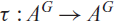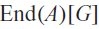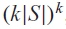Let G be a group and A a set equipped with a collection of finitary operations. We study cellular automata 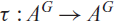$$\tau :{A^G} \to {A^G}$$ that preserve the operations AG of induced componentwise from the operations of A. We show τ that is an endomorphism of AG if and only if its local function is a homomorphism. When A is entropic (i.e. all finitary operations are homomorphisms), we establish that the set EndCA(G;A), consisting of all such endomorphic cellular automata, is isomorphic to the direct limit of Hom(AS, A), where S runs among all finite subsets of G. 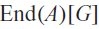In particular, when A is an R-module, we show that EndCA(G;A) is isomorphic to the group algebra $${\rm{End}}(A)[G]$$ . Moreover, when A is a finite Boolean algebra, we establish that the number of endomorphic cellular automata over AG admitting a memory set S is precisely 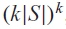$${(k|S|)^k}$$ , where k is the number of atoms of A.

Let B be a Boolean algebra and G a group of automorphisms of B. Define an equivalence relation ∼ on B by letting x ∼ y if there are x1, x2,…,xn, y1, y2, …yn in B such that x is the disjoint union of the xi, y is the disjoint union of the yi, and for each i there is a member of G taking xi to yi. The equivalence classes under ∼ are called equidecomposability types. Addition of equidecomposability types is given by (x) + (y) = (x V y) provided x ∧ y = 0. An example is given of a complete Boolean algebra B and a group G of automorphisms of B with X, Y ∊ B such that (X) + (X) = (Y) + (Y) but (X) ≠ (Y), answering a question of Wagon (see [5 p. 231 problem 14]). Moreover B may be taken to be the algebra of Borel subsets of Cantor space modulo sets of the first category. It is also remarked that in this case equidecomposability types do not form a weak cardinal algebra.

The principle of duality for Boolean algebra states that if an identity ƒ = g is valid in every Boolean algebra and if we transform ƒ = g into a new identity by interchanging (i) the two lattice operations and (ii) the two lattice bound elements 0 and 1, then the resulting identity ƒ = g is also valid in every Boolean algebra. Also, the equational theory of Boolean algebras is finitely based. Believing in the cosmic order of mathematics, it is only natural to ask whether the equational theory of Boolean algebras can be generated by a finite irredundant set of identities which is already closed for the duality mapping. Here we provide one such equational basis.