Traditionally, the role of general topology in model theory has been mainly limited to the study of compacta that arise in first-order logic. In this context, the topology tends to be so trivial that it turns into combinatorics, motivating a widespread approach that focuses on the combinatorial component while usually hiding the topological one. This popular combinatorial approach to model theory has proved to be so useful that it has become rare to see more advanced topology in model-theoretic articles. Prof. Franklin D. Tall has led the re-introduction of general topology as a valuable tool to push the boundaries of model theory. Most of this thesis is directly influenced by and builds on this idea.
The first part of the thesis will answer a problem of T. Gowers on the undefinability of pathological Banach spaces such as Tsirelson space. The topological content of this chapter is centred around Grothendieck spaces.
In a similar spirit, the second part will show a new connection between the notion of metastability introduced by T. Tao and the topological concept of pseudocompactness. We shall make use of this connection to show a result of X. Caicedo, E. Dueñez, J. Iovino in a much simplified manner.
The third part of the thesis will carry a higher set-theoretic content as we shall use forcing and descriptive set theory to show that the well-known theorem of M. Morley on the trichotomy concerning the number of models of a first-order countable theory is undecidable if one considers second-order countable theories instead.
The only part that did not originate from model-theoretic questions will be the fourth one. We show that 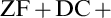 $\operatorname {ZF} + \operatorname {DC} +$“all Turing invariant sets of reals have the perfect set property” implies that all sets of reals have the perfect set property. We also show that this result generalizes to all countable analytic equivalence relations. This result provides evidence in favour of a long-standing conjecture asking whether Turing determinacy implies the axiom of determinacy.
$\operatorname {ZF} + \operatorname {DC} +$“all Turing invariant sets of reals have the perfect set property” implies that all sets of reals have the perfect set property. We also show that this result generalizes to all countable analytic equivalence relations. This result provides evidence in favour of a long-standing conjecture asking whether Turing determinacy implies the axiom of determinacy.
Abstract prepared by Clovis Hamel
E-mail: [email protected]