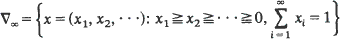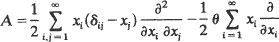Research Article
The infinitely-many-neutral-alleles diffusion model
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 429-452
-
- Article
- Export citation
An analysis of sex in random environments, I
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 453-463
-
- Article
- Export citation
On multitype branching processes in a random environment
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 464-497
-
- Article
- Export citation
Maximum likelihood estimation for branching processes with immigration
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 498-509
-
- Article
- Export citation
Choosing the best of the current crop
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 510-532
-
- Article
- Export citation
Uniform approximation to distributions of extreme order statistics
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 533-547
-
- Article
- Export citation
The asymptotic time to failure of a bundle of fibers with random slacks
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 548-566
-
- Article
- Export citation
On a general storage problem and its approximating solution
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 567-602
-
- Article
- Export citation
Queues with non-stationary input stream: Ross's conjecture
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 603-618
-
- Article
- Export citation
Asymptotic exponentiality of the tail of the waiting-time distribution in a Ph/Ph/C queue
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 619-630
-
- Article
- Export citation
Front Matter
APR volume 13 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. f1-f2
-
- Article
- Export citation
Back Matter
APR volume 13 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. b1-b2
-
- Article
- Export citation