1. INTRODUCTION
A strapdown Inertial Navigation System (INS) is a dead reckoning system, basically formed of a cluster of accelerometers and gyroscopes used to sense acceleration and rotation components in three dimensions. Inertial navigation systems rely on rate and acceleration measurements and initial position, velocity and attitude information to provide position and velocity. However, errors in sensor readings caused by bias, scale factors, thermal/magnetic effects, other non-linearities and initialisation offsets cause an accumulation of navigation errors.
A popular approach is to use an additional information source in order to improve the accuracy of the inertial navigation system. In most modern integrated navigation applications, the external aid sensor utilised is a type of satellite radio navigation with low cost, high accuracy and global coverage such as the Global Positioning System (GPS). GPS integrated INS systems (GPS/INS) have become the major navigation tool in recent years for applications such as automotive, robotics and unmanned autonomous vehicles.
In a GPS/INS system, GPS not only improves the navigation accuracy during operation but also provides the initial position and velocity information to the system. However, the acquisition of initial attitude information is not straightforward and it cannot be directly obtained from GPS.
Low cost systems initialise the pitch and roll angles using accelerometer-measured gravitational field vector. Heading is initialised using either magnetometer-measured earth's magnetic field (Li and Wang, Reference Li and Wang2013) or non-holonomic constraints and GPS velocity vector (Dissanayake et al., Reference Dissanayake, Sukkarieh, Nebot and Durrant-Whyte2001). Unfortunately, these approaches cannot be applied in helicopter, quadrotor and all wheel drive applications in which the magnetometer data is not reliable and non-holonomic constraints are not valid. Apart from initialisation, another problem arises when the GPS signal is lost during operation. Low cost GPS/INS systems handle GPS outages by switching from the GPS/INS mode to the Attitude Heading Reference System (AHRS) mode (Wendel et al., Reference Wendel, Meister, Schlaile and Trommer2006). An AHRS outputs roll, pitch and yaw (heading) angles. However, the heading error grows without bounds if the magnetometer data is not reliable. In such a case, GPS/INS mode begins with a large heading error as soon as the GPS signal is reacquired. Thus, both the initial alignment and realignment are problematic and yield large heading errors when the magnetometers and the vehicle dynamics/constraints cannot be used in the navigation system.
In order to circumvent the large heading error problem, in-motion alignment techniques are applied. In-motion alignment uses different external aiding devices and can be applied to the systems with different accuracy levels.
Various in-motion alignment techniques are studied in the literature. Pham (Reference Pham1992) developed Kalman filter mechanization in the wander azimuth frame and defined the heading error state as wander angle error to achieve the coarse alignment of an inertial navigation system mounted on a flying platform. In Scherzinger (Reference Scherzinger1996), an extended psi-angle model with large heading error is introduced. Kong et al. (Reference Kong, Nebot and Durrant-Whyte1999) developed a non-linear INS error model to account for large heading errors. This model eliminates the necessity to switch from coarse to fine alignment and proposes a single filter for alignment. However, this model suffers from complex non-linear operations. Rogers (Reference Rogers2001) compared two large azimuth INS error models developed in the wander azimuth frame and gave the performance results of these models with real flight test data. All these models are developed for coarse alignment in the systems with large azimuth error and the filter implementation model is modified after the wander azimuth error uncertainty reaches a small value. Han and Wang (Reference Han and Wang2009) proposed a mechanism for initial alignment with GPS aiding. In this model, initial heading misalignment of the system is modelled as sine and cosine of platform heading misalignment. Thus, the observability of the error is increased with respect to the models using sine and cosine of wander azimuth angle. Li et al. (Reference Li, Wu, Wang and Lu2013) introduced an initial alignment scheme using Doppler Velocity Log (DVL) measurements. Hong et al. (Reference Hong, Lee and Park2004) introduced a different attitude error model to handle the large heading error. The model divides the attitude errors into heading and levelling errors using a horizontal frame and provides high observability and fast convergence. Hong et al. (Reference Hong, Lee and Park2004) used this model for the alignment of an INS on an Autonomous Underwater Vehicle (AUV) aided by a Super-Short Baseline (SSBL). In the study, GPS aiding is not considered and no experimental results are supplemented other than the simulation results.
This paper extends the idea of Hong et al. (Reference Hong, Lee and Park2004) and addresses the development of a low cost GPS/INS system that works under large heading errors with high performance. The proposed approach has the capability to decrease heading errors as large as 180° very quickly. The basic idea of the system is to implement a Kalman filter based on a large heading error model for the GPS/INS integration. The proposed GPS/INS system does not have a special alignment procedure and eliminates the need for external heading observations. This approach enables GPS/INS system to perform under circumstances such as large initial heading errors and accumulated heading errors after a long period of GPS loss.
In the next section, a brief description of a GPS/INS system using the well-known small angle assumption error model is introduced. In Section 3, the integration of INS with GPS under large heading uncertainty is described, including some remarks on the usage of GPS measurements and the system observability. The system performance and its comparison to GPS/INS system based on the small attitude error model are given with the road test in Section 4 and the paper concludes in Section 5.
2. CONVENTIONAL GPS/INS MODEL
2.1. Strapdown Inertial Navigation System
The navigation system implemented works in local level mechanization such that it calculates attitude and body velocity with respect to North-East-Down (NED) frame. In this type of mechanization, the velocity is expressed in the local geographic coordinate system as north-east-down in order to maintain the navigation accuracy over large distances on earth. Here, the rate of change of the vehicle speed with respect to earth is expressed as:
where ωie is the rate of earth with respect to inertial frame and ωen is the rate of navigation frame with respect to earth. Substituting ![]() ${\bf \dot v}_e^i = {\bf f} - {\bf \omega} _{ie} x{\bf v}_e + {\bf g}$ into Equation (1), we have
${\bf \dot v}_e^i = {\bf f} - {\bf \omega} _{ie} x{\bf v}_e + {\bf g}$ into Equation (1), we have
Expressing Equation (2) in the navigation frame:
where fb is the specific force measured by the accelerometers, gn is the gravity vector represented in navigation frame and Cbn is the body to navigation transformation matrix. The Direction Cosine Matrix (DCM), Cbn, propagates as
where ![]() ${\bf \Omega} _{nb}^b $ is the skew symmetric matrix of rate of body frame
${\bf \Omega} _{nb}^b $ is the skew symmetric matrix of rate of body frame ![]() ${\bf \omega} _{nb}^b $, with respect to navigation frame expressed in body frame, and
${\bf \omega} _{nb}^b $, with respect to navigation frame expressed in body frame, and
The position is expressed in terms of latitude (L), longitude (λ) and height (h) and propagates as
Using these equations, the INS computes the navigation output at a rate of 100 Hz for the experiments conducted throughout this paper. It is important to note that an inertial navigation system is a dead reckoning system and any lack of precision is passed from one evaluation to the next and the navigation solution drifts with time. In this study, GPS measurements are integrated to the system via an extended Kalman filter in order to bound the navigation errors.
2.2. INS error dynamic model for small attitude error
The propagation step of the Kalman filter depends on the error state dynamics of the INS. The error state vector of the inertial system includes position, velocity, and attitude errors in addition to the accelerometer and gyroscope errors.
Under the small attitude error assumption, true direction cosine matrix, Cbn, is related to the computed direction cosine matrix, ![]() ${\bf \tilde C}_b^n $, as follows:
${\bf \tilde C}_b^n $, as follows:
and the attitude error dynamics are obtained as:
Velocity and position error dynamics are
and
where ε is the tilt angle vector, δ vn the velocity error in navigation frame, δL, δλ and δh the north, east and height position errors, respectively. In addition to these nine error states standing for inertial equation errors, another six states are used in order to model the accelerometer and gyro bias errors, as first-order Markov processes:
where w is white noise and τ a and τ g are time constants. Thus, the GPS/INS filter has 15 states.
2.3. Integration filter
The GPS/INS system benefits from the bounded error characteristics of the GPS and the high frequency characteristics of the INS at the same time by integrating them via a Kalman filter. Under the assumption of a small attitude error, a 15-state Kalman filter is used in order to integrate the INS and the GPS systems. The integration filter uses a dynamic error model (Section 2.2) to create the continuous state transition matrix, F, for the error states, which is then discretized using the first order Taylor series approximation to yield Φ=I+FΔt where Δt is chosen as one second and Kalman propagation of the covariance
is done at 1 Hz for our application.
The Kalman update is triggered at every GPS measurement (1 Hz) using:
 $$\eqalign{ & {\bf K} = {\bf P}^ - {\bf H}^T ({\bf HP}^ - {\bf H}^T + {\bf R})^{ - 1} \cr & \delta {\bf x} = {\bf Ky} \cr & {\bf P}^ + = ({\bf I} - {\bf KH}){\bf P}^ -} $$
$$\eqalign{ & {\bf K} = {\bf P}^ - {\bf H}^T ({\bf HP}^ - {\bf H}^T + {\bf R})^{ - 1} \cr & \delta {\bf x} = {\bf Ky} \cr & {\bf P}^ + = ({\bf I} - {\bf KH}){\bf P}^ -} $$where δ x is the estimated error states, y the difference between GPS measurements (position and velocity) and INS measurements, K the Kalman gain matrix, P the state covariance matrix, R the measurement covariance matrix, Q the input covariance matrix and H the measurement matrix where the position and velocity errors are observed.
In a conventional GPS/INS system, R=diag ([2 2 3 0·1 0·1 0·1]2) is chosen based on the GPS output uncertainties. At initial P, the diagonal matrix has diagonal entities of state variances, where standard deviations of position, velocity and attitude are 5 m, 0·1 m/s and 1 mrad, respectively. The initial bias values of the accelerometers and gyroscopes are taken as 10 mg and 10°/hr. The Q matrix is created using the inertial sensors’ noise statistics.
2.4. Conventional GPS/INS performance
2.4.1. Test setup
The conventional integrated navigation system is mounted on a van and tested on a 3-minute route. The vehicle starts the test from stationary and moves with a 30 km/h average speed.
The vehicle contains the GPS/INS integrated navigation system employing an IMU, navigation computer and a GPS receiver. The IMU contains three 10°/hr gyroscopes and one 10 mg three-axis accelerometer in an orthogonal arrangement. The GPS/INS system contains a microprocessor for navigation computation and a Novatel OEM receiver for navigation purposes. A laptop computer is used to store GPS and IMU data and another computer is employed for system monitoring purposes. Raw IMU data was logged at 400 Hz while the GPS data was logged at 1 Hz. Both GPS and IMU data were stored through a serial port on the laptop computer. During the test, GPS/INS navigation solutions were also recorded to analyse the performance of the integrated navigation system.
The van test was carried out in an open field with minimal buildings and trees around. A 180 second test was conducted on the site. The closed path circles around a 300×300 m area and generates a closed path of more than one kilometre long.
During the road test, the number of visible satellites dropped especially in the vicinity of the building corners. Although the road test started and finished with seven visible satellites, the number of visible satellites dropped to four at the 100th second of the test. As a result, the accuracy of the GPS height channel decreased abruptly. However, the GPS/INS system managed to stabilise the height channel to ±2 metres accuracy.
2.4.2. Navigation results
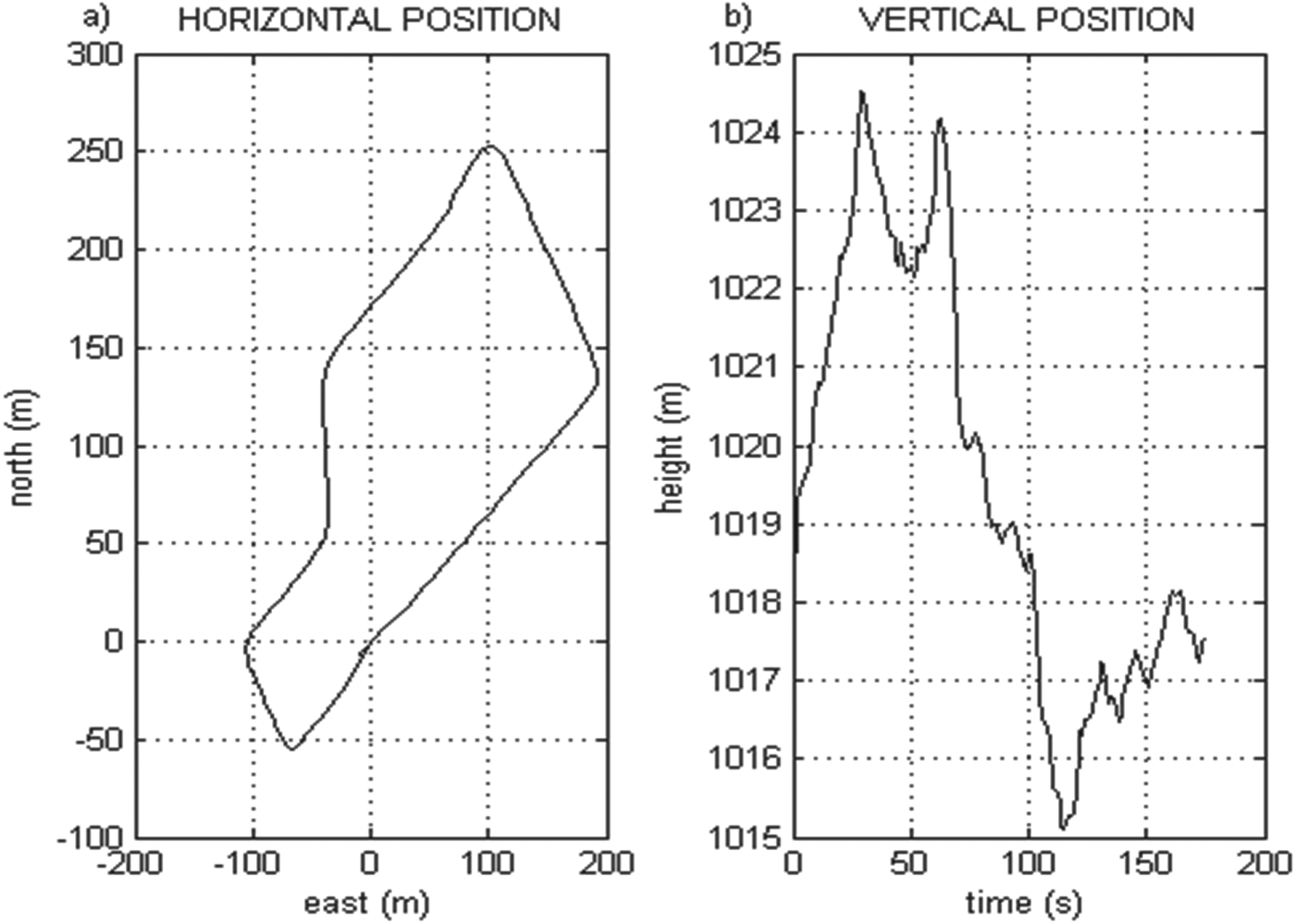
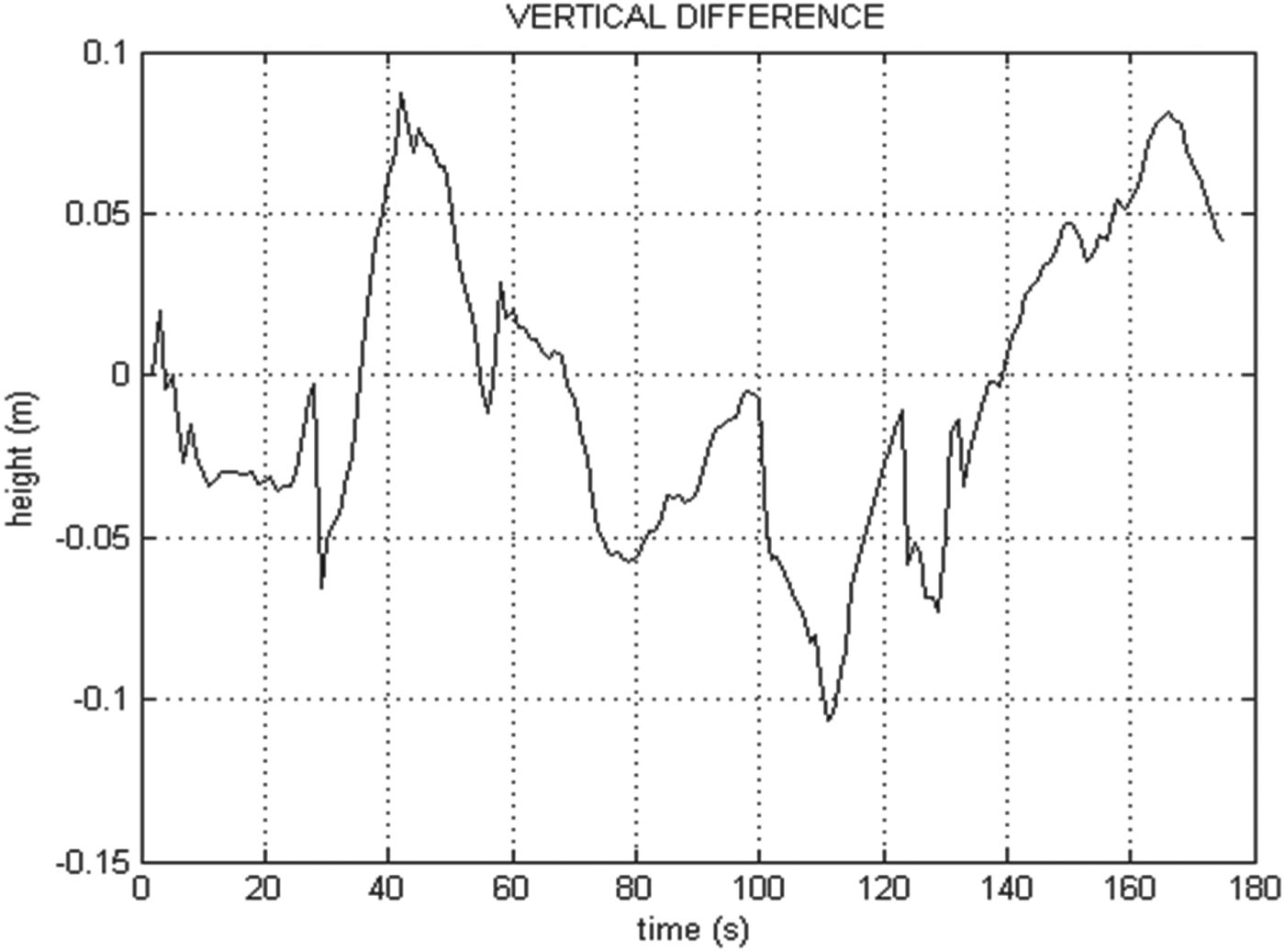
During the road test the GPS position, velocity, and GPS/INS position, velocity and attitude data were recorded for approximately 180 seconds. Figure 1 presents the horizontal and vertical solutions provided by the conventional GPS/INS system described in Section 2.

Figure 1. (a) Horizontal navigation using conventional GPS/INS. (b) Vertical profile of the test route output by conventional GPS/INS.
3. GPS/INS MODEL FOR LARGE HEADING ERROR
3.1. INS error dynamic model for large heading error
A Direction Cosine Matrix (DCM), Cbn, holds the attitude information in between the body and navigation frames. Cbn is represented by roll (ϕ) , pitch (θ), and yaw-heading (ψ) angles and can be divided into Cbh and Chn matrices.
 $${\bf C}_b^n = \underbrace {\left[ {\matrix{ {\cos \psi} & { - \sin \psi} & 0 \cr {\sin \psi} & {\cos \psi} & 0 \cr 0 & 0 & 1 \cr}} \right]}_{{\bf C}_h^n} \underbrace {\left[ {\matrix{ {\cos \theta} & {\sin \phi \sin \theta} & {\cos \phi \sin \theta} \cr 0 & {\cos \phi} & { - \sin \phi} \cr { - \sin \theta} & {\sin \phi \cos \theta} & {\cos \phi \cos \theta} \cr}} \right]}_{{\bf C}_b^h} $$
$${\bf C}_b^n = \underbrace {\left[ {\matrix{ {\cos \psi} & { - \sin \psi} & 0 \cr {\sin \psi} & {\cos \psi} & 0 \cr 0 & 0 & 1 \cr}} \right]}_{{\bf C}_h^n} \underbrace {\left[ {\matrix{ {\cos \theta} & {\sin \phi \sin \theta} & {\cos \phi \sin \theta} \cr 0 & {\cos \phi} & { - \sin \phi} \cr { - \sin \theta} & {\sin \phi \cos \theta} & {\cos \phi \cos \theta} \cr}} \right]}_{{\bf C}_b^h} $$where h stands for horizontal frame. Assuming small roll and pitch misalignments (ε x, εy), true Cbh, is related to the computed ![]() ${\bf \tilde C}_b^h $ as follows:
${\bf \tilde C}_b^h $ as follows:
 $${\bf \tilde C}_b^h = (I_{3x3} - {\bf \varepsilon} x){\bf C}_b^h, \quad {\bf \varepsilon} x = \,\left[ {\matrix{ 0 & 0 & {\varepsilon _y} \cr 0 & 0 & { - \varepsilon _x} \cr { - \varepsilon _y} & {\varepsilon _x} & 0 \cr}} \right]$$
$${\bf \tilde C}_b^h = (I_{3x3} - {\bf \varepsilon} x){\bf C}_b^h, \quad {\bf \varepsilon} x = \,\left[ {\matrix{ 0 & 0 & {\varepsilon _y} \cr 0 & 0 & { - \varepsilon _x} \cr { - \varepsilon _y} & {\varepsilon _x} & 0 \cr}} \right]$$As a result of large heading error, the computed ![]() ${\bf \tilde C}_h^n $ is related to true Chn as:
${\bf \tilde C}_h^n $ is related to true Chn as:
 $${\bf \tilde C}_h^n = {\bf C}_h^n + \delta {\bf C}_h^n = \,{\bf C}_h^n + \,\,\left[ {\matrix{ {\delta \cos \psi} & { - \delta \sin \psi} & 0 \cr {\delta \sin \psi} & {\delta \cos \psi} & 0 \cr 0 & 0 & 0 \cr}} \right]$$
$${\bf \tilde C}_h^n = {\bf C}_h^n + \delta {\bf C}_h^n = \,{\bf C}_h^n + \,\,\left[ {\matrix{ {\delta \cos \psi} & { - \delta \sin \psi} & 0 \cr {\delta \sin \psi} & {\delta \cos \psi} & 0 \cr 0 & 0 & 0 \cr}} \right]$$From Equations (15) and (16), the body to navigation attitude error is calculated as:
 $$ \eqalign{\delta {\bi C}_b^n = & {\bi \tilde C}_h^n {\bi \tilde C}_b^h - {\bi C}_b^n \cr = & \left( {\delta {\bi C}_h^n - {\bi C}_h^n {\bi \varepsilon }x} \right){\bi C}_b^h } $$
$$ \eqalign{\delta {\bi C}_b^n = & {\bi \tilde C}_h^n {\bi \tilde C}_b^h - {\bi C}_b^n \cr = & \left( {\delta {\bi C}_h^n - {\bi C}_h^n {\bi \varepsilon }x} \right){\bi C}_b^h } $$The DCM error is rewritten as:
 $$\delta {\bf C}_b^n = {\bf DC}_b^h = \left[ {\matrix{ {\delta \cos \psi} & { - \delta \sin \psi} & { - \varepsilon _x \sin \psi - \varepsilon _y \cos \psi} \cr {\delta \sin \psi} & {\delta \cos \psi} & {\varepsilon _x \cos \psi - \varepsilon _x \sin \psi} \cr {\varepsilon _y} & { - \varepsilon _x} & 0 \cr}} \right]{\bf C}_b^h $$
$$\delta {\bf C}_b^n = {\bf DC}_b^h = \left[ {\matrix{ {\delta \cos \psi} & { - \delta \sin \psi} & { - \varepsilon _x \sin \psi - \varepsilon _y \cos \psi} \cr {\delta \sin \psi} & {\delta \cos \psi} & {\varepsilon _x \cos \psi - \varepsilon _x \sin \psi} \cr {\varepsilon _y} & { - \varepsilon _x} & 0 \cr}} \right]{\bf C}_b^h $$The sine and cosine of yaw error is chosen as the heading error states since the error Equation (18) is nonlinear in yaw error, while it is linear in γ 1=δ sin ψ and γ 2=δ cos ψ. Thus, INS attitude error is represented by four states of γ 1, γ 2, ε x and ε y and
 $${\bf D} = \left[ {\matrix{ {\gamma _2} & { - \gamma _1} & { - \varepsilon _x \sin \psi - \varepsilon _y \cos \psi} \cr {\gamma _1} & {\gamma _2} & {\varepsilon _x \cos \psi - \varepsilon _x \sin \psi} \cr {\varepsilon _y} & { - \varepsilon _x} & 0 \cr}} \right]$$
$${\bf D} = \left[ {\matrix{ {\gamma _2} & { - \gamma _1} & { - \varepsilon _x \sin \psi - \varepsilon _y \cos \psi} \cr {\gamma _1} & {\gamma _2} & {\varepsilon _x \cos \psi - \varepsilon _x \sin \psi} \cr {\varepsilon _y} & { - \varepsilon _x} & 0 \cr}} \right]$$Differentiating Equation (19), one obtains the way the attitude errors propagate in time. After some algebraic manipulations, the derivative becomes
Ωnhh and δΩnbn are the skew-symmetric matrices of ![]() ${\bf \omega} _{nh}^h $ and
${\bf \omega} _{nh}^h $ and ![]() $\delta {\bf \omega} _{nb}^n $.
$\delta {\bf \omega} _{nb}^n $.
 $$\eqalign{ & {\bf \omega} _{nh}^h = [\matrix{ 0 & 0 & { - \dot \psi} \cr} ]^T \cr & \dot \psi = \omega _y \sin \phi \sec \theta + \omega _z \cos \phi \sec \theta \cr & \delta {\bf \omega} _{nb}^n = [\matrix{ {\delta \omega _n} & {\delta \omega _e} & {\delta \omega _d} \cr} ]^T = {\bf DC}_b^h {\bf \omega} _{ib}^b + {\bf C}_b^n \delta {\bf \omega} _{ib}^b - \left( {\delta {\bf \omega} _{ie}^n + \delta {\bf \omega} _{en}^n} \right)} $$
$$\eqalign{ & {\bf \omega} _{nh}^h = [\matrix{ 0 & 0 & { - \dot \psi} \cr} ]^T \cr & \dot \psi = \omega _y \sin \phi \sec \theta + \omega _z \cos \phi \sec \theta \cr & \delta {\bf \omega} _{nb}^n = [\matrix{ {\delta \omega _n} & {\delta \omega _e} & {\delta \omega _d} \cr} ]^T = {\bf DC}_b^h {\bf \omega} _{ib}^b + {\bf C}_b^n \delta {\bf \omega} _{ib}^b - \left( {\delta {\bf \omega} _{ie}^n + \delta {\bf \omega} _{en}^n} \right)} $$where ωy and ωz are the body rates. Using Equation (21) in Equation (20), the attitude error equations are obtained as follows:
 $$\eqalign{\dot \varepsilon _x & = - \dot \psi \varepsilon _y - \cos \psi \kern1pt \delta \omega _n - \sin \psi \kern1pt \delta \omega _e \cr \dot \varepsilon _y & = - \dot \psi \varepsilon _x + \sin \psi \kern1pt\delta \omega _n - \cos \psi \kern1pt \delta \omega _e \cr \dot \gamma _1 & = \dot \psi \gamma _2 + \cos \psi \kern1pt \delta \omega _d \cr \dot \gamma _2 & = - \dot \psi \gamma _1 - \sin \psi \kern1pt \delta \omega _d} $$
$$\eqalign{\dot \varepsilon _x & = - \dot \psi \varepsilon _y - \cos \psi \kern1pt \delta \omega _n - \sin \psi \kern1pt \delta \omega _e \cr \dot \varepsilon _y & = - \dot \psi \varepsilon _x + \sin \psi \kern1pt\delta \omega _n - \cos \psi \kern1pt \delta \omega _e \cr \dot \gamma _1 & = \dot \psi \gamma _2 + \cos \psi \kern1pt \delta \omega _d \cr \dot \gamma _2 & = - \dot \psi \gamma _1 - \sin \psi \kern1pt \delta \omega _d} $$Velocity error is the difference between true velocity and computed velocity.
We obtain the following differential equations by differentiating Equation (23)
Although, the δ Cbn term of the velocity error dynamics given in Equations (9) and (24) differs under large heading error, the differential equations of position error and sensor biases remain the same as the error equations in Section 2.2.
3.2. GPS measurement model
As stated in Section 2.3, GPS/INS filters introduced in this study use GPS position and velocity measurements as external observations. However, the measurement equations developed for large heading error is different from the ones used in the conventional approach. This difference is due to lever arm compensation that requires body to navigation frame transformation. The position of INS with respect to GPS antenna centre is given by
where LAb is the three-dimensional lever arm vector in body frame and
 $${\bf T} = \left[ {\matrix{ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\left( {R_n + h} \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left( {R_n + h} \right)}$}}} & 0 & 0 \cr 0 & {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\left( {R_e + h} \right)\cos L}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left( {R_e + h} \right)\cos L}$}}} & 0 \cr 0 & 0 & { - 1} \cr}} \right]$$
$${\bf T} = \left[ {\matrix{ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\left( {R_n + h} \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left( {R_n + h} \right)}$}}} & 0 & 0 \cr 0 & {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\left( {R_e + h} \right)\cos L}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left( {R_e + h} \right)\cos L}$}}} & 0 \cr 0 & 0 & { - 1} \cr}} \right]$$is used to convert north, east and down components of the lever arm into latitude, longitude and height. Using Equation (25), position measurement of the system is
and inserting Equation (18) into Equation (27) it becomes
Investigating the position measurement equation, it is seen that the heading error is directly observable under the non-zero lever arm condition and the quality of the heading depends on the length of the lever arm. However, using a false lever arm term or totally excluding the lever arm may cause filter divergence.
Comparing Equation (28) to the Super Short Baseline (SSBL) measurement given in Hong et al. (Reference Hong, Lee and Park2004), it is obvious that the GPS position measurement is much more effective than the SSBL measurement in heading estimation. This is due to the fact that the SSBL provides the position solution directly while the GPS gives a position solution with a lever arm offset that increases the heading observability.
The second measurement provided by GPS is velocity. The velocity of INS with respect to the antenna velocity is as follows:
Using the above relation, velocity measurement is
 $$\eqalign{\delta {\bf v}_{meas} = \ & {\bf \tilde v}_{INS} - {\bf \dot {\tilde C}}_b^n {\bf L\tilde A}^b - {\bf v}_{ANT} \cr = \ & \delta {\bf v} + {\bf \dot C}_b^n \delta {\bf LA}^b + \delta {\bf \dot C}_b^n {\bf LA}^b} $$
$$\eqalign{\delta {\bf v}_{meas} = \ & {\bf \tilde v}_{INS} - {\bf \dot {\tilde C}}_b^n {\bf L\tilde A}^b - {\bf v}_{ANT} \cr = \ & \delta {\bf v} + {\bf \dot C}_b^n \delta {\bf LA}^b + \delta {\bf \dot C}_b^n {\bf LA}^b} $$Using Equation (4) and the derivative of Equation (18) in Equation (31), the measurement is rearranged as
where δ Ωnbn is the skew symmetric matrix of δ ωnbn given in Equation (21).
The velocity measurement given in Equation (31) differs from the position measurement in terms of heading observability. The heading error in Equation (31) is coupled with the rotation rate as well as the lever arm. Thus, the quality of the heading depends not only on the length of the lever arm but also the instantaneous rotation of the vehicle. High rotation rates yield faster heading convergence.
GPS position and velocity measurements inherently involve attitude errors and provide direct observability of the large heading error. This enhances the system performance and enables fast heading convergence even under low dynamics. Moreover, it is possible to increase the convergence speed by increasing the length of the lever arm.
3.3. Kalman filter corrections
A Kalman filter based on the error dynamics given in Section 3.1 and the measurements described in Section 3.2 is used to generate corrections for diminishing the position, velocity, attitude and inertial sensor errors. As a result, the overall GPS/INS output becomes driftless with bounded uncertainty. The Kalman estimated error states are as follows:
The estimated errors are fed back to the inertial sensors and inertial navigation system after every update step of Kalman filter. Corrections to the navigation system are realized as:
 $$\eqalign{& {\bf p} = {\bf \tilde p} - \delta {\bf p} \cr & {\bf v} = {\bf \tilde v} - \delta {\bf v} \cr & {\bf C}_b^n = {\bf \tilde C}_b^n - {\bf DC}_b^h \cr & {\bf f}^b = {\bf \tilde f}^b - \delta {\bf f}^b \cr & {\bf \omega} ^b = {\bf \tilde \omega} ^b - \delta {\bf \omega} ^b} $$
$$\eqalign{& {\bf p} = {\bf \tilde p} - \delta {\bf p} \cr & {\bf v} = {\bf \tilde v} - \delta {\bf v} \cr & {\bf C}_b^n = {\bf \tilde C}_b^n - {\bf DC}_b^h \cr & {\bf f}^b = {\bf \tilde f}^b - \delta {\bf f}^b \cr & {\bf \omega} ^b = {\bf \tilde \omega} ^b - \delta {\bf \omega} ^b} $$The position, velocity and sensor bias corrections are straightforward. The attitude correction can be realized by using the estimated γ 1, γ 2, ε x and ε y states and current values of roll (ϕ) and pitch (θ) angles as follows:
 $$\delta {\bf C}_b^n = \left[ {\matrix{ {\gamma _2} & { - \gamma _1} & { - \varepsilon _x \sin \psi - \varepsilon _y \cos \psi} \cr {\gamma _1} & {\gamma _2} & {\varepsilon _x \cos \psi - \varepsilon _x \sin \psi} \cr {\varepsilon _y} & { - \varepsilon _x} & 0 \cr}} \right]\left[ {\matrix{ {\cos \theta} & {\sin \phi \sin \theta} & {\cos \phi \sin \theta} \cr 0 & {\cos \phi} & { - \sin \phi} \cr { - \sin \theta} & {\sin \phi \cos \theta} & {\cos \phi \cos \theta} \cr}} \right]$$
$$\delta {\bf C}_b^n = \left[ {\matrix{ {\gamma _2} & { - \gamma _1} & { - \varepsilon _x \sin \psi - \varepsilon _y \cos \psi} \cr {\gamma _1} & {\gamma _2} & {\varepsilon _x \cos \psi - \varepsilon _x \sin \psi} \cr {\varepsilon _y} & { - \varepsilon _x} & 0 \cr}} \right]\left[ {\matrix{ {\cos \theta} & {\sin \phi \sin \theta} & {\cos \phi \sin \theta} \cr 0 & {\cos \phi} & { - \sin \phi} \cr { - \sin \theta} & {\sin \phi \cos \theta} & {\cos \phi \cos \theta} \cr}} \right]$$However, heading corrections that can be tens of degrees can cause numerical instability. In order to prevent loss of orthonormality in Cbn, an orthonormalization process is run after every correction step.
4. EXPERIMENTAL RESULTS
4.1. Test setup
The land vehicle set-up employed in the proposed GPS/INS system is exactly the same as the one given in Section 2.4.1. The test was conducted for 180 seconds and the raw IMU data, GPS data and GPS/INS data were collected throughout the test. The proposed system's navigation data was obtained by post-processing of the raw IMU data and the GPS data using models given in Section 3.
4.2. Test results
In this section the GPS/INS computed navigation solution obtained during the road test (Figure 1) is employed as reference. The conventional system given in Section 2 and the proposed system given in Section 3 are compared to this reference.
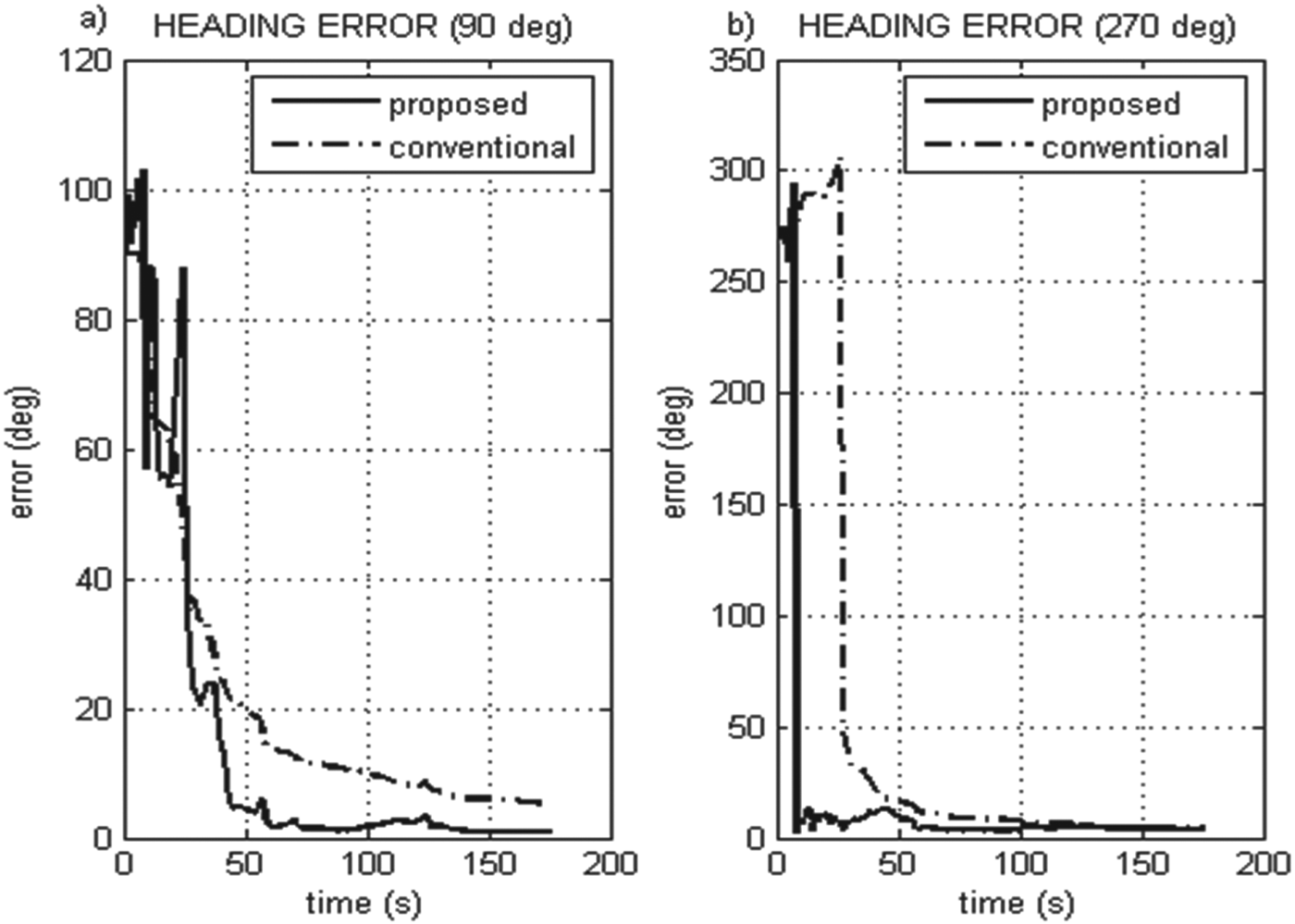
Collected GPS and IMU data are used to simulate the conventional and the proposed systems with different initial heading errors. The heading solutions under an initial error of ±90° are given in Figure 2.

Figure 2. Heading error comparison of proposed and conventional systems with a) 90° and b) −90° initial heading error.
It is seen in Figure 2 that the proposed system shows higher performance with 90° and −90° initial heading error and converges faster compared to the system using the small angle error assumption. In the proposed system, the heading error decreases below 5° in 40 seconds. However, the heading error of the conventional system does not reach 5° during the entire test.
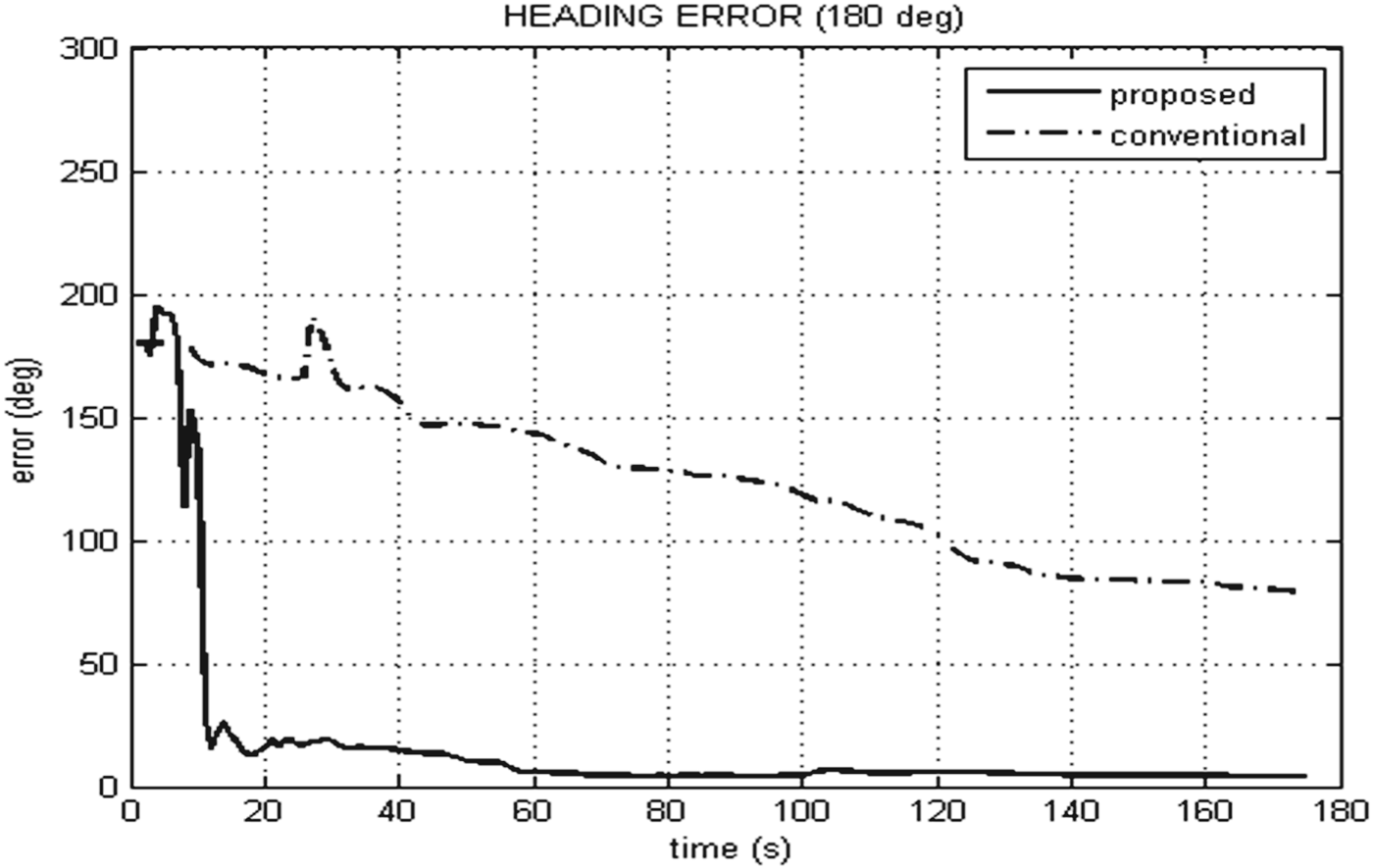
The behaviour of the compared systems with 180° initial heading error is more striking. As seen in Figure 3, the proposed system converges while the conventional one does not in this case. The proposed system attains 4° heading error at the end of the test.

Figure 3. Heading error comparison of proposed and conventional systems with 180° initial heading error.
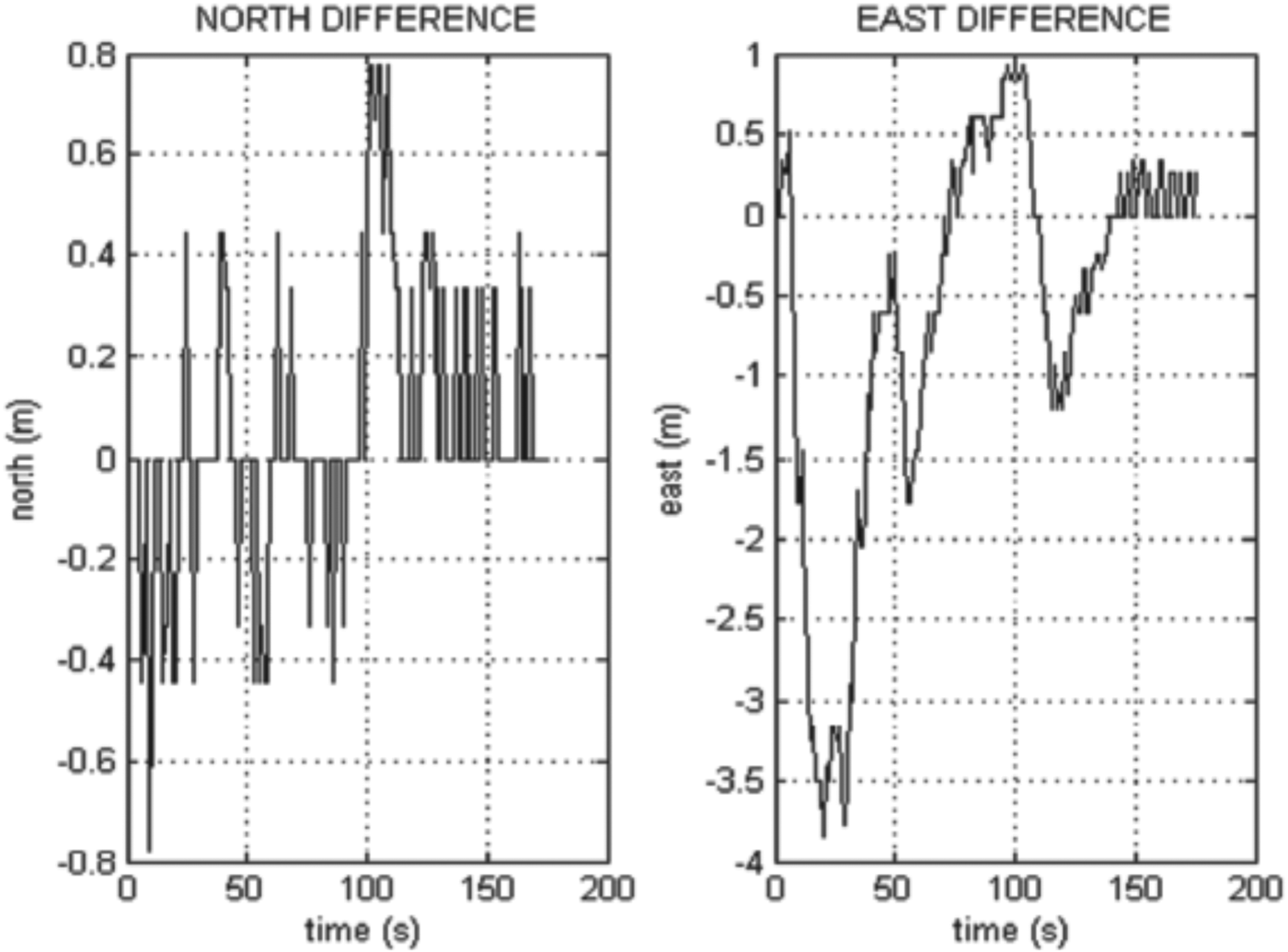
It is also important to see that the position solution of the proposed system with 180° initial heading error is similar to the position of the reference system (Figures 4 and 5). Thus, the proposed system's navigation solutions can be used from the beginning of the mission.

Figure 4. Horizontal position errors of the proposed system with 180° initial heading error.

Figure 5. Vertical position error of the proposed system with 180° initial heading error.
5. CONCLUSION
The conventional GPS/INS system performs inadequately in the case of large heading errors. This imposes a special alignment procedure employing external heading observations in low cost systems. However, using such an extra heading measurement may not be always possible. Therefore, an alternative approach to GPS/INS integration was presented and it was shown that this approach diminishes the attitude errors and allows the inertial system to navigate more accurately without any external aid. In this new approach, GPS position and velocity measurements inherently involve attitude errors and provide direct observability of the large heading error. Thus, the system achieves fast heading convergence even under low dynamics. The proposed approach has the capability to decrease the large heading errors quickly and to start the strapdown navigation computations under poor heading conditions.
Comparisons showed that the new integration structure performs extremely well in the road test and the GPS measurements provide high observability on the heading states. The system is shown to be capable of decreasing 180° heading error to less than 4° during the test period.
The proposed method is very powerful for low cost GPS/INS systems that cannot use any external heading information. The technique can be especially useful for helicopter, quadrotor and all wheel drive applications in which the magnetometer data is not reliable and non-holonomic constraints are not valid.