List of Symbols

1. Introduction
The latest assessment report of the Intergovernmental Panel on Climate Change (AR5) reports that both the Greenland and Antarctic ice sheets have lost mass over the past 20 years and for Greenland the rate of ice loss appears to be accelerating (Reference Vaughan and StockerVaughan and others, 2013). The two ice sheets alone have contributed some 14 mm to sea-level rise over this period. Much of the evidence for these changes has come from repeated measurements of ice-sheet elevation using satellite or airborne altimeters and this ‘geodetic’ method will continue to play an important part in monitoring future changes in ice-sheet mass balance.
It is clearly important to know the length of time required to acquire sufficient elevation measurements to deduce a mass-balance trend. Short-term fluctuations in accumulation, surface temperature and the density of newly fallen snow produce short-term fluctuations in elevation which affect the accuracy of estimates of the long-term mass-balance trend. How long must the elevation time series be before the uncertainty in the mass-balance trend is less than the trend itself?
The answer to this question depends both on the magnitude and autocorrelation of the input fluctuations and on the response of the ice sheet to these inputs. For example, the time needed to detect a trend in mean annual accumulation of the same order as the standard deviation of the annual variations, with probability 0.9, is 29 years for a typical lag-1 autocorrelation of 0.1 m w.e. (Reference WeatherheadWeatherhead and others, 1998). However, the underlying snow and ice adapts to increased snowfall by an increased downward motion (and vice versa) so that each year’s snowfall is not translated directly into a proportional change in surface height. This nonlinear response reduces the time taken to establish an elevation trend by an amount that we need to determine.
Reference Van der VeenVan der Veen (1993) looked at the effect of fluctuations in accumulation using a simple ice-flow model to describe the ice-sheet response. He concluded that for the Greenland ice sheet an observation period of about 10 years would be sufficient to measure climatically significant changes in ice thickness caused by accumulation. More comprehensively, Reference Arthern and WinghamArthern and Wingham (1998) looked at the effects of fluctuations in accumulation, surface temperature and surface density using a snow densification model for the upper part of the ice sheet. They derived response times to step perturbations in accumulation, surface temperature and surface density for sites in Greenland and Antarctica. For an accumulation perturbation of 10% the response time (half the time required to reach equilibrium) ranged from 6 to 16 years. The response to surface density perturbations was more rapid (3–8 years) and that to surface temperature considerably slower (45–90 years). However, the densification model did not include the effect of temperature variations in the upper 2 m of the firn, where a rapid response would be expected (Reference Zwally and LiZwally and Li, 2002).
Given the limitations of current models, there is an advantage in observing the effect of input fluctuations on the ice sheet directly. As part of the calibration and validation (cal/val) activities in support of CryoSat-2 we have measured elevation change rates in the dry snow zone of the Greenland ice sheet over a period of 7 years and, using repeated measurements of density, have been able to quantify the contribution of the short-term fluctuations to the error in determining the mass-balance trend over this period from the elevation trend. We show that this error is reduced to the level of the mass-balance trend itself over the 7 year period and that this is therefore a minimum estimate for the time needed to determine the trend.
2. Theory
We are concerned with three types of short-term fluctuation that can affect the elevation of the snow surface:
-
The mass fluctuation: an increase in the accumulation rate (at fixed snow density) will raise the surface.
-
The surface density fluctuation: an increase in the surface density (at fixed accumulation rate) will lower the surface.
-
The compaction fluctuation: an increase in the rate of snow compaction will lower the surface.
In a previous paper, which reported on data collected over the first 2 years of the CryoSat-2 cal/val project (Reference Morris and WinghamMorris and Wingham, 2011), we gave a detailed theoretical analysis which showed how these fluctuations contribute to the error in determining mass balance from elevation. Here we give a summary of the key equations, without repetition of their full (and somewhat complex) derivation.
Consider a column of densifying firn with surface height z = h
S in an inertial frame {x, z, t} and a base, fixed in the inertial frame, at sufficient depth that the firn has reached the density of ice, ρ
i. We assume that the vertical mass flux per unit area at the surface of the column, ![]() , and the vertical mass flux at the base,
, and the vertical mass flux at the base, ![]() , are the only sources of mass gain or loss. We neglect mass loss through the walls of the column, on the grounds that the length of the column is small compared with the thickness of the ice. Because the time periods we are concerned with are short, we suppose that
, are the only sources of mass gain or loss. We neglect mass loss through the walls of the column, on the grounds that the length of the column is small compared with the thickness of the ice. Because the time periods we are concerned with are short, we suppose that ![]() is constant both in time and space. That is, we are excluding the effect of changes in ice dynamics, basal melting rate and isostatic uplift rate on mass flux at the base of the column. The rate of change of surface height,
is constant both in time and space. That is, we are excluding the effect of changes in ice dynamics, basal melting rate and isostatic uplift rate on mass flux at the base of the column. The rate of change of surface height, ![]() , associated with fluctuations in accumulation and near-surface density, is then
, associated with fluctuations in accumulation and near-surface density, is then
where ρ
S is the snow density at the surface and ![]() the compaction velocity. The compaction velocity is the difference between the velocities of the surface and base of the column in the inertial frame and
the compaction velocity. The compaction velocity is the difference between the velocities of the surface and base of the column in the inertial frame and ![]() ,
, ![]() are the material velocities at the surface and base, respectively. The change in mass balance arising from change in mass of the firn column is
are the material velocities at the surface and base, respectively. The change in mass balance arising from change in mass of the firn column is ![]() .
.
Setting ![]() equal to
equal to ![]() will lead to an error in the estimate of the mass-balance trend which, written as an equivalent rate of change of height, is
will lead to an error in the estimate of the mass-balance trend which, written as an equivalent rate of change of height, is
Using Eqn (1) this becomes
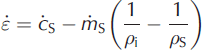
Integrating Eqn (2) over time gives the error, Δε, over time Δt as
where Δm
S is the mass per unit area of the accumulation layer, Δh
S is the change in surface elevation and Δm
F is the mass lost per unit area at the base of the column over the observation time interval. If Δl is the depth of snow accumulated over time Δt, the mean density of the accumulation layer ![]() . Reference Morris and WinghamMorris and Wingham (2011) show that Eqn (3) integrates to give
. Reference Morris and WinghamMorris and Wingham (2011) show that Eqn (3) integrates to give
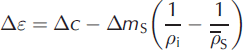
with an approximation error which increases with Δt. The approximation error is 10% for Δt = 5 years, which should therefore be regarded as an upper limit for the time interval between observations.
We expand the variables on the right-hand side of Eqn (5) as

where the time-invariant unperturbed variables Δm
0, ![]() and Δc
0 are related by the steady-state equation
and Δc
0 are related by the steady-state equation
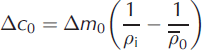
and the perturbations Δm
1, ![]() and Δc
1 are the time-varying fluctuations from these values that give rise to error Δε.
and Δc
1 are the time-varying fluctuations from these values that give rise to error Δε. ![]() is the harmonic mean of ρ
0(s). Substitution from Eqn (6) leads to the expression
is the harmonic mean of ρ
0(s). Substitution from Eqn (6) leads to the expression
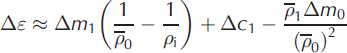
where second-order terms have been discarded on the assumption that the perturbations are small compared with the unperturbed variables. The error Δε can only be expressed in terms of three separate contributions from the fluctuations if Δm
0 and ![]() are such that this condition is fulfilled.
are such that this condition is fulfilled.
For discrete sites xj weighted by wj the spatial mean of Δε = Δt is given by

Where ![]() is the cross-product (Δεj
/Δt)(Δεk
/Δt). For a population of spatial means, the same equation holds, with
is the cross-product (Δεj
/Δt)(Δεk
/Δt). For a population of spatial means, the same equation holds, with ![]() interpreted as the root mean square over the population and
interpreted as the root mean square over the population and ![]() as the covariance of Δε/Δt.
as the covariance of Δε/Δt.
Given field measurements of Δm
S, ![]() and Δc at a given site, we choose suitable values for the time-invariant variables Δm
0,
and Δc at a given site, we choose suitable values for the time-invariant variables Δm
0, ![]() and Δc
0 (Section 5) and then derive the time-varying fluctuations Δm
1,
and Δc
0 (Section 5) and then derive the time-varying fluctuations Δm
1, ![]() and Δc
1 from Eqn (6). Equation (8) then gives us the error Δε at that site. The average error over a wider area is calculated using errors from several sites in Eqn (9).
and Δc
1 from Eqn (6). Equation (8) then gives us the error Δε at that site. The average error over a wider area is calculated using errors from several sites in Eqn (9).
3. The Cryosat Traverse
The CryoSat traverse includes a 365 km section of the Expéditions Glaciologiques Internationales au Groenland (EGIG) line from site T05 to site T41, and a 184 km track north to Summit Station (Fig. 1). The lower section of the traverse, from T05 to near T12, lies in the ‘percolation zone’ (Reference Scott, Nienow, Mair, Parry, Morris and WinghamScott and others, 2006). The upper section, from T21 to Summit Stations, lies in the ‘dry snow zone’ where melt incidents can occur in some summers but do not produce significant ice layering in the snow.

Fig. 1. The CryoSat traverse. Sites T05 to T41 lie along the EGIG line.
Repeated one-way traverses were made in spring and autumn 2004 and spring and summer 2006. In summer 2010 a round trip to T21 was made from Summit Station, during which profiles were taken at sites on the outward and return legs. In summer 2011 measurements were made solely on the outward leg from Summit Station to T21. Thus we have data covering 7 years for the dry snow zone and 2.2 years for the percolation and transition zones.
The positions and climatological characteristics of the sites are given in Table 1, which gives two values for the mean annual accumulation. The profile value, āp, was determined by counting annual density peaks (Reference Morris and WinghamMorris and Wingham, 2011) in the upper 10–14 m of snow and applies to the period during which this surface layer is built up, Δt p, which ranges from 8 to 19 years. The recent value, ār, was determined by direct measurement of the mass added over the measurement period, Δt r, which ranges from 2 to 7 years. In the dry snow zone ār is lower than āp, though not significantly so, given the uncertainties in the means. This is consistent with the decrease in precipitation over the Greenland ice sheet from 2006 to 2010 shown by the European Centre for Medium-Range Weather Forecasts (ECMWF) re-analysis data, after a period of increasing precipitation since 1990 (e.g. Reference VernonVernon and others, 2013).
Table 1. Climatological conditions at the CryoSat traverse sites. x is the distance along the traverse and T * m is the mean annual temperature, with values estimated from lapse rates in parentheses. The mean annual accumulation rate determined from the spring 2004 profiles, āp, is for the period Δt p and ār is the accumulation rate over the measurement period, Δt r. Elevation is given as the height above ellipsoid
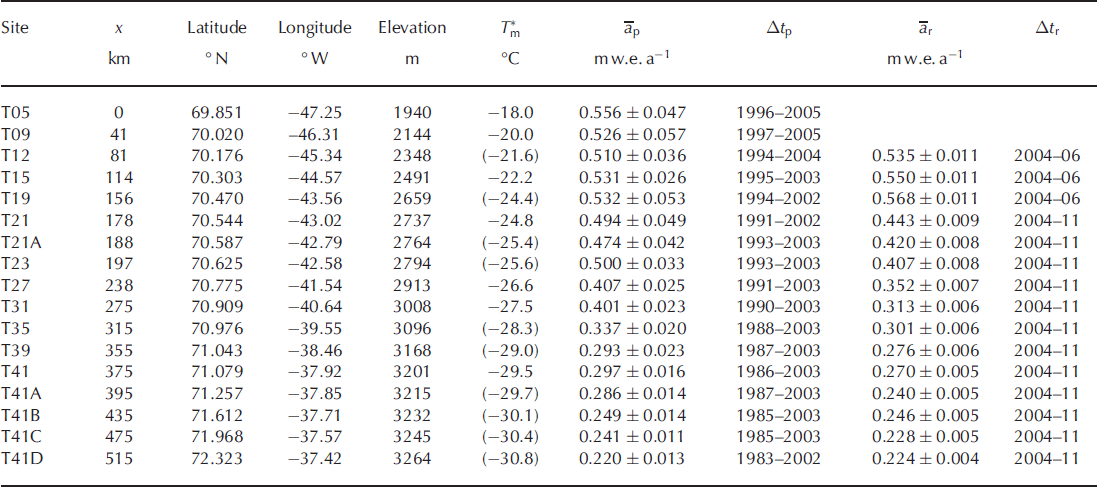
Mean annual temperatures date from pre-1990 measurements (Reference Merlivat, Ravoire, Vergnaud and LoriusMerlivat and others, 1973; Reference Anklin, Stauffer, Geis and WagenachAnklin and others, 1994). Over the past 20 years an increase in mean summer surface air temperature has been observed both at Swiss Camp, 86 km west-southwest of T05, and at Summit Station (Reference HannaHanna and others, 2014) with 2007 and 2010 being particularly warm years.
4. Methods
The density profiles were measured using a neutron probe, which forms part of the Ice Geophysical Logging System developed by Reference Morris and CooperMorris and Cooper (2003). It contains an annular source of fast neutrons around a cylindrical detector of slow neutrons. The fast neutrons lose energy by scattering in the snow and the count rate of slow neutrons arriving back at the detector is related to snow density, ρ. A 5 cm diameter access hole is augered in the snow and the probe moved slowly upwards using a small winch. Since the neutron emission is a random process, there is a random error in the count rate, leading to a random error, σρ
, in density. This can be reduced by increasing the counting period, or, in the case of continuous profiling, reducing the winch speed. At the minimum winch speed of 1 mm s−1, at which a 10 m hole can be logged in about 3 hours, σρ
/ρ ≈ 2%. Theoretical calibration equations have been derived by Reference MorrisMorris (2008) and, together with laboratory experiments, show that for a given density, count rate decreases with the diameter of the access hole and the offset of the probe axis from the centre of the hole. The systematic error in density, ![]() , can be minimized by careful drilling and by ensuring that the probe rests against the side-wall of the access hole so the offset is known. An error of 5% in diameter produces
, can be minimized by careful drilling and by ensuring that the probe rests against the side-wall of the access hole so the offset is known. An error of 5% in diameter produces ![]() . Very near the surface both snow and atmosphere are included in the measurement volume, so the apparent snow density decreases.
. Very near the surface both snow and atmosphere are included in the measurement volume, so the apparent snow density decreases.
In the first year of the traverse, access holes drilled in the spring were protected by snow blocks and resurveyed in the autumn. Later a technique of protecting the holes with 1 m lengths of white plastic tubing was used. This allowed the holes to be re-profiled without disturbing the newly accumulated surface layer. However, over the 4 year gap in measurements between 2006 and 2010 all sites were lost, so new holes had to be augered. The data therefore come from a mixture of repeat measurements in the same hole and pairs of measurements in different holes separated by 5–10 m.
Figure 2 shows density profiles for 2004, 2006, 2010 and 2011 at site T41 as an example of the data obtained using the neutron probe. The profiles show the variation between denser winter snow and less dense snow formed during the summer from a mixture of surface hoar and precipitation. The density peaks lie in winter snow, but are formed during the following summer, when higher temperatures promote densification in the near-surface layer. In Figure 2a each curve measured after 2004 has been positioned on the depth scale so that its lowest recognizable density feature lies at the same level as the same feature in the previous profile. In Figure 2b the profiles have been positioned on the water equivalent depth scale so that the peaks match. The mass of snow between given peaks does not change with time. At most sites profiles were obtained to around 13 m depth, sufficient to cover the first stage of densification during which the snow densifies to around 0.55 g cm−3 by grain-boundary sliding and bonds start to form between grains.
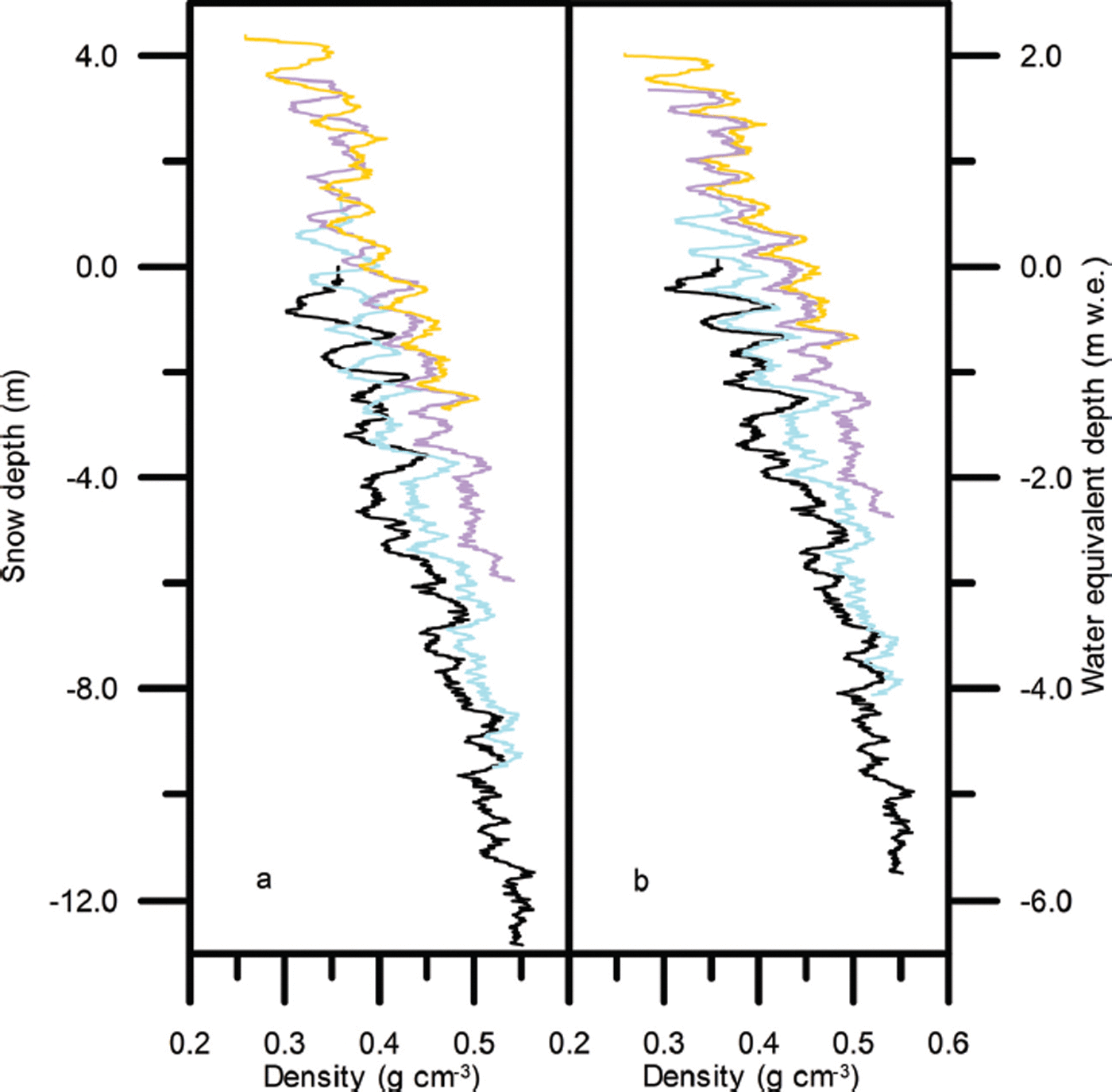
Fig. 2. Density profiles from site T41 measured in spring 2004 (——),summer 2006 (——),summer 2010 (——)and summer 2011 (——) plotted against (a) depth and (b) water equivalent depth with arbitrary zero at the spring 2004 surface.
Dual-frequency GPS measurements of the position of a point on the snow surface were made at each site. In addition to these GPS elevation measurements, the point was marked with a 4m aluminium pole and the relative height of the surface (with respect to the bottom of the pole) was also recorded. The pole was installed 1 m from the access hole to avoid disturbing the snow to be profiled.
5. Analysis
At this point we need to introduce a densification equation in order to (1) define ![]() , the unperturbed value of the harmonic mean density of a layer accumulated over time Δt at a given site and (2) estimate the compaction below the depth of our last density measurement. Following Reference Morris and WinghamMorris and Wingham (2011), we assume a densification model of the form first proposed by Reference Herron and LangwayHerron and Langway (1980). The time-varying models proposed by Reference Arthern, Vaughan, Rankin, Mulvaney and ThomasArthern and others (2010) and Reference Morris and WinghamMorris and Wingham (2014) reduce to this form in the steady-state case.
, the unperturbed value of the harmonic mean density of a layer accumulated over time Δt at a given site and (2) estimate the compaction below the depth of our last density measurement. Following Reference Morris and WinghamMorris and Wingham (2011), we assume a densification model of the form first proposed by Reference Herron and LangwayHerron and Langway (1980). The time-varying models proposed by Reference Arthern, Vaughan, Rankin, Mulvaney and ThomasArthern and others (2010) and Reference Morris and WinghamMorris and Wingham (2014) reduce to this form in the steady-state case.

where ![]() is strain rate, ρ
0(s) the density at depth s below the surface and k
0 is a site-dependent constant. We assume k
0 depends on local temperature but not on accumulation so Eqn (10) can be integrated to give a linear expression in s
is strain rate, ρ
0(s) the density at depth s below the surface and k
0 is a site-dependent constant. We assume k
0 depends on local temperature but not on accumulation so Eqn (10) can be integrated to give a linear expression in s
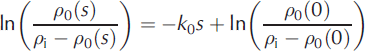
at each site. Profiles of ρ
0 are estimated by fitting this curve to the measured density profiles. In particular, we obtain estimates of the density at the surface, ρ
0(0), and the harmonic mean density, ![]() , over an accumulation layer of thickness Δl.
, over an accumulation layer of thickness Δl.
When the measured density profile is accurate over most of the accumulation layer, Δm
S and ![]() can be determined separately. For those periods when this is not possible, usually because the layer is too thin, we can at least identify the ratio
can be determined separately. For those periods when this is not possible, usually because the layer is too thin, we can at least identify the ratio ![]() .
.
The Eulerian elevation change Δh S for each site is determined by repeated GPS measurements of the ellipsoidal height of the snow surface at each access hole (to give the Lagrangian elevation change) followed by addition of the (negative) convective elevation change, Δx ∂h S = ∂x (Reference Morris and WinghamMorris and Wingham, 2011). Above T41 the convective elevation changes are negligible compared with the instrumental error in Δh S. Below T23 the correction for convective elevation change is significant, especially over the longer time periods.
The surface height change Δh S may also be determined by comparison of repeated density profiles. Δh S is related to Δl by

Where ![]() is the harmonic mean density of material element N over time Δt and Δc
1N
is the fluctuation in compaction below N. (Note that Reference Morris and WinghamMorris and Wingham (2011) used the lowest common density peak to define N, but here we use the lowest common recognizable density feature to gain a little more depth.) We assume N is deep enough for Δc
1N
to be negligible. Elevation change rates can also be determined from the pole measurements, using the same method as for comparison of density profiles, with the further assumption of a small downward velocity for the pole of 0.025 m a−1 (Reference Morris and WinghamMorris and Wingham, 2011).
is the harmonic mean density of material element N over time Δt and Δc
1N
is the fluctuation in compaction below N. (Note that Reference Morris and WinghamMorris and Wingham (2011) used the lowest common density peak to define N, but here we use the lowest common recognizable density feature to gain a little more depth.) We assume N is deep enough for Δc
1N
to be negligible. Elevation change rates can also be determined from the pole measurements, using the same method as for comparison of density profiles, with the further assumption of a small downward velocity for the pole of 0.025 m a−1 (Reference Morris and WinghamMorris and Wingham, 2011).
Equation (12) includes two unknowns, that is, the time-invariant mass input, Δm 0, and the mass output, Δm F. Given Δm 0 we can estimate Δm F by matching the height changes determined from GPS and density measurements. There is a difficulty in that we do not know a priori on what timescale Δm 0 should be estimated. In this paper we use both the profile mean annual accumulation rate, āp, which implies a timescale of 8–19 years, and the recent accumulation rate, ār over 2–7 years, to estimate Δm 0. In order to understand the implications of the choice of Δm 0 on the contributions to the error from mass and compaction fluctuations it is useful to write
where any systematic error, Δm
*, in the estimate, ![]() , produces a systematic error Δc
* in c
0 by Eqn (7). The fluctuation estimates
, produces a systematic error Δc
* in c
0 by Eqn (7). The fluctuation estimates ![]() and
and ![]() are then given by
are then given by

Hence

where

is the estimate for Δm F for a particular time period, determined by optimizing Eqn (15) to obtain the best match with the GPS data.
6. Results
6.1. Mean surface density
Figure 3a shows the (arithmetic) mean density of various surface layers. The data for summer 2006–summer 2010 and summer 2006–summer 2011 are consistent with the best straight line through the spring 2004–spring 2006 data:

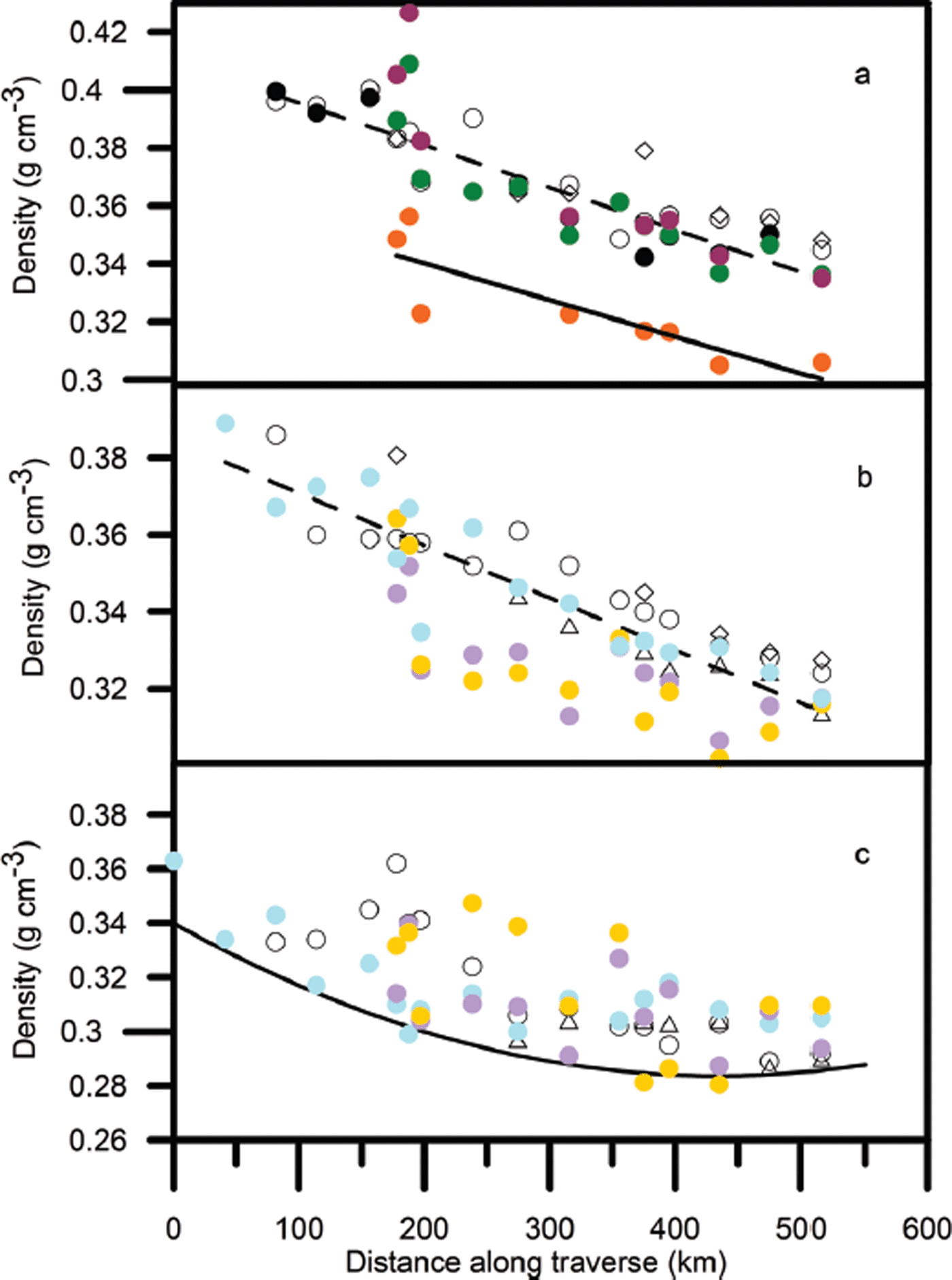
Fig. 3. (a) The mean density, ![]() , of snow accumulated over the periods spring 2004–spring 2006 (•), spring 2004–summer 2006 (•), autumn 2004–summer 2006 (0), summer 2010–summer 2006 (•), summer 2011–summer 2006 (•) and summer 2011–summer 2010 (•). The dashed line is the best fit to the spring 2004–spring 2006 data and the solid line the best fit to the summer 2010– summer 2011 data. (b) The time-invariant density at the snow surface, ρ
0(0), derived from profiles measured in spring 2004 (•), autumn 2004 (◊), spring 2006 (Δ), summer 2006 (•), summer 2010 (•) and summer 2011 (•). The dashed line is the best fit to the summer 2006 data. (c) The minimum density observed in profiles measured in spring 2004 (o), spring 2006 (Δ), summer 2006 (•), summer 2010 (•) and summer 2011 (•). The curve is an upper estimate of the minimum value of
, of snow accumulated over the periods spring 2004–spring 2006 (•), spring 2004–summer 2006 (•), autumn 2004–summer 2006 (0), summer 2010–summer 2006 (•), summer 2011–summer 2006 (•) and summer 2011–summer 2010 (•). The dashed line is the best fit to the spring 2004–spring 2006 data and the solid line the best fit to the summer 2010– summer 2011 data. (b) The time-invariant density at the snow surface, ρ
0(0), derived from profiles measured in spring 2004 (•), autumn 2004 (◊), spring 2006 (Δ), summer 2006 (•), summer 2010 (•) and summer 2011 (•). The dashed line is the best fit to the summer 2006 data. (c) The minimum density observed in profiles measured in spring 2004 (o), spring 2006 (Δ), summer 2006 (•), summer 2010 (•) and summer 2011 (•). The curve is an upper estimate of the minimum value of ![]() .
.
but the summer 2010–summer 2011 mean densities are clearly lower. The best straight line through these data is

The time-invariant density at the surface, ρ 0(0), shown in Figure 3b shows that the 2010 and 2011 estimates of ρ 0(0) generally lie below the best straight line through the summer 2006 estimates
However, from Figure 3c, the minimum densities recorded at each site in 2010 and 2011 still fit within the envelope given by the curve

6.2. Mass-balance trend
The estimated trend in the mass balance of the firn column, ![]() , is shown in Table 2. Trends have been calculated for each site, using
, is shown in Table 2. Trends have been calculated for each site, using ![]() and
and ![]() . Data for periods <1 year have been excluded. The number of measurements available at each site, n, is greater above T21, so the values are more reliable. Between T21 and T41A the mass-balance trend is more negative when
. Data for periods <1 year have been excluded. The number of measurements available at each site, n, is greater above T21, so the values are more reliable. Between T21 and T41A the mass-balance trend is more negative when ![]() is used to estimate the mass input. This is not only because in this region
is used to estimate the mass input. This is not only because in this region ![]() (Table 1), but also because the estimate of Δm
F changes slightly with
(Table 1), but also because the estimate of Δm
F changes slightly with ![]() . Seven sites above T23 are in balance with the profile accumulation. Taking all sites together, the output flux is in balance with
. Seven sites above T23 are in balance with the profile accumulation. Taking all sites together, the output flux is in balance with ![]() but significantly greater than
but significantly greater than ![]() .
.
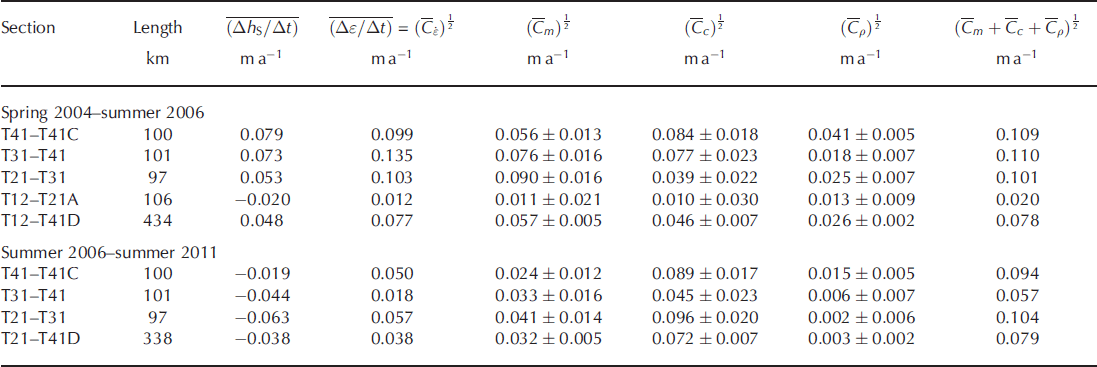
Table 2. Estimated mass-balance trend at the CryoSat traverse sites
6.3. Elevation change rate
Figure 4 shows the elevation change rates over the periods 2006–10, 2006–11, 2010–11 and 2004–06. The grey points show data from density profiles and pole measurements made within 1 m of the GPS measurements, which are shown in black. The uncertainty in ΔhS for the grey points is estimated from the error in ![]() (5%), the instrumental error in Δl(±10.02 m) and an estimated 5% error in
(5%), the instrumental error in Δl(±10.02 m) and an estimated 5% error in ![]() and is larger than the uncertainty in the GPS measurements. The choice of
and is larger than the uncertainty in the GPS measurements. The choice of ![]() affects the position of the grey points slightly, but the agreement with the GPS measurements is not affected. Figure 4b shows a loss in elevation from 2006 to 2011, whereas Figure 4d shows a small increase in elevation for all sites above T21A for the previous 2 years. Much of the recent elevation decrease occurred in 2010–11 (Fig. 4c).
affects the position of the grey points slightly, but the agreement with the GPS measurements is not affected. Figure 4b shows a loss in elevation from 2006 to 2011, whereas Figure 4d shows a small increase in elevation for all sites above T21A for the previous 2 years. Much of the recent elevation decrease occurred in 2010–11 (Fig. 4c).

Fig. 4. The rate of change in surface elevation Δh
S = Δt. (a) Summer 2006–summer 2010, (b) summer 2006–summer 2011, (c) summer 2010– summer 2011 and (d) spring 2004–summer 2006. Determined from GPS (•), density profile (•) and pole (◊) measurements. Calculated using ![]() .
.
6.4. The error in mass-balance trend arising from short-term fluctuations
Figure 5 shows the cross-product ![]() for sites xi
and xj
as a function of distance along the traverse for four periods for which we have data at all sites from T21 to T41D. Sites xi
lie on the horizontal axes and sites xj
on the vertical axes. Figure 5a, for a time interval of 1 year, shows a similar pattern to the spatial covariance of the annual mass contribution to Δε/Δt shown by Reference Morris and WinghamMorris and Wingham (2011), with
for sites xi
and xj
as a function of distance along the traverse for four periods for which we have data at all sites from T21 to T41D. Sites xi
lie on the horizontal axes and sites xj
on the vertical axes. Figure 5a, for a time interval of 1 year, shows a similar pattern to the spatial covariance of the annual mass contribution to Δε/Δt shown by Reference Morris and WinghamMorris and Wingham (2011), with ![]() varying by ±10.05 m2 a−2 on the 100 km scale. As the time interval increases, the range of
varying by ±10.05 m2 a−2 on the 100 km scale. As the time interval increases, the range of ![]() decreases. Figure 5b, for a time interval of 2.2 years, shows maximum values of ∼0.03 m2 a−2 around T31 and T41A. Figure 5c, for 5 years, has maximum values of ∼0.01 m2 a−2 between T27 and T31 and Figure 5d, for 7 years, has maximum values of ∼0.0015 m2 a−2 around T41B. From Eqn (9) the spatial mean error,
decreases. Figure 5b, for a time interval of 2.2 years, shows maximum values of ∼0.03 m2 a−2 around T31 and T41A. Figure 5c, for 5 years, has maximum values of ∼0.01 m2 a−2 between T27 and T31 and Figure 5d, for 7 years, has maximum values of ∼0.0015 m2 a−2 around T41B. From Eqn (9) the spatial mean error, ![]() , for the region xi
to xj
is given by averaging
, for the region xi
to xj
is given by averaging ![]() and then taking the square root. Figure 5 demonstrates that the spatial mean error decreases both as the length of the region (the spatial scale) increases and as the time interval increases. After 2.2 years the maximum point value is 0.17 m s−1 and the 338 km scale value is 0.10ms−1. After 7 years the maximum point value is 0.04 m s−1 and the 338 km scale value is 0.01 m s−1.
and then taking the square root. Figure 5 demonstrates that the spatial mean error decreases both as the length of the region (the spatial scale) increases and as the time interval increases. After 2.2 years the maximum point value is 0.17 m s−1 and the 338 km scale value is 0.10ms−1. After 7 years the maximum point value is 0.04 m s−1 and the 338 km scale value is 0.01 m s−1.
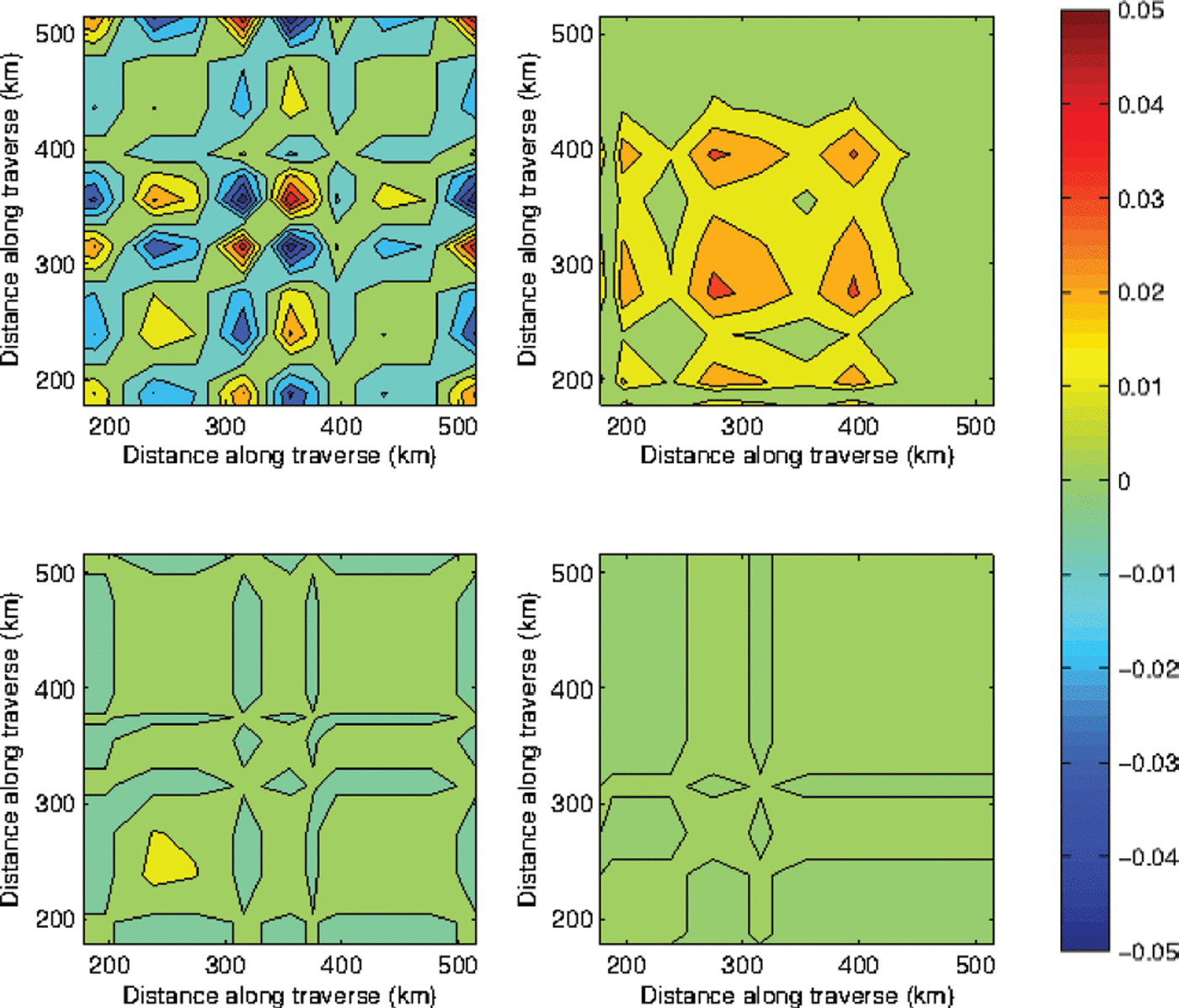
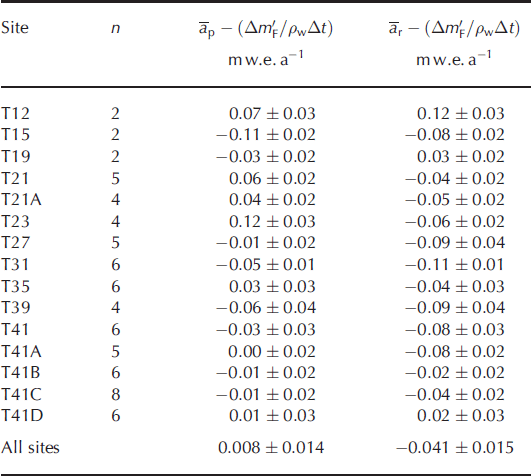
Fig. 5. The cross-product ![]() of errors Δε/Δt over the periods (a) summer 2010–summer 2011, (b) spring 2004–summer 2006, (c) summer 2006–summer 2011 and (d) spring 2004–summer 2011. The contours are at intervals of 0.01 m2 a−2. Sites xi
lie on the horizontal axis and sites xj
on the vertical axis. By definition
of errors Δε/Δt over the periods (a) summer 2010–summer 2011, (b) spring 2004–summer 2006, (c) summer 2006–summer 2011 and (d) spring 2004–summer 2011. The contours are at intervals of 0.01 m2 a−2. Sites xi
lie on the horizontal axis and sites xj
on the vertical axis. By definition ![]() is symmetrical about the diagonal along which j = k.
is symmetrical about the diagonal along which j = k.
Figure 6a shows the decrease in the spatial mean error with time since the start of elevation observations in 2004. Points for means taken over sub-regions of about 100 km are scattered around the values for the whole region from T21 to T41D. Figure 6b shows the decrease in mean elevation change rate for the same period. After 7 years the observed mean elevation change rate is approaching the value expected for a mass-balance change of −0.041 m w.e. a−1 i.e. −0.045 m a−1. In other words, after 7 years the elevation time series is long enough to deduce the estimated mass-balance trend (Table 2) with an error less than its magnitude, provided that elevations are averaged over about 100 km or more.
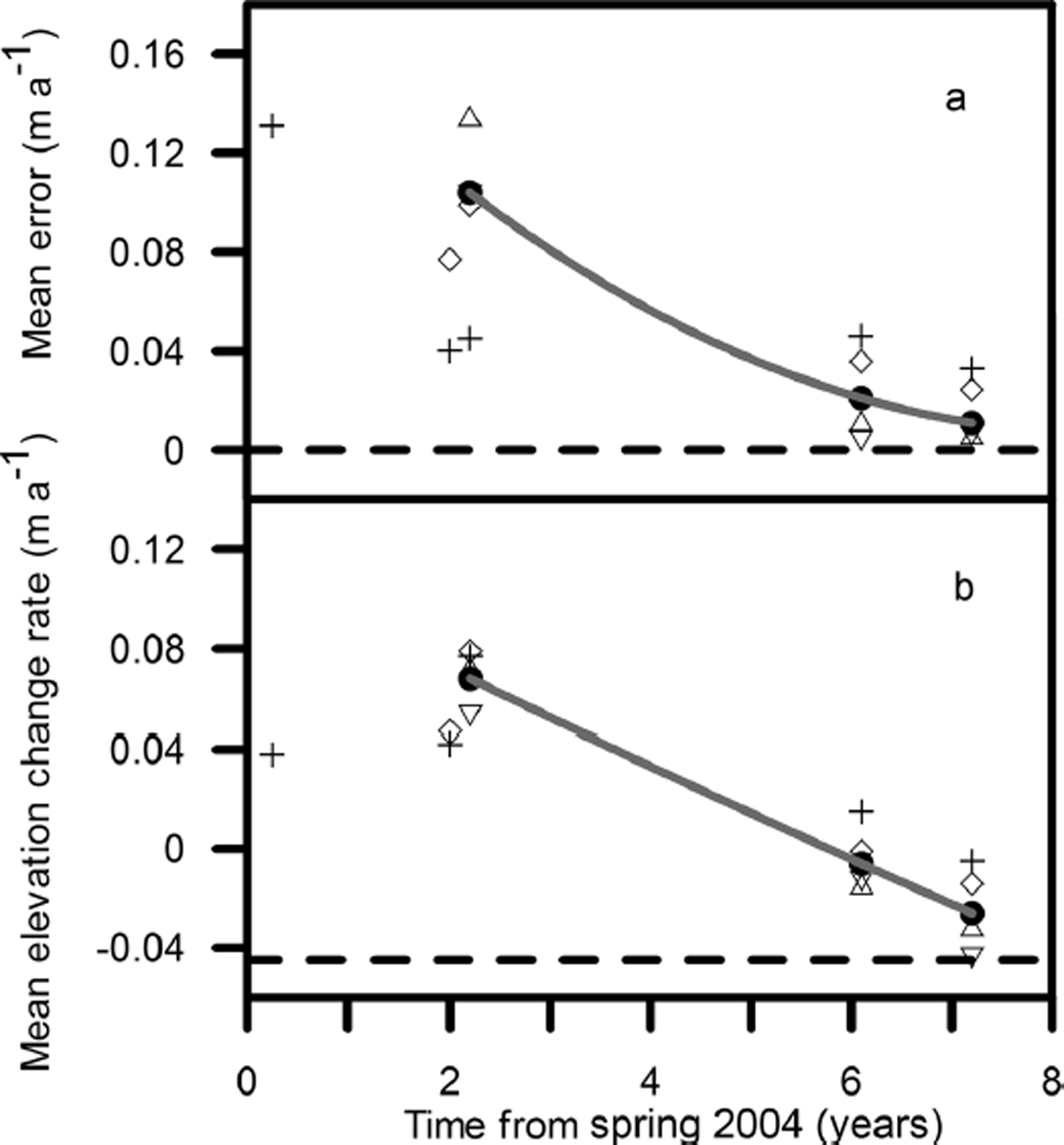
Fig. 6. (a) The mean error, ![]() , and (b) the mean elevation change rate,
, and (b) the mean elevation change rate, ![]() , as a function of time from the first field observations in spring 2004. Spatial averages are taken over T41B–T41D (80 km; +), T41–T41C (100 km; ◊), T31–T41 (101 km; Δ), T21–T31 (97 km; ∇) and T21–T41D (338 km; •). The solid curves are second-order polynomial fits to the T21–T41D data. After 7 years, the mean error is of the same order as the long-term trend in elevation. The dashed line in (b) shows the mean mass-balance trend for all sites, −0.045 m ice equivalent a−1.
, as a function of time from the first field observations in spring 2004. Spatial averages are taken over T41B–T41D (80 km; +), T41–T41C (100 km; ◊), T31–T41 (101 km; Δ), T21–T31 (97 km; ∇) and T21–T41D (338 km; •). The solid curves are second-order polynomial fits to the T21–T41D data. After 7 years, the mean error is of the same order as the long-term trend in elevation. The dashed line in (b) shows the mean mass-balance trend for all sites, −0.045 m ice equivalent a−1.
6.5. Contributions to the error
Figures 7 and 8 show the various contributions to the error from short-term fluctuations for Δt ≥ 2 years and using the two different methods of estimating Δm
0. The density fluctuations are unaffected by the choice of ![]() . On average their contribution to the total error is ∼20% and the combined contribution from mass and compaction fluctuations is ∼80%. However, the magnitudes of the mass and compaction fluctuations taken individually are very different.
. On average their contribution to the total error is ∼20% and the combined contribution from mass and compaction fluctuations is ∼80%. However, the magnitudes of the mass and compaction fluctuations taken individually are very different.
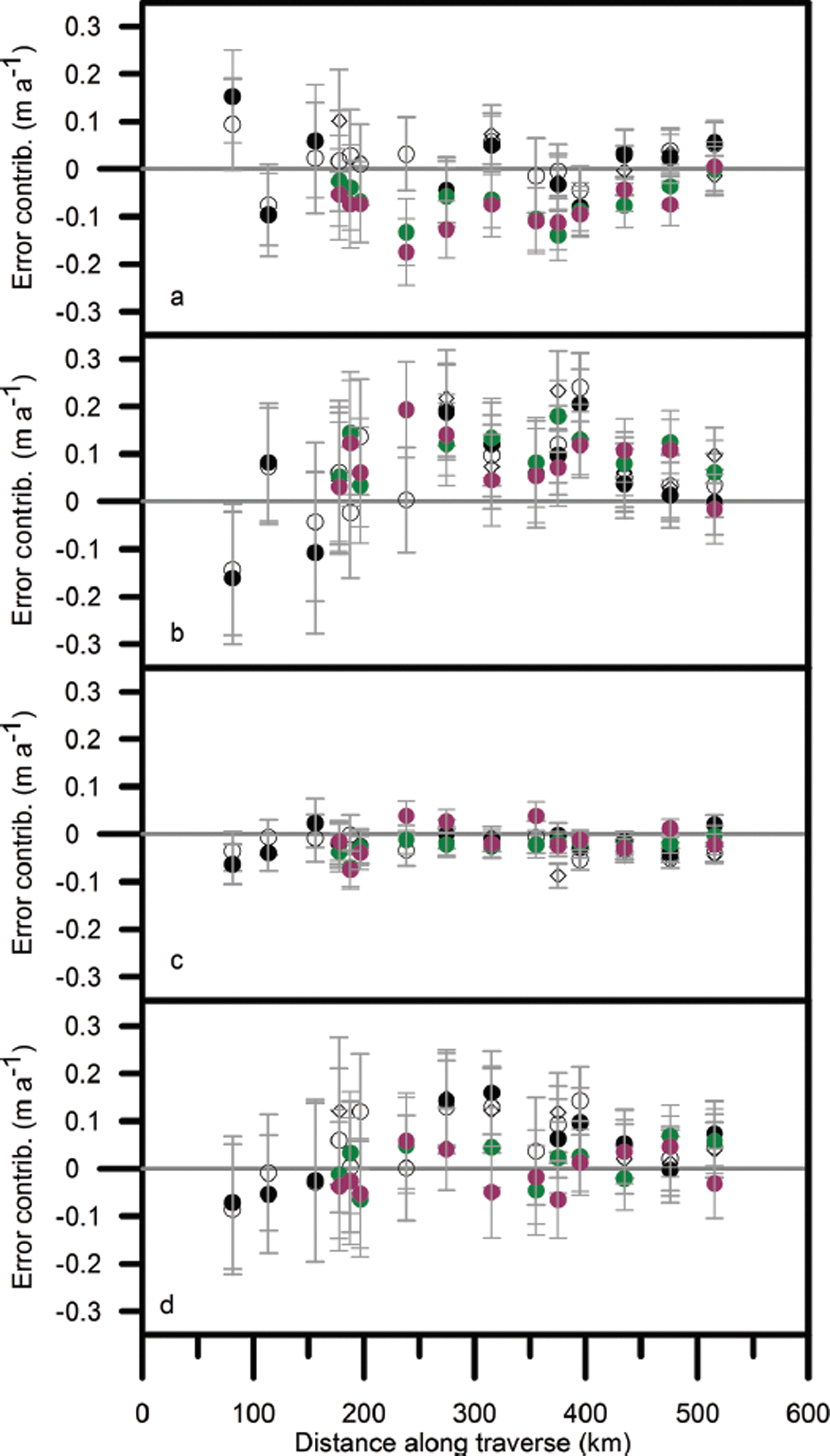
Fig. 7. The contribution of (a) mass (b) compaction and (c) density fluctuations to the error in mass-balance trend Δε/Δt (shown in (d)) over the periods spring 2004–summer 2006 (•), autumn 2004– summer 2006 (◊), spring 2004–spring 2006 (0), summer 2010–summer 2006 (•) and summer 2011–summer 2006 (•). Calculated using ![]() .
.
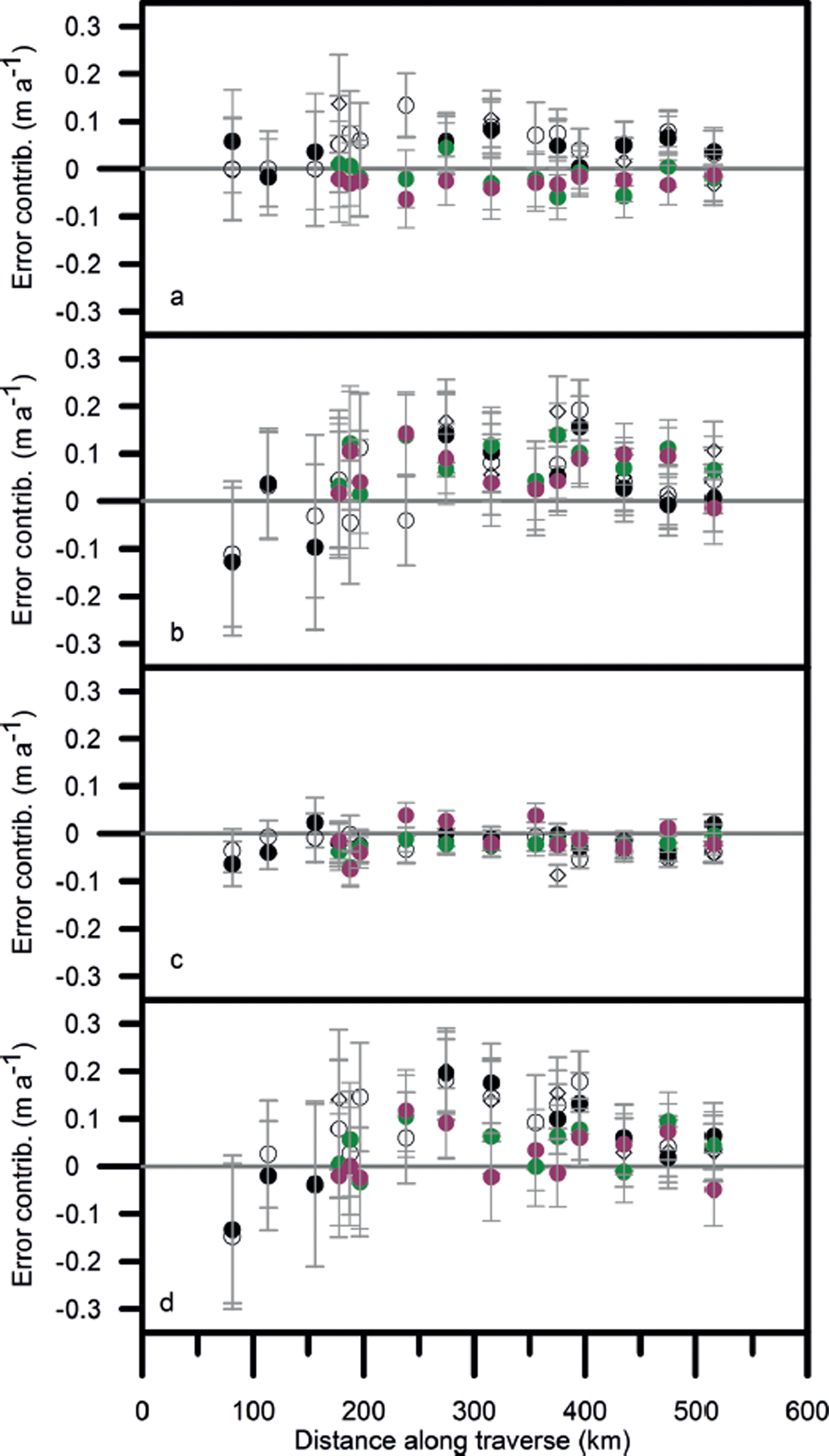
Fig. 8. Same as Figure 7, but calculated using ![]() .
.
In Figure 7 the contribution to the error from mass fluctuations is relatively large and appears to mirror, and thus offset, the contribution from compaction fluctuations. In Figure 8 the error from mass fluctuations is reduced and there does not seem to be a correlation with the compaction fluctuations. This suggests that in the first case a significant error Δm * in the estimate of Δm 0 is producing systematic errors in the mass and compaction contributions.
Figures 9 and 10 show the various contributions to the error for the shorter periods with Δt ≤ 2 years and the two different methods of estimating Δm
0. For both the short summer periods, and four of the measurements over 2010–11, the mean density of the accumulation layer is not well known. In these cases ![]() must be estimated in order to separate the contributions from mass and density. The minimum density observed in the profile is used as an estimate for
must be estimated in order to separate the contributions from mass and density. The minimum density observed in the profile is used as an estimate for ![]() in summer (Reference Morris and WinghamMorris and Wingham, 2011) and the missing 2010–11 values are interpolated using Eqn (18). The resulting estimated contribution from mass fluctuations is shown in Figures 9c and 10c. For the two summer periods the contribution from density fluctuations is 0.05–0.150 m a−1 throughout the traverse; for the year 2010–11 this decreases to −0.01 to 0.05 m a−1. Comparison of the two figures shows that the mass and compaction fluctuations are again reduced in magnitude when the recent accumulation is used to estimate Δm
0.
in summer (Reference Morris and WinghamMorris and Wingham, 2011) and the missing 2010–11 values are interpolated using Eqn (18). The resulting estimated contribution from mass fluctuations is shown in Figures 9c and 10c. For the two summer periods the contribution from density fluctuations is 0.05–0.150 m a−1 throughout the traverse; for the year 2010–11 this decreases to −0.01 to 0.05 m a−1. Comparison of the two figures shows that the mass and compaction fluctuations are again reduced in magnitude when the recent accumulation is used to estimate Δm
0.
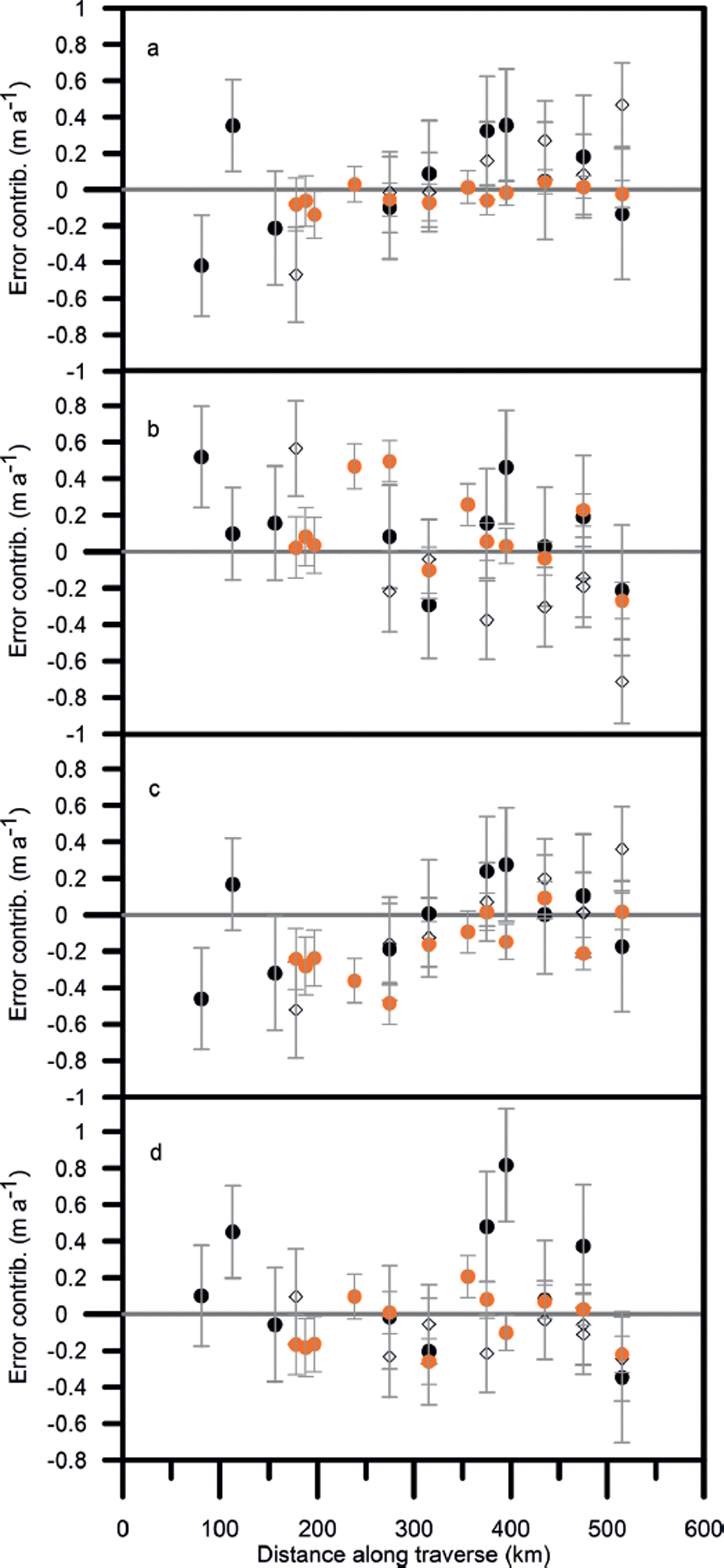
Fig. 9. The contribution of (a) mass and density, (b) compaction and (c) mass fluctuations to the error in mass-balance trend Δε/Δt (shown in (d)) over the periods spring 2004–autumn 2004 (◊), spring 2006–summer 2006 (•) and summer 2011–summer 2010 (•). Calculated using ![]() .
.
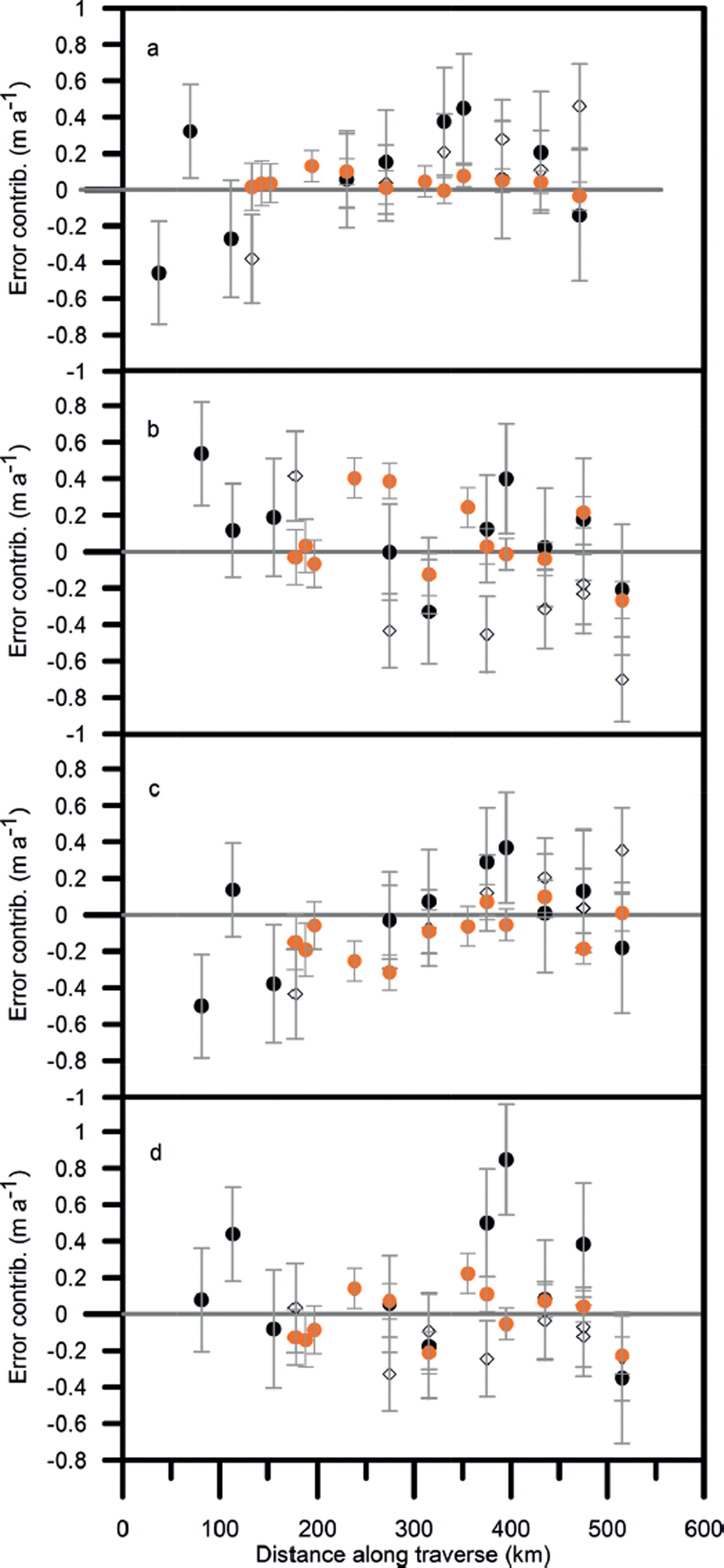
Fig. 10. Same as Figure 9, but calculated using ![]() .
.
6.6. Relation between mass and compaction contributions
In order to investigate any possible correlation between the major contributions we calculate the gradients and correlation coefficients of a linear regression of the estimated compaction contribution, ![]() , on the estimated mass contribution,
, on the estimated mass contribution, ![]() , for both estimates of Δm
0. These are shown in Table 3, which also shows the gradient
, for both estimates of Δm
0. These are shown in Table 3, which also shows the gradient ![]() calculated from Eqn (7) using the harmonic mean surface densities
calculated from Eqn (7) using the harmonic mean surface densities ![]() for each site and time period. This expresses the long-term relation between mass and compaction contributions to elevation.
for each site and time period. This expresses the long-term relation between mass and compaction contributions to elevation.
Table 3. Gradients of linear regression of ![]() on
on ![]() with coefficients of determination, r
2
with coefficients of determination, r
2
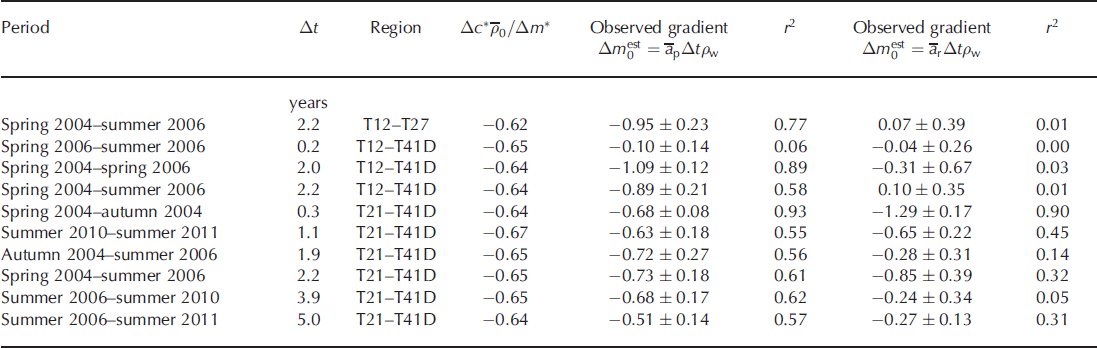
When the profile accumulation rate is used, it appears that Δc
* and Δm
* are large enough to ensure that, in all but two cases, the gradient of the regression line of ![]() on
on ![]() is not significantly different from the value expected for the long-term response. The terms Δc
1 and Δm
1 merely add apparently random fluctuations which reduce the coefficient of regression. When the recent accumulation rate is used, the picture becomes more complex. In most cases the correlation is weak or nonexistent; the only strong correlation occurs for spring 2004– autumn 2004. Gradient estimates are in most cases less than the long-term values, but not significantly so. The general picture suggests that Δc
* and Δm
* are now smaller and the gradients are more influenced by the relationship between Δc
1 and Δm
1.
is not significantly different from the value expected for the long-term response. The terms Δc
1 and Δm
1 merely add apparently random fluctuations which reduce the coefficient of regression. When the recent accumulation rate is used, the picture becomes more complex. In most cases the correlation is weak or nonexistent; the only strong correlation occurs for spring 2004– autumn 2004. Gradient estimates are in most cases less than the long-term values, but not significantly so. The general picture suggests that Δc
* and Δm
* are now smaller and the gradients are more influenced by the relationship between Δc
1 and Δm
1.
6.7. Spatial correlation of contributions
Reference Morris and WinghamMorris and Wingham (2011) calculated ![]() and
and ![]() for each of the contributions to the error for the spring 2004–summer 2006 period using the profile accumulation rate to give the best estimate for Δm
0. Table 4 shows these cross-products recalculated using recent precipitation. The mean elevation rate still decreases with elevation and it is still the case that the only section for which the mean error,
for each of the contributions to the error for the spring 2004–summer 2006 period using the profile accumulation rate to give the best estimate for Δm
0. Table 4 shows these cross-products recalculated using recent precipitation. The mean elevation rate still decreases with elevation and it is still the case that the only section for which the mean error, ![]() , is less than
, is less than ![]() is T12–T21A. However,
is T12–T21A. However, ![]() is now much closer to
is now much closer to ![]() for all sections. For T12–T41D,
for all sections. For T12–T41D, ![]() and
and ![]() , i.e. the contributions are essentially uncorrelated. Table 3 confirms this with a value of r
2 = 0.01 for this section and period. The summer 2006–summer 2011 period has a higher, though still weak, correlation between mass and compaction contributions, with r
2 = 0.31 for T21–T41D, and Table 4 shows
, i.e. the contributions are essentially uncorrelated. Table 3 confirms this with a value of r
2 = 0.01 for this section and period. The summer 2006–summer 2011 period has a higher, though still weak, correlation between mass and compaction contributions, with r
2 = 0.31 for T21–T41D, and Table 4 shows ![]() is significantly greater than
is significantly greater than ![]() for all sections.
for all sections.
Table 4. The mean elevation change rate, mean error and root-mean cross-products for two example periods
7. Discussion
In Section 6.2 we showed that output mass flux at the base of the firn column over the period 2004–11 is in balance with the profile accumulation over the 12–19 years before 2004 at seven sites in the upper part of the traverse. In the lower part the picture is less clear, but for all sites taken together the balance with pre-2004 accumulation remains.
The measurements of elevation change made over the traverse (Section 6.2) show that the response to a period of increasing precipitation in 2004–06, followed by decreasing precipitation from 2006–10, has been an increase in elevation to 2006 and a decrease thereafter. These data are consistent with Ice, Cloud and land Elevation Satellite (ICESat) laser altimeter measurements of elevation change of 0–0.1 m a−1 over the period 2003–07 (Reference Pritchard, Arthern, Vaughan and EdwardsPritchard and others, 2009) and CryoSat-2 radar altimeter measurements of –0.1 to −0.3 m a−1 from 2011–12 (Reference Helm, Humbert and MillerHelm and others, 2014). The cumulative elevation change rate declines with time from 2004 (Fig. 6). After 7 years it is close to the 2004–11 firn column mass-balance trend in ice equivalent depth.
In order to reduce speckle error, satellite radar altimeter data have to be spatially averaged over a scale of about 100 km. This averaging also reduces the uncertainty in the mass-balance trend derived from these data (Section 6.4). The mean values of the error Δε/Δt over approximately 100 km sections of the traverse decrease with time and are scattered around the mean for the 328 km section from T21– T41D. The half-time for the decrease is around 4 years.
We may compare this with the half-times calculated by Reference Arthern and WinghamArthern and Wingham (1998) for a return to steady-state conditions after step perturbations in accumulation, surface snow density and surface temperature for a site with ![]() , ρ
0(0) = 0.36 g cm−3 and
, ρ
0(0) = 0.36 g cm−3 and ![]() , conditions similar to the mid-range of EGIG line points. The half-times are 6, 3 and 45 years, respectively. For the CryoSat traverse the contribution of fluctuations in surface density to the error is relatively small (Section 6.5); the important contributions come from accumulation and from compaction produced by changes in both accumulation and temperature. A half-time of 4 years for the error suggests that either the temperature effect is negligible or, as we believe, that the appropriate half-time is ≪45 years.
, conditions similar to the mid-range of EGIG line points. The half-times are 6, 3 and 45 years, respectively. For the CryoSat traverse the contribution of fluctuations in surface density to the error is relatively small (Section 6.5); the important contributions come from accumulation and from compaction produced by changes in both accumulation and temperature. A half-time of 4 years for the error suggests that either the temperature effect is negligible or, as we believe, that the appropriate half-time is ≪45 years.
Using the CryoSat traverse data, Reference Morris and WinghamMorris and Wingham (2014) have derived an empirical densification equation which allows the effect of changes in accumulation and temperature on compaction to be estimated. The instantaneous response of compaction to accumulation is −0.33 to −0.95 ma−1 (m w.e.)−1, leading to values of ![]() ranging from −0.15 to −0.35. The response to a step increase in surface temperature is −0.11 to −0.20 m a−1 K−1. This includes a relatively rapid response to summer warming in the upper 2 m, not included in the Reference Arthern and WinghamArthern and Wingham (1998) analysis. Reference Morris and WinghamMorris and Wingham (2014) suggested that these responses would reinforce each other for the CryoSat sites, on the grounds that increased accumulation is normally associated with higher temperatures, since most of the precipitation is associated with cyclonic activity. However, recent summers (2007–11) in Greenland have been drier than normal, as a result of more frequent anticyclonic conditions (Reference HannaHanna and others, 2014), and also warmer, with an exceptionally warm summer in 2010. This would provide an explanation for the range of observed gradients
ranging from −0.15 to −0.35. The response to a step increase in surface temperature is −0.11 to −0.20 m a−1 K−1. This includes a relatively rapid response to summer warming in the upper 2 m, not included in the Reference Arthern and WinghamArthern and Wingham (1998) analysis. Reference Morris and WinghamMorris and Wingham (2014) suggested that these responses would reinforce each other for the CryoSat sites, on the grounds that increased accumulation is normally associated with higher temperatures, since most of the precipitation is associated with cyclonic activity. However, recent summers (2007–11) in Greenland have been drier than normal, as a result of more frequent anticyclonic conditions (Reference HannaHanna and others, 2014), and also warmer, with an exceptionally warm summer in 2010. This would provide an explanation for the range of observed gradients ![]() (Table 3) and the predominately weak correlations. Even though we have come closer to a good estimate of the short-term fluctuations by using the recent accumulation rate, the expected increase in compaction with increased accumulation is obscured by uncorrelated temperature effects. Further investigation of the causes of the compaction fluctuations along the EGIG line will require a snow model to determine energy and mass fluxes within the firn and a meteorological model to provide surface boundary conditions.
(Table 3) and the predominately weak correlations. Even though we have come closer to a good estimate of the short-term fluctuations by using the recent accumulation rate, the expected increase in compaction with increased accumulation is obscured by uncorrelated temperature effects. Further investigation of the causes of the compaction fluctuations along the EGIG line will require a snow model to determine energy and mass fluxes within the firn and a meteorological model to provide surface boundary conditions.
Another exceptionally warm event occurred in July 2012, after our observation period. For a few days there was melting over much of the ice sheet and, in some places, rain. At Summit the surface snow became slushy and then refroze to form a 2 cm crust; at the North Greenland Eemian Ice drilling site (NEEM, 77.45°N, 51.05°W), which has a similar mean annual temperature to T39 on the EGIG line, a 1 cm surface crust was observed and melt layers formed at depths of around 5, 20 and 69 cm (Reference NghiemNghiem and others, 2012). We can assume that similar melt layers formed along the EGIG line. For periods long enough for all the melt layers to lie in Δl, the effect of melting is to increase ![]() , with no change in Δm
1. Abnormally high temperatures also increase
, with no change in Δm
1. Abnormally high temperatures also increase ![]() and possibly c
1 if they penetrate below Δl. We may therefore speculate that the contribution of surface density fluctuations to the error in determining mass balance over 2011–13 could be greater than the relatively minor contribution over a period of similar length from 2004 to 2006.
and possibly c
1 if they penetrate below Δl. We may therefore speculate that the contribution of surface density fluctuations to the error in determining mass balance over 2011–13 could be greater than the relatively minor contribution over a period of similar length from 2004 to 2006.
In this case study we found that about 7 years of ice elevation measurements, averaged on the 300 km scale, were required to detect the small trend in ice-sheet mass balance we believe exists along the EGIG line. This is consistent with the findings of a recent analysis of 3 years of CryoSat-2 radar altimetric data over the Antarctic (Reference McMillanMcMillan and others, 2014). In this study a backscatter correction was applied to the radar altimeter heights to account for spurious fluctuations correlated with changes in the echo power (Reference Wingham, Ridout, Scharroo, Arthern and ShumWingham and others, 1998), leaving fluctuations in accumulation as the major contributor to observed ice-sheet elevation change over much of the ice sheet. The observed changes, averaged on the basin scale, were mostly smaller than the expected contribution from these fluctuations. As the authors point out, the 3 year measurement period was too short to detect any long-term mass imbalance in these areas.
Acknowledgements
This project is a contribution to the calibration and validation of the European Space Agency (ESA) CryoSat satellite altimeter and is supported by ESA and by the UK Natural Environment Research Council (NERC) Consortium grant NER/O/S/2003/00620. We are grateful to the NERC Geophysical Equipment Facility and the University of Edinburgh for the loan of Leica GPS systems. Logistic support for the traverses was provided by CH2M HILL Polar Services, G. Somers, J. Pailthorpe, H. Chamberlain, M. Hignell and J. Sweeny gave invaluable assistance in the field and T. Benham provided Figure 1. Finally, we thank R. Arthern for useful discussions and our Scientific Editor, H. Fricker, and two anonymous reviewers for helpful comments.
















