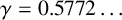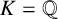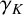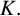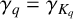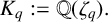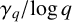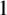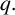1 Introduction
For a number field K, the Euler–Kronecker constant
![]() $\gamma _K$
is given by
$\gamma _K$
is given by
 $$ \begin{align*} \gamma_K:=\lim_{s \to 1^+}\bigg(\frac{\zeta_K'(s)}{\zeta_K(s)} + \frac{1}{s-1}\bigg), \end{align*} $$
$$ \begin{align*} \gamma_K:=\lim_{s \to 1^+}\bigg(\frac{\zeta_K'(s)}{\zeta_K(s)} + \frac{1}{s-1}\bigg), \end{align*} $$
where
![]() $\zeta _K(s)$
is the Dedekind zeta-function for
$\zeta _K(s)$
is the Dedekind zeta-function for
![]() $K.$
The Euler–Mascheroni constant
$K.$
The Euler–Mascheroni constant
![]() $\gamma =0.5772\ldots \!$
is the
$\gamma =0.5772\ldots \!$
is the
![]() $K={\mathbb Q}$
case, where
$K={\mathbb Q}$
case, where
![]() $\zeta _{{\mathbb Q}}(s)=\zeta (s)$
is the Riemann zeta-function. We consider the constants
$\zeta _{{\mathbb Q}}(s)=\zeta (s)$
is the Riemann zeta-function. We consider the constants
![]() $\gamma _q=\gamma _{K_q}$
for cyclotomic fields
$\gamma _q=\gamma _{K_q}$
for cyclotomic fields
![]() $K_q:={\mathbb Q}(\zeta _q)$
, where
$K_q:={\mathbb Q}(\zeta _q)$
, where
![]() $q\in {\mathbb Z}^{+}$
and
$q\in {\mathbb Z}^{+}$
and
![]() $\zeta _q$
is a primitive qth root of unity.
$\zeta _q$
is a primitive qth root of unity.
The recent interest in the distribution of the
![]() $\gamma _q$
is inspired by work of Ihara [Reference Ihara and Ginzburg4, Reference Ihara and Rodier5]. He proposed, for every
$\gamma _q$
is inspired by work of Ihara [Reference Ihara and Ginzburg4, Reference Ihara and Rodier5]. He proposed, for every
![]() $\varepsilon> 0$
, that there is a
$\varepsilon> 0$
, that there is a
![]() $Q (\varepsilon )$
for which
$Q (\varepsilon )$
for which
for every integer
![]() $q \ge Q (\epsilon )$
, where
$q \ge Q (\epsilon )$
, where
![]() $0 < c_1 \le c_2 < 2$
are absolute constants. This conjecture was disproved by Ford et al. in [Reference Ford, Luca and Moree2] assuming a strong form of the Hardy–Littlewood k-tuple conjecture. However, assuming the Elliott–Halberstam conjecture (see [Reference Elliott and Halberstam1]), these same authors also proved that the conjecture holds for almost all primes
$0 < c_1 \le c_2 < 2$
are absolute constants. This conjecture was disproved by Ford et al. in [Reference Ford, Luca and Moree2] assuming a strong form of the Hardy–Littlewood k-tuple conjecture. However, assuming the Elliott–Halberstam conjecture (see [Reference Elliott and Halberstam1]), these same authors also proved that the conjecture holds for almost all primes
![]() $q,$
with
$q,$
with
![]() $c_1 = c_2 = 1.$
We recall the Elliott–Halberstam Conjecture as formulated in terms of the Von Mangoldt function
$c_1 = c_2 = 1.$
We recall the Elliott–Halberstam Conjecture as formulated in terms of the Von Mangoldt function
![]() $\Lambda (n),$
the Chebyshev function
$\Lambda (n),$
the Chebyshev function
![]() $\psi (x)$
and Euler’s totient function
$\psi (x)$
and Euler’s totient function
![]() $\varphi (n).$
$\varphi (n).$
Elliott–Halberstam Conjecture (EH).
If we let
 $$ \begin{align*}E(x;m,a):=\sum_{\substack{p\equiv a \pmod m\\ p\leq x\ {\mathrm{prime}}}} \Lambda(p) -\frac{\psi(x)}{\varphi(m)},\end{align*} $$
$$ \begin{align*}E(x;m,a):=\sum_{\substack{p\equiv a \pmod m\\ p\leq x\ {\mathrm{prime}}}} \Lambda(p) -\frac{\psi(x)}{\varphi(m)},\end{align*} $$
then for every
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $A>0$
, we have
$A>0$
, we have
 $$ \begin{align*}\sum_{m\le x^{1-\varepsilon}}\max_{(a,m) = 1}\lvert{E(x;m,a)}\rvert\ll_{A,\varepsilon} \frac{x}{(\log x)^A}.\end{align*} $$
$$ \begin{align*}\sum_{m\le x^{1-\varepsilon}}\max_{(a,m) = 1}\lvert{E(x;m,a)}\rvert\ll_{A,\varepsilon} \frac{x}{(\log x)^A}.\end{align*} $$
Assuming EH, Ford et al. proved (see [Reference Ford, Luca and Moree2, Theorem 6(i)]), for every
![]() $\varepsilon> 0$
, that
$\varepsilon> 0$
, that
for almost all primes q (that is, the number of exceptional
![]() $q \le x$
is
$q \le x$
is
![]() $o(\pi (x))$
as
$o(\pi (x))$
as
![]() $x\to \infty $
). Here we extend and refine this result to all integers
$x\to \infty $
). Here we extend and refine this result to all integers
![]() $q.$
$q.$
Theorem 1.1. Under EH, for
![]() $Q\rightarrow +\infty $
, we have
$Q\rightarrow +\infty $
, we have
 $$ \begin{align*} \frac{1}{Q}\sum_{Q<q\le 2Q} \lvert{\gamma_q - \log q}\rvert = o(\log Q), \end{align*} $$
$$ \begin{align*} \frac{1}{Q}\sum_{Q<q\le 2Q} \lvert{\gamma_q - \log q}\rvert = o(\log Q), \end{align*} $$
where the sum is over integers q.
Remark 1.2. Theorem 1.1 shows that EH implies that the distribution of
![]() $\gamma _q /\!\log q$
in
$\gamma _q /\!\log q$
in
![]() $[Q, 2Q]$
converges to the one point distribution supported on
$[Q, 2Q]$
converges to the one point distribution supported on
![]() $1$
.
$1$
.
To prove Theorem 1.1, we use the work of Fouvry [Reference Fouvry3] that allowed him to unconditionally prove that
 $$ \begin{align*}\frac{1}{Q}\sum_{Q<q\le 2Q}\gamma_q=\log Q+O(\log\log Q).\end{align*} $$
$$ \begin{align*}\frac{1}{Q}\sum_{Q<q\le 2Q}\gamma_q=\log Q+O(\log\log Q).\end{align*} $$
Our conditional result is a point-wise refinement of Fouvry’s asymptotic formula under EH.
2 Proof of Theorem 1.1
For brevity, we shall assume that the reader is familiar with Fouvry’s paper [Reference Fouvry3]. The key formula is (see (3) of [Reference Fouvry3]) the following expression for
![]() $\gamma _q$
in terms of logarithmic derivatives of Dirichlet L-functions:
$\gamma _q$
in terms of logarithmic derivatives of Dirichlet L-functions:
 $$ \begin{align} \gamma_q = \gamma + \sum_{1<q^*|q\ }\sum_{\chi^*\!\bmod q^*}\frac{L'(1,\chi^*)}{L(1,\chi^*)}. \end{align} $$
$$ \begin{align} \gamma_q = \gamma + \sum_{1<q^*|q\ }\sum_{\chi^*\!\bmod q^*}\frac{L'(1,\chi^*)}{L(1,\chi^*)}. \end{align} $$
Here the inner sum runs over the primitive Dirichlet characters
![]() $\chi ^*$
modulo
$\chi ^*$
modulo
![]() $q^*$
.
$q^*$
.
We follow the strategy and notation in [Reference Fouvry3], which makes use of the modified Chebyshev function
 $$ \begin{align*} \psi(x;q,a):=\sum_{\substack{n\leq x\\ n\equiv a \pmod q}} \Lambda(n), \end{align*} $$
$$ \begin{align*} \psi(x;q,a):=\sum_{\substack{n\leq x\\ n\equiv a \pmod q}} \Lambda(n), \end{align*} $$
and the integral
 $$ \begin{align*} \Phi_{\chi^*}(x):=\frac{1}{x-1}\int_{1}^x \bigg(\sum_{n\leq t}\frac{\Lambda(n)}{n}\chi^*(n)\bigg) \,dt. \end{align*} $$
$$ \begin{align*} \Phi_{\chi^*}(x):=\frac{1}{x-1}\int_{1}^x \bigg(\sum_{n\leq t}\frac{\Lambda(n)}{n}\chi^*(n)\bigg) \,dt. \end{align*} $$
However, we replace the sums
![]() $\Gamma _i(Q)$
and
$\Gamma _i(Q)$
and
![]() $\Gamma _{1,j}(Q)$
defined in [Reference Fouvry3] with the pointwise terms
$\Gamma _{1,j}(Q)$
defined in [Reference Fouvry3] with the pointwise terms
![]() $\gamma _i(q)$
and
$\gamma _i(q)$
and
![]() $\gamma _{1,j}(q)$
. Following the approach in [Reference Fouvry3], which is based on (2.1), we have
$\gamma _{1,j}(q)$
. Following the approach in [Reference Fouvry3], which is based on (2.1), we have
where
 $$ \begin{align*}A(q)&=\sum_{q^*|q} \,{\sum_{\chi^*\mod q^*}} \frac{L'}{L}(1,\chi^*)+\Phi_{\chi^*}(x), \\B(q)&=\sum_{\substack{\chi \bmod q\\ \chi\neq \chi_0}} \Phi_{\chi}(x)-\sum_{q^*|q}\,{\sum_{\chi^*\mod q^*}} \Phi_{\chi^*}(x), \\\gamma_2(q)&=\frac{1}{x-1}\int_1^x \frac{\varphi(q)\psi(t;q,1)-\psi(t)}{t} \,dt, \\\gamma_3(q)&=\frac{1}{x-1}\int_1^x \sum_{\substack{n\leq t\\(n,q) \neq 1}} \frac{\Lambda(n)}{n}\,dt, \\\gamma_{1,1}(q)&=\frac{1}{x-1}\int_1^x\int_1^{\min(q,t)}\bigg(\frac{\varphi(q)\psi(u;q,1)-\psi(u)}{u^2}\,du\bigg)\,dt, \\\gamma_{1,2}(q)&=\frac{1}{x-1}\int_1^x\int_{\min(q,t)}^{\min(x_1,t)}\bigg(\frac{\varphi(q)\psi(u;q,1)-\psi(u)}{u^2}\,du\bigg)\,dt, \\\gamma_{1,3}(q)&=\frac{1}{x-1}\int_1^x\int_{\min(x_1,t)}^t \bigg(\frac{\varphi(q)\psi(u;q,1)-\psi(u)}{u^2}\,du\bigg)\,dt. \end{align*} $$
$$ \begin{align*}A(q)&=\sum_{q^*|q} \,{\sum_{\chi^*\mod q^*}} \frac{L'}{L}(1,\chi^*)+\Phi_{\chi^*}(x), \\B(q)&=\sum_{\substack{\chi \bmod q\\ \chi\neq \chi_0}} \Phi_{\chi}(x)-\sum_{q^*|q}\,{\sum_{\chi^*\mod q^*}} \Phi_{\chi^*}(x), \\\gamma_2(q)&=\frac{1}{x-1}\int_1^x \frac{\varphi(q)\psi(t;q,1)-\psi(t)}{t} \,dt, \\\gamma_3(q)&=\frac{1}{x-1}\int_1^x \sum_{\substack{n\leq t\\(n,q) \neq 1}} \frac{\Lambda(n)}{n}\,dt, \\\gamma_{1,1}(q)&=\frac{1}{x-1}\int_1^x\int_1^{\min(q,t)}\bigg(\frac{\varphi(q)\psi(u;q,1)-\psi(u)}{u^2}\,du\bigg)\,dt, \\\gamma_{1,2}(q)&=\frac{1}{x-1}\int_1^x\int_{\min(q,t)}^{\min(x_1,t)}\bigg(\frac{\varphi(q)\psi(u;q,1)-\psi(u)}{u^2}\,du\bigg)\,dt, \\\gamma_{1,3}(q)&=\frac{1}{x-1}\int_1^x\int_{\min(x_1,t)}^t \bigg(\frac{\varphi(q)\psi(u;q,1)-\psi(u)}{u^2}\,du\bigg)\,dt. \end{align*} $$
To complete the proof, for
![]() $\varepsilon>0$
, we let
$\varepsilon>0$
, we let
![]() $x := q^{100}$
and
$x := q^{100}$
and
![]() $x_1 := q^{1 + \varepsilon }$
. Apart from
$x_1 := q^{1 + \varepsilon }$
. Apart from
![]() $\gamma _{1,1}(q),$
which gives the
$\gamma _{1,1}(q),$
which gives the
![]() $-\log q$
terms in Theorem 1.1, we shall show that these summands are all small.
$-\log q$
terms in Theorem 1.1, we shall show that these summands are all small.
Estimation of
![]() $A(q)$
: By Proposition 1 and Remark (i) of [Reference Fouvry3],
$A(q)$
: By Proposition 1 and Remark (i) of [Reference Fouvry3],
 $$ \begin{align*}\sum_{q=Q}^{2Q} \lvert{A(q)}\rvert =O(Q).\end{align*} $$
$$ \begin{align*}\sum_{q=Q}^{2Q} \lvert{A(q)}\rvert =O(Q).\end{align*} $$
Estimation of
![]() $B(q)$
: For
$B(q)$
: For
![]() $B(q)$
, by (26) and Lemma 3 of [Reference Fouvry3], we simplify
$B(q)$
, by (26) and Lemma 3 of [Reference Fouvry3], we simplify
 $$ \begin{align*}B(q)&=-\frac{1}{x-1}\int_{1}^x \sum_{q^*|q}\ \sum_{\chi^*\,\mod q^*} \sum_{\substack{n \leq t\\(n,q)>1}} \frac{\Lambda(n)\chi^*(n)}{n} \,dt \\&= -\frac{1}{x-1}\int_{1}^x \sum_{q^*|q}\ \sum_{\chi^*\,\mod q^*}\ \sum_{\substack{p^v\leq t\\ p|q}} \frac{\log p\cdot\chi^*(p^v)}{p^v} \,dt \\&= -\frac{1}{x-1}\int_1^x \sum_{q^*|q}\ \sum_{\substack{p^v\leq t \\ p|q\\ p\nmid q^*}}\ \sum_{\substack{d|(p^v-1,q^*)}}\frac{\log p}{p^v} \cdot \varphi(d) \mu\bigg(\frac{q^*}{d}\bigg) \,dt \\&= -\frac{1}{x-1}\int_1^x \sum_{\substack{p^v\leq t\\ p|q}}\ \sum_{\substack{d|p^v-1}}\frac{\log p}{p^v}\cdot\varphi(d) \sum_{\substack{q^*|q\\d|q^*\\ p\nmid q^*}}\mu\bigg(\frac{q^*}{d}\bigg) \,dt. \end{align*} $$
$$ \begin{align*}B(q)&=-\frac{1}{x-1}\int_{1}^x \sum_{q^*|q}\ \sum_{\chi^*\,\mod q^*} \sum_{\substack{n \leq t\\(n,q)>1}} \frac{\Lambda(n)\chi^*(n)}{n} \,dt \\&= -\frac{1}{x-1}\int_{1}^x \sum_{q^*|q}\ \sum_{\chi^*\,\mod q^*}\ \sum_{\substack{p^v\leq t\\ p|q}} \frac{\log p\cdot\chi^*(p^v)}{p^v} \,dt \\&= -\frac{1}{x-1}\int_1^x \sum_{q^*|q}\ \sum_{\substack{p^v\leq t \\ p|q\\ p\nmid q^*}}\ \sum_{\substack{d|(p^v-1,q^*)}}\frac{\log p}{p^v} \cdot \varphi(d) \mu\bigg(\frac{q^*}{d}\bigg) \,dt \\&= -\frac{1}{x-1}\int_1^x \sum_{\substack{p^v\leq t\\ p|q}}\ \sum_{\substack{d|p^v-1}}\frac{\log p}{p^v}\cdot\varphi(d) \sum_{\substack{q^*|q\\d|q^*\\ p\nmid q^*}}\mu\bigg(\frac{q^*}{d}\bigg) \,dt. \end{align*} $$
We note that the innermost sum
 $$ \begin{align*}\sum_{\substack{q^*|q\\ d|q^* \\ p\nmid q^*}}\mu\bigg(\frac{q^*}{d}\bigg)\end{align*} $$
$$ \begin{align*}\sum_{\substack{q^*|q\\ d|q^* \\ p\nmid q^*}}\mu\bigg(\frac{q^*}{d}\bigg)\end{align*} $$
is always
![]() $0$
or
$0$
or
![]() $1$
, so we conclude that
$1$
, so we conclude that
![]() $B(q) \leq 0$
for any q. Proposition 2 of [Reference Fouvry3] gives
$B(q) \leq 0$
for any q. Proposition 2 of [Reference Fouvry3] gives
 $$ \begin{align*}\sum_{q=Q}^{2Q}B(q)=O(Q),\end{align*} $$
$$ \begin{align*}\sum_{q=Q}^{2Q}B(q)=O(Q),\end{align*} $$
and so we have
 $$ \begin{align*}\sum_{q=Q}^{2Q}\lvert{B(q)}\rvert =O(Q).\end{align*} $$
$$ \begin{align*}\sum_{q=Q}^{2Q}\lvert{B(q)}\rvert =O(Q).\end{align*} $$
Estimation of
![]() $\gamma _2(q)$
: By Lemma 8 of [Reference Fouvry3], uniformly in Q with
$\gamma _2(q)$
: By Lemma 8 of [Reference Fouvry3], uniformly in Q with
![]() $u\geq 1,$
we have
$u\geq 1,$
we have
 $$ \begin{align*}\sum_{q=Q}^{2Q} \psi(u;q,1) \ll u.\end{align*} $$
$$ \begin{align*}\sum_{q=Q}^{2Q} \psi(u;q,1) \ll u.\end{align*} $$
Therefore,
 $$ \begin{align*}\sum_{q=Q}^{2Q} \lvert{\varphi(q)\psi(t;q,1)-\psi(t)}\rvert =O(Qt),\end{align*} $$
$$ \begin{align*}\sum_{q=Q}^{2Q} \lvert{\varphi(q)\psi(t;q,1)-\psi(t)}\rvert =O(Qt),\end{align*} $$
and so we conclude that
 $$ \begin{align*}\sum_{q=Q}^{2Q} \lvert{\gamma_{2}(q)}\rvert = O(Q).\end{align*} $$
$$ \begin{align*}\sum_{q=Q}^{2Q} \lvert{\gamma_{2}(q)}\rvert = O(Q).\end{align*} $$
Estimation of
![]() $\gamma _3(q)$
: By definition,
$\gamma _3(q)$
: By definition,
![]() $\gamma _3$
is positive, so by (36) of [Reference Fouvry3],
$\gamma _3$
is positive, so by (36) of [Reference Fouvry3],
 $$ \begin{align*}\sum_{q=Q}^{2Q} \lvert{\gamma_{3}(q)}\rvert =O(Q).\end{align*} $$
$$ \begin{align*}\sum_{q=Q}^{2Q} \lvert{\gamma_{3}(q)}\rvert =O(Q).\end{align*} $$
Estimation of
![]() $\gamma _{1,1}(q)$
: Since
$\gamma _{1,1}(q)$
: Since
![]() $\psi (u;q,1)=0$
for
$\psi (u;q,1)=0$
for
![]() $u<q$
, we have
$u<q$
, we have
 $$ \begin{align*} \gamma_{1,1}(q)=-\frac{1}{x-1}\int_1^x \bigg(\int_1^{\min(q,t)}\frac{\psi(u)}{u^2} \,du \bigg) \,dt. \end{align*} $$
$$ \begin{align*} \gamma_{1,1}(q)=-\frac{1}{x-1}\int_1^x \bigg(\int_1^{\min(q,t)}\frac{\psi(u)}{u^2} \,du \bigg) \,dt. \end{align*} $$
Dividing both sides of (41) of [Reference Fouvry3] by Q,
Estimation of
![]() $\gamma _{1,2}(q)$
: By the same proof as (42) of [Reference Fouvry3], we have
$\gamma _{1,2}(q)$
: By the same proof as (42) of [Reference Fouvry3], we have
 $$ \begin{align*} \sum_{q=Q}^{2Q} \lvert{\gamma_{1,2}(q)}\rvert \ll \varepsilon Q\log Q. \end{align*} $$
$$ \begin{align*} \sum_{q=Q}^{2Q} \lvert{\gamma_{1,2}(q)}\rvert \ll \varepsilon Q\log Q. \end{align*} $$
Summing the above estimates, we conclude unconditionally that
 $$ \begin{align*} \frac{1}{Q}\sum_{q=Q}^{2Q} \lvert{\gamma_q-\log q}\rvert =\frac{1}{Q}\sum_{q=Q}^{2Q} \lvert{\gamma_{1,3}(q)}\rvert + O(\varepsilon \log Q). \end{align*} $$
$$ \begin{align*} \frac{1}{Q}\sum_{q=Q}^{2Q} \lvert{\gamma_q-\log q}\rvert =\frac{1}{Q}\sum_{q=Q}^{2Q} \lvert{\gamma_{1,3}(q)}\rvert + O(\varepsilon \log Q). \end{align*} $$
Estimation of
![]() $\gamma _{1,3}(q)$
: If we assume Conjecture EH holds, then we have (as in Lemma 7 of [Reference Fouvry3]) that
$\gamma _{1,3}(q)$
: If we assume Conjecture EH holds, then we have (as in Lemma 7 of [Reference Fouvry3]) that
 $$ \begin{align*} \sum_{\substack{q\le 2Q\\ (q,a)=1}}\varphi(q)\bigg\vert{\psi(x;q,a)-\frac{\psi(x)}{\varphi(q)}}\bigg\vert=O_A\big(Qx(\log x)^{-A+2}\big). \end{align*} $$
$$ \begin{align*} \sum_{\substack{q\le 2Q\\ (q,a)=1}}\varphi(q)\bigg\vert{\psi(x;q,a)-\frac{\psi(x)}{\varphi(q)}}\bigg\vert=O_A\big(Qx(\log x)^{-A+2}\big). \end{align*} $$
Therefore,
 $$ \begin{align*} \frac{1}{Q} \sum_{q=Q}^{2Q}\lvert{\gamma_{1,3}(q)}\rvert=O_{\epsilon,A}(\log^{-A} Q). \end{align*} $$
$$ \begin{align*} \frac{1}{Q} \sum_{q=Q}^{2Q}\lvert{\gamma_{1,3}(q)}\rvert=O_{\epsilon,A}(\log^{-A} Q). \end{align*} $$
By combining these estimates, we obtain the main result
 $$ \begin{align*} \frac{1}{Q}\sum_{q=Q}^{2Q}\lvert{\gamma_q-\log q}\rvert=o(\log Q). \end{align*} $$
$$ \begin{align*} \frac{1}{Q}\sum_{q=Q}^{2Q}\lvert{\gamma_q-\log q}\rvert=o(\log Q). \end{align*} $$
Acknowledgements
The authors thank Pieter Moree for helpful discussions regarding his work with Ford and Luca. We thank the referee for suggestions that improved the exposition in this paper.