An integrated Structure-from-Motion and time-lapse technique for quantifying ice-margin dynamics

Abstract

Fine resolution topographic data derived from methods such as Structure from Motion (SfM) and Multi-View Stereo (MVS) have the potential to provide detailed observations of geomorphological change, but have thus far been limited by the logistical constraints of conducting repeat surveys in the field. Here, we present the results from an automated time-lapse camera array, deployed around an ice-marginal lake on the western margin of the Greenland ice sheet. Fifteen cameras acquired imagery three-times per day over a 426 day period, yielding a dataset of ~19 000 images. From these data we derived 18 point clouds of the ice-margin across a range of seasons and successfully identified calving events (ranging from 234 to 1475 m² in area and 815–8725 m³ in volume) induced by ice cliff undercutting at the waterline and the collapse of spalling flakes. Low ambient light levels, locally reflective surfaces and the large survey range hindered analysis of smaller scale ice-margin dynamics. Nevertheless, this study demonstrates that an integrated SfM-MVS and time-lapse approach can be employed to generate long-term 3-D topographic datasets and thus quantify ice-margin dynamics at a fine spatio-temporal scale. This approach provides a template for future studies of geomorphological change.

1. INTRODUCTION

The number and area of ice-marginal lakes are increasing globally in response to contemporary deglaciation (Carrivick and Tweed, 2013). Ice-marginal lakes can influence the dynamics of glaciers via a series of thermo-mechanical controls, including: enhanced basal water pressure, buoyancy and sliding (e.g. Anderson and others, 2005; Riesen and others, 2010; Tsutaki and others, 2011); terminus floatation (e.g. Naruse and Skvarca, 2000; Mayer and others, 2008; Tsutaki and others, 2013); and perhaps most importantly, the initiation of calving (Warren and others, 2001; van der Veen, 2002). Their development often leads to the formation of a positive feedback mechanism whereby ice-margin recession promotes lake expansion, which further accelerates glacier mass loss (e.g. Kirkbride, 1993; Warren and others, 1995; Boyce and others, 2007; Trussel and others, 2013). However, the effects of ice-marginal lakes on glacier dynamics remain poorly understood and tend to be omitted from mechanistic models of glacier change and sea-level rise because of a scarcity of quantitative field data from calving ice margins (Benn and others, 2007).

Existing satellite and airborne remote-sensing approaches are generally unable to capture the high spatio-temporal variability of physical changes at lacustrine ice margins. Satellite-based techniques have been used extensively to study ice-margin dynamics, structure and extent (Quincey and Luckman, 2009), but the trade-off between spatial resolution and frequency of repeat survey can prevent the acquisition of imagery at the optimal spatial and temporal scales for the investigation of ice-marginal processes. Airborne remote sensing can provide imagery at much finer spatial, spectral and temporal resolutions (Abdalati and others, 2001), but the expense of repeat overflights often precludes acquiring a dense dataset of observations. Similarly, many field-based techniques encounter spatial and temporal limitations. For example, repeat optical or dGPS surveys of stakes installed on glacier termini are commonly employed to measure changes in ice-margin extent, elevation and velocity (e.g. Anderson and others, 2005; Sugiyama and others, 2007; Tsutaki and others, 2011). However, such surveys necessarily possess a coarse spatial resolution and may only be resurveyed weekly or seasonally. Where frequent (i.e. sub-daily) resurveys of stakes have been reported these surveys are rarely sustained beyond several weeks (e.g. Walder and others, 2006; Podrasky and others, 2014). In addition, the spatial coverage of physical surveys at ice margins is often restricted by zones of deep crevassing and extensive calving activity.

Ground-based remote-sensing techniques provide an alternative approach for the collection of high-resolution topographic data from inaccessible and dangerous locations. Most notably, the advent of terrestrial laser scanning (TLS) has enabled the rapid generation of high-accuracy topographic datasets, with fine (sub-metre) spatial resolution, broad spatial coverage and sub-daily temporal capability. Recent applications of TLS in glaciology include the monitoring of glacier surface melt (Gabbud and others, 2015), mass balance (Fischer and others, 2016), thermo-erosional notch propagation (Petlicki and others, 2015) and the quantification of aerodynamic surface roughness (Smith and others, 2016). However, the necessity for manual on-site operation of TLS limits its suitability for capturing ice-marginal lake/glacier interactions, particularly calving activity (the timing of which is largely unpredictable), or for generating fine temporal resolution datasets of ice-margin dynamics across an entire season. Besides the considerable expense of the equipment and its associated software, the application of TLS in ice-marginal environments is further constrained by significant reductions in point density and point accuracy caused by poor laser reflection within near-infrared wavelengths from wet or melting surfaces (e.g. Deems and others, 2013; Gabbud and others, 2015; Petlicki and others, 2015).

In recent years advances in Structure-from-Motion (SfM) and Multi-View Stereo (MVS) techniques have enabled the generation of topographic datasets with spatial resolutions and accuracies comparable to, and in many cases surpassing, those generated via traditional photogrammetry, ground-based TLS and airborne Light Detection and Ranging (LiDAR) (Westoby and others, 2012; Fonstad and others, 2013; Smith and others, 2015). Key advantages of the SfM-MVS approach are its affordability, fast data processing times and ease of data acquisition – requiring only a consumer grade digital camera or mobile phone (Micheletti and others, 2015). SfM-MVS techniques have recently been used to measure seasonal changes in glacier dynamics (e.g. Whitehead and others, 2013; Immerzeel and others, 2014) and to investigate discrete tidewater calving events (Ryan and others, 2015). However, in common with TLS surveys, glacial SfM-MVS-based studies are limited by the logistical constraints of collecting repeat surveys in the field and thus typically comprise week-long to month-long datasets at best. Furthermore, the infrequent acquisition of data can increase the superimposition and coalescence of geomorphological events (e.g. Abellán and others, 2014) and is therefore a major obstacle to identifying and isolating mechanistic drivers and triggers of geomorphological change.

Time-lapse photography has been extensively employed in glaciology to generate long-term (seasonal – annual) datasets of glacier change (e.g. Amundson and others, 2010; Danielson and Sharp, 2013; Murray and others, 2015; Petlicki and others, 2015) and can facilitate the acquisition of imagery at fine-temporal resolutions. Consequently, the integration of SfM-MVS and time-lapse techniques has remarkable potential for generating long-term 3-D topographic datasets, and hence revealing mechanistic drivers and triggers of geomorphological change. However, to date a combined approach remains relatively unexplored, in part due to the perceived difficulties of establishing and maintaining an automated camera network capable of acquiring the necessary image datasets (e.g. Eltner and others, 2016).

This study therefore aims to demonstrate how an integrated SfM-MVS and time-lapse approach can be employed to acquire and analyse fine spatio-temporal resolution datasets of ice-margin dynamics. We deploy the method at a dynamic lacustrine-terminating margin of the Greenland ice sheet to assess the viability of the method in a hostile and challenging environment.

2. STUDY SITE

This study focuses on an ice-marginal lake (67°08′10″N, 50°04′25″W) adjacent to the northern margin of Russell Glacier, which is a predominately land-terminating outlet glacier in western Greenland (Fig. 1). The ~1 km² lake is impounded by a 1.5 km long ice dam, and is notable for a series of well-documented drainage events in the summer months (e.g. Sugden and others, 1985; Russell, 1989; Mernild and Hasholt, 2009; Russell and others, 2011; Mikkelsen and others, 2013). The freeboard of the ice margin ranges from 10 to 60 m depending on the elevation of the lake surface. Analysis of satellite radar interferometry indicates ice surface velocities in the vicinity of the ice-dammed lake are ~30 ma⁻¹ (Rignot and Mouginot, 2012), while field surveys of basal ice velocities along the northern margin of Russell Glacier are in the range 20–43 ma⁻¹ (Chandler and others, 2005).

Fig. 1. Study location on the northern margin of Russell Glacier, western Greenland (inset) and camera array geometry. Heavier blue shading represents increased camera overlap.

3. METHODS

SfM-MVS employs digital photogrammetric and computer vision methods to simultaneously resolve camera position and 3-D feature geometry using multiple digital photos as the primary input (Snavely and others, 2006; Fonstad and others, 2013). The output of the technique is a point cloud, comprising identifiable features from the image dataset, which can be scaled and georeferenced using ground control points (GCPs) situated within the survey area or by using measurements of camera positions during image acquisition. Comprehensive reviews of the underlying principles of SfM-MVS, and its recent applications in geographical research are presented in Smith and others (2015), Eltner and others (2016) and Carrivick and others (2016). Typically, image acquisition for SfM-MVS is performed manually using a single camera carried around the survey reach on foot or mounted to an airborne platform (e.g. unmanned aerial vehicle, kite, gyrocopter). Consequently, the scheduling and duration of field seasons acts as an arbitrary constraint on image acquisition and therefore data collection. Additionally, James and Robson (2014a) noted that single camera SfM-MVS image acquisition is impractical for capturing rapid, dynamic events, where high rates of change instead necessitate continuous, simultaneous image collection from multiple cameras.

3.1. Time-lapse camera array setup

In an effort to extend the duration of image acquisition indefinitely we devised and installed an automated time-lapse ‘camera array’ at the Russell Glacier study site. The aim of the array was to develop an autonomous, affordable and low-maintenance technique for prolonged high-frequency SfM-MVS image acquisition, capable of withstanding the extremes of the Greenland climate. The array was populated with 15 LtL Acorn 5210A 12 megapixel (interpolated from 5 megapixel) trail cameras with a 6 mm focal length and 52° angle of view. The camera model was selected for its programmability, high image quality, multiple power sources and – given the high number of cameras required – affordability (costing ~£120 each). Power was supplied internally using eight disposable lithium AA batteries, which were favoured because of their low self-discharge and capacity to remain operative in temperatures as low as −40 °C. Photovoltaic cells were discounted as a power source due to the minimal midwinter daylight at 67° north and the high likelihood of burial by snow. Fluctuations in ambient lighting conditions and shadows during conventional SfM-MVS surveys can interfere with the keypoint matching stage of the SfM process (James and Robson, 2012; Bemis and others, 2014). Consequently, camera clocks were synchronised manually to an external handheld GPS receiver and programmed to trigger simultaneously at 09:00, 13:00 and 17:00 hours daily. The timing of image acquisition was designed to minimise battery use (thereby extending the operational longevity of the camera array) and make optimal use of the available daylight during the winter months.

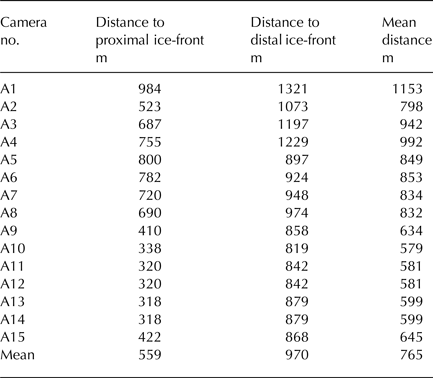
The camera array was installed along the lake shore in the summer of 2014, with a range of orthogonal (side looking) and oblique (front looking) viewpoints employed to maximise coverage of the ice margin and mitigate the ‘doming’ effect associated with near parallel view orientations (James and Robson, 2014b) (Fig. 1). The positions of some cameras were adjusted in response to quality control of the setup, which was performed in the field by downloading the preliminary imagery to a laptop running SfM-MVS software and generating test point clouds. A more even distribution of cameras around the lake was not possible because the orientation and dip of local topography diminished viewsheds of the ice margin along sections of the shore. However, each camera was individually orientated towards the ice margin so that its field of view possessed at least 30% overlap with that of another camera. The average viewing distance of the cameras to the active ice front was 765 m (Table 1). In contrast to other static camera set-ups we did not use tripods, camera mounts or enclosures to stabilise or protect the cameras (cf. Rivera and others, 2012; Danielson and Sharp, 2013; Rosenau and others, 2013). Instead the cameras were stationed on the ground and buttressed laterally and overhead with boulders to minimise movement and offer protection from the weather and wildlife (Fig. 2). The camera array operated continuously for a total of 426 days, extending from 27 July 2014 to 24 September 2015. The only maintenance performed during the operating period occurred on 22–23 May 2015 and comprised the download of existing imagery, replacement of batteries and the reset of one camera, which had been dislodged from its station.

Fig. 2. Example of a trail camera installation at the lake shore.

Table 1. Survey range between the cameras and ice margin

3.2. Ground control points

A network of 18 GCPs, consisting of stable landscape features (e.g. large boulders, exposed bedrock bluffs) located immediately either side of the ice margin was surveyed using a Leica System 500 dGPS in July 2014 to enable georeferencing of the point clouds derived from the image dataset. We used a temporary base station mounted ~5 km from the lake. Its position was obtained by post-processing 10 h of observations recorded at 1 minute intervals against the Kellyville International Geodetic System network continuous receiver, yielding a 3-D accuracy of ±0.01 m. GCPs around the lake margin were then surveyed in real time static mode (using the geometric mean of 120 static readings) and post-processed against the base-station, yielding an overall 3-D accuracy of ±0.05 m. Owing to the dynamic nature of the field site GCPs could not be located on the ice margin itself, and dynamic lighting conditions dictated that in many surveys only a subset of GCPs could be identified in the camera imagery.

3.3. Point cloud processing

Following recovery of the cameras in September 2015 the image dataset was used to generate point clouds of ice-margin topography using the commercial software Agisoft Photoscan Professional v.1.2.5 (available from http://www.agisoft.com), with further analysis performed in the open source software CloudCompare v.2.7 (CloudCompare, 2016). Owing to the limited GCP coverage across the ice front, pre-calibration of camera parameters was undertaken using a calibrated target. Focal length, principal point and three radial distortion parameters were included in the final camera model. Camera calibration parameters and imagery were imported into Agisoft Photoscan where the lake and sky were masked from the remaining workflow prior to the running of bundle adjustment algorithms to construct the sparse point clouds. Reprojection filters were then applied to remove the ~10% of points with the lowest localisation accuracies (as determined by the least squares minimisation of errors within the bundle adjustment process). Reconstruction uncertainty filters were also used to identify noise in the clouds induced by the relatively small baselines between some neighbouring cameras, resulting in a further ~10% of points being removed. The sparse clouds were then scaled and georeferenced by importing GCP coordinates and marking visible GCPs in the camera imagery, before running MVS algorithms to generate the final dense point clouds. In this application, GCPs were used only to scale and georeference the cloud and were not used to refine camera models and determine cloud shape (so-called ‘optimization’ within Agisoft Photoscan).

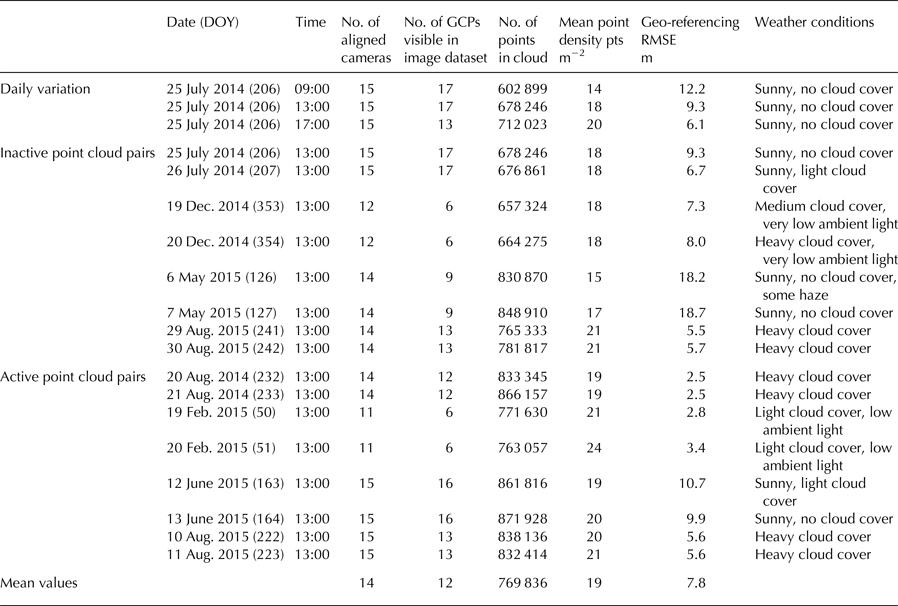
To demonstrate the potential of the approach, 18 point clouds were chosen to reflect different seasons (and thus weather and ambient lighting conditions), GCP distributions (which were also largely a function of illumination) and periods of ice-front activity and inactivity (Table 2). Initial analysis of the point clouds indicated significant daily variability in point cloud parameters, particularly point cloud density and GCP visibility. Point clouds derived from 13:00 images were selected for all subsequent analyses as they returned both high point densities and high GCP visibility. Image sets were paired and categorised as being ‘active’ i.e. some change in ice-front morphology was observed, and ‘inactive’ i.e. no change in morphology was observed. Distances between cloud pairs were subsequently computed in CloudCompare using the multi-scale model-to-model cloud comparison (M3C2) algorithm developed by Lague and others (2013). The M3C2 tool was used to determine surface normals along the ice-front and subsequently calculate distances between core points subsampled from the input clouds. Normal and projection scales of 40 and 6 m, respectively, were applied to minimise the influence of local surface roughness along the ice-front (which produced highly complex normals at lower scales) while maintaining the efficiency of the calculation. Provisional differencing of the inactive point cloud pairs revealed significant regions of change in peripheral survey areas, notably the stable lake shores (Fig. 3). Analysis of the camera array geometry indicated that the observed changes corresponded with low camera overlap (Fig. 4); consequently, all point clouds were trimmed to the sector of ice-front possessing greatest camera coverage prior to further analysis.

Fig. 3. Schematic of point cloud differencing workflow. (a & b) Point clouds from 13:00 on 25 and 26 July 2014 respectively; (c) the resultant output of the M3C2 cloud differencing algorithm; and (d) the M3C2 output trimmed to the sector of ice-front possessing greatest camera coverage (note the black square denotes the location of 30 m² patch). The differencing of inactive cloud pairs provides a measure of internal consistency in cloud geometry. The changes detected on the stable lake shores are indicative of poor camera coverage in peripheral survey areas.

Fig. 4. Aerial view of dense point cloud derived from imagery acquired at 13:00 on 25 July 2014, illustrating the spatial extent of cloud reconstruction and camera overlap. Black bars delineate the trimmed section of ice margin used for analysis.

Table 2. Seasonal variations in point cloud parameters

The real-world accuracy of point clouds is conventionally measured against an independently derived reference dataset. However, an assessment of cloud accuracy is not a necessity for our technique, because differences between clouds can still be measured provided there is internal consistency in cloud geometry. To provide an assessment of cloud consistency the means and standard deviations of distances between inactive point cloud pairs were measured along the trimmed ice margin (Fig. 3d; Table 3). Analysis of the data showed that in the worst case scenario 95% (±2 standard deviations) of distances between inactive point cloud pairs were within 3.72 m of the mean recorded change. Consequently, we adopted a threshold of 4 m to distinguish statistically significant changes from noise when differencing the active point cloud pairs. This cautious approach is commensurate with the scale of change that this SfM survey is designed to detect, as even relatively minor lacustrine calving events are typically tens to hundreds of cubic metres in volume. Further standard deviation measurements were taken from a 30 m² patch in the centre of the ice-front (Fig. 3d), revealing that a detection threshold of ~2 m could be viable for the sections of the point cloud with greatest camera coverage (Table 3). The 2.5-D Volume tool in CloudCompare was subsequently used to calculate the volumes of any changes lying beyond the respective 2 and 4 m error thresholds. Volumes were computed by cropping the respective cloud pairs to the region of change, orienting them to an arbitrary plane and projecting a grid (with a cell size of 1 m²) through a rasterised copy of the cropped clouds.

Table 3. Standard deviations and mean changes for inactive point cloud pairs

4. RESULTS

4.1. Camera array viability and point cloud construction

Analysis of the image dataset illustrates the capacity of the automated camera array setup for capturing long-term (> annual) records of ice-margin change. The cameras recorded ~19 000 images of the ice margin over a 426 day period and remained fully operative despite repeated burial by snow and local temperatures reaching −33 °C in February 2015. The cameras remained in position for the duration of the study, with the exception of camera A2, which was dislodged from its position in the late summer of both 2014 and 2015, most likely by wildlife. Relatively minor drifts in camera orientation were also observed over the study period in response to freezing and thawing ground ice. The availability of cameras and GCPs for point cloud generation fluctuated in the winter months in response to snowfall (Table 2). Cameras were able to continue capturing viable imagery in the aftermath of moderate snowfall (<10 cm depth), though light snowfalls were often sufficient to prevent the identification of GCPs in the camera imagery. To a lesser extent some GCPs were also obscured in the spring and summer months by vegetation growth immediately in the foreground of some camera stations.

The construction of ice-margin point clouds was viable at least once per day for 93.5% (398 days) of the study period, with burial by snow or poor weather conditions (including mist, rain and snowfall) obscuring the ice margin on the remaining days. The longest period with no viable images for point cloud generation occurred between 23 and 29 of December 2014. The relatively small number of images employed in the SfM-MVS analysis expedited data processing, with ~2.5 h required to complete the Agisoft Photoscan workflow for each point cloud (using 8 GB of RAM and an Intel i5 quad-core processor operating at 3.2 GHz). The most time consuming stage of the workflow was the manual identification of GCPs in the camera imagery, without which dense point cloud construction would have been possible on a sub-hour timescale. The spatial extent of the generated point clouds comprised the majority of the lacustrine ice margin and terrain immediately adjacent to the eastern and western lake shores (Figs. 4, 5). Reconstruction of the westernmost section of the lacustrine ice margin was prohibited by poor camera coverage, which may explain the relatively high georeferencing errors given that GCPs were also located at the edges of the survey area (Table 2). Generation of the ice-surface topography was limited by extensive crevassing along the ice margin (Figs. 3, 5).

Fig. 5. (a) Cropped image of ice margin recorded at 13:00 on 25 July 2014 from camera A12; (b) corresponding view of the derived dense-point cloud; and (c) enlargement of area bounded by dashed line in panel b, with detail illustrating the effect of crevasse peaks on point cloud reconstruction of the ice-sheet surface. Note for scale the vertical height of the ice-margin is ~50 m.

4.2. Point cloud parameters

Point cloud parameters exhibited notable variance throughout the study, with the number of points in each ice-front ranging from ~600 000 to ~870 000 and ice-front point densities falling between 14 and 24 points per m² (Table 2). Ambient lighting, weather conditions and the elevation of the lake surface all acted as controls on point cloud size and density. Smaller point clouds, with lower point densities were generally associated with low ambient light availability (particularly in midwinter) or elevated lake levels thereby minimising the subaerial portion of the ice margin. Larger point clouds and point densities were generally associated with brighter conditions and/or low lake levels. The impact of ambient light levels on point cloud alignment was investigated by superimposing successive point clouds sharing identical processing parameters and weather conditions, and with no visible changes in ice-front position or morphology. Overlaying all three clouds from 25 July 2014 revealed close alignment between the 13:00 and 17:00 clouds (mean change 0.48 m), however the 09:00 cloud was misaligned with the 13:00 and 17:00 clouds by a mean distance of −5.71 and −5.15 m, respectively. The sole difference in the image datasets used to derive the three clouds was the illumination of the ice margin, which was in full sun at 17:00, partially shaded at 13:00 and both heavily shaded and exhibiting strong glare from the lake surface at 09:00 (cf. imagery in Fig. 6a). Analysis of the feature matches detected during sparse point cloud construction demonstrated that poor illumination of the ice margin corresponded with fewer accepted feature matches (Fig. 6). Additionally, contrasting weather conditions (and thus light levels) were also observed to cause poor alignment between point cloud pairs. Consequently, measurements of ice-margin change via point cloud differencing were limited to point cloud pairs exhibiting consistent weather conditions and ambient lighting.

Fig. 6. (a) Images recorded by camera A11 on 25 July 2014 showing daily variation in lighting conditions and accepted and rejected feature matches (blue and white circles respectively); (b) corresponding histograms of reprojection error for accepted feature matches; and (c) reprojection error for individual points in the sparse point clouds derived from the 09:00 (i), 13:00 (ii) and 17:00 (iii) imagery.

In the absence of an independently derived reference dataset, analysis of the georeferencing RMSE (the error metric generated by the scaling and georeferencing of a point cloud) can be used as an approximate gauge of model quality. Table 2 illustrates that georeferencing RMSEs varied substantially across the study, with values for individual point clouds ranging from 2.5 to 18.7 m. The data show no significant relationship between georeferencing RMSE and the number of aligned cameras, or the number of visible GCPs. Instead, higher RMSEs generally correspond with bright, clear weather conditions, whereas low RMSEs are associated with lower ambient light levels caused by heavy cloud cover or the low elevation of the winter sun (Table 2).

4.3. Quantification of ice-margin dynamics

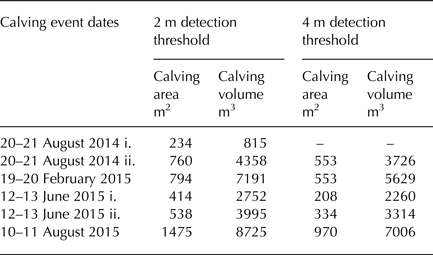
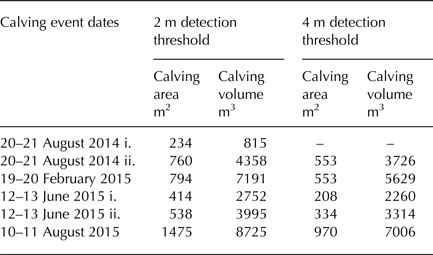
The differencing of active point cloud pairs effectively identified examples of ice-margin change throughout the operation of the camera array, including calving events induced by ice cliff undercutting at the waterline (Fig. 7a), the collapse of spalling flakes along the ice-front (Figs. 7b–d), and the resultant accumulation of ice debris on the frozen lake surface (Figs. 7b, c). The detection of smaller magnitude ice-margin dynamics (e.g. advance/recession of the ice-front) was prohibited by the relatively large magnitude of the detection threshold and the short periods between image acquisition. The 2 m threshold was sufficient to closely delineate most calving activity, whereas the higher 4 m threshold omitted thin sections of ice peripheral to some calving events, and in one case, an event in its entirety (e.g. Fig. 7a (i)). Analysis of the point clouds derived from midwinter imagery (Fig. 7b) indicated that the lower 2 m threshold may lie beyond the margin of error when ambient light levels are low and/or the number of cameras available for alignment is limited (Table 2). Observed calving events at the 2 m threshold ranged from 234 to 1475 m² in area and 815–8725 m³ in volume (Table 4). Calving area measurements were more sensitive than volume measurements to changes in the detection threshold, with an increase in threshold to 4 m prompting mean reductions in calving area and volume of ~60 and ~25%, respectively.

Fig. 7. Camera imagery and M3C2 outputs for calving events identified in the active point cloud pairs. Events are dated: (a) 20–21 August 2014; (b) 19–20 February 2015; (c) 12–13 June 2015; and (d) 10–11 August 2015. Note for scale the vertical height of the ice margin is ~50 m.

Table 4. Area and volume calculations for calving events displayed in Fig. 7. Note ‘i’ and ‘ii’ denote distinct calving events detected in the same active point cloud pair (see Fig. 7)

5. DISCUSSION

The above data effectively indicate that an integrated SfM-MVS and time-lapse approach can be used to analyse ice-margin dynamics at a hitherto unprecedented spatio-temporal resolution. However, there are significant challenges associated with generating prolonged 3-D topographic records of ice margins in the High Arctic. The parameters that influence point cloud coverage, density and accuracy are explored here, along with some strategies for improving point cloud quality.

5.1. Camera array geometry

At the most fundamental level, the geometry of the camera array exerts considerable control over point cloud accuracy, coverage and density. A limited number of camera stations with poor distribution can cause distortions and gaps in point clouds (Bemis and others, 2014), while parallel image orientations can induce a systematic doming effect (James and Robson, 2014b). Good spatial coverage and convergent image geometries (where cameras are orientated towards the feature of interest) are therefore necessary to mitigate against such systematic errors. However, the angle of convergence is critical because angles of >25° between adjacent camera stations can prevent the identification of keypoint correspondences because of apparent dissimilarities in surface texture (Bemis and others, 2014; Smith and others, 2015). The setup of the camera array at Russell Glacier facilitated convergent image acquisition, with the majority of cameras orientated towards the centre of the ice margin (Fig. 1). However, local topography prevented a uniform distribution of camera stations along the lake shore. Instead cameras were stationed in three primary groups (A1–A4; A5–A8; A8–A15), which had low intra-group angular changes between camera stations, but necessarily possessed significant inter-group angular changes, most notably between groups A1–A4 and A5–A8 (Fig. 1). Consequently, analysis of the keypoint matching stage of the workflow revealed that cameras A1–A4 contributed significantly fewer matches to the final point cloud, a problem later exacerbated by the loss of camera A2. The use of camera arrays therefore requires careful consideration of camera station distribution in order to minimise angles between neighbouring cameras; in some cases it may be preferable to limit the desired area of coverage, rather than deploy an isolated camera or group of cameras. In addition, the refinement of camera array geometry can be facilitated prior to its automation by the production of test point clouds in the field and careful analysis of the keypoint matches returned by each camera in the setup.

5.2. Ambient lighting effects

The poor alignment of point cloud pairs in response to divergent ambient lighting or weather conditions was expected. Shadows are well documented to reduce key point matching in affected areas (Bemis and others, 2014; Gienko and Terry, 2014) and increase absolute error in point clouds (Gómez-Gutiérrez and others, 2014). In addition to shadows, glare and high-contrast imagery are also unfavourable for point cloud accuracy and density (Fig. 6). Illumination of the feature of interest is therefore of particular importance to time-lapse SfM-MVS studies, where complications arise due to variable weather conditions and solar elevation. This challenge is exacerbated by the highly reflective surfaces (ice and water) typical in glacial environments, particularly when the sun is low. Consequently, prolonged time-lapse studies in glacial environments will frequently contend with unfavourable lighting for image acquisition, therefore the setup of camera stations should follow careful consideration of: (i) the orientation of the cameras in relation to the feature of interest; (ii) the influence of local topography on shading; (iii) the path of the sun (daily and seasonally); (iv) prevailing weather conditions; and (v) locally reflective surfaces. One method to mitigate unfavourable conditions would be to factor redundancy into the timings for image acquisition by deliberately oversampling (e.g. collecting images at twice the rate desired); though it is important to consider the resultant impact on camera battery life and memory capacity.

It should also be noted that achieving all the desired qualities of a point cloud (e.g. good spatial coverage, high point density and low georeferencing RMSE) is likely to be a significant challenge for surveys of this nature. For example, our data tentatively indicate that low georeferencing RMSEs are achieved under lower ambient light levels, whereas larger clouds with greater point densities are associated with brighter conditions. Prioritising which of these qualities takes precedence should be determined by the objectives of the survey. For example, the minimisation of georeferencing RMSEs should take precedence where the real-world accuracy of a point cloud is paramount, whereas point cloud size and density can be prioritised in situations where the quantification of relative changes between successive clouds (generated from the same survey setup) is the primary objective.

5.3. Point cloud error

Isolation of individual error sources in SfM-MVS point clouds is challenging due to the number of confounding variables that determine accuracy (Smith and others, 2015), relating to both survey design and underlying photogrammetric methods (James and others, 2017). The error inherent in topographic reconstruction is closely related to the distance between the feature of interest and the sensor, with conventional SfM-MVS surveys demonstrating a linear degradation of precision with increased survey range. Smith and Vericat (2015) analysed 50 extant SfM-MVS datasets and identified a relative precision ratio of 1:650 for SfM-MVS surveys, indicating model error of ~1 m at survey ranges of ~650 m (which in itself is sub-optimal, as James and Robson (2012) suggest that measurement precisions of 1:1000 of the survey range should be achievable). Survey ranges in our study varied between 318 and 1321 m, with a mean range of 765 m (Table 1). While external validation data were unavailable in this study, this broadly compares with the distribution of errors observed when comparing two point clouds over an ‘inactive’ interval (Table 3). The poor projection accuracy of GCPs that were located at the periphery of the survey, and thus were observed in relatively few images, would explain why errors are higher than expected (Table 2).

5.4. GCP distribution

The dynamism and, in many cases, inaccessibility of ice margins poses a challenge for the distribution of GCPs, which are conventionally stationed throughout the entirety of a survey area (James and Robson, 2012; Smith and others, 2015). In addition, surveys that extend beyond the confines of GCP stations often exhibit increased point cloud error (Javemick and others, 2014; Smith and others, 2015). Consequently, future implementations of this camera array approach should aim to improve the distribution of GCP stations where possible. The two GCP clusters employed in this study were necessarily peripheral to the survey area, being located >500 m from the centre of the ice margin and, like the lake shores themselves, possessing relatively poor camera coverage (Fig. 4). Accordingly, georeferencing RMSEs in similar setups are likely to be several orders of magnitude greater than conventional surveys where optimal GCP distribution and camera overlap can be achieved. The scale of the survey range also requires sizable GCP targets, which increase the likelihood of misidentifying the precise reference point, which can be further exacerbated by fluctuating light levels. Stable landscape features are the most viable option for establishing a GCP network at long survey ranges (>1 km), where dedicated GCP targets are likely to be impracticable. For example, in this setup we estimate that dedicated targets would need to be >1 m in diameter to be resolvable in the camera imagery. In addition, any such markers would need to be sufficiently sturdy to withstand Arctic winter weather and the attentions of local wildlife (e.g. musk-ox, Arctic fox).

Possible methods to mitigate the impact of peripheral GCPs on cloud accuracy would be to supplement the GCP network with multiple telemetric dGPS units stationed on the ice itself, or to survey and incorporate the positions of the camera stations in the bundle adjustment. Low-budget, high-precision dGPS units have become increasingly available in recent years (Völksen and Mayer, 2015; Jones and others, 2016) and could facilitate concurrent measurements of 3-D ice motion. However, their successful application would again require that the dGPS units (or their associated targets) were accurately resolvable in the camera imagery.

5.5. Camera clocks and workflow automation

Despite their low-cost, the cameras were remarkably resilient to the cold and harsh conditions of the study site. Upon their retrieval internal camera clocks were assessed against a handheld GPS clock to determine the presence of any clock drift. The comparison revealed that all the camera clocks had drifted significantly from their original synchronisation; with the final set of images (scheduled for 13:00 on the 24 September 2015) acquired over a period of 27 min between 13:21 and 13:48. Although the period of image acquisition remained within the 30 min survey duration recommended by Bemis and others (2014) (to mitigate complications caused by changes to shadow length, weather and surface albedo), clock drift could be a significant barrier to the acquisition of topographic datasets from highly dynamic environments where data is required on a minute-by-minute basis, such as the lava flows observed in James and Robson (2014a). Methods for improving camera clock calibration and mitigating clock drift are outlined in Welty and others (2013), although it should be noted that the necessary integration of cameras and GPS receivers would increase the power requirements of any prospective camera array setup. We anticipate that the analysis of high-temporal resolution topographic datasets could be expedited by automation of the processing workflow and use of batch processing capabilities, although variable image quality is likely to provide a barrier to full automation. Rigorous testing of camera performance and provisional analytical workflows are therefore recommended before automation of a camera array in the field.

5.6. Detection of ice-margin dynamics

As evidenced in this study the types of ice-margin dynamics that are resolvable using the time-lapse camera array approach will be determined by point cloud accuracy and survey interval. For example, while point clouds with relatively low accuracies (>2 m) are likely to be sufficient for capturing calving events, higher accuracies (<1 m) are required to capture small-scale glacier changes, such as ice cliff advance/retreat, ice surface thinning/thickening, crevasse and ice fall serac dynamics or, perhaps in the context of water-terminating ice margins, flexure, fracture and floatation. When compared with existing approaches for quantifying ice-margin changes, the differencing of 3-D point clouds is advantageous because any topographic change can be calculated along the normal direction of the cliff face, thereby avoiding the amalgamation of 3-D topographic change (resulting from melt and horizontal and vertical motion) that exists in vertical DEM differencing (e.g. Thompson and others, 2016). In addition, mechanisms controlling any ice-margin topographic change can be evaluated in 3-D, revealing hitherto hard-to-detect phenomena such as thermo-erosional undercutting by ice-marginal lake water. Consequently, the deployment of camera arrays at ice margins could afford considerable potential for improving knowledge of ice-marginal processes, including the spatial and seasonal distribution of calving events, the contribution of calving (e.g. total volume) to mass balance, and calving responses to external drivers including weather, water temperature and water level.

5.7. Appraisal against TLS

Our data suggest that the camera array presents an effective alternative to TLS for the acquisition of topographic datasets in glacial environments. The point clouds generated in this study possessed similar point densities to those derived via glacial TLS investigations at comparable scales (e.g. Gabbud and others, 2015); however, the camera array technique offers several further advantages over TLS. Most notably the cost of a TLS system (>£40 000) greatly exceeds that of a camera array (in this case ~£1800), even when accounting for software licenses (e.g. Agisoft Photoscan Professional ~£3000 for commercial purposes). Additionally, complex glacier geometries are likely to require multiple scanning stations, which increase the complexity and duration of both TLS setup and post-processing. Finally, the automation of the camera array facilitates prolonged data acquisition well beyond the financial and climatic constraints of manual TLS operation.

6. CONCLUSIONS AND RECOMMENDATIONS

This study has presented the first set-up, operation and analysis of data from a time-lapse camera array to generate multi-temporal topographic surveys of a lacustrine-terminating ice margin. These instruments and methods are shown to be far more practical than field-based measurements, such as ablation stake monitoring, and of far greater spatio-temporal resolution than airborne or ground-based remote sensing. They therefore have significant potential for revealing mechanistic drivers and triggers of geomorphological change, not only for lacustrine ice margins, but also for other rapidly-changing glacial environments such as ice-falls and, with due consideration of the baseline distances involved, marine ice margins.

Our recommendations for the deployment of time-lapse camera arrays to acquire topographic datasets note that these instruments and methods are very much still in development and face considerable challenges, particularly in glaciological applications. However, the following practical guidance should improve the setup, and therefore data quality, of future camera array-based investigations:

• • The types of ice margin and other glacier dynamics that are resolvable using this approach will be determined by point cloud accuracy and survey interval. Consequently, the setup of the camera array and survey frequency must be tailored to the specific aims of any investigation.

• • Ambient light levels determine both image quality and GCP visibility, therefore the positioning of camera and GCP stations should follow careful consideration of: (i) the orientation of the cameras in relation to the feature of interest; (ii) the influence of local topography on shading; (iii) the path of the sun (daily and seasonally); (iv) prevailing weather conditions; and (v) locally reflective surfaces, particularly ice, snow and water.

• • The likelihood of camera failure or disturbance will increase with prolonged operation, consequently camera arrays should be designed to allow some redundancy in operative cameras while still maintaining sufficient image overlap for point cloud generation.

• • Similarly, redundancy of GCPs should also be factored into the setup to account for dynamic lighting and variable ground conditions, including snowfall and vegetation growth.

• • The sub-optimal distribution of GCPs in similar camera array setups is likely to produce georeferencing RMSEs several orders of magnitude greater than conventional SfM-MVS surveys. However, where access and survey range permit, this problem could be addressed by distributing multiple telemetric dGPS units (and associated targets) within the survey area.

• • Quality control of the camera array setup should be performed in the field prior to full automation by downloading preliminary imagery to a laptop running SfM-MVS software and generating test point clouds, with particular attention given to the number of keypoint matches returned by individual cameras.

• • Increasing the rate of image acquisition (i.e. oversampling) can mitigate the effect of changing weather conditions on image quality and limit the superimposition of geomorphological processes. However, the frequency of image acquisition must also reflect memory capacity and power availability, particularly when a finite power source is used, or where prevailing weather conditions, snowfall or daylight hours curtail the efficacy of photovoltaic cells.

Further opportunities for the development and scope of camera array-based glaciological investigations will be facilitated by rapid advances in the technical specifications of time-lapse cameras and an increased affordability. Significantly, camera models are increasingly equipped with MMS or WiFi connectivity, enabling the immediate transmission of imagery from connected locations. Integration with a fully automated workflow for data analysis could therefore permit real time analysis of geomorphological change. The incorporation of sensors into a camera array network could also facilitate the operation of cameras in response to external triggers (for example using seismic or motion sensors to activate the array during large calving events). Finally, the rapid development of software is also likely to significantly increase the range of variables that can be derived from camera array-based investigations; for example James and others (2016) present open access software capable of quantifying the horizontal and vertical ice velocity components of a glacier from an oblique terrestrial time-lapse image sequence.