Published online by Cambridge University Press: 26 October 2022
Given a sequence 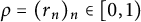 $\varrho =(r_n)_n\in [0,1)$ tending to
$\varrho =(r_n)_n\in [0,1)$ tending to 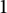 $1$, we consider the set
$1$, we consider the set 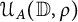 ${\mathcal {U}}_A({\mathbb {D}},\varrho )$ of Abel universal functions consisting of holomorphic functions f in the open unit disk
${\mathcal {U}}_A({\mathbb {D}},\varrho )$ of Abel universal functions consisting of holomorphic functions f in the open unit disk 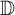 $\mathbb {D}$ such that for any compact set K included in the unit circle
$\mathbb {D}$ such that for any compact set K included in the unit circle 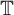 ${\mathbb {T}}$, different from
${\mathbb {T}}$, different from 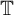 ${\mathbb {T}}$, the set
${\mathbb {T}}$, the set 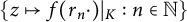 $\{z\mapsto f(r_n \cdot )\vert _K:n\in \mathbb {N}\}$ is dense in the space
$\{z\mapsto f(r_n \cdot )\vert _K:n\in \mathbb {N}\}$ is dense in the space 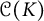 ${\mathcal {C}}(K)$ of continuous functions on K. It is known that the set
${\mathcal {C}}(K)$ of continuous functions on K. It is known that the set 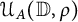 ${\mathcal {U}}_A({\mathbb {D}},\varrho )$ is residual in
${\mathcal {U}}_A({\mathbb {D}},\varrho )$ is residual in 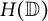 $H(\mathbb {D})$. We prove that it does not coincide with any other classical sets of universal holomorphic functions. In particular, it is not even comparable in terms of inclusion to the set of holomorphic functions whose Taylor polynomials at
$H(\mathbb {D})$. We prove that it does not coincide with any other classical sets of universal holomorphic functions. In particular, it is not even comparable in terms of inclusion to the set of holomorphic functions whose Taylor polynomials at 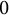 $0$ are dense in
$0$ are dense in 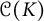 ${\mathcal {C}}(K)$ for any compact set
${\mathcal {C}}(K)$ for any compact set 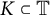 $K\subset {\mathbb {T}}$ different from
$K\subset {\mathbb {T}}$ different from 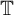 ${\mathbb {T}}$. Moreover, we prove that the class of Abel universal functions is not invariant under the action of the differentiation operator. Finally, an Abel universal function can be viewed as a universal vector of the sequence of dilation operators
${\mathbb {T}}$. Moreover, we prove that the class of Abel universal functions is not invariant under the action of the differentiation operator. Finally, an Abel universal function can be viewed as a universal vector of the sequence of dilation operators 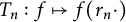 $T_n:f\mapsto f(r_n \cdot )$ acting on
$T_n:f\mapsto f(r_n \cdot )$ acting on 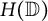 $H(\mathbb {D})$. Thus, we study the dynamical properties of
$H(\mathbb {D})$. Thus, we study the dynamical properties of 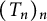 $(T_n)_n$ such as the multiuniversality and the (common) frequent universality. All the proofs are constructive.
$(T_n)_n$ such as the multiuniversality and the (common) frequent universality. All the proofs are constructive.
The authors are supported by the grant ANR-17-CE40-0021 of the French National Research Agency ANR (project Front).