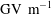1. Introduction
Currently, high electron energies of tens of GeV are achieved with radio-frequency (RF) linear accelerators that operate in the GHz frequency range with a typical length of a few kilometers[Reference Neal1]. In idealized conditions, breakdown[Reference Wangler2] limits the accelerating electric field to the order of a few hundreds of ![]() $\mathrm{MV\ m}^{-1}$. In practice, gradients reach values of
$\mathrm{MV\ m}^{-1}$. In practice, gradients reach values of ![]() $25\ \mathrm{MV\ m}^{-1}$ when operating at room temperature[Reference Neal1] and
$25\ \mathrm{MV\ m}^{-1}$ when operating at room temperature[Reference Neal1] and ![]() $35\ \mathrm{MV\ m}^{-1}$ in their superconductive counterpart[Reference Behnke, Brau, Foster, Fuster, Harrison, McEwan Paterson, Peskin, Stanitzki, Walker and Yamamoto3].
$35\ \mathrm{MV\ m}^{-1}$ in their superconductive counterpart[Reference Behnke, Brau, Foster, Fuster, Harrison, McEwan Paterson, Peskin, Stanitzki, Walker and Yamamoto3].
In the past two decades, with the immense progress in laser technology, laser plasma accelerators have become able generate hundreds of ![]() $\mathrm{GV\ m}^{-1}$[Reference Esarey, Schroeder and Leemans4–Reference Hooker6]. In this scheme, high intensity focused laser pulses with lengths of the order of the plasma wavelength generate an intense wake. The plasma wake, which trails behind the laser pulse with the same group velocity, can accelerate electrons from the plasma itself. Work is in progress to accelerate electrons that do not originate in the plasma.
$\mathrm{GV\ m}^{-1}$[Reference Esarey, Schroeder and Leemans4–Reference Hooker6]. In this scheme, high intensity focused laser pulses with lengths of the order of the plasma wavelength generate an intense wake. The plasma wake, which trails behind the laser pulse with the same group velocity, can accelerate electrons from the plasma itself. Work is in progress to accelerate electrons that do not originate in the plasma.
Based on the chirped pulse amplification (CPA) technique[Reference Strickland and Mourou7], pulsed laser technology facilitates focus on plasma target pulses with intensities as high as ![]() $10^{18}\ \mathrm{W\ cm}^{-2}$ and duration of the order of femtoseconds (
$10^{18}\ \mathrm{W\ cm}^{-2}$ and duration of the order of femtoseconds (![]() $10^{-15}$ s) for a laser wavelength of
$10^{-15}$ s) for a laser wavelength of ![]() $1\ \mu \mathrm{m}$ that is optimized to a plasma density of
$1\ \mu \mathrm{m}$ that is optimized to a plasma density of ![]() $10^{18}\ \mathrm{cm}^{-3}$. In a series of experiments reported in 2004[Reference Mangles, Murphy, Najmudin, Thomas, Collier, Dangor, Divall, Foster, Gallacher, Hooker, Jaroszynski, Langley, Mori, Norreys, Tsung, Viskup, Walton and Krushelnick8–Reference Faure, Glinec, Pukhov, Kiselev, Gordienko, Lefebvre, Rousseau, Burgy and Malka10], quasi-monoenergetic e-beams with energies of the order of 100 MeV have been demonstrated. More recently, several groups have demonstrated quasi-monoenergetic e-beams with energies of up to 2 GeV[Reference Wang, Zgadzaj, Fazel, Li, Yi, Zhang, Henderson, Chang, Korzekwa, Tsai, Pai, Quevedo, Dyer, Gaul, Martinez, Bernstein, Borger, Spinks, Donovan, Khudik, Shvets, Ditmire and Downer11].
$10^{18}\ \mathrm{cm}^{-3}$. In a series of experiments reported in 2004[Reference Mangles, Murphy, Najmudin, Thomas, Collier, Dangor, Divall, Foster, Gallacher, Hooker, Jaroszynski, Langley, Mori, Norreys, Tsung, Viskup, Walton and Krushelnick8–Reference Faure, Glinec, Pukhov, Kiselev, Gordienko, Lefebvre, Rousseau, Burgy and Malka10], quasi-monoenergetic e-beams with energies of the order of 100 MeV have been demonstrated. More recently, several groups have demonstrated quasi-monoenergetic e-beams with energies of up to 2 GeV[Reference Wang, Zgadzaj, Fazel, Li, Yi, Zhang, Henderson, Chang, Korzekwa, Tsai, Pai, Quevedo, Dyer, Gaul, Martinez, Bernstein, Borger, Spinks, Donovan, Khudik, Shvets, Ditmire and Downer11].
An intense wake may also develop by replacing the laser pulse with an energetic e-beam in plasma, and it is shown experimentally[Reference Blumenfeld, Clayton, Decker, Hogan, Huang, Ischebeck, Iverson, Joshi, Katsouleas, Kirby, Lu, Marsh, Mori, Muggli, Oz, Siemann, Walz and Zhou12] that an initial bunch of 40 GeV can generate an intense wake of the order of ![]() $50\ \mathrm{GV\ m}^{-1}$, which results in acceleration of a trailing bunch to an energy of about 80 GeV with about 16% energy spread. The total number of injected electrons in the bunch is
$50\ \mathrm{GV\ m}^{-1}$, which results in acceleration of a trailing bunch to an energy of about 80 GeV with about 16% energy spread. The total number of injected electrons in the bunch is ![]() $10^{10}$ and the spot size is
$10^{10}$ and the spot size is ![]() $10\ \mu \mathrm{m}$, whereas the number of electrons accelerated to 80 GeV is about
$10\ \mu \mathrm{m}$, whereas the number of electrons accelerated to 80 GeV is about ![]() $240\times 10^{6}$. For comparison, in a dielectric loaded waveguide, a 60 MeV bunch of electrons can generate Cerenkov gradients of
$240\times 10^{6}$. For comparison, in a dielectric loaded waveguide, a 60 MeV bunch of electrons can generate Cerenkov gradients of ![]() $250\ \mathrm{MV\ m}^{-1}$[Reference Peralta, Soong, England, Colby, Wu, Montazeri, McGuinness, McNeur, Leedle, Walz, Sozer, Cowan, Schwartz, Travish and Byer13]. The total number of injected electrons in the bunch is
$250\ \mathrm{MV\ m}^{-1}$[Reference Peralta, Soong, England, Colby, Wu, Montazeri, McGuinness, McNeur, Leedle, Walz, Sozer, Cowan, Schwartz, Travish and Byer13]. The total number of injected electrons in the bunch is ![]() $3\times 10^{6}$ and the spot size is
$3\times 10^{6}$ and the spot size is ![]() $10\ \mu \mathrm{m}$, whereas the number of accelerated electrons is about
$10\ \mu \mathrm{m}$, whereas the number of accelerated electrons is about ![]() $70\times 10^{3}$.
$70\times 10^{3}$.
In the paradigm analyzed here, the gradients are more modest (order of ![]() $1\ \mathrm{GV\ m}^{-1}$) and it is conceptually closer to a conventional two-beam acceleration scheme. It relies on transferring energy stored from the active medium to a train of electron bunches – see Refs. [Reference Schächter14, Reference Schächter15]. In contrast to previously mentioned schemes, where the energy for the acceleration comes from either energetic laser pulses or an energetic electron bunch, in this scheme the energy comes from excited atoms. In the first approach of this scheme, an electron bunch injected into an active medium generates a wake comprised of a broadband spectrum of evanescent waves. Since the active medium is a resonant medium, only the fraction of the wake spectrum that is close to the resonance frequency of the medium will be amplified. Thus, it is proposed to inject a spatially modulated bunch with periodicity equal to the resonance wavelength so that a large portion of the wake spectrum lies in the vicinity of the resonance frequency of the medium. As a result, the amplified wake accelerates directly the injected bunch. This approach has been demonstrated in an experiment performed at Brookhaven National Laboratory Accelerator Test Facility (BNL-ATF)[Reference Banna, Berezovsky and Schächter16], in which a density modulated bunch with an energy of 45 MeV gained energy of 200 keV from an active
$1\ \mathrm{GV\ m}^{-1}$) and it is conceptually closer to a conventional two-beam acceleration scheme. It relies on transferring energy stored from the active medium to a train of electron bunches – see Refs. [Reference Schächter14, Reference Schächter15]. In contrast to previously mentioned schemes, where the energy for the acceleration comes from either energetic laser pulses or an energetic electron bunch, in this scheme the energy comes from excited atoms. In the first approach of this scheme, an electron bunch injected into an active medium generates a wake comprised of a broadband spectrum of evanescent waves. Since the active medium is a resonant medium, only the fraction of the wake spectrum that is close to the resonance frequency of the medium will be amplified. Thus, it is proposed to inject a spatially modulated bunch with periodicity equal to the resonance wavelength so that a large portion of the wake spectrum lies in the vicinity of the resonance frequency of the medium. As a result, the amplified wake accelerates directly the injected bunch. This approach has been demonstrated in an experiment performed at Brookhaven National Laboratory Accelerator Test Facility (BNL-ATF)[Reference Banna, Berezovsky and Schächter16], in which a density modulated bunch with an energy of 45 MeV gained energy of 200 keV from an active ![]() $\mathrm{CO}_{2}$ gas mixture.
$\mathrm{CO}_{2}$ gas mixture.
For a description of the paradigm, we start with a general description of the system followed by a simplified model used to investigate the essential phenomena involved. A trigger bunch propagates in a vacuum channel surrounded by a low loss dielectric layer which is thick enough to sustain the 8–10 atm pressure of the ![]() $\mathrm{CO}_{2}$ mixture consisting of the active medium. The latter in turn is confined by a Bragg waveguide which facilitates excitation of the active medium on the one hand and allows full confinement of a resonant Cherenkov wake. One of the eigenmodes is amplified by the active medium and many wavelengths behind the trigger bunch the former accelerates a trailing bunch. For the sake of simplicity, the analysis that follows relies on a metallic waveguide that contains the gaseous active medium.
$\mathrm{CO}_{2}$ mixture consisting of the active medium. The latter in turn is confined by a Bragg waveguide which facilitates excitation of the active medium on the one hand and allows full confinement of a resonant Cherenkov wake. One of the eigenmodes is amplified by the active medium and many wavelengths behind the trigger bunch the former accelerates a trailing bunch. For the sake of simplicity, the analysis that follows relies on a metallic waveguide that contains the gaseous active medium.
Initially, a triggering bunch of electrons generates a Cerenkov wake with electric field in the longitudinal direction, which in turn is amplified by the active medium - stimulated emission process. As the wake field is amplified, the population inversion in the active medium is reduced and, as a result, the spatial gain is also reduced. When the spatial gain is zero, the wake reaches saturation and it can accelerate a second bunch of electrons trailing behind the triggering bunch.
Previous study of this scheme used a linear model[Reference Schächter15, Reference Schächter17–Reference Voin and Schächter19] and a simplified nonlinear model[Reference Schächter, Colby and Siemann20]. In the linear model, where a constant population inversion density (PID) is assumed, the wake is exponentially amplified. Since the propagating wake in the cylindrical waveguide propagates in an oblique angle, it reflects multiple times from the boundaries. As a result, the effective propagation path is longer than if the wake were propagating in a boundless medium. For a structure of a given length, the effective gain of the wake is enhanced. The simplified nonlinear model assumes the propagation of one electromagnetic (EM) mode[Reference Schächter, Colby and Siemann20]; it does not account for the multiple reflections of the wake from the waveguide boundary and only the dynamics of the polarization field is considered.
In this paper we extend the previous linear model[Reference Voin, Kimura and Schächter18, Reference Voin and Schächter19] and include the nonlinear dynamics of the active medium. The extended model can describe the wake saturation level and the interval of time in which the wake reaches saturation. While the previously mentioned approaches[Reference Voin, Kimura and Schächter18–Reference Schächter, Colby and Siemann20] predict the saturation process qualitatively, the present approach is far more quantitative.
This paper is organized as follows. Section 2 presents the dynamics equations that describe the Cerenkov wake amplification by the active medium. It also describes the dynamics of the polarization and the population inversion density. In Section 3 the single-mode resonance condition, the value of the saturated wake and the saturation length are calculated analytically. In addition, we calculate for a single mode the width or the spot size of the longitudinal wake. In Section 4 we show numerically for a modulated trigger bunch the dynamics of the wake and the population inversion density for a ![]() $\mathrm{CO}_{2}$ gas mixture. We conclude (Section 5) with discussion and conclusions.
$\mathrm{CO}_{2}$ gas mixture. We conclude (Section 5) with discussion and conclusions.
2. Formulation of the problem
The structure of interest consists of a cylindrical metallic waveguide of radius ![]() $R$ filled with an active medium (see Figure 1). Far from the resonance of the active medium it is assumed that the dielectric coefficient of the medium is
$R$ filled with an active medium (see Figure 1). Far from the resonance of the active medium it is assumed that the dielectric coefficient of the medium is ![]() $\varepsilon _{r}$ and it is frequency independent. A bunch of electrons, the trigger bunch, is injected into the structure with velocity
$\varepsilon _{r}$ and it is frequency independent. A bunch of electrons, the trigger bunch, is injected into the structure with velocity ![]() $\beta c$ larger than the Cerenkov velocity
$\beta c$ larger than the Cerenkov velocity ![]() $c/\sqrt{\varepsilon _{r}}$, where
$c/\sqrt{\varepsilon _{r}}$, where ![]() $c$ is the speed of light in vacuum. Assuming azimuthal symmetry, the bunch excites an entire manifold of transverse magnetic (TM) modes which propagate behind[Reference Schächter21]. Each mode consists of longitudinal and radial electric field components (
$c$ is the speed of light in vacuum. Assuming azimuthal symmetry, the bunch excites an entire manifold of transverse magnetic (TM) modes which propagate behind[Reference Schächter21]. Each mode consists of longitudinal and radial electric field components (![]() $E_{z},E_{r}$) as well as an azimuthal magnetic field (
$E_{z},E_{r}$) as well as an azimuthal magnetic field (![]() $H_{\phi }$).
$H_{\phi }$).

Figure 1. Schematic description of the accelerating structure. A trigger bunch propagates in a cylindrical metallic waveguide of radius ![]() $R$ filled with an active medium. This bunch is injected into the structure with velocity
$R$ filled with an active medium. This bunch is injected into the structure with velocity ![]() $\beta c$ larger than the Cerenkov velocity
$\beta c$ larger than the Cerenkov velocity ![]() $c/\sqrt{\varepsilon _{r}}$ and generates an entire manifold of TM modes which propagate behind. One of the eigenmodes is amplified by the active medium and many wavelengths behind the trigger bunch the former accelerates a trailing train bunch.
$c/\sqrt{\varepsilon _{r}}$ and generates an entire manifold of TM modes which propagate behind. One of the eigenmodes is amplified by the active medium and many wavelengths behind the trigger bunch the former accelerates a trailing train bunch.
This superposition of TM modes, also known as the wake field, travels at the same speed as the trigger bunch. Among this infinite manifold of TM modes only those with frequency equal to or close enough to the resonance frequency of the active medium, ![]() $\omega _{0}$, will be amplified through the stimulated emission process. Thus, the EM field has the following generic form
$\omega _{0}$, will be amplified through the stimulated emission process. Thus, the EM field has the following generic form
where each field ![]() $\psi \; (\psi \in \{E_{z},E_{r},H_{\phi }\})$ depends on the radial coordinate,
$\psi \; (\psi \in \{E_{z},E_{r},H_{\phi }\})$ depends on the radial coordinate, ![]() $r$, and a variable that follows the e-beam,
$r$, and a variable that follows the e-beam, ![]() $T\equiv t-z/\beta c$. Specifically, for field
$T\equiv t-z/\beta c$. Specifically, for field ![]() $\psi =E_{z}$ the index of the Bessel function of the first kind is
$\psi =E_{z}$ the index of the Bessel function of the first kind is ![]() $\nu =0$ and for
$\nu =0$ and for ![]() $\psi =\{E_{r},H_{\phi }\}$ the index is
$\psi =\{E_{r},H_{\phi }\}$ the index is ![]() $\nu =1$. In addition, the radial wavenumber is
$\nu =1$. In addition, the radial wavenumber is ![]() $k_{s}\equiv p_{s}/R$, where
$k_{s}\equiv p_{s}/R$, where ![]() $p_{s}$ is defined through
$p_{s}$ is defined through ![]() $J_{0}(k_{s}R)=0\; (s=1,2,3,\ldots)$ since
$J_{0}(k_{s}R)=0\; (s=1,2,3,\ldots)$ since ![]() $E_{z}(T,r=R)=0$. Finally, the dependence of each mode on
$E_{z}(T,r=R)=0$. Finally, the dependence of each mode on ![]() $T$ is given by
$T$ is given by ![]() $\psi _{s}(T)$.
$\psi _{s}(T)$.
Similarly to the EM fields, the current density of the trigger bunch is assumed to be of the form
where ![]() $\theta (x)$ is the Heaviside step function and
$\theta (x)$ is the Heaviside step function and ![]() $I(T)$ is the e-beam longitudinal current envelope. Assuming that the spatially modulated bunch profile is given by
$I(T)$ is the e-beam longitudinal current envelope. Assuming that the spatially modulated bunch profile is given by ![]() $f(T)$ then the current envelope is
$f(T)$ then the current envelope is ![]() $I(T)=I_{0}f(T)$, where the modulated current is
$I(T)=I_{0}f(T)$, where the modulated current is ![]() $I_{0} =Q_{b} \beta c/L_{b}$. Here, the total charge is
$I_{0} =Q_{b} \beta c/L_{b}$. Here, the total charge is ![]() $Q_{b} = -eN_{b}$, where
$Q_{b} = -eN_{b}$, where ![]() $-e$ is the electron charge and
$-e$ is the electron charge and ![]() $N_{b}$ is the number of macro-particles that comprise the bunch;
$N_{b}$ is the number of macro-particles that comprise the bunch; ![]() $L_{b}$ is the bunch length.
$L_{b}$ is the bunch length.
Having in mind that the growth rate is much smaller than the resonance frequency, the dynamics of the fields can be separated into two major time scales: the ‘fast’ and the ‘slow’ time scales. The ‘fast’ time scale is the medium resonance period of time ![]() $1/\omega _{0}$ whereas the ‘slow’ time scale associated with the growth rate of the field envelopes,
$1/\omega _{0}$ whereas the ‘slow’ time scale associated with the growth rate of the field envelopes, ![]() $\psi _{s}(T)$, is
$\psi _{s}(T)$, is ![]() $1/\omega _{p}$, where
$1/\omega _{p}$, where ![]() $\omega _{p}=\omega _{0} \sqrt{\frac{2N_{0}\mu ^{2}}{\varepsilon _{0} \hslash \omega _{0}}} \ll \omega _{0}$ is the ‘plasma frequency’ of the active medium. Here,
$\omega _{p}=\omega _{0} \sqrt{\frac{2N_{0}\mu ^{2}}{\varepsilon _{0} \hslash \omega _{0}}} \ll \omega _{0}$ is the ‘plasma frequency’ of the active medium. Here, ![]() $N_{0}$ is the initial PID,
$N_{0}$ is the initial PID, ![]() $\mu =\mu _{12}/\sqrt3$ is the average dipole moment and
$\mu =\mu _{12}/\sqrt3$ is the average dipole moment and ![]() $\mu _{12}$ is the dipole moment. The parameter
$\mu _{12}$ is the dipole moment. The parameter ![]() $\hslash $ is the reduced Planck constant and
$\hslash $ is the reduced Planck constant and ![]() $\varepsilon _{0}$ is the vacuum permittivity. Thus, the dynamics of the wake and the active medium can be described by the slowly varying envelope approximation. Consequently, the dynamics of the normalized EM fields derived from the Ampere and Faraday laws read
$\varepsilon _{0}$ is the vacuum permittivity. Thus, the dynamics of the wake and the active medium can be described by the slowly varying envelope approximation. Consequently, the dynamics of the normalized EM fields derived from the Ampere and Faraday laws read
 $$\begin{eqnarray} \frac {\partial \bar {E}_{z,s}}{\partial \tau } &=& -i\bar {\omega }_{0} \bar {E}_{z,s} + \frac {\bar {k}_{s} }{2\sqrt {\varepsilon _{r} } }\bar {E}_{+,s} + \frac {\bar {k}_{s} }{2\sqrt {\varepsilon _{r} } }\bar {E}_{-,s}\nonumber \\ && + \, \frac {2}{\varepsilon _{r} }\bar {P}_{z,s} - \frac {2}{\varepsilon _{r} }\bar {J}_{s} f ,\label {eq3}\end{eqnarray}$$
$$\begin{eqnarray} \frac {\partial \bar {E}_{z,s}}{\partial \tau } &=& -i\bar {\omega }_{0} \bar {E}_{z,s} + \frac {\bar {k}_{s} }{2\sqrt {\varepsilon _{r} } }\bar {E}_{+,s} + \frac {\bar {k}_{s} }{2\sqrt {\varepsilon _{r} } }\bar {E}_{-,s}\nonumber \\ && + \, \frac {2}{\varepsilon _{r} }\bar {P}_{z,s} - \frac {2}{\varepsilon _{r} }\bar {J}_{s} f ,\label {eq3}\end{eqnarray}$$ The expression ![]() $\frac{2}{\varepsilon _{r}} \bar{J}_{s}f$ is the normalized bunch current, where
$\frac{2}{\varepsilon _{r}} \bar{J}_{s}f$ is the normalized bunch current, where ![]() $\bar{J}_{s} = \frac{I_{0}}{\pi R^{2}}\frac{J_{c} (k_{s} R_{b})}{J_{1} (k_{s} R)}\frac{\sqrt{\varepsilon _{r}}}{\omega _{0} \mu N_{0}}$,
$\bar{J}_{s} = \frac{I_{0}}{\pi R^{2}}\frac{J_{c} (k_{s} R_{b})}{J_{1} (k_{s} R)}\frac{\sqrt{\varepsilon _{r}}}{\omega _{0} \mu N_{0}}$, ![]() $J_{c} (x)\equiv 2J_{1} (x)/x$ and
$J_{c} (x)\equiv 2J_{1} (x)/x$ and ![]() $f = f(\tau )$ describes the electron bunch profile in the longitudinal direction. In this study, the bunch injected at
$f = f(\tau )$ describes the electron bunch profile in the longitudinal direction. In this study, the bunch injected at ![]() $\tau = \tau _{0}$ with a length of
$\tau = \tau _{0}$ with a length of ![]() $\bar{{L}}_{b} = L_{b} \omega _{A} /\beta c$ has a profile of
$\bar{{L}}_{b} = L_{b} \omega _{A} /\beta c$ has a profile of ![]() $f(\tau _{0} <\tau <\tau _{1})=1$,
$f(\tau _{0} <\tau <\tau _{1})=1$, ![]() $f(\tau =\tau _{0} )=1/2,\, f(\tau =\tau _{1})=1/2$ and zero otherwise, where
$f(\tau =\tau _{0} )=1/2,\, f(\tau =\tau _{1})=1/2$ and zero otherwise, where ![]() $\tau _{1} = \tau _{0} +\bar{{L}}_{b}$.
$\tau _{1} = \tau _{0} +\bar{{L}}_{b}$.
The active medium is modeled semi-classically as a two-level system within the framework of the dipole approximation[Reference Pantell and Puthoff22, Reference Boyd23]. In addition, it is assumed that only stimulated emission can reduce the population inversion density and collisions of the second kind are neglected here. The response of the active medium to the wake is through the normalized polarization fields ![]() $\bar{P}_{z}$ and
$\bar{P}_{z}$ and ![]() $\bar{P}_{r}$,
$\bar{P}_{r}$,
The dynamics of the PID, ![]() $\bar{N}$, reads
$\bar{N}$, reads
Finally, the set of equations introduced in Equations (2.3)–(2.8) conserves energy,
where the total energy is
![]() $\bar{W}_{s}^{(EM,lo)} = \frac{\varepsilon _{r}}{4} |\bar{E}_{z,s}|^{2}$ is the energy density associated with the longitudinal electric field and
$\bar{W}_{s}^{(EM,lo)} = \frac{\varepsilon _{r}}{4} |\bar{E}_{z,s}|^{2}$ is the energy density associated with the longitudinal electric field and ![]() $\bar{W}_{s}^{(EM,tr)} = \frac{\varepsilon _{r}}{8} (\Delta \varepsilon _{-} |\bar{E}_{+,s}|^{2} + \Delta \varepsilon _{+} |\bar{E}_{-,s}|^{2})$ is the transverse component counterpart. Also, the energy density of the active medium is
$\bar{W}_{s}^{(EM,tr)} = \frac{\varepsilon _{r}}{8} (\Delta \varepsilon _{-} |\bar{E}_{+,s}|^{2} + \Delta \varepsilon _{+} |\bar{E}_{-,s}|^{2})$ is the transverse component counterpart. Also, the energy density of the active medium is ![]() $\bar{W}_{N} =\bar{N}$, and the energy of the bunch is denoted by
$\bar{W}_{N} =\bar{N}$, and the energy of the bunch is denoted by ![]() $\bar{W}_{s}^{(B)} = \bar{J}_{s} \int _0^\tau \! f(\tau ') \frac{1}{2} [\bar{E}_{z,s} (\tau ') + \bar{E}_{z,s}^{\ast } (\tau ')]d\tau '$.
$\bar{W}_{s}^{(B)} = \bar{J}_{s} \int _0^\tau \! f(\tau ') \frac{1}{2} [\bar{E}_{z,s} (\tau ') + \bar{E}_{z,s}^{\ast } (\tau ')]d\tau '$.
3. Analytical assessments
In this section we determine analytically the single-mode resonance condition, the value of the saturated wake and the saturation length. In addition, we calculate for a single mode the spot size of the longitudinal wake.
In the considered structure only the modes with frequencies adjacent to the resonance frequency will be amplified. In our model it is possible to find the modes that will be amplified from the dynamics of ![]() $\bar{E}_{z,s}$ as follows. Substitution of
$\bar{E}_{z,s}$ as follows. Substitution of ![]() $\bar{E}_{+,s}$ and
$\bar{E}_{+,s}$ and ![]() $\bar{E}_{-,s}$ from Equations (2.4) and (2.5), respectively, into Equation (2.3) results in
$\bar{E}_{-,s}$ from Equations (2.4) and (2.5), respectively, into Equation (2.3) results in
 $$\begin{eqnarray} \frac {\partial \bar {E}_{z,s} }{\partial \tau } &=& -i \Delta \bar {\omega }_{s} \bar {E}_{z,s} -i \frac {2\bar {k}_{s}}{\beta \varepsilon _{r} \sqrt {\varepsilon _{r}} \varepsilon _{c} \bar {\omega }_{0}} \bar {P}_{r,s} + \frac {2}{\varepsilon _{r}} \bar {P}_{z,s} \\ && +\, i\frac {\bar {k}_{s}}{2\bar {\omega }_{0} \sqrt {\varepsilon _{r}}} \frac {\partial }{\partial \tau } (\bar {E}_{+,s} + \bar {E}_{-,s}) - \frac {2}{\varepsilon _{r}} \bar {J}_{s} f, \label {eq11} \end{eqnarray}$$
$$\begin{eqnarray} \frac {\partial \bar {E}_{z,s} }{\partial \tau } &=& -i \Delta \bar {\omega }_{s} \bar {E}_{z,s} -i \frac {2\bar {k}_{s}}{\beta \varepsilon _{r} \sqrt {\varepsilon _{r}} \varepsilon _{c} \bar {\omega }_{0}} \bar {P}_{r,s} + \frac {2}{\varepsilon _{r}} \bar {P}_{z,s} \\ && +\, i\frac {\bar {k}_{s}}{2\bar {\omega }_{0} \sqrt {\varepsilon _{r}}} \frac {\partial }{\partial \tau } (\bar {E}_{+,s} + \bar {E}_{-,s}) - \frac {2}{\varepsilon _{r}} \bar {J}_{s} f, \label {eq11} \end{eqnarray}$$ Thus, the single resonance occurs when the dispersion relation of the waveguide (left-hand side of Equation (3.2)) coincides with that of the electron (right-hand side of Equation (3.2)) at the resonant frequency (![]() $\omega _{0}$) of the medium.
$\omega _{0}$) of the medium.
The dynamics of the wake can be divided into three parts. In the first part of the amplification, where the PID is weakly depleted i.e., ![]() $\bar{N}\simeq 1$, known also as the linear regime, the solution of Equations (2.3)–(2.7) assuming a single-mode longitudinal wake is
$\bar{N}\simeq 1$, known also as the linear regime, the solution of Equations (2.3)–(2.7) assuming a single-mode longitudinal wake is
 $$\begin{eqnarray} \bar {E}_{z,s0} &=& i \frac {\bar {J}_{s}}{\varepsilon _{r}} \left [A_{1} \int _0^\tau \!e^{i\Omega _{1} (\tau -\tau ')}f(\tau ')d\tau ' \right . \\ && \left . +\, A_{2} \int _0^\tau \!e^{i\Omega _{2} (\tau -\tau ')}f(\tau ')d\tau ' \right ] ,\label {eq13} \end{eqnarray}$$
$$\begin{eqnarray} \bar {E}_{z,s0} &=& i \frac {\bar {J}_{s}}{\varepsilon _{r}} \left [A_{1} \int _0^\tau \!e^{i\Omega _{1} (\tau -\tau ')}f(\tau ')d\tau ' \right . \\ && \left . +\, A_{2} \int _0^\tau \!e^{i\Omega _{2} (\tau -\tau ')}f(\tau ')d\tau ' \right ] ,\label {eq13} \end{eqnarray}$$ $$\begin{equation} \label {eq14} \Omega _{1,2} = i \frac {\Delta \bar {\omega }}{4} \left (1 \pm \sqrt {1 + \frac {16\bar {N}}{\varepsilon _{c} \Delta \bar {\omega }^{2}}} \right ), \end{equation}$$
$$\begin{equation} \label {eq14} \Omega _{1,2} = i \frac {\Delta \bar {\omega }}{4} \left (1 \pm \sqrt {1 + \frac {16\bar {N}}{\varepsilon _{c} \Delta \bar {\omega }^{2}}} \right ), \end{equation}$$ where it is assumed that ![]() $|\Omega _{1,2}|\ll \bar{\omega }_{0}$ and
$|\Omega _{1,2}|\ll \bar{\omega }_{0}$ and ![]() $\bar{N}$ is constant. In the limit of
$\bar{N}$ is constant. In the limit of ![]() $\frac{1}{\sqrt{\varepsilon _{c}}}\gg \Delta \bar{\omega }$ and
$\frac{1}{\sqrt{\varepsilon _{c}}}\gg \Delta \bar{\omega }$ and ![]() $\bar{N} = 1$ the growth rate is
$\bar{N} = 1$ the growth rate is
and the decay rate is
At the limit of ![]() $\tau \gg \tau _{0}$ and
$\tau \gg \tau _{0}$ and ![]() $\beta \to 1$ the longitudinal wake is
$\beta \to 1$ the longitudinal wake is
Clearly, in the linear regime the wake is growing exponentially. Moreover, for a trigger bunch satisfying the Cerenkov condition or ![]() $\varepsilon _{c}\to 0$ the growth rate can be significantly larger than the medium bandwidth
$\varepsilon _{c}\to 0$ the growth rate can be significantly larger than the medium bandwidth ![]() $\Delta \bar{\omega }$. This is in contrast to the growth rate of source-free EM pulse propagation in an active medium which is limited by the medium’s bandwidth
$\Delta \bar{\omega }$. This is in contrast to the growth rate of source-free EM pulse propagation in an active medium which is limited by the medium’s bandwidth ![]() $\Delta \bar{\omega }$.
$\Delta \bar{\omega }$.
In the second part of the amplification the PID is significantly depleted (![]() $|\bar{N}|\ll 1$) as a result of the stimulated emission (right-hand side of Equation (2.8)), thus reducing the effective gain of the medium. In this nonlinear regime of amplification, where the PID is getting depleted and the wake is intense, both the amplified wake and the PID can experience Rabi oscillations[Reference Siegman24] before reaching the third regime of deep saturation. In the latter case the PID is completely depleted (
$|\bar{N}|\ll 1$) as a result of the stimulated emission (right-hand side of Equation (2.8)), thus reducing the effective gain of the medium. In this nonlinear regime of amplification, where the PID is getting depleted and the wake is intense, both the amplified wake and the PID can experience Rabi oscillations[Reference Siegman24] before reaching the third regime of deep saturation. In the latter case the PID is completely depleted (![]() $\bar{N}\simeq 0$) and as a result the effective gain is zero. Hence, the medium is transparent to the propagating wake and the interaction reaches full saturation.
$\bar{N}\simeq 0$) and as a result the effective gain is zero. Hence, the medium is transparent to the propagating wake and the interaction reaches full saturation.
The value of the saturated wake can be found from the energy conservation (Equation (2.9)). Assuming that ![]() $\bar{N}(\tau =0)=1$ and at
$\bar{N}(\tau =0)=1$ and at ![]() $\tau = 0$ most of the energy is stored in the active medium rather than the trigger bunch (
$\tau = 0$ most of the energy is stored in the active medium rather than the trigger bunch (![]() $\bar{W}_{b,s}(\tau )\ll 1$) then Equation (2.9) becomes
$\bar{W}_{b,s}(\tau )\ll 1$) then Equation (2.9) becomes
In the saturation regime where ![]() $\bar{N}(\tau = \tau _{sat}) = 0$ one can obtain from Equation (3.9) that the value of the saturated wake is
$\bar{N}(\tau = \tau _{sat}) = 0$ one can obtain from Equation (3.9) that the value of the saturated wake is
and in real units it reads
Clearly, the value of the saturated wake is proportional to the square root of the initial PID, ![]() $N_{0}$. Moreover, since for a large mode number (
$N_{0}$. Moreover, since for a large mode number (![]() $s\gg 1$)
$s\gg 1$) ![]() $|J_{1}(p_{s}\simeq s\pi )| \sim \sqrt{2/\pi ^{2}s}$, the saturation value is proportional to the square root of the mode number or (from Equation (3.2)) the waveguide radius.
$|J_{1}(p_{s}\simeq s\pi )| \sim \sqrt{2/\pi ^{2}s}$, the saturation value is proportional to the square root of the mode number or (from Equation (3.2)) the waveguide radius.
To determine the saturation time we first evaluate the time interval of the quasi-linear regime and then the nonlinear regime. We define the time interval of the quasi-linear regime to be from the point where the trigger bunch ends (![]() $\tau = \tau _{1}$) until the point where the PID reaches its first time zero,
$\tau = \tau _{1}$) until the point where the PID reaches its first time zero, ![]() $\tau _{d}\colon \bar{N}(\tau =\tau _{1} + \tau _{d}) = 0$. Motivated by the linear regime (see Equations (3.4) and (3.7)), where the amplitude during
$\tau _{d}\colon \bar{N}(\tau =\tau _{1} + \tau _{d}) = 0$. Motivated by the linear regime (see Equations (3.4) and (3.7)), where the amplitude during ![]() $\tau _{1} <\tau <\tau _{1} +\tau _{d} $ satisfies
$\tau _{1} <\tau <\tau _{1} +\tau _{d} $ satisfies
wherein ![]() $\bar{\Omega }$ is virtually constant, in the nonlinear regime this term is assumed to vary according to the PID, namely,
$\bar{\Omega }$ is virtually constant, in the nonlinear regime this term is assumed to vary according to the PID, namely, ![]() $\bar{\Omega } = i\Omega _{1} \sqrt{\bar{N}} \simeq \frac{\sqrt{\bar{N}}}{\sqrt{\varepsilon _{c}} - \frac{\Delta \bar{\omega }}{4}}$. Using Equation (3.9) the nonlinear growth rate is
$\bar{\Omega } = i\Omega _{1} \sqrt{\bar{N}} \simeq \frac{\sqrt{\bar{N}}}{\sqrt{\varepsilon _{c}} - \frac{\Delta \bar{\omega }}{4}}$. Using Equation (3.9) the nonlinear growth rate is ![]() $\bar{\Omega }(\tau ) = \bar{\Omega }_{0} \sqrt{1-\frac{1}{2}\varepsilon _{r} |\bar{E}_{z,s0}(\tau )|^{2}}$, where
$\bar{\Omega }(\tau ) = \bar{\Omega }_{0} \sqrt{1-\frac{1}{2}\varepsilon _{r} |\bar{E}_{z,s0}(\tau )|^{2}}$, where ![]() $\bar{\Omega }_{0} = \frac{1}{\sqrt{\varepsilon _{c}}} - \frac{\Delta \bar{\omega }}{4}$. The solution of Equation (3.12) at the first depletion point in real units is
$\bar{\Omega }_{0} = \frac{1}{\sqrt{\varepsilon _{c}}} - \frac{\Delta \bar{\omega }}{4}$. The solution of Equation (3.12) at the first depletion point in real units is
where the wake just behind the trigger bunch (calculated from Equation (3.3)) is
 $$\begin{eqnarray} \bar {E}_{z,s0} (\tau = \tau _{1}) &=& i \frac {\bar {J}_{s0}}{\varepsilon _{r}} \left \{ - \frac {A_{1}}{i\Omega _{1}} [1-e^{i\Omega _{1} (\tau _{1} -\tau _{0} )}]\right . \\ && \left . - \frac {A_{2}}{i\Omega _{2}} [1-e^{i\Omega _{2} (\tau _{1} -\tau _{0} )}] \right \}. \label {eq24} \end{eqnarray}$$
$$\begin{eqnarray} \bar {E}_{z,s0} (\tau = \tau _{1}) &=& i \frac {\bar {J}_{s0}}{\varepsilon _{r}} \left \{ - \frac {A_{1}}{i\Omega _{1}} [1-e^{i\Omega _{1} (\tau _{1} -\tau _{0} )}]\right . \\ && \left . - \frac {A_{2}}{i\Omega _{2}} [1-e^{i\Omega _{2} (\tau _{1} -\tau _{0} )}] \right \}. \label {eq24} \end{eqnarray}$$ where ![]() $\bar{\omega }_{R} = \sqrt{ \varepsilon _{r} (|\bar{E}_{z,s0}|^{2} + |\frac{\bar{E}_{+,s0} - \bar{E}_{-,s0}}{2} |^{2} )}$ is the normalized Rabi frequency.
$\bar{\omega }_{R} = \sqrt{ \varepsilon _{r} (|\bar{E}_{z,s0}|^{2} + |\frac{\bar{E}_{+,s0} - \bar{E}_{-,s0}}{2} |^{2} )}$ is the normalized Rabi frequency.
Since ![]() $\bar{E}_{\pm } \approx \frac{i\bar{k}_{s0}}{\bar{\omega }_{0} \sqrt{\varepsilon _{r}} \Delta \varepsilon _{\mp }}\bar{E}_{z,s0}$, the Rabi frequency in physical units is
$\bar{E}_{\pm } \approx \frac{i\bar{k}_{s0}}{\bar{\omega }_{0} \sqrt{\varepsilon _{r}} \Delta \varepsilon _{\mp }}\bar{E}_{z,s0}$, the Rabi frequency in physical units is ![]() $\omega _{R}^{2} = \omega _{R,0}^{2} \frac{J_{1}^{2} (p_{s0})}{\varepsilon _{c}}$, where
$\omega _{R}^{2} = \omega _{R,0}^{2} \frac{J_{1}^{2} (p_{s0})}{\varepsilon _{c}}$, where ![]() $\omega _{R,0} = \frac{\mu |E_{z,s0}|}{\sqrt{\varepsilon _{r}} \hslash }$ is in the same form as the Rabi frequency in a homogeneous medium.
$\omega _{R,0} = \frac{\mu |E_{z,s0}|}{\sqrt{\varepsilon _{r}} \hslash }$ is in the same form as the Rabi frequency in a homogeneous medium.
For a relativistic bunch that travels close to the Cerenkov velocity (![]() $\beta \to 1$ and
$\beta \to 1$ and ![]() $\varepsilon _{c} \ll 1$) the Rabi frequency is
$\varepsilon _{c} \ll 1$) the Rabi frequency is ![]() $\bar{\omega }_{R} \approx |\bar{E}_{z,s0}|/\sqrt{\varepsilon _{c}}$. Hence, in the nonlinear regime where
$\bar{\omega }_{R} \approx |\bar{E}_{z,s0}|/\sqrt{\varepsilon _{c}}$. Hence, in the nonlinear regime where ![]() $| \bar{E}_{z,s0}|\approx |\bar{E}_{sat}| = \sqrt{2/\varepsilon _{r}}$ the wake oscillates at
$| \bar{E}_{z,s0}|\approx |\bar{E}_{sat}| = \sqrt{2/\varepsilon _{r}}$ the wake oscillates at
and the solution of Equation (3.15) is
where ![]() $\tau ' = \tau _{1} + \tau _{d}$ and
$\tau ' = \tau _{1} + \tau _{d}$ and ![]() $\bar{N}_{0}^{'} = \frac{\partial \bar{N}}{\partial \tau }|_{\tau =\tau '}$. Thus, we define according to Equation (3.17) the time in which the oscillations of the PID relax to be
$\bar{N}_{0}^{'} = \frac{\partial \bar{N}}{\partial \tau }|_{\tau =\tau '}$. Thus, we define according to Equation (3.17) the time in which the oscillations of the PID relax to be
Therefore, from Equations (3.13) and (3.18) the saturation time is given by
and in real units it is
where ![]() $\Omega = \frac{\omega _{p}}{2\sqrt{\varepsilon _{r} \varepsilon _{c}}} - \frac{\Delta \omega }{4}$ is the linear growth rate for
$\Omega = \frac{\omega _{p}}{2\sqrt{\varepsilon _{r} \varepsilon _{c}}} - \frac{\Delta \omega }{4}$ is the linear growth rate for ![]() $\beta \to 1$ and
$\beta \to 1$ and ![]() $\varepsilon _{c} \ll 1$. In addition,
$\varepsilon _{c} \ll 1$. In addition, ![]() $\bar{E}_{z,s0} (\tau _{1})$ is given in Equation (3.14).
$\bar{E}_{z,s0} (\tau _{1})$ is given in Equation (3.14).
Finally, the theoretical spot size, ![]() $R_{sp}$, of the longitudinal wake can be calculated through
$R_{sp}$, of the longitudinal wake can be calculated through ![]() $J_{0}(p_{s0}R_{sp}/R)=0$. Since the first zero of
$J_{0}(p_{s0}R_{sp}/R)=0$. Since the first zero of ![]() $J_{0}(x)$ is
$J_{0}(x)$ is ![]() ${\sim }2.4$ and from the single-resonance condition
${\sim }2.4$ and from the single-resonance condition ![]() $p_{s0} = R\frac{\omega _{0}}{c}\sqrt{\varepsilon _{r} \varepsilon _{c}}$, we obtain that the spot size of the longitudinal wake is
$p_{s0} = R\frac{\omega _{0}}{c}\sqrt{\varepsilon _{r} \varepsilon _{c}}$, we obtain that the spot size of the longitudinal wake is
4. Simulations
In this section we show the wake dynamics for an active ![]() $\mathrm{CO}_{2}$ gas mixture with the set of parameters that is given in Table 1.
$\mathrm{CO}_{2}$ gas mixture with the set of parameters that is given in Table 1.
Table 1. Structure parameters of our studied example. Note that the set of parameters used here is the same as in Ref. [Reference Pantell and Puthoff22].

Since the bunch profile is continuously changing except for a finite number of points where it can have first-order discontinuity, the initial conditions of all the envelopes are set to zero but the initial PID is ![]() $\bar{N}(\tau =0)=1$.
$\bar{N}(\tau =0)=1$.
Figure 2 shows the wake and the medium dynamics on the waveguide axis (![]() $r=0$). In this example the trigger bunch (Figures 2(a) and (b) dashed curves) which appears at
$r=0$). In this example the trigger bunch (Figures 2(a) and (b) dashed curves) which appears at ![]() $\tau =\tau _{0}=0.05$ and ends at
$\tau =\tau _{0}=0.05$ and ends at ![]() $\tau =\tau _{1}=0.0813$ (corresponding to a bunch length of
$\tau =\tau _{1}=0.0813$ (corresponding to a bunch length of ![]() $L_{b}=300\ \mu \mathrm{m}$) generates the initial wake. As seen in Figure 2(a), the wake (solid curve) amplification begins in the linear regime, where the PID (dashed–dotted curve) is weakly depleted (
$L_{b}=300\ \mu \mathrm{m}$) generates the initial wake. As seen in Figure 2(a), the wake (solid curve) amplification begins in the linear regime, where the PID (dashed–dotted curve) is weakly depleted (![]() $\bar{N}(\tau ) \approx \bar{N}(0) = 1$). In this regime the growth rate of the medium is constant, which results in exponential amplification of the wake (Figure 2(b)).
$\bar{N}(\tau ) \approx \bar{N}(0) = 1$). In this regime the growth rate of the medium is constant, which results in exponential amplification of the wake (Figure 2(b)).

Figure 2. (a) The dynamics of the wake ![]() $\bar{E}_{z}(\tau ,r=0)$ on the axis (solid curve), the PID,
$\bar{E}_{z}(\tau ,r=0)$ on the axis (solid curve), the PID, ![]() $\bar{N}$ (dashed–dotted curve), and the trigger bunch profile,
$\bar{N}$ (dashed–dotted curve), and the trigger bunch profile, ![]() $f$ (dashed curve). The value of the saturated wake
$f$ (dashed curve). The value of the saturated wake ![]() $|\bar{E}_{sat}|=\sqrt{2}$ is shown by the dotted curve. (b) A comparison of the nonlinear wake dynamics in real units (solid curve) with the linear wake dynamics (dots). In addition, the profile of the bunch is drawn as a reference (dashed curve).
$|\bar{E}_{sat}|=\sqrt{2}$ is shown by the dotted curve. (b) A comparison of the nonlinear wake dynamics in real units (solid curve) with the linear wake dynamics (dots). In addition, the profile of the bunch is drawn as a reference (dashed curve).

Figure 3. The mode spectrum of the wake ![]() $|E_{z,s}(\beta cT = 10\ \mathrm{cm},r=0)|$. Here, the single-resonance mode is
$|E_{z,s}(\beta cT = 10\ \mathrm{cm},r=0)|$. Here, the single-resonance mode is ![]() $s0=360$.
$s0=360$.
As the wake is amplified the PID is depleted. In this nonlinear regime of amplification, where the PID is significantly reduced and the wake is intense, Figure 2(a) shows that the amplified wake and the PID experience Rabi oscillations. Finally, when the PID relaxes to zero, the effective gain of the medium is zero and the wake reaches deep saturation.
Figure 2(a) shows that the normalized wake reaches a saturation value similar to the theoretical calculation (Equation (3.10) with ![]() $\varepsilon _{r}\simeq 1$) of
$\varepsilon _{r}\simeq 1$) of ![]() $\bar{E}_{sat} = \sqrt{2}$. Also, the normalized saturation time in this example is
$\bar{E}_{sat} = \sqrt{2}$. Also, the normalized saturation time in this example is ![]() $\tau _{sat}^{sim} = \tau _{d}^{sim} + \tau _{r}^{sim} = 1.32$, where the depletion time is
$\tau _{sat}^{sim} = \tau _{d}^{sim} + \tau _{r}^{sim} = 1.32$, where the depletion time is ![]() $ \tau _{d}^{sim} = 0.8448$ and the relaxation time is
$ \tau _{d}^{sim} = 0.8448$ and the relaxation time is ![]() $\tau _{r}^{sim} = 0.512$. These time parameters are in good agreement with the theoretical formulas (Equations (3.13) and (3.18)) of
$\tau _{r}^{sim} = 0.512$. These time parameters are in good agreement with the theoretical formulas (Equations (3.13) and (3.18)) of ![]() $\tau _{d}^{th} = 0.8448$,
$\tau _{d}^{th} = 0.8448$, ![]() $\tau _{r}^{th} = 0.508$ and
$\tau _{r}^{th} = 0.508$ and ![]() $\tau _{sat}^{th} = 1.353$.
$\tau _{sat}^{th} = 1.353$.
Figure 2(b) shows in a logarithmic scale the nonlinear wake amplification in physical units of ![]() $\mathrm{V\ m}^{-1}$. Clearly, in the linear regime the wake (solid curve) grows exponentially and it saturates about 6 cm behind the trigger bunch to a value of
$\mathrm{V\ m}^{-1}$. Clearly, in the linear regime the wake (solid curve) grows exponentially and it saturates about 6 cm behind the trigger bunch to a value of ![]() $0.7\ \mathrm{GV\ m}^{-1}$. In addition, Figure 2(b) shows in the linear regime good agreement between the nonlinear wake dynamics (solid curve) and the linear wake dynamics (dots) which is calculated for
$0.7\ \mathrm{GV\ m}^{-1}$. In addition, Figure 2(b) shows in the linear regime good agreement between the nonlinear wake dynamics (solid curve) and the linear wake dynamics (dots) which is calculated for ![]() $\bar{N}(\tau ) = 1$.
$\bar{N}(\tau ) = 1$.
Similarly to the linear regime approach[Reference Voin, Kimura and Schächter18, Reference Voin and Schächter19], the waveguide radius is chosen such that only a single TM mode will be in resonance with the active medium. Indeed, Figure 3 shows at ![]() $\tau = 1.67$ that among the first 500 modes of
$\tau = 1.67$ that among the first 500 modes of ![]() $\bar{E}_{z,s}$ that are calculated in the simulation only
$\bar{E}_{z,s}$ that are calculated in the simulation only ![]() $s0=360$ is the dominant mode.
$s0=360$ is the dominant mode.
Figure 4 shows the two-dimensional plot of the longitudinal wake. At ![]() $\tau =0.95$, corresponding to
$\tau =0.95$, corresponding to ![]() $z-\beta ct=50\; \mathrm{mm}$, Figures 4(b) and (c) show that the radius of the spot is about
$z-\beta ct=50\; \mathrm{mm}$, Figures 4(b) and (c) show that the radius of the spot is about ![]() $100\ \mu \mathrm{m}$, which is smaller than the waveguide radius of
$100\ \mu \mathrm{m}$, which is smaller than the waveguide radius of ![]() $R = 50.6475\ \mathrm{mm}$. This spot size radius is in good agreement with our theoretical expression (Equation (3.21)) of
$R = 50.6475\ \mathrm{mm}$. This spot size radius is in good agreement with our theoretical expression (Equation (3.21)) of ![]() $107.6\ \mu \mathrm{m}$. This means that such a wake can accelerate a second bunch of electrons with a beam radius of less than a hundred microns.
$107.6\ \mu \mathrm{m}$. This means that such a wake can accelerate a second bunch of electrons with a beam radius of less than a hundred microns.

Figure 4. (a) A two-dimensional plot of the longitudinal wake ![]() $|E_{z}|$. The green rectangle is the location of the trigger bunch. (b) The same as (a) but in the region that is marked in magenta in (a). (c) The radial dependence of the wake at
$|E_{z}|$. The green rectangle is the location of the trigger bunch. (b) The same as (a) but in the region that is marked in magenta in (a). (c) The radial dependence of the wake at ![]() $z - \beta ct = 50\ \mathrm{mm}$.
$z - \beta ct = 50\ \mathrm{mm}$.
The energy balance of the structure shown in Figure 5 reveals that initially most of the energy comes from the active medium (Figure 5(c)) and only a small fraction of it comes from the trigger bunch (Figure 5(b)). In the steady state of the amplification all the stored energy from the active medium is transferred to EM energy (Figure 5(a)) such that the energy of the longitudinal wake, ![]() $\bar{W}^{(EM,lo)} = \sum _s{\bar{W}_{s}^{(EM,lo)}}$, is the same as that of the transverse wake,
$\bar{W}^{(EM,lo)} = \sum _s{\bar{W}_{s}^{(EM,lo)}}$, is the same as that of the transverse wake, ![]() $\bar{W}^{(EM,tr)} = \sum _s {\bar{W}_{s}^{(EM,tr)}}$. In addition, the stored energy of level 1 in the active medium,
$\bar{W}^{(EM,tr)} = \sum _s {\bar{W}_{s}^{(EM,tr)}}$. In addition, the stored energy of level 1 in the active medium, ![]() $\bar{W}_{N1}(\tau ) = \frac{1}{2} [\bar{W}_{tot}(\tau = 0) - \bar{W}_{N}(\tau )]$, is equal to that of level 2,
$\bar{W}_{N1}(\tau ) = \frac{1}{2} [\bar{W}_{tot}(\tau = 0) - \bar{W}_{N}(\tau )]$, is equal to that of level 2, ![]() $\bar{W}_{N2} (\tau ) = \frac{1}{2} [\bar{W}_{tot} (\tau =0) + \bar{W}_{N}(\tau )]$ (Figure 5(c)), which means that in the steady state the total stored energy in the active medium is zero,
$\bar{W}_{N2} (\tau ) = \frac{1}{2} [\bar{W}_{tot} (\tau =0) + \bar{W}_{N}(\tau )]$ (Figure 5(c)), which means that in the steady state the total stored energy in the active medium is zero, ![]() $\bar{W}_{N} = \bar{W}_{N2} - \bar{W}_{N1}=0$. The deviation from energy conservation
$\bar{W}_{N} = \bar{W}_{N2} - \bar{W}_{N1}=0$. The deviation from energy conservation ![]() $\eta (\%) = 100 \times |\bar{W}_{tot} (\tau ) - \bar{W}_{tot} (\tau =0)|/\bar{W}_{tot} (\tau =0)$ is shown in Figure 5(d) and can be used for the numerical simulation error which in our example is about
$\eta (\%) = 100 \times |\bar{W}_{tot} (\tau ) - \bar{W}_{tot} (\tau =0)|/\bar{W}_{tot} (\tau =0)$ is shown in Figure 5(d) and can be used for the numerical simulation error which in our example is about ![]() $6\times 10^{-5}\%$.
$6\times 10^{-5}\%$.

Figure 5. The energy conservation. Here, ![]() $\bar{W}_{N1}$ is the energy of the ground state and
$\bar{W}_{N1}$ is the energy of the ground state and ![]() $\bar{W}_{N2}$ is the energy of the excited state; (d) shows the deviation from energy conservation.
$\bar{W}_{N2}$ is the energy of the excited state; (d) shows the deviation from energy conservation.
As mentioned previously, the shape of the single-mode wake is sensitive to the active medium bandwidth, ![]() $\Delta \bar{\omega }$, and the Cerenkov parameter,
$\Delta \bar{\omega }$, and the Cerenkov parameter, ![]() $\varepsilon _{c}$. These two parameters affect the Rabi frequency
$\varepsilon _{c}$. These two parameters affect the Rabi frequency ![]() $\bar{\omega }_{R}$ and the relaxation time
$\bar{\omega }_{R}$ and the relaxation time ![]() $\tau _{r}$. Figure 6 shows the dynamics of the wake for different Cerenkov and bandwidth parameters. The solid curve corresponds to the same wake dynamics as in Figure 6(a) with
$\tau _{r}$. Figure 6 shows the dynamics of the wake for different Cerenkov and bandwidth parameters. The solid curve corresponds to the same wake dynamics as in Figure 6(a) with ![]() $\bar{\omega }_{R} = 37.6$ and
$\bar{\omega }_{R} = 37.6$ and ![]() $\Delta \bar{\omega } = 39.4$. As seen for a Cerenkov parameter five times larger than our former example (dashed curve) the number of Rabi oscillations is significantly lowered. However, the saturation length,
$\Delta \bar{\omega } = 39.4$. As seen for a Cerenkov parameter five times larger than our former example (dashed curve) the number of Rabi oscillations is significantly lowered. However, the saturation length, ![]() $\tau _{sat}$, is greatly increased as a result of increased
$\tau _{sat}$, is greatly increased as a result of increased ![]() $\tau _{d}$—see Equation (3.13). It may be possible to suppress the Rabi oscillation when the medium bandwidth is enlarged. However, increasing the bandwidth can result in multi-mode interaction if
$\tau _{d}$—see Equation (3.13). It may be possible to suppress the Rabi oscillation when the medium bandwidth is enlarged. However, increasing the bandwidth can result in multi-mode interaction if ![]() $|\Delta \bar{\omega }_{s}| < \Delta \bar{\omega }$. Figure 6(a) shows (dotted curve) that for a bandwidth that is five times larger the shape of the wake in the steady-state regime has a steady oscillation which results from multi-mode coupling. In this example,
$|\Delta \bar{\omega }_{s}| < \Delta \bar{\omega }$. Figure 6(a) shows (dotted curve) that for a bandwidth that is five times larger the shape of the wake in the steady-state regime has a steady oscillation which results from multi-mode coupling. In this example, ![]() $|\Delta \bar{\omega }_{s_{0} \pm 1}| = 75 < 88.06 = \Delta \bar{\omega }$, whereas for the first single-mode propagation we have
$|\Delta \bar{\omega }_{s_{0} \pm 1}| = 75 < 88.06 = \Delta \bar{\omega }$, whereas for the first single-mode propagation we have ![]() $|\Delta \bar{\omega }_{s_{0}\pm 1}| = 167 > 39.4 = \Delta \bar{\omega }$, where
$|\Delta \bar{\omega }_{s_{0}\pm 1}| = 167 > 39.4 = \Delta \bar{\omega }$, where ![]() $s_{0} = 360$. Figure 6(b) shows the mode spectrum of the wake. As seen for large bandwidth (dotted curve), the adjacent modes (
$s_{0} = 360$. Figure 6(b) shows the mode spectrum of the wake. As seen for large bandwidth (dotted curve), the adjacent modes (![]() $s=359$ and 361) participate in the wake dynamics shown in Figure 6(a) (dotted curve).
$s=359$ and 361) participate in the wake dynamics shown in Figure 6(a) (dotted curve).

Figure 6. The wake dynamics (a) and the wake spectrum (b) for various Cerenkov parameters and bandwidths. The solid curve corresponds to ![]() $\varepsilon _{c}=\varepsilon _{c,0}$ and
$\varepsilon _{c}=\varepsilon _{c,0}$ and ![]() $\Delta \omega = \Delta \omega _{0}$, where
$\Delta \omega = \Delta \omega _{0}$, where ![]() $\varepsilon _{c,0}$ and
$\varepsilon _{c,0}$ and ![]() $\Delta \omega _{0}$ are the Cerenkov and bandwidth parameters as in Figure 2. The dotted curve corresponds to
$\Delta \omega _{0}$ are the Cerenkov and bandwidth parameters as in Figure 2. The dotted curve corresponds to ![]() $\varepsilon _{c}=\varepsilon _{c,0}$ and
$\varepsilon _{c}=\varepsilon _{c,0}$ and ![]() $\Delta \omega = 5\Delta \omega _{0}$. The dashed curve corresponds to
$\Delta \omega = 5\Delta \omega _{0}$. The dashed curve corresponds to ![]() $\varepsilon _{c}=5\varepsilon _{c,0}$ and
$\varepsilon _{c}=5\varepsilon _{c,0}$ and ![]() $\Delta \omega = \Delta \omega _{0}$.
$\Delta \omega = \Delta \omega _{0}$.
The two major parameters that characterize our scheme are the value of the wake at the saturation and the saturation length. The sensitivities of these two quantities to the other parameters of the scheme are revealed in Figure 7. Specifically, Figure 7 shows the dependence of the value of the saturated wake (Figure 7(a)) and the saturation time (Figure 7(b)) on the waveguide radius, the dielectric constant, the active medium bandwidth, the bunch energy and the bunch radius. Clearly, the saturation value of the wake is significantly dependent on the waveguide radius, ![]() $R$, the medium bandwidth,
$R$, the medium bandwidth, ![]() $\Delta \omega $, and the parameter
$\Delta \omega $, and the parameter ![]() $\varepsilon _{r} -1$, which is proportional to the Cerenkov parameter
$\varepsilon _{r} -1$, which is proportional to the Cerenkov parameter ![]() $\varepsilon _{c}$.
$\varepsilon _{c}$.

Figure 7. The dependence of the saturation value (a) and saturation length (b) on the waveguide and trigger bunch parameters. Here, the index 0 represents the parameter value as in Figure 2 or Ref. [Reference Voin, Kimura and Schächter18].
For a relativistic beam the scaling law of the saturated wake on the structure parameters can be explained by our analytical calculations (Equation (3.11)) and the single-resonance condition of ![]() $p_{s} = R (\omega _{0}/c) \sqrt{\varepsilon _{r} \varepsilon _{c}}$ (see Equation (3.2)),
$p_{s} = R (\omega _{0}/c) \sqrt{\varepsilon _{r} \varepsilon _{c}}$ (see Equation (3.2)),
where it is assumed that ![]() $\bar{N} \propto \Delta \bar{\omega }$ (because of
$\bar{N} \propto \Delta \bar{\omega }$ (because of ![]() $\omega _{p} = \omega _{0} \sqrt{\frac{2N_{0} \mu ^{2}}{\varepsilon _{0} \hslash \omega _{0}}}$ and
$\omega _{p} = \omega _{0} \sqrt{\frac{2N_{0} \mu ^{2}}{\varepsilon _{0} \hslash \omega _{0}}}$ and ![]() $\omega _{p} = \sqrt{2c\Delta \omega \alpha }$, where
$\omega _{p} = \sqrt{2c\Delta \omega \alpha }$, where ![]() $\alpha $ is the small signal gain). This means that the waveguide radius and bandwidth strongly affect the saturation – compared with the Cerenkov parameter. In addition, for a relativistic beam the saturation value does not depend on the beam radius and energy.
$\alpha $ is the small signal gain). This means that the waveguide radius and bandwidth strongly affect the saturation – compared with the Cerenkov parameter. In addition, for a relativistic beam the saturation value does not depend on the beam radius and energy.
Similarly, the scaling law of the saturation time on the structure parameters can be explained by our analytical calculations of the saturation time (Equations (3.14) and (3.20)) and the single resonance condition of ![]() $p_{s} = R(\omega _{0} /c)\sqrt{\varepsilon _{r}\varepsilon _{c}}$ (see Equation (3.2)),
$p_{s} = R(\omega _{0} /c)\sqrt{\varepsilon _{r}\varepsilon _{c}}$ (see Equation (3.2)),
For a single resonant mode, the saturation time is strongly dependent on the Cerenkov parameter and the medium bandwidth but weakly dependent on the waveguide radius and beam spot size. Indeed, Figure 7(b) confirms the scaling law in Equation (4.2), but not for the waveguide radius at ![]() $\chi = 0.2$.
$\chi = 0.2$.
At this point the saturation time is significantly large because the deviation from satisfying the resonance condition is larger than for a larger waveguide radius ![]() $(\chi >0.2)$. Specifically, for
$(\chi >0.2)$. Specifically, for ![]() $R=0.2R_{0}$ the deviation from the nearest resonance mode is
$R=0.2R_{0}$ the deviation from the nearest resonance mode is ![]() $\Delta \bar{\omega }_{s} (s=72)=167$, whereas for
$\Delta \bar{\omega }_{s} (s=72)=167$, whereas for ![]() $R=0.5R_{0}$ the deviation is
$R=0.5R_{0}$ the deviation is ![]() $\Delta \bar{\omega }_{s}(s=180)=42$. When the waveguide radius is close to satisfying a single resonance, then there is a small dependence on the saturation time, as confirmed by the logarithmic dependence in Equation (4.2). Otherwise the wake growth rate is significantly reduced.
$\Delta \bar{\omega }_{s}(s=180)=42$. When the waveguide radius is close to satisfying a single resonance, then there is a small dependence on the saturation time, as confirmed by the logarithmic dependence in Equation (4.2). Otherwise the wake growth rate is significantly reduced.
5. Discussion and conclusions
In this paper we present the nonlinear aspects of a new scheme of electron acceleration by an active medium. In contrast to plasma-based accelerators, where the energy for generating the intense wake originates in the intense laser pulse, in our scheme the energy source is stored in excited atoms/molecules. Most importantly, we have shown that a centimeter-sized cylindrical waveguide filled with a ![]() $\mathrm{CO}_{2}$ gas mixture can generate gradients of the order of
$\mathrm{CO}_{2}$ gas mixture can generate gradients of the order of ![]() $\mathrm{GV\ m}^{-1}$ traveling at the trigger bunch velocity.
$\mathrm{GV\ m}^{-1}$ traveling at the trigger bunch velocity.
We analyzed the dynamics of the wake and the active medium both analytically and numerically. Our numerical simulations indicate that the dynamics of the wake can be divided into three regimes. In the first regime, known as the linear regime, the PID is nearly constant (![]() $\bar{N}\simeq 1$). Hence, the gain of the medium is constant which results in exponential growth of the wake. The second regime starts when the amplified wake reaches high intensity, and the PID is significantly reduced (
$\bar{N}\simeq 1$). Hence, the gain of the medium is constant which results in exponential growth of the wake. The second regime starts when the amplified wake reaches high intensity, and the PID is significantly reduced (![]() $\bar{N}\ll 1$) by the stimulated emission effect. In this regime both the PID and the wake can experience Rabi oscillations. The Rabi frequency in our confined structure can be significantly larger than in a boundless medium. More specifically, this frequency is inversely proportional to the square root of both the Cerenkov parameter and the mode number. Finally, in the third regime, when the Rabi oscillations are relaxed, the PID reaches complete depletion (
$\bar{N}\ll 1$) by the stimulated emission effect. In this regime both the PID and the wake can experience Rabi oscillations. The Rabi frequency in our confined structure can be significantly larger than in a boundless medium. More specifically, this frequency is inversely proportional to the square root of both the Cerenkov parameter and the mode number. Finally, in the third regime, when the Rabi oscillations are relaxed, the PID reaches complete depletion (![]() $\bar{N}\simeq 0$) and the wake reaches deep saturation.
$\bar{N}\simeq 0$) and the wake reaches deep saturation.
Energy conservation proves that most of the initial energy originates from the active medium, and in the deep saturation regime half of the initial stored energy is transferred to the longitudinal EM field component and the other half is transferred to the transverse EM field components.
To obtain maximum performance from our studied structure we should fulfill the following constraints. First, it is desired to design the structure for single-resonance-mode operation to obtain a constant value of the wake in the saturation regime. In order to avoid multi-mode propagation of adjacent frequencies, the active medium bandwidth should be narrow enough. Second, the spot size of the wake should be large enough in order to accelerate most of the trailing train bunch. We found that for single-mode propagation a large spot size is achieved for a small Cerenkov parameter. The last requirement is obviously the generation of a high gradient in a short saturation length.
On one hand, we have found that for a relativistic trigger bunch the saturation value is strongly dependent on the waveguide radius and the medium bandwidth but weakly dependent on the Cerenkov parameter. On the other hand, we have found that for single-mode propagation and a relativistic trigger bunch the saturation length is strongly dependent on the Cerenkov parameter and the medium bandwidth but weakly dependent on the waveguide and electron beam radius. Consequently, optimal performance may be achieved with a large waveguide radius filled with a high density of excited atoms and a trigger bunch that travels at a velocity slightly above the Cerenkov velocity. Interestingly, the short saturation length of the wake may be used as a seed pulse for backward Raman amplification in plasma[Reference Malkin, Shvets and Fisch25].
For a proper perspective, it is important to comment that the high value of the gradient is limited by self-focusing and ionization effects[Reference Boyd23], which are not analyzed here, but which may be overcome by using a vacuum channel, as previously mentioned in Section 1.
In spite of the relatively modest gradient, compared with laser plasma accelerators, our paradigm may benefit from a few aspects. First, our scheme can support staging[Reference Kimura, van Steenbergen, Babzien, Ben-Zvi, Campbell, Cline, Dilley, Gallardo, Gottschalk, He, Kusche, Liu, Pantell, Pogorelsky, Quimby, Skaritka, Steinhauer and Yakimenko26, Reference Dunning, Hemsing, Hast, Raubenheimer, Weathersby and Xiang27] in a fairly natural way. Second, our setup, in principle, does not seem to suffer from instabilities that may evolve in plasma at a high repetition rate. A typical repetition rate for laser plasma accelerators is less than 1 Hz for 100 J laser pulses with fs duration in a laser plasma accelerator[Reference Hooker6]. The various laser wake acceleration schemes in plasma take advantage of the fact that on the fs time scale all ion instabilities are far below threshold; at high repetition rate these instabilities may develop[Reference Kruer28]. Their suppression may require a dramatic reduction of the laser power.
Regarding our paradigm as a new source of coherent radiation excited by a trigger bunch, it possesses important features that distinguish it from a conventional laser driven by spontaneous emission. The most remarkable ones are the excitation of a specific mode number and wake propagation at the same phase and group velocity as the trigger bunch.
Acknowledgement
This work was supported by the Bi-National Science Foundation (BSF).