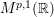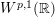1 Introduction
Wiener [Reference Wiener15] studied the class
![]() $A(\mathbb{T})$
of all continuous functions on the torus
$A(\mathbb{T})$
of all continuous functions on the torus
![]() $\mathbb{T}$
with the absolutely convergent Fourier series, and proved that
$\mathbb{T}$
with the absolutely convergent Fourier series, and proved that
![]() $F(z)=1/z$
operates on
$F(z)=1/z$
operates on
![]() $A(\mathbb{T})$
. Lévy [Reference Lévy9] gave an extension of this result by showing that an analytic function operates on
$A(\mathbb{T})$
. Lévy [Reference Lévy9] gave an extension of this result by showing that an analytic function operates on
![]() $A(\mathbb{T})$
, which is called the Wiener–Lévy Theorem. After that, there are many papers about operating functions on the same function spaces with respect to Fourier series by Helson, Kahane, Katznelson, Rudin, and so forth (see [Reference Helson, Kahane, Katznelson and Rudin6, Reference Rudin10]).
$A(\mathbb{T})$
, which is called the Wiener–Lévy Theorem. After that, there are many papers about operating functions on the same function spaces with respect to Fourier series by Helson, Kahane, Katznelson, Rudin, and so forth (see [Reference Helson, Kahane, Katznelson and Rudin6, Reference Rudin10]).
In this paper, we give the characterization of operating functions on modulation spaces
![]() $M^{p,1}(\mathbb{R})$
and Wiener amalgam spaces
$M^{p,1}(\mathbb{R})$
and Wiener amalgam spaces
![]() $W^{p,1}(\mathbb{R})$
. The modulation spaces
$W^{p,1}(\mathbb{R})$
. The modulation spaces
![]() $M^{p,q}$
and the Wiener amalgam spaces
$M^{p,q}$
and the Wiener amalgam spaces
![]() $W^{p,q}$
are two function spaces introduced by Feichtinger [Reference Feichtinger, Krishna, Radha and Thangavelu4]. The precise definition of these spaces will be given in Section 2, but the main idea of these spaces is to consider the space variable and the variable of its Fourier transform simultaneously. Let
$W^{p,q}$
are two function spaces introduced by Feichtinger [Reference Feichtinger, Krishna, Radha and Thangavelu4]. The precise definition of these spaces will be given in Section 2, but the main idea of these spaces is to consider the space variable and the variable of its Fourier transform simultaneously. Let
![]() $F$
be a complex-valued function on
$F$
be a complex-valued function on
![]() $\mathbb{R}^{2}$
and
$\mathbb{R}^{2}$
and
![]() $X=M^{p,1}(\mathbb{R})$
or
$X=M^{p,1}(\mathbb{R})$
or
![]() $W^{p,1}(\mathbb{R})$
. If
$W^{p,1}(\mathbb{R})$
. If
![]() $F(\text{Re}f,\text{Im}f)\in X$
for every
$F(\text{Re}f,\text{Im}f)\in X$
for every
![]() $f\in X$
, then we say that
$f\in X$
, then we say that
![]() $F$
operates on
$F$
operates on
![]() $X$
.
$X$
.
Concerning modulation spaces, Wiener amalgam spaces and operating functions, the following theorem is known.
Theorem A.
(Bhimani [Reference Bhimani2], Bhimani and Ratnakumar [Reference Bhimani and Ratnakumar3]) Let
![]() $1\leqslant p<\infty$
and
$1\leqslant p<\infty$
and
![]() $F$
be a complex-valued function on
$F$
be a complex-valued function on
![]() $\mathbb{R}^{2}$
. Suppose
$\mathbb{R}^{2}$
. Suppose
![]() $X=M^{p,1}(\mathbb{R})$
or
$X=M^{p,1}(\mathbb{R})$
or
![]() $W^{p,1}(\mathbb{R})$
. If
$W^{p,1}(\mathbb{R})$
. If
![]() $F$
operates on
$F$
operates on
![]() $X$
, then
$X$
, then
![]() $F$
is a real analytic function on
$F$
is a real analytic function on
![]() $\mathbb{R}^{2}$
with
$\mathbb{R}^{2}$
with
![]() $F(0)=0$
. Conversely, if
$F(0)=0$
. Conversely, if
![]() $F$
is a real analytic on
$F$
is a real analytic on
![]() $\mathbb{R}^{2}$
with
$\mathbb{R}^{2}$
with
![]() $F(0)=0$
, then
$F(0)=0$
, then
![]() $F$
operates on
$F$
operates on
![]() $M^{1,1}(\mathbb{R})(=W^{1,1}(\mathbb{R}))$
.
$M^{1,1}(\mathbb{R})(=W^{1,1}(\mathbb{R}))$
.
We remark that Theorem A answers negatively the open problem posed by Ruzhansky–Sugimoto–Wang [Reference Ruzhansky, Sugimoto and Wang11] about the general power type nonlinearity of the form
![]() $|u|^{\unicode[STIX]{x1D6FC}}u$
. In [Reference Bhimani2] and [Reference Bhimani and Ratnakumar3], they also propose an open problem: is the condition in Theorem A sufficient or not for
$|u|^{\unicode[STIX]{x1D6FC}}u$
. In [Reference Bhimani2] and [Reference Bhimani and Ratnakumar3], they also propose an open problem: is the condition in Theorem A sufficient or not for
![]() $p>1$
? This paper gives an affirmative answer to this problem. Our result is as follows.
$p>1$
? This paper gives an affirmative answer to this problem. Our result is as follows.
Theorem 1.1. Let
![]() $1\leqslant p<\infty$
and
$1\leqslant p<\infty$
and
![]() $F$
be a real analytic function on
$F$
be a real analytic function on
![]() $\mathbb{R}^{2}$
with
$\mathbb{R}^{2}$
with
![]() $F(0)=0$
. Suppose
$F(0)=0$
. Suppose
![]() $X=M^{p,1}(\mathbb{R})$
or
$X=M^{p,1}(\mathbb{R})$
or
![]() $W^{p,1}(\mathbb{R})$
. Then
$W^{p,1}(\mathbb{R})$
. Then
![]() $F$
operates on
$F$
operates on
![]() $X$
.
$X$
.
Since
![]() $F(s,t)=\frac{1}{(1+s^{2})(1+t^{2})}$
is a real analytic function on
$F(s,t)=\frac{1}{(1+s^{2})(1+t^{2})}$
is a real analytic function on
![]() $\mathbb{R}^{2}$
, we obtain
$\mathbb{R}^{2}$
, we obtain
![]() $F(\text{Re}f,\text{Im}f)\in X$
for all
$F(\text{Re}f,\text{Im}f)\in X$
for all
![]() $f\in X$
by Theorem 1.1.
$f\in X$
by Theorem 1.1.
Combining Theorems A and 1.1, we have the following characterization of operating functions on
![]() $M^{p,1}(\mathbb{R})$
and
$M^{p,1}(\mathbb{R})$
and
![]() $W^{p,1}(\mathbb{R})$
.
$W^{p,1}(\mathbb{R})$
.
Corollary 1.2. Let
![]() $1\leqslant p<\infty$
and
$1\leqslant p<\infty$
and
![]() $F$
be a complex-valued function on
$F$
be a complex-valued function on
![]() $\mathbb{R}^{2}$
. Suppose
$\mathbb{R}^{2}$
. Suppose
![]() $X=M^{p,1}(\mathbb{R})$
or
$X=M^{p,1}(\mathbb{R})$
or
![]() $W^{p,1}(\mathbb{R})$
. Then
$W^{p,1}(\mathbb{R})$
. Then
![]() $F$
operates on
$F$
operates on
![]() $X$
if and only if
$X$
if and only if
![]() $F$
is a real analytic function with
$F$
is a real analytic function with
![]() $F(0)=0$
.
$F(0)=0$
.
2 Preliminaries
The following notation will be used throughout this article. We write
![]() ${\mathcal{S}}(\mathbb{R})$
to denote the Schwartz space of all complex-valued rapidly decreasing infinitely differentiable functions on
${\mathcal{S}}(\mathbb{R})$
to denote the Schwartz space of all complex-valued rapidly decreasing infinitely differentiable functions on
![]() $\mathbb{R}$
and
$\mathbb{R}$
and
![]() ${\mathcal{S}}^{\prime }(\mathbb{R})$
to denote the space of tempered distributions on
${\mathcal{S}}^{\prime }(\mathbb{R})$
to denote the space of tempered distributions on
![]() $\mathbb{R}$
, that is, the topological dual of
$\mathbb{R}$
, that is, the topological dual of
![]() ${\mathcal{S}}(\mathbb{R})$
. The Fourier transform is defined by
${\mathcal{S}}(\mathbb{R})$
. The Fourier transform is defined by
![]() $\widehat{f}(\unicode[STIX]{x1D709})=\int _{\mathbf{R}}f(x)e^{-ix\cdot \unicode[STIX]{x1D709}}dx$
and the inverse Fourier transform by
$\widehat{f}(\unicode[STIX]{x1D709})=\int _{\mathbf{R}}f(x)e^{-ix\cdot \unicode[STIX]{x1D709}}dx$
and the inverse Fourier transform by
![]() $f^{\vee }(x)=(2\unicode[STIX]{x1D70B})^{-1}\widehat{f}(-x)$
. We also write
$f^{\vee }(x)=(2\unicode[STIX]{x1D70B})^{-1}\widehat{f}(-x)$
. We also write
![]() $C_{c}^{\infty }(\mathbb{R})$
to denote the set of all complex-valued infinitely differentiable functions on
$C_{c}^{\infty }(\mathbb{R})$
to denote the set of all complex-valued infinitely differentiable functions on
![]() $\mathbb{R}$
with compact support.
$\mathbb{R}$
with compact support.
2.1 Real analytic function
A complex-valued function
![]() $F$
on
$F$
on
![]() $\mathbb{R}^{2}$
is said to be real analytic on
$\mathbb{R}^{2}$
is said to be real analytic on
![]() $\mathbb{R}^{2}$
if for each
$\mathbb{R}^{2}$
if for each
![]() $(s_{0},t_{0})\in \mathbb{R}^{2}$
,
$(s_{0},t_{0})\in \mathbb{R}^{2}$
,
![]() $F$
has a power series expansion
$F$
has a power series expansion
which converges absolutely in a neighborhood of
![]() $(s_{0},t_{0})$
.
$(s_{0},t_{0})$
.
2.2 Short-time Fourier transform
Let
![]() $f\in {\mathcal{S}}^{\prime }(\mathbb{R})$
and
$f\in {\mathcal{S}}^{\prime }(\mathbb{R})$
and
![]() $g\in {\mathcal{S}}(\mathbb{R})$
. Then the short-time Fourier transform
$g\in {\mathcal{S}}(\mathbb{R})$
. Then the short-time Fourier transform
![]() $V_{g}f$
of
$V_{g}f$
of
![]() $f$
with respect to the window
$f$
with respect to the window
![]() $g$
is defined by
$g$
is defined by
2.3 Modulation spaces
Let
![]() $1\leqslant p,q\leqslant \infty$
and
$1\leqslant p,q\leqslant \infty$
and
![]() $g\in {\mathcal{S}}(\mathbb{R})\setminus \{0\}$
. Then the modulation space
$g\in {\mathcal{S}}(\mathbb{R})\setminus \{0\}$
. Then the modulation space
![]() $M^{p,q}(\mathbb{R})=M^{p,q}$
consists of all
$M^{p,q}(\mathbb{R})=M^{p,q}$
consists of all
![]() $f\in {\mathcal{S}}^{\prime }(\mathbb{R})$
such that the norm
$f\in {\mathcal{S}}^{\prime }(\mathbb{R})$
such that the norm
 $$\begin{eqnarray}\Vert f\Vert _{M^{p,q}(\mathbb{R})}=\left(\int _{\mathbb{R}}\left(\int _{\mathbb{R}}|V_{g}f(x,\unicode[STIX]{x1D709})|^{p}dx\right)^{q/p}d\unicode[STIX]{x1D709}\right)^{1/q}\end{eqnarray}$$
$$\begin{eqnarray}\Vert f\Vert _{M^{p,q}(\mathbb{R})}=\left(\int _{\mathbb{R}}\left(\int _{\mathbb{R}}|V_{g}f(x,\unicode[STIX]{x1D709})|^{p}dx\right)^{q/p}d\unicode[STIX]{x1D709}\right)^{1/q}\end{eqnarray}$$
is finite (with usual modifications if
![]() $p=\infty$
or
$p=\infty$
or
![]() $q=\infty$
).
$q=\infty$
).
We note that since
![]() $V_{g}\overline{f}(x,\unicode[STIX]{x1D709})=\overline{V_{\overline{g}}f(x,-\unicode[STIX]{x1D709})}$
, we have
$V_{g}\overline{f}(x,\unicode[STIX]{x1D709})=\overline{V_{\overline{g}}f(x,-\unicode[STIX]{x1D709})}$
, we have
We collect basic properties of modulation spaces in the following lemma (see [Reference Feichtinger, Krishna, Radha and Thangavelu4, Reference Gröchenig5, Reference Ruzhansky, Sugimoto and Wang11–Reference Toft14] for more details).
Lemma 2.1.
(1) The space
 $M^{p,q}(\mathbb{R})$
is a Banach space, whose definition is independent of the choice of
$M^{p,q}(\mathbb{R})$
is a Banach space, whose definition is independent of the choice of
 $g$
. More precisely, we have for
$g$
. More precisely, we have for $$\begin{eqnarray}\Vert f\Vert _{M_{[g_{0}](\mathbb{R})}^{p,q}}\leqslant C\Vert g\Vert _{M_{[g_{0}](\mathbb{R})}^{1,1}}\Vert f\Vert _{M_{[g](\mathbb{R})}^{p,q}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert f\Vert _{M_{[g_{0}](\mathbb{R})}^{p,q}}\leqslant C\Vert g\Vert _{M_{[g_{0}](\mathbb{R})}^{1,1}}\Vert f\Vert _{M_{[g](\mathbb{R})}^{p,q}}\end{eqnarray}$$
 $f\in M^{p,q}(\mathbb{R})$
and
$f\in M^{p,q}(\mathbb{R})$
and
 $g_{0},g\in {\mathcal{S}}(\mathbb{R}^{n})\setminus \{0\}$
, where
$g_{0},g\in {\mathcal{S}}(\mathbb{R}^{n})\setminus \{0\}$
, where  $$\begin{eqnarray}\Vert f\Vert _{M_{[g]}^{p,q}(\mathbb{R})}=\left\Vert \Vert V_{g}f(x,\unicode[STIX]{x1D709})\Vert _{L^{p}(\mathbb{R}_{x})}\right\Vert _{L^{q}(\mathbb{R}_{\unicode[STIX]{x1D709}})}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert f\Vert _{M_{[g]}^{p,q}(\mathbb{R})}=\left\Vert \Vert V_{g}f(x,\unicode[STIX]{x1D709})\Vert _{L^{p}(\mathbb{R}_{x})}\right\Vert _{L^{q}(\mathbb{R}_{\unicode[STIX]{x1D709}})}.\end{eqnarray}$$
(2)
 $M^{p,min\{p,p^{\prime }\}}(\mathbb{R}^{n}){\hookrightarrow}L^{p}(\mathbb{R}^{n}){\hookrightarrow}M^{p,max\{p,p^{\prime }\}}(\mathbb{R}^{n}).$
In particular, we have
$M^{p,min\{p,p^{\prime }\}}(\mathbb{R}^{n}){\hookrightarrow}L^{p}(\mathbb{R}^{n}){\hookrightarrow}M^{p,max\{p,p^{\prime }\}}(\mathbb{R}^{n}).$
In particular, we have
 $M^{2,2}(\mathbb{R}^{n})=L^{2}(\mathbb{R}^{n})$
.
$M^{2,2}(\mathbb{R}^{n})=L^{2}(\mathbb{R}^{n})$
.(3)
 $M^{p,1}(\mathbb{R})\subset C(\mathbb{R})$
, that is,
$M^{p,1}(\mathbb{R})\subset C(\mathbb{R})$
, that is,
 $f$
is continuous on
$f$
is continuous on
 $\mathbb{R}$
if
$\mathbb{R}$
if
 $f\in M^{p,1}(\mathbb{R})$
.
$f\in M^{p,1}(\mathbb{R})$
.(4) If
 $p_{1}\leqslant p_{2}$
and
$p_{1}\leqslant p_{2}$
and
 $q_{1}\leqslant q_{2}$
, then
$q_{1}\leqslant q_{2}$
, then
 $M^{p_{1},q_{1}}(\mathbb{R}){\hookrightarrow}M^{p_{2},q_{2}}(\mathbb{R})$
.
$M^{p_{1},q_{1}}(\mathbb{R}){\hookrightarrow}M^{p_{2},q_{2}}(\mathbb{R})$
.(5)
 $(\text{Density and duality})$
If
$(\text{Density and duality})$
If
 $p,q<\infty$
, then
$p,q<\infty$
, then
 ${\mathcal{S}}(\mathbb{R})$
is dense in
${\mathcal{S}}(\mathbb{R})$
is dense in
 $M^{p,q}(\mathbb{R})$
and
$M^{p,q}(\mathbb{R})$
and
 $(M^{p,q}(\mathbb{R}))^{\prime }=M^{p^{\prime },q^{\prime }}(\mathbb{R})$
.
$(M^{p,q}(\mathbb{R}))^{\prime }=M^{p^{\prime },q^{\prime }}(\mathbb{R})$
.(6)
 $(\text{Multiplication})$
If
$(\text{Multiplication})$
If
 $\frac{1}{p_{1}}+\frac{1}{p_{2}}=\frac{1}{p}$
and
$\frac{1}{p_{1}}+\frac{1}{p_{2}}=\frac{1}{p}$
and
 $\frac{1}{q_{1}}+\frac{1}{q_{2}}=\frac{1}{q}+1$
, then Moreover, we have
$\frac{1}{q_{1}}+\frac{1}{q_{2}}=\frac{1}{q}+1$
, then Moreover, we have $$\begin{eqnarray}\Vert fg\Vert _{M^{p,q}(\mathbb{R})}\leqslant C\Vert f\Vert _{M^{p_{1},q_{1}}(\mathbb{R})}\Vert g\Vert _{M^{p_{2},q_{2}}(\mathbb{R})},\quad f,g\in {\mathcal{S}}(\mathbb{R}).\end{eqnarray}$$
that is,
$$\begin{eqnarray}\Vert fg\Vert _{M^{p,q}(\mathbb{R})}\leqslant C\Vert f\Vert _{M^{p_{1},q_{1}}(\mathbb{R})}\Vert g\Vert _{M^{p_{2},q_{2}}(\mathbb{R})},\quad f,g\in {\mathcal{S}}(\mathbb{R}).\end{eqnarray}$$
that is, $$\begin{eqnarray}\Vert fg\Vert _{M^{p,1}(\mathbb{R})}\leqslant C\Vert f\Vert _{M^{p,1}(\mathbb{R})}\Vert g\Vert _{M^{p,1}(\mathbb{R})},\quad f,g\in M^{p,1}(\mathbb{R}),\end{eqnarray}$$
$$\begin{eqnarray}\Vert fg\Vert _{M^{p,1}(\mathbb{R})}\leqslant C\Vert f\Vert _{M^{p,1}(\mathbb{R})}\Vert g\Vert _{M^{p,1}(\mathbb{R})},\quad f,g\in M^{p,1}(\mathbb{R}),\end{eqnarray}$$
 $M^{p,1}(\mathbb{R})$
is a multiplication algebra.
$M^{p,1}(\mathbb{R})$
is a multiplication algebra.(7)
 $(\text{Convolution})$
If
$(\text{Convolution})$
If
 $\frac{1}{p_{1}}+\frac{1}{p_{2}}=\frac{1}{p}+1$
and
$\frac{1}{p_{1}}+\frac{1}{p_{2}}=\frac{1}{p}+1$
and
 $\frac{1}{q_{1}}+\frac{1}{q_{2}}=\frac{1}{q}$
, then
$\frac{1}{q_{1}}+\frac{1}{q_{2}}=\frac{1}{q}$
, then  $$\begin{eqnarray}\Vert f\ast g\Vert _{M^{p,q}(\mathbb{R})}\leqslant C\Vert f\Vert _{M^{p_{1},q_{1}}(\mathbb{R})}\Vert g\Vert _{M^{p_{2},q_{2}}(\mathbb{R})},\quad f,g\in {\mathcal{S}}(\mathbb{R}).\end{eqnarray}$$
$$\begin{eqnarray}\Vert f\ast g\Vert _{M^{p,q}(\mathbb{R})}\leqslant C\Vert f\Vert _{M^{p_{1},q_{1}}(\mathbb{R})}\Vert g\Vert _{M^{p_{2},q_{2}}(\mathbb{R})},\quad f,g\in {\mathcal{S}}(\mathbb{R}).\end{eqnarray}$$
(8)
 $(\text{Dilation property})$
There exists constants
$(\text{Dilation property})$
There exists constants
 $C,C^{\prime }>0$
such that for
$C,C^{\prime }>0$
such that for $$\begin{eqnarray}\displaystyle \Vert f_{\unicode[STIX]{x1D706}}\Vert _{M^{\infty ,1}(\mathbb{R})} & {\leqslant} & \displaystyle C\Vert f\Vert _{M^{\infty ,1}(\mathbb{R})},\quad f\in M^{\infty ,1}(\mathbb{R}),\nonumber\\ \displaystyle \Vert (f_{\unicode[STIX]{x1D706}})^{\wedge }\Vert _{M^{1,\infty }(\mathbb{R})} & {\leqslant} & \displaystyle C^{\prime }\Vert \widehat{f}\Vert _{M^{1,\infty }(\mathbb{R})},\quad \widehat{f}\in M^{1,\infty }(\mathbb{R})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert f_{\unicode[STIX]{x1D706}}\Vert _{M^{\infty ,1}(\mathbb{R})} & {\leqslant} & \displaystyle C\Vert f\Vert _{M^{\infty ,1}(\mathbb{R})},\quad f\in M^{\infty ,1}(\mathbb{R}),\nonumber\\ \displaystyle \Vert (f_{\unicode[STIX]{x1D706}})^{\wedge }\Vert _{M^{1,\infty }(\mathbb{R})} & {\leqslant} & \displaystyle C^{\prime }\Vert \widehat{f}\Vert _{M^{1,\infty }(\mathbb{R})},\quad \widehat{f}\in M^{1,\infty }(\mathbb{R})\nonumber\end{eqnarray}$$
 $0<\unicode[STIX]{x1D706}\leqslant 1$
. Here we denote
$0<\unicode[STIX]{x1D706}\leqslant 1$
. Here we denote
 $f_{\unicode[STIX]{x1D706}}(x)=f(\unicode[STIX]{x1D706}x)$
.
$f_{\unicode[STIX]{x1D706}}(x)=f(\unicode[STIX]{x1D706}x)$
.
2.4 Wiener amalgam spaces
Let
![]() $1\leqslant p,q\leqslant \infty$
and
$1\leqslant p,q\leqslant \infty$
and
![]() $g\in {\mathcal{S}}(\mathbb{R})\setminus \{0\}$
. Then the Wiener amalgam space
$g\in {\mathcal{S}}(\mathbb{R})\setminus \{0\}$
. Then the Wiener amalgam space
![]() $W^{p,q}(\mathbb{R})=W^{p,q}$
consists of all
$W^{p,q}(\mathbb{R})=W^{p,q}$
consists of all
![]() $f\in {\mathcal{S}}^{\prime }(\mathbb{R})$
such that the norm
$f\in {\mathcal{S}}^{\prime }(\mathbb{R})$
such that the norm
 $$\begin{eqnarray}\Vert f\Vert _{W^{p,q}(\mathbb{R})}=\left(\int _{\mathbb{R}}\left(\int _{\mathbb{R}}|V_{g}f(x,\unicode[STIX]{x1D709})|^{q}d\unicode[STIX]{x1D709}\right)^{p/q}dx\right)^{1/p}\end{eqnarray}$$
$$\begin{eqnarray}\Vert f\Vert _{W^{p,q}(\mathbb{R})}=\left(\int _{\mathbb{R}}\left(\int _{\mathbb{R}}|V_{g}f(x,\unicode[STIX]{x1D709})|^{q}d\unicode[STIX]{x1D709}\right)^{p/q}dx\right)^{1/p}\end{eqnarray}$$
is finite (with usual modifications if
![]() $p=\infty$
or
$p=\infty$
or
![]() $q=\infty$
).
$q=\infty$
).
We remark that since
![]() $V_{g}f(x,\unicode[STIX]{x1D709})=(2\unicode[STIX]{x1D70B})^{-1}e^{-ix\cdot \unicode[STIX]{x1D709}}V_{\widehat{g}}\widehat{f}(\unicode[STIX]{x1D709},-x)$
, we have
$V_{g}f(x,\unicode[STIX]{x1D709})=(2\unicode[STIX]{x1D70B})^{-1}e^{-ix\cdot \unicode[STIX]{x1D709}}V_{\widehat{g}}\widehat{f}(\unicode[STIX]{x1D709},-x)$
, we have
for some positive constants
![]() $C_{1}$
and
$C_{1}$
and
![]() $C_{2}$
. This implies that the definition of
$C_{2}$
. This implies that the definition of
![]() $W^{p,q}$
is independent of the choice of
$W^{p,q}$
is independent of the choice of
![]() $g$
since the modulation space
$g$
since the modulation space
![]() $M^{q,p}$
is independent of the choice of
$M^{q,p}$
is independent of the choice of
![]() $g$
. For the same reason,
$g$
. For the same reason,
![]() $W^{p,q}$
has the following properties.
$W^{p,q}$
has the following properties.
Lemma 2.2. Let
![]() $1\leqslant p,p_{1},p_{2},q,q_{1},q_{2}\leqslant \infty$
and
$1\leqslant p,p_{1},p_{2},q,q_{1},q_{2}\leqslant \infty$
and
![]() $\frac{1}{p}+\frac{1}{p^{\prime }}=1=\frac{1}{q}+\frac{1}{q^{\prime }}$
.
$\frac{1}{p}+\frac{1}{p^{\prime }}=1=\frac{1}{q}+\frac{1}{q^{\prime }}$
.
(1)
 $M^{p,1}(\mathbb{R}){\hookrightarrow}W^{p,1}(\mathbb{R})$
.
$M^{p,1}(\mathbb{R}){\hookrightarrow}W^{p,1}(\mathbb{R})$
.(2)
 $W^{p,1}(\mathbb{R})\subset C(\mathbb{R})$
, that is,
$W^{p,1}(\mathbb{R})\subset C(\mathbb{R})$
, that is,
 $f$
is continuous on
$f$
is continuous on
 $\mathbb{R}$
if
$\mathbb{R}$
if
 $f\in W^{p,1}(\mathbb{R})$
.
$f\in W^{p,1}(\mathbb{R})$
.(3) If
 $p_{1}\leqslant p_{2}$
and
$p_{1}\leqslant p_{2}$
and
 $q_{1}\leqslant q_{2}$
, then
$q_{1}\leqslant q_{2}$
, then
 $W^{p_{1},q_{1}}(\mathbb{R}){\hookrightarrow}W^{p_{2},q_{2}}(\mathbb{R})$
.
$W^{p_{1},q_{1}}(\mathbb{R}){\hookrightarrow}W^{p_{2},q_{2}}(\mathbb{R})$
.(4)
 $(\text{Multiplication})$
If
$(\text{Multiplication})$
If
 $\frac{1}{p_{1}}+\frac{1}{p_{2}}=\frac{1}{p}$
and
$\frac{1}{p_{1}}+\frac{1}{p_{2}}=\frac{1}{p}$
and
 $\frac{1}{q_{1}}+\frac{1}{q_{2}}=\frac{1}{q}+1$
, then Moreover, we have
$\frac{1}{q_{1}}+\frac{1}{q_{2}}=\frac{1}{q}+1$
, then Moreover, we have $$\begin{eqnarray}\Vert fg\Vert _{W^{p,q}(\mathbb{R})}\leqslant C\Vert f\Vert _{W^{p_{1},q_{1}}(\mathbb{R})}\Vert g\Vert _{W^{p_{2},q_{2}}(\mathbb{R})},\quad f,g\in {\mathcal{S}}(\mathbb{R}).\end{eqnarray}$$
that is,
$$\begin{eqnarray}\Vert fg\Vert _{W^{p,q}(\mathbb{R})}\leqslant C\Vert f\Vert _{W^{p_{1},q_{1}}(\mathbb{R})}\Vert g\Vert _{W^{p_{2},q_{2}}(\mathbb{R})},\quad f,g\in {\mathcal{S}}(\mathbb{R}).\end{eqnarray}$$
that is, $$\begin{eqnarray}\Vert fg\Vert _{W^{p,1}(\mathbb{R})}\leqslant C\Vert f\Vert _{W^{p,1}(\mathbb{R})}\Vert g\Vert _{W^{p,1}(\mathbb{R})},\quad f,g\in W^{p,1}(\mathbb{R}),\end{eqnarray}$$
$$\begin{eqnarray}\Vert fg\Vert _{W^{p,1}(\mathbb{R})}\leqslant C\Vert f\Vert _{W^{p,1}(\mathbb{R})}\Vert g\Vert _{W^{p,1}(\mathbb{R})},\quad f,g\in W^{p,1}(\mathbb{R}),\end{eqnarray}$$
 $W^{p,1}(\mathbb{R})$
is a multiplication algebra.
$W^{p,1}(\mathbb{R})$
is a multiplication algebra.(5)
 $(\text{Dilation property})$
There exists constant
$(\text{Dilation property})$
There exists constant
 $C>0$
such that Here we denote
$C>0$
such that Here we denote $$\begin{eqnarray}\displaystyle & \Vert f_{\unicode[STIX]{x1D706}}\Vert _{W^{\infty ,1}(\mathbb{R})}\leqslant C\Vert f\Vert _{W^{\infty ,1}(\mathbb{R})},\quad 0<\unicode[STIX]{x1D706}\leqslant 1,~f\in W^{\infty ,1}(\mathbb{R}). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \Vert f_{\unicode[STIX]{x1D706}}\Vert _{W^{\infty ,1}(\mathbb{R})}\leqslant C\Vert f\Vert _{W^{\infty ,1}(\mathbb{R})},\quad 0<\unicode[STIX]{x1D706}\leqslant 1,~f\in W^{\infty ,1}(\mathbb{R}). & \displaystyle \nonumber\end{eqnarray}$$
 $f_{\unicode[STIX]{x1D706}}(x)=f(\unicode[STIX]{x1D706}x)$
.
$f_{\unicode[STIX]{x1D706}}(x)=f(\unicode[STIX]{x1D706}x)$
.
We also recall the following characterization of modulation spaces
![]() $M^{p,1}(\mathbb{R})$
and Wiener amalgam spaces
$M^{p,1}(\mathbb{R})$
and Wiener amalgam spaces
![]() $W^{p,1}(\mathbb{R})$
.
$W^{p,1}(\mathbb{R})$
.
Definition 2.3. Let
![]() $1\leqslant p\leqslant \infty$
and
$1\leqslant p\leqslant \infty$
and
![]() $f$
be a function defined on
$f$
be a function defined on
![]() $\mathbb{R}$
. Suppose
$\mathbb{R}$
. Suppose
![]() $X=M^{p,1}(\mathbb{R})$
or
$X=M^{p,1}(\mathbb{R})$
or
![]() $W^{p,1}(\mathbb{R})$
.
$W^{p,1}(\mathbb{R})$
.
(1) Let
 $x_{0}\in \mathbb{R}$
. If there exist a neighborhood
$x_{0}\in \mathbb{R}$
. If there exist a neighborhood
 $V$
of
$V$
of
 $x_{0}$
and a function
$x_{0}$
and a function
 $g\in X$
satisfying
$g\in X$
satisfying
 $f(x)=g(x)$
for every
$f(x)=g(x)$
for every
 $x\in V$
, then we say
$x\in V$
, then we say
 $f$
belongs to
$f$
belongs to
 $X$
locally at a point
$X$
locally at a point
 $x_{0}\in \mathbb{R}$
.
$x_{0}\in \mathbb{R}$
.(2) If there exist a compact set
 $K\subset \mathbb{R}$
and
$K\subset \mathbb{R}$
and
 $h\in X$
satisfying
$h\in X$
satisfying
 $f(x)=h(x)$
for all
$f(x)=h(x)$
for all
 $x\in \mathbb{R}\setminus K$
, then we say
$x\in \mathbb{R}\setminus K$
, then we say
 $f$
belongs to
$f$
belongs to
 $X$
at
$X$
at
 $\infty$
.
$\infty$
.
We denote by
![]() $X_{loc}$
, the space of functions that are locally in
$X_{loc}$
, the space of functions that are locally in
![]() $X$
at each point
$X$
at each point
![]() $x_{0}\in \mathbb{R}$
.
$x_{0}\in \mathbb{R}$
.
Lemma 2.4. (cf. [Reference Bhimani2, Lemma 4.3], [Reference Bhimani and Ratnakumar3, Propositions 3.12 and 3.13], [Reference Katznelson8])
Let
![]() $1\leqslant p\leqslant \infty$
and
$1\leqslant p\leqslant \infty$
and
![]() $f$
be a function defined on
$f$
be a function defined on
![]() $\mathbb{R}$
. Suppose
$\mathbb{R}$
. Suppose
![]() $X=M^{p,1}(\mathbb{R})$
or
$X=M^{p,1}(\mathbb{R})$
or
![]() $W^{p,1}(\mathbb{R})$
.
$W^{p,1}(\mathbb{R})$
.
(1)
 $f\in X_{loc}$
, if and only if
$f\in X_{loc}$
, if and only if
 $\unicode[STIX]{x1D711}f\in X$
for every
$\unicode[STIX]{x1D711}f\in X$
for every
 $\unicode[STIX]{x1D711}\in C_{c}^{\infty }(\mathbb{R})$
.
$\unicode[STIX]{x1D711}\in C_{c}^{\infty }(\mathbb{R})$
.(2)
 $f$
belongs to
$f$
belongs to
 $X$
at
$X$
at
 $\infty$
, if and only if there exists a function
$\infty$
, if and only if there exists a function
 $\unicode[STIX]{x1D711}\in C_{c}^{\infty }(\mathbb{R})$
such that
$\unicode[STIX]{x1D711}\in C_{c}^{\infty }(\mathbb{R})$
such that
 $(1-\unicode[STIX]{x1D711})f\in X$
.
$(1-\unicode[STIX]{x1D711})f\in X$
.(3) If
 $f\in X_{loc}$
and
$f\in X_{loc}$
and
 $f$
belongs to
$f$
belongs to
 $X$
at
$X$
at
 $\infty$
, then
$\infty$
, then
 $f\in X$
.
$f\in X$
.
2.5 The space
 $A(\mathbb{T})$
$A(\mathbb{T})$
Let
![]() $\mathbb{T}=\mathbb{R}/2\unicode[STIX]{x1D70B}\mathbb{Z}$
be the torus. Then the space
$\mathbb{T}=\mathbb{R}/2\unicode[STIX]{x1D70B}\mathbb{Z}$
be the torus. Then the space
![]() $A(\mathbb{T})$
consists of all continuous function on
$A(\mathbb{T})$
consists of all continuous function on
![]() $\mathbb{T}$
having an absolutely convergent Fourier series, that is, the function
$\mathbb{T}$
having an absolutely convergent Fourier series, that is, the function
![]() $f$
for which
$f$
for which
Lemma 2.5. [Reference Kahane7, pp. 56–57]
Let
![]() $\unicode[STIX]{x1D706}\in (0,1)$
and define the
$\unicode[STIX]{x1D706}\in (0,1)$
and define the
![]() $2\unicode[STIX]{x1D70B}$
-periodic function
$2\unicode[STIX]{x1D70B}$
-periodic function
![]() $\mathbf{V}_{\unicode[STIX]{x1D706}}\in C(\mathbb{T})$
by
$\mathbf{V}_{\unicode[STIX]{x1D706}}\in C(\mathbb{T})$
by
where
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(x)=\max \{0,1-\frac{|x|}{\unicode[STIX]{x1D706}}\}.$
Moreover, we define
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(x)=\max \{0,1-\frac{|x|}{\unicode[STIX]{x1D706}}\}.$
Moreover, we define
for
![]() $x_{0}\in \mathbb{R}$
. Then for every
$x_{0}\in \mathbb{R}$
. Then for every
![]() $g\in A(\mathbb{T})$
with
$g\in A(\mathbb{T})$
with
![]() $g(x_{0})=0$
, we have
$g(x_{0})=0$
, we have
![]() $\Vert \mathbf{V}_{\unicode[STIX]{x1D706}}^{x_{0}}g\Vert _{A(\mathbb{T})}\rightarrow 0$
as
$\Vert \mathbf{V}_{\unicode[STIX]{x1D706}}^{x_{0}}g\Vert _{A(\mathbb{T})}\rightarrow 0$
as
![]() $\unicode[STIX]{x1D706}\rightarrow 0$
.
$\unicode[STIX]{x1D706}\rightarrow 0$
.
We state the following lemma whose proof is almost a repetition of arguments in Bényi and Oh [Reference Bényi and Oh1, Proposition B.1] and Bhimani [Reference Bhimani2, Proposition 3.3].
Lemma 2.6. Let
![]() $1\leqslant p\leqslant \infty$
and
$1\leqslant p\leqslant \infty$
and
![]() $\unicode[STIX]{x1D719}\in C_{c}^{\infty }(\mathbb{R})$
with
$\unicode[STIX]{x1D719}\in C_{c}^{\infty }(\mathbb{R})$
with
![]() $\text{supp }\unicode[STIX]{x1D719}\subset (k\unicode[STIX]{x1D70B},(k+2)\unicode[STIX]{x1D70B})$
for some
$\text{supp }\unicode[STIX]{x1D719}\subset (k\unicode[STIX]{x1D70B},(k+2)\unicode[STIX]{x1D70B})$
for some
![]() $k\in \mathbb{Z}$
. Suppose
$k\in \mathbb{Z}$
. Suppose
![]() $X=M^{p,1}(\mathbb{R})$
or
$X=M^{p,1}(\mathbb{R})$
or
![]() $W^{p,1}(\mathbb{R})$
. Then there exist positive constants
$W^{p,1}(\mathbb{R})$
. Then there exist positive constants
![]() $C_{\unicode[STIX]{x1D719}}^{1}$
and
$C_{\unicode[STIX]{x1D719}}^{1}$
and
![]() $C_{\unicode[STIX]{x1D719}}^{2}$
(which depend on
$C_{\unicode[STIX]{x1D719}}^{2}$
(which depend on
![]() $\unicode[STIX]{x1D719}$
but do not depend on
$\unicode[STIX]{x1D719}$
but do not depend on
![]() $k$
) such that
$k$
) such that
and
3 The Proof of Theorem 1.1
We first prove that if
![]() $F$
is real analytic, then
$F$
is real analytic, then
![]() $F(\text{Re}f,\text{Im}f)\in X_{loc}$
for every
$F(\text{Re}f,\text{Im}f)\in X_{loc}$
for every
![]() $f\in X$
.
$f\in X$
.
Proposition 3.1. Let
![]() $1\leqslant p<\infty$
and
$1\leqslant p<\infty$
and
![]() $F$
be a complex-valued real analytic function on
$F$
be a complex-valued real analytic function on
![]() $\mathbb{R}^{2}$
with
$\mathbb{R}^{2}$
with
![]() $F(0)=0$
. If
$F(0)=0$
. If
![]() $f\in X$
, then
$f\in X$
, then
![]() $F(\text{Re}f,\text{Im}f)$
belongs to
$F(\text{Re}f,\text{Im}f)$
belongs to
![]() $X$
locally at
$X$
locally at
![]() $x_{0}$
for all
$x_{0}$
for all
![]() $x_{0}\in \mathbb{R}$
.
$x_{0}\in \mathbb{R}$
.
Proof. Let
![]() $f\in X$
and
$f\in X$
and
![]() $x_{0}\in \mathbb{R}$
. Set
$x_{0}\in \mathbb{R}$
. Set
![]() $f(x_{0})=s_{0}+it_{0}$
with
$f(x_{0})=s_{0}+it_{0}$
with
![]() $s_{0},t_{0}\in \mathbb{R}$
. Since
$s_{0},t_{0}\in \mathbb{R}$
. Since
![]() $F$
is real analytic, for some
$F$
is real analytic, for some
![]() $\unicode[STIX]{x1D6FF}>0$
$\unicode[STIX]{x1D6FF}>0$
and
if
![]() $|s-s_{0}|<\unicode[STIX]{x1D6FF}$
and
$|s-s_{0}|<\unicode[STIX]{x1D6FF}$
and
![]() $|t-t_{0}|<\unicode[STIX]{x1D6FF}$
.
$|t-t_{0}|<\unicode[STIX]{x1D6FF}$
.
Let
![]() $\unicode[STIX]{x1D719}\in C_{c}^{\infty }(\mathbb{R})$
such that
$\unicode[STIX]{x1D719}\in C_{c}^{\infty }(\mathbb{R})$
such that
![]() $\unicode[STIX]{x1D719}(x)=1$
near
$\unicode[STIX]{x1D719}(x)=1$
near
![]() $x_{0}$
and
$x_{0}$
and
![]() $\text{supp }\unicode[STIX]{x1D719}\subset (x_{0}-\frac{1}{10},x_{0}+\frac{1}{10})$
, and define
$\text{supp }\unicode[STIX]{x1D719}\subset (x_{0}-\frac{1}{10},x_{0}+\frac{1}{10})$
, and define
![]() $g_{j}$
$g_{j}$
![]() $(j=1,2)$
by
$(j=1,2)$
by
We note that
![]() $\unicode[STIX]{x1D719}g_{j}\in X$
and
$\unicode[STIX]{x1D719}g_{j}\in X$
and
![]() $(\unicode[STIX]{x1D719}g_{j})(x_{0})=0$
for
$(\unicode[STIX]{x1D719}g_{j})(x_{0})=0$
for
![]() $j=1,2$
. Thus by Lemma 2.6 we can easily see
$j=1,2$
. Thus by Lemma 2.6 we can easily see
![]() $\unicode[STIX]{x1D719}g_{j}\in A(\mathbb{T})$
. So, by Lemma 2.5 we obtain
$\unicode[STIX]{x1D719}g_{j}\in A(\mathbb{T})$
. So, by Lemma 2.5 we obtain
![]() $\Vert \mathbf{V}_{\unicode[STIX]{x1D706}}^{x_{0}}\unicode[STIX]{x1D719}g_{j}\Vert _{A(\mathbb{T})}\rightarrow 0$
as
$\Vert \mathbf{V}_{\unicode[STIX]{x1D706}}^{x_{0}}\unicode[STIX]{x1D719}g_{j}\Vert _{A(\mathbb{T})}\rightarrow 0$
as
![]() $\unicode[STIX]{x1D706}\rightarrow 0.$
Thus, for any
$\unicode[STIX]{x1D706}\rightarrow 0.$
Thus, for any
![]() $\unicode[STIX]{x1D700}\in (0,\unicode[STIX]{x1D6FF})$
there exists
$\unicode[STIX]{x1D700}\in (0,\unicode[STIX]{x1D6FF})$
there exists
![]() $\unicode[STIX]{x1D706}_{0}>0$
such that
$\unicode[STIX]{x1D706}_{0}>0$
such that
for
![]() $\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}_{0}$
, where
$\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}_{0}$
, where
![]() $C_{X}$
denotes the constant with
$C_{X}$
denotes the constant with
Hence by Lemma 2.6 again, we obtain
for
![]() $\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}_{0}$
. Now we define
$\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}_{0}$
. Now we define
for
![]() $\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}_{0}$
. Since
$\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}_{0}$
. Since
![]() $\unicode[STIX]{x1D700}<\unicode[STIX]{x1D6FF}$
and
$\unicode[STIX]{x1D700}<\unicode[STIX]{x1D6FF}$
and
![]() $a_{00}=0$
, by Lemmas 2.1 and 2.2 we have
$a_{00}=0$
, by Lemmas 2.1 and 2.2 we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{m,n=0}^{\infty }\Vert a_{mn}(\unicode[STIX]{x1D719}\mathbf{V}_{\unicode[STIX]{x1D706}}^{x_{0}}\unicode[STIX]{x1D719}g_{1})^{m}(\unicode[STIX]{x1D719}\mathbf{V}_{\unicode[STIX]{x1D706}}^{x_{0}}\unicode[STIX]{x1D719}g_{2})^{n}\Vert _{X}\nonumber\\ \displaystyle & & \displaystyle \qquad \leqslant C_{X}\mathop{\sum }_{m,n=0}^{\infty }|a_{mn}|~\Vert (\unicode[STIX]{x1D719}\mathbf{V}_{\unicode[STIX]{x1D706}}^{x_{0}}\unicode[STIX]{x1D719}g_{1})^{m}\Vert _{X}\Vert \unicode[STIX]{x1D719}(\mathbf{V}_{\unicode[STIX]{x1D706}}^{x_{0}}\unicode[STIX]{x1D719}g_{2})^{n}\Vert _{X}\nonumber\\ \displaystyle & & \displaystyle \qquad \leqslant C_{X}\mathop{\sum }_{m,n=0}^{\infty }|a_{mn}|\unicode[STIX]{x1D700}^{m+n}<\infty ,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{m,n=0}^{\infty }\Vert a_{mn}(\unicode[STIX]{x1D719}\mathbf{V}_{\unicode[STIX]{x1D706}}^{x_{0}}\unicode[STIX]{x1D719}g_{1})^{m}(\unicode[STIX]{x1D719}\mathbf{V}_{\unicode[STIX]{x1D706}}^{x_{0}}\unicode[STIX]{x1D719}g_{2})^{n}\Vert _{X}\nonumber\\ \displaystyle & & \displaystyle \qquad \leqslant C_{X}\mathop{\sum }_{m,n=0}^{\infty }|a_{mn}|~\Vert (\unicode[STIX]{x1D719}\mathbf{V}_{\unicode[STIX]{x1D706}}^{x_{0}}\unicode[STIX]{x1D719}g_{1})^{m}\Vert _{X}\Vert \unicode[STIX]{x1D719}(\mathbf{V}_{\unicode[STIX]{x1D706}}^{x_{0}}\unicode[STIX]{x1D719}g_{2})^{n}\Vert _{X}\nonumber\\ \displaystyle & & \displaystyle \qquad \leqslant C_{X}\mathop{\sum }_{m,n=0}^{\infty }|a_{mn}|\unicode[STIX]{x1D700}^{m+n}<\infty ,\nonumber\end{eqnarray}$$
and thus
![]() $G\in X.$
Moreover, since
$G\in X.$
Moreover, since
![]() $\unicode[STIX]{x1D719}(x)=1$
near
$\unicode[STIX]{x1D719}(x)=1$
near
![]() $x_{0}$
, we have
$x_{0}$
, we have
near
![]() $x_{0}$
, and thus
$x_{0}$
, and thus
 $$\begin{eqnarray}\displaystyle G(x) & = & \displaystyle \mathop{\sum }_{m,n=0}^{\infty }a_{mn}(\text{Re}f(x)-s_{0})^{m}(\text{Im}f(x)-t_{0})^{n}\nonumber\\ \displaystyle & = & \displaystyle F(\text{Re}f,\text{Im}f)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle G(x) & = & \displaystyle \mathop{\sum }_{m,n=0}^{\infty }a_{mn}(\text{Re}f(x)-s_{0})^{m}(\text{Im}f(x)-t_{0})^{n}\nonumber\\ \displaystyle & = & \displaystyle F(\text{Re}f,\text{Im}f)\nonumber\end{eqnarray}$$
near
![]() $x_{0}$
. This completes the proof.◻
$x_{0}$
. This completes the proof.◻
Next, we prove that if
![]() $F$
is real analytic, then
$F$
is real analytic, then
![]() $F(\text{Re}f,\text{Im}f)$
belongs
$F(\text{Re}f,\text{Im}f)$
belongs
![]() $X$
at
$X$
at
![]() $\infty$
for every
$\infty$
for every
![]() $f\in X$
. For this, we prepare the following proposition.
$f\in X$
. For this, we prepare the following proposition.
Proposition 3.2. Let
![]() $1\leqslant p<\infty$
and
$1\leqslant p<\infty$
and
![]() $f\in X$
. For any
$f\in X$
. For any
![]() $\unicode[STIX]{x1D700}>0$
, there exists a real-valued function
$\unicode[STIX]{x1D700}>0$
, there exists a real-valued function
![]() $\unicode[STIX]{x1D6F9}\in C_{c}^{\infty }(\mathbb{R})$
such that
$\unicode[STIX]{x1D6F9}\in C_{c}^{\infty }(\mathbb{R})$
such that
Proof. Let
![]() $f\in X$
,
$f\in X$
,
![]() $\unicode[STIX]{x1D700}>0$
and
$\unicode[STIX]{x1D700}>0$
and
![]() $\unicode[STIX]{x1D719}$
be a real-valued function in
$\unicode[STIX]{x1D719}$
be a real-valued function in
![]() $C_{c}^{\infty }(\mathbb{R})$
with
$C_{c}^{\infty }(\mathbb{R})$
with
![]() $\unicode[STIX]{x1D719}(0)=1$
. Since
$\unicode[STIX]{x1D719}(0)=1$
. Since
![]() ${\mathcal{S}}(\mathbb{R})$
is dense in
${\mathcal{S}}(\mathbb{R})$
is dense in
![]() $X$
, there exists
$X$
, there exists
![]() $g\in {\mathcal{S}}(\mathbb{R})$
such that
$g\in {\mathcal{S}}(\mathbb{R})$
such that
where
![]() $C_{0}$
is decided later. We also recall the fact that for any
$C_{0}$
is decided later. We also recall the fact that for any
![]() $g\in {\mathcal{S}}(\mathbb{R})(\subset M^{1,1}(\mathbb{R})=W^{1,1}(\mathbb{R}))$
, there exists
$g\in {\mathcal{S}}(\mathbb{R})(\subset M^{1,1}(\mathbb{R})=W^{1,1}(\mathbb{R}))$
, there exists
![]() $\unicode[STIX]{x1D706}_{0}\in (0,1)$
such that
$\unicode[STIX]{x1D706}_{0}\in (0,1)$
such that
for
![]() $\unicode[STIX]{x1D706}\in (0,\unicode[STIX]{x1D706}_{0})$
, where
$\unicode[STIX]{x1D706}\in (0,\unicode[STIX]{x1D706}_{0})$
, where
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}(x)=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D706}x)$
(see for example [Reference Bhimani and Ratnakumar3, Proposition 3.14]).
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}(x)=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D706}x)$
(see for example [Reference Bhimani and Ratnakumar3, Proposition 3.14]).
Now we define
![]() $\unicode[STIX]{x1D6F9}\in C_{c}^{\infty }(\mathbb{R})$
by
$\unicode[STIX]{x1D6F9}\in C_{c}^{\infty }(\mathbb{R})$
by
![]() $\unicode[STIX]{x1D6F9}(x)=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D706}x)$
. Then we have
$\unicode[STIX]{x1D6F9}(x)=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D706}x)$
. Then we have
 $$\begin{eqnarray}\displaystyle \Vert (1-\unicode[STIX]{x1D6F9})f\Vert _{X} & {\leqslant} & \displaystyle \Vert (1-\unicode[STIX]{x1D6F9})(f-g)\Vert _{X}+\Vert (1-\unicode[STIX]{x1D6F9})g\Vert _{X}\nonumber\\ \displaystyle & = & \displaystyle \Vert f-g-\unicode[STIX]{x1D6F9}(f-g)\Vert _{X}+\Vert (1-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}})g\Vert _{X}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \Vert f-g\Vert _{X}+C\Vert \unicode[STIX]{x1D6F9}\Vert _{Y}\Vert f-g\Vert _{X}+\Vert (1-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}})g\Vert _{M^{1,1}(\mathbb{R})}\nonumber\\ \displaystyle & {<} & \displaystyle (1+C\Vert \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}\Vert _{Y})\Vert f-g\Vert _{X}+\frac{\unicode[STIX]{x1D700}}{2},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert (1-\unicode[STIX]{x1D6F9})f\Vert _{X} & {\leqslant} & \displaystyle \Vert (1-\unicode[STIX]{x1D6F9})(f-g)\Vert _{X}+\Vert (1-\unicode[STIX]{x1D6F9})g\Vert _{X}\nonumber\\ \displaystyle & = & \displaystyle \Vert f-g-\unicode[STIX]{x1D6F9}(f-g)\Vert _{X}+\Vert (1-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}})g\Vert _{X}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \Vert f-g\Vert _{X}+C\Vert \unicode[STIX]{x1D6F9}\Vert _{Y}\Vert f-g\Vert _{X}+\Vert (1-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}})g\Vert _{M^{1,1}(\mathbb{R})}\nonumber\\ \displaystyle & {<} & \displaystyle (1+C\Vert \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}\Vert _{Y})\Vert f-g\Vert _{X}+\frac{\unicode[STIX]{x1D700}}{2},\nonumber\end{eqnarray}$$
for
![]() $\unicode[STIX]{x1D706}\in (0,\unicode[STIX]{x1D706}_{0})$
, where
$\unicode[STIX]{x1D706}\in (0,\unicode[STIX]{x1D706}_{0})$
, where
![]() $Y=M^{\infty ,1}$
(if
$Y=M^{\infty ,1}$
(if
![]() $X=M^{p,1}$
) or
$X=M^{p,1}$
) or
![]() $=W^{\infty ,1}$
(if
$=W^{\infty ,1}$
(if
![]() $X=W^{p,1}$
). By Lemmas 2.1 and 2.2 we have
$X=W^{p,1}$
). By Lemmas 2.1 and 2.2 we have
for
![]() $\unicode[STIX]{x1D706}\in (0,\unicode[STIX]{x1D706}_{0})$
. Hence we have
$\unicode[STIX]{x1D706}\in (0,\unicode[STIX]{x1D706}_{0})$
. Hence we have
Corollary 3.3. Let
![]() $1\leqslant p<\infty$
and
$1\leqslant p<\infty$
and
![]() $f_{1},\ldots ,f_{N}\in X$
. For any
$f_{1},\ldots ,f_{N}\in X$
. For any
![]() $\unicode[STIX]{x1D700}>0$
, there exists a real-valued function
$\unicode[STIX]{x1D700}>0$
, there exists a real-valued function
![]() $\unicode[STIX]{x1D6F9}\in C_{c}^{\infty }(\mathbb{R})$
such that
$\unicode[STIX]{x1D6F9}\in C_{c}^{\infty }(\mathbb{R})$
such that
Proposition 3.4. Let
![]() $1\leqslant p<\infty$
and
$1\leqslant p<\infty$
and
![]() $F$
be a real analytic function on
$F$
be a real analytic function on
![]() $\mathbb{R}^{2}$
with
$\mathbb{R}^{2}$
with
![]() $F(0)=0$
. If
$F(0)=0$
. If
![]() $f\in X$
, then there exists
$f\in X$
, then there exists
![]() $H\in X$
such that
$H\in X$
such that
except for some compact set in
![]() $\mathbb{R}$
.
$\mathbb{R}$
.
Proof. Let
![]() $f\in X$
. Since
$f\in X$
. Since
![]() $F$
is real analytic, for some
$F$
is real analytic, for some
![]() $\unicode[STIX]{x1D6FF}>0$
$\unicode[STIX]{x1D6FF}>0$
and
if
![]() $|s|<\unicode[STIX]{x1D6FF}$
and
$|s|<\unicode[STIX]{x1D6FF}$
and
![]() $|t|<\unicode[STIX]{x1D6FF}$
. By Corollary 3.3 there exists a real-valued function
$|t|<\unicode[STIX]{x1D6FF}$
. By Corollary 3.3 there exists a real-valued function
![]() $\unicode[STIX]{x1D6F9}\in C_{c}^{\infty }(\mathbb{R})$
such that
$\unicode[STIX]{x1D6F9}\in C_{c}^{\infty }(\mathbb{R})$
such that
where
![]() $C_{X}$
denotes the constant with
$C_{X}$
denotes the constant with
From this and Lemmas 2.1 and 2.2,
converges in
![]() $X.$
Since
$X.$
Since
![]() $\unicode[STIX]{x1D6F9}\in C_{c}^{\infty }(\mathbb{R})$
,
$\unicode[STIX]{x1D6F9}\in C_{c}^{\infty }(\mathbb{R})$
,
![]() $H(x)=F(\text{Re}f(x),\text{Im}f(x))$
except for some compact set in
$H(x)=F(\text{Re}f(x),\text{Im}f(x))$
except for some compact set in
![]() $\mathbb{R}$
.◻
$\mathbb{R}$
.◻
Acknowledgments
The authors wish to thank the anonymous referee for carefully reading their paper and for providing some helpful comments. This work was supported by JSPS KAKENHI, Grant Numbers JP16K17606, JP26400129.