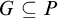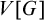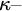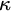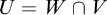ON RESTRICTIONS OF ULTRAFILTERS FROM GENERIC EXTENSIONS TO GROUND MODELS

1 Introduction

Let P be a forcing notion and $G\subseteq P$ its generic subset. Suppose that we have in $V[G]$ a $\kappa{-}$ complete ultrafilter ^{1 , 2} W over $\kappa $ . Set $U=W\cap V$ .

We will deal here with the following three basic questions:

1. 1. Is U in V?

2. 2. Suppose that $U \in V$ . How many extensions of U to $\kappa{-}$ complete ultrafilters do we have in $V[G]$ ?

3. 3. What is $j_W\upharpoonright V$ ?

Note that it is possible that U not in V and even $\kappa $ is not a measurable in V. The result is due to Kunen—just start with measurable cardinal $\kappa $ and iterate with Easton support at each inaccessible the forcing of Suslin tree followed by adding a branch to it. At $\kappa $ itself add only a Suslin tree. Denote the resulting extension by $V_1$ . Clearly, $\kappa $ is not a measurable in $V_1$ . However, after a further forcing which adds a branch to the Suslin tree it will be a measurable cardinal back.

Hamkins [10] introduced a gap forcing ³ and showed that if P is such a forcing with a gap below $\kappa $ , then $U\in V$ and $j_W\upharpoonright V$ is definable in V. ⁴

Assume that there is no inner model with a Woodin cardinal. Then by the celebrated results of Jensen and Steel [11], the core model $\mathcal K$ exists and then by Schindler [17], $j_W\upharpoonright V$ is an iterated ultrapower of $\mathcal K$ by its extenders.

Note that $j_W\upharpoonright V$ need not be definable in V already if there is a measurable limit of measurables.

Namely, we add first a Cohen real r to V, and then, iterate with Easton support (as in [7, Section 6]) the following forcing $Q_\nu $ below such measurable $\kappa $ : for every $\nu <\kappa $ , let ${\langle } \nu _n \mid n<\omega {\rangle }$ be the first $\omega $ many measurable cardinals above $\nu $ . Let $Q_\nu $ be the Magidor iteration [15] of Prikry forcings which change cofinality of $\nu _n$ , but only if $r(n)=0$ .

The purpose of the present paper is to extend the Hamkins approach to a wider class of forcing notions.

Our prime interest will be in Prikry type forcing notions.

Magidor in his celebrated paper [15] showed that the first measurable cardinal can be a strongly compact.

The method was to use the Magidor (full support) iteration of Prikry forcings and this way to destroy measurable cardinals.

Another approach was used by Kimchi and Magidor (see [1])—they destroyed measurability by adding a non-reflecting stationary subset to measurables. The iteration used was the Easton support iteration. Note that this type of forcing falls into the Hamkins schema.

Here we will deal with this type of iterated forcing notions and in addition to Easton and full supports, we will consider also a nonstationary support.

2 Some sufficient conditions

Proposition 2.1. Let $V[G]$ is a generic extension of V by a forcing P.

Suppose that $\kappa $ is a measurable cardinal in $V[G]$ and W is a $\kappa{-}$ complete ultrafilter over $\kappa $ .

Let $U=V\cap W$ . Then $U \in V$ if the following hold:

1. 1. all cardinals of V in the interval $[\kappa , (2^\kappa )^V]$ are preserved,

2. 2. no fresh subsets are added to a cardinal $\lambda $ , ⁵ $ \kappa \leq \lambda \leq (2^\kappa )^V$ .

Proof Let $\delta =(2^\kappa )^V$ . For every $f\!:\delta \leftrightarrow \mathcal P(\kappa )$ in V set

$$ \begin{align*}X_f=\{\alpha<\delta \mid f(\alpha) \in W\}.\end{align*} $$

Clearly, if for some such $f, X_f \in V$ , then also $U \in V$ .

Suppose that $X_f $ never is in $ V$ .

Define, for such f’s, $\alpha _f\leq \delta $ be the least $\alpha $ such that $X_f \cap \alpha \not \in V$ .

Set

$$ \begin{align*}\alpha^*=\min\{\alpha_f \mid f:\delta \leftrightarrow \mathcal P^V(\kappa), f \in V\}.\end{align*} $$

Claim. $\alpha ^*<\kappa $ .

Proof Suppose otherwise. By the first two assumption of the theorem, $\alpha ^*$ cannot be a cardinal in the interval $[\kappa ,\delta ]$ .

So, there is a cardinal $\eta , \kappa \leq \eta <\delta $ such that $\eta <\alpha ^*<\eta ^+$ .

Pick, in V, $g:\delta \leftrightarrow \delta $ such that $g\upharpoonright \eta $ maps $\eta $ onto $\alpha ^*$ .

Then $X_{f\circ g}\cap \eta \not \in V$ , and hence, $\alpha _{f\circ g}\leq \eta $ .

But $\eta <\alpha ^*\leq \alpha _{f\circ g}$ . Contradiction.

So, $\alpha ^*<\kappa $ . Fix $f:\delta \leftrightarrow \mathcal P(\kappa )$ with $\alpha _f=\alpha ^*$ . So, the set

$$ \begin{align*}X_f \cap \alpha^*=\{\alpha<\alpha^* \mid f(\alpha) \in W\}\not \in V.\end{align*} $$

Work in $V[G]$ . Set $A_0=\bigcap _{\alpha \in X_f \cap \alpha ^*} f(\alpha )$ and $A_1=\bigcap _{\alpha \in \alpha ^* \setminus X_f } \kappa \setminus f(\alpha )$ . Both sets are in W due to $\kappa{-}$ completeness. So, $A=A_0\cap A_1 \in W$ , as well. Pick $\zeta \in A_0\cap A_1$ .

Then

$$ \begin{align*}\{\alpha<\alpha^* \mid \zeta\in f(\alpha)\}=X_f \cap \alpha^*,\end{align*} $$

but clearly, $\{\alpha <\alpha ^* \mid \zeta \in f(\alpha )\}$ is in V.

So, $X_f \cap \alpha ^* \in V$ . Contradiction.

Remark 2.2. 1. By Hamkins it is possible to collapse cardinals without adding new fresh subsets to them. Just add a Cohen real and then do the collapse.

2. The conditions of the theorem are not necessary by no means. For example, starting with a supercompact cardinal $\kappa $ , one can collapse $\kappa ^+$ preserving supercompactness (after making an appropriate preparation) and still it will be possible to find W a normal measure in the extension such that $W\cap V \in V$ .

3. Originally we used a stronger assumption which suffices for the further applications:

every bounded subset of $\kappa $ is added by some subforcing $R\lessdot P$ of cardinality $<\kappa $ .

Magidor pointed out that it is possible to drop it. The final lines of the argument are due to him.

4. Note that if $\delta $ is the least regular cardinal of V which has a new subset in $V[G]$ , then every cardinal $\tau $ of cofinality $\delta $ in V will have a fresh subset. In particular our assumption implies that there is no such $\tau $ ’s in the interval $[\kappa , (2^\kappa )^V]$ .

Our main interest will be in the case $2^\kappa =\kappa ^+$ .

Proposition 2.3. Let U be a $\kappa{-}$ complete ultrafilter over $\kappa $ in V. Let $V[G]$ be a generic extension of V by a forcing P. Suppose that for every $A\subseteq \kappa $ in $V[G]$ there is $p \in G$ such that .

Suppose that in $V[G]$ there is a $\kappa{-}$ complete ultrafilter which extends U.

Then, in $V[G]$ , is a $\kappa{-}$ complete ultrafilter which extends U. Moreover, $U^*$ is the unique $\kappa{-}$ complete ultrafilter which extends U.

Proof Suppose that W is a $\kappa{-}$ complete ultrafilter which extends U in $V[G]$ . Clearly, then $W\cap V=U$ .

Also,

$$ \begin{align*}U=\{A\subseteq \kappa \mid A\in V \text{ and } [id]_W \in j_W(A)\}.\end{align*} $$

Consider $j_W:V[G]\to M_W$ . Then, $M_W=M[j_W(G)]$ . ⁶

Define $k:M_U \to M$ by setting $k([f]_U)=[f]_W$ .

Lemma 2.4. k is an elementary embedding.

Proof Clearly, k respects $\in $ and $=$ .

Let $\varphi (v_1,\ldots ,v_n)$ be a formula and $f_1,\ldots ,f_n$ be functions in V from $\kappa $ .

Suppose that

$$ \begin{align*}M_U\models \varphi([f_1]_U,\ldots,[f_n]_U).\end{align*} $$

Then

$$ \begin{align*}\{\nu<\kappa \mid V\models \varphi(f_1(\nu),\ldots,f_n(\nu)\}\in U\subseteq W.\end{align*} $$

So,

$$ \begin{align*}M_W\models (M\models \varphi([f_1]_W,\ldots,[f_n]_W)).\end{align*} $$

Hence,

$$ \begin{align*}M\models \varphi([f_1]_W,\ldots,[f_n]_W).\\[-30pt]\end{align*} $$

Lemma 2.5. $j_W\upharpoonright V= k\circ j_U$ .

Proof Let $x \in V$ . Then $j_W(x) = [c_x]_W$ , where $c_x$ is the constant function with value x. So,

$$ \begin{align*}j_W(x) = [c_x]_W=k([c_x]_U)=k(j_U(x)),\end{align*} $$

and we are done.

Now, let A be subset of $ \kappa $ in $V[G]$ . Then, there is $p \in G$ such that

Suppose that

Apply k.

Then

Recall that $M_W=M[j_W(G)]$ . So, $j_W(p)\in j_W(G)$ , and then, in $M_W$ ,

Hence, $A \in W$ .

This shows that $U^*=W$ , and we are done.

Let us show the following:

Proposition 2.6. Let U be a $\kappa{-}$ complete ultrafilter over $\kappa $ in V. Let $V[G]$ be a generic extension of V by a forcing P. Then the following two conditions are equivalent:

1. 1. for every $A\subseteq \kappa $ in $V[G]$ there is $p \in G$ such that

2. 2. U generates an ultrafilter in $V[G]$ , i.e., $\{ A\subseteq \kappa \mid \exists B\in U (B\subseteq A)\}$ is an ultrafilter in $V[G]$ .

Proof $(1)\Rightarrow (2)$ .

Let $A\subseteq \kappa $ in $V[G]$ and suppose that there is $p \in G$ such that

. Let, in V,

Then, $B\in U$ , by the Los Theorem. In addition, $B\subseteq A$ , since $p\in G$ .

$(2)\Rightarrow (1)$ . Let $A\subseteq \kappa $ in $V[G]$ and suppose that $A\supseteq B$ , for some $B\in U$ .

Pick $p\in G$ such that

. Then, in $M_U$ ,

By the assumption, U generates an ultrafilter, hence for every $A\subseteq \kappa $ in $V[G]$ , either A or $\kappa \setminus A$ contain an element of U. So, (1) holds.

Clearly, the condition (2) of the proposition provides the uniqueness.

Concerning the completeness of U in extensions, we do not know the following:

Question. Suppose that U is a $\kappa{-}$ complete (or normal) ultrafilter over $\kappa $ in V. Let $V[G]$ be a generic extension of V by a forcing P. Is it possible that U generates an ultrafilter in $V[G]$ which is not $\sigma{-}$ complete?

Assuming some forms of covering it is possible to argue that U must be complete in the extension. Let us state a simplest form of this type of arguments.

Proposition 2.7. Assume $2^\kappa =\kappa ^+$ . Let U be a $\kappa{-}$ complete filter over $\kappa $ in V. Let $V[G]$ be a generic extension of V by a forcing P. Suppose that both $\kappa $ and $\kappa ^+$ remain regular in $V[G]$ .

Then the filter generated by U remains $\kappa{-}$ complete in $V[G]$ . ⁷

In addition, if U was normal in V, then it remains $\kappa ^+$ -directed in $V[G]$ . ⁸

Proof Let us deal with $\kappa{-}$ completeness. Directedness is similar.

We assume $2^\kappa =\kappa ^+$ holds in V. Hence, $U=\{B_\alpha \mid \alpha <\kappa ^+\}$ .

Now let $a\subseteq \kappa ^+, |a|<\kappa $ in $V[G]$ . Pick $f:\kappa \to \sup (a)+1$ in V to be onto. Then, due to regularity of $\kappa $ , there is $\delta <\kappa $ , such that $f"\delta \supseteq a$ . Set $b=f"\delta $ . Clearly, $b\in V$ and $|b|<\kappa $ there. Then

$$ \begin{align*}\bigcap_{\alpha\in a}B_\alpha\supseteq \bigcap_{\alpha\in b}B_\alpha \in U.\\[-35pt]\end{align*} $$

The following is a slight generalization of 2.3:

Proposition 2.8. Let U be a $\kappa{-}$ complete ultrafilter over $\kappa $ in V. Suppose that $i:V\to N$ is an elementary embedding such that for some $\delta $ , $U=\{ X \subseteq \kappa \mid \delta \in i(X)\}$ . Let $V[G]$ be a generic extension of V by a forcing P. Suppose that for every $A\subseteq \kappa $ in $V[G]$ there is $p \in G$ such that .

Then U generates an ultrafilter in $V[G]$ .

Proof Define $\sigma :M_U \to N$ by setting $\sigma ([f]_U)=i(f)(\delta )$ .

Then $i=\sigma \circ j_U$ and $\sigma ([id]_U)=\delta $ . So, by elementarity of $\sigma $ ,

for every $p \in P$ and a name

. In particular, the assumption of the proposition implies that for every $A\subseteq \kappa $ in $V[G]$ there is $p \in G$ such that

. Now the conclusion follows by 2.6.

It is tempting to try to apply the above proposition together with Friedman, Magidor [6] in order to obtain $2^\kappa>\kappa ^+$ but there is a normal ultrafilter generated by $\kappa ^+$ many sets. The problem is that a non-trivial forcing should be made over $\kappa $ itself and, then statements of the form are decided by $p^\frown j(p)\setminus \kappa +1$ and not by $j(p)$ alone, since in $j(p)$ the $\kappa{-}$ th coordinate is just empty.

We have the following parallel to 2.6 statement for normal ultrafilters:

Proposition 2.9. Let U be a normal ultrafilter over $\kappa $ in V. Let $V[G]$ be a generic extension of V by a forcing P. Then the following two conditions are equivalent:

1. 1. for every regressive function f on $\kappa $ in $V[G]$ , there is $p \in G$ such that

2. 2. U generates a normal ultrafilter in $V[G]$ , i.e., $W=\{ A\subseteq \kappa \mid \exists B\in U (B\subseteq A)\}$ is a normal ultrafilter in $V[G]$ .

Proof $(1)\Rightarrow (2)$ .

Let f be a regressive function on $\kappa $ in $V[G]$ and suppose that there is $p \in G$ such that for some $\alpha <\kappa $ ,

. Let, in V,

Then, $B\in U$ , by the Los Theorem. In addition, $B\subseteq \{\nu <\kappa \mid f(\nu )=\alpha \}$ , since $p\in G$ .

$(2)\Rightarrow (1)$ . Let f be a regressive function on $\kappa $ in $V[G]$ and suppose that for some $\alpha <\kappa $ , the set $A=\{\nu <\kappa \mid f(\nu )=\alpha \}\in W$ .

Then, $A\supseteq B$ , for some $B\in U$ .

Pick $p\in G$ such that

. Then, in $M_U$ ,

So, (1) holds.

The following question seems natural:

Question. Suppose that U is a normal ultrafilter over $\kappa $ in V. Let $V[G]$ be a generic extension of V by a forcing P. Is it possible that U generates a $\kappa{-}$ complete ultrafilter in $V[G]$ which is not normal?

3 Nonstationary support iteration of Prikry type forcing notions

An iterated forcing with nonstationary support was introduced by Jensen [3] in his famous work on codding the universe by a real, Friedman and Magidor [6] used it to solve a long standing problem on number of normal measures, Ben-Neria [4], Ben-Neria and Unger [5], Apter and Cummings [2] found more interesting applications.

Definition 3.1. An iterated forcing notion $P_\eta $ of length $\eta $ is an iteration with nonstationary support if for every $\gamma \leq \eta $ :

1. 1. If $\gamma $ is not inaccessible, then $P_\gamma $ is the inverse limit of ${\langle } P_\alpha \mid \alpha <\gamma {\rangle }$ .

2. 2. If $\gamma $ is inaccessible, then $P_\gamma $ is the set of conditions in the inverse limit of ${\langle } P_\alpha \mid \alpha <\gamma {\rangle }$ whose support is a nonstationary subset of $\gamma $ .

Definition 3.2. A triple ${\langle } \mathcal P, \leq , \leq ^*{\!\rangle }$ is called a Prikry type forcing notion iff

1. 1. $\leq , \leq ^*$ are two partial orderings of a set $\mathcal P$ .

2. 2. $\leq ^*\subseteq \leq $ .

3. 3. For every statement $\varphi $ of the forcing language ${\langle } \mathcal P,\leq {\rangle }$ and every $q \in \mathcal P$ , there is $p\in \mathcal P$ , $p\geq ^* q$ which decides $\varphi $ .

Suppose now that is a nonstationary support iteration of a Prikry type forcing notions such that for every $\beta <\kappa $ the following hold:

1. 1. is trivial unless $\beta $ is an inaccessible (or measurable),

2. 2. is $\beta{-}$ strategically closed,

3. 3. is less than the first inaccessible cardinal above $\beta $ .

Two specific forcing notions of this type in which we are interested are

1. A. The Prikry forcing for changing cofinality of a measurable $\beta $ to $\omega $ .

2. B. The forcing for adding a stationary non-reflecting subset to $\beta $ which consists of inaccessible cardinals, for a Mahlo cardinal $\beta $ .

   In this case $\leq =\leq ^*$ .

The basic properties of this type of iterations are identical to the Easton or full support iterations, see for example [7]. We refer to Ben-Neria and Unger [5] for iterating Prikry forcings and to Apter and Cummings [1] for iterating forcings adding a stationary non-reflecting subset, with non-stationary support.

Suppose that $\kappa $ is a measurable cardinal and U a normal ultrafilter over $\kappa $ .

Assume that on a set I of $\beta $ ’s in U the forcing is trivial.

The next lemma follows basically an argument of Friedman and Magidor [6].

Lemma 3.3. Let $G_\kappa $ be generic subset of $P_\kappa $ . Then the set $H=\{j_U(p)\setminus \kappa \mid p \in G_\kappa \}$ ⁹ is $M_U[G_\kappa ]{-}$ generic for ${\langle } j_U(P_\kappa )/G_\kappa , \leq ^*{\!\rangle } $ .

Proof Let be a name which is forced, say by the weakest condition in $P_\kappa $ , to be a dense open subset of . Pick a function F which represents in the ultrapower $M_U$ .

Assume, for simplification of the notation, that for every $\beta \in I$ , $F(\beta )$ is forced by the weakest condition in $P_\beta $ to be a dense open subset of ${\langle } P_\kappa /P_\beta , \leq ^*{\!\rangle }$ .

Fix $p \in P_\kappa $ . We define by induction a $\leq ^*$ -increasing sequence ${\langle } p_i \mid i<\kappa {\rangle }$ of extensions of p and a decreasing sequence ${\langle } C_i \mid i<\kappa {\rangle } $ of closed unbounded subsets of $\kappa $ such that for every $i<\kappa $ the following hold:

1. 1. $C_i \cap {\textrm {supp}}(p_i)=\emptyset $ ,

2. 2. $p\upharpoonright {i} \Vdash p_{i}\setminus {i} \in F({i})$ , if $i \in I\cap \bigcap _{j<i}C_j$ ,

3. 3. $p_i \upharpoonright {i +1}=p_{i'}\upharpoonright {i+1}$ , for every $i<i'<\kappa $ .

Proceed as follows.

Set $p_0=p$ . Let $C_0$ be a club disjoint with ${\textrm {supp}}(p_0)$ . Set $i_0=\min (I\cap C_0)$ .

For every $i<i_0$ , set $p_i=p_0$ and $C_i=C_0$ .

Now let $p_{i_0}\geq ^* p_0$ be such that $p_{i_0}\upharpoonright i_0=p_0\upharpoonright i_0$ and $p\upharpoonright i_0 \Vdash p_{i_0}\setminus i_0 \in F(i_0)$ .

Let $C_{i_0}$ be a proper club subset of $C_0$ which is disjoint from ${\textrm {supp}}(p_{i_0})$ .

Suppose now that $p_j,C_j$ are defined for every $j<i$ . Define $p_i$ and $C_i$ . If there is $i'<i$ such that $C_{i'}=C_j$ , for every $j, i'\leq j<i$ , then we proceed as above.

Suppose that this is not the case. Note that then $i \not \in {\textrm {supp}}(p_j)$ , for every $j<i$ .

Set $C_i'=\bigcap _{j<i}C_j$ . There is a $\leq ^*$ -extension of the sequence ${\langle } p_j \mid j<i{\rangle }$ . Just put together the conditions using the inductive assumption (3) above and the strategic closure. Note that $|P_{\xi }|$ is below the first inaccessible above $\xi $ , so we have enough strategic closure in order to proceed. The only problematic coordinate may be i itself, however, $i \not \in {\textrm {supp}}(p_j)$ , for every $j<i$ , and so we will have the i-th coordinate just empty.

This is actually the crucial point in the use of nonstationary support.

Now, if $i \not \in I$ , then set $C_i = C_i'$ and $p_i=p_i'$ .

If $i \in I$ , we proceed as above using $p_i'$ and $C_i'$ .

This completes the construction.

Now set $C=\Delta _{i<\kappa }C_i$ and put the sequence ${\langle } p_i \mid i<\kappa {\rangle }$ into a single condition $p^*$ using the inductive assumption (3) above.

Then for every $i \in C\cap I$ , $p\upharpoonright i \Vdash p_i\setminus i+1\leq ^* p^*\setminus i+1.$

Hence, $p^*\upharpoonright i \Vdash p^*\setminus i+1 \in F(i)$ .

Finally, in $M_U$ , .

Recall that $p \in P_\kappa $ was arbitrary. So there is such $p^* $ in $G_\kappa $ .

Now it is easy to show that $\kappa $ remains a measurable cardinal in $V[G_\kappa ]$ .

Namely set

Lemma 3.4. $U^*$ is a normal ultrafilter over $\kappa $ in $V[G_\kappa ]$ .

Proof Note that for every $X\subseteq \kappa $ in $V[G_\kappa ]$ , the set

is a $\leq ^*{-}$ dense open in $M_U[G_\kappa ]$ , by the Prikry condition of the forcing $ j_U(P_\kappa )/G_\kappa $ . Now, use Lemma 3.3.

The proof of Lemma 3.3 gives the following ¹⁰ :

Lemma 3.5. Let $ p\in P_{\kappa } $ and $ I\subseteq \kappa $ be a stationary subset such that for every $\beta \in I$ , $Q_\beta $ is trivial $($ for example, I consists of accessible or non-measurable cardinals, etc. $)$ . For every $ \beta \in I $ , let $ F(\beta ) $ be a $ P_{\beta } $ -name for a $ \leq ^* $ -dense open subset of $ P_{\kappa } \setminus \beta $ above $ p\setminus \beta $ , and assume that this is forced by $ p\restriction {\beta } $ . Then there exist $p^* \geq ^{*} p$ and a club $ C\subseteq \kappa $ such that for every $\beta \in C\cap I$ ,

$$ \begin{align*}p^* \restriction{\beta} \Vdash p^* \setminus \beta \in F(\beta).\end{align*} $$

Lemma 3.6. Suppose that $\kappa $ was a supercompact in V and there is no inaccessible $($ or measurable $)$ cardinals above it, then it will be a strongly compact in $V[G_\kappa ]$ .

Proof Let U be as above and $\lambda $ be a regular cardinal above $\kappa $ . Fix a normal ultrafilter F over $\mathcal P_\kappa (\lambda )$ .

Consider the embedding $j=j_{j_U(F)}\circ j_U: V\to M$ .

We have the following:

1. A. ,

2. B. $M_U \cap {}^{j_U(\lambda )}M \subseteq M$ ,

3. C. $j_U(\lambda )<j(\kappa )=j_{j_U(F)}(j_U(\kappa ))$ .

Now instead of deciding statements we would like to decide or .

Note that

So, the former decisions will define a uniform $\kappa{-}$ complete ultrafilter over $\lambda $ . Similar, the latter will define a fine $\kappa{-}$ complete ultrafilter over $\mathcal P_\kappa (\lambda )$ , since for every $\alpha <\lambda $ ,

Apply Lemma 3.3. The set $H=\{j_U(p)\setminus \kappa \mid p \in G_\kappa \}$ is $M_U[G_\kappa ]$ -generic for ${\langle } j_U(P_\kappa )/G_\kappa , \leq ^*{\!\rangle } $ . Construct also (in $V[G_\kappa ]$ ) an $M_U[G_\kappa ,H]$ -generic set R for ${\langle } Q_{j_U(\kappa )}, \leq ^*_{Q_{j_U(\kappa )}} {\!\rangle }$ . Note that in case of the Prikry forcings iteration this will be just an atomic forcing, since any two conditions with the same trunk will be compatible.

Next, consider $j_{j_U(F)}:M_U \to M$ . It is an ultrapower embedding by a normal ultrafilter $j_U(F)$ over $\mathcal P_{j_U(\kappa )}(j_U(\lambda ))$ of $M_U$ .

Take . Actually, only H is moved. By supercompactness, it can be made into a single condition s. Just take the union of all supports of this conditions, it is a union of less than $j(\kappa )$ nonstationary subsets of $j(\kappa )$ , and so is nonstationary etc. Also, note that $j_U(\kappa )$ does not belong to ${\textrm {supp}}(s)$ , since $j_U(F)$ is normal.

Now, using the closure, find in $M_U[G_\kappa ,H,R]$ an $M[G_\kappa ,H,R]$ -generic subset S for the forcing ${\langle } j(P_\kappa )/ G_\kappa *H*R, \leq ^*{\!\rangle }$ with $s \in S$ .

Finally, for every $D \in M[G_\kappa ]$ which is a dense open for the forcing ${\langle } j(P_\kappa )/ G_\kappa , \leq ^* {\!\rangle }$ there will be $p \in G_\kappa $ and $q \in R*S$ such that $j_U(p)^\frown q \geq j(p)$ and $j_U(p)^\frown q \in D$ .

The next lemma shows that strongness implies tallness in such extensions. Apter and Cummings were first to show this (see Lemma 2.30 of [2]).

The argument below follows their lines.

Lemma 3.7. Suppose that $\kappa $ was a strong cardinal in V and there is no inaccessible $($ or measurable $)$ cardinals above it, then it will be a tall cardinal in $V[G_\kappa ]$ .

Proof (sketch)

Let E be a $(\kappa , \lambda )$ -extender for some regular $\lambda>\kappa $ . Proceed as in the previous lemma, only use E instead of F and $j=j_{j_U(E)}\circ j_U: V\to M$ . We do not construct a $\leq ^*$ -master condition sequence now, but rather use the image of a $\leq ^*$ -generic over $M_{E(\kappa )}$ to generate a $\leq ^*$ -generic over $M_{E}$ , and then over M, where $E(\kappa )=\{X\subseteq \kappa \mid \kappa \in j_E(X)\}$ is the normal measure of E.

4 Applications

If there is a supercompact cardinal, then, by Solovay (see, for example [12]) there are many normal ultrafilters. But what about strongly compact?

Question. Suppose that there is a strongly compact cardinal, does it follow that there is more than one normal ultrafilter?

Questions of this type appear in the book The Higher Infinite, by Kanamori [12].

Goldberg informed us that he and Woodin gave a negative answer starting from a measurable which is a limit of supercompact cardinals and the Ultrapower Axiom (UA). We will show this from a single supercompact and UA.

The following consequence of UA over a supercompact cardinal $\kappa $ will be used:

1. (ℵ) There exists a unique normal measure over $\kappa $ which concentrates on non-measurable cardinals.

Goldberg proved series of striking consequences of UA (see for example [9]). The statement above is one of them.

Using the argument of 3.6 it is possible to show that ( $\aleph $ ) does not imply UA.

Let us start with the following observation:

Proposition 4.1. Let $\kappa $ be a cardinal. Force with $Cohen(\omega )*Col(\kappa ^+,2^\kappa )$ . Let H be a generic.

Suppose that $\kappa $ is a measurable in $V[H]$ and W is a $\kappa{-}$ complete ultrafilter over $\kappa $ .

Then $U=V\cap W$ is in V ¹¹ and W is a unique extension of it to $V[H]$ .

Proof $U=V\cap W$ is in V by the Hamkins Gap Theorem, since $j_W\upharpoonright V$ is definable in V and

$$ \begin{align*}U=\{X\subseteq \kappa \mid X\in V \text{ and } [id]_W \in j_W\upharpoonright V(X)\}.\end{align*} $$

Now, by Kunen-Paris [14], generates a generic subset $H^*$ of $j_U(Cohen(\omega )*Col(\kappa ^+,2^\kappa ))$ over $M_U$ .

Then, in $V[H]$ , is a $\kappa {-}$ complete ultrafilter which extends U. By 2.3, $U^*$ is the unique $\kappa {-}$ complete ultrafilter which extends U and so $W=U^*$ .

The forcing used above may destroy supercompactness of $\kappa $ . In order to preserve it let us use instead the nonstationary support iteration of the forcings $Col(\alpha ^+,2^\alpha )$ for every inaccessible (or Mahlo) $\alpha \leq \kappa $ .

Denote this iteration up to stage $\kappa $ by $P_\kappa $ and let $P_{\kappa +1}=P_\kappa *Col(\kappa ^+,2^\kappa )$ . Let $G_\kappa $ be a generic subset of $P_\kappa $ and H a generic for $Col(\kappa ^+,2^\kappa )$ over $V[G_\kappa ]$ .

Proposition 4.2. Suppose that $\kappa $ is a supercompact cardinal in V and there is no inaccessible cardinal above it.

Then it remains such in $V[G_\kappa ,H]$ . If W is a $\kappa{-}$ complete ultrafilter over $\kappa $ in $V[G_\kappa ,H]$ .

Then $U=V\cap W$ is in V and W is a unique extension of it in $V[G_\kappa ,H]$ .

Proof The argument for supercompactness is rather standard. Namely, let $\lambda>2^\kappa $ be a regular cardinal and let F be a normal ultrafilter over $\mathcal P_\kappa (\lambda )$ in V. We will extend the embedding $j_F:V\to M_F$ to an elementary embedding $j^*:V[G_\kappa ,H] \to M_F[G_\kappa ^*,H^*]$ .

Thus consider first . Note that $\kappa $ does not appear in supports of its elements due to normality of F. So, we can using the closure of the forcing and the ultrapower, combine elements of this set into a single condition s in $j_F(P_\kappa *Col(\kappa ^+,2^\kappa ))/ G_\kappa *H$ . Finally, build a master condition sequence above s for $M_F[G_\kappa *H]$ .

Now let us deal with second part of the statement.

Let W be a $\kappa{-}$ complete ultrafilter over $\kappa $ in $V[G_\kappa ,H]$ .

Again, as in 4.1, by Hamkins Gap Theorem, $U=V\cap W \in V$ (a gap now, for example, at the second inaccessible below $\kappa $ ). Still, generates a generic subset $G^**H^*$ of $j_U(P_\kappa *Col(\kappa ^+,2^\kappa ))$ over $M_U$ . We can apply 3.3 together with Kunen–Paris for this.

The final stage is as in 4.1.

Now the following follows:

Corollary 4.3. Suppose that $\kappa $ is a supercompact cardinal with no inaccessible cardinal above it and with a unique normal measure which concentrates on non-measurable cardinals.

Then there is a generic extension in which $2^\kappa =\kappa ^+$ and $\kappa $ is still a supercompact cardinal with a unique normal measure which concentrates on non-measurable cardinals.

Now we are ready to prove the result:

Theorem 4.4. Suppose that $\kappa $ is a supercompact cardinal with a unique normal measure which concentrates on non-measurable cardinals and $2^\kappa =\kappa ^+$ .

Assume that there is no inaccessible cardinals above $\kappa $ .

Let $P_\kappa $ be the forcing adding non-reflecting stationary subset of inaccessibles to every measurable cardinal below $\kappa $ with the nonstationary support. Let $G_\kappa \subseteq P_\kappa $ be a generic.

Then, in $V[G_\kappa ]$ , $\kappa $ is a strongly compact, the only measurable cardinal and there is a unique normal measure. ¹²

Proof By Lemma 3.6, $\kappa $ is strongly compact in $V[G_\kappa ]$ . Clearly, it is a unique measurable there.

Let W be a normal ultrafilter over $\kappa $ in $V[G_\kappa ]$ . Note that W concentrates on cardinals which are non-measurable in V. Just otherwise, $\kappa $ will be a measurable in the ground model of $M_W$ , and so, a non-reflecting stationary set S should be added there. But such S will be stationary in $V[G_\kappa ]$ as well, since ${}^\kappa M_W\subseteq M_W$ . However, $\kappa $ is a measurable cardinal in $V[G_\kappa ]$ .

By Hamkins [10], no new fresh subsets are added to $\kappa ,\kappa ^+$ . So, by 2.1, $U=W\cap V$ is in V. Hence, U is a normal ultrafilter on $\kappa $ in V which concentrates on non-measurable cardinals.

By our assumption, U is a unique ultrafilter like these.

Now, 2.3 and 3.3 complete the argument.

Now let us turn to the Prikry forcings. We will be to show a parallel result for a nonstationary iteration:

Theorem 4.5. Suppose that $\kappa $ is a supercompact cardinal with a unique normal measure which concentrates on non-measurable cardinals and $2^\kappa =\kappa ^+$ .

Assume that there is no inaccessible cardinals above $\kappa $ .

Let $P_\kappa $ be a nonstationary support iteration of Prikry forcing changing cofinality of every measurable cardinal below $\kappa $ to $\omega $ . Let $G_\kappa \subseteq P_\kappa $ be a generic.

Then, in $V[G_\kappa ]$ , $\kappa $ is a strongly compact, the only measurable cardinal and there is a unique normal measure.

The proof repeats completely the proof of 4.4, only we cannot appeal anymore to Hamkins result about fresh subsets, since now we use a forcing which is not strategically closed. Instead, let us argue directly that there is no fresh subsets of $\kappa $ and of $\kappa ^+$ in $V[G_\kappa ]$ .

Let us do this for all three supports—Easton, full and nonstationary (see [7] for Easton and full supports).

We start with $\kappa $ .

Lemma 4.6. Let $V[G]$ be a generic extension of V by a forcing P which preserves $\kappa ^+$ . Suppose that there is a normal ultrafilter W over $\kappa $ in $V[G]$ such that ${U=V\cap W \in V}$ .

Assume that there is a set $X\in U$ such that for every $\alpha \in X$ , GCH holds at $\alpha $ in V.

Then there is no fresh subsets of $\kappa $ in $V[G]$ .

Proof Suppose otherwise. Let A be a fresh subset of $\kappa $ . Consider $j_W:V[G]\to M_W$ . Then $M_W=M[j_W(G))]$ . By freshness of A, we have then

$$ \begin{align*}A=j_W(A)\cap \kappa \in M.\end{align*} $$

Set $k([f]_U)=[f]_W$ . By 2.4, it is an elementary embedding from $M_U$ to M. The critical point of k (if exists) should be $>\kappa ^+$ , due to the canonical functions from $\kappa $ to $\kappa $ .

Finally, both $M_U$ and M satisfy GCH at $\kappa $ . Hence, $A\in M_U\subseteq V$ . Contradiction.

We can conclude the following:

Corollary 4.7. Easton, full and nonstationary support iterations of Prikry type forcing notions of a measurable length $\kappa $ which satisfy the assumptions of 4.6 do not add fresh subsets to $\kappa $ .

In particular, assuming $2^\kappa =\kappa ^+$ , Easton, full and nonstationary support iterations of Prikry forcings do not add fresh subsets to $\kappa $ .

Let us deal now with $\kappa ^+$ .

The following lemma is obvious:

Lemma 4.8. Let $\lambda $ be a regular cardinal and P be a forcing notion of cardinality $<\lambda $ . Then P does not add fresh subsets to $\lambda $ .

Proof Suppose otherwise. Let $G\subseteq P $ be a generic and let A be a fresh subset of $\lambda $ in $V[G]$ . For every $\nu \in A$ pick a condition $p_\nu \in G$ which decides . By regularity of $\lambda $ , there is a single $p\in G$ which decides for unboundedly many $\nu $ ’s. Set B to be the union of such decisions made by p. Clearly, $B\in V$ and . So, $A=B\in V$ . Contradiction.

As a corollary we obtain:

Corollary 4.9. Easton support iterations of Prikry type forcing notions each of cardinality $<\kappa $ of a regular length $\kappa $ do not add fresh subsets to $\kappa ^+$ .

Using a similar idea, it is possible to show the following:

Lemma 4.10. Let $P_\kappa $ be a full support iteration of Prikry type forcing notions of a regular length $\kappa $ such that

• • ,

• • if and , then there is .

For example a full support iteration of Prikry forcings is like this.

Then $P_\kappa $ does not add fresh subsets to $\kappa ^+$ .

Proof Suppose otherwise. Let $G_\kappa \subseteq P_\kappa $ be a generic and let A be a fresh subset of $\lambda $ in $V[G]$ .

Fix some . For every $\nu \in A$ pick a condition $p^\nu \in G_\kappa , p^\nu \geq s $ which decides . Then there is a finite $a^\nu \subseteq \kappa $ such that at every coordinate $\beta <\kappa $ outside of $a^\nu $ , .

By regularity of $\kappa ^+$ , there will be a single a such that $a=a_\nu $ , for unboundedly many $\nu $ ’s.

By shrinking more if necessary, we can assume that there is a single condition $q \in P_{\max (a)+1}$ such that $q=p^\nu \upharpoonright \max (a)+1$ , for unboundedly many $\nu $ ’s.

Then, by the assumption of the lemma, if $t \in P_\kappa $ , $t\upharpoonright \max (a)+1=q$ and $t\setminus \max (a)+1\geq ^* s\setminus \max (a)+1$ then t is compatible with all such $p^\nu $ ’s.

Set

Clearly, $B\in V$ and $A=B$ . Contradiction.

Finally let us deal with a nonstationary support iteration.

Lemma 4.11. Let $ I\subseteq \kappa $ be a stationary subset which includes all accessible cardinals and let be a nonstationary support iteration of a Prikry type forcing notions of a regular length $\kappa $ such that for every $\beta <\kappa $ the following hold:

1. 1. is trivial for every $\beta \in I$ ,

2. 2. is $\beta {-}$ strategically closed,

3. 3. is less than the first inaccessible cardinal above $\beta $ .

Then $P_\kappa $ does not add fresh subsets to $\kappa ^+$ .

Proof Assume that is a $ P_{\kappa } $ -name for a fresh function in $ 2^{\kappa ^{+}} $ , and this is forced by the weakest condition in $ P_{\kappa } $ .

At least one of is non-trivial, since otherwise a generic extension will be just V.

Case 1. There exists $ \mu \in I $ which is above the first $\beta <\kappa $ for which

is non-trivial, and a condition $ p^* \in P_{\mu } $ which forces that the following property holds:

(here, $ G_{\mu } $ is the canonical name for the generic set for $ P_{\mu } $ ). By extending $ p^* $ , we can decide the value of $ p $ in the statement above, and thus assume that $ p^* \geq p $ . Let

be a $ P_{\mu } $ -name for $ s $ from the above property, and assume that this is forced by $ p^* $ .

Fix a $ P_{\mu } $ -name for a strategy, , for the second player in the game of length $ \mu +1 $ , which witnesses the $ \mu +1 $ -strategically closure of $ \langle P\setminus \mu , \leq ^* \rangle $ . Note that such a strategy exists since $ \mu \in I$ . Assume that $ p^* $ forces the is such a strategy.

Let us apply the same methods as in the main lemma in [10]. We construct, in $ V $ , a binary tree of conditions, and a tree of functions $ \langle b_{\sigma } \colon \sigma \in {}^{\mu>}2 \rangle $ such that , and for every $ \sigma \in {}^{\mu>}2$ :

1. 1. .

2. 2. .

3. 3. If $ \mbox {lh}(\sigma ) $ is limit, then $ p^* $ forces that is an upper bound, with respect to the direct extension order, of .

4. 4. $ b_{\sigma } $ is an end extension of $ b_{\sigma \restriction { \xi }} $ for every $ \xi <\mbox {lh}(\sigma ) $ .

5. 5. For every $ \xi <\mbox {lh}(\sigma ) $ , $ p^* $ forces that is the sequence of moves of the first player in the game, where the second player plays according to the strategy $ \tau $ .

Now assume that $ g\subseteq P_{\mu } $ is generic over $ V $ with $ p^* \in g $ . In $ V\left [g\right ] $ , let $ h\in 2^{<\mu } $ be the characteristic function of a new subset of $\mu $ . Clearly, $ h \notin V $ . $ h $ defines a branch through the binary tree, . The forcing $ P\setminus \mu $ has a direct extension order which is more than $ \mu {-}$ closed, so there exists an upper bound for the conditions in the branch, of the form . It forces that

$$ \begin{align*}b= \bigcup_{\xi<\mu} b_{h\restriction { \xi }}\end{align*} $$

is an initial segment of . Therefore, $ b\in V $ , and thus $ h $ can be defined, in $ V $ , using the binary tree and the set $ b $ . This is a contradiction to the choice of $ h $ .

Case 2. For every $ \mu \in I $ which is above the first $\beta <\kappa $ for which

is non-trivial, every condition in $ P_{\mu } $ forces that

so, for every $ \mu \in I $ , the following set is forced to be $ \leq ^* $ -dense open in $ P\setminus \mu $ :

Note that we used here the fact that $ \left | G_{\mu } \right |$ is below the first inaccessible above $ \mu $ , and $ P\setminus \mu $ has a direct extension order which has enough strategic closure (since $ \mu $ is in I).

Let us apply lemma 3.5. There exists $ p\in P_{\kappa } $ and a club $ C\subseteq \kappa $ such that for every $ \mu \in C\cap I$ ,

$$ \begin{align*}p\restriction{ \mu} \Vdash p\setminus \mu \in e(\mu).\end{align*} $$

Now, assume that $ G\subseteq P_{\kappa } $ is generic over $ V $ and $ p\in G $ . For every $ \xi <\kappa ^{+} $ , there exists $ p_{\xi }\in G $ above $ p $ which decides . For every such $ \xi $ , there exists $ \mu _{\xi } \in C\cap I $ such that coordinates above $ \mu _{\xi } $ in $ p_{\xi } $ are direct extensions of $ p $ . There exists $ \mu ^*<\kappa $ such that, for unboundedly many values of $ \xi <\kappa ^{+}$ , $ \mu _{\xi } = \mu ^* $ . Similarly, there exists $ p^* \in P_{\mu ^*} $ such that for unboundedly many values of $ \xi <\kappa ^{+} $ , $ p_{\xi }\restriction { \mu ^* } = p^* $ . Let $ q = {p^*}^{\frown } p\setminus {\mu ^*} $ . So $ q\in G $ has the following property: For every $ \xi <\kappa ^{+} $ there exists $ r_{\xi }\in P\setminus {\mu ^*} $ such that $ {q\restriction { {\mu ^*} }}^{\frown } r_{\xi } \in G $ decides and $ q\restriction {{\mu ^*}} \Vdash r_{\xi }\geq ^* q\setminus {\mu ^*}$ .

Let $ q' \in G $ be a condition which forces that the property above holds for $ \check {q} $ .

In $ V $ , let $ g \colon \kappa ^{+} \to 2 $ be the union of all the functions which are forced to be an initial segment of , by some direct extension of $ q $ of the form $ {q\restriction { {\mu ^*} }}^{\frown } r $ , where $ q\restriction {{\mu ^*}} \Vdash r\geq ^* q\setminus {\mu ^*} $ . $ g $ is a function since $ q\setminus {\mu ^*}= p\setminus {\mu ^*}\in e({\mu ^*}) $ .

Finally, let us note that $ q' $ forces that , a contradiction.

Note that neither Easton (specially) and full support share the uniqueness properties of a nonstationary support. However, we still have the following conclusions:

Theorem 4.12. Suppose the following:

1. 1. $\kappa $ is a measurable cardinal.

2. 2. $2^\kappa =\kappa ^+$ .

3. 3. $P_\kappa $ is an Easton support iteration of Prikry type forcing notions each of cardinality $<\kappa $ .

   Let $G_\kappa \subseteq P_\kappa $ be a generic.

4. 4. There is a normal ultrafilter F in V over $\kappa $ which extends to a normal ultrafilter in $V[G_\kappa ]$ and a set $X\in F$ such that for every $\alpha \in X$ , GCH holds in V at $\alpha $ .

Then for every $\kappa{-}$ complete ultrafilter W over $\kappa $ in $V[G_\kappa ]$ , $U=V\cap W$ is in V.

Proof Note that $|P_\kappa |=\kappa $ , and so, $\kappa ^+$ is preserved and $2^\kappa =\kappa ^+$ in $V[G_\kappa ]$ .

By Lemma 4.6, no fresh subsets are added to $\kappa $ and by Corollary 4.9, no fresh subsets are added to $\kappa ^+$ .

Now, by Proposition 2.1, $U\in V$ .

Theorem 4.13. Suppose the following:

1. 1. $\kappa $ is a measurable cardinal.

2. 2. $2^\kappa =\kappa ^+$ .

3. 3. $P_\kappa $ be a full support iteration of Prikry type forcing notions such that

   • • ,

   • • if and , then there is .

   Let $G_\kappa \subseteq P_\kappa $ be a generic.

4. 4. There is a normal ultrafilter F in V over $\kappa $ which extends to a normal ultrafilter in $V[G_\kappa ]$ and a set $X\in F$ such that for every $\alpha \in X$ , GCH holds in V at $\alpha $ .

Then for every $\kappa{-}$ complete ultrafilter W over $\kappa $ in $V[G_\kappa ]$ , $U=V\cap W$ is in V.

Proof Note that $P_\kappa $ preserves $\kappa ^+$ and $2^\kappa =\kappa ^+$ in $V[G_\kappa ]$ .

By Lemma 4.6, no fresh subsets are added to $\kappa $ and by Lemma 4.10, no fresh subsets are added to $\kappa ^+$ .

Now, by Proposition 2.1, $U\in V$ .

The work by Ben-Neria [4] allows to say more about number of possible extensions of ultrafilters from V to a full support iterations $V[G_\kappa ]$ . Let $P_\kappa $ be just the usual Magidor (full support) iteration of Prikry forcings [15].

Following [4], denote

$$ \begin{align*}\Delta=\{\nu<\kappa \mid \nu \text{ is a measurable cardinal} \}.\end{align*} $$

Let $d:\Delta \to \kappa $ is the function which takes a measurable in V cardinal $\nu $ to the first element of its Prikry sequence.

Ben-Neria proved in [4, Proposition 3.4] assuming , that there is a unique normal measure in $V[G_\kappa ]$ that does not concentrates on $d"\Delta $ . He make use of existence of the core model and restrictions of ultrapower embeddings to it.

It is not hard to replace this inner models part by appealing to 4.13. So, the following holds:

Theorem 4.14. Suppose that $\kappa $ is a supercompact cardinal with a unique normal measure which concentrates on non-measurable cardinals and $2^\kappa =\kappa ^+$ .

Assume that there is no inaccessible cardinals above $\kappa $ .

Let $P_\kappa $ be a full support iteration of Prikry forcing changing cofinality of every measurable cardinal below $\kappa $ to $\omega $ . Let $G_\kappa \subseteq P_\kappa $ be a generic.

Then, in $V[G_\kappa ]$ , $\kappa $ is a strongly compact, the only measurable cardinal and there is a unique normal measure which does not concentrate on $d"\Delta $ .

Let us return to 4.4, 4.5, but use a bit more strength of the Ultrapower Axiom.

By Goldberg [9], there exists not only a unique normal measure over a supercompact $\kappa $ which concentrates over non-measurable cardinals, but also a unique normal measure which concentrates on measurable cardinals of the Mitchell order 1 (i.e., having a unique normal measure), of the Mitchell order 2 etc.

Let $\eta <\kappa $ . Now, instead of ( $\aleph $ ) above we assume the following consequence of UA:

$(\beth )_\eta $ For every $\tau <\eta $ there exists a unique normal measure of the Mitchell order $\tau $ over $\kappa $ .

The following follows from 4.2:

Corollary 4.15. Suppose that $\kappa $ is a supercompact cardinal with no inaccessible cardinal above it and $(\beth )_\eta $ holds.

Then there is a generic extension in which no new subsets are added to $\eta $ , $2^\kappa =\kappa ^+$ and $\kappa $ is still a supercompact cardinal and $(\beth )_\eta $ holds.

Now we can deduce the following:

Theorem 4.16. Suppose that $\kappa $ is a supercompact cardinal, $(\beth )_\eta $ holds and $2^\kappa =\kappa ^+$ .

Assume that there is no inaccessible cardinals above $\kappa $ .

Let $P_\kappa $ be the forcing adding non-reflecting stationary subset of inaccessibles (or alternatively the Prikry forcing) for every measurable cardinal below $\kappa $ of the Mitchell order $\geq \eta $ with the nonstationary support. Let $G_\kappa \subseteq P_\kappa $ be a generic.

Then, in $V[G_\kappa ]$ , $\kappa $ is a strongly compact, there is no measurable cardinals of the Mitchell order $\geq \eta $ and $(\beth )_\eta $ holds.

Proof We repeat the arguments of 4.4, 4.5, only use $I=\{\nu <\kappa \mid \text { the Mitchell order of } \nu <\eta \}$ instead of $I=\{\nu <\kappa \mid \nu \text { is not measurable} \}$ .

By Lemma 3.6, $\kappa $ is strongly compact in $V[G_\kappa ]$ .

Let W be a normal ultrafilter over $\kappa $ in $V[G_\kappa ]$ . Note that W concentrates on cardinals which has the Mitchell order $<\eta $ , in V. Just otherwise, $\kappa $ will be a measurable in the ground model of $M_W$ of the Mitchell order $\geq \eta $ , and so, a non-reflecting stationary set S or a Prikry sequence should be added there. Say that a non-reflecting stationary set S was added. But such S will be stationary in $V[G_\kappa ]$ as well, since ${}^\kappa M_W\subseteq M_W$ . However, $\kappa $ is a measurable cardinal in $V[G_\kappa ]$ .

By Hamkins [10], for non-reflecting stationary set or by 4.6, 4.11, for Prikry, no new fresh subsets are added to $\kappa ,\kappa ^+$ . So, by 2.1, $U=W\cap V$ is in V. Hence, U is a normal ultrafilter on $\kappa $ in V which concentrates on measurable cardinals of the Mitchell order $<\eta $ .

Then, by $\kappa{-}$ completeness, there is $\zeta <\eta $ such that U concentrates exactly on measurable cardinals of the Mitchell order $\zeta $ .

By our assumption, U is a unique ultrafilter like these.

Now, 2.3 and 3.3 complete the argument.

It is possible to continue and preserving strong compactness of $\kappa $ to turn it into the first measurable with exactly $\eta $ normal measures.

We force with the full support iteration of the Prikry forcings below $\kappa $ and turn every measurable $\nu <\kappa $ into a cardinal of cofinality $\omega $ .

Then by Magidor [15], $\kappa $ will remain strongly compact cardinal. The number of normal measures over $\kappa $ will remain $\eta $ , by the arguments of Ben-Neria [4] and 4.13, used to replace the inner models part in his argument. So, the following holds:

Theorem 4.17. Suppose that $\kappa $ is a supercompact cardinal, $(\beth )_\eta $ holds and $2^\kappa =\kappa ^+$ .

Assume that there is no inaccessible cardinals above $\kappa $ .

Then there is a generic extension adding no new subsets to $\eta $ , in which $\kappa $ is a strongly compact, least measurable and there are exactly $\eta $ normal measures.

Proof (sketch)

We preserve the notation of [4]: .

Proceed as on p. 382 of [4].

Let W be a normal ultrafilter over $\kappa $ and $\Gamma \in W$ . $\Gamma \in W$ implies which in turn,implies that in $M_W = M[G_W]$ , $|d^{-1}(\{\kappa \})|= 1$ . Denote $\mu = d^{-1}(\kappa )$ . Consider, in $V[G]$ ,

$$ \begin{align*}W_\mu=\{ X\subseteq \kappa \mid \mu \in j_W(X)\}.\end{align*} $$

It is a $\kappa{-}$ complete ultrafilter over $\kappa $ which is Rudin–Keisler equivalent to W, since d is one to one on . In particular, $j_W=j_{W_\mu }$ .

We have $\Delta \in W_\mu $ and $\mu \in j_W(\Delta )$ .

Set $U_\mu =W_\mu \cap V$ . Then by 2.1 and 4.10, $U_\mu \in V$ .

Lemma 4.18. $U_\mu $ is a normal ultrafilter in V.

Proof Proceed as in 3.6 of [4]. Suppose otherwise. Then there is a regressive f which represents $\kappa $ in the ultrapower $M_{U_\mu }$ .

We will find a condition $q \in G$ such that , which is impossible, since , and so, $d(\mu )>\kappa $ in $M_W$ .

For every $p \in P_\kappa $ define $ p^{-f}\geq ^* p$ by reducing the (name of) every measure one set $X_\nu (p)$ for all $\nu \in \Delta $ such that

$$ \begin{align*}p^{-f}\upharpoonright \nu\Vdash X_\nu(p^{-f} ) = X_\nu(p)\setminus ( f(\nu)+1).\end{align*} $$

The definition of $ p^{-f}$ implies that there is a finite subset $b \subseteq \Delta $ such that for every $\nu \in \Delta \setminus b$ , .

Now, using the density argument, find such $ p^{-f}\in G$ . Then

since $\Delta \in W_\mu $ and $\kappa \leq k(\kappa )=k([f]_{U_\mu })=[f]_{W_\mu }=j_{W_\mu }(f)(\mu )=j_W(f)(\mu )$ , where $k:M_{U_\mu }\to M_{W_\mu }$ defined as usual: $k([h]_{U_\mu })=[h]_{W_\mu }$ .

Let us argue now that $W=U^{\times }_\mu $ . It is sufficient to prove that $W\supseteq U^{\times }_\mu $ . As in [4], it is enough to show that $d"A \in W$ , for every $A \in U_\mu $ .

Let $A\in U_\mu $ , then $A\in W_\mu \supseteq U_\mu $ , and so, $d"A \in W=d_*W_\mu $ .

It is possible to give an alternative proof of Apter and Cummings [2] result about tall cardinals. We use exactly the same construction as in the previous theorem, only a strong cardinal replaces a supercompact.

Theorem 4.19. Suppose that $\kappa $ is a strong cardinal, $(\beth )_\eta $ holds and $2^\kappa =\kappa ^+$ .

Assume that there is no inaccessible cardinals above $\kappa $ .

Then there is a generic extension adding no new subsets to $\eta $ , in which $\kappa $ is a tall cardinal, least measurable and there are exactly $\eta $ normal measures.

Note that by results of Mitchell, see [16], the property $(\beth )_\eta $ holds in inner models with a strong cardinal.

5 Elementary embeddings

Let $P_\kappa $ be either Easton or full or nonstationary support iteration of Prikry type forcing notions, $G_\kappa \subseteq P_\kappa $ generic, W a normal ultrafilter over $\kappa $ in $V[G_\kappa ]$ and $U=V\cap W \in V$ . So, $j_W: V[G] \to M_W=M[j_W(G_\kappa )]$ .

In this section we would like to analyze $j_W\upharpoonright V:V\to M$

In order to do so, let us study the elementary embedding $k:M_U \to M$ defined by setting $k([f]_U)=[f]_W$ .

If k is the identity, then $j_W$ is just an extension of $j_U$ . However, even when the Hamkins Gap Theorem [10] applies, k need not be the identity. Starting with a single measurable, it is possible to construct a generic extension in which $j_W\upharpoonright V$ is, for example, the ultrapower embedding with $U\times U$ .

Let us first try to understand possibilities for the critical point of k, assuming that k is not the identity map.

Clearly, ${\textrm {crit}}(k)>\kappa ^+$ , due to the canonical functions.

Let us start with the Easton support iteration.

5.1 Easton support

We will start with two examples in which ${\textrm {crit}}(k)=(\kappa ^{++})^{M_U}$ .

Example 1. Assume GCH. Let $A \subseteq \kappa $ be such that $\kappa \setminus A$ contains $\kappa{-}$ many measurable cardinals.

Let be the Easton support iteration, where for every $\beta <\kappa $ , $Q_\beta $ is trivial, unless $\beta $ is a measurable in $V^{P_\beta }$ and $\beta \not \in A$ . If this is the case, then $Q_\beta $ is the Prikry forcing with a normal measure over $\beta $ .

Suppose that there is a $(\kappa ,\kappa ^{++})$ -extender E in V such that A belongs to its normal measure $E(\kappa )=\{X\subseteq \kappa \mid \kappa \in j_E(X)\}$ . Denote $E(\kappa )$ by U.

Set $\delta =(\kappa ^{++})^{M_{E(\kappa )}}$ . Consider F on $\kappa ^2$ defined as follows:

$$ \begin{align*}Z\in F \text{ iff } (\kappa, \delta) \in j_E(Z).\end{align*} $$

Denote by $i:M_{E(\kappa )} \to M_E$ the natural embedding derived from $j_E$ . Then $\delta $ will be its critical point. Let $[id]_F=(\kappa , \delta _F)$ . Then $|\delta _F|=\kappa ^+$ , since $M_E\models |\delta |=\kappa ^+$ .

Now let $G_\kappa $ be a generic subset of $P_\kappa $ .

Define an extension W of $U=E(\kappa )$ in $ V[G_\kappa ]$ as follows.

Consider $j_F:V\to M_F$ . Let $\mu $ be the least measurable of $M_F$ above $\kappa $ which is not in $j_F(A)$ .

We define $\leq ^*$ -increasing sequence of conditions ${\langle } q_\alpha \mid \alpha <\kappa ^+{\!\rangle }$ in $j_F(P_\kappa )/G_\kappa $ meeting all $\leq ^*$ -dense sets of $M_F[G_\kappa ]$ , only start with a condition which puts $\delta $ to be the first member of the Prikry sequence for $\mu $ .

Set $X\in W$ iff there is $p \in G_\kappa $ and $\alpha <\kappa ^+$ such that .

Then W will be a normal measure over $\kappa $ in $V[G]$ , $W\cap V=U$ .

In addition we will have $\delta <(\kappa ^{++})^{M_W}$ , since the function f

$$ \begin{align*}\nu\mapsto \text{the first element of the Prikry sequence of the least measurable cardinal above } \nu\end{align*} $$

$$ \begin{align*}\text{ which is not in } A\end{align*} $$

will represent $\delta $ in $M_W$ and the set

$$ \begin{align*}\{\nu<\kappa \mid f(\nu)<\nu^{++}\} \in W,\end{align*} $$

by its definition.

Example 2. Let us use adding a non-reflecting stationary sets instead of the Prikry forcing.

Proceed exactly as in the first example only start the master condition sequence ${\langle } q_\alpha \mid \alpha <\kappa ^+{\!\rangle }$ in $j_F(P_\kappa )/G_\kappa $ meeting all $\leq ^*$ -dense sets of $M_F[G_\kappa ]$ , with only start with a condition which puts $\delta $ to be the first member of the generic stationary non-reflecting subset of $\mu $ .

Then, as above, we will have ${\textrm {crit}}(k)=(\kappa ^{++})^{M_U}$ .

Recall that by Hamkins [10], $j_W\upharpoonright V$ , and so k, are definable over V, whenever the forcing $P_\kappa $ has a gap below $\kappa $ . Also, $j_W(V)=\bigcup _{\alpha \in On}j_W((V_\alpha )^V)$ is definable in V.

Remark. There is no need in a $(\kappa , \kappa ^{++})$ -extender in order to produce such examples, i.e., with ${\textrm {crit}}(k)=(\kappa ^{++})^{M_U}$ . It is possible to start with a measurable $\kappa $ which is a limit of measurable cardinals.

Let us sketch the idea. Start with V in which $\kappa $ is a limit of measurable cardinals. Let U be a normal ultrafilter over $\kappa $ which concentrates on non-measurable cardinals. We will use an extensions of $U\times U$ and of $U\times U\times U$ as replacements of U and F of the previous construction.

Denote $j_U(\kappa )$ by $\kappa _1$ , $j_{U\times U}(\kappa )$ by $\kappa _2$ and $j_{U\times U\times U}(\kappa )$ by $\kappa _3$ . We force (with a suitable preparation) a Cohen function $f_\kappa :\kappa \to \kappa $ . Then do collapses $Col(\nu ^+,<f_\kappa (\nu ))$ , on a set $\nu $ ’s in U. Set the value of the corresponding $f_{\kappa _2}(\kappa )$ to be $\kappa _1$ in $M_{U\times U}$ . Set $f_{\kappa _3}(\kappa )$ to be $\kappa _2$ in $M_{U\times U\times U}$ .

5.2 More examples

We would like to use iterations of Prikry forcings in order to construct examples with $j_W\upharpoonright V$ not definable in V, but still $W\cap V\in V$ . This type of situation is different from those produced by the Hamkins Gap Theorem [10].

Let us observe that the methods above do not allow to construct models with $j_W(V)$ definable (in V), but $j_W\upharpoonright V$ is not.

The next proposition shows a definability of $j_W(V)$ together with non-definability of $j_W\upharpoonright V$ should be rather strong, if consistent.

Proposition 5.1. Suppose that the core model $\mathcal K$ exists and V is a generic extension of $\mathcal K$ , i.e., for some forcing notion $P\in \mathcal K$ and some $H\subseteq P$ generic over $\mathcal K$ , $V=\mathcal K[H]$ . ¹³

Suppose that $V^*\supseteq V$ is a generic extension of V (or both have the same core model) and $j^*:V^* \to M^*$ is an elementary embedding such that $j^*(V)$ is definable in V.

Then, also, $j^*\upharpoonright V$ is definable in V.

Proof Denote the V-class $j^*(V)$ by M. Let $j=j^*\upharpoonright V$ .

By elementarity, $M=j(\mathcal K)[H']$ , where $H'=j(H)$ is $\mathcal K^M=j(\mathcal K)$ -generic over $\mathcal K^M$ .

$\mathcal K^M$ is a class in V, so we can compare inside V with the real $\mathcal K$ (by using least disagreements). This will produce the embedding $i:\mathcal K \to \mathcal K^M$ . Given $\mathcal K^M$ , such i is unique.

So, $j\upharpoonright K=i$ and i is definable in K.

Now,

So, we can define j using i and $H'$ .

Remark 5.2. The assumption that $V^*\supseteq V$ is a generic extension of V or at least both have the same core model, is necessary. Just otherwise, we can take $V=L[U]$ and $V^*=L[\vec {W}]$ , where $\vec {W}$ contains at least two measures, and then, form $j^*$ by iterating the second measure.

Start with a GCH model with a measurable cardinal $\kappa $ which is a limit of measurables. We can assume, for simplicity that $V=\mathcal K$ , but it is not necessary.

First we force with Easton support product the Cohen forcing which adds a Cohen function $h_\nu :\nu ^+\to \nu ^+$ to every inaccessible $\nu <\kappa $ . Let ${\langle } R_\alpha , {C}_\beta \mid \beta <\kappa , \alpha \leq \kappa {\rangle }$ be this forcing.

By Kunen–Paris (see for example Kanamori’s book [12] on this), it preserves measurability of every measurable cardinal.

Let us be more specific here.

Let $\eta \leq \kappa $ be a measurable in the ground model. Fix some normal ultrafilter $U(\eta )$ which concentrates on non-measurable cardinals. Let $j_\eta =j_{U(\eta )}:V\to M_{U(\eta )}=M_\eta $ be the corresponding elementary embedding.

We define in the extension $\eta $ -many normal ultrafilters which extend $U(\eta )$ , but have the same ultrapower.

Consider the relevant for $\eta $ part of the forcing, i.e., $R_{\eta }$ . It adds Cohen functions $\vec {h}={\langle } h_\nu \mid \nu < \eta \text { is an inaccessible} {\rangle }$ .

Pick in $V[\vec {h}]$ , a sequence such that

• • , for every inaccessible $\nu <\eta $ ,

• • is $M_\eta {-}$ generic for the forcing $j_\eta (R_{\eta })$ .

Denote $V[\vec {h}]$ by $V'$ and $M_\eta [\vec {h}']$ by $M_\eta '$ . Then $j_\eta $ extends to and is the ultrapower of $V'$ by an extension of of $U_\eta $ .

Let . Now, for every $i<\eta $ , let us change the value to i. Denote the result by .

Set

Clearly that such is in $M_\eta '$ and it is $j_\eta (R_{\eta })$ -generic over $M_\eta $ .

We have so, .

Define

according to

, i.e., by setting

Define the corresponding ultrafilter

$$ \begin{align*}U_{\eta, i}'=\{ X\subseteq \eta \mid \eta \in j_{\eta, i}'(X)\}.\end{align*} $$

Note that such ’s will be different.

Namely, let $i, i'<\eta , i\not = i'$ . Then the set

and the set

Clearly this sets are disjoint.

Now, let us define in $V'$ an iteration of Prikry forcings (either Easton, non-stationary or full support can be used for this).

Set .

Let ${\langle } \eta _\xi \mid \xi <\kappa {\rangle }$ be the increasing enumeration of all measurable cardinals $\tau <\kappa $ .

Define an iteration with either nonstationary or full support. ¹⁴

For every $\beta <\kappa $ , let $Q_\beta $ be trivial, unless $\beta $ is a measurable in $V^{'P_\beta }$ . Let $Q_{\eta _0}$ be the Prikry forcing with . Let be the canonical name of the Prikry sequence for $Q_{\eta _0}$ .

Now, suppose that $ 0<\xi <\kappa $ and $P_{\eta _\xi }$ is defined. Define $Q_{\eta _\xi }$ .

If $\xi $ is a limit ordinal then let $Q_{\eta _\xi }$ be the Prikry forcing with .

If $\xi =\xi '+k$ , where $\xi '$ is a limit and $k,0<k<\omega $ , then let $Q_{\eta _\xi }$ be the Prikry forcing with .

Let $G_\kappa $ be a generic subset of $P_\kappa $ . Then U extends in $V'[G_\kappa ]$ to a normal ultrafilter W. We have $W\cap V=U\in V'$ .

Let us argue that $j_W\upharpoonright V'$ is not definable in $V'$ .

Recall that $j_W= k\circ j_U$ .

Thus, $j_W\upharpoonright V'$ is an iterated ultrapower of $V'$ by its measures. So, U must be applied first, since $\kappa $ is the critical point and it is not measurable in the ultrapower. Let be the list of all measurable cardinals below $j_U(\kappa )$ in $M_U$ . So the next cardinal addressed should be which is the first measurable above $\kappa $ in $M_U$ . The recipe that now we should apply the Prikry forcing with . However, is an ordinal of cofinality $\kappa ^+$ and cardinals are preserved. So, an iterated ultrapower with the measure should be used $\omega $ -many times in order to produce the desired Prikry sequence, see [8], for a non-stationary support and [13], for a full support. Then we proceed to , , etc.

Now if $j_W\upharpoonright V'$ was definable in $V'$ , then we will be able to reconstruct the Prikry over $V'$ sequence ${\langle } \eta _0^n\mid n<\omega {\rangle }$ .

Namely, consider the sets in $M_U$ . Only image $k(X_{\eta _\kappa , i})$ from them which contains a final segment of the Prikry sequence for is . Which means that $\eta ^0_0$ reconstructible from the iteration. Proceed similar with each $n, 0<n<\omega $ .