Magnetic Field and Early Evolution of Circumstellar Disks

Abstract

The magnetic field plays a central role in the formation and evolution of circumstellar disks. The magnetic field connects the rapidly rotating central region with the outer envelope and extracts angular momentum from the central region during gravitational collapse of the cloud core. This process is known as magnetic braking. Both analytical and multidimensional simulations have shown that disk formation is strongly suppressed by magnetic braking in moderately magnetised cloud cores in the ideal magnetohydrodynamic limit. On the other hand, recent observations have provided growing evidence of a relatively large disk several tens of astronomical units in size existing in some Class 0 young stellar objects. This introduces a serious discrepancy between the theoretical study and observations. Various physical mechanisms have been proposed to solve the problem of catastrophic magnetic braking, such as misalignment between the magnetic field and the rotation axis, turbulence, and non-ideal effect. In this paper, we review the mechanism of magnetic braking, its effect on disk formation and early evolution, and the mechanisms that resolve the magnetic braking problem. In particular, we emphasise the importance of non-ideal effects. The combination of magnetic diffusion and thermal evolution during gravitational collapse provides a robust formation process for the circumstellar disk at the very early phase of protostar formation. The rotation induced by the Hall effect can supply a sufficient amount of angular momentum for typical circumstellar disks around T Tauri stars. By examining the combination of the suggested mechanisms, we conclude that the circumstellar disks commonly form in the very early phase of protostar formation.

1 INTRODUCTION

Circumstellar disks are formed around protostars during the gravitational collapse of molecular cloud core. Because the disks are the formation sites of planets, the formation and evolution processes of the disk essentially determine the initial conditions for planet formation. Hence, understanding disk formation and evolution is crucial for constructing a comprehensive theory for planet formation. An accurate description of the angular momentum evolution is required to investigate the disk evolution because the centrifugal force mainly balances the gravitational force of the central protostar.

Formation of a circumstellar disk around a very young protostar had been believed to be a natural consequence of angular momentum conservation in the gravitationally collapsing molecular cloud core. Observations of cloud cores have shown that they have finite angular momentum (e.g., Goodman et al. 1993; Caselli et al. 2002).

Many studies of the cloud core collapse without a magnetic field have been conducted (Boss & Bodenheimer 1979; Bate 1998; Truelove et al. 1998; Matsumoto & Hanawa 2003; Commerçon et al. 2008; Attwood et al. 2009; Walch et al. 2009; Machida, Inutsuka, & Matsumoto 2010; Stamatellos, Whitworth, & Hubber 2012; Walch, Whitworth, & Girichidis 2012; Tsukamoto & Machida 2013; Tsukamoto, Machida, & Inutsuka 2013), and it is now well established that a relatively large disk with a size of r ~ 100 AU is formed during the early phase of protostar formation and fragmentation also occurs in the unmagnetised cores.

However, the magnetic field changes this simple process of disk formation. During the gravitational collapse, a toroidal magnetic field is created and the magnetic tension decelerates the gas rotation, removing the angular momentum. This process is known as magnetic braking. Its importance in circumstellar disk formation was recognised in the past decade, although there had been several theoretical studies regarding magnetic braking (Gillis, Mestel, & Paris 1974, 1979; Mouschovias & Paleologou 1979, 1980), focusing mostly on the angular momentum evolution of molecular clouds or cores. Simulations in which the ideal magnetohydrodynamics (MHD) approximation is adopted and the magnetic field is aligned with the rotation vector have shown that disk formation is almost completely suppressed in moderately magnetised cloud cores by magnetic braking (Allen, Li, & Shu 2003; Price & Bate 2007b; Mellon & Li 2008; Hennebelle & Fromang 2008).

Several mechanisms have been suggested to reduce the magnetic braking efficiency. For example, misalignment between the magnetic field and the rotation vector and turbulence are suggested as mechanisms that weaken magnetic braking in the ideal MHD limit (Hennebelle & Ciardi 2009; Joos, Hennebelle, & Ciardi 2012; Santos-Lima, de Gouveia Dal Pino, & Lazarian 2012; Seifried et al. 2013; Joos et al. 2013; Li, Krasnopolsky, & Shang 2013). Non-ideal effects (Ohmic diffusion, the Hall effect, and ambipolar diffusion), which arise from the finite conductivity in the cloud core, also serve as mechanisms that change the magnetic braking efficiency (Duffin & Pudritz 2009; Machida & Matsumoto 2011; Krasnopolsky, Li, & Shang 2011; Li, Krasnopolsky, & Shang 2011; Tomida et al. 2013; Tomida, Okuzumi, & Machida 2015; Tsukamoto et al. 2015b; Masson et al. 2015; Tsukamoto et al. 2015a).

In this paper, we review recent progress on the influence of the magnetic field on the formation and early evolution of the circumstellar disk. The paper is organised as follows. We review the observed properties of cloud cores in Section 2 and summarise gravitational collapse of cloud cores in Section 3. The main part of this paper, Sections 4 to 6, covers recent studies of disk formation and early evolution in magnetised cloud cores. In Section 7, we summarise our current understanding of disk formation and early evolution, and discuss future perspectives.

2 OBSERVATIONAL PROPERTIES OF MOLECULAR CLOUD CORES

In this section, we give an overview of the observational properties of molecular cloud cores.

2.1 Rotation of the cores

An important parameter of the cloud core is its rotation energy. Rotation of cloud cores is often observationally measured using the velocity gradient obtained from the NH₃ (1,1) inversion transition line or N₂H⁺ (1 − 0) rotational transition line (Goodman et al. 1993; Barranco & Goodman 1998; Caselli et al. 2002; Pirogov et al. 2003). On the other hand, simulations of cloud core formation are performed to theoretically investigate core rotation (Offner, Klein, & McKee 2008; Dib et al. 2010). Figure 1 shows the histograms of β_rot ≡ E _rot/E _grav from Dib et al. (2010), where E _rot and E _grav are the rotational and gravitational energy of the core, respectively. In this figure, both the observation (black dotted lines) and simulation results (coloured lines) are plotted. The peaks of both lines show that the cores typically have a β_rot value of ~ 0.01. Hence, both the observations and the simulations suggest that the rotational energy of a typical cloud core is about 1% of its gravitational energy.

Figure 1. Histogram of β_rot( ≡ E _rot/E _grav) of cloud cores obtained using the simulations of Dib et al. (2010) (coloured lines) and observations of Goodman et al. (1993), Barranco & Goodman (1998), and Caselli et al. (2002) (black lines). This figure appears as Figure 6 of Dib et al. (2010). Coloured lines in the upper panels show β_rot with a low density threshold for n _th = 2.0 × 10⁴ cm^{− 3}, whereas, those in the lower panels show β_rot with a high density threshold for n _th = 8.0 × 10⁴ cm^{− 3}. The low and high density thresholds correspond roughly to the excitation density for the NH₃ (J − K)=(1,1) transition and the N₂H⁺ (1 − 0) emission lines, respectively. The observational results obtained for the NH₃ (J − K)=(1,1) transition (upper panels) and the N₂H⁺ (1 − 0) emission line (lower panels) are plotted with black-dashed lines. The NH₃ core observations are from Goodman et al. (1993) and Barranco & Goodman (1998) and the N₂H⁺ data are from Caselli et al. (2002). The left and right panels show the results with strong and weak initial magnetic fields. The initial plasma β in the left and right panels are β = 0.1 and β = 1, respectively.

2.2 Turbulence in the cores

The molecular cloud has a complex internal velocity structure over a wide range of scales that is interpreted as turbulent motion (Larson 1981) and, even at the cloud core scale, there exist non-thermal motions (Barranco & Goodman 1998). Burkert & Bodenheimer (2000) showed that a random Gaussian velocity field with P(k)∝k ^{− 4} can explain the observed rotational properties of the cores. Note that P(k)∝k ^{− 4} is very similar to the Kolmogorov spectrum P(k)∝k ^{− 11/3}. Thus, it is expected that turbulence exists in cloud cores although coherent rotation is often assumed in the theoretical study of the cloud core collapse (e.g., Bate 1998; Matsumoto & Hanawa 2003; Walch et al. 2009; Tsukamoto & Machida 2011). The turbulent velocity inside the cores is typically subsonic (Ward-Thompson et al. 2007).

2.3 Magnetic field in the core

Another important physical quantity is the strength of the magnetic field. The strength of the magnetic field is often expressed using the mass-to-flux ratio relative to the critical mass-to-flux ratio (Mouschovias & Spitzer 1976),

(1) $$\begin{eqnarray} \mu =\frac{(M/\Phi )_{\rm core}}{(M/\Phi )_{\rm crit}}=\frac{(M/\Phi )_{\rm core}}{(0.53/3\pi ) \sqrt{5/G}}. \end{eqnarray}$$

When μ < 1, the magnetic pressure is strong enough to support the cloud core against its self-gravity. The critical value, $(M/\Phi )_{\rm crit}=0.53/3\pi \sqrt{5/G}$ is derived for a spherically symmetric cloud core. This critical value is often used in theoretical study. Another critical mass-to-flux ratio is derived for the stability of disks and expressed as (Nakano & Nakamura 1978),

(2) $$\begin{eqnarray} \lambda =\frac{(\Sigma /\boldsymbol{B})_{\rm core}}{(\Sigma /\boldsymbol{B})_{\rm crit}}=\frac{(\Sigma /\boldsymbol{B})_{\rm core}}{(4\pi ^2 G)^{-1/2}}. \end{eqnarray}$$

This is often used in observational study.

The magnetic field strength of the molecular clouds and cores can be measured using the Zeeman effect (Crutcher et al. 1993, 1996; Falgarone et al. 2008; Troland & Crutcher 2008; Crutcher 2012). Figure 2 shows the observation of the magnetic field of the cloud cores using the OH Zeeman effect. This figure appears as Figure 2 of Troland & Crutcher (2008). They found that the mean value of the mass-to-flux ratio of the observed cloud cores is λ_obs = 4.8 ± 0.4. By applying a geometrical correction, they showed that the mean mass-to-flux ratio of the cloud cores is λ ~ 2. Hence, most cores are supercritical, meaning that the magnetic field is not strong enough to support the cloud core by magnetic pressure. However, the energy of the magnetic field in cores with λ ~ 2 could be several tens of percent of its gravitational energy, which is much larger than the rotation velocity. Therefore, the magnetic field is expected to affect the gas dynamics during gravitational collapse.

Figure 2. Observed line-of-sight magnetic field strength B _los plotted as a function of the H₂ column density [N ₂₁ = 10^{− 21} n(cm^{− 2})]. This figure appears as Figure 2 of Troland & Crutcher (2008). Error bars indicate 1σ. The mass-to-flux ratio normalised by the critical value is given as λ = 7.6 × 10^{− 21} N ₂₁/B _los. The solid line represents the weighted mean value for the mass-to-flux ratio λ = 4.8 ± 0.4, whereas the dashed line represents the value for λ = 1.

3 GRAVITATIONAL COLLAPSE OF CLOUD CORE

In this section, we discuss gravitational collapse of molecular cloud cores. Some terminology is also introduced in this section.

Once the core becomes massive enough and gravitationally unstable, dynamical collapse of the cloud core begins. At the beginning of the collapse, radiation cooling by dust thermal emission is sufficiently effective, and the gas temperature remains almost isothermal at a temperature T = 10 K. During this isothermal collapse phase, the magnetic field is essentially frozen into the gas. When the Lorentz force is weak and negligible, the collapse can be described well as spherically symmetric collapse. Larson (1969) has shown that the isothermal gravitational collapse proceeds self-similarly. As a result, the density profile in the isothermal collapse phase has a central flat profile; the radius is characterised by the Jeans length λ_J and the outer envelope has ρ∝r ^{− 2}, as shown in Larson (1969). In the spherically symmetric collapse phase, the magnetic field evolves as B∝ρ^2/3.

As the isothermal spherical collapse proceeds, the magnetic field is amplified, and the plasma β ≡ P _gas/P _mag) decreases as β∝ρ^{− 1/3}, where P _gas and P _mag are the gas and magnetic pressure, respectively. Hence, at some point, the Lorentz force becomes effective and begins to deflect the gas motion toward the direction parallel to the magnetic field. This breaks the spherically symmetric collapse. The gas density increases by the parallel accretion, while the magnetic field strength remains almost constant.

As a result of parallel accretion, the gas moves to the equatorial plane, forming a sheet-like structure known as a pseudodisk (Galli & Shu 1993). Figure 3 shows the density map of the pseudodisk formed in the simulation of Tsukamoto et al. (2015a), for example. Its radius is typically r ≳ 100 AU at the protostar formation epoch. Because of the inward dragging of the magnetic field, the magnetic field configuration exhibits an hourglass shape (Tomisaka, Ikeuchi, & Nakamura 1988a; Galli & Shu 1993) and a current sheet exists at its midplane. The hourglass shape of the magnetic field is also inferred from observations (Girart, Rao, & Marrone 2006; Cortes & Crutcher 2006; Gonçalves, Galli, & Girart 2008). The figure also shows that the velocity is almost parallel to the magnetic field except around the midplane indicating that the gas moves parallel to the magnetic field. Note that the pseudodisk is not rotationally supported although its morphology is disk-like.

Figure 3. Density structure of the pseudodisk in x–z plane. This figure is obtained using simulation results in which all of the non-ideal effects are considered and the magnetic field and rotation vector are parallel. The simulation corresponds to model Ortho defined in Tsukamoto et al. (2015a) and the simulation setup is described in detail in the paper. At this epoch, the central protostar is formed. The red and white arrows indicate the velocity field and direction of the magnetic field, respectively.

The gas continues to accrete toward the central region mainly through the pseudodisk. If the disk-like structure is maintained, the magnetic field increases as B _c∝ρ^1/2 _c because the central magnetic field and density evolve as B _c∝R ^{− 2} and ρ_c∝R ^{− 2} H ^{− 1}∝R ^{− 4}, respectively, and hence B _c∝ρ^1/2 _c. Here, we assumed that the scale-height of the pseudodisk is given by $H_{\rm c}=c_{\rm s}^2/(G \Sigma )=c_{\rm s}/\sqrt{G \rho _{\rm c}}$ .

When the central density reaches ρ ~ 10^{− 13}g cm^{− 3}, compressional heating overtakes radiative cooling, and the gas begins to evolve adiabatically. As a result, gravitational collapse temporarily stops and a quasi-hydrostatic core, commonly known as the first core or the adiabatic core, forms (Larson 1969; Masunaga & Inutsuka 1999; Vaytet et al. 2012, 2013). In cores with very weak or no magnetic field, a disk several tens of AU in size can form around first core before protostar formation (Bate 1998; Matsumoto & Hanawa 2003; Walch et al. 2009; Tsukamoto & Machida 2011; Tsukamoto et al. 2015c). In the first core phase, the temperature evolves as T∝ρ^{γ − 1}, where γ is the adiabatic index (γ = 5/3 for T ≲ 100 K, and γ = 7/5 for 100 ≲ T ≲ 2000 K). As we will discuss below, in the first core, magnetic diffusion becomes effective, and the gas and the magnetic field are temporarily decoupled until the central temperature reaches ~ 1000 K, and thermal ionisation provides sufficient ionisation.

When the central temperature of the first core reaches ~ 2000 K, the hydrogen molecules begin to dissociate. This endothermic reaction changes the effective adiabatic index to γ_eff = 1.1, and gravitational collapse resumes, which is known as the second collapse. Finally, when the molecular hydrogen is completely dissociated, the gas evolves adiabatically again, and gravitational collapse at the centre finishes. The adiabatic core formed at the centre is the protostar (or the second core). After the protostar forms, it evolves by mass accretion from the envelope (the remnant of the host cloud core), and, at some point, a circumstellar disk is formed around the protostar.

4 MAGNETIC BRAKING AND SUPPRESSION OF DISK FORMATION

In this section, we review angular momentum transfer by the magnetic field, focusing in particular on magnetic braking. We investigate the most simple case, in which the ideal MHD approximation is adopted, the magnetic field and rotation axis are parallel, and the core rotation is coherent. The effects of misalignment and turbulence are discussed in Section 5 and the effects of non-ideal MHD effect are discussed in Section 6.

4.1. Timescale of magnetic braking

An estimate of the magnetic braking timescale would be useful for understanding the basic characteristics of magnetic braking. As shown in many previous studies (Mouschovias & Paleologou 1979, 1980; Mouschovias 1985; Nakano 1989; Tomisaka, Ikeuchi, & Nakamura 1990), the magnetic braking timescale t _b can be estimated as the time in which the torsional Alfvén waves sweep an amount of gas in the outer envelope for which the moment of inertia I _ext(t _b) equals that of the central region I _c. This condition is expressed as

(3) $$\begin{eqnarray} I_{\rm ext}(t_{\rm b})=I_{\rm c}. \end{eqnarray}$$

By solving this equation for a specified geometry of the central region and outer envelope, we can obtain the magnetic braking timescale.

In the simplest geometry, the central collapsing region is modelled as a uniform cylinder with a density ρ_c, radius R _c, and scale height H _c threaded by a uniform magnetic field parallel to the rotation axis. The density of the outer envelope, ρ_ext is assumed to be constant. In this geometry, I _ext(t _b) = πρ_ext R ⁴ _c v _A t _b and I _c = πρ_c R ⁴ _c H _c, where v _A denotes the Alfvén velocity of the outer envelope. Thus, t _b is given as (Mouschovias 1985)

(4) $$\begin{eqnarray} t_{\rm b}=\frac{\rho _{\rm c}}{\rho _{\rm ext}}\frac{H_{\rm c}}{v_{\rm A}}. \end{eqnarray}$$

Using the mass of the cylinder, M = 2πρ_c R ² _c H _c, and the magnetic flux Φ = πR ² _c B, we can rewrite Equation (4) as

(5) $$\begin{eqnarray} t_{\rm b} = \left( \frac{\pi }{\rho _{\rm ext}} \right)^{1/2} \frac{M}{\Phi }. \end{eqnarray}$$

This shows that the magnetic braking timescale in this simple geometry is determined only by the mass-to-flux ratio of the central region and the density of the outer envelope. This timescale can be regarded as the upper limit in the collapsing cloud core because, as shown in Figure 3, the magnetic field has an hourglass shape in the gravitationally collapsing cloud core. In this more realistic configuration, the correction factor ( < 1) resulting from the magnetic field geometry is multiplied by the braking timescale.

As illustrated schematically in Figure 4, in the hourglass configuration, the magnetic field fans out in the vertical direction. If we neglect the moment of inertia of the transitional region, I _ext(t _b) is given as

(6) $$\begin{eqnarray} I_{\rm ext}(t_{\rm b})=\pi \rho _{\rm ext} R_{\rm ext}^4 v_{\rm A} t_{\rm b}. \end{eqnarray}$$

Using I _c = πρ_c R ⁴ _c H _c and Equation (6), we can obtain the magnetic braking timescale of the disk with hourglass magnetic field geometry as (Mouschovias 1985)

(7) $$\begin{eqnarray} t_{\rm b,f}=\left( \frac{\pi }{\rho _{\rm ext}} \right)^{1/2} \left(\frac{M}{\Phi }\right) \left(\frac{R_{\rm c}}{R_{\rm ext}}\right)^2. \end{eqnarray}$$

Here, we assume that R _ext = (B _c/B _ext)^1/2 R _c because of the conservation of the magnetic flux. This shows that the magnetic braking timescale could become much shorter than t _b in Equation (5) because (R _c/R _ext) < 1.

Figure 4. Schematic figure of the geometry assumed in the derivation of Equations (6) and (7). R _c, H _c, and ρ_c are the radius, scale height, and density of the central cylinder, respectively. R _ext, ρ_ext are the radius of flux-tube and density of outer envelope, respectively.

The ratio of the radii, (R _c/R _ext) is highly uncertain. Furthermore, the density structure of the envelope evolves with time. These uncertainties make the analytical treatment of magnetic braking difficult (see, however, Nakano 1989; Tomisaka et al. 1990; Krasnopolsky & Königl 2002; Dapp & Basu 2010; Dapp, Basu, & Kunz 2012, for example). Therefore, multidimensional simulation of the collapsing cloud core is an important tool for investigating the effect of magnetic braking in a realistic magnetic field configuration.

4.2. Numerical simulations of magnetic braking

Using a two-dimensional ideal MHD simulation starting from cylindrical isothermal cloud cores, Tomisaka (2000) clearly showed that much of the angular momentum is removed from the central region by magnetic braking and outflow. He showed that about two-thirds of the initial specific angular momentum is removed from the central region during the runaway collapse phase, and more is removed after the formation of the first core by outflow and magnetic braking. At the end of the simulation, most of the specific angular momentum has been removed from the central region (a reduction of 10⁴ from the initial value). His simulation clearly indicates the importance of angular momentum transfer by the magnetic field.

Allen et al. (2003) showed that magnetic braking in the main accretion phase is significant and that much of the angular momentum is removed from the accreting gas using two-dimensional ideal MHD simulations starting from singular isothermal toroids. They pointed out that the magnetic braking efficiency is enhanced by hourglass like magnetic field geometry around the pseudodisk because the magnetic field is strengthened and the reduction factor (R _c/R _ext)² in the timescale of Equation (7) becomes small. Because of the two enhancement mechanisms for magnetic braking in the pseudodisk, magnetic braking plays an important role in the angular momentum evolution of accreting gas. Note that most of the gas accretes onto the central star through the pseudodisk, and angular momentum removal in the pseudodisk strongly affects formation and evolution of the circumstellar disk around the protostar.

This significant removal of angular momentum in the ideal MHD limit was later confirmed using two- or three-dimensional simulations (Banerjee & Pudritz 2006; Price & Bate 2007b; Hennebelle & Fromang 2008; Mellon & Li 2008; Machida et al. 2011b; Bate, Tricco, & Price 2014). These studies focused on the quantitative aspect of magnetic braking, i.e., how strong a magnetic field is required for suppression of the disk formation. Price & Bate (2007b) showed that disk formation is strongly suppressed when the mass-to-flux ratio of entire core is μ ≲ 4 using three-dimensional smoothed particle hydrodynamics (SPH) simulations with a uniform cloud core. Hennebelle & Fromang (2008) also performed three-dimensional simulations using a uniform cloud core with adaptive mesh refinement (AMR) code ramses and also concluded that disk formation is suppressed at a slightly greater value of the mass-to-flux ratio μ ≲ 5. Mellon & Li (2008) performed two-dimensional ideal MHD simulations using rotating singular isothermal toroids as the initial condition and showed that circumstellar disk formation is suppressed in a cloud core with μ ≲ 10.

Most of studies mentioned above (Tomisaka 2000; Allen et al. 2003; Price & Monaghan 2007; Hennebelle & Fromang 2008; Mellon & Li 2008; Machida et al. 2011b) used the isothermal or piecewise polytropic equation of state (EOS), and the influence of the realistic temperature evolution on the magnetic braking rate was unclear. Three-dimensional radiative ideal MHD simulations with AMR and nested grid codes were performed by Commerçon et al. (2010) and Tomida et al. (2010). They showed that the magnetic braking is significant even when the radiative transfer is included. Especially, Commerçon et al. (2010) showed that the fragmentation that occurs in their simulation with μ = 20 is suppressed in that with μ = 5 implying that significant angular momentum removal occurs and disk formation is strongly suppressed. Bate et al. (2014) conducted radiative ideal MHD simulations of a collapsing cloud core using SPH. They employed a uniform cloud core as the initial condition. They also showed that disk formation is suppressed when μ ≲ 5 at the protostar formation epoch. Their results seem to be consistent with previous studies using the simplified EOS, and radiative transfer would not change magnetic braking efficiency significantly in the ideal MHD limit. Note, however, that the fragmentation of the first core or the disk is significantly affected by the temperature. Thus, radiative transfer is important when we consider fragmentation (Commerçon et al. 2010; Tsukamoto et al. 2015c).

In summary, the previous study indicates that disk formation is strongly suppressed by magnetic braking in the Class 0 phase with an observed magnetic field strength μ ~ 2 (Troland & Crutcher 2008) in ideal MHD limit and with aligned magnetic field and rotation vector. On the other hand, there is growing evidence that a relatively large ( ~ 50 AU) disk exists in some Class 0 young stellar objects (YSOs) (Murillo et al. 2013; Ohashi et al. 2014; Sakai et al. 2014). Therefore, obtaining the physical mechanisms that resolve discrepancy between the observations and the theoretical study is the main issue of the recent theoretical study.

4.3. Consideration of initial conditions

As we have seen above, the mass-to-flux ratio of the initial cloud core normalised by the critical value, μ = (M/Φ)/(M/Φ)_crit, is often used as an indicator of the strength of the magnetic field. This seems to be reasonable because, as we have seen in Section 4.1, the magnetic braking timescale is proportional to the mass-to-flux ratio of the central region. However, the mass-to-flux ratio M/Φ is generally a function of the radius, and the M/Φ around the centre of the initial core can be much larger or smaller than the value for the entire cloud core depending on the density profile and magnetic field profile of the initial core. Thus, we should take care of not only the mass-to-flux ratio of the entire core but also the initial density and initial magnetic field profile of the core when we compare the results of previous study.

To illustrate this point, we show the profiles of the mass-to-flux ratios of the two most commonly used initial density profiles, i.e., those of a uniform sphere and a Bonnor–Ebert sphere in Figure 5. The uniform sphere is used in Price & Bate (2007a), Hennebelle & Fromang (2008), Bate et al. (2014), Tsukamoto et al. (2015a), and Tsukamoto et al. (2015b) and the Bonnor–Ebert sphere is used mainly in Japanese community (Matsumoto & Tomisaka 2004; Inutsuka, Machida, & Matsumoto 2010; Machida & Matsumoto 2011; Machida, Inutsuka, & Matsumoto 2011a; Tomida et al. 2013, 2015). The profile of the mass-to-flux ratio of the Bonnor–Ebert sphere depends greatly on its central density, cut-off radius, and total mass. Thus, the mass-to-flux ratio of the central region is different among previous studies that used the Bonnor–Ebert sphere. Here, for example, we select the Bonnor–Ebert sphere from model 1 (μ = 1) of Machida & Matsumoto (2011).

Figure 5. Profile of mass-to-flux ratios of Bonnor–Ebert sphere and uniform sphere normalised by the critical value $(M/\Phi )_{\rm crit}=0.53/(3\pi ) \sqrt{5/G}$ as a function of included mass, M(r) = ∫ ^r ₀ρ(r′)4πr′² dr′. Solid line represents the profile of the Bonnor–Ebert sphere with μ = 1 used in Machida, Inutsuka, & Matsumoto (2011b). Dashed, dotted, and dash–dotted lines represent the profiles of uniform spheres with μ = 1, 4 and 7.5, respectively. Note that Machida et al. (2011b) used a different critical value, $(M/\Phi )_{\rm crit}=0.48/3\pi \sqrt{5/G}$ (Tomisaka, Ikeuchi, & Nakamura 1988b; Tomisaka et al. 1988a) and the value of the solid line is slightly smaller than that shown in Figure 2 of the original paper.

Figure 5 shows the profile of mass-to-flux ratio of Bonnor–Ebert sphere used in Machida et al. (2011b) and uniform spheres threaded by constant magnetic field as a function of the included mass, M(r) = ∫ ^r ₀ρ(r′)4πr′² dr′. The figure shows that, in the Bonnor–Ebert sphere, the mass-to-flux ratio around the centre of the core is μ(M) ~ 2 at $M \sim 0.2 \text{M}_\odot$ (solid line) even with μ = 1 for the entire cloud core. On the other hand, μ(M) becomes ~ 2 at $M \sim 0.2 \text{M}_\odot$ in a uniform sphere with μ = 4 (dotted line). If we fix the mass-to-flux ratio at the central region, the Bonnor–Ebert sphere with the mass-to-flux ratio of μ = 1 corresponds to a uniform sphere with μ ~ 7. Thus, the mass-to-flux ratios around the centre could have severalfold difference depending on the density profiles. Note that the magnetic energy is proportional to |B|² and that the severalfold difference in the magnetic field strength results in a difference of more than an order of magnitude in the magnetic energy. Thus, we should pay attention to the initial density profile when we compare previous results.

An illustrative example regarding this issue can be found in Machida et al. (2011b). They conducted three-dimensional simulations starting from a supercritical Bonnor–Ebert sphere. They showed that, even with a relatively strong magnetic field of μ = 1, the circumstellar disks can be formed. This is surprising and seems to contradict other results. However, it does not contradict to other results. This difference may come from the difference of the magnetic field strength around the centre of the cloud core. In their subsequent paper (Machida, Inutsuka, & Matsumoto 2014), it is shown that disk formation is more strongly suppressed when a uniform sphere is assumed.

5 MECHANISMS THAT WEAKEN MAGNETIC BRAKING IN THE IDEAL MHD LIMIT

5.1. Turbulence

The theoretical study we mentioned above adopted idealised cloud cores; i.e., the core has coherent rotation such as rigid rotation and the rotation vector and magnetic field are parallel. A realistic molecular cloud core, however, is expected to have a turbulent velocity field and its rotation vector is misaligned from the magnetic field. In this section, we review the suggested mechanisms that weaken the magnetic braking efficiency in the ideal MHD limit.

Santos-Lima et al. (2012) suggested that turbulence in the cloud core weakens magnetic braking. They compared the simulation results for a coherently rotating core and a turbulent core and found that a rotationally supported disk is formed only in the turbulent cloud core. Similar results were obtained by Seifried et al. (2013). Santos-Lima et al. (2012) pointed out that random motion due to turbulence causes small-scale magnetic reconnections and provides an effective magnetic resistivity that enables removal of the magnetic flux from the central region. As a result, in their simulations, a disk with a size of r ~ 100 AU is formed even in ideal MHD limit.

However, their results were obtained in the presence of supersonic turbulence with a Mach number of four, which is much larger than the value expected from observations (the core typically has subsonic turbulence). Furthermore, they employed a uniform grid with a relatively large grid size of Δx ~ 15 AU. In ideal MHD simulations, reconnection occurs at the scale of numerical resolution. Thus, a numerical convergence test is strongly desired to confirm that turbulence-induced reconnection really plays a role in disk formation.

Joos et al. (2013) checked the numerical convergence of simulations of turbulent cloud core collapse with the AMR simulation code ramses. They performed two simulations using exactly the same initial conditions while varying the numerical resolution (they resolved the Jeans length with 10 or 20 meshes) and found that the mass of the disk at a given time varies by about a factor of two (Figure A.1 of Joos et al. 2013). This result suggests that their simulations do not converge and further investigation is desired to quantify the influence of turbulent reconnection on disk formation.

5.2. Misalignment between magnetic field and rotation vector

Another possible mechanism that weakens the magnetic braking is misalignment between the magnetic field and rotation vector. In many previous studies, it is assumed for simplicity that the rotation vector is completely aligned with the magnetic field. However, in real molecular cloud cores, the magnetic field (B) and rotation vector ( Ω ) would be mutually misaligned. The recent observations with CARMA suggest that the direction of the molecular outflows, which may trace the normal direction of the disk, and the direction of the magnetic field on a scale of 1 000 AU have no correlation (Hull et al. 2013).

In pioneering study on magnetic braking (Mouschovias 1985), the perpendicular Ω ⊥B configuration was also considered. The magnetic braking timescale in the the perpendicular configuration is given as (Mouschovias 1985)

(8) $$\begin{eqnarray} t_{\rm b,\perp }=2 \left( \frac{\pi }{\rho _{\rm c}} \right)^\frac{1}{2}\frac{M}{\Phi }. \end{eqnarray}$$

In the derivation, it is assumed that Alfvén waves propagate isotropically on the equatorial plane, and, as a consequence, B(r)∝r ^{− 1} because of ∇ · B = 0. The ratio of the magnetic braking timescale of parallel and perpendicular configurations from Equations (5) and (8) is given as

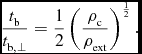(9) $$\begin{eqnarray} \frac{t_{\rm b}}{t_{\rm b,\perp }}=\frac{1}{2}\left(\frac{\rho _{\rm c}}{\rho _{\rm ext}} \right)^{\frac{1}{2}}. \end{eqnarray}$$

This shows that the timescale in perpendicular case is much smaller than that in the parallel case because ρ_c ≫ ρ_ext, meaning that the magnetic braking in the perpendicular case is much stronger than that in the parallel case. However, in realistic case, fanned-out configuration of magnetic field should be considered as shown in Figure 4. Thus, the ratio of the timescale becomes

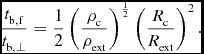(10) $$\begin{eqnarray} \frac{t_{\rm b,f}}{t_{\rm b,\perp }}=\frac{1}{2}\left(\frac{\rho _{\rm c}}{\rho _{\rm ext}} \right)^{\frac{1}{2}}\left(\frac{R_{\rm c}}{R_{\rm ext}}\right)^2. \end{eqnarray}$$

This shows that magnetic braking timescale of the perpendicular case can be larger than that of the parallel case when $\left(R_{\rm c}/R_{\rm ext}\right)^2 \left(\rho _{\rm c}/\rho _{\rm ext} \right)^{\frac{1}{2}} <1$ . However, whether the magnetic braking in the perpendicular case is weaker than that in the parallel case is not obvious because it is difficult to quantitatively compare (R _c/R _ext)² and $\left(\rho _{\rm c}/\rho _{\rm ext} \right)^{\frac{1}{2}}$ from the analytic discussions.

Several multidimensional simulations have been performed to investigate the magnetic braking in the misaligned configuration, however, the results are inconsistent among the previous studies (Matsumoto & Tomisaka 2004; Machida et al. 2006; Hennebelle & Ciardi 2009; Joos et al. 2012; Li et al. 2013). Matsumoto & Tomisaka (2004) conducted ideal MHD simulations of the collapsing cloud core using a Bonnor–Ebert sphere. They investigated the angular momentum evolution of the prestellar collapse phase and reported that the angular momentum of the central region is more efficiently removed when the magnetic field and rotation vector are perpendicular. This is consistent with the classical estimate of Mouschovias & Paleologou (1979). In Figure 6, we show the angular momentum evolution of the central region obtained in Matsumoto & Tomisaka (2004). The figure shows that the angular momentum in the central region in the perpendicular case (SF90) is much smaller than that in the parallel case (SF00).

Figure 6. Evolution of central angular momentum as a function of maximum (or central) density ρ_max. Here, J ≡ ∫_{ρ > 0.1ρmax} (r × v)ρ d V and M ≡ ∫_{ρ > 0.1ρmax} ρ d V. This figure appears as Figure 12 of Matsumoto & Tomisaka (2004). Models SF00, SF45, and SF90 denote the simulation results with a mutual angle between the initial magnetic field and the initial rotation vector of θ = 0°, 45°, and 90°. The dashed line denotes J/M ² for an unmagnetised simulation. The solid lines denote the angular momentum parallel to the local magnetic field, J _∥/M ², whereas dotted lines denote the angular momentum perpendicular to the local magnetic field, J _⊥/M ². Dash–dotted line denotes J _∥ for a simulation with a weak magnetic field and dashed line denotes J for a simulation without magnetic field. Diamonds denote the stage of the first core formation epoch. Solid line of SF00 and dotted line of SF90 clearly show that the angular momentum around the central region with a perpendicular magnetic field is much smaller than that with a parallel magnetic field.

On the other hand, Hennebelle & Ciardi (2009) reported that the efficiency of the magnetic braking decreases as the mutual angle between the magnetic field and the rotation axis increases and is minimum in the perpendicular configuration using centrally condensed cloud core with magnetic field whose intensity is proportional to the total column density through the core. They pointed out that disk formation becomes possible in the misaligned cloud cores even in the ideal MHD limit. Joos et al. (2012) also conducted the ideal MHD simulations with the same density profile of Hennebelle & Ciardi (2009). Figure 7 is taken from Figure 4 of Joos et al. (2012) and shows that mean specific angular momentum of the central dense region in a perpendicular core (red lines) is about two times larger than that in a parallel core (blue lines). This is clearly opposite to the result shown in Figure 6. The influence of misalignment was also investigated by Li et al. (2013) with uniform density sphere. They also reported that the angular momentum of the central region is much large in the perpendicular case and concluded that the disk formation becomes possible when μ ≳ 4. They pointed out that the angular momentum removal by outflow plays an important role in the parallel configuration.

Figure 7. Evolution of mean specific angular momentum as a function of time. This figure appears as Figure 4 in Joos et al. (2012). Here, the mean specific angular momentum is defined as $j \equiv \frac{1}{M} \int _{\rho >\rho _{\rm c}}(\boldsymbol{r \times v} )\rho \, d \boldsymbol{V}$ and M ≡ ∫_{ρ > ρc} ρ d V. Evolution with μ = 5 and three different thresholds, ρ_c that correspond to n = 10¹⁰, 10⁹, 10⁸cm^{− 3} is shown.

It is still unclear why the discrepancy between the results of Hennebelle & Ciardi (2009), Joos et al. (2012), Li et al. (2013), and Matsumoto & Tomisaka (2004) arises. One possible explanation is the difference in the initial conditions. As discussed above, the magnetic braking timescale in the perpendicular configuration can be larger or smaller than that in the parallel configuration depending on the assumptions of the envelope structure and magnetic field configurations. Hence, the difference in the initial conditions may explain the discrepancy although further studies on the effect of misalignment on the magnetic braking efficiency are required.

6 INFLUENCE OF NON-IDEAL MHD EFFECTS ON DISK FORMATION

So far, we have reviewed the mechanisms that weaken magnetic braking in the ideal MHD limit. In a realistic molecular cloud core, however, the ideal MHD approximation, in which infinite conductivity is assumed, is not always valid because of the small ionisation degree. Thus, non-ideal effects may affect the formation and evolution of circumstellar disks. In this section, we review the influence of non-ideal MHD effects on disk formation.

In a weakly ionised gas, collisions between neutral, positively charged, and negatively charged particles cause finite conductivity, and non-ideal effects arise. The non-ideal effects appear as correction terms in the induction equation if we neglect the inertia of the charged particles. The induction equation with non-ideal terms is given as

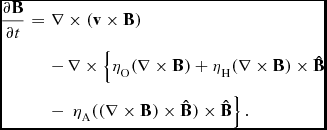(11) $$\begin{eqnarray} \frac{\partial \boldsymbol{B}}{\partial t} &=& \nabla \times (\boldsymbol{v}\times \boldsymbol{B})\nonumber \\ &&-\, \nabla \times \left\lbrace \eta _{\rm O} (\nabla \times \boldsymbol{B}) +\eta _{\rm H} (\nabla \times \boldsymbol{B}) \times \boldsymbol{\hat{B}} \right.\nonumber\\ &&-\, \left. \eta _{\rm A} ((\nabla \times \boldsymbol{B}) \times \boldsymbol{\hat{B}}) \times \boldsymbol{\hat{B}}\right\rbrace . \end{eqnarray}$$

The second, third, and fourth terms on the right-hand side of Equation (11) describe Ohmic diffusion, the Hall term, and ambipolar diffusion, respectively. Here, η_O, η_H, and η_A are the Ohmic, Hall, and ambipolar diffusion coefficients, respectively. These quantities are calculated from the microscopic force balance of ions, electrons, and charged dust aggregates.

Detailed calculations of the abundance of charged particles are required to quantify how the non-ideal effects influence disk formation. For example, we show the evolution of the abundance of ions, electrons, and charged dusts inside the cloud core as a function of the density in Figure 8. This figure appears as Figure 1 of Nakano et al. (2002). The figure shows that the relative abundance of the charged particles decreases as the density increases. The figure also shows that the dominant charge carriers are ions and electrons in the low density region n _H ≲ 10⁶cm^{− 3} and g⁺ and g⁻ are the dominant carriers in the high density region 10¹⁰ < n _Hcm^{− 3}.

Figure 8. Abundances of various charged particles as a function of the density of hydrogen nuclei. This figure appears as Figure 1 of Nakano, Nishi, & Umebayashi (2002). Here, n _H denotes the number density of hydrogen nuclei. Solid and dotted lines represent the number densities of ions, and electrons relative to n _H, respectively. Dashed lines labelled g ^x represent the number densities relative to n _H of grains of charge xe summed over the radius. The ionisation rate of a H₂ molecule by cosmic rays outside the cloud core is taken to be $\zeta _0=10^{-17} \text{ s}^{-1}$ . M⁺ and m⁺ collectively denote metal ions such as Mg⁺, Si⁺, and Fe⁺ and molecular ions such as HCO⁺, respectively. The MRN dust size distribution (Mathis, Rumpl, & Nordsieck 1977) with $a_{\rm min}=0.005\ \mu \text{m}$ and $a_{\rm max}=0.25\ \mu \text{m}$ is assumed.

6.1 Ohmic and ambipolar diffusion

6.1.1 Magnetic flux-loss in the first core phase

The effect of Ohmic and ambipolar diffusions in the collapsing cloud core has been thoroughly investigated by Nakano and his collaborators using an analytic approach (Nakano 1984; Nakano & Umebayashi 1986; Umebayashi & Nakano 1990; Nishi, Nakano, & Umebayashi 1991; Nakano et al. 2002). They investigated the influence of magnetic diffusion during cloud core collapse by comparing the diffusion timescale of magnetic field and the free-fall timescale.

Figure 9 shows the typical evolution of the magnetic diffusion timescale in the cloud core. The magnetic diffusion timescale becomes smaller than the free-fall timescale at a density of n _crit ~ 10¹¹cm^{− 3}, and much of the magnetic flux is removed from the gas in the central region when the central density reaches n _crit. They pointed out that this flux-loss is caused mainly by Ohmic diffusion. The critical density varies according to the dust model. Nishi et al. (1991) investigated the dependence of the critical density on the dust model and found that the critical density varies in the range of 10¹⁰cm^{− 3} ≲ n _crit ≲ 10¹¹cm^{− 3}.

Figure 9. Timescales of magnetic flux-loss for cloud cores. This figure appears as Figure 3 of Nakano et al. (2002). The flux-loss timescale t _B is shown for field strengths of B = B _cr (solid lines) and B = 0.1B _cr (dashed lines), where B _cr approximately corresponds to the magnetic field strength of μ ~ 1 [the exact value of B _cr can be found in Equation (30) of Nakano et al. (2002)]. The Ohmic diffusion time t _od is also shown as dash–dotted lines. Two ionisation rates by cosmic rays outside the cloud core, $\zeta _0=10^{-17}\, \text{s}^{-1}$ (thick lines: standard case) and $\zeta _0=10^{-16}\, \text{s}^{-1}$ (thin lines), are considered. The other parameters are the same as in Figure 8. Dotted line indicates the free-fall time t _ff = [3π/(32Gρ)]^1/2.

As discussed in Section 3, the pressure-supported first core is formed when the central density reaches n ~ 10¹⁰cm^{− 3}, and significant flux-loss occurs in the first core phase. Furthermore, the duration of the first core phase is much longer than the free-fall timescale and the magnetic flux-loss may occur at a density less than n _crit. Thus, it is expected that the magnetic field and the gas are decoupled in the first core and that the magnetic braking is no longer important in it.

6.1.2 Formation of circumstellar disk in the first core phase

Multidimensional MHD simulations with magnetic diffusion have been conducted and have revealed its influence on early disk evolution (Duffin & Pudritz 2009; Machida & Matsumoto 2011; Li et al. 2011; Tomida et al. 2013, 2015; Tsukamoto et al. 2015b; Masson et al. 2015). As we described above, the magnetic field and the gas is decoupled in the first core. Decoupling between the magnetic field and the gas in the first core leads to a very important consequence for disk formation because the first core is the precursor of the circumstellar disk. Machida & Matsumoto (2011) conducted numerical simulations that followed formation of the protostar without any sink technique. They clearly showed that the first core directly becomes the circumstellar disk after the second collapse. In Figure 10, we show the structure of the forming circumstellar disk inside the first core at the protostar formation epoch. Because the first core has finite angular momentum and magnetic braking is no longer important in it, the gas cannot accrete directly onto the second core owing to centrifugal force. Therefore, the circumstellar disk inevitably forms just after protostar formation.

Figure 10. Remnant of the first core (orange isodensity surface) and forming circumstellar disk (red isodensity surface) plotted in three dimensions. This figure appears as Figure 3 of Machida & Matsumoto (2011). Density distributions on the x = 0, y = 0, and z = 0 planes are projected onto each wall surface. Velocity vectors on the z = 0 plane are also projected onto the bottom wall surface.

The disk formation at the protostar formation epoch was later confirmed by more sophisticated simulations that included radiative transfer and Ohmic and ambipolar diffusion (Tomida et al. 2013, 2015; Tsukamoto et al. 2015b; Masson et al. 2015). All of them reported formation of a circumstellar disks at the protostar formation epoch due to magnetic diffusion, although slight differences exist in the initial size of the circumstellar disk (1AU ≲ r ≲ 10AU), which may arise from differences in the initial conditions, EOS, or resistivity models. Because the magnetic field and the gas are inevitably decoupled in the first core, we robustly conclude that the circumstellar disk with a size of r ≳ 1 AU is formed at the protostar formation epoch.

The circumstellar disk serves as a reservoir for angular momentum. As pointed out in the classical theory of an accretion disk (Lynden-Bell & Pringle 1974), the gas accreted onto the disk leaves most of the angular momentum in the disk and accretes onto the protostar. Therefore, a small disk can grow in the subsequent evolution phase even though it is small at its formation epoch.

6.1.3 Properties and long term evolution of newborn disk

The newborn circumstellar disk is expected to be more massive than the newborn protostar at its formation epoch. This was clearly noted by Inutsuka et al. (2010). Figure 11 shows a schematic figure of the evolution of the characteristic mass scale during gravitational collapse and the accretion phase. The masses of the newborn protostar and the first core are roughly determined by the Jeans mass and are approximately 10^{− 3} and $10^{-2}\, \text{M}_\odot$ , respectively (Masunaga, Miyama, & Inutsuka 1998; Masunaga & Inutsuka 1999). In addition, the newborn circumstellar disk acquires most of the mass of the first core. Thus, the circumstellar disk is more massive than the central protostar at its formation epoch. In such a massive disk, gravitational instability (GI) serves as an important angular momentum transfer mechanism. Later, Machida et al. (2011b), Tsukamoto et al. (2015b) confirmed that a newborn disk is actually massive, and GI may serve as the angular momentum transfer mechanism in the early phase of circumstellar disk evolution.

Figure 11. Schematic of evolution of the characteristic mass during gravitational collapse of the molecular cloud cores. This figure appears as Figure 2 of Inutsuka et al. (2010). The vertical axis denotes mass (in units of solar mass) and the horizontal axis denotes time (in years). The red curve on the left-hand side indicates the characteristic mass of the collapsing molecular cloud core, which corresponds to the Jeans mass. Note that the mass of the first core is much larger than that of the central protostar at its birth. The right-hand side describes the evolution after protostar formation. Because the first core changes into the circumstellar disk, the disk mass remains larger than the mass of the protostar in its early evolutionary phase. The protostar mass increases monotonically owing to mass accretion from the disk and becomes larger than the mass of the disk at some point.

The disk evolves by mass accretion from the envelope. How the disk size increases in the Class 0 phase depends strongly on the amount of angular momentum carried into the disk. Using long-term simulations with a sink cell, Machida et al. (2011b) showed that a disk can grow to the 100 AU scale when the envelope is depleted (i.e., at the end of the Class 0 phase). Note that magnetic braking becomes weak once the envelope is depleted because the magnetic braking timescale depends on the envelope density [see, Equations (5) and (7)].

6.2 Hall effect

The Hall effect has an unique feature in that it can actively induce rotation by generating a toroidal magnetic field from a poloidal magnetic field (Wardle & Ng 1999). In this subsection, we review the influence of the Hall effect on circumstellar disk formation and evolution.

For understanding how magnetic field evolves with the Hall effect, we rewrite the Hall term in the induction equation as

(12) $$\begin{eqnarray} -\nabla \times \left\lbrace \eta _{\rm H} (\nabla \times \boldsymbol{B}) \times \boldsymbol{\hat{B}}\right\rbrace =\nabla \times \left( \boldsymbol{v}_{\rm Hall} \times \boldsymbol{B}\right) . \end{eqnarray}$$

Here, the drift velocity induced by the Hall term is defined as

(13) $$\begin{eqnarray} \boldsymbol{v}_{\rm Hall}=-\eta _{\rm H} \frac{(\nabla \times \boldsymbol{B})_\perp }{|\boldsymbol{B}|}=-\eta _{\rm H}\frac{c \boldsymbol{J}_\perp }{4 \pi |\boldsymbol{B}|}, \end{eqnarray}$$

where c is the speed of light. The right-hand side of Equation (12) has the same form as the ideal MHD term. The Equations (12) and (13) show that the magnetic field moves along J _⊥ with a speed of |v _Hall|.

During gravitational collapse, an hourglass-shaped magnetic field is generally realised (see Figure 3). In this configuration, a toroidal current exists at the midplane and the Hall term generates a toroidal magnetic field by twisting the magnetic field lines toward the azimuthal direction. The toroidal magnetic field exerts a toroidal magnetic tension and induces gas rotation. Consequently, the gas starts to rotate even when it does not rotate initially. This phenomenon was actually observed in the simulations of Krasnopolsky et al. (2011) and Li et al. (2011).

The characteristic rotation velocity induced by the Hall effect can be estimated from the Hall drift velocity v _Hall because the toroidal component of the ideal term and the Hall term cancel each other out when the rotation velocity is equal to the azimuthal component of the Hall drift velocity v _{Hall, ϕ}. Thus, the rotation velocity of the gas tends to converge to v _ϕ = v _{Hall, ϕ}. Using the numerical simulations in which only Hall effect is considered, Krasnopolsky et al. (2011) showed that the rotation velocity actually converges to v _{Hall, ϕ}.

Here, we estimate the Hall-induced rotation velocity in the pseudodisk in which a current sheet exists at the midplane. The rotation velocity induced by the Hall term is roughly estimated as

(14) $$\begin{eqnarray} v_{\rm \phi } \sim \frac{\eta _{\rm H}}{|B_{\rm z}|}\frac{|B_{\rm r,s}|}{H}. \end{eqnarray}$$

Here, H, B _z, and B _{r, s} are the scale height, vertical magnetic field at the midplane, and radial magnetic field at the surface of the pseudodisk, respectively, and we assumed |∇ × B| ~ |B _{r, s}|/H. It is clear from the Equation (14) that, because η_H is proportional to |B|, the Hall-induced rotation velocity is an increasing function of the strength of the magnetic field. By employing the monopole approximation B _{r, s} ~ Φ_pdisk/(2πr ²) which is used in Contopoulos, Ciolek, & Königl (1998), Krasnopolsky & Königl (2002), and Braiding & Wardle (2012b, 2012a) and using the relation of Φ_pdisk = M _pdisk/(μ_pdisk(M/Φ)_crit), we can estimate the Hall-induced rotation velocity as

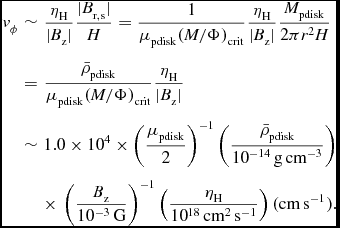(15) $$\begin{eqnarray} v_{\rm \phi } &\sim& \frac{\eta _{\rm H}}{|B_{\rm z}|}\frac{|B_{\rm r,s}|}{H} = \frac{1}{\mu _{\rm pdisk} (M/\Phi )_{\rm crit}} \frac{\eta _{\rm H}}{|B_{\rm z}|}\frac{M_{\rm pdisk}}{2 \pi r^2 H}\nonumber\\ &=&\frac{\bar{\rho }_{\rm pdisk}}{\mu _{\rm pdisk} (M/\Phi )_{\rm crit}} \frac{\eta _{\rm H}}{|B_{\rm z}|} \nonumber\\ &\sim& 1.0 \times 10^{4} \times \left( \frac{\mu _{\rm pdisk}}{2}\right)^{-1} \left( \frac{\bar{\rho }_{\rm pdisk}}{10^{-14} \,{\rm g\,cm}^{-3} } \right)\nonumber \\ &&\times\, \left( \frac{B_{\rm z}}{10^{-3} \,{\rm G}} \right)^{-1} \left( \frac{\eta _{\rm H}}{ 10^{18} \,{\rm cm}^{2} \,{\rm s}^{-1} }\right) ({\rm cm\,s^{-1}}). \end{eqnarray}$$

Here, Φ_pdisk, μ_pdisk, M _pdisk, and $ \bar{\rho }_{\rm pdisk}$ are the magnetic flux, the mass-to-flux ratio normalised by the critical value, the mass, and the mean density of the pseudodisk, respectively. Note that B _z is the vertical magnetic field at a radius, on the other hand, B _{r, s} is determined by the magnetic flux within a radius. Therefore, we need two different pieces of information (μ_pdisk and B _z) for magnetic field. Note also that Φ_pdisk (and hence B _{r, s}) increases as the total mass in the central region is increased by mass accretion if there is no efficient magnetic flux loss mechanism. Hence, the Hall-induced rotation would be strengthened in the later evolution phase. The corresponding specific angular momentum induced by the Hall term is estimated as

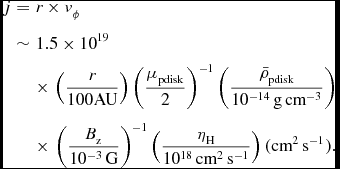(16) $$\begin{eqnarray} j&=&r\times v_{\rm \phi }\nonumber \\ &\sim& 1.5 \times 10^{19} \nonumber\\ && \times\,\left( \frac{r}{100 {\rm AU}} \right) \left( \frac{\mu _{\rm pdisk}}{2}\right)^{-1} \left( \frac{\bar{\rho }_{\rm pdisk}}{10^{-14} \,{\rm g\,cm}^{-3} } \right) \nonumber\\ && \times\,\left( \frac{B_{\rm z}}{10^{-3} \,{\rm G}} \right)^{-1} \left( \frac{\eta _{\rm H}}{ 10^{18} \,{\rm cm}^{2} \,{\rm s}^{-1} }\right) ({\rm cm^2\,s^{-1}}). \end{eqnarray}$$

Once a circumstellar disk is formed, the accreting gas leaves the most of the angular momentum in the disk and finally accretes onto the central protostar. Thus, during protostar formation, the disk acquires an angular momentum of

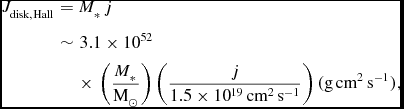(17) $$\begin{eqnarray} J_{\rm disk, Hall}&=&M_*\,j \nonumber\\ &\sim& 3.1\times 10^{52} \nonumber\\ &&\times\,\left( \frac{M_*}{\text{M}_\odot } \right)\left( \frac{j}{1.5 \times 10^{19} \,{\rm cm^2\,s^{-1}}} \right) ({\rm g\,cm^2\,s^{-1}}), \end{eqnarray}$$

where M _* is the final mass of the central protostar.

On the other hand, the total angular momentum of a Keplerian disk with Σ∝r ^{− 3/2} is given as

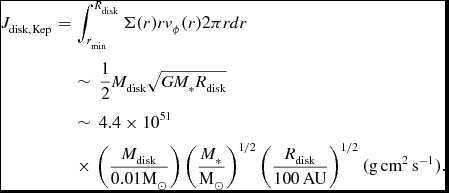(18) $$\begin{eqnarray} J_{\rm disk, Kep}&=&\int _{r_{\rm min}}^{R_{\rm disk}} \Sigma (r) r v_{\phi }(r) 2 \pi r dr \nonumber\\ &&\sim \,\frac{1}{2} M_{\rm disk}\sqrt{G M_* R_{\rm disk}} \nonumber\\ &&\sim\, 4.4 \times 10^{51} \nonumber\\ &&\times\,\left( \frac{M_{\rm disk}}{0.01 \text{M}_\odot } \right) \left( \frac{M_*}{ \text{M}_\odot } \right)^{1/2}\left( \frac{R_{\rm disk}}{100 \,{\rm AU}} \right)^{1/2} ({\rm g\,cm^2\,s^{-1}}). \nonumber\\ \end{eqnarray}$$

Thus, the Hall term alone can supply a sufficient amount of the angular momentum for explaining a circumstellar disk with a mass and radius of $0.01 \text{M}_\odot$ and 100 AU, respectively, which roughly correspond to typical values of the disks around T Tauri stars (Andrews & Williams 2005, 2007; Williams & Cieza 2011) .

In realistic situations, the inherent rotation of cloud cores and magnetic diffusion introduce complicated gas dynamics. When the rotation of the cloud core is also considered, a very interesting phenomenon arises. As we can see from the induction equation, the Hall term is not invariant against inversion of the magnetic field (B → −B) and its effect on the gas rotation differs depending on whether the rotation vector and magnetic field of the host cloud core are parallel or antiparallel (Wardle & Ng 1999; Braiding & Wardle 2012a, b). For η_H < 0 which is almost always valid in the cloud cores, when the rotation vector and magnetic field are antiparallel, the Hall-induced rotation and the inherent rotation are in the same direction, and hence, the Hall term weakens the magnetic braking. On the other hand, the Hall term strengthens the magnetic braking in the parallel case because the Hall term induces inverse rotation against the inherent rotation of the cloud core.

Krasnopolsky et al. (2011) investigated the effect of the Hall term on disk formation using two-dimensional simulations. They focused on the dynamical behaviour induced by the Hall term by neglecting Ohmic and ambipolar diffusion and by employing a constant Hall coefficient, Q _Hall ≡ η_H|B|. They showed that a circumstellar disk r ≳ 10 AU in size can form as a result of only the Hall term when the Hall coefficient is Q _Hall ≳ 3 × 10²⁰cm²s^{− 1}G^{− 1}. Another interesting finding is that the formation of an envelope that rotates in the direction opposite to that of disk rotation. Because of the conservation of the angular momentum, the spin-up due to the Hall term at the midplane of the pseudodisk generates a negative angular momentum flux along the magnetic field line. This causes spin-down of the upper region, and the upper region eventually begins to rotate in the direction opposite to that of disk rotation.

Li et al. (2011) investigated the effect of the Hall term in two-dimensional simulations that included all the non-ideal MHD effects using a realistic diffusion model and started from uniform cloud cores. They confirmed that Hall-induced rotation occurs even when other non-ideal effects are considered. They also showed that the formation of a counter-rotating envelope. They showed that the Hall-induced rotation velocity can reach v _ϕ ~ 10⁵(cms^{− 1}) at r = 10¹⁴(cm) (this corresponds to the radius of the their inner boundary), which means that the accreting gas has a specific angular momentum of j ~ 10¹⁹(cm²s^{− 1}) (Figure 11 of Li et al. 2011). This is consistent with the value estimated using Equation (16).

Tsukamoto et al. (2015a) conducted three-dimensional simulations, that included all the non-ideal effects as well as radiative transfer. They followed the first core formation phase and resolved protostar formation without any sink technique. Therefore, their simulations did not suffer from numerical artefacts introduced by the sink or inner boundary. A drawback of this treatment is that they could not follow the long-term evolution of the disk after protostar formation because the numerical timestep became very small. In Figure 12, we show a density map of the central regions of the simulations conducted in Tsukamoto et al. (2015a). The left panel shows the result of the simulation in which initial magnetic field and the rotation vector are in parallel configuration. On the other hand, the right panel shows that in which initial magnetic field and the rotation vector are in antiparallel configuration. The right panel clearly shows that a disk ~ 20 AU in size formed at the protostar formation epoch On the other hand, the left panel shows that a disk 1 AU in size formed even with the parallel configuration. They also showed that the magnetic field and the gas are decoupled in the disk in the right panel, and that the magnetic braking is no longer important in it. Although the disk is formed in both cases, the difference in its size in the parallel and antiparallel cases is significant. Thus, they argued that the disks in Class 0 YSOs can be subcategorised according to the parallel and antiparallel nature of their host cloud cores and suggested that the systems with parallel and antiparallel configurations should be called as ortho-disks and para-disks, respectively. They also confirmed that a negatively rotating envelope is formed and suggested that this envelope may be observable in future observations of Class 0 YSOs.

Figure 12. Density map of newborn disks formed in a cloud core with parallel configuration (left, model Ortho) and antiparallel configuration (right, model Para). This figure is taken from Figure 1 of Tsukamoto et al. (2015a) but it has been modified to clarify the formation of the disk in the model Ortho. In the simulations, all the non-ideal effects are considered. The only difference between the initial conditions of the models Ortho and Para is the direction of the magnetic field. Inset at upper left in the left-hand panel shows an enlarged density map around the centre of the model Ortho. It shows that a disk ~ 1 AU in size is formed at the centre in the parallel case. The right panel shows that a disk ~ 20 AU in size is formed at the centre in the antiparallel case. We confirmed that both disks are rotationally supported. The non-axisymmetric spiral arms in the right panel are created by gravitational instability. We confirmed that Toomre’s Q value was Q ~ 1.

Up to the present, Wurster, Price, & Bate (2015) have made the most comprehensive study regarding the impact of non-ideal MHD effects on disk evolution. They investigated the influences of each non-ideal MHD effect both independently and together using three-dimensional simulations. They pointed out that, among the three non-ideal effects, the Hall effect is the most important process for disk size. This suggests that including the Hall effect is crucial for investigating the formation and evolution process of circumstellar disks in magnetised cloud cores. They pointed out that an anticorrelation between the size and speed of the outflow and the size of the disk. This suggests that angular momentum transfer by the outflow is also important. In their simulations, a negatively rotating envelope is also formed. Note that the negatively rotating envelopes are formed in all multidimensional simulations with the Hall effect (Krasnopolsky et al. 2011; Li et al. 2011; Tsukamoto et al. 2015a; Wurster et al. 2015) and its formation seems to be robust. Therefore, the detection of a negatively rotating envelope would provide clear evidence that the Hall effect actually influences the angular momentum evolution.

7 SUMMARY AND FUTURE PERSPECTIVES

7.1. Summary

In this paper, we reviewed the formation and evolution processes of circumstellar disks in magnetised cloud cores, focusing in particular on the influence of magnetic braking. In the ideal MHD approximation and with an aligned magnetic field, magnetic braking is very efficient and, circumstellar disk formation is almost completely suppressed in a moderately magnetised cloud core (its mass-to-flux ratio is μ ~ 2) (Allen et al. 2003; Hennebelle & Fromang 2008; Mellon & Li 2008). This introduced a serious discrepancy between the observations and theory and was considered a very serious problem for disk formation theory.

However, various physical mechanisms have been proposed to solve the problem of catastrophic magnetic braking. For example, the misalignment between the magnetic field and the rotation axis (Hennebelle & Ciardi 2009; Joos et al. 2012) or turbulence (Santos-Lima et al. 2012; Seifried et al. 2013) in the cloud core may weaken magnetic braking. Ohmic and ambipolar diffusions remove much of the magnetic flux in the first core and make it possible for circumstellar disks a few AU in size to form at the formation epoch of the protostar (Machida & Matsumoto 2011; Tomida et al. 2013, 2015; Tsukamoto et al. 2015c; Masson et al. 2015). The spin-up effect of the Hall term increases the specific angular momentum of the accretion flow and the disk radius at the protostar formation epoch (Krasnopolsky et al. 2011; Tsukamoto et al. 2015a). A combination of these mechanisms solves the magnetic braking problem, and we can robustly conclude that the disk is formed in the early evolution phase of the protostar, although its quantitative features, such as the disk radius and mass, are still under debate. Therefore, the simple question of whether a disk can form is no longer a central issue, and we should move on to more specific problems of disk evolution.

7.2. Future perspectives

Determining the angular momentum transfer mechanisms in the Class 0 phase may be the most important unresolved issue. To data, GI and magneto-rotational instability (MRI) are considered to be the two major mechanisms of angular momentum transport within the disk (Armitage 2011). Further, magneto-centrifugal wind (Blandford & Payne 1982) has recently received attention as a mechanism that can remove angular momentum from a disk (Tomisaka 2000, 2002; Bai & Stone 2013; Bai 2013; Gressel et al. 2015). How these mechanisms contribute to disk evolution and how the relative importance of GI, MRI, and magneto-centrifugal wind changes during disk evolution are still unclear. Surface density and temperature determine whether the disk is stable against GI and the size of the MRI dead zone. Magnetic field strength is closely related to the saturation level of MRI (Sano et al. 2004; Suzuki, Muto, & Inutsuka 2010) and strength of magneto-centrifugal wind. Thus, to answer the question, we must quantitatively investigate the long-term evolution of the surface density, temperature, and magnetic field of disk by considering all the relevant physical mechanisms.

The formation process of binaries or multiples in the Class 0 phase and its relation to disk evolution is another important issue. Fragmentation of the disk or the first core is considered a promising mechanism for binary formation (Matsumoto & Hanawa 2003; Machida et al. 2005, 2008; Kratter et al. 2010; Tsukamoto & Machida 2013; Tsukamoto et al. 2015c). However, for realistic values of the magnetic field and rotation velocity (μ ~ 1 and β_rot ~ 0.01, respectively), the fragmentation in the early phase of the protostar formation seems to be strongly suppressed. In particular, the formation of a binary with a separation of several tens of AU would be very difficult for realistic values (see, Figure 12 of Machida et al. 2008). On the other hand, the binary or multiple fraction of solar-type stars is about 0.6, which is quite high (Duquennoy & Mayor 1991). Furthermore, the median orbital period of binaries is 190 yrs indicating that the typical separation is several tens of AU. This introduces a discrepancy between the observations and theoretical studies, that should be resolved in future studies. To determine whether fragmentation of the first core or the disk is the dominant formation mechanism of multiples, we should investigate how often the fragmentation of the disk and the first core can occur in cloud cores and whether the frequency of fragmentation is sufficient to explain the number of binaries or multiples fraction.

Dust coagulation in the disk and its impact on disk evolution is also an important issue. It is expected that dust coagulation occurs and that the size distribution of the dust particles in the disk changes (Dullemond & Dominik 2005; Okuzumi 2009). Once dust coagulation occurs and the dust size distribution changes during disk evolution, the magnetic resistivity is affected, and the gas dynamics can also be altered owing to this. Then, the dust coagulation process may be modified by the gas dynamics. Therefore, it is possible that the large-scale disk and the small scale dust distribution co-evolve. Such a co-evolution process of dust and the disk would be important not only for the evolution of YSOs but also for formation process of planetesimals.