Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T05:06:54.878Z Has data issue: false hasContentIssue false
  • English
  • Français

The Ideal Generation Conjecture for 28 Points in P3

Published online by Cambridge University Press:  20 November 2018

Leslie G. Roberts
Leslie G. Roberts*
Affiliation:
Queen's University, Kingston, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The ideal generation conjecture has recently been proved for general points in 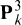, (k a field) [1], [6]. The proof in [1] is by induction. One of the starting points for the induction (called A(5) in [1]) is proved in [6]. The theoretical proof of A(5) in [6] seems to be very difficult, apparently even more difficult than the induction. Because of this, and also because [6] is not publically available, I feel it is worth knowing that A(5) can be proved numerically with modest readily available computing facilities. In this note I discuss the computation involved, and give a few explicit examples. In the course of working out these examples I found 26 points in 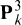, that satisfy the ideal generation conjecture, but which cannot be extended to 27 or 28 points satisfying the ideal generation conjecture. This phenomenon can be interpreted combinatorially, leading to an infinite number of similar examples.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 5 , 01 October 1986 , pp. 1228 - 1238
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Ballico, E., Generators for the homogeneous ideal of s general points in P 3 , (preprint).CrossRefGoogle Scholar
2. Geramita, A. V., Gregory, D. and Roberts, L., Monomial ideals and points in projective space, Journal of Pure and Applied Algebra 40 (1986), 33–62.Google Scholar
3. Geramita, A. V. and Orecchia, F., On the Cohen-Macaulay type of s lines in An + 1 J. Alg. 70 (1981), 116–140.Google Scholar
4. Hartshorne, R., Connectedness of the Hilbert scheme, Publ. Math. Inst, des Hautes Etudes Sci. 29 (1966), 261–304.Google Scholar
5. Hartshorne, R., Algebraic geometry (Springer-Verlag, 1977).CrossRefGoogle Scholar
6. Hirschowitz, A., letter to R. Hartshorne, (1983).Google Scholar