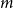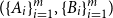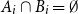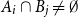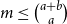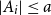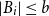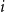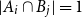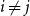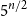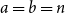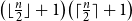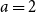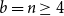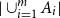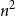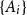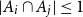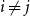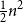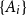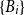Problems and results on 1-cross-intersecting set pair systems

Abstract

The notion of cross-intersecting set pair system of size $m$ , $ (\{A_i\}_{i=1}^m, \{B_i\}_{i=1}^m )$ with $A_i\cap B_i=\emptyset$ and $A_i\cap B_j\ne \emptyset$ , was introduced by Bollobás and it became an important tool of extremal combinatorics. His classical result states that $m\le\binom{a+b}{a}$ if $|A_i|\le a$ and $|B_i|\le b$ for each $i$ . Our central problem is to see how this bound changes with the additional condition $|A_i\cap B_j|=1$ for $i\ne j$ . Such a system is called $1$ -cross-intersecting. We show that these systems are related to perfect graphs, clique partitions of graphs, and finite geometries. We prove that their maximum size is

• at least $5^{n/2}$ for $n$ even, $a=b=n$ ,

• equal to $\bigl (\lfloor \frac{n}{2}\rfloor +1\bigr )\bigl (\lceil \frac{n}{2}\rceil +1\bigr )$ if $a=2$ and $b=n\ge 4$ ,

• at most $|\cup _{i=1}^m A_i|$ ,

• asymptotically $n^2$ if $\{A_i\}$ is a linear hypergraph ( $|A_i\cap A_j|\le 1$ for $i\ne j$ ),

• asymptotically ${1\over 2}n^2$ if $\{A_i\}$ and $\{B_i\}$ are both linear hypergraphs.

1. Introduction, results

The notion of cross-intersecting set pair systems (SPSs) was introduced by Bollobás [4] and it became a standard tool of extremal set theory. Because of its importance, there are many proofs (e.g., Lovász [19], Kalai [16]) and generalisations (e.g., Alon [1], Füredi [7]). For applications and extensions of the concept, the surveys of Füredi [8] and Tuza [21, 22] are recommended.

A cross-intersecting SPS of size $m\ge 2$ consists of finite sets $A_1,\ldots,A_m$ and $B_1,\ldots,B_m$ such that

\begin{equation*}A_i\cap B_i=\emptyset \mathrm {\ for\ every\ } 1\le i \le m,\end{equation*}

\begin{equation*}A_i\cap B_j\ne \emptyset \mathrm {\ for\ every\ } 1\le i\ne j \le m.\end{equation*}

We will consider further constrains but always keep these two basic properties.

Bollobás’ theorem [4] states that

(1) \begin{equation} m\le\binom{a+b}{a} \end{equation}

must hold for any cross-intersecting SPS if we have $|A_i|\le a$ and $|B_i|\le b$ for each $i$ . This size can be achieved by the standard example, taking all $a$ -element sets of an $(a\!+\!b)$ -element set for the $A_i$ -s and their complements as $B_i$ -s.

Let ${\mathcal{A}}=\{A_i\}_{i=1}^m$ and ${\mathcal{B}}=\{B_i\}_{i=1}^m$ . The SPS is denoted by $({\mathcal{A}},{\mathcal{B}})=\{(A_i,B_i)\}_{i=1}^{m}$ . An SPS is $(a,b)$ -bounded if $|A_i|\le a$ and $|B_i|\le b$ for each $i$ .

An SPS $(\mathcal{A},\mathcal{B})$ is $1$ -cross-intersecting if $|A_i\cap B_j|=1$ for each $i\ne j$ . Our aim is to find good estimates for the size under this condition. This leads to interesting but seemingly difficult problems.

Our results are summarised in the next five subsections. In two warm-up sections, we show that an $1$ -cross-intersecting $(n,n)$ -bounded SPS $(\mathcal{A},\mathcal{B})$ can have exponential size and that its size is bounded by the sizes of the vertex sets of $\mathcal{A}$ (and $\mathcal{B}$ ). We show how the latter provides an alternate ending of Gasparian’s proof of Lovász’s perfect graph theorem. The next two subsections present our main results: sharp bound of the size in the $(2,n)$ -bounded case (Theorem 1.4) and asymptotically best bounds for the size in the $(n,n)$ -bounded case when ${\mathcal{A}},{\mathcal{B}}$ are linear (Theorem 1.6) and when ${\mathcal{A}},{\mathcal{B}}$ are $1$ -intersecting (Theorem 1.7). Then, we show the connection of $1$ -cross-intersecting SPS-s with clique partition of graphs.

Although the main results of this article are about $1$ -intersecting families, we propose the problem in a very general setting in Section 2. The proof of the upper bounds are in Sections 3 and 4. The constructions giving the lower bounds are in Section 5. We conclude with some open problems in Section 6.

1.1 $1$ -cross-intersecting SPS of exponential sizes

A $1$ -cross-intersecting $(n,n)$ -bounded SPS can have exponential size.

Proposition 1.1. If there exist an $(a_1,b_1)$ -bounded $1$ -cross-intersecting SPS of size $m_1$ and an $(a_2,b_2)$ -bounded $1$ -cross-intersecting SPS of size $m_2$ then there exists an $(a_1\!+\!a_2, b_1\!+\!b_2)$ -bounded $1$ -cross-intersecting SPS of size $m_1\cdot m_2$ .

The proof of this, and most other proofs, are postponed to later sections.

Starting from the standard example (with $a=b=1$ and $m=2$ ), Proposition 1.1 yields an $(n,n)$ -bounded $1$ -cross-intersecting SPS of size $2^n$ , exponential in $n$ . Define the $(2,2)$ -bounded $1$ -cross-intersecting SPS, called ${\mathcal H}(2,2)$ , using the edges of a five cycle and its complement. The five pairs $ (\{i, i\!+\!1\},\{i\!+\!2, i\!+\!4\} )$ are taken modulo $5$ . Then Proposition 1.1 gives the following.

Corollary 1.2. There exists an $(n,n)$ -bounded $1$ -cross-intersecting SPS of size $5^{n/2}$ if $n$ is even and of size $2\cdot 5^{(n-1)/2}$ if $n$ is odd.

This is the best lower bound we know. It remains a challenge to decrease the upper bound of essentially $\binom{2n}{n}$ in (1) for an $(n,n)$ -bounded $1$ -cross-intersecting SPS.

Corollary 1.2 gives a $(3,3)$ -bounded $1$ -cross-intersecting SPS of size $10$ , in fact two different ones, with $12$ and with $15$ vertices, depending on the order we apply Proposition 1.1. We have a third example, the pairs $(\{i, i\!+\!1, i\!+\!2\}, \{i\!+\!3, i\!+\!6, i\!+\!9\})$ taken modulo $10$ , it has $10$ vertices. Samuel Spiro ([email protected]) informed us that his computer programme successfully checked that $10$ is indeed the largest size of such a family.

1.2 $1$ -cross-intersecting SPS and perfect graphs

One particular feature of a $1$ -cross-intersecting SPS $(\mathcal{A},\mathcal{B})$ is that its size is bounded by the sizes of the vertex sets of $\mathcal{A}$ (and $\mathcal{B}$ ). This can be considered as a variant of Fischer’s inequality, and does not hold for general SPS.

Proposition 1.3. Assume that $(\mathcal{A},\mathcal{B})$ is $1$ -cross-intersecting and $V\,:\!=\,\cup{\mathcal{A}}$ . Then the characteristic vectors of the edges of $\mathcal{A}$ are linearly independent in ${\mathbb R}^V$ .

A special case of Proposition 1.3 relates to perfect graphs and can be used in Gasparian’s proof [6, 11] of Lovász’s characterisation [18] of perfect graphs: a graph $G$ is perfect if and only if

(2) \begin{equation} |V(H)|\le \alpha (H)\omega (H) \end{equation}

holds for all induced subgraphs $H$ of $G$ .

To prove the nontrivial part, Gasparian showed that if a minimal imperfect graph $G$ would satisfy (2) then there is a $1$ -cross-intersecting SPS of size $m=\alpha (G)\omega (G)+1$ defined by independent sets and complete subgraphs of $G$ . By Proposition 1.3, $|V(G)|\ge \alpha (G)\omega (G)+1$ , contradicting (2).

1.3 $(2,n)$ -bounded $1$ -cross-intersecting SPS

Here, we state the best bound for the size of $(2,n)$ -bounded $1$ -cross-intersecting SPS showing that the main term of the upper bound $\frac{1}{2}(n+2)(n+1)$ in (1) can be halved.

Theorem 1.4. Let $n\ge 4$ , and let $(\mathcal{A},\mathcal{B})$ be a $(2,n)$ -bounded $1$ -cross-intersecting SPS of size $m$ . Then

\begin{equation*}m\le \left (\left \lfloor \frac {n}{2}\right \rfloor +1\right )\left (\left \lceil \frac {n}{2}\right \rceil +1\right ).\end{equation*}

This bound is the best possible. For $n=2, 3$ the exact values are $m=5, 7$ .

1.4 $1$ -cross-intersecting SPS in linear hypergraphs

A hypergraph $\mathcal{H}$ is called linear if the intersection of any two different edges has at most one vertex. $\mathcal{H}$ is called $1$ -intersecting if $|H\cap H'|=1$ for all $H, H'\in{\mathcal{H}}$ whenever $H\neq H'$ .

If one of $(\mathcal{A},\mathcal{B})$ , say $\mathcal{A}$ , in an SPS is linear, then the size of this SPS is bounded by $n^2+O(n)$ (without any assumption on $|B_i\cap B_j|,|A_i\cap B_j|$ ).

Proposition 1.5. Suppose that $({\mathcal{A}},{\mathcal{B}})$ is an $(n,n)$ -bounded cross-intersecting SPS of size $m$ such that $\mathcal{A}$ is a linear hypergraph. Then $m \le n^2 +n+1$ .

When $\mathcal{A}$ and $\mathcal{B}$ are both linear, and they form a $1$ -cross-intersecting SPS then this bound can be approximately halved.

Theorem 1.6. Suppose that $({\mathcal{A}},{\mathcal{B}})$ is an $(n,n)$ -bounded $1$ -cross-intersecting SPS of size $m$ such that both $\mathcal{A}$ and $\mathcal{B}$ are linear hypergraphs. Then $m \le \frac{1}{2}n^2 +n+1$ .

A further small decrement comes if in addition $\mathcal{A}$ and $\mathcal{B}$ are both 1-intersecting hypergraphs. Then their union ${\mathcal{H}}={\mathcal{A}}\cup{\mathcal{B}}$ can be considered as a ‘geometry’ where two lines intersect in at most one point, and every line has exactly one parallel line.

Theorem 1.7. Assume that $(\mathcal{A},\mathcal{B})$ is an $(n,n)$ -bounded $1$ -cross-intersecting SPS of size $m$ such that both $\mathcal{A}$ and $\mathcal{B}$ are $1$ -intersecting. Then $m \le\binom{n}{2}+1$ for $n\gt 2$ . If $n\ge 4$ and equality holds, then $\mathcal{H}$ is $n$ -uniform and $n$ -regular $(|A_i|=|B_i|=n$ for $i=1,\dots,m$ and $d_{\mathcal{A}}(v)=d_{\mathcal{B}}(v)=n)$ .

In Section 5, we give constructive lower bounds. Constructions 5.1, 5.2 and 5.3 show that the upper bounds in this subsection are asymptotically the best possible.

1.5 $1$ -cross-intersecting SPS and clique partitions of graphs

The notion of $1$ -cross-intersecting SPS is closely related to the concept of clique and biclique partitions. A clique partition of a graph $G$ is a partition of the edge set of $G$ into complete graphs. Similarly, a biclique partition of a bipartite graph $B$ is a partition of the edge set of $B$ into complete bipartite graphs (bicliques). The minimum number of cliques (bicliques) needed for the clique (or biclique) partitions are well studied, see, for example [13]. Our problem relates to another parameter of clique (biclique) partitions. The thickness of a clique (biclique) partition of a graph (bipartite graph) is the minimum $s$ such that every vertex of the graph (bipartite graph) is in at most $s$ cliques (bicliques). Let $T_{2m}$ be the cocktail party graph, i.e., the complete graph $K_{2m}$ from which a perfect matching is removed. Let $B_{2m}$ be the bipartite graph obtained from the complete bipartite graph $K_{m,m}$ by removing a perfect matching.

Assume that $(\mathcal{A},\mathcal{B})$ is an $(n,n)$ -bounded $1$ -cross-intersecting SPS of size $m$ , and ${\mathcal{H}}={\mathcal{A}}\cup{\mathcal{B}}$ . The dual of this hypergraph, ${\mathcal{H}}^*$ , has vertex set

\begin{equation*}V^*=\{x_1,\dots,x_m,y_1,\dots,y_m\}\end{equation*}

where $x_i,y_i$ correspond to $A_i,B_i$ . The hyperedges of ${\mathcal{H}}^*$ correspond to vertices of $\mathcal{H}$ . Since $|A_i\cap B_j|=1$ for $i\ne j$ , every pair $x_i,y_j$ for $i\ne j$ is covered exactly once by a hyperedge of ${\mathcal{H}}^*$ . On the other hand, $|A_i\cap B_i|=0$ for every $i$ so the pairs $x_i,y_i$ are not covered by any hyperedge of ${\mathcal{H}}^*$ . Thus the complete graphs induced by the hyperedges of ${\mathcal{H}}^*$ form a biclique partition of thickness $n$ of the bipartite graph $B_{2m}$ .

If we have the additional assumption that $\mathcal{A}$ and $\mathcal{B}$ are both 1-intersecting then the pairs $x_i,x_j$ and the pairs $y_i,y_j$ are also covered exactly once by the hyperedges of ${\mathcal{H}}^*$ . Thus in this case the complete graphs induced by the hyperedges of ${\mathcal{H}}^*$ form a clique partition of thickness $n$ of the cocktail party graph $T_{2m}$ .

The above argument gives the following.

Theorem 1.8. The maximum $m$ such that $B_{2m}$ has a biclique partition of thickness $n$ is equal to the maximum size of an $(n,n)$ -bounded $1$ -cross-intersecting SPS. The maximum $m$ such that $T_{2m}$ has a clique partition of thickness $n$ is equal to the maximum size of an $(n,n)$ -bounded $1$ -cross-intersecting SPS in which $\mathcal{A}$ and $\mathcal{B}$ are also $1$ -intersecting.

2. Notation and general setting

Let $a, b$ positive integers and $I_A, I_B, I_{\mathrm{cross}}$ three sets of non-negative integers. We denote by $m(a, b, I_A, I_B, I_{\mathrm{cross}})$ the maximum size $m$ of a cross-intersecting SPS $(\mathcal{A},\mathcal{B})$ with the following conditions.

1. 1. $A_i\cap B_i=\emptyset$ for every $1\le i \le m$ ,

2. 2. $|A_i|\le a$ for every $1\le i\le m$ ,

3. 3. $|B_i|\le b$ for every $1\le i\le m$ ,

4. 4. $|A_i\cap A_j|\in I_A$ for every $1\le i\ne j\le m$ ,

5. 5. $|B_i\cap B_j|\in I_B$ for every $1\le i\ne j\le m$ ,

6. 6. $0\lt |A_i\cap B_j|\in I_{\mathrm{cross}}$ for every $1\le i\ne j\le m$ .

To avoid trivialities we always suppose that $0\not \in I_{\mathrm{cross}}$ , also that $m\geq 2$ . If a constraint in 4)–6) is vacuous (i.e., either $\{ 0,1, \dots, a\} \subseteq I_A$ or $\{ 0,1, \dots, b\} \subseteq I_B$ or $\{ 1, \dots, \min \{ a,b\}\} \subseteq I_{\mathrm{cross}}$ ) then we use the symbol $*$ to indicate this. With this notation Bollobás’ theorem [4] states

\begin{equation*}m(a, b, *, *, *)=\binom{a+b}{a},\end{equation*}

and our Theorem 1.4 states (for $n\geq 4$ )

\begin{equation*}m(2, n, *, *, 1)=\left (\left \lfloor \frac {n}{2}\right \rfloor +1\right )\left (\left \lceil \frac {n}{2}\right \rceil +1\right ).\end{equation*}

In the rest of the results we deal with the case $a=b=n$ and use the abbreviation of placing $n$ as an index

\begin{equation*} m_n(I_A, I_B, I_{\mathrm {cross}})\,:\!=\,m(n, n, I_A, I_B, I_{\mathrm {cross}}).\end{equation*}

Since in this paper the main results are about linear hypergraphs, we will have $I_A$ (and also $I_B$ ) is either $\{ 0,1\}$ ( $\mathcal{A}$ is a linear hypergraph), or $\{ 1\}$ ( $\mathcal{A}$ is a 1-intersecting hypergraph), or $*$ . Instead of writing $I_A=\{ 1\}$ we write ‘ $1{\textrm{-int}}$ ’, instead of $I_A=\{ 0, 1\}$ we write ‘ $01{\textrm{-int}}$ ’, and for $I_{\mathrm{cross}}= \{ 1\}$ we use just ‘1’ (as we did above).

Adding more restrictions can only decrease the maximum size, so we have

(3) \begin{equation} m_n(1{\textrm{-int}}, 1{\textrm{-int}}, 1)\le m_n(1{\textrm{-int}},{01{\textrm{-int}}}, 1)\le m_n({01{\textrm{-int}}},{01{\textrm{-int}}}, 1). \end{equation}

In fact, we examined all 18 cases for $m_n(I_A, I_B, I_{\mathrm{cross}})$ where $I_A$ and $I_B$ are chosen from $\{ 1\}$ , $\{ 0, 1\}$ , or $*$ and $I_{\mathrm{cross}}$ is either $\{ 1\}$ or $*$ . By symmetry they define twelve functions. Summarizing our results, $m_n(*, *, 1)$ and $m_n(*, *, *)$ are exponential as a function of $n$ , the other cases are polynomial. Three of them, mentioned in (3), are asymptotically $\frac{1}{2}n^2$ while the other seven are asymptotically $n^2$ .

Several problems under assumptions similar to $1$ -cross-intersecting SPS have been studied before, see, e.g., [3, 5, 9, 21] and more recently in [12, 20].

3. $1$ -cross-intersecting SPS – proofs

Proposition 1.1. If there exist an $(a_1,b_1)$ -bounded $1$ -cross-intersecting SPS of size $m_1$ and an $(a_2,b_2)$ -bounded $1$ -cross-intersecting SPS of size $m_2$ then there exists an $(a_1\!+\!a_2, b_1\!+\!b_2)$ -bounded $1$ -cross-intersecting SPS of size $m_1\cdot m_2$ .

Proof. We have to show that

\begin{equation*}m(a_1\!+\!a_2, b_1\!+\!b_2, *, *, 1)\ge m(a_1, b_1, *, *, 1)\cdot m(a_2, b_2, *, *, 1).\end{equation*}

Consider $t=m(a_2, b_2, *, *, 1)$ pairwise disjoint ground sets $V_1,\dots,V_t$ and for all $i\in [t]$ a copy $({\mathcal{A}}_i,{\mathcal{B}}_i)$ of a construction giving an $(a_1,b_1)$ -bounded $1$ -cross-intersecting SPS of size $s$ such that ${\mathcal{A}}_i=\{A_{i,1},\dots,A_{i,s}\},\;{\mathcal{B}}_i=\{B_{i,1},\dots,B_{i,s}\}$ , where $s=m(a_1, b_1, *, *, 1)$ . Let $({\mathcal{A}},{\mathcal{B}})$ be a copy of an $(a_2,b_2)$ -bounded $1$ -cross-intersecting SPS of size $t$ on the ground set $V$ such that ${\mathcal{A}}=\{A_1,\dots,A_t\},\;{\mathcal{B}}=\{B_1,\dots,B_t\}$ , where $V$ is disjoint from all $V_i$ -s. For any $1\le i\le t,\; 1\le j\le s$ define

\begin{equation*}{A_{i,j}^{\prime}}=A_{i,j}\cup A_i, \; {B_{i,j}^{\prime}}=B_{i,j}\cup B_i.\end{equation*}

The pairs $({A_{i,j}^{\prime}},{B_{i,j}^{\prime}})$ form a $1$ -cross-intersecting SPS such that $|{A_{i,j}^{\prime}}|\le a_1+a_2$ and $|{B_{i,j}^{\prime}}|\le$ $b_1+b_2$ .

Proposition 1.3. Assume that $(\mathcal{A},\mathcal{B})$ is $1$ -cross-intersecting and $V\,:\!=\,\cup{\mathcal{A}}$ . Then the characteristic vectors of the edges of $\mathcal{A}$ are linearly independent in ${\mathbb R}^V$ .

Proof. Let ${\textbf{a}}_i$ (resp. ${\textbf{b}}_i$ ) denote the characteristic vector of $A_i$ (resp. $B_i$ ), i.e. ${\textbf{a}}_i(v)=1$ for $v\in V$ if and only if $v\in A_i$ . Otherwise the coordinates are $0$ . Suppose that

\begin{equation*} \sum _{i=1}^m \lambda _i {\textbf {a}}_i = {\boldsymbol {0}}.\end{equation*}

Take the dot product of both sides of this equation with ${\textbf{b}}_j$ . Since $|A_i\cap B_j|=1$ for $i\ne j$ and $|A_i\cap B_j|=0$ for $i=j$ , we get that

\begin{equation*}\left (\sum _{i=1}^m \lambda _i\right )-\lambda _j=0.\end{equation*}

Adding these for all $j$ yields $(m-1) (\sum _{i=1}^m \lambda _i )=0$ . Consequently (using $m\gt 1$ ) $\sum _{i=1}^m \lambda _i=0$ . Thus $\lambda _j=0$ for all $j$ .

Theorem 1.4. Let $n\ge 4$ , and let $(\mathcal{A},\mathcal{B})$ be a $(2,n)$ -bounded $1$ -cross-intersecting SPS of size $m$ . Then

\begin{equation*}m\le \left (\left \lfloor \frac {n}{2}\right \rfloor +1\right )\left (\left \lceil \frac {n}{2}\right \rceil +1\right ).\end{equation*}

This bound is the best possible. For $n=2, 3$ the exact values are $m=5, 7$ .

Proof. Let $(\mathcal{A},\mathcal{B})$ be a $(2,n)$ -bounded $1$ -cross-intersecting SPS of size $m$ . It is convenient to assume that $\mathcal{A}$ is two-uniform (a graph without multiple edges) and $\mathcal{B}$ is an $n$ -uniform hypergraph. (For smaller sets dummy vertices can be added).

Consider the simple graph $\mathcal{A}$ .

Lemma 3.1. If $\mathcal{A}$ contains a cycle then $m\le 2n+1$ .

Proof. The $n$ -set $B_i$ must be an independent transversal for all edges other than $A_i$ (i.e., intersects all edges of $\mathcal{A}$ except $A_i$ but does not contain any edge of $\mathcal{A}$ ) and disjoint from the edge $A_i$ . Suppose that the graph $\mathcal{A}$ contains an even cycle with edges $A_1=(x_1,x_2),A_2=(x_2,x_3).\dots A_{2k}=(x_{2k},x_1)$ . Since $B_1$ is an independent transversal for all edges other than $A_1$ , we have $x_3\in B_1$ which implies $x_4\notin B_1$ , and so on, finally $x_{2k}\notin B_1,\; x_1\in B_1$ contradicting $A_1\cap B_1=\emptyset$ . Thus $\mathcal{A}$ has no even cycles.

If there is an odd cycle $C$ with $k$ vertices, it cannot contain a diagonal, since any diagonal would create an even cycle, contradicting the previous paragraph. If there is an edge $A_i$ with exactly one vertex, say $x_1$ on $C$ , then the argument of the previous paragraph implies $x_2\in B_i,\; x_3\notin B_i,\dots, x_1\in B_i$ , contradiction. Also, if there is an edge $A_i$ with no vertex on $C$ then $B_i$ must intersect all edges of $C$ so it cannot be an independent transversal. Thus in this case $m\le |C| \le 2n+1$ .

Assume next that $\mathcal{A}$ is an acyclic graph.

Lemma 3.2. Assume that $T\subseteq{\mathcal{A}}$ is a non-star tree component with $t$ edges. Then

\begin{equation*}\max _{A_i\in T} |B_i\cap V(T)|\ge \left \lceil {t\over 2}\right \rceil .\end{equation*}

Proof. Let $P=x,y,z,z_2, \dots$ be a maximal path of $T$ , set $A_1=\{x,y\},A_2=\{y,z\}$ . Let $S\subseteq V(T)$ the set of leaves connected to $y$ . Note that $t\geq 3$ , $|V(T)|=t+1$ , $\;N_T(y)=S\cup \{ z\}$ and $x\in S$ . Then $B_1\cap V(T)$ is the set $X$ of vertices with odd distance from $y$ in the tree $T-x$ . On the other hand, $B_2\cap V(T)$ is the set $X'=S\cup D$ where $D$ is the set of vertices with odd distance from $z$ in the tree $T-(S\cup \{ y\})$ . Then $|X|+|X'|=t+|S|-1\ge t$ . Therefore

\begin{equation*} \max \{|B_1\cap V(T)|, |B_2\cap V(T)|\} =\max \{ |X|, |X'|\} \ge \left \lceil {t\over 2}\right \rceil . \end{equation*}

Assume that there is a non-star tree component $T$ in $\mathcal{A}$ with $t$ edges, $A_1,\dots,A_t$ , $(t\ge 3)$ . We define another $(2,n)$ -bounded $1$ -cross-intersecting SPS $(\mathcal{A'},\mathcal{B'})$ of size $m$ . Let ${\mathcal{A}}'$ be the graph defined by replacing $T$ with $S$ , where $S$ is the union of two vertex disjoint stars $S_1$ and $S_2$ with centres $s_1,s_2$ having $ \lceil{t\over 2} \rceil$ and $ \lfloor{t\over 2} \rfloor$ edges, respectively. We keep all edges of the other components of $\mathcal{A}$ , i.e., ${\mathcal{A}}'= ({\mathcal{A}}\setminus E(T))\cup E(S)$ .

For $i=1,\dots,t$ in case of ${A_{i}^{\prime}}\in E(S_\alpha )$ let $C_i$ be the complement of ${A_{i}^{\prime}}$ in the star $S_\alpha$ together with the centre of the other star of $S$ , i.e., $C_i= (V(S_\alpha )\setminus {A_{i}^{\prime}} )\cup \{ s_{3-\alpha }\}$ . Note that $|C_i|$ is either $\lfloor{t\over 2}\rfloor$ or $\lceil{t\over 2}\rceil$ . According to Lemma 3.2 there is a hyperedge, say $B_1$ , with $|B_1\cap V(T)|\ge \lceil{t\over 2} \rceil$ . Define ${\mathcal{B}}'$ as follows.

\begin{equation*}B_i^{\prime}\,:\!=\,\left \{\begin {array}{ll} C_i\cup (B_1\setminus V(T)) &\qquad \text {for } 1\leq i\leq t, \\ \{ s_1, s_2\}\cup (B_i\setminus V(T))& \qquad \text {for } i\gt t. \end {array}\right . \end{equation*}

Claim 3.3. $({{\mathcal{A}}'},{{\mathcal{B}}'})$ is a $(2,n)$ -bounded $1$ -cross-intersecting SPS of size $m$ .

Proof. It is clear that $({{\mathcal{A}}'},{{\mathcal{B}}'})$ is a $1$ -cross-intersecting SPS of size $m$ . To prove that it is $(2,n)$ - bounded, assume first that $1\le i\le t$ . Then

\begin{equation*} |B_i^{\prime}|= |C_i|+|B_1\setminus V(T))| \le \left \lceil {t/2}\right \rceil +\left ( |B_1|-\left \lceil {t/2}\right \rceil \right )=|B_1|\leq n. \end{equation*}

If $i\gt t$ , we have

\begin{equation*}|B_i^{\prime}|= 2+|B_i\setminus V(T)|\le |B_i\cap V(T)|+|B_i\setminus V(T)|\leq n,\end{equation*}

where the inequality $2\le |B_i\cap V(T)|$ holds because $T$ is not a star.

Applying Claim 3.3 repeatedly, we may assume that all components of $\mathcal{A}$ are stars, $S_1,\dots,S_k$ , where $S_i$ has $t_i\ge 1$ edges. For any edge $A_j\in S_i$ , $n\ge |B_j|=t_i-1+k-1$ . Adding these inequalities for $i=1,\dots,k$ , we obtain that $kn\ge m-2k+k^2$ which leads to $k(n+2-k)\ge m$ . Hence

\begin{equation*}m\leq k(n+2-k)\leq \Bigl (\left \lfloor {n\over 2}\right \rfloor +1\Bigr )\Bigl (\left \lceil {n\over 2}\right \rceil +1\Bigr ). \end{equation*}

Taking together the bounds for odd cycles and acyclic graphs, we get that

\begin{equation*}m\le \max \left \{2n+1,\; \Bigl (\left \lfloor {n\over 2}\right \rfloor +1\Bigr )\Bigl (\left \lceil {n\over 2}\right \rceil +1\Bigr )\right \}.\end{equation*}

For $n=2,3$ the first term is larger, for $n=4$ they are equal, and for $n\ge 5$ the second term takes over. This proves the upper bound for $m$ .

The matching lower bound for $n\ge 4$ comes from Proposition 1.1 applied to the standard construction with values $(1,\lceil{n\over 2}\rceil )$ and $(1,\lfloor{n\over 2}\rfloor )$ . For $n=2$ the hypergraph ${\mathcal H}(2,2)$ works (defined in Subsection 1.1). For $n=3$ we can define ${\mathcal H}(2,3)$ as the pairs $ (\{i, i\!+\!1\}, \{i\!+\!2, i\!+\!4, i\!+\!6\} )$ taken modulo $7$ .

4. $1$ -cross-intersecting linear SPS – upper bounds

For $v\in V$ , we denote by $d_{\mathcal{A}}(v),\; d_{\mathcal{B}}(v),\; d_{\mathcal{H}}(v)$ the degree of $v$ in the hypergraphs ${\mathcal{A}},{\mathcal{B}},{\mathcal{H}}$ , respectively.

Proposition 1.5. Suppose that $({\mathcal{A}},{\mathcal{B}})$ is an $(n,n)$ -bounded cross-intersecting SPS of size $m$ such that $\mathcal{A}$ is a linear hypergraph. Then $m \le n^2 +n+1$ .

Proof. Our first observation here is the following.

Claim 4.1. $d_{\mathcal{A}}(v)\le n+1$ for each vertex $v$ .

Proof. Suppose $v\in A_1\cap \ldots \cap A_{n+2}$ . Then $v\not \in B_i$ for $i\le n+2$ and in $\bigcup _{i=1}^{n+2}A_i\setminus \{v\}$ the sets $A_i^{\prime}=A_i\setminus \{v\}$ are pairwise disjoint. The set $B_{n+2}$ must intersect each ${A_{1}^{\prime}},\ldots,{A_{n+1}^{\prime}}$ which is impossible.

Consider $B_{n^2+n+2}$ . For $1\le i\le n^2+n+1$ the set $A_i$ intersects $B_{n^2+n+2}$ , so there is a vertex $v\in B_{n^2+n+2}$ with $d_A(v)\gt n+1$ , a contradiction.

Theorem 1.6. Suppose that $({\mathcal{A}},{\mathcal{B}})$ is an $(n,n)$ -bounded $1$ -cross-intersecting SPS of size $m$ such that both $\mathcal{A}$ and $\mathcal{B}$ are linear hypergraphs. Then $m \le \frac{1}{2}n^2 +n+1$ .

Proof. Suppose that $({\mathcal{A}},{\mathcal{B}})$ is an $(n,n)$ -bounded $1$ -cross-intersecting SPS of size $m$ such that both $\mathcal{A}$ and $\mathcal{B}$ are linear hypergraphs. We have $m_2({01{\textrm{-int}}},{01{\textrm{-int}}}, 1)\leq 5$ by Theorem 1.4 so we may suppose that $n\geq 3$ . If $m\leq 2n+2$ then there is nothing to prove, so from now on, we may suppose that $m\geq 2n+3$ .

We claim that for every $v\in V$ , $d_{\mathcal{A}}(v)$ , $d_{\mathcal{B}}(v)\le n$ . Indeed, $d_{\mathcal{A}}(v)\leq n+1$ (and in the same way $d_{\mathcal{B}}(v)\le n+1$ ) is obvious from Claim 4.1. Suppose $d_{\mathcal{A}}(v)= n+1$ , say $v\in A_1\cap \dots \cap A_{n+1}$ then $m\gt 2n+2\geq d_{\mathcal{A}}(v)+d_{\mathcal{B}}(v)$ so there is a pair $A_i,B_i$ with $i\gt n+1$ such that $v\notin A_i\cup B_i$ . Thus $B_i$ cannot intersect all $A_j$ -s containing $v$ , proving the claim.

Since $(\mathcal{A},\mathcal{B})$ is $1$ -cross-intersecting we have $\sum _{v\in B_i} d_{\mathcal{A}}(v)=m-1$ for each $B_i$ . Adding up these $m$ equations we get

(4) \begin{equation} \sum _v d_{\mathcal{A}}(v)d_{\mathcal{B}}(v)=m^2-m. \end{equation}

Let ${\mathcal{A}}_i$ be the set of $A_j$ -s that intersect $A_i$ and different from $A_i$ . Our crucial observation is that if $A_i$ and $A_j$ do not intersect then

(5) \begin{equation} |{\mathcal{A}}_i|+|{\mathcal{A}}_j|\leq n^2. \end{equation}

Indeed, the left-hand side of (5) equals to $\sum _{\ell : \ell \neq i,j} |A_\ell \cap (A_i\cup A_j)|$ . For two disjoint sets $X,Y$ we say that a pair $(x,y)$ joins $X,Y$ if $x\in X,y\in Y$ . For $\ell \neq i,j$ we have $|A_\ell \cap (A_i\cup A_j)|\leq 2$ . In case of $|A_\ell \cap (A_i\cup A_j)|= 2$ , we select two pairs $(x,y),(x',y')$ joining $A_i,A_j$ , namely $(x,y)=A_\ell \cap (A_i\cup A_j)$ and $(x',y')=B_\ell \cap (A_i\cup A_j)$ . In case of $|A_\ell \cap (A_i\cup A_j)|= 1$ we select one pair $(x,y)$ joining $A_i,A_j$ , namely $(x,y)=B_\ell \cap (A_i\cup A_j)$ . These pairs are distinct because

\begin{equation*}|A_{\ell }\cap B_{\ell '}|\le 1,|A_{\ell }\cap A_{\ell '}|\le 1, |B_{\ell }\cap B_{\ell '}|\le 1. \end{equation*}

Since there are $n^2$ pairs between $A_i$ and $A_j$ we obtain that $\sum _{\ell : \ell \neq i,j} |A_\ell \cap (A_i\cup A_j)|\leq n^2$ , completing the proof of (5).

If $A_i\cap A_j=\{v\}$ then we will prove that

(6) \begin{equation} |{\mathcal{A}}_i|+|{\mathcal{A}}_j|\leq (n-1)^2+d_{\mathcal{A}}(v)+d_{\mathcal{B}}(v) \leq n^2+1. \end{equation}

Indeed, as before,

\begin{equation*} |{\mathcal {A}}_i|+|{\mathcal {A}}_j|=\sum _{\ell : \ell \neq i} |A_\ell \cap A_i| +\sum _{\ell : \ell \neq j} |A_\ell \cap A_j|. \end{equation*}

For every $\ell \neq i,j$ we select (at most) two pairs joining $A_i\setminus \{ v\}$ to $A_j\setminus \{ v\}$ , namely $A_\ell \cap ((A_i\setminus \{ v\})\cup (A_j\setminus \{ v\}))$ and $B_\ell \cap ((A_i\setminus \{ v\})\cup (A_j\setminus \{ v\}))$ . In this way we selected at least $ |A_\ell \cap A_i|+|A_\ell \cap A_j|$ distinct pairs except if $v\in A_\ell \cup B_\ell$ . In the latter case we still have selected at least $ |A_\ell \cap A_i|+|A_\ell \cap A_j|-1$ pairs. So the left-hand side of (6) is at most the number of pairs joining $A_i\setminus \{ v\}$ to $A_j\setminus \{ v\}$ plus $d_{\mathcal{A}}(v)+d_{\mathcal{B}}(v)$ . This completes the proof of (6).

Next we prove that

(7) \begin{equation} \sum _{v\in V} d_{\mathcal{A}}(v)^2 \leq m\left (\frac{1}{2}n^2 + n + \frac{1}{2}\right ). \end{equation}

Add up inequalities (5) and (6) for all $1\leq i\lt j\leq m$

\begin{equation*} \frac {1}{m-1}\sum _{1\leq i\lt j\leq m} |{\mathcal {A}}_i|+|{\mathcal {A}}_j| \leq \frac {1}{m-1}\binom{m}{2} (n^2+1)= m\left (\frac {1}{2}n^2 + \frac {1}{2}\right ). \end{equation*}

Here, the left-hand side is

\begin{equation*} \sum _{1\leq i\leq m} |{\mathcal {A}}_i|= \sum _{1\leq i\leq m}\left ( \sum _{v\in A_i} (d_{\mathcal {A}}(v)\!-\!1)\right ) =\sum _{v\in V} \left (d_{\mathcal {A}}(v)^2-d_{\mathcal {A}}(v)\right )= \left (\sum _{v\in V} d_{\mathcal {A}}(v)^2\right ) -mn. \end{equation*}

The last two displayed formulas yield (7) and equality can hold only if (5) was not used. Note that similar upper bound must hold for $ \sum _{v\in V} d_{\mathcal{B}}(v)^2$ , too.

Apply (7) to $\mathcal{A}$ and to $\mathcal{B}$ and subtract the double of (4). We obtain

\begin{align*} 0\leq \sum _{v\in V} (d_{\mathcal{A}}(v)-d_{\mathcal{B}}(v))^2 & = \sum _{v} d_{\mathcal{A}}(v)^2 + \sum _{v} d_{\mathcal{A}}(v)^2 -2\sum _v d_{\mathcal{A}}(v)d_{\mathcal{B}}(v) \\ &\leq 2m\left ( \frac{1}{2}n^2 + n + \frac{1}{2}\right ) -2m(m-1)= 2m \left ( \frac{1}{2}n^2 + n + \frac{3}{2}-m\right ). \end{align*}

This implies $m\leq \frac{1}{2}n^2 + n + \frac{3}{2}$ . As a last step, we show that this inequality is strict completing the proof of the upper bound on $m$ . Indeed, equality can hold only if (5) was never used to $\mathcal{A}$ neither to $\mathcal{B}$ . This implies that $\mathcal{A}$ and $\mathcal{B}$ are 1-intersecting and because of (6) there exists a $v$ with $d_{\mathcal{A}}(v)=d_{\mathcal{B}}(v)=n$ . Suppose

\begin{equation*}v\in A_1\cap \dots \cap A_n\cap B_{n+1}\cap \dots \cap B_{2n}.\end{equation*}

Then $A_{n+1}\cap B_{n+2}=\emptyset$ because $A_{n+1}\cap B_i$ , $B_{n+2}\cap A_i$ are nonempty for $i=1,\dots,n$ . This contradicts the $1$ -intersection property.

Theorem 1.7. Assume that $(\mathcal{A},\mathcal{B})$ is an $(n,n)$ -bounded $1$ -cross-intersecting SPS of size $m$ such that both $\mathcal{A}$ and $\mathcal{B}$ are $1$ -intersecting. Then $m \le\binom{n}{2}+1$ for $n\gt 2$ . If $n\ge 4$ and equality holds, then $\mathcal{H}$ is $n$ -uniform and $n$ -regular $(|A_i|=|B_i|=n$ for $i=1,\dots,m$ and $d_{\mathcal{A}}(v)=d_{\mathcal{B}}(v)=n)$ .

Proof. Recall that ${\mathcal{H}}={\mathcal{A}}\cup{\mathcal{B}}$ . First, consider the case when there exists a vertex $v$ with $d_{\mathcal{H}}(v)\geq n+1$ , say $v\in A_i\cup B_i$ for $i\in \{1, 2, \dots, n+1 \}$ . Then one of the members of $\{ A_{n+2}, B_{n+2}\}$ does not cover $v$ , say, $v\notin A_{n+2}$ . Then, $A_{n+2}$ cannot intersect all members of $\{ A_i, B_i\}_{1\leq i\leq n+1}$ containing $v$ , a contradiction. So in this case $m=n+1$ and we are done.

From now on, we may suppose that $m\gt n+1$ , and $d_{\mathcal{H}}(v)\leq n$ for all $v\in V$ . Since only $B_1$ is disjoint from $A_1$ we get

\begin{equation*} 2m=|{\mathcal {H}}|= 2+ \sum _{v\in A_1} (d_{\mathcal {H}}(v)-1)\leq 2+ n(n-1). \end{equation*}

and we conclude that $m\le\binom{n}{2}+1$ . If $n\ge 4$ and equality holds, then all vertices of $A_1$ (and of all other hyperedges) must have degree $n$ .

5. Constructing cross-intersecting linear hypergraphs

Here, we give constructions of large cross-intersecting SPS-s such that $\mathcal{A}$ is an intersecting linear hypergraph. Constructions 5.1 and 5.2 show that

(8) \begin{align} n^2-o(n^2)&\le m_n(1{\textrm{-int}}, 1{\textrm{-int}}, *), \end{align}

(9) \begin{align} n^2-o(n^2)&\le m_n(1{\textrm{-int}}, *, 1). \end{align}

Since the right-hand sides of these inequalities are bounded above by $m_n({01{\textrm{-int}}}, *, *)$ (which is at most $n^2+n+1$ ), Proposition 1.5 is asymptotically the best possible. Construction 5.3 shows that

(10) \begin{equation} \frac{1}{2}n^2-o(n^2)\le m_n(1{\textrm{-int}}, 1{\textrm{-int}}, 1). \end{equation}

Hence, Theorems 1.6 and 1.7 are also asymptotically the best possible.

We use that the function $m_n(I_A, I_B, I_{\textrm{cross}})$ is monotone increasing in $n$ so we have to make constructions only for a dense set of special values of $n$ .

Beyond Bertrand’s postulate (for each real $x\gt 1$ there always exists a prime $p$ with $x\lt p\lt 2x$ ) we need Hoheisel’s theorem [14] about the density of primes: There are constants $x_0$ and $0.5\le \alpha \lt 1$ such that for all $x\ge x_0$ the interval

(11) \begin{equation} [x-x^{\alpha }, x] \,\,\, \textrm{contains a prime number}. \end{equation}

The currently known best $\alpha$ is $0.525$ by Baker, Harman, and Pintz [2].

5.1 Building blocks: double stars and affine planes

The vertex set of a double star of size $s$ consists of $\{v_{i,j}\;|\; 1\le i,\; j\le s,\; i\ne j\}$ and two additional special vertices $w_a$ and $w_b$ . Let $A_i\,:\!=\,\{w_a\}\cup \{v_{i,j}\;|\; 1\le j\le s,\; j\ne i\}$ and $B_i\,:\!=\,\{w_b\}\cup \{v_{j,i}\;|\; 1\le j\le s,\; j\ne i\}$ for $i=1,\ldots,s$ . Then $({\mathcal{A}},{\mathcal{B}})$ is a $1$ -cross-intersecting SPS of size $s$ containing $s$ -element sets such that both $\mathcal{A}$ and $\mathcal{B}$ are 1-intersecting. The double star shows that $m_n(1{\textrm{-int}}, 1{\textrm{-int}}, 1)\geq n$ for all $n$ (consequently, $m_n(1{\textrm{-int}}, 1{\textrm{-int}}, *)\geq n$ and $m_n(1{\textrm{-int}}, *, 1)\geq n$ ).

The affine plane AG $(2,q)=(P,{\mathcal{L}})$ is a $q$ -uniform hypergraph with a $q^2$ element vertex set $P$ , such that each edge $L\in{\mathcal{L}}$ (called line) has $q$ vertices ( points), and $\mathcal{L}$ can be split into $q+1$ parts ${\mathcal{L}} ={\mathcal{L}}_1\cup{\mathcal{L}}_2\cup \dots \cup{\mathcal{L}}_{q+1}$ (directions or parallel classes of lines) such that each parallel class contains $q$ lines, ${\mathcal{L}}_\delta = \{L_{1, \delta }, \dots, L_{q, \delta }\}$ , the members of a parallel class are pairwise disjoint, but two lines from distinct classes always meet in a single point. It is known that an AG $(2,q)$ exists if $q$ is prime.

In the next subsection, we give three different (but similar) constructions to prove the lower bounds (8)–(10). Each construction will use an associated Extension twice, where an Extension starts with a weaker construction of the same type and combine it with AG $(2,q)$ for getting a stronger construction. In the following, $p$ and $q$ will always denote odd primes.

5.2 Extensions of the affine plane

Extension I. Let $({\mathcal{A}}',{\mathcal{B}}' )$ be a cross-intersecting SPS of size at least $q$ . For each $1\leq \delta \leq q+1$ take a new copy of $({\mathcal{A}}',{\mathcal{B}}' )$ so that the ground sets of the $q+1$ copies are pairwise disjoint and also disjoint from AG $(2,q)$ . For $i=1,\ldots,q$ let $({A_{i,\delta }^{\prime}}, {B_{i,\delta }^{\prime}})$ be the disjoint pairs in the $\delta$ th copy.

Let ${\mathcal{C}}_1(q,{\mathcal{A}}')$ be the family of $q^2+q$ sets $A_{i,\delta }\,:\!=\,L_{i,\delta }\cup {A_{i,\delta }^{\prime}}$ , and let ${\mathcal{C}}_1(q,{\mathcal{B}}')$ be the family of $q^2+q$ sets $B_{i,\delta }\,:\!=\,L_{i+1,\delta }\cup {B_{i,\delta }^{\prime}}$ . Here, $L_{q+2, \delta }\,:\!=\, L_{1, \delta }$ .

Claim 5.1. $({\mathcal{C}}_1(q,{\mathcal{A}}'),{\mathcal{C}}_1(q,{\mathcal{B}}'))$ is a cross-intersecting SPS. If ${\mathcal{A}}'$ and ${\mathcal{B}}'$ are $1$ -intersecting hypergraphs, then so do ${\mathcal{C}}_1(q,{\mathcal{A}}')$ and ${\mathcal{C}}_1(q,{\mathcal{B}}')$ .

Proof. Indeed, $A_{i,\delta }\cap B_{j,\gamma }= (L_{i,\delta }\cap L_{j+1, \gamma }) \cup ({A_{i,\delta }^{\prime}}\cap {B_{j,\gamma }^{\prime}})$ . This is the singleton $L_{i,\delta }\cap L_{j+1,\gamma }$ for $\delta \ne \gamma$ , it contains the nonempty set ${A_{i,\delta }^{\prime}}\cap {B_{j,\delta }^{\prime}}$ for $\delta =\gamma$ and $i\neq j$ , and it is empty for $({i,\delta })=(j,\gamma )$ .

In the case ${\mathcal{A}}'$ is 1-intersecting and $({i,\delta })\neq (j,\gamma )$ we get that $A_{i,\delta }\cap A_{j,\gamma }= (L_{i,\delta }\cap L_{j, \gamma }) \cup ({A_{i,\delta }^{\prime}}\cap {A_{j,\gamma }^{\prime}})$ , a singleton.

Construction 5.1. We prove (8), i.e., $m_n(1{\textrm{-int}}, 1{\textrm{-int}}, *)\ge n^2- 10 n^{1+\alpha }\ge n^2-o(n^2)$ .

Claim 5.1 implies that whenever $q$ is an odd prime and $m_s(1{\textrm{-int}}, 1{\textrm{-int}}, *)\geq q$ then

(12) \begin{equation} m_{q+s}(1{\textrm{-int}}, 1{\textrm{-int}}, *) \geq q^2+q. \end{equation}

Since $m_{s}(1{\textrm{-int}}, 1{\textrm{-int}}, *) \geq s$ by the double star, apply (12) for $(q,s)=(p,p)$ . We get $m_{2p}(1{\textrm{-int}}, 1{\textrm{-int}}, *)\ge p^2+p$ for all primes $p\gt 2$ .

Suppose $n\gt 2x_0$ . There is a prime $q$ between $n-5n^\alpha$ and $n-4n^\alpha$ by (11) and there is another prime $p$ between $n^\alpha$ and $2n^\alpha$ . Since $m_{2p}(1{\textrm{-int}}, 1{\textrm{-int}}, *)\geq p^2+p\gt n^{2\alpha }\gt n \gt q$ one can apply (12) with $s\,:\!=\,2p$

\begin{equation*} m_{n}(1{\textrm {-int}}, 1{\textrm {-int}}, *)\geq m_{q+2p}(1{\textrm {-int}}, 1{\textrm {-int}}, *) \geq q^2+q \gt n^2- 10 n^{1+\alpha }. \end{equation*}

Note that $|A_{i,\delta }\cap B_{j,\gamma }|$ can be as large as $q+1$ (for $i=j+1$ ).

Next we prove (9) and (10). The proofs are rather similar to the one presented above, so we leave out most of the details.

Extension II. Let $({\mathcal{A}}',{\mathcal{B}}' )$ be a $1$ -cross-intersecting SPS of size at least $q-1$ . For each $1\leq \delta \leq q+1$ take a new copy of $({\mathcal{A}}',{\mathcal{B}}' )$ so that the ground sets of the $q+1$ copies are pairwise disjoint and also disjoint from AG $(2,q)$ . For $i=1,\ldots,q-1$ let $({A_{i,\delta }^{\prime}}, {B_{i,\delta }^{\prime}})$ be the disjoint pairs in the $\delta$ th copy.

Let ${\mathcal{C}}_2(q,{\mathcal{A}}')$ be the family of $q^2-1$ sets $A_{i,\delta }\,:\!=\,L_{i,\delta }\cup {A_{i,\delta }^{\prime}}$ , and let ${\mathcal{C}}_2(q,{\mathcal{B}}')$ be the family of $q^2-1$ sets $B_{i,\delta }\,:\!=\,L_{q,\delta }\cup {B_{i,\delta }^{\prime}}$ .

Claim 5.2. $({\mathcal{C}}_2(q,{\mathcal{A}}'),{\mathcal{C}}_2(q,{\mathcal{B}}'))$ is a $1$ -cross-intersecting SPS. If ${\mathcal{A}}'$ is a $1$ -intersecting hypergraph, then so does ${\mathcal{C}}_2(q,{\mathcal{A}}')$ .

Construction 5.2. We prove (9), i.e., $m_n(1{\textrm{-int}}, *, 1)\ge n^2- o(n)$ .

Claim 5.2 implies that whenever $q$ is an odd prime and $m_s(1{\textrm{-int}}, *, 1)\geq q-1$ then

(13) \begin{equation} m_{q+s}(1{\textrm{-int}}, *, 1) \geq q^2-1. \end{equation}

Since $m_{s}(1{\textrm{-int}}, *, 1) \geq s$ by the double star, apply (13) for $(q,s)=(p,p-1)$ . We get $m_{2p-1}(1{\textrm{-int}}, *,1)\ge p^2-1$ for all primes $p\gt 2$ .

There is a prime $q$ between $n-5n^\alpha$ and $n-4n^\alpha$ and there is another prime $p$ between $n^\alpha$ and $2n^\alpha$ . Since $m_{2p-1}(1{\textrm{-int}}, *, 1)\geq p^2-1 \gt n^{2\alpha }-1 \geq n \gt q$ one can apply (13) with $s\,:\!=\,2p-1$

\begin{equation*} m_{n}(1{\textrm {-int}}, *,1)\geq m_{q+2p-1}(1{\textrm {-int}}, *,1) \geq q^2-1 \gt n^2- 10 n^{1+\alpha }. \end{equation*}

Note that ${\mathcal{C}}_2(q,{\mathcal{B}}')$ is not linear.

Extension III. Let $({\mathcal{A}}',{\mathcal{B}}' )$ be a $1$ -cross-intersecting SPS of size at least $(q-1)/2$ . For each $1\leq \delta \leq q+1$ take a new copy of $({\mathcal{A}}',{\mathcal{B}}' )$ so that the ground sets of the $q+1$ copies are pairwise disjoint and also disjoint from AG $(2,q)$ . For $i=1,\ldots,(q-1)/2$ let $({A_{i,\delta }^{\prime}}, {B_{i,\delta }^{\prime}})$ be the disjoint pairs in the $\delta$ th copy.

Let ${\mathcal{C}}_3(q,{\mathcal{A}}')$ be the family of $(q^2-1)/2$ sets $A_{i,\delta }\,:\!=\,L_{i,\delta }\cup {A_{i,\delta }^{\prime}}$ , and let ${\mathcal{C}}_3(q,{\mathcal{B}}')$ be the family of $(q^2-1)/2$ sets $B_{i,\delta }\,:\!=\,L_{i+(q-1)/2,\delta }\cup {B_{i,\delta }^{\prime}}$ .

Claim 5.3. $({\mathcal{C}}_3(q,{\mathcal{A}}'),{\mathcal{C}}_3(q,{\mathcal{B}}'))$ is a $1$ -cross-intersecting SPS. If ${\mathcal{A}}'$ and ${\mathcal{B}}'$ are $1$ -intersecting hypergraphs, then so do ${\mathcal{C}}_3(q,{\mathcal{A}}')$ and ${\mathcal{C}}_3(q,{\mathcal{B}}')$ .

Construction 5.3. We prove (10), i.e., $m_n(1{\textrm{-int}}, 1{\textrm{-int}}, 1)\ge \frac{1}{2}n^2-o(n^2)$ .

Claim 5.3 implies that whenever $q$ is an odd prime and $m_s(1{\textrm{-int}}, 1{\textrm{-int}}, 1)\geq (q-1)/2$ then

(14) \begin{equation} m_{q+s}(1{\textrm{-int}}, 1{\textrm{-int}}, 1) \geq (q^2-1)/2. \end{equation}

Since $m_{s}(1{\textrm{-int}}, 1{\textrm{-int}}, 1) \geq s$ by the double star, apply (14) for $(q,s)=(p,(p-1)/2)$ . We get $m_{(3p-1)/2}(1{\textrm{-int}}, 1{\textrm{-int}},1)\ge (p^2-1)/2$ for all primes $p\gt 2$ .

There is a prime $q$ between $n-5n^\alpha$ and $n-4n^\alpha$ and there is another prime $p$ between $n^\alpha$ and $2n^\alpha$ . Since $m_{(3p-1)/2}(1{\textrm{-int}}, 1{\textrm{-int}}, 1)\geq (p^2-1)/2 \gt n^{2\alpha }/2 \geq n \gt q$ one can apply (14) with $s\,:\!=\,(3p-1)/2$

\begin{equation*} m_{n}(1{\textrm {-int}}, 1{\textrm {-int}},1)\geq m_{q+(3p-1)/2}(1{\textrm {-int}}, 1{\textrm {-int}},1) \geq \frac {1}{2}(q^2-1) \gt \frac {1}{2}n^2- 5 n^{1+\alpha }. \end{equation*}

6. Conjectures, open problems

We conjectured [10] that there exists a positive $\varepsilon$ such that $m_n(*, *, 1)\le (1-\varepsilon )\binom{2n}{n}$ for every $n\ge 2$ . This was proved by Holzman [15] in the following stronger form. If $a, b\geq 2$ , then $m(a, b,1)\leq (29/30)\binom{a+b}{a}$ . More recently, Kostochka, McCourt, and Nahvi [17] showed that the factor $29/30$ in this bound can be replaced by $5/6$ , which is the best possible since $m(2,2,1)=5$ .

Although Constructions 5.1 and 5.3 together with Proposition 1.5 and Theorem 1.6 show that

\begin{equation*}\lim _{n\to \infty } \frac {m_n(1{\textrm {-int}}, 1{\textrm {-int}}, 1)}{m_n(1{\textrm {-int}}, 1{\textrm {-int}}, *)}=\lim _{n\to \infty } \frac {m_n({01{\textrm {-int}}}, {01{\textrm {-int}}}, 1)}{m_n({01{\textrm {-int}}}, {01{\textrm {-int}}}, *)}=\frac {1}{2},\end{equation*}

we strongly believe that the following is also true.

Conjecture 1.

\begin{equation*}\lim _{n\to \infty } \frac {m_n(*, *, 1)}{m_n(*, *, *)}=0.\end{equation*}

We obtained some tight results for $m(a, b, I_A, I_B, I_{\mathrm{cross}})$ in the case $a=b$ and also in the case $a=2$ . There is plenty of room for further investigations.