Experimental and theoretical studies of the interactions of alanine onto surfaces of olivine and montmorillonite: relevance in astrobiology

Abstract

Amino acids have been detected in some meteorites and are readily synthesized in prebiotic experiments. These molecules may have been precursors of oligomers and polymers in the early Earth. These reactions were likely to happen in the protected confined spaces on the porous surface of olivine and in the interlayer nanospace of montmorillonite. This study describes experimental and theoretical research on the sorption of l-alanine onto surfaces of silicate minerals, olivine and montmorillonite. Kinetics of the sorption of this amino acid at different pH media was performed. This sorption has been also studied at atomic scale by means of quantum mechanical calculations finding that this sorption is energetically favourable. These results strongly support the premise that minerals could have actively participated in prebiotic reactions.

Introduction

The emergence of life on early Earth likely hinged upon the intricate interplay between organic compounds and mineral substrates. Organic materials served as essential precursors for the synthesis of complex biopolymers through prebiotic reactions, boosting chemical evolution on our planet. The origins of these organic molecules extend beyond Earth's boundaries, with compounds synthesized both locally and delivered via extraterrestrial bodies such as meteorites, comets and interstellar dust (Dass et al., 2016). This influx of water, volatiles and organic compounds onto Earth's surface, as suggested by studies (Oro et al., 1980; Alexander et al., 2012; Albarede et al., 2013; Marty et al., 2016), could have played a pivotal role in priming the conditions for life's emergence.

Of the most relevant organic molecules, amino acids stand out as key components essential for life's processes. Their significance is underscored by their structural diversity, including chirality, making them focal points in prebiotic chemistry investigations (Glavin et al., 2018). Amino acids are common in chondritic meteorites, with glycine (Gly) and alanine (Ala) notably prevalent, as evidenced by analyses of the Murchison meteorite (Botta and Bada, 2002; Burton et al., 2012; Cobb and Pudritz, 2014; Elsila et al., 2016; Koga and Naraoka, 2017).

In the context of Earth's early environment, the presence of minerals, particularly clays, was expected and significant (Hazen et al., 2008). Clays have been implicated in sorption experiments involving amino acids, offering insights into their potential role as concentrators of organic molecules (Lambert, 2008; Farias et al., 2014; Escamilla-Roa et al., 2017; de Castro Silva et al., 2020; Samulewski et al., 2021; Nkoh et al., 2022). Despite these investigations, questions persist regarding the sorption behaviour of amino acids onto other mineral substrates (Escamilla-Roa and Sainz-Díaz, 2014).

In this study, we investigate the sorption behaviour of l-alanine onto olivine and montmorillonite, minerals commonly found on meteorites and plausibly present on early Earth. Through a comprehensive analysis encompassing sorption kinetics, isotherms and pH profiles, augmented by theoretical modelling, we aim to elucidate the role of these minerals as potential concentrators of amino acids. This information will allow us to better understand the possible relevance of the interactions of organics–minerals for astrobiological research.

Materials and methods

All the reactants were from the highest purity commercially available. l-Alanine (C₃H₇NO₂), nitric acid (HNO₃), sulphuric acid (H₂SO₄), potassium hydroxide (KOH), potassium chloride (KCl), hydrochloric acid (HCl), ethanol (C₂H₅OH), potassium nitrate (KNO₃), tin(II) chloride (SnCl₂) and ethylene glycol (C₂H₆O₂) used in this study were from Sigma Aldrich^®. The montmorillonite (Mt) [Al_1.67Mg_0.33Si₄O₁₀(OH)₂nH₂O] is a Wyoming SWy-1 smectite, obtained from the University of Missouri-Columbia, Source Clay Minerals Repository. The olivine was purchased in a mineral store, and it was characterized by X-ray diffraction (XRD) and scanning electron microscopy in a JEOL JXA-8900R by energy-dispersive X-ray spectroscopy. The olivine (Oliv) used in this study appertains to the end-member forsterite, since magnesium is in greater proportion (49%) than the iron (10.33%). The water used in all the experiments was deionized in a Milli-Q Plus Millipore^® ultrapure water system.

Cleaning of the material

The glassware was cleaned with a warm sulphuric–nitric acid mixture (1 : 1) for 30 min. After that, it was rinsed with distilled water and heated in a furnace for 3 h at 200°C to avoid organic contamination.

Determination of the point of zero charge

The point of zero charge (pzc) was determined for both minerals, montmorillonite and olivine, by two methods: pH change (Gillman and Uehara, 1980; Uehara and Gillman, 1980; de Souza et al., 2013), and titration curves (Ibanez et al., 2008).

pH change (method 1, pzc)

This method is useful to estimate the pH value where one or more components of the surficial charge vanish. For each mineral two samples were prepared; the first contained the mineral and deionized water (1.5 ml); the second, the mineral and 1.5 ml of a solution of KCl (0.1 mol⋅l⁻¹). In the case of olivine, 600 mg of the mineral were added to each tube, for montmorillonite 30 mg of the clay were employed. Samples were stirred for 24 h, and then the pH of each sample was determined. The pzc was determined according to

(1)$${\rm p}{\rm H}_{{\rm pzc}} = 2{\rm p}{\rm H}_{{\rm KCl}}-{\rm p}{\rm H}_{{\rm H}_2{\rm O}}$$

where pH_pzc = point of zero charge; pH_KCl = the measured pH of the sample with the KCl solution; ${\rm p}{\rm H}_{{\rm H}_2{\rm O}}$ = measured pH of the sample with water.

Titration curves (method 2, pznpc)

pznpc means the point of zero net proton charge. This method allows estimating the surficial charge on a particle, due to adsorbed protons, where it approaches zero. To estimate this value, two titration curves were constructed: one for the sample without the mineral, and the other for the sample containing one of the minerals (olivine or montmorillonite). In the case of the curve without the mineral, 3 ml of KNO₃ (0.1 mol·l⁻¹) were added to 6 ml of deionized water, the sample was stirred and then 1 ml of KOH (0.01 mol⋅l⁻¹) was added. The sample was stirred again, and the pH was measured. Titration was done by adding volumes of HNO₃ (0.1 ml, 0.01 mol·l⁻¹) to the sample; the pH was measured after each addition until the value did not change.

For the samples with mineral, 3 ml of KNO₃ (0.1 mol⋅l⁻¹) were added to 6 ml of deionized water, the sample was stirred; then 50 mg of the mineral were added. The sample was stirred for 10 min more. Afterwards, 1 ml of KOH (0.01 mol·l⁻¹) was added and the pH was measured. Titration was also done with HNO₃, with volumes of 0.1 ml (0.01 mol·l⁻¹), that were added to the sample. The pH was measured after each addition until it did not change. The volume of employed HNO₃ was plotted against the measured pH for each curve. The pznpc is graphically found as the value where both curves intersect.

Amino acid quantification by ultraviolet–visible spectroscopy

Ninhydrin derivatives were prepared to quantify the amino acid following the next procedure: 1 ml of the amino acid solution was mixed with 1 ml of a ninhydrin solution [1 g of ninhydrin, 12.5 ml of acetate buffer (pH = 5.5), 1.25 ml of tin(II) chloride solution (0.6 g of SnCl₂ in 6 ml of ethylene glycol); and 37.5 ml of ethylene glycol], the mixture was stirred. Then, the sample was heated in a water bath (at 96°C) for 10 min. After cooling, 2 ml of an ethanol–water solution (50 : 50) were added to the sample. The absorbance (at λ = 570 nm) was measured in a Varian^® Cary 100 Scan spectrophotometer. Calibration curves were obtained for each amino acid, from 1 × 10⁻⁵ to 1 × 10⁻³ mol·l⁻¹. The supernatant was also treated as previously described.

Sorption experiments

Sorption experiments were made to evaluate the interaction of the amino acid (Ala) with the minerals. Aliquots of 3 ml of a solution of Ala ()1 × 10⁻³ mol⋅l⁻¹) were mixed with 100 (±0.25) mg of the mineral, olivine (Oliv–Ala) or montmorillonite (Mt–Ala). The samples were stirred for 24 h. We performed experiments at different pH values. To evaluate the role of pH in the sorption of the amino acid, three different sets of experiments were made: at the natural pH of solutions (pH ≈ 6.5), at acidic (pH = 2) and at basic (pH = 12) conditions. The pH was adjusted by the addition of drops of an HCl solution (0.01 mol·l⁻¹) or a NaOH solution (0.01 mol⋅l⁻¹). After stirring (for 24 h), the pH was measured, and the samples were centrifuged at 15 000 RPM for 30 min. The supernatant was analysed by ultraviolet–visible spectroscopy and the solid phase was lyophilized for further analyses. All experiments were conducted in triplicate.

Sorption kinetics experiments

These experiments allow determining the time required for the maximum sorption of the amino acid on the mineral. In total, 100 mg of the mineral (either olivine or montmorillonite) were mixed with 3 ml of the amino acid (Ala, 1 × 10⁻³ mol l⁻¹, pH = 2), then it was stirred for 1 h. The procedure was repeated, but increasing the stirring time, for 1, 2, 4, 6, 14 and 24 h. Samples were centrifuged at 15 000 RPM for 30 min. The supernatant was derivatized and analysed as described previously. All the experiments were conducted in triplicate.

Desorption experiments

These experiments were performed to check the reversibility of the bonding between the amino acid and minerals. Distilled water (3 ml) was placed in a culture tube, and then 100 mg of each sample (Oliv–Ala; Mt–Ala) were added. The sample was stirred for 1 h and then centrifuged for 25 min at 24 000 RPM. This procedure was conducted by duplicate to determine the total amount of amino acid that could be recovered.

Isotherms

Aliquots (3 ml) of the amino acid solution (Ala, 1 × 10⁻³ mol·l⁻¹, pH = 2) were mixed with 100 mg of the mineral (olivine or montmorillonite), and they were stirred for 24 h at room temperature (25°C). Samples were centrifuged and the concentration at equilibrium of the amino acid in the supernatant was determined by the ninhydrin method. The concentration of amino acid sorbed was plotted against the amount of amino acid at equilibrium. The latter was calculated by the difference between the initial concentration and the amount measured in the supernatant. All the experiments were made in triplicate.

For all data, adjustments were made to find out which model best described the process. Adjustments were made for Langmuir, Freundlich and Brunauer, Emmett and Teller (BET) isotherm models in their non-linear form; since the parameters calculated with non-linear fits better represent the sorption characteristics than their fits to linear forms (Subramanyam and Das, 2009).

Langmuir model

According to this model, the sorption occurs in monolayers, and all the sorption sites have the same energy (homogeneous surface) (Ayawei et al., 2017). The below equation describes this model:

(2)$$q_{\rm e} = q_{\rm m}\displaystyle{{k_{\rm L}C_{\rm e}} \over {1 + k_{\rm L}C_{\rm e}}}$$

where C _e is the concentration of the adsorbate at equilibrium, k _L is the equilibrium constant of the adsorption reaction, an thus it is associated with free energy adsorption and q _m is the maximum sorption capacity. From the value of k _L, a dimensionless constant called separation factor R _L can be calculated:

(3)$$R_{\rm L} = \displaystyle{1 \over {1 + k_{\rm L}C_0}}$$

Freundlich model

Unlike the Langmuir isotherm model, Freundlich model describes the sorption process on heterogeneous surfaces. The Freundlich isotherm expresses how heterogeneous the surface area is (Freundlich, 1909). This model also includes the distribution of the active sites and their energies, and is described by the following equation:

(4)$$q_{\rm e} = k_{\rm F}C_{\rm e}^{1/n} $$

where k _F is the Freundlich constant that is indicative of the sorption capacity and 1/n is the sorption intensity, which is related to the energy distribution and heterogeneity of the sorption sites. When n > 1, sorption is favourable; if n = 1 the isotherm has a linear form and when n < 1, sorption is not favourable (Giles et al., 1974).

BET model

The BET model is used for multilayer sorption of gases into solids. Ebadi et al. (2009) proposed an adaptation of the BET equation that can be applied to liquids. This form considers two separate equilibrium constants, one for the first layer and other for the upper layers:

(5)$$q_{\rm e} = q_{\rm m}\displaystyle{{k_{\rm S}C_{\rm e}} \over {( {1-k_{\rm L}C_{\rm e}} ) ( {1-k_{\rm L}C_{\rm e} + k_{\rm S}k_{\rm L}C_{\rm e}} ) }}$$

where q _m is the maximum sorption capacity of the first layer, k _S is the equilibrium constant of the first layer and k _L is the equilibrium constant for the upper layers. In the case where the sorption is single layered, BET is equivalent to the Langmuir model.

XRD analysis

Powder XRD analysis was performed on the mineral samples with and without amino acid. Samples were powdered in agate mortar. Oriented aggregates were prepared on glass plates. The measurements were carried out using an EMPYREAN X-ray diffractometer with CuKα (λ = 1.5406 Å) radiation and a PIXcel3D detector.

Thermogravimetric analysis

Thermogravimetric analysis (TGA) and differential thermogravimetric analysis were performed with a LINSEIS STA PT 1600 calorimeter, previously calibrated with gold and indium standards using alumina crucibles. The heating rate was 10°C min⁻¹ in the 30–1000°C temperature range.

Computational modelling

Models

The amino acid molecular structures were drawn by using the Materials Studio graphical package (‘BIOVIA Materials Studio – BIOVIA – Dassault systèmes^®,’ n.d.) considering the experimental information. Bearing in mind the pH of the media, several forms were generated, a neutral zwitterionic one for a neutral pH (Ala), a Na carboxylate form (Ala–Na) for a high pH media and ammonium chloride salt (AlaH_Cl) for a low pH media. All of them were placed in a cubic periodical box of 13 × 13 × 13 Å³.

For the hydrated models, periodical boxes were filled with each amino acid form with water molecules by using a Monte Carlo method optimizing the structures reaching a density close to 1 g cm⁻³.

Two models of montmorillonite were created as crystals by using periodical boundary conditions: one (Mt) with the same chemical composition to the experimental one with the unit cell composition of Na_0.5(Al_3.5Mg_0.5)Si₈(OH)₄O₂₀, and another one with a higher interlayer charge (Mt1) Na(Al₃Mg)Si₈(OH)₄O₂₀. In all cases, a 2 × 1 × 1 supercell was created in order to have enough space for adsorption of each amino acid without interferences with vicinal cells in the periodical systems. Several hydration levels were studied with two and three water molecules per Na⁺ cation.

Computational methodology

Quantum mechanical calculations were performed based on density functional theory (DFT) by using the Quantum Espresso (QE) code (Giannozzi et al., 2017). The generalized gradient approximation and the Perdew–Burke–Ernzerhof (PBE) functional for the exchange–correlation functional (Perdew et al., 1996) were used along with projector-augmented wave pseudopotentials (Blöchl, 1994). Empirical dispersion corrections were used according to the DFT-D3 scheme (Grimme et al., 2010). Other calculation parameters were taken from their optimization for similar systems previously (Misaela et al., 2022) obtaining an energy cut-off = 100 Ry, charge density cut-off (rho) = 400 Ry and a 3 × 2 × 1 k points grid of the Brillouin zone.

The periodical boxes of the hydrated amino acids were filled by means of a Monte Carlo method at 298 K with 100 loading steps using the COMPASS force fields (‘BIOVIA Materials Studio – BIOVIA – Dassault systèmes^®,’ n.d.), where each amino acid form is surrounded by enough water molecules for a density of 1 g cm⁻³.

Results and discussion

pzc of minerals

In aqueous solution a mineral develops charges on its surface, either by the reaction with ions in the solution or by isomorphic substitutions in its structure. These charges can be of three types: structural charges, that do not depend on pH; a charge that depends on the amount of H⁺ absorbed or desorbed at the interface of the mineral surface and the aqueous solution and third, the charge conferred by the sorbed ions, different from H⁺ or OH⁻ (Stumm, 1992). The pzc has been defined as the pH value at which the sum of the three types of superficial charges equals zero. This value is defined at certain values of temperature, pressure and composition of the aqueous solution (Stumm, 1992). However the potentiometric titration curves only provide information about the charge due to the adsorbed protons (Zuyi and Taiwei, 2003). The pzc shows how the whole mineral surface changes as a function of pH. At pH values below the pzc, mineral surface is positively charged and above the pH of the superficial charge is negative.

The measured values of zero charge point for both minerals differ from other published values. In the case of olivine, the determined values were 10.14 (pzc) and 7.08 (pznpc) using method 1 (pH change) and method 2 (titration curves), respectively (Supplementary Table 1). When compared to other studies (Luce and Parks, 1973; Ney, 1973; Pokrovsky and Schott, 2000; Oelkers et al., 2009; Cárdenas-Espinosa and Vargas, 2010; de Souza et al., 2013), it was found that there is a big difference between the reported values (Supplementary Table 1). Those measurements range from ~4 to ~10. This difference could be attributed to different factors, being one of the most important the mineral sample, as the origin and thus geochemical composition of the mineral is fundamental for its behaviour; it is also relevant the method used for pzc determination.

Regarding montmorillonite, the measured values were 6.8 (pzc) and 7.1 (pznpc). Montmorillonite is a mineral that holds structural charge; in these clays (2 : 1) the pznc determined by a titration curve (at a given ionic strength) is almost equivalent to pzc (Duc et al., 2005). According to the values estimated by us, pzc and pznc are close, but not the same. The values of pzc measured for montmorillonite in this study also differ from other reported values (Supplementary Table 2). Duc et al. (2005) suggest that the method is the main responsible of the differences; but there are other critical points such as: the clay purification protocol; the storage conditions of purified clay and the analytical method selected to determine the zero-point charge. Unlike the reported studies in this research a previous purification step was not performed, as we wanted to keep the sample as natural as possible. The analytical conditions used here were also different. The ionic strength of the medium strongly affects the zero-point charge determination for montmorillonite; as the ionic strength increases the value decreases (Hao et al., 2018), this coincides with the results obtained here. When a 1 M solution of KCl was employed, the measured value was 6.8, while the use of a 0.01 mol·l⁻¹ of KNO₃ resulted in a value of 7.1. In summary, the determination of pzc in different minerals is strongly dependent on the geochemical composition of the mineral, and the method employed.

Sorption studies

Sorption on olivine

The sorption of l-alanine in olivine is pH dependent as shown in Fig. 1. The highest sorption values correspond to the lowest pH. For example, at pH 4.6 alanine is sorbed at 38.2% ± 1.14 on olivine. At this pH sorption can occur by opposite charge attraction between the olivine positive surface and the negative carboxyl group of the zwitterion form of alanine that constitutes the 99.4% of the species. However, at pH 9.7 the amount of alanine sorbed is just 14.7%. ± 1.5. At this pH, the sorption takes place through the interaction of the carbonyl group of the amino acid in the form of a zwitterion; or the negatively charged amino acid, and the positive surface of olivine. The differences among the percentages of sorption at those different pH values can be explained assuming that the number of positively charged sites on the mineral surface is higher at pH 4.6 than at pH 9.7, since this last value is closest to the pzc of olivine, either 10.14 or 7.08.

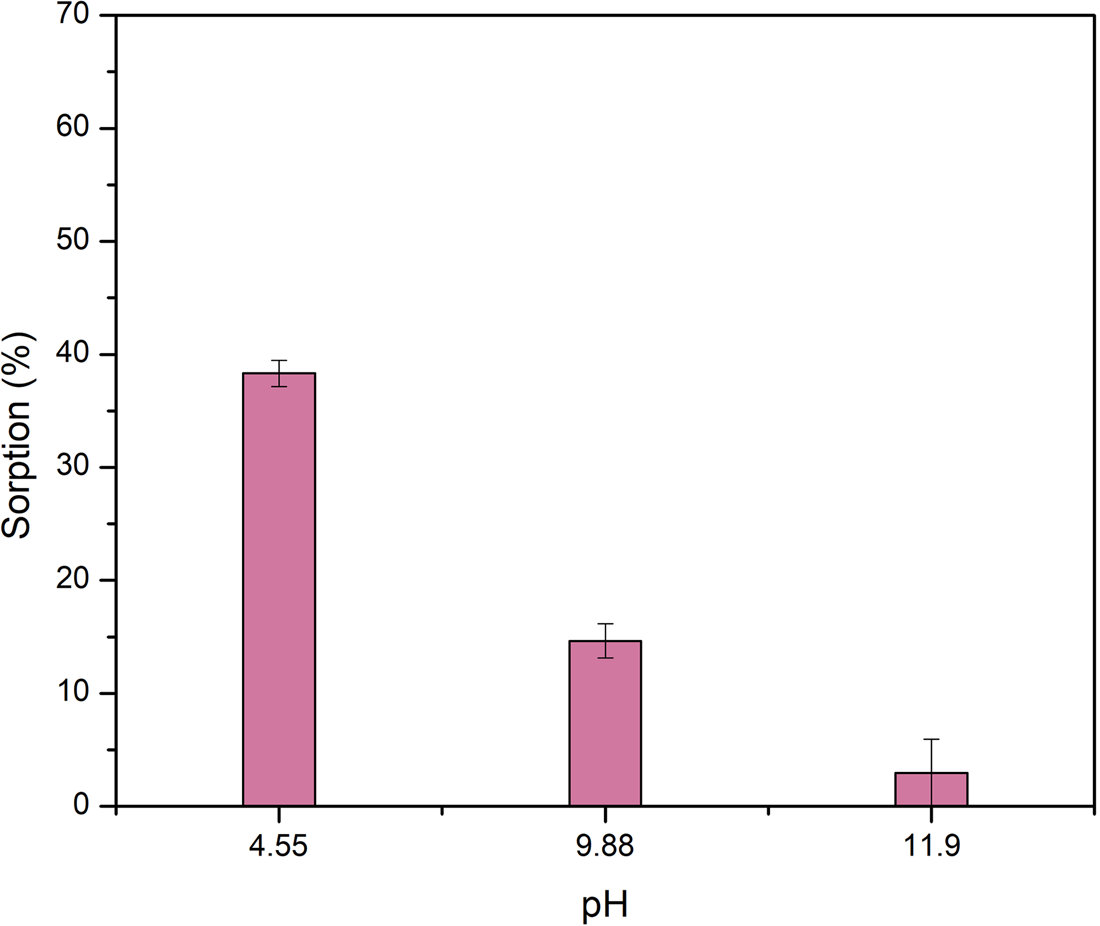
Figure 1. Sorption of l-alanine into olivine as a function of the final pH. There is a strong dependency of the amount of alanine sorbed and the value of pH, as this last becomes more alkaline, the sorption diminishes. Lines in columns are the standard deviations.

In acidic medium, magnesium and iron of olivine participate in exchange reactions with H⁺, as a result, they are released to the aqueous medium as cations (Wogelius and Walther, 1991; Lacroix et al., 2014; Oelkers et al., 2018). As the olivine surface lost both magnesium and iron, it starts to resemble compositionally the surface of SiO₂ due to the polymerization of the SiO₄⁴⁻ groups (Pokrovsky and Schott, 2000). However, this is proposed as the first step in olivine reaction with water at acidic pH. In further steps the surface loses both Mg and Si (Oelkers et al., 2018). King et al. (2014) propose that at acidic pH an amorphous Mg-silicate phase in the olivine surface is due to dissolution and precipitation of the mineral. In this surface the groups available for interaction with alanine are siloxane (Si–O–Si), magnesil (Si–O–Mg–O–OH) and silanol (Si–OH). At pH 4.6 more than 99% of the molecule of Ala is in the zwitterionic form; therefore, at this acidic pH the interaction of the organic molecules could be due interaction between the carboxylic and positive charged SiOH₂⁺ groups, that constitute the most reactive group.

At basic pH (~11.9) the sorption of l-Ala on the olivine surface was not observed. This coincides with the fact that at this pH value, the amino acid and the mineral surface are negatively charged (Fig. 1), and the sorption cannot proceed via opposite charges attraction. The results here obtained indicate that the amino acid is mainly sorbed on olivine by opposite charge attraction. Another possibility is the formation of surface complexes between alanine and Mg or Fe in olivine. It is known that in acidic pH organic ligands such as oxalate, formic acid, ascorbic acid and potassium acid phthalate can form complexes with metal ions in olivine (Wogelius and Walther, 1991; Olsen and Donald Rimstidt, 2008; Prigiobbe and Mazzotti, 2011). The negatively charged carboxylic group in alanine zwitterion can bond to the Mg or Fe in olivine.

Sorption in montmorillonite

The sorption of Ala on montmorillonite is also dependent on the pH (Fig. 2), which coincides with the behaviour of other organic molecules and the clay, like nucleobases (Meléndez-López et al., 2017) or other amino acids (Greenland et al., 1962; Friebele et al., 1980; Ramos and Huertas, 2013; Farias et al., 2014). In general, sorption percentages decrease as pH increases; this also agrees with other studies. The highest percentage of sorption occurs at acidic pH (2.6), with a percentage of 56.2 ± 3.1%.

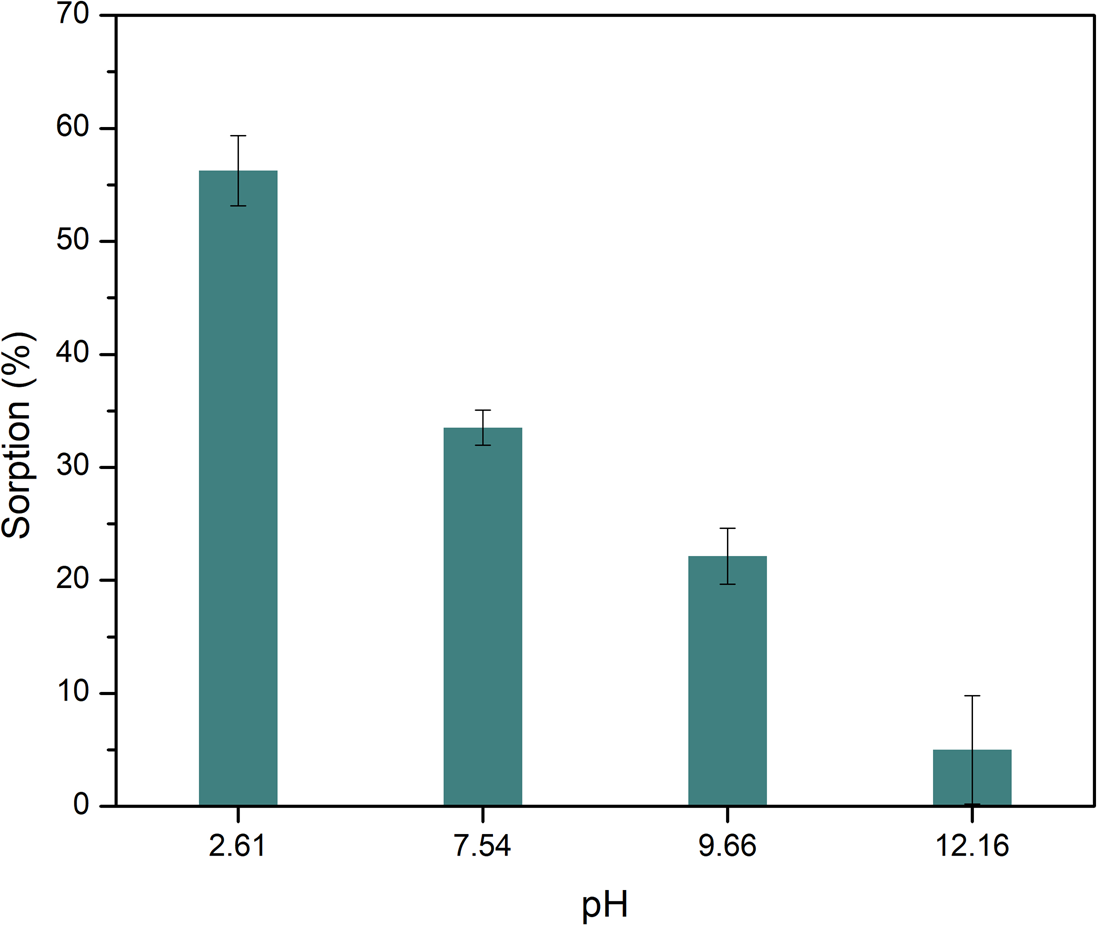
Figure 2. Sorption of l-Ala on montmorillonite as a function of final pH. The change in alkalinity produces a decrease in the sorption of the amino acid. Lines represent the standard deviation for the measurements. Sorption is favoured at acidic media.

Montmorillonite has surficial pH-dependent charges as the amino acids. At pH 12 the amino acid is negatively charged, like the mineral, so the adsorption could not occur by opposite charges attraction. At pH 7.5 the mineral surface is negatively charged, while amino acids are in the zwitterion form, thus sorption of amino acids can occur; this occurs through the protonated amino group of Ala. The amino acid is positively charged at pH 2, and sorption can occur by a cation exchange process in the interlayer space. In olivine the sorption is produced in the external surface, that is smaller than in interlayer space of montmorillonite, thus the sorption in olivine is lower than in montmorillonite.

Kinetics of sorption

These experiments allow the determination of the time required for alanine, to be absorbed on the minerals. Our results indicate that sorption occurs quickly on montmorillonite (Fig. 3), in less than 1 h. While in the case of olivine, the amino acid is slowly sorbed, and after 24 h of stirring the maximum sorption is attained (Fig. 4). At acidic pH (~2) the amino acid is positively charged, and the adsorption is produced by a cation exchange mechanism that occurs in the interlayer space of montmorillonite. The interlayers of montmorillonite are negatively charged, which facilitate the entry of positively charged molecules; this occurs easily and results in fast sorption kinetics.

Figure 3. Sorption kinetics of l-Ala on sodium montmorillonite. At the beginning of the experiment (0.5 h) the sorption is 23.7.3 ± 2.2%, as the sorption time increases the sorption diminishes, reaching a minimum close to 15%. A decrease in the amount sorbed can be related to the rise in pH. The subsequent increase in adsorption could be due to the slow diffusion of alanine into the interlayer region.

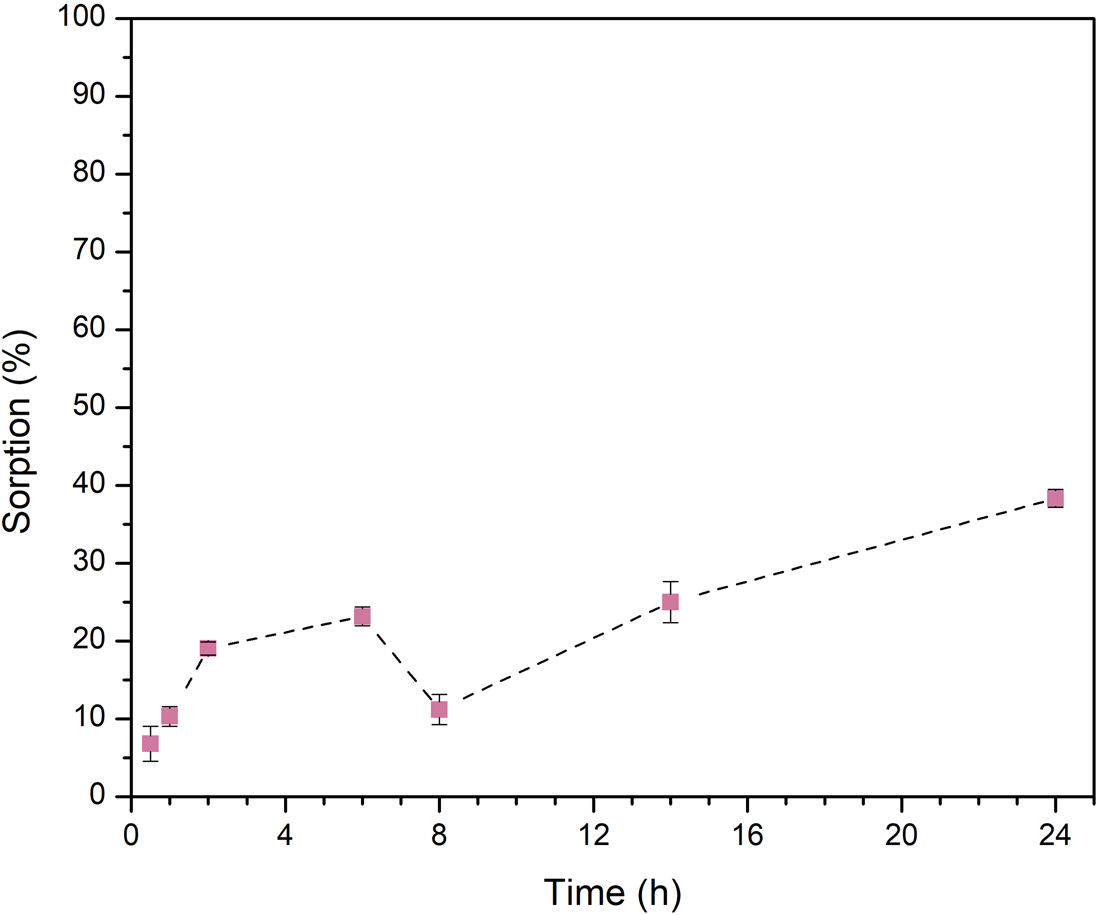
Figure 4. Sorption kinetics of l-Ala onto olivine. In general, the sorption of the amino acid on the mineral increases with contact time, except after 8 h, but then it increases again. Results are the average of three independent measurements.

However, in the case of olivine, there is a repulsion interaction between the surface and the molecules. This is probably due to the fact that both, the amino acid and the mineral, are positively charged.

Desorption experiments

The amino acids are not easily desorbed from minerals. After the desorption experiments variable amounts of the molecule remain adsorbed (Table 1). In the case of the experiments with montmorillonite, greater desorption percentages were observed (Mt–Ala, 42.65%), and the desorption occurs after 2 h, this could be related to an increase of pH in the system. An ionic exchange reaction in the interlamellar channel occurs, Na⁺ is released while H⁺ is adsorbed on the clay (Wanner et al., 1994), as the H⁺ in the medium diminishes the pH increases.

Table 1. Desorption of alanine from olivine and montmorillonite

^a The percentage of desorption is the corresponding fraction of the sorbed amount.

Even if sorption is smaller on olivine (Oliv–Ala, 16.37%) almost no desorption was observed (Oliv–Ala, 0.09%). Escamilla-Roa and Moreno (2012) proposed that glycine bounds to olivine by both chemisorption and physisorption processes, depending on the configuration of the amino acid and the possibility of interaction with the surface. In our results, the small desorption of alanine from olivine could be explained if chemisorption occurs, and there was the formation of chemical bonds between the molecules and the surface of the mineral. More studies are needed to confirm if chemisorption could occur between Ala and olivine.

Sorption isotherms

The values obtained from isotherms are a comparison between the amount of the organics sorbed in the mineral and the concentration in the aqueous phase; also, they provide us information about the nature of the sorption. Oliv–Ala system shows a good fit to all models, for concentrations from 1 × 10⁻⁴ to 1 × 10⁻³ mol⋅l⁻¹ (Table 2); the Mt–Ala system does not fit any of the tested models. It has been published that the sorption isotherms for amino acids mostly correspond to the Langmuir model (Greenland et al., 1962, 1965; Dashman and Stotzky, 1982; Kalra et al., 2000; Parbhakar et al., 2007; Ramos and Huertas, 2013). However, it is well known that in montmorillonite cation exchange occurs; and this process is a different mechanism to the one described by the Langmuir model. It is important to emphasize that the concentration of organics in those studies are greater than the ones used in the present research. Ramos and Huertas (2013) demonstrated that at low concentrations the sorption of glycine occurs in the edges of the montmorillonite and cation exchange only occurs at higher concentrations.

Table 2. Parameters calculated by the adjustment of isotherms to the three models tested: Langmuir, Freundlich and BET

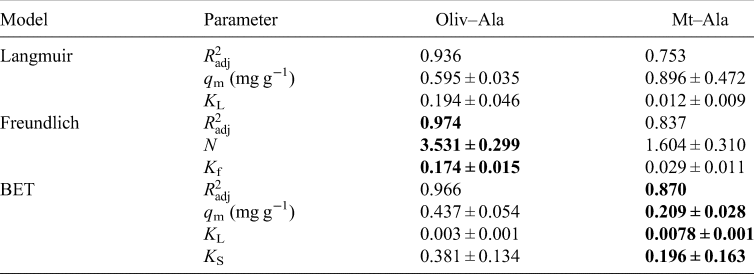
Note: The best adjustments for each experiment are shown in bold.

In the case of the Oliv–Ala system (Fig. 5) all the tested models fit the experimental data, since the calculated $R_{{\rm adj}}^2$ is >0.9. The Freundlich model fits the best; this suggests heterogeneous sites for adsorption with a non-uniform distribution of heat of sorption over the surface (Freundlich, 1909). This can be indicative of the different surface groups of olivine that can interact with alanine. The value of n obtained from the fitting is greater than 1 (Table 2) indicating a favourable sorption process.

Figure 5. Isotherm models fit of l-Ala sorption onto olivine. The data better adjust to the Freundlich model, suggesting that sorption occurs in a heterogeneous surface with different energy.

As already mentioned above, there was not a good adjustment of none of the tested models to the Mt–Ala data ($R_{{\rm adj}}^2$ is <0.9). This is probably due to the large errors caused by the clay, whose origin is natural. Natural materials are not homogeneous due to irregularities in mineral surfaces, which can cause variations in the adsorption of l-alanine (dos Santos et al., 2016; Galvez-Martinez et al., 2019; Cruz-Hernández et al., 2022). After saturation, the amount sorbed is independent of the concentration, and this is the maximum amount of sorption. In the Mt –Ala isotherm the maximum adsorption capacity is not reached at the concentrations used. As mentioned before, the mechanism of adsorption of glycine into montmorillonite is concentration dependent. At an initial concentration of 1.5 × 10⁻⁴ mol⋅l⁻¹ and pH below 7, the mechanism of sorption of glycine in montmorillonite is probably due to the electrostatic interaction between the positively charged montmorillonite edges and the COO⁻ group of the zwitterion (Ramos et al., 2011; Ramos and Huertas, 2013). This can also happen in the Mt–Ala system since the pK values are similar to the values for glycine. We studied the sorption at lower and higher concentrations of alanine (1.5 × 10⁻⁴ mol⋅l⁻¹). Thus, the Mt–Ala isotherm obtained includes both the electrostatic interaction and the cation exchange mechanisms. We propose that isotherm does not fit well to the models because in the range of concentrations studied the two mechanisms are present (Fig. 6).

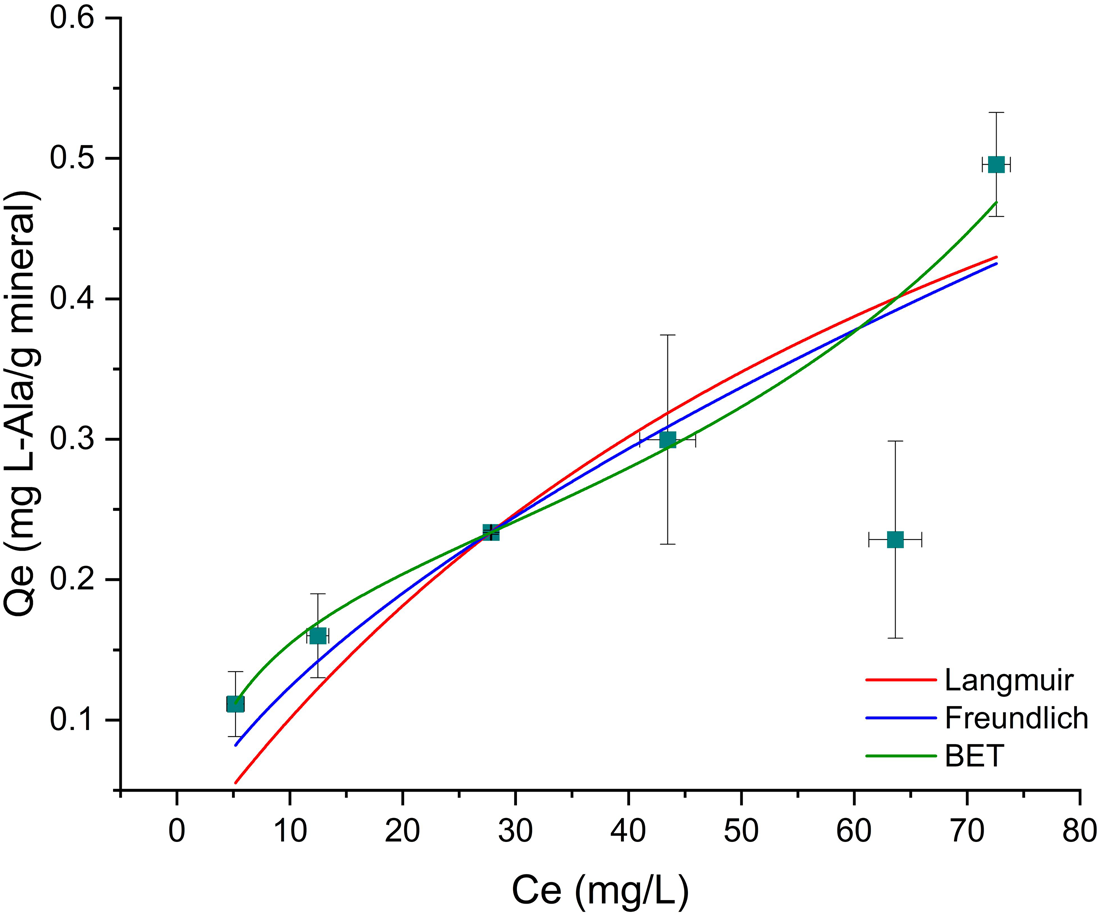
Figure 6. Isotherm models for l-Ala sorption onto montmorillonite. The data do not fit to any model.

Powder XRD

The powder XRD diffractogram of the pristine Mt samples showed the little presence of quartz and a clear d(001) spacing of 11.99 Å. The Mt–Ala sample showed a d(001) spacing of 13.17 Å (Fig. 7). This increase of interlayer space indicates that the alanine is intercalated in this interlayer of Mt.

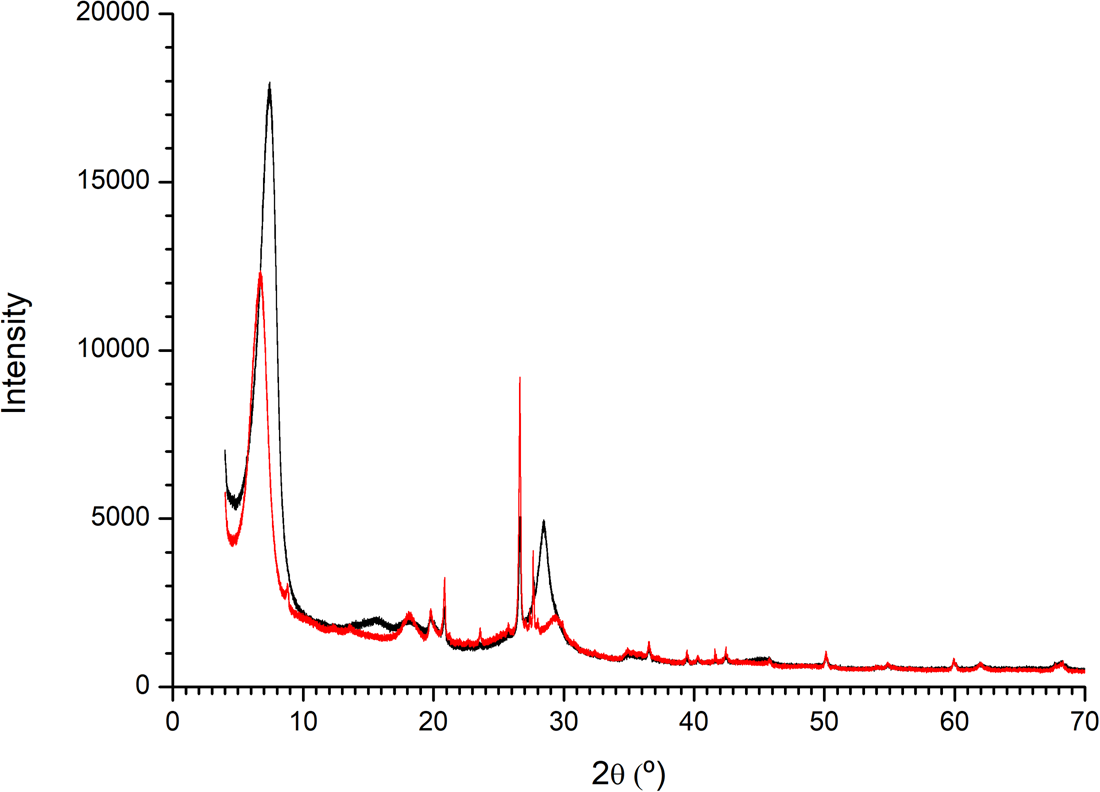
Figure 7. XRD diffractogram of montmorillonite and montmorillonite–l-Ala samples. There is an increase in the interlayer space of the clay when the amino acid is sorbed.

Thermogravimetric analysis

TGA of the pristine Mt showed a weight loss of 12% at 30–200°C corresponding to the water content and another weight loss at 600–720°C corresponding to the dihydroxylation process of clay mineral. A similar profile was observed in the Mt–Ala material with a water loss of 5.8% (Fig. 8).

Figure 8. TGA of montmorillonite (Mt) and Mt–Ala samples. For Mt two weight losses were observed, the first one at 30–200°C (water content), and the second at 600–720°C (dihydroxylation process). In the case of Mt–Ala material both losses were also observed at different intensities.

Molecular modelling

The alanine (Ala) molecule maintains the zwitterionic form in the hydrated box, where the Monte Carlo packing procedure needed 30 water molecules for reaching a density of 1 g cm⁻³ in a periodical cubic box of 10 × 10 × 10 Å³. After the optimization with QE, the ammonium group forms hydrogen bonds with the water O atoms, d(NH…OH) = 1.70–1.97 Å. The carboxylate O atoms form hydrogen bonds with the surrounding water H atoms, d(CO…HO) = 1.69–1.82 Å (Fig. 9(a)).

Figure 9. Optimized structures of the hydration box of Ala (a), AlaNa (b) and AlaH_Cl (c). The C, Na, Cl, N, O and H atoms are in grey, purple, green, blue, red and clear-grey colours, respectively.

The hydration cell of AlaNa needed a cubic periodical box of 13 × 13 × 13 Å³ with 69 water molecules. The optimized structure with QE shows hydrogen bonds between amino N atom and water H atom, d(CN…HO) = 1.68 Å, between the amino H atoms and the water O atoms d(NH…OH) = 2.27 Å and between the carboxylate O atoms and the water H atoms, d(CO…HO) = 1.67–1.83 Å. The Na⁺ cation is coordinated with water O atoms, d(Na…OH) = 2.40–2.62 Å (Fig. 9(b)). On the other hand, the hydrated salt of chlorhydrate of alanine (AlaH_Cl) needed 71 water molecules in a periodical cubic box of 13 × 13 × 13 Å³. This structure optimized by QE shows hydrogen bonds between the carboxylic H atom and the water O atom, d(COH…OH) = 1.55–2.04 Å, and between the ammonium H atoms and the water O atoms, d(NH…OH) = 1.69 Å (Fig. 9(c)).

The optimized crystal structure of the supercell 2 × 1 × 1 of Mt with four water molecules per 2 × 1 × 1 supercell (a = 10.42 Å, b = 9.05 Å, c = 11.97 Å, α = 85.7°, ® = 91.8°, © = 89.9°, d(001) = 11.96 Å) is consistent with experimental values, d(001) spacing = 11.99 Å.

All forms of alanine (Ala, AlaNa and AlaH_Cl) were initially placed in the centre of the interlayer space of Mt. The fully optimized adsorption complex of the neutral zwitterionic form (Ala) showed that the amino acid reminds in the centre of the interlayer confined space of Mt (Fig. 10(a)). The carboxylate group is coordinating the Na⁺ cation and the water molecules are connected by hydrogen bonds. The crystallographic cell parameters are also consistent with experimental values (a = 10.39 Å, b = 9.03 Å, c = 12.72 Å, α = 88.7°, ® = 92.1°, © = 89.9°). The d(001) spacing of this adsorption complex with four water molecules per supercell was 12.71 Å, being smaller than our experimental value (13.17 Å). This difference can be attributed to a different content of water. An additional Mt–Ala model with a higher amount of water, six water molecules per 2 × 1 × 1 supercell of Mt was generated and optimized obtaining a similar structure with d(001) = 12.92 Å, approaching to our experimental value. The optimized structure of AlaNa intercalated in Mt, corresponding to the adsorption at high pH medium, showed that AlaNa remained in the centre on interlayer space with similar distances with both mineral surfaces (Fig. 10(c)). The Na⁺ cation from Mt is coordinated by water molecules and the amino H atom, whereas the Na⁺ cation from AlaNa remains coordinates with the carboxylic O atoms. The crystal structure was similar with a d(001) spacing of 12.61 Å. In the optimized model of AlaH intercalated into Mt, corresponding to the adsorption at low pH medium, the adsorption process was by cation exchange where a Na⁺ cation is exchanged by the alanyl ammonium one. The amino acid molecule remained also in the centre of interlayer and the d(001) spacing was 12.72 Å. In all cases of adsorption complexes, the d(001) spacings were close to the experimental values confirming the formation of a monolayer of amino acid in the interlayer of Mt observed in our experimental kinetics studies. The main interatomic interactions have been highlighted by dotted lines in Figs. 9 and 10. These interactions are mainly hydrogen bonds in the confined interlayer space and coordination bonds with Na cations. Hence, unlike olivine case, the adsorption mechanism in montmorillonite is not purely electrostatic but cation exchange stabilized by hydrogen bonds in the confined interlayer space and surface electrostatic interactions.

Figure 10. Optimized crystal structures of the adsorption complexes of Mt with Ala (a, b), with AlaNa (c, d) and with AlaHCl (e, f). Views from the (100) plane (a, c, e) and from (001) plane (b, d, f). The Si, Al, Mg, C, Na, N, O and H atoms are in yellow, pink, green, grey, purple, blue, red and clear-grey colours, respectively.

The adsorption energy was calculated from the energy balance of the components of each reaction and three scenarios were considered:

1. (i) Neutral adsorption in non-aqueous media:

   $${\rm Mt} + {\rm Ala} = {\rm Mt}-{\rm Ala}$$

where the adsorption energy will be: E _ads = E _Mt−Ala − E _Mt − E _Ala

1. (a) Neutral adsorption in aqueous media:

   $${\rm Mt} + {\rm Alaw} = {\rm Mt}-{\rm Ala} + {\rm w}$$

where the adsorption energy is: E _ads = E _Mt−Ala + E _w − E _Mt − E _Alaw.

E _Mt−Ala being the energy of the adsorption complex of the amino acid form intercalated into Mt; E _w the energy of the periodical box of water molecules; E _Mt the energy of Mt and E _Alaw the energy of the periodical box of amino acids form with the same number of water molecules.

1. (a) Cation exchange adsorption:

   $${\rm MtNa} + {\rm AlaHClw} = {\rm Mt}-{\rm Ala} + {\rm NaClw}$$

where the adsorption energy is: E _ads = E _Mt−Ala + E _NaClw − E _MtNa − E _AlaHClw.

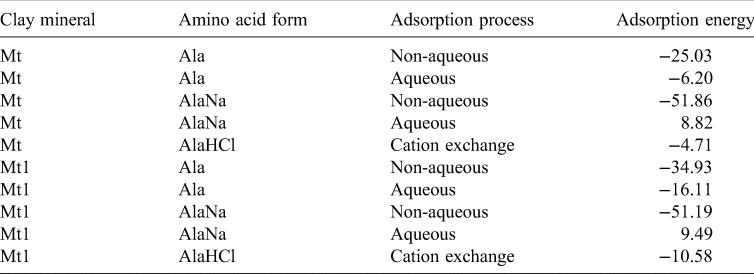
For this last reaction a periodical cubic box of NaCl was created and optimized with the same water molecules that the hydrated protonated form of alanine, AlaHCl. All adsorption processes were energetically favourable, except for AlaNa under aqueous conditions. The same results were obtained with the Mt1 model with a higher interlayer charge (Table 3).

Table 3. Adsorption energies (in kcal mol⁻¹) of the intercalation processes

Relevance on astrobiology

Bernal (1949) first proposed that organics can be trapped and protected within a clay mineral matrix. In general, our experiments show that l-Ala is more extensively sorbed on montmorillonite than on olivine at different pH values. However, we also noticed the amino acid sorption onto olivine, even at lower percentages. This reinforces the idea of the main role of minerals in chemical evolution processes, not only clays but also other minerals. We determined that the sorption of the amino acids on the minerals occurs at different rates: on montmorillonite it is fast (~1 h), while on olivine it takes almost 24 h, and this could be related to the nature of the organics, but mainly to the adsorption surface. Clays behave as extraordinary sorbents for organic molecules, but the effect of other minerals cannot be neglected.

Minerals are ubiquitous now, and undoubtedly, they were present in places where chemical evolution occurred, both on our planet and in extraterrestrial bodies. The strong association of organic molecules and hydrous clay minerals on meteorites has been demonstrated (Pearson et al., 2002; Garvie and Buseck, 2007). Probably, the ability to host clay minerals is the main reason for the abundance of organics in carbonaceous chondrites, since other aqueously generated mineral phases do not show the same behaviour (Pearson et al., 2002). The aqueous alteration process of the parent body could have trapped and concentrated the organic molecules (Ponnamperuma et al., 1982).

Carbonaceous chondrites exhibit evidence of the action of low temperature alteration on their parent bodies (Schulte and Shock, 2004; Le Guillou et al., 2014). These events, when water was present as a liquid, could have allowed the formation of clay minerals and simultaneously the sorption of organics. Even more, as some ions were present in solution, they could have induced small pH changes in the surroundings, depending on the abundance of some ions (both cations and anions) and water. Even if these events were sporadic and short length, they could have occurred enabling the selective sorption of organics under different conditions. In our study, we experimentally demonstrated that sorption is dependent of the organics, the nature of minerals and the physicochemical conditions; so more studies are needed to fully understand the dynamics of sorption and to link them to processes occurring on meteorites.

The relevance of these events for chemical evolution is huge; as organic materials could have been sorbed on minerals, they could have been protected against degradation, especially if sorption occurred on clays. In this manner, when meteorites reached the surface of a planet (e.g. the Earth), organics could endure. Molecules are found when meteoritic samples are directly analysed, since their bond to minerals, this interaction could have guaranteed their permanence. From a prebiotic point of view, this fact strongly supports the idea of the contribution of extraterrestrial material on the chemical evolution of Earth. Additionally, these processes could also have occurred on the early Earth, where minerals were conspicuous. The diversity of minerals on the prebiotic Earth surely promoted the sorption of the organics on the different minerals.

Conclusion

Several conclusions stem from our experiments. First, alanine is sorbed on both minerals (olivine and montmorillonite) through a pH-dependent process. The acidic environment favours the sorption of the molecules on minerals. Alanine binds more extensively to montmorillonite. In the clay, the main sorption mechanism is cation exchange, occurring mainly in the interlamellar channel, and in a lesser extent at the edges of crystals. In the case of olivine, a different mechanism based on electrostatic forces on the surface is proposed. It was not possible to fully desorb all the amino acid, especially in the case of olivine-bearing experiments; this could indicate the formation of chemical bonds between surfaces and organics.

The computational modelling methodology used in this study is consistent with the experimental results. The main geometrical features of the calculated models of alanine adsorption indicate that only one layer of amino acid is adsorbed into the confined space of montmorillonite, confirming the results observed experimentally. Most of the intercalation processes into clay minerals are energetically favourable, except for the adsorption process at high pH.

More experiments are needed to understand the details of the interactions of organics with minerals; however, our results coincide with observations that strongly support the association of organics with clays on meteorites. The amino acids could have been protected against degradation when sorbed or immobilized, allowing the concentration or complexation of organic molecules both on terrestrial and extraterrestrial environments.

Even if there is a myriad of studies in this regard, yet the precise sorption mechanism of amino acids onto minerals is not fully understood. Here lies the relevance of our results; they reinforce the participation of surfaces in prebiotic chemistry and add to the comprehension of the process. One must be careful in the extrapolation of the behaviour of amino acids in presence of minerals, since it is a contingent event, as it depends on many variables.