No CrossRef data available.
Article contents
ON THE SHORTEST DISTANCE FUNCTION IN CONTINUED FRACTIONS
Published online by Cambridge University Press: 23 June 2023
Abstract
Let 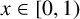 $x\in [0,1)$ be an irrational number and let
$x\in [0,1)$ be an irrational number and let 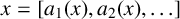 $x=[a_{1}(x),a_{2}(x),\ldots ]$ be its continued fraction expansion with partial quotients
$x=[a_{1}(x),a_{2}(x),\ldots ]$ be its continued fraction expansion with partial quotients 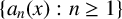 $\{a_{n}(x): n\geq 1\}$. Given a natural number m and a vector
$\{a_{n}(x): n\geq 1\}$. Given a natural number m and a vector 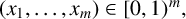 $(x_{1},\ldots ,x_{m})\in [0,1)^{m},$ we derive the asymptotic behaviour of the shortest distance function
$(x_{1},\ldots ,x_{m})\in [0,1)^{m},$ we derive the asymptotic behaviour of the shortest distance function 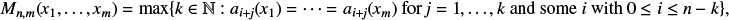 $$ \begin{align*} M_{n,m}(x_{1},\ldots,x_{m})=\max\{k\in \mathbb{N}: a_{i+j}(x_{1})=\cdots= a_{i+j}(x_{m}) \ \text{for}~ j=1,\ldots,k \mbox{ and some } i \mbox{ with } 0\leq i \leq n-k\}, \end{align*} $$
$$ \begin{align*} M_{n,m}(x_{1},\ldots,x_{m})=\max\{k\in \mathbb{N}: a_{i+j}(x_{1})=\cdots= a_{i+j}(x_{m}) \ \text{for}~ j=1,\ldots,k \mbox{ and some } i \mbox{ with } 0\leq i \leq n-k\}, \end{align*} $$
which represents the run-length of the longest block of the same symbol among the first n partial quotients of  $(x_{1},\ldots ,x_{m}).$ We also calculate the Hausdorff dimension of the level sets and exceptional sets arising from the shortest distance function.
$(x_{1},\ldots ,x_{m}).$ We also calculate the Hausdorff dimension of the level sets and exceptional sets arising from the shortest distance function.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
This work is supported by National Natural Science Foundation of China (NSFC), No. 12201476.



