Introduction
The perspective that I am proposing in this book is firmly anchored in the so-called Complex (Adaptive) Systems (CAS) approach that has been developed over the last forty or so years, in both Europe and the USA. It is the approach that the multidisciplinary ARCHAEOMEDES team experimented with under my direction in the 1990s, looking at a wide range of sustainability issues in all the countries of the Northern Mediterranean rim (van der Leeuw Reference van der Leeuw1998b). In this chapter, I am heavily drawing on that real-life and real-world experiment, which was the first in the world.
Systems Science
In order to understand the approach and the context in which the CAS approach has emerged and is being used, I need to go back a little bit in the history of science, to the development of noncomplex systems science around World War II and its immediate aftermath. One cannot point to a single person to whom the basic ideas of systems science go back – some argue for predecessors as early as pre-Socratic Greece and Heraclitus of Ephesus (c. 535–c. 475 BCE). Clearly there were major scientists whose ideas were moving in this direction from as early as the seventeenth century: Leibnitz (1646–1716), Joule (1818–1889), Clausius (1822–1888), and Gibbs (1839–1903) among them.
For our current purposes, two names are forever associated with this approach, Norbert Wiener and Ludwig von Bertalanffy. The applied mathematician Wiener published his Cybernetics or Control and Communication in the Animal and the Machine in 1948, while the biologist von Bertalanffy launched his General Systems Theory in 1946, and brought it all together in General System Theory: Foundations, Development, Applications in 1968. But a substantive number of others were major contributors, among them Niklas Luhmann (Reference Luhmann1989), Gregory Bateson (Reference Bateson1972, Reference Bateson1979), W. Ross Ashby (Reference Ashby1956), C. West Churchman (Reference Churchman1968), Humberto Maturana (Reference Maturana and Varela1979 with F. Varela), Herbert Simon (Reference Simon1969), and John von Neumann (Reference Von Neumann and Burks1966). The approach rapidly spread across many disciplines, including engineering, physics, biology, and psychology. Early pioneers to apply it to sustainability issues are Gilberto Gallopin (Reference Gallopin1980, Reference Gallopin1994) and Hartmut Bossel (Bossel et al. Reference Bossel, Klaczko and Müller1976; Bossel Reference Bossel1986).
Systems science shifted the emphasis from the study of parts of a whole, on which mechanistic science had been founded in the Enlightenment, to studying the organization of the ways in which these parts interact, recognizing that the interactions of the parts are not static and constant (structural) but dynamic. The introduction of systems science, in that respect, is a first step away from the very fragmented scientific landscape that developed after the university reform movement of the 1850s. Some of the scientists involved, such as von Bertalanffy (Reference Von Bertalanffy1949) and Miller (Reference Miller1995) went as far as to aim for a universal approach to understanding systems in many disciplines.
An example of the importance of systems thinking in the social sciences is presented in Chapter 5, mapping system state transitions in the Mexican agricultural system under the impact of growing urban populations in North America. Such thinking focuses on the organization that links various active elements that impact on each other. They are linked through feedback loops that can either be negative (damping oscillations so that the system remains more or less in equilibrium) or positive (enhancing the amplitude and frequency of oscillations). In the earlier phases of the development of systems thinking the focus was on systems in equilibrium (so-called homeostatic systems, such as those keeping the temperature in a room stable by means of a thermostat) and thus on negative (stabilizing) feedback loops. However, from the 1960s the importance of morphogenetic systems (in which feedbacks amplify and therefore lead to changes in the system’s dynamic structure) was increasingly recognized (e.g., Maruyama Reference Maruyama1963, Reference Maruyama1977). Such positive feedbacks are involved in all living systems. This shift in perspective also implied that systems needed to be seen as open rather than closed because to change and grow systems need to draw upon resources from the outside, specifically energy, matter, and information. Positive feedbacks in open systems are responsible for their growth and adaptation, but can also lead to their decay. If living systems were only composed of positive feedback loops, they would quickly get out of control. Real-life systems therefore always combine both positive and negative feedback loops.
Complex Systems
The introduction of positive feedbacks and morphogenetic systems clearly prefigured the emergence of the wider Complex Systems (CS) approach. This is a specific development of General Systems Theory that originated in the late 1970s and early 1980s both in the USA (Gell-Mann Reference Gell-Mann1995; Cowan Reference Cowan2010); Holland (Reference Holland1995, Reference Holland1998, Reference Holland2014; Arthur Reference Arthur, Durlauf and Lane1997; Anderson Reference Anderson, Arrow and Pines1988, with Arrow and Pines), and in Europe (Morin Reference Morin1977–2004; Prigogine Reference Prigogine and Nicolis1980; Prigogine & Stengers Reference Prigogine and Stengers1984; Nicolis & Prigogine Reference Nederveen Pieterse1989). It is focused on explaining emergence and novelty in highly complex systems, such as those that create what we called “wicked” problems in Chapter 2. It has many characteristics of an ex-ante approach. Moreover, it is not reductionist, viewing systems as (complex) open ones, subject to ontological uncertainty (the impossibility to predict outcomes of system dynamics, cf. Lane et al. Reference Lane and Maxfield2005). It moves us “from being to becoming” (Prigogine Reference Prigogine and Nicolis1980), emphasizing the importance of processes, dynamics, and historical trajectories in explaining observed situations, and the very high dimensionality of most processes and phenomena.
When focused, as in this book, on integrated socioenvironmental systems and sustainability, the CS approach is focused on the mutual adaptive interactions between societies and their environments, and thus we speak of Complex Adaptive Systems (CAS). It emphasizes the importance of a transdisciplinary science that encompasses both natural and societal phenomena, fusing different disciplinary approaches into a single holistic one. It also shifts our emphasis away from defining entities and phenomena toward an approach that includes looking at the importance of contexts and relationships. This chapter will first briefly outline the most important differences between the Newtonian (classic) scientific approach and the CAS approach by means of examples drawn from different spheres of life. Then it will show, in the form of an example, how such an approach can change our perspective.
The Flow Is the Structure
The basic change in perspective involved is presented by Prigogine (Reference Prigogine and Nicolis1980) as moving from considering the flow that emerges when one pulls the plug out of a basin full of water as a disturbance (and the full basin as the stable system) to considering the flow as the (temporary, dynamic) structure and the full basin as the random movement of particles. He illustrates this by referring to the emergence of Rayleigh-Bénard convection cells when one heats a pan of oil or water.
As soon as a potential (in this case of temperature) is applied across the fluid, particles start moving back and forth across that potential (in this case the heat potential between the heated pan and the cooler air above it), that moves the hot particles in the liquid from the bottom of the dish to the top in the center of each cell, and the cooler cells back from the top to the bottom at its edges. That causes a structuring of their movement into individual, tightly packed cells. The flow of the particles transforms random movement into structured movement.
But the important lesson to retain from this example is the simple change in perspective on what is a structure and what is not, from which it follows that flows are dynamic structures (rather than static ones) generated by potentials. Irreversible direction (and thus change) therefore becomes the focus, rather than undirectedness or reversibility (Prigogine Reference Prigogine1977; Prigogine & Nicolis Reference Prigogine and Nicolis1980). Along with the perspective, the questions asked change as well, as do the kinds of data collected, and indeed the kind of phenomena that arouse interest. We will see in Chapter 9 that if we transpose Prigogine’s idea of dissipative flows (flows that dissipate randomness or entropy) into the domain of socioenvironmental systems, the idea of “dissipative flow structures” (as Prigogine calls them) provides us with a very powerful tool to develop a unified perspective on human societal institutions. For example, the banking system consists of a set of institutions and rules around the flow of wealth, from poor to rich and vice versa. Large migrations as we see today in Europe are flow structures triggered by a huge differential in ease of life between war-torn/poor, and peaceful/wealthy places.
Structural Transformation
As we see in Chapter 5, the problem of understanding the long-term behavior of (natural and societal) systems that undergo state changes is inextricably bound up with questions of origins and emergence (van der Leeuw Reference van der Leeuw, Fiches and van der Leeuw1990), which we might more generally and neutrally subsume under the heading of structural transformation.
The central issue in any discussion of complex dynamics concerns the problem of emergence, rather than existence (Prigogine Reference Prigogine and Nicolis1980). Understanding the structural development of emergent phenomena is not only the key to a better characterization of complexity, but to an understanding of the relationship between order and disorder. While these are easily defined and distinguished in physical systems, for example, this is much less obvious for societies. What is an ordered or an un- or disordered society? The same is true for the concept of equilibrium. Again, in physical systems one can observe the state of equilibrium (non-change) relatively easily, but in societal systems this is more difficult. Among other things it depends on the scale of observation.
How do such dynamic systems emerge? It is a characteristic phenomenon of complex systems that they are considered self-organizing, owing to the interactions between entities in the system. In societal systems, individuals interact in many different ways, and the result of those interactions is the (dynamic) structure of the society, which can be observed as a pattern (see Figure 7.1). That pattern, in turn, impacts upon the interacting individuals or other entities. To a large extent, these processes are also the ones that are implicated in the construction and evolution of the spatial inhomogeneity that we recognize in landscapes.
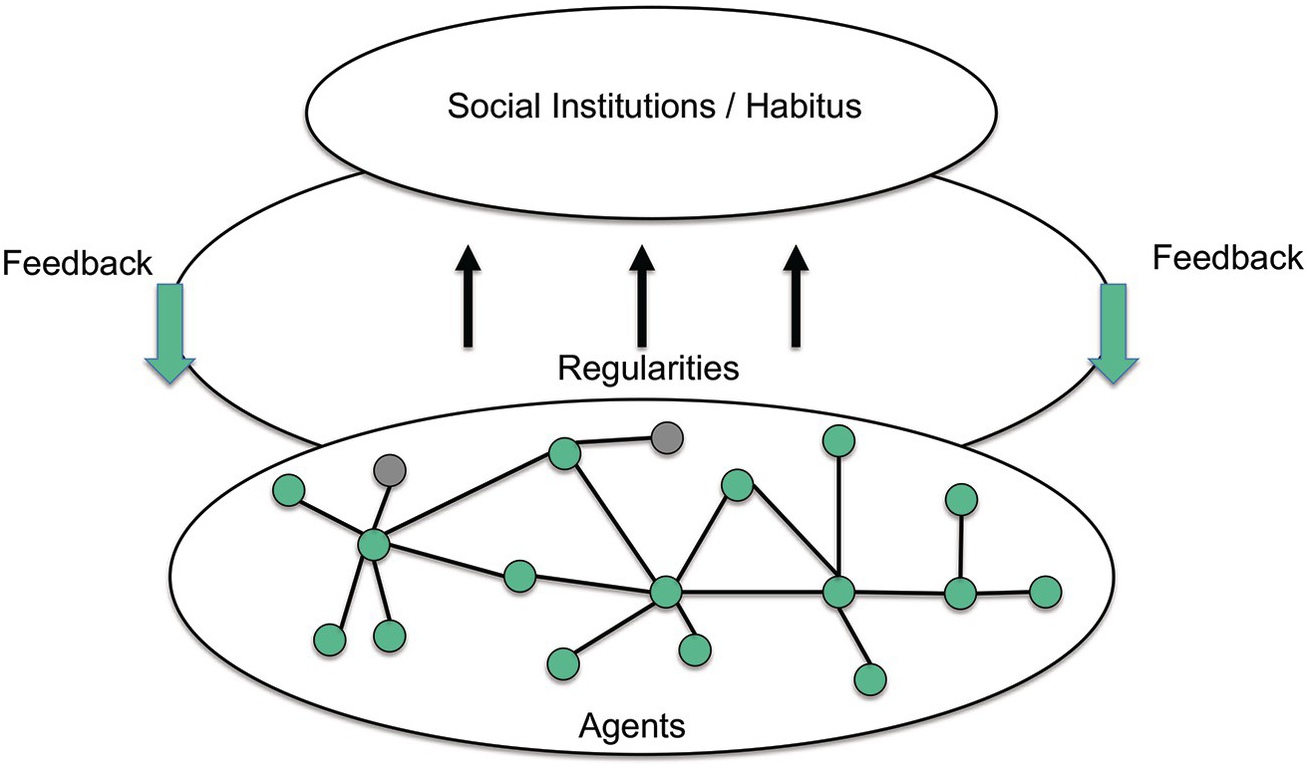
Figure 7.1: Interactions between individual entities at the lower level create patterns observable at the higher level which, in turn, impact on the interactions between individual entities.
The most important part of the realignment I propose by applying CAS is to actively supplant evolutionary ideas of progressive and incremental unfolding in favor of models that recognize the nonlinear dynamical aspects of structures, and thus underline the importance of instability and discontinuity in the process of societal transformation and -evolution. In that context, I also need to point to another essential concept that has played a major role in the development of this approach: the concept of phase transitions. The reader will encounter this concept extensively in the third part of this book. It is the idea that the underlying dynamics of a self-organizing system can reach a state in which they will change their behavior fundamentally. The conditions under which this happens may be predictable, but the result of the changes is not, and different states of the restructured system may emerge. For example, the temperature and humidity under which snowflakes appear are entirely predictable, but the geometric features of the flakes themselves are nevertheless entirely unpredictable. These are phase transitions that have, of course, been observed since the early history of mankind. But complex systems theorists have developed interesting and novel ways to understand such structural changes in dynamics, pointing out that zones of predictability and unpredictability can coexist. In the social sciences, such phase changes are generally referred to as tipping points. (For a detailed introduction to this topic see for example Scheffer Reference Scheffer2009.)
History and Unpredictability
A fundamental characteristic of the CAS approach to emergence is the fact that it emphasizes both history and unpredictability. By considering observed patterns at a macro-level as the result of interactions between independent entities at a level below, at once the relationships between these entities are of fundamental importance to explain the patterns observed, and because the entities are independent it is impossible to predict their collective behavior, so that in the case of complex adaptive systems the pattern observed is also unpredictable.
A good case in point is the major traffic jam that prevents one from getting to the airport that I mentioned in Chapter 2. All the drivers who are part of it have their own reasons for driving and their own planned trajectories. As their paths cross and intersect, there are points where their movements impact on each other to the point of immobilizing them. Situations like this cannot be explained a posteriori. The only way to understand them is by identifying and studying the history of the dynamics involved at the level of the individual participants. Helbing very successfully applied this approach to pedestrian traffic problems and has now been extending it to more general societal challenges (e.g., 2015, 2016).
The closest well-known theoretical position in the social sciences is that of Bourdieu (Reference Bourdieu1977) and Giddens (Reference Giddens1979, Reference Giddens1984), who emphasize the relationship between individual behavior and collective behavior patterns (habitus to use their term) that are anchored in a society through customs and beliefs. To understand a group’s habitus one needs to go back in time and identify the dynamics that were responsible for originating the habitus’s different components.
Because the complex systems approach is ex-ante in its study of the emergence of phenomena, it describes such phenomena in terms of possibilities and (at best) probabilities, in effect pointing to multiple futures and options. It can therefore not predict with any certainty as is done when a (reductionist) cause-and-effect chain is assumed. At best it can, under certain circumstances, point to places in a system’s trajectory when one change or another is probable.
Underlying this change in perspective is the following reflection. Any attempt to deal with the morphogenetic properties of dynamic systems must acknowledge the important role played by unforeseen events and the fact that actions often combine to produce phenomena we might define as the spontaneous structuring of order. The observation that apparently spontaneous spatiotemporal patterning can occur in systems far from equilibrium, first made by Rashevsky (Reference Rashevsky1940) and Turing (Reference Turing1952), was then developed by Prigogine and coworkers. These have coined the term “order through fluctuation” to describe the process (e.g., Nicolis & Prigogine Reference Nicolis and Prigogine1977).
The fundamental point is that non-equilibrium behavior – an intrinsic property of many systems, both natural and social – can act as a source of self-organization, and hence may be the driving force behind qualitative restructuring (state change) as the system evolves from one state to another. This assumes that dynamic structures rely on the action of fluctuations that are damped below a critical threshold and have little effect on the system, but can become amplified beyond this threshold and generate a new macroscopic order (Prigogine Reference Prigogine and Nicolis1980). Evolution thus occurs as a series of phase transitions between disordered and ordered states; as successive bifurcations generating new ordered structures (Figure 7.2). An interesting example of this is the logistic map developed to look at the dynamics between population reproduction (where the current population is small) and population starvation (where the growth will decrease at a rate proportional to the value obtained by taking the theoretical “carrying capacity” of the environment less the current population).
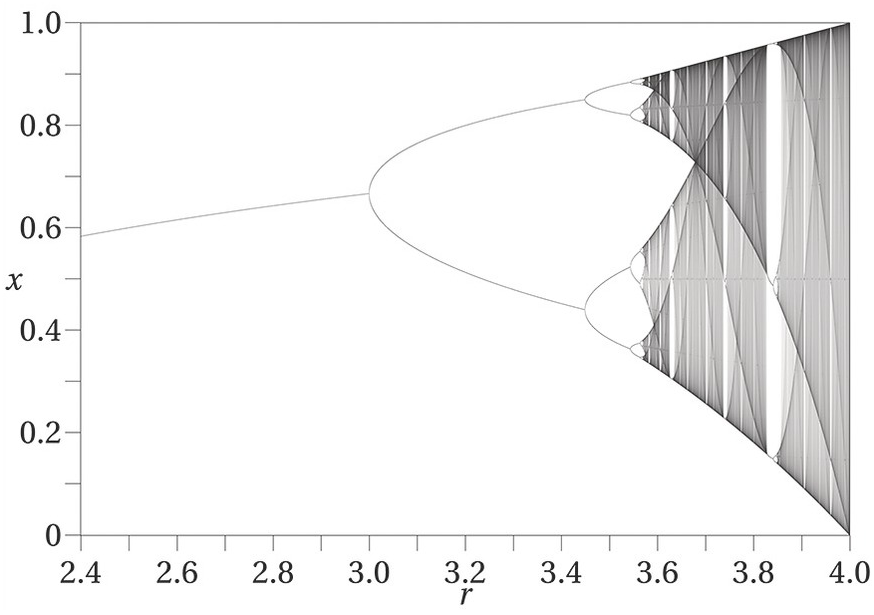
Figure 7.2 Bifurcation diagram of a logistic population dynamic. For a detailed explanation see https://en.wikipedia.org/wiki/Logistic_map.
In this perspective, instability, far from being an aberration within stable systems, becomes fundamental to the production of resilience in complex systems.1 The long-term evolution of structure can be seen as a history of discontinuity in geographical (or other kinds of) space; i.e., history not as a finely spun homogeneous fabric, but as being punctuated by a sequence of phase changes resulting from both intentional and unintentional actions, such as have been postulated for biological evolution by Gould and Eldredge (1972). Such discontinuities are in fact thresholds of change (“tipping points” in more recent popular parlance), where the role of agency and/or idiosyncratic behaviors assumes paramount significance in the production and reproduction of structures.
Chaotic Dynamics and Emergent Behavior
For biological, ecological, and, by implication, societal systems, the discovery of self-induced complex dynamics is of profound importance, since we can now identify a powerful source of emergent behavior. Far from promoting any pathological trait, aperiodic oscillations resident in chaotic dynamics perform a significant operational role in the evolution of the system, principally by increasing the degrees of freedom within which it operates. This is another way of saying that chaos promotes flexibility, which in turn promotes diversity.
In turn, this throws light on some of the problems inherent in the concept of adaptation, a difficult concept in the study of evolution. Briefly put, since the existence of chaos severely calls into question concepts such as density-dependent growth in (human and) biological populations, we might be able to see a theoretical solution in the coexistence of multiple attractors (see below) defining a flexible domain of adaptation, rather than any single state. We thus arrive at a paradox where chaos and change become responsible for enhancing the robustness or the resilience of the system.
From a philosophical perspective, it might be said that the first thing that a nonlinear, dynamic, or complex systems perspective does is to effectively destroy historical causation as a linear, progressive, unfolding of events. It forces us to reconceptualize history as a series of contingent structurations that are the outcome of an interplay between deterministic and stochastic processes (see Monod 2014). The manifest equilibrium tendencies of linear systems concepts also stand in contrast to their nonlinear counterparts by virtue of the fact that nonlinear systems possess the ability to generate emergent behavior and have the potential for multiple domains of stability that may appear to be qualitatively different.
Nonlinear systems can thus be described as occupying a state space or possibility space within which multiple domains of attraction exist. For societal systems, this is a consequence of the fact that they are governed by positive feedback or self-reinforcing processes, and that they are coupled to environmental forces that are either stochastic or periodically driven.
Diversity and Self-Reinforcing Mechanisms
Clearly, the conditions around which systemic configurations become unstable and subsequently reorganize or change course have no inherent predictability; the diversity that characterizes all living behavior guarantees this. It is this diversity that is critically important from an evolutionary perspective because it accounts for the systems’ “evolutionary drive” (Allen & McGlade Reference Allen and McGlade1987b, 726). The existence of idiosyncratic and stochastic risk-taking behaviors acts to maintain a degree of evolutionary slack within systems; error-making strategies are thus crucially important (Allen & McGlade Reference Allen and McGlade1987a). In fact, without the operation of such non-optimal and unstable behaviors, we effectively reduce the degrees of freedom in the system and hence severely constrain its creative potential for evolutionary transformation.
One of the enduring issues isolated by the above methods is the importance of positive feedback or “self-reinforcing mechanisms,” as Arthur (Reference Arthur, Anderson, Arrow and Pines1988, 10) has characterized them. Processes such as reproduction, co-operation, and competition at the interface of individual and community levels can, under specific conditions of enhancement, generate unstable and potentially transformative behavior. Instability is seen as a product of self-reinforcing dynamic structures operating within sets of relationships and at higher aggregate levels of community organization. This is clearly the case in a range of phenomena, from population dynamics to the complex exchange and redistribution processes such as occur in most food and trade webs. Of crucial importance to an understanding of these issues is the fact that networks of relationships are prone to collapse or transformation, independent of the application of any external force, process, or information. Instability is an intrinsic part of the internal dynamic of the system.
Focus on Relations and Networks
The relational aspect of the complex systems approach is another major innovation in its own right. Much of our western thinking is in essence categorization – or entity – based. In a fascinating essay, “Tlön, Uqbar, Orbis Tertius,” Borges (Reference Borges1944) evokes how nouns and entities (things) are essential to much of western thinking by arguing that in a world where there are no nouns – or where nouns are composites of other parts of speech, created and discarded according to a whim – and (thus) no things, most of western philosophy becomes impossible. Without nouns about which to state propositions, there can be no a priori deductive reasoning from first principles. Without history, there can be no teleology. If there can be no such thing as observing the same object at different times, there is no possibility of a posteriori inductive reasoning (generalizing from experience). Ontology – the philosophy of what it means to be – is then an alien concept. Such a worldview requires denying most of what would normally be considered common sense reality in western society.
Accepting that entities are essential to much of our western intellectual tradition raises a question about verbs. A language without verbs cannot define, study, or even conceive of relationships, whether between entities, different moments in time, or different locations in space. Verbs, and relationships, are essential to conceive of process, interaction, growth, and decay. In moving from being to becoming, emphasizing that structures are dynamic, the complex systems approach brings these two perspectives together, highlighting the need in our science, as in our society, to think and express ourselves in terms of both entities and relationships.
This in turn has triggered one of the major innovations of the complex systems approach: the conception of processes as occurring in networks that link participating entities. Currently one of the cutting edges of the complex systems approach, popularized by Watts (Reference Watts2003), this is an important innovation in many domains of social science research, with a certain emphasis on mapping the links (edges in network parlance) that link entities (called nodes in network science), and drawing up hypotheses about the ways in which the structure of the links impacts the processes driven by the participant entities (Hu et al. Reference Hu, Shi, Ming, Tao, Leeson, van der Leeuw, Renn and Jaeger2017). These networks can often be decomposed in clusters with more or less frequent interactions, thus allowing us to view the dynamics of interaction as occurring in a hierarchy of such clusters.
Whereas it is acknowledged in the natural and life sciences that the organization of complex systems in such clusters is a major factor in determining their trajectories, this is much less generally accepted in some of the social sciences, where the idea persists that looking at individuals and at the whole population (by means of statistical tools) is sufficient. Lane et al. (Reference Lane, Maxfield, Read, van der Leeuw, Lane, Pumain, van der Leeuw and West2009) argue for adopting an organization perspective in the social sciences, as identification of different levels of organization seems especially relevant because societies are composed of many different network levels between individuals and their societies. At each such level, the networked participants differ, and so do their ideas, concepts, and language.
Deterministic Chaos
The complexity of dynamical systems is in large part a consequence of the existence of multiple modes of operation. Much of the inherent instability in, e.g., exchange systems, reflects the dominance of highly nonlinear interactions. It is the role of such nonlinearities that has led to observations on the emergence of erratic, aperiodic fluctuations in the behavior of biological populations (May & Oster Reference May and Oster1976) and in the spread of epidemics (Schaffer & Kot Reference Schaffer and Kot1985a, Reference Schaffer and Kotb). These highly irregular fluctuations (often dismissed as environmental “noise”) are manifestations of deterministic chaos. The important contribution of this work (Lorenz Reference Lorenz1963; Li & Yorke Reference Li and Yorke1975) is that it demonstrates that chaotic behavior is a property of systems unperturbed by extraneous noise. As a result of subsequent observations in the physical, chemical, and biological sciences, we now assume that the seeds of aperiodic, chaotic trajectories are embedded in all self-replicating systems. The systems involved have no inherent equilibrium but are characterized by the existence of multiple equilibria and sets of coexisting attractors to which the system is drawn and between which it may oscillate.
Another important characteristic displayed by all chaotic systems, whether social, biological, or physical, is that, given any observational point, it is impossible to make accurate long term predictions (in the conventional scientific sense) of their behavior. This property has come to be known as “sensitivity to initial conditions” (Ruelle Reference Ruelle1979, 408), and simply means that nearby trajectories will diverge, on average exponentially. In popular language, this is known as the “butterfly effect” – the idea that the flapping of the wings of a butterfly somewhere in the world may engender major changes elsewhere. Or, in terms of the well-known science fiction writer Ray Bradbury (Reference Bradbury1952), that someone treading on a piece of grass in the distant past may have an impact on a presidential election of today …
Attractors
The evolution of a dynamical system is acted out in so-called phase space. Imagine the simple example of the motion of a pendulum (Figure 7.3a and b). If it is allowed to move back and forth from some initial starting condition, we can describe its state by recourse to speed and position. From whatever starting values of position and velocity, it returns to its initial vertical state, damped by gravity, air resistance, and other forms of energy dissipation. The phase-space in which the pendulum dynamics are acted out is defined by a set of coordinates, displacement, and velocity. All motions converge asymptotically toward an equilibrium state referred to as a point attractor, since it “attracts” all trajectories in the phase space to one position. Moreover, the system’s long-term predictability is guaranteed.

Figure 7.3 Different kinds of attractor. For explanation see text.
A second type of attractor common in dynamical systems is a limit cycle. The representation of this in phase space indicates periodic cyclical motion (Figure 7.3c), and like the point attractor it is stable and guarantees long-term predictability.
But, unlike the point attractor, the periodic motion is not damped to the point that the system eventually moves to a single, motionless, state. Instead, it continues to cycle.
A third form of attractor is known as a torus; it resembles the surface of a doughnut (Figure 7.3d). Systems governed by a torus are quasi-periodic, i.e., a periodic motion is modulated by another operating on a different frequency. This combination produces a time series whose structure is not clear, and under certain circumstances can be mistaken for chaos, notwithstanding the fact that the torus is ultimately governed by wholly predictable dynamics. An important facet of toroidal attractors is that although they are not especially common, quasi-periodic motion is often observed during the transition from one typical type of motion to another. As Stewart (Reference Stewart1989, 105) points out, toroidal attractors can provide a useful point of departure for analyses of more complex aperiodicities such as chaos.
There are many other ways in which various combinations of periodicities may describe a system’s behavior, but the most complex attractor of all is the so-called strange or chaotic attractor (Figure 7.3e). This is characterized by motion that is neither periodic nor quasi-periodic, but completely aperiodic, such that prediction of the long-term behavior of its time evolution is impossible. Nonetheless, over long time periods regularities may emerge, which give the attractor a degree of global stability, even though at a local level it is completely unstable. An additional feature of chaotic attractors is that they are characterized by noninteger or fractal dimensions (Farmer et al. Reference Farmer, Ott and Yorke1983). Each of the lines in the phase space trajectory, when greatly magnified, is seen to be composed of additional lines that themselves are structured in like manner. This infinite structure is characteristic of fractal geometries such as Mandelbrot sets (Mandelbrot Reference Mandelbrot1982).
As a final observation in this classification of dynamical systems and attracting sets, we should note that beyond the complexity of low-dimensional strange attractors we encounter the full-blown chaos characterized by turbulence; indeed, to a large extent, the quintessential manifestation of chaotic behavior is to be found in turbulent flows, for example in liquids or gases. Examples of this highly erratic state are a rising column of smoke, or the eddies behind a boat or an aircraft wing.
Multi-Scalarity
The links in a complex systems network can occur at very different spatiotemporal and organizational scales, and the multi-scalarity of the complex systems perspective is one of its important characteristics. Traditionally we select only two or three of those scales (macro, meso, and/or micro) to analytically investigate the processes involved. In most cases, that will give us a rather limited and arbitrary insight in what is actually going on. Hence, dynamic modeling of the interactions between many different spatiotemporal scales has become an important tool in CAS work. In landscape ecology, for example, Allen and colleagues (Reference Allen and Starr1982, Reference Atlan1992) have developed an approach in which they sort component dynamics of a complex system based on their clock time, distinguishing different levels in a temporal hierarchy. In such a hierarchy, components with a faster clock time can react more rapidly to changing circumstances, whereas the components with a slower clock time tend to stabilize the system as a whole.
This has in the last decade and a half led to the elaboration of novel tools to understand the dynamics of complex multi-scalar systems, drawing heavily on different modeling techniques, whether defining the dynamic levels in terms of differential equations or doing so in agent-based models through the definition of the rules that the agents follow.
Occam’s Razor
Yet another important aspect of the complex systems approach is the fact that we can no longer heed the old precept that, when confronted with two different solutions, choosing the simpler of the two is best. Indeed, that “rule of parsimony” – which is also called Occam’s Razor after a medieval Franciscan friar, scholastic philosopher, and theologian (c. 1287–1347) – is one of the important building blocks of reductionist science. It leads to striving for scientific clarity by reducing the number of dimensions of a phenomenon or process, and thus ignoring seemingly irrelevant yet pertinent information. That in turn facilitates the kind of linear cause-and-effect narratives that we find increasingly counterproductive in our attempts at understanding the world around us.
The complex systems approach, on the other hand, searches for the emergence of novelty, and is thus focused on increases in the dimensionality of processes being investigated. It is the fundamental opposite of the traditional reductionist approach. Rather than assuming that phenomena are simple, or can be explained by simple assumptions, it assumes that our observations are the result of interactions between complex, multidimensional processes, and therefore need to be understood in such terms.
Some Epistemological Implications
Before we conclude this chapter, we need to devote a few words to some of the epistemological implications of the complex systems approach. One of these concerns the nature of subject–object relationships. As it is acknowledged that the “real world” cannot be known, the object with which the person investigating a problem has to cope is no longer the real world, but his/her own perception of that world. Thus, new relationships are added to those between the scientist and the objects of his or her research, notably between the researcher and his perceptions of the phenomena studied: the observer’s subjectivity is acknowledged and taken as the basis of all understanding, even if the methodology involved is a scientific one (van der Leeuw Reference van der Leeuw, Renfrew, Rowlands and Segraves1982).
This change in perspective is of crucial importance because it loosens the (implicit and often unconscious) tie between the models used and the observed real world. Implied is an alternative to the search for the (one) truth that we have so long strived for in (neo) positivist science. Rather than study the past as closely as possible in the hope that it will be able to explain everything, we need to acknowledge that studying a range of outcomes, investigating a range of causes, or building a range of models of the behavior of a system is a more valuable focus. These models may be known, whilst the phenomena can never be known, if only because the infinity of the number of their dimensions implies that all knowledge must remain incomplete. Thus, the focus is on generating multiple models that help an essentially intuitive capacity for insight to understand the phenomena studied. It brings the awareness that models are at once more and less than the reality that we strive to perceive. Although explanation and prediction may be schematically symmetrical, and are argued by some positivist philosophers of science (e.g., Salmon 1984) to be logically symmetrical as well, the fact that the one uses closed categories and the other open ones implies that they are substantively absolutely asymmetrical. As scientists, we have to acquiesce in this because it is all we will ever be able to work with. And it opens up the potential to do much more than we have hitherto thought.
Other implications concern the nature of change. I have already mentioned that in the traditional approach change does, or does not, manage to transform something preexistent into something new. Change is a transition between two stable states. In the CAS perspective developed here, change is presumed to be fundamental and never to cease (even though the rate of change may be slow). This approaches the historical ideas of Braudel (e.g., Reference Braudel1949, 1979), who saw change as fundamental and relative, occurring at different rates so that compared with the speed of short-term change, long-term change may seem to equal stability. Stability is thus a research device that does not occur in the real world. Making use of it is concomitant with using an absolute, non-experiential timescale. One’s perception of time is necessarily relative and both dependent on the position of the observer and related to the rate of change that occurs. Both these aspects are part of our everyday experience, summed up by the anomaly that when we are very busy, we seem to be able to fit more experiences (thoughts, emotions) into what at the time seems a period that goes very fast, because we hardly stop to think. On the other hand, in a period when we have little to do, time seems to stretch endlessly. Yet, looking back on our lives, we seem to have been subject to a sort of Doppler effect, because the periods in which much happened seem longer than those in which little occurred, even though measured in days, months, and years they are not. Thus, to construct a state of absolute stability, it is necessary to avail oneself of neutral time or absolute time, which is independent of our experience.
The nature of change is – not surprisingly – also different in the two approaches. In the traditional systems approach (when the situation is not one of oscillation within goal-range), developments converge, so that diversity is reduced and information is made to disappear. In short, developments through time are thought to accord with the Second Law of Thermodynamics. But that approach is only suited to the study of non-living phenomena in closed systems. The dynamical (complex adaptive) systems approach, on the other hand, focuses on divergence, on growth. It is therefore best suited to research on change in an amplification network, such as the mutual amplification mechanisms that effect changes in ecosystems, whereas the analytical approach prevails in the study of the structure of established relationships, such as genetic codes.
Finally, the way in which the level of generalities and that of details relate to each other is quite revealing of the underlying approach chosen by a researcher. Owing to its after-the-fact perspective, the analytical approach has more of a tendency to stress the generalities to explain the details. On the other hand, a perspective that is not sure of its perception of the phenomena as they present themselves, or even of the fact that it perceives them all, is less able to point to specific general elements, but is more likely to see the result as the interaction of all (or most of) the perceived details involved. Such an explanation would be in terms of the patterns resulting from the interactions of individual decisions, their similarities, and their differences, as well as their relationships to each other. Such explanations would necessarily be of a proximate nature.




