Hostname: page-component-6587cd75c8-67gbf Total loading time: 0 Render date: 2025-04-24T06:06:16.162Z Has data issue: false hasContentIssue false
  • English
  • Français

Flows with free boundaries and hydrodynamic singularities

Published online by Cambridge University Press:  31 January 2024

Evgenii A. Karabut Open the ORCID record for Evgenii A. Karabut [Opens in a new window]  and
Elena N. Zhuravleva Open the ORCID record for Elena N. Zhuravleva [Opens in a new window]
Evgenii A. Karabut*
Affiliation:
Lavrentyev Institute of Hydrodynamics, Siberian Branch, RAS, Novosibirsk, 630090, Russia
Elena N. Zhuravleva
Affiliation:
Lavrentyev Institute of Hydrodynamics, Siberian Branch, RAS, Novosibirsk, 630090, Russia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

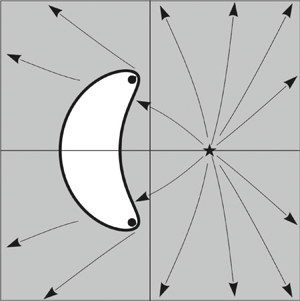
Plane unsteady potential flows of an ideal incompressible fluid with a free boundary are considered in the absence of external forces and surface tension. Examples of exact solutions in situations where the entire boundary of the domain occupied by the fluid is completely free are constructed. There may be polar singularities of the complex velocity function inside the fluid, which corresponds to the presence of a source or a sink there.

JFM classification

Mathematical Foundations: Topological fluid dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 980 , 10 February 2024 , A23
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Dirichlet, G.L. 1861 Untersuchungen uber ein problem der hydrodynamik. J. Reine Angew. Math. 58, 181–216.Google Scholar
Dyachenko, A.I., Dyachenko, S.A., Lushnikov, P.M. & Zakharov, V.E. 2019 Dynamics of poles in two-dimensional hydrodynamics with free surface: new constants of motion. J. Fluid Mech. 874, 891–925.CrossRefGoogle Scholar
Dyachenko, A.I., Dyachenko, S.A., Lushnikov, P.M. & Zakharov, V.E. 2021 Short branch cut approximation in two-dimensional hydrodynamics with free surface. Proc. R. Soc. A 477 (2249), 20200811.CrossRefGoogle Scholar
John, F. 1953 Two-dimensional potential flows with a free boundary. Commun. Pure Appl. Math. VI, 497–503.CrossRefGoogle Scholar
Karabut, E.A. 1991 Semi-analytical investigation of unsteady free-boundary flows. Intl Ser. Numer. Math. 99, 215–224.Google Scholar
Karabut, E.A., Petrov, A.G. & Zhuravleva, E.N. 2019 Semi-analytical study of the Voinovs problem. Euro. J. Appl. Math. 30, 298–337.CrossRefGoogle Scholar
Karabut, E.A. & Zhuravleva, E.N. 2014 Unsteady flows with a zero acceleration on the free boundary. J. Fluid Mech. 754, 308–331.CrossRefGoogle Scholar
Karabut, E.A., Zhuravleva, E.N. & Zubarev, N.M. 2020 Application of transport equations for constructing exact solutions for the problem of motion of a fluid with a free boundary. J. Fluid Mech. 890, A13.CrossRefGoogle Scholar
Kuznetsov, E.A., Spector, M.D. & Zakharov, V.E. 1994 Formation of singularities on the free surface of an ideal fluid. Phys. Rev. E 49 (2), 1283–1290.CrossRefGoogle ScholarPubMed
Liu, J.-G. & Pego, R.L. 2021 In search of local singularities in ideal potential flows with free surface. arXiv:2108.00445Google Scholar
Longuet-Higgins, M.S. 1972 A class of exact, time-dependent, free-surface flows. J. Fluid Mech. 55 (3), 529–543.CrossRefGoogle Scholar
Lushnikov, P.M. & Zubarev, N.M. 2018 Exact solutions for nonlinear development of a Kelvin–Helmholtz instability for the counterflow of superfluid and normal components of Helium II. Phys. Rev. Lett. 120, 204504.CrossRefGoogle ScholarPubMed
Mestnikova, A.A. & Starovoitov, V.N. 2019 Steady free surface potential flow of an ideal fluid due to a singular sink on the flat bottom. Nonlinear Anal. 49, 111–136.CrossRefGoogle Scholar
Ovsiannikov, L.V. 1967 General equations and examples. In Problem of Unsteady Motion of the Fluid with a Free Boundary, Novosibirsk.Google Scholar
Polubarinova-Kochina, P.Y. 1945 On moving of the oil-bearing contour. Dokl. Akad. Nauk SSSR 47 (4), 254–257.Google Scholar
Zubarev, N.M. & Kuznetsov, E.A. 2014 Singularity formation on a fluid interface during the Kelvin–Helmholtz instability development. J. Expl Theor. Phys. 119 (1), 169–178.CrossRefGoogle Scholar