1. INTRODUCTION
With the rapid demands of the situation awareness capability in the military and civilian surveillance and navigation systems, it is vitally important to fuse all the information from different sensors to obtain accurate target location estimation and comprehensive attribute information. However, before the benefits of fusion can be realized, the sensor registration problem (or alignment) must be addressed because of the existence of unavoidable systematic biases which make the measurements deviate from the true locations (see Feng and Ochieng, Reference Feng and Ochieng2006). In this situation, when different sensors' measurements are transformed to a common reference frame for fusion, the estimation accuracy will be decreased, also, data disassociation and redundant tracks will occur, which can seriously harm the fusion. Fortunately, many error registration methods were developed to estimate these biases and compensate sensor measurements which include parameter estimation methods (see Chen et al., Reference Chen, Wang, Jia and Progri2012); however, these methods are based on the stationary radar networks, and the systematic biases in consideration include range, the gain of range, azimuth, and elevation biases which are usually referred to as offset biases.
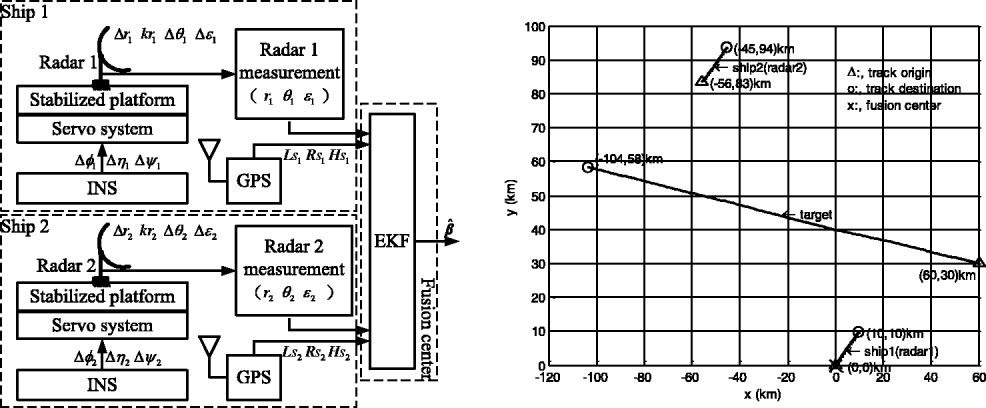
As distinct from stationary radar, mobile radar measurements contain attitude biases of platform at the same time (Progri et al., Reference Progri, Nicholson, Upton, Upadhyay and Vander Velde1998; Progri, Reference Progri2011; Setoodeh et al., Reference Setoodeh, Khatatian and Farjah2007; Falcone et al., Reference Falcone, Progri, Olson and Beam1998). Attitude biases, which means yaw, pitch, and roll biases, can be caused by the accumulated biases in the gyros in the Inertial Measurements Units (IMU) of the Inertial Navigation System (INS) (King Reference King1997). They influence radar measurements in two ways, according to different radar installation methods.
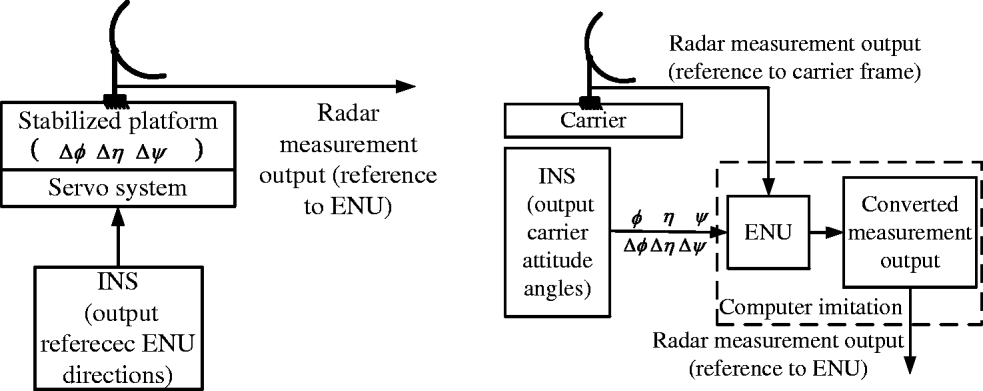
• As shown in Figure 1(a), the first type consists of large ship-borne radar which is installed on the gyro-stabilized platforms and can steadily follow systems referenced on local East-North-Up (ENU) coordinate environments. For the ENU frame, its origin o locates at the centre of the gyro-stabilized platform, three mutually orthogonal axes x, y, and z refer to the directions of East, North and Up, respectively. The plane xoy is horizontal.
• As shown in Figure 1(b), the second type consists of airborne radar which is directly fixed on platforms and rotates with platforms simultaneously.
For the first type, radar directly provides target coordinates in ENU reference frame. For the second type, the measurements are made in the measurement frame (Upadhyay et al., Reference Upadhyay, Progri, Lomas and Buckler1999) which should be converted to the ENU frame by using attitude angles provided by the INS. The common characteristic for both types of mobile radars is that they all need real-time attitude angle information of the platform to rectify radar sensitive axes which contain attitude biases (Hide et al., Reference Hide, Moore and Hill2007). Since the mechanisms of both types of mobile radar measurements are different, the registration models for them are different, too. In the paper, only the first type is discussed for length limitation, the second type will be discussed later.
Unlike stationary radars, the difficulty for mobile radar registration lies in the estimation of offset biases and attitude biases simultaneously. However, both types of biases are coupled and the coupling influences of attitude biases on radar measurements are nonlinear, time-varying, and related to the relative positions of the target. These influences assume as varying radar measurement errors which cannot be distinguished from radar native offset biases. Although it is difficult to estimate both types of biases separately, Cruz et al. (Reference Cruz, Alouani, Rice and Blair1992); Helmick and Rice (Reference Helmick and Rice1993) have made some efforts.
A two-stepped method was adopted by Cruz et al. (Reference Cruz, Alouani, Rice and Blair1992), which first estimated radar offset biases using a Kalman Filter (KF) without considering the influences of the attitude biases; that is, all the attitude biases were assumed to be zeros. Subsequently, another KF was used merely to estimate the attitude biases by using the measurements rectified by the offset bias estimations obtained in the first step. This method in fact ignored the coupling between two different kinds of biases. The model proposed by Helmick and Rice (Reference Helmick and Rice1993) considered the coupling adequately, but their methods assumed that the sensors were close enough (e.g., they located on the same platform). For models proposed by Cruz et al. (Reference Cruz, Alouani, Rice and Blair1992) and Helmick and Rice (Reference Helmick and Rice1993), they both selected the relative offset biases and relative attitude biases as the system state variables. As a result, their methods could not get absolute bias estimations of each sensor. Chen et al. (Reference Chen, Wang, Jia and Progri2012) proposed Attitude Bias Conversion Mode (ABCM), which converted the attitude biases into radar measurement errors to establish the registration equations, and used the Unscented Kalman Filter (UKF) to estimate the biases. The estimation results of ABCM for pitch and roll biases are zeros because the equivalent measurement error expressions caused by the attitude biases include the target coordinates which are big in magnitudes and limit the attitude bias estimations. Also, they proved that the linearization is not the reason for the poor estimations of attitude biases.
Based on the ABCM, we study the mobile 3-D radar registration problem where both offset biases and attitude biases are included in radar measurements. The Earth-Centred Earth-Fixed Frame (ECEF) (Kim and Smyton Reference Kim and Smyton1988 and Zhou et al., Reference Zhou, Leung and Blanchette1999) is selected as the reference frame because it can maintain higher coordinate conversion accuracy in a large space. As distinct from Chen et al. (Reference Chen, Wang, Jia and Progri2012), the equivalent measurement errors caused by the attitude biases are derived and the dependencies of the azimuth and yaw biases are proved. Then, an Optimized Bias Estimation Model (OBEM) is developed whose state vector does NOT contain the pitch and roll biases, However, the estimation result of the elevation bias contains their influences. Since the dimensions of the state vector are small, OBEM can reduce the computational costs and has better performance than ABCM. OBEM can estimate the absolute biases of both radars.

Figure 1. Measurement from moving platform radar.
For the purposes of discussion, it is assumed that all the biases are constants (since attitude biases are slowly varying biases); both radars have accurate position information of themselves; they are synchronized and have the same sampling intervals.
Progri (Reference Progri2011, Chapter 5) provides the most comprehensive description on best blind adaptive algorithms which could be utilized for future applications of mobile radar error registration algorithms of both stationary and non-stationary radars.
The main contributions of this paper are:
• The All Augmented Model (AAM) is proposed after analysing radar measurement models.
• Based on AAM, the dependencies between azimuth and yaw biases and the equivalent measurement error expressions caused by the attitude biases are given.
• OBEM is proposed according to the second bullet above, and its performance is tested by a simulated track.
Compared with the AAM and the ‘Attitude Bias Conversion Mode - Square Root Unscented Kalman Filter’ (ABCM-SRUKF), the OBEM has fewer state variables and the best estimation performance for the absolute systematic biases. This paper is organized as follows. In Section 2, a basic mathematical model is developed for the first kind of mobile radar according to the measurement generating mechanism. Then the coupling influence expressions are derived and the observability of AAM is analysed to introduce OBEM. The alignment algorithms are tested in Section 3 with simulated track data. Finally, in Section 4, the results of this study are provided.
2. MATHEMATICAL MODEL
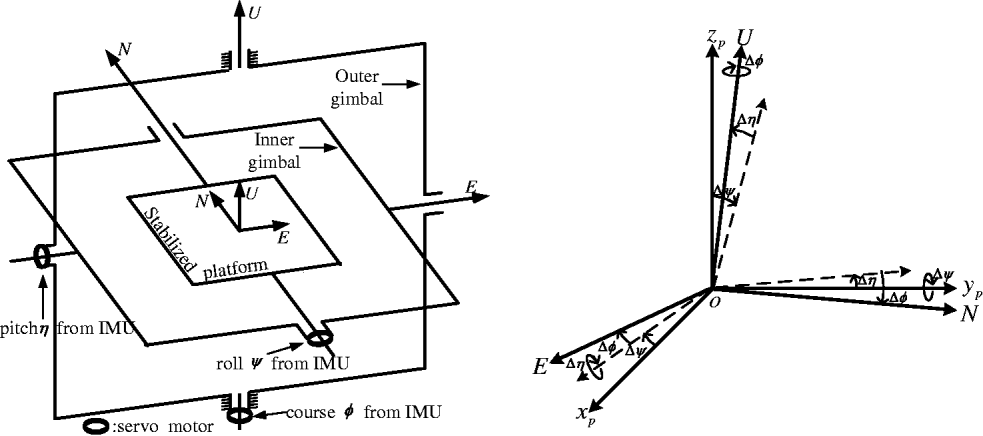
The problem addressed in this work can be stated as follows. Consider the ith radar, where i = {1,2}, which is installed on the ith moving ship. The geographic coordinates of the ith ship are latitude Ls i, longitude Rs i, and altitude H i, which are known in real time. Three-axis gyro-stabilized platform (King, Reference King1997) of radar can steadily track the local ENU frame as shown in Figure 2. A stabilized platform is installed on the carrier through inner and outer gimbals sequentially; the gimbals are free to rotate with respect to one another. The spin axis of platform points to the North, the inner gimbal points to East, and the outer gimbal points to Up, respectively. There are three orthogonal IMUs installed on the platform whose stable axes point to East, North, and Up, respectively. The annunciators of IMUs which are fixed on the IMU stable axes output pitch, roll, and yaw angles of the platform relative to ENU frame, respectively. When carrier's attitude angles change, they can drive the platform to rotate simultaneously. Since the stable axis of IMU is invariable, it can measure the variation of the attitude angle relative to its stable axis and output electric signals proportional to the attitude angle magnitude. Then, the electric signals are sent to the servo system to drive the motor to rotate with the corresponding axis of the platform in the opposite direction and the same magnitude to the attitude angle, which can compensate the rotation of the carrier. Thus the axes of the platform can steadily point to East, North and Up all the time.

Figure 2. Working principle diagram of the stabilized platform (left) and conversion from the platform frame to ENU (right).

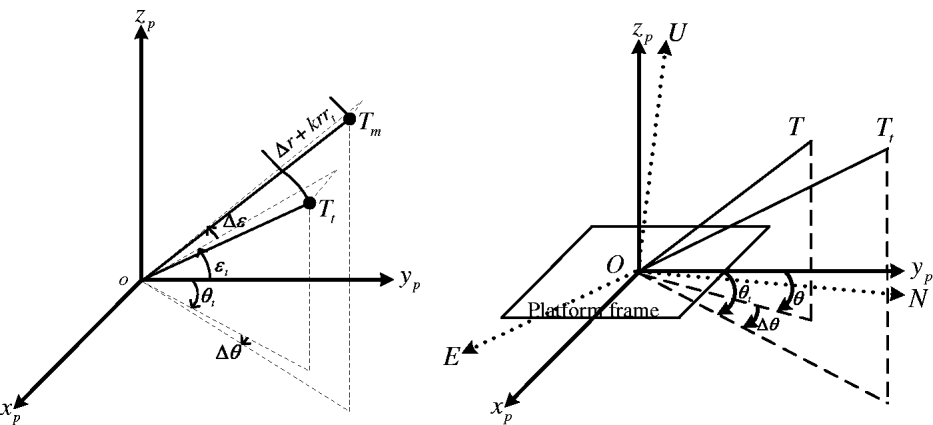
Figure 3. Connection between the radar offset biases and their measurements without considering random measurement noises (left) and the mechanism of the azimuth measurements (right).
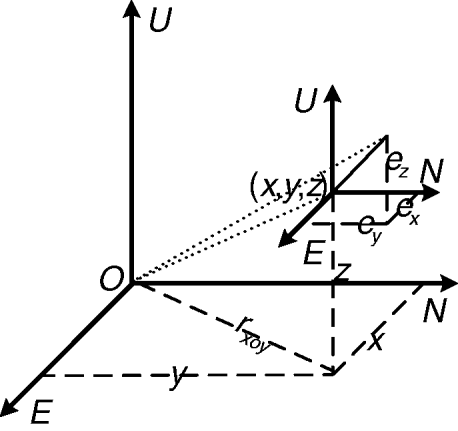
We define the output Cartesian coordinates of the gyro-stabilized platform as the platform frame. The platform frame has the same origin with ENU, but its axes have angle biases with the corresponding axes of ENU. These biases are attitude biases. Figure 2 (right) shows the conversion process from the platform frame to ENU, where x p, yp, and z p denotes x-, y-, and z- axes of the platform coordinates respectively, and the axes drawn in dashed lines are intermediate axes. As shown in Figure 2 (right), the transformation of the target coordinates from the platform frame to ENU is accomplished by first rotating about the y-axis of the platform frame by the roll bias Δψ, then rotating about the intermediate x-axis by the pitch bias Δη, and rotating about the final z-axis by the yaw bias Δφ. Customarily, the polarities of Δφ and ∆ψ abide by the left-hand rule, and Δη abides by the right-hand rule. For the ECEF frame (Zhou et al., Reference Zhou, Leung and Blanchette1999), its origin locates at the centre of the Earth; its x-axis passes through the Greenwich meridian; its z-axis coincides with the Earth's axis of rotation; its y-axis lies in the equatorial plane to form a right-handed system of coordinate axes.
Radar measurements are based on the measurement frame which shares the same origin with the platform frame. In order to analyse the composition of radar measurements, Figure 3 (left) gives the connection between radar offset biases and their measurements without considering random measurement noises. As for random noises, they are additive.

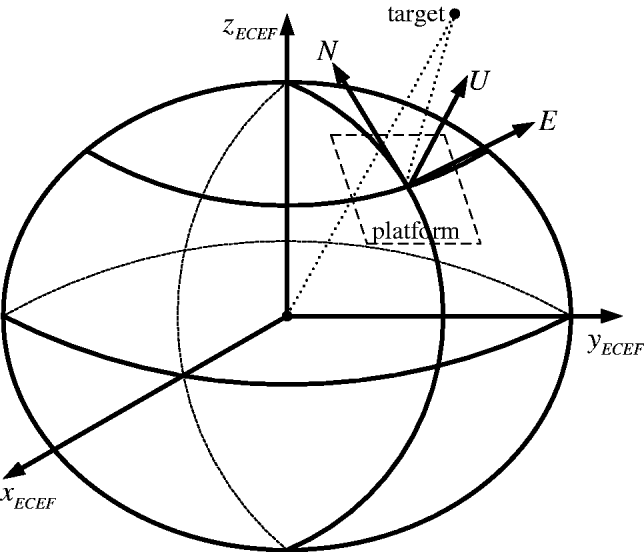
Figure 4. The conversion of the True Target Coordinates (TTC) from the radar measurement to the ECEF.
In Figure 3 (left), T t denotes the true location of the target, and T m denotes the radar measurement which contains offset biases only. The dashed lines denote the projection to planes x poyp and y pozp, respectively. From Figure 3 (left), we know that there are azimuth and elevation biases between the corresponding coordinate axes of the measurement frame and the platform frame. The measurements from the ith radar include the range r i, azimuth θ i (as shown in Figure 3 [right]), the true North direction corresponds to θ = 0, and the clockwise direction denotes the increment of θ which can be seen in Earle (Reference Earle2008), and elevation ε i. These measurements contain the true target position information (such as the true range r it, azimuth θ it and elevation ε it); radar offset biases (such as the range bias Δr i, the gain of range k ri which arises for atmospheric refraction, azimuth Δθ i and elevation bias Δε i); attitude biases (such as yaw bias Δφ i, pitch Δη i and roll Δψ i); and random measurement noises (such as the range noise δ ri, azimuth δ θi and elevation δ εi). The random measurement noises are zero-mean, Gaussian white with known standard deviations.
The main work for mobile radar registration is to estimate radar offset biases and attitude biases simultaneously using both radars' raw measurements. Usually, the following steps are adopted to establish the mathematic models. As shown in Figure 4, first, radar offset biases and random measurement errors included in the raw measurements are removed to obtain the True Target Coordinates (TTC) in the platform frame. Then, the TTC in the ENU frame are obtained by using rotation transformation caused by the attitude biases. Finally, the conversion from the ENU to the ECEF frame is used to obtain the TTC in the common reference frame.
The theoretical basis for the alignment algorithm is that the true coordinates of the same target included in both radars' raw measurements are equal when they are converted to a common reference frame. The main procedures are as follows.
2.1. True Target Coordinates in Platform Frame
Let the column vector Xi_p(k) = [x i_p(k), y i_p(k), z i_p(k)]T denote the TTC in the ith radar platform frame at observation time k, where the superscript ‘T’ denotes a matrix or vector transposition. Each element in Xi_p is a nonlinear function of radar raw measurements, radar offset biases, and random measurement noises. Since the biases and noises are small in magnitudes, then, Xi_p can be approximated by the first-order Maclaurin series expansion as:
where:
 $$\{\bf X}_i (k) = {\bf X}_{i - p} (k)|_{_{{\bi w}_i (k) = 0}^{{\bi \beta} _i = 0}} = \left[ {\matrix{ {r_i (k){\rm sin}(\theta _i (k)){\rm cos}\;(\varepsilon _i (k))} \cr {r_i (k){\rm cos}\;(\theta _i (k)){\rm cos}\;(\varepsilon _i (k))} \cr {r_i (k){\rm sin}(\varepsilon _i (k))} \cr}} \right];\left. {{\bf A}_i (k) = \displaystyle{{\partial {\bf X}_{i\_p} (k)} \over {\partial {\bi \beta} _i (k)}}} \right|_{_{{\bi w}_i (k) = 0}^{{\bi \beta} _i = 0}} ;$$
$$\{\bf X}_i (k) = {\bf X}_{i - p} (k)|_{_{{\bi w}_i (k) = 0}^{{\bi \beta} _i = 0}} = \left[ {\matrix{ {r_i (k){\rm sin}(\theta _i (k)){\rm cos}\;(\varepsilon _i (k))} \cr {r_i (k){\rm cos}\;(\theta _i (k)){\rm cos}\;(\varepsilon _i (k))} \cr {r_i (k){\rm sin}(\varepsilon _i (k))} \cr}} \right];\left. {{\bf A}_i (k) = \displaystyle{{\partial {\bf X}_{i\_p} (k)} \over {\partial {\bi \beta} _i (k)}}} \right|_{_{{\bi w}_i (k) = 0}^{{\bi \beta} _i = 0}} ;$$and:
 $$\left. {{\bf C}_i (k) = \displaystyle{{\partial {\bf X}_{i\_p} (k)} \over {\partial {\bi w}_i (k)}}} \right|_{_{{\bi w}_i (k) = 0}^{{\bi \beta} _i = 0}} ;{\bf \beta} _i (k) = [\Delta r_i, k_{ri}, \Delta \theta _i, \Delta \varepsilon _i ]^T ;\;{\rm and}\;{\bf w}_i (k) = [\delta _{ri} (k),\delta _{\theta i} (k),\delta _{\varepsilon i} (k)]^T $$
$$\left. {{\bf C}_i (k) = \displaystyle{{\partial {\bf X}_{i\_p} (k)} \over {\partial {\bi w}_i (k)}}} \right|_{_{{\bi w}_i (k) = 0}^{{\bi \beta} _i = 0}} ;{\bf \beta} _i (k) = [\Delta r_i, k_{ri}, \Delta \theta _i, \Delta \varepsilon _i ]^T ;\;{\rm and}\;{\bf w}_i (k) = [\delta _{ri} (k),\delta _{\theta i} (k),\delta _{\varepsilon i} (k)]^T $$It should be noted that the range error caused by the gain of the range bias is correlated with the true target range, however, it cannot be obtained in practice, and it can be approximated by the range measurement.
2.2. Transition from the Platform Frame to the ENU
The transition from the platform frame to the ENU can be described by three sequential rotating transformations. Each transformation can be described as one rotation matrix. According to the polarity definition of the attitude biases and rotating transformation order, we can get the following rotation matrix:
2.2.1. Roll Bias Rotation Matrix
 $${\bf T}_{\Delta \psi} = \left[ {\matrix{ {{\rm cos}\;\Delta \psi} & 0 & { - {\rm sin}\Delta \psi} \cr 0 & 1 & 0 \cr {{\rm sin}\Delta \psi} & 0 & {{\rm cos}\;\Delta \psi} \cr}} \right];$$
$${\bf T}_{\Delta \psi} = \left[ {\matrix{ {{\rm cos}\;\Delta \psi} & 0 & { - {\rm sin}\Delta \psi} \cr 0 & 1 & 0 \cr {{\rm sin}\Delta \psi} & 0 & {{\rm cos}\;\Delta \psi} \cr}} \right];$$2.2.2. Pitch Bias Rotation Matrix
 $${\bf T}_{\Delta \eta} = \left[ {\matrix{ 1 & 0 & 0 \cr 0 & {{\rm cos}\;\Delta \eta} & { - {\rm sin}\Delta \eta} \cr 0 & {{\rm sin}\Delta \eta} & {{\rm cos}\;\Delta \eta} \cr}} \right];$$
$${\bf T}_{\Delta \eta} = \left[ {\matrix{ 1 & 0 & 0 \cr 0 & {{\rm cos}\;\Delta \eta} & { - {\rm sin}\Delta \eta} \cr 0 & {{\rm sin}\Delta \eta} & {{\rm cos}\;\Delta \eta} \cr}} \right];$$2.2.3. Yaw Bias Rotation Matrix
 $${\bf T}_{\Delta \phi} = \left[ {\matrix{ {{\rm cos}\;\Delta \phi} & {{\rm sin}\Delta \phi} & 0 \cr { - {\rm sin}\Delta \phi} & {{\rm cos}\;\Delta \phi} & 0 \cr 0 & 0 & 1 \cr}} \right].$$
$${\bf T}_{\Delta \phi} = \left[ {\matrix{ {{\rm cos}\;\Delta \phi} & {{\rm sin}\Delta \phi} & 0 \cr { - {\rm sin}\Delta \phi} & {{\rm cos}\;\Delta \phi} & 0 \cr 0 & 0 & 1 \cr}} \right].$$The rotation matrices given above are orthogonal matrices which satisfy TT = T−1. According to Equations (2)–(4), the TTC in the ENU frame can be written as:
where:
Ti_ENU2p denotes the rotation matrix from ENU to the platform frame.
Ti_2pENU denotes the inverse transformation of Ti_ENU2p.
Both of them are orthogonal matrices, that is, ![]() ${\bf T}_{i\_p2ENU}^{ - 1} = {\bf T}_{i\_p2ENU}^{\rm T} = {\bf T}_{i\_ENU2p} $ and:
${\bf T}_{i\_p2ENU}^{ - 1} = {\bf T}_{i\_p2ENU}^{\rm T} = {\bf T}_{i\_ENU2p} $ and:
 $${\bf T}_{i\_p2ENU} = \left[ {\matrix{ {t_{i\_p2ENU} (1,1)} \hfill & {t_{i\_p2ENU} (1,2)} \hfill & {t_{i\_p2ENU} (1,3)} \hfill \cr {t_{i\_p2ENU} (2,1)} \hfill & {t_{i\_p2ENU} (2,2)} \hfill & {t_{i\_p2ENU} (2,3)} \hfill \cr {t_{i\_p2ENU} (3,1)} \hfill & {t_{i\_p2ENU} (2,3)} \hfill & {t_{i\_p2ENU} (3,3)} \hfill \cr}} \right]$$
$${\bf T}_{i\_p2ENU} = \left[ {\matrix{ {t_{i\_p2ENU} (1,1)} \hfill & {t_{i\_p2ENU} (1,2)} \hfill & {t_{i\_p2ENU} (1,3)} \hfill \cr {t_{i\_p2ENU} (2,1)} \hfill & {t_{i\_p2ENU} (2,2)} \hfill & {t_{i\_p2ENU} (2,3)} \hfill \cr {t_{i\_p2ENU} (3,1)} \hfill & {t_{i\_p2ENU} (2,3)} \hfill & {t_{i\_p2ENU} (3,3)} \hfill \cr}} \right]$$where:
Equation (7) can be approximated by the first-order Maclaurin series expansion about attitude biases as:
 $$\{\bf T}_{i\_p2ENU} \approx {\bf I} + \left[ {\matrix{ 0 \hfill & 1 \hfill & 0 \hfill \cr { - 1} \hfill & 0 \hfill & 0 \hfill \cr 0 \hfill & 0 \hfill & 0 \hfill \cr}} \right]\Delta \phi _i + \left[ {\matrix{ 0 \hfill & 0 \hfill & 0 \hfill \cr 0 \hfill & 0 \hfill & { - 1} \hfill \cr 0 \hfill & 1 \hfill & 0 \hfill \cr}} \right]\Delta \eta _i + \left[ {\matrix{ 0 \hfill & 0 \hfill & { - 1} \hfill \cr 0 \hfill & 0 \hfill & 0 \hfill \cr 1 \hfill & 0 \hfill & 0 \hfill \cr}} \right]\Delta \psi _i = {\bf I} + \Delta _i }$$
$$\{\bf T}_{i\_p2ENU} \approx {\bf I} + \left[ {\matrix{ 0 \hfill & 1 \hfill & 0 \hfill \cr { - 1} \hfill & 0 \hfill & 0 \hfill \cr 0 \hfill & 0 \hfill & 0 \hfill \cr}} \right]\Delta \phi _i + \left[ {\matrix{ 0 \hfill & 0 \hfill & 0 \hfill \cr 0 \hfill & 0 \hfill & { - 1} \hfill \cr 0 \hfill & 1 \hfill & 0 \hfill \cr}} \right]\Delta \eta _i + \left[ {\matrix{ 0 \hfill & 0 \hfill & { - 1} \hfill \cr 0 \hfill & 0 \hfill & 0 \hfill \cr 1 \hfill & 0 \hfill & 0 \hfill \cr}} \right]\Delta \psi _i = {\bf I} + \Delta _i }$$where: I is a 3 × 3 identity matrix,and:
 $$\Delta _i = \left[ {\matrix{ 0 \hfill & {\Delta \phi _i} \hfill & { - \Delta \psi _i} \hfill \cr { - \Delta \phi _i} \hfill & 0 \hfill & { - \Delta \eta _i} \hfill \cr {\Delta \psi _i} \hfill & {\Delta \eta _i} \hfill & 0 \hfill \cr}} \right]$$
$$\Delta _i = \left[ {\matrix{ 0 \hfill & {\Delta \phi _i} \hfill & { - \Delta \psi _i} \hfill \cr { - \Delta \phi _i} \hfill & 0 \hfill & { - \Delta \eta _i} \hfill \cr {\Delta \psi _i} \hfill & {\Delta \eta _i} \hfill & 0 \hfill \cr}} \right]$$Substituting Equations (1), (8) into Equation (5), we have:

Figure 5. Conversion from the ENU to the ECEF frame.
2.3. Transition from the ENU to the ECEF
Given the geographic coordinates of the ith radar, the TTC in the ECEF can be given as (Zhou et al., Reference Zhou, Leung and Blanchette1999):
where:
Xis(k) denotes the ECEF coordinates of the ith radar.
Ti(k) is the rotation matrix.
Both variables are only correlated with the geographic coordinates of the ith radar at time k. The geometry of the target coordinates in the ECEF is shown in Figure 5.
2.4. All Augmented Model for Estimation
Substituting Equation (10) into Equation (11), we can obtain:
According to the fact that:
The registration equations can be established (for simplicity, time argument ‘k’ is omitted in the following equations) as:
Omitting the higher order terms, Equation (14) can be approximated as:
Usually, for moving platform radar registration equations, the offset and attitude biases of both radars are written sequentially in the state vector as:
According to Equation (16), Equation (15) can be rearranged as:
where:
 $$\{\bf D}_i = \left[ {\matrix{ {x_i a_i d_i - y_i c_i} \tab {y_i b_i d_i + z_i a_i d_i} \tab {x_i b_i d_i + z_i c_i} \cr {x_i a_i c_i + y_i c_id_i} \tab {y_i b_i c_i + z_i a_i c_i} \tab {x_i b_i c_i - z_i d_i} \cr { - x_i b_i} \tab {y_i a_i - z_i b_i} \tab {x_i a_i} \cr}} \right]{\rm and}\left\{ {\matrix{ {a_i = {\rm sin}Ls_i} \hfill \cr {b_i = {\rm cos}\;Ls_i} \hfill \cr {c_i = \sin Rs_i} \hfill \cr {d_i = \cos Rs_i} \hfill \cr}} \right.$$
$$\{\bf D}_i = \left[ {\matrix{ {x_i a_i d_i - y_i c_i} \tab {y_i b_i d_i + z_i a_i d_i} \tab {x_i b_i d_i + z_i c_i} \cr {x_i a_i c_i + y_i c_id_i} \tab {y_i b_i c_i + z_i a_i c_i} \tab {x_i b_i c_i - z_i d_i} \cr { - x_i b_i} \tab {y_i a_i - z_i b_i} \tab {x_i a_i} \cr}} \right]{\rm and}\left\{ {\matrix{ {a_i = {\rm sin}Ls_i} \hfill \cr {b_i = {\rm cos}\;Ls_i} \hfill \cr {c_i = \sin Rs_i} \hfill \cr {d_i = \cos Rs_i} \hfill \cr}} \right.$$For constant systematic bias model (Bar-Shalom, Reference Bar-Shalom2001), the state equation can be written as:
According to Equations (17) and (20), a KF can be used to estimate the systematic biases (Xu et al., Reference Xu, Li, Rizos and Xu2010). Since this model selects all the offset biases and attitude biases as state vector, we call this model an AAM. AAM is a primary method of mobile radar registration, but it does not consider the coupling influences of the attitude biases on radar offset biases. Consequently, the estimations of radar offset biases are inaccurate. In view of this, the coupling influences are analysed below.
2.5. Analysis of Coupling Influences of Attitude Biases
2.5.1. Proposition 1
For dynamic equations consisting of Equations (17) and (20), if azimuth and yaw biases are combined to form a new variable, the system is observable.
2.5.2. Proof
Assuming a discrete linear time-varying system, its state and measurement equations can be described as:
Then the system is called N-step observable if, and only if, its observation matrix M satisfies (Peters and Iglesias, Reference Peters and Iglesias1997 and Bar-Shalom, Reference Bar-Shalom2001):
 $${\bf M}(k,k - N + 1) = \sum\limits_{i = k - N + 1}^k {{\bf F}^T (k,i){\bf H}^T (i){\bf H}(i)} {\bf F}(k,i) \gt 0,$$
$${\bf M}(k,k - N + 1) = \sum\limits_{i = k - N + 1}^k {{\bf F}^T (k,i){\bf H}^T (i){\bf H}(i)} {\bf F}(k,i) \gt 0,$$where:
F(k,i) denotes the state transition matrix from time instant i to k.
H(i) is the measurement matrix at time i.
N is a positive integer which is unrelated to k.
According to Equations (17), (20) and (22), the observation matrix of AAM can be written as:
 $${\bf M}(k,k - N + 1) = \sum\limits_{i = k - N + 1}^k {{\bf H}^T (i){\bf H}(i)} = \sum\limits_{i = k - N + 1}^k {{\bf S}(i)}, $$
$${\bf M}(k,k - N + 1) = \sum\limits_{i = k - N + 1}^k {{\bf H}^T (i){\bf H}(i)} = \sum\limits_{i = k - N + 1}^k {{\bf S}(i)}, $$where H(i) = [T1(i)A1(i), − T2(i)A2(i), D1(i), − D2(i)] is a 3 × 14 matrix and S(i) = HT(i)H(i) is a 14 × 14 matrix.
In Equation (23), omitting time index, each element in matrix S can be written as:
 $$S_{ij} = \sum\limits_{u = 1}^3 {{\bf H}_{iu}^T {\bf H}_{uj}} = \sum\limits_{u = 1}^3 {{\bf H}_{ui} {\bf H}_{uj}}, $$
$$S_{ij} = \sum\limits_{u = 1}^3 {{\bf H}_{iu}^T {\bf H}_{uj}} = \sum\limits_{u = 1}^3 {{\bf H}_{ui} {\bf H}_{uj}}, $$where S ij denotes the ith row and the jth column element in the matrix S.
In Equation (15), only the term T1Δ1X1 contains attitude biases of platform 1, and it can be written as:
where a1 = [Δφ 1, Δη 1, Δψ 1]T.
In linear Equation (15), the coefficients of radar 1 azimuth bias can be written as:
 $${\bf T}_1 {\bf A}_1 (:,3) = \left\{ {\matrix{ {\left[ \eqalign{ & c_1 r_1 {\rm cos} \ \theta _1 {\rm cos} \ \varepsilon _1 - a_1 b_1 r_1 {\rm sin}\, \theta _1 {\rm cos} \ \varepsilon _1 \cr & - d_1 r_1 {\rm cos} \ \theta _1 {\rm cos} \ \varepsilon _1 - a_1 c_1 r_1 {\rm sin} \, \theta _1 {\rm cos} \ \varepsilon _1 \cr & \quad \quad \quad \quad b_1 r_1 {\rm sin} \, \theta _1 {\rm cos} \ \varepsilon _1} \right]} \cr {\matrix{ = \hfill & {\left[ {\matrix{ {y_1 c_1 - x_1 a_1 d_1} \cr { - y_1 d_1 - x_1 a_1 c_1} \cr {x_1 b_1} \cr}} \right]} \hfill \cr}} \cr}} \right.;\left\{ {\matrix{ {a_1 = {\rm sin}\;Ls_1} \hfill \cr {b_1 = {\rm cos} \ Ls_1} \hfill \cr {c_1 = {\rm sin} \ Rs_1} \hfill \cr {d_1 = {\rm cos} \ Rs_1} \hfill \cr}} \right.$$
$${\bf T}_1 {\bf A}_1 (:,3) = \left\{ {\matrix{ {\left[ \eqalign{ & c_1 r_1 {\rm cos} \ \theta _1 {\rm cos} \ \varepsilon _1 - a_1 b_1 r_1 {\rm sin}\, \theta _1 {\rm cos} \ \varepsilon _1 \cr & - d_1 r_1 {\rm cos} \ \theta _1 {\rm cos} \ \varepsilon _1 - a_1 c_1 r_1 {\rm sin} \, \theta _1 {\rm cos} \ \varepsilon _1 \cr & \quad \quad \quad \quad b_1 r_1 {\rm sin} \, \theta _1 {\rm cos} \ \varepsilon _1} \right]} \cr {\matrix{ = \hfill & {\left[ {\matrix{ {y_1 c_1 - x_1 a_1 d_1} \cr { - y_1 d_1 - x_1 a_1 c_1} \cr {x_1 b_1} \cr}} \right]} \hfill \cr}} \cr}} \right.;\left\{ {\matrix{ {a_1 = {\rm sin}\;Ls_1} \hfill \cr {b_1 = {\rm cos} \ Ls_1} \hfill \cr {c_1 = {\rm sin} \ Rs_1} \hfill \cr {d_1 = {\rm cos} \ Rs_1} \hfill \cr}} \right.$$where F(:, i) denotes the ith column vector in the matrix F.
According to Equations (19) and (26):
Equation (27) means that the coefficients of the yaw bias of platform 1 in Equation (17) are in proportion to the coefficients of the azimuth bias of radar 1. That is, in Equation (24), H(:, 3) = − H(:, 9). According to Equation (24), S i3 = Σu = 13HiuTHu3 = Σu = 13HuiHu3 = −S i9. Similarly, for radar 2, s i7 = −s i12. So, the observation matrix M is not a positive definite matrix. According to the definition of Equation (22), the system is unobservable.
On the contrary, if we subtract the yaw bias from the azimuth bias to form a new variable, then, the dimension of state vector in Equation (17) will be reduced from 14 to 12. From Equation (23), when N ≥ 4 and the positions of the target are different at each sampling instant, the observation matrix M can be guaranteed to be positive definite, according to the definition in Equation (22), the system is observable.
Assuming radar measurement errors caused by the attitude biases can be described as Δr c(aT), Δθ c(aT), and Δɛ c(aT); a = [Δφ, Δη, Δψ]T which denote range, azimuth, and elevation errors, respectively, then, the following proposition holds.
2.5.3. Proposition 2
For measurement errors caused by the attitude biases, when attitude biases are small, the following results can be obtained:
(a) Δr c = 0 + o(a);
(b)
 $\Delta \theta _c = - \Delta \phi + \displaystyle{{yz\Delta \psi - xz\Delta \eta} \over {x^2 + y^2}} + o({\bf a})$;
$\Delta \theta _c = - \Delta \phi + \displaystyle{{yz\Delta \psi - xz\Delta \eta} \over {x^2 + y^2}} + o({\bf a})$;
and:
(c)
 $\Delta \varepsilon _c = \displaystyle{{ - x\Delta \psi - y\Delta \eta} \over {\sqrt {x^2 + y^2}}} + o({\bf a})$
$\Delta \varepsilon _c = \displaystyle{{ - x\Delta \psi - y\Delta \eta} \over {\sqrt {x^2 + y^2}}} + o({\bf a})$
2.5.4. Proof
Using the first-order approximation, Equation (10) can be written as:
The last term of the left hand side of Equation (28b) is the error expression caused by the attitude biases. Omitting the subscript ‘i’, it can be rewritten as:
 $$\left[ {\matrix{ {e_x} \hfill \cr {e_y} \hfill \cr {e_z} \hfill \cr}} \right] = - \Delta X = - \left[ {\matrix{ 0 \hfill & {\Delta \phi} \hfill & { - \Delta \psi} \hfill \cr { - \Delta \phi} \hfill & 0 \hfill & { - \Delta \eta} \hfill \cr {\Delta \psi} \hfill & {\Delta \eta} \hfill & 0 \hfill \cr}} \right]\left[ {\matrix{ x \hfill \cr y \hfill \cr z \hfill \cr}} \right]$$
$$\left[ {\matrix{ {e_x} \hfill \cr {e_y} \hfill \cr {e_z} \hfill \cr}} \right] = - \Delta X = - \left[ {\matrix{ 0 \hfill & {\Delta \phi} \hfill & { - \Delta \psi} \hfill \cr { - \Delta \phi} \hfill & 0 \hfill & { - \Delta \eta} \hfill \cr {\Delta \psi} \hfill & {\Delta \eta} \hfill & 0 \hfill \cr}} \right]\left[ {\matrix{ x \hfill \cr y \hfill \cr z \hfill \cr}} \right]$$where e x, ey, and e z denote the errors in x, y, and z coordinates, respectively.
According to Equation (29), the measurement errors caused by the attitude biases can be written as follows.
2.5.4.1. Range Error Caused by the Attitude Biases
The range error can be given by:
Substituting Equation (29) into Equation (30), Equation (30) can be approximated by the first order Maclaurin series as (for details see Appendix A):
Equation (31) manifests that the range error caused by the attitude biases is approximately zero.
2.5.4.2. Azimuth Error Caused by the Attitude Biases
Assuming the true azimuth of target is θ and the additional azimuth caused by the attitude biases is Δθ c, there are two cases to be discussed to calculate Δθ c, according to the different locations of the target.
2.5.4.3. The Target Does Not Locate on the x-Axis of the ENU Frame
By the definition of azimuth, we have:
then:
Substituting Equations (32), (33) into Equation (34), the first order approximation of Equation (34) can be written as:
Equation (35) can be approximated further as:
2.5.4.4. The Target Locates on the x-Axis of the ENU Frame
In this case:
where r xoy denotes the projection of the target range on xoy plane of the ENU frame. Substituting Equation (37) into Equation (29) gives:
According to Equation (37) and Equation (38), the azimuth error can be described as:
Equation (39) can be approximated as:
In fact, Equation (40) is included in Equation (36). Considering the fact that r xoy≫z, the result of Equation (36) manifests that the yaw bias is the main factor in causing radar azimuth measurement error and the effects of pitch and roll biases can be omitted. According to the analyses above, Δθ c is approximately −Δφ.
2.5.4.5. Elevation Error Caused by the Attitude Biases
Similarly, assuming the true elevation of the target is ɛ, the additional elevation error caused by the attitude biases is Δɛ c.
Then:
Substituting Equations (41) and (42) into Equation (43), using first order approximation, Equation (43) can be written as:
Further approximation for Equation (44) can be written as:
Equation (45) indicates that the elevation error is mainly caused by the roll and pitch biases, its magnitudes are related to the position of the target.
2.6. Optimized Bias Estimation Model (OBEM)
Proposition 1 and Equation (36) suggest that both of the platforms’ yaw biases should be deleted in the state vector Equation (16). The azimuth biases left are in fact equivalent to the subtraction of the yaw biases from azimuth biases. Since the azimuth and yaw biases are constants, the azimuth biases left are constants, too, which coincide with the state Equation (20) used for a KF. So, the remaining azimuth bias variables can be estimated accurately.
According to Equation (45), the equivalent elevation error is mainly caused by the roll and pitch biases. Its magnitude is not a constant and changes with different target locations, however, the variations are small in each sampling period, and the invariant part manifests the dependencies between the elevation bias and yaw, pitch biases. Since the dependencies are strong, when selecting system state vector, it is practical to abandon both pitch and roll biases and the remained elevation bias variable in fact contains their influences. In view of this, the state vector can be written as:
Since the state vector is selected optimally, we call this model the Optimized Bias Estimation Model (OBEM).

Figure 6. The complete algorithm flowchart for OBEM using first-order linearized model.
Rearranging Equation (15) in terms of Equation (46), the equivalent measurement equation is given by:
where:
Since the systematic biases are constants, the state equation can be described as:
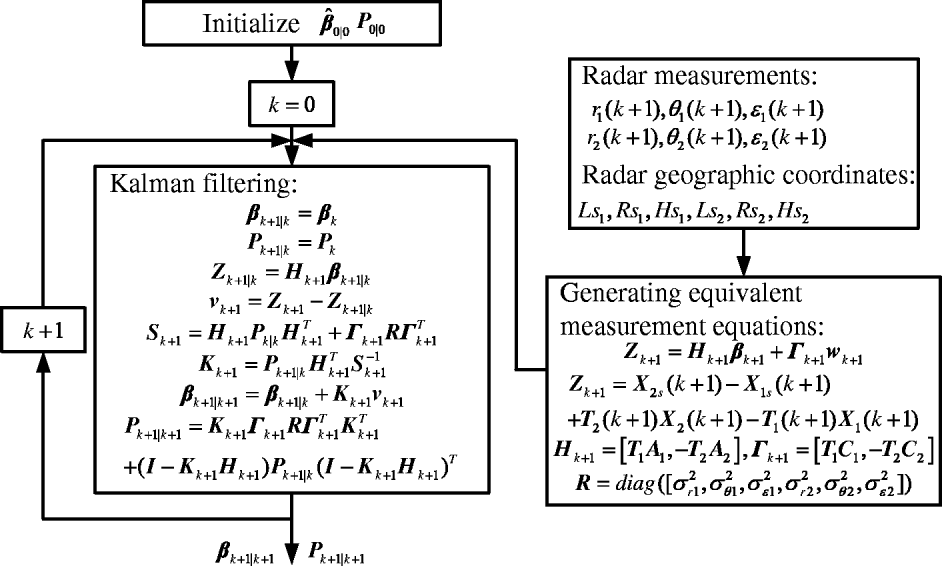
Equations (47) and (49) constitute the linearized dynamic equations; a KF can be used to estimate these biases. The complete algorithm flowchart is described in Figure 6.
3. SIMULATION RESULTS
The alignment algorithms are tested by generating a common track for two radars installed on different ships. The system test setup block diagram is depicted in Figure 7 (left). Since the comparison between OBEM and ABCM-SRUKF has been made (Chen et al., Reference Chen, Wang, Jia and Progri2012) and the results given are comprehensive, OBEM is only compared with AAM in this section. Assuming that ship 1 and ship 2 are moving with constant velocity model, and the initial geographical coordinates are [40°, 116°, 10 m], [40·75°, 115·34°, 10 m], respectively. The initial states of both ships in their native ENU frame are [0,10 m/s, 0, 10 m/s, 0, 0]. In state vector, the variables denote x-coordinate (East), x-velocity, y-coordinate (North), y-velocity, z-coordinate (Up), and z-velocity, respectively. The standard deviations of both ships’ process noises are equal to those which are given in x, y, and z coordinates by 0·1 m/s2, 0·1 m/s2, and 0 m/s2, respectively. Fusion centre locates at the initial position of ship 1. The constant velocity model is also used for the target. The initial state of the target in fusion centre is [60 km, −170 m/s, 30 km, 30 m/s, 5 km, 1 m/s]. The standard deviations of the process noise in x, y, and z coordinates are set to 1 m/s2, 1 m/s2, and 0·1 m/s2, respectively. The geometry of radar and target is shown in Figure 7 (right). The true offset biases of both radars are assumed to be constant and equal as Δr i = 300 m, k ri = 0.01, Δθ i = 2°, and Δɛ i = 2°, respectively. The standard deviations of random measurement noises for both radars are σ ri = 50 m, ![]() $\sigma _{\theta _i} = 0{\cdot}5{\rm ^{\circ}} $, and
$\sigma _{\theta _i} = 0{\cdot}5{\rm ^{\circ}} $, and ![]() $\sigma _{\varepsilon _i} = 0{\cdot}5{\rm ^{\circ}} $, respectively. The attitude biases of both platforms are also assumed to be constant and equal as Δφ i = 2°, Δη i = 1°, and Δψ i = 1°, respectively. It is assumed that both radars are synchronized with the same sampling intervals T = 5 s. 200 scans of the target are simulated and the number of Monte Carlo runs is set to 100. Figures 8–10 contain all the simulation results.
$\sigma _{\varepsilon _i} = 0{\cdot}5{\rm ^{\circ}} $, respectively. The attitude biases of both platforms are also assumed to be constant and equal as Δφ i = 2°, Δη i = 1°, and Δψ i = 1°, respectively. It is assumed that both radars are synchronized with the same sampling intervals T = 5 s. 200 scans of the target are simulated and the number of Monte Carlo runs is set to 100. Figures 8–10 contain all the simulation results.

Figure 7. System test setup block diagram (left) and the geometry of radar and target (right).

Figure 8. RMSE of radar bias estimation. (a) gross range bias; (b) elevation bias; (c) the subtraction of the yaw bias from azimuth bias.
Figure 8 contains the Root Mean Square Errors (RMSE) of the offset biases of radar 1 and radar 2, respectively, where:
The solid lines represent the results of AAM.
The dashed lines represent OBEM.
The red lines represent radar 1.
The blue lines represent radar 2.
(a) is the gross range bias which is the sum of the range bias and the range bias induced by the gain of the range.
(b) is the elevation bias.
(c) is the subtraction of the yaw bias from azimuth bias.
The main difference between the OBEM and AAM is the estimation accuracy of the elevation bias; OBEM performs better than AAM, which verifies Proposition 2. (c) shows that the RMSE of the subtraction of yaw bias from azimuth bias is less than 0·5°, which verifies Proposition 1.
The RMSEs of pitch and roll biases estimated by AAM are given in Figure 9. The results show that the estimations deviate from the true values significantly because of the strong dependencies. Since the real model has strong nonlinearity, and OBEM in the paper is a first-order Extended Kalman Filter (EKF), linearization will inevitably cause big estimation errors.

Figure 9. RMSE of platform's pitch and roll bias estimation in AAM.

Figure 10. RMSE of target location in xyz-coordinates after rectifying radar 1 measurements by bias estimations. (a) x-coordinates; (b) y-coordinates; (c) z-coordinates.
An UKF, whose theoretical basis is unscented transformation, does not need linearization. The calculated covariances of UKF can coincide with the practical situation well (Lee and Jekeli, Reference Lee and Jekeli2010; Zhou et al., Reference Zhou, Knedlik and Loffeld2010). However for an EKF, the calculated covariances deviate from the true values significantly because of the linearization. So, the UKF estimations are expected to be closer to the true values than the EKF (Jwo and Lai, Reference Jwo and Lai2009). In view of this, we will use UKF for OBEM in our future work.
Figure 10 are the RMSEs of the rectified measurements in each axis of the ENU frame, where the raw measurements are subtracted by the estimated offset biases, then, they are compensated by using attitude bias rotation matrix as described by Equation (7). Since the dependencies between azimuth bias and yaw bias, the subtraction of yaw bias from azimuth bias is used as azimuth estimation and the yaw bias is set to zero when compensating the raw measurements. In Figure 10, (a) represents x-coordinate; (b) represents y-coordinate; (c) represents z-coordinate, and the black lines represent the raw measurements which deviate from the true locations considerably; the red lines represent the results of using the estimation of an OBEM. In this situation, the roll and pitch bias estimations are both assumed to be zero; the blue lines represent the results of using all the estimations of AAM; and the green lines represent using all the estimations of an AAM except roll and pitch biases. The results of these figures show that the OBEM outperforms the AAM when their estimations are used to rectify radar raw measurements.
4. SUMMARY AND CONCLUSIONS
The problem of aligning two mobile 3-D radars which simultaneously have the offset biases and attitude biases was examined. First, the physical registration models were given. Second, the coupling error expressions caused by the attitude biases were derived and the observability analysis was made for the system. Thirdly, according to the analyses, the OBEM for registration was proposed, which combined the azimuth and yaw biases as one variable, and omitted the roll and pitch biases in the state vector. Fourthly, comparing the AAM and the ABCM, which use all the offset and attitude biases as state vector, the OBEM has smaller dimension in the state vector and could reduce the computational costs (see Goris et al., Reference Goris, Gray and Mareels1997). Fifthly, the OBEM can improve the elevation bias estimation performance because it isolates the influences of poor estimation results of roll and pitch biases.
Another characteristic of the OBEM is that the model does not need to know the true course, pitch, and roll of the platform, which saves much bandwidth and decreases the coupling influences of the attitude angles to a great extent. The OBEM in the paper did not consider the position errors of radars. The same sampling intervals and the same sampling instant for the common target were assumed for both radars. However, in physical system, these assumptions should be considered carefully. How they influence the estimation of the biases, how to model, how they affect each other etc., should be studied further in the future.
ACKNOWLEDGEMENTS
This work was supported in part by the National Natural Science Foundation of China 61032001, 61102165, 61002006 and Special Foundation Program for Mountain Tai Scholars of China.
APPENDIX A
The following are the derivations of the equivalent measurement errors caused by the attitude biases, as shown in Figure A1.
A1. DERIVATION OF EQUATION (31)
Equation (31) can be approximated by the first order Maclaurin series expansion as:
 $$\{\Delta r_c (\Delta \phi, \Delta \eta, \Delta \psi ) = \left\{ {\matrix{ {\quad \quad \quad r(x,y,z,e_x, e_y, e_z )|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}} + \left. {\displaystyle{{2(x + e_x )y + 2(y + e_y )( - x)} \over {2r(x,y,z,e_x, e_y, e_z )}}} \right|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}}\cdot \Delta \phi} \hfill \cr { + \left. {\displaystyle{{2(y + e_y )( - z) + 2(z + e_z )y} \over {2r(x,y,z,e_x, e_y, e_z )}}} \right|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}} \cdot \left. {\Delta \eta + \displaystyle{{2(x + e_x )( - z) + 2(z + e_z )x} \over {2r(x,y,z,e_x, e_y, e_z )}}} \right|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}}. \Delta \psi} \hfill \cr \matrix{\quad \quad \quad \quad \quad \quad + o(\Delta \phi, \Delta \eta, \Delta \psi ) - \sqrt {x^2 + y^2 + z^2} \hfill \cr \quad \quad \quad \quad \quad \quad \quad \quad \quad = o(\Delta \phi, \Delta \eta, \Delta \psi ) \hfill} \hfill \cr}} \right.}$$
$$\{\Delta r_c (\Delta \phi, \Delta \eta, \Delta \psi ) = \left\{ {\matrix{ {\quad \quad \quad r(x,y,z,e_x, e_y, e_z )|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}} + \left. {\displaystyle{{2(x + e_x )y + 2(y + e_y )( - x)} \over {2r(x,y,z,e_x, e_y, e_z )}}} \right|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}}\cdot \Delta \phi} \hfill \cr { + \left. {\displaystyle{{2(y + e_y )( - z) + 2(z + e_z )y} \over {2r(x,y,z,e_x, e_y, e_z )}}} \right|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}} \cdot \left. {\Delta \eta + \displaystyle{{2(x + e_x )( - z) + 2(z + e_z )x} \over {2r(x,y,z,e_x, e_y, e_z )}}} \right|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}}. \Delta \psi} \hfill \cr \matrix{\quad \quad \quad \quad \quad \quad + o(\Delta \phi, \Delta \eta, \Delta \psi ) - \sqrt {x^2 + y^2 + z^2} \hfill \cr \quad \quad \quad \quad \quad \quad \quad \quad \quad = o(\Delta \phi, \Delta \eta, \Delta \psi ) \hfill} \hfill \cr}} \right.}$$where:
A2. DERIVATION OF EQUATION (36)
The geometry of the true target location and its ghost location affected by the attitude biases is at Figure A1. According to Equations (30), (33)–(35):

Figure A1. The geometry of the true target location and its ghost location affected by the attitude biases.
Taking attitude biases as variables, Equation (A3) can be first order approximated as:
 $$\{\tan (\Delta \theta _c ) = \left\{ {\matrix{ {\displaystyle{{{\textstyle{{(x + e_x )} \over {(y + e_y )}}} - {\textstyle{x \over y}}} \over {1 + {\textstyle{{x(x + e_x )} \over {y(y + e_y )}}}}} =} \cr {\displaystyle{{y(x + e_x ) - x(y + e_y )} \over {y(y + e_y ) + x(x + e_x )}} =} \cr {\left\{ {\matrix{ {\left. {\displaystyle{{ye_x - xe_y} \over {y(y + e_y ) + x(x + e_x )}}} \right|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}} + \left. {\displaystyle{{ - (x^2 + y^2 )^2} \over {(y(y + e_y ) + x(x + e_x ))^2}}} \right|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}}. \Delta \phi +} \cr {\left. {\displaystyle{{ - xz(y(y + e_y ) + x(x + e_x ))} \over {(y(y + e_y ) + x(x + e_x ))^2}}} \right|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}} \cdot \left. {\Delta \eta + \displaystyle{{yz(y(y + e_y ) + x(x + e_x ))} \over {(y(y + e_y ) + x(x + e_x ))^2}}} \right|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}} \cdot \Delta \psi + o(\Delta \phi, \Delta \eta, \Delta \psi ) =} \cr}} \right.} \cr { - \Delta \phi + \displaystyle{{yz\Delta \psi - xz\Delta \eta} \over {x^2 + y^2}} + o(\Delta \phi, \Delta \eta, \Delta \psi )} \cr}} \right.}$$
$$\{\tan (\Delta \theta _c ) = \left\{ {\matrix{ {\displaystyle{{{\textstyle{{(x + e_x )} \over {(y + e_y )}}} - {\textstyle{x \over y}}} \over {1 + {\textstyle{{x(x + e_x )} \over {y(y + e_y )}}}}} =} \cr {\displaystyle{{y(x + e_x ) - x(y + e_y )} \over {y(y + e_y ) + x(x + e_x )}} =} \cr {\left\{ {\matrix{ {\left. {\displaystyle{{ye_x - xe_y} \over {y(y + e_y ) + x(x + e_x )}}} \right|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}} + \left. {\displaystyle{{ - (x^2 + y^2 )^2} \over {(y(y + e_y ) + x(x + e_x ))^2}}} \right|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}}. \Delta \phi +} \cr {\left. {\displaystyle{{ - xz(y(y + e_y ) + x(x + e_x ))} \over {(y(y + e_y ) + x(x + e_x ))^2}}} \right|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}} \cdot \left. {\Delta \eta + \displaystyle{{yz(y(y + e_y ) + x(x + e_x ))} \over {(y(y + e_y ) + x(x + e_x ))^2}}} \right|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}} \cdot \Delta \psi + o(\Delta \phi, \Delta \eta, \Delta \psi ) =} \cr}} \right.} \cr { - \Delta \phi + \displaystyle{{yz\Delta \psi - xz\Delta \eta} \over {x^2 + y^2}} + o(\Delta \phi, \Delta \eta, \Delta \psi )} \cr}} \right.}$$A3. DERIVATION OF EQUATION (43)
According to Equations (30), (40–42):
Similarly to Equation (A4), taking attitude biases as variables, Equation (A5) can be first order approximated as:
 $$\{\tan (\Delta \varepsilon _c ) = \left\{ {\matrix{ {\displaystyle{{\displaystyle{{z + e_z} \over {\sqrt {(x + e_x )^2 + (y + e_y )^2}}} - \displaystyle{z \over {\sqrt {x^2 + y^2}}}} \over {1 + \displaystyle{{z + e_z} \over {\sqrt {(x + e_x )^2 + (y + e_y )^2}}} \displaystyle{z \over {\sqrt {x^2 + y^2}}}}} =} \cr \matrix{\left. {\displaystyle{{\partial \tan (\Delta \varepsilon _c )} \over {\partial \Delta \phi}}} \right|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}} \cdot \Delta \phi + \left. {\displaystyle{{\partial \tan (\Delta \varepsilon _c )} \over {\partial \Delta \eta}}} \right|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}} \cdot \left. {\Delta \eta \displaystyle{{\partial \tan (\Delta \varepsilon _c )} \over {\partial \Delta \psi}}} \right|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}} \cdot \Delta \psi + o(\Delta \phi, \Delta \eta, \Delta \psi ) = \hfill \cr \quad \quad \quad \quad \quad \quad \displaystyle{{ - x\Delta \psi - y\Delta \eta} \over {\sqrt {x^2 + y^2}}} + o(\Delta \phi, \Delta \eta, \Delta \psi ) \hfill} \cr}} \right.}$$
$$\{\tan (\Delta \varepsilon _c ) = \left\{ {\matrix{ {\displaystyle{{\displaystyle{{z + e_z} \over {\sqrt {(x + e_x )^2 + (y + e_y )^2}}} - \displaystyle{z \over {\sqrt {x^2 + y^2}}}} \over {1 + \displaystyle{{z + e_z} \over {\sqrt {(x + e_x )^2 + (y + e_y )^2}}} \displaystyle{z \over {\sqrt {x^2 + y^2}}}}} =} \cr \matrix{\left. {\displaystyle{{\partial \tan (\Delta \varepsilon _c )} \over {\partial \Delta \phi}}} \right|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}} \cdot \Delta \phi + \left. {\displaystyle{{\partial \tan (\Delta \varepsilon _c )} \over {\partial \Delta \eta}}} \right|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}} \cdot \left. {\Delta \eta \displaystyle{{\partial \tan (\Delta \varepsilon _c )} \over {\partial \Delta \psi}}} \right|_{\matrix{ {\Delta \phi = 0} \hfill \cr {\Delta \eta = 0} \hfill \cr {\Delta \psi = 0} \hfill \cr}} \cdot \Delta \psi + o(\Delta \phi, \Delta \eta, \Delta \psi ) = \hfill \cr \quad \quad \quad \quad \quad \quad \displaystyle{{ - x\Delta \psi - y\Delta \eta} \over {\sqrt {x^2 + y^2}}} + o(\Delta \phi, \Delta \eta, \Delta \psi ) \hfill} \cr}} \right.}$$where:
 $$\\displaystyle{{\partial \tan (\Delta \varepsilon _c )} \over {\partial \Delta \phi}} = - \displaystyle{{c(x,y,e_x, e_y )} \over {a(x,y,z,e_x, e_y, e_z )}}\left[ {z + \displaystyle{{\sqrt {x^2 + y^2} b(x,y,z,e_x, e_y, e_z )} \over {a(x,y,z,e_x, e_y, e_z )}}} \right]$$
$$\\displaystyle{{\partial \tan (\Delta \varepsilon _c )} \over {\partial \Delta \phi}} = - \displaystyle{{c(x,y,e_x, e_y )} \over {a(x,y,z,e_x, e_y, e_z )}}\left[ {z + \displaystyle{{\sqrt {x^2 + y^2} b(x,y,z,e_x, e_y, e_z )} \over {a(x,y,z,e_x, e_y, e_z )}}} \right]$$ $$ \eqalign{\displaystyle{{\partial \tan (\Delta \varepsilon _c )} \over {\partial \Delta \eta}} = \tab \displaystyle{{ - y\sqrt {x^2 + y^2} - zd(x,y,z,e_x, e_y )} \over {a(x,y,z,e_x, e_y, e_z )}} \cr \tab - \displaystyle{{\left[ {\sqrt {x^2 + y^2} d(x,y,z,e_x, e_y ) - yz} \right]b(x,y,z,e_x, e_y, e_z )} \over {a(x,y,z,e_x, e_y, e_z )^2}}} $$
$$ \eqalign{\displaystyle{{\partial \tan (\Delta \varepsilon _c )} \over {\partial \Delta \eta}} = \tab \displaystyle{{ - y\sqrt {x^2 + y^2} - zd(x,y,z,e_x, e_y )} \over {a(x,y,z,e_x, e_y, e_z )}} \cr \tab - \displaystyle{{\left[ {\sqrt {x^2 + y^2} d(x,y,z,e_x, e_y ) - yz} \right]b(x,y,z,e_x, e_y, e_z )} \over {a(x,y,z,e_x, e_y, e_z )^2}}} $$ $$\eqalign{\displaystyle{{\partial \tan (\Delta \varepsilon _c )} \over {\partial \Delta \psi}} = & \displaystyle{{ - x\sqrt {x^2 + y^2} - zf\,(x,y,z,e_x, e_y )} \over {a(x,y,z,e_x, e_y, e_z )}} \cr & - \displaystyle{{\left[ {\sqrt {x^2 + y^2} f\,(x,y,z,e_x, e_y ) - xz} \right]b(x,y,z,e_x, e_y, e_z )} \over {a(x,y,z,e_x, e_y, e_z )^2}}} $$
$$\eqalign{\displaystyle{{\partial \tan (\Delta \varepsilon _c )} \over {\partial \Delta \psi}} = & \displaystyle{{ - x\sqrt {x^2 + y^2} - zf\,(x,y,z,e_x, e_y )} \over {a(x,y,z,e_x, e_y, e_z )}} \cr & - \displaystyle{{\left[ {\sqrt {x^2 + y^2} f\,(x,y,z,e_x, e_y ) - xz} \right]b(x,y,z,e_x, e_y, e_z )} \over {a(x,y,z,e_x, e_y, e_z )^2}}} $$ $$c(x,y,e_x, e_y ) = \displaystyle{{ - 2y(x + e_x ) + 2x(y + e_y )} \over { {\2}\root \of {(x + e_x )^2 + (y + e_y )^2}}} $$
$$c(x,y,e_x, e_y ) = \displaystyle{{ - 2y(x + e_x ) + 2x(y + e_y )} \over { {\2}\root \of {(x + e_x )^2 + (y + e_y )^2}}} $$ $$d(x,y,z,e_x, e_y ) = \displaystyle{{2z(y + e_y )} \over { {\2} \root\of {(x + e_x )^2 + (y + e_y )^2}}} $$
$$d(x,y,z,e_x, e_y ) = \displaystyle{{2z(y + e_y )} \over { {\2} \root\of {(x + e_x )^2 + (y + e_y )^2}}} $$ $$f(x,y,z,e_x, e_y ) = \displaystyle{{2z(x + e_x )} \over { {\2}\root \of {(x + e_x )^2 + (y + e_y )^2}}} $$
$$f(x,y,z,e_x, e_y ) = \displaystyle{{2z(x + e_x )} \over { {\2}\root \of {(x + e_x )^2 + (y + e_y )^2}}} $$A4. SUMMARY
The results manifest that all the attitude biases can be converted to radar measurement errors. The attitude biases have no effects on radar range measurements; the yaw bias mainly affects radar azimuth measurement; and the roll and pitch biases mainly affect radar elevation measurements, their effects are related with the target location.