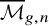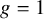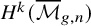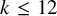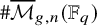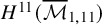1 Introduction
The Langlands program makes a number of striking predictions about the Hodge structures and Galois representations that appear in the cohomology of moduli spaces of stable curves; see [Reference Chenevier and Renard8, Section 1.2] and [Reference Bergström, Faber and Payne4, Reference Bergström and Faber3]. While the conjectured correspondence with algebraic cuspidal automorphic representations of conductor 1 remains out of reach, these representations have been classified up to weight 22 [Reference Chenevier and Lannes7], and some of the resulting predictions can now be verified unconditionally. Bergström, Faber and the third author recently proved that
![]() $H^k(\overline {\mathcal {M}}_{g,n})$
vanishes for all odd
$H^k(\overline {\mathcal {M}}_{g,n})$
vanishes for all odd
![]() $k \leq 9$
and all g and n [Reference Bergström, Faber and Payne4]. For
$k \leq 9$
and all g and n [Reference Bergström, Faber and Payne4]. For
![]() $k = 11$
, the conjectural correspondence predicts that
$k = 11$
, the conjectural correspondence predicts that
![]() $H^{11}(\overline {\mathcal {M}}_{g,n})$
is isomorphic to a direct sum of copies of
$H^{11}(\overline {\mathcal {M}}_{g,n})$
is isomorphic to a direct sum of copies of
![]() $H^{11}(\overline {\mathcal {M}}_{1,11})$
and hence should vanish in all cases where
$H^{11}(\overline {\mathcal {M}}_{1,11})$
and hence should vanish in all cases where
![]() $\overline {\mathcal {M}}_{g,n}$
is unirational. We confirm this prediction unconditionally and show that
$\overline {\mathcal {M}}_{g,n}$
is unirational. We confirm this prediction unconditionally and show that
![]() $H^{11}(\overline {\mathcal {M}}_{g,n})$
vanishes in an even wider range of cases.
$H^{11}(\overline {\mathcal {M}}_{g,n})$
vanishes in an even wider range of cases.
Theorem 1.1. The cohomology group
![]() $H^{11}(\overline {\mathcal {M}}_{g,n})$
is nonzero if and only if
$H^{11}(\overline {\mathcal {M}}_{g,n})$
is nonzero if and only if
![]() $g = 1$
and
$g = 1$
and
![]() $n \geq 11$
.
$n \geq 11$
.
For
![]() $g = 1$
and
$g = 1$
and
![]() $n \geq 11$
,
$n \geq 11$
,
![]() $H^{11}(\overline {\mathcal {M}}_{1,n})$
is isomorphic to a direct sum of
$H^{11}(\overline {\mathcal {M}}_{1,n})$
is isomorphic to a direct sum of
![]() $\binom {n-1}{10}$
copies of
$\binom {n-1}{10}$
copies of
![]() $H^{11}(\overline {\mathcal {M}}_{1,11})$
[Reference Getzler14]; in particular, it decomposes as
$H^{11}(\overline {\mathcal {M}}_{1,11})$
[Reference Getzler14]; in particular, it decomposes as
![]() $H^{11,0}(\overline {\mathcal {M}}_{1,n}) \oplus H^{0,11}(\overline {\mathcal {M}}_{1,n})$
. We show that
$H^{11,0}(\overline {\mathcal {M}}_{1,n}) \oplus H^{0,11}(\overline {\mathcal {M}}_{1,n})$
. We show that
![]() $H^{11,0}(\overline {\mathcal {M}}_{1,n})$
is generated by the pullbacks of the distinguished generator of
$H^{11,0}(\overline {\mathcal {M}}_{1,n})$
is generated by the pullbacks of the distinguished generator of
![]() $H^{11,0}(\overline {\mathcal {M}}_{1,11})$
, which corresponds to the weight 12 cusp form
$H^{11,0}(\overline {\mathcal {M}}_{1,11})$
, which corresponds to the weight 12 cusp form
![]() $\Delta $
for
$\Delta $
for
![]() $\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
, under the
$\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
, under the
![]() $\binom {n}{11}$
forgetful maps and describe the relations among these generators. In this way, we show that
$\binom {n}{11}$
forgetful maps and describe the relations among these generators. In this way, we show that
![]() $H^{11,0}(\overline {\mathcal {M}}_{1,n})$
is an irreducible
$H^{11,0}(\overline {\mathcal {M}}_{1,n})$
is an irreducible
![]() $\mathbb {S}_{n}$
-representation isomorphic to the Specht module
$\mathbb {S}_{n}$
-representation isomorphic to the Specht module
![]() $V_{n-10,1^{10}}$
.
$V_{n-10,1^{10}}$
.
Next, we address the Hodge structures and Galois representations that appear in other low degrees. The Langlands program predicts that the cohomology of
![]() $\overline {\mathcal {M}}_{g,n}$
should be pure Hodge–Tate in all even degrees less than or equal to 20. This prediction was previously confirmed only in the cases where these cohomology groups are known to be generated by tautological classes, for example, for
$\overline {\mathcal {M}}_{g,n}$
should be pure Hodge–Tate in all even degrees less than or equal to 20. This prediction was previously confirmed only in the cases where these cohomology groups are known to be generated by tautological classes, for example, for
![]() $g \leq 2$
[Reference Keel18, Reference Getzler14, Reference Petersen23], for
$g \leq 2$
[Reference Keel18, Reference Getzler14, Reference Petersen23], for
![]() $k \leq 2$
[Reference Arbarello and Cornalba1], and for
$k \leq 2$
[Reference Arbarello and Cornalba1], and for
![]() $k = 4$
and
$k = 4$
and
![]() $g \geq 8$
[Reference Polito25]. Our second result extends the confirmation of this prediction to a much wider range of cases. The proof is a double induction on g and n. The base cases are given by recent results of the first two authors, who showed that
$g \geq 8$
[Reference Polito25]. Our second result extends the confirmation of this prediction to a much wider range of cases. The proof is a double induction on g and n. The base cases are given by recent results of the first two authors, who showed that
![]() $H^*(\overline {\mathcal {M}}_{g,n})$
is tautological for
$H^*(\overline {\mathcal {M}}_{g,n})$
is tautological for
![]() $g \geq 3$
and
$g \geq 3$
and
![]() $2g + n \leq 14$
[Reference Canning and Larson5].
$2g + n \leq 14$
[Reference Canning and Larson5].
Theorem 1.2. For any even
![]() $k \leq 12$
, the cohomology group
$k \leq 12$
, the cohomology group
![]() $H^{k}(\overline {\mathcal {M}}_{g,n})$
is pure Hodge–Tate.
$H^{k}(\overline {\mathcal {M}}_{g,n})$
is pure Hodge–Tate.
It remains an open problem whether
![]() $H^k(\overline {\mathcal {M}}_{g,n})$
is generated by algebraic cycle classes for even
$H^k(\overline {\mathcal {M}}_{g,n})$
is generated by algebraic cycle classes for even
![]() ${4 \leq k \leq 12}$
.
${4 \leq k \leq 12}$
.
As an application of these two theorems, we show that the point count
![]() $\#\overline {\mathcal {M}}_{g,n}(\mathbb {F}_q)$
is surprisingly well approximated by a polynomial in q.
$\#\overline {\mathcal {M}}_{g,n}(\mathbb {F}_q)$
is surprisingly well approximated by a polynomial in q.
Corollary 1.3. Assume
![]() $g \geq 2$
, and let
$g \geq 2$
, and let
![]() $d = \dim \overline {\mathcal {M}}_{g,n}$
. Then
$d = \dim \overline {\mathcal {M}}_{g,n}$
. Then
 $$\begin{align*}\#\overline{\mathcal{M}}_{g,n}(\mathbb{F}_q) = \sum_{i=0}^6 h^{2i}(\overline{\mathcal{M}}_{g,n}) q^{d-i} + O(q^{d-13/2}).\end{align*}$$
$$\begin{align*}\#\overline{\mathcal{M}}_{g,n}(\mathbb{F}_q) = \sum_{i=0}^6 h^{2i}(\overline{\mathcal{M}}_{g,n}) q^{d-i} + O(q^{d-13/2}).\end{align*}$$
Remark 1.4. The point count
![]() $\#\overline {\mathcal {M}}_{0,n}(\mathbb {F}_q)$
is a polynomial in q, for all n, as is
$\#\overline {\mathcal {M}}_{0,n}(\mathbb {F}_q)$
is a polynomial in q, for all n, as is
![]() $\# \overline {\mathcal {M}}_{1,n}(\mathbb {F}_q)$
for
$\# \overline {\mathcal {M}}_{1,n}(\mathbb {F}_q)$
for
![]() $n \leq 10$
. For
$n \leq 10$
. For
![]() $n \geq 11$
,
$n \geq 11$
,
![]() $\# \overline {\mathcal {M}}_{1,n}(\mathbb {F}_q)$
was determined by Getzler [Reference Getzler14]; it has an approximation to order
$\# \overline {\mathcal {M}}_{1,n}(\mathbb {F}_q)$
was determined by Getzler [Reference Getzler14]; it has an approximation to order
![]() $O(q^{n-13/2})$
by a polynomial in q minus the correction term
$O(q^{n-13/2})$
by a polynomial in q minus the correction term
![]() $\binom {n-1}{10} \tau (q)$
, where
$\binom {n-1}{10} \tau (q)$
, where
![]() $\tau (q)$
denotes the coefficient of q in the Fourier expansion of the weight
$\tau (q)$
denotes the coefficient of q in the Fourier expansion of the weight
![]() $12$
cusp form
$12$
cusp form
![]() $\Delta $
for
$\Delta $
for
![]() $\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
.
$\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
.
Unlike the cohomology groups in smaller odd degrees,
![]() $H^{13}(\overline {\mathcal {M}}_{g,n})$
is nonvanishing in a wide range of cases, including for large g, as are all higher degree odd cohomology groups. Indeed, Pikaart showed that
$H^{13}(\overline {\mathcal {M}}_{g,n})$
is nonvanishing in a wide range of cases, including for large g, as are all higher degree odd cohomology groups. Indeed, Pikaart showed that
![]() $H^{13}(\overline {\mathcal {M}}_{g,n})$
is nonvanishing for
$H^{13}(\overline {\mathcal {M}}_{g,n})$
is nonvanishing for
![]() $n \geq 10$
and g sufficiently large, as is
$n \geq 10$
and g sufficiently large, as is
![]() $H^{33}(\overline {\mathcal {M}}_g)$
[Reference Pikaart24]. Similar nonvanishing statements in higher degrees follow immediately, by Hard Lefschetz. The bounds on g that come from Pikaart’s method are large, typically in the thousands. For instance, van Zelm computes that Pikaart’s method yields
$H^{33}(\overline {\mathcal {M}}_g)$
[Reference Pikaart24]. Similar nonvanishing statements in higher degrees follow immediately, by Hard Lefschetz. The bounds on g that come from Pikaart’s method are large, typically in the thousands. For instance, van Zelm computes that Pikaart’s method yields
![]() $H^{33}(\overline {\mathcal {M}}_{g,1}) \neq 0$
for
$H^{33}(\overline {\mathcal {M}}_{g,1}) \neq 0$
for
![]() $g \geq 8069$
. The bounds for
$g \geq 8069$
. The bounds for
![]() $H^{13}(\overline {\mathcal {M}}_{g,10})$
and
$H^{13}(\overline {\mathcal {M}}_{g,10})$
and
![]() $H^{33}(\overline {\mathcal {M}}_{g})$
are not explicitly stated in the literature, but there is substantial evidence that such bounds should be far from optimal. While Pikaart’s constructions prove the existence of nontautological algebraic cycle classes on
$H^{33}(\overline {\mathcal {M}}_{g})$
are not explicitly stated in the literature, but there is substantial evidence that such bounds should be far from optimal. While Pikaart’s constructions prove the existence of nontautological algebraic cycle classes on
![]() $\overline {\mathcal {M}}_g$
for
$\overline {\mathcal {M}}_g$
for
![]() $g \geq 16192$
, van Zelm proved that this holds for
$g \geq 16192$
, van Zelm proved that this holds for
![]() $g \geq 12$
[Reference van Zelm28]. Also, Bergström and Faber have recently shown that
$g \geq 12$
[Reference van Zelm28]. Also, Bergström and Faber have recently shown that
![]() $H^{13}(\overline {\mathcal {M}}_{2,n}) \neq 0$
for
$H^{13}(\overline {\mathcal {M}}_{2,n}) \neq 0$
for
![]() $n \geq 10$
. They also prove that the nonvanishing of
$n \geq 10$
. They also prove that the nonvanishing of
![]() $H^{13}(\overline {\mathcal {M}}_{3,n})$
for
$H^{13}(\overline {\mathcal {M}}_{3,n})$
for
![]() $n \geq 10$
follows from conjectural parts of the Langlands correspondence. Here, we prove the latter statement unconditionally, extend it to all higher genera, and also improve Pikaart’s bound for the nonvanishing of
$n \geq 10$
follows from conjectural parts of the Langlands correspondence. Here, we prove the latter statement unconditionally, extend it to all higher genera, and also improve Pikaart’s bound for the nonvanishing of
![]() $H^{33}(\overline {\mathcal {M}}_g)$
.
$H^{33}(\overline {\mathcal {M}}_g)$
.
Theorem 1.5. Assume
![]() $k \leq 11$
. Let
$k \leq 11$
. Let
![]() $g_1,\dots ,g_k$
be distinct positive integers, and set
$g_1,\dots ,g_k$
be distinct positive integers, and set
![]() $g=1 + g_1+\cdots +g_k$
. Then
$g=1 + g_1+\cdots +g_k$
. Then
In particular,
![]() $H^{13}(\overline {\mathcal {M}}_{g,n})\neq 0$
for
$H^{13}(\overline {\mathcal {M}}_{g,n})\neq 0$
for
![]() $g\geq 2$
and
$g\geq 2$
and
![]() $n\geq 10$
, and
$n\geq 10$
, and
![]() $H^{33}(\overline {\mathcal {M}}_g)\neq 0$
for
$H^{33}(\overline {\mathcal {M}}_g)\neq 0$
for
![]() $g\geq 67$
.
$g\geq 67$
.
As a further application, we prove the existence of nontautological classes in the Chow rings
![]() $A^*(\overline {\mathcal {M}}_{g,n})$
in a number of cases where this was not previously known.
$A^*(\overline {\mathcal {M}}_{g,n})$
in a number of cases where this was not previously known.
Corollary 1.6. Consider
![]() $\overline {\mathcal {M}}_{g,n}$
as a stack over
$\overline {\mathcal {M}}_{g,n}$
as a stack over
![]() $\mathbb {C}$
. For any
$\mathbb {C}$
. For any
![]() $(g,n)$
as in Theorem 1.5, the quotient
$(g,n)$
as in Theorem 1.5, the quotient
![]() $A^*(\overline {\mathcal {M}}_{g,n})/R^*(\overline {\mathcal {M}}_{g,n})$
is uncountable, as is the subgroup of
$A^*(\overline {\mathcal {M}}_{g,n})/R^*(\overline {\mathcal {M}}_{g,n})$
is uncountable, as is the subgroup of
![]() $A^*(\overline {\mathcal {M}}_{g,n})$
generated by cycles algebraically equivalent to zero.
$A^*(\overline {\mathcal {M}}_{g,n})$
generated by cycles algebraically equivalent to zero.
This provides many new examples of
![]() $(g,n)$
for which
$(g,n)$
for which
![]() $A^*(\overline {\mathcal {M}}_{g,n})$
is not tautological. In particular, the existence of nontautological Chow classes is new for
$A^*(\overline {\mathcal {M}}_{g,n})$
is not tautological. In particular, the existence of nontautological Chow classes is new for
![]() $(4,n)$
with
$(4,n)$
with
![]() $9\leq n\leq 16$
; for
$9\leq n\leq 16$
; for
![]() $(5,n)$
with
$(5,n)$
with
![]() $9\leq n\leq 13$
; for
$9\leq n\leq 13$
; for
![]() $(6,n)$
with
$(6,n)$
with
![]() $9\leq n\leq 11$
and for
$9\leq n\leq 11$
and for
![]() $(7,8)$
and
$(7,8)$
and
![]() $(7,9)$
.
$(7,9)$
.
Existence results for nontautological classes come in two flavors. There are cases where one can write down explicit examples of nontautological Chow classes. Graber and Pandharipande gave the first such example when
![]() $(g,n)=(2,20)$
[Reference Graber and Pandharipande17]. Van Zelm generalized their example to show the existence of explicit nontautological Chow classes on
$(g,n)=(2,20)$
[Reference Graber and Pandharipande17]. Van Zelm generalized their example to show the existence of explicit nontautological Chow classes on
![]() $\overline {\mathcal {M}}_{g,n}$
for
$\overline {\mathcal {M}}_{g,n}$
for
![]() $2g+n\geq 24$
and
$2g+n\geq 24$
and
![]() $g\geq 2$
[Reference van Zelm28]. A nice feature of these examples is that they are nontautological in both Chow and cohomology. There are also the inexplicit nontautological Chow classes, which arise from the existence of odd cohomology. The first such examples are for
$g\geq 2$
[Reference van Zelm28]. A nice feature of these examples is that they are nontautological in both Chow and cohomology. There are also the inexplicit nontautological Chow classes, which arise from the existence of odd cohomology. The first such examples are for
![]() $g=1, n\geq 11$
, where the existence of a holomorphic 11-form implies that
$g=1, n\geq 11$
, where the existence of a holomorphic 11-form implies that
![]() $A_{0}(\overline {\mathcal {M}}_{1,n})$
is infinite dimensional [Reference Roĭtman26]. Bergström and Faber showed that there is odd cohomology on
$A_{0}(\overline {\mathcal {M}}_{1,n})$
is infinite dimensional [Reference Roĭtman26]. Bergström and Faber showed that there is odd cohomology on
![]() $\overline {\mathcal {M}}_{2,n}$
for
$\overline {\mathcal {M}}_{2,n}$
for
![]() $n\geq 10$
[Reference Bergström and Faber3], implying that there are nontautological Chow classes as well, by results of Kimura and Totaro [Reference Kimura19, Reference Totaro27]; see Theorem 7.1. The examples provided by Corollary 1.6 are also of this inexplicit form. We do not know whether all of the nontautological classes in these inexplicit cases are homologically equivalent to zero.
$n\geq 10$
[Reference Bergström and Faber3], implying that there are nontautological Chow classes as well, by results of Kimura and Totaro [Reference Kimura19, Reference Totaro27]; see Theorem 7.1. The examples provided by Corollary 1.6 are also of this inexplicit form. We do not know whether all of the nontautological classes in these inexplicit cases are homologically equivalent to zero.
1.1 Methods
Arbarello and Cornalba introduced an inductive method for studying cohomology groups of
![]() $\overline {\mathcal {M}}_{g,n}$
and applied this to prove the vanishing of
$\overline {\mathcal {M}}_{g,n}$
and applied this to prove the vanishing of
![]() $H^k(\overline {\mathcal {M}}_{g,n})$
for
$H^k(\overline {\mathcal {M}}_{g,n})$
for
![]() $k \in \{1,3,5\}$
[Reference Arbarello and Cornalba1]. The same method was used to prove vanishing for
$k \in \{1,3,5\}$
[Reference Arbarello and Cornalba1]. The same method was used to prove vanishing for
![]() $k \in \{7,9\}$
after establishing the additional base cases needed to run the induction, via point counting over finite fields [Reference Bergström, Faber and Payne4]. Our proof of Theorems 1.1 and 1.2 start from the observation that the same induction can be used to control the Hodge structures and Galois representations that appear in
$k \in \{7,9\}$
after establishing the additional base cases needed to run the induction, via point counting over finite fields [Reference Bergström, Faber and Payne4]. Our proof of Theorems 1.1 and 1.2 start from the observation that the same induction can be used to control the Hodge structures and Galois representations that appear in
![]() $H^k(\overline {\mathcal {M}}_{g,n})$
even when these groups do not vanish. The first two authors recently established the base cases needed for
$H^k(\overline {\mathcal {M}}_{g,n})$
even when these groups do not vanish. The first two authors recently established the base cases needed for
![]() $k \leq 12$
[Reference Canning and Larson5]. Running this induction when k is even leads directly to Theorem 1.2. Doing so for
$k \leq 12$
[Reference Canning and Larson5]. Running this induction when k is even leads directly to Theorem 1.2. Doing so for
![]() $k = 11$
shows that
$k = 11$
shows that
![]() $H^{11}(\overline {\mathcal {M}}_{g,n})$
injects into a direct sum of copies of
$H^{11}(\overline {\mathcal {M}}_{g,n})$
injects into a direct sum of copies of
![]() $H^{11}(\overline {\mathcal {M}}_{1,11})$
(Proposition 3.5). This is enough to confirm the prediction that
$H^{11}(\overline {\mathcal {M}}_{1,11})$
(Proposition 3.5). This is enough to confirm the prediction that
![]() $H^{11}(\overline {\mathcal {M}}_{g,n})$
vanishes whenever
$H^{11}(\overline {\mathcal {M}}_{g,n})$
vanishes whenever
![]() $\overline {\mathcal {M}}_{g,n}$
is unirational, but a different argument is needed to prove that it vanishes whenever
$\overline {\mathcal {M}}_{g,n}$
is unirational, but a different argument is needed to prove that it vanishes whenever
![]() $g \geq 2$
.
$g \geq 2$
.
The Arbarello–Cornalba induction uses the excision sequence for the pair of
![]() $\overline {\mathcal {M}}_{g,n}$
with its boundary
$\overline {\mathcal {M}}_{g,n}$
with its boundary
![]() $\partial \mathcal {M}_{g,n}:=\overline {\mathcal {M}}_{g,n}\smallsetminus \mathcal {M}_{g,n}$
, along with the map
$\partial \mathcal {M}_{g,n}:=\overline {\mathcal {M}}_{g,n}\smallsetminus \mathcal {M}_{g,n}$
, along with the map
given by pullback to the normalization of the boundary. Our proof of Theorem 1.1 uses the observation that the map (1.1) is the first arrow in a natural chain complex whose jth term may be identified with the cohomology of the normalization of the closure of the codimension j boundary strata with coefficients in a natural local system, the determinant of the permutation representation on the branches of the boundary divisor. This complex has several natural interpretations: It is the kth weight-graded piece of the Feynman transform of the modular operad that takes the value
![]() $\mathbb {Q}$
for every
$\mathbb {Q}$
for every
![]() $(g,n)$
[Reference Getzler and Kapranov16]. It is also the weight k row in the
$(g,n)$
[Reference Getzler and Kapranov16]. It is also the weight k row in the
![]() $E_1$
-page of a natural spectral sequence obtained via Poincaré duality from Deligne’s weight spectral sequence for the pair
$E_1$
-page of a natural spectral sequence obtained via Poincaré duality from Deligne’s weight spectral sequence for the pair
![]() $(\overline {\mathcal {M}}_{g,n}, \partial \mathcal {M}_{g,n})$
and has a natural interpretation as a decorated graph complex [Reference Payne and Willwacher20, Section 2.3].
$(\overline {\mathcal {M}}_{g,n}, \partial \mathcal {M}_{g,n})$
and has a natural interpretation as a decorated graph complex [Reference Payne and Willwacher20, Section 2.3].
For
![]() $k = 11$
, we examine the first two maps in this complex. Assuming that
$k = 11$
, we examine the first two maps in this complex. Assuming that
![]() $H^{11}(\overline {\mathcal {M}}_{2,n})$
vanishes for all n, a double induction on g and n shows that
$H^{11}(\overline {\mathcal {M}}_{2,n})$
vanishes for all n, a double induction on g and n shows that
![]() $H^{11}(\overline {\mathcal {M}}_{g,n})$
vanishes whenever
$H^{11}(\overline {\mathcal {M}}_{g,n})$
vanishes whenever
![]() $g> 2$
. In Section 4.3, we prove the needed base cases, that is, the vanishing of
$g> 2$
. In Section 4.3, we prove the needed base cases, that is, the vanishing of
![]() $H^{11}(\overline {\mathcal {M}}_{2,n})$
for all n, by explicit calculations using the generators and relations for
$H^{11}(\overline {\mathcal {M}}_{2,n})$
for all n, by explicit calculations using the generators and relations for
![]() $H^{11}(\overline {\mathcal {M}}_{1,n})$
. It should also be possible to deduce these base cases from results of Petersen [Reference Petersen23, Reference Petersen22]; see Remark 4.3.
$H^{11}(\overline {\mathcal {M}}_{1,n})$
. It should also be possible to deduce these base cases from results of Petersen [Reference Petersen23, Reference Petersen22]; see Remark 4.3.
1.2 Structure of the paper
In Section 2, we recall how to extract
![]() $H^{11}(\overline {\mathcal {M}}_{1,n})$
with its Hodge structure or Galois representation from the work of Getzler [Reference Getzler14]. We then describe generators and relations for this group and describe the
$H^{11}(\overline {\mathcal {M}}_{1,n})$
with its Hodge structure or Galois representation from the work of Getzler [Reference Getzler14]. We then describe generators and relations for this group and describe the
![]() $\mathbb {S}_n$
-action and the pullback under tautological morphisms in terms of these generators. In Section 3, we recall the inductive method of Arbarello and Cornalba and use it to prove Theorem 1.2. In Section 4, we present the inductive argument for vanishing of
$\mathbb {S}_n$
-action and the pullback under tautological morphisms in terms of these generators. In Section 3, we recall the inductive method of Arbarello and Cornalba and use it to prove Theorem 1.2. In Section 4, we present the inductive argument for vanishing of
![]() $H^{11}(\overline {\mathcal {M}}_{g,n})$
for
$H^{11}(\overline {\mathcal {M}}_{g,n})$
for
![]() $g> 2$
, using the weight spectral sequence, assuming the vanishing for
$g> 2$
, using the weight spectral sequence, assuming the vanishing for
![]() $g = 2$
. We then prove the vanishing in the necessary base cases, for
$g = 2$
. We then prove the vanishing in the necessary base cases, for
![]() $g = 2$
, using the explicit generators and relations for
$g = 2$
, using the explicit generators and relations for
![]() $g = 1$
. In Sections 5, 6 and 7, we prove Corollary 1.3, Theorem 1.5 and Corollary 1.6, respectively.
$g = 1$
. In Sections 5, 6 and 7, we prove Corollary 1.3, Theorem 1.5 and Corollary 1.6, respectively.
1.3 Notations and conventions
We denote by
![]() $H^{k}(\overline {\mathcal {M}}_{g,n})$
either the
$H^{k}(\overline {\mathcal {M}}_{g,n})$
either the
![]() $\mathbb {Q}$
-Hodge structure
$\mathbb {Q}$
-Hodge structure
![]() $H^{k}((\overline {\mathcal {M}}_{g,n})_{\mathbb {C}},\mathbb {Q})$
or the absolute Galois representation
$H^{k}((\overline {\mathcal {M}}_{g,n})_{\mathbb {C}},\mathbb {Q})$
or the absolute Galois representation
![]() $H^{k}_{\mathrm{\acute{e}t}}((\overline {\mathcal {M}}_{g,n})_{\overline {\mathbb {Q}}},\mathbb {Q}_{\ell })$
. We write
$H^{k}_{\mathrm{\acute{e}t}}((\overline {\mathcal {M}}_{g,n})_{\overline {\mathbb {Q}}},\mathbb {Q}_{\ell })$
. We write
![]() $\mathsf {L}$
for the Tate motive. We say that
$\mathsf {L}$
for the Tate motive. We say that
![]() $H^k(\overline {\mathcal {M}}_{g,n})$
is pure Hodge–Tate if it is isomorphic to a direct sum of the Betti or
$H^k(\overline {\mathcal {M}}_{g,n})$
is pure Hodge–Tate if it is isomorphic to a direct sum of the Betti or
![]() $\ell $
-adic realizations of powers of
$\ell $
-adic realizations of powers of
![]() $\mathsf {L}$
. We write
$\mathsf {L}$
. We write
![]() $\mathsf {S}_{12}$
for the motive associated to the weight
$\mathsf {S}_{12}$
for the motive associated to the weight
![]() $12$
modular form
$12$
modular form
![]() $\Delta $
, whose Betti and
$\Delta $
, whose Betti and
![]() $\ell $
-adic realizations are
$\ell $
-adic realizations are
![]() $H^{11}(\overline {\mathcal {M}}_{1,11})$
. We denote by
$H^{11}(\overline {\mathcal {M}}_{1,11})$
. We denote by
![]() $A^*(X)$
the Chow ring with rational coefficients of a variety or Deligne–Mumford stack X.
$A^*(X)$
the Chow ring with rational coefficients of a variety or Deligne–Mumford stack X.
2 Genus
 $1$
$1$
In this section, we give explicit generators and relations for
![]() $H^{11}(\overline {\mathcal {M}}_{1,n})$
and describe the
$H^{11}(\overline {\mathcal {M}}_{1,n})$
and describe the
![]() $\mathbb {S}_n$
-action and the pullback to boundary divisors in terms of these generators. These formulas will be used in Section 4.3.2, in our proof that
$\mathbb {S}_n$
-action and the pullback to boundary divisors in terms of these generators. These formulas will be used in Section 4.3.2, in our proof that
![]() $H^{11}(\overline {\mathcal {M}}_{2,n}) = 0$
.
$H^{11}(\overline {\mathcal {M}}_{2,n}) = 0$
.
2.1 Dimension and Hodge structure
We start by explaining how to extract
![]() $H^{11}(\overline {\mathcal {M}}_{1,n})$
with its Hodge structure or Galois representation from [Reference Getzler14]. Getzler gives generating functions that determine the cohomology groups
$H^{11}(\overline {\mathcal {M}}_{1,n})$
with its Hodge structure or Galois representation from [Reference Getzler14]. Getzler gives generating functions that determine the cohomology groups
![]() $H^{*}(\overline {\mathcal {M}}_{1,n})$
with their
$H^{*}(\overline {\mathcal {M}}_{1,n})$
with their
![]() $\mathbb {S}_n$
-actions. These formulas simplify substantially when forgetting the
$\mathbb {S}_n$
-actions. These formulas simplify substantially when forgetting the
![]() $\mathbb {S}_n$
-action, so we begin by using Getzler’s formula to extract
$\mathbb {S}_n$
-action, so we begin by using Getzler’s formula to extract
![]() $H^{11}(\overline {\mathcal {M}}_{1,n})$
nonequivariantly. Below, as in [Reference Getzler14], we write
$H^{11}(\overline {\mathcal {M}}_{1,n})$
nonequivariantly. Below, as in [Reference Getzler14], we write
![]() $\mathsf {L}$
for the Tate motive and
$\mathsf {L}$
for the Tate motive and
![]() $\mathsf {S}_{2k+2}$
for the Hodge structure associated to the space of cusp forms of weight
$\mathsf {S}_{2k+2}$
for the Hodge structure associated to the space of cusp forms of weight
![]() $2k+2$
(see [Reference Getzler14, p. 489] for definition). We note that
$2k+2$
(see [Reference Getzler14, p. 489] for definition). We note that
![]() $\mathsf {S}_{2k+2} = 0$
for
$\mathsf {S}_{2k+2} = 0$
for
![]() $k \leq 4$
.
$k \leq 4$
.
Lemma 2.1. The cohomology group
![]() $H^{11}(\overline {\mathcal {M}}_{1,n})$
is a direct sum of
$H^{11}(\overline {\mathcal {M}}_{1,n})$
is a direct sum of
![]() ${n-1 \choose 10}$
copies of
${n-1 \choose 10}$
copies of
![]() $\mathsf {S}_{12}$
.
$\mathsf {S}_{12}$
.
Proof. Let
![]() $\mathsf {e}^{\mathbb {S}_n}(\mathcal {M})$
denote the
$\mathsf {e}^{\mathbb {S}_n}(\mathcal {M})$
denote the
![]() $\mathbb {S}_n$
-equivariant Euler characteristic of
$\mathbb {S}_n$
-equivariant Euler characteristic of
![]() $\mathcal {M}$
in the Grothendieck ring of equivariant mixed Hodge structures. Getzler defines two families of generating functions
$\mathcal {M}$
in the Grothendieck ring of equivariant mixed Hodge structures. Getzler defines two families of generating functions
![]() $\mathbf {a}_i = \sum \mathsf {e}^{\mathbb {S}_n}(\mathcal {M}_{i,n})$
and
$\mathbf {a}_i = \sum \mathsf {e}^{\mathbb {S}_n}(\mathcal {M}_{i,n})$
and
![]() $\mathbf {b}_i = \sum \mathsf {e}^{\mathbb {S}_n}(\overline {\mathcal {M}}_{i,n})$
. For
$\mathbf {b}_i = \sum \mathsf {e}^{\mathbb {S}_n}(\overline {\mathcal {M}}_{i,n})$
. For
![]() $i = 0$
or
$i = 0$
or
![]() $1$
, these generating functions are power series in the Hodge structures
$1$
, these generating functions are power series in the Hodge structures
![]() $\mathsf {L}$
and
$\mathsf {L}$
and
![]() $\mathsf {S}_{2k+2}$
whose coefficients are symmetric functions.
$\mathsf {S}_{2k+2}$
whose coefficients are symmetric functions.
To get to the ordinary Euler characteristic generating function
![]() $\mathsf {e}(\mathcal {M})$
from
$\mathsf {e}(\mathcal {M})$
from
![]() $\mathsf {e}^{\mathbb {S}_n}(\mathcal {M})$
, we apply Getzler’s
$\mathsf {e}^{\mathbb {S}_n}(\mathcal {M})$
, we apply Getzler’s
![]() $\mathrm {rk}$
functor, which is defined by setting the power sums to
$\mathrm {rk}$
functor, which is defined by setting the power sums to
![]() $p_1 = x$
and
$p_1 = x$
and
![]() $p_n = 0$
for
$p_n = 0$
for
![]() $n> 0$
. It sends
$n> 0$
. It sends
![]() $\mathsf {e}^{\mathbb {S}_n}(\overline {\mathcal {M}}_{i,n})$
to
$\mathsf {e}^{\mathbb {S}_n}(\overline {\mathcal {M}}_{i,n})$
to
![]() $\mathsf {e}(\overline {\mathcal {M}}_{i,n}) \frac {x^n}{n!}$
[Reference Getzler14, p. 484]. We shall write
$\mathsf {e}(\overline {\mathcal {M}}_{i,n}) \frac {x^n}{n!}$
[Reference Getzler14, p. 484]. We shall write
![]() $a_i = \mathrm {rk}(\mathbf {a}_i)$
and
$a_i = \mathrm {rk}(\mathbf {a}_i)$
and
![]() $b_i = \mathrm {rk}(\mathbf {b}_i)$
, which are power series in
$b_i = \mathrm {rk}(\mathbf {b}_i)$
, which are power series in
![]() $\mathsf {L}$
and
$\mathsf {L}$
and
![]() $\mathsf {S}_{2k+2}$
when
$\mathsf {S}_{2k+2}$
when
![]() $i = 0$
or
$i = 0$
or
![]() $1$
. For example,
$1$
. For example,
 $$\begin{align*}b_0 = \mathrm{rk}(\mathbf{b}_0) = \sum_{n \geq 3} \mathsf{e}(\overline{\mathcal{M}}_{0,n}) \frac{x^n}{n!}. \end{align*}$$
$$\begin{align*}b_0 = \mathrm{rk}(\mathbf{b}_0) = \sum_{n \geq 3} \mathsf{e}(\overline{\mathcal{M}}_{0,n}) \frac{x^n}{n!}. \end{align*}$$
Important for us is that
For
![]() $b_1$
, we are interested in the coefficient of
$b_1$
, we are interested in the coefficient of
![]() $\frac {x^n}{n!}\mathsf {S}_{12}$
, which is equal to the negative of the multiplicity of
$\frac {x^n}{n!}\mathsf {S}_{12}$
, which is equal to the negative of the multiplicity of
![]() $\mathsf {S}_{12}$
in
$\mathsf {S}_{12}$
in
![]() $H^{11}(\overline {\mathcal {M}}_{1,n})$
by construction. Applying
$H^{11}(\overline {\mathcal {M}}_{1,n})$
by construction. Applying
![]() $\mathrm {rk}$
to [Reference Getzler14, Theorem 2.5] relates
$\mathrm {rk}$
to [Reference Getzler14, Theorem 2.5] relates
![]() $b_1$
to
$b_1$
to
![]() $a_1$
. Note that the symbol
$a_1$
. Note that the symbol
![]() $\circ $
in [Reference Getzler14, Theorem 2.5] denotes plethysm of symmetric functions; applying
$\circ $
in [Reference Getzler14, Theorem 2.5] denotes plethysm of symmetric functions; applying
![]() $\mathrm {rk}$
turns this plethysm into composition of functions, as can be seen from the properties characterizing plethysm in [Reference Getzler13, Section 5.2]. In particular, we find
$\mathrm {rk}$
turns this plethysm into composition of functions, as can be seen from the properties characterizing plethysm in [Reference Getzler13, Section 5.2]. In particular, we find
The terms built from
![]() $a_0$
cannot contribute to the coefficient of
$a_0$
cannot contribute to the coefficient of
![]() $\mathsf {S}_{12}$
. (We note that there is a small error in [Reference Getzler14, Theorem 2.5], which is corrected in [Reference Consani and Faber9, p. 306], but it occurs in these terms built from
$\mathsf {S}_{12}$
. (We note that there is a small error in [Reference Getzler14, Theorem 2.5], which is corrected in [Reference Consani and Faber9, p. 306], but it occurs in these terms built from
![]() $a_0$
, and thus will not affect the outcome of our calculation.)
$a_0$
, and thus will not affect the outcome of our calculation.)
To expand the right-hand side of equation (2.1), apply
![]() $\mathrm {rk}$
to the equation for
$\mathrm {rk}$
to the equation for
![]() $\mathbf {a}_1$
in [Reference Getzler14, p. 489], and then plug in
$\mathbf {a}_1$
in [Reference Getzler14, p. 489], and then plug in
![]() $x + b_0'$
for x (so substitute
$x + b_0'$
for x (so substitute
![]() $p_1 = x+b_0'$
and
$p_1 = x+b_0'$
and
![]() $p_n = 0$
for
$p_n = 0$
for
![]() $n> 1$
):
$n> 1$
):
 $$ \begin{align*} \begin{split} a_1 (x + b_0') &= \mathrm{res}_0{} \Bigg[ \frac{(1 + x + b_0')^{1 - \omega -\mathsf{L}/\omega + \mathsf{L}}-1}{1 - \omega -\mathsf{L}/\omega + \mathsf{L}} \\ & \qquad\qquad\times \left(\sum_{k=1}^\infty \left(\frac{\mathsf{S}_{2k+2} + 1}{\mathsf{L}^{2k+1}}\right) \omega^{2k} - 1\right)(\omega - \mathsf{L}/\omega )d\omega \Bigg] {}. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} a_1 (x + b_0') &= \mathrm{res}_0{} \Bigg[ \frac{(1 + x + b_0')^{1 - \omega -\mathsf{L}/\omega + \mathsf{L}}-1}{1 - \omega -\mathsf{L}/\omega + \mathsf{L}} \\ & \qquad\qquad\times \left(\sum_{k=1}^\infty \left(\frac{\mathsf{S}_{2k+2} + 1}{\mathsf{L}^{2k+1}}\right) \omega^{2k} - 1\right)(\omega - \mathsf{L}/\omega )d\omega \Bigg] {}. \end{split} \end{align*} $$
In the middle parenthesized term,
![]() $\mathsf {S}_{12}$
is multiplied by
$\mathsf {S}_{12}$
is multiplied by
![]() $\omega ^{10}/\mathsf {L}^{11}$
. Since we need to take the residue at
$\omega ^{10}/\mathsf {L}^{11}$
. Since we need to take the residue at
![]() $0$
with respect to
$0$
with respect to
![]() $\omega $
, the coefficient of
$\omega $
, the coefficient of
![]() $\mathsf {S}_{12}$
appears when the other terms combine to give
$\mathsf {S}_{12}$
appears when the other terms combine to give
![]() $\mathsf {L}^{11}/\omega ^{11}$
. To get
$\mathsf {L}^{11}/\omega ^{11}$
. To get
![]() $\mathsf {L}^{11}/\omega ^{11}$
, we must use the
$\mathsf {L}^{11}/\omega ^{11}$
, we must use the
![]() $-\mathsf {L}/\omega $
piece of the
$-\mathsf {L}/\omega $
piece of the
![]() $(\omega - \mathsf {L}/\omega )$
term. Similarly, when we expand the first term, only the powers of
$(\omega - \mathsf {L}/\omega )$
term. Similarly, when we expand the first term, only the powers of
![]() $\mathsf {L}/\omega $
are relevant. From this, we see that the coefficient of
$\mathsf {L}/\omega $
are relevant. From this, we see that the coefficient of
![]() $\mathsf {S}_{12}$
in the above display is the negative of the coefficient of
$\mathsf {S}_{12}$
in the above display is the negative of the coefficient of
![]() $y^{10}$
in
$y^{10}$
in
 $$\begin{align*}\frac{(1 + x + b_0')^{1 + y}}{1+y} = \frac{e^{x(1+y)}}{1 + y} + \langle \mathsf{L} \rangle = \sum_{n = 1}^\infty \frac{x^n}{n!}(y+1)^{n-1} + \langle \mathsf{L} \rangle. \end{align*}$$
$$\begin{align*}\frac{(1 + x + b_0')^{1 + y}}{1+y} = \frac{e^{x(1+y)}}{1 + y} + \langle \mathsf{L} \rangle = \sum_{n = 1}^\infty \frac{x^n}{n!}(y+1)^{n-1} + \langle \mathsf{L} \rangle. \end{align*}$$
In conclusion,
![]() $H^{11}(\overline {\mathcal {M}}_{1,n})$
consists of
$H^{11}(\overline {\mathcal {M}}_{1,n})$
consists of
![]() ${n-1 \choose 10}$
copies of
${n-1 \choose 10}$
copies of
![]() $\mathsf {S}_{12}$
.
$\mathsf {S}_{12}$
.
Getzler’s formulas also encode the
![]() $\mathbb {S}_n$
-action on
$\mathbb {S}_n$
-action on
![]() $H^{11}(\overline {\mathcal {M}}_{1,n})$
. We recover this information in a different way, by describing generators on which the
$H^{11}(\overline {\mathcal {M}}_{1,n})$
. We recover this information in a different way, by describing generators on which the
![]() $\mathbb {S}_n$
-action is evident, as follows.
$\mathbb {S}_n$
-action is evident, as follows.
2.2 Generators and their pullbacks
To begin, in the case
![]() $n = 11$
, Lemma 2.1 tells us
$n = 11$
, Lemma 2.1 tells us
The weight
![]() $12$
cusp form of
$12$
cusp form of
![]() $\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
gives rise to a distinguished generator
$\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
gives rise to a distinguished generator
![]() $\omega \in H^{11,0}(\overline {\mathcal {M}}_{1,11})$
; see [Reference Faber and Pandharipande12, p. 14] for an explicit geometric construction. It is evident from this construction (or from [Reference Getzler14]) that
$\omega \in H^{11,0}(\overline {\mathcal {M}}_{1,11})$
; see [Reference Faber and Pandharipande12, p. 14] for an explicit geometric construction. It is evident from this construction (or from [Reference Getzler14]) that
![]() $\mathbb {S}_{11}$
acts by the sign representation.
$\mathbb {S}_{11}$
acts by the sign representation.
We now describe a natural collection of forms in
![]() $H^{11,0}(\overline {\mathcal {M}}_{1,n})$
, which we will soon see are generators. These forms come from pulling back the distinguished generator of
$H^{11,0}(\overline {\mathcal {M}}_{1,n})$
, which we will soon see are generators. These forms come from pulling back the distinguished generator of
![]() $H^{11,0}(\overline {\mathcal {M}}_{1,11})$
under the various forgetful maps
$H^{11,0}(\overline {\mathcal {M}}_{1,11})$
under the various forgetful maps
![]() $\overline {\mathcal {M}}_{1,n} \to \overline {\mathcal {M}}_{1,11}$
. Precisely, given an ordered subset
$\overline {\mathcal {M}}_{1,n} \to \overline {\mathcal {M}}_{1,11}$
. Precisely, given an ordered subset
![]() $A \subset \{1, \ldots , n\}$
with
$A \subset \{1, \ldots , n\}$
with
![]() $|A| = 11$
, write
$|A| = 11$
, write
![]() $f_A\colon \overline {\mathcal {M}}_{1,n} \to \overline {\mathcal {M}}_{1,A} \cong \overline {\mathcal {M}}_{1,11}$
for the projection map and define
$f_A\colon \overline {\mathcal {M}}_{1,n} \to \overline {\mathcal {M}}_{1,A} \cong \overline {\mathcal {M}}_{1,11}$
for the projection map and define
![]() $\omega _A := f_A^*\omega \in H^{11,0}(\overline {\mathcal {M}}_{1,n})$
.
$\omega _A := f_A^*\omega \in H^{11,0}(\overline {\mathcal {M}}_{1,n})$
.
The pullbacks of these forms to boundary divisors follow a simple rule. By the Künneth formula, the only boundary divisors of
![]() $\overline {\mathcal {M}}_{1,n}$
with nonzero
$\overline {\mathcal {M}}_{1,n}$
with nonzero
![]() $H^{11}$
are those of the form
$H^{11}$
are those of the form
where
![]() $|B| \geq 10$
and
$|B| \geq 10$
and
![]() $\iota _B\colon D_B \to \overline {\mathcal {M}}_{1,n}$
is the map that glues p to q. In this case, projection onto the first factor
$\iota _B\colon D_B \to \overline {\mathcal {M}}_{1,n}$
is the map that glues p to q. In this case, projection onto the first factor
![]() $\mathrm {pr}_1\colon D_B \to \overline {\mathcal {M}}_{1,B \cup p}$
induces an isomorphism
$\mathrm {pr}_1\colon D_B \to \overline {\mathcal {M}}_{1,B \cup p}$
induces an isomorphism
Given ordered subsets A and B of
![]() $\{1, \ldots , n\}$
with
$\{1, \ldots , n\}$
with
![]() $|A| = 11$
and
$|A| = 11$
and
![]() $|A \cap B| = 10$
, there is a unique element
$|A \cap B| = 10$
, there is a unique element
![]() $i \in A$
such that
$i \in A$
such that
![]() $i \notin B$
. Let
$i \notin B$
. Let
![]() $\epsilon (A)$
denote the ordered set obtained from A by replacing i with p, so
$\epsilon (A)$
denote the ordered set obtained from A by replacing i with p, so
![]() $\epsilon (A)$
is a subset of B. If
$\epsilon (A)$
is a subset of B. If
![]() $|A \cap B| = 11$
so that A is already contained in B, then we set
$|A \cap B| = 11$
so that A is already contained in B, then we set
![]() $\epsilon (A) = A$
.
$\epsilon (A) = A$
.
Lemma 2.2. Given a boundary divisor
![]() $\iota _B\colon D_B \to \overline {\mathcal {M}}_{1,n}$
, and
$\iota _B\colon D_B \to \overline {\mathcal {M}}_{1,n}$
, and
![]() $A \subset \{1, \ldots ,n\}$
with
$A \subset \{1, \ldots ,n\}$
with
![]() $|A| = 11$
, we have
$|A| = 11$
, we have
 $$\begin{align*}\iota_B^*\omega_A = \begin{cases} \mathrm{pr}_1^*\omega_{\epsilon(A)} & \text{if }|A \cap B| \geq 10 \\ 0 & \text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}\iota_B^*\omega_A = \begin{cases} \mathrm{pr}_1^*\omega_{\epsilon(A)} & \text{if }|A \cap B| \geq 10 \\ 0 & \text{otherwise.} \end{cases} \end{align*}$$
Proof. First, suppose
![]() $|A \cap B| \leq 9$
, so
$|A \cap B| \leq 9$
, so
![]() $|A \cap B^c|\geq 2$
. Then there is a commutative diagram
$|A \cap B^c|\geq 2$
. Then there is a commutative diagram

where the horizontal maps glue p to q and the vertical maps forget markings not in A. In this case, the image of
![]() $f_A\circ \iota _B$
is a proper boundary divisor in
$f_A\circ \iota _B$
is a proper boundary divisor in
![]() $\overline {\mathcal {M}}_{1,A}$
, which has no holomorphic
$\overline {\mathcal {M}}_{1,A}$
, which has no holomorphic
![]() $11$
-forms. Hence, the pullback of the generator of
$11$
-forms. Hence, the pullback of the generator of
![]() $H^{11,0}(\overline {\mathcal {M}}_{1,A})$
to
$H^{11,0}(\overline {\mathcal {M}}_{1,A})$
to
![]() $D_B$
vanishes.
$D_B$
vanishes.
Now, suppose
![]() $|A \cap B| \geq 10$
, so
$|A \cap B| \geq 10$
, so
![]() $|A \cap B^c| \leq 1$
. Then, the lower left hand term in diagram (2.4) must be replaced by
$|A \cap B^c| \leq 1$
. Then, the lower left hand term in diagram (2.4) must be replaced by
![]() $\overline {\mathcal {M}}_{(A \cap B) \cup p}$
. Thus, there is another commutative diagram
$\overline {\mathcal {M}}_{(A \cap B) \cup p}$
. Thus, there is another commutative diagram

where if
![]() $|A \cap B| = 10$
, we identify p with the unique symbol of A not contained in B.
$|A \cap B| = 10$
, we identify p with the unique symbol of A not contained in B.
2.3 Relations and the
 $\mathbb {S}_n$
-action
$\mathbb {S}_n$
-action
The group
![]() $\mathbb {S}_n$
acts on the subsets
$\mathbb {S}_n$
acts on the subsets
![]() $A \subset \{1, \ldots , n\}$
and correspondingly on the subspace of
$A \subset \{1, \ldots , n\}$
and correspondingly on the subspace of
![]() $H^{11,0}(\overline {\mathcal {M}}_{1,n})$
generated by the
$H^{11,0}(\overline {\mathcal {M}}_{1,n})$
generated by the
![]() $\omega _A$
. Note that, for any permutation
$\omega _A$
. Note that, for any permutation
![]() $\sigma $
in the subgroup of
$\sigma $
in the subgroup of
![]() $\mathbb {S}_n$
fixing A, we have
$\mathbb {S}_n$
fixing A, we have
![]() $\omega _{\sigma (A)} = \operatorname {\mathrm {sign}}(\sigma ) \omega _{A}$
.
$\omega _{\sigma (A)} = \operatorname {\mathrm {sign}}(\sigma ) \omega _{A}$
.
To identify our representation, we briefly recall some of the combinatorial objects that arise in the representation theory of
![]() $\mathbb {S}_n$
.
$\mathbb {S}_n$
.
A tabloid is an equivalence class of tableaux, which identifies tableaux up to reordering rows. Given a tableau T, we write
![]() $\{T\}$
for the corresponding tabloid. Given a partition
$\{T\}$
for the corresponding tabloid. Given a partition
![]() $\lambda $
of n, we denote by
$\lambda $
of n, we denote by
![]() $M_{\lambda }$
the vector space with basis given by tabloids of shape
$M_{\lambda }$
the vector space with basis given by tabloids of shape
![]() $\lambda $
. The Specht module generator associated to a tableau T is the vector
$\lambda $
. The Specht module generator associated to a tableau T is the vector
where
![]() $\mathrm {C}_T \subset \mathbb {S}_n$
is the subgroup that preserves the columns of T setwise. The subspace of
$\mathrm {C}_T \subset \mathbb {S}_n$
is the subgroup that preserves the columns of T setwise. The subspace of
![]() $M_{\lambda }$
generated by the vectors (2.6) as T runs over all tableaux is an irreducible representation called the Specht module
$M_{\lambda }$
generated by the vectors (2.6) as T runs over all tableaux is an irreducible representation called the Specht module
![]() $V_\lambda $
. The Specht module generators associated to the standard tableaux on
$V_\lambda $
. The Specht module generators associated to the standard tableaux on
![]() $\lambda $
form a basis for
$\lambda $
form a basis for
![]() $V_{\lambda }$
.
$V_{\lambda }$
.
To each ordered subset
![]() $A \subset \{1, \ldots , n\}$
of size
$A \subset \{1, \ldots , n\}$
of size
![]() $11$
, we associate a tableau
$11$
, we associate a tableau
![]() $T_A$
of shape
$T_A$
of shape
![]() $(n-10,1^{10})$
which has the symbols of A in order down the first column and the rest of the first row filled in increasing order.
$(n-10,1^{10})$
which has the symbols of A in order down the first column and the rest of the first row filled in increasing order.
Proposition 2.3. There is an
![]() $\mathbb {S}_n$
-equivariant isomorphism
$\mathbb {S}_n$
-equivariant isomorphism
![]() $H^{11,0}(\overline {\mathcal {M}}_{1,n}) \xrightarrow {\sim } V_{n-10,1^{10}}$
taking
$H^{11,0}(\overline {\mathcal {M}}_{1,n}) \xrightarrow {\sim } V_{n-10,1^{10}}$
taking
![]() $\omega _A$
to the Specht module generator associated to
$\omega _A$
to the Specht module generator associated to
![]() $T_A$
.
$T_A$
.
Proof. The dimension of the Specht module
![]() $V_{n-10,1^{10}}$
is the number of standard tableaux of shape
$V_{n-10,1^{10}}$
is the number of standard tableaux of shape
![]() $(n-10,1^{10})$
, which is
$(n-10,1^{10})$
, which is
![]() ${n-1 \choose 10}$
. Therefore, by Lemma 2.1, it will suffice to give a
${n-1 \choose 10}$
. Therefore, by Lemma 2.1, it will suffice to give a
![]() $\mathbb {S}_n$
-equivariant map from the subspace of
$\mathbb {S}_n$
-equivariant map from the subspace of
![]() $H^{11,0}(\overline {\mathcal {M}}_{1,n})$
generated by
$H^{11,0}(\overline {\mathcal {M}}_{1,n})$
generated by
![]() $\{\omega _A\}$
to
$\{\omega _A\}$
to
![]() $V_{n-10,1^{10}}$
that takes
$V_{n-10,1^{10}}$
that takes
![]() $\omega _A$
to the Specht module generator associated to A.
$\omega _A$
to the Specht module generator associated to A.
We are going to study the image of subspace generated by
![]() $\{\omega _A\}$
under the pullback map
$\{\omega _A\}$
under the pullback map
where B is an ordered subset of
![]() $\{1, \ldots , n\}$
and
$\{1, \ldots , n\}$
and
![]() $D_B$
is as in equation (2.2). Let
$D_B$
is as in equation (2.2). Let
![]() $W_B$
be the element in the target of the map (2.7) which has component
$W_B$
be the element in the target of the map (2.7) which has component
![]() $\mathrm {pr}_1^*\omega \in H^{11,0}(D_B)$
and
$\mathrm {pr}_1^*\omega \in H^{11,0}(D_B)$
and
![]() $0$
in all other components. The collection of ordered subsets B of size
$0$
in all other components. The collection of ordered subsets B of size
![]() $10$
is in bijection with tabloids on
$10$
is in bijection with tabloids on
![]() $(n-10,1^{10})$
, where
$(n-10,1^{10})$
, where
![]() $B^c$
fills the row and B (in order) fills the column. Thus, the right-hand side is identified with the vector space of tabloids
$B^c$
fills the row and B (in order) fills the column. Thus, the right-hand side is identified with the vector space of tabloids
![]() $M_{n-10,1^{10}}$
; given a tabloid
$M_{n-10,1^{10}}$
; given a tabloid
![]() $\{T\}$
corresponding to B we write
$\{T\}$
corresponding to B we write
![]() $W_{\{T\}} = W_B$
.
$W_{\{T\}} = W_B$
.
Fix
![]() $A \subset \{1, \ldots , n\}$
with
$A \subset \{1, \ldots , n\}$
with
![]() $|A| = 11$
. If
$|A| = 11$
. If
![]() $B \subset A$
, with
$B \subset A$
, with
![]() $|B| = 10$
, then A is a permutation of
$|B| = 10$
, then A is a permutation of
![]() $i \cup B$
for some
$i \cup B$
for some
![]() $i \notin B$
. Let
$i \notin B$
. Let
![]() $\sigma _{A \to B}\colon i \cup B \to A$
denote the corresponding permutation. By Lemma 2.2, the image of
$\sigma _{A \to B}\colon i \cup B \to A$
denote the corresponding permutation. By Lemma 2.2, the image of
![]() $\omega _A$
under the map (2.7) is
$\omega _A$
under the map (2.7) is
which is the Specht module generator defined in the expression (2.6), and the proposition follows.
Corollary 2.4. The forms
![]() $\{ \omega _A : 1 \in A, A\text { increasing} \}$
form a basis for
$\{ \omega _A : 1 \in A, A\text { increasing} \}$
form a basis for
![]() $H^{11}(\overline {\mathcal {M}}_{1,n})$
.
$H^{11}(\overline {\mathcal {M}}_{1,n})$
.
Corollary 2.5. The pullback map
![]() $H^{11,0}(\overline {\mathcal {M}}_{1,n}) \to \bigoplus _{\substack {|B| = 10}} H^{11,0}(D_{B})$
is injective.
$H^{11,0}(\overline {\mathcal {M}}_{1,n}) \to \bigoplus _{\substack {|B| = 10}} H^{11,0}(D_{B})$
is injective.
Remark 2.6. Dan Petersen suggested an alternate method to obtain several of the results in this section, which avoids the manipulations with generating functions in Lemma 2.1. We sketch his argument here. Let
![]() $f^{1}:\mathcal {E}\rightarrow \mathcal {M}_{1,1}$
denote the universal elliptic curve and
$f^{1}:\mathcal {E}\rightarrow \mathcal {M}_{1,1}$
denote the universal elliptic curve and
![]() $\mathcal {E}^{n}$
denote the n-fold fiber product of
$\mathcal {E}^{n}$
denote the n-fold fiber product of
![]() $\mathcal {E}$
with itself over
$\mathcal {E}$
with itself over
![]() $\mathcal {M}_{1,1}$
. Note that
$\mathcal {M}_{1,1}$
. Note that
![]() $\mathcal {M}_{1,n}$
is an open substack of
$\mathcal {M}_{1,n}$
is an open substack of
![]() $\mathcal {E}^{n-1}$
. By the long exact sequences for the pairs
$\mathcal {E}^{n-1}$
. By the long exact sequences for the pairs
![]() $(\overline {\mathcal {M}}_{1,n},\mathcal {M}_{1,n})$
and
$(\overline {\mathcal {M}}_{1,n},\mathcal {M}_{1,n})$
and
![]() $(\mathcal {E}^{n-1},\mathcal {M}_{1,n})$
, we see that there are natural isomorphisms
$(\mathcal {E}^{n-1},\mathcal {M}_{1,n})$
, we see that there are natural isomorphisms
One can then study the Leray spectral sequence for the smooth morphism
![]() $f^{n-1}:\mathcal {E}^{n-1}\rightarrow \mathcal {M}_{1,1}$
. Let
$f^{n-1}:\mathcal {E}^{n-1}\rightarrow \mathcal {M}_{1,1}$
. Let
![]() $\mathbb {V}$
denote the local system
$\mathbb {V}$
denote the local system
![]() $R^1f^1_*\mathbb {Q}$
. Then by the Künneth formula,
$R^1f^1_*\mathbb {Q}$
. Then by the Künneth formula,
The pure cohomology
![]() $W_{11}H^{11}(\mathcal {E}^{n-1})$
arises from the
$W_{11}H^{11}(\mathcal {E}^{n-1})$
arises from the
![]() $\binom {n-1}{10}$
summands
$\binom {n-1}{10}$
summands
![]() $\mathbb {V}[-1]^{\otimes 10}$
, each of which gives a copy of
$\mathbb {V}[-1]^{\otimes 10}$
, each of which gives a copy of
![]() $\mathsf {S}_{12}$
. This gives Lemma 2.1. To identify the
$\mathsf {S}_{12}$
. This gives Lemma 2.1. To identify the
![]() $\mathbb {S}_n$
representation as in Proposition 2.3, one first notes that as an
$\mathbb {S}_n$
representation as in Proposition 2.3, one first notes that as an
![]() $\mathbb {S}_{n-1}$
representation, we have
$\mathbb {S}_{n-1}$
representation, we have
By the Pieri formula and the branching rule for the symmetric group, it follows that as an
![]() $\mathbb {S}_n$
representation,
$\mathbb {S}_n$
representation,
3 Applying the Arbarello–Cornalba induction
We start by recalling the inductive method of Arbarello and Cornalba [Reference Arbarello and Cornalba1], by excision of the boundary and pullback to its normalization. We then apply this method to prove Theorem 1.2 and a preliminary proposition about the degree
![]() $11$
cohomology of
$11$
cohomology of
![]() $\overline {\mathcal {M}}_{g,n}$
.
$\overline {\mathcal {M}}_{g,n}$
.
3.1 Restricting to boundary divisors
Consider the excision long exact sequence associated to the boundary
![]() $\partial \mathcal {M}_{g,n}=\overline {\mathcal {M}}_{g,n}\smallsetminus \mathcal {M}_{g,n}$
:
$\partial \mathcal {M}_{g,n}=\overline {\mathcal {M}}_{g,n}\smallsetminus \mathcal {M}_{g,n}$
:
Note that this sequence is in fact a long exact sequence of mixed Hodge structures or
![]() $\ell $
-adic Galois representations. In particular, when
$\ell $
-adic Galois representations. In particular, when
![]() $H^{k}_c(\mathcal{M}_{g,n}) = 0$
, there is an injective morphism
$H^{k}_c(\mathcal{M}_{g,n}) = 0$
, there is an injective morphism
Let
![]() $\widetilde {\partial \mathcal {M}}_{g,n}$
denote the normalization of
$\widetilde {\partial \mathcal {M}}_{g,n}$
denote the normalization of
![]() $\partial \mathcal {M}_{g,n}$
. Arbarello and Cornalba improve on the injectivity of the map (3.1), as follows.
$\partial \mathcal {M}_{g,n}$
. Arbarello and Cornalba improve on the injectivity of the map (3.1), as follows.
Lemma 3.1 (Lemma 2.6 of [Reference Arbarello and Cornalba1]).
Suppose
![]() $H^k_c(\mathcal {M}_{g,n})=0$
. Then the pullback
$H^k_c(\mathcal {M}_{g,n})=0$
. Then the pullback
is injective.
For fixed k, the following proposition gives vanishing of compactly supported cohomology in all but an explicit finite collection of cases.
Proposition 3.2 (Proposition 2.1 of [Reference Bergström, Faber and Payne4]).
Assume
![]() $g\geq 1$
.
$g\geq 1$
.
 $$ \begin{align*} H^k_c(\mathcal{M}_{g,n})=0 \text{ for } \begin{cases}\kern-10pt & k<2g \text{ and } n=0,1 \\ \kern-10pt & k<2g-2+n \text{ and } n\geq 2. \end{cases} \end{align*} $$
$$ \begin{align*} H^k_c(\mathcal{M}_{g,n})=0 \text{ for } \begin{cases}\kern-10pt & k<2g \text{ and } n=0,1 \\ \kern-10pt & k<2g-2+n \text{ and } n\geq 2. \end{cases} \end{align*} $$
3.2 The case of even degrees
 $k \leq 12$
$k \leq 12$
Let
![]() $RH^*(\overline {\mathcal {M}}_{g,n})\subset H^*(\overline {\mathcal {M}}_{g,n})$
be the tautological cohomology ring. Tautological classes are algebraic and defined over
$RH^*(\overline {\mathcal {M}}_{g,n})\subset H^*(\overline {\mathcal {M}}_{g,n})$
be the tautological cohomology ring. Tautological classes are algebraic and defined over
![]() $\mathbb {Z}$
, so if
$\mathbb {Z}$
, so if
![]() $H^k(\overline {\mathcal {M}}_{g,n}) = RH^k(\overline {\mathcal {M}}_{g,n})$
, then
$H^k(\overline {\mathcal {M}}_{g,n}) = RH^k(\overline {\mathcal {M}}_{g,n})$
, then
![]() $H^k(\overline {\mathcal {M}}_{g,n})$
is pure Hodge–Tate. The next lemma provides the necessary base cases for the inductive argument.
$H^k(\overline {\mathcal {M}}_{g,n})$
is pure Hodge–Tate. The next lemma provides the necessary base cases for the inductive argument.
Lemma 3.3. If
![]() $2g - 2 + n \leq 12$
and
$2g - 2 + n \leq 12$
and
![]() $k \leq 12$
is even, then
$k \leq 12$
is even, then
![]() $H^k(\overline {\mathcal {M}}_{g,n})$
is pure Hodge–Tate.
$H^k(\overline {\mathcal {M}}_{g,n})$
is pure Hodge–Tate.
Proof. For
![]() $g = 0$
and any n, all cohomology is tautological [Reference Keel18], as is all even cohomology for
$g = 0$
and any n, all cohomology is tautological [Reference Keel18], as is all even cohomology for
![]() $g = 1$
[Reference Petersen21], and for
$g = 1$
[Reference Petersen21], and for
![]() $g = 2$
and
$g = 2$
and
![]() $n < 20$
[Reference Petersen23]. Finally, for
$n < 20$
[Reference Petersen23]. Finally, for
![]() $g \geq 3$
, all cohomology is tautological for
$g \geq 3$
, all cohomology is tautological for
![]() $2g - 2 +n \leq 12$
[Reference Canning and Larson5, Theorem 1.4].
$2g - 2 +n \leq 12$
[Reference Canning and Larson5, Theorem 1.4].
Proof of Theorem 1.2.
We induct on g and n. By Lemma 3.3, we can assume
![]() $2g-2+n>k$
. By Lemma 3.2, we have an injection
$2g-2+n>k$
. By Lemma 3.2, we have an injection
Each component of
![]() $\widetilde {\partial \mathcal {M}}_{g,n}$
is a quotient by a finite group of
$\widetilde {\partial \mathcal {M}}_{g,n}$
is a quotient by a finite group of
![]() $\overline {\mathcal {M}}_{g-1,n+2}$
or
$\overline {\mathcal {M}}_{g-1,n+2}$
or
![]() $\overline {\mathcal {M}}_{g_1,n_1+1}\times \overline {\mathcal {M}}_{g_2,n_2+1}$
, where
$\overline {\mathcal {M}}_{g_1,n_1+1}\times \overline {\mathcal {M}}_{g_2,n_2+1}$
, where
![]() $g_1+g_2=g$
,
$g_1+g_2=g$
,
![]() $n_1 + n_2 = n$
, and
$n_1 + n_2 = n$
, and
![]() $2g_i-2+n_i>0$
. By induction on g, we know
$2g_i-2+n_i>0$
. By induction on g, we know
![]() $H^k(\overline {\mathcal {M}}_{g-1,n+2})$
is pure Hodge–Tate. Meanwhile, note that
$H^k(\overline {\mathcal {M}}_{g-1,n+2})$
is pure Hodge–Tate. Meanwhile, note that
![]() $H^j(\overline {\mathcal {M}}_{g',n'})=0$
for all
$H^j(\overline {\mathcal {M}}_{g',n'})=0$
for all
![]() $(g',n')$
and odd
$(g',n')$
and odd
![]() $j \leq k/2 \leq 6$
by [Reference Arbarello and Cornalba1]. Hence, the Künneth formula shows that
$j \leq k/2 \leq 6$
by [Reference Arbarello and Cornalba1]. Hence, the Künneth formula shows that
 $$ \begin{align} H^{k}(\overline{\mathcal{M}}_{g_1,n_1+1}\times\overline{\mathcal{M}}_{g_2,n_2+1})=\bigoplus_{i=0}^{k/2} H^{2i}(\overline{\mathcal{M}}_{g_1,n_1+1})\otimes H^{k-2i}(\overline{\mathcal{M}}_{g_2,n_2+1}). \end{align} $$
$$ \begin{align} H^{k}(\overline{\mathcal{M}}_{g_1,n_1+1}\times\overline{\mathcal{M}}_{g_2,n_2+1})=\bigoplus_{i=0}^{k/2} H^{2i}(\overline{\mathcal{M}}_{g_1,n_1+1})\otimes H^{k-2i}(\overline{\mathcal{M}}_{g_2,n_2+1}). \end{align} $$
Inductively, we know that the right-hand side of equation (3.3) is pure Hodge–Tate. Thus, the map (3.2) is an injection of
![]() $H^k(\overline {\mathcal {M}}_{g,n})$
into a Hodge structure or Galois representation that is pure Hodge–Tate, and it follows that
$H^k(\overline {\mathcal {M}}_{g,n})$
into a Hodge structure or Galois representation that is pure Hodge–Tate, and it follows that
![]() $H^k(\overline {\mathcal {M}}_{g,n})$
is pure Hodge–Tate as well.
$H^k(\overline {\mathcal {M}}_{g,n})$
is pure Hodge–Tate as well.
3.3 The case of degree
 $k=11$
$k=11$
The base cases required to run an analogous induction for
![]() $k = 11$
are those where
$k = 11$
are those where
![]() $H^{11}(\overline {\mathcal {M}}_{g,n})$
does not inject into
$H^{11}(\overline {\mathcal {M}}_{g,n})$
does not inject into
![]() $H^{11}(\widetilde {\partial \mathcal {M}}_{1,11})$
. Recent results of the first two authors rule out any such bases cases with
$H^{11}(\widetilde {\partial \mathcal {M}}_{1,11})$
. Recent results of the first two authors rule out any such bases cases with
![]() $g \geq 2$
.
$g \geq 2$
.
Lemma 3.4. If
![]() $g \geq 2$
, then
$g \geq 2$
, then
![]() $H^{11}(\overline {\mathcal {M}}_{g,n}) \to H^{11}(\widetilde {\partial \mathcal {M}}_{g,n})$
is injective.
$H^{11}(\overline {\mathcal {M}}_{g,n}) \to H^{11}(\widetilde {\partial \mathcal {M}}_{g,n})$
is injective.
Proof. If
![]() $2g - 2 + n> 11$
, this follows by combining Lemma 3.1 and Proposition 3.2. If
$2g - 2 + n> 11$
, this follows by combining Lemma 3.1 and Proposition 3.2. If
![]() $2g - 2 + n \leq 11$
and
$2g - 2 + n \leq 11$
and
![]() $g \geq 2$
, then [Reference Canning and Larson5, Theorem 1.4] shows
$g \geq 2$
, then [Reference Canning and Larson5, Theorem 1.4] shows
![]() $H^{11}(\overline {\mathcal {M}}_{g,n}) = 0$
.
$H^{11}(\overline {\mathcal {M}}_{g,n}) = 0$
.
Proposition 3.5. For any g, there is an injection
Proof. The result is known for
![]() $g \leq 1$
, so we may assume
$g \leq 1$
, so we may assume
![]() $g \geq 2$
. By Lemma 3.4, we have an injection
$g \geq 2$
. By Lemma 3.4, we have an injection
Each component of
![]() $\widetilde {\partial \mathcal {M}}_{g,n}$
is a quotient by a finite group of
$\widetilde {\partial \mathcal {M}}_{g,n}$
is a quotient by a finite group of
![]() $\overline {\mathcal {M}}_{g-1,n+2}$
or
$\overline {\mathcal {M}}_{g-1,n+2}$
or
![]() $\overline {\mathcal {M}}_{g_1,n_1+1}\times \overline {\mathcal {M}}_{g_2,n_2+1}$
, where
$\overline {\mathcal {M}}_{g_1,n_1+1}\times \overline {\mathcal {M}}_{g_2,n_2+1}$
, where
![]() $k_1+k_2=n$
,
$k_1+k_2=n$
,
![]() $2g_i-2+n_i>0$
. Because
$2g_i-2+n_i>0$
. Because
![]() $H^k(\overline {\mathcal {M}}_{g',n'})=0$
for all
$H^k(\overline {\mathcal {M}}_{g',n'})=0$
for all
![]() $(g',n')$
and
$(g',n')$
and
![]() $k=1,3,5,7,9$
[Reference Arbarello and Cornalba1, Reference Bergström, Faber and Payne4], the Künneth formula shows that
$k=1,3,5,7,9$
[Reference Arbarello and Cornalba1, Reference Bergström, Faber and Payne4], the Künneth formula shows that
Note that either
![]() $g_1<g$
or
$g_1<g$
or
![]() $g_1=g$
and
$g_1=g$
and
![]() $n_1+1<n$
, and analogously for
$n_1+1<n$
, and analogously for
![]() $(g_2,n_2)$
. Therefore, there is an injective morphism of Hodge structures from
$(g_2,n_2)$
. Therefore, there is an injective morphism of Hodge structures from
![]() $H^{11}(\overline {\mathcal {M}}_{g,n})$
into a direct sum of Hodge structures of the form
$H^{11}(\overline {\mathcal {M}}_{g,n})$
into a direct sum of Hodge structures of the form
![]() $H^{11}(\overline {\mathcal {M}}_{\gamma ,\nu })$
, where
$H^{11}(\overline {\mathcal {M}}_{\gamma ,\nu })$
, where
![]() $\gamma <g$
or
$\gamma <g$
or
![]() $\gamma =g$
and
$\gamma =g$
and
![]() $\nu <n$
. By double induction on g and n and using that
$\nu <n$
. By double induction on g and n and using that
![]() $H^{11}(\overline {\mathcal {M}}_{0,n}) = 0$
and
$H^{11}(\overline {\mathcal {M}}_{0,n}) = 0$
and
![]() $H^{11}(\overline {\mathcal {M}}_{1,n}) = 0$
for
$H^{11}(\overline {\mathcal {M}}_{1,n}) = 0$
for
![]() $n \leq 10$
, we conclude that there is an injective morphism of Hodge structures or
$n \leq 10$
, we conclude that there is an injective morphism of Hodge structures or
![]() $\ell $
-adic Galois representations
$\ell $
-adic Galois representations
4 An induction via the weight spectral sequence
In this section, we prove the vanishing of
![]() $H^{11}(\overline {\mathcal {M}}_{g,n})$
for
$H^{11}(\overline {\mathcal {M}}_{g,n})$
for
![]() $g \geq 2$
. We do so by identifying the injection
$g \geq 2$
. We do so by identifying the injection
![]() $H^{11}(\overline {\mathcal {M}}_{g,n}) \hookrightarrow H^{11}(\widetilde {\partial \mathcal {M}}_{g,n})$
(Lemma 3.4) as the first map in a complex and showing that the next map in the complex is injective. The complex we use is obtained from the
$H^{11}(\overline {\mathcal {M}}_{g,n}) \hookrightarrow H^{11}(\widetilde {\partial \mathcal {M}}_{g,n})$
(Lemma 3.4) as the first map in a complex and showing that the next map in the complex is injective. The complex we use is obtained from the
![]() $E_1$
-page in the weight spectral sequence associated to the compactification
$E_1$
-page in the weight spectral sequence associated to the compactification
![]() $\overline {\mathcal {M}}_{g,n}$
of
$\overline {\mathcal {M}}_{g,n}$
of
![]() $\mathcal {M}_{g,n}$
[Reference Deligne10], via Poincaré duality. It is also the weight 11 summand of the Feynman transform of the modular operad
$\mathcal {M}_{g,n}$
[Reference Deligne10], via Poincaré duality. It is also the weight 11 summand of the Feynman transform of the modular operad
![]() $H^*(\overline {\mathcal {M}}_{g,n})$
[Reference Getzler and Kapranov16], and therefore has a natural graph complex interpretation [Reference Payne and Willwacher20, Section 2.3].
$H^*(\overline {\mathcal {M}}_{g,n})$
[Reference Getzler and Kapranov16], and therefore has a natural graph complex interpretation [Reference Payne and Willwacher20, Section 2.3].
4.1 The first two maps in the weight k complex
Let
![]() $\Gamma $
denote a stable n-marked graph of genus g; the underlying graph is connected, each vertex v is labeled by an integer
$\Gamma $
denote a stable n-marked graph of genus g; the underlying graph is connected, each vertex v is labeled by an integer
![]() $g_v$
and the valence of the vertex v is denoted
$g_v$
and the valence of the vertex v is denoted
![]() $n_v$
. The stability condition is that
$n_v$
. The stability condition is that
![]() $2g_v+n_v-2> 0$
. Set
$2g_v+n_v-2> 0$
. Set
![]() $\overline {\mathcal {M}}_{\Gamma }=\prod _v \overline {\mathcal {M}}_{g_v,n_v}$
. There is the natural gluing map
$\overline {\mathcal {M}}_{\Gamma }=\prod _v \overline {\mathcal {M}}_{g_v,n_v}$
. There is the natural gluing map
The normalization of
![]() $\xi _{\Gamma }(\overline {\mathcal {M}}_{\Gamma })$
is isomorphic to
$\xi _{\Gamma }(\overline {\mathcal {M}}_{\Gamma })$
is isomorphic to
![]() $\overline {\mathcal {M}}_{\Gamma }/\operatorname {\mathrm {Aut}}(\Gamma )$
. Thus, the first map in the weight k complex, the pullback of
$\overline {\mathcal {M}}_{\Gamma }/\operatorname {\mathrm {Aut}}(\Gamma )$
. Thus, the first map in the weight k complex, the pullback of
![]() $H^k$
to the normalization of the boundary, can be rewritten as:
$H^k$
to the normalization of the boundary, can be rewritten as:
The target of the jth map in the weight k complex is
![]() $\bigoplus _{|E(\Gamma )|=j} (H^{k}(\overline {\mathcal {M}}_{\Gamma }) \otimes \det E(\Gamma ))^{\operatorname {\mathrm {Aut}} \Gamma }.$
Here,
$\bigoplus _{|E(\Gamma )|=j} (H^{k}(\overline {\mathcal {M}}_{\Gamma }) \otimes \det E(\Gamma ))^{\operatorname {\mathrm {Aut}} \Gamma }.$
Here,
![]() $\det E(\Gamma )$
denotes the determinant of the permutation representation of
$\det E(\Gamma )$
denotes the determinant of the permutation representation of
![]() $\operatorname {\mathrm {Aut}}(\Gamma )$
acting on the set of edges. We will only need the first and second maps.
$\operatorname {\mathrm {Aut}}(\Gamma )$
acting on the set of edges. We will only need the first and second maps.
Let us describe the second map. We define
 $$ \begin{align} \bigoplus_{|E(\Gamma) = 1|} H^{k}(\overline{\mathcal{M}}_{\Gamma})^{\operatorname{\mathrm{Aut}}(\Gamma)} \xrightarrow{ \ \beta \ } \bigoplus_{|E(\Gamma) = 2|} (H^{k}(\overline{\mathcal{M}}_{\Gamma}) \otimes \det E(\Gamma))^{\operatorname{\mathrm{Aut}}(\Gamma)} \end{align} $$
$$ \begin{align} \bigoplus_{|E(\Gamma) = 1|} H^{k}(\overline{\mathcal{M}}_{\Gamma})^{\operatorname{\mathrm{Aut}}(\Gamma)} \xrightarrow{ \ \beta \ } \bigoplus_{|E(\Gamma) = 2|} (H^{k}(\overline{\mathcal{M}}_{\Gamma}) \otimes \det E(\Gamma))^{\operatorname{\mathrm{Aut}}(\Gamma)} \end{align} $$
as follows. For each graph
![]() $\Gamma $
with two edges, choose an ordering of the edges
$\Gamma $
with two edges, choose an ordering of the edges
![]() $E(\Gamma )= \{e_1, e_2\}$
and say
$E(\Gamma )= \{e_1, e_2\}$
and say
![]() $e_i$
corresponds to the node obtained by gluing the marked points
$e_i$
corresponds to the node obtained by gluing the marked points
![]() $p_i$
and
$p_i$
and
![]() $q_i$
. Let
$q_i$
. Let
![]() $\phi _i(\Gamma )$
denote the graph with one edge obtained by contracting
$\phi _i(\Gamma )$
denote the graph with one edge obtained by contracting
![]() $e_i$
. Gluing
$e_i$
. Gluing
![]() $p_i$
and
$p_i$
and
![]() $q_i$
induces a map
$q_i$
induces a map
![]() $\xi _i\colon \overline {\mathcal {M}}_{\Gamma } \to \overline {\mathcal {M}}_{\phi _i(\Gamma )}$
, which in turn gives a map
$\xi _i\colon \overline {\mathcal {M}}_{\Gamma } \to \overline {\mathcal {M}}_{\phi _i(\Gamma )}$
, which in turn gives a map
![]() $\xi _i^*\colon H^{k}(\overline {\mathcal {M}}_{\phi _i(\Gamma )}) \to H^{k}(\overline {\mathcal {M}}_{\Gamma })$
. This induces
$\xi _i^*\colon H^{k}(\overline {\mathcal {M}}_{\phi _i(\Gamma )}) \to H^{k}(\overline {\mathcal {M}}_{\Gamma })$
. This induces
If
![]() $E(\Gamma )$
is a nontrivial representation of
$E(\Gamma )$
is a nontrivial representation of
![]() $\operatorname {\mathrm {Aut}}(\Gamma )$
, then
$\operatorname {\mathrm {Aut}}(\Gamma )$
, then
![]() $\xi _2 = \xi _1 \circ \sigma $
, where
$\xi _2 = \xi _1 \circ \sigma $
, where
![]() $\sigma \colon \overline {\mathcal {M}}_{\Gamma } \to \overline {\mathcal {M}}_{\Gamma }$
is the automorphism that simultaneously swaps
$\sigma \colon \overline {\mathcal {M}}_{\Gamma } \to \overline {\mathcal {M}}_{\Gamma }$
is the automorphism that simultaneously swaps
![]() $p_1$
with
$p_1$
with
![]() $p_2$
and
$p_2$
and
![]() $q_1$
with
$q_1$
with
![]() $q_2$
(corresponding to the automorphism of
$q_2$
(corresponding to the automorphism of
![]() $\Gamma $
that swaps the two edges). In particular, it follows that the image of
$\Gamma $
that swaps the two edges). In particular, it follows that the image of
![]() $\xi _1^* - \xi _2^*$
lies in the subspace
$\xi _1^* - \xi _2^*$
lies in the subspace
![]() $(H^{k}(\overline {\mathcal {M}}_{\Gamma }) \otimes \det E(\Gamma ))^{\operatorname {\mathrm {Aut}}(\Gamma )} \subset H^{k}(\overline {\mathcal {M}}_{\Gamma })$
. Then
$(H^{k}(\overline {\mathcal {M}}_{\Gamma }) \otimes \det E(\Gamma ))^{\operatorname {\mathrm {Aut}}(\Gamma )} \subset H^{k}(\overline {\mathcal {M}}_{\Gamma })$
. Then
![]() $\beta $
is defined by taking the sum over all two-edge graphs. Then
$\beta $
is defined by taking the sum over all two-edge graphs. Then
![]() $\beta \circ \alpha = 0$
because each component is the difference of the pullbacks under two copies of the same gluing maps.
$\beta \circ \alpha = 0$
because each component is the difference of the pullbacks under two copies of the same gluing maps.
4.2 Proof of Theorem 1.1, assuming it holds for
 $g = 2$
$g = 2$
We first give a short inductive proof of Theorem 1.1, assuming that
![]() $H^{11}(\overline {\mathcal {M}}_{2,n}) = 0$
for all n. Fix
$H^{11}(\overline {\mathcal {M}}_{2,n}) = 0$
for all n. Fix
![]() $k = 11$
and
$k = 11$
and
![]() $g \geq 3$
. By Lemma 3.4, the map
$g \geq 3$
. By Lemma 3.4, the map
![]() $\alpha $
in (4.1) is injective. We claim that the map
$\alpha $
in (4.1) is injective. We claim that the map
![]() $\beta $
in (4.2) is also injective. The theorem follows from this claim since
$\beta $
in (4.2) is also injective. The theorem follows from this claim since
![]() $\beta \circ \alpha = 0$
.
$\beta \circ \alpha = 0$
.
Consider the domain of
![]() $\beta $
, which is
$\beta $
, which is
![]() $\bigoplus _{|E(\Gamma ) = 1|} H^{k}(\overline {\mathcal {M}}_{\Gamma })^{\operatorname {\mathrm {Aut}}(\Gamma )}$
. If
$\bigoplus _{|E(\Gamma ) = 1|} H^{k}(\overline {\mathcal {M}}_{\Gamma })^{\operatorname {\mathrm {Aut}}(\Gamma )}$
. If
![]() $\Gamma $
has a single vertex with a loop edge, then
$\Gamma $
has a single vertex with a loop edge, then
![]() $H^{11}(\overline {\mathcal {M}}_\Gamma )^{\operatorname {\mathrm {Aut}}(\Gamma )} = H^{11}(\overline {\mathcal {M}}_{g-1,n+2})^{\mathbb {S}_2}$
, which vanishes by induction on g.
$H^{11}(\overline {\mathcal {M}}_\Gamma )^{\operatorname {\mathrm {Aut}}(\Gamma )} = H^{11}(\overline {\mathcal {M}}_{g-1,n+2})^{\mathbb {S}_2}$
, which vanishes by induction on g.
Suppose
![]() $\Gamma $
has two vertices joined by an edge. Then
$\Gamma $
has two vertices joined by an edge. Then
![]() $\overline {\mathcal {M}}_\Gamma = \overline {\mathcal {M}}_{a, A \cup p} \times \overline {\mathcal {M}}_{b, A^c \cup q}$
. By the Künneth formula and the vanishing of lower degree odd cohomology,
$\overline {\mathcal {M}}_\Gamma = \overline {\mathcal {M}}_{a, A \cup p} \times \overline {\mathcal {M}}_{b, A^c \cup q}$
. By the Künneth formula and the vanishing of lower degree odd cohomology,
Assume
![]() $a \geq b$
. By induction on g and n,
$a \geq b$
. By induction on g and n,
![]() $H^{11}(\overline {\mathcal {M}}_\Gamma )$
vanishes unless
$H^{11}(\overline {\mathcal {M}}_\Gamma )$
vanishes unless
![]() $b = 1$
and
$b = 1$
and
![]() $|A^c| \geq 10$
, in which case it is
$|A^c| \geq 10$
, in which case it is
![]() $H^{11}(\overline {\mathcal {M}}_{1,A^c \cup q})$
. Note that, in this case,
$H^{11}(\overline {\mathcal {M}}_{1,A^c \cup q})$
. Note that, in this case,
![]() $\operatorname {\mathrm {Aut}}(\Gamma )$
is trivial.
$\operatorname {\mathrm {Aut}}(\Gamma )$
is trivial.

Figure 1 The graph
![]() $\Gamma $
on the left and
$\Gamma $
on the left and
![]() $\Gamma '$
on the right.
$\Gamma '$
on the right.
Let
![]() $\Gamma '$
be the graph obtained by attaching a loop to the vertex of genus
$\Gamma '$
be the graph obtained by attaching a loop to the vertex of genus
![]() $g-1$
(and decreasing its genus accordingly), as shown in Figure 1. As in equation (4.4), we know that
$g-1$
(and decreasing its genus accordingly), as shown in Figure 1. As in equation (4.4), we know that
![]() $H^{11}(\overline {\mathcal {M}}_{\Gamma '})$
contains
$H^{11}(\overline {\mathcal {M}}_{\Gamma '})$
contains
![]() $H^{11}(\overline {\mathcal {M}}_{1,A^c \cup q})$
as a summand. Then
$H^{11}(\overline {\mathcal {M}}_{1,A^c \cup q})$
as a summand. Then
![]() $\beta $
maps
$\beta $
maps
![]() $H^{11}(\overline {\mathcal {M}}_{\Gamma })$
injectively into this summand of
$H^{11}(\overline {\mathcal {M}}_{\Gamma })$
injectively into this summand of
![]() $H^{11}(\overline {\mathcal {M}}_{\Gamma '})$
, and it follows that
$H^{11}(\overline {\mathcal {M}}_{\Gamma '})$
, and it follows that
![]() $\beta $
is injective, as claimed.
$\beta $
is injective, as claimed.
4.3 Proof of Theorem 1.1 for
 $g = 2$
$g = 2$
The proof that
![]() $H^{11}(\overline {\mathcal {M}}_{g,n}) = 0$
for all n follows a similar strategy to the inductive argument for
$H^{11}(\overline {\mathcal {M}}_{g,n}) = 0$
for all n follows a similar strategy to the inductive argument for
![]() $g\geq 3$
. By Lemma 3.4, we know that
$g\geq 3$
. By Lemma 3.4, we know that
![]() $\alpha $
is injective, and we claim that
$\alpha $
is injective, and we claim that
![]() $\beta $
is also injective. The theorem follows from this claim. However, the proof that
$\beta $
is also injective. The theorem follows from this claim. However, the proof that
![]() $\beta $
is injective is more involved in this case.
$\beta $
is injective is more involved in this case.
We begin by describing some of the components of
![]() $\beta $
as concretely as possible.
$\beta $
as concretely as possible.
Example 4.1. Suppose
![]() $\Gamma $
is the leftmost graph in Figure 3. In this case,
$\Gamma $
is the leftmost graph in Figure 3. In this case,
![]() $\phi _1(\Gamma )$
and
$\phi _1(\Gamma )$
and
![]() $\phi _2(\Gamma )$
are not isomorphic, so each component of
$\phi _2(\Gamma )$
are not isomorphic, so each component of
![]() $\beta |_{H^{11}(\overline {\mathcal {M}}_\Gamma )}$
is one of the usual restriction maps, up to sign.
$\beta |_{H^{11}(\overline {\mathcal {M}}_\Gamma )}$
is one of the usual restriction maps, up to sign.
Example 4.2. Suppose
![]() $\Gamma $
is the rightmost graph in Figure 3. In this case,
$\Gamma $
is the rightmost graph in Figure 3. In this case,
![]() $\phi _1(\Gamma ) \cong \phi _2(\Gamma )$
. Let
$\phi _1(\Gamma ) \cong \phi _2(\Gamma )$
. Let
![]() $\sigma \colon \overline {\mathcal {M}}_{\Gamma } \to \overline {\mathcal {M}}_{\Gamma }$
be the automorphism that simultaneously swaps
$\sigma \colon \overline {\mathcal {M}}_{\Gamma } \to \overline {\mathcal {M}}_{\Gamma }$
be the automorphism that simultaneously swaps
![]() $p_1$
with
$p_1$
with
![]() $p_2$
and
$p_2$
and
![]() $q_1$
with
$q_1$
with
![]() $q_2$
(corresponding to the automorphism of
$q_2$
(corresponding to the automorphism of
![]() $\Gamma $
swapping the two edges). Then
$\Gamma $
swapping the two edges). Then
![]() $\xi _2 = \xi _1 \circ \sigma $
. By Proposition 2.3, we know
$\xi _2 = \xi _1 \circ \sigma $
. By Proposition 2.3, we know
![]() $\sigma ^*\colon H^{11}(\overline {\mathcal {M}}_{\Gamma }) \to H^{11}(\overline {\mathcal {M}}_{\Gamma })$
is multiplication by
$\sigma ^*\colon H^{11}(\overline {\mathcal {M}}_{\Gamma }) \to H^{11}(\overline {\mathcal {M}}_{\Gamma })$
is multiplication by
![]() $-1$
. It follows that
$-1$
. It follows that
![]() $\beta |_{H^{11}(\overline {\mathcal {M}}_{\Gamma })}$
is again one of the usual restriction maps, up to rescaling.
$\beta |_{H^{11}(\overline {\mathcal {M}}_{\Gamma })}$
is again one of the usual restriction maps, up to rescaling.
We will show that, for each
![]() $1$
-edge graph
$1$
-edge graph
![]() $\Gamma $
there is a collection of
$\Gamma $
there is a collection of
![]() $2$
-edge graphs
$2$
-edge graphs
![]() $\{\Gamma _i\}$
such that
$\{\Gamma _i\}$
such that
![]() $\beta $
maps
$\beta $
maps
![]() $H^{11}(\overline {\mathcal {M}}_{\Gamma })^{\operatorname {\mathrm {Aut}}(\Gamma )}$
injectively into
$H^{11}(\overline {\mathcal {M}}_{\Gamma })^{\operatorname {\mathrm {Aut}}(\Gamma )}$
injectively into
![]() $\bigoplus _i (H^{11}(\overline {\mathcal {M}}_{\Gamma _i}) \otimes \det (E_{\Gamma _i}))^{\operatorname {\mathrm {Aut}}(\Gamma _i)}$
. Moreover, we order the one-edge graphs in such a way that, at each step, none of the two-edge graphs
$\bigoplus _i (H^{11}(\overline {\mathcal {M}}_{\Gamma _i}) \otimes \det (E_{\Gamma _i}))^{\operatorname {\mathrm {Aut}}(\Gamma _i)}$
. Moreover, we order the one-edge graphs in such a way that, at each step, none of the two-edge graphs
![]() $\{\Gamma _i\}$
admit edge contractions to any of the one-edge graphs that came earlier in the order. In this way, we see that
$\{\Gamma _i\}$
admit edge contractions to any of the one-edge graphs that came earlier in the order. In this way, we see that
![]() $\beta $
can be represented by a block upper diagonal matrix with injective blocks, and hence is injective, as required.
$\beta $
can be represented by a block upper diagonal matrix with injective blocks, and hence is injective, as required.
For
![]() $n \leq 9$
, the cohomology
$n \leq 9$
, the cohomology
![]() $H^*(\overline {\mathcal {M}}_{2,n})$
is tautological [Reference Canning and Larson5], and hence
$H^*(\overline {\mathcal {M}}_{2,n})$
is tautological [Reference Canning and Larson5], and hence
![]() $H^{11}(\overline {\mathcal {M}}_{2,n}) = 0$
, as required. The cases
$H^{11}(\overline {\mathcal {M}}_{2,n}) = 0$
, as required. The cases
![]() $n = 10$
and
$n = 10$
and
![]() $11$
can be handled by an argument similar to that used for the cases
$11$
can be handled by an argument similar to that used for the cases
![]() $n \geq 12$
, below, but the details are more involved. Instead, we note that
$n \geq 12$
, below, but the details are more involved. Instead, we note that
![]() $\overline {\mathcal {M}}_{2,n}$
is rational in these cases [Reference Casnati6], and hence,
$\overline {\mathcal {M}}_{2,n}$
is rational in these cases [Reference Casnati6], and hence,
![]() $H^{11,0}(\overline {\mathcal {M}}_{2,n}) = 0$
. By Proposition 3.5, it follows that
$H^{11,0}(\overline {\mathcal {M}}_{2,n}) = 0$
. By Proposition 3.5, it follows that
![]() $H^{11}(\overline {\mathcal {M}}_{2,n}) = 0$
. For the remainder of this subsection, we therefore assume
$H^{11}(\overline {\mathcal {M}}_{2,n}) = 0$
. For the remainder of this subsection, we therefore assume
![]() $n \geq 12$
.
$n \geq 12$
.
There are three types of
![]() $1$
-edge graphs to consider: those with a vertex of genus
$1$
-edge graphs to consider: those with a vertex of genus
![]() $2$
, those with a unique vertex of genus
$2$
, those with a unique vertex of genus
![]() $1$
and a self-edge and those with two vertices of genus
$1$
and a self-edge and those with two vertices of genus
![]() $1$
.
$1$
.
4.3.1 Graphs with a genus
 $2$
vertex
$2$
vertex
Let
![]() $\Gamma $
be a graph with one edge and a genus
$\Gamma $
be a graph with one edge and a genus
![]() $2$
vertex. Then
$2$
vertex. Then
![]() $\overline {\mathcal {M}}_{\Gamma } = \overline {\mathcal {M}}_{2,A \cup p} \times \overline {\mathcal {M}}_{0, A^c \cup q}$
. Because
$\overline {\mathcal {M}}_{\Gamma } = \overline {\mathcal {M}}_{2,A \cup p} \times \overline {\mathcal {M}}_{0, A^c \cup q}$
. Because
![]() $|A \cup p| < n$
, we see that
$|A \cup p| < n$
, we see that
![]() $H^{11}(\overline {\mathcal {M}}_{2,A \cup p}) = 0$
by induction. By the Künneth formula and the vanishing of lower degree odd cohomology,
$H^{11}(\overline {\mathcal {M}}_{2,A \cup p}) = 0$
by induction. By the Künneth formula and the vanishing of lower degree odd cohomology,
![]() $H^{11}(\overline {\mathcal {M}}_{\Gamma })=0$
.
$H^{11}(\overline {\mathcal {M}}_{\Gamma })=0$
.
4.3.2 Graphs with a single genus 1 vertex
Let
![]() $\Gamma $
be the graph with one vertex of genus
$\Gamma $
be the graph with one vertex of genus
![]() $1$
, n legs and one self-edge. Consider
$1$
, n legs and one self-edge. Consider
![]() $\overline {\mathcal {M}}_{\Gamma } = \overline {\mathcal {M}}_{1,n+2}$
labeled
$\overline {\mathcal {M}}_{\Gamma } = \overline {\mathcal {M}}_{1,n+2}$
labeled
![]() $\{1, \ldots , n, p_1, q_1\}$
, where
$\{1, \ldots , n, p_1, q_1\}$
, where
![]() $p_1, q_1$
are glued together to get curves with dual graph
$p_1, q_1$
are glued together to get curves with dual graph
![]() $\Gamma $
. As in Section 2.2, given a subset
$\Gamma $
. As in Section 2.2, given a subset
![]() $B \subset \{1, \ldots , n, p_1, q_1\}$
of cardinality
$B \subset \{1, \ldots , n, p_1, q_1\}$
of cardinality
![]() $10$
, we let
$10$
, we let
![]() $D_B = \overline {\mathcal {M}}_{1,B \cup p_2} \times \overline {\mathcal {M}}_{0, B^c \cup q_2}$
. (This is nonempty because
$D_B = \overline {\mathcal {M}}_{1,B \cup p_2} \times \overline {\mathcal {M}}_{0, B^c \cup q_2}$
. (This is nonempty because
![]() $n \geq 12$
.) There are four flavors of subsets B: both of
$n \geq 12$
.) There are four flavors of subsets B: both of
![]() $p_1, q_1$
are in B; neither
$p_1, q_1$
are in B; neither
![]() $p_1$
nor
$p_1$
nor
![]() $q_1$
is in B; only
$q_1$
is in B; only
![]() $p_1$
is in B; or only
$p_1$
is in B; or only
![]() $q_1$
is in B. These correspond to
$q_1$
is in B. These correspond to
![]() $4$
types of codimension
$4$
types of codimension
![]() $1$
strata under the map
$1$
strata under the map
![]() $D_B \to \overline {\mathcal {M}}_{1,n+2}$
that glues
$D_B \to \overline {\mathcal {M}}_{1,n+2}$
that glues
![]() $p_2$
and
$p_2$
and
![]() $q_2$
(see Figure 2).
$q_2$
(see Figure 2).

Figure 2 The four flavors of
![]() $D_B$
.
$D_B$
.
For each subset B, let
![]() $\Gamma _B$
be the two-edge graph obtained by further gluing
$\Gamma _B$
be the two-edge graph obtained by further gluing
![]() $p_1$
and
$p_1$
and
![]() $q_1$
(see Figure 3). Note that
$q_1$
(see Figure 3). Note that
![]() $\overline {\mathcal {M}}_{\Gamma _B} = D_B$
. We want to show that
$\overline {\mathcal {M}}_{\Gamma _B} = D_B$
. We want to show that
is injective.
When we glue
![]() $p_1$
and
$p_1$
and
![]() $q_1$
, the last two types of subsets B give the same type of two-edge graph
$q_1$
, the last two types of subsets B give the same type of two-edge graph
![]() $\Gamma _B$
:
$\Gamma _B$
:

Figure 3 Gluing
![]() $p_1$
and
$p_1$
and
![]() $q_1$
.
$q_1$
.
Swapping
![]() $p_1$
and
$p_1$
and
![]() $q_1$
preserves the first two maps
$q_1$
preserves the first two maps
![]() $D_B \to \overline {\mathcal {M}}_{1,n+2}$
but exchanges the other two. Correspondingly, the edge representation is trivial in the first two cases and nontrivial in cases three and four.
$D_B \to \overline {\mathcal {M}}_{1,n+2}$
but exchanges the other two. Correspondingly, the edge representation is trivial in the first two cases and nontrivial in cases three and four.
By Corollary 2.5, we have an injection
Now,
![]() $\mathbb {S}_2$
acts on both sides by swapping
$\mathbb {S}_2$
acts on both sides by swapping
![]() $p_1$
and
$p_1$
and
![]() $q_1$
. Taking
$q_1$
. Taking
![]() $\mathbb {S}_2$
-invariants of both sides, we have an injection from
$\mathbb {S}_2$
-invariants of both sides, we have an injection from
![]() $H^{11}(\overline {\mathcal {M}}_{1,n+2})^{\mathbb {S}_2}$
into
$H^{11}(\overline {\mathcal {M}}_{1,n+2})^{\mathbb {S}_2}$
into
 $$\begin{align*}\bigoplus_{\substack{\{p_1, q_1\} \subset B \text{ or } \{p_1,q_1\} \subset B^c \\ |B| = 10} } H^{11}(D_B)^{\mathbb{S}_2} \oplus \bigoplus_{\substack{p_1 \in B \text{ and } q_1 \notin B \\ |B| = 10}}[H^{11}(D_B) \oplus H^{11}(D_{(B\smallsetminus p_1) \cup q_1})]^{\mathbb{S}_2}.\end{align*}$$
$$\begin{align*}\bigoplus_{\substack{\{p_1, q_1\} \subset B \text{ or } \{p_1,q_1\} \subset B^c \\ |B| = 10} } H^{11}(D_B)^{\mathbb{S}_2} \oplus \bigoplus_{\substack{p_1 \in B \text{ and } q_1 \notin B \\ |B| = 10}}[H^{11}(D_B) \oplus H^{11}(D_{(B\smallsetminus p_1) \cup q_1})]^{\mathbb{S}_2}.\end{align*}$$
The first collection of terms is
![]() $(H^{11}(\overline {\mathcal {M}}_{\Gamma _B}) \otimes \det E(\Gamma _B))^{\mathbb {S}_2}$
for the graphs
$(H^{11}(\overline {\mathcal {M}}_{\Gamma _B}) \otimes \det E(\Gamma _B))^{\mathbb {S}_2}$
for the graphs
![]() $\Gamma _B$
of the first and second flavor in Figure 3, which have trivial edge representation. For the terms in square brackets, we have
$\Gamma _B$
of the first and second flavor in Figure 3, which have trivial edge representation. For the terms in square brackets, we have
![]() $H^{11}(D_B) \cong H^{11}(D_{(B\smallsetminus p_1)\cup q_1})$
and the
$H^{11}(D_B) \cong H^{11}(D_{(B\smallsetminus p_1)\cup q_1})$
and the
![]() $\mathbb {S}_2$
-action switches the two factors. Hence, the space of
$\mathbb {S}_2$
-action switches the two factors. Hence, the space of
![]() $\mathbb {S}_2$
-invariants is
$\mathbb {S}_2$
-invariants is
![]() $H^{11}(\overline {\mathcal {M}}_{\Gamma _B})$
. When
$H^{11}(\overline {\mathcal {M}}_{\Gamma _B})$
. When
![]() $p_1 \in B$
and
$p_1 \in B$
and
![]() $q_1 \notin B$
, note that
$q_1 \notin B$
, note that
![]() $\Gamma _B$
is the type of graph considered in Example 4.2. In particular
$\Gamma _B$
is the type of graph considered in Example 4.2. In particular
![]() $\operatorname {\mathrm {Aut}}(\Gamma _B)$
acts by the sign representation, so
$\operatorname {\mathrm {Aut}}(\Gamma _B)$
acts by the sign representation, so
![]() $(H^{11}(\overline {\mathcal {M}}_{\Gamma _B}) \otimes \det E(\Gamma _B))^{\operatorname {\mathrm {Aut}}(\Gamma _B)} = H^{11}(\overline {\mathcal {M}}_{\Gamma _B})$
. In summary, we have given an injection
$(H^{11}(\overline {\mathcal {M}}_{\Gamma _B}) \otimes \det E(\Gamma _B))^{\operatorname {\mathrm {Aut}}(\Gamma _B)} = H^{11}(\overline {\mathcal {M}}_{\Gamma _B})$
. In summary, we have given an injection
4.3.3 Graphs with two genus
 $1$
vertices
$1$
vertices
Suppose
![]() $\Gamma $
has two genus
$\Gamma $
has two genus
![]() $1$
vertices, so
$1$
vertices, so
We may assume
![]() $|A^c| \leq |A|$
. Figure 4 shows three types of graphs that will be used in the three cases of the argument. Note that none of them have a loop, so none admit edge contractions to the one-edge graphs of Section 4.3.2.
$|A^c| \leq |A|$
. Figure 4 shows three types of graphs that will be used in the three cases of the argument. Note that none of them have a loop, so none admit edge contractions to the one-edge graphs of Section 4.3.2.

Figure 4 The graphs in Cases 1, 2 and 3.
Case 1:
![]() $|A^c| = 0$
. By Corollary 2.5, there is an injection
$|A^c| = 0$
. By Corollary 2.5, there is an injection
 $$\begin{align*}H^{11}(\overline{\mathcal{M}}_{\Gamma}) = H^{11}(\overline{\mathcal{M}}_{1,A \cup p}) \hookrightarrow \bigoplus_{\substack{B \subset A \\ |B| = 10}} H^{11}(\overline{\mathcal{M}}_{1, B \cup p'}) = H^{11}(\overline{\mathcal{M}}_{\Psi_B}),\end{align*}$$
$$\begin{align*}H^{11}(\overline{\mathcal{M}}_{\Gamma}) = H^{11}(\overline{\mathcal{M}}_{1,A \cup p}) \hookrightarrow \bigoplus_{\substack{B \subset A \\ |B| = 10}} H^{11}(\overline{\mathcal{M}}_{1, B \cup p'}) = H^{11}(\overline{\mathcal{M}}_{\Psi_B}),\end{align*}$$
where
![]() $\Psi _B$
is the first graph in Figure 4, which has
$\Psi _B$
is the first graph in Figure 4, which has
Case 2:
![]() $|A^c| = 1$
. Again, by Corollary 2.5, there is an injection
$|A^c| = 1$
. Again, by Corollary 2.5, there is an injection
 $$\begin{align*}H^{11}(\overline{\mathcal{M}}_{\Gamma}) = H^{11}(\overline{\mathcal{M}}_{1,A \cup p}) \hookrightarrow \bigoplus_{\substack{B \subset A \\ |B| = 10}} H^{11}(\overline{\mathcal{M}}_{1, B \cup p'}) = H^{11}(\overline{\mathcal{M}}_{\Psi_B'}),\end{align*}$$
$$\begin{align*}H^{11}(\overline{\mathcal{M}}_{\Gamma}) = H^{11}(\overline{\mathcal{M}}_{1,A \cup p}) \hookrightarrow \bigoplus_{\substack{B \subset A \\ |B| = 10}} H^{11}(\overline{\mathcal{M}}_{1, B \cup p'}) = H^{11}(\overline{\mathcal{M}}_{\Psi_B'}),\end{align*}$$
where this time
![]() $\Psi _B'$
is the second graph in Figure 4, which has
$\Psi _B'$
is the second graph in Figure 4, which has
Note that our assumptions
![]() $n \geq 12$
and
$n \geq 12$
and
![]() $|A^c| = 1$
ensure
$|A^c| = 1$
ensure
![]() $|A \smallsetminus B| \geq 1$
, so the middle genus
$|A \smallsetminus B| \geq 1$
, so the middle genus
![]() $0$
vertex has at least
$0$
vertex has at least
![]() $3$
markings. Note that no edge contraction of
$3$
markings. Note that no edge contraction of
![]() $\Psi _B'$
gives a one-edge graph
$\Psi _B'$
gives a one-edge graph
![]() $\Gamma $
of the type in Case 1 or a different
$\Gamma $
of the type in Case 1 or a different
![]() $\Gamma $
of the type in Case 2.
$\Gamma $
of the type in Case 2.
Case 3:
![]() $|A^c| \geq 2$
. Choose any
$|A^c| \geq 2$
. Choose any
![]() $i, j \in A^c$
and
$i, j \in A^c$
and
![]() $k, \ell \in A$
and define
$k, \ell \in A$
and define
and
Associated to these are two-edge graphs
![]() $\Phi _A$
and
$\Phi _A$
and
![]() $\Phi _{A^c}$
so that
$\Phi _{A^c}$
so that
and contracting the edge connecting
![]() $p'$
and
$p'$
and
![]() $q'$
gives
$q'$
gives
![]() $\Gamma $
. See the last graph in Figure 4 for a picture of
$\Gamma $
. See the last graph in Figure 4 for a picture of
![]() $\Phi _A$
. Notice that no edge contraction of
$\Phi _A$
. Notice that no edge contraction of
![]() $\Phi _A$
or
$\Phi _A$
or
![]() $\Phi _{A^c}$
gives a one-edge graph appearing in Cases 1 or 2 above or a different one-edge graph of the type in Case 3.
$\Phi _{A^c}$
gives a one-edge graph appearing in Cases 1 or 2 above or a different one-edge graph of the type in Case 3.
By the Künneth formula,
 $$ \begin{align*} H^{11}(\overline{\mathcal{M}}_{\Gamma}) &=H^{11}(\overline{\mathcal{M}}_{1,A\cup p})\oplus H^{11}(\overline{\mathcal{M}}_{1,A^c\cup q}), \\ H^{11}(\overline{\mathcal{M}}_{\Phi_A})&=H^{11}(\overline{\mathcal{M}}_{1,A\cup p})\oplus H^{11}(\overline{\mathcal{M}}_{1,(A^c\smallsetminus \{i,j\})\cup \{q,p'\}}), \end{align*} $$
$$ \begin{align*} H^{11}(\overline{\mathcal{M}}_{\Gamma}) &=H^{11}(\overline{\mathcal{M}}_{1,A\cup p})\oplus H^{11}(\overline{\mathcal{M}}_{1,A^c\cup q}), \\ H^{11}(\overline{\mathcal{M}}_{\Phi_A})&=H^{11}(\overline{\mathcal{M}}_{1,A\cup p})\oplus H^{11}(\overline{\mathcal{M}}_{1,(A^c\smallsetminus \{i,j\})\cup \{q,p'\}}), \end{align*} $$
and
It follows that
![]() $H^{11}(\overline {\mathcal {M}}_{\Gamma })$
injects into the sum
$H^{11}(\overline {\mathcal {M}}_{\Gamma })$
injects into the sum
Remark 4.3. It should also be possible to deduce the vanishing of
![]() $H^{11}(\overline {\mathcal {M}}_{2,n})$
from the work of Dan Petersen as follows. There are exact sequences
$H^{11}(\overline {\mathcal {M}}_{2,n})$
from the work of Dan Petersen as follows. There are exact sequences
Specializing to
![]() $k=11$
, we see that
$k=11$
, we see that
By [Reference Petersen23, Theorem 2.1 and Remark 2.2], there is an isomorphism
where
![]() $A^q$
and
$A^q$
and
![]() $B^q$
are certain direct sums of Tate twists of symplectic local systems. The cohomology of these local systems has been determined by Petersen in [Reference Petersen22]. Petersen’s work makes significant use of high-powered machinery, including mixed Hodge modules, perverse sheaves, the decomposition theorem for the map
$B^q$
are certain direct sums of Tate twists of symplectic local systems. The cohomology of these local systems has been determined by Petersen in [Reference Petersen22]. Petersen’s work makes significant use of high-powered machinery, including mixed Hodge modules, perverse sheaves, the decomposition theorem for the map
![]() $\mathcal {M}_{2,n}^{\mathrm {ct}}\rightarrow \mathcal {M}_{2}^{\mathrm {ct}}$
and the Eichler–Shimura isomorphism concerning modular forms. The proof we present here is relatively elementary and highlights a combinatorial perspective on the vanishing of
$\mathcal {M}_{2,n}^{\mathrm {ct}}\rightarrow \mathcal {M}_{2}^{\mathrm {ct}}$
and the Eichler–Shimura isomorphism concerning modular forms. The proof we present here is relatively elementary and highlights a combinatorial perspective on the vanishing of
![]() $H^{11}(\overline {\mathcal {M}}_{2,n})$
.
$H^{11}(\overline {\mathcal {M}}_{2,n})$
.
5 Application to point counting
The weighted count of
![]() $\mathbb {F}_q$
points on a Deligne–Mumford stack X is
$\mathbb {F}_q$
points on a Deligne–Mumford stack X is
 $$\begin{align*}\#X(\mathbb{F}_q):=\sum_{x\in |X(\mathbb{F}_q)|} \frac{1}{\# \operatorname{\mathrm{Aut}} (x)}, \end{align*}$$
$$\begin{align*}\#X(\mathbb{F}_q):=\sum_{x\in |X(\mathbb{F}_q)|} \frac{1}{\# \operatorname{\mathrm{Aut}} (x)}, \end{align*}$$
where
![]() $|X(\mathbb {F}_q)|$
denotes the set of isomorphism classes of the groupoid
$|X(\mathbb {F}_q)|$
denotes the set of isomorphism classes of the groupoid
![]() $X(\mathbb {F}_q)$
. This point count is related to the trace of the Frobenius map
$X(\mathbb {F}_q)$
. This point count is related to the trace of the Frobenius map
![]() $\Phi _q$
on cohomology by Behrend’s Grothendieck–Lefschetz trace formula [Reference Behrend2, Theorem 3.1.2]:
$\Phi _q$
on cohomology by Behrend’s Grothendieck–Lefschetz trace formula [Reference Behrend2, Theorem 3.1.2]:
Using this formula in the case
![]() $X=\overline {\mathcal {M}}_{g,n}$
leads to the proof of Corollary 1.3.
$X=\overline {\mathcal {M}}_{g,n}$
leads to the proof of Corollary 1.3.
Proof of Corollary 1.3.
Let
![]() $d = \dim \overline {\mathcal {M}}_{g,n} = 3g - 3 + n$
. The eigenvalues of Frobenius acting on
$d = \dim \overline {\mathcal {M}}_{g,n} = 3g - 3 + n$
. The eigenvalues of Frobenius acting on
![]() $H^k_{\mathrm{\acute{e}t}}((\overline {\mathcal {M}}_{g,n})_{\overline {\mathbb {F}}_q}, \mathbb {Q}_{\ell })$
are Weil numbers of weight k, meaning that under any embedding
$H^k_{\mathrm{\acute{e}t}}((\overline {\mathcal {M}}_{g,n})_{\overline {\mathbb {F}}_q}, \mathbb {Q}_{\ell })$
are Weil numbers of weight k, meaning that under any embedding
![]() $\overline {\mathbb {Q}}_\ell \hookrightarrow \mathbb {C}$
they have absolute value
$\overline {\mathbb {Q}}_\ell \hookrightarrow \mathbb {C}$
they have absolute value
![]() $q^{k/2}$
[Reference Deligne11]. Thus, the point count
$q^{k/2}$
[Reference Deligne11]. Thus, the point count
![]() $\#\overline {\mathcal {M}}_{g,n}(\mathbb {F}_q)$
is determined up to
$\#\overline {\mathcal {M}}_{g,n}(\mathbb {F}_q)$
is determined up to
![]() $O(q^{d - 13/2})$
by the eigenvalues of Frobenius on
$O(q^{d - 13/2})$
by the eigenvalues of Frobenius on
![]() $H^{2d-k}(\overline {\mathcal {M}}_{g,n})$
for
$H^{2d-k}(\overline {\mathcal {M}}_{g,n})$
for
![]() $k \leq 12$
. Theorem 1.2 and Poincaré duality tells us that Frobenius acts on the even cohomology
$k \leq 12$
. Theorem 1.2 and Poincaré duality tells us that Frobenius acts on the even cohomology
![]() $H^{2d - k}(\overline {\mathcal {M}}_{g,n})$
for
$H^{2d - k}(\overline {\mathcal {M}}_{g,n})$
for
![]() $k \leq 12$
by
$k \leq 12$
by
![]() $q^{d - k/2}$
. Moreover, the groups
$q^{d - k/2}$
. Moreover, the groups
![]() $H^{2d-k}(\overline {\mathcal {M}}_{g,n})$
vanish for odd
$H^{2d-k}(\overline {\mathcal {M}}_{g,n})$
vanish for odd
![]() $k \leq 9$
by [Reference Arbarello and Cornalba1, Reference Bergström, Faber and Payne4]. Thus, up to
$k \leq 9$
by [Reference Arbarello and Cornalba1, Reference Bergström, Faber and Payne4]. Thus, up to
![]() $O(q^{d-13/2})$
, the only other contribution to
$O(q^{d-13/2})$
, the only other contribution to
![]() $\#\overline {\mathcal {M}}_{g,n}(\mathbb {F}_{q})$
is from
$\#\overline {\mathcal {M}}_{g,n}(\mathbb {F}_{q})$
is from
![]() $H^{2d-11}(\overline {\mathcal {M}}_{g,n})$
, which vanishes when
$H^{2d-11}(\overline {\mathcal {M}}_{g,n})$
, which vanishes when
![]() $g \geq 2$
by Theorem 1.1 and Poincaré duality.
$g \geq 2$
by Theorem 1.1 and Poincaré duality.
6 Higher odd cohomology groups
In this section, we prove Theorem 1.5. The main tool is the push-pull formula. This formula is proven for manifolds in [Reference Yamaguchi29, Corollary 2.2]. The proof for orbifolds or smooth Deligne–Mumford stacks goes through analogously.
Lemma 6.1. Suppose
![]() $i\colon X\hookrightarrow Y$
is a closed embedding of codimension d between smooth Deligne–Mumford stacks. Let
$i\colon X\hookrightarrow Y$
is a closed embedding of codimension d between smooth Deligne–Mumford stacks. Let
![]() $N_{X/Y}$
denote the normal bundle. Then for any cohomology class
$N_{X/Y}$
denote the normal bundle. Then for any cohomology class
![]() $\alpha \in H^*(X)$
$\alpha \in H^*(X)$
Proof of Theorem 1.5.
Set
![]() $g=1 + \sum _{i=1}^{k} g_i$
. Assume
$g=1 + \sum _{i=1}^{k} g_i$
. Assume
![]() $\{g_i\}$
is ordered so that
$\{g_i\}$
is ordered so that
![]() $g_1<\dots <g_k$
. It suffices to prove the result for
$g_1<\dots <g_k$
. It suffices to prove the result for
![]() $\overline {\mathcal {M}}_{g,11-k}$
, as the pull back maps
$\overline {\mathcal {M}}_{g,11-k}$
, as the pull back maps
are injective for all n. Consider the gluing morphism
attaching the marked point on the
![]() $\overline {\mathcal {M}}_{g_i,1}$
component to the ith marked point on
$\overline {\mathcal {M}}_{g_i,1}$
component to the ith marked point on
![]() $\overline {\mathcal {M}}_{1,11}$
. Let
$\overline {\mathcal {M}}_{1,11}$
. Let
![]() ${\alpha \in H^{11,0}(\overline {\mathcal {M}}_{1,11})}$
be a nonzero holomorphic
${\alpha \in H^{11,0}(\overline {\mathcal {M}}_{1,11})}$
be a nonzero holomorphic
![]() $11$
-form. We will show that
$11$
-form. We will show that
It suffices to show that
![]() $\xi ^*\xi _*(\alpha \otimes 1\otimes \cdots \otimes 1)$
is nonzero. If
$\xi ^*\xi _*(\alpha \otimes 1\otimes \cdots \otimes 1)$
is nonzero. If
![]() $g_1\neq 1$
, set
$g_1\neq 1$
, set
If
![]() $g_1=1$
, set
$g_1=1$
, set
We will show that
Let
![]() $\Gamma _{g,11-k}$
denote the stable graph with
$\Gamma _{g,11-k}$
denote the stable graph with
![]() $k+1$
vertices as follows. One vertex is of genus
$k+1$
vertices as follows. One vertex is of genus
![]() $1$
with
$1$
with
![]() $11-k$
half-edges, and the rest of the vertices are of genus
$11-k$
half-edges, and the rest of the vertices are of genus
![]() $g_i$
. There is exactly one edge between the first vertex and each of the latter vertices, and no other edges, unless
$g_i$
. There is exactly one edge between the first vertex and each of the latter vertices, and no other edges, unless
![]() $g_1=1$
in which case we allow ourselves to replace the
$g_1=1$
in which case we allow ourselves to replace the
![]() $g_1$
vertex with a genus
$g_1$
vertex with a genus
![]() $0$
vertex with a self-edge (see Figure 5).
$0$
vertex with a self-edge (see Figure 5).

Figure 5 The graphs
![]() $\Gamma _{g,11-k}$
.
$\Gamma _{g,11-k}$
.
Let
![]() $V_{g,11-k}$
denote the open substack of
$V_{g,11-k}$
denote the open substack of
![]() $\overline {\mathcal {M}}_{g,11-k}$
parametrizing curves whose dual graphs are obtained from
$\overline {\mathcal {M}}_{g,11-k}$
parametrizing curves whose dual graphs are obtained from
![]() $\Gamma _{g,11-k}$
by edge contraction. Then
$\Gamma _{g,11-k}$
by edge contraction. Then
factors through the open substack
![]() $V_{g,11-k}$
. The induced map
$V_{g,11-k}$
. The induced map
is a closed embedding between smooth stacks of codimension k. Here, we are using that the genera
![]() $g_1,\dots ,g_k$
are distinct. Let
$g_1,\dots ,g_k$
are distinct. Let
![]() $\beta $
denote the restriction of
$\beta $
denote the restriction of
![]() $\alpha $
to
$\alpha $
to
![]() $\mathcal {M}_{1,11}$
, which is nonzero (for example, by [Reference Getzler15]). By Lemma 6.1
$\mathcal {M}_{1,11}$
, which is nonzero (for example, by [Reference Getzler15]). By Lemma 6.1
Let
![]() $\psi _{g_j}$
denote the (unique)
$\psi _{g_j}$
denote the (unique)
![]() $\psi $
class on the
$\psi $
class on the
![]() $(j+1)$
st component of U. Let
$(j+1)$
st component of U. Let
![]() $\psi _j$
denote the jth
$\psi _j$
denote the jth
![]() $\psi $
class on
$\psi $
class on
![]() $\mathcal {M}_{1,11}$
. It is well-known that
$\mathcal {M}_{1,11}$
. It is well-known that
 $$\begin{align*}c_k(N_i)=\prod_{j=1}^k(-\psi_j\otimes 1\otimes \cdots\otimes 1-1\otimes \cdots\otimes \psi_{g_j}\otimes\cdots\otimes 1). \end{align*}$$
$$\begin{align*}c_k(N_i)=\prod_{j=1}^k(-\psi_j\otimes 1\otimes \cdots\otimes 1-1\otimes \cdots\otimes \psi_{g_j}\otimes\cdots\otimes 1). \end{align*}$$
See, for example, the discussion in [Reference Graber and Pandharipande17, Section A.4]. Because
![]() $H^{13}(\mathcal {M}_{1,11})=0$
[Reference Getzler15], all products of the form
$H^{13}(\mathcal {M}_{1,11})=0$
[Reference Getzler15], all products of the form
![]() $\beta \psi _{j}$
vanish. Therefore,
$\beta \psi _{j}$
vanish. Therefore,
7 Application to Chow rings
We denote by
![]() $A^*(X)$
the Chow ring of X with
$A^*(X)$
the Chow ring of X with
![]() $\mathbb {Q}$
-coefficients.
$\mathbb {Q}$
-coefficients.
Theorem 7.1 (Kimura [Reference Kimura19], Totaro [Reference Totaro27]).
Suppose that X is a smooth, proper Deligne–Mumford stack over
![]() $\mathbb {C}$
. If
$\mathbb {C}$
. If
![]() $A^*(X)$
is a countable
$A^*(X)$
is a countable
![]() $\mathbb {Q}$
-vector space, then the cycle class map
$\mathbb {Q}$
-vector space, then the cycle class map
is an isomorphism.
Proof. First, note that X is defined over a subfield
![]() $E \subset \mathbb {C}$
that is finitely generated over
$E \subset \mathbb {C}$
that is finitely generated over
![]() $\mathbb {Q}$
and hence countable. Suppose
$\mathbb {Q}$
and hence countable. Suppose
![]() $A^*(X)$
is countable. Then there is a countable extension F of E such that
$A^*(X)$
is countable. Then there is a countable extension F of E such that
![]() $A^*(X_{F})\rightarrow A^*(X)$
is surjective. Let G be a finitely generated extension of F. Then G can be embedded in
$A^*(X_{F})\rightarrow A^*(X)$
is surjective. Let G be a finitely generated extension of F. Then G can be embedded in
![]() $\mathbb {C}$
, so we have a morphism
$\mathbb {C}$
, so we have a morphism
Each of the maps above is injective by [Reference Kimura19, Proposition 3.2]. Because the composite is surjective, it follows that the first morphism is also surjective. By [Reference Totaro27, Theorem 4.1], it follows that the motive of
![]() $X_F$
is pure Hodge–Tate, and thus the motive of X is as well. Note that [Reference Totaro27, Theorem 4.1] is stated for schemes, but the same proof goes through for Deligne–Mumford stacks. In particular, the cycle class map is an isomorphism.
$X_F$
is pure Hodge–Tate, and thus the motive of X is as well. Note that [Reference Totaro27, Theorem 4.1] is stated for schemes, but the same proof goes through for Deligne–Mumford stacks. In particular, the cycle class map is an isomorphism.
Proof of Corollary 1.6.
The tautological ring
![]() $R^*(\overline {\mathcal {M}}_{g,n})$
is a finite-dimensional
$R^*(\overline {\mathcal {M}}_{g,n})$
is a finite-dimensional
![]() $\mathbb {Q}$
-vector space by [Reference Graber and Pandharipande17, Corollary 1]. By Theorem 7.1, we know that
$\mathbb {Q}$
-vector space by [Reference Graber and Pandharipande17, Corollary 1]. By Theorem 7.1, we know that
![]() $A^*(\overline {\mathcal {M}}_{g,n})$
is uncountable whenever there is odd cohomology. Therefore, the quotient
$A^*(\overline {\mathcal {M}}_{g,n})$
is uncountable whenever there is odd cohomology. Therefore, the quotient
![]() $A^*(\overline {\mathcal {M}}_{g,n})/R^*(\overline {\mathcal {M}}_{g,n})$
is uncountable for the values of
$A^*(\overline {\mathcal {M}}_{g,n})/R^*(\overline {\mathcal {M}}_{g,n})$
is uncountable for the values of
![]() $(g,n)$
in Theorem 1.5. It follows that the subgroup of
$(g,n)$
in Theorem 1.5. It follows that the subgroup of
![]() $A^*(\overline {\mathcal {M}}_{g,n})$
generated by cycles algebraically equivalent to zero is also uncountable since the Hilbert scheme has only countably many connected components.
$A^*(\overline {\mathcal {M}}_{g,n})$
generated by cycles algebraically equivalent to zero is also uncountable since the Hilbert scheme has only countably many connected components.
Acknowledgements
We are grateful to Jonas Bergström, Carel Faber, Dan Petersen and Burt Totaro for helpful conversations. We especially thank Burt Totaro for suggesting an improvement of an earlier version of Theorem 7.1, and thus Corollary 1.6, and Dan Petersen for suggesting the proof sketch in Remark 2.6. We thank the referee for helpful comments on an earlier version of this article.
Competing interests
The authors have no competing interest to declare.
Funding statement
S.C. was partially supported by NSF RTG grant DMS-1502651 and a Hermann–Weyl–Instructorship from the Forschungsinstitut für Mathematik at ETH Zürich.This research was partially conducted during the period H.L served as a Clay Research Fellow. S.P. was supported in part by NSF grants DMS-2001502 and DMS-2053261.