No CrossRef data available.
Published online by Cambridge University Press: 20 March 2023
We introduce the combinatorial notion of a q-factorization graph intended as a tool to study and express results related to the classification of prime simple modules for quantum affine algebras. These are directed graphs equipped with three decorations: a coloring and a weight map on vertices, and an exponent map on arrows (the exponent map can be seen as a weight map on arrows). Such graphs do not contain oriented cycles and, hence, the set of arrows induces a partial order on the set of vertices. In this first paper on the topic, beside setting the theoretical base of the concept, we establish several criteria for deciding whether or not a tensor product of two simple modules is a highest-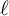 $\ell $-weight module and use such criteria to prove, for type A, that a simple module whose q-factorization graph has a totally ordered vertex set is prime.
$\ell $-weight module and use such criteria to prove, for type A, that a simple module whose q-factorization graph has a totally ordered vertex set is prime.
This work was developed as part of the Ph.D. project of the second author, which was supported by a PICME grant. The work of the first author was partially supported by CNPq grants 304261/2017-3 and 402449/2021-5, and Fapesp grant 2018/23690-6.