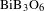High efficiency second harmonic generation of nanojoule-level femtosecond pulses in the visible based on BiBO

Abstract

We demonstrate high efficiency second harmonic generation (SHG) of near infrared femtosecond pulses using a $\text{BiB}_{3}\text{O}_{6}$ crystal in a single-pass tight focusing geometry setup. A frequency doubling efficiency of $63\%$ is achieved, which is, to the best of our knowledge, the highest value ever reported in the femtosecond regime for such low energy (nJ-level) pumping pulses. Theoretical analyses of the pumping scheme focusing waist and the SHG efficiency are performed, by numerically solving the three wave mixing coupled equations in the plane-wave scenario and by running simulations with a commercial full 3D code. Simulations show a good agreement with the experimental data regarding both the efficiency and the pulse spectral profile. The simulated SHG pulse temporal profile presents the characteristic features of the group velocity mismatch broadening in a ‘thick’ crystal.

1 Introduction

In the past few decades, an increasing demand for coherent and ultrafast laser sources in the 350–530 nm spectral range, ultraviolet (UV) to visible, has been arising for significant industrial and scientific applications^[1–4]. This has resulted in the development and use of nonlinear second harmonic generation (SHG) of near infrared (near-IR) radiation, from commercial Ti:sapphire lasers (700–1060 nm). High repetition rate (HRR) SHG is extensively employed, for example, in quantum optics^{[2, 5]}, enabling low probability events to be studied with adequate statistics. Furthermore, HRR SHG sources have been used to pump other nonlinear processes, like optical parametric generation (OPG)^[6] and optical parametric amplification (OPA)^[7] stages or optical parametric oscillator (OPO)^[8], in order to extend the wavelength range available in the femtosecond HRR regime.

SHG is a powerful and robust technique for wavelength extension. For low pump intensity, the efficiency $\unicode[STIX]{x1D6FE}$ of the phase-matched SHG depends linearly on the pump intensity and quadratically on the crystal length and the effective nonlinear crystal coefficient $d_{\text{eff}}$ .

Moreover, it is well known that the efficiency depends on the matching between the pump spectrum and the spectral acceptance bandwidth provided by the frequency doubling crystals^[9]. Conversion efficiency is increased and harmonic temporal pulse broadening is minimized in the ultrashort laser pulse regime if the group velocity mismatch (GVM) in the nonlinear crystal is sufficiently small compared to the fundamental pulse duration. This requirement is met by using a thin crystal, but this condition results in a low conversion efficiency for most of the frequency doubling crystals, unless high intensity pump pulses are used. However, the damage thresholds of the crystals and other nonlinear effects, such as $\unicode[STIX]{x1D712}^{(3)}$ processes^[10], can limit the efficiency.

Because the SHG process efficiency depends strongly on the frequency doubling crystal, over the years there has been a continuous search for new nonlinear optical materials^[11]. Bismuth borate, $\text{BiB}_{3}\text{O}_{6}$ (BiBO)^[12–14], is a nonlinear material with unique optical properties for frequency conversion in the visible and UV^[15–17] that has recently seen a surge of interest. It combines the advantages of well-known materials, such as BBO and LBO, with enhanced optical nonlinearity, as in $\text{KTiOPO}_{4}$ (KTP)^{[11, 18–20]} or in poled crystals^{[11, 21, 22]}. In addition, it offers other advantages such as flexible propagation geometries and small double refraction^{[11, 16, 23]}. However, BiBO presents some disadvantages, such as a larger walk-off angle, which can be minimized by employing a thin crystal thanks to the high nonlinear coefficient.

Another option for having a nonlinear coefficient higher than that of BiBO is $\text{KNbO}_{3}$ ^[24], but its opaqueness below 420 nm, the requirement of large negative/positive temperatures for phase matching and losses due to blue light induced infrared absorption effect, limits its use^{[25, 26]}. Periodically poled crystals such as periodically poled KTP (PPKTP)^{[11, 22, 27]} and periodically poled $\text{LiNbO}_{3}$ (PPLN)^{[11, 21, 28, 29]} have high nonlinearity, but compared to BiBO they have constraints in use due to poling complexities, low optical quality and higher cost^{[30, 31]}.

In the pulsed regime, for pulses hundreds of fs long (ultrashort regime) and with high average power, single-pass SHG with $50\%$ conversion efficiency has been reported for 1.65 W of fundamental power at 800 nm^[17], $41\%$ conversion efficiency for 2.7 W at 1033 nm^[32] and $46.5\%$ conversion efficiency for 5 W at 1060 nm^[33]; whereas efficiencies as high as $68\%$ are reported for high energy picosecond pulses (short regime)^[23] at 1064 nm.

In almost all CW and pulsed SHG studies, a high conversion efficiency was achieved at large input powers^{[16, 17, 23, 34]}, while for low input powers the conversion efficiencies decreased significantly due to the linear dependence on the input power. By using BiBO in an external cavity in the ultrashort regime and for nJ-level pulses, a 53% frequency doubling efficiency was reported^[35].

In this paper, we present a high SHG efficiency for low input powers by implementing a BiBO crystal in a single-pass SHG tight focusing geometry in the short wavelength region of the visible spectrum. The SHG efficiency reaches $63\%$ for an input energy of ${\sim}4$  nJ/pulse (average power ${\sim}300$  mW), which is, to the best of our knowledge, the highest SHG efficiency ever reported for the femtosecond pulsed regime at the nJ level. In addition to this, we perform a theoretical analysis of the SHG efficiency. A simulation code was developed solving numerically the wave mixing equation in the plane-wave scenario, including broadening processes like GVM and group delay dispersion (GDD), crystal losses and spatial walk-off. In addition, a commercial full 3D code was used to study the optimal focusing waist to drive the nonlinear process and to support the experimental results retrieved. The simulated SHG efficiency behavior, both with 1D plane-wave code and the 3D code, for different input intensities, is compared to the experimental data, showing a good agreement. The spectral bandwidth retrieved matches the experimental data and the temporal profile is also retrieved.

2 SHG efficiency considerations

Here we discuss the role and optimization of the main parameters affecting SHG efficiency. This problem is related to finding an optimized spatial configuration (beam size and focusing geometry) according to the pulse length (which together with the energy defines the peak intensity), crystal length and crystal nonlinear coefficient. This is shown in the definition of the phase-matched SHG efficiency,

(1) $$\begin{eqnarray}\unicode[STIX]{x1D6FE}=\frac{8\unicode[STIX]{x1D70B}^{2}d_{\text{eff}}^{2}}{\unicode[STIX]{x1D716}_{0}c\unicode[STIX]{x1D706}_{0}^{2}n_{0}^{3}}L_{\text{cry}}^{2}I_{\text{p}}\text{sinc}^{2}\,\left(\frac{\unicode[STIX]{x0394}kL_{\text{cry}}}{2}\right),\end{eqnarray}$$

where $c$ is the speed of light, $\unicode[STIX]{x0394}k$ is the phase mismatch, $\unicode[STIX]{x1D716}_{0}$ is the vacuum permittivity, $I_{\text{p}}$ is the pump intensity, $L_{\text{cry}}$ is the crystal length, $d_{\text{eff}}$ the nonlinear crystal coefficient and $n_{0}$ the refractive index at the fundamental wavelength $\unicode[STIX]{x1D706}_{0}$ .

The beam size should be optimized in order to maximize the intensity in the crystal as well as to preserve a given Rayleigh length ( $L_{\text{Ray}}$ ). This length should match half the crystal length, ensuring that the beam intensity is kept at the same level inside the crystal; on the other hand, the so-called interaction length will be shortened leading to a smaller efficiency.

The crystal nonlinear coefficient, walk-off and the GVM parameters depend strongly on the operating wavelength. The latter two, like the beam size, will limit the interaction length. For a given wavelength, the nonlinear interaction geometry must ensure that pump and SHG pulses are spatially and temporally overlapped over the full crystal length. Strong walk-off and GVM effects will lead to temporal and spatial slippage, limiting the effective crystal length and leading to a less efficient SHG. Finally, the acceptance bandwidth of the crystal ensures that for a given length the different spectral components are phase-matched.

As we show in the following sections, the numerically optimized interplay of the different parameters can lead to high efficiency even in the low-power regime. In order to understand and validate our experimental parameters and results, we present supporting simulations that reproduce them adequately. For the pump beam waist, we use a full 3D code to perform a study on the SHG efficiency vs. the waist diameter with full energy at 1030 nm (Section 5.1). Regarding the effective interaction length, simulations were performed both with the 1D plane-wave code with a 1.1 mm long crystal, taking into account the interaction length, and with a full 3D code with a 2 mm effective length, taking into account the spatial effect and a 2D treatment of the walk-off (Section 5.2). These findings can be readily applied to different parameters in the same ultrashort, low-power regime.

3 Experimental setup

The experimental setup, as shown in Figure 1, consists of an energy-controlled pumping laser focused on a BiBO nonlinear crystal and undergoing direct single-pass second harmonic generation. The frequency-doubled source is successively collimated and guided into the diagnostics. The pumping laser is a Kerr lens mode-locked commercial oscillator (Coherent Mira 900F) that produces, in its current configuration, tunable pulses in the spectral range 980–1060 nm. It is pumped by a CW solid-state laser (Coherent Verdi V-10) providing up to $10$  W at $532$  nm. When operated at maximum power, the laser provides a linearly polarized output beam in TEM $_{00}$ spatial profile. Depending on the operating wavelength (as shown below, Section 4.1), the pulses have an energy of a few nJ, a pulse length from 115 fs to 190 fs and a repetition rate of 75.54 MHz. Pulse polarization and energy are set by a stage of polarizers and filters (EC) at the oscillator exit.

Figure 1. Experimental setup in SHG experiment. $\unicode[STIX]{x1D706}/2,\unicode[STIX]{x1D706}/4$ : waveplates; EC: pump energy control; FL: focusing lens; C: nonlinear crystal; CL: collimating lens; DM: dichroic mirror; FM: flip mirror; SM: spectrometer; CAM: camera; PM: power meter; SA: spectrum analyzer; PC: computer.

The focusing scheme relies on a short focal length ( $f_{\text{FL}}\sim 6$  cm) achromatic lens. This choice allows a good spatial quality, minimizing aberrations (e.g., chromatic) in the tight focal spot. A study on the optimal waist radius was performed (see Section 5.1). The optimal waist diameter (full width at half-maximum, FWHM) is $w_{0}\sim 22~\unicode[STIX]{x03BC}\text{m}$ and the associated Rayleigh length, $L_{\text{Ray}}\sim 400~\unicode[STIX]{x03BC}\text{m}$ , is long enough to maintain the gain over the length of the crystal.

The pulses are focused in the middle plane of the $2$  mm long, $5~\text{mm}\times 5$  mm aperture $\text{BiB}_{3}\text{O}_{6}$ nonlinear crystal, which is cut at $\unicode[STIX]{x1D703}=169.4^{\circ }$ and $\unicode[STIX]{x1D719}=90^{\circ }$ in the optical $yz$ -plane for Type-I (ee $\rightarrow$ o) phase matching at normal incidence. The crystal is antireflection coated on both faces for $1030$  nm and $515$  nm. For this phase-matching geometry, the spatial walk-off angle is $\unicode[STIX]{x1D70C}\sim 23$  mrad; the corresponding group velocity mismatch is $\unicode[STIX]{x1D6FD}=133.3$  fs/mm and the nonlinear coefficient is $d_{\text{eff}}=3.02$  pm/V. The crystal is assembled on a rotational mount and set up on a double roto-translational stage to allow tuning:

• ∙ its orientation and tilt to fulfill the phase-matching conditions,

• ∙ its position to match the focal spot (maximum intensity),

and to achieve high efficiency SHG. The optimization of the phase-matching conditions and maximization of the efficiency are achieved by using a waveplate to slightly adjust the pump polarization. After the frequency doubling crystal, a collimating lens (CL) is used for beam transport of the SHG source. A dichroic mirror (DM) is placed in the SHG direction of propagation at $45^{\circ }$ , to split the SHG beam and the undepleted pump ( $\text{HR}\sim 99.5\%$ , $\text{HT}\sim 95\%$ ). After the wavelength splitting, both the SHG and the undepleted pump are fully characterized by different diagnostics: CCD cameras (CAM1, CAM2) to characterize their spatial profile, spectrometers (SM1, SM2) to understand the supported temporal length and a power meter (PM). The pumping beam was fully characterized by using these diagnostics to estimate the initial average power and to retrieve its spatial and spectral profile. The spatial profiles of the pump and the SHG beams are shown in Figure 2. Moreover, a homemade scanning autocorrelator (minimum resolvable pulsewidth ${\sim}80$  fs) was used to estimate the temporal lengths of the pumping beam at different operation wavelengths.

Figure 2. Comparison between pump and SHG spatial profile, respectively.

4 Experimental results

4.1 Spectral and temporal characterization of IR pulses

The full characterization of the oscillator pulses is a crucial point in order to understand the parameters, such as pulse intensity, involved in the nonlinear interaction in the crystal for different wavelengths. Firstly, we fully characterized the oscillator pulses at four different wavelengths (980, 1000, 1030 and 1054 nm), covering its entire operational range. Figure 3 shows the corresponding autocorrelation traces. The data was fitted for $1030$  nm pulses (Figure 3, top left) and the retrieved temporal length is $116$  fs (in all autocorrelation calculations a Gaussian shape is assumed). The same procedure was applied for the other three wavelengths and the experimental data can be seen in Table 1. As seen from the data, the shortest duration is available for $1030$  nm pulses. This is expected because the dispersion compensation stage inside the commercial oscillator is optimized for this wavelength, so shifting the wavelength introduces temporal broadening effects.

Figure 3. Autocorrelation measurement of the pulse at 1030, 1054, 1000 and 980 nm for top left, top right, bottom left and bottom right, respectively.

Figure 4 shows the corresponding spectral intensity profiles at the same operating wavelengths. The results are also reported in Table 1, with the corresponding transform-limited pulse length ( $\unicode[STIX]{x1D70F}_{\text{pulse}}^{\text{TL}}$ ).

Figure 4. Input (red) and depleted (orange) signal spectra for 1030, 1054, 1000 and 980 nm pulses.

Table 1. Autocorrelation and spectral experimental data. $\unicode[STIX]{x1D70F}_{\text{AC}}$ – FWHM of the autocorrelation trace, $\unicode[STIX]{x1D70F}_{\text{pulse}}$ – retrieved Gaussian FWHM pulse length, $\unicode[STIX]{x0394}\unicode[STIX]{x1D706}$ – spectral FWHM bandwidth and $\unicode[STIX]{x1D70F}_{\text{pulse}}^{\text{TL}}$ – supported (transform-limited) pulse length.

At $1030$  nm the pulses are well compressed, almost close to transform limited ( $r_{1030}=\unicode[STIX]{x1D70F}_{\text{pulse}}/\unicode[STIX]{x1D70F}_{\text{pulse}}^{\text{TL}}=1.06$ ). For the other three wavelengths the dispersion compensation is slightly less efficient but nevertheless good: $r_{980}=1.22,r_{1000}=1.35,r_{1054}=1.22$ .

4.2 SHG efficiency measurements

The output pulse energy from the oscillator was adjusted by two filter wheels, a coarse one producing steps of half neutral density from 0 to 4.5 and a fine one producing steps of 0.1 neutral density from 0 to 0.5. A previous calibration was performed in order to eliminate any alignment or spectral dependency of the combined attenuation. In Figure 5, the second harmonic generated average power ( $P_{\text{SHG}}$ ) is plotted as a function of the input average power ( $P_{\text{in}}$ ). Due to the pump source characteristics, the maximum SHG pulse energy is wavelength-dependent. The highest converted power is obtained for 1000 nm, although at a higher input power with respect to the other three wavelengths.

Figure 5. SHG power versus input power at different wavelengths.

Figure 6 shows the corresponding SHG efficiency, which reaches $63\%$ at $1030$  nm and around $60\%$ at $1000$  nm at the maximum average power and energy available, respectively, for each wavelength. For the other two cases:

• ∙ at 1054 nm the available average power is not enough to enable an efficiency above $40\%$ . Since the experimental data for 1030 nm and 1054 nm are virtually superimposed and because of the similar pulse length, it is expectable that at higher powers a similar efficiency ( ${\sim}60\%$ ) will be obtained;

• ∙ at 980 nm the lower efficiency can be attributed to coating-induced losses from the nonlinear crystal and the focusing optics.

The efficiency comparison between different wavelengths is more clear and intuitive when plotted as a function of the intensity. The beam focusing geometry was maintained during all the experiment (the focal spot wavelength dependency was taken into account), the temporal lengths were known and the energy was an imposed parameter for all the wavelengths, so the average power axis ( $P_{\text{in}}$ ) was converted in the intensity axis, as in Figure 7. This graph shows that even though higher input intensities are available at $1000$  nm, the SHG is more efficient at $1030$  nm. The reason for this difference in efficiency is linked to the crystal cut angle and coating being optimized for $1030$  nm.

Figure 6. SHG efficiency versus input energy and average power for different wavelengths.

Figure 7. Comparison (measured and simulated data) of the SHG efficiency as a function of the input intensity for different wavelengths.

It may be assumed that by using the same geometry and crystals with adequate cut angles and coatings, the losses can be minimized. Moreover, by keeping the same input intensity we can exceed the 60% efficiency for both 980 nm and 1000 nm, since the nonlinear coefficient increases for smaller wavelengths, up to $3.27$  pm/V at $980$  nm. While the energy available from the oscillator does not enable reaching a clear saturation regime of the SHG process, as in Figure 6 or Figure 7, it is apparent that behavior is being approached.

4.3 SHG spectral measurements

Figure 8 shows the measured spectral intensity of the SHG at 1030 nm pump wavelength. The same measurements were performed for the other three pumping wavelengths. Each spectrum was fitted with a Gaussian function in order to determine its bandwidth and the supported pulse temporal length (Table 2). It is noticeable that the minimum supported pulse widths are longer with respect to those of the pumping pulses, which is expected when ultrashort pulses undergo nonlinear effects or propagate through dispersive media (crystals, glasses, etc.).

Figure 8. Experimental and simulated second harmonic generation spectrum of 1030 nm pumping beam.

Table 2. SHG spectral experimental data. $\unicode[STIX]{x0394}\unicode[STIX]{x1D706}$ represents the FWHM bandwidth of the SHG spectrum and $\unicode[STIX]{x1D70F}_{\text{SHG}}^{\text{TL}}$ the retrieved FWHM of the supported SHG pulse temporal length assuming Gaussian shape.

5 Theoretical simulation and discussion

5.1 Optimal focusing of the oscillator

Simulations with a commercial full 3D code^[36] were performed. Figure 9 shows the SHG efficiency at 1030 nm as a function of the pump beam waist diameter. Two energies (3.7 and 3.8 nJ) were considered for the simulation in order to evaluate the stability of the SHG process. The efficiency is maximized for the 20–24  $\unicode[STIX]{x03BC}\text{m}$ waist diameter range (FWHM) for $I\sim 8$  GW/cm $^{2}$ and $L_{\text{cry}}=2$  mm at 1030 nm. For smaller diameters, $L_{\text{Ray}}$ will be shorter and the process will be driven strongly for a short interaction length. For broader waists, the intensity is reduced and even though $L_{\text{Ray}}$ is longer, the interaction length will be limited in practice by $L_{w_{\text{off}}}\sim 1$  mm, $L_{\text{GVM}}\sim 1$  mm and $L_{\text{BW}}\sim 1.3$  mm.

Figure 9. SHG efficiency versus focal spot diameter at two different energies: 3.7 and 3.8 nJ for the same crystal length.

5.2 SHG efficiency simulations

To support the experimental results, simulations were made with a noncommercial code solving the wave mixing coupled equations for optical parametric processes^[10] in a BiBO crystal and with a commercial full 3D code, 2D–SP–SNLO. In the developed code, the system of equations is solved for the fields envelope in a plane-wave scenario. The 1D code does not take into account spatial effects like diffraction or birefringence, nor high order temporal effects such as cascaded nonlinear effects. Although walk-off is a 2D spatial effect, it can be inserted as a lossy term^[37] with its coefficient estimated as

(2) $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{w_{\text{off}}}=\frac{1}{L_{w_{\text{off}}}}=\frac{\unicode[STIX]{x1D70C}}{\sqrt{\unicode[STIX]{x1D70B}}R_{s}}\end{eqnarray}$$

with $R_{s}$ the radius of the signal beam.

The system of equations solved is

(3) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}A_{p}}{\unicode[STIX]{x2202}z}+\frac{1}{v_{p}}\frac{\unicode[STIX]{x2202}A_{p}}{\unicode[STIX]{x2202}t}=iK_{p}A_{p}^{\ast }A_{s}\exp (i\unicode[STIX]{x0394}kz), & \displaystyle\end{eqnarray}$$

(4) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}A_{s}}{\unicode[STIX]{x2202}z}+\frac{1}{v_{s}}\frac{\unicode[STIX]{x2202}A_{s}}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FC}_{w_{\text{off}}}A_{s}=iK_{s}A_{p}^{2}\exp (-i\unicode[STIX]{x0394}kz), & \displaystyle\end{eqnarray}$$

with

(5) $$\begin{eqnarray}K_{p,s}=\frac{2\unicode[STIX]{x1D70B}d_{\text{eff}}}{n_{p,s}\unicode[STIX]{x1D706}_{p,s}}\end{eqnarray}$$

respectively for pump and signal, $\unicode[STIX]{x1D706}_{p,s}$ the wavelength, $n_{p,s}$ the refractive index, $v_{p,s}$ the group velocity, $\unicode[STIX]{x0394}k$ the phase mismatch and $z$ the propagation direction. In Equations (3) and (4), it is noticeable that the term that takes into account the GDD is not included. The choice of not including the GDD term was done because in $2$  mm of BiBO the broadening that a $100$  fs pulse undergoes is negligible. A perfect phase-matching scenario is assumed ( $\unicode[STIX]{x0394}k\rightarrow 0$ ) so that $\exp (\pm i\unicode[STIX]{x0394}kz)\rightarrow 1$ . The previous set of equations was not solved by adopting the ‘split step’ method but by using an alternative, ‘static’ approach working in the temporal domain, as follows.

• ∙ Change the variables $\unicode[STIX]{x1D709}=z$ and $\unicode[STIX]{x1D70F}_{s,p}=t-(z/v_{s,p})$ for each equation.

• ∙ At each space slice inside the crystal, one pulse temporal slice interacts with a different slice of the other interacting pulse because of GVM; so $A_{p}(\unicode[STIX]{x1D709},t)$ interacts with

  (6) $$\begin{eqnarray}A_{s}\left(\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F}_{s}+\frac{z}{v_{p}}\right)=A_{s}(\unicode[STIX]{x1D709},t-\unicode[STIX]{x1D709}\unicode[STIX]{x1D6FD}),\end{eqnarray}$$
  and the system of equations becomes
  (7) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}A_{p}(\unicode[STIX]{x1D709},t)}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}=iK_{p}A_{p}^{\ast }(\unicode[STIX]{x1D709},t-\unicode[STIX]{x1D709}\unicode[STIX]{x1D6FD})A_{s}(\unicode[STIX]{x1D709},t-\unicode[STIX]{x1D709}\unicode[STIX]{x1D6FD}), & \displaystyle\end{eqnarray}$$
  (8) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}A_{s}(\unicode[STIX]{x1D709},t)}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}-\unicode[STIX]{x1D6FC}_{w_{\text{off}}}A_{s}(\unicode[STIX]{x1D709},t)=iK_{s}A_{p}^{2}(\unicode[STIX]{x1D709},t-\unicode[STIX]{x1D709}\unicode[STIX]{x1D6FD}). & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

• ∙ Equations (7) and (8) are discretized with a modified Euler implicit method. An iterative process allows calculating the behavior of the fields.

Equations (7) and (8) just describe, as pointed out, the simple scenario of the central wavelength with $\unicode[STIX]{x0394}k\rightarrow 0$ . The code takes into account the entire pulse spectrum (for $\unicode[STIX]{x0394}k\neq 0$ ), not just the central phase-matched wavelength. The simulation code was benchmarked with the free commercial code, PW–SP–SNLO^[36]. The results are in good agreement and the developed code has also been generalized to simulate other nonlinear processes, such as OPA and OPO.

The simulations were performed for several input intensities, ranging from ${\sim}$ 1 GW/cm $^{2}$ to ${\sim}$ 8 GW/cm $^{2}$ , covering the range available for the 1030 nm operational wavelength. Figure 7 shows the experimental data for each wavelength and three different sets of simulations at 1030 nm: using the developed plane-wave code for 1.1 mm and 2 mm long crystals and using the ‘modified’ 2D–SP–SNLO code for a 2 mm long crystal (including the entire pulse spectrum).

The behavior of the calculated efficiencies is in good agreement with the experimental data. As expected, the measured SHG efficiency is lower, by about $15\%$ , than the theoretical/simulated one with the plane-wave/short pulse developed code for $L_{\text{cry}}=2$  mm due to the code assumptions, namely the use of plane waves, the lack of 2D spatial effects, losses (e.g., from crystal absorbance, coating) and 2D treatment of the walk-off effect.

It was found that by considering an effective crystal length of $L_{\text{int}}=L_{\text{cry}}=1.1$  mm, because of different limiting factors of the crystal length in nonlinear processes: $L_{w_{\text{off}}}\sim 1$  mm ( $\unicode[STIX]{x1D70C}\sim 23$  mrad), $L_{\text{foc}}\sim 1$  mm ( $L_{\text{Ray}}\sim 0.5$  mm), $L_{\text{GVM}}\sim 1$ mm ( $\text{GVM}\sim 133$  fs/mm) and $L_{\text{BW}}\sim 1.3$  mm ( $\text{BW}\text{acc}\sim 0.25~\text{nm}\cdot \text{mm}$ ), the gap between the simulation and experimental data is lower than in the previous case, about $4\%$ . The adjustment to the measured data was optimized, leading to the conclusion that the 1D treatment (approximated as a lossy term) of the walk-off effect was overestimating the SHG efficiency simulation data.

The remaining discrepancy is explained by the plane-wave assumption, as can be inferred by noticing the excellent agreement of the full 3D simulation with the experimental points. Furthermore, in Figure 7 we can notice that for low ( $0{-}1.5$  GW/cm $^{2}$ ) intensities the simulation points are not completely overlapped with the experimental data for 1030 nm. In this region, the signal-to-noise ratio was not optimal, so this disagreement was expected.

5.3 SHG pulse temporal–spectral profile simulations

The temporal length of the SHG pulses was theoretically/numerically retrieved using the simulation code developed to treat the nonlinear interaction process. In Figure 10, the temporal profile of the SHG pulse for the $1030$  nm operating wavelength is shown. The noticeably asymmetric shape is due to the increased effects of GVM in long (2 mm BiBO in this case) crystals.

Figure 10. Second harmonic generation simulation determining the temporal length of the SHG pulse.

While the SHG green pulse and pumping pulse propagate together through the crystal, the trailing edge of the SHG pulse is increasingly stretched, since it is generated by a progressively more depleted, less intense fundamental pulse^{[15, 17]} because of the difference in their group velocities. This leads to the characteristic asymmetry and longer second harmonic pulse length. As mentioned before, in this scenario the GVM effect is the most important broadening effect.

At this point, the Gaussian fit of the simulation data was performed, tuning the amplitude, the position of the maximum and the width (FWHM), yielding $\unicode[STIX]{x1D70F}_{\text{SHG}}=143$  fs.

The spectral profile was also retrieved (Figure 8). The spectral bandwidth retrieved, fitting the simulation data, is 2.95 nm in good agreement with the experimental spectrum. Using the spectral measurements in Section 4.3, we can calculate the ratio between $\unicode[STIX]{x1D70F}_{\text{SHG}}$ and $\unicode[STIX]{x1D70F}_{\text{SHG}}^{\text{TL}}$ to be around $r_{515}=1.11$ . This means that by starting with almost transform-limited pulses we are able to retrieve almost transform-limited SHG pulses.

Furthermore, it can be argued that using a smaller crystal to avoid the pulse-broadening GVM effect while keeping the same single-pass gain ( $L_{\text{cry}}\sim 2L_{\text{Ray}}$ ) will allow producing SHG sources with transform-limited temporal parameters. The last condition is important in any experiment where the SHG pulses will act as pumping beam for optical parametric generation or amplification.

6 Conclusion

In conclusion, we have experimentally demonstrated high efficiency frequency doubling of nanojoule-level femtosecond pulses in the near-IR range using a Type-I BiBO crystal placed in a single-pass tight focusing geometry setup, leading to high quality SHG in the visible.

At 1030 nm, a frequency doubling efficiency of $63\%$ is achieved for a low energy ( ${\sim}4$  nJ) input beam (average power of ${\sim}300$  mW). A significant improvement in the conversion efficiency is shown compared to usual single-pass SHG efficiency using a pump beam waist of ${\sim}25~\unicode[STIX]{x03BC}$ m at the doubling nonlinear crystal.

Furthermore, we performed simulations solving the SHG wave mixing equations, in the plane-wave scenario, to evaluate the theoretical efficiency across all the power range, showing good agreement between the experimental and theoretical curves. The developed simulation code helped us also to estimate the SHG pulse temporal profiles; almost transform-limited SHG pulses ( ${\sim}$ 143 fs, 1.1 times the transform limit temporal length) are generated and by using a smaller length crystal the input pulse temporal length can be preserved.

Our work highlights the importance of the interaction spatial configuration, crystal length and nonlinear coefficient parameters. The record efficiency was made possible by optimizing the above-mentioned parameters: the tight focal spot, according to 3D simulation, using an achromatic focusing lens to enhance the spatial quality and to minimize the aberrations preserving high intensity; the crystal ( $d_{\text{eff}}$ , acceptance bandwidth, GVM, walk-off) and its length ( $L_{\text{cry}}\sim L_{\text{int}}$ , depending on the crystal parameters) to keep a high gain at the chosen operational wavelength.

These results allow for standard nJ-level commercial oscillators to be efficiently frequency doubled and used as pump sources for HRR optical parametric amplifiers (OPAs) or optical parametric oscillators (OPOs), yielding short temporal length pulses, high spatial quality beams and tunable systems. The SHG source developed will be the pumping system of a femtosecond OPO based on BiBO ranging from $750$  nm to $1030$  nm, parameters of relevance for large-scale laser architectures based on optical parametric chirped pulse amplification (OPCPA), e.g., as a master oscillator or a fs off-harmonic probe beam.