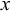Surprisingly robust violations of stochastic dominance despite splitting training: A quasi-adversarial collaboration

Abstract

First-order stochastic dominance is a core principle in rational decision-making. If lottery A has a higher or equal chance of winning an amount $x $ or more compared to lottery B for all x, and a strictly higher chance for at least one $x $, then A should be preferred over B. Previous research suggests that violations of this principle may result from failures in recognizing coalescing equivalence. In Expected Utility Theory (EUT) and Cumulative Prospect Theory (CPT), gambles are represented as probability distributions, where probabilities of equivalent events can be combined, ensuring stochastic dominance. In contrast, the Transfer of Attention Exchange (TAX) model represents gambles as trees with branches for each probability and outcome, making it possible for coalescing and stochastic dominance violations to occur. We conducted two experiments designed to train participants in identifying dominance by splitting coalesced gambles. By toggling between displays of coalesced and split forms of the same choice problem, participants were instructed to recognize stochastic dominance. Despite this training, violations of stochastic dominance were only minimally reduced, as if people find it difficult—or even resist—shifting from a trees-with-branches representation (as in the TAX model) to a cognitive recognition of the equivalence among different representations of the same choice problem.

1. Introduction

Consider the choice between gambles $G^- $ and $G^+ $ in Figure 1. Gamble $G^+ $ offers outcomes of £12, £14, and £96 with probabilities 0.05, 0.05, and 0.90, respectively. Gamble $G^- $ offers outcomes of £12, £90, and £96 with probabilities 0.10, 0.05, and 0.85. Which would you prefer? Birnbaum (2006) found that over 70% of participants preferred $G^- $ , a striking violation of stochastic dominance: when the probability of winning $x $ or more in lottery A is greater than or equal to that in lottery B for all $x $ , and strictly greater for at least one $x $ , A should be preferred over B. In our example, $G^+ $ dominates $G^- $ , yet many participants still prefer $G^- $ , despite it being objectively worse.

Figure 1 Cultivating and weeding out violations of stochastic dominance (after Birnbaum, 2008).

Violating stochastic dominance involves choosing an objectively worse option, making the high and persistent rates of these violations particularly troubling, as they suggest that people may make irrational decisions in critical domains, including medical, financial, or personal choices. The finding that a majority of people tend to make these seemingly irrational decisions underscores the need for a better understanding of their origins (Birnbaum, 1997, 1999, 2005; Birnbaum and Navarrete, 1998; Birnbaum et al., 1999).

Birnbaum (1997) developed a recipe for creating these violations based on descriptive, configural weight models. The recipe is illustrated in Figure 1: Start with a root gamble $G_0 = (x,1-p; y,p) $ , where $y> x > 0 $ . First, split the lower branch of $G_0 $ into two outcomes, one with a slightly higher value $x^+ $ (where $y> x^+ > x $ ), creating a better gamble $G^+ = (x,1-p-q; x^+,q; y,p) $ . Then, split the upper branch of $G_0 $ into two outcomes, one with a slightly lower value $y^- $ (where $x < y^- < y $ ), creating a worse gamble $G^- = (x,1-p; y^-,r; y,p-r) $ . Notice how $G^+ $ dominates $G_0 $ , and $G_0 $ dominates $G^- $ .

Under the descriptive models guiding this recipe, this initial round of splitting induces violations of stochastic dominance in binary lottery choices, leading to the selection of $G^- $ over $G^+ $ , $G^- $ over $G_0 $ , or $G_0 $ over $G^+ $ . However, if lotteries $G^+ $ and $G^- $ are split again to create objectively equivalent options displayed in canonical split form (i.e., with equal probabilities on their corresponding branches), as seen in lotteries $GS^+ $ and $GS^- $ , the models predict that violations of dominance should be eliminated, leading to a preference for $GS^+ $ over $GS^- $ .

Such violations of dominance carry far-reaching theoretical and practical implications. Respecting dominance is implied or assumed by many descriptive theories but not by others. Expected Utility Theory (EUT), Cumulative Prospect Theory (CPT), and Rank and Sign-Dependent Utility (RSDU) models satisfy this property (Gonzalez and Wu, 1999; Luce and Fishburn, 1991; Quiggin, 1993; Tversky and Kahneman, 1992), while configural weight models such as Rank Affected Multiplicative Weights (RAM) and Transfer of Attention Exchange (TAX) theories allow for violations (Birnbaum and Chavez, 1997; Birnbaum and Navarrete, 1998). So, the property of stochastic dominance provides a means of testing among descriptive theories. Birnbaum’s recipe was specifically developed to compare these configural weight models (RAM and TAX) against CPT and RSDU models.

In Birnbaum’s models, lotteries are treated as trees with branches, where each branch represents a probability-consequence pair. When a branch is split, the resulting ‘splinters’ receive more total weight than the original branch. A lottery can be improved by splitting branches with higher consequences, or worsened by splitting branches with lower consequences, potentially leading to violations of stochastic dominance.

These implications contrast with those of EUT and CPT, where gambles are represented as probability distributions over outcomes, allowing for the coalescing of branches with identical outcomes by summing their probabilities. Under these models, stochastic dominance is never violated.

More technically, if a person adheres to outcome monotonicity, coalescing, and transitivity, they should satisfy stochastic dominance within this recipe. Outcome monotonicity states that increasing an outcome in a gamble, while keeping everything else constant, should improve that gamble. Coalescing equivalence asserts that adding the probabilities of branches with identical values within a gamble or splitting a branch into splinters with the same total probability should not alter preferences. Finally, transitivity implies that if a person prefers A to B and B to C, then they should also prefer A to C.

To illustrate, consider equivalent versions of $G_0 $ , denoted as $G_0' $ and $G_0" $ , that reflect different splits of the same gamble. In the first round of splitting, coalescing $G_0' = (x,1-p-q; x,q; y,p) $ makes it equivalent to $G_0 $ . By outcome monotonicity, $G^+ = (x,1-p-q; x^+,q; y,p) \succ G_0' $ , meaning $G^+ \succ G_0 $ . Similarly, coalescing $G_0" = (x,1-p; y,r; y,p-r) $ makes it equivalent to $G_0 $ , and by outcome monotonicity, $ G^- = (x,1-p; y^-,r; y,p-r) \prec G_0" $ , so $G^- \prec G_0 $ . Therefore, by transitivity, $G^+ \succ G^- $ . After the second round of splitting, dominance is satisfied due to outcome monotonicity alone, leading to $GS^+ \succ GS^- $ .

RSDU, CPT, and EUT assume or imply all three of these principles and therefore cannot explain systematic violations of stochastic dominance in the choice between $G^+$ and $G^-$ . RAM and TAX models, on the contrary, imply transitivity and outcome monotonicity, but violate coalescing, and therefore they can imply violations of dominance in this recipe. In fact, they imply $G^- \succ G^+$ in this example choice problem, based on parameters estimated from previous research (Birnbaum and Navarrete, 1998); however, those models retain consequence monotonicity and transitivity so they satisfy dominance in the choice between $GS^+$ and $GS^-$ . Indeed, numerous experimental studies with these choice problems appear consistent with the hypothesis that violations of dominance are primarily due to violations of coalescing, rather than to violations of outcome monotonicity or transitivity (Birnbaum, 1997, 1999, 2005; Birnbaum and Navarrete, 1998; Birnbaum et al., 2016; Birnbaum et al., 1999).

The finding that violations of coalescing equivalence are the likely cause of violations of stochastic dominance in these studies raises the question of whether there is a format in which coalescing can be satisfied. To explore this, Birnbaum (2004, 2006), Birnbaum et al. (2008), Birnbaum and Martin (2003) conducted a series of studies that manipulated various aspects of the decision-making scenario. These included probability format (probabilities represented via text, pie charts, bar charts, frequencies, or lists), branch splitting (gambles presented in split or coalesced form), and event-framing (outcomes framed using the same or different colours of marbles on corresponding branches). While the probability format, display format and event framing had minimal effects, branch splitting versus coalescing had large effects and appeared to be the primary factors driving violations of stochastic dominance.

2. Training people to detect dominance

Because first-order stochastic dominance is a normative principle as well as a property that distinguishes descriptive decision models, it is of both practical and theoretical importance to learn what can be done to help people “see” and conform to this principle. How easy is it to markedly reduce the kind of violations that have been observed in previous studies? In our quasi-adversarial collaboration, some but not all of us thought that training participants to split coalesced gambles would markedly increase adherence to first-order stochastic dominance in the $G^+ $ and $G^- $ choice.

Birnbaum (1999, 2001) reported that people with greater education were less likely to violate stochastic dominance: high school graduates, those with bachelor’s degrees, and those with PhDs had violation rates of about 70%, 60%, and 50%, respectively. Furthermore, PhDs who had read a journal article or book on decision making had a violation rate of only 42%. From this correlation, Birnbaum (Birnbaum, 1999, 2000) speculated that training might reduce violation rates, but he was of the opinion that to be effective, this training might require a graduate-level course.

We conducted two experiments to test the effects of training on the incidence of violations of stochastic dominance. In the first experiment, participants were trained using an animation that illustrated the splitting and coalescing of branches.¹ In the animation, participants could toggle between the two views in Figure 2. As they toggled, solid vertical lines appeared and faded, to highlight the splitting and coalescing of branches. To pre-empt our results, we found that while the training did have a reliable effect, the reduction in the rate of dominance violations was small. To investigate specific conjectures as to why the training produced only small improvements in satisfying dominance, we conducted a second experiment.

Figure 2 Training illustration: Splitting gambles in experiment 1.Note: This screenshot is from the training phase, illustrating a choice where $G^- $ is the top gamble and $G^+ $ is the bottom gamble. During the training phase, participants could toggle between two views. As they toggled, solid vertical lines appeared and faded, highlighting the splitting and coalescing of the gamble branches. A video of the training animation is available at https://github.com/neil-stewart/stoc_dom_2/blob/main/screenshots/toggle.mp4.

A related issue in training—and part of our quasi-dispute—is whether people make choices between risky prospects through intuitive judgments or through analytic, reflective thinking. Dual-process notions of cognition distinguish a fast, intuitive system (‘unconscious interence’, ID, or System 1) and a slower, reflective system (‘conscious thinking’, Super-Ego, or System 2) (Kahneman, Frederick, et al., 2002; Kahneman and Frederick, 2005; Sloman, 1996; Stanovich and West, 2000). Our dispute may relate to how intuitive computations of value, generated by biological mechanisms of the kind described by Helmholtz (1866/1962), Freud (Ellenberger, 1956), and Shepard (Shepard, 2004)—what some now call ‘System 1’ can persist in generating perception-based computations, despite efforts to engage language-based ‘System 2’ processes.

3. Experiment 1

Experiment 1 examined whether training participants to recognize the equivalence between choice problems presented in coalesced and canonically split forms would substantially reduce violations of stochastic dominance. The training was intended to help participants detect dominance by visualizing a choice problem between gambles in split form. The experiment aimed first to determine whether these violations were due to failures in outcome monotonicity or coalescing equivalence, and second, to assess whether the training effectively reduced dominance violations.

3.1. Method

3.1.1. Participants

A total of 1,309 participants were recruited from Amazon Mechanical Turk (MTurk), a crowdsourcing platform commonly used for running online studies. Both the sample size and experimental design were preregistered, and the preregistration details can be accessed at https://aspredicted.org/r272a.pdf. All materials used in the study are available at https://github.com/neil-stewart/stoc_dom_2.

3.1.2. Stimuli and instructions

The experiment involved three choices (as shown in Table 1).

Table 1 Choice problems tested Experiment 1

At the start of the experiment, participants were presented with a choice between two gambles. Each gamble was defined as a lottery with either 20 tickets (for Gamble G) or 25 tickets (for Gamble F). In each trial presentation (and thus independently for each participant), the gambles in a choice were randomly allocated to the top or bottom positions. Participants were informed that cash prizes were printed on each ticket, and that one ticket would be drawn at random from the chosen lottery. A selected participant would win the amount printed on the randomly drawn ticket.

To make stochastic dominance more obvious during training, the gambles were displayed in a matrix-aligned format, where probabilities were represented by lottery tickets. The branches were aligned horizontally, and the number of tickets in each branch determined their horizontal spacing, allowing for easy visual comparison. This layout was designed to promote vertical eye movements, enabling participants to easily compare prizes across lotteries. We expected that stochastic dominance would be readily discernible in this display and would be apparent to participants both during and after the training.²

The instructions given to participants, as well as the sequence of gambles displayed in each condition, are provided in Supplementary Figure S1 and Supplementary Table S1. The appearance of the training provided is shown in Figure 2.

3.1.3. Design

As specified in the preregistered experimental design, participants were randomly assigned with equal probabilities to three between-subject conditions: 435 participants were allocated to the Coalesced-Identical Condition, 436 to the Coalesced-Different Condition, and 438 to the Transparent Condition. These conditions varied in the version of the choice problem presented and whether participants received an explanation on how to recognize dominance (as shown in Table 2). During training, the coalesced and split forms of lotteries derived from Gamble G were used for the Coalesced-Identical Condition, while those from Gamble F were used for the Coalesced-Different Condition.

Table 2 Experimental conditions for Experiment 1

Note: Screenshots illustrating the sequence of choice problems presented in each condition can be found in Supplementary Table S1.

In the Coalesced-Identical Condition, participants completed two main trials, both involving the choice between $G^- $ vs. $G^+ $ . Prior to the second main trial, participants underwent a separate training phase, also using the $G^- $ vs. $G^+ $ choice. During training, participants were instructed to compare each ticket in both gambles by their payouts, identifying which gamble offered a payment at least as good as the other for each ticket. They were required to toggle between coalesced and split representations at least six times before moving on to the second trial.

The Coalesced-Different Condition was structured similarly to the Coalesced-Identical Condition, but with the F version of the gambles used in place of the G version in the first trial and during the training phase. This condition was designed to test whether the training would generalize to a different, but similar, choice problem. In the Transparent Condition, participants were presented with the canonical split forms of the gambles, comparing $GS^- $ vs. $GS^+ $ .

3.2. Results

The proportion of participants violating stochastic dominance is displayed in Figure 3, along with 95% confidence intervals. As preregistered, we excluded submissions from participants with duplicate IP addresses and removed the fastest and slowest 5% of responses in each condition.

Figure 3 Rates of violations of stochastic dominance in Experiment 1.Note: Error bars represent 95% confidence intervals.

The final sample included 1,072 participants after exclusions: 343 in the Coalesced-Identical Condition; 344 in the Coalesced-Different Condition; and 385 in the Transparent Condition. The reported proportions reflect these exclusions. The conclusions of our analyses remain the same with or without these exclusions (see Supplementary Figure S2).

We first analyze the results from the initial trials, before training. According to EUT, CPT, and RSDU—theories that assume coalescing—we would expect few violations of stochastic dominance, aside from random error. Yet, the data indicate a high frequency of violations: 68% of participants violated dominance in the $G^- $ vs. $G^+ $ choice, which is significantly higher than the 18% violation rate in the split form of the same choice, $ GS^- $ vs. $GS^+ $ , $\chi ^2(1,N = 728) = 186.8, p < .001 $ . Similarly, 71% of participants violated dominance in the $F^- $ vs. $F^+ $ choice, again significantly higher than the violation rate in the $GS^- $ vs. $GS^+ $ choice, $\chi ^2(1,N = 729) = 206.2, p < .001 $ .³

Appendix Table A1 shows the distribution of dominance violations before and after training, aggregated across all conditions.⁴ Since responses for versions G and F were similar, we combined conditions Coalesced Identical and Coalesced Different (the two training conditions), resulting in a sample of 687 participants. Among these, 258 participants (37.6%) changed their responses following the intervention; 166 participants (24.2%) shifted from violating to not violating dominance, while 92 participants (13.4%) shifted in the opposite direction, leading to an overall 0.11 reduction in the proportion of participants violating dominance (95% CI: [0.06, 0.15]). A McNemar’s test revealed a statistically significant improvement after training, $\chi ^2(1) = 20.7,\ p < .001 $ . The odds ratio for improvement is 1.80 (95% CI: [1.39, 2.35]), indicating a positive, but modest effect of the training.

During training, participants toggled between the split and coalesced forms of the gambles an average of 7.34 times (SD = 2.70). Those who toggled more frequently were less likely to violate dominance on the second trial, with each additional toggle (beyond the required minimum) associated with a 1.8% decrease in violation likelihood (95% CI: [0.42%, 3.1%]). After training, response times generally decreased as participants became more familiar with the task (see Figure S4 in the Supplementary Material); however, participants who satisfied stochastic dominance tended to have longer reaction times, possibly reflecting greater care, more attention, or more thought (see Figure 4). Together, these findings suggest that more active engagement with the task may be linked to improved satisfaction of stochastic dominance.

Figure 4 Histogram of reaction times by stochastic dominance violation in Experiment 1.Note: The first column shows reaction times for trials without violations of stochastic dominance, and the second for trials with violations. Each row corresponds to a different condition before and after training. Dashed lines indicate mean reaction times.

In sum, these findings are compatible with the theory that people mostly satisfy outcome monotonicity, as reflected by the low rates of violations in the $ GS^- $ vs. $GS^+ $ choice, and often fail to adhere to coalescing, as indicated by the much higher rates of violations in the $G^- $ vs. $G^+ $ and $F^- $ vs. $F^+ $ choices. Furthermore, results show this gap is only slightly reduced by training designed to reveal that the split and coalesced forms of the choice problems are equivalent.

4. Experiment 2

Experiment 1 showed that rates of violation of stochastic dominance after training were only slightly lower than before. Experiment 2 investigated five conjectures, including some suggested by colleagues, to explain why high rates of dominance violations persisted and why training had only a modest effect in Experiment 1.

Conjecture C1 is the null hypothesis that the training had no effect and that the observed reduction in violations after training was simply a practice effect from making a second choice on the same problem. Birnbaum et al. (2016) (Figure 2) reported that violation rates decreased with repeated exposure to the task, even without training. To test C1, Experiment 2 included a control group that received no training between the first and second presentations of the main choice problem. We compared the control group’s second-round responses with those of the experimental group, which received training between the first and second presentations.

Conjecture C2 states that people who violate dominance do so knowingly—not because they believe the dominated gamble has a higher chance of a favorable outcome, but due to other factors. This conjecture implies a conscious choice to favor the dominated gamble despite understanding its lower likelihood of a better result. To test C2, Experiment 2 first asked participants to state their preferred gamble and then to identify which option they believed was more likely to yield a better outcome. C2 implies that participants should judge that the dominant gamble has a higher likelihood of a favorable outcome yet still prefer the dominated gamble.

Conjecture C3 asserts that if people were allowed to express indifference as well as preference, judgments of preference would not show systematic violations of dominance. Experiment 2 tested C3 by including two groups that were allowed to express ‘indifference’, in which case there should be no systematic violations of dominance when people say they are not indifferent.

Conjecture C4 proposes that training would have been more effective if participants had not made choices before training. Once participants make initial choices, they tend to repeat them (for consistency), even if training shows their initial choices were incorrect. Experiment 2 tested C4 by comparing a group that made no initial choice before training with a group that did make an initial choice.

Conjecture C5 is that the observed effect of training may be biased by changes in error rates following training. For instance, training might produce no systematic benefit on true preferences and yet it might appear to reduce violations. For example, if training merely confuses participants without changing true preferences, it would increase random errors, causing the observed violation rate to approach 0.5. Alternately, training may have produced larger true systematic benefits than observed, with effects masked by changes in error rates. Experiment 2 tested these possibilities by including repeated presentations of the choice problems, allowing the use of the true and error model to separately estimate random error rates and the rate of true (systematic) violation before and after training.

4.1. Method

4.1.1. Participants

For Experiment 2, we recruited 1,998 participants via Prolific. The experiment was preregistered at https://aspredicted.org/BGD_Y9L. Experimental materials are available in the Supplementary Material.

4.1.2. Stimuli and instructions

The experiment followed the same setup as Experiment 1, where participants chose between two gambles. Each gamble was defined as a lottery with a set number of tickets, and participants were told that a ticket would be drawn at random from the chosen lottery, with one participant winning the amount printed on the ticket. As in Experiment 1, the gambles were displayed in a matrix format, with branches aligned horizontally and spaced according to the number of tickets to facilitate easy visual comparison.

The instructions given to participants, as well as the sequence of gambles displayed in each condition, are provided in Figure S5 and Tables S2–S6 in the Supplementary Material. The appearance of the training provided is shown in Figure S6 in the Supplementary Material.

4.1.3. Design

As in the preregistered experimental design, participants were randomly assigned to five between-subject conditions with equal probability: 402 were allocated to Condition 1, 395 to Condition 2, 401 to Condition 3, 398 to Condition 4, and 402 to the Control Condition. Table 3 describes the choice problems presented in each condition. As in Experiment 1, gambles were randomly allocated to the top and the bottom positions, and counterbalanced between replications.

Table 3 Experimental conditions for Experiment 2

Note: The table outlines the sequence of choice problems for each condition. The ‘Problems Prior to Training’ and ‘Post-Training’ columns list the gamble choices in the order participants faced them, while the ‘Training’ column indicates if any training was provided. The question column describes the questions posed to participants during each choice problem before and after training. In all conditions, participants chose between two options unless otherwise noted (Condition 3). During the training phase, participants were always asked ‘Select the option you prefer’, with two response options.

In the Control Condition, participants received no training. They were presented with gambles $G^+ $ vs. $G^- $ , asked to select their preferred option, followed by a 20-second pause, during which the screen displayed the message ‘Please wait a moment for the next set of choices to appear’, after which the next trial began. They received the same choice again (with positions of the gambles counterbalanced).

Conditions 1 to 4 included the training task of Experiment 1, which demonstrated the equivalence of the choice in canonically split and coalesced forms.

Condition 1 mirrored the Control Condition, but with the training task replacing the pause of the Control condition. Condition 1 and the Control Condition tested Conjecture C1, assessing whether the improvements observed in Experiment 1 were due to training or simply due to increased practice with the task. As shown in the table, these two conditions included replications, so they were also used to test Conjecture C5, via a true and error model analysis.

In Condition 2, participants answered two questions for each pair of gambles: ‘Select the option you prefer’ and ‘Which is more likely to yield a better outcome?’ These questions aimed to distinguish between participants’ preferences and their understanding of objective probabilities, while also prompting them to focus on the overall structure of probabilities and outcomes. According to Conjecture C2, most people will correctly recognize that $G^+ $ is more likely to produce a better outcome, but will continue to choose $G^- $ .

To help participants distinguish between preference and likelihood of a better outcome, two types of filler gambles were included in Conditions 2 and 3: ( $CR$ vs. $DR$ and $ER$ vs. $FR$ , shown in Table 4). In $CR$ vs. $DR$ , $DR$ is more likely to yield a better outcome because it offers better outcomes on a greater number of tickets, despite CR having a higher Expected Value (EV). Conversely, in ER vs. FR, FR is objectively better in both likelihood and EV. These fillers were intended to reveal to participants that preference and likelihood can align or diverge, encouraging participants to distinguish the dependent variables of subjective preference from their objective evaluation of the probabilities in the gambles.

Table 4 Filler choice problems used in Experiment 2

Condition 3 expanded on Condition 2 by introducing options to express indifference. Participants answered the same two questions as in Condition 2, with additional response options: ‘I am indifferent’ for the preference question, and ‘They are both equally likely to yield a better outcome’ for the likelihood question. This modification aimed to assess whether violations of dominance reflect genuine preferences for dominated gambles or mere difficulty in distinguishing between options. This condition also presented a pair of objectively identical gambles, $G^+ $ and its split version $GS^+ $ , to test for perceived equivalence before and after training.

Finally, Condition 4 began with an upfront training task on probability aggregation using G gambles, followed by choices between $G^+ $ and $G^- $ . This condition was included to rule out the possibility that violations persisted following training in Experiment 1 because participants may have stuck with their initial choice before training, due to a commitment to their first expressed preference. According to Conjecture C4, the effect of training should be greater in this condition, as people do not need to overcome commitment to violations expressed before training.

Figure 5 Rates of violations of stochastic dominance in Experiment 2.Note: Incidence of stochastic dominance violations in the choice problems $G^+ $ versus $G^- $ before and after training, along with 95% confidence intervals.

4.2. Results

Figure 5 displays the proportion of participants who preferred $G^-$ , violating stochastic dominance in the choice problems $G^+ $ vs. $G^- $ before and immediately after training; horizontal bars show 95% confidence intervals. Filled circles show rates of violation of stochastic dominance before training, and triangles indicate rates of violation after training. The overall pattern in the figure shows that the results are similar to those in Experiment 1, and although there may be differences among the conditions, none of the variations of procedure reduced the rate of violations to anywhere near the level produced by the split version of the choice problem.⁵

Test of Conjecture C1: Are the observed before–after improvements due to practice in the task rather than training? In the Control condition, where participants experienced only a brief pause between trials and no training, 42 participants who initially violated dominance satisfied it after the pause, while 45 participants who initially satisfied dominance later violated it. In contrast, in Condition 1, where participants received training instead of a pause, 75 participants who initially violated dominance satisfied it after training, while only 33 shifted to violating it. Thus, after training in Condition 1 and after the pause in the Control condition, the violation rate was lower in Condition 1 (59%) than in the Control group (66%), a statistically significant difference, $\chi ^2(1) = 4.17, p < .05$ . Moreover, a difference-in-difference analysis comparing the before-and-after changes in the Control group with those in Condition 1 indicated that training in Condition 1 led to an 11.2% reduction in the likelihood of violations (95% CI: [4.5%, 17.9%]), above and beyond the changes observed in the Control group.⁶ We, therefore, reject Conjecture C1 in favor of the hypothesis that the observed improvements were due to training rather than task familiarity alone.

Table 5 summarizes the number of participants with two ( $f_11$ in the table), one ( $f_10+f_01$ ), or zero violations ( $f_00)$ after the pause or training in both the Control and Condition 1 groups. The Control group had 38 more participants with two violations and 23 fewer participants with zero violations compared to Condition 1, $\chi ^2(2)=7.48$ . Additionally, in the generalization test (which evaluated whether training on the choice between $G^+$ and $G^-$ generalized to the choice between $F^+$ and $F^-$ ), Condition 1 had 40 fewer participants than the Control group with two violations and 47 more with no violations after training, $\chi ^2(2)=14.31$ . These findings, which incorporate the replication data, also require us to reject the null hypothesis of Conjecture C1 in favor of the conclusion that the training caused a reduction in the rate of violations.

Table 5 Observed frequencies of response patterns and parameter estimates of true and error model - Experiment 2

Note: The model uses preference reversals by the same person to repeated measures of the same choice problem to estimate error rates. Parameters are estimated from Condition 1 (trials 2 to 5 post-training) and the Control condition (trials 2 to 5 after a waiting period, no training). $\mathbf {f_{11}}$ : Number of participants who violated dominance in both choice problems. $\mathbf {f_{10}}$ : Violated dominance in the first choice problem, but satisfied it in the second. $\mathbf {f_{01}}$ : Satisfied dominance in the first problem but violated it in the second. $\mathbf {f_{00}}$ : Satisfied dominance in both choice problems. $\mathbf {p}$ : Estimated probability of violating dominance in the choice problems. $\mathbf {e}$ : Estimated probability of making an error in the choice. $\mathbf {G}$ : Index of fit of TE model, distributed Chi-Square with 1 df. Choice Problems 2 and 4: $G^+ $ versus $G^- $ . Choice Problems 3 and 5: $F^+ $ versus $F^- $ .

Test of Conjecture C5: Is the reduction of observed violations due to a change in the error rate, or is it due to a true change in systematic preferences? Both the Control Condition and Condition 1 included repeated trials of the $G^+ $ vs. $G^- $ and $F^- $ vs. $F^+ $ choice problems after training or after the control pause. The use of replicates allowed us to apply the True and Error (TE) Model (Birnbaum and Quispe-Torreblanca, 2018), which distinguishes between true violations and those produced by random error. The TE model analysis confirmed that training led to about 10%–15% reductions in true rate of violations (see Table 5). Following training, the $G^+ $ vs. $G^- $ and $F^- $ vs. $F^+ $ choice problems in Condition 1 had true violation rates of 0.629 and 0.591, with error rates of 0.164 and 0.115, respectively, compared to the corresponding Control group values following the pause of 0.724 and 0.738 with error rates of 0.137 and 0.127, respectively. Therefore, the data are not consistent with Conjecture C5, but instead imply that training reduced true preferences for the dominated gambles.

Conjecture C2: Do people violate stochastic dominance knowingly, or do they think that the dominated gamble is more likely to yield a better outcome? Condition 2 included two questions: ‘Select the option you prefer’ and ‘Which is more likely to yield a better outcome?’ Figure 5 shows that the rate of saying that the dominated gamble is more likely to yield the better outcome is high and not very different from the rate of preferring the dominated gamble.

Table 6 provides a crosstabulation of 4 responses (two dependent variables, before and after training) in Condition 2. The 4 most frequent patterns of responses, in decreasing frequency are (a) 196 participants (first row) chose $G^-$ over $G^+$ , violating dominance, and said (incorrectly) that $G^-$ is more likely to give a better outcome, and did the same before and after training; (b) 86 individuals chose $G^-$ and said $G^-$ is more likely to give a better outcome before training, but reversed both responses after training; (c) 57 people chose $G^+$ and consistently said $G^+$ was preferred before and after training; (d) 25 people initially favored $G^+$ on both responses but (surprisingly) switched to preferring $G^-$ after training, saying it was better. Only 31 (8% of 395) people had one of the other 12 response patterns; these participants did not always choose the gamble they said was more likely to give a better outcome. In sum, the vast majority say the gamble they chose was more likely to give the better outcome, including those who violated dominance. This result is not consistent with C2, which held that people violate dominance despite knowing that $G^-$ is less likely to yield a better outcome.

Table 6 Participant responses in Condition 2 of Experiment 2 for choice problem $G^+ $ vs. $G^- $

Conjecture C3: Are violations of dominance merely an artifact of a binary forced choice procedure? Condition 3 is the same as Condition 2, except participants were able to express indifference and to say that both gambles were equally likely to yield a better outcome.

Table 7 provides a crosstabulation of responses in Condition 3, as in Table 6. The four most frequent response patterns match those of Condition 2, and their order of relative magnitude is the same. Very few participants expressed indifference (only 17 of 401 before training and only 6 after training), and few thought both gambles equally likely to yield better outcome. As in Condition 2, most participants who expressed a preference said their chosen gamble was more likely to yield a better outcome.

Table 7 Participant responses in Condition 3 of Experiment 2 for choice problem $G^+ $ vs. $G^- $

Comparing Conditions 2 and 3, note that Condition 3 had 109 (of 401) people who switched from violating dominance to satisfying it, and 25 who switched in the opposite direction; In Condition 2, the corresponding numbers were 86 to 25 (of 395); in addition, the number who persisted in violating dominance before and after was lower in Condition 3 (140) than in Condition 2 (196), suggesting that the training effect appears slightly larger in Condition 3 than 2.

In terms of before-after differences in overall rates of dominance violations, Condition 2 showed a statistically significant reduction from 77.2% to 61.3%, a decrease of 15.9%, while Condition 3 showed a similarly significant reduction from 73.6% to 53.4%, a decrease of 20.2%. The difference between conditions, however, was minimal and nonsignificant ( $-$ 4.3%; 95% CI: [ $-$ 12.3%, 3.8%]). Likewise, training significantly reduced failures to recognize that gamble $G^+ $ was more likely to yield a better outcome than gamble $G^- $ , with a decrease of 16.7% in Condition 2 and 17.2% in Condition 3. This small difference between conditions in training effects was also nonsignificant ( $-$ 0.5%, 95% CI: [ $-$ 8.8%, 7.8%]). Although there might be some minor effect of having the option to respond with indifference, we cannot reject the null hypothesis that this manipulation produced no improvement in training. Overall, adding the option to respond ‘I am indifferent’ failed to eliminate or markedly reduce the violations of stochastic dominance in the first choice, and failed to significantly alter training effects compared to Condition 2; therefore, the data do not provide evidence to argue as in Conjecture C3 that people who violate stochastic dominance are actually indifferent and merely choosing the dominated alternative systematically for some other reason.

In Condition 2, almost half of the sample failed to identify $DR$ as more likely to yield a better outcome than $CR$ , with correct responses dropping from 51.1% to 38.9% post-training. In Condition 3, correct responses similarly declined from 37.9% to 29.7%, with more than half of the sample failing to identify $DR$ as the more likely option, suggesting that at least some participants might have focused on overall value rather than likelihood in these problems.⁷

Condition 3 also included a pair of objectively identical gambles, $G^+ $ and its split version $GS^+ $ , to test whether participants would recognize their equivalence before and after training. Before training, 67.1% of participants (269 out of 401) failed to respond ‘indifferent’ when asked to select their preferred option, but 26.8% of these shifted to indifference after training (see Figure 6, bottom panel). Similarly, 59.6% (239 out of 401) did not identify the equivalence when asked which gamble was more likely to yield a better outcome before training, with 30.9% of these shifting responses to indicate both options were equally likely to yield a better outcome after training.⁸ Although training had some effect, a sizeable portion of participants still failed to identify this equivalence between the gambles, even though $G^+ $ versus $GS^+ $ comparison should have been straightforward.

Figure 6 Participants’ responses when given the opportunity to express indifference (Condition 3 of Experiment 2).Note: Participants’ responses in Condition 3 to questions about which gamble they prefer and which is more likely to yield a better outcome in the choice problems $G^+ $ vs. $G^- $ (top panel) and $G^+ $ vs. $GS^+ $ (bottom panel), along with 95% confidence intervals.

Testing Conjecture C4: Are high violation rates and modest effects of training due to participants sticking with their initial pre-training choices that violated dominance? In Condition 4, participants made no choices prior to the training task, so their choice between $G^+ $ and $G^- $ after training could not be influenced by commitment to a previously expressed choice. This procedure produced a slightly lower rate of violations by $-3.68\%$ (95% CI: [ $-$ 10.54%, 3.19%]), a difference that was not statistically significant; see also Figure 5. We thus retain the hypothesis that this manipulation had no effect and reject the hypothesis that it produced a large enough effect to substantially reduce the violations of stochastic dominance.

The new conditions of Experiment 2 replicate the main results from Experiment 1: violations of stochastic dominance are substantial, and training has significant but small effects. Aggregating Conditions 1 to 3, where participants received training, 402 participants changed their responses after the intervention: 294 participants shifted from violating to not violating dominance, while 108 shifted in the opposite direction. McNemar’s test revealed a statistically significant benefit, $\chi ^2(1) = 85.137$ , $p < 0.001 $ . The odds ratio for improvement was 2.72 (95% CI: [2.18, 3.43]), which was slightly larger than in Experiment 1.

As found in Experiment 1, participants of Experiment 2 who toggled more frequently between the split and coalesced forms of the choice problem during training were less likely to violate dominance in the subsequent test ( $r=$ $-$ 0.12). On average, participants toggled 9.22 times (SD = 7.61). Each additional toggle reduced the likelihood of violations by an average of 0.8% (95% CI: [0.5%, 1.2%]). The correlation between the number of toggles and violations of dominance in the pre-training phase was again not significant ( $r=$ 0.02), making it hard to argue that people who toggle are less prone to violations.⁹

5. Discussion

Although some of us thought the training would be compelling, it had only a small (though significant and replicable) effect on reducing violations of dominance, which remained high. Birnbaum’s findings on violations of stochastic dominance appear to be more robust than (some of us) thought.

Consistent with previous studies (summarized in Birnbaum, 2008), our data revealed much higher rates of dominance violations when choices problems were presented in coalesced form ( $G^+ $ vs. $G^- $ ) compared to the canonical split form ( $GS^+ $ vs. $ GS^- $ ). According to certain descriptive theories of risky decision making, such as cumulative prospect theory (Tversky and Kahneman, 1992), and the editing rule of combination in original prospect theory (Kahneman and Tversky, 1979), these two choice problems should be equivalent; however, evidence shows they are not. Apparently, people do not spontaneously combine branches in the split form of the choice, nor do they spontaneously split the gambles in the coalesced form.

Because previous findings appeared consistent with the theory that people satisfy monotonicity but violate coalescing, we sought to train people to recognize the equivalence of split and coalesced forms of the choice problems. Some of us were surprised that the training had such small effects. Either the training did not succeed in teaching this equivalence, or most participants failed to apply it in subsequent trials.

Though the training’s success in reducing violations was limited, we did observe a positive correlation between the frequency of toggling between the split and coalesced forms and the likelihood of satisfying dominance. Although this correlation was not pre-registered, it was observed in both of our experiments. Perhaps a stronger effect might have been observed had we set a higher minimum number of toggles or provided additional motivation to engage with the training.

Alternatively, it is also possible that participants who were more intelligent, careful, motivated, or diligent were the ones who derived benefit from the treatment, and also spent more time with the training. Possibly related to this interpretation, we found that responses that satisfied dominance also had longer average reaction times. According to this interpretation, increasing the required number toggles may not have had much additional effect.

Experiment 2 refuted or found no evidence for five conjectures proposed to account for the high rates of violations of dominance and/or the minimal effects of training. Results of Experiment 2 showed that the effect of training is not merely a consequence of practice in the task and that the violations of stochastic dominance and the effects of training cannot be attributed to effects on random errors. Experiment 2 also found that most participants who violated dominance judged (incorrectly) that the dominated gamble was more likely to yield a better outcome, that dominance violations are not substantially reduced when people are allowed to express indifference, and that even when a person makes no initial choice before training, the violations after training persist. Although there may be some small effects of the manipulations that were proposed to reduce violations or increase the effects of training, we found no convincing evidence to reject the proposition that they had minimal effects, and we could reject the proposition that they had large effects.

It is worth noting that our findings do not suggest that violations of stochastic dominance are frequent in all choice problems, as shown by our results with choices presented in canonical split form (Transparent Condition in Experiment 1, Figure 3). They are, however, relatively frequent in the particular recipe we tested and found to be quite robust. Nevertheless, Birnbaum (1999) noted that violations of dominance tend to decrease with higher education levels, possibly due to intelligence or mathematical training. The correlation between the number of toggles and adherence to dominance in our study may similarly relate to education or cognitive ability.

Our findings raise questions about models describing risky choice and their ability to capture violations of coalescing. According to models like CPT, EU, or RSDU, where gambles are represented as probability distributions, training should not be necessary to learn how to split coalesced gambles. The fact that many participants continue to violate stochastic dominance even when they have just been taught how to split seems consistent with the idea that people represent gambles as trees with distinct branches, as in the RAM and TAX models. Perhaps this tree-based representation may be resistant to attempts at restructuring the choice problems, even when doing so would facilitate satisfying stochastic dominance.

Overall, our findings suggest that participants often relied on intuitive evaluations despite training intended to counteract those intuitions in a single type of problem. The limited effect of the training seems consistent with other findings, such as those of Meyer and Frederick’s (2023) research on the bat-and-ball problem, which showed that intuitive errors often persist even when reflection is encouraged and mistakes are pointed out.

It is important to acknowledge that while our study aimed to train people to recognize and satisfy dominance in specific choice problems, it would be even more challenging to develop training that would apply to a wider range of situations. In real-world situations, decision problems often lack numerical probabilities, and the decision maker may need to rely on subjective estimates. Furthermore, many choice problems lack a dominance relationship, so training in detecting dominance by itself is not a complete program in making better decisions. These limitations highlight the need for further research to develop effective methods for promoting dominance satisfaction across a wider range of decision-making scenarios.

Our Quasi-Adversarial collaboration began in a pub in Newcastle in 2010, prompted by a semi-dispute over a central question: Shouldn’t it be straightforward to induce people to detect and conform to dominance in the recipe of Figure 1? According to the prospect theory of Kahneman and Tversky, 1979, people initially perform an editing process of a choice problem and follow the editing phase with an intuitive calculation of value. The editing phase, operating by language-based (Ego/Superego, ‘System 2’) rules includes an unspecified dominance detector, whereas the equations of value represented an Id-based, unconscious, ‘System 1’ value calculator that need not satisfy dominance. If people have a dominance detector that is only partially effective, sufficient to recognize dominance in choices like that between $G_0$ and $G^+$ , but not in the ‘more complex’ choice between $G^+$ and $G^-$ , then it should be possible to observe systematic violations of transitivity. However, in one branch of our collaboration, Birnbaum et al. (2016) were unable to find much evidence, if any, that more than a small number of participants might have utilized such a partial dominance detector. This report shows that despite all our efforts, we were able to find only a small improvement by training people to detect dominance. We have not reported here a number of other, largely futile, attempts to make the dominance relation ‘transparent’ to participants.