Introduction
Race differences in intelligence
Cavalli-Sforza et al. (Reference Cavalli-Sforza, Menozzi and Piazza1994) analysed data for 120 alleles from 43 populations and found ten major ‘clusters’, but traditionally the term ‘race’ is used; their taxonomy is based on the largest number of alleles and the largest number of populations (see Lynn, Reference Lynn2015, pp. 18–21, for a description of other taxonomies). Following Cavalli-Sforza et al., Lynn (Reference Lynn2015, p. 21) distinguished between ten races: (1) Bushmen and Pygmies, (2) sub-Saharan Africans, (3) South Asians and North Africans, (4) Europeans, (5) East Asians, (6) Arctic Peoples, (7) Native American Indians, (8) South-east Asians, (9) Pacific Islanders and (10) Australian Aborigines and Aboriginal New Guineans. The South Asians and North Africans include the peoples of Bangladesh, India, Pakistan, Iraq, Iran, the Gulf states, the Near East and Turkey. Europeans, North Africans and South Asians have been traditionally referred to as Caucasians (Lynn, Reference Lynn2015, p. 129). In the present paper, the term ‘Whites’ will be used to describe the cluster/race of ‘Europeans’ and the term ‘Blacks’ will be used to describe sub-Saharan Africans. Within the races, sub-races (or sub-clusters) can be distinguished – for instance, the sub-Saharan cluster is made up of sub-races of West Africans, Nilotics, Ethiopians and Bantus (Lynn, Reference Lynn2015, p. 57).
There are many instances of racial groups differing in their mean intelligence score (David & Lynn, Reference David and Lynn2007; Rindermann et al., Reference Rindermann, Baumeister and Groper2014; Rindermann & Thompson, Reference Rindermann and Thompson2016). Jensen (Reference Jensen1980, Reference Jensen1998) showed large differences between Blacks and Whites, and te Nijenhuis et al. (Reference te Nijenhuis, de Jong, Evers and van der Flier2004) showed large differences between Dutch and non-Western immigrants. Generally, Whites are the highest scoring race in these comparison studies, but when non-Jewish Whites are being compared with East Asians or Jews it is the non-Jewish White group that have the lower IQ scores (Lynn & Vanhanen, Reference Lynn and Vanhanen2002; Lynn, Reference Lynn2011).
Explaining race differences in intelligence: Spearman’s hypothesis
Jensen (Reference Jensen1985) hypothesized that the differences in Black and White scores on the subtests of an IQ battery showed a clear pattern: namely, large differences on the subtests with a high cognitive complexity (high g loadings), and small differences on subtests with a low cognitive complexity (low g loadings). Jensen (Reference Jensen1998, p. 372) wrote that the strong form of this so-called Spearman’s hypothesis states that the variation in the size of the mean Black/White (B/W) difference across various tests is solely a positive function of variation in the tests’ g loadings – the larger the g loading for a given test, the greater the mean B/W difference on that test. The weak form of Spearman’s hypothesis states that the variation in the size of the mean B/W difference across various tests is mainly a positive function of variation in the tests’ g loading, but certain lower-order group factors may also contribute some smaller part of each B/W difference. Jensen (Reference Jensen1998) showed the method of correlated vectors (MCV) can be used to test the weak form of Spearman’s hypothesis and, when comparing Blacks and Whites, subtests of an IQ battery measuring short-term memory or spatial rotation are further from the regression line than predicted by their g loadings. This means that when matched on their g score, Blacks have better mean scores on short-term memory than Whites, and lower mean scores on spatial rotation. Jensen (Reference Jensen1998) supplied a large amount of proof for Spearman’s hypothesis, and concluded that it is a law-like phenomenon.
Initially, Spearman’s hypothesis was reserved for Black/White differences in the US, but nowadays it is more broadly applied to race differences in general. Spearman’s hypothesis has been confirmed comparing different races. For instance, te Nijenhuis et al. (Reference te Nijenhuis, Willigers, Dragt and van der Flier2016c) showed strong support for Spearman’s hypothesis by comparing the scores of ethnic Dutch and non-Western immigrants. Recent meta-analyses also confirmed Spearman’s hypothesis for Amerindians (te Nijenhuis et al., Reference te Nijenhuis, van den Hoek and Armstrong2015d) and Black adults (te Nijenhuis & van den Hoek, Reference te Nijenhuis and van den Hoek2016). Spearman’s hypothesis has been confirmed in comparisons between sub-races as well: for instance, non-Jewish Whites versus Jews in the US, and European Jews versus Oriental Jews in Israel (te Nijenhuis et al., Reference te Nijenhuis, David, Metzen and Armstrong2014a). Therefore, there is extensive literature showing large-scale support for various tests of Spearman’s hypothesis.
However, a careful study of the literature shows there are a few cases where the hypothesis is in fact not confirmed. For instance, both Kane (Reference Kane2007) and Dalliard (2013) compared Whites with East Asians and found a negative correlation between g loadings and race differences. Jensen and Faulstich (Reference Jensen and Faulstich1988) compared the IQ scores of Black and White prisoners and the g loadings of the subtests did not correlate with racial differences on the same subtests. Lastly, Armstrong et al. (Reference Armstrong, Woodley and Lynn2014) compared the IQ scores of the Sámi and Finns and did not find support for Spearman’s hypothesis. However, te Nijenhuis et al. (Reference te Nijenhuis, van den Hoek, Metzen and David2017b) argued that the aforementioned studies all share an unusual Verbal/Performance profile, which strongly influences the outcomes of tests of Spearman’s hypothesis.
Spearman’s hypothesis is often tested using the Wechsler batteries, where the Performance subtests have, on average, lower g loadings than the Verbal subtests, and in most group comparisons the group differences on the Performance subtests are smaller than the group differences on the Verbal subtests. So, the generally lower-g Performance subtests yield generally smaller values of d and the generally higher-g Verbal subtests show generally higher values of d, which means Spearman’s hypothesis is strongly confirmed. However, what the groups mentioned above appear to have in common is smaller ds on Verbal subtests and larger ds on Performance subtests and so the generally higher-g-loaded Verbal subtests showed the smaller group differences and the generally lower-g-loaded Performance subtests show the larger group differences. This profile of higher g combined with lower d and lower g combined with higher d will not lead to support of Spearman’s hypothesis (te Nijenhuis et al., Reference te Nijenhuis, van den Hoek, Metzen and David2017b, p. 53). Te Nijenhuis et al. (Reference te Nijenhuis, van den Hoek, Metzen and David2017b) carried out a series of meta-analyses to investigate this concern. Spearman’s hypothesis showed no supporting evidence, but bypassing the unusual Verbal/Performance profile by testing it separately on Verbal subtests and Performance subtests led to a confirmation in 57% (25 out of 44) of the comparisons. There are more positive correlations for the Verbal subtests than for the Performance subtests; one could speculate that East Asians tend to excel on subtests of Spatial rotation, which becomes an outlier in a test of Spearman’s hypothesis, and outliers are known to strongly influence the size of correlations, especially correlations based upon a small number of observations. The authors conclude the anomalies appear to be more in line with Spearman’s hypothesis than previously thought (te Nijenhuis et al., Reference te Nijenhuis, van den Hoek, Metzen and David2017b, p. 52).
Te Nijenhuis et al. (Reference te Nijenhuis, Al-Shahomee, van den Hoek, Allik, Grigoriev and Dragt2015a) described how Spearman’s hypothesis has also been confirmed using instruments other than intelligence test batteries. Firstly, there are elementary cognitive tasks (ECTs) that measure the time it takes a person to process information presented in these very simple tasks, which do not call upon previously acquired knowledge or skills and scarcely resemble conventional psychometric tests (Jensen, Reference Jensen1993). Secondly, there are Situational Judgment Tests (SJTs) and Assessment Centre (AC) exercises, which are popular instruments in selection psychology. The SJTs assess an applicant’s judgment regarding situations encountered in the workplace, while ACs allow applicants to demonstrate that they possess an important job skill (Goldstein et al., Reference Goldstein, Yusko, Braverman, Smith and Chung1998; Whetzel et al., Reference Whetzel, McDaniel and Nguyen2008). Thirdly, Goldstein et al. (Reference Goldstein, Yusko and Nicolopoulos2001) showed that B/W differences in managerial competencies were in line with Spearman’s hypothesis. Fourthly, racial differences in cognitive ability measures used in employment and educational settings confirm Spearman’s hypothesis (te Nijenhuis et al., Reference te Nijenhuis, Evers and Mur2000; Roth et al., Reference Roth, Bevier, Bobko, Switzer and Tyler2001).
The method of correlated vectors (MCV) has also been used by researchers who do not explicitly state they use the technique. For instance, Tesser (Reference Tesser1993) showed that attitudes higher in heritability are responded to more quickly, and are more resistant to change. Another example is Dahlke and Sackett (Reference Dahlke and Sackett2017), who, in a study in personnel selection psychology, examined a large number of predictors of job performance, including integrity tests, biodata, Situational Judgment Tests, occupational interests, assessment centres and structured interviews. They found that the instruments with the highest cognitive-ability saturation show the largest B/W differences.
The nomological net of MCV study outcomes yields three clusters
Many studies have been carried out using MCV, and Rushton (Reference Rushton1998) suggested when the MCV resulted in strong, positive correlations they should be called ‘Jensen effects’. One could then argue that strong, negative correlations should be called ‘anti-Jensen effects’. When the outcome of MCV is the absence of a substantial correlation, it is concluded there are neither Jensen effects nor anti-Jensen effects. One important reason many studies explore the correlations between IQ battery subtest g loadings and other variables, is that such research may help answer a fundamental question in the social sciences: what is the main cause of racial differences?
Opinions differ on the value of MCV, with Flynn (Reference Flynn2013, pp. 19–20) being quite critical: ‘… actually, its results cannot really discriminate even in favour of biological versus cultural’. Flynn (Reference Flynn2013, p. 25) wrote further: ‘… to disentangle cultural and genetic factors … MCV is useless …’. Flynn does not conclude that the MCV has no value, but that it does not settle the question of the causes of Black/White differences in IQ scores; Flynn states that the MCV can be used to test interesting hypotheses about brain physiology (see: Flynn, Reference Flynn2018, Box 1). Rushton (Reference Rushton1999, p. 837), in contrast, wrote positively on ‘the discriminating power of the Jensen effect’. The present authors review a large number of findings from the nomological net of studies based on MCV, including the anomalous studies that give unexpected outcomes from the perspective of Jensen’s research programme, and argue that the MCV is a valuable tool for disentangling genetic and environmental factors.
Jensen (Reference Jensen1985) developed the method of correlated vectors and compared a substantial number of samples of Blacks and Whites to find that g loadings and group differences were strongly related. Jensen (Reference Jensen1998) began exploring the nomological net of outcomes of studies using MCV and showed many strong, positive correlations for various brain variables. He also found that most Flynn effect gains did not show positive correlations with g loadings. Rushton (Reference Rushton1999; see also Flynn, Reference Flynn1999a, Reference Flynn1999b, Reference Flynn2000a, Reference Flynn2000b) started exploring a part of the nomological net of MCV by checking whether various within-group data could predict various between-group differences. The within-group data were inbreeding depression scores from Japan and g-factor loadings from the US. Rushton argued one kind of between-group difference, Black/White differences, could be predicted by the within-group data, but another kind of between-group difference – Flynn effect gains – could not be predicted by the within-group data. Rushton (Reference Rushton1999) was the first to have combined various datasets that used MCV, added additional datasets to which he applied MCV, created a correlation matrix of all the correlations between the various vectors, and then applied factor analysis. This resulted in two factors – a genetic factor with loadings of heritability, inbreeding depression, g loadings and B/W differences, and an environmental factor on which various Flynn effect gains loaded. So, Rushton’s analysis of a limited number of variables resulted in two clusters. Te Nijenhuis et al.’s (Reference te Nijenhuis, Bakhiet, van den Hoek, Repko, Allik, Žebec and Abduljabbar2016a) table 1 presents a larger number of studies using MCV than Jensen (Reference Jensen1998) and Rushton (Reference Rushton1999), all of which are incorporated in the present paper’s Table 1, including additional relevant studies. Rushton’s pioneering efforts advanced the discussion, but the present authors argue the outcomes of the current larger collection of studies using MCV can best be described using three clusters instead of two.
Table 1. Studies on the correlation between a g vector and a second vector
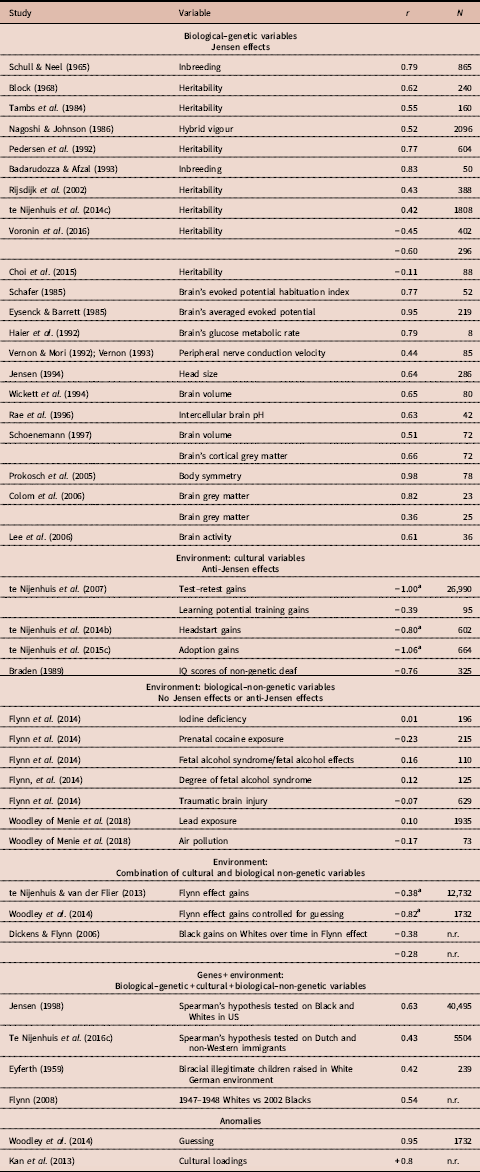
n.r.=not reported or could not be obtained.
Many of the correlations were taken from Jensen (Reference Jensen1998), but the authors of the original studies are listed in the table. Schöenemann (Reference Schönemann1997) is cited in Jensen (Reference Jensen1998, p. 147); sample sizes were not reported by Jensen and were taken from Schöenemann’s dissertation. Haier et al. (Reference Haier, Siegel, Tang, Abel and Buchsbaum1992) shows there is an inverse relationship between brain glucose metabolic rate and psychometric measures of intelligence. A negative correlation is reported and the sign was reversed by the present authors. Colom et al. (Reference Colom, Jung and Haier2006) reported a collection of 28 correlations (Table 3) and 26 correlations (Table 5) on grey brain matter yielding the average correlation shown in the present table. In their Table 2, Lee et al. (Reference Lee, Choi, Gray, Cho, Chae and Lee2006) reported data on activity in several brain regions. The average value of the sixteen correlations is reported in the present table. Prokosch et al. (Reference Prokosch, Yeo and Miller2005) reported data on IQ scores and body symmetry. They also reported the association between the rank-order of g loadings of five cognitive tests and its body symmetry association. Their data were used to compute the rank-order correlation between rank-ordered g loadings and body symmetry association, which is r s=0.98. Schull and Neel (Reference Schull and Neel1965) tested 865 children from consanguineous marriages and 989 children from non-consanguineous marriages. Jensen (1983) used the same data. Badaruddozza and Afzal (Reference Badaruddoza and Afzal1993) tested 50 inbred and 50 non-inbred control children. Braden (Reference Braden1989) reported the correlation of the differences in IQ scores between normal and hearing-impaired individuals and g loadings. Braden reported a median r=−0.76 for six studies, but the three largest studies were criticized by Isham and Kamin (Reference Isham and Kamin1993). The r=−0.76 was taken as an estimate of the mean correlation for the remaining three studies (combined N=325).
Figures in bold are based upon meta-analyses.
This table, including the notes, is taken mostly ad verbatim from the notes of Table 1 in te Nijenhuis et al. (Reference te Nijenhuis, Bakhiet, van den Hoek, Repko, Allik, Žebec and Abduljabbar2016a).
a These correlations are corrected for statistical artefacts.
In contrast with Flynn (Reference Flynn2008), the present authors defend the position that MCV is successful in separating biological–genetic variables from environmental variables, and also successful in separating two environmental variables, namely cultural variables on the one hand and biological–non-genetic variables on the other hand. Biological–genetic factors show strong Jensen effects, cultural factors show strong anti-Jensen effects and biological–non-genetic factors show neither Jensen effects nor anti-Jensen effects, but show correlations with g loadings quite close to zero. It is also possible for outcomes to reflect the action of two or more factors simultaneously. The Flynn effect is a prime example, reflecting both cultural and biological–non-genetic effects, resulting in a meta-analytical rho=−0.38 (corrected for statistical artefacts) (te Nijenhuis & van der Flier, Reference te Nijenhuis and van der Flier2013). Score gains over time of Blacks in comparison to Whites (Dickens & Flynn, Reference Dickens and Flynn2006) is another example of both cultural and biological–non-genetic effects combining to yield a correlation with g loadings of r=−0.38 for children and r=−0.28 for adults. However, using MCV on certain variables leads to anomalies: values of r or meta-analytical rho that do not fit into the theoretically expected cluster. Preferably all or most of these anomalies need to be explained from a specific theoretical perspective – in this case the perspective of Jensen’s research programme that the MCV can be used to show a strong genetic component in racial differences in IQ scores (see: Lakatos, Reference Lakatos1970).
The first cluster consists of biological–genetic variables for which the large majority of studies show Jensen effects. Ten correlations are on genetic factors, namely heritability, inbreeding and hybrid vigour. A recent meta-analysis of Japanese studies on heritability showed smaller values, which contrasts with older studies, which showed strong positive correlations; however, two recent studies even displayed negative correlations. Twelve correlations are from studies on the brain, which measured variables such as head size, brain size and various activities of the brain; all these brain-related variables have been shown to be clearly heritable or can be expected to be clearly heritable.
The second cluster consists of environmental, cultural variables and all of the studies show anti-Jensen effects, especially the ones based on large samples or meta-analyses. Learning potential training gains show a quite substantial negative correlation, and Headstart gains, adoption gains and the differences in IQ scores between normal and hearing-impaired individuals show strong negative correlations. A very large meta-analysis on test–retest studies shows a large negative correlation.
The third cluster consists of environmental, biological–non-genetic variables and all studies show no clear Jensen effects and no clear anti-Jensen effects. The correlations with g loadings are virtually all small or quite close to zero for iodine deficiency, prenatal cocaine exposure, fetal alcohol syndrome and traumatic brain injury.
The interpretation of the r value from an individual study of biological–non-genetic factors can sometimes be less than straightforward. In a fictitious example, an individual study on the effects of improved nutrition may show the largest gain on a specific broad ability, while another individual study on the effects of taking vitamins may show the largest gain on another broad ability. If the gain is predominantly on a high-g broad ability, then the value of r will be somewhat higher than 0 and may give the impression of a modest Jensen effect. If the gain is predominantly on a low-g broad ability, then the value of r will be somewhat lower than 0. To illustrate, if the strongest increase was to be found on a reasoning subtest (high g) then this would lead to a higher value of the correlation. Conversely, if the strongest increase was to be found on a visual speed subtest (low g) then this would lead to a negative value of the correlation. This example illustrates a weakness of the method of correlated vectors: at the level of individual studies, the discriminative power of MCV is not perfect. At the level of individual studies using MCV it can be difficult to empirically distinguish a modest-size Jensen effect for a biological–genetic variable from the absence of a Jensen effect for a biological–non-genetic variable. This is why data aggregation is so important (see: Rushton et al., Reference Rushton, Brainerd and Pressley1983): a meta-analysis of a specific biological–non-genetic factor will result in a mean, which generally is a quite reliable outcome.
Flynn et al. (Reference Flynn, te Nijenhuis and Metzen2014) found that the mean of five meta-analyses testing for Jensen effects on biological–non-genetic variables led to an average value of 0.00. So, in the scenario that all kinds of biological–non-genetic variables affect all kinds of narrow abilities in a quite random way, one would expect a variety of r values from individual studies or even for rhos from meta-analyses of one specific variable to be relatively close to zero, approximately between r≈−0.3 and r≈+0.3. However, the overall value for a large number of meta-analyses on very different biological–non-genetic variables would be expected to theoretically situate at 0.
Three clusters have been described above: biological–genetic factors, cultural factors and biological–non-genetic factors. Some variables fit perfectly into one cluster; others are (theoretically) expected to fit into two or even three clusters at the same time. There are four possible combinations of the three clusters and Table 1 lists the outcomes of MCV of the empirically tested relevant variables for two combinations of clusters. Two other combinations of clusters have not been studied empirically, and examples are supplied of variables for each of the two combinations. Some of the combinations of clusters chosen for specific examples are somewhat tentative, because theoretical considerations and empirical outcomes of studies using MCV do not always point in the same direction. In light of this, argumentation was supplied for the present authors’ choice of specific cluster combinations for these examples below.
The Flynn effect reflects score gains over time and obviously cultural factors, such as schooling, and biological–non-genetic factors, such as nutrition, are operating simultaneously, so one would theoretically expect a combined effect that reflects both clusters of variables. The meta-analytical correlation with g loadings of rho=−0.38 (corrected for statistical artefacts; te Nijenhuis & van der Flier, Reference te Nijenhuis and van der Flier2013) is in line with this interpretation, as it lies between the values of rho≈−1 for cultural factors and rho≈0 for biological–non-genetic factors.
With concern to score gains over time, Dickens and Flynn (Reference Dickens and Flynn2006) reported that both the scores of Blacks and Whites are increasing, and they further argued that Black scores are increasing somewhat more quickly, thereby reducing the B/W score gap to a certain degree. Dickens and Flynn maintain this is an environmental effect, and the present authors contend it is most likely that cultural factors and biological–non-genetic factors are acting simultaneously, so one would theoretically expect a combined effect reflecting both clusters of variables. Dickens and Flynn reported gains from the Wechsler Adult Intelligence Scale-Revised (WAIS-R) to the WAIS-III and, for the full sample of adults, reported an r=−0.28; while for gains from the WISC-R to WISC-IV they reported r=−0.38.
In past research, race differences in IQ scores have displayed Jensen effects in almost all cases, making it a law-like phenomenon (Jensen, Reference Jensen1998; te Nijenhuis et al., Reference te Nijenhuis, Willigers, Dragt and van der Flier2016c). Jensen (Reference Jensen1998) reported a mean r=0.63 for various B/W comparisons and te Nijenhuis et al. reported a mean r=0.42 for various Dutch/non-Western immigrant comparisons. It is emphasized that g loadings do not have a correlation of 1.00 with race differences in IQ, so there is still room for the influence of cultural and biological–non-genetic variables. Jensen (Reference Jensen1998) has shown the MCV comes with a lot of measurement error, and correcting for various sources of psychometric error strongly increases the value of the observed correlation; Jensen (Reference Jensen1998, p. 383) argued that the true correlation between B/W differences and g loadings is r≈0.90. This strong Jensen effect for B/W differences means biological–genetic variables are more important in explaining racial differences in IQ scores than environmental variables. Thus, theoretically an effect of+1 for tests of Spearman’s hypothesis would not be expected, and that is indeed reflected in the large-scale empirical research on the topic.
Jensen (Reference Jensen1998) stressed that Spearman’s hypothesis should be tested on representative samples, so Jensen’s own studies are on representative samples of Blacks and Whites with representative environments for both groups. However, James Flynn (Reference Flynn2008, pp. 88–97) posed a fundamental theoretical question, namely whether a powerful environment can make Jensen effects for racial differences disappear (rho=0, or rho=−1, or a value in between). Whether a very strong environment is able to overpower the force of genes remains an empirical question.
As a result, Flynn (Reference Flynn2008) came up with an excellent theoretical idea: to compare the scores on the Wechsler of Whites in 1947–1948 with the scores of Blacks in 2002. Taking the White 1947–1948 mean of 100, the 2002 Blacks score 104, so not equal to 1947–1948 Whites, but even a few points better. The Black mean IQ from 1947–1948 received a boost of no less than 15+4=19 IQ points over a period of 54.5 years. The 54.5 years between 1947–1948 and 2002 saw a dramatic increase in the quality of the environment. Conversely, the 1947–1948 Whites are kept frozen in their 1947–1948 environment, and only the Blacks of 2002 reaped the IQ benefits of the dramatically improved environment over time. In making this comparison, Flynn illustrates empirically that a strongly improved environment can lead to a very large increase in Black IQ scores, but evokes the question of whether these very strong environmental effects for Blacks lead to the disappearance of the Jensen effect. Flynn (Reference Flynn2008, p. 311) reported a value of r=0.54, which means this unprecedented, massive improvement of the environment was not sufficient to make the Jensen effects disappear. Flynn (Reference Flynn2008, p. 311) also tested Spearman’s hypothesis for Blacks and Whites for the WISC-R in 1972 and the WISC-IV in 2002 and reported r=0.71 and r=0.59, respectively. Based on a large number of tests of Spearman’s hypothesis based on high-quality samples, Jensen (Reference Jensen1998) reported an average effect size of r=0.63. The data suggest the dramatic difference in environment between Blacks and Whites only results in a quite modest reduction in the size of the Jensen effect. If such a massive environmental change, leading to a 19-point IQ gain, cannot efface the Jensen effect (and, at best, possibly only leads to a quite modest reduction of the effect size) it is not plausible to assume that less-powerful environmental changes that lead to comparable or lower IQ effects, such as Headstart and cross-racial adoption and schooling, will erase the Jensen effect for B/W differences either.
Flynn (Reference Flynn2008) claimed that Eyferth’s (Reference Eyferth1959) modest-sized study of biracial children in Germany displayed no Jensen effect. However, it will be shown in a careful analysis of the data that this conclusion is clearly not warranted. Eyferth (Reference Eyferth1959) studied mixed-race children in Germany, the offspring of Black US soldiers and White German women, and compared them with the offspring of White US soldiers and White German women, constituting an interesting natural experiment. US Blacks have approximately 75% sub-Saharan African genes and 25% European genes (Jensen, Reference Jensen1998, p. 432), and therefore it is reasonable to estimate these biracial German children had approximately 65% White genes and 35% Black genes. The mothers were single parents, so the environment was 100% White. It is theoretically possible that the 100% White environment was so much stronger than the 35% Black genes that the Jensen effect disappeared.
Unfortunately, Flynn (Reference Flynn2008, pp. 88–91) did not make the same statistical choices as made by Jensen in numerous articles on MCV when he applied MCV to Eyferth’s data. The first non-optimal choice of methods concerns the correct correlation coefficient. Jensen carried out many tests of Spearman’s hypothesis and virtually always used the value of Pearson’s r to gauge the strength of the effect, and the value of Spearman’s rho to test for significance. However, Flynn used the value of Spearman’s rho for the effect size and did not argue this choice. The values of Pearson’s r, however, were mentioned in the appendix of the book (Flynn, Reference Flynn2008, pp. 313–314). The second non-optimal choice of methods concerns leaving out the mean scores on the subtest Coding; Flynn (Reference Flynn2008, p. 90) at least strongly suggested he preferred to omit this data point because it more clearly evoked the expected pattern of the absence of a Jensen effect. Jensen (Reference Jensen1998, p. 374) argued that only demonstrably biased tests, such as those with language bias when testing recent immigrants, should be excluded. In his requirements for a proper application of the method of correlated vectors Jensen (Reference Jensen1998, pp. 372–374) stated: ‘The tests must be sufficiently diverse in content, task demands, and factor structure to allow significant differences between the g loadings of the various tests.’ So, one needs to have a good range of g values and this clearly argues for inclusion of the specific value for Coding. Leaving out the value for the subtest Coding would lead to severe restriction of range, which would attenuate the correlation. However, Flynn luckily still reported the values of the correlations with and without the Coding data point in his box 15; it is clear though, that the conclusions in the text are based strongly upon the dataset without Coding.
The value of r=0.42 best expresses the way g loadings predict group differences, and this is a quite strong Jensen effect. As Jensen (Reference Jensen1998) found a mean value of 0.63 for a large number of studies of B/W differences, it is clear the value for the Eyferth study is quite a bit lower. It is also clearly lower than the value of r=0.54 when comparing Whites from 1947–1948 with Blacks from 2002, with a gap of more than half a century between them. As a result, the study could be interpreted as suggesting the Jensen effect is reduced, but the conclusion that the Jensen effect disappears is clearly not warranted. Undoubtedly, and in light of the aforementioned problems, this study does not deserve too much emphasis on its own; the best way forward would involve finding comparable studies and testing them for Jensen effects. For example, checking outcomes of cross-racial adoption studies for Jensen effects: are the values substantially lower than r=0.63? Another option would be checking the IQ scores of biracial children and also testing them for Jensen effects: are the values close to r=0.42 or close to r=0.63? New studies should be included in a future meta-analysis, which would then allow strong conclusions to be drawn. However, in defence of Flynn (Reference Flynn2008), it should be noted he explicitly states that one should be careful when drawing strong conclusions from this single, limited dataset.
In light of this, it is concluded that two strong environments – 54.5 years of environmental improvement in the Flynn effect and a 100% White German environment for biracial children that are approximately 35% Black – cannot efface the Jensen effect. If these two strong environments cannot make the Jensen effect disappear, it is difficult to imagine that comparably strong or less strong environments will succeed. However, the data suggest strong environments can make the Jensen effect modestly less powerful. One perfectly clear matter is that only carrying out additional studies and combining them into a meta-analysis will allow strong conclusions to be determined.
To the best of the authors’ knowledge, no studies using MCV on a combination of biological–genetic and cultural factors have been carried out. However, outcomes from specific studies may be used – for instance, Headstart studies with Black children only, as Headstart gains show a meta-analytical rho=–0.80 (te Nijenhuis et al., Reference te Nijenhuis, Jongeneel-Grimen and Kirkegaard2014b), so one could argue they have been established as cultural effects. Another example includes studies of cross-racial adoption, where IQ scores of adopted Black children would be compared with IQ scores of the general White population. Adoption gains would arguably be classified as full cultural effects, because they show very strong anti-Jensen effects: rho=−1 (te Nijenhuis et al., Reference te Nijenhuis, Jongeneel-Grimen and Armstrong2015c). A third example would compare Black IQ scores after test–retest or test training against either White IQ scores before test–retest or a nationally representative sample of Whites; test–retest gains have been shown to correlate rho=−1 with g loadings (te Nijenhuis et al., Reference te Nijenhuis, van Vianen and van der Flier2007).
To the best of the authors’ knowledge, no studies using MCV on a combination of biological–genetic and biological–non-genetic factors have been carried out. However, outcomes from specific studies may be used, where first an example is supplied of a score increase followed by an example of a score decrease. The first example is nutrition gain for studies of only Black children being compared with a nationally representative White sample, or nutrition gain studies comparing a control group of White children and an experimental group of Black children. The second example is traumatic brain injury studies comprised of only Black children/adults, where their scores are compared with White norm samples of IQ scores.
Nutrition is an example of a biological–non-genetic variable with a quite small effect, generally just a few IQ points. Such a quite small effect does not have a strong influence on the outcome of the genetic effect reflected in a Jensen effect. In theory, a substantial number of biological–non-genetic variables acting simultaneously could have a quite strong influence on IQ scores of a group, and could even make a Jensen effect substantially less strong, and in some cases, even disappear. Thus, the total pattern of biological–non-genetic effects at the level of broad or even narrow abilities is most vital. In theory, various biological–non-genetic variables each having a small effect on one specific broad ability might lead to a large change in scores on one or more subtests measuring that broad ability, which then might strongly influence the size of the correlation. Jensen (Reference Jensen1998, pp. 500–509) argued there are a great deal of biological–non-genetic effects. Many of them have a small effect on the population, although for some individuals one variable may have large effects. In order to theoretically overpower the influence of genes, one must combine many biological–non-genetic variables to have a strong effect. However, when a single biological–non-genetic variable has a strong effect, the variable might be able to strongly reduce the Jensen effect. Clearly, more empirical studies are needed.
Anomalies in the nomological net of studies using MCV
Table 1 shows that MCV is successful in separating genetic variables from environmental variables, and separating cultural variables from biological–non-genetic variables. The impression left by Table 1 is not crystal clear as applying MCV also leads to a couple of anomalies. Lakatos (Reference Lakatos1970) described that finding and trying to explain anomalies plays an important role in advancing or destroying research programmes. Next, three studies are presented as anomalies in Jensen’s research programme on racial differences in intelligence using MCV. All three cases show cultural effects that are claimed to be Jensen effects: the Brand effect, cultural loadings of IQ tests, and basketball training analogies by Flynn.
Flynn has made an effective attempt to find empirical facts that function as anomalies in the Jensen research programme of studying variables using MCV. Flynn (Reference Flynn2008) presented the outcomes of the Eyferth (Reference Eyferth1959) study as an anomaly, but the present authors have illustrated that this study shows a quite strong Jensen effect, so it cannot be considered anomalous anymore. Besides, another study in which a comparison was made between a Black group and a White group such that the Black group had the advantage of experiencing 54.5 years of environmental improvements showed a comparable Jensen effect.
Woodley et al. (Reference Woodley, te Nijenhuis, Must and Must2014) described how guessing answers on IQ subtests improves scores over generations and that the effects of guessing are largest for the most g-loaded subtests, meaning there is a clear Jensen effect. They termed this the Brand effect, after the British intelligence researcher Chris Brand, who was the first to propose this as a potential cause of the Flynn effect. To the best of the authors’ knowledge, there is no study showing the heritability of guessing on IQ tests to be biologically–genetically determined, so most likely this should be considered a cultural variable. As cultural variables should show an anti-Jensen effect, the finding of a clear Jensen effect for the Brand effect is a clear anomaly.
Kan et al. (Reference Kan, Wicherts, Dolan and Van der Maas2013) made ratings of the culture-loadedness of IQ subtests and found this correlated positively with both subtest g loading (r=0.82 for the WISC and r=0.83 for the WAIS) and subtest heritabilities (r=0.30 for the WISC and r=0.40 for the WAIS). This can be seen as an anomaly due to the fact it is a variable meant to reflect culture that shows a strong Jensen effect.
Cook and Campbell (Reference Cook and Campbell1979) stated that measures should have construct validity, and that convergent validity and discriminant validity together demonstrate construct validity. Convergent validity occurs when measures of constructs that are expected to correlate do so; in this case, a measure of cultural loadings should correlate with other measures of cultural factors. Discriminant validity occurs when constructs that are not expected to relate accordingly do not; in this case, a measure of cultural loadings should not correlate with genetic variables. However, due to the very strong correlation with g loadings, cultural loadings will strongly correlate positively with all genetic variables in Table 1 and strongly correlate negatively with all cultural variables in Table 1. It is concluded that Kan et al.’s measure of cultural loading currently lacks construct validity and, in the words of TV character Ricky Ricardo from I Love Lucy: ‘You have some ‘splaining to do’. Te Nijenhuis and co-authors have argued repeatedly that, when working with MCV, an individual study should be seen as a contribution to a future meta-analysis and only the meta-analysis allows drawing strong conclusions (Woodley et al., Reference Woodley, te Nijenhuis, Must and Must2014). The Kan et al. findings need to be replicated using other IQ tests and all the studies then must be meta-analysed.
Flynn (Reference Flynn2012, pp. 133–134), presented an anomaly using sports analogies, where it is argued environmental factors lead to a Jensen effect in outcomes. Based on Jensen’s (Reference Jensen1998) suppositions, one would argue only biological–genetic factors can produce a Jensen effect, thus, when it is convincingly shown environmental factors also produce Jensen effects, this would present a serious anomaly which could theoretically jeopardize Jensen’s research programme. It is clear this is an important argument for Flynn, as he and some of his co-authors use it frequently (see: Flynn, Reference Flynn2013; see: Nisbett et al., Reference Nisbett, Aronson, Blair, Dickens, Flynn and Halpern2012, p. 504). Flynn’s (Reference Flynn2012) basketball analogies are quoted here at length:
Does the fact that the performance gap between the races is larger the more complex the task tell us anything about genes versus environment? Imagine that one group has better genes for height and reflex arc but suffers from a less rich basketball environment (less incentive, worse coaching, less play). The environmental disadvantage will expand the between-group performance gap as complexity rises, just as much as genetic deficit would. I have not played basketball since high school. Recently, I found that I could still make nine out of ten layups. But I have fallen far behind on the more difficult shots: my attempts at a fade away jump shot from the edge of the circle are ludicrous. The skill gap between basketball “unchallenged” players and those still active will be more pronounced the more difficult the task. In sum, someone exposed to a poor environment hits what I call a ‘complexity ceiling’. Clearly, the existence of this ceiling does not differentiate whether the performance gap is due to genes or environment. (Flynn, 2012, pp. 133–134)
The present authors beg to differ with Professor Flynn, and argue that Flynn’s thought experiments crumble upon contact with large-scale empirical data on practice and training on IQ tests. Flynn writes accessible books with engaging thought experiments to drive home his points. However, the downside lies in the fact that, in his basketball examples, he neglects to report on correlation matrices of basketball tasks and does not supply the means and SDs – preferably from nationally representative samples of basketball players – needed to express the effects of practice on various basketball tasks in standardized scores (ds). So, without reliable ratings of complexity of basketball tasks – the equivalent of g loadings of IQ tests – and standardized scores (ds) on basketball tasks, it is technically not possible to test for Jensen effects.
Luckily, these kinds of data can be found relatively easily in the combined literature on the effects of practice and training on IQ tests as well as in the literature on testing for Jensen effects, so the present authors transformed Flynn’s basketball-based examples into IQ-test-based examples. This means the present authors’ conclusions are based on a sound empirical foundation whereas Flynn’s are not.
Technically, Jensen effects exist when tasks with low cognitive complexity show small standardized group differences and when tasks with high cognitive complexity show large standardized group differences. The fundamental mistake in Flynn’s basketball example is the assumption that, after training, difficult tasks accompany large standardized differences between groups and easy tasks accompany small standardized differences between groups. However, Ericsson (Reference Ericsson1996) has shown that intensive practice can lead to gains of many SDs on easy tasks (see: also: Fleishman & Hempel, Reference Fleishman and Hempel1955).
Flynn (Reference Flynn2012) and Nisbett et al. (Reference Nisbett, Aronson, Blair, Dickens, Flynn and Halpern2012, p. 504) actually gave three basketball examples. First, Nisbett et al. (Reference Nisbett, Aronson, Blair, Dickens, Flynn and Halpern2012) put forth two groups that were comparable with regard to their basketball talent, but received different amounts of practice. Second, Flynn (Reference Flynn2012, pp. 133–134) stated that one group had better genes for basketball than the other group, and the two groups received different amounts of practice. Third, Flynn (Reference Flynn2012) put forward an example of an out-of-shape person playing basketball after not playing for half a century (Flynn, Reference Flynn2012, pp. 133–134). These three basketball-task examples will now be transformed into IQ-test examples, but first some relevant IQ findings are discussed.
It is historically well-known that after taking an IQ battery twice, the total score goes up by about a third of a standard deviation (Jensen, Reference Jensen1980). In their meta-analysis, te Nijenhuis et al. (Reference te Nijenhuis, van Vianen and van der Flier2007) studied the gains on all subtests of an IQ battery and found the standardized gains were largest on subtests with the lowest g loadings and smallest on subtests with the highest g loadings, demonstrating that test–retest gains are perfect anti-Jensen effects (rho=−1). A smaller, but even more directly relevant study, by te Nijenhuis et al. (Reference te Nijenhuis, Voskuijl and Schijve2001) illustrates training before taking IQ tests also yields an anti-Jensen effect. Additionally, a study on learning potential training in South Africa exhibits the largest standardized gains on the easiest items and the smallest standardized gains on the most difficult items (r=−0.30) (te Nijenhuis et al., Reference te Nijenhuis, van Vianen and van der Flier2007).
First, consider Nisbett et al.’s (Reference Nisbett, Aronson, Blair, Dickens, Flynn and Halpern2012, p. 504) example of two comparably talented groups with differing practice times. Assume both groups are genetically identical with exactly the same mean scores on all tests of an IQ battery. Then, group A is not allowed to train and practise with IQ tests, whereas group B trains and practises a substantial number of times. The active group will show a large standardized gain on easy subtests and small standardized gains on difficult subtests. So, group A and B will show large standardized differences on lower-g subtests and smaller standardized differences on higher-g subtests. In other words, the group differences will show an anti-Jensen effect.
Second, consider Flynn’s (Reference Flynn2012) first basketball example where group A has better genes and receives worse training, while group B has worse genes and receives better training. Let’s assume group A’s genetic advantage leads to a mean score of 101 compared with a mean score of 100 for group B. Again, group A is not allowed to train and practise with IQ tests, whereas group B trains and practises a substantial number of times. The active group will show the largest standardized gains on easy subtests and the smallest standardized gains on difficult subtests, resulting in group B outscoring group A on the total IQ score. So, group A and B will show large standardized differences on lower-g subtests and smaller standardized differences on higher-g subtests, which means the differences will also exhibit an anti-Jensen effect.
Third, consider Flynn’s second basketball example, where a person who has been out-of-practice for half a century tries again. The out-of-practice basketball player that plays worse than same-age practised players is comparable to a person who took an IQ battery 50 years ago, versus a group of persons who took an IQ test every year for the past 50 years, and, due to their practice, are now skilled in taking IQ tests. As practice on IQ tests leads to large standardized gains on low-g tests and small standardized gains on high-g tests, the persons who took IQ tests every year will have large standardized gains on low-g tests, moderate standardized gains on medium-g subtests and the smallest gains on high-g tests. Even if you practise quite a lot, high-g tests remain difficult and responding to the items never becomes automated. For instance, the difficult words in a high-g, new verbal analogies test remain difficult, even if after frequent practising on other verbal analogies tests with non-overlapping words. So, when comparing a group of out-of-practice test-takers with a group of practised test-takers, larger between-group standardized differences (d) accompany lower g loadings and smaller standardized differences accompany higher g loadings; in other words, this results not in a Jensen effect as Flynn argues, but in an anti-Jensen effect.
Flynn hypothesizes a scenario where cultural effects lead to Jensen effects. However, every cultural effect studied empirically so far shows clear anti-Jensen effects; for instance, test training, test coaching, adoption and learning potential (see Table 1). Even Flynn’s own data (Dickens & Flynn, Reference Dickens and Flynn2006) on Black IQ gains over Whites over time show these environmental variables do not yield Jensen effects, but clear anti-Jensen effects. Moreover, to make a strong claim that environmental effects also lead to Jensen effects requires stronger proof than just thought experiments, which are generally considered to supply weaker evidence than empirical studies.
In sum, Flynn (Reference Flynn2012, Reference Flynn2013; Nisbett et al., Reference Nisbett, Aronson, Blair, Dickens, Flynn and Halpern2012) presented basketball analogies that in fact are not anomalies, in addition to cultural loadings that show appalling construct validity, such that they are not clear-cut anomalies either. However, the Brand effect illustrating a Jensen effect remains a clear anomaly in the Jensen research programme and future studies will no doubt discover other anomalies that require further explanation.
Flynn (Reference Flynn2012, Reference Flynn2013) has played an important role in criticizing Jensen’s research programme by focusing on anomalies. However, it is also important to consider the whole nomological net of studies using MCV (see: Rushton, Reference Rushton1999) to assess the evidence in its entirety (see: Carnap, Reference Carnap1947). It is Flynn’s right to focus on anomalies, but one should not lose sight that what remains standing after a process of scientific scrutiny is an exception to the rule. MCV does a pretty good job of sorting variables into three clusters, albeit not a perfect job.
Anomalies can potentially destroy a theory, but in this case, 1) Spearman’s hypothesis is a law-like phenomenon, 2) there is massive support in a nomological net of studies and the number of anomalies is small and is getting smaller, not bigger and 3) all kinds of innovative predictions continue to be generated from Jensen’s research programme and are being overwhelmingly confirmed empirically.
It is then concluded that the pattern in race differences is more similar to the pattern in biological–genetic variables than to the pattern in cultural variables or the pattern in biological–non-genetic variables. These outcomes suggest biological–genetic variables are more important than cultural and biological–non-genetic variables in explaining race differences in IQ scores.
The psychometric meta-analytic—MCV hybrid model
Schmidt (Reference Schmidt1992) stated that the main function of a study is to be added to a future meta-analysis, because only the amount of information in a meta-analysis carries enough weight to allow the drawing of strong conclusions. The data points from the studies cited above can also be seen as contributions to future meta-analyses. It is important that the same statistical techniques are used in all the papers, so that various empirical studies can be combined, leading to cumulativeness in science.
There are several different forms of error in study results and they all have an impact on the result of a meta-analysis, where they modify the study correlation. Study errors or imperfections are called artefacts and some of these errors can be corrected (Schmidt & Hunter, Reference Schmidt and Hunter2015). Jensen (Reference Jensen1998, chapter 10) showed that he was thoroughly familiar with these corrections for statistical artefacts and showed in an embryonic form what a psychometric meta-analysis of studies using MCV should look like. Jensen invited Jan te Nijenhuis to develop what is now called the psychometric meta-analytical–MCV hybrid model, or PMA–MCV hybrid model for short. In the first application of this hybrid model (te Nijenhuis et al., Reference te Nijenhuis, van Vianen and van der Flier2007) in a meta-analysis of test–retest effects corrections for five artefacts were carried out: sampling error, reliability of the g vector, reliability of the d vector, range restriction in g loadings and imperfectly measuring the construct of g. In later applications of the PMA–MCV hybrid model the corrections were improved (see: te Nijenhuis & van der Flier, Reference te Nijenhuis and van der Flier2013; te Nijenhuis et al., Reference te Nijenhuis, Jongeneel-Grimen and Kirkegaard2014b; te Nijenhuis et al., Reference te Nijenhuis, Jongeneel-Grimen and Armstrong2015c; te Nijenhuis et al., Reference te Nijenhuis, Bakhiet, van den Hoek, Repko, Allik, Žebec and Abduljabbar2016a, Reference te Nijenhuis, Willigers, Dragt and van der Flier2016c).
In many meta-analyses sampling error explains the majority of the variance between studies. In the published meta-analyses using the hybrid model sampling error was reflected in the sample size of the study, and this generally led to a quite modest amount of variance explained, which is unusual. The present authors are now of the opinion that the sampling error is reflected in the number of units in a vector, which equals the number of subtests when using an IQ battery. So, an IQ battery with four subtests has more sampling error than an IQ battery with 24 subtests. It is expected that the number of subtests will explain much more variance between the data points in a meta-analysis than sample size.
The values of the correlation between g loadings and race differences are reduced through the imperfect reliability of the g vector of intelligence tests. However, it is possible to estimate the reliability of the vector of g loadings by correlating different g loadings of comparable samples. Various studies show, as expected, reliability is an asymptotic function of sample size (for instance, te Nijenhuis et al., Reference te Nijenhuis, Jongeneel-Grimen and Kirkegaard2014b). The next step is to correct the observed correlations for unreliability: g loadings based on large samples are reliable and lead to small upward corrections, whereas g loadings based on small samples are unreliable and lead to large upward corrections. The PMA–MCV hybrid model has as an advantage that g loadings do not need to be taken from the sometimes small-N study itself, but high-quality g loadings based on large samples from test manuals can be used. So, the sample size for this correction is generally not based on the study itself, but on the generally much larger N from the test manual.
The value of r(g×d) is also reduced by the reliability of the d vector. It is possible to estimate the reliability of the d vector by correlating d vectors of comparable samples. Various studies show that, as expected, the reliability of the d vector is an asymptotic function of sample size (for instance, te Nijenhuis et al., Reference te Nijenhuis, Jongeneel-Grimen and Armstrong2015c). The groups in a test of Spearman’s hypothesis are generally not equal in sample size: for instance, with 200 Blacks and 1500 Whites. Following te Nijenhuis and van der Flier (Reference te Nijenhuis and van der Flier2013), it was chosen to compute the harmonic N for each comparison made, using the formula:
where N is the number of scores and x i is the individual score.
The sample size is always taken from the original study, and the values are therefore generally much smaller than for the sample size for the correction for the reliability of the g vector, making the corrections quite strongly independent. Now that sampling error is based on the number of subtests in an IQ battery, the two corrections for unreliability of the two vectors have become independent from the correction for sampling error.
Jensen (Reference Jensen1998, pp. 381–382) showed that restriction in the magnitude of g loadings strongly attenuates the correlation between g loadings and standardized group differences. Hunter and Schmidt (Reference Hunter and Schmidt1990, pp. 47–49) stated that the solution to variation in range is to define a reference population and express all correlations in terms of it; various reference populations can be taken. The deviation from perfect construct validity in g attenuates the value of r(g×d). IQ batteries with a lot of subtests measure g better than short IQ batteries. Te Nijenhuis et al. (Reference te Nijenhuis, van Vianen and van der Flier2007) corrected for imperfectly measuring the construct of g with a correction of approximately 10%.
Woodley et al. (Reference Woodley, te Nijenhuis, Must and Must2014) made clear that the MCV is clearly not a strong statistic when used in isolation, but when it is combined with the strong methodology of Psychometric Meta-Analysis (PMA) (Schmidt & Hunter, Reference Schmidt and Hunter2015) it can result in a robust statistic, yielding strong, highly stable meta-analytical outcomes. The PMA–MCV hybrid model has already been successfully used in various publications (see: te Nijenhuis et al., Reference te Nijenhuis, van Vianen and van der Flier2007, Reference te Nijenhuis, Jongeneel-Grimen and Kirkegaard2014b, Reference te Nijenhuis, Jongeneel-Grimen and Armstrong2015c, Reference te Nijenhuis, Bakhiet, van den Hoek, Repko, Allik, Žebec and Abduljabbar2016a, Reference te Nijenhuis, Willigers, Dragt and van der Flier2016c; te Nijenhuis & van der Flier, Reference te Nijenhuis and van der Flier2013). Woodley et al. stated that there are at least four advantages of combining the MCV with PMA. First, various classical corrections for statistical artefacts can be carried out, leading to an improved view of relations between the constructs measured by the instruments in the studies. Second, there is information on the variance between studies in the meta-analysis, and this variance is generally large; a collection of quite comparable studies will generally lead to highly different outcomes due to the strong impact of various statistical artefacts. In the meta-analysis of Flynn effect gains (te Nijenhuis et al., Reference te Nijenhuis and van der Flier2013) 100% of the variance between studies was explained and in the meta-analysis on test–retest IQ gains (te Nijenhuis et al., Reference te Nijenhuis, van Vianen and van der Flier2007) 99% of the variance between studies was explained. Third, small studies sometimes report g loadings that are based on a small N, so the g vectors are quite unreliable, but they can simply be substituted by g loadings from high-quality samples, thereby strongly reducing the unreliability. Fourth, 100% of the published datasets can be used, including quite small ones (Woodley et al., Reference Woodley, te Nijenhuis, Must and Must2014).
Replicating the subtest-level nomological net at the item level
The large amount of research at the level of subtests can be seen as contributing to a nomological net of interrelations between constructs and measures (Cronbach & Meehl, Reference Cronbach and Meehl1955) with g loadings in the centre, and where the genetic variables are clearly distinguished from the environmental variables. There is quite a bit of good evidence that the subtest-level nomological net can also be partially replicated at the item level. First, there is a substantial number of studies of Spearman’s hypothesis at the level of items, most of them making comparisons between various groups. Second, a South African learning potential study showed a negative correlation between g loadings of items and score gains on items (te Nijenhuis et al., Reference te Nijenhuis, van Vianen and van der Flier2007). Third, the results of applying the PMA–MCV hybrid model are very similar at the subtests level and the item level (see: te Nijenhuis et al., Reference te Nijenhuis, Bakhiet, van den Hoek, Repko, Allik, Žebec and Abduljabbar2016a). The studies summarized above are described in more detail below.
However, although there are quite a few studies in the nomological net at the item level, the studies are not yet as numerous and broad as those in the nomological net at the subtest level. The present study is an attempt at replicating and broadening the nomological net at the item level. A fundamental assumption in the present study is that items of an IQ test function similarly to subtests of an IQ battery.
A substantial number of tests of Spearman’s hypothesis have also been carried out using the items of Raven’s Progressive Matrices (RPM). This work was pioneered by Phil Rushton (Rushton & Skuy, Reference Rushton and Skuy2000), after intensive consulting with the person that was at that time considered the world’s leading psychometrician, Arthur Jensen. The g loadings of items were estimated using the correlation of item scores with the total score on the RPM, which is generally considered a very good measure of g (Jensen, Reference Jensen1998). These g loadings were then correlated with the differences in pass rates between races. Rushton and his co-authors carried out a series of studies in Africa and Serbia (Rushton & Skuy, Reference Rushton and Skuy2000; Rushton, Reference Rushton2002; Rushton et al., Reference Rushton, Skuy and Fridjhon2003; Rushton et al., Reference Rushton, Čvorović and Bons2007). It was found that sub-Saharan African/White differences were greater on those items of the RPM with the highest item-total correlations. Rushton et al. (Reference Rushton, Čvorović and Bons2007) found that differences in intelligence between the Roma (Gypsy) community of Serbia and majority Serbians were most pronounced on the most g-loaded items of the Raven. More recently, Díaz et al. (Reference Díaz, Sellami, Infanzón, Lanzón and Lynn2012) used the RPM to compare a White Spanish sample with a sample of Moroccans, which even resulted in a negative correlation (r=−0.20). Te Nijenhuis et al. (Reference te Nijenhuis, Al-Shahomee, van den Hoek, Allik, Grigoriev and Dragt2015a) compared a group of Libyan secondary school children with other groups of secondary school children from Bosnia and Herzegovina, Estonia, Ukraine, Russia, South Africa, Ireland and Chile. The analyses were carried out on nine comparisons between the Libyan children and the other children with a mean-weighted r with a value of 0.61. Te Nijenhuis et al. (Reference te Nijenhuis, Al-Shahomee, van den Hoek, Grigoriev and Repko2015b) also compared groups of Libyan university students and adults with comparable groups from South Africa, Spain and Russia, and a group of Roma from Serbia. Spearman’s hypothesis was strongly confirmed with a mean-weighted r with a value of 0.73. Te Nijenhuis et al. (Reference te Nijenhuis, Grigoriev and van den Hoek2016b) carried out a study where groups of Kazakh, Korean, Tatar and Uzbek children from Kazakhstan were compared with a group of Russian children from Kazakhstan yielding a mean-weighted r of 0.67. In one of the largest studies, te Nijenhuis et al. (Reference te Nijenhuis, Bakhiet, van den Hoek, Repko, Allik, Žebec and Abduljabbar2016a) compared a group of Sudanese children and adolescents (N=7226) with other groups of children and adolescents from Denmark, Cyprus, Croatia, Bosnia, South Africa, Estonia, Ukraine, Ireland, Russia and Chile (total N=13,105) yielding a sample-size-weighted r with a value of 0.70. Te Nijenhuis et al. (Reference te Nijenhuis, Batterjee, van den Hoek, Allik and Sukhanovskiy2017a) compared a group of Saudi children and adolescents (N=3209) with other groups of children and adolescents from Denmark, Cyprus, Croatia, Bosnia, South Africa, Estonia, Ukraine, Ireland, Russia and Chile (total N=9333) yielding a mean-weighted r with a value of 0.44. Finally, Al-Shahomee et al. (Reference Al-Shahomee, te Nijenhuis, van den Hoek, Spanoudis and Žebec2017) compared a group of young Libyan children (N=900) with other groups of young children from Denmark, Cyprus and Croatia (total N=1847) yielding a mean-weighted r of 0.67. It is concluded that when Whites are compared with lower-scoring races at the level of items there is an overwhelming confirmation of Spearman’s hypothesis. However, there is simply no test of Spearman’s hypothesis at the item level where Whites are the lower-scoring race; there is a clear gap in the empirical literature. In the present study Korean university students are compared with other university students, including Whites, where the Whites are now the lower-scoring race.
Scores on IQ tests are known to be the best predictors of success in work settings and school settings (Schmidt & Hunter, Reference Schmidt and Hunter1998). However, it is also known that IQ scores can be increased, for instance by means of participation in learning potential training programmes. Te Nijenhuis et al. (Reference te Nijenhuis, van Vianen and van der Flier2007) showed that these score gains, which are fully environmental, are not linked to the g score: the correlation between score gains and the g loadedness of item scores was −0.39.
A substantial number of psychometric meta-analyses have already been published using data at the level of the subtests of an IQ battery (see references above), but only one study applied psychometric meta-analytical techniques to a large database of nineteen group comparisons, some of them using large to very large samples (see: te Nijenhuis et al., Reference te Nijenhuis, Bakhiet, van den Hoek, Repko, Allik, Žebec and Abduljabbar2016a). It is clear that the results are highly similar, supporting the claim that the PMA–MCV hybrid model functions similarly for subtests and items.
Sampling error is defined as a function of the number of elements in a vector – in this case, the number of items in the various versions of the Raven’s Progressive Matrices. The more items there are in a version of the Raven, the better the test of Spearman’s hypothesis, and the higher the value of the resulting correlation. As the Standard Progressive Matrices (SPM) has 60 items, and the Advanced Progressive Matrices (APM) has 36 items, based on psychometric theory one would expect on average a higher outcome for the SPM. Moreover, more elements in a vector also implies that the construct of g will be measured better than with fewer elements in a vector, which is a second statistical argument to expect a higher outcome for the SPM. Te Nijenhuis et al. (Reference te Nijenhuis, Bakhiet, van den Hoek, Repko, Allik, Žebec and Abduljabbar2016a) in their Table 2 gave an overview of all the studies testing Spearman’s hypothesis at the item level and clearly the outcomes for the APM were substantially lower.
Table 2. g loadings for the Korean WAIS-R (K-WAIS) subtests by age group
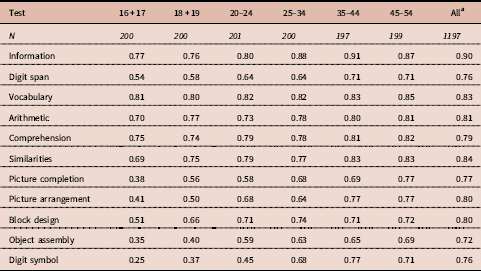
a All=average intercorrelations of the tests for all six age groups.
The various meta-analyses at the level of subtests where a vector of g loadings is correlated with a second vector show a picture of the distribution of the reliability of the g vector and a picture of the distribution of the reliability of the d vector and they are very similar. In all cases the small studies have the lowest reliability and the largest studies have the highest reliability and there is an asymptotic relation between sample size and reliability, as psychometric theory predicts. Te Nijenhuis et al. (Reference te Nijenhuis, Bakhiet, van den Hoek, Repko, Allik, Žebec and Abduljabbar2016a, Figures 2 and 3) reported comparable pictures, but then for reliability of vectors of items. A comparison of these two groups of figures showed that their shapes were very similar.
Criticism of MCV at the level of subtests: Schönemann (Reference Schönemann1997)
MCV has been criticized by Schönemann (Reference Schönemann1997) as necessarily generating positive correlations. The present authors strongly disagree with the position taken in Schönemann (Reference Schönemann1997), and would even argue that there is strong consensus among researchers publishing on MCV that this paper has been refuted (see also te Nijenhuis & van den Hoek, Reference te Nijenhuis and van den Hoek2016). First, the position that MCV automatically leads to positive correlations has been strongly undermined empirically. There are many studies, including meta-analyses, some of them very large, showing zero or negative correlations. Non-positive correlations are simply ubiquitous. Voronin et al. (Reference Voronin, te Nijenhuis and Malykh2016) showed negative correlations for heritability, as did Choi et al. (Reference Choi, Cho and Lee2015). Flynn et al. (Reference Flynn, te Nijenhuis and Metzen2014) applied MCV to iodine deficiency, prenatal cocaine exposure, fetal alcohol syndrome/fetal alcohol effects, degree of fetal alcohol syndrome and traumatic brain injury and the average correlation was 0.00. Te Nijenhuis and van der Flier (Reference te Nijenhuis and van der Flier2013) carried out a meta-analysis of Flynn effect gains and showed negative correlations. Woodley et al. (Reference Woodley, te Nijenhuis, Must and Must2014) showed negative effects for Flynn effect gains corrected for guessing. Te Nijenhuis et al. (Reference te Nijenhuis, van Vianen and van der Flier2007) showed negative correlations for test–retest gains and learning potential training gains. Te Nijenhuis et al. (Reference te Nijenhuis, Jongeneel-Grimen and Kirkegaard2014b) showed negative correlations for Headstart gains and te Nijenhuis et al. (Reference te Nijenhuis, Jongeneel-Grimen and Armstrong2015c) showed negative correlations for adoption gains. Braden (Reference Braden1989) showed negative correlations for IQ scores of the non-genetic deaf. Three studies have been identified where Spearman’s hypothesis was not confirmed: 1) Jensen & Faulstich (Reference Jensen and Faulstich1988), who compared the IQ scores of Black and White prisoners; 2) Dalliard (2013), who compared Whites with East Asians; and 3) Armstrong et al. (Reference Armstrong, Woodley and Lynn2014), who compared the IQ scores of the Sámi and Finns. Second, in a classic paper in Multivariate Behavioral Research, Dolan (Reference Dolan1997) clearly showed that Schönemann’s refutation was simply incorrect on statistical grounds. In sum, Schönemann’s paper has been refuted, both empirically and statistically (te Nijenhuis & van den Hoek, Reference te Nijenhuis and van den Hoek2016).
Criticism of MCV at the level of subtests: Dolan (Reference Dolan2000) and Ashton and Lee (Reference Ashton and Lee2005) attacking a strawman
The MCV has been criticized by various researchers (e.g. Dolan, Reference Dolan2000; Ashton & Lee, Reference Ashton and Lee2005; Hunt, Reference Hunt2011, pp. 363–365), and is considered controversial by some, notwithstanding its frequent use in research. The present authors therefore defend the choice made in detail, where extensive use is made of the argumentation by Woodley et al. (Reference Woodley, te Nijenhuis, Must and Must2014). First, it is remarked that all authors are attacking a strawman: they don’t attack the PMA–MCV hybrid model, but only r(g×d). The PMA–MCV was already present in Jensen (Reference Jensen1998, chapter 10) – albeit in embryonic form – which the criticizing authors all cited, so they were familiar with, or should have been familiar with, the content of Jensen’s highly influential book. The PMA–MCV in its first full version was presented in 2007 (te Nijenhuis et al., Reference te Nijenhuis, van Vianen and van der Flier2007), but none of the authors after 2007 ever addressed the full-fledged model. Woodley et al. (Reference Woodley, te Nijenhuis, Must and Must2014) came up with a detailed defence of the critique of the PMA–MCV hybrid model as preferable to Dolan’s version of MGCFA, but the critics never replied to this.
Woodley et al. stated that most of the criticism of the MCV is resting on two problematic premises. First, Jensen (Reference Jensen1998, pp. 380–383) showed that there are four statistical artefacts that strongly attenuate the outcomes of the MCV, namely unreliability of the g vector, unreliability of the d vector, restriction of range in g loadings and imperfectly measuring the construct of g (see Schmidt & Hunter, Reference Schmidt and Hunter2015, for a detailed description). So, Jensen was well aware that his method was not perfect and showed that controlling for these statistical artefacts strongly increased the value of the correlations between the g vector and the d vector. It has been shown that samples of limited size can yield unreliable outcomes (Dolan, Reference Dolan2000), which is consistent with Jensen’s previous statements. Second, Jensen (Reference Jensen1998, pp. 372–374) clearly stated that fairly representative samples should be used, a large enough number of tests should be used and that in terms of content these tests must also be diverse. So, for instance, not only verbal tests or not only reasoning tests should be used. It has been shown that analyses involving unbalanced collections of tests yield outcomes that make little sense (Ashton & Lee, Reference Ashton and Lee2005); however, Jensen made it clear that unbalanced samples should not be used. Therefore, there is little in these criticisms that Jensen did not anticipate years before (Woodley et al., Reference Woodley, te Nijenhuis, Must and Must2014).
Woodley et al. mentioned how Hunt (Reference Hunt2011, p. 365) and Dolan (Reference Dolan2000) advised the use of Multigroup Confirmatory Factor Analysis (MCGFA), but this leads to the loss of all four advantages of the use of the PMA–MCV hybrid model. First, in the studies published by Dolan the corrections for statistical artefacts common in PMA–MCV (Schmidt & Hunter, Reference Schmidt and Hunter2015) were not applied. So, it is to be expected that the outcomes from single studies using MGCFA will in many cases differ very strongly from the outcomes based on the combination of MCV and PMA, using various studies. It would be theoretically possible to correct for these statistical artefacts, but it would mean that the values of a substantial number of additional parameters would need to be estimated, requiring even larger sample sizes. Second, because the focus is on individual datasets there is no information on the variance between studies compiled in a meta-analysis. However, the meta-analyses of te Nijenhuis and co-authors show there is a large amount of variance between studies, and that it is essential to explain the variance with statistical artefacts. Third, g loadings from huge samples are better than the g loadings from small or medium-sized samples (see: Jensen, Reference Jensen1998), but Dolan’s choice of MGCFA did not include importing better g loadings from other samples. It would be possible to import better g loadings, but it would mean that the values of additional parameters would need to be estimated, requiring even larger sample sizes. Fourth, MGCFA can only be carried out on quite large samples, so the many small datasets simply cannot be analysed, which means the information contained in them is lost for the purposes of accumulation. In many fields of research only small-scale experiments can be carried out, based on Ns that are simply too small for the use of MGCFA. Also, Dolan requires that at least the correlation matrices have to be available, which puts a clear limitation on the number of datasets that can be analysed. Of the studies used in the two meta-analyses by te Nijenhuis and his co-authors the large majority of studies could simply not be analysed with MGCFA, leading to a potentially enormous waste of scientific data (Woodley et al., Reference Woodley, te Nijenhuis, Must and Must2014). Obviously, a statistical technique that can only be applied to a very small selection of datasets has strong drawbacks.
Kline (Reference Kline2011, p. 11) stated that structural equation modelling (SEM) is a large-sample technique, and that certain kinds of statistical estimates, such as standard errors, may not be accurate when the sample size is not large. The likelihood of technical problems in the analyses is greater too. Kline asked the question of what a large enough sample size is when using SEM, and stated that a complex model generally requires a larger N than a simple model, because the values of more parameters need to be estimated. Larger samples are necessary for the results to be sufficiently stable. The type of estimation algorithm used in the analysis affects sample size too. There are several estimation methods in SEM, and some types need very large samples, because of assumptions they make about the data. Another factor involves the distributional characteristics of the data. Large samples are needed when the distributions of continuous outcome variables are non-normal in shape and their associations with one another are non-linear. Kline (Reference Kline2011, p. 12) could be read as suggesting that N=200 per group is the bare minimum for the use of SEM, and most likely only for simple models. Kline cited a study by Barrett (Reference Barrett2007) suggesting that generally papers using SEM with fewer than 200 research participants should not be published. So, non-simple models need much larger samples.
Dolan used a form of SEM called Multigroup Confirmatory Factor Analysis (MGCFA) to test Spearman’s hypothesis and he appeared to be well aware of the need for large samples when testing his highly complex models, because he generally used large samples. For instance, Roorda et al. (Reference Roorda, Dolan and Wicherts2004) re-analysed the dataset of Lynn and Owen (Reference Lynn and Owen1994) with N=1056 Whites, N=1093 Blacks and N=1063 Indians, and the dataset of te Nijenhuis and van der Flier (1997) with N=806 Whites. Dolan (Reference Dolan2000) re-analysed the dataset from Jensen and Reynolds (Reference Jensen and Reynolds1982) with N=1868 Whites and N=305 Blacks. It appears that datasets with a large enough N for Dolan’s purposes are so difficult to come by that Dolan even had to revert to the use of computer-generated data (see: Lubke et al., Reference Lubke, Dolan and Kelderman2001). Stating the obvious, datasets based on computer-generated data are never included in meta-analyses, which suggests they play only a minimal role in the cumulativeness of science (see: Schmidt, Reference Schmidt1992). The samples generally used by Dolan are easily several times larger than the majority of the samples analysed using the PMA–MCV hybrid model. Moreover, Nunnally (Reference Nunnally1978) states that techniques based on traditional statistical models make more efficient use of data.
Interestingly, for some questions both MGCFA and the PMA–MCV hybrid model have been employed. Wicherts et al. (Reference Wicherts, Dolan, Oosterveld, van Baal, Boomsma and Span2004) contributed to the study of the Flynn effect, the study of IQ gains over generations, and found, using MGCFA, unsurprisingly, that test scores could not be compared over generations. They went on to show that Flynn effect gains and B/W group differences are highly dissimilar. Te Nijenhuis and van der Flier (Reference te Nijenhuis and van der Flier2013) used the PMA–MCV hybrid model and showed that g loadings correlate substantially negatively with the Flynn effect gains. As g loadings have been already shown to strongly correlate with B/W differences (Jensen, Reference Jensen1998), one can also draw the conclusion that Flynn effect gains and Black/White group differences are highly dissimilar. However, the MGCFA analyses required access to the original correlation matrices, complex computations, and large sample sizes, whereas the PMA–MCV analyses were much simpler and all samples in the literature reporting the information on a sufficient number of subtests could be used, including small samples. It would seem that PMA–MCV is more efficient in reaching the same conclusion than MGCFA.
Finally, Dolan’s use of MGCFA has also received criticism from various experts in psychometrics. For instance, Frisby and Beaujean (Reference Frisby and Beaujean2015) argued that a bi-factor model was preferable to MGCFA when it comes to extracting g. They also argued that in the bi-factor approach the g factor and non-g factors are independent, so that it leads to a better-quality examination of the influence of the g factors and non-g factors on cognitive scores. Another example is Irwing (Reference Irwing2012), who stated that a profound difficulty with MGCFA is that most analyses have failed to separate out measurement issues from structural analyses. Moreover, he stated that probably the most serious problem is that factors are correlated, and therefore the conclusions are influenced by the order of testing. Irwing therefore chose a quite different approach to Dolan.
Criticism of MCV at the level of items: Wicherts (Reference Wicherts2018) attacking a strawman
Wicherts (Reference Wicherts2017, Reference Wicherts2018) criticized the use of MCV at the level of items, and argued that item-level data should be analysed using Item Response Theory and not analyses based on MCV. Astonishingly, although Wicherts has published papers critical of MCV, in a paper on the heritability and culture-loadedness of subtests of IQ batteries published in the high-impact Psychological Science (Kan et al., Reference Kan, Wicherts, Dolan and Van der Maas2013) he used the very same technique.
Wicherts’ criticism at the item level strongly brings back memories of Schönemann’s (Reference Schönemann1997) criticism at the subtest level that MCV will always, or virtually always, lead to a positive correlation. The many negative and zero-order correlations from subtest-level studies employing MCV have refuted Schönemann’s position. Wicherts’ position that there should almost always be a positive correlation is also weakened by the quite strong negative correlation (r=–0.39) found in a study on learning potential at the item level (te Nijenhuis et al., Reference te Nijenhuis, van Vianen and van der Flier2007), which after corrections for artefacts might easily become r=–0.60. Moreover, Díaz et al. (Reference Díaz, Sellami, Infanzón, Lanzón and Lynn2012) used the items of the Raven’s Progressive Matrices to compare a White Spanish sample with a sample of Moroccans and found r=–0.20. Arguably they found this negative correlation because they employed g loadings of school children, which are less appropriate for their sample of adults (see: te Nijenhuis et al., Reference te Nijenhuis, Bakhiet, van den Hoek, Repko, Allik, Žebec and Abduljabbar2016a). This most likely also means that using the g loadings from the wrong age group could lead to many additional negative correlations.
Wicherts (Reference Wicherts2018) took the position that relations studied in Spearman’s hypothesis at the item level are quite complex, and this is perfectly in line with the PMA–MCV hybrid model’s use of no less than five corrections for statistical artefacts at the same time. Indeed, although the formulas for the five individual corrections for statistical artefacts in the Schmidt and Hunter (Reference Schmidt and Hunter2015) book are relatively straightforward, the combination of formulas for corrections for various statistical artefacts make PMA–MCV highly complex. Having said that, quite a few of the studies at the item level show very high observed correlations, and when these observed high correlations are corrected for statistical artefacts, in quite a few cases they will become even higher, which lessens the plausibility of the lack of linearity.
Asendorpf et al. (Reference Asendorpf, Conner, de Fruyt, de Houwer and Denissen2013), of which Wicherts was a co-author, recommended increasing the number of replications in psychology. However, this is not reflected in his or his co-author Dolan’s work on Spearman’s hypothesis. Dolan and co-authors contributed a very modest number of studies on Spearman’s hypothesis using MGCFA at the subtest level to the empirical literature, which makes for a very modest future meta-analysis that does not even allow something as basic as a moderator analysis. So, this research adds very little to the progress of science in terms of cumulativeness of findings.
Zickar and Broadfoot (Reference Zickar and Broadfoot2009, p. 50) made a comparison between Item Response Theory (IRT) and Classical Test Theory (CTT), and they stated that IRT models have more parameters to estimate, so they are more complex than CTT models. This means that sample sizes will need to be larger with IRT if one wants to measure IRT parameters with equal precision as their CTT counterparts, and the sample sizes are largest for the most complex IRT models. Zickar and Broadfoot (p. 50) stated that there is no consensus on the sample sizes required for the use of IRT models, but they observed that most IRT studies rely on sample sizes over 200. They stated that CTT-based approaches might be the only viable option when researchers have only small samples available. So, choosing to rely solely on IRT makes it more difficult to carry out meta-analyses.
New empirical tests of whether the subtest-level nomological net replicates item-level studies
The present authors take the position that with concern to Spearman’s hypothesis, subtests and items function fundamentally the same, within the frame of the PMA–MCV hybrid model. So, it is hypothesized that the subtest-level nomological net will replicate with item-level studies, in this case comparing a sample of young Korean adults taking the Advanced Progressive Matrices with eight groups of other young adults taking the same test. Four hypotheses are tested that test predictions from the PMA–MCV hybrid model.
First, Jews have a higher mean IQ than non-Jewish Whites, and it has been shown at the level of subtests, that a Jewish–non-Jewish White comparison also confirms Spearman’s hypothesis (te Nijenhuis et al., Reference te Nijenhuis, David, Metzen and Armstrong2014a). As East Asians have a higher mean IQ than Whites, it is hypothesized that in a comparison of Koreans and Whites at the item level Spearman’s hypothesis will be confirmed.
The second hypothesis is based upon the idea that the total score on the Raven is a high-quality measure of g, but that the Full Scale score of the Wechsler is even a better measure of g. It is hypothesized that computing the g loadings of the items of the Raven with either the Raven-g or the Wechsler-g will lead to the same conclusions, namely a clear confirmation of Spearman’s hypothesis.
The third hypothesis concerns a comparison between the 60-item Standard Progressive Matrices (SPM) and the 36-item Advanced Progressive Matrices (APM). As the number of items reflects both sampling error and the degree to which the construct of g is measured perfectly, it is expected that the values of r(g×d) will be lower for the APM than for the SPM. More precisely, it is expected that the mean value of r(g×d) for the APM in the present study will be lower than the weighted mean or r=0.70 of all the nineteen comparisons based on the SPM in the largest study to date, by te Nijenhuis et al. (Reference te Nijenhuis, Bakhiet, van den Hoek, Repko, Allik, Žebec and Abduljabbar2016a), based on N=7226 Sudanese children and N=13,105 other children.
The fourth hypothesis concerns the reliability of the d vector, of which it has been shown that larger Ns go with larger values of r(g×d) in studies of MCV at the level of subtests. It is hypothesized that there will be a substantial correlation between r(g×d) and N harmonic in the eight comparisons.
Methods
The purpose of this study was to test Spearman’s hypothesis at the item level using a sample of young adults from Korea, which were compared with eight other samples. The method of correlated vectors (MCV) was used to correlate the between-group difference scores (d) and the g loadings, thereby testing whether the magnitude of the differences between races is a function of the g loadings.
Instruments
All Korean participants took both the Raven’s Advanced Progressive Matrices Set II (APM) and the Korean version of the Wechsler Adult Intelligence Scale-Revised (WAIS-R). There are four versions of the Raven: the Standard Progressive Matrices (SPM) for the ages of 6 years to adulthood; the Coloured Progressive Matrices, an easier version of the test designed for children aged 5 to 12; the Advanced Progressive Matrices (APM), a harder version of the test designed for older adolescents and adults with higher ability; and the Standard Progressive Matrices Plus (SPM plus), an extended version of the SPM offering more discrimination among more able young adults. For all samples, the Raven’s Advanced Progressive Matrices (APM; Raven et al., Reference Raven, Raven and Court1998) was used to assess their intelligence. The APM consists of 36 diagrammatic puzzles, each with a missing part that the test taker attempts to identify from several options. The total score is a very good measure of g, the general factor of intelligence, at least within Western countries (Jensen, Reference Jensen1980). The APM is considered a high-quality, non-verbal intelligence test and therefore it can be used to compare samples from different countries, especially the highly educated samples that were used in the present study (see: Jensen, Reference Jensen1980, Reference Jensen1998). The various versions of the Raven have been used in thousands of studies all over the world.
The K-WAIS is the Korean version of the WAIS-R and consists of eleven subtests that measure diverse cognitive abilities: Information, Comprehension, Vocabulary, Similarities, Block Design, Object Assembly, Picture Completion, Digit Span, Arithmetic, Digit Symbol and Picture Arrangement (Yum et al., Reference Yum, Park, Oh, Kim and Lee1992). (To avoid confusion, it is stated explicitly that the K-WAIS is not based on the US-WAIS, but on the US-WAIS-R.)
Data
The samples were all matched on age to ensure comparability.
Korean sample
The study protocol was approved by the relevant institutional review boards (Seoul National University, Catholic University of Korea), and written informed consent was obtained from participants. A total of 289 healthy volunteers aged 20.7±2.8 (mean±SD) were recruited from the community with advertisements (156 males, 133 females). They were from the greater Seoul region, and took the test in 2006. In 2006, 80% or more of Korean high school students became university students, and 40% or more people lived in the greater Seoul region (Gyeonggi-do). This sample included a total of 88 healthy twin volunteers consisting of 24 monozygotic (MZ) and 20 dizygotic (DZ) same-sex twin pairs. Following standard practice, one individual from each twin pair was chosen at random.
All students (N=245) took the K-WAIS and the APM, but item scores were only available for n=205 students; the sample had a mean K-WAIS FSIQ of 115.9 (SD=14.28) and a mean APM score of 27.59 (SD=5.89).
White samples
The Russian White sample (Lapteva & Valueva, Reference Lapteva and Valueva2010; Lapteva, Reference Lapteva2012) contained 199 psychology students from several institutes of higher education in Moscow between the ages of 17 and 30. To compare them optimally with the Korean sample one participant over 27 was removed, giving a 17–27 age range for the Russians; this group was compared with the Korean 17–27 age group. They had a mean APM score of 22.1.
The White South African comparison sample was comprised of two similar samples which were combined. The first sample (Rushton et al., Reference Rushton, Skuy and Bons2004) consisted of 72 White participants from the University of Witwatersrand between the ages of 17 and 23. The second sample (Rushton et al., Reference Rushton, Skuy and Fridjhon2003) consisted of 67 White participants from the University of Witwatersrand between the ages of 17 and 23. The percentage correct on the items was combined by taking the weighted mean of the two samples. This was then compared with the Korean 17–23 age group. They had a mean APM score of 28.9.
Black samples
The Black South African comparison sample was also comprised of two similar samples which were combined. The first sample (Rushton et al., Reference Rushton, Skuy and Bons2004) consisted of 177 Black participants from the University of Witwatersrand between the ages of 17 and 23. The second sample (Rushton et al., Reference Rushton, Skuy and Fridjhon2003) consisted of 187 Black participants from the University of Witwatersrand between the ages of 17 and 23. The percentage correct on the items was combined by taking the weighted mean of the two samples. This was then compared with the Korean 17–23 age group. They had a mean APM score of 22.2
East Indian sample
The East Indian South African comparison sample was also comprised of two similar samples which were combined. The first sample (Rushton et al., Reference Rushton, Skuy and Bons2004) consisted of 57 East Indian participants from the University of Witwatersrand between the ages of 17 and 23. The second sample (Rushton et al., Reference Rushton, Skuy and Fridjhon2003) consisted of 40 East Indian participants from the University of Witwatersrand between the ages of 17 and 23. The percentage correct on the items was combined by taking the weighted mean of the two samples. This was then compared with the Korean 17–23 age group. They had a mean APM score of 25.1.
Hispanic sample
The Peruvian sample from Mayaute and Vásquez (Reference Mayaute and Vásquez2015) contained a total of 2081 university students from different universities in Lima, with an age range of 18–27. This sample was compared with the 18–27 age group of the Korean sample. They had a mean APM score of 21.1.
Mixed samples
The Canadian sample from Vigneau and Bors (Reference Vigneau and Bors2005) consisted of 506 first-year psychology students from the University of Toronto between the ages of 17 and 30. The study did not describe the ethnic makeup of the sample but the sample was assumed to be of mixed ethnicity. The sample was compared with the 17–27 age group from the Korean data. They had a mean APM score of 22.2.
The two US samples are from a study by Alderton and Larson (Reference Alderton and Larson1990) and contained two samples of Navy recruits aged 17–34. The first sample consisted of 874 subjects (64.5% White, 19.6% Black, 12.3% Hispanics, 0.9% Asian, 1.8 Filipino and 0.9% other) and the second sample consisted of 857 subjects (68.2% White, 13.4% Black, 14.7% Hispanic, 1.2% Asian, 1.6% Filipino and 0.9% other). Both samples were compared with the 17–27 age group from the Korean data. They had mean APMs score of, respectively, 17.9 and 16.5.
Statistical analyses
Calculating d
To apply MCV a d score is required, which is generally the standardized difference between races. In the present study the differences were expressed in percentages, and to compute the difference scores the score of the lower scoring race was deducted from the score of the higher scoring race. The remaining percentage was used as the difference score or d.
Calculating g
To calculate the g loadings at the item level, the quite large Korean dataset was used and these g loadings were computed in two ways. First, the scores on each item were correlated with the total score on the APM, since the total score of the APM is a good indicator of g. Second, because scores on all K-WAIS subtests were available, K-WAIS g scores could also be computed. Use was made of the correlation matrices reported in the K-WAIS manual to compute the g loadings for all K-WAIS subtests for each of the six age groups and then the average g loadings were computed for the six age groups, yielding a total N=1197 (see Table 2). A K-WAIS g score was then computed by multiplying the z score on each subtest by the subtest’s g loading and adding up the eleven products. This K-WAIS g score was then correlated with the score on each APM item. This correlation with the g score of a broad test battery should give a theoretically improved g score, as the g score of a Wechsler battery is a better measure of g than the total score of the APM (see: Jensen, Reference Jensen1998, chapter 10). The present authors’ reading of the literature is that the g loading of the APM total score is approximately 0.75 and the g loading of the Wechsler Full Scale score is approximately 0.95. The two different g vectors were then compared by computing their correlation.
Results
Table 3 gives an overview of the various data necessary for testing Spearman’s hypothesis. Using the g loadings from the Korean datasets it was found that correlations between g and d ranged from 0.23 to 0.74 with a weighted mean score of 0.63 using the APM g score and 0.56 using the K-WAIS g score, based on 36 observations (N=36). So, this means that in a comparison where Whites are the lower-scoring race Spearman’s hypothesis is also confirmed. It also means that computing the g loadings of the items of the Raven with either the Raven-g or the Wechsler-g leads to the same conclusion: Spearman’s hypothesis is clearly confirmed in both instances. The correlation between the item-total correlations for all items and the APM full score and the item-total correlations for all items and the K-WAIS g score was 0.89, so the vectors of g loadings are quite strongly interchangeable. Using the item g loadings based upon the Raven’s APM-g, the mean value of r(g×d) based on the eight comparisons in Table 4 is 0.63, which is a bit lower than the N harmonic-weighted mean of r=0.70 of all nineteen comparisons using the Standard Progressive Matrices in the large-scale study by te Nijenhuis et al. (Reference te Nijenhuis, Bakhiet, van den Hoek, Repko, Allik, Žebec and Abduljabbar2016a). There is a clear correlation between r(g×d) and N harmonic of r=0.34 for the APM-g and r=0.39 for the WAIS-g. So, the larger the sample size the stronger the correlation.
Table 3. g loadings using the Korean Raven’s score and the K-WAIS score and differences between Koreans and other groups on the items of the APM
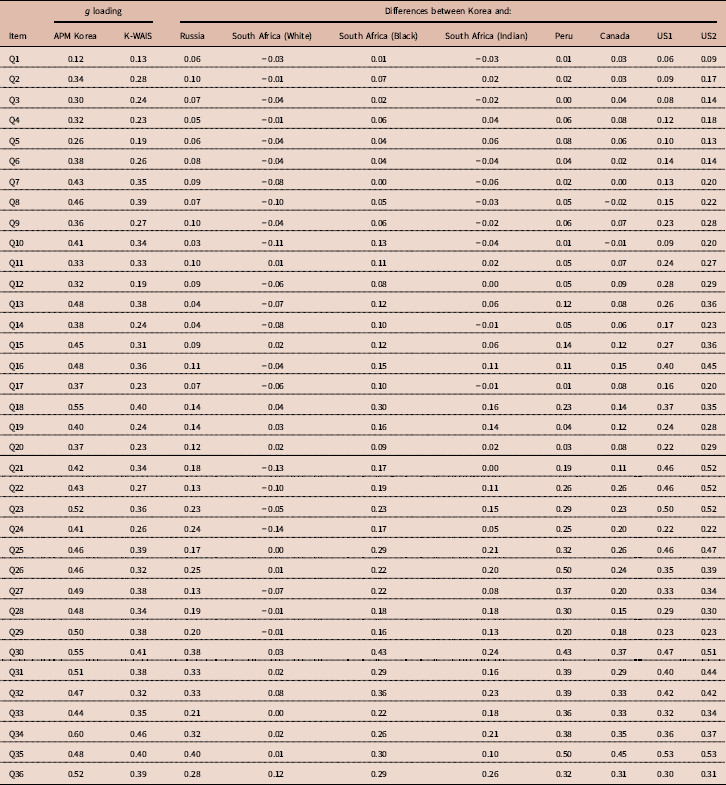
Table 4. Overview of studies with correlations between g loadings and Korean/non-Korean differences
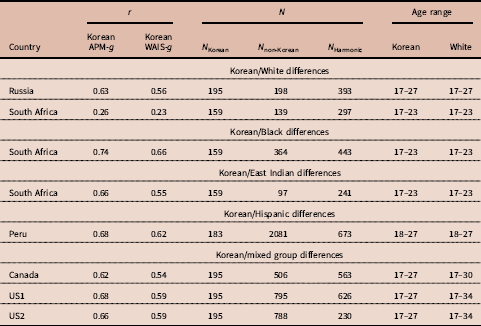
N harmonic is computed using the formula:
![]() $N_{{\rm harmonic}} {\equals}{4 \over {{1 \over {n_{1} }}{\plus}{1 \over {n_{2} }}}}$
$N_{{\rm harmonic}} {\equals}{4 \over {{1 \over {n_{1} }}{\plus}{1 \over {n_{2} }}}}$
where N is the number of ethnic groups and where n 1 and n 2 are the number of participants in groups 1 and 2, respectively.
APM=Advanced Progressive Matrices; K-WAIS=Korean Wechsler Adult Intelligence Scale.
In a post-hoc analysis, a d score was computed by taking the Korean APM score and subtracting the APM scores of all other groups. This d score for every comparison was then correlated with the size of the Jensen effect which yielded r=−0.74 when using g loadings based on the Raven and r=−0.77 when using g loadings based on the K-WAIS. This means that samples with APM scores most similar to the APM score of the Koreans have the smallest Jensen effects and that samples that differ the most from the APM score of the Koreans have the strongest Jensen effects. However, a replication using more data points is required before strong conclusions can be drawn.
Discussion
It was hypothesized that, with concern to Spearman’s hypothesis, subtests and items function fundamentally the same, so that the subtest-level nomological net was hypothesized to replicate with item-level studies, in this case comparing various sample of young adults taking the Advanced Progressive Matrices. East Asians have a higher mean IQ than Whites and the first finding in a comparison of Koreans with lower-scoring Whites, Spearman’s hypothesis was clearly confirmed. The second finding of this study was that computing the g loadings of the items of the Raven with either the Raven-g or the Wechsler-g led to the same conclusion: namely, a clear confirmation of Spearman’s hypothesis. The third finding was that tests of Spearman’s hypothesis yielded less-strong outcomes when the 36-item Advanced Progressive Matrices were used than when the 60-item Standard Progressive Matrices were used, although the difference was not large. The fourth finding was that there is a substantial correlation between sample size and the outcome of Spearman’s hypothesis; so, the larger the sample size the stronger the correlation. This pattern had already been found at the level of subtests and now it has also been found at the level of items. So, all four hypotheses were confirmed, showing that a part of the subtest-level nomological net replicates at the item level, strengthening the position that with concern to Spearman’s hypothesis subtests and items function fundamentally the same.
This study has several points of interest. First, Spearman’s hypothesis tested at the level of items states that differences between races on the items of an IQ test are a function of the g loadings of these items, such that there are small differences between races on items with low g loadings and large differences between races on items with high g loadings. A dataset of APM item scores of Korean young adults was analysed and compared with the APM scores of other groups of young adults from five different countries. Spearman’s hypothesis was strongly confirmed for eight comparisons with a mean-weighted r with a value of 0.64 when using the APM g score and 0.55 when using the K-WAIS g score. This means that Spearman’s hypothesis is not only confirmed for comparisons of Whites and lower-scoring races, but also for comparisons of Whites and a higher-scoring race.
Second, this finding also throws a different light on the meta-analysis by te Nijenhuis et al. (Reference te Nijenhuis, van den Hoek, Metzen and David2017b), showing that Spearman’s hypothesis at the level of subtests is only partially supported for East Asians. The Wechsler subtests show the Verbal/Performance distinction, but the items of the Raven are in comparison highly homogeneous. The present findings strongly suggest the differences between Koreans on the one hand and other groups on the other hand are strongly on g, but that at the level of subtests the Verbal/Performance profile of East Asians blocks the view. It is concluded that Spearman’s hypothesis is supported for one group of East Asians, namely Koreans, which means that one of the anomalies at the level of subtests is more in line with Spearman’s hypothesis than previously thought, and that Spearman’s hypothesis is a more general phenomenon than previously thought. It may be that testing the other anomalous groups with the Raven instead of the Wechsler will again lead to confirmation of Spearman’s hypothesis; more research is needed.
Third, MCV at the level of subtests has been applied to a large number of phenomena and the large majority of studies on biological–genetic variables show a strong positive correlation with g loadings. Almost all studies on environmental (cultural and biological–non-genetic) variables show a substantial to strong negative correlation with g loadings. It is clear that the pattern in race differences at the item level is more similar to the pattern in biological–genetic variables than to the pattern in environmental variables. The outcomes suggest that biological–genetic variables are more important than environmental variables in explaining race differences in IQ scores.
Fourth, what is new in the present study is that not Whites are compared with lower-scoring races, but that in this case the Whites are the lower-scoring race in comparison to the higher-scoring Koreans. Just as it appears that there might be a biological–genetic component to the score difference between Whites and races that score lower, it appears that there also might be a biological–genetic component to the higher IQ score of the Koreans.
The study has its limitations. First, only a modest number of groups of a specific age were compared with each other. Replication studies using groups from other East Asian countries, such as China, Japan, Taiwan and Mongolia, and other age groups, should be carried out to test the generalizability of the findings. A replication study comparing non-Jewish Whites and Whites should also be carried out. Another limitation is that the samples are not representative of the general population; they are predominantly students at institutes of higher learning. This limits the generalizability of the present findings. In a future meta-analysis, it can be checked whether representativeness of samples acts as a moderator; for instance, whether it leads to systematically lower correlations. To be able to draw reliable conclusions from moderator analysis using theoretically interesting moderator variables a large number of different studies need to be included in the future meta-analysis (Schmidt & Hunter, Reference Schmidt and Hunter2015).
Only a small part of the large nomological net of studies at the level of subtests has been replicated at the level of items, so more replications are needed. For instance, are there negative correlations at the item level for Flynn effect gains, test–retest gains and Headstart gains?
Using meta-analysis to advance scientific theories and cumulativeness
Woodley et al. (Reference Woodley, te Nijenhuis, Must and Must2014) stated that the outcomes of the collection of studies carried out with the MCV look very much like the outcomes of the collection of studies in personnel selection predicting job performance with IQ tests before the advent of meta-analysis. Predictive validities for the same job from different studies yielded highly variable outcomes. However, it has been shown (Schmidt & Hunter, Reference Schmidt and Hunter1977) that because most of the samples were quite small, there was a massive amount of sampling error. Correcting for this statistical artefact and a small number of others led to a dramatic reduction of the large variance between the studies in many meta-analyses. Gottfredson (Reference Gottfredson1997) stated that the outcomes based on a large number of studies all of a sudden became crystal clear and started making theoretical sense; this was a true paradigm shift in selection psychology. Dolan (Reference Dolan2000) and Wicherts (Reference Wicherts2018) focused on individual studies, and limited themselves to those with large samples. Analysing many studies with MCV and meta-analysing the many studies testing Spearman’s hypothesis using subtests of an IQ battery has already led to clear outcomes (see: te Nijenhuis et al. (Reference te Nijenhuis, Bakhiet, van den Hoek, Repko, Allik, Žebec and Abduljabbar2016a) for a review of these studies) and has the potential to lead to improvements in theory within the field of intelligence research. It was argued in an editorial published in Intelligence that more psychometric meta-analyses should be carried out within the field of intelligence research (Schmidt & Hunter, Reference Schmidt and Hunter1999). Stating the obvious, in order to be able to carry out a future meta-analysis original new studies, such as the present one, need to be published in scientific journals.
Schmidt (Reference Schmidt1992) stressed that the way research is carried out should be changed, and that researchers should think more meta-analytically. For instance, an individual study, even one with a large sample size, contains just a modest amount of information; the only amount of information that allows clear conclusions is the amount of information contained in a meta-analysis. So, individual studies should be seen as contributions to a future meta-analysis. With meta-analytical aggregation in mind it is important that the same or comparable statistical techniques are used. When every study uses a different statistical technique, this will hamper the development of cumulative knowledge in psychology (Schmidt, Reference Schmidt1992). The present authors therefore have a clear preference for using the same statistical techniques used in previous studies of Spearman’s hypothesis at the item level.
A future meta-analysis allows carrying out various corrections for statistical artefacts. Various meta-analyses based on MCV already show that these corrections strongly change the observed values (te Nijenhuis et al., Reference te Nijenhuis, van Vianen and van der Flier2007; te Nijenhuis & van der Flier, Reference te Nijenhuis and van der Flier2013), as was already predicted by Jensen (Reference Jensen1998, chapter 10). A recent large-scale study of Spearman’s hypothesis at the item level, using a substantial number of comparison groups, already employed some basic corrections for reliability of the g vector, reliability of the d vector and restriction of range of g loadings, and also showed that the observed correlations increased substantially (te Nijenhuis et al., Reference te Nijenhuis, Bakhiet, van den Hoek, Repko, Allik, Žebec and Abduljabbar2016a).
Suggestions for follow-up research
Rushton (Reference Rushton1999) argued that one should not focus on a limited number of MCV outcomes, but on a substantial part of the nomological net of constructs, measures and their interrelationships of studies using MCV. In line with this, the present authors conclude that MCV has been used in a large number of studies and there is a lot that is already known. The overwhelming majority of outcomes of MCV studies can neatly be grouped into three clusters, or into various combinations of the three clusters, with just a modest number of anomalies. Some of these anomalies can be explained, some cannot be considered strong anomalies, but others remain puzzles. The present authors believe the MCV research programme initiated by Arthur Jensen (Reference Jensen1985) to illustrate that racial differences have both genetic and environmental causes is still progressive. Clearly, for this research programme to remain progressive, theoretically novel predictions must be made and then confirmed empirically, leading to extension of the nomological net of variables studied using MCV, and both existing and new anomalies must be given more attention in an attempt to reconcile them with the majority of current findings (see: Lakatos, Reference Lakatos1970). The findings which Flynn (Reference Flynn2012, Reference Flynn2013) and Dickens and Flynn (Reference Dickens and Flynn2006) consider anomalous in Jensen’s MCV research programme can, after scrutiny, actually be found to be in accordance with Jensen’s research programme. Flynn deserves praise for devising various theoretically innovative predictions, some of which have been tested empirically, while others still require testing. Therefore, as stated above, there is a lot that is already known from studies using MCV, but it is also clear that there are still missing pieces of the puzzle because a substantial number of variables and hypotheses have not yet been tested empirically. The suggestions for follow-up research are ordered by the three clusters of variables and the four combinations of clusters that were described in the Introduction. A reviewer proposed several interesting suggestions for follow-up research, some of which might lead to anomalous findings that require explanations; the reviewer also suggested a discussion of specific published findings, with a focus on anomalies. Where relevant, other topics are also discussed.
The biological–genetic factors could be further explored. Jensen (Reference Jensen1998) already did an excellent job exploring the literature, but many more variables could be investigated. For instance, te Nijenhuis et al. (Reference te Nijenhuis, Choi, Choi, Lee, Seo, Kim and Lee2018) found that a gene predictive of the onset of Alzheimer’s – when measuring the disease’s associated decline in intelligence with neurocognitive tasks – shows a Jensen effect.
Cultural factors could be further explored, for instance, with regards to schooling. Schooling gains should not necessarily give a strong anti-Jensen effect, because schooling is clearly an important cause of the Flynn effect (Jensen, Reference Jensen1998) and Flynn convincingly argues that educators care little about the g-loadedness of school topics or IQ tests, and simply want to raise the level of skills important for functioning in modern Western society.
Another cultural variable to explore is stereotype threat. Stereotype threat theory (Steele, Reference Steele1997) argues that people who feel themselves to be at risk of confirming their group stereotypes score lower on IQ tests. Flore and Wicherts (Reference Flore and Wicherts2015) have shown that research outcomes have been strongly influenced by publication bias, so, at best, there is a very modest effect. It is expected stereotype threat decrements in IQ would display anti-Jensen effects.
The biological–non-genetic factors could be further explored. Flynn et al. (Reference Flynn, te Nijenhuis and Metzen2014) and Woodley et al. (Reference Woodley of Menie, te Nijenhuis, Shibaev, Li and Smit2018) studied variables that decreased IQ scores, but variables that increase IQ scores should also receive attention. Some variables that increase IQ scores include nutrition and taking vitamin pills.
Variables that are a combination of biological–genetic, cultural and biological–genetic factors should be further explored, and various ways of doing so will be described.
Jensen (Reference Jensen1998) stated that Spearman’s hypothesis is a law-like phenomenon, at least for Black/White comparisons in the US; comparisons of others races and sub-races in almost all cases confirm Spearman’s hypothesis. Various racial groups in the US have been compared with Whites, but Spearman’s hypothesis has not yet been meta-analytically tested on Hispanics and Puerto Ricans. Also, no studies have been carried out using IQ scores of Australian Aborigines. Many groups can still be compared to explore these differences: for instance, Russia has many minorities on which little IQ testing has been carried out (see: Shibaev & Lynn, Reference Shibaev and Lynn2015, Reference Shibaev and Lynn2017).
There are large differences in IQ within the White racial group or cluster in Europe. Lynn and Vanhanen (Reference Lynn and Vanhanen2012) showed large differences between European countries: for instance, mean IQ is 99 for Germany and 92 for Greece. Jensen effects are established for comparisons between races, but many fewer comparisons between sub-races have been carried out, so it should be tested, for instance, how strongly German–Greek comparisons show Jensen effects. Another example that would be interesting to compare involves new immigrants to the US as well as descendants of those immigrants from either higher-IQ White European countries (i.e. German-Americans) versus lower-IQ White European countries (i.e. Greek-Americans). A theoretically interesting comparison of groups is possible when the immigrants are not representative of their mother countries, as might be the case for Irish-Americans and Polish-Americans (see: Sowell, Reference Sowell1981).
Jensen (Reference Jensen1985) started with his research on Spearman’s hypothesis by comparing Blacks and Whites, but now Spearman’s hypothesis has come to mean a comparison between different racial groups. Jensen (Reference Jensen1998, p. 371) stated that if Spearman’s hypothesis becomes an established fact, then the main source of differences on IQ tests between Blacks and Whites is the same as the main source of differences on IQ tests within each racial group, namely g. To establish if g is the main cause of differences on IQ tests within each racial group more extensive testing is required. Finding more Jensen effects within various racial groups would strengthen the conclusion that between-group differences have the same main cause as within-group differences.
If g is the main source of differences on IQ tests between individuals within the Black group and within the White group, then, for instance, one would expect a Jensen effect for a comparison of average-IQ Whites and high-IQ gifted Whites, in addition to a Jensen effect for a comparison of average-IQ Whites and low-IQ MR Whites. One would also expect a Jensen effect for a comparison of school types, as the children and students in the different school types differ in mean IQ.
Lynn (Reference Lynn2010) showed that there are large regional differences between the north and the south of Italy – both White groups. Similarly, regional differences in IQ have been reported between the different regions of the UK (Carl, Reference Carl2016a, Reference Carlb), Spain (Lynn, Reference Lynn2012), Turkey (Lynn et al., Reference Lynn, Sakar and Cheng2015), Japan (Kura, Reference Kura2013) and between northern and southern Egypt (Dutton et al., Reference Dutton, Bakhiet, Ziada, Essa, Ali and Alqafari2018). These regional differences should also show Jensen effects.
An interesting question is whether the outcomes of tests of Spearman’s hypothesis comparing Blacks and Whites are dependent on the number of Black genes in the Black population. Does the value of r get lower with a smaller percentage of Black genes? Spearman’s hypothesis was tested on sub-Saharan Blacks in Zimbabwe, who are 100% Black, comparing them with US Whites, leading to r=0.36 (Rushton & Jensen, Reference Rushton and Jensen2003). Spearman’s hypothesis was also tested on Blacks in the US, who are approximately 75% Black, leading to a mean r=0.63 (Jensen, Reference Jensen1998). Te Nijenhuis et al. (Reference te Nijenhuis, Willigers, Dragt and van der Flier2016c) showed a value of r=0.43 for immigrants in the Netherlands, of which Blacks from Surinam comprise a large part and are most likely genetically comparable to US Blacks. The biracial German children in the Eyferth (Reference Eyferth1959) study were most likely 35% Black, and Flynn (Reference Flynn2008) reported r=0.42. A clear relationship between ancestry and the strength of the correlation is not apparent, but this may be due to the small number of studies carried out on African Blacks and on biracial individuals. Spearman’s hypothesis should be tested on other sub-Saharan African and biracial samples to empirically quantify what happens to the value of r. It would also be interesting to see how far Spearman’s hypothesis can be generalized. The Eyferth study shows there are Jensen effects for children who are approximately 35% Black; will Jensen effects also be present when that percentage is substantially lower? Some new studies need to be added to the literature.
James Flynn has proposed testing whether the Jensen effects persist when, for instance, Whites and Blacks are transplanted to another society. As a result, they would function in an environment created by, or strongly influenced by, people from another race. Similarities can be drawn to studies of cross-racial adoption, where often Black children are reared by White families, but these studies have not been analysed using MCV. If the race differences in IQ tests are most strongly influenced by genes, then Spearman’s hypothesis will be confirmed, but if the new environment has a stronger influence than the genes, Spearman’s hypothesis will not be confirmed. Several of these transplantation studies have already been carried out, and they are described below, but more systematic work needs to be done.
Enslaved sub-Saharan African Blacks were transported to various parts of the world, for instance to the Arab world; the US, where a small group of emancipated slaves went back to Africa to live in Liberia; and in Surinam and the Netherlands Antilles, where large groups went to the Netherlands, after which some returned to South America and the Caribbean. Sub-Saharan Africans grew up in a Black environment, but the descendants of Black slaves in the US and the Netherlands grew up in an environment created by the White majority. After comparing African Blacks and US Blacks, Rushton and Jensen (Reference Rushton and Jensen2003) reported a confirmation of Spearman’s hypothesis: r=0.36. Tests of Spearman’s hypothesis have been confirmed for Blacks in the US (mean r=0.63; Jensen, Reference Jensen1998) and Blacks in the Netherlands (mean r=43 for non-Western immigrants in general; te Nijenhuis et al., Reference te Nijenhuis, Willigers, Dragt and van der Flier2016c).
It would be interesting to test Spearman’s hypothesis on the descendants of US Black immigrants in Liberia. They transitioned from being slaves, to being freed slaves, to being Westernized Black colonizers in a sub-Saharan African country. It would also be interesting to test Spearman’s hypothesis on the descendants of Black slaves in the Arab world, where slavery was only officially abolished in Saudi Arabia and Yemen in 1962.
Until the end of Apartheid in 1994, South Africa had a dominant White culture, which subsequently began transforming into a dominant Black culture. Politically, the Whites went from being a powerful minority to a powerless minority, and conversely the Blacks went from being a powerless majority to a powerful majority. If group differences are still genetically determined, Spearman’s hypothesis should show comparable outcomes before and after Apartheid. If the environment becomes more important than the genes, then Spearman’s hypothesis should not be confirmed.
Colonial India consisted of present-day Pakistan, India and Bangladesh. The inhabitants emigrated to many places, including Great Britain, South Africa and Surinam (and then on to the Netherlands in some cases). In all these places they lived in a White culture, with the exception of post-Apartheid South Africa, where the White culture changed into a predominantly Black culture. Descendants of Indian immigrants in Surinam emigrated to the Netherlands on a large scale after Surinam gained its independence in 1975. Spearman’s hypothesis was tested 40 times in the Netherlands and yielded a mean r=43 for non-Western immigrants in general, including many Indians (te Nijenhuis et al., Reference te Nijenhuis, Willigers, Dragt and van der Flier2016c). The Indian immigrants in Surinam were taught Dutch in school and had at least some familiarity with Dutch culture.
Te Nijenhuis et al. (Reference te Nijenhuis, van den Hoek, Metzen and David2017b) carried out a meta-analysis of Spearman’s hypothesis tested on East Asian samples, leading to a mean rho=−0.27 for the Verbal scales and rho=0.44 for the Performal scales. Amerindians are the descendants of North Asian migrants and showed a Jensen effect of rho=0.62 in a meta-analysis (te Nijenhuis et al., Reference te Nijenhuis, van den Hoek and Armstrong2015d). Latin-American Hispanics are the descendants of Amerindians and Europeans and several studies have shown Jensen effects for Latin-American Hispanic immigrants in the US. Hartmann et al. (Reference Hartmann, Kruuse and Nyborg2007) used a sample based on data from the Centre for Disease Control and a second sample based on data from the National Longitudinal Survey of Youth (NLSY79) in the US to find r=0.71 and r=0.74, respectively. Kane (Reference Kane2007) used the Universal Nonverbal Intelligence Test (UNIT) and reported r=0.42, and Dalliard (2013) used the Differential Ability Scales-II (DAS-II), which yielded r=0.70.
After the end of the Middle Ages, Whites became very powerful and colonized large parts of the world, creating White-influenced environments. With concern to the testing of Spearman’s hypothesis, Whites in South Africa constitute an interesting natural experiment. Before the end of Apartheid, Whites politically were a powerful minority, and after the end of Apartheid Whites became a politically a quite powerless minority in a Black-ruled country. If genes still play the strongest role, the outcome of Spearman’s hypothesis should be positive, whereas if the environment overpowers the genes, Spearman’s hypothesis should have a negative outcome.
Jews can be considered a part of the White race, and in the so-called diaspora, have left their native Israel to live in a large number of other countries. Jews in Western European countries arguably live in an environment strongly created by non-Jewish Whites, but also with a clear Jewish influence. Te Nijenhuis et al.’s (Reference te Nijenhuis, David, Metzen and Armstrong2014a) meta-analysis compared US Jews with US gentiles, which yielded a value of rho=0.80. The Jewish state was officially founded in 1948 and the culture was, from the outset, strongly determined by European Jews. Te Nijenhuis et al.’s (Reference te Nijenhuis, David, Metzen and Armstrong2014a) meta-analysis compared European Jews and Oriental Jews in Israel, which yielded a value of rho=0.87.
In conclusion, Spearman’s hypothesis is confirmed in the overwhelming majority of empirical studies where people of a specific race or sub-race live in a country or a region where the culture of another race or sub-race is dominant. However, more research is needed to test the strength of the patterns in the data analysed thus far. Various theoretically interesting comparisons have yet to be made, or are based on only one or a small number of datasets. Moreover, as the outcomes of individual studies are strongly influenced by various sources of measurement order, only the outcomes of psychometric meta-analyses allow strong conclusions about the patterns in the data.
Reviewer James Flynn also suggested using samples of elite Blacks, for instance the 50% who score at or above the Black mean of 85. The Black SD=12 (Jensen, Reference Jensen1998), and the Naylor-Shine table for determining the mean score of those selected in a selection procedure (Cascio & Boudreau, Reference Cascio and Boudreau2011) tells us they have a mean IQ score of 95, so just below the White mean of 100; these Blacks will have better genes and better environments than the rest of the Black population. A Jensen effect would suggest genes play the most important role; an anti-Jensen effect would suggest the superior environment plays a more important role. Another potential research design would compare highest-SES Blacks with a representative sample of Whites. Naglieri and Jensen (Reference Naglieri and Jensen1987) already played with this idea by testing Spearman’s hypothesis on 86 matched pairs of Black and White primary-school children and found a strong Jensen effect (r=0.78). An even stronger test could be made by taking the IQ scores of Black students admitted to elite universities and comparing them with a representative White sample.
A combination of genetic and cultural variables could also be explored. Reviewer James Flynn suggested studying race differences where the lower-scoring race is influenced by a non-standard environment. A brilliant example is found in Flynn (Reference Flynn2008), which compared 1947–1948 Whites with 2002 Blacks displaying a clear Jensen effect, albeit one that is smaller than is generally found in B/W comparisons. An important question is how strongly do Flynn’s findings comparing previous-generation Whites with more-recent-generations Blacks generalize. For instance, using Black and White scores on the WISC-V and Black and White scores on the various versions of the Stanford-Binet could improve generalizability. Additionally, it would be interesting to investigate whether the decline in the Jensen effect’s strength is reliable, and then whether the decline in the Jensen effect is dependent upon the time gap, which acts as a measure of the strength of the change in the environment.
Four other research designs could also be studied. First, in cross-racial adoption studies IQ scores have been shown to increase, but is there still a Jensen effect? Please note the present authors list adoption studies under cultural effects because a meta-analysis has shown a strong anti-Jensen effect: r=−1. Second, many learning potential studies have been carried out; do the scores of Black children after learning potential training still show strong Jensen effects? Third, Headstart studies show huge gains, but do the scores of Black children at the end of Headstart programmes still show Jensen effects? Fourth, test–retest studies show modest score gains; do the scores of Black children at the end of the retest show a Jensen effect when compared with White children without a retest?
A combination of cultural and biological–non-genetic factors should be investigated further. The Flynn effect and Black gains on Whites over time in the Flynn effect have been studied extensively already. Flynn (Reference Flynn2008, pp. 83–88) stated that the IQ-score gaps between Blacks and Whites get larger with increasing age and he believes this is an environmental effect. If this is the case, then arguably both cultural and biological–non-genetic factors are at work simultaneously, which theoretically should result in a modest-sized anti-Jensen effect.
Various research designs can be used to study a combination of biological–genetic and biological–non-genetic factors; one example is provided focusing on score increases and another focusing on score decreases. The first design involves carrying out nutrition studies with Black and White children and testing for Jensen effects comparing White children in the control group and Black children in the experimental group. The second design entails carrying out traumatic-brain-injury studies comparing Black research participants with a White norm sample.
Conclusion: Spearman’s hypothesis is still a law-like phenomenon
The present authors urge Wicherts to take his own recommendations to carry out replications (Asendorpf et al., Reference Asendorpf, Conner, de Fruyt, de Houwer and Denissen2013) seriously, using self-collected data, instead of carrying out yet another study based on computer-generated data. A psychometric meta-analysis based on at least ten individual studies of empirical datasets using the techniques advocated by Wicherts would not be considered an attack on a strawman, but a serious reaction to the until now completely ignored psychometric meta-analytic–MCV hybrid model, including the many replications by Rushton and co-authors and te Nijenhuis and co-authors. The present authors also urge Wicherts to focus less on statistics and to not ignore the bigger theoretical picture.
Just suppose Wicherts (Reference Wicherts2018) is correct that Spearman’s hypothesis cannot be tested at the item level using MCV. Then there would still be a massive amount of evidence on IQ batteries, measures of simple reaction time, school achievement tests, training achievement tests, safety suitability tests, Assessment Centres, Situational Judgment Test and a combination of all the assessment instruments used for personnel selection. So, even if Wicherts was right, there would hardly be a dent in the totality of evidence, and Spearman’s hypothesis, based upon the outcomes of studies so far, would still be a law-like phenomenon. However, studies of Spearman’s hypothesis on groups that are maximally culturally different from Whites, such as Kalahari Bushmen, Pygmies and traditionally living Aborigines in Australia, have not been carried out, so it remains to be established empirically whether Jensen Spearman’s hypothesis can be generalized to all cultures. For Jensen’s research programme to remain progressive the various theoretical predictions made in the Discussion need to be tested and the majority confirmed empirically.
Acknowledgments
This work was supported by the Original Technology Research Program for Brain Science of the National Research Foundation (NRF) funded by the Korean government, MSIT (NRF-2014M3C7A1046041) and by the Samsung Research Funding & Incubation Center of Samsung Electronics under Project Number SRFC-IT1601-05. The authors would like to thank an anonymous reviewer and James Flynn for their constructive feedback which aided in improving the paper.
Ethical approval
The study protocol was approved by the relevant institutional review boards (Seoul National University, Catholic University of Korea), and written informed consent was obtained from all participants.
Conflicts of Interest
The authors have no conflicts of interest to declare.
Funding
This work was supported by the Original Technology Research Program for Brain Science of the National Research Foundation (NRF) funded by the Korean government, MSIT (NRF-2014M3C7A1046041), and by a research grant from Chosun University.






