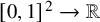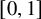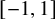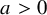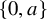1. Introduction
A graph G has vertex set
![]() $V(G)$
and edge set
$V(G)$
and edge set
![]() $E(G)$
. All graphs are assumed to be simple, without loops or multiple edges. Given two simple graphs G and H, let
$E(G)$
. All graphs are assumed to be simple, without loops or multiple edges. Given two simple graphs G and H, let
![]() $\operatorname {hom}(H, G)$
denote the number of homomorphisms from H to G, which is the set of maps from
$\operatorname {hom}(H, G)$
denote the number of homomorphisms from H to G, which is the set of maps from
![]() $V(H)$
to
$V(H)$
to
![]() $V(G)$
that send edges of H to edges of G. Furthermore, let
$V(G)$
that send edges of H to edges of G. Furthermore, let
![]() $t(H,G):=\frac {\operatorname {hom}(H,G)}{|V(G)|^{|V(H)|}}$
denote the homomorphism density of H in G, that is, the probability that a random map from
$t(H,G):=\frac {\operatorname {hom}(H,G)}{|V(G)|^{|V(H)|}}$
denote the homomorphism density of H in G, that is, the probability that a random map from
![]() $V(H)$
to
$V(H)$
to
![]() $V(G)$
is a homomorphism. One can extend the usual definition of graph homomorphisms to include target graphs G with edge weights
$V(G)$
is a homomorphism. One can extend the usual definition of graph homomorphisms to include target graphs G with edge weights
![]() $\mathbf {w}: E(G) \to \mathbb {R}$
, denoted as
$\mathbf {w}: E(G) \to \mathbb {R}$
, denoted as
![]() $G_{\mathbf {w}}$
:
$G_{\mathbf {w}}$
:
 $$ \begin{align*}\operatorname{hom}(H,G_{\mathbf{w}}) := \sum_{\substack{{\varphi:} V(H){\rightarrow} V(G_{\mathbf{w}}):\\ \varphi \text{ is a homomorphism}}} \prod_{\{i,j\}\in E(H)} w_{\varphi(i), \varphi(j)}.\end{align*} $$
$$ \begin{align*}\operatorname{hom}(H,G_{\mathbf{w}}) := \sum_{\substack{{\varphi:} V(H){\rightarrow} V(G_{\mathbf{w}}):\\ \varphi \text{ is a homomorphism}}} \prod_{\{i,j\}\in E(H)} w_{\varphi(i), \varphi(j)}.\end{align*} $$
We can define
![]() $t(H, G_{\mathbf {w}}) := \frac {\operatorname {hom}(H, G_{\mathbf {w}})}{|V(G_{\mathbf {w}})|^{|V(H)|}}$
analogously. If the edge weights
$t(H, G_{\mathbf {w}}) := \frac {\operatorname {hom}(H, G_{\mathbf {w}})}{|V(G_{\mathbf {w}})|^{|V(H)|}}$
analogously. If the edge weights
![]() ${\mathbf {w}}$
of
${\mathbf {w}}$
of
![]() $G_{\mathbf {w}}$
only take values in
$G_{\mathbf {w}}$
only take values in
![]() $\{0,1\}$
, we recover the usual definitions of homomorphism numbers and densities.
$\{0,1\}$
, we recover the usual definitions of homomorphism numbers and densities.
One of the central topics in extremal combinatorics is the study of algebraic inequalities between homomorphism densities. For example, the famous Sidorenko conjecture [Reference Sidorenko19] states that
![]() $t(H,G)-t(K_2,G)^{|E(H)|}\geq 0$
for any bipartite graph H and any graph G. Since
$t(H,G)-t(K_2,G)^{|E(H)|}\geq 0$
for any bipartite graph H and any graph G. Since
![]() $t(H_i,G_{\mathbf {w}})\cdot t(H_j,G_{\mathbf {w}})=t(H_iH_j,G_{\mathbf {w}})$
, where
$t(H_i,G_{\mathbf {w}})\cdot t(H_j,G_{\mathbf {w}})=t(H_iH_j,G_{\mathbf {w}})$
, where
![]() $H_iH_j$
is the disjoint union of
$H_iH_j$
is the disjoint union of
![]() $H_i, H_j$
, any polynomial inequality can be seen as a linear inequality. Formally, define a quantum graph f to be a finite formal linear combination of graphs
$H_i, H_j$
, any polynomial inequality can be seen as a linear inequality. Formally, define a quantum graph f to be a finite formal linear combination of graphs
![]() $\sum _{1 \leq i \leq k} c_i H_i$
, where
$\sum _{1 \leq i \leq k} c_i H_i$
, where
![]() $k \in \mathbb {N}_+$
,
$k \in \mathbb {N}_+$
,
![]() $c_i \in \mathbb {R}$
, and
$c_i \in \mathbb {R}$
, and
![]() $H_i$
’s are finite graphs [Reference Freedman, Lovász and Schrijver5]. Many extremal combinatorics questions can be reformulated as asking whether
$H_i$
’s are finite graphs [Reference Freedman, Lovász and Schrijver5]. Many extremal combinatorics questions can be reformulated as asking whether
is valid for all graphs
![]() $G_{\mathbf {w}}$
(for certain classes of edge weights
$G_{\mathbf {w}}$
(for certain classes of edge weights
![]() $\mathbf {w}$
).
$\mathbf {w}$
).
It is often useful to study the nonnegativity of quantum graphs using language and tools from graph limits, a deep theory recently developed by Lovász et al. (see, e.g., [Reference Lovász13, Reference Borgs, Chayes, Lovász, Sós and Vesztergombi2, Reference Borgs, Chayes, Lovász, Sós and Vesztergombi3]). Given a bounded measurable function
![]() $W: [0,1]^2 \to \mathbb {R}$
, one can define the homomorphism density of H in W as
$W: [0,1]^2 \to \mathbb {R}$
, one can define the homomorphism density of H in W as
 $$ \begin{align*}t(H,W) := \int_{[0,1]^{|V(H)|}} \prod_{\{i,j\}\in E(H)} W(x_i, x_j)d x_1 \dots d x_{|V(H)|}.\end{align*} $$
$$ \begin{align*}t(H,W) := \int_{[0,1]^{|V(H)|}} \prod_{\{i,j\}\in E(H)} W(x_i, x_j)d x_1 \dots d x_{|V(H)|}.\end{align*} $$
There are three natural classes of graph limits [Reference Lovász13]. The first one is
![]() $\mathcal {W}$
, the set of kernels, defined as the set of bounded symmetric measurable functions
$\mathcal {W}$
, the set of kernels, defined as the set of bounded symmetric measurable functions
![]() $W:[0,1]^2 \to \mathbb {R}$
. The second one is
$W:[0,1]^2 \to \mathbb {R}$
. The second one is
![]() $\mathcal {W}_0$
, the set of graphons, that is, kernels where
$\mathcal {W}_0$
, the set of graphons, that is, kernels where
![]() $W(x,y) \in [0,1]$
for all
$W(x,y) \in [0,1]$
for all
![]() $x,y \in [0,1]^2$
. The last one is
$x,y \in [0,1]^2$
. The last one is
![]() $\mathcal {W}_1$
, defined as the set of kernels W with
$\mathcal {W}_1$
, defined as the set of kernels W with
![]() $\|W\|_\infty \leq 1$
. More generally, we define
$\|W\|_\infty \leq 1$
. More generally, we define
![]() $\mathcal {W}_a$
for some
$\mathcal {W}_a$
for some
![]() $a> 0$
as the set of kernels W with
$a> 0$
as the set of kernels W with
![]() $\|W\|_\infty \leq a$
. Note that this notation is consistent with
$\|W\|_\infty \leq a$
. Note that this notation is consistent with
![]() $\mathcal {W}_1$
but not with
$\mathcal {W}_1$
but not with
![]() $\mathcal {W}_0$
.
$\mathcal {W}_0$
.
There are many classical extremal combinatorics questions which deal not only with
![]() $\mathcal {W}_0$
but also with other kernels allowing negative values in the range. For example, it is known that
$\mathcal {W}_0$
but also with other kernels allowing negative values in the range. For example, it is known that ![]() does not hold in general for kernels
does not hold in general for kernels
![]() $W \in \mathcal {W}_{1/2}$
whereas
$W \in \mathcal {W}_{1/2}$
whereas ![]() does [Reference Thomason20, Reference Sidorenko18]. In general, the theory of Ramsey multiplicity or localness of graph inequalities can be rephrased as certifying the nonnegativity of polynomial inequalities for kernels W in some class whose range includes negative values (e.g., [Reference Lovász11, Reference Lovász12, Reference Král, Volec and Wei10, Reference Fox and Wei6, Reference Král, Noel, Norin, Volec and Wei9, Reference Lovász13]). As a consequence of the results in [Reference Borgs, Chayes, Lovász, Sós and Vesztergombi2], an answer to the following question raised by Lovász would essentially give a complete solution to extremal combinatorics questions on graph homomorphism densities.
does [Reference Thomason20, Reference Sidorenko18]. In general, the theory of Ramsey multiplicity or localness of graph inequalities can be rephrased as certifying the nonnegativity of polynomial inequalities for kernels W in some class whose range includes negative values (e.g., [Reference Lovász11, Reference Lovász12, Reference Král, Volec and Wei10, Reference Fox and Wei6, Reference Král, Noel, Norin, Volec and Wei9, Reference Lovász13]). As a consequence of the results in [Reference Borgs, Chayes, Lovász, Sós and Vesztergombi2], an answer to the following question raised by Lovász would essentially give a complete solution to extremal combinatorics questions on graph homomorphism densities.
Problem 1.1 (Problem 20, Lovász [Reference Lovász11])
Which quantum graphs f satisfy
![]() $t(f, W) \geq 0$
for every
$t(f, W) \geq 0$
for every
![]() $W \in \mathcal {W}$
(or for every
$W \in \mathcal {W}$
(or for every
![]() $W \in \mathcal {W}_0$
)?
$W \in \mathcal {W}_0$
)?
There have been many developments in solving some instances of Problem 1.1 (e.g., [Reference Freedman, Lovász and Schrijver5, Reference Razborov16, Reference Lovász and Szegedy14]). In particular, many known results follow from writing the quantum graph f as a sum of squares or, equivalently, through a sequence of cleverly applied Cauchy–Schwarz inequalities [Reference Razborov16, Reference Freedman, Lovász and Schrijver5, Reference Lovász and Szegedy14, Reference Lovász13]. An important question is the computational difficulty of deciding whether a given polynomial inequality is valid. In Problem 17 of [Reference Lovász11], Lovász asked, ‘Does every algebraic inequality between the subgraph densities
![]() $t(F,W)$
that holds for all
$t(F,W)$
that holds for all
![]() $W \in \mathcal {W}_0$
follow from a finite number of semidefiniteness inequalities?’ Hatami and Norin showed that the answer to this question is negative in their breakthrough paper [Reference Hatami and Norine7]. In fact, their main result in [Reference Hatami and Norine7] is that the problem of determining the validity of a polynomial inequality between homomorphism densities for
$W \in \mathcal {W}_0$
follow from a finite number of semidefiniteness inequalities?’ Hatami and Norin showed that the answer to this question is negative in their breakthrough paper [Reference Hatami and Norine7]. In fact, their main result in [Reference Hatami and Norine7] is that the problem of determining the validity of a polynomial inequality between homomorphism densities for
![]() $W \in \mathcal {W}_0$
is undecidable. This shows that there is no unified algorithm or effective certificate to determine the positivity of
$W \in \mathcal {W}_0$
is undecidable. This shows that there is no unified algorithm or effective certificate to determine the positivity of
![]() $t(f, W)$
for any
$t(f, W)$
for any
![]() $W \in \mathcal {W}_0$
and negatively answers the following question raised by Lovász for the special case
$W \in \mathcal {W}_0$
and negatively answers the following question raised by Lovász for the special case
![]() $W \in \mathcal {W}_0$
.
$W \in \mathcal {W}_0$
.
Problem 1.2 (Problem 21, Lovász [Reference Lovász11])
Is it true that for every quantum graph f, where
![]() $t(f, W) \geq 0$
for all
$t(f, W) \geq 0$
for all
![]() $W \in \mathcal {W}$
, there exist quantum graphs g and h, each expressible as a sum of squares of labeled quantum graphs, so that
$W \in \mathcal {W}$
, there exist quantum graphs g and h, each expressible as a sum of squares of labeled quantum graphs, so that
![]() $f + gf = h$
?
$f + gf = h$
?
The undecidability result and the corresponding problem of effective certification of nonnegativity were left open for general weights. We show that the problem of determining whether a given graph density inequality is valid is undecidable for any set of kernels which contains all kernels with range
![]() $\{0,a\}$
for some nonzero
$\{0,a\}$
for some nonzero
![]() $a\in \mathbb {R}$
. In particular, it is undecidable for each of the three natural classes of graph limits,
$a\in \mathbb {R}$
. In particular, it is undecidable for each of the three natural classes of graph limits,
![]() $\mathcal {W}_0, \mathcal {W}$
and
$\mathcal {W}_0, \mathcal {W}$
and
![]() $\mathcal {W}_a$
, thus generalizing the work of [Reference Hatami and Norine7]. We give a single unified proof for any kernel class
$\mathcal {W}_a$
, thus generalizing the work of [Reference Hatami and Norine7]. We give a single unified proof for any kernel class
![]() $\mathcal {W}^*$
that contains all kernels with range
$\mathcal {W}^*$
that contains all kernels with range
![]() $\{0,1\}$
. The case of kernels containing all kernels with range
$\{0,1\}$
. The case of kernels containing all kernels with range
![]() $\{0,a\}$
follows quickly by rescaling the kernels by the factor of
$\{0,a\}$
follows quickly by rescaling the kernels by the factor of
![]() $\frac {1}{a}$
, which also rescales the corresponding polynomial inequalities. We also note that by compactness [Reference Borgs, Chayes, Lovász, Sós and Vesztergombi2], nonnegativity of a polynomial inequality on all kernels W with range
$\frac {1}{a}$
, which also rescales the corresponding polynomial inequalities. We also note that by compactness [Reference Borgs, Chayes, Lovász, Sós and Vesztergombi2], nonnegativity of a polynomial inequality on all kernels W with range
![]() $\{0,1\}$
is equivalent to nonnegativity on all kernels
$\{0,1\}$
is equivalent to nonnegativity on all kernels
![]() $W\in \mathcal {W}_0$
.
$W\in \mathcal {W}_0$
.
Theorem 1.3. For any set of kernels
![]() $\mathcal {W}^*$
which contains all kernels with range
$\mathcal {W}^*$
which contains all kernels with range
![]() $\{0,1\}$
as a subset, the following problem is undecidable:
$\{0,1\}$
as a subset, the following problem is undecidable:
-
○ Instance: A positive integer k, finite graphs
 $H_1, \dots , H_k$
and real numbers
$H_1, \dots , H_k$
and real numbers
 $c_1, \dots , c_k$
.
$c_1, \dots , c_k$
. -
○ Question: Does the inequality
 $\sum _{i=1}^k c_i t(H_i, W) \geq 0$
hold for all
$\sum _{i=1}^k c_i t(H_i, W) \geq 0$
hold for all
 $W\in \mathcal {W}^*$
?
$W\in \mathcal {W}^*$
?
In particular, it holds when
![]() $\mathcal {W}^*$
is
$\mathcal {W}^*$
is
![]() $\mathcal {W}$
,
$\mathcal {W}$
,
![]() $\mathcal {W}_0$
or
$\mathcal {W}_0$
or
![]() $\mathcal {W}_a$
, for
$\mathcal {W}_a$
, for
![]() $a>0$
.
$a>0$
.
The above theorem quickly implies a negative answer to Problem 1.2 for any kernel class which contains all kernels with range
![]() $\{0,1\}$
as a subset. For nice choices of kernel classes, we have the following more general result on nonexistence of certificates of nonnegativity.
$\{0,1\}$
as a subset. For nice choices of kernel classes, we have the following more general result on nonexistence of certificates of nonnegativity.
Corollary 1.4. There exists a quantum graph f with
![]() $t(f,W)\geq 0$
for all
$t(f,W)\geq 0$
for all
![]() $W \in \mathcal {W}$
(or
$W \in \mathcal {W}$
(or
![]() $\mathcal {W}_1$
) for which there are no quantum graphs
$\mathcal {W}_1$
) for which there are no quantum graphs
![]() $g,h$
, each expressible as a sum of squares of labeled quantum graphs such that
$g,h$
, each expressible as a sum of squares of labeled quantum graphs such that
![]() $gf = h$
.
$gf = h$
.
The solution of Problem 1.2 follows along the same lines as the proof of Corollary 1.4, which we will present in Subsection 2.3.
In addition, our result also implies the undecidability result for homomorphism numbers
![]() $\operatorname {hom}(H_i, G_{\mathbf {w}})$
instead of densities
$\operatorname {hom}(H_i, G_{\mathbf {w}})$
instead of densities
![]() $t(H_i, W)$
when the range of
$t(H_i, W)$
when the range of
![]() $\mathbf {w}$
contains at least two values including
$\mathbf {w}$
contains at least two values including
![]() $0$
. This follows from the fact that any polynomial inequality involving homomorphism densities
$0$
. This follows from the fact that any polynomial inequality involving homomorphism densities
![]() $t(H_i, G_{\mathbf {w}})$
is equivalent to a polynomial inequality involving homomorphism numbers
$t(H_i, G_{\mathbf {w}})$
is equivalent to a polynomial inequality involving homomorphism numbers
![]() $\operatorname {hom}(H_i, G_{\mathbf {w}})$
by adding isolated vertices to
$\operatorname {hom}(H_i, G_{\mathbf {w}})$
by adding isolated vertices to
![]() $H_i$
’s if necessary. Note that in the case when the edge weights
$H_i$
’s if necessary. Note that in the case when the edge weights
![]() $\mathbf {w}$
have binary range
$\mathbf {w}$
have binary range
![]() $\{0,1\}$
, an earlier result of Ioannidis and Ramakrishnan [Reference Ioannidis and Ramakrishnan8] showed undecidability of inequalities between homomorphism numbers
$\{0,1\}$
, an earlier result of Ioannidis and Ramakrishnan [Reference Ioannidis and Ramakrishnan8] showed undecidability of inequalities between homomorphism numbers
![]() $\operatorname {hom}(H_i, G)$
.
$\operatorname {hom}(H_i, G)$
.
1.1. Proof idea and challenges
We first sketch the idea of Ioannidis and Ramakrishnan’s short proof [Reference Ioannidis and Ramakrishnan8] of the undecidability of inequalities between homomorphism numbers
![]() $\operatorname {hom}(H_i, G)$
as a motivation for the proof for homomorphism densities. As in [Reference Hatami and Norine7], this proof is also deduced from Matiyasevich’s solution to Hilbert’s 10th problem, stated below.
$\operatorname {hom}(H_i, G)$
as a motivation for the proof for homomorphism densities. As in [Reference Hatami and Norine7], this proof is also deduced from Matiyasevich’s solution to Hilbert’s 10th problem, stated below.
Theorem 1.5 (Matiyasevich [Reference Matiyasevich15])
Given a positive integer k and a polynomial
![]() $p(x_1, \ldots , x_k)$
with integer coefficients, the problem of determining whether there exist
$p(x_1, \ldots , x_k)$
with integer coefficients, the problem of determining whether there exist
![]() $x_1, \ldots , x_k \in \mathbb {Z}$
such that
$x_1, \ldots , x_k \in \mathbb {Z}$
such that
![]() $p(x_1, \ldots , x_k) <0$
is undecidable.
$p(x_1, \ldots , x_k) <0$
is undecidable.
By changing
![]() $x_i$
to
$x_i$
to
![]() $-x_i$
when necessary, it is therefore also undecidable to determine whether a polynomial with integer coefficients is always nonnegative for
$-x_i$
when necessary, it is therefore also undecidable to determine whether a polynomial with integer coefficients is always nonnegative for
![]() $x_i$
’s taking values in
$x_i$
’s taking values in
![]() $\mathbb {N}$
. Thus, it suffices to show that for any polynomial with integer coefficients
$\mathbb {N}$
. Thus, it suffices to show that for any polynomial with integer coefficients
![]() $p(x_1, \dots , x_k)$
, there is a quantum graph f such that
$p(x_1, \dots , x_k)$
, there is a quantum graph f such that
![]() $p(x_1, \dots , x_k) \geq 0$
for all
$p(x_1, \dots , x_k) \geq 0$
for all
![]() $x_i \in \mathbb {N}$
if and only if
$x_i \in \mathbb {N}$
if and only if
![]() $\operatorname {hom}(f, G) \geq 0$
for all G. Let
$\operatorname {hom}(f, G) \geq 0$
for all G. Let
![]() $H_1, \dots ,H_k$
be finite connected graphs with no homomorphisms from one to another and such that each
$H_1, \dots ,H_k$
be finite connected graphs with no homomorphisms from one to another and such that each
![]() $H_i$
has no nontrivial homomorphism to itself. It is not hard to show that such graphs exist. Since
$H_i$
has no nontrivial homomorphism to itself. It is not hard to show that such graphs exist. Since
![]() $\operatorname {hom}(H_i, G) \operatorname {hom}(H_j, G) = \operatorname {hom}(H_i H_j, G)$
, there is a quantum graph f such that for any graph G,
$\operatorname {hom}(H_i, G) \operatorname {hom}(H_j, G) = \operatorname {hom}(H_i H_j, G)$
, there is a quantum graph f such that for any graph G,
Crucially, since
![]() $\operatorname {hom}(H_i, G) \in \mathbb {N}$
, we have that
$\operatorname {hom}(H_i, G) \in \mathbb {N}$
, we have that
![]() $p\geq 0$
for any
$p\geq 0$
for any
![]() $x_1, \dots , x_k \in \mathbb {N}$
implies that
$x_1, \dots , x_k \in \mathbb {N}$
implies that
![]() $\operatorname {hom}(f, G) \geq 0$
for all G. On the other hand, for each k-tuple of values
$\operatorname {hom}(f, G) \geq 0$
for all G. On the other hand, for each k-tuple of values
![]() $a_1, \dots , a_k \in \mathbb {N}$
, there is a graph G such that
$a_1, \dots , a_k \in \mathbb {N}$
, there is a graph G such that
![]() $t(H_i, G) = a_i$
, for example, by letting G be the disjoint union of
$t(H_i, G) = a_i$
, for example, by letting G be the disjoint union of
![]() $a_i$
copies of
$a_i$
copies of
![]() $H_i$
.
$H_i$
.
One challenge in generalizing this simple proof to show the undecidability of homomorphism density inequalities is that
![]() $t(H_i, G)$
is not necessarily an integer. In [Reference Hatami and Norine7], Hatami and Norin used a result of Bollobás [Reference Bollobás4] that the convex hull of the set of all possible pairs of edge-triangle densities, that is, pairs
$t(H_i, G)$
is not necessarily an integer. In [Reference Hatami and Norine7], Hatami and Norin used a result of Bollobás [Reference Bollobás4] that the convex hull of the set of all possible pairs of edge-triangle densities, that is, pairs
![]() $(t(K_2, W), t(K_3, W))$
for
$(t(K_2, W), t(K_3, W))$
for
![]() $W \in \mathcal {W}_0$
, is the convex hull of points
$W \in \mathcal {W}_0$
, is the convex hull of points
![]() $(1,1)$
and
$(1,1)$
and
![]() $\left (\frac {n-1}{n}, \frac {(n-2) (n-1)}{n^2}\right )$
for
$\left (\frac {n-1}{n}, \frac {(n-2) (n-1)}{n^2}\right )$
for
![]() $n\in \mathbb {N}$
. These extreme points thus provide the needed integer points. This integrality feature alone does not lead to undecidability since nonnegativity of univariate polynomials on integers is a decidable problem.
$n\in \mathbb {N}$
. These extreme points thus provide the needed integer points. This integrality feature alone does not lead to undecidability since nonnegativity of univariate polynomials on integers is a decidable problem.
Given a polynomial
![]() $p(x_1, \dots , x_k)$
in k variables, starting from a particular base graph F, Hatami and Norin use a delicate and intricate construction of a quantum graph f based on different variations of blow-ups of F. As in the proof of the undecidability of homomorphism number inequalities, one needs k ‘independent’ copies of the convex hull to ‘plug in’
$p(x_1, \dots , x_k)$
in k variables, starting from a particular base graph F, Hatami and Norin use a delicate and intricate construction of a quantum graph f based on different variations of blow-ups of F. As in the proof of the undecidability of homomorphism number inequalities, one needs k ‘independent’ copies of the convex hull to ‘plug in’
![]() $x_1, \dots , x_k$
. Hatami and Norin achieve this by measuring some conditional graph densities, conditioned on the set of graph homomorphisms
$x_1, \dots , x_k$
. Hatami and Norin achieve this by measuring some conditional graph densities, conditioned on the set of graph homomorphisms
![]() $\phi : V(F) \to V(G)$
. They construct the quantum graph f so that for any graph G,
$\phi : V(F) \to V(G)$
. They construct the quantum graph f so that for any graph G,
where
![]() $c_\phi $
’s are constants,
$c_\phi $
’s are constants,
![]() $p^*$
is a polynomial whose nonnegativity is closely related to that of p and
$p^*$
is a polynomial whose nonnegativity is closely related to that of p and
![]() $x_i(\phi )$
and
$x_i(\phi )$
and
![]() $y_i(\phi )$
’s are closely related to the density of
$y_i(\phi )$
’s are closely related to the density of
![]() $K_2$
and
$K_2$
and
![]() $K_3$
in some subgraphs
$K_3$
in some subgraphs
![]() $G_i(\phi )$
of G depending on
$G_i(\phi )$
of G depending on
![]() $\phi $
. When
$\phi $
. When
![]() $p \geq 0$
for integer-valued variables, they show that
$p \geq 0$
for integer-valued variables, they show that
![]() $p^*\geq 0$
by the integrality feature of the aforementioned convex hull and the fact that each individual
$p^*\geq 0$
by the integrality feature of the aforementioned convex hull and the fact that each individual
![]() $\phi $
enables k copies of this convex hull. A crucial fact is that since the weights
$\phi $
enables k copies of this convex hull. A crucial fact is that since the weights
![]() $\mathbf {w}$
of
$\mathbf {w}$
of
![]() $G_{\mathbf {w}}$
are nonnegative (in fact, they are in
$G_{\mathbf {w}}$
are nonnegative (in fact, they are in
![]() $\{0,1\}$
), the constants
$\{0,1\}$
), the constants
![]() $c_\phi $
are always nonnegative. These two facts imply
$c_\phi $
are always nonnegative. These two facts imply
![]() $t(f,G) \geq 0$
for any G.
$t(f,G) \geq 0$
for any G.
There are several difficulties in extending this approach to more arbitrary weights
![]() $\mathbf {w}$
in
$\mathbf {w}$
in
![]() $G_{\mathbf {w}}$
, or equivalently to more general classes of kernels. First, much less is known about possible tuples of graph densities with
$G_{\mathbf {w}}$
, or equivalently to more general classes of kernels. First, much less is known about possible tuples of graph densities with
![]() $W \in \mathcal {W}$
and even less if we consider more general classes of kernels. There are certainly fewer valid inequalities when negative weights are allowed. For instance, it is still an open question to characterize all graphs G that such
$W \in \mathcal {W}$
and even less if we consider more general classes of kernels. There are certainly fewer valid inequalities when negative weights are allowed. For instance, it is still an open question to characterize all graphs G that such
![]() $t(G,W)\geq 0$
for all
$t(G,W)\geq 0$
for all
![]() $W\in \mathcal {W}$
[Reference Lovász11]. If we try to record again all pairs of edge-triangle densities
$W\in \mathcal {W}$
[Reference Lovász11]. If we try to record again all pairs of edge-triangle densities
![]() $(t(K_2, W), t(K_3, W))$
but for
$(t(K_2, W), t(K_3, W))$
but for
![]() $W \in \mathcal {W}$
instead of
$W \in \mathcal {W}$
instead of
![]() $\mathcal {W}_0$
, then any point in
$\mathcal {W}_0$
, then any point in
![]() $\mathbb {R}^2$
is achievable. Second, the construction that Hatami and Norin used heavily relies on
$\mathbb {R}^2$
is achievable. Second, the construction that Hatami and Norin used heavily relies on
![]() $c_\phi $
being nonnegative, which is not the case in general for
$c_\phi $
being nonnegative, which is not the case in general for
![]() $W \in \mathcal {W}$
. Lastly, the process to obtain multiple copies of the convex hull with the integrality feature relies on individual
$W \in \mathcal {W}$
. Lastly, the process to obtain multiple copies of the convex hull with the integrality feature relies on individual
![]() $\phi $
’s and cannot be used in our setting by the previous argument.
$\phi $
’s and cannot be used in our setting by the previous argument.
Our proof strategy is to show that the convex hull of ratios of densities of some carefully chosen graphs has the integrality feature even when
![]() $W \in \mathcal {W}$
. We then directly realize multiple copies of the convex hull by using an explicit family of graphs instead of going through a sum depending on
$W \in \mathcal {W}$
. We then directly realize multiple copies of the convex hull by using an explicit family of graphs instead of going through a sum depending on
![]() $\phi $
. Remarkably, the convex hull is the same regardless of the weights we use, either
$\phi $
. Remarkably, the convex hull is the same regardless of the weights we use, either
![]() $\mathcal {W}_0$
,
$\mathcal {W}_0$
,
![]() $\mathcal {W}_1$
or
$\mathcal {W}_1$
or
![]() $\mathcal {W}$
. Another advantage of our proof technique is that we associate each polynomial to an explicit quantum graph.
$\mathcal {W}$
. Another advantage of our proof technique is that we associate each polynomial to an explicit quantum graph.
1.1.1. Main results in detail
We use
![]() $\mathfrak {W}$
to denote the collection of sets of kernels that contain all kernels with range
$\mathfrak {W}$
to denote the collection of sets of kernels that contain all kernels with range
![]() $\{0,1\}$
as a subset. We introduce the components of our quantum graphs. A necklace
$\{0,1\}$
as a subset. We introduce the components of our quantum graphs. A necklace
![]() $N_{c,q}$
is a cycle of length c where each edge is replaced by a clique of size q. (See Figure 1 as an example and Definitions 2.1 and 2.2 for details). We study the convex hull of the profile recording the pairs of ratios of densities
$N_{c,q}$
is a cycle of length c where each edge is replaced by a clique of size q. (See Figure 1 as an example and Definitions 2.1 and 2.2 for details). We study the convex hull of the profile recording the pairs of ratios of densities
 $$ \begin{align*}\left(\frac{t(N_{8,q},W)}{t(N_{4,q}, W)^2}, \frac{t(N_{12,q}, W)}{t(N_{4,q}, W)^3} \right)\end{align*} $$
$$ \begin{align*}\left(\frac{t(N_{8,q},W)}{t(N_{4,q}, W)^2}, \frac{t(N_{12,q}, W)}{t(N_{4,q}, W)^3} \right)\end{align*} $$
as W varies over
![]() $\mathcal {W}^*$
for some
$\mathcal {W}^*$
for some
![]() $\mathcal {W}^*\in \mathfrak {W}$
, for which
$\mathcal {W}^*\in \mathfrak {W}$
, for which
![]() $t(N_{4,q},W)\neq 0$
. We call the set of all possible pairs for all values of q between
$t(N_{4,q},W)\neq 0$
. We call the set of all possible pairs for all values of q between
![]() $2$
and
$2$
and
![]() $\ell $
, the
$\ell $
, the
![]() $\ell $
-necklace profile and denote it as
$\ell $
-necklace profile and denote it as
![]() $\mathcal {D}_{\leq \ell }$
(see Definition 2.14). Points in the
$\mathcal {D}_{\leq \ell }$
(see Definition 2.14). Points in the
![]() $\ell $
-necklace profile lie in
$\ell $
-necklace profile lie in
![]() $\mathbb {R}^{2l-2}$
since we are recording
$\mathbb {R}^{2l-2}$
since we are recording
![]() $l-1$
different pairs.
$l-1$
different pairs.

Figure 1 A
![]() $4$
-necklace of length 5:
$4$
-necklace of length 5:
![]() $N_{5,4}$
.
$N_{5,4}$
.
Let
![]() $\mathcal {R} \subset \mathbb {R}^2$
be the convex hull of
$\mathcal {R} \subset \mathbb {R}^2$
be the convex hull of
![]() $(0,0)$
with the points
$(0,0)$
with the points
![]() $\left (\frac {1}{n},\frac {1}{n^2}\right )$
for
$\left (\frac {1}{n},\frac {1}{n^2}\right )$
for
![]() $n \in \mathbb {N}$
(see Figure 2). We note that
$n \in \mathbb {N}$
(see Figure 2). We note that
![]() $\mathcal {R}$
is a compact convex set. Our first main ingredient is that the convex hull of the
$\mathcal {R}$
is a compact convex set. Our first main ingredient is that the convex hull of the
![]() $\ell $
-necklace profile
$\ell $
-necklace profile
![]() $\mathcal {D}_{\leq \ell }$
is simply the direct product of
$\mathcal {D}_{\leq \ell }$
is simply the direct product of
![]() $\ell -1$
copies of
$\ell -1$
copies of
![]() $\mathcal {R}$
inside
$\mathcal {R}$
inside
![]() $\mathbb {R}^{2\ell -2}$
for any
$\mathbb {R}^{2\ell -2}$
for any
![]() $\ell \geq 2$
and any kernel class
$\ell \geq 2$
and any kernel class
![]() $\mathcal {W}^*\in \mathfrak {W}$
.
$\mathcal {W}^*\in \mathfrak {W}$
.
Theorem 1.6. Let
![]() $T\subset \mathbb {R}^{2\ell -2}$
be the convex hull of the
$T\subset \mathbb {R}^{2\ell -2}$
be the convex hull of the
![]() $\ell $
-necklace profile
$\ell $
-necklace profile
![]() $\mathcal {D}_{\leq \ell }$
as W varies over all kernels in
$\mathcal {D}_{\leq \ell }$
as W varies over all kernels in
![]() $\mathcal {W}^*$
,
$\mathcal {W}^*$
,
![]() $\mathcal {W}^*\in \mathfrak {W}$
. We have that
$\mathcal {W}^*\in \mathfrak {W}$
. We have that

Figure 2 Region
![]() $\mathcal {R}$
that contains
$\mathcal {R}$
that contains
![]() $\mathcal {D}_q$
for every
$\mathcal {D}_q$
for every
![]() $q\geq 2$
.
$q\geq 2$
.
We will prove this result in Claim 2.12 and Proposition 2.15 where the latter is the harder result. We observe that the set
![]() $\mathcal {R}$
is an affine-linear transformation of the convex hull of
$\mathcal {R}$
is an affine-linear transformation of the convex hull of
![]() $(K_2,K_3)$
densities in
$(K_2,K_3)$
densities in
![]() $\mathcal {W}_0$
proved by Bollobás [Reference Bollobás4], and therefore it has the same integrality feature. We can then follow the same reduction as Hatami and Norin to obtain our main theorem, Theorem 1.3. In particular, we will prove that deciding whether a polynomial expression in densities of necklaces
$\mathcal {W}_0$
proved by Bollobás [Reference Bollobás4], and therefore it has the same integrality feature. We can then follow the same reduction as Hatami and Norin to obtain our main theorem, Theorem 1.3. In particular, we will prove that deciding whether a polynomial expression in densities of necklaces
![]() $N_{c,q}$
is nonnegative for
$N_{c,q}$
is nonnegative for
![]() $W\in \mathcal {W}^*$
for any
$W\in \mathcal {W}^*$
for any
![]() $\mathcal {W^*}\in \mathfrak {W}$
is undecidable. In particular, the result holds for
$\mathcal {W^*}\in \mathfrak {W}$
is undecidable. In particular, the result holds for
![]() $\mathcal {W}$
,
$\mathcal {W}$
,
![]() $\mathcal {W}_0$
and
$\mathcal {W}_0$
and
![]() $\mathcal {W}_a$
.
$\mathcal {W}_a$
.
In Section 2.1, we first establish basic properties of necklaces and graph profiles in general and then study the profile of ratios of necklaces (see Definition 2.6). In Section 2.2, we obtain several independent copies of the profile. Finally, in Section 2.3, we prove the main result. In the appendix, we give an alternate proof of our result.
2. Proof of Theorem 1.3
2.1. Properties of graph profiles involving necklaces
The main result in this section is Theorem 1.6, which is the key to prove our main theorem (Theorem 1.3). We first formalize the operation of replacing edges by cliques that was mentioned in the introduction in relation to necklaces.
Definition 2.1. Given some graph G and some integer
![]() $q\geq 2$
, the q-ification of G is the graph obtained as follows: For every edge of G, add
$q\geq 2$
, the q-ification of G is the graph obtained as follows: For every edge of G, add
![]() $q-2$
vertices that are all pairwise adjacent and that are all adjacent to the two vertices of the selected edge. In other words, each edge of G gets replaced by a clique of size q.
$q-2$
vertices that are all pairwise adjacent and that are all adjacent to the two vertices of the selected edge. In other words, each edge of G gets replaced by a clique of size q.
Figure 1 is a
![]() $4$
-ification of
$4$
-ification of
![]() $G = C_5$
. Necklaces can thus be defined through the q-ification of cycles.
$G = C_5$
. Necklaces can thus be defined through the q-ification of cycles.
Definition 2.2. Let
![]() $c \geq 3, q \geq 2$
be positive integers. Let
$c \geq 3, q \geq 2$
be positive integers. Let
![]() $N_{c,q}$
be the q-ification of the cycle of length c. We call
$N_{c,q}$
be the q-ification of the cycle of length c. We call
![]() $N_{c,q}$
the q-necklace of length c.
$N_{c,q}$
the q-necklace of length c.
As it will soon become clear, to understand the density
![]() $t(N_{c,q}, W)$
, we need to work with an auxiliary function corresponding to W. Before defining this auxiliary function, we first define conditional density. A rooted graph is a graph with one or more vertices distinguished as roots. Suppose
$t(N_{c,q}, W)$
, we need to work with an auxiliary function corresponding to W. Before defining this auxiliary function, we first define conditional density. A rooted graph is a graph with one or more vertices distinguished as roots. Suppose
![]() $H^{\bullet \dots \bullet }$
is a rooted graph with k roots, where
$H^{\bullet \dots \bullet }$
is a rooted graph with k roots, where
![]() $v_1, \dots , v_k$
are the roots and
$v_1, \dots , v_k$
are the roots and
![]() $v_{k+1}, \dots , v_{|V(H)|}$
are the remaining vertices of H. Fix
$v_{k+1}, \dots , v_{|V(H)|}$
are the remaining vertices of H. Fix
![]() $x_1, \dots , x_k \in [0,1]$
, and define the conditional density
$x_1, \dots , x_k \in [0,1]$
, and define the conditional density
 $$ \begin{align*}t_{x_1,\dots, x_k}(H^{\bullet \dots \bullet}, W) = \int_{[0,1]^{|V(H)|-k}} \prod_{\{i,j\}\in E(H)} W(x_i, x_j)d x_{k+1} \dots dx_{|V(H)|}.\end{align*} $$
$$ \begin{align*}t_{x_1,\dots, x_k}(H^{\bullet \dots \bullet}, W) = \int_{[0,1]^{|V(H)|-k}} \prod_{\{i,j\}\in E(H)} W(x_i, x_j)d x_{k+1} \dots dx_{|V(H)|}.\end{align*} $$
In other words, this is the density of H in W, where vertex
![]() $v_i$
is mapped to
$v_i$
is mapped to
![]() $x_i$
for each
$x_i$
for each
![]() $1 \leq i \leq k$
.
$1 \leq i \leq k$
.
Definition 2.3. Given
![]() $W \in \mathcal {W}$
, consider a symmetric measurable function
$W \in \mathcal {W}$
, consider a symmetric measurable function
![]() $M_{W,q}: [0,1]^2 \to \mathbb {R}$
such that
$M_{W,q}: [0,1]^2 \to \mathbb {R}$
such that
![]() $M_{W,q}(x,y) = t_{x,y}(K_q^{\bullet \bullet }, W)$
, where
$M_{W,q}(x,y) = t_{x,y}(K_q^{\bullet \bullet }, W)$
, where
![]() $K_q^{\bullet \bullet }$
is the complete graph on q vertices with two roots.
$K_q^{\bullet \bullet }$
is the complete graph on q vertices with two roots.
Definition 2.4. Given a graph G, we define
![]() $M_{G, q} := M_{W_G, q}$
, where
$M_{G, q} := M_{W_G, q}$
, where
![]() $W_G$
is the graphon associated with G defined as follows. Partition
$W_G$
is the graphon associated with G defined as follows. Partition
![]() $[0,1]$
into
$[0,1]$
into
![]() $|V(G)|$
intervals
$|V(G)|$
intervals
![]() $I_1, \dots , I_{|V(G)|}$
of equal length. Let
$I_1, \dots , I_{|V(G)|}$
of equal length. Let
![]() $W_G(x,y)=1$
if and only if
$W_G(x,y)=1$
if and only if
![]() $x \in I_i$
and
$x \in I_i$
and
![]() $y \in I_j$
and
$y \in I_j$
and
![]() $(i,j) \in E(G)$
, and
$(i,j) \in E(G)$
, and
![]() $W_G(x,y)=0$
otherwise.
$W_G(x,y)=0$
otherwise.
It can be easily seen that
![]() $t(H, G) = t(H, W_G)$
. Trivially, by Definition 2.3, we have for any graph G and any
$t(H, G) = t(H, W_G)$
. Trivially, by Definition 2.3, we have for any graph G and any
![]() $W' \in \mathcal {W}$
that
$W' \in \mathcal {W}$
that
Since
![]() $M_{W, q}$
is bounded and symmetric, its spectrum is countable, with real eigenvalues
$M_{W, q}$
is bounded and symmetric, its spectrum is countable, with real eigenvalues
![]() $|\lambda _1| \geq |\lambda _2| \geq \dots $
. Moreover,
$|\lambda _1| \geq |\lambda _2| \geq \dots $
. Moreover,
![]() $\sum _i |\lambda _i|^s<\infty $
for any positive integer s (see, e.g., [Reference Lovász13]).
$\sum _i |\lambda _i|^s<\infty $
for any positive integer s (see, e.g., [Reference Lovász13]).
Lemma 2.5. Let
![]() $W \in \mathcal {W}$
. Then
$W \in \mathcal {W}$
. Then
![]() $t(N_{c,q},W)=\sum _{i} \lambda _i^c$
, where
$t(N_{c,q},W)=\sum _{i} \lambda _i^c$
, where
![]() $\lambda _1, \lambda _2, \ldots $
are the eigenvalues of
$\lambda _1, \lambda _2, \ldots $
are the eigenvalues of
![]() $M_{W,q}$
.
$M_{W,q}$
.
Proof. Since
![]() $M_{W,q}$
is again in
$M_{W,q}$
is again in
![]() $\mathcal {W}$
, the result follows as
$\mathcal {W}$
, the result follows as
![]() $t(N_{c,q}, W) = t(C_c, M_{W,q}) = \sum _i \lambda _i^c$
. The last equality follows from a standard argument through the spectral decomposition of
$t(N_{c,q}, W) = t(C_c, M_{W,q}) = \sum _i \lambda _i^c$
. The last equality follows from a standard argument through the spectral decomposition of
![]() $M_{W,q}$
(e.g., see [Reference Lovász13]).
$M_{W,q}$
(e.g., see [Reference Lovász13]).
We now investigate the profiles of ratios of necklaces.
Definition 2.6. For an integer
![]() $q \geq 2$
, let
$q \geq 2$
, let
 $$ \begin{align*}\mathcal{D}_q:=\text{cl}\left(\left \{ \left(\frac{t(N_{8,q},W)}{t(N_{4,q},W)^2}, \frac{t(N_{12,q},W)}{t(N_{4,q},W)^3}\right) \mid W \in \mathcal{W} \text{ and }t(N_{4,q},W)\neq 0 \right\}\right).\end{align*} $$
$$ \begin{align*}\mathcal{D}_q:=\text{cl}\left(\left \{ \left(\frac{t(N_{8,q},W)}{t(N_{4,q},W)^2}, \frac{t(N_{12,q},W)}{t(N_{4,q},W)^3}\right) \mid W \in \mathcal{W} \text{ and }t(N_{4,q},W)\neq 0 \right\}\right).\end{align*} $$
For a particular W, we let
![]() $x_q(W):=\frac {t(N_{8,q},W)}{t(N_{4,q},W)^2}$
and
$x_q(W):=\frac {t(N_{8,q},W)}{t(N_{4,q},W)^2}$
and
![]() $y_q(W):=\frac {t(N_{12,q},W)}{t(N_{4,q},W)^3}$
.
$y_q(W):=\frac {t(N_{12,q},W)}{t(N_{4,q},W)^3}$
.
We first note the following simple lemma where we obtain a bound on the boundary curve of
![]() $\mathcal {D}_q$
. This lower bound will serve the same purpose as the Goodman lower bound did in [Reference Hatami and Norine7].
$\mathcal {D}_q$
. This lower bound will serve the same purpose as the Goodman lower bound did in [Reference Hatami and Norine7].
Lemma 2.7. For any
![]() $W \in \mathcal {W}$
such that
$W \in \mathcal {W}$
such that
![]() $t(N_{4,q},W)\neq 0$
,
$t(N_{4,q},W)\neq 0$
,
![]() $0\leq x_q(W), y_q(W) \leq 1$
. Equivalently,
$0\leq x_q(W), y_q(W) \leq 1$
. Equivalently,
![]() $\mathcal {D}_q\subseteq [0,1]^2$
. In addition, for any
$\mathcal {D}_q\subseteq [0,1]^2$
. In addition, for any
![]() $(x,y)\in \mathcal {D}_q$
, we have that
$(x,y)\in \mathcal {D}_q$
, we have that
![]() $y\geq x^2$
.
$y\geq x^2$
.
Proof. By Lemma 2.5, we know that
![]() $x_q(W)=\frac {\sum _{i} \lambda _i^8}{\left (\sum _{i} \lambda _i^4\right )^2}$
. Thus,
$x_q(W)=\frac {\sum _{i} \lambda _i^8}{\left (\sum _{i} \lambda _i^4\right )^2}$
. Thus,
![]() $x_q(W) \leq 1$
by the Cauchy–Schwarz inequality. The fact that
$x_q(W) \leq 1$
by the Cauchy–Schwarz inequality. The fact that
![]() $y_q(W) \in [0,1]$
follows from the same argument.
$y_q(W) \in [0,1]$
follows from the same argument.
We are left to show that
![]() $y_q(W) \geq x_q(W)^2$
holds for every
$y_q(W) \geq x_q(W)^2$
holds for every
![]() $W \in \mathcal {W}$
. By Lemma 2.5, it suffices to show that
$W \in \mathcal {W}$
. By Lemma 2.5, it suffices to show that
 $$ \begin{align*}\frac{\sum_{i} \lambda_i^{12}}{\left(\sum_{i} \lambda_i^4\right)^3}\geq \left(\frac{\sum_{i} \lambda_i^8}{\left(\sum_{i} \lambda_i^4\right)^2}\right)^2.\end{align*} $$
$$ \begin{align*}\frac{\sum_{i} \lambda_i^{12}}{\left(\sum_{i} \lambda_i^4\right)^3}\geq \left(\frac{\sum_{i} \lambda_i^8}{\left(\sum_{i} \lambda_i^4\right)^2}\right)^2.\end{align*} $$
This is equivalent to showing that
![]() $\sum _{i} \lambda _i^4 \sum _{i} \lambda _i^{12} \geq (\sum _{i} \lambda _i^8)^2$
which follows from Hölder’s inequality.
$\sum _{i} \lambda _i^4 \sum _{i} \lambda _i^{12} \geq (\sum _{i} \lambda _i^8)^2$
which follows from Hölder’s inequality.
We now want to show that a sparse but infinite set of points on
![]() $y=x^2$
is realizable for every
$y=x^2$
is realizable for every
![]() $\mathcal {D}_q$
. The following lemma and theorem build up to a result that serves the purpose of Bollobás’ result used in [Reference Hatami and Norine7].
$\mathcal {D}_q$
. The following lemma and theorem build up to a result that serves the purpose of Bollobás’ result used in [Reference Hatami and Norine7].
Lemma 2.8. Let
![]() $q\geq 2$
be an integer. The points
$q\geq 2$
be an integer. The points
![]() $(\frac {1}{r}, \frac {1}{r^2})$
are in
$(\frac {1}{r}, \frac {1}{r^2})$
are in
![]() $\mathcal {D}_q$
for every positive integer r.
$\mathcal {D}_q$
for every positive integer r.
Proof. Let
![]() $I_1, \dots , I_r$
be r intervals of equal length that partition
$I_1, \dots , I_r$
be r intervals of equal length that partition
![]() $[0,1]$
. Let W be a graphon where
$[0,1]$
. Let W be a graphon where
![]() $W(x,y)=1$
if and only if both
$W(x,y)=1$
if and only if both
![]() $x, y \in I_i$
for some
$x, y \in I_i$
for some
![]() $1 \leq i \leq r$
. Equivalently, one can consider W as the limit object of graphs consisting of the disjoint union of r cliques of equal size. By Definition 2.3,
$1 \leq i \leq r$
. Equivalently, one can consider W as the limit object of graphs consisting of the disjoint union of r cliques of equal size. By Definition 2.3,
![]() $M_{W,q}(x,y)=0$
if
$M_{W,q}(x,y)=0$
if
![]() $x,y$
are not in the same
$x,y$
are not in the same
![]() $I_i$
for any
$I_i$
for any
![]() $1 \leq i \leq r$
, and
$1 \leq i \leq r$
, and
![]() $M_{W,q}(x,y) = \frac {1}{r^{q-2}}$
if and only if both
$M_{W,q}(x,y) = \frac {1}{r^{q-2}}$
if and only if both
![]() $x,y\in I_i$
for some
$x,y\in I_i$
for some
![]() $1 \leq i \leq r$
. Each block of
$1 \leq i \leq r$
. Each block of
![]() $M_{W,q}$
(restricted to
$M_{W,q}$
(restricted to
![]() $I_i \times I_i$
) has eigenvalues
$I_i \times I_i$
) has eigenvalues
![]() $\frac {1}{r^{q-2}}$
with multiplicity one and the remaining eigenvalues are zero. Thus, the eigenvalues of
$\frac {1}{r^{q-2}}$
with multiplicity one and the remaining eigenvalues are zero. Thus, the eigenvalues of
![]() $M_{W,q}$
are
$M_{W,q}$
are
![]() $\frac {1}{r^{q-1}}$
with multiplicity r and zero for the remaining ones. Thus, by Lemma 2.5,
$\frac {1}{r^{q-1}}$
with multiplicity r and zero for the remaining ones. Thus, by Lemma 2.5,
![]() $x_q(W) = \frac {1}{r}$
and
$x_q(W) = \frac {1}{r}$
and
![]() $y_q(W) = \frac {1}{r^2}$
.
$y_q(W) = \frac {1}{r^2}$
.
Lemma 2.9. Let
![]() $q\geq 2$
be an integer. For every
$q\geq 2$
be an integer. For every
![]() $W \in \mathcal {W}$
and every positive integer r, if
$W \in \mathcal {W}$
and every positive integer r, if
![]() $x_q(W) \in \left [\frac {1}{r+1}, \frac {1}{r}\right ]$
, then we have
$x_q(W) \in \left [\frac {1}{r+1}, \frac {1}{r}\right ]$
, then we have
![]() $y_q(W) \geq L(x_q(W))$
, where
$y_q(W) \geq L(x_q(W))$
, where
Proof. Let
![]() $\mathbf {X}$
be the space of
$\mathbf {X}$
be the space of
![]() $\mathbf {x} = (x_1, x_2, \dots )$
, where
$\mathbf {x} = (x_1, x_2, \dots )$
, where
![]() $\mathbf {x} \geq \mathbf {0}$
,
$\mathbf {x} \geq \mathbf {0}$
,
![]() $x_1 \geq x_2 \geq \ldots $
, and
$x_1 \geq x_2 \geq \ldots $
, and
![]() $\mathbf {x} \in \mathbb {R}^s$
for any positive integer s. Let
$\mathbf {x} \in \mathbb {R}^s$
for any positive integer s. Let
![]() $e_j(\mathbf {x}):=\sum _{1 \leq i_1 < \ldots < i_j } x_{i_1}\cdots x_{i_j}$
be the jth elementary symmetric polynomial, and let
$e_j(\mathbf {x}):=\sum _{1 \leq i_1 < \ldots < i_j } x_{i_1}\cdots x_{i_j}$
be the jth elementary symmetric polynomial, and let
![]() $p_j(\mathbf {x}):=\sum _{i} x_i^j$
be the jth power sum. Note that when
$p_j(\mathbf {x}):=\sum _{i} x_i^j$
be the jth power sum. Note that when
![]() $\mathbf {x} \in \mathbf {X}$
,
$\mathbf {x} \in \mathbf {X}$
,
![]() $e_j(\mathbf {x}), p_j(\mathbf {x})$
’s are well defined. To prove the result, we first look at the convex hull of
$e_j(\mathbf {x}), p_j(\mathbf {x})$
’s are well defined. To prove the result, we first look at the convex hull of
![]() $e_2(\mathbf {x})$
and
$e_2(\mathbf {x})$
and
![]() $e_3(\mathbf {x})$
when
$e_3(\mathbf {x})$
when
![]() $e_1(\mathbf {x})=1$
before moving to the convex hull of the profile of
$e_1(\mathbf {x})=1$
before moving to the convex hull of the profile of
![]() $p_2(\mathbf {x})$
and
$p_2(\mathbf {x})$
and
![]() $p_3(\mathbf {x})$
when
$p_3(\mathbf {x})$
when
![]() $p_1(\mathbf {x})=1$
and then transforming this appropriately to get the desired result.
$p_1(\mathbf {x})=1$
and then transforming this appropriately to get the desired result.
Claim 2.10. For any
![]() $c_2, c_3\in \mathbb {R}$
, we have that
$c_2, c_3\in \mathbb {R}$
, we have that
![]() $c_2e_2(\mathbf {x}) + c_3 e_3(\mathbf {x}) \geq 0$
for every
$c_2e_2(\mathbf {x}) + c_3 e_3(\mathbf {x}) \geq 0$
for every
![]() $\mathbf {x}\in \mathbf {X}$
and
$\mathbf {x}\in \mathbf {X}$
and
![]() $e_1(\mathbf {x})=1$
if and only if
$e_1(\mathbf {x})=1$
if and only if
![]() $c_2e_2(\mathbf {x}) + c_3 e_3(\mathbf {x}) \geq 0$
for
$c_2e_2(\mathbf {x}) + c_3 e_3(\mathbf {x}) \geq 0$
for
![]() $x_1=\ldots = x_m = \frac {1}{m}$
and
$x_1=\ldots = x_m = \frac {1}{m}$
and
![]() $x_{m+1}=x_{m+2}=\ldots =0$
for every integer
$x_{m+1}=x_{m+2}=\ldots =0$
for every integer
![]() $m\geq 1$
.
$m\geq 1$
.
Proof. The forward direction is trivial since
![]() $x_1=\ldots = x_m = \frac {1}{m}$
and
$x_1=\ldots = x_m = \frac {1}{m}$
and
![]() $x_{m+1}=x_{m+2}=\ldots =0$
satisfies
$x_{m+1}=x_{m+2}=\ldots =0$
satisfies
![]() $\mathbf {x} \geq \mathbf {0}$
and
$\mathbf {x} \geq \mathbf {0}$
and
![]() $e_1(\mathbf {x})=1$
.
$e_1(\mathbf {x})=1$
.
For the converse, suppose
![]() $c_2e_2(\mathbf {x}) + c_3 e_3(\mathbf {x}) \geq 0$
for
$c_2e_2(\mathbf {x}) + c_3 e_3(\mathbf {x}) \geq 0$
for
![]() $x_1=\ldots = x_m = \frac {1}{m}$
and
$x_1=\ldots = x_m = \frac {1}{m}$
and
![]() $x_{m+1}=x_{m+2}=\ldots =0$
for every
$x_{m+1}=x_{m+2}=\ldots =0$
for every
![]() $m\in \mathbb {N}$
. Let
$m\in \mathbb {N}$
. Let
![]() $f(\mathbf {x}):=c_2e_2(\mathbf {x}) + c_3 e_3(\mathbf {x})$
. It suffices to show that
$f(\mathbf {x}):=c_2e_2(\mathbf {x}) + c_3 e_3(\mathbf {x})$
. It suffices to show that
Since
![]() $\{\mathbf {x}\in \mathbf {X} : e_1(\mathbf {x})=1\}$
is compact, we can assume that the minimum is attained on some
$\{\mathbf {x}\in \mathbf {X} : e_1(\mathbf {x})=1\}$
is compact, we can assume that the minimum is attained on some
![]() $\mathbf {x} \in \mathbf {X}$
, and among all optimal solutions, we pick one of largest
$\mathbf {x} \in \mathbf {X}$
, and among all optimal solutions, we pick one of largest
![]() $\ell ^2$
norm.
$\ell ^2$
norm.
We prove the claim by local adjustment of this optimal solution
![]() $\mathbf {x}$
when fixing
$\mathbf {x}$
when fixing
![]() $x_i+x_j$
for some given
$x_i+x_j$
for some given
![]() $i < j$
, where
$i < j$
, where
![]() $x_i, x_j> 0$
. By the definition of f, there are functions
$x_i, x_j> 0$
. By the definition of f, there are functions
![]() $f_1, f_2, f_3$
that only depend on
$f_1, f_2, f_3$
that only depend on
![]() $\mathbf {x}^{i,j}$
, that is,
$\mathbf {x}^{i,j}$
, that is,
![]() $\mathbf {x}$
where we delete the entries
$\mathbf {x}$
where we delete the entries
![]() $x_i, x_j$
so that
$x_i, x_j$
so that
If
![]() $f_1(\mathbf {x}^{i,j})\geq 0$
, then by turning
$f_1(\mathbf {x}^{i,j})\geq 0$
, then by turning
![]() $x_i$
into
$x_i$
into
![]() $x_i + x_j$
and
$x_i + x_j$
and
![]() $x_j$
into zero, the value of f does not decrease while the
$x_j$
into zero, the value of f does not decrease while the
![]() $\ell ^2$
norm of the solution strictly increases, which is a contradiction after reordering
$\ell ^2$
norm of the solution strictly increases, which is a contradiction after reordering
![]() $x_i$
’s. Thus,
$x_i$
’s. Thus,
![]() $f_1(x_3, \ldots , x_n)<0$
. Holding
$f_1(x_3, \ldots , x_n)<0$
. Holding
![]() $x_i+x_j$
fixed, one can see that
$x_i+x_j$
fixed, one can see that
![]() $f(\mathbf {x})$
is minimized when
$f(\mathbf {x})$
is minimized when
![]() $x_i=x_j$
. Similarly, we can show that all nonzero entries in
$x_i=x_j$
. Similarly, we can show that all nonzero entries in
![]() $\mathbf {x}$
are equal. Thus, there is a positive integer m such that
$\mathbf {x}$
are equal. Thus, there is a positive integer m such that
![]() $x_1=\ldots =x_m = \frac {1}{m}$
, as desired.
$x_1=\ldots =x_m = \frac {1}{m}$
, as desired.
Note that this implies that the convex hull of
![]() $\{(e_2(\mathbf {x}), e_3(\mathbf {x}))\mid \mathbf {x}\in \mathbf {X}, e_1(\mathbf {x}) = 1\}$
is the same as the convex hull of
$\{(e_2(\mathbf {x}), e_3(\mathbf {x}))\mid \mathbf {x}\in \mathbf {X}, e_1(\mathbf {x}) = 1\}$
is the same as the convex hull of
![]() $\{(e_2(\mathbf {x}), e_3(\mathbf {x}))\mid x_1=\ldots = x_m = \frac {1}{m} \text { and } x_{m+1}= x_{m+2} = \ldots =0 \text { for some } m\in \mathbb {N}\}$
or equivalently by evaluating, as the convex hull of
$\{(e_2(\mathbf {x}), e_3(\mathbf {x}))\mid x_1=\ldots = x_m = \frac {1}{m} \text { and } x_{m+1}= x_{m+2} = \ldots =0 \text { for some } m\in \mathbb {N}\}$
or equivalently by evaluating, as the convex hull of
![]() $\{(\frac {m-1}{2m}, \frac {(m-1)(m-2)}{6m^2}) \mid m\in \mathbb {N}\}$
. Also note that this is equivalent to Bollobás’ result [Reference Bollobás4] and that the exact profile can be fully understood as an easy corollary from Razborov’s work [Reference Razborov17].
$\{(\frac {m-1}{2m}, \frac {(m-1)(m-2)}{6m^2}) \mid m\in \mathbb {N}\}$
. Also note that this is equivalent to Bollobás’ result [Reference Bollobás4] and that the exact profile can be fully understood as an easy corollary from Razborov’s work [Reference Razborov17].
Claim 2.11. The convex hull of
![]() $\{(p_2(\mathbf {x}), p_3(\mathbf {x}))\mid \mathbf {x}\in \mathbf {X}, p_1(\mathbf {x}) = 1\}$
is equal to the convex hull of
$\{(p_2(\mathbf {x}), p_3(\mathbf {x}))\mid \mathbf {x}\in \mathbf {X}, p_1(\mathbf {x}) = 1\}$
is equal to the convex hull of
![]() $\{(\frac {1}{m}, \frac {1}{m^2})| m\in \mathbb {N}\}$
.
$\{(\frac {1}{m}, \frac {1}{m^2})| m\in \mathbb {N}\}$
.
Proof. In general, through Newton’s identities, we know that
![]() $p_2(\mathbf {x})=(e_1(\mathbf {x}))^2-2e_2(\mathbf {x})$
, and
$p_2(\mathbf {x})=(e_1(\mathbf {x}))^2-2e_2(\mathbf {x})$
, and
![]() $p_3(\mathbf {x})=(e_1(\mathbf {x}))^3-3e_1(\mathbf {x})e_2(\mathbf {x})+3e_3(\mathbf {x})$
. Since we are setting
$p_3(\mathbf {x})=(e_1(\mathbf {x}))^3-3e_1(\mathbf {x})e_2(\mathbf {x})+3e_3(\mathbf {x})$
. Since we are setting
![]() $e_1(\mathbf {x})=p_1(\mathbf {x})=1$
, we have
$e_1(\mathbf {x})=p_1(\mathbf {x})=1$
, we have
![]() $p_2(\mathbf {x})=1-2e_2(\mathbf {x})$
and
$p_2(\mathbf {x})=1-2e_2(\mathbf {x})$
and
![]() $p_3(\mathbf {x})=1-3e_2(\mathbf {x})+3e_3(\mathbf {x})$
, and so the convex hull of
$p_3(\mathbf {x})=1-3e_2(\mathbf {x})+3e_3(\mathbf {x})$
, and so the convex hull of
![]() $\{(p_2(\mathbf {x}), p_3(\mathbf {x}))\mid \mathbf {x}\in \mathbf {X}, p_1(\mathbf {x}) = 1\}$
will be an affine transformation of the convex hull of
$\{(p_2(\mathbf {x}), p_3(\mathbf {x}))\mid \mathbf {x}\in \mathbf {X}, p_1(\mathbf {x}) = 1\}$
will be an affine transformation of the convex hull of
![]() $\{(e_2(\mathbf {x}), e_3(\mathbf {x}))\mid \mathbf {x}\in \mathbf {X}, e_1(\mathbf {x}) = 1\}$
. Under this map, the points
$\{(e_2(\mathbf {x}), e_3(\mathbf {x}))\mid \mathbf {x}\in \mathbf {X}, e_1(\mathbf {x}) = 1\}$
. Under this map, the points
![]() $(\frac {m-1}{2m}, \frac {(m-1)(m-2)}{6m^2})$
go to
$(\frac {m-1}{2m}, \frac {(m-1)(m-2)}{6m^2})$
go to
![]() $(\frac {1}{m}, \frac {1}{m^2})$
, and so the statement holds.
$(\frac {1}{m}, \frac {1}{m^2})$
, and so the statement holds.
Claim 2.12. The convex hull of
![]() $\{(x_q(W), y_q(W)) \mid W \in \mathcal {W}, t(N_{4,q}, W) \neq 0\}$
is contained in the convex hull of
$\{(x_q(W), y_q(W)) \mid W \in \mathcal {W}, t(N_{4,q}, W) \neq 0\}$
is contained in the convex hull of
![]() $\{(\frac {1}{m}, \frac {1}{m^2})| m\in \mathbb {N}\}$
.
$\{(\frac {1}{m}, \frac {1}{m^2})| m\in \mathbb {N}\}$
.
Proof. Note for any real
![]() $\alpha \neq 0$
and any
$\alpha \neq 0$
and any
![]() $W \in \mathcal {W}$
,
$W \in \mathcal {W}$
,
![]() $x_q(W) =x_q(\alpha W)$
, and
$x_q(W) =x_q(\alpha W)$
, and
![]() $y_q(W) = y_q(\alpha W)$
. Also notice that
$y_q(W) = y_q(\alpha W)$
. Also notice that
![]() $t(N_{4,q}, \alpha W) =\alpha ^{4\binom {q}{2}}t(N_{4,q}, W)$
. Thus, whenever
$t(N_{4,q}, \alpha W) =\alpha ^{4\binom {q}{2}}t(N_{4,q}, W)$
. Thus, whenever
![]() $t(N_{4,q}, W)\neq 0$
, we may assume
$t(N_{4,q}, W)\neq 0$
, we may assume
![]() $|t(N_{4,q}, W)| = 1$
by properly scaling W. Since
$|t(N_{4,q}, W)| = 1$
by properly scaling W. Since
![]() $t(N_{4,q}, W) \geq 0$
by Lemma 2.5, we assume
$t(N_{4,q}, W) \geq 0$
by Lemma 2.5, we assume
![]() $t(N_{4,q}, W) = 1$
. Therefore, the convex hull of
$t(N_{4,q}, W) = 1$
. Therefore, the convex hull of
![]() $\{(x_q(W), y_q(W)) \mid W \in \mathcal {W}, t(N_{4,q}, W) \neq 0\}$
is the same as the convex hull of
$\{(x_q(W), y_q(W)) \mid W \in \mathcal {W}, t(N_{4,q}, W) \neq 0\}$
is the same as the convex hull of
![]() $\{(t(N_{8,q}, W), t(N_{12,q}, W)) \mid W \in \mathcal {W}, t(N_{4,q}, W) = 1\}$
.
$\{(t(N_{8,q}, W), t(N_{12,q}, W)) \mid W \in \mathcal {W}, t(N_{4,q}, W) = 1\}$
.
Let ![]() be the spectrum of
be the spectrum of
![]() $M_{W,q}$
, where
$M_{W,q}$
, where
![]() $|\lambda _1| \geq |\lambda _2| \geq \dots $
. By letting
$|\lambda _1| \geq |\lambda _2| \geq \dots $
. By letting
![]() $x_i=\lambda _i^4$
for every i, we have that
$x_i=\lambda _i^4$
for every i, we have that
![]() $\mathbf {x} = (x_1, x_2, \dots ) \in \mathbf {X}$
. By Lemma 2.5,
$\mathbf {x} = (x_1, x_2, \dots ) \in \mathbf {X}$
. By Lemma 2.5, ![]() ,
, ![]() and
and ![]() . So by Claim 2.11, the convex hull of
. So by Claim 2.11, the convex hull of
![]() $\{(t(N_{8,q}, W), t(N_{12,q}, W)) \mid W \in \mathcal {W} \text { such that }t(N_{4,q}, W)=1\}$
is contained in the convex hull of
$\{(t(N_{8,q}, W), t(N_{12,q}, W)) \mid W \in \mathcal {W} \text { such that }t(N_{4,q}, W)=1\}$
is contained in the convex hull of
![]() $\{(\frac {1}{m}, \frac {1}{m^2})| m\in \mathbb {N}\}$
, as desired.
$\{(\frac {1}{m}, \frac {1}{m^2})| m\in \mathbb {N}\}$
, as desired.
This ends the proof of Lemma 2.9.
We give a name to the region in the statement of Lemma 2.9. Note that this region does not depend on the choice of q.
Definition 2.13. Let
![]() $\mathcal {R}:=\{(x,y)\in [0,1]^2: y\leq x \text { and } y \geq \frac {2r+1}{r(r+1)}x-\frac {1}{r(r+1)} \text { for } \frac {1}{r+1}\leq x \leq \frac {1}{r} \text { for } r\in \mathbb {N}\}$
(see Figure 2). Observe that
$\mathcal {R}:=\{(x,y)\in [0,1]^2: y\leq x \text { and } y \geq \frac {2r+1}{r(r+1)}x-\frac {1}{r(r+1)} \text { for } \frac {1}{r+1}\leq x \leq \frac {1}{r} \text { for } r\in \mathbb {N}\}$
(see Figure 2). Observe that
![]() $\mathcal {D}_q\subseteq \mathcal {R}$
for every integer
$\mathcal {D}_q\subseteq \mathcal {R}$
for every integer
![]() $q\geq 2$
. Notice that
$q\geq 2$
. Notice that
![]() $\mathcal {R}$
is the convex hull of the points
$\mathcal {R}$
is the convex hull of the points
![]() $\{(1/n, 1/n^2), n \in \mathbb {N}\}$
.
$\{(1/n, 1/n^2), n \in \mathbb {N}\}$
.
2.2. Obtaining k independent copies of
 $\mathcal {D}_q$
$\mathcal {D}_q$
In Lemma 2.8, we realized an infinite sparse set of points on
![]() $y=x^2$
for every
$y=x^2$
for every
![]() $\mathcal {D}_q$
. In the next section, as explained in the proof outline, in order to simultaneously plug in independent values for each
$\mathcal {D}_q$
. In the next section, as explained in the proof outline, in order to simultaneously plug in independent values for each
![]() $x_i$
in
$x_i$
in
![]() $p(x_1, \dots , x_k) \in \mathbb {Z}[x]$
, it will be useful to simultaneously realize
$p(x_1, \dots , x_k) \in \mathbb {Z}[x]$
, it will be useful to simultaneously realize
![]() $(\frac {1}{r_q},\frac {1}{r_q^2})\in \mathcal {D}_q$
with a single construction for different positive integer
$(\frac {1}{r_q},\frac {1}{r_q^2})\in \mathcal {D}_q$
with a single construction for different positive integer
![]() $r_q$
’s for every
$r_q$
’s for every
![]() $2 \leq q \leq \ell $
(in the sense of Proposition 2.15). To do so, we now use q-ification again on a construction due to Alon [Reference Alon1].
$2 \leq q \leq \ell $
(in the sense of Proposition 2.15). To do so, we now use q-ification again on a construction due to Alon [Reference Alon1].
Recall that
![]() $x_q(W):=\frac {t(N_{8,q},W)}{t(N_{4,q},W)^2}$
and
$x_q(W):=\frac {t(N_{8,q},W)}{t(N_{4,q},W)^2}$
and
![]() $y_q(W):=\frac {t(N_{12,q},W)}{t(N_{4,q},W)^3}$
.
$y_q(W):=\frac {t(N_{12,q},W)}{t(N_{4,q},W)^3}$
.
Definition 2.14. For
![]() $\ell \in \mathbb {N}$
such that
$\ell \in \mathbb {N}$
such that
![]() $\ell \geq 2$
, let
$\ell \geq 2$
, let
Our goal in this subsection is to prove the following proposition.
Proposition 2.15. For any set of positive integers
![]() $r_2, \ldots , r_\ell $
,
$r_2, \ldots , r_\ell $
,
![]() $(\frac {1}{r_2}, \frac {1}{r_2^2},\frac {1}{r_3}, \frac {1}{r_3^2}, \ldots , \frac {1}{r_\ell }, \frac {1}{r_\ell ^2})\in \mathcal {D}_{\leq \ell }$
.
$(\frac {1}{r_2}, \frac {1}{r_2^2},\frac {1}{r_3}, \frac {1}{r_3^2}, \ldots , \frac {1}{r_\ell }, \frac {1}{r_\ell ^2})\in \mathcal {D}_{\leq \ell }$
.
Note that Theorem 1.6 follows from Proposition 2.15.
To prove Proposition 2.15, we need a construction of W for any given
![]() $r_2, \dots , r_\ell $
. The starting point of our construction W is a disjoint union of blocks, each of the style described in the next definition.
$r_2, \dots , r_\ell $
. The starting point of our construction W is a disjoint union of blocks, each of the style described in the next definition.
Definition 2.16. Let
![]() $A(k,2)$
be an (unweighted) triangle-free graph with n vertices that is d-regular and where the second largest eigenvalue (in absolute value) of the adjacency matrix of
$A(k,2)$
be an (unweighted) triangle-free graph with n vertices that is d-regular and where the second largest eigenvalue (in absolute value) of the adjacency matrix of
![]() $A(k,2)$
is
$A(k,2)$
is
![]() $\lambda $
, where
$\lambda $
, where
![]() $n=\Theta (2^{3k})$
,
$n=\Theta (2^{3k})$
,
![]() $d=\Theta (2^{2k})$
and
$d=\Theta (2^{2k})$
and
![]() $\lambda =\Theta (2^k)$
. Here, the constants in
$\lambda =\Theta (2^k)$
. Here, the constants in
![]() $\Theta $
are absolute constants. For an integer
$\Theta $
are absolute constants. For an integer
![]() $q\geq 3$
, let
$q\geq 3$
, let
![]() $A(k,q)$
be the q-ification of
$A(k,q)$
be the q-ification of
![]() $A(k,2)$
.
$A(k,2)$
.
The graphs
![]() $A(k,2)$
are known as
$A(k,2)$
are known as
![]() $(n,d,\lambda )$
-graphs in the literature and were first constructed by Alon in [Reference Alon1]. Since
$(n,d,\lambda )$
-graphs in the literature and were first constructed by Alon in [Reference Alon1]. Since
![]() $A(k,2)$
has
$A(k,2)$
has
![]() $\frac {nd}{2}=\Theta (2^{5k-1})$
edges and since the q-ification introduces
$\frac {nd}{2}=\Theta (2^{5k-1})$
edges and since the q-ification introduces
![]() $q-2$
vertices for every edge of
$q-2$
vertices for every edge of
![]() $A(k,2)$
,
$A(k,2)$
,
![]() $A(k,q)$
has
$A(k,q)$
has
![]() $n+(q-2)\frac {dn}{2}=\Theta (2^{3k}+(q-2)2^{5k-1})$
vertices. The original vertices coming from
$n+(q-2)\frac {dn}{2}=\Theta (2^{3k}+(q-2)2^{5k-1})$
vertices. The original vertices coming from
![]() $A(k,2)$
have degree
$A(k,2)$
have degree
![]() $d(q-1)$
, and the new vertices have degree
$d(q-1)$
, and the new vertices have degree
![]() $q-1$
. Further, the original vertices are each contained in
$q-1$
. Further, the original vertices are each contained in
![]() $d~q$
-cliques, whereas the new vertices are contained in exactly one q-clique.
$d~q$
-cliques, whereas the new vertices are contained in exactly one q-clique.
In the proof of Proposition 2.15, each block of our construction W will look like
![]() $A(k_s, s)$
for some appropriately chosen
$A(k_s, s)$
for some appropriately chosen
![]() $k_s$
for each
$k_s$
for each
![]() $2 \leq s \leq \ell $
. Thus, to understand
$2 \leq s \leq \ell $
. Thus, to understand
![]() $t(N_{4,q}, W), t(N_{8, q}, W)$
and
$t(N_{4,q}, W), t(N_{8, q}, W)$
and
![]() $t(N_{12, q}, W)$
, we need to understand
$t(N_{12, q}, W)$
, we need to understand
![]() $M_{A(k_s, s), q}$
(as defined in Definition 2.4) and bound its eigenvalues to apply Lemma 2.5. Recall that
$M_{A(k_s, s), q}$
(as defined in Definition 2.4) and bound its eigenvalues to apply Lemma 2.5. Recall that
![]() $W_G$
is the graphon corresponding to graph G.
$W_G$
is the graphon corresponding to graph G.
Lemma 2.17. For
![]() $s, q \geq 2$
, suppose
$s, q \geq 2$
, suppose
![]() $A(k,s)$
has
$A(k,s)$
has
![]() $n_s$
vertices. Then
$n_s$
vertices. Then
![]() $M_{A(k,s),q}=\binom {s-2}{q-2}\frac {W_{A(k,s)}}{n_s^{q-2}}$
. In particular, this means that
$M_{A(k,s),q}=\binom {s-2}{q-2}\frac {W_{A(k,s)}}{n_s^{q-2}}$
. In particular, this means that
![]() $M_{A(k,q),q}=W_{A(k,q)}$
.
$M_{A(k,q),q}=W_{A(k,q)}$
.
Proof. Since
![]() $A(k,2)$
contains no clique of size 3, the only s-cliques in
$A(k,2)$
contains no clique of size 3, the only s-cliques in
![]() $A(k,s)$
are those that correspond to edges in
$A(k,s)$
are those that correspond to edges in
![]() $A(k,2)$
. In fact, these s-cliques are the only maximal cliques in
$A(k,2)$
. In fact, these s-cliques are the only maximal cliques in
![]() $A(k,s)$
. Therefore, every edge of
$A(k,s)$
. Therefore, every edge of
![]() $A(k,s)$
is in exactly
$A(k,s)$
is in exactly
![]() $\binom {s-2}{q-2}~q$
-clique, so
$\binom {s-2}{q-2}~q$
-clique, so
![]() $M_{A(k,s),q}=\frac {\binom {s-2}{q-2}}{n_s^{q-2}}M_{A(k,s),2}$
. The proof is complete since
$M_{A(k,s),q}=\frac {\binom {s-2}{q-2}}{n_s^{q-2}}M_{A(k,s),2}$
. The proof is complete since
![]() $M_{A(k,s),2} = W_{A(k,s)}$
by Equation (2.1).
$M_{A(k,s),2} = W_{A(k,s)}$
by Equation (2.1).
Lemma 2.18. The top eigenvalue of the adjacency matrix of graph
![]() $A(k,s)$
is
$A(k,s)$
is
![]() $\Theta (2^{2k})$
, while all the other eigenvalues are at most
$\Theta (2^{2k})$
, while all the other eigenvalues are at most
![]() $O(2^k)$
. Here, the asymptotic is as
$O(2^k)$
. Here, the asymptotic is as
![]() $k \to \infty $
and s is a fixed constant.
$k \to \infty $
and s is a fixed constant.
Proof. Since
![]() $A(k,2)$
is an induced subgraph of
$A(k,2)$
is an induced subgraph of
![]() $A(k,s)$
, by the eigenvalue interlacing theorem, the largest eigenvalue of
$A(k,s)$
, by the eigenvalue interlacing theorem, the largest eigenvalue of
![]() $A(k,s)$
is at least that of
$A(k,s)$
is at least that of
![]() $A(k,2)$
, which is
$A(k,2)$
, which is
![]() $\Theta (2^{2k})$
. On the other hand, the largest eigenvalue is also at most the maximum degree of
$\Theta (2^{2k})$
. On the other hand, the largest eigenvalue is also at most the maximum degree of
![]() $A(k,s)$
, which again is
$A(k,s)$
, which again is
![]() $\Theta (2^{2k})$
.
$\Theta (2^{2k})$
.
We now prove the second claim. For any edge
![]() $e = (u,v)$
in
$e = (u,v)$
in
![]() $A(k,2)$
, let
$A(k,2)$
, let
![]() $U_e$
be the
$U_e$
be the
![]() $s-2$
vertices created for e in
$s-2$
vertices created for e in
![]() $A(k, s)$
. Let
$A(k, s)$
. Let
![]() $\lambda $
be an eigenvalue of
$\lambda $
be an eigenvalue of
![]() $A(k,s)$
and
$A(k,s)$
and
![]() $\mathbf {v}$
its eigenvector, and assume
$\mathbf {v}$
its eigenvector, and assume
![]() $|\lambda | \gg \Theta (1)$
. For any
$|\lambda | \gg \Theta (1)$
. For any
![]() $w \in U_e$
, we have
$w \in U_e$
, we have
By subtracting two such equations if
![]() $|U_e| \geq 2$
, we obtain
$|U_e| \geq 2$
, we obtain
![]() $\mathbf {v}(w) = \mathbf {v}(w')$
for any
$\mathbf {v}(w) = \mathbf {v}(w')$
for any
![]() $w, w' \in U_e$
since
$w, w' \in U_e$
since
![]() $\lambda \neq -1$
. Plugging this back into Equation (2.2) and using
$\lambda \neq -1$
. Plugging this back into Equation (2.2) and using
![]() $|U_e| = s-2$
, we have
$|U_e| = s-2$
, we have
![]() $(\lambda -s+3)\mathbf {v}(w) = \mathbf {v}(v)+ \mathbf {v}(u)$
for any
$(\lambda -s+3)\mathbf {v}(w) = \mathbf {v}(v)+ \mathbf {v}(u)$
for any
![]() $w \in U_e$
. Furthermore, we have that
$w \in U_e$
. Furthermore, we have that
 $$ \begin{align} \sum_{w \in U_{(u,v)}}\mathbf{v}(w) = \frac{s-2}{\lambda-s+3}(\mathbf{v}(v)+ \mathbf{v}(u)). \end{align} $$
$$ \begin{align} \sum_{w \in U_{(u,v)}}\mathbf{v}(w) = \frac{s-2}{\lambda-s+3}(\mathbf{v}(v)+ \mathbf{v}(u)). \end{align} $$
Consider any original vertex v in
![]() $A(k,2)$
. We then have
$A(k,2)$
. We then have
 $$\begin{align*}\lambda \mathbf{v}(v) = \sum_{u: (u,v)\in E(A(k,2)) } \left(\mathbf{v}(u) + \sum_{w \in U_{(u,v)}} \mathbf{v}(w)\right) =\sum_{u: (u,v)\in E(A(k,2)) } \left(\mathbf{v}(u) + \frac{s-2}{\lambda-s+3}(\mathbf{v}(v)+ \mathbf{v}(u))\right), \end{align*}$$
$$\begin{align*}\lambda \mathbf{v}(v) = \sum_{u: (u,v)\in E(A(k,2)) } \left(\mathbf{v}(u) + \sum_{w \in U_{(u,v)}} \mathbf{v}(w)\right) =\sum_{u: (u,v)\in E(A(k,2)) } \left(\mathbf{v}(u) + \frac{s-2}{\lambda-s+3}(\mathbf{v}(v)+ \mathbf{v}(u))\right), \end{align*}$$
where the second equality follows from Equation (2.3). By rearranging and recalling that each vertex in
![]() $A(k,2)$
has degree
$A(k,2)$
has degree
![]() $d = \Theta (2^{2k})$
, we have that
$d = \Theta (2^{2k})$
, we have that
 $$ \begin{align} \left(\lambda - \frac{d(s-2)}{\lambda-s+3}\right) \mathbf{v}(v) =\left( 1+ \frac{s-2}{\lambda-s+3}\right) \sum_{u: (u,v)\in E(A(k,2)) } \mathbf{v}(u). \end{align} $$
$$ \begin{align} \left(\lambda - \frac{d(s-2)}{\lambda-s+3}\right) \mathbf{v}(v) =\left( 1+ \frac{s-2}{\lambda-s+3}\right) \sum_{u: (u,v)\in E(A(k,2)) } \mathbf{v}(u). \end{align} $$
We now move
![]() $1+\frac {s-2}{\lambda -s+3}$
to the left (this quantity is nonzero since
$1+\frac {s-2}{\lambda -s+3}$
to the left (this quantity is nonzero since
![]() $|\lambda |$
is large). Thus,
$|\lambda |$
is large). Thus,
 $$\begin{align*}f(\lambda) := \frac{\lambda - \frac{d(s-2)}{\lambda-s+3}}{ 1+ \frac{s-2}{\lambda-s+3}} \end{align*}$$
$$\begin{align*}f(\lambda) := \frac{\lambda - \frac{d(s-2)}{\lambda-s+3}}{ 1+ \frac{s-2}{\lambda-s+3}} \end{align*}$$
has to be an eigenvalue of
![]() $A(k,2)$
, with the same eigenvector as
$A(k,2)$
, with the same eigenvector as
![]() $\mathbf {v}$
when restricted to vertices in
$\mathbf {v}$
when restricted to vertices in
![]() $A(k,2)$
.
$A(k,2)$
.
We can now prove the second part of the lemma by contradiction. If
![]() $\lambda $
is not the largest eigenvalue of
$\lambda $
is not the largest eigenvalue of
![]() $A(k,s)$
but
$A(k,s)$
but
![]() $\frac {2^k}{\lambda } = o(1)$
as
$\frac {2^k}{\lambda } = o(1)$
as
![]() $k \to \infty $
, then
$k \to \infty $
, then
![]() $f(\lambda ) = \Theta (\lambda ) \gg 2^k$
since s is a fixed constant and
$f(\lambda ) = \Theta (\lambda ) \gg 2^k$
since s is a fixed constant and
![]() $d = \Theta (2^{2k})$
. However, the only eigenvalue of
$d = \Theta (2^{2k})$
. However, the only eigenvalue of
![]() $A(k,2)$
much larger than
$A(k,2)$
much larger than
![]() $\Theta (2^k)$
is the top eigenvalue, which is d. Thus,
$\Theta (2^k)$
is the top eigenvalue, which is d. Thus,
![]() $f(\lambda )=d$
. Rearranging the equation
$f(\lambda )=d$
. Rearranging the equation
![]() $f(\lambda )=d$
, any eigenvalue
$f(\lambda )=d$
, any eigenvalue
![]() $\lambda $
satisfying
$\lambda $
satisfying
![]() $\frac {2^k}{\lambda } = o(1)$
is a root of
$\frac {2^k}{\lambda } = o(1)$
is a root of
![]() $\lambda (\lambda - s +3) - d(s-2) = d(\lambda - s + 3 + s-2)$
. The product of the roots of this quadratic equation is
$\lambda (\lambda - s +3) - d(s-2) = d(\lambda - s + 3 + s-2)$
. The product of the roots of this quadratic equation is
![]() $-d(s-2)-d$
. Since we have shown the largest eigenvalue of
$-d(s-2)-d$
. Since we have shown the largest eigenvalue of
![]() $A(k,s)$
is at least d, the magnitude for the other root is at most
$A(k,s)$
is at least d, the magnitude for the other root is at most
![]() $\frac {d(s-2)+d}{d} = O(1)$
. Since
$\frac {d(s-2)+d}{d} = O(1)$
. Since
![]() $A(k, s)$
is connected, the largest eigenvalue has multiplicity one. This leads to a contradiction to our assumption on
$A(k, s)$
is connected, the largest eigenvalue has multiplicity one. This leads to a contradiction to our assumption on
![]() $\lambda $
.
$\lambda $
.
Corollary 2.19. Fix
![]() $s \geq q \geq 2$
. The top eigenvalue of
$s \geq q \geq 2$
. The top eigenvalue of
![]() $M_{A(k,s),q}$
is
$M_{A(k,s),q}$
is
![]() $\Theta (2^{2k-5k(q-1)})$
, and all the other eigenvalues are at most
$\Theta (2^{2k-5k(q-1)})$
, and all the other eigenvalues are at most
![]() $O(2^{k-5k(q-1)})$
.
$O(2^{k-5k(q-1)})$
.
Proof. This is a direct consequence of Lemmas 2.17 and 2.18 and the fact that
![]() $A(k,s)$
has
$A(k,s)$
has
![]() $n_s = \Theta (2^{5k})$
vertices. Here, notice that the eigenvalues of
$n_s = \Theta (2^{5k})$
vertices. Here, notice that the eigenvalues of
![]() $M_{A(k,s),2}= W_{A(k,s)}$
are the ones of the adjacency matrix of
$M_{A(k,s),2}= W_{A(k,s)}$
are the ones of the adjacency matrix of
![]() $A(k,s)$
scaled by
$A(k,s)$
scaled by
![]() $\frac {1}{n_s}$
.
$\frac {1}{n_s}$
.
Lemma 2.20. All but at most
![]() $O(2^{3k})$
eigenvalues of
$O(2^{3k})$
eigenvalues of
![]() $A(k,s)$
are
$A(k,s)$
are
![]() $O(1)$
. Thus, all but at most
$O(1)$
. Thus, all but at most
![]() $O(2^{3k})$
eigenvalues of
$O(2^{3k})$
eigenvalues of
![]() $M_{A(k,s),q}$
are
$M_{A(k,s),q}$
are
![]() $O(2^{-5k(q-1)})$
.
$O(2^{-5k(q-1)})$
.
Proof. Let the eigenvalues of
![]() $A_{k,s}$
be
$A_{k,s}$
be
![]() $\lambda _1\geq \lambda _2 \geq \ldots $
. Let n be the number of vertices in
$\lambda _1\geq \lambda _2 \geq \ldots $
. Let n be the number of vertices in
![]() $A(k,2)$
, which is
$A(k,2)$
, which is
![]() $\Theta (2^{3k})$
. By the interlacing theorem applied to adjacency matrices, we know that
$\Theta (2^{3k})$
. By the interlacing theorem applied to adjacency matrices, we know that
![]() $\lambda _{1+n}$
is at most the largest eigenvalue of the adjacency matrix of the graph obtained by removing the n original vertices in
$\lambda _{1+n}$
is at most the largest eigenvalue of the adjacency matrix of the graph obtained by removing the n original vertices in
![]() $A(k,2)$
vertices from
$A(k,2)$
vertices from
![]() $A(k,s)$
. This induced subgraph consists of the disjoint union of cliques of size
$A(k,s)$
. This induced subgraph consists of the disjoint union of cliques of size
![]() $q-2$
and thus has eigenvalues that are at most
$q-2$
and thus has eigenvalues that are at most
![]() $q-3$
. So
$q-3$
. So
![]() $\lambda _{1+n}\leq q-3$
. Similarly, each eigenvalue in
$\lambda _{1+n}\leq q-3$
. Similarly, each eigenvalue in
![]() $K_{q-3}$
is at least
$K_{q-3}$
is at least
![]() $-1$
, thus all but at most n eigenvalues are at least
$-1$
, thus all but at most n eigenvalues are at least
![]() $-1$
.
$-1$
.
We are now ready to prove Proposition 2.15.
Proof of Proposition 2.15
For each
![]() $2 \leq s \leq \ell $
, let
$2 \leq s \leq \ell $
, let
![]() $k_s = (\ell -s + 1)K$
for some large positive integer K. All the asymptotics in this proof are as
$k_s = (\ell -s + 1)K$
for some large positive integer K. All the asymptotics in this proof are as
![]() $K \to \infty $
, and the constants are in terms of
$K \to \infty $
, and the constants are in terms of
![]() $\ell $
and
$\ell $
and
![]() $r_s$
’s. Let graphon W correspond to the disjoint union of
$r_s$
’s. Let graphon W correspond to the disjoint union of
![]() $G_2$
,
$G_2$
,
![]() $G_3$
,
$G_3$
,
![]() $\ldots $
,
$\ldots $
,
![]() $G_\ell $
, where
$G_\ell $
, where
![]() $G_s$
consists of
$G_s$
consists of
![]() $r_s$
disjoint copies of
$r_s$
disjoint copies of
![]() $A(k_s,s)$
. Each
$A(k_s,s)$
. Each
![]() $A(k_s,s)$
has
$A(k_s,s)$
has
![]() $n_s = \Theta (2^{5k_s})$
vertices, and let
$n_s = \Theta (2^{5k_s})$
vertices, and let
![]() $N = \sum _s r_s n_s$
be the total number of vertices in the graph. Thus, each block in
$N = \sum _s r_s n_s$
be the total number of vertices in the graph. Thus, each block in
![]() $M_{W,q}$
corresponding to
$M_{W,q}$
corresponding to
![]() $A(k_s, s)$
is
$A(k_s, s)$
is
![]() $M_{A(k_s,s),q}$
scaled by
$M_{A(k_s,s),q}$
scaled by
![]() $\frac {n_s^{q-2}}{N^{q-2}}$
. When fixing
$\frac {n_s^{q-2}}{N^{q-2}}$
. When fixing
![]() $s, q$
, let
$s, q$
, let
![]() $\mu _{s,q,i}$
be the i-th largest eigenvalue of
$\mu _{s,q,i}$
be the i-th largest eigenvalue of
![]() $M_{A(k_s,s),q}$
multiplied by
$M_{A(k_s,s),q}$
multiplied by
![]() $n_s^{q-2} \cdot n_s$
.
$n_s^{q-2} \cdot n_s$
.
Thus, by Lemma 2.5,
 $$ \begin{align*} x_q(W)&=\frac{\sum_{s=2}^\ell r_s\left(\sum_{i} \mu_{s,q,i} ^8\right)}{\left(\sum_{s=2}^\ell r_s\left(\sum_i \mu_{s,q,i}^4\right)\right)^2}=\frac{\sum_{s=q}^\ell r_s\left(\sum_{i} \mu_{s,q,i}^8\right)}{\left(\sum_{s=q}^\ell r_s\left(\sum_i \mu_{s,q,i}^4\right)\right)^2}. \end{align*} $$
$$ \begin{align*} x_q(W)&=\frac{\sum_{s=2}^\ell r_s\left(\sum_{i} \mu_{s,q,i} ^8\right)}{\left(\sum_{s=2}^\ell r_s\left(\sum_i \mu_{s,q,i}^4\right)\right)^2}=\frac{\sum_{s=q}^\ell r_s\left(\sum_{i} \mu_{s,q,i}^8\right)}{\left(\sum_{s=q}^\ell r_s\left(\sum_i \mu_{s,q,i}^4\right)\right)^2}. \end{align*} $$
The last equality holds because when
![]() $s < q$
,
$s < q$
,
![]() $M_{A(k,s),q}$
is zero by Lemma 2.17.
$M_{A(k,s),q}$
is zero by Lemma 2.17.
When
![]() $\ell \geq s \geq q \geq 2$
, by Corollary 2.19,
$\ell \geq s \geq q \geq 2$
, by Corollary 2.19,
![]() $\mu _{s,q,1}= \Theta (2^{k_s(2-5(q-1))}) n_s^{q-1} = \Theta (2^{2{k_s}})$
. Furthermore, by Corollary 2.19 and Lemma 2.20,
$\mu _{s,q,1}= \Theta (2^{k_s(2-5(q-1))}) n_s^{q-1} = \Theta (2^{2{k_s}})$
. Furthermore, by Corollary 2.19 and Lemma 2.20,
 $\sum _i \mu _{s,q,i}^4 = \mu _{s,q,1}^4 + \sum _{i \geq 2}\mu _{s,q,i}^4 = \mu _{s,q,1}^4 + O(2^{3k_s})\cdot O(2^{4k_s(1-5(q-1))}) n_s^{q-1} + n_s O(2^{-20k_s(q-1)}) = (1+o(1)) \mu _{s,q,1}^4$
. In addition, when
$\sum _i \mu _{s,q,i}^4 = \mu _{s,q,1}^4 + \sum _{i \geq 2}\mu _{s,q,i}^4 = \mu _{s,q,1}^4 + O(2^{3k_s})\cdot O(2^{4k_s(1-5(q-1))}) n_s^{q-1} + n_s O(2^{-20k_s(q-1)}) = (1+o(1)) \mu _{s,q,1}^4$
. In addition, when
![]() $s> q$
,
$s> q$
,
![]() $\mu _{s,q,1}^4= \Theta (2^{8k_s}) = o(2^{8k_q}) = o(\mu _{q,q,1}^4)$
. Thus, the denominator of
$\mu _{s,q,1}^4= \Theta (2^{8k_s}) = o(2^{8k_q}) = o(\mu _{q,q,1}^4)$
. Thus, the denominator of
![]() $x_q(W)$
is
$x_q(W)$
is
![]() $(\sum _{p=q}^\ell (1+o(1))r_s\mu _{s,q,1}^4)^2 = (1+o(1))r_s^2\mu _{q,q,1}^4$
. Similarly, by the same computation, the numerator of
$(\sum _{p=q}^\ell (1+o(1))r_s\mu _{s,q,1}^4)^2 = (1+o(1))r_s^2\mu _{q,q,1}^4$
. Similarly, by the same computation, the numerator of
![]() $x_q(W)$
is
$x_q(W)$
is
![]() $\sum _{s=q}^\ell (1+o(1))r_s\mu _{s,q,1}^8 = (1+o(1))r_s\mu _{q,q,1}^8$
. Thus,
$\sum _{s=q}^\ell (1+o(1))r_s\mu _{s,q,1}^8 = (1+o(1))r_s\mu _{q,q,1}^8$
. Thus,
![]() $x_q(W) = \frac {1+o(1)}{r_q}$
. Similarly,
$x_q(W) = \frac {1+o(1)}{r_q}$
. Similarly,
![]() $y_q(W) = \frac {1+o(1)}{r_q^2}$
. Again here
$y_q(W) = \frac {1+o(1)}{r_q^2}$
. Again here
![]() $o(1)$
is when
$o(1)$
is when
![]() $K \to \infty $
. Since this result holds for any
$K \to \infty $
. Since this result holds for any
![]() $2 \leq q \leq \ell $
, the claim follows.
$2 \leq q \leq \ell $
, the claim follows.
We end this section by highlighting the fact that even though our profiles are over
![]() $W \in \mathcal {W}$
, all our constructions use
$W \in \mathcal {W}$
, all our constructions use
![]() $W \in \mathcal {W}_0$
, and thus the same results hold had we started with profiles for
$W \in \mathcal {W}_0$
, and thus the same results hold had we started with profiles for
![]() $W \in \mathcal {W}^*$
for any
$W \in \mathcal {W}^*$
for any
![]() $\mathcal {W}^* \in \mathfrak {W}$
.
$\mathcal {W}^* \in \mathfrak {W}$
.
2.3. Completion of the proof
By Matiyasevich’s solution to Hilbert’s 10th problem [Reference Matiyasevich15], determining the nonnegativity of a polynomial with integer-valued variables is undecidable. We follow the same strategy as Hatami and Norin in [Reference Hatami and Norine7] to reduce our problem to the decidability of polynomials with integer variables. We use the integrality feature of the graph profiles proved in Lemma 2.8 and Proposition 2.15 of Subsection 2.1.
Lemma 2.21. Given a positive integer
![]() $\ell \geq 7$
and a polynomial
$\ell \geq 7$
and a polynomial
![]() $p(x_2, \ldots , x_\ell )$
with integer coefficients, the problem of determining whether there exist
$p(x_2, \ldots , x_\ell )$
with integer coefficients, the problem of determining whether there exist
![]() $x_2, \ldots , x_\ell \in \{\frac {1}{n} | n\in \mathbb {N}\}$
such that
$x_2, \ldots , x_\ell \in \{\frac {1}{n} | n\in \mathbb {N}\}$
such that
![]() $p(x_2, \ldots , x_\ell ) <0$
is undecidable.
$p(x_2, \ldots , x_\ell ) <0$
is undecidable.
Proof. Consider a polynomial
![]() $\bar {p}(y_2, \ldots , y_\ell )$
with integer coefficients. Note that
$\bar {p}(y_2, \ldots , y_\ell )$
with integer coefficients. Note that
![]() $\bar {p}(y_2, \ldots , y_\ell ) \geq 0$
for all
$\bar {p}(y_2, \ldots , y_\ell ) \geq 0$
for all
![]() $y_2, \ldots , y_\ell \in \mathbb {N}$
if and only if the polynomial with integer coefficients
$y_2, \ldots , y_\ell \in \mathbb {N}$
if and only if the polynomial with integer coefficients
 $$ \begin{align*}p(x_2, \ldots, x_\ell):=\left(\prod_{q=2}^{\ell}x_q^{\text{deg}(\bar{p})}\right)\bar{p}\left(\frac{1}{x_2}, \ldots, \frac{1}{x_\ell} \right)\end{align*} $$
$$ \begin{align*}p(x_2, \ldots, x_\ell):=\left(\prod_{q=2}^{\ell}x_q^{\text{deg}(\bar{p})}\right)\bar{p}\left(\frac{1}{x_2}, \ldots, \frac{1}{x_\ell} \right)\end{align*} $$
is nonnegative for all
![]() $x_2, \ldots , x_\ell \in \{\frac {1}{n}: n\in \mathbb {N}\}$
. Hence, the problem is undecidable.
$x_2, \ldots , x_\ell \in \{\frac {1}{n}: n\in \mathbb {N}\}$
. Hence, the problem is undecidable.
Just as in [Reference Hatami and Norine7], we need to relate the nonnegativity of a polynomial with variables in
![]() $\{\frac {1}{n} \mid n\in \mathbb {N}\}$
to the nonnegativity of polynomials involving homomorphism densities. By Lemma 2.9, the convex hull
$\{\frac {1}{n} \mid n\in \mathbb {N}\}$
to the nonnegativity of polynomials involving homomorphism densities. By Lemma 2.9, the convex hull
![]() $\mathcal {D}_q$
has the integrality feature for every
$\mathcal {D}_q$
has the integrality feature for every
![]() $2\leq q \leq \ell $
. To use this fact, we first need to create an auxiliary polynomial as in Lemma 5.4 in [Reference Hatami and Norine7] so that the original polynomial is nonnegative on
$2\leq q \leq \ell $
. To use this fact, we first need to create an auxiliary polynomial as in Lemma 5.4 in [Reference Hatami and Norine7] so that the original polynomial is nonnegative on
![]() $\{\frac {1}{n}\mid n\in \mathbb {N}\}$
if and only if the auxiliary polynomial is nonnegative on
$\{\frac {1}{n}\mid n\in \mathbb {N}\}$
if and only if the auxiliary polynomial is nonnegative on
![]() $\mathcal {R}^{\ell -1}$
. We modify slightly the construction of the auxiliary polynomial presented in [Reference Hatami and Norine7] and reproduce the proof in the appendix for completion.
$\mathcal {R}^{\ell -1}$
. We modify slightly the construction of the auxiliary polynomial presented in [Reference Hatami and Norine7] and reproduce the proof in the appendix for completion.
Lemma 2.22. Let p be a polynomial in variables
![]() $x_2, \ldots , x_\ell $
. Let M be the sum of the absolute values of the coefficients of p multiplied by
$x_2, \ldots , x_\ell $
. Let M be the sum of the absolute values of the coefficients of p multiplied by
![]() $100 \text {deg}(p)$
. Define
$100 \text {deg}(p)$
. Define
![]() $\bar {p}\in \mathbb {R}[x_2, \ldots , x_\ell , y_2, \ldots , y_\ell ]$
as
$\bar {p}\in \mathbb {R}[x_2, \ldots , x_\ell , y_2, \ldots , y_\ell ]$
as
 $$ \begin{align*}\bar{p}:=p\prod_{q=2}^\ell x_q^6 + M \left(\sum_{q=2}^\ell y_q - x_q^2\right).\end{align*} $$
$$ \begin{align*}\bar{p}:=p\prod_{q=2}^\ell x_q^6 + M \left(\sum_{q=2}^\ell y_q - x_q^2\right).\end{align*} $$
Then the following are equivalent:
-
1.
 $\bar {p}(x_2, \ldots , x_\ell , y_2, \ldots , y_\ell )<0$
for some
$\bar {p}(x_2, \ldots , x_\ell , y_2, \ldots , y_\ell )<0$
for some
 $x_2, \ldots , x_\ell , y_2, \ldots , y_\ell $
with
$x_2, \ldots , x_\ell , y_2, \ldots , y_\ell $
with
 $(x_q, y_q)\in \mathcal {R}$
for every
$(x_q, y_q)\in \mathcal {R}$
for every
 $2\leq q \leq \ell $
;
$2\leq q \leq \ell $
; -
2.
 $p(x_2, \ldots , x_\ell )<0$
for some
$p(x_2, \ldots , x_\ell )<0$
for some
 $x_2, \ldots , x_\ell \in \{\frac {1}{n}:n\in \mathbb {N}\}$
.
$x_2, \ldots , x_\ell \in \{\frac {1}{n}:n\in \mathbb {N}\}$
.
Lemma 2.23. Given a polynomial p in
![]() $\ell -1$
variables, there is a quantum graph
$\ell -1$
variables, there is a quantum graph
![]() $f(p)$
such that for any
$f(p)$
such that for any
![]() $W \in \mathcal {W}$
,
$W \in \mathcal {W}$
,
 $$ \begin{align} t(f(p), W):= \bar{p}\left(\frac{t(N_{8,2},W)}{t(N_{4,2},W)^2}, \ldots, \frac{t(N_{8,\ell},W)}{t(N_{4,\ell},W)^2}, \frac{t(N_{12,2},W)}{t(N_{4,2},W)^3}, \ldots, \frac{t(N_{12,\ell},W)}{t(N_{4,\ell},W)^3}\right)\prod_{q=2}^\ell t(N_{4,q},W)^{3\mathrm{deg}(p)}. \end{align} $$
$$ \begin{align} t(f(p), W):= \bar{p}\left(\frac{t(N_{8,2},W)}{t(N_{4,2},W)^2}, \ldots, \frac{t(N_{8,\ell},W)}{t(N_{4,\ell},W)^2}, \frac{t(N_{12,2},W)}{t(N_{4,2},W)^3}, \ldots, \frac{t(N_{12,\ell},W)}{t(N_{4,\ell},W)^3}\right)\prod_{q=2}^\ell t(N_{4,q},W)^{3\mathrm{deg}(p)}. \end{align} $$
Proof. The right-hand side of Equation (2.5) is a polynomial in
![]() $t(N_{4,q}, W), t(N_{8,q},W), t(N_{12,q},W)$
for
$t(N_{4,q}, W), t(N_{8,q},W), t(N_{12,q},W)$
for
![]() $2\leq q \leq \ell $
. Thus, there is a quantum graph
$2\leq q \leq \ell $
. Thus, there is a quantum graph
![]() $f(p)$
where Equation (2.5) holds.
$f(p)$
where Equation (2.5) holds.
Lemma 2.24. The following two statements are equivalent.
-
○
 $p(x_2, \ldots , x_\ell )<0$
for some
$p(x_2, \ldots , x_\ell )<0$
for some
 $x_2, \ldots , x_\ell \in \{\frac {1}{n}:n\in \mathbb {N}\}$
.
$x_2, \ldots , x_\ell \in \{\frac {1}{n}:n\in \mathbb {N}\}$
. -
○
 $t(f(p),W) < 0$
for some
$t(f(p),W) < 0$
for some
 $W \in \mathcal {W}$
.
$W \in \mathcal {W}$
.
Proof. If
![]() $p(x_2, \ldots , x_\ell )\geq 0$
for all
$p(x_2, \ldots , x_\ell )\geq 0$
for all
![]() $x_2, \dots , x_\ell \in \{\frac {1}{n}: n\in \mathbb {N}\}^{\ell -1}$
, then
$x_2, \dots , x_\ell \in \{\frac {1}{n}: n\in \mathbb {N}\}^{\ell -1}$
, then
![]() $\bar {p}(x_2, \ldots , x_\ell , y_2, \ldots , y_\ell )\geq 0$
for every
$\bar {p}(x_2, \ldots , x_\ell , y_2, \ldots , y_\ell )\geq 0$
for every
![]() $x_2, \ldots , x_l, y_2, \ldots , y_\ell $
such that
$x_2, \ldots , x_l, y_2, \ldots , y_\ell $
such that
![]() $(x_q,y_q)\in \mathcal {R}$
for every
$(x_q,y_q)\in \mathcal {R}$
for every
![]() $2\leq q \leq \ell $
by Lemma 2.22. Therefore,
$2\leq q \leq \ell $
by Lemma 2.22. Therefore,
![]() $t(f(p),W)\geq 0$
for every
$t(f(p),W)\geq 0$
for every
![]() $W \in \mathcal {W}$
by Equation (2.5) and Lemma 2.8.
$W \in \mathcal {W}$
by Equation (2.5) and Lemma 2.8.
On the other hand, if
![]() $p(x_2', \ldots , x_\ell ') < 0$
where for each
$p(x_2', \ldots , x_\ell ') < 0$
where for each
![]() $2 \leq q \leq \ell $
, we have that
$2 \leq q \leq \ell $
, we have that
![]() $x_q' = \frac {1}{n_q}$
for some
$x_q' = \frac {1}{n_q}$
for some
![]() $n_q \in \mathbb {N}$
, then by the construction of
$n_q \in \mathbb {N}$
, then by the construction of
![]() $\bar p$
,
$\bar p$
,
![]() $\bar {p}(\frac {1}{n_2}, \ldots , \frac {1}{n_\ell }, \frac {1}{n_2^2}, \ldots , \frac {1}{n_\ell ^2})< 0$
. By Proposition 2.15, there is a sequence of
$\bar {p}(\frac {1}{n_2}, \ldots , \frac {1}{n_\ell }, \frac {1}{n_2^2}, \ldots , \frac {1}{n_\ell ^2})< 0$
. By Proposition 2.15, there is a sequence of
![]() $W_n$
’s such that
$W_n$
’s such that
![]() $\frac {t(N_{8,q},W_n)}{t(N_{4,q},W_n)^2} \rightarrow \frac {1}{n_q}$
and
$\frac {t(N_{8,q},W_n)}{t(N_{4,q},W_n)^2} \rightarrow \frac {1}{n_q}$
and
![]() $\frac {t(N_{12,q},W_n)}{t(N_{4,q},W_n)^3}\rightarrow \frac {1}{n_q^2}$
for each
$\frac {t(N_{12,q},W_n)}{t(N_{4,q},W_n)^3}\rightarrow \frac {1}{n_q^2}$
for each
![]() $2 \leq q \leq \ell $
as
$2 \leq q \leq \ell $
as
![]() $n\rightarrow \infty $
. Thus, again by Equation (2.5) and the continuity of polynomial
$n\rightarrow \infty $
. Thus, again by Equation (2.5) and the continuity of polynomial
![]() $\bar p$
, there is a W such that
$\bar p$
, there is a W such that
![]() $t(f(p),W) < 0$
.
$t(f(p),W) < 0$
.
We can now finish the proof of Theorem 1.3.
Again, note that the same holds if we look at the version of this theorem where we replace graph homomorphisms by homomorphism numbers.
Proof of Corollary 1.4
This follows from the same argument that Lovász presented in [Reference Lovász13] for the positivstellensatz of graphs. Consider two Turing machines where the input is a quantum graph f with rational coefficients. One machine is searching for sums of squares
![]() $g, h$
, where
$g, h$
, where
![]() $gf =h$
; the other machine is searching for graphs
$gf =h$
; the other machine is searching for graphs
![]() $G_{\mathbf {w}}$
, where the range of
$G_{\mathbf {w}}$
, where the range of
![]() $\mathbf {w}$
is
$\mathbf {w}$
is
![]() $\mathbb {Z}$
. Both are well defined algorithms. If either machine halts, we know
$\mathbb {Z}$
. Both are well defined algorithms. If either machine halts, we know
![]() $f \geq 0$
or not. However, by our undecidability result Theorem 1.3, there must be an f where both machines never halt.
$f \geq 0$
or not. However, by our undecidability result Theorem 1.3, there must be an f where both machines never halt.
A Proof of Lemma 2.22
Proof. If
![]() $(2)$
holds, then for each
$(2)$
holds, then for each
![]() $x_q$
we have
$x_q$
we have
![]() $(x_q, x_q^2)\in \mathcal {R}$
by the definition of
$(x_q, x_q^2)\in \mathcal {R}$
by the definition of
![]() $\mathcal {R}$
, and setting
$\mathcal {R}$
, and setting
![]() $y_q:=x_q^2$
gives
$y_q:=x_q^2$
gives
![]() $\bar {p}(x_2, \ldots , x_\ell , y_2, \ldots , y_\ell )=p(x_2, \ldots , x_\ell )\prod _{q=2}^\ell x_q^6<0$
. Therefore,
$\bar {p}(x_2, \ldots , x_\ell , y_2, \ldots , y_\ell )=p(x_2, \ldots , x_\ell )\prod _{q=2}^\ell x_q^6<0$
. Therefore,
![]() $(2)$
implies
$(2)$
implies
![]() $(1)$
.
$(1)$
.
Suppose now that
![]() $(1)$
holds. Observe that decreasing
$(1)$
holds. Observe that decreasing
![]() $y_q$
decreases the value of
$y_q$
decreases the value of
![]() $\bar {p}$
, and we can thus assume without loss of generality that
$\bar {p}$
, and we can thus assume without loss of generality that
![]() $y_q$
is as small as possible while still having
$y_q$
is as small as possible while still having
![]() $(x_q, y_q)\in \mathcal {R}$
, that is,
$(x_q, y_q)\in \mathcal {R}$
, that is,
![]() $y_q=L(x_q)$
. So we have
$y_q=L(x_q)$
. So we have
 $$ \begin{align*}\tilde{p}(x_2, \ldots, x_\ell):=\bar{p}(x_2, \ldots, x_\ell, y_2, \ldots, y_\ell)=p(x_2, \ldots, x_\ell)\prod_{q=2}^\ell x_q^6+ M\left(\sum_{q=2}^\ell L(x_q) - x_q^2\right)<0.\end{align*} $$
$$ \begin{align*}\tilde{p}(x_2, \ldots, x_\ell):=\bar{p}(x_2, \ldots, x_\ell, y_2, \ldots, y_\ell)=p(x_2, \ldots, x_\ell)\prod_{q=2}^\ell x_q^6+ M\left(\sum_{q=2}^\ell L(x_q) - x_q^2\right)<0.\end{align*} $$
For every
![]() $2 \leq q \leq \ell $
, let
$2 \leq q \leq \ell $
, let
![]() $r_q$
be a positive integer such that
$r_q$
be a positive integer such that
![]() $x_q \in \left [\frac {1}{r_q+1}, \frac {1}{r_q}\right ]$
. Fixing
$x_q \in \left [\frac {1}{r_q+1}, \frac {1}{r_q}\right ]$
. Fixing
![]() $r_2, \ldots , r_\ell $
, we may assume that
$r_2, \ldots , r_\ell $
, we may assume that
![]() $x_2, \ldots , x_\ell $
are chosen in the corresponding intervals to minimize
$x_2, \ldots , x_\ell $
are chosen in the corresponding intervals to minimize
![]() $\tilde {p}$
. We claim that we then have that
$\tilde {p}$
. We claim that we then have that
![]() $x_q \in \{\frac {1}{n}:n\in \mathbb {N}\}$
for every
$x_q \in \{\frac {1}{n}:n\in \mathbb {N}\}$
for every
![]() $2 \leq q \leq \ell $
. Suppose not: Suppose that
$2 \leq q \leq \ell $
. Suppose not: Suppose that
![]() $x_{q^*} \in (\frac {1}{r_{q^*}+1}, \frac {1}{r_{q^*}})$
for some
$x_{q^*} \in (\frac {1}{r_{q^*}+1}, \frac {1}{r_{q^*}})$
for some
![]() $q^*$
. By the choice of
$q^*$
. By the choice of
![]() $x_{q^*}$
, we have that
$x_{q^*}$
, we have that
![]() $\frac {\partial \tilde {p}}{\partial x_{q^*}}=0$
. We will derive a contradiction by a sequence of observations.
$\frac {\partial \tilde {p}}{\partial x_{q^*}}=0$
. We will derive a contradiction by a sequence of observations.
First, note that since each
![]() $x_q\in (0,1]$
and
$x_q\in (0,1]$
and
![]() $\text {deg}(p)\geq 1$
, we have that
$\text {deg}(p)\geq 1$
, we have that
 $$ \begin{align*} \bigg|\frac{\partial}{\partial x_{q^*}}\left( p(x_2, \ldots, x_\ell) \prod_{q=2}^\ell x_q^6\right)\bigg| &= p \cdot 6x_{q^*}^5\cdot \prod_{q\in [\ell]\backslash\{1,q^*\}} x_q^6 + \frac{\partial p}{\partial x_{q^*}} \cdot \prod_{q=2}^\ell x_q^6 \\ & \leq \sum_i |c_i| \cdot 6x_{q^*}^5 \cdot 1 + \text{deg}(p)\sum_{i} |c_i|\cdot x_{q^*}^6\\ & \leq 7 \text{deg}(p) \sum_{i} |c_i| x_{q^*}^5 =7 \frac{M}{100} x_{q^*}^5 \leq \frac{M}{12 r_{q^*}^5}, \end{align*} $$
$$ \begin{align*} \bigg|\frac{\partial}{\partial x_{q^*}}\left( p(x_2, \ldots, x_\ell) \prod_{q=2}^\ell x_q^6\right)\bigg| &= p \cdot 6x_{q^*}^5\cdot \prod_{q\in [\ell]\backslash\{1,q^*\}} x_q^6 + \frac{\partial p}{\partial x_{q^*}} \cdot \prod_{q=2}^\ell x_q^6 \\ & \leq \sum_i |c_i| \cdot 6x_{q^*}^5 \cdot 1 + \text{deg}(p)\sum_{i} |c_i|\cdot x_{q^*}^6\\ & \leq 7 \text{deg}(p) \sum_{i} |c_i| x_{q^*}^5 =7 \frac{M}{100} x_{q^*}^5 \leq \frac{M}{12 r_{q^*}^5}, \end{align*} $$
where
![]() $\sum _i |c_i|$
is the sum of the absolute values of the coefficients of p.
$\sum _i |c_i|$
is the sum of the absolute values of the coefficients of p.
Therefore, since
![]() $\frac {\partial \tilde {p}}{\partial x_{q^*}}=0$
, we have
$\frac {\partial \tilde {p}}{\partial x_{q^*}}=0$
, we have
 $\frac {1}{12r_{q^*}^5} \geq |L'(x_{q^*})-2x_{q^*}|=\bigg | 2z - 2x_{q^*}\bigg |$
, where
$\frac {1}{12r_{q^*}^5} \geq |L'(x_{q^*})-2x_{q^*}|=\bigg | 2z - 2x_{q^*}\bigg |$
, where
![]() $z=\frac {r_{q^*}+\frac {1}{2}}{r_{q^*}(r_{q^*}+1)}$
. Then the previous inequality can be rewritten as
$z=\frac {r_{q^*}+\frac {1}{2}}{r_{q^*}(r_{q^*}+1)}$
. Then the previous inequality can be rewritten as
 $$ \begin{align*}|z-x_{q^*}| \leq \frac{1}{24r_{q^*}^5}.\end{align*} $$
$$ \begin{align*}|z-x_{q^*}| \leq \frac{1}{24r_{q^*}^5}.\end{align*} $$
Now, note that
![]() $L'(x)-2x=\frac {2r+1}{r(r+1)}-2x$
is monotone on the interval
$L'(x)-2x=\frac {2r+1}{r(r+1)}-2x$
is monotone on the interval
![]() $\left [\frac {1}{r_{q^*}+1},{\frac {1}{r_{q^*}}}\right ]$
which contains both
$\left [\frac {1}{r_{q^*}+1},{\frac {1}{r_{q^*}}}\right ]$
which contains both
![]() $x_{q^*}$
and z and that this expression yields
$x_{q^*}$
and z and that this expression yields
![]() $0$
when
$0$
when
![]() $x=z$
. It follows that
$x=z$
. It follows that
 $$ \begin{align*} L(x_{q^*})-x^2_{q^*} &\geq (L(z)-z^2)-|(L(x_{q^*})-x_{q^*}^2)'||z-x_{q^*}|\\ & \geq \frac{1}{4r_{q^*}^2(r_{q^*}+1)^2}-2\left(\frac{1}{24r_{q^*}^5}\right)^2 \geq \frac{1}{16r_{q^*}^4}-2\left(\frac{1}{24r_{q^*}^5}\right)^2=\frac{1}{18r_{q^*}^4}. \end{align*} $$
$$ \begin{align*} L(x_{q^*})-x^2_{q^*} &\geq (L(z)-z^2)-|(L(x_{q^*})-x_{q^*}^2)'||z-x_{q^*}|\\ & \geq \frac{1}{4r_{q^*}^2(r_{q^*}+1)^2}-2\left(\frac{1}{24r_{q^*}^5}\right)^2 \geq \frac{1}{16r_{q^*}^4}-2\left(\frac{1}{24r_{q^*}^5}\right)^2=\frac{1}{18r_{q^*}^4}. \end{align*} $$
Finally, note that
![]() $\sum _{q=2}^{\ell } L(x_q)-x_q^2 \geq L(x_{q^*})-x_{q^*}^2$
since
$\sum _{q=2}^{\ell } L(x_q)-x_q^2 \geq L(x_{q^*})-x_{q^*}^2$
since
![]() $L(x_q)-x_q^2 \geq 0$
for every q. So, putting everything together, we thus have that
$L(x_q)-x_q^2 \geq 0$
for every q. So, putting everything together, we thus have that
 $$ \begin{align*}\tilde{p}(x_2, \ldots, x_\ell) \geq -\frac{M}{100} x_{q^*}^6+M(L(x_{q^*})-x_{q^*}^2) \geq M \left( \frac{1}{18r_{q^*}^4} - \frac{1}{100 r_{q^*}^6}\right)> 0, \end{align*} $$
$$ \begin{align*}\tilde{p}(x_2, \ldots, x_\ell) \geq -\frac{M}{100} x_{q^*}^6+M(L(x_{q^*})-x_{q^*}^2) \geq M \left( \frac{1}{18r_{q^*}^4} - \frac{1}{100 r_{q^*}^6}\right)> 0, \end{align*} $$
which is a contradiction. Therefore, the claim that
![]() $x_q\in \{\frac {1}{n} : n\in \mathbb {N}\}$
for every
$x_q\in \{\frac {1}{n} : n\in \mathbb {N}\}$
for every
![]() $2\leq q \leq \ell $
holds. We therefore have that
$2\leq q \leq \ell $
holds. We therefore have that
![]() $0>\tilde {p}(x_2, \ldots , x_{\ell }) = p(x_2, \ldots , x_\ell ) \prod _{q=2}^\ell x_q^6,$
which shows that
$0>\tilde {p}(x_2, \ldots , x_{\ell }) = p(x_2, \ldots , x_\ell ) \prod _{q=2}^\ell x_q^6,$
which shows that
![]() $(2)$
holds since
$(2)$
holds since
![]() $\prod _{q=2}^\ell x_q^6\geq 0$
.
$\prod _{q=2}^\ell x_q^6\geq 0$
.
B Alternative proof
We provide an alternative proof to Theorem 1.3. The advantage of this proof is that it is easier to obtain k independent copies of the convex hull, although the description of the quantum graph is slightly more complicated.
In some steps of this proof, it is easier to work with induced copies of H in G. Given graphs H and G, an induced homomorphism from H to G is a mapping
![]() $V(H) \to V(G)$
that preserves both adjacency and nonadjacency. Given a graph H and
$V(H) \to V(G)$
that preserves both adjacency and nonadjacency. Given a graph H and
![]() $W \in \mathcal {W}$
, we can define the induced density as
$W \in \mathcal {W}$
, we can define the induced density as
 $$\begin{align*}t_{\text{ind}}(H, W) := \int_{[0,1]^{|V(H)|}} \prod_{\{i,j\}\in E(H)} W(x_i, x_j)\prod_{\{i,j\}\notin E(H)} (1-W(x_i, x_j))d x_{1} \dots dx_{|V(H)|}. \end{align*}$$
$$\begin{align*}t_{\text{ind}}(H, W) := \int_{[0,1]^{|V(H)|}} \prod_{\{i,j\}\in E(H)} W(x_i, x_j)\prod_{\{i,j\}\notin E(H)} (1-W(x_i, x_j))d x_{1} \dots dx_{|V(H)|}. \end{align*}$$
Thus, if
![]() $W_G$
is the graphon associated with a simple graph G,
$W_G$
is the graphon associated with a simple graph G,
![]() $t_{\text {ind}}(H, W_G)$
is essentially the density of induced copies of H in G. We can similarly define conditional induced density. Suppose
$t_{\text {ind}}(H, W_G)$
is essentially the density of induced copies of H in G. We can similarly define conditional induced density. Suppose
![]() $H^{\bullet \dots \bullet }$
has k roots, then
$H^{\bullet \dots \bullet }$
has k roots, then
 $$ \begin{align*}t_{\text{ind}, x_1,\dots, x_k}(H^{\bullet \dots \bullet}, W) := \!\int_{[0,1]^{|V(H)|-k}} \prod_{\{i,j\}\in E(H)} W(x_i, x_j) \prod_{\{i,j\}\notin E(H)}\! (1-W(x_i, x_j)) d x_{k+1} \dots dx_{|V(H)|}.\end{align*} $$
$$ \begin{align*}t_{\text{ind}, x_1,\dots, x_k}(H^{\bullet \dots \bullet}, W) := \!\int_{[0,1]^{|V(H)|-k}} \prod_{\{i,j\}\in E(H)} W(x_i, x_j) \prod_{\{i,j\}\notin E(H)}\! (1-W(x_i, x_j)) d x_{k+1} \dots dx_{|V(H)|}.\end{align*} $$
Let
![]() $\mathcal {H}$
be the set of connected rooted graphs
$\mathcal {H}$
be the set of connected rooted graphs
![]() $H^{\bullet \bullet }$
where (1) the two roots are adjacent and (2) the graph is symmetric with respect to the two roots, that is, there is an induced homomorphism
$H^{\bullet \bullet }$
where (1) the two roots are adjacent and (2) the graph is symmetric with respect to the two roots, that is, there is an induced homomorphism
![]() $V(H) \to V(H)$
which maps the two roots to one another. Let
$V(H) \to V(H)$
which maps the two roots to one another. Let
![]() $N_{c, H^{\bullet \bullet }}$
be the graph obtained by gluing each edge e of the cycle
$N_{c, H^{\bullet \bullet }}$
be the graph obtained by gluing each edge e of the cycle
![]() $C_c$
to an induced copy of H by identifying the two roots of
$C_c$
to an induced copy of H by identifying the two roots of
![]() $H^{\bullet \bullet }$
with the end vertices of e. Let
$H^{\bullet \bullet }$
with the end vertices of e. Let
![]() $\mathbf {N}_{c, H^{\bullet \bullet }}$
be the set of all possible graphs that contain
$\mathbf {N}_{c, H^{\bullet \bullet }}$
be the set of all possible graphs that contain
![]() $N_{c, H^{\bullet \bullet }}$
as a spanning subgraph and where there can be additional edges formed by any pair of vertices belonging to copies of H that were glued to different edges of
$N_{c, H^{\bullet \bullet }}$
as a spanning subgraph and where there can be additional edges formed by any pair of vertices belonging to copies of H that were glued to different edges of
![]() $C_c$
. To lighten the notation, we let
$C_c$
. To lighten the notation, we let
 $$\begin{align*}t_{\text{ind}}(\mathbf{N}_{c,H^{\bullet \bullet}}, W) := \sum_{F \in \mathbf{N}_{c,H^{\bullet \bullet}}} t_{\text{ind}}(F, W). \end{align*}$$
$$\begin{align*}t_{\text{ind}}(\mathbf{N}_{c,H^{\bullet \bullet}}, W) := \sum_{F \in \mathbf{N}_{c,H^{\bullet \bullet}}} t_{\text{ind}}(F, W). \end{align*}$$
For example, if
![]() $H = K_2^{\bullet \bullet }$
, then
$H = K_2^{\bullet \bullet }$
, then
![]() $N_{c, H^{\bullet \bullet }}$
is
$N_{c, H^{\bullet \bullet }}$
is
![]() $C_c$
and
$C_c$
and
![]() $\mathbf {N}_{c, H^{\bullet \bullet }}$
is all the graphs on c vertices containing
$\mathbf {N}_{c, H^{\bullet \bullet }}$
is all the graphs on c vertices containing
![]() $C_c$
as a subgraph. Thus,
$C_c$
as a subgraph. Thus,
![]() $t_{\text {ind}}(\mathbf {N}_{c, K_2^{\bullet \bullet }},W) = t(C_c, W)$
.
$t_{\text {ind}}(\mathbf {N}_{c, K_2^{\bullet \bullet }},W) = t(C_c, W)$
.
The first part of the proof is almost the same as in Subsection 2.1. We introduce the following definition to understand
![]() $t_{\text {ind}}(\mathbf {N}_{c,H^{\bullet \bullet }}, W)$
.
$t_{\text {ind}}(\mathbf {N}_{c,H^{\bullet \bullet }}, W)$
.
Definition B.1. Given
![]() $W \in \mathcal {W}$
, consider a symmetric measurable function
$W \in \mathcal {W}$
, consider a symmetric measurable function
![]() $M_{W,H^{\bullet \bullet }}: [0,1]^2 \to \mathbb {R}$
such that
$M_{W,H^{\bullet \bullet }}: [0,1]^2 \to \mathbb {R}$
such that
![]() $M_{W,H^{\bullet \bullet }}(x,y) = t_{\text {ind}, x,y}(H^{\bullet \bullet }, W)$
.
$M_{W,H^{\bullet \bullet }}(x,y) = t_{\text {ind}, x,y}(H^{\bullet \bullet }, W)$
.
This definition is a generalization of Definition 2.3. Indeed, when
![]() $H^{\bullet \bullet } = K_q^{\bullet \bullet }$
,
$H^{\bullet \bullet } = K_q^{\bullet \bullet }$
,
![]() $M_{W,H^{\bullet \bullet }}$
is the same as
$M_{W,H^{\bullet \bullet }}$
is the same as
![]() $M_{W,q}$
from Definition 2.3. The following lemma is immediate.
$M_{W,q}$
from Definition 2.3. The following lemma is immediate.
Lemma B.2. Let
![]() $W \in \mathcal {W}$
. Then
$W \in \mathcal {W}$
. Then
![]() $t_{\mathrm {ind}}(\mathbf {N}_{c, H^{\bullet \bullet }}, W)=\sum _{i} \lambda _i^c$
, where
$t_{\mathrm {ind}}(\mathbf {N}_{c, H^{\bullet \bullet }}, W)=\sum _{i} \lambda _i^c$
, where
![]() $\lambda _1, \lambda _2, \ldots $
are the eigenvalues of
$\lambda _1, \lambda _2, \ldots $
are the eigenvalues of
![]() $M_{W,H^{\bullet \bullet }}$
.
$M_{W,H^{\bullet \bullet }}$
.
By exactly the same proof as in Lemma 2.7, if we let
 $$ \begin{align*}\mathcal{D}_{H^{\bullet \bullet},q}:=\text{cl}\left(\left \{ \left(\frac{t_{\text{ind}}(\mathbf{N}_{8,H^{\bullet \bullet}},W)}{t_{\text{ind}}(\mathbf{N}_{4,H^{\bullet \bullet}},W)^2}, \frac{t_{\text{ind}}(\mathbf{N}_{12,H^{\bullet \bullet}},W)}{t_{\text{ind}}(\mathbf{N}_{4,H^{\bullet \bullet}},W)^3}\right) \mid W \in \mathcal{W} \text{ and }t_{\text{ind}}(\mathbf{N}_{4,H^{\bullet \bullet}},W)\neq 0 \right\}\right),\end{align*} $$
$$ \begin{align*}\mathcal{D}_{H^{\bullet \bullet},q}:=\text{cl}\left(\left \{ \left(\frac{t_{\text{ind}}(\mathbf{N}_{8,H^{\bullet \bullet}},W)}{t_{\text{ind}}(\mathbf{N}_{4,H^{\bullet \bullet}},W)^2}, \frac{t_{\text{ind}}(\mathbf{N}_{12,H^{\bullet \bullet}},W)}{t_{\text{ind}}(\mathbf{N}_{4,H^{\bullet \bullet}},W)^3}\right) \mid W \in \mathcal{W} \text{ and }t_{\text{ind}}(\mathbf{N}_{4,H^{\bullet \bullet}},W)\neq 0 \right\}\right),\end{align*} $$
then
![]() $\mathcal {D}_{H^{\bullet \bullet },q}\subseteq [0,1]^2$
. In addition, for any
$\mathcal {D}_{H^{\bullet \bullet },q}\subseteq [0,1]^2$
. In addition, for any
![]() $(x,y)\in \mathcal {D}_{H^{\bullet \bullet },q}$
, we have that
$(x,y)\in \mathcal {D}_{H^{\bullet \bullet },q}$
, we have that
![]() $y\geq x^2$
. Furthermore, by Lemma B.2, Lemma 2.9 holds here too. Recall from Definition 2.13 that
$y\geq x^2$
. Furthermore, by Lemma B.2, Lemma 2.9 holds here too. Recall from Definition 2.13 that
![]() $\mathcal {R}$
is the convex hull of the points
$\mathcal {R}$
is the convex hull of the points
![]() $\{(\frac {1}{n}, \frac {1}{n^2}) \mid n \in \mathbb {N}\}$
to obtain the following lemma.
$\{(\frac {1}{n}, \frac {1}{n^2}) \mid n \in \mathbb {N}\}$
to obtain the following lemma.
Lemma B.3. We have that
![]() $\mathcal {D}_{H^{\bullet \bullet },q}\subseteq \mathcal {R}$
.
$\mathcal {D}_{H^{\bullet \bullet },q}\subseteq \mathcal {R}$
.
The second part of the proof serves the purpose of Subsection 2.2. Given k different
![]() $H^{\bullet \bullet }$
, we now proceed to show that we can obtain k independent copies of the convex hull. In particular, we prove the following result, which serves the purpose of Proposition 2.15. This proof is simpler than the proof of Proposition 2.15, which is the main result in Subsection 2.2.
$H^{\bullet \bullet }$
, we now proceed to show that we can obtain k independent copies of the convex hull. In particular, we prove the following result, which serves the purpose of Proposition 2.15. This proof is simpler than the proof of Proposition 2.15, which is the main result in Subsection 2.2.
Proposition B.4. Let
![]() $H_1^{\bullet \bullet }, \dots , H_\ell ^{\bullet \bullet }$
be
$H_1^{\bullet \bullet }, \dots , H_\ell ^{\bullet \bullet }$
be
![]() $\ell $
different graphs in
$\ell $
different graphs in
![]() $\mathcal {H}$
with no induced homomorphism from one to another. Furthermore, assume that each
$\mathcal {H}$
with no induced homomorphism from one to another. Furthermore, assume that each
![]() $H_i$
has a vertex cut set of size at least three and contains a triangle and that there is no induced homomorphism
$H_i$
has a vertex cut set of size at least three and contains a triangle and that there is no induced homomorphism
![]() $V(H_i)\to V(H_i)$
which does not fix the set of the two roots. Let
$V(H_i)\to V(H_i)$
which does not fix the set of the two roots. Let
 $$\begin{align*}x_i(W) =\frac{t_{\mathrm{ind}}(\mathbf{N}_{8,H_i^{\bullet \bullet}},W)}{t_{\mathrm{ind}}(\mathbf{N}_{4,H_i^{\bullet \bullet}},W)^2}, \ \ y_i(W) = \frac{t_{\mathrm{ind}}(\mathbf{N}_{12,H_i^{\bullet \bullet}},W)}{t_{\mathrm{ind}}(\mathbf{N}_{4,H_i^{\bullet \bullet}},W)^3}, \ \ \text{and} \end{align*}$$
$$\begin{align*}x_i(W) =\frac{t_{\mathrm{ind}}(\mathbf{N}_{8,H_i^{\bullet \bullet}},W)}{t_{\mathrm{ind}}(\mathbf{N}_{4,H_i^{\bullet \bullet}},W)^2}, \ \ y_i(W) = \frac{t_{\mathrm{ind}}(\mathbf{N}_{12,H_i^{\bullet \bullet}},W)}{t_{\mathrm{ind}}(\mathbf{N}_{4,H_i^{\bullet \bullet}},W)^3}, \ \ \text{and} \end{align*}$$
Then for any set of positive integers
![]() $r_1, \ldots , r_\ell $
,
$r_1, \ldots , r_\ell $
,
![]() $(\frac {1}{r_1}, \frac {1}{r_1^2},\frac {1}{r_2}, \frac {1}{r_2^2}, \ldots , \frac {1}{r_\ell }, \frac {1}{r_\ell ^2})\in \mathcal {D}^{\prime }_{\leq \ell }$
.
$(\frac {1}{r_1}, \frac {1}{r_1^2},\frac {1}{r_2}, \frac {1}{r_2^2}, \ldots , \frac {1}{r_\ell }, \frac {1}{r_\ell ^2})\in \mathcal {D}^{\prime }_{\leq \ell }$
.
Proof. For a positive integer k, let
![]() $A(k)$
be the following graph constructed by Alon [Reference Alon1]:
$A(k)$
be the following graph constructed by Alon [Reference Alon1]:
![]() $A(k)$
is a triangle-free graph with
$A(k)$
is a triangle-free graph with
![]() $n=\Theta (2^{3k})$
vertices that is
$n=\Theta (2^{3k})$
vertices that is
![]() $d = \Theta (2^{2k})$
-regular and for which the second largest eigenvalue (in absolute value) is
$d = \Theta (2^{2k})$
-regular and for which the second largest eigenvalue (in absolute value) is
![]() $\Theta (2^k)$
. For each
$\Theta (2^k)$
. For each
![]() $1 \leq i \leq \ell $
, let
$1 \leq i \leq \ell $
, let
![]() $G_i(k)$
be the graph obtained by replacing each edge of
$G_i(k)$
be the graph obtained by replacing each edge of
![]() $A(k)$
by a copy of
$A(k)$
by a copy of
![]() $H_i^{\bullet \bullet }$
, identifying the two roots to the end vertices of the edge. For simplicity, write
$H_i^{\bullet \bullet }$
, identifying the two roots to the end vertices of the edge. For simplicity, write
![]() $G_i(k), A(k)$
as
$G_i(k), A(k)$
as
![]() $G_i, A$
, respectively.
$G_i, A$
, respectively.
Let G be the disjoint union of
![]() $r_i$
copies of
$r_i$
copies of
![]() $G_i$
for
$G_i$
for
![]() $1 \leq i \leq \ell $
. Let N be the number of vertices in G. We now study
$1 \leq i \leq \ell $
. Let N be the number of vertices in G. We now study
![]() $t_{\text {ind}}(\mathbf {N}_{c, H_i^{\bullet \bullet }}, G)$
. Fix i so that, by definition, we are only looking for induced copies of
$t_{\text {ind}}(\mathbf {N}_{c, H_i^{\bullet \bullet }}, G)$
. Fix i so that, by definition, we are only looking for induced copies of
![]() $H_i$
. Note that since
$H_i$
. Note that since
![]() $H_i$
contains a triangle and A is triangle-free, there is no copy of
$H_i$
contains a triangle and A is triangle-free, there is no copy of
![]() $H_i$
in A. Since
$H_i$
in A. Since
![]() $H_i$
is connected and has a vertex cut set of size at least three, each induced copy of
$H_i$
is connected and has a vertex cut set of size at least three, each induced copy of
![]() $H_i$
in G has to come from one single copy of
$H_i$
in G has to come from one single copy of
![]() $H_j$
for some j which is glued to some original edge in A. Since there is no induced copy of
$H_j$
for some j which is glued to some original edge in A. Since there is no induced copy of
![]() $H_i$
in
$H_i$
in
![]() $H_j$
for
$H_j$
for
![]() $j\neq i$
, the only induced copies of
$j\neq i$
, the only induced copies of
![]() $H_i$
has to come from
$H_i$
has to come from
![]() $G_i$
and not
$G_i$
and not
![]() $G_j$
for
$G_j$
for
![]() $j \neq i$
. Furthermore, since all induced homomorphisms from
$j \neq i$
. Furthermore, since all induced homomorphisms from
![]() $H_i$
to itself fix the set of roots, only the original edges in
$H_i$
to itself fix the set of roots, only the original edges in
![]() $A \subset G_i$
could yield an induced copy of
$A \subset G_i$
could yield an induced copy of
![]() $H_i^{\bullet \bullet }$
while identifying the end vertices of the edge to the roots (exactly one copy). Thus, by definition,
$H_i^{\bullet \bullet }$
while identifying the end vertices of the edge to the roots (exactly one copy). Thus, by definition,
![]() $M_{G, H_i^{\bullet \bullet }}$
is always zero unless
$M_{G, H_i^{\bullet \bullet }}$
is always zero unless
![]() $x,y \in [0,1]^2$
correspond to two end vertices of an edge in
$x,y \in [0,1]^2$
correspond to two end vertices of an edge in
![]() $A \subset G_i$
, in which case
$A \subset G_i$
, in which case
![]() $M_{G, H_i^{\bullet \bullet }}(x,y)=\frac {1}{N^{|V(H_i)|-2}}$
. Let
$M_{G, H_i^{\bullet \bullet }}(x,y)=\frac {1}{N^{|V(H_i)|-2}}$
. Let
![]() $\lambda _1 \geq \lambda _2 \dots $
be the eigenvalues of
$\lambda _1 \geq \lambda _2 \dots $
be the eigenvalues of
![]() $M_{G, H_i^{\bullet \bullet }}$
. Note that they are precisely the eigenvalues of A, each duplicated
$M_{G, H_i^{\bullet \bullet }}$
. Note that they are precisely the eigenvalues of A, each duplicated
![]() $r_i$
times while scaled by the same nonzero scalar. Thus, if
$r_i$
times while scaled by the same nonzero scalar. Thus, if
![]() $|\mu _1|> |\mu _2| \geq \dots $
are the eigenvalues of the adjacency matrix of graph A, then by Lemma B.2 and the properties of
$|\mu _1|> |\mu _2| \geq \dots $
are the eigenvalues of the adjacency matrix of graph A, then by Lemma B.2 and the properties of
![]() $A(k)$
, we have
$A(k)$
, we have
 $$\begin{align*}x_i(W_{G}) = \frac{r_i\sum_j \mu_j^8}{(r_i\sum_j \mu_j^4)^2} = \frac{1}{r_i}\frac{(d^8 + n O(d^{1/2})^8)}{((d^4 + n O(d^{1/2})^4))^2} = \frac{1}{r_i}\frac{d^8 + \Theta(d^{1.5}) O(d^{1/2})^8}{(d^4 + \Theta(d^{1.5}) O(d^{1/2})^4)^2} \to \frac{1}{r_i}, \end{align*}$$
$$\begin{align*}x_i(W_{G}) = \frac{r_i\sum_j \mu_j^8}{(r_i\sum_j \mu_j^4)^2} = \frac{1}{r_i}\frac{(d^8 + n O(d^{1/2})^8)}{((d^4 + n O(d^{1/2})^4))^2} = \frac{1}{r_i}\frac{d^8 + \Theta(d^{1.5}) O(d^{1/2})^8}{(d^4 + \Theta(d^{1.5}) O(d^{1/2})^4)^2} \to \frac{1}{r_i}, \end{align*}$$
where we use
![]() $d = \Theta (2^{2k})$
and
$d = \Theta (2^{2k})$
and
![]() $k \to \infty $
. Similarly, we have
$k \to \infty $
. Similarly, we have
![]() $y_i(W_G) \to 1/r_i^2$
as
$y_i(W_G) \to 1/r_i^2$
as
![]() $k \to \infty $
.
$k \to \infty $
.
There are many ways to construct graphs
![]() $H_i$
’s satisfying the assumptions in Proposition B.4. For example, one can build each
$H_i$
’s satisfying the assumptions in Proposition B.4. For example, one can build each
![]() $H_i$
from a Cayley graph, fixing two vertices as roots and then changing some of its nonneighbors to neighbors. As long as the degrees of these two roots are larger than the degrees of the other vertices, there will be no induced homomorphism from
$H_i$
from a Cayley graph, fixing two vertices as roots and then changing some of its nonneighbors to neighbors. As long as the degrees of these two roots are larger than the degrees of the other vertices, there will be no induced homomorphism from
![]() $H_i$
to itself that does not fix the set of roots. Similarly, if
$H_i$
to itself that does not fix the set of roots. Similarly, if
![]() $H_i$
and
$H_i$
and
![]() $H_j$
have different degree sequences while
$H_j$
have different degree sequences while
![]() $|V(H_i)| = |V(H_j)|$
, then there is no induced homomorphism from one to another.
$|V(H_i)| = |V(H_j)|$
, then there is no induced homomorphism from one to another.
We can now complete the proof of Theorem 1.3 using the same argument as in Subsection 2.3. Given a polynomial p in variables
![]() $x_1, \ldots , x_\ell $
, let
$x_1, \ldots , x_\ell $
, let
![]() $\bar p$
be defined in the same way as in Lemma 2.22. First, note that by the definition of
$\bar p$
be defined in the same way as in Lemma 2.22. First, note that by the definition of
![]() $t_{\text {ind}}$
, we have that for each graph H, there is a quantum graph g such that for any
$t_{\text {ind}}$
, we have that for each graph H, there is a quantum graph g such that for any
![]() $W \in \mathcal {W}$
,
$W \in \mathcal {W}$
,
![]() $t_{\text {ind}}(H, W) = t(g, W)$
. Therefore, there is a quantum graph
$t_{\text {ind}}(H, W) = t(g, W)$
. Therefore, there is a quantum graph
![]() $f(p)$
such that
$f(p)$
such that
 $$ \begin{align} t(f(p), W):= \bar{p}\left(\frac{t_{\text{ind}}(\mathbf{N}_{8,H_1^{\bullet \bullet}},W)}{t_{\text{ind}}(\mathbf{N}_{4,H_1^{\bullet \bullet}},W)^2}, \ldots, \frac{t_{\text{ind}}(\mathbf{N}_{8,H_\ell^{\bullet \bullet}},W)}{t_{\text{ind}}(\mathbf{N}_{4,H_\ell^{\bullet \bullet}},W)^2}, \frac{t_{\text{ind}}(\mathbf{N}_{12,H_1^{\bullet \bullet}},W)}{t_{\text{ind}}(\mathbf{N}_{4,H_1^{\bullet \bullet}},W)^3}, \ldots, \frac{t_{\text{ind}}(\mathbf{N}_{12,H_\ell^{\bullet \bullet}},W)}{t_{\text{ind}}(\mathbf{N}_{4,H_\ell^{\bullet \bullet}},W)^3}\right) \nonumber \\ \prod_{i=1}^\ell t_{\text{ind}}(\mathbf{N}_{4,H_\ell^{\bullet \bullet}},W)^{3\text{deg}(p)}. \end{align} $$
$$ \begin{align} t(f(p), W):= \bar{p}\left(\frac{t_{\text{ind}}(\mathbf{N}_{8,H_1^{\bullet \bullet}},W)}{t_{\text{ind}}(\mathbf{N}_{4,H_1^{\bullet \bullet}},W)^2}, \ldots, \frac{t_{\text{ind}}(\mathbf{N}_{8,H_\ell^{\bullet \bullet}},W)}{t_{\text{ind}}(\mathbf{N}_{4,H_\ell^{\bullet \bullet}},W)^2}, \frac{t_{\text{ind}}(\mathbf{N}_{12,H_1^{\bullet \bullet}},W)}{t_{\text{ind}}(\mathbf{N}_{4,H_1^{\bullet \bullet}},W)^3}, \ldots, \frac{t_{\text{ind}}(\mathbf{N}_{12,H_\ell^{\bullet \bullet}},W)}{t_{\text{ind}}(\mathbf{N}_{4,H_\ell^{\bullet \bullet}},W)^3}\right) \nonumber \\ \prod_{i=1}^\ell t_{\text{ind}}(\mathbf{N}_{4,H_\ell^{\bullet \bullet}},W)^{3\text{deg}(p)}. \end{align} $$
Then the rest of the proof follows from the same argument as in Subsection 2.3.
Competing interest
The authors have no competing interest to declare.
Funding statement
Grigoriy Blekherman was partially supported by NSF grant DMS-1901950. Annie Raymond was partially supported by NSF grant DMS-2054404. Fan Wei was partially supported by NSF grants DMS-2401414 and DMS-2404167.