Diet–animal fractionation of nitrogen stable isotopes reflects the efficiency of nitrogen assimilation in ruminants

Abstract

The natural abundance of ¹⁵N in animal proteins (δ¹⁵N_animal) is greater than that in the diet consumed by the animals (δ¹⁵N_diet), with a discrimination factor (Δ¹⁵N = δ¹⁵N_animal− δ¹⁵N_diet) that is known to vary according to nutritional conditions. The objectives of the present study were to test the hypothesis that Δ¹⁵N variations depend on the efficiency of nitrogen utilisation (ENU) in growing beef cattle, and to identify some of the physiological mechanisms responsible for this N isotopic fractionation in ruminants. Thus, we performed the regression of the Δ¹⁵N of plasma proteins obtained from thirty-five finishing beef cattle fed standard and non-conventional diets against different feed efficiency indices, including ENU. We also performed the regression of the Δ¹⁵N of different ruminant N pools (plasma and milk proteins, urine and faeces) against different splanchnic N fluxes obtained from multi-catheterised lactating dairy cows. The Δ¹⁵N of plasma proteins was negatively correlated with feed efficiency indices in beef cattle, especially ENU (body protein gain/N intake) and efficiency of metabolisable protein (MP) utilisation (body protein gain/MP intake). Although Δ¹⁵N obtained from different N pools in dairy cows were all negatively correlated with ENU, the highest correlation was found when Δ¹⁵N was calculated from plasma proteins. Δ¹⁵N showed no correlation with urea-N recycling or rumen NH₃ absorption, but exhibited a strong correlation with liver urea synthesis and splanchnic amino acid metabolism, which points to a dominant role of splanchnic tissues in the present N isotopic fractionation study.

The human population is expected to increase about 34 % by 2050, creating a 50 % increase in the demand for dairy and beef products on existing natural and land resources^{( 1 )}. In this context, current livestock production systems need to evolve towards improving the efficiency with which ruminants transform feeds into foods (feed conversion efficiency (FCE); body-weight (BW) gain or milk yield/DM intake), which is lower and more variable than in other farmed species^{( 2 )}. However, in practice, assessing animal FCE is costly and laborious, mainly due to the need to accurately quantify individual feed intakes over a long period.

The efficiency of nitrogen utilisation (ENU; animal N gain or milk N secretion/N intake) is an important component of FCE in growing beef cattle^{( 3 )} and dairy cows^{( 4 )}, and is also directly related to environmental N pollution associated with livestock production^{( 5 )}. However, ENU is even more laborious and difficult to measure than FCE because it also requires analysis of feed N content, refusal N content, and animal BW gain or milk yield. Predictions of ENU require good knowledge of the multiple factors that affect N partitioning across digestive and metabolic compartments, or alternatively the use of indicators that reflect N utilisation at rumen and whole-body levels.

N naturally exists in the form of two stable isotopes, i.e. light ¹⁴N and the far less abundant heavy ¹⁵N. It has long been known that the natural relative abundance of ¹⁵N (δ¹⁵N) in human or animal tissues is greater than that in the diet they consume^{( 6 , 7 )}. This diet–animal ¹⁵N fractionation or δ¹⁵N difference between an individual and its diet (Δ¹⁵N = δ¹⁵N_animal− δ¹⁵N_diet) has traditionally been considered relatively constant (the so-called ‘trophic shift’: Δ¹⁵N approximately 3·4 ‰^{( 8 )}), allowing ecologists to infer ‘what-eats-what’ within the food web and thus elucidate part of the trophic structure of the ecosystem. However, results from the last few decades have shown high variability in Δ¹⁵N in response to a variety of nutritional and physiopathological conditions in human subjects and animals^{( 9 , 10 )} that is sometimes even higher than the assumed value of the trophic shift^{( 11 )}. This may suggest that Δ¹⁵N variations could reflect modulations of certain N metabolic fluxes induced by different environmental conditions. In the last few years, Δ¹⁵N has been related to protein gain in pregnant women^{( 12 )} and efficiency of feed N conversion to body protein in monogastric animals^{( 13 – 15 )}. After first emerging as a promising biomarker of N partitioning in ruminants^{( 16 , 17 )}, this same methodology has successfully been applied to predict ENU in lactating dairy cows^{( 18 )} and to predict FCE in growing cattle fed a unique diet^{( 3 )}. However, other well-controlled ruminant experiments^{( 19 , 20 )} have found no relationship between ENU and Δ¹⁵N, highlighting the need for further research. Despite the huge potential value of Δ¹⁵N in a range of scientific investigations, there has been little focus on the underlying physiological and biochemical mechanisms^{( 21 )}. Many authors, especially ecologists, have stressed the need to understand the physiological basis of diet–animal ¹⁵N fractionation^{( 9 – 11 , 22 )} by identifying the fractionating pathways involved so as to better understand the underlying mechanisms and significance of Δ¹⁵N variability^{( 23 )}. Thus, we set out to (1) demonstrate a relationship between Δ¹⁵N and ENU in growing beef cattle fed contrasting diets used in livestock farming, and (2) identify some of the potential physiological mechanisms responsible for the diet–animal fractionation of N stable isotopes by means of a metabolic experiment using multi-catheterised dairy cows. To achieve these goals, we used samples and individual data from two published experiments^{( 24 , 25 )}.

Materials and methods

The experiments were conducted in compliance with the National Legislation on Animal Care (Certificate of Authorization to Experiment on Living Animals, No. 004495, Ministry of Agriculture, France).

Expt 1 (beef cattle)

A total of thirty-six post-weaning Charolais young bulls (initial BW 360 (sem 33) kg, average age approximately 8 months) were used in a randomised complete block design experiment. After weaning, animals were allotted into four homogeneous groups (n 9 per group) according to pre-weaning performances. Each group was randomly assigned to one of four experimental diets, which were based on two silage types (S), either maize silage or pre-wilted grass silage. Diets were iso-net energy and iso-crude protein (CP) in composition but supplied at two different intake levels (I; ad libitum (high) v. restricted (low)) to promote theoretical average daily gains of 1600 and 1400 g/d, respectively, according to the INRA (Institut National de la Recherche Agronomique) feeding system^{( 26 )}. Restricted intake levels were achieved by limiting concentrate supply, with forage supplied ad libitum in all the four dietary treatments. Diets based on maize silage were supplemented with a standard concentrate (on average, 19 % maize grain, 37 % wheat, 40 % rapeseed meal and 2 % urea, on a DM basis), while diets based on grass silage were supplemented with by-products (on average, 54 % citrus pulp and 44 % wheat-based dry distiller grains, on a DM basis). The animals were housed in free stalls equipped with electronic gates (Dairy gate^®; EFEI) to measure individual daily feed intake. Forages were distributed once daily, whereas concentrates were supplied twice at about 08.00 and 16.00 hours. The experiment was preceded by a 4-week transition period to allow the animals to adapt to the treatment diets. All the young bulls were slaughtered at a carcass weight constant endpoint (420 (sem 11) kg, corresponding to 705 (sem 22) kg live weight), and, therefore, average time to slaughter varied according to the treatment diets from 202 to 251 d. The first bull slaughtered was on 21 May, and from then on, four to six bulls were slaughtered every week until 3 July. Average feed efficiencies for each dietary treatment have been reported previously in Sepchat et al. ^{( 24 )}, and individual values were used here for correlation analysis with isotopic measurements.

The animals were weighed and feeds were individually sampled fortnightly. Daily amounts of forages and concentrates as well as individual refusals, if any, were precisely weighed to calculate individual feed intakes throughout the experiment. DM was measured twice per week for ingredients and daily for refusals (103°C, 48 h). Feed samples pooled over the whole experiment were stored at − 20°C before analysis.

Subcutaneous adipose tissue was sampled to determine the diameter of adipose cells and, thus, the empty body fat weight at the beginning of the trial. At baseline, all animals were biopsied from the middle of a triangle formed by the tail base, ischial tuberosity and last lumbar vertebrae under local anaesthesia (4 ml Lidocaine^®/cow).

Blood samples from all animals were collected by jugular venepuncture the day before the first slaughter using a 10 ml blood Vacutainer tube containing sodium heparin. Blood samples were immediately stored on ice until centrifugation (2500  g for 20 min at 4°C) to separate the plasma, which was stored at − 80°C until plasma protein isolation and N isotopic analysis of natural abundance.

At slaughter, empty BW and carcass weight were recorded. Kidneys, heart and pelvic fat (visceral fat) as well as subcutaneous fat were removed and weighed to measure the fat content of the non-carcass compartment. Tissue dissection of the sixth rib was conducted to estimate carcass fat content according to the method described by Robelin & Geay^{( 27 )}.

Expt 2 (dairy cows)

A total of five multiparous Jersey cows in mid-lactation, averaging 365 (sem 28) kg BW and 78 (sem 12) d in milk at the onset of the experiment were used in a 4 × 4 Latin square design, with the fifth cow used as an extra observation^{( 25 )}. Chronic indwelling catheters were surgically implanted into the major splanchnic vessels before peak lactation. We formulated four isoenergetic diets to test the effects of dietary CP content (low (12·0 %) and normal (16·5 %)) and dietary carbohydrate composition (CHO; 350 g starch and 310 g neutral detergent fibre/kg DM (starch diets), and 45 g starch and 460 g neutral detergent fibre/kg DM (fibre diets)). Diet composition, feed distribution, infusions and sampling procedures have been detailed in Cantalapiedra-Hijar et al. ^{( 25 )}. The dairy cows were subjected to four experimental periods lasting 27 d each. Average net splanchnic fluxes of nitrogenous fractions as well as milk N efficiency have been reported in the study of Cantalapiedra-Hijar et al. ^{( 25 )}. Individual values were used here for the analysis of correlations with isotopic measurements. Measured net portal fluxes of NH₃-N and urea-N are considered here as proxies for rumen NH₃ absorption and urea-N recycling^{( 28 )}, respectively, while the net hepatic flux of urea-N and the splanchnic irreversible loss rate of amino acids are termed ‘liver urea synthesis’ and ‘splanchnic amino acid metabolism’, respectively.

Amino acid flux (irreversible loss rate or unidirectional flux representing the amino acid flux towards protein synthesis and oxidation) metabolised by the splanchnic tissues (portal-drained viscera (PDV) and liver) was measured using an isotopic dilution method with continuous infusion of [1-¹³C]Leu and [²H₅]Phe^{( 29 )}. On day 26 of each period, a silicone rubber catheter was inserted into one jugular vein, and on day 27, a sterile solution containing 9·0 g/l of [1-¹³C]Leu and 4·2 g/l of [²H₅]Phe (99 atom % excess; Cambridge Isotope Laboratories, Inc.) was infused (Harvard apparatus, Models 22 and PHD2000) via a jugular catheter at the rate of 2·5 (sem 0·14) mmol/h for 8 h (08.00 to 16.00 hours) after a priming dose of 2·5 mmol. Blood was collected from the mesenteric artery and from portal and hepatic veins into heparinised syringes twice during the hour preceding the infusion and then hourly from 3 to 8 h after the start of tracer infusion to determine plasma free [1-¹³C]Leu and [²H₅]Phe enrichments by GC–MS. In addition, blood from the mesenteric artery, urine (acidified (pH < 2) with 1000 ml of 1·9 m-H₂SO₄), faeces and milk were also collected before the tracer infusion.

Laboratory analysis

Adipose tissue samples were fixed with OsO₄, as described previously^{( 30 )}. Adipocytes were dispersed in 8 m-urea solution and examined by microscopy to determine the diameter of approximately 300 adipose cells.

Before analysis, feed and refusal samples were thawed, dried at 60°C for 48 h and ground to 1 mm. The DM and Kjeldahl N contents of the samples were determined according to the Association of Official Analytical Chemists^{( 31 )}. Dietary metabolisable protein (MP) contents were calculated from the chemical composition of the analysed ingredients^{( 26 )}.

For metabolic tracer analysis across the splanchnic tissues, plasma free [²H₅]Phe and [1-¹³C]Leu enrichments were determined by GC–MS (Trace GC/Automass Multi, Thermofinnigan) after isolation of amino acids by cation exchange (AG-50 H+ resin; Bio-Rad). Before isotopic analysis of natural abundance levels, plasma and milk samples stored at − 80°C were thawed at 4°C overnight and their protein fraction was isolated by precipitation with sulfosalicylic acid (200 μl into 2 ml of sample; 1 g/ml). After 1 h storage at 4°C and centrifugation (4500  g for 20 min at 4°C), the supernatant and pellet were separated. The pellet was rinsed three times with MilliQ water and then freeze-dried. Furthermore, bulk faecal and urine samples were analysed for N stable isotopic analysis of natural abundance (δ¹⁵N).

Alanine aminotransferase and aspartate aminotransferase plasma concentrations were analysed enzymatically using kinetic test kits (RC1160-04 and RC1157-02, respectively) provided by Sobioda.

Natural abundance analysis of nitrogen stable isotopes

The N stable isotopic composition (δ¹⁵N, i.e. natural relative abundance of the rare stable isotope of N) of plasma protein and diet ingredients (dairy cow and beef cattle experiments) and of milk protein, faeces and urine (dairy cow experiment) was determined using an isotope-ratio mass spectrometer (Isoprime; VG Instruments) coupled to an elemental analyser (EA Vario Micro Cube; Elementar). Internal standards (tyrosine) were included in every run to correct for possible variations in the raw values determined by the mass spectrometer. Typical replicate measurement errors for these reference materials were ± 0·1 ‰. Results are expressed using the delta notation according to the following equation:

$$\begin{eqnarray} \delta ^{15}N = (( R _{sample}/ R _{standard}) - 1)\times 1000, \end{eqnarray}$$

where R _sample and R _standard are the N isotope ratio between the heavier isotope and the lighter isotope (¹⁵N:¹⁴N) for the sample being analysed and the internationally defined standard (atmospheric N₂, R _standard= 0·0036765), respectively, and δ is the delta notation in parts per 1000 (‰) relative to the standard. The N percentages in the metabolic pools and diet ingredients analysed by elemental analyser-isotope ratio mass spectrometry (EA-IRMS) were determined using the elemental analyser, with tyrosine as the standard.

Calculations and statistical analysis

Protein gain

At the onset of the experiment, empty body weight (EBW₀) was estimated from live weight (LW₀) according to the allometric equation proposed by Robelin & Daenicke^{( 32 )}. Total adipose tissue weight (TAD₀, kg) and empty body lipid weight (LIP₀, kg) were estimated via the adipose cell diameter (ACD) using equations proposed by Garcia & Agabriel^{( 33 )}, i.e.

$$\begin{eqnarray} TAD_{0} = 5.211\times exp^{(0.0114\,\times \,ACD)}, \end{eqnarray}$$

$$\begin{eqnarray} LIP_{0} = 1 .134\times TAD _{0}^{0.992}. \end{eqnarray}$$

Empty body protein weight at the onset of the experiment (PROT₀, kg) was calculated from EBW₀ and LIP₀ as follows:

$$\begin{eqnarray} PROT_{0} = 0.2\times (EBW_{0} - LIP_{0}). \end{eqnarray}$$

Carcass fat content was estimated from the tissue dissection of the sixth rib^{( 27 )} and the measured EBW₀ and fat content of the non-carcass compartment. Total adipose tissue weight at slaughter (TAD₁) equals measured non-carcass fat content plus estimated carcass fat content. Empty body protein weight at slaughter (PROT₁, kg) was deduced from TAD₁ as indicated before. Whole-body protein gain was finally calculated as PROT₁− PROT₀.

Feed efficiency indices

The theoretical MP requirement for maintenance in the beef cattle experiment was calculated as 3·25 g of MP/kg of mean metabolic BW throughout the experiment^{( 26 )} whereas the MP intake available for protein gain was calculated as MP intake minus theoretical MP for maintenance. Energy-corrected milk yield (ECM, kg/d) in the dairy experiment was calculated to account for differences in milk composition (g/d) as follows:

$$\begin{eqnarray} ECM = ((0.038)\times crude fat + 0.024\times CP + 0.017\times lactose)/3.14. \end{eqnarray}$$

FCE was calculated as whole-body gain (beef) or ECM yield (dairy) divided by DM intake. ENU was calculated as total whole-body protein gain (beef) or milk N yield (dairy) per feed N intake. The efficiency of metabolisable energy utilisation (EMEU) or efficiency of metabolisable protein utilisation (EMPU) was calculated similarly, but the input is expressed as metabolisable energy and MP intake, respectively. Finally, the efficiency of metabolisable protein utilisation for gain (EMPUg) was calculated as whole-body protein gain divided by MP intake available for growth.

Isotopic measures

The irreversible loss rate of leucine in the PDV and phenylalanine in the liver was calculated as detailed in Savary-Auzeloux et al. ^{( 29 )}, taking the artery and hepatic vein as the amino acid precursor pool for PDV and liver measures, respectively.

Δ¹⁵N was calculated as δ¹⁵N of the considered pool (plasma and milk proteins, urine and faeces) minus δ¹⁵N of the diet, where δ¹⁵N of the diet was calculated as the average of δ¹⁵N of each ingredient weighted by the percentage of N the ingredient represents in the diet.

Statistical analyses

All statistical analyses were performed using R software (version 3·0·1)^{( 34 )}. For the beef cattle experiment, a linear model was used as follows:

$$\begin{eqnarray} Y _{ ij } = \mu + S _{ i } + I _{ j } + S \times I _{ ij } + \varepsilon _{ ij }, \end{eqnarray}$$

where Y _ij is the dependent variable; μ is the overall mean; S _i is the fixed effect of silage type (maize v. grass); I _j is the fixed effect of intake level (low v. high); S× I _ij is the fixed effect of the interaction between S and I; and ε _ij is the random residual error. For the dairy cow experiment, a mixed linear model that included a random intercept term for each animal was used. The mixed model was fitted using the lme procedure within the nlme package. Statistical analyses were carried out as a 4 × 4 Latin square, following the model:

$$\begin{eqnarray} Y _{ ijkl } = \mu + P _{ i } + C _{ j } + CHO_{ k } + CP_{ l } + CHO\times CP_{ kl } + \varepsilon _{ ijkl }, \end{eqnarray}$$

where Y _ijkl is the dependent variable; μ is the overall mean; P _i is the fixed effect of the experimental period i= 1–4; C _j is the random effect of cow j= 1–5; CHO _k is the fixed effect of dietary carbohydrate composition (starch v. fibre); CP _l is the fixed effect of dietary CP level (12·0 v. 16·5 %); CHO × CP_kl is the fixed effect of the interaction between CHO and CP; and ε_ijkl is the random residual error. Mean values are reported as least-squares means with pooled standard error values due to missing observations.

For both experiments, when the interaction between main effects was significant the dietary treatment means were compared using Tukey's honest significant difference (HSD) multiple comparison. The significance of treatment effect was set at P< 0·05.

Regression analysis between observed (non-adjusted) data of Δ¹⁵N measured in different N pools and feed efficiency indices and other metabolic measures was performed using the lm procedure in R. The cut-off value suggesting that an observation is an extreme outlier was set at DFFITS (difference in fit, standardised) >2√(p/n), where p is the number of parameters estimated in the model and n is the total number of observations. Because no significant quadratic effect was found for any relationship (P>0·10), all results presented here were derived from linear regression analysis.

Results

Expt 1 (beef cattle)

Of the initial thirty-six animals, one did not finish the experiment due to health problems and another was removed from the final statistical analysis because it was considered an outlier according to the DFFITS analysis (n 34).

As shown in Table 1, diets based on maize silage had higher (P< 0·001) δ¹⁵N values and promoted higher (P< 0·001) δ¹⁵N of plasma proteins and lower (P< 0·001) N isotopic fractionation of plasma proteins (Δ¹⁵N_{plasma protein}= δ¹⁵N_animal− δ¹⁵N_diet) compared with diets based on grass silage. Diets supplied at a high intake level had lower (P< 0·001) δ¹⁵N values compared with diets supplied at a low intake level but only with diets based on maize silage (S× I; P< 0·001). There was no effect of I on δ¹⁵N of plasma proteins (P= 0·98) nor on Δ¹⁵N_{plasma protein} (P= 0·58), but differences across intake levels were different between maize and grass silage (S× I; P≤ 0·02). A difference of 0·82 ‰ was found between the diets with the lowest (maize silage at a low intake level) and highest (grass silage at a low intake level) Δ¹⁵N_{plasma protein} mean values.

Table 1 Nitrogen isotopic fractionation (δ¹⁵N_{plasma protein}−δ¹⁵N_diet) in beef cattle fed the experimental diets (Mean values with their standard errors)

S, effect of silage type (maize v. grass); I, effect of intake level (low v. high).

^a,b,cMean values within a row with unlike superscript letters were significantly different (P< 0·05).

Table 2 shows the coefficient of correlation between several feed efficiency indices and Δ¹⁵N_{plasma protein} obtained in growing beef cattle fed the experimental diets. All feed efficiency variables were positively correlated with each other. In our experimental conditions (classical and non-conventional growing beef diets at two feeding levels), almost two-thirds of variation in FCE was explained by a simple linear model based on ENU (FCE = 0·074( ± 0·013)+0·418( ± 0·056) × ENUG; r ² 0·63; P< 0·001), and this correlation was slightly improved when using metabolic efficiencies (EMEU, EMPU and EMPUg, 0·82 ≤ r≤ 0·85). Δ¹⁵N_{plasma protein} averaged 3·56 ‰, and showed a significant (P< 0·001) and negative correlation with FCE (r − 0·66), ENU (r − 0·72), EMPU (r − 0·78) and EMPUg (r − 0·82). In contrast, Δ¹⁵N_{plasma protein} showed a significant (P= 0·002) but weaker correlation with EMEU (r − 0·51). Figure 1 shows how Δ¹⁵N_{plasma protein} decreased as ENU and EMPUg increased (P< 0·001; 0·72 ≤ r≤ 0·82) in beef cattle: the more efficiently the beef cattle used dietary protein and MP, the lower the δ¹⁵N difference between plasma proteins and diet (Δ¹⁵N_{plasma protein}).

Table 2 Relationships between nitrogen isotopic fractionation of plasma proteins (Δ¹⁵N_{plasma protein}=δ¹⁵N_{plasma proteins}−δ¹⁵N_diet) and different feed efficiency indices in growing beef cattle (Mean values with their standard errors, n 34)

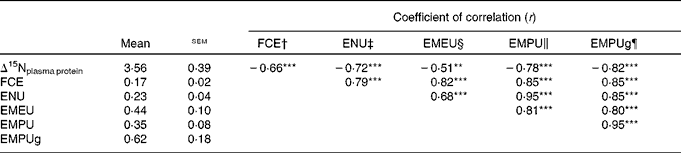
FCE, feed conversion efficiency; ENU, efficiency of N utilisation; EMEU, efficiency of metabolisable energy utilisation; EMPU, efficiency of metabolisable protein utilisation; EMPUg, efficiency of metabolisable protein utilisation for protein gain.

** P< 0·01, *** P< 0·001.

† FCE = body-weight gain/DM intake.

‡ ENU = body protein gain/crude protein intake.

§ EMEU = body net energy gain/metabolisable energy intake.

∥ EMPU = body protein gain/metabolisable protein intake.

¶ EMPUg = body protein gain/(metabolisable protein intake − metabolisable protein requirement for maintenance).

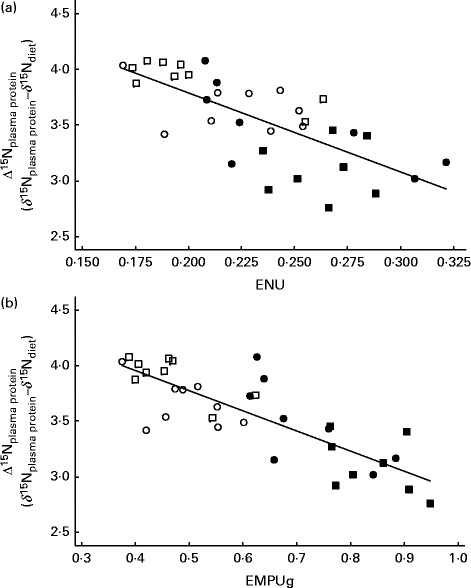
Fig. 1 Relationships between ¹⁵N enrichment over diet of plasma proteins (Δ¹⁵N_{plasma protein}) and (a) efficiency of N utilisation (ENU; body protein gain/crude protein intake) and (b) efficiency of metabolisable protein utilisation for protein gain (EMPUg; body protein gain/(metabolisable protein intake − metabolisable protein requirement for maintenance)) in growing beef cattle. Fitted equations are as follows: Δ¹⁵N_{plasma protein}= 5·21( ± 0·28) − 7·11( ± 1·19) × ENU (n 34; P< 0·001; r ² 0·52; residual SE (RSE) = 0·277) and Δ¹⁵N_{plasma protein}= 4·68( ± 0·14) − 1·82( ± 1·22) × EMPUg (n 34; P< 0·001; r ² 0·68; RSE = 0·224). ■, Diet based on maize silage at a low intake level; ●, diet based on maize silage at a high intake level; □, diet based on pre-wilted grass silage at a low intake level; ○, diet based on pre-wilted grass silage at a high intake level.

Expt 2 (dairy cows)

All available data from the original experiment were used for the regression analysis, except for ENU and liver urea synthesis where one data for each was declared an extreme outlier based on the DFFITS analysis (therefore, n 18 for ENU and n 15 for liver urea synthesis). The effect of period was not significant (P>0·05; data not shown) for any of the studied variables.

As shown in Table 3, starch diets had higher (P≤ 0·001) δ¹⁵N values and promoted higher δ¹⁵N of plasma and milk proteins (P≤ 0·006) and lower Δ¹⁵N_{plasma protein} (P= 0·008) and Δ¹⁵N_urine (P= 0·02) compared with fibre diets. A trend for starch diets to promote lower Δ¹⁵N_faeces compared with fibre diets was also found (P= 0·06). CHO affected neither the δ¹⁵N values of faeces and urine nor the Δ¹⁵N_{milk protein} values (P= 0·22). Low-CP diets (12·0 %CP) had higher (P< 0·001) δ¹⁵N values and promoted lower Δ¹⁵N of plasma and milk proteins (P≤ 0·003), faeces and urine (P= 0·08) compared with normal-CP diets (16·5 % CP).

Table 3 Nitrogen isotopic fractionation (δ¹⁵N_animal−δ¹⁵N_diet, ‰) from different animal pools in lactating dairy cows fed the experimental diets (Least-squares mean values with their pooled standard errors)

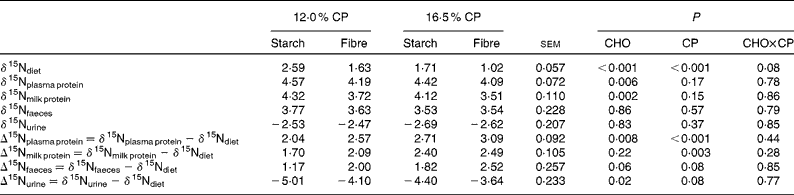
CHO, effect of dietary carbohydrate composition (starch v. fibre); CP, effect of crude protein (CP) level (12·0 % CP v. 16·5 % CP).

As shown in Table 4, Δ¹⁵N_{plasma protein} and Δ¹⁵N_{milk protein} averaged 2·60 (sem 0·44) and 2·18 (sem 0·38) ‰, respectively, and showed no significant correlation (P≥ 0. 14) with FCE (ECM yield/kg DM intake), but a strong negative correlation with ENU (r − 0·91 and − 0·74, respectively; P< 0·001). Urine was depleted (Δ¹⁵N_urine= − 4·32 (sem 0·7) ‰) and faeces were enriched (Δ¹⁵N_faeces= 1·86 (sem 0·69) ‰) in ¹⁵N compared with original diet contents, and the Δ¹⁵N of these two N excretion pools were also negatively correlated with ENU (P< 0·001, r − 0·76 and − 0·73, respectively) and not correlated with FCE (P≥ 0·12). Measures of Δ¹⁵N from different ruminant N pools were all significantly and positively correlated (0·48 ≤ r≤ 0·82), but the Δ¹⁵N of plasma proteins gave the best correlation with ENU (r − 0·91). The relationships between ENU and Δ¹⁵N of plasma and milk proteins are shown in Fig. 2, together with the relationships between ENU and Δ¹⁵N in the urine and faeces. Thus, the more efficiently the dairy cow transformed feed N into milk protein, the lower its Δ¹⁵N values in all of the ruminant N pools analysed (plasma and milk proteins, faeces and urine).

Table 4 Relationships between nitrogen isotopic fractionation of different nitrogen pools (Δ¹⁵N=δ¹⁵N_animal−δ¹⁵N_diet) and their relationships with feed efficiency in dairy cows (Mean values with their standard errors)

* P< 0·05, *** P< 0·001.

† FCE = energy-corrected milk yield/feed DM intake.

‡ ENU = milk N yield/feed N intake.

Fig. 2 ¹⁵N enrichment or depletion over diet of (a) animal protein (plasma protein (Δ¹⁵N_{plasma protein}) and milk protein (Δ¹⁵N_{milk protein})) and (b) nitrogen excretion pools (urine (Δ¹⁵N_urine) and faeces (Δ¹⁵N_faeces)) according to the efficiency of nitrogen utilisation (ENU; milk N/N intake) in lactating dairy cows. ■, 12·0 % CP-starch diet; ●, 12·0 % CP-fibre diet; □, 16·5 % CP-starch diet; ○, 16·5 % CP-fibre diet. Regression equations (n 18) are as follows: (1) Δ¹⁵N_{plasma protein}= 6·43( ± 0·45) − 12·0( ± 1·39) × ENU (r ² 0·82; RSE = 0·192; P< 0·001); (2) Δ¹⁵N_{milk protein}= 4·92( ± 0·64) − 8·58( ± 2·0) × ENU (r ² 0·54; RSE = 0·275; P< 0·001); (3) Δ¹⁵N_faeces= 7·11( ± 1·08) − 16·4( ± 3·37) × ENU (r ² 0·60; RSE = 0·465; P< 0·001); (4) Δ¹⁵N_urine= 0·76( ± 1·09) − 15·8( ± 3·39) × ENU (r ² 0·58; RSE = 0·468; P< 0·001).

In addition, as shown in Table 5, Δ¹⁵N_{plasma protein} showed a significant and positive correlation with liver urea synthesis (r 0·77, P< 0·001) and splanchnic amino acid metabolism (0·79 ≤ r≤ 0·84; P< 0·001, on its correlation with the amino acid flux towards protein synthesis and oxidation measured as the irreversible loss rate of leucine and phenylalanine across the PDV and liver, respectively). In contrast, no significant relationship was found between Δ¹⁵N_{plasma protein} and rumen NH₃-N absorption (net portal flux of NH₃-N; r 0·42; P= 0·07) or urea-N recycling (net portal flux of urea-N; r 0·35; P= 0·14). Figure 3 shows how Δ¹⁵N_{plasma protein} increased (P< 0·001) as liver urea synthesis and splanchnic metabolic utilisation of amino acids increased. Despite good correlations between Δ¹⁵N and hepatic ureagenesis, no correlation (0·08 ≤ r≤ 0·12; P≥ 0·619) was found, as determined by the regression of Δ¹⁵N against plasma activities of the main transaminases (alanine and aspartate transaminases).

Table 5 Relationships between the nitrogen isotopic fractionation of plasma proteins (Δ¹⁵N_{plasma protein}) and nitrogen fluxes in lactating dairy cows*

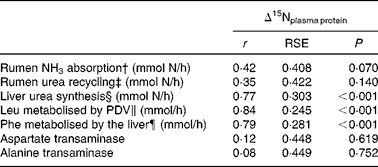
* n 19 except for ENU (n 18), liver urea-N synthesis (n 15) and Phe metabolised by the liver (n 16).

† Net portal flux of NH₃-N.

‡ Net portal flux of urea-N.

§ Net hepatic flux of urea-N.

∥ Irreversible loss rate of leucine across the portal-drained viscera.

¶ Irreversible loss rate of phenylalanine across the liver.

Fig. 3 Relationships between ¹⁵N enrichment over diet of plasma proteins (Δ¹⁵N_{plasma protein}) and (a) liver urea synthesis, (b) leucine metabolised by the portal-drained viscera (Leu ILR-PDV) and (c) phenylalanine metabolised by the liver (Phe ILR-Liver). ■, 12·0 % CP-starch diet; ●, 12·0 % CP-fibre diet; □, 16·5 % CP-starch diet; ○, 16·5 % CP-fibre diet. Fitted equations are as follows: Δ¹⁵N_{plasma protein}= 1·39( ± 0·29)+0·0081 ( ± 0·0019) × liver urea synthesis (n 15; r ² 0·59; P< 0·001); Δ¹⁵N_{plasma protein}= 1·49( ± 0·19)+0·076( ± 0·012) × Leu ILR-PDV (n 19; r ² 0·71; P< 0·001); Δ¹⁵N_{plasma protein}= 0·86( ± 0·37)+0·160( ± 0·034) × Phe ILR-Liver (n 16; r ² 0·63; P< 0·001).

Discussion

Δ¹⁵N of animal proteins and efficiency of nitrogen utilisation

As expected from other ruminant^{( 18 , 35 , 36 )} and non-ruminant^{( 14 , 15 )} studies, animal proteins were naturally ¹⁵N-enriched relative to diet, with mean trophic shift values in line with previous observations in dairy cows (2·37 ‰^{( 36 )} and 3·19 ‰^{( 18 )}) and growing cattle (3·58^{( 3 )} and 3·8^{( 37 )}). The results found herein for beef cattle and confirmed for dairy cows^{( 18 )} demonstrated that the efficiency with which feed N is assimilated into animal proteins is negatively correlated with the N isotopic fractionation (i.e. the δ¹⁵N difference) between animal proteins and animal diet. In fact, diets in the present study were ranked in terms of Δ¹⁵N similarly to the reported ENU in the beef cattle^{( 24 )} and dairy cow^{( 25 )} experiments. This explains, for instance, why an S× I interaction effect was found in beef cattle for Δ¹⁵N_{plasma protein} or why the dietary CP level significantly affected Δ¹⁵N_{plasma protein} and Δ¹⁵N_{milk protein} in dairy cows. Thus, the more efficiently the animals utilise dietary N, the closer the δ¹⁵N values between animal proteins and diet (i.e. the lower the trophic shift). In this sense, higher Δ¹⁵N values have been reported as ruminants were fed high- v. low-N diets^{( 11 , 38 )} in accordance with the expected lower ENU as N intake increases in cattle^{( 39 )}. Likewise, Δ¹⁵N has been positively correlated with N intake in non-ruminant species^{( 21 )} and negatively to efficiency of protein accretion in fish^{( 14 )}. This may suggest that variations in Δ¹⁵N could be primarily driven by the efficiency with which dietary N is assimilated into animal proteins. Known factors affecting Δ¹⁵N, such as dietary protein quality and quantity^{( 10 , 11 , 15 )}, habitat and climate^{( 40 )}, physiological state or pathological conditions^{( 41 , 42 )}, could, therefore, all have an impact on Δ¹⁵N via changes in the efficiency of N assimilation into animal proteins through a shift in the relative partitioning of dietary N into anabolic v. catabolic pathways.

The period of time elapsed between a diet shift, and the sampling of animal proteins is an important issue when analysing Δ¹⁵N data. Indeed, isotopic data should be interpreted with caution when this period of time is not long enough to allow animal tissues to incorporate the isotopic composition of the new diet through their specific protein turnover rates^{( 15 )}. This might be the case in cross-over design experiments with short experimental periods similar to the dairy cow experiment conducted in the present study (with four successive diet-shift periods lasting 27 d each) as well as other ruminant studies reported in the literature^{( 19 , 20 )}. In such cases, there could be a potential bias if the Δ¹⁵N measurements at the end of each successive diet shift are significantly influenced by the initial isotopic values (i.e. memory effect). However, assuming a fractional synthesis rate of plasma proteins in ruminants ranging from 6·5^{( 43 )} to 11·5 %/d^{( 44 )}, the calculated proportion of isotopic equilibrium reached after 27 d from the last diet shift would range from 83 to 96 % for our non-growing dairy cows according to the classical single-compartment first-order kinetic model used to describe isotopic trajectories^{( 45 )}. These estimates are in line with predictions of a recently developed multi-compartmental model^{( 46 )}: Δ¹⁵N values of plasma proteins, faeces and urine should have reached 80–90 % of their final isotopic equilibrium values at 27 d post-diet shift. This non-steady state condition has probably not biased the present results as only a minor fraction of the sampled pools (less than 20 % in all cases) did not actually reflect metabolic adaptations to the diet being tested, but adaptations to the previous diet due to a memory effect. In contrast, this limitation would not apply for the beef cattle experiment, since the period of time used between the diet shift and blood sampling (230 d) was long enough to ensure that plasma proteins has reached isotopic equilibrium^{( 47 )}. Future research on isotopic fractionation of ¹⁵N in ruminants should respect a minimum of 45 d post-diet shift before blood sampling in order to ensure isotopic equilibrium (time frame necessary to reach 95 % of isotopic equilibrium assuming a value of 6·5 %/d for plasma protein turnover).

Mechanisms involved in ¹⁵N fractionation in ruminants

Ruminants, unlike monogastric species, can show substantial N isotopic fractionation during digestion^{( 17 , 34 , 35 )}, and this has been cited as one of the main reasons why Δ¹⁵N has not always correlated with efficiency of N assimilation in ruminant experiments^{( 16 , 19 , 20 )}. The fact that Δ¹⁵N_{plasma protein} showed no correlation with rumen NH₃-N absorption or urea-N recycling was unexpected^{( 17 , 23 )}, and could indicate that under our experimental conditions, most of the Δ¹⁵N variability originated from animal metabolism rather than rumen N efficiency (microbial protein synthesis/rumen available N^{( 42 )}) or urea-N recycling.

It has been speculated^{( 34 )} and demonstrated in vitro ^{( 17 )} that rumen bacteria preferentially use ¹⁴N- over ¹⁵N-NH₃ to synthesise their own proteins, leading to higher absorption of ¹⁵N-enriched NH₃ (and thus urea-N excreted in the urine) and ¹⁵N-depleted microbial protein (and thus absorbed amino acids and eventually body proteins) as NH₃ taken up by rumen bacteria (i.e. rumen N efficiency) increases. Moreover, as N isotopic fractionation only takes place during the incorporation of NH₃-N into bacterial proteins^{( 17 )}, the use of preformed amino acids and peptides rather than NH₃ for microbial protein synthesis would further decrease the isotopic fractionation. Only about 20 % of bacterial protein is derived from non-NH₃ sources at typical rumen conditions^{( 48 )}; however, an increase in bacterial growth has been associated with the addition of amino acids and peptides in in vitro cultures through a direct incorporation of preformed amino acids into microbial protein^{( 48 )}. Therefore, rumen N utilisation would affect N isotopic fractionation in the same way as metabolic N utilisation^{( 13 )}, with both contributing to decrease Δ¹⁵N as their efficiencies increase. Given that rumen N metabolism has been identified as the most important factor contributing to ENU in ruminants^{( 49 )}and that N isotopic fractionation in animals is thought to occur before the urea synthesis cycle^{( 8 )}, the well-demonstrated N isotopic fractionation by rumen bacteria could by itself explain the good correlation between Δ¹⁵N and ENU found here and in other^{( 18 )} ruminant experiments. However, the many metabolic routes by which NH₃-N could potentially be isotopically discriminated (i.e. NH₃ incorporated into bacterial proteins and urea-N recycling, and NH₃ absorption through the rumen wall^{( 16 )}) might complicate this simple reasoning. This could explain why we did not find any correlations between Δ¹⁵N and rumen NH₃-N absorption or why under certain feeding conditions Δ¹⁵N did not negatively correlate with ENU^{( 16 , 18 )}. Interestingly, Sutoh et al. ^{( 16 )} found significant δ¹⁵N differences in animal proteins but not in rumen protein bacteria (the main amino acid source in most ruminant feeding conditions^{( 50 )}) and similar δ¹⁵N values for plasma urea but not in rumen NH₃ (the main N donor to urea synthesis in ruminants^{( 51 )}) when sheep were fed iso-N diets supplemented or not with sucrose. They concluded that metabolic pathways involved in urea synthesis could have explained the findings. In this regard, Cabrita et al. ^{( 52 )} argued that the weaker, although significant, relationship (r ² 0·29) between ENU and Δ¹⁵N of milk protein (casein) compared with other studies^{( 18 )} could have been ascribed to the relatively little variations in hepatic deamination and transamination among the experimental diets, with variations in rumen efficiency having the predominant effect on ENU. These results suggest that although rumen efficiency seems to be involved in the N isotopic fractionation, variations in animal N metabolism are probably the most important determinants of Δ¹⁵N.

¹⁵N trophic shift (i.e. positive Δ¹⁵N) is thought to originate in part from whole-body amino acid metabolism^{( 6 , 13 )} and ureagenesis^{( 7 , 36 )}. The rationale is that transamination and deamination enzymes are likely to preferentially convert amino groups containing ¹⁴N over ¹⁵N^{( 53 , 54 )}, resulting in the excretion of the isotopically lighter ¹⁴N and retention of the isotopically heavier ¹⁵N^{( 23 )}. Moreover, it has been hypothesised that the extent of anabolic (protein synthesis) and catabolic (urea synthesis) use of absorbed amino acids in the liver may modulate the magnitude of Δ¹⁵N^{( 13 )}. Indeed, in line with a limited dataset obtained in different species^{( 9 , 10 , 14 , 15 )}, a negative relationship between Δ¹⁵N and efficiency of protein assimilation is expected, since the δ¹⁵N values of body proteins would remain close to those in the diet as urea production decreases with increasing proportion of dietary amino acids incorporated into body protein. In this sense, liver urea synthesis was positively correlated with Δ¹⁵N in the present study, supporting the concept of ¹⁵N fractionation during ureagenesis. However, we did not find a relationship between plasma transaminase concentrations and Δ¹⁵N here despite the fact that plasma aspartate aminotransferase concentration has been shown to correlate negatively with feed efficiency in some ruminant studies^{( 55 )}.

Moreover, splanchnic amino acid metabolism (measured as the irreversible loss rate of leucine and phenylalanine across the PDV and liver, respectively, and representing their anabolic (protein synthesis) and catabolic (oxidation) utilisation) showed a significant and positive relationship with Δ¹⁵N. Given that splanchnic tissues are considered to contribute between 30 and 50 % of total protein flux in cattle^{( 56 )} and between 20 and 40 % of whole-body amino acid oxidation^{( 57 )}, they are expected to exert a major influence on ENU^{( 57 )}. The question is whether the relationship between splanchnic amino acid metabolism and ¹⁵N fractionation is contingent on splanchnic amino acid oxidation rather than splanchnic protein synthesis. In principle, ¹⁵N fractionation is less likely to occur during protein synthesis because the amino group is not involved in amino acid activation and binding to transfer RNA^{( 58 )}, but more research is needed to validate this hypothesis.

Δ¹⁵N in nitrogen excretion pools compared with animal proteins

Consistent with other studies^{( 18 , 35 , 36 )}, ruminant faeces and urine were naturally ¹⁵N-enriched and ¹⁵N-depleted in relation to the diet. It should be noted that the Δ¹⁵N of the urine (δ¹⁵N_urine− δ¹⁵N_diet) and faeces (δ¹⁵N_faeces− δ¹⁵N_diet) also showed significant negative correlations with ENU in the dairy cow experiment. Indeed, Δ¹⁵N of the urine was significantly and positively correlated with Δ¹⁵N of plasma proteins (r 0·76, P< 0·001), with a fairly constant ¹⁵N enrichment of plasma proteins relative to the urine for all animals (6·92 (sem 0·46)), in line with other ruminant^{( 18 )} and non-ruminant^{( 13 , 15 )} studies. The N end products resulting from liver amino acid metabolism have previously been reported to exhibit ‘isotope ratio disproportionation^{( 13 )}’, namely a ¹⁵N enrichment of the plasma protein and a ¹⁵N depletion of the urea (and thus urine) produced in the liver compared with their common precursor. So, it seems that the proportional enrichment of plasma proteins as ENU decreases would affect to the same extent the ¹⁵N depletion of urine as predicted in rats from the equations proposed by Sick et al. ^{( 13 )}. In contrast, no relationship between δ¹⁵N in animal proteins and urine was found in sheep^{( 16 )}, which could suggest that the 2-week diet adaptation period used in that study was not long enough to reach steady-state conditions.

The Δ¹⁵N of the faeces was significantly and positively correlated with Δ¹⁵N of plasma and milk proteins, in agreement with others^{( 16 )}, and thus was also showed significantly and negatively correlated with ENU. Metabolic faecal N (non-reabsorbed endogenous protein) contributes significantly to total faecal N excretion in ruminants (from 20 to 50 %^{( 59 , 60 )}), so high contamination of the undigested feed N with endogenously enriched ¹⁵N proteins is thus expected. Based on the fact that contribution of endogenous proteins (animal) to total N excreted in the faeces is related to DM intake^{( 25 , 50 )}, and that we found no differences in DM intake among our dietary treatments^{( 27 )}, a proportional ¹⁵N enrichment of the faeces would parallel the observed increase in animal proteins with decreasing ENU.

Efficiency of nitrogen utilisation: sources of variation and isotopic biomarkers

The results from the beef cattle experiment showed that the EMPUg explained almost three-quarters of FCE variability across the four feeding conditions tested. In contrast to the efficiency of metabolisable energy use for growth (kg), EMPUg evolve similarly to FCE across the lifetime of the animal, i.e. they both decrease as lipid content of BW gain increases with age^{( 61 )}. Thus, evidence suggests that EMPUg contributes significantly to overall feed efficiency and thus to performance, although the factors involved in its high variability (EMPUg ranged from 0·38 to 0·95 in our conditions) are not completely understood^{( 62 )}. In ruminants, the efficiency with which MP is converted to net protein for gain or milk is variable, and has been demonstrated to be significantly affected by (1) level of protein^{( 63 )} and energy^{( 64 )} supplies, (2) absorbed amino acid profile^{( 65 )}, (3) contribution of lipids to BW gain^{( 61 )}, (4) milk production level^{( 66 )}, among other factors. In addition, other non-identified features related to the animals could contribute to the high between-animal variability usually found in EMPUg (EMPUg ranged from 0·37 to 0·60 in animals fed the same diet in the beef cattle experiment). The challenge today is to integrate all of this variability into ration-balancing models that avoid the use of fixed metabolic efficiency coefficients that lead to erroneous predictions. For instance, as cited by Dijkstra et al. ^{( 67 )}, a decrease in EMPUg for milk protein yield from 0·85 (maximum theoretical efficiency^{( 68 )}) to 0·64 (conversion efficiency factor assumed by most feeding systems) or even 0·38 (maximum within-experiment efficiency (marginal) from PDI system data^{( 69 )}) results in maximal ENU for a standard cow of 0·43, 0·37 and 0·26, respectively. New feeding systems should be able to integrate this high variability in EMPUg to better predict ruminant feed requirements and performances. The present results showed that Δ¹⁵N could be used as a biomarker- of EMPUg in growing young bulls fed different diets, but more studies are needed to evaluate its potential use in real-world farming systems.

Conclusions

The results found herein showed that the efficiency with which feed N is assimilated into animal proteins is a major factor driving the variations in ¹⁵N fractionation between different ruminant N pools (plasma and milk proteins, faecal and urinary N) and diet, and suggests that splanchnic amino acid metabolism could play a key role in the N isotopic fractionation observed in ruminants. ¹⁵N fractionation between animal and diet could potentially be used in ruminant feeding practice to encompass the variability in the conversion of MP into animal proteins; however, more controlled studies are needed to address and validate this point.