Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T03:31:14.819Z Has data issue: false hasContentIssue false
  • English
  • Français

ENDOSCOPY FOR HECKE CATEGORIES, CHARACTER SHEAVES AND REPRESENTATIONS

Part of: Linear algebraic groups and related topics (Co)homology theory Representation theory of groups

Published online by Cambridge University Press:  28 May 2020

GEORGE LUSZTIG  and
ZHIWEI YUN
GEORGE LUSZTIG
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, 77 Massachusetts Ave, Cambridge, MA 02139, USA; [email protected]
ZHIWEI YUN
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, 77 Massachusetts Ave, Cambridge, MA 02139, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a reductive group 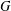$G$ over a finite field, we show that the neutral block of its mixed Hecke category with a fixed monodromy under the torus action is monoidally equivalent to the mixed Hecke category of the corresponding endoscopic group 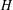$H$ with trivial monodromy. We also extend this equivalence to all blocks. We give two applications. One is a relationship between character sheaves on 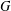$G$ with a fixed semisimple parameter and unipotent character sheaves on the endoscopic group 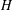$H$, after passing to asymptotic versions. The other is a similar relationship between representations of 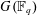$G(\mathbb{F}_{q})$ with a fixed semisimple parameter and unipotent representations of 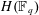$H(\mathbb{F}_{q})$.

MSC classification

Primary: 20G40: Linear algebraic groups over finite fields
Secondary: 14F05: Sheaves, derived categories of sheaves and related constructions 14F43: Other algebro-geometric (co)homologies (e.g., intersection, equivariant, Lawson, Deligne (co)homologies) 20C08: Hecke algebras and their representations 20C33: Representations of finite groups of Lie type
Type
Algebra
Information
Forum of Mathematics, Pi , Volume 8 , 2020 , e12
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020

References

Beilinson, A., Bernstein, J. and Deligne, P., ‘Faisceaux pervers’, inAnalysis and Topology on Singular Spaces, I, Astérisque (Soc. Math. France, Paris, 1982), 5–171.Google Scholar
Ben-Zvi, D. and Nadler, D., The character theory of a complex group, Preprint, 2009, arXiv:0904.1247.Google Scholar
Bernstein, J. and Lunts, V., Equivariant Sheaves and Functors, Lecture Notes in Mathematics, 1578 (Springer, Berlin, 1994), iv+139 pp.CrossRefGoogle Scholar
Bezrukavnikov, R. and Finkelberg, M., ‘Equivariant Satake category and Kostant-Whittaker reduction’, Mosc. Math. J. 8(1) (2008), 39–72.CrossRefGoogle Scholar
Bezrukavnikov, R., Finkelberg, M. and Ostrik, V., ‘Character D-modules via Drinfeld center of Harish-Chandra bimodules’, Invent. Math. 188 (2012), 589–620.CrossRefGoogle Scholar
Bezrukavnikov, R. and Yun, Z., ‘On Koszul duality for Kac-Moody groups (with appendices by Zhiwei Yun) Represent’, Theory 17 (2013), 1–98.Google Scholar
Deligne, P. and Lusztig, G., ‘Representations of reductive groups over finite fields’, Ann. of Math. (2) 103 (1976), 103–161.CrossRefGoogle Scholar
Deligne, P., ‘La conjecture de Weil II’, Publ. Math. Inst. Hautes Études Sci. 52 (1980), 137–252.CrossRefGoogle Scholar
Ginsburg, V., ‘Perverse sheaves and ℂ∗ -actions’, J. Amer. Math. Soc. 4(3) (1991), 483–490.Google Scholar
Joyal, A. and Street, R., ‘Tortile Yang-Baxter operators in tensor categories’, J. Pure Appl. Alg. 71 (1991), 43–51.CrossRefGoogle Scholar
Kazhdan, D. and Lusztig, G., ‘Representations of Coxeter groups and Hecke algebras’, Invent. Math. 53 (1979), 165–184.CrossRefGoogle Scholar
Lusztig, G., Characters of Reductive Groups Over Finite Fields, Proceedings of the International Congress of Mathematicians, Vol. 1, 2 (Warsaw, 1983), 877–880. PWN, Warsaw, 1984.Google Scholar
Lusztig, G., Characters of Reductive Groups Over a Finite Field, Annals of Mathematics Studies, 107 (Princeton University Press, Princeton, NJ, 1984), xxi+384 pp.CrossRefGoogle Scholar
Lusztig, G., ‘Character sheaves, I’, Adv. Math. 56(3) (1985), 193–237.CrossRefGoogle Scholar
Lusztig, G., ‘Character sheaves, V’, Adv. Math. 61(2) (1986), 103–155.CrossRefGoogle Scholar
Lusztig, G., ‘On the representations of reductive groups with disconnected center’, Astérisque 168 (1988), 157–166.Google Scholar
Lusztig, G., ‘Character sheaves on disconnected groups VII’, Represent. Theory 9 (2005), 209–266.CrossRefGoogle Scholar
Lusztig, G., ‘Irreducible representations of finite spin groups’, Represent. Theory 12 (2008), 1–36.CrossRefGoogle Scholar
Lusztig, G., ‘Character sheaves on disconnected groups X’, Represent. Theory 13 (2009), 82–140.CrossRefGoogle Scholar
Lusztig, G., ‘Truncated convolution of character sheaves’, Bull. Inst. Math. Acad. Sin. (N.S.) 10(1) (2015), 1–72.Google Scholar
Lusztig, G., ‘Unipotent representations as a categorical centre’, Represent. Theory 19 (2015), 211–235.CrossRefGoogle Scholar
Lusztig, G., ‘Non-unipotent character sheaves as a categorical centre’, Bull. Inst. Math. Acad. Sin. (N.S.) 11(4) (2016), 603–731.Google Scholar
Lusztig, G., ‘Non-unipotent representations and categorical centres’, Bull. Inst. Math. Acad. Sin. (N.S.) 12(3) (2017), 205–296.Google Scholar
Lusztig, G., ‘Conjugacy classes in reductive groups and two-sided cells’, Bull. Inst. Math. Acad. Sinica (N.S.) 14 (2019), 265–293.Google Scholar
MacLane, S., Categories for the Working Mathematician (Second Edition), Graduate Texts in Mathematics, 5 Springer, New York, 1998, xii+314 pp.Google Scholar
Majid, S., ‘Representations, duals and quantum doubles of monoidal categories, Rend’, Circ. Mat. Palermo 26 (1991), 197–206.Google Scholar
Soergel, W., ‘Kategorie 𝓞, perverse Garben und Moduln über den Koinvarianten zur Weylgruppe’, J. Amer. Math. Soc. 3(2) (1990), 421–445.Google Scholar
Soergel, W., ‘Kazhdan-Lusztig-Polynome und unzerlegbare Bimoduln über Polynomringen’, J. Inst. Math. Jussieu 6(3) (2007), 501–525.CrossRefGoogle Scholar
Steinberg, R., Endomorphisms of linear algebraic groups, Memoirs of the American Mathematical Society, 80 (American Mathematical Society, Providence, R.I., 1968).CrossRefGoogle Scholar
Yokonuma, T., ‘Sur la structure des anneaux de Hecke d’un groupe de Chevalley fini’, C. R. Acad. Sci. Paris Ser. A 264 (1967), A334–A347.Google Scholar
Yun, Z., Rigidity in Automorphic Representations and Local Systems, Current Developments in Mathematics (2013), 73–168, Int. Press, Somerville, MA, 2014.CrossRefGoogle Scholar
Yun, Z., Higher signs for Coxeter groups, Preprint, 2019, arXiv:1908.03672.Google Scholar