Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-12-03T00:27:57.325Z Has data issue: false hasContentIssue false
  • English
  • Français

Computing the effectively computable bound in Baker's inequality for linear forms in logarithms

Published online by Cambridge University Press:  17 April 2009

A.J. van der Poorten  and
J.H. Loxton
A.J. van der Poorten
Affiliation:
School of Mathematics, University of New South Wales, Kensington, New South Wales.
J.H. Loxton
Affiliation:
School of Mathematics, University of New South Wales, Kensington, New South Wales.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For certain number theoretical applications, it is useful to actually compute the effectively computable constant which appears in Baker's inequality for linear forms in logarithms. In this note, we carry out such a detailed computation, obtaining bounds which are the best known and, in some respects, the best possible. We show inter alia that if the algebraic numbers α1, …, αn all lie in an algebraic number field of degree D and satisfy a certain independence condition, then for some n0(D) which is explicitly computed, the inequalities (in the standard notation)

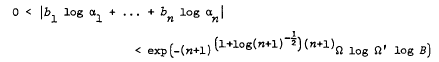
have no solution in rational integers b1, …, bn (bn ≠ 0) of absolute value at most B, whenever n ≥ n0(D). The very favourable dependence on n is particularly useful.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 15 , Issue 1 , August 1976 , pp. 33 - 57
Copyright
Copyright © Australian Mathematical Society 1976

References

[1]Baker, A., “Linear forms in the logarithms of algebraic numbers (IV)”, Mathematika 15 (1968), 204–216.CrossRefGoogle Scholar
[2]Baker, A., “A sharpening of the bounds for linear forms in logarithms”, Acta Arith. 21 (1972), 117–129.CrossRefGoogle Scholar
[3]Baker, A., “A central theorem in transcendence theory”, Diophantine approximation and its applications, 1–23 (Proc. Conf. Diophantine Approximation and its Applications, Washington, 1972. Academic Press [Harcourt-Brace Jovanovich], New York, London, 1973).Google Scholar
[4]Baker, A., “A sharpening of the bounds for linear forms in logarithms II”, Acta Arith. 24 (1973), 33–36.CrossRefGoogle Scholar
[5]Baker, Alan, Transcendental number theory (Cambridge University Press, Cambridge, 1975).CrossRefGoogle Scholar
[6]Baker, A., “A sharpening of the bounds for linear forms in logarithms III”, Acta Arith. 27 (1975), 247–252.CrossRefGoogle Scholar
[7]Baker, A., “The theory of linear forms in logarithms”, Proceedings of a Conference, Cambridge, 1976 (to appear).Google Scholar
[8]Cijsouw, Pieter L. and Waldschmidt, Michel, “Linear forms and simultaneous approximations”, submitted.Google Scholar
[9]Чудновский, Г.В. [G.V. Čudnovskiĭ], “Аналитические методы в диофантовых прибдижениях” [Analytic methods in diophantine approximation] (Preprint, Akad. Nauk USSB Inst. Mat. Kiev, 1974.Google Scholar
[10]Фельдман, Н.И. [N.I. Fel'dman], “Зффективное степенное усиление теоремы лиувилля” [An effective sharpening of the exponent in Liouville's theorem], Izv. Akad. Nauk. SSSR Ser. Mat. 35 (1971), 973–990.Google ScholarPubMed
[11]van der Poorten, Alfred J., “On Baker's inequality for linear forms in logarithms”, Math. Proc. Cambridge Philos. Soc. (to appear).Google Scholar
[12]van der Poorten, A.J., “Linear forms in logarithms in the p–adic case”, Proceedings of a Conference,Cambridge, 1976 (to appear).Google Scholar
[13]Shorey, T.N., “On gaps between numbers with a large prime factor, II”, Acta Arith. 25 (1973-1974), 365–373.CrossRefGoogle Scholar
[14]Shorey, T.N., “On linear forms in the logarithms of algebraic numbers”, Acta Arifh. (to appear).Google Scholar
[15]Stark, H.M., “Further advances in the theory of linear forms in logarithms”, Diophantine approximation and its applications, 255–293 (Proc. Conf. Diophantine Approximation and its Applications, Washington, 1972. Academic Press [Harcourt-Brace Jovanovich], New York, London, 1973).Google Scholar
[16]Tijdeman, R., “On the equation of Catalan”, Acta Arith. (to appear).Google Scholar