1. INTRODUCTION
With the development of worldwide transportation, polar navigation technology has become a research hotspot in the field of positioning and navigation. Due to its special geographical characteristics, common navigation methods such as satellite navigation, radio navigation and geomagnetic navigation do not always work efficiently in polar regions (Ngwira et al., Reference Ngwira, McKinnell and Cilliers2010; Andalsvik and Jacobsen, Reference Andalsvik and Jacobsen2014). Inertial navigation, which is resistant to the changes of terrain, weather, magnetic field and other external factors, is superior in high latitude areas compared to other navigation methods (Fei and Lin, Reference Fei and Lin2011).
For applications involving movement relative to the surface of the Earth, such as ships and airplanes, the local geographic frame is being now widely used as the navigation frame. All the outputs are given with regard to the local-level frame and the attitude angles are defined as roll, pitch and yaw, which are the Euler angles from the attitude matrix 
$C_n^b $. These attitude angles referred to the local horizontal plane are much easier to handle and can be immediately used by much equipment, such as radar and celestial navigation star sensors. This mechanisation is also convenient for Integrated Navigation Systems (INS), such as INS/MCP (Magnetic Compass Pilot), INS/Altimeter and INS/CNS (Celestial Navigation System).
However, in polar regions, the rapid gathering of meridians makes the traditional geographic coordinate system ineffective because the system fails to give valid directions (Maclure, Reference Maclure1949). All mechanisms using traditional longitude and latitude as the position reference fail to provide accurate navigation in polar regions (Yao et al., Reference Yao, Xu and Tong2015).
ECEF (Earth-Centred, Earth-Fixed) mechanisation is a navigation solution for polar regions, in which all the outputs are given with regard to the Earth frame and the attitude angles are defined as the angles between the body frame and the Earth frame (Zhou et al., Reference Zhou, Qin and Fu2013). When roll, pitch and yaw are required, these attitude angles between the body frame and the local geographical frame can be easily obtained from the matrix 
${\bi C}_e^b $ by using the local position. But at the poles, because both z-axes of the ECEF frame and the local geographical frame are parallel, the yaw is no longer unique. Besides, the accuracy of roll, pitch and yaw transformed from 
${\bi C}_e^b $ will degrade with the increase of the latitude and the transformation is thus inaccurate due to the position error.
Thus a transverse mechanisation was presented as an alternative to the ECEF mechanisation in polar regions, which is more immediate and convenient because the definition of the attitude angles is based on a local horizontal plane just like that in the traditional geographical frame. In addition, the horizontal attitude angles in the transverse navigation system are much easier to measure with accelerometers when the vessel is in non-accelerating moving mode other than at the attitude angles defined in ECEF.
In the transverse navigation algorithm, a new Earth model was established where the pole is set on the equator (Broxmeyer and Leondes, Reference Broxmeyer and Leondes1964). The mechanism of transverse navigation under the spherical Earth model is presented in Li et al. (Reference Li, Ben, Yu and Sun2015). Its corresponding damping technology and system reset process have been studied. However, as the Earth is an ellipsoid, further research should be conducted to examine and ensure the validity of the transverse navigation system under the ellipsoidal Earth model. Meanwhile, the performance of the transverse navigation system in non-polar areas has not yet been investigated, and there is a lack of assessment regarding the application regions of the transverse navigation system (Xu and Dou, Reference Xu and Dou2014).
When evaluating the performance of the transverse navigation system in polar regions, purely simulated data has been applied (Yao et al., Reference Yao, Xu and Tong2015; Zhou et al., Reference Zhou, Qin and Fu2013; Broxmeyer and Leondes, Reference Broxmeyer and Leondes1964; Li et al., Reference Li, Ben, Yu and Sun2015; Xu and Dou, Reference Xu and Dou2014), which may not reflect the real environment in field tests. To compensate for this, a novel experimental approach is proposed by means of using the data in the mid-latitude field test to simulate the corresponding information at high latitudes. Considering the difference between polar and non-polar regions, some compensations and transformations were implemented to build a field test equivalent to one in polar regions. Details are illustrated in Section 4.
The purpose of this research is to build a transverse navigation system under the ellipsoidal Earth model and study the corresponding mechanisms. In addition, the performance of the proposed transverse navigation system is evaluated in both polar and non-polar regions. The paper is organised as follows. The transverse Earth coordinate system is introduced and its mechanism is derived under the ellipsoidal Earth model in Section 2. In Section 3, in order to determine its application regions, the error propagation characteristics of the proposed transverse navigation system are studied. In Section 4, to evaluate the performance of the proposed algorithm, a field test in a non-polar region was implemented and the corresponding simulation for a polar region using the real non-polar data was also conducted. Finally, conclusions are drawn in Section 5.
2. THE TRANSVERSE NAVIGATION MECHANISM UNDER THE ELLIPSOIDAL EARTH MODEL
2.1. The effect of the ellipsoidal Earth model on the transverse navigation system
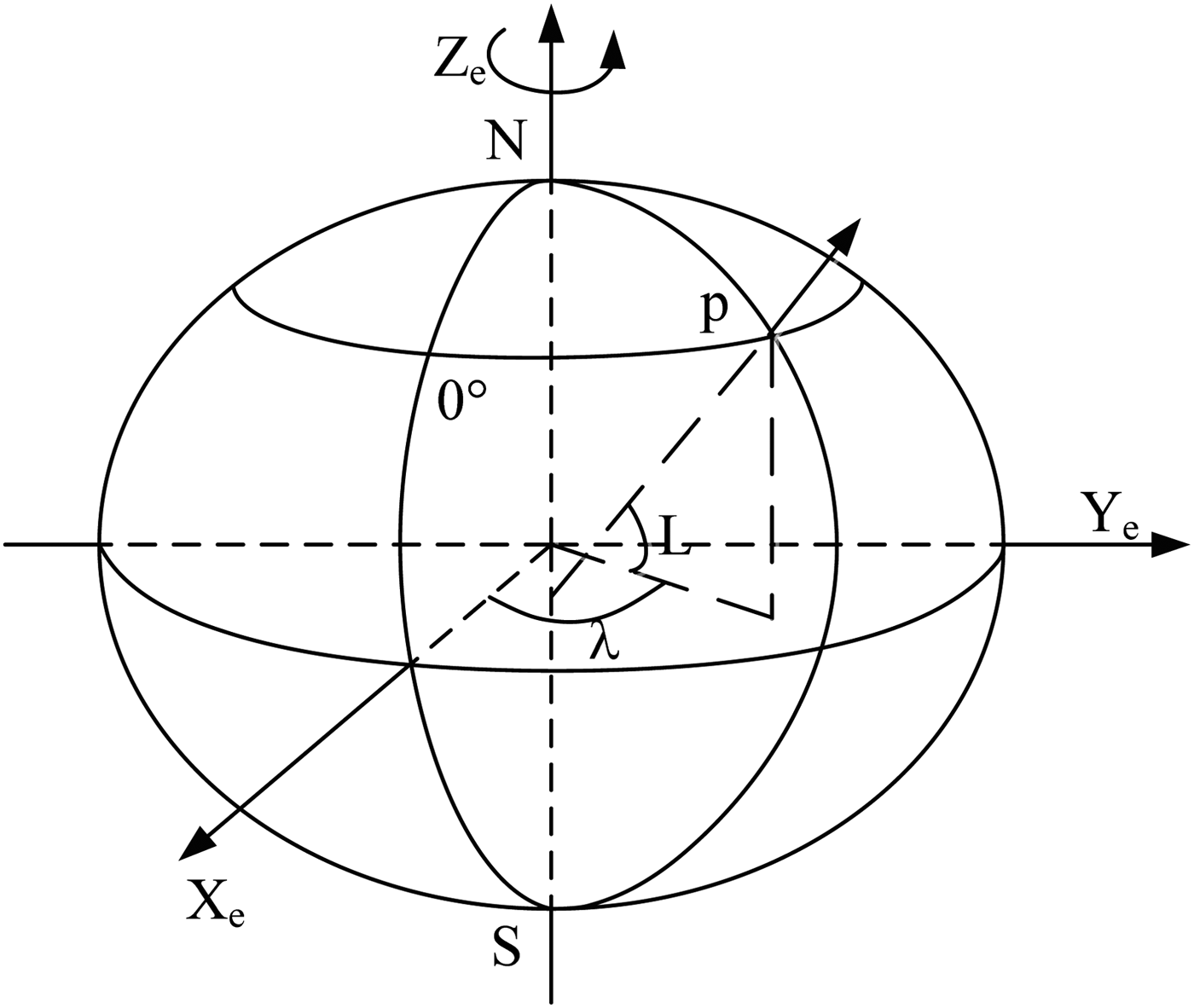
In the traditional coordinate system, as shown in Figure 1, the line of longitude is an imaginary arc on the Earth's surface from the North Pole to the South Pole. Along with the Earth's rotation axis, it forms a plane perpendicular to the equatorial plane. The line of latitude is a circle on the Earth's surface, which forms a plane that is parallel to the equatorial plane. The included angle formed by the local meridian plane of point P and the prime meridian plane is the longitude of point P, written as λ. The angle between the normal and the equatorial plane is the latitude of point P written as L.
Figure 1. Traditional definition of latitude and longitude.
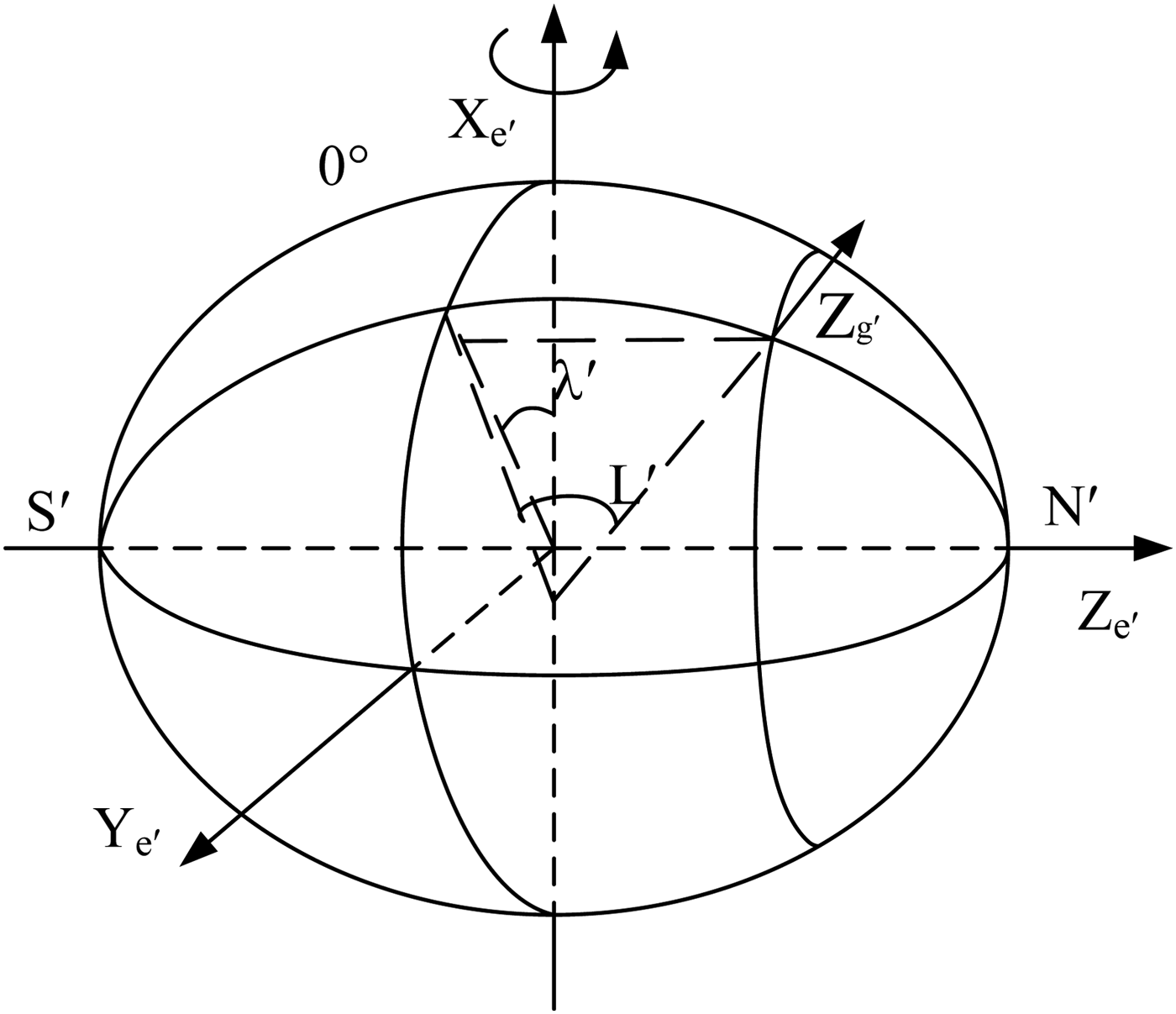
The transverse navigation mechanism under the spherical Earth model (Broxmeyer and Leondes, Reference Broxmeyer and Leondes1964; Liu et al., Reference Liu, Wang, Wang and Feng2013) gives the definition of transverse latitude and longitude, which is similar to the traditional coordinate system, as shown in Figure 2. After the rotation, the transverse Earth-fixed frame is achieved. The X e′ axis of the transverse Earth-fixed frame points towards the North pole, the Z e′ axis points at 90°E, in the traditional equatorial plane. The Y e′ axis is chosen to form a right-handed coordinate system. The transverse longitude λ′ is the included angle between the transverse prime meridian plane and the local meridian plane. L′ is the angle between the normal and the transverse equatorial plane.
Figure 2. Definition of transverse latitude and longitude according to the traditional coordinates.
However, since the Earth is an ellipsoid, the definition of transverse latitude and longitude that is similar to the traditional definition of latitude and longitude may raise problems. The reasons are:
1) The line of transverse latitude, which is parallel to the transverse equatorial plane, forms an ellipse rather than a circle. As a consequence, different points on the same line of transverse latitude in Figure 2 will possess different latitudes L′.
2) The transverse longitude λ′, which is the included angle between the transverse prime meridian plane and the local meridian plane, is unequal to the angle between the normal and the prime meridian plane.
3) The radii of the meridian and the prime vertical should be achieved on the basis of the normal of the local-level plane, which the construction of transverse latitude and longitude above does not utilise. Therefore there are errors in the calculation of radii of the meridian and the prime vertical.
4) The transverse geographic frame g′, which is obtained by the rotation of the transverse Earth-fixed frame according to L′ and λ′, is not a local-level frame, and there is a small angle between Z g′ axis and the normal. Thus, the integral of the velocity along Z g′ cannot represent the growth in altitude, which makes the frame g′ meaningless.
Furthermore, because the error of height in inertial navigation is divergent, using a local-level frame as the navigation frame can separate the volatile factors, which can be easily mitigated by altitude information from other sources, such as altimeters (Cheng et al., Reference Cheng, Wang and Wang2013). Therefore a new local-level frame is preferred in this research.
2.2. Definitions in transverse navigation and parameter transformation
The following definitions are established:
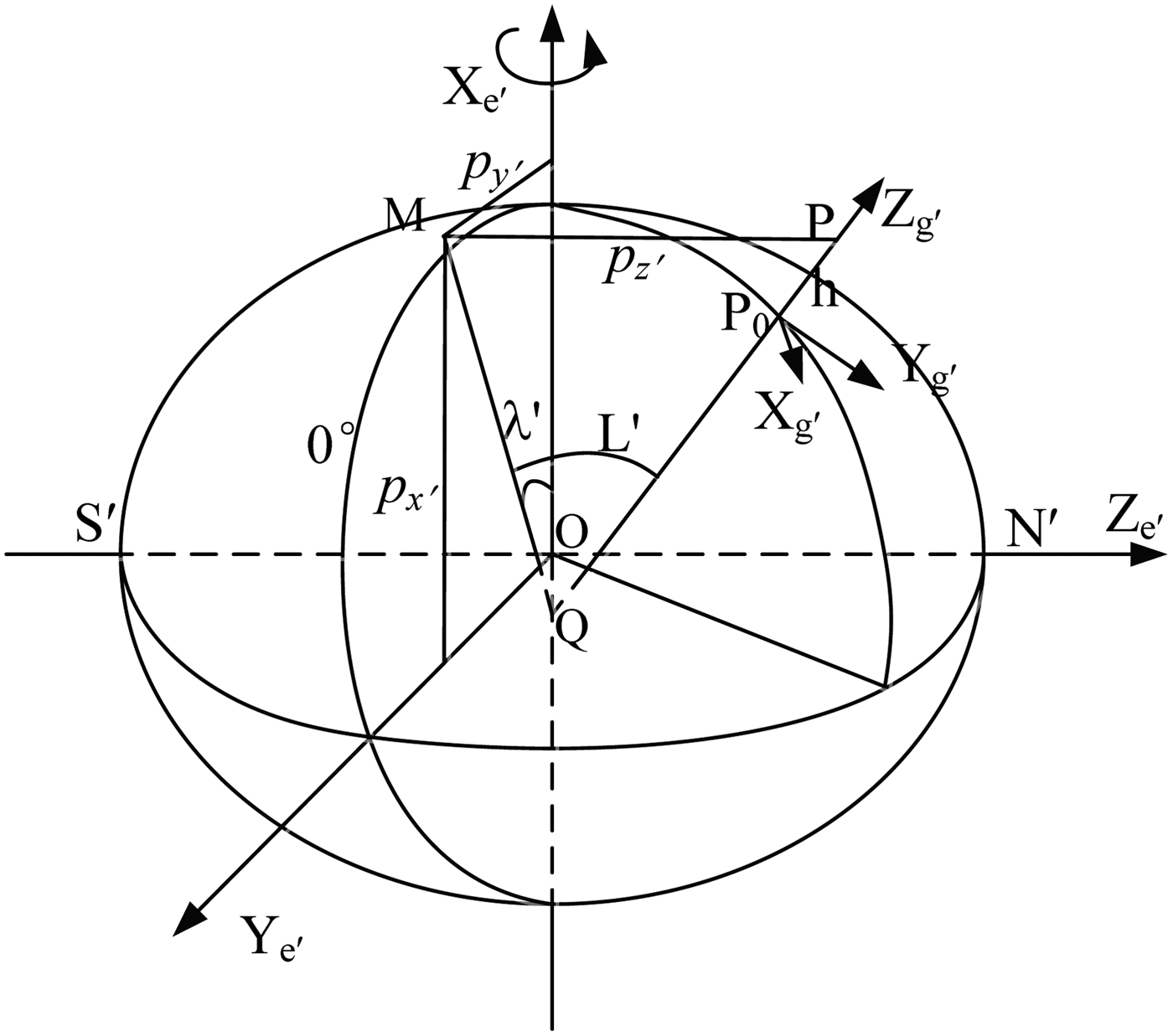
1) Transverse Earth- fixed frame e′: Denote the intersection of 90° E and the equatorial plane as the transverse north pole N′. X e′ axis is pointing towards the North pole, where Z e′ axis points at N′. Y e′ axis extends from the intersection of the prime meridian and the equatorial plane.
2) Transverse longitude λ′ and latitude L′: As shown in Figure 3, point P is the vehicle and line P 0P is the normal of the local-level plane. The included angle of P 0P and the transverse equatorial plane is denoted as L′. Transverse longitude λ′ is the included angle between line QM and X e′, where M is the projection of P in the equatorial plane.
Figure 3. Definition of transverse latitude and longitude under the ellipsoidal Earth model.
3) Transverse north and east: Transverse north is along the intersecting line of plane PMQ and the local-level plane of P 0. Transverse east is along the intersecting line of the local-level plane and the plane parallel to the transverse equatorial plane, which contains point P 0.
4) Transverse geographic frame g′: The origin is at the mass centre of the object. Z g′ is the vector along the normal of the local-level plane upwards. X g′ points at the transverse east and Y g′ points at the transverse north.
According to the analysis above, the points that share the same latitude or longitude are located in different planes due to the elliptical shape of the Earth. Thus the transverse longitude and latitude is only a description of the position.
The position of point P in the geocentric rectangular coordinate system can be written as 
$\left[ {\matrix{x & y & z \cr}} \right]^T $, while in the transverse geocentric rectangular coordinate system it is denoted as 
$\left[ {\matrix{{x^{\prime}} & {y^{\prime}} & {z^{\prime}} \cr}} \right]^T $. The relation between them is
$$\left[ {\matrix{ x & y & z \cr}} \right]^T = \left[ {\matrix{ {y^{\prime}} & {z^{\prime}} & {x^{\prime}} \cr}} \right]^T $$Thus the direction cosine matrix of transformation from the traditional Earth-fixed frame e to frame e′ is
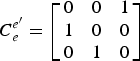$${\bi C}_e^{e^{\prime}} = \left[ {\matrix{ 0 & 0 & 1 \cr 1 & 0 & 0 \cr 0 & 1 & 0 \cr}} \right] $$Based on the relationship between the geodetic coordinate system and the geocentric rectangular coordinate system, λ′ and L′ can be obtained as
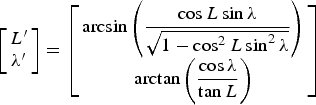$$\left[ {\matrix{ {L^{\prime}} \cr {\rm \lambda ^{\prime}} \cr}} \right] = \left[ {\matrix{ {\arcsin \left( {\displaystyle{{\cos L\sin \rm \lambda} \over {\sqrt {1 - \cos ^2 L\sin ^2 \rm \lambda}}}} \right)} \cr {\arctan \left( {\displaystyle{{\cos \rm \lambda} \over {\tan L}}} \right)} \cr}} \right] $$and the conversion equation is shown as
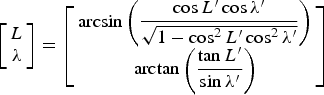$$\left[ {\matrix{ L \cr \rm \lambda \cr}} \right] = \left[ {\matrix{ {\arcsin \left( {\displaystyle{{\cos L^{\prime}\cos \rm \lambda ^{\prime}} \over {\sqrt {1 - \cos ^2 L^{\prime}\cos ^2 \rm \lambda ^{\prime}}}}} \right)} \cr {\arctan \left( {\displaystyle{{\tan L ^{\prime}} \over {\sin \rm \lambda ^{\prime}}}} \right)} \cr}} \right] $$Since the transverse geographic frame g′ and the traditional geographic frame g are both local-level frames, there is only an included angle β between them in Z g′ (Z g). The corresponding direction cosine matrix of transformation is
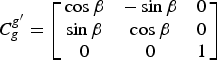$${\bi C}_g^{g^{\prime}} = \left[ {\matrix{ {\cos \beta} & { - \sin \beta} & 0 \cr {\sin \beta} & {\cos \beta} & 0 \cr 0 & 0 & 1 \cr}} \right] $$where
$$\cos \beta = \displaystyle{{ - \sin L\sin \rm \lambda} \over {\sqrt {1 - \cos ^2 L\sin ^2 \rm \lambda}}} = \displaystyle{{ - \sin L^{\prime}\cos \rm \lambda ^{\prime}} \over {\sqrt {1 - \cos ^2 L^{\prime}\cos ^2 \rm \lambda ^{\prime}}}} $$
$$\sin \beta = \displaystyle{{\cos \rm \lambda} \over {\sqrt {1 - \cos ^2 L\sin ^2 \rm \lambda}}} = \displaystyle{{\sin \rm \lambda ^{\prime}} \over {\sqrt {1 - \cos ^2 L^{\prime}\cos ^2 \rm \lambda ^{\prime}}}} $$2.3. The transverse navigation mechanism
Using the transverse geographic frame as the navigation frame, the differential equations of the velocity and the direction cosine matrix of attitude are
$${\dot{\bi C}}_b^{g^{\prime}} = {\bi C}_b^{g^{\prime}} \left( {{\bi \omega}_{g^{\prime}b}^b \times} \right)$$
$$\dot{\bi v}^{g^{\prime}} = {\bi C}_b^{g^{\prime}}\, {\bi f}^b - \left( {2{\bi C}_{e^{\prime}}^{g^{\prime}} {\bi \omega} _{ie^{\prime}}^{e^{\prime}} + {\bi \omega} _{e^{\prime}g^{\prime}}^{g^{\prime}}} \right) \times {\bi v}^{g^{\prime}} + {\bi G}^{g^{\prime}} $$
where Gg′ is the projection of the gravity vector in the transverse geographic frame g′, and 
$\left( {{\bi \omega} _{g^{\prime}b}^b \times} \right)$ is the skew-symmetric matrix of 
${\bi \omega} _{g^{\prime}b}^b $, the angular rate of body frame b to frame g′ in frame b.
With the gyros' output 
${\bi \omega} _{ib}^b $, we can obtain
$${\bi \omega} _{g^{\prime}b}^b = {\bi \omega} _{ib}^b - {\bi \omega} _{ig^{\prime}}^b = {\bi \omega} _{ib}^b - {\bi C}_{g^{\prime}}^b ({\bi \omega} _{ie^{\prime}}^{g^{\prime}} + {\bi \omega} _{e^{\prime}g^{\prime}}^{g^{\prime}} ) $$where
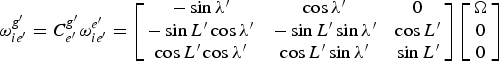$${\bi \omega} _{ie^{\prime}}^{g^{\prime}} = {\bi C}_{e^{\prime}}^{g^{\prime}} {\bi \omega} _{ie^{\prime}}^{e^{\prime}} = \left[ {\matrix{ { - \sin \lambda ^{\prime}} & {\cos \lambda ^{\prime}} & 0 \cr { - \sin L^{\prime}\cos \lambda ^{\prime}} & { - \sin L^{\prime}\sin \lambda ^{\prime}} & {\cos L^{\prime}} \cr {\cos L^{\prime}\cos \lambda ^{\prime}} & {\cos L^{\prime}\sin \lambda ^{\prime}} & {\sin L^{\prime}} \cr}} \right]\left[ {\matrix{ \Omega \cr 0 \cr 0 \cr}} \right] $$
Ω is the Earth's rotation rate. Here, 
${\bi C}_{e^{\prime}}^{g^{\prime}} $ is obtained through similar calculations as the traditional 
${\bi C}_e^g $, but λ′ and L′ from the ellipsoidal model is used instead.
Meanwhile, we can obtain other parameters as follows:
$${\bi \omega} _{e^{\prime}g^{\prime}}^{g^{\prime}} = {\bi C}_g^{g^{\prime}} {\bi \omega} _{eg}^g + \left[ {\matrix{ 0 & 0 & { - \dot \beta} \cr}} \right]^T $$
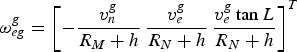$${\bi \omega} _{eg}^g = \left[ { - \displaystyle{{v_n^g} \over {R_M + h}} \, \displaystyle{{v_e^g} \over {R_N + h}} \, \displaystyle{{v_e^g \tan L} \over {R_N + h}}} \right]^T $$
$${\bi v}^g = {\bi C}_{g^{\prime}}^g {\bi v}^{g^{\prime}} $$
$$\dot \beta = - \displaystyle{{\cos L\cos ^2 \beta} \over {(R_N + h)\sin L}}v_e^g - \displaystyle{{\sin \beta \cos \beta \cos L} \over {(R_M + h)\sin L}}v_n^g $$where v n and v e are northward and eastward velocities in the corresponding frame. R M and R N are the radii of the meridian and the prime vertical, respectively.
Substituting Equations (4) and (5) and Equations (13)–(15) into Equation (12), we can obtain
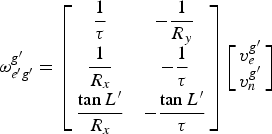$${\bi \omega} _{e^{\prime}g^{\prime}}^{g^{\prime}} = \left[ {\matrix{ {\displaystyle{1 \over \tau}} & { - \displaystyle{1 \over {R_y}}} \cr {\displaystyle{1 \over {R_x}}} & { - \displaystyle{1 \over \tau}} \cr {\displaystyle{{\tan L^{\prime}} \over {R_x}}} & { - \displaystyle{{\tan L^{\prime}} \over \tau}} \cr}} \right]\left[ {\matrix{ {v_e^{g^{\prime}}} \cr {v_n^{g^{\prime}}} \cr}} \right]$$where
$$\eqalign{& \displaystyle{1 \over \tau} = \left( {\displaystyle{1 \over {R_M + h}} - \displaystyle{1 \over {R_N + h}}} \right)\sin \beta \cos \beta \cr & \displaystyle{1 \over {R_x}} = \displaystyle{{\sin ^2 \beta} \over {R_M + h}} + \displaystyle{{\cos ^2 \beta} \over {R_N + h}} \cr & \displaystyle{1 \over {R_y}} = \displaystyle{{\cos ^2 \beta} \over {R_M + h}} + \displaystyle{{\sin ^2 \beta} \over {R_N + h}}}$$
$$\eqalign{& R_M = \displaystyle{{R_e (1 - q)^2} \over {\left( {1 - \left( {2 - q} \right)q\cos ^2 L^{\prime}\cos ^2 \rm \lambda ^{\prime}} \right)^{3/2}}} \cr & R_N = \displaystyle{{R_e} \over {\left( {1 - \left( {2 - q} \right)q\cos ^2 L^{\prime}\cos ^2 \rm \lambda ^{\prime}} \right)^{1/2}}}}$$R e is the length of the semi major axis and q is the ellipticity of the Earth.
${\bi \omega} _{e^{\prime}g^{\prime}}^{g^{\prime}} $ could also be attained by calculating the rate of change in λ′ and L′ according to the relationship between e′ and g′
$${\bi \omega} _{e^{\prime}g^{\prime}}^{g^{\prime}} = \left[ {\matrix{ { - \dot L^{\prime}} \cr 0 \cr 0 \cr}} \right] + \left[ {\matrix{ 1 & 0 & 0 \cr 0 & {\sin L^{\prime}} & {\cos L^{\prime}} \cr 0 & { - \cos L^{\prime}} & {\sin L^{\prime}} \cr}} \right]\left[ {\matrix{ 0 \cr 0 \cr {\dot {\rm \lambda} ^{\prime}} \cr}} \right] = \left[ {\matrix{ { - \dot L^{\prime}} \cr {\dot {\rm \lambda} ^{\prime}\cos L^{\prime}} \cr {\dot {\rm \lambda} ^{\prime}\sin L^{\prime}} \cr}} \right]$$Comparing Equation (16) with Equation (19), the differential equations of λ′ and L′ are
$$\eqalign{& \dot L^{\prime} = - \displaystyle{1 \over \tau} v_e^{g^{\prime}} + \displaystyle{1 \over {R_y}} v_n^{g^{\prime}} \cr & {\dot {\rm \lambda}} ^{\prime} = \displaystyle{1 \over {R_x \cos L^{\prime}}}v_e^{g^{\prime}} - \displaystyle{1 \over {\tau \cos L^{\prime}}}v_n^{g^{\prime}}} $$It can be seen that the updates of transverse longitude and latitude involve eastward and northward velocities simultaneously. This is quite different from the mechanism under the spherical Earth model and is a result of the characteristics of an ellipsoid.
P′, R′ and H′ are pitch, roll and yaw in the transverse navigation system respectively. They represent the relationship between frame b and frame g′ as shown in the following matrix
$$\eqalign{&{\bi C}_{g^{\prime}}^b = \left[ {\matrix{ {\cos R^{\prime}\cos H^{\prime} + \sin R^{\prime}\sin H^{\prime}\sin P^{\prime}} & { - \cos R^{\prime}\sin H^{\prime} + \sin R^{\prime}\cos H^{\prime}\sin P^{\prime}}\cr {\sin H^{\prime}\cos P^{\prime}} & {\cos H^{\prime}\cos P^{\prime}}\cr {\sin R^{\prime}\cos H^{\prime} - \cos R^{\prime}\sin H^{\prime}\sin P^{\prime}} & { - \sin R^{\prime}\sin H^{\prime} - \cos R^{\prime}\cos H^{\prime}\sin P^{\prime}}}} \right. \cr&\quad\qquad \left. {\matrix{ { - \sin R^{\prime}\cos P^{\prime}} \cr {\sin P^{\prime}} \cr {\cos R^{\prime}\cos P^{\prime}}}} \right]}$$
Let 
${\bi C}_{g^{\prime}}^b = \left[ {C_{ij}} \right]$ (i,j = 1,2,3), and we can have
$$\eqalign{& P^{\prime} = \arcsin \left( {C_{23}} \right) \cr & R^{\prime} = \arctan \left( { - \displaystyle{{C_{13}} \over {C_{33}}}} \right) \cr & H^{\prime} = \arctan \left( {\displaystyle{{C_{21}} \over {C_{22}}}} \right)} $$3. ERROR ANALYSIS OF THE TRANSVERSE NAVIGATION SYSTEM AND ITS APPLICATION REGIONS
The errors of the transverse navigation system are analysed similarly to the traditional inertial navigation system (Lv et al., Reference Lv, Lai, Liu and Nie2014; Liu et al., Reference Liu, Wang, Wang and Feng2013). The derivative of the misalignment angle vector φ, which contains angles between the true transverse geographic frame and the actual transverse navigation frame, is
$$\dot{\bi \varphi} ^{g^{\prime}} = - \left( {{\bi \omega} _{ig^{\prime}}^{g^{\prime}} \times} \right){\bi \varphi} ^{g^{\prime}} + \delta {\bi \omega} _{ig^{\prime}}^{g^{\prime}} - {\bi C}_b^{g^{\prime}} {\bi \varepsilon} ^b$$where ε represents gyro drift.
The transverse velocity error model is
$$\eqalign{\delta \dot{\bi v}^{g^{\prime}} & = - ((\delta {\bi \omega} _{ie^{\prime}}^{g^{\prime}} \times ) + (\delta {\bi \omega} _{ig^{\prime}}^{g^{\prime}} \times )){\bi v}^{g^{\prime}} - (({\bi \omega} _{ie^{\prime}}^{g^{\prime}} \times ) + ({\bi \omega} _{ig^{\prime}}^{g^{\prime}} \times ))\delta {\bi v}^{g^{\prime}} + \cr & \quad {\bi C}_b^{g^{\prime}} \nabla ^b - \left( {{\bi \varphi} ^{g^{\prime}} \times} \right){\bi f}^b + \delta {\bi G}^{{\bi g^{\prime}}}} $$
where 
$\nabla $ represents accelerometer bias.
The position information is provided in the transverse ellipsoidal Earth model. Its error model is
$$\eqalign{& \delta \dot L^{\prime} = - \displaystyle{1 \over \tau} \delta v_e^{g^{\prime}} + \displaystyle{1 \over {R_y}} \delta v_n^{g^{\prime}} \cr & \delta \dot \lambda ^{\prime} = \displaystyle{1 \over {R_x \cos L^{\prime}}}\delta v_e^{g^{\prime}} - \displaystyle{1 \over {\tau \cos L^{\prime}}}\delta v_n^{g^{\prime}} + \displaystyle{{\tan L^{\prime}} \over {\cos L^{\prime}}}\left(\displaystyle{{v_e^{g^{\prime}}} \over {R_x}} - \displaystyle{{v_n^{g^{\prime}}} \over \tau} \right)\delta L^{\prime}} $$From Equations (23) and (24), it can be seen that the error model of the transverse navigation system shares the same structure with the traditional inertial navigation system. In fact, the selection of different navigation frames will not affect the accuracy of the positioning. However, the transverse system succeeds in giving right directions in polar regions while the traditional mechanism fails.
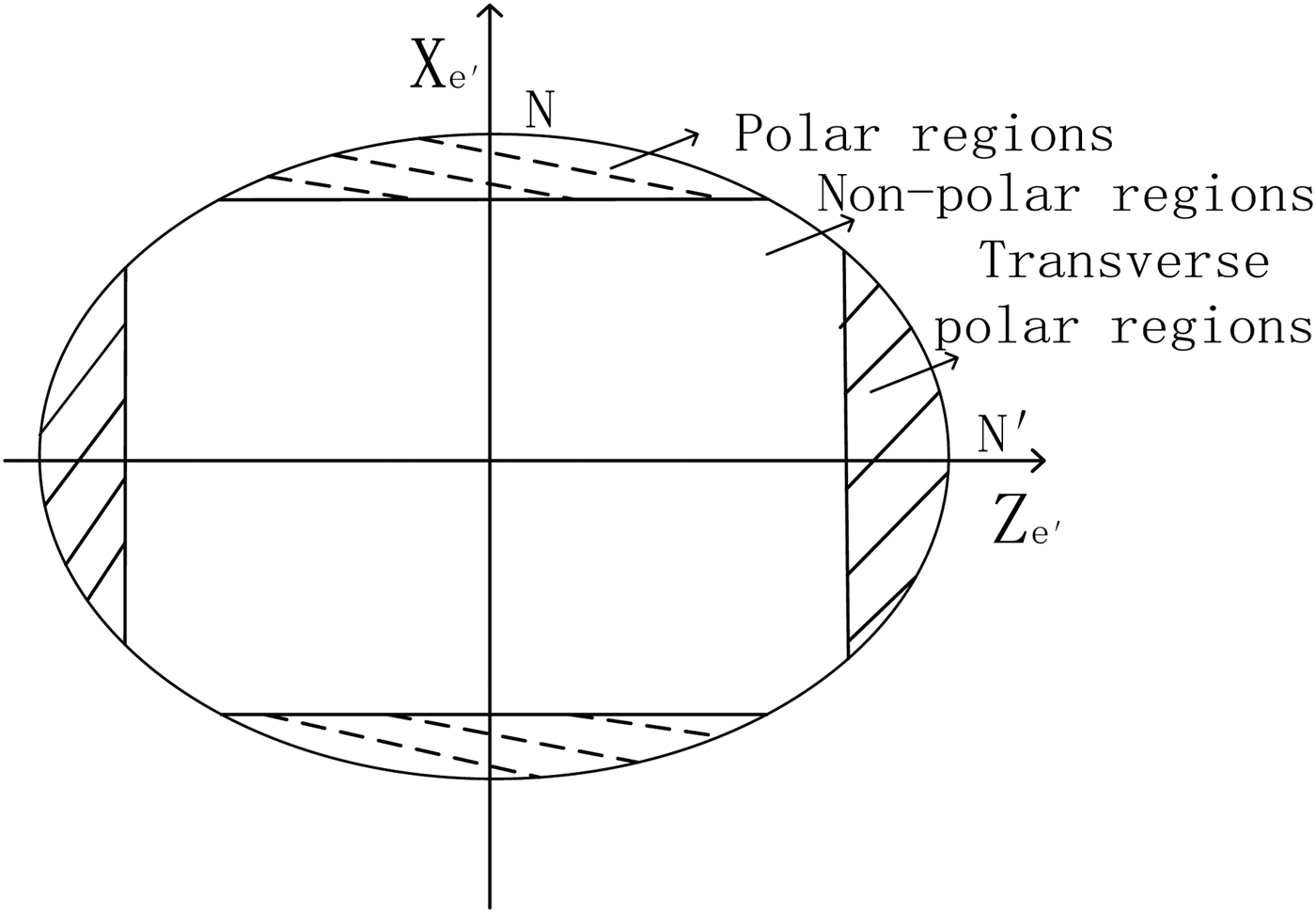
As shown in Equation (25), in the ellipsoidal Earth model, the errors of L′ and λ′ are more complex than those in the spherical model. Polar regions, which are far away from the transverse poles, have low transverse latitudes L′. Thus, cos L′ approaches 1 and the transverse navigation system works properly in these areas. Most non-polar regions with low transverse latitudes can still use the transverse navigation system to support accuracy. However, in the areas near the transverse poles, because of the high L′, cos L′ converges to 0 and the error of the transverse longitude diverges sharply. The transverse yaw fails to indicate the direction due to the convergence of the lines of transverse longitude.
Figure 4 illustrates the three different kinds of regions on the Earth. It is known that the traditional inertial navigation algorithm is invalid in polar regions. Therefore the transverse navigation algorithm has been proposed, which however does not work in transverse polar regions according to the error analysis above. In most non-polar regions, the transverse navigation system can operate properly, just like the traditional navigation system in mid-latitude regions. Thus, the application region of the proposed transverse system is not limited to polar regions, and research and field work should be done to evaluate the performance of transverse navigation system in non-polar regions, which is often easily ignored.
Figure 4. The division of regions.
4. EXPERIMENTAL RESULTS
In this section, the performance of the proposed algorithm in both polar and non-polar regions is evaluated. As discussed in Section 3, transverse navigation could also work in non-polar regions, and thus a field test was operated in Nanjing (118°E, 32°N), a mid-latitude area, to investigate the applicability of the presented algorithm in non-polar regions.
For polar regions, the practical deployment of the proposed method would require a distant journey to the North or South Pole. Simulations were made in related research (Zhou et al., Reference Zhou, Qin and Fu2013; Broxmeyer and Leondes, Reference Broxmeyer and Leondes1964; Li et al., Reference Li, Ben, Yu and Sun2015; Xu and Dou, Reference Xu and Dou2014). However, solely simulated data fails to show the impact of a real environment. To avoid this, an original and novel specific approach was adopted for the deployment and evaluation of the proposed algorithm in polar regions.
4.1. Transverse navigation in non-polar regions
A vehicle test was conducted to evaluate the performance of the proposed algorithm in Nanjing, Jiangsu Province, China. Parameters of gyros and the accelerometers are shown in Table 1. The reference navigation data are given by the loose couple of PHINS developed by French firm IXBLUE and the FlexPark6 GNSS receiver developed by NovAtel. The performance of the PHINS in GPS aided mode: both pitch and roll errors are less than 0.01°, heading error is less than 0.01°. PHINS and the inertial measurement unit (IMU) are fixed on the same mounting plate shown in Figure 5. Figure 6 is the navigation experimental car and the GNSS receiver antenna is marked.
Figure 5. Installation diagram.
Figure 6. Experimental car.
Table 1. The parameters of the inertial measurement unit.
The test lasted for 1·3 hours and the update rate was 200 Hz. It was conducted in Jianglonghu campus of Southeast University of Nanjing. Figure 7 shows the navigation trajectory from the reference systems and this track is marked on a map using Google Earth, shown in Figure 8.
Figure 7. Navigation track.
Figure 8. Navigation track on map.
To make a valid comparison of the transverse navigation system and the traditional inertial navigation system, the two systems were operated simultaneously and inputs of the gyros and accelerometers were transmitted to both systems synchronously. For the transverse inertial navigation system, the information of attitude, velocity and position was transformed into the system first to set the initial parameters of the proposed method. Then the transverse inertial navigation system was put to operation to update the navigation parameters. After each update period, the outputs, which were under the transverse navigation system, were transformed back into the traditional navigation system to compare with the reference. Figures 9–11 show the errors of attitude, velocity and position in the two systems. The red line denotes the transverse output, while the blue line indicates the output under the traditional strapdown inertial navigation system.
Figure 9. Position errors in non-polar region.
Figure 10. Velocity errors in non-polar region.
Figure 11. Attitude errors in non-polar region.
It can be seen that the proposed transverse navigation system performs as well as the traditional inertial navigation system. For the transverse navigation system, the latitude and longitude errors are both 0·01°. The eastward and northward velocity errors are smaller than 1 m/s respectively and the errors of pitch and roll are within 0·07°. The error of yaw has a tendency to increase, which is 0·1° at the end of the test.
Some small difference between the two navigation systems is shown in Figures 9–11. This is due to the non-commutativity error. As different navigation frames are utilised in the two systems, the rotating axes and the rotating order are diverse, which affects the calculation results (Babich, Reference Babich2014; Krobka, Reference Krobka2010).
In conclusion, the transverse algorithm satisfies the demand of accurate navigation in mid-latitude regions.
4.2. Transverse navigation in polar regions
A novel approach was adopted for the evaluation of the performance of the proposed algorithm in polar regions, avoiding solely simulated data. The data of IMU and the reference information of PHINS from the field test are still utilised to simulate the field test in polar regions. However, considering the difference between polar and non-polar regions, some compensations and transformations should be made to simulate the field test in polar regions.
4.2.1. Experimental preparation
The idea of simulating field tests in polar regions using the field test information from non-polar regions is to maintain the vehicle's attitude and velocity relative to the ground. The initial position is moved to a high latitude point in polar regions. Due to the different curvatures in various latitudes, the navigation track in non-polar regions cannot be transported parallel to polar regions. Parallel transport of the navigation track performed on the ground by vehicles in non-polar regions will lead to the suspension of the track in the air in polar regions.
Thus, the reference latitude and longitude information in polar regions is reconstructed using the reference velocity information.
$$\eqalign{& L_{new}^{(N)} = L_{new}^{(0)} + \sum\limits_{i = 1}^N {\displaystyle{{v_n^{g(i)}} \over {R_{Mnew}^{(i)}}}} \cdot \Delta T \cr & \rm \lambda _{new}^{(N)} = \rm \lambda _{new}^{(0)} + \sum\limits_{i = 1}^N {\displaystyle{{v_e^{g(i)}} \over {R_{Nnew}^{(i)} \cos L_{new}^{(i)}}}} \cdot \Delta T} $$
$$\eqalign{& R_{Mnew}^{(i)} = \displaystyle{{R_e (1 - q)^2} \over {\left( {1 - \left( {2 - q} \right)q\sin ^2 L_{new}^{\left( i \right)}} \right)^{3/2}}} \cr & R_{Nnew}^{(i)} = \displaystyle{{R_e} \over {\left( {1 - \left( {2 - q} \right)q\sin ^2 L_{new}^{\left( i \right)}} \right)^{1/2}}}}$$where superscript (i) indicates the number of time intervals and ΔT indicates the update period. The subscript “new” means the reconstruction of the parameter. It can be seen from the equation that the latitude, longitude and radii of the meridian and prime vertical are different from the original ones. The velocity relative to the ground is still the original one because the purpose of this special simulation is to reconstruct the same movement relative to the Earth. Unlike the reference latitude and longitude information, the reference altitude, attitude and velocity need no reconstruction.
On the other hand, the IMU data also needs some compensation. First, 
${\bi \omega} _{ib}^b $, the data from gyros, needs to be transformed to suit polar regions. As the attitude relative to Earth remains unchanged, 
${\bi \omega} _{gb}^b $ is the same in both polar and non-polar regions.
$${\bi \omega} _{gb}^b = {\bi \omega} _{ib}^b - {\bi \omega} _{ig}^b = {\bi \omega} _{ibnew}^b - {\bi \omega} _{ignew}^b$$
Thus, the new gyro data 
${\bi \omega} _{ibnew}^b $ in polar regions can be calculated,
$${\bi \omega} _{ibnew}^b = {\bi \omega} _{ib}^b - {\bi \omega} _{ig}^b + {\bi \omega} _{ignew}^b = {\bi \omega} _{ib}^b - {\bi C}_g^b \left( {{\bi \omega} _{ig}^g - {\bi \omega} _{ignew}^g} \right)$$
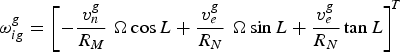$${\bi \omega} _{ig}^g = \left[ { - \displaystyle{{v_n^g} \over {R_M}} \,\, \Omega \cos L + \displaystyle{{v_e^g} \over {R_N}} \,\, \Omega \sin L + \displaystyle{{v_e^g} \over {R_N}} \tan L} \right]^{\!T}$$where Ω is the Earth's rotation rate.
$${\bi \omega} _{ignew}^g = \left[ { - \displaystyle{{v_n^g} \over {R_{Mnew}}} \,\, \Omega \cos L_{new} + \displaystyle{{v_e^g} \over {R_{Nnew}}} \,\, \Omega \sin L_{new} + \displaystyle{{v_e^g} \over {R_{Nnew}}} \tan L_{new}} \right]^{\!T}$$
where direction cosine matrix 
${\bi C}_g^b $ and velocity vg remain the same as it is in the non-polar regions to ensure the same movement relative to Earth.
Furthermore, fb, the measurement of the accelerometer also needs compensation. As the velocity relative to Earth remains unchanged, 
$\dot{\bi v}^g $ is the same in both polar and non-polar regions.
$$\dot{\bi v}^g = {\bi f}^g - \left( {{\bi \omega} _{ie}^g + {\bi \omega} _{ig}^g} \right) \times {\bi v}^g + {\bi G}^g = {\bi f}_{new}^g - \left( {{\bi \omega} _{ienew}^g + {\bi \omega} _{ignew}^g} \right) \times {\bi v}^g + {\bi G}_{new}^g $$
Thus, new accelerometer data 
${\bi f}_{new}^b $ in polar regions can be calculated,
$${\bi f}_{new}^b = {\bi C}_g^b \left( {{\bi C}_b^g \,{\bi f}^b - \left( {{\bi \omega} _{ie}^g + {\bi \omega} _{ig}^g - {\bi \omega} _{ienew}^g - {\bi \omega} _{ignew}^g} \right) \times {\bi v}^g + {\bi G}^g - {\bi G}_{new}^g} \right)$$
$${\bi \omega} _{ie}^g = \left[ {\matrix{ 0 & {\Omega \cos L} & {\Omega \sin L} \cr}} \right]^T $$
$${\bi \omega} _{ienew}^g = \left[ {\matrix{ 0 & {\Omega \cos L_{new}} & {\Omega \sin L_{new}} \cr}} \right]^T $$4.2.2. Experimental results
A simulated field test was conducted for polar regions. The initial longitude is the same as that in the vehicle test in Section 4.1. The initial latitude is set to be 88°N. The parameters of IMU and the update rate remained the same. Figure 12 is the navigation trajectory in the polar region.
Figure 12. Navigation track in polar region.
It can be seen from Figure 12 that the range of longitude is wider compared to how it is in the mid-latitude region, which reflects the convergence of longitude in polar regions. The errors of attitude, velocity and position of the two systems in polar regions are shown in Figures 13 to 15.
Figure 13. Position errors in polar region.
Figure 14. Velocity errors in polar region.
Figure 15. Attitude errors in polar region.
It can be seen that the proposed transverse navigation system outperforms the traditional inertial navigation system in polar regions.
For the traditional navigation system, the errors of longitude and yaw reach 0·5° in 1·3 hours, which is too long for an inertial navigation system to navigate accurately. This trend becomes worse with the time. For navigation in polar regions, where external correction information hardly exists, the errors are less tolerable.
For the transverse navigation system, the latitude error is 0·02°, while the longitude error is 0·005°. The divergent error of yaw is much smaller than it is in the traditional navigation system, which is 0·1° at the end of the test.
Comparisons can also be made between the navigation results in polar and non-polar regions. It is shown that for the same vehicle movement relative to Earth, the traditional navigation system performs quite differently in polar and non-polar regions. However, the proposed transverse navigation system can ensure accuracy in both areas. This coincides with the theoretical analysis in Section 3, which affirms the applicability of the proposed algorithm in both polar and most non-polar regions.
To summarise, the traditional navigation system cannot meet the demand of accurate positioning in polar regions, while the transverse navigation system can.
6. CONCLUSION
In this research, a transverse navigation mechanism under the ellipsoidal Earth model is proposed to address the theoretical error resulting from the inaccurate spherical Earth model. The corresponding error analysis is conducted to specify the scope of applications of the proposed algorithm. According to the theoretical analysis, the proposed navigation system is capable of working in both polar regions and most non-polar areas. A field test was conducted on one of the campuses of Southeast University in Nanjing to evaluate the performance of the transverse navigation system. Meanwhile, a novel experimental approach using field test data from a mid-latitude area to simulate the IMU data and reference information in polar regions, was utilised to investigate the performance of the proposed transverse navigation system in polar environments. From the experiment results it can be concluded that the proposed transverse navigation system can ensure the same accuracy as the traditional inertial navigation system in mid-latitude regions. However, when applied to navigation in polar regions, this new mechanism outperforms the traditional method, achieving much lower errors in longitude and yaw.
ACKNOWLEDGMENTS
This work was supported in part by the National Natural Science Foundation (Grants 61473085,51175082,61273056), this support is greatly appreciated.
