Published online by Cambridge University Press: 12 March 2014
We consider IOpen, the subsystem of PA (Peano Arithmetic) with the induction scheme restricted to quantifier-free formulas.
We prove that each model of IOpen can be embedded in a model where the equation 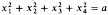 has a solution. The main lemma states that there is no polynomial f{x,y) with coefficients in a (nonstandard) DOR M such that ∣f(x,y) ∣ < 1 for every (x,y) Є C, where C is the curve defined on the real closure of M by C: x2 + y2 = a and a > 0 is a nonstandard element of M.
has a solution. The main lemma states that there is no polynomial f{x,y) with coefficients in a (nonstandard) DOR M such that ∣f(x,y) ∣ < 1 for every (x,y) Є C, where C is the curve defined on the real closure of M by C: x2 + y2 = a and a > 0 is a nonstandard element of M.
Please note a has been issued for this article.