1 Introduction
In a recent article in this journal, Oppenheimer and Monin (Reference Oppenheimer and Monin2009) raised the possibility that people’s judgments about the past history of a random process might display the same biases as their predictions of future outcomes. Oppenheimer and Monin focussed on the gambler’s fallacy — the belief that a streak of one outcome raises the probability of the other outcome above the base rate (e.g., Tune, Reference Tune1964). The most common explanation of the gambler’s fallacy is that people employ a representativeness heuristic — they believe in the “law of small numbers” (Tverysky & Kahneman, Reference Tversky and Kahneman1971), such that small samples should be representative of the underlying probabilities: a run of one outcome needs to be “balanced out” by the occurrence of the opposite outcome.
Oppenheimer and Monin (Reference Oppenheimer and Monin2009) suggested that the gambler’s fallacy might also operate when people reconstruct the past history of a random process. Rather than having participants predict future outcomes, they asked people to estimate the number of trials that had preceded the occurrence of a particular event. For example, participants were asked to imagine walking into a room to find a man flipping a coin five times, either producing a streak of five heads or a mix of three heads and two tails. Participants were then asked how many times the man had flipped the coin before they entered the room. The estimates of participants in the streak condition were much larger than those of participants in the non-streak condition. This result generalizes: across a wide variety of domains, Oppenheimer and Monin found that the estimated number of previous trials was greater when the outcome was subjectively unlikely, an effect they refer to as the retrospective gambler’s fallacy.
This effect is important because it suggests that the heuristics and biases that shape our predictions of the future also colour our reconstruction of the past (see Olivola & Oppenheimer, Reference Olivola and Oppenheimer2008, for an additional exploration of this idea). However, it is notable that the focus of Oppenheimer and Monin’s (Reference Oppenheimer and Monin2009) work is not on the gambler’s fallacy as traditionally conceived. Rather than examining judgments about the outcomes of previous trials in a manner analogous to the prediction of future outcomes, the authors focussed on estimates of the number of preceding trials. As Oppenheimer and Monin note: “The most straightforward instantiation of the retrospective gambler’s fallacy would be formally identical to the gambler’s fallacy, only in the past… While this would be a natural extension of the gambler’s fallacy, it has, to our knowledge, never been tested” (p. 326).
The current experiment supplements Oppenhemier & Monin’s (Reference Oppenheimer and Monin2009) work by providing such a test. Participants were told about a streak of one outcome and asked either to predict the next outcome or to infer the outcome of the trial before the streak. As an additional manipulation, the data-generating process was varied: for some participants it was a physical process likely to be regarded as random (coin flipping) whilst for others it was a skill-based action (basketball shooting). The motivation for this was that, although the gambler’s fallacy is widespread, some judgment domains produce the opposite bias — the belief that a streak of one outcome increases the probability of that outcome (Gilovich, Vallone, & Tversky, Reference Gilovich, Vallone and Tversky1985). This bias is referred to as the hot hand fallacy or, more neutrally, as belief in the hot hand (see Alter & Oppenheimer, 2008, for a recent review) and seems to occur for processes which are regarded as non-random and which involve an element of human skill (Ayton & Fischer, Reference Ayton and Fischer2004; Burns & Corpus, Reference Burns and Corpus2004; for comparable results in other domains, see e.g., Matthews & Stewart, Reference Matthews and Stewart2009a, 2009b; for an interesting theoretical discussion, see Sun & Wang, Reference Sun and Wang2010.) The current experiment therefore asked: Do judgments about the past show the same biases as predictions of the future, and are these effects differentially influenced by the nature of the random outcomes?
2 Method
2.1 Participants
A total of 207 people (aged 16–78; mean age 28.85 years, SD = 13.02; 96 male) participated on a voluntary basis. Participants were recruited via a form of snowball sampling. Initially, a group of undergraduate psychology students participated at the start of a class; all were naive to the purposes of the experiment. Each student was then given the materials to test four other participants, one in each condition. (A small number of students who missed the initial session also completed this data collection.) The students were encouraged to recruit from a wide range of friends, colleagues, co-workers etc. It was emphasized that participants should not take part more than once, and that the students should check whether prospective participants had already taken part before administering the task.Footnote 1
2.2 Design and procedure
The study employed a 2×2 design with scenario (coin flip or basketball shot) and time (inferring the past or predicting the future) as between-subject variables. Each participant read a description of a streak. In the coin condition, the data-generating process was a coin toss and the streak was a run of four heads; in the basketball condition, it was a person practicing basketball and the streak was a run of four successful shots. In both cases it was explained that the long-term probability of each outcome is .5. (This equilibration of base rates is important if the results of the two conditions are to be comparable; see Burns & Corpus, Reference Burns and Corpus2004). Participants in the future condition were asked to predict the next outcome in the sequence; those in the past condition were asked to indicate the outcome of the trial immediately before the streak. Participants indicated their judgments on a nine-point scale. On this scale, 9 indicated a certainty of an outcome of the same type as the streak and 1 indicated certainty of the opposite outcome; 5 indicated that both outcomes were equally likely. A verbally-anchored rating scale was used in case the broad spectrum of participants meant that not all were confident about numerically estimating probabilities. Care was taken to ensure that the structure and wording of each scenario was as similar as possible; the full text of each is reproduced in the Appendix.
3 Results
Figure 1 shows the distribution of responses for each condition; the mean and standard deviations of the judgments are included on the plots. The modal response in all conditions is 5, showing that a large number of participants show no bias. Oppenheimer & Monin (Reference Oppenheimer and Monin2009) note a similar result. However, inspection of the mean judgments shows that the average judgments differ between the conditions. A 2×2 between-subjects ANOVA showed that the streak was judged more likely to end in the coin scenario than in the basketball scenario, F(1,203) = 13.38, p < .001, partial η2 = .06. There was no effect of time and no interaction (both Fs less than 1). (The data show some violations of normality, but the sample sizes are large and there is no heterogeneity of variance so the ANOVA is likely to be robust. Moreover, a series of non-parametric Mann-Whitney tests produced the same pattern of results.)
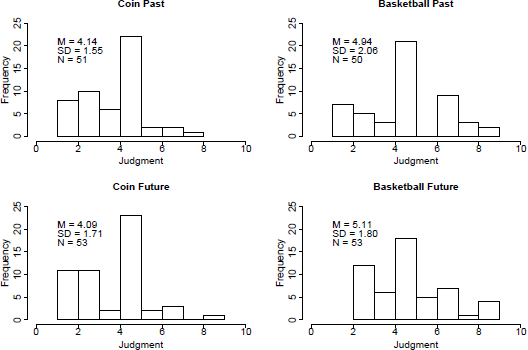
Figure 1: Distribution of responses for each condition.
One-sample t-tests were used to see whether the mean judgments in each condition differed from the mid-point of the rating scale. For both of the Coin conditions, there was a highly significant tendency to expect streak termination (t(50) = −3.98, p<.001 for the Coin Past condition; t(52) = −3.85, p<.001 for the Coin Future condition.) Judgements in the Basketball conditions showed no bias (ts < 1).Footnote 2
4 Discussion
The results may be simply summarized. After being told that a coin had come up heads four times in a row, participants judged that it was more likely to come up tails on the next flip. This is the gambler’s fallacy. When asked about the outcome of the flip preceding the streak, participants displayed exactly the same bias. When told about an identical sequence of outcomes from a process involving an element of human skill – basketball shooting – participants showed no sign of the gambler’s fallacy, either when predicting the future or reconstructing the past.
The results from the coin conditions supplement Oppenheimer and Monin (Reference Oppenheimer and Monin2009) and support their conclusion that the biases which shape our predictions of the future operate in an apparently identical manner when we make inferences about the past. This is an important point to establish, not least because of the importance of inference and reconstruction as mnemonic strategies (e.g., Dooling & Christiaansen, Reference Dooling and Christiaansen1977).
The difference between the coin flip and basketball conditions mirrors that found in previous work, and lends credence to the idea that people’s perceptions of the data-generating process are an important determinant of the gambler’s and hot hand fallacies. The basketball scenario in the current experiment was very similar to that used by Burns and Corpus (Reference Burns and Corpus2004), whose participants likewise judged the probability of streak continuation to be about 50%. The basketball judgments did not (on average) demonstrate belief in the hot hand; whether scenarios which elicit such a belief will affect inferences about the past remains an important topic for subsequent research.
One strength of the current experiment is that it used a retrospective judgment task which is directly equivalent to the future prediction tasks used in studies of the gambler’s fallacy. Oppenheimer and Monin (Reference Oppenheimer and Monin2009) had people estimate the number of trials that preceded a particular outcome. As these authors point out, the participants may have misinterpreted their task and estimated the number of trials needed if one were waiting to obtain the outcome — which will, on average, take longer for rare events. The task used here is not susceptible to such a misinterpretation.
A question arises about terminology. Oppenheimer and Monin (Reference Oppenheimer and Monin2009) found that rare events are taken to indicate a larger number of preceding trials, and refer to this as the retrospective gambler’s fallacy. However, the gambler’s fallacy is more usually taken to involve a judgment about the probability of a particular outcome — specifically, the probability that a streak will continue. Oppenheimer and Monin’s results show that people regard rare outcomes as indicative of longer preceding trial sequences, consistent with a belief in representativeness that extends to the reconstruction of the past. Although representativeness is often advanced as an explanation for the gambler’s fallacy, the two are not synonymous and there are other theoretical explanations for people’s biased judgments about the probability of streak continuation (e.g., Ayton & Fischer, Reference Ayton and Fischer2004). Referring to Oppenheimer and Monin’s result as the retrospective gambler’s fallacy risks confusing the empirical phenomenon with the theoretical explanation. The effect discovered by Oppenheimer and Monin might better be referred to as “retrospective representativeness”, or perhaps “retrospective belief in the law of small numbers”, with the term “retrospective gambler’s fallacy” being reserved for situations where a streak is taken to indicate that the unobserved preceding event was of the opposite type – that is, for the phenomenon revealed by the current experiment. Both phenomena are likely to be manifestations of the same underlying beliefs about random sequences, and both indicate that the heuristics and biases that shape our predictions of the future operate in the same way when we attempt to reconstruct the past.
Appendix
4.1 Instructions for Coin Past condition
Consider flipping a fair coin. In the long run, it comes up heads and tails about equally often. The last four flips in a row have all come up heads. You do not know whether the flip before that came up heads or tails, but if you had to guess, what would you say? To indicate your judgment, circle one of the numbers below. Larger numbers indicate greater confidence that the coin came up heads, from 1 (“definitely tails”) to 9 (“definitely heads”).
4.2 Instructions for Coin Future condition
Consider flipping a fair coin. In the long run, it comes up heads and tails about equally often. The last four flips in a row have all come up heads. You do not know whether the next flip will come up heads or tails, but if you had to guess, what would you say? To indicate your judgment, circle one of the numbers below. Larger numbers indicate greater confidence that the coin will come up heads, from 1 (“definitely tails”) to 9 (“definitely heads”).
4.3 Instructions for Coin Past condition
Consider a basketball player who is practicing throwing the ball through the ring from a certain distance. In the long run, his shots go in and miss about equally often. His last four shots in a row have all gone in. You do not know whether the shot before that went in or missed, but if you had to guess, what would you say? To indicate your judgment, circle one of the numbers below. Larger numbers indicate greater confidence that the shot went in, from 1 (“definitely missed”) to 9 (“definitely went in”).
4.4 Instructions for Coin Future condition
Consider a basketball player who is practicing throwing the ball through the ring from a certain distance. In the long run, his shots go in and miss about equally often. His last four shots in a row have all gone in. You do not know whether the next shot will go in or miss, but if you had to guess, what would you say? To indicate your judgment, circle one of the numbers below. Larger numbers indicate greater confidence that the shot will go in, from 1 (“definitely miss”) to 9 (“definitely go in”).



