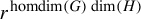1. Introduction
This article is concerned with the complexity of discrete subsets of locally compact groups, which obey some form of aperiodic order. An extensive discussion of this can be found in the thesis by the author [Reference Kaiser27]. In this paper, our focus is on the Lie group case and in a following paper, we will extend the argumentation to hyperbolic spaces.
For discrete subsets of locally compact abelian groups, notably for discrete subsets of
![]() ${\mathbb {R}}^n$
, there is an established notion of complexity based on the study of the so-called patch counting function [Reference Arnoux, Mauduit, Shiokawa and Tamura1, Reference Baryshnikov5, Reference Haynes, Koivusalo and Walton21, Reference Julien26, Reference Lagarias30, Reference Lagarias and Pleasants32, Reference Moody37, Reference Moody38, Reference Vuillon50]. More recently, there has been an approach to extend results about discrete subsets of locally abelian groups to general locally compact groups [Reference Beckus, Hartnick and Pogorzelski7–Reference Björklund, Hartnick and Pogorzelski10].
${\mathbb {R}}^n$
, there is an established notion of complexity based on the study of the so-called patch counting function [Reference Arnoux, Mauduit, Shiokawa and Tamura1, Reference Baryshnikov5, Reference Haynes, Koivusalo and Walton21, Reference Julien26, Reference Lagarias30, Reference Lagarias and Pleasants32, Reference Moody37, Reference Moody38, Reference Vuillon50]. More recently, there has been an approach to extend results about discrete subsets of locally abelian groups to general locally compact groups [Reference Beckus, Hartnick and Pogorzelski7–Reference Björklund, Hartnick and Pogorzelski10].
In the present article, we contribute to this program by extending the notion of complexity to discrete subsets of non-abelian locally compact groups. More specifically, we are going to generalize an approach of Julien [Reference Julien26], and Haynes, Koivusalo and Walton [Reference Haynes, Koivusalo and Walton21]. While the theory works in full generality, we will obtain our strongest results in the case of two-step-nilpotent Lie groups.
1.1. Aperiodic order in the Euclidean case
Consider the abelian group
![]() $({\mathbb {R}}^n, +)$
as a metric group with respect to the standard Euclidean metric. A set
$({\mathbb {R}}^n, +)$
as a metric group with respect to the standard Euclidean metric. A set
![]() $\Lambda \subset {\mathbb {R}}^n$
is called locally finite if for all bounded sets
$\Lambda \subset {\mathbb {R}}^n$
is called locally finite if for all bounded sets
![]() $B \subset {\mathbb {R}}^n$
, the intersection
$B \subset {\mathbb {R}}^n$
, the intersection
![]() $\Lambda \cap B$
is finite. For these sets, one can define the patch counting function
$\Lambda \cap B$
is finite. For these sets, one can define the patch counting function
![]() $p(r)$
(see Definition 1.2) as a measure of their complexity. Examples of locally finite sets are lattices. Their complexity functions are constant 1, meaning that lattices are highly structured. In the case of aperiodic ordered sets, the patch counting function is growing at least linearly [Reference Lagarias30, Reference Lagarias and Pleasants32, Reference Moody37, Reference Moody38, Reference Vuillon50]. A locally finite set with
$p(r)$
(see Definition 1.2) as a measure of their complexity. Examples of locally finite sets are lattices. Their complexity functions are constant 1, meaning that lattices are highly structured. In the case of aperiodic ordered sets, the patch counting function is growing at least linearly [Reference Lagarias30, Reference Lagarias and Pleasants32, Reference Moody37, Reference Moody38, Reference Vuillon50]. A locally finite set with
![]() $p(r)< \infty $
for all
$p(r)< \infty $
for all
![]() $r>0$
is called a set with finite local complexity or an FLC set.
$r>0$
is called a set with finite local complexity or an FLC set.
There are two important methods to construct FLC sets, either by substitution or by cut-and-project. We are interested in the cut-and-project approach, which is due to Yves Meyer, who is a pioneer in the field of aperiodic order and laid the foundation for much of our common knowledge in the 1960s [Reference Meyer34–Reference Meyer36]. The idea in the cut-and-project approach is to consider a lattice
![]() $\Gamma $
in the product
$\Gamma $
in the product
![]() ${\mathbb {R}}^n \times {\mathbb {R}}^d$
. Then one chooses a subset
${\mathbb {R}}^n \times {\mathbb {R}}^d$
. Then one chooses a subset
![]() $W \subset {\mathbb {R}}^d$
, which is called the window. The projection of
$W \subset {\mathbb {R}}^d$
, which is called the window. The projection of
![]() $({\mathbb {R}}^n \times W) \cap \Gamma $
to
$({\mathbb {R}}^n \times W) \cap \Gamma $
to
![]() ${\mathbb {R}}^n$
results in a point set, which is called a cut-and-project set. Under some extra conditions, this cut-and-project set is an FLC set, and in this case, it is called the model set defined by the data
${\mathbb {R}}^n$
results in a point set, which is called a cut-and-project set. Under some extra conditions, this cut-and-project set is an FLC set, and in this case, it is called the model set defined by the data
![]() $\Lambda ({\mathbb {R}}^n, {\mathbb {R}}^d, \Gamma , W)$
. Such sets have been studied from different perspectives, see for example [Reference Baake, Huck and Strungaru3, Reference Haynes, Koivusalo and Walton21, Reference Hof24, Reference Lagarias29, Reference Moody39].
$\Lambda ({\mathbb {R}}^n, {\mathbb {R}}^d, \Gamma , W)$
. Such sets have been studied from different perspectives, see for example [Reference Baake, Huck and Strungaru3, Reference Haynes, Koivusalo and Walton21, Reference Hof24, Reference Lagarias29, Reference Moody39].
The approach has also been generalized to abelian locally compact second countable groups, see for example [Reference Schlottmann42, Reference Schlottmann43].
In the 1980s, the popularity of this field was pushed by the discovery of quasi-crystals [Reference Shechtman, Blech, Gratias and Cahn45]. After this discovery, physicists, crystallographers and mathematicians worked on models to describe these newly discovered aperiodic structures. Physicists are primarily interested in quasi-crystals in
![]() ${\mathbb {R}}^n$
for
${\mathbb {R}}^n$
for
![]() $n \leq 3$
, but mathematically, the restriction on the dimension is unnatural and therefore was rapidly dropped. A history of the developments in this time can be found in the book by Senechal [Reference Senechal44]. The characterizing property of a quasi-crystal is pure-point diffraction, which is a global property and was studied in [Reference Baake and Lenz4, Reference Dworkin13, Reference Hof22, Reference Hof23, Reference Lagarias31]. Another line of research is to characterize the structure of an aperiodic ordered set by some local data, namely its repetitivity or its complexity [Reference Lagarias30, Reference Lagarias and Pleasants32, Reference Moody37, Reference Moody38, Reference Vuillon50]. For a comprehensive overview of the field, see [Reference Baake and Grimm2].
$n \leq 3$
, but mathematically, the restriction on the dimension is unnatural and therefore was rapidly dropped. A history of the developments in this time can be found in the book by Senechal [Reference Senechal44]. The characterizing property of a quasi-crystal is pure-point diffraction, which is a global property and was studied in [Reference Baake and Lenz4, Reference Dworkin13, Reference Hof22, Reference Hof23, Reference Lagarias31]. Another line of research is to characterize the structure of an aperiodic ordered set by some local data, namely its repetitivity or its complexity [Reference Lagarias30, Reference Lagarias and Pleasants32, Reference Moody37, Reference Moody38, Reference Vuillon50]. For a comprehensive overview of the field, see [Reference Baake and Grimm2].
This paper will focus on understanding the complexity of model sets. We want to determine how the complexity function
![]() $p(r)$
behaves asymptotically.
$p(r)$
behaves asymptotically.
Definition 1.1. (Patch)
Let X be a metric space,
![]() $\Lambda \subset X$
a locally finite subset,
$\Lambda \subset X$
a locally finite subset,
![]() $\unicode{x3bb} \in \Lambda $
and
$\unicode{x3bb} \in \Lambda $
and
![]() $r\in {\mathbb {R}}^+$
. Then the r-patch
$r\in {\mathbb {R}}^+$
. Then the r-patch
![]() $P_r(\unicode{x3bb} )$
is the constellation of points from
$P_r(\unicode{x3bb} )$
is the constellation of points from
![]() $\Lambda $
around
$\Lambda $
around
![]() $\unicode{x3bb} $
, which have distance at most r to
$\unicode{x3bb} $
, which have distance at most r to
![]() $\unicode{x3bb} $
, that is,
$\unicode{x3bb} $
, that is,
![]() $ P_r(\unicode{x3bb} ):= B_r(\unicode{x3bb} ) \cap \Lambda $
.
$ P_r(\unicode{x3bb} ):= B_r(\unicode{x3bb} ) \cap \Lambda $
.
If G is a locally compact second countable (lcsc) group, the set of patches of radius r impose an equivalence relation on the elements of
![]() $\Lambda \subset G$
by
$\Lambda \subset G$
by
We will denote the r-equivalence class of
![]() $\unicode{x3bb} $
by
$\unicode{x3bb} $
by
and the set of all equivalence classes by
Definition 1.2. (Complexity function)
Let G be an lcsc group and
![]() $\Lambda \subset G$
a locally finite subset. Then the complexity function
$\Lambda \subset G$
a locally finite subset. Then the complexity function
![]() $p(r)$
is given by
$p(r)$
is given by
The function p is also called the patch-counting function and first appeared in the work by Lagarias and Pleasants [Reference Lagarias and Pleasants32], where it is denoted by
![]() $N_X$
. Note that model sets carry more information than the underlying point set itself, and this can be used to determine the complexity function. Some early work in this context is done in [Reference Arnoux, Mauduit, Shiokawa and Tamura1, Reference Baryshnikov5] for some special cases and low dimensions. A general approach first appeared in the paper by Julien [Reference Julien26], where the main idea is that each class of patches corresponds to a certain region inside the window, the so called acceptance domain. Optimal results can be obtained in the case of polytopal windows, that is, when W is a convex polytope. The ideas of Julien were picked up by Koivusalo and Walton [Reference Koivusalo and Walton28], who proved the following theorem. We will assume the stabilizers of the hyperplanes which bound the window are trivial; in the original theorem, the role of these stabilizers is addressed.
$N_X$
. Note that model sets carry more information than the underlying point set itself, and this can be used to determine the complexity function. Some early work in this context is done in [Reference Arnoux, Mauduit, Shiokawa and Tamura1, Reference Baryshnikov5] for some special cases and low dimensions. A general approach first appeared in the paper by Julien [Reference Julien26], where the main idea is that each class of patches corresponds to a certain region inside the window, the so called acceptance domain. Optimal results can be obtained in the case of polytopal windows, that is, when W is a convex polytope. The ideas of Julien were picked up by Koivusalo and Walton [Reference Koivusalo and Walton28], who proved the following theorem. We will assume the stabilizers of the hyperplanes which bound the window are trivial; in the original theorem, the role of these stabilizers is addressed.
Theorem 1.3. (Koivusalo and Walton [Reference Koivusalo and Walton28, Theorem 7.1])
Consider a model set
![]() $\Lambda ({\mathbb {R}}^n, {\mathbb {R}}^d, \Gamma , W)$
with a polytopal window W. Assume that the stabilizers of the hyperplanes which bound the window are trivial. Then the complexity grows asymptotically as
$\Lambda ({\mathbb {R}}^n, {\mathbb {R}}^d, \Gamma , W)$
with a polytopal window W. Assume that the stabilizers of the hyperplanes which bound the window are trivial. Then the complexity grows asymptotically as
![]() $p(r) \asymp r^{n \cdot d}$
.
$p(r) \asymp r^{n \cdot d}$
.
1.2. Aperiodic order beyond the Euclidean case
A natural generalization of FLC sets in
![]() ${\mathbb {R}}^n$
is to consider FLC sets in arbitrary locally compact groups equipped with some metric. We will be interested in studying their complexity functions. We emphasize that in doing so, the choice of metric is important. By the restriction to lcsc groups, a theorem of Struble [Reference Struble47] guarantees the existence of a ‘nice’ metric. ‘Nice’ means in this context that the metric is right-invariant, proper and compatible. So we will study metric groups, in which the metric fulfils these properties. This is the setup in which the Euclidean ideas are generalized [Reference Beckus, Hartnick and Pogorzelski7–Reference Björklund, Hartnick and Pogorzelski10, Reference Lenz and Strungaru33].
${\mathbb {R}}^n$
is to consider FLC sets in arbitrary locally compact groups equipped with some metric. We will be interested in studying their complexity functions. We emphasize that in doing so, the choice of metric is important. By the restriction to lcsc groups, a theorem of Struble [Reference Struble47] guarantees the existence of a ‘nice’ metric. ‘Nice’ means in this context that the metric is right-invariant, proper and compatible. So we will study metric groups, in which the metric fulfils these properties. This is the setup in which the Euclidean ideas are generalized [Reference Beckus, Hartnick and Pogorzelski7–Reference Björklund, Hartnick and Pogorzelski10, Reference Lenz and Strungaru33].
The cut-and-project approach also applies in this more general setup [Reference Björklund, Hartnick and Pogorzelski10]. The question we want to answer is how the approach of Julien, and Koivusalo and Walton can be translated to this more general setup? This question was asked during the 2017 Oberwolfach workshop ‘Spectral Structures and Topological Methods in Mathematical Quasicrystals’ for the Heisenberg group by Tobias Hartnick and Henna Koivusalo.
1.3. Results on two-step homogeneous Lie groups
Ideally, one would like to describe the complexity of FLC sets for all lcsc groups. However, this turns out to be quite challenging so we will have to introduce some more restrictions. In particular, since we want to follow the approach of Julien [Reference Julien26], and Koivusalo and Walton [Reference Koivusalo and Walton28], we need a notion of hyperplanes. So a first question is in which groups can we define hyperplanes?
We will consider homogeneous Lie groups. These groups are nilpotent, real, finite-dimensional, connected, simply connected and admit a family of dilations which replace the scalar multiplication. For a detailed discussion of such groups, we refer to the book by Fischer and Ruzhansky [Reference Fischer and Ruzhansky14]. For this class of groups, it is possible to identify the underlying set of the Lie group G with the corresponding Lie algebra
![]() ${\mathfrak {g}}$
. Since
${\mathfrak {g}}$
. Since
![]() ${\mathfrak {g}}$
is a vector space, we can define hyperplanes in the usual sense. An example of such a group is the Heisenberg group.
${\mathfrak {g}}$
is a vector space, we can define hyperplanes in the usual sense. An example of such a group is the Heisenberg group.
Moreover, these groups admit a canonical quasi-isometry class of homogeneous norms, which provide the same complexity resolving the aforementioned issue of dependence on the choice of metric. It turns out that balls with respect to such norms have exact polynomial growth, that is, the volume of a ball
![]() $B_r(e)$
grows as
$B_r(e)$
grows as
![]() $r^{\alpha }$
. The exponent of this growth is called the homogeneous dimension of the homogeneous Lie group.
$r^{\alpha }$
. The exponent of this growth is called the homogeneous dimension of the homogeneous Lie group.
A second restriction has to be made since we also need that the group acts on the space of hyperplanes in the vector space underlying
![]() ${\mathfrak {g}}$
. We can show that this is the case exactly if the Lie group has nilpotency degree one or two, that is, if it is abelian or two-step nilpotent. For higher nilpotency degree, the action of the group bends the hyperplanes into algebraic hypersurfaces.
${\mathfrak {g}}$
. We can show that this is the case exactly if the Lie group has nilpotency degree one or two, that is, if it is abelian or two-step nilpotent. For higher nilpotency degree, the action of the group bends the hyperplanes into algebraic hypersurfaces.
Naively, one would expect that the complexity function of a model set
![]() $\Lambda (G,H, \Gamma , W)$
would depend on the dimension of the Lie groups G and H, that is,
$\Lambda (G,H, \Gamma , W)$
would depend on the dimension of the Lie groups G and H, that is,
![]() $p(r)\asymp r^{\dim (G)\dim (H)}$
, or if not, their homogeneous dimensions, that is,
$p(r)\asymp r^{\dim (G)\dim (H)}$
, or if not, their homogeneous dimensions, that is,
![]() $p(r) \asymp r^{{\mathrm {homdim}}(G){\mathrm {homdim}}(H)}$
, but surprisingly, both turn out to be false. In fact, the two factors behave differently. On the G-side, the homogeneous dimension replaces the dimension, while on the H-side, it does not. More precisely, we prove the following theorem, which is the main theorem of this paper.
$p(r) \asymp r^{{\mathrm {homdim}}(G){\mathrm {homdim}}(H)}$
, but surprisingly, both turn out to be false. In fact, the two factors behave differently. On the G-side, the homogeneous dimension replaces the dimension, while on the H-side, it does not. More precisely, we prove the following theorem, which is the main theorem of this paper.
Theorem 1.4. (Informal version of the main theorem, Theorem 5.1)
Consider a model set
![]() $\Lambda (G, H, \Gamma , W)$
with a convex polytopal window W, and G and H two-step nilpotent homogeneous Lie groups. Assume that the stabilizer of the hyperplanes which bound the window is trivial. Then the complexity grows asymptotically as
$\Lambda (G, H, \Gamma , W)$
with a convex polytopal window W, and G and H two-step nilpotent homogeneous Lie groups. Assume that the stabilizer of the hyperplanes which bound the window is trivial. Then the complexity grows asymptotically as
![]() $p(r) \asymp r^{{\mathrm {homdim}}(G) \cdot \dim (H)}$
.
$p(r) \asymp r^{{\mathrm {homdim}}(G) \cdot \dim (H)}$
.
1.4. Method of proof
The proof of the main theorem consists of four steps. The first three are similar to the Euclidean case, while the fourth one uses different techniques.
First, we will establish the connection between the equivalence classes of patches and the acceptance domains in §2. This is a translation from the Euclidean case considered in [Reference Koivusalo and Walton28]. The only difference is that we have to be a bit more careful since our groups are, in general, non-abelian. The established result is the same as in the Euclidean case.
Definition 1.5. Let
![]() $\Lambda (G,H, \Gamma , W)$
be a model set, with
$\Lambda (G,H, \Gamma , W)$
be a model set, with
![]() $G, H$
lcsc groups,
$G, H$
lcsc groups,
![]() $\Gamma \subset G \times H$
a uniform lattice and
$\Gamma \subset G \times H$
a uniform lattice and
![]() $W\subset H$
a non-empty, pre-compact,
$W\subset H$
a non-empty, pre-compact,
![]() $\Gamma $
-regular window. Further, let
$\Gamma $
-regular window. Further, let
![]() $\unicode{x3bb} \in \Lambda $
and
$\unicode{x3bb} \in \Lambda $
and
![]() $r>0$
, then
$r>0$
, then
 $$ \begin{align*} \bigg(\bigcap_{\mu \in {\mathcal{S}}_r(\unicode{x3bb})}\mu \mathring{W}\bigg)\cap \bigg(\bigcap_{\mu \in {\mathcal{S}}_r(\unicode{x3bb})^{\mathrm{C}}} \mu W^{\mathrm{C}} \bigg)=:W_r(\unicode{x3bb}) \end{align*} $$
$$ \begin{align*} \bigg(\bigcap_{\mu \in {\mathcal{S}}_r(\unicode{x3bb})}\mu \mathring{W}\bigg)\cap \bigg(\bigcap_{\mu \in {\mathcal{S}}_r(\unicode{x3bb})^{\mathrm{C}}} \mu W^{\mathrm{C}} \bigg)=:W_r(\unicode{x3bb}) \end{align*} $$
is called the r-acceptance domain of
![]() $\unicode{x3bb} $
, where
$\unicode{x3bb} $
, where
![]() $S_r$
is the set of points in
$S_r$
is the set of points in
![]() $\Gamma $
which project into
$\Gamma $
which project into
![]() $W W^{-1}$
and are within radius r of the origin, see Definition 2.7 for a formal definition.
$W W^{-1}$
and are within radius r of the origin, see Definition 2.7 for a formal definition.
Theorem 2.2. (Acceptance domains versus equivalence classes)
Let
![]() $\Lambda (G,H, \Gamma , W)$
be a model set, with
$\Lambda (G,H, \Gamma , W)$
be a model set, with
![]() $G, H$
lcsc groups,
$G, H$
lcsc groups,
![]() $\Gamma \subset G \times H$
a uniform lattice and
$\Gamma \subset G \times H$
a uniform lattice and
![]() $W\subset H$
a non-empty, pre-compact,
$W\subset H$
a non-empty, pre-compact,
![]() $\Gamma $
-regular window, then
$\Gamma $
-regular window, then
Further, for
![]() $\unicode{x3bb} \not \sim _r \unicode{x3bb} '$
, we have
$\unicode{x3bb} \not \sim _r \unicode{x3bb} '$
, we have
Finally, we have
 $$ \begin{align*} \overline{W} = \bigcup_{\unicode{x3bb} \in A_r^G}\overline{W_r(\unicode{x3bb})}. \end{align*} $$
$$ \begin{align*} \overline{W} = \bigcup_{\unicode{x3bb} \in A_r^G}\overline{W_r(\unicode{x3bb})}. \end{align*} $$
We will give the precise definition of
![]() ${\mathcal {S}}_r(\unicode{x3bb} )$
in §2 and of
${\mathcal {S}}_r(\unicode{x3bb} )$
in §2 and of
![]() $A_r^H(\unicode{x3bb} )$
in Definition 1.12. For now, think of
$A_r^H(\unicode{x3bb} )$
in Definition 1.12. For now, think of
![]() $A_r^H(\unicode{x3bb} )$
as the projection of all the points in the equivalence class of
$A_r^H(\unicode{x3bb} )$
as the projection of all the points in the equivalence class of
![]() $\unicode{x3bb} $
to H. Further,
$\unicode{x3bb} $
to H. Further,
![]() ${\mathcal {S}}_r(\unicode{x3bb} )$
and
${\mathcal {S}}_r(\unicode{x3bb} )$
and
![]() ${\mathcal {S}}_r^{\mathrm {C}}(\unicode{x3bb} )$
are roughly speaking a decomposition of the possible neighbours of
${\mathcal {S}}_r^{\mathrm {C}}(\unicode{x3bb} )$
are roughly speaking a decomposition of the possible neighbours of
![]() $\unicode{x3bb} $
projected to H.
$\unicode{x3bb} $
projected to H.
As a second step, we establish a lattice point counting argument in §3.
Proposition 3.1. (Growth lemma)
Let G and H be lcsc groups. For a model set
![]() $\Lambda (G,H, \Gamma , W)$
with a uniform lattice
$\Lambda (G,H, \Gamma , W)$
with a uniform lattice
![]() $\Gamma \subset G \times H$
and a bounded open set
$\Gamma \subset G \times H$
and a bounded open set
![]() ${\emptyset \neq A \subset H}$
, the asymptotic growth of the number of lattice points inside
${\emptyset \neq A \subset H}$
, the asymptotic growth of the number of lattice points inside
![]() $B^G_r(e) \times A$
is bounded by
$B^G_r(e) \times A$
is bounded by
for some constants
![]() $k_1,k_2>0$
as
$k_1,k_2>0$
as
![]() $r \to \infty $
.
$r \to \infty $
.
Remark 1.6. For the asymptotic behaviour, we use the common notation
![]() $g(t) \ll f(t)$
which means
$g(t) \ll f(t)$
which means
![]() $\limsup \limits _{t \to \infty }\vert {g(t)}/{f(t)} \vert < \infty $
. If both
$\limsup \limits _{t \to \infty }\vert {g(t)}/{f(t)} \vert < \infty $
. If both
![]() $g(t) \ll f(t)$
and
$g(t) \ll f(t)$
and
![]() $g(t) \gg f(t)$
hold, we write
$g(t) \gg f(t)$
hold, we write
![]() $g(t) \asymp f(t)$
.
$g(t) \asymp f(t)$
.
This result connects the number of lattice points in sets of a certain form to the measure of these sets. The standard proof is via ergodic theory, but we will give a more elementary proof.
In the third step, we show in §5 that we can estimate the number of acceptance domains by extending the boundary of the window. This is also done in [Reference Koivusalo and Walton28]; the new regions inside the window are called cut regions in this paper. Again, the result we obtain is the same as in the Euclidean case. However, we have to overcome a major difference in its proof since in the Euclidean case, the group acts on a hyperplane by translations, which preserves the directions of the hyperplane. Or formulated differently, a translation does not rotate a hyperplane. In our general setup, the group action can rotate hyperplanes, leading to a new phenomenon.
The following theorem is a combination of Lemmas 5.2, 5.3 and Proposition 5.23.
Theorem 1.7. (Cut regions versus acceptance domains)
For a polytopal model set
![]() $\Lambda (G,H,\Gamma ,W)$
, where the window is bounded by
$\Lambda (G,H,\Gamma ,W)$
, where the window is bounded by
![]() $P_1,\ldots ,P_N$
, and G and H at most two-step nilpotent homogeneous Lie groups, we have
$P_1,\ldots ,P_N$
, and G and H at most two-step nilpotent homogeneous Lie groups, we have
 $$ \begin{align*} \vert A_r^H\vert \leq \# \pi_0 \bigg( H \setminus \bigcup_{\mu\in{\mathcal{S}}_r} \bigcup_{i=1}^N \mu P_i\bigg). \end{align*} $$
$$ \begin{align*} \vert A_r^H\vert \leq \# \pi_0 \bigg( H \setminus \bigcup_{\mu\in{\mathcal{S}}_r} \bigcup_{i=1}^N \mu P_i\bigg). \end{align*} $$
For a certain ball
![]() $B_h(c_W)\subset W$
, we also have
$B_h(c_W)\subset W$
, we also have
 $$ \begin{align*} \# \pi_0 \bigg( B_h(c_W) \setminus \bigcup_{i=1}^N \bigcup_{\mu \in U_i(r)} \mu P_i \bigg) \leq \vert A_r^H \vert. \end{align*} $$
$$ \begin{align*} \# \pi_0 \bigg( B_h(c_W) \setminus \bigcup_{i=1}^N \bigcup_{\mu \in U_i(r)} \mu P_i \bigg) \leq \vert A_r^H \vert. \end{align*} $$
The last step is devoted to solving the problem with the rotating hyperplanes, see §6. To do so, we use the theory of hyperplane arrangements; this tool was not needed in the abelian case. The research of such arrangements has a long history and goes back as far as [Reference Schläfli41], whereas more modern approaches are due to Grünbaum [Reference Grünbaum18–Reference Grünbaum20] and Zaslavsky [Reference Zaslavsky51]. Two sources for a survey of the field are the book by Dimca [Reference Dimca12] and the lecture notes by Stanley [Reference Stanley46]. An important tool for our combinatorial argument is by Beck [Reference Beck6]. We need a special version of Beck’s theorem. To prove this version of Beck’s theorem, we need some combinatorial inputs from [Reference Székely48]. This lets us extend the standard counting formulae to our specific context and we can prove the following theorem, which will then finish the proof of the main theorem.
Theorem 6.1. (Higher dimensional local dual of Beck’s theorem)
Let
![]() ${\mathcal {H}}$
be a hyperplane arrangement in
${\mathcal {H}}$
be a hyperplane arrangement in
![]() ${\mathbb {R}}^d$
and let
${\mathbb {R}}^d$
and let
![]() $B \subset {\mathbb {R}}^d$
be convex. Further, let
$B \subset {\mathbb {R}}^d$
be convex. Further, let
![]() ${\mathcal {H}}$
consist of d families
${\mathcal {H}}$
consist of d families
![]() $F_1,\ldots ,F_d$
with
$F_1,\ldots ,F_d$
with
![]() $\vert F_i \vert = {n}/{d}$
and such that for all
$\vert F_i \vert = {n}/{d}$
and such that for all
![]() $(f_1,\ldots ,f_d) \in F_1 \times \cdots \times F_d$
, we have
$(f_1,\ldots ,f_d) \in F_1 \times \cdots \times F_d$
, we have
![]() $B \cap \bigcap _{i=1}^d f_i = \{p\}$
for some point
$B \cap \bigcap _{i=1}^d f_i = \{p\}$
for some point
![]() $p \in B$
. Moreover, assume that there is a constant
$p \in B$
. Moreover, assume that there is a constant
![]() $c < {1}/{100}$
such that at most
$c < {1}/{100}$
such that at most
![]() $c \cdot \vert F_i \vert $
hyperplanes from
$c \cdot \vert F_i \vert $
hyperplanes from
![]() $F_i$
can intersect in one point. Then there exists a constant
$F_i$
can intersect in one point. Then there exists a constant
![]() $c_d$
, depending on the dimension d, such that the number of intersection points in B exceeds
$c_d$
, depending on the dimension d, such that the number of intersection points in B exceeds
![]() $c_d \cdot n^d$
, that is,
$c_d \cdot n^d$
, that is,
![]() $\vert F_{0,B} \vert \geq c_d \cdot n^d$
.
$\vert F_{0,B} \vert \geq c_d \cdot n^d$
.
1.5. General results for lcsc groups
As discussed above, our restriction to homogeneous Lie groups is necessary for the proof of the main theorem, but the individual steps work in greater generality. Acceptance domains and cut regions can be defined for all connected lcsc groups, and the polytopal condition on the window is not needed for this approach.
1.6. Notation
Throughout this text, G and H will always be locally compact second countable groups,
![]() $\Gamma \subset G \times H$
a uniform lattice and
$\Gamma \subset G \times H$
a uniform lattice and
![]() $W \subset H$
a precompact
$W \subset H$
a precompact
![]() $\Gamma $
-regular, that is,
$\Gamma $
-regular, that is,
![]() $\partial W \cap \pi _H(\Gamma ) = \emptyset $
, subset with non-empty interior, which is called the window. Why these restrictions on W are required will be explained in Proposition A.2. Further, we denote the projection on G by
$\partial W \cap \pi _H(\Gamma ) = \emptyset $
, subset with non-empty interior, which is called the window. Why these restrictions on W are required will be explained in Proposition A.2. Further, we denote the projection on G by
![]() $\pi _G$
and on H by
$\pi _G$
and on H by
![]() $\pi _H$
.
$\pi _H$
.
Definition 1.8. A triple
![]() $(G,H, \Gamma )$
is called a cut-and-project scheme (CPS) if
$(G,H, \Gamma )$
is called a cut-and-project scheme (CPS) if
![]() $\pi _G\vert _\Gamma $
is injective and
$\pi _G\vert _\Gamma $
is injective and
![]() $\pi _H(\Gamma )$
is dense in H. The set
$\pi _H(\Gamma )$
is dense in H. The set
is called a model set if
![]() $(G,H, \Gamma )$
is a cut-and-project scheme. Here we use the notation
$(G,H, \Gamma )$
is a cut-and-project scheme. Here we use the notation
![]() $\Gamma _H := \pi _H(\Gamma )$
and
$\Gamma _H := \pi _H(\Gamma )$
and
![]() $\tau := \pi _H \circ (\pi _G \vert _\Gamma )^{-1}$
.
$\tau := \pi _H \circ (\pi _G \vert _\Gamma )^{-1}$
.
Remark 1.9. Observe that we do not consider non-uniform model sets, so in our terminology of a model set, the lattice is always uniform.
We will always put a G (respectively H) in the index if we consider the projection of an object to the factor G (respectively H). Figure 1 visualizes the relation between the different groups in this setup.
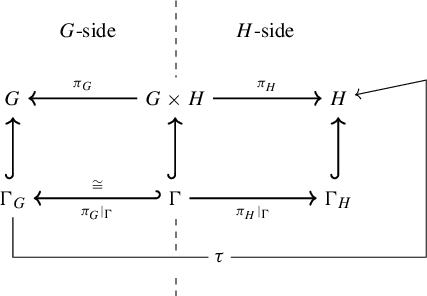
Figure 1 Visualization of a CPS.
To study complexity, we need a metric that will always be associated to a norm by
![]() $d(x,y):= \vert x y^{-1}\vert $
. In the case of homogeneous Lie groups, we have an homogeneous norm on G and H, which we will denote by
$d(x,y):= \vert x y^{-1}\vert $
. In the case of homogeneous Lie groups, we have an homogeneous norm on G and H, which we will denote by
![]() $\vert \cdot \vert _G$
,
$\vert \cdot \vert _G$
,
![]() $\vert \cdot \vert _H$
; if it is clear which norm we consider, we drop the index.
$\vert \cdot \vert _H$
; if it is clear which norm we consider, we drop the index.
Definition 1.10. (Delone)
Let X be a metric space, a subset
![]() $\Lambda \subset X$
is called
$\Lambda \subset X$
is called
![]() $(R,r)$
-Delone if:
$(R,r)$
-Delone if:
-
(a) it is R-relatively dense, that is,
 $$ \begin{align*} \text{there exists } R>0\quad \text{for all } x \in X : B_R(x) \cap \Lambda \neq \emptyset; \end{align*} $$
$$ \begin{align*} \text{there exists } R>0\quad \text{for all } x \in X : B_R(x) \cap \Lambda \neq \emptyset; \end{align*} $$
-
(b) it is r-uniformly discrete, that is,
 $$ \begin{align*} \text{there exists } r>0\quad \text{for all } \unicode{x3bb}, \mu \in \Lambda: d(\unicode{x3bb},\mu) \geq r. \end{align*} $$
$$ \begin{align*} \text{there exists } r>0\quad \text{for all } \unicode{x3bb}, \mu \in \Lambda: d(\unicode{x3bb},\mu) \geq r. \end{align*} $$
If one is not interested in the parameters R and r, one simply speaks of a Delone set.
Remark 1.11. By Proposition A.2, model sets are Delone sets.
Definition 1.12. (Pre-acceptance domains)
Let
![]() $\Lambda (G,H, \Gamma , W)$
be a model set. The image of
$\Lambda (G,H, \Gamma , W)$
be a model set. The image of
![]() $A_r^G(\unicode{x3bb} )$
under the map
$A_r^G(\unicode{x3bb} )$
under the map
![]() $\tau $
is called the r-pre-acceptance domain of
$\tau $
is called the r-pre-acceptance domain of
![]() $\unicode{x3bb} $
:
$\unicode{x3bb} $
:
We denote the set of all pre-acceptance domains by
![]() $A_r^H$
.
$A_r^H$
.
2. How to measure complexity?
In this section, we will explain how one can determine the complexity function of a given FLC set, e.g. a model set
![]() $\Lambda (G, H, \Gamma , W)$
, where
$\Lambda (G, H, \Gamma , W)$
, where
![]() $G=(G,d_G)$
and
$G=(G,d_G)$
and
![]() $H=(H,d_H)$
are metric locally compact second countable groups. The statements in this section are translations from the Euclidean case, we refer to the paper of Koivusalo and Walton [Reference Koivusalo and Walton28] for this setup. We will take a closer look at how the complexity function p is connected to local constellations, which are called patches, in the FLC set. We will then establish a connection between these patches and certain regions in the window W.
$H=(H,d_H)$
are metric locally compact second countable groups. The statements in this section are translations from the Euclidean case, we refer to the paper of Koivusalo and Walton [Reference Koivusalo and Walton28] for this setup. We will take a closer look at how the complexity function p is connected to local constellations, which are called patches, in the FLC set. We will then establish a connection between these patches and certain regions in the window W.
Definition 2.1. (Finite local complexity)
Let
![]() $\Lambda \subset G$
be an FLC subset. If the complexity function of
$\Lambda \subset G$
be an FLC subset. If the complexity function of
![]() $\Lambda $
is finite for all r, we say that
$\Lambda $
is finite for all r, we say that
![]() $\Lambda $
has finite local complexity. There are several ways of viewing this condition, compare Lemma A.1.
$\Lambda $
has finite local complexity. There are several ways of viewing this condition, compare Lemma A.1.
Theorem 2.2. (Acceptance domains)
Let
![]() $\Lambda (G,H, \Gamma , W)$
be a model set, with
$\Lambda (G,H, \Gamma , W)$
be a model set, with
![]() $G, H$
lcsc groups,
$G, H$
lcsc groups,
![]() $\Gamma \subset G \times H$
a uniform lattice and
$\Gamma \subset G \times H$
a uniform lattice and
![]() $W\subset H$
a non-empty, pre-compact,
$W\subset H$
a non-empty, pre-compact,
![]() $\Gamma $
-regular window, then
$\Gamma $
-regular window, then
 $$ \begin{align} A_r^H(\unicode{x3bb}) \subset \bigg(\bigcap_{\mu \in {\mathcal{S}}_r(\unicode{x3bb})}\mu \mathring{W}\bigg)\cap \bigg(\bigcap_{\mu \in {\mathcal{S}}_r(\unicode{x3bb})^{\mathrm{C}}} \mu W^{\mathrm{C}} \bigg)=:W_r(\unicode{x3bb}), \end{align} $$
$$ \begin{align} A_r^H(\unicode{x3bb}) \subset \bigg(\bigcap_{\mu \in {\mathcal{S}}_r(\unicode{x3bb})}\mu \mathring{W}\bigg)\cap \bigg(\bigcap_{\mu \in {\mathcal{S}}_r(\unicode{x3bb})^{\mathrm{C}}} \mu W^{\mathrm{C}} \bigg)=:W_r(\unicode{x3bb}), \end{align} $$
where
![]() ${\mathcal {S}}_r(\unicode{x3bb} )$
will be defined in Definition 2.7. The
${\mathcal {S}}_r(\unicode{x3bb} )$
will be defined in Definition 2.7. The
![]() $W_r(\unicode{x3bb} )$
are called r-acceptance domains of
$W_r(\unicode{x3bb} )$
are called r-acceptance domains of
![]() $\unicode{x3bb} $
. Further, for
$\unicode{x3bb} $
. Further, for
![]() $\unicode{x3bb} \not \sim _r \unicode{x3bb} '$
, we have
$\unicode{x3bb} \not \sim _r \unicode{x3bb} '$
, we have
Finally, we have
 $$ \begin{align} \overline{W} = \bigcup_{\unicode{x3bb} \in A_r^G}\overline{W_r(\unicode{x3bb})}. \end{align} $$
$$ \begin{align} \overline{W} = \bigcup_{\unicode{x3bb} \in A_r^G}\overline{W_r(\unicode{x3bb})}. \end{align} $$
Remark 2.3. The terminology is due to Koivusalo and Walton [Reference Koivusalo and Walton28]. In their paper, they treat the case of model sets
![]() $\Lambda ({\mathbb {R}}^d,{\mathbb {R}}^n,\Gamma , W)$
and extend on Julien’s paper [Reference Julien26], which first introduced the idea of considering a decomposition of the window.
$\Lambda ({\mathbb {R}}^d,{\mathbb {R}}^n,\Gamma , W)$
and extend on Julien’s paper [Reference Julien26], which first introduced the idea of considering a decomposition of the window.
Corollary 2.4.
![]() $p(r)=\vert \{W_r(\unicode{x3bb} ) \mid \unicode{x3bb} \in \Lambda \}\vert =\vert A_r^H\vert $
.
$p(r)=\vert \{W_r(\unicode{x3bb} ) \mid \unicode{x3bb} \in \Lambda \}\vert =\vert A_r^H\vert $
.
The rest of the section is devoted to the proof of the theorem and we begin by working towards the definition of
![]() $S_r(\unicode{x3bb} )$
.
$S_r(\unicode{x3bb} )$
.
Definition 2.5. (Displacements)
Let
![]() $\Lambda $
be a CPS. We define the displacements of
$\Lambda $
be a CPS. We define the displacements of
![]() $\unicode{x3bb} \in \Lambda $
as
$\unicode{x3bb} \in \Lambda $
as
Lemma 2.6. [Reference Koivusalo and Walton28, Lemma 2.1]
Let
![]() $\unicode{x3bb} \in \Lambda $
and
$\unicode{x3bb} \in \Lambda $
and
![]() $\mu \in G$
. If
$\mu \in G$
. If
![]() $\mu \unicode{x3bb} \in \Lambda $
, then
$\mu \unicode{x3bb} \in \Lambda $
, then
![]() $\mu \in \Gamma _G$
. However, if
$\mu \in \Gamma _G$
. However, if
![]() $\mu \in \Gamma _G$
,
$\mu \in \Gamma _G$
,
In particular,
![]() $\tau (\mathrm {Disp}(\unicode{x3bb} )) \subset \mathring {W}\mathring {W}^{-1}$
.
$\tau (\mathrm {Disp}(\unicode{x3bb} )) \subset \mathring {W}\mathring {W}^{-1}$
.
Proof. Since
![]() $\unicode{x3bb} , \mu \unicode{x3bb} \kern1.3pt{\in}\kern1.3pt \Lambda $
, we find elements
$\unicode{x3bb} , \mu \unicode{x3bb} \kern1.3pt{\in}\kern1.3pt \Lambda $
, we find elements
![]() $\gamma , \delta \kern1.3pt{\in}\kern1.3pt \Gamma $
such that
$\gamma , \delta \kern1.3pt{\in}\kern1.3pt \Gamma $
such that
![]() $\pi _G(\gamma )\kern1.3pt{=}\kern1.3pt\unicode{x3bb} $
,
$\pi _G(\gamma )\kern1.3pt{=}\kern1.3pt\unicode{x3bb} $
,
![]() ${\pi _G(\delta )\kern1.3pt{=}\kern1.3pt(\mu \unicode{x3bb} )^{-1}}$
. Then
${\pi _G(\delta )\kern1.3pt{=}\kern1.3pt(\mu \unicode{x3bb} )^{-1}}$
. Then
![]() $\gamma \delta \in \Gamma $
and
$\gamma \delta \in \Gamma $
and
![]() $\pi _G(\gamma \delta )= \unicode{x3bb} (\mu \unicode{x3bb} )^{-1} = \mu ^{-1} \in \Gamma _G$
, and therefore
$\pi _G(\gamma \delta )= \unicode{x3bb} (\mu \unicode{x3bb} )^{-1} = \mu ^{-1} \in \Gamma _G$
, and therefore
![]() $\mu \in \Gamma _G$
.
$\mu \in \Gamma _G$
.
Now let
![]() $\mu \in \Gamma _G$
. By definition,
$\mu \in \Gamma _G$
. By definition,
![]() $\mu \unicode{x3bb} \in \Lambda $
if and only if
$\mu \unicode{x3bb} \in \Lambda $
if and only if
![]() $\tau (\mu \unicode{x3bb} ) \in \mathring {W}$
and since
$\tau (\mu \unicode{x3bb} ) \in \mathring {W}$
and since
![]() $\tau $
is a homomorphism, this is equivalent to
$\tau $
is a homomorphism, this is equivalent to
![]() $\tau (\mu ) \in \mathring {W} \tau (\unicode{x3bb} )^{-1}$
and
$\tau (\mu ) \in \mathring {W} \tau (\unicode{x3bb} )^{-1}$
and
![]() $\tau (\unicode{x3bb} ) \in \tau (\mu )^{-1}\mathring {W}$
.
$\tau (\unicode{x3bb} ) \in \tau (\mu )^{-1}\mathring {W}$
.
To understand patches on the H-side of the model set, we transport the information of the displacements to this side. Since we always consider patches in dependence of r, we only need displacements of magnitude at most r (see Figure 2).
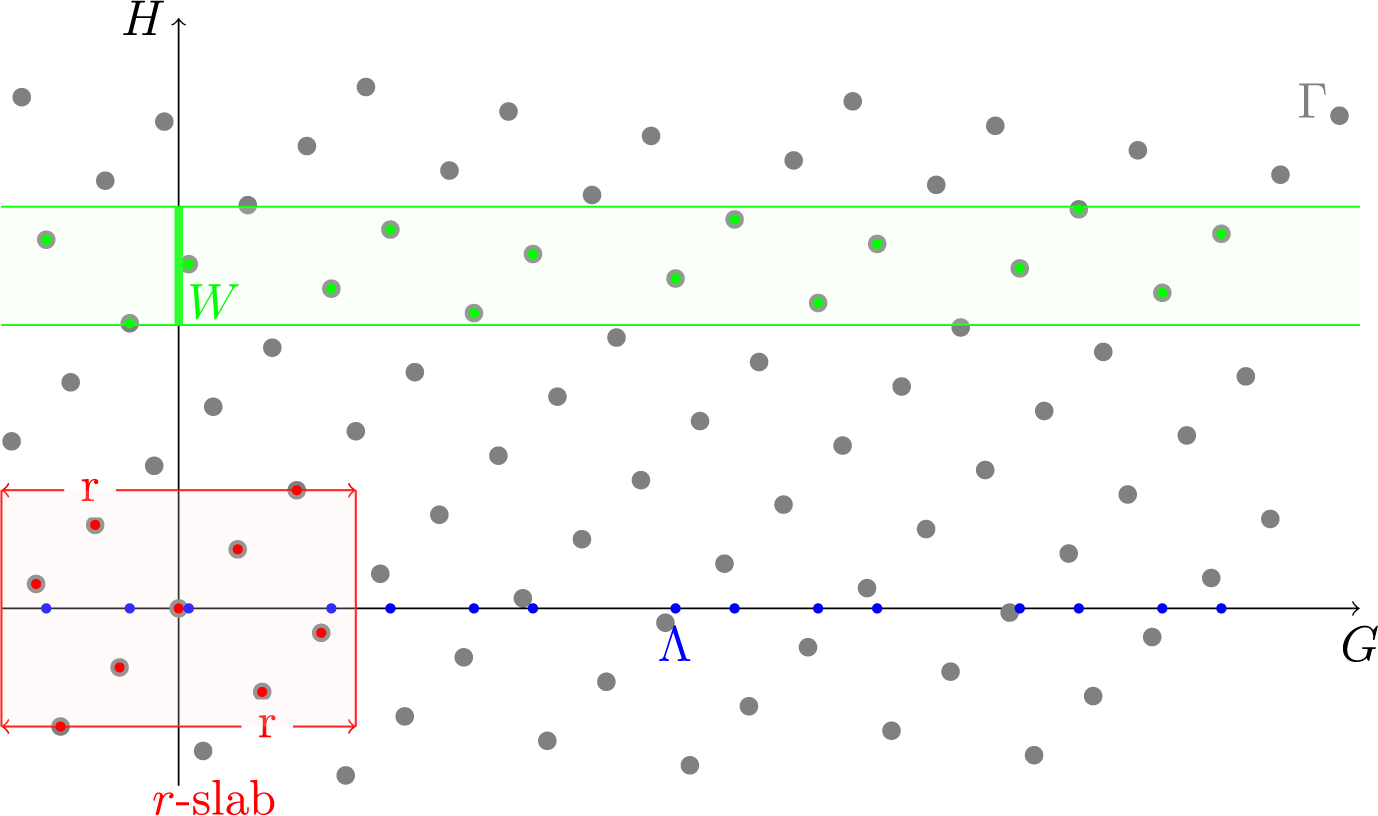
Figure 2 Preimage of the slab for a fixed r in the setting of an
![]() ${\mathbb {R}} \times {\mathbb {R}}$
model set.
${\mathbb {R}} \times {\mathbb {R}}$
model set.
Definition 2.7. (r-slab)
Let
![]() $\Lambda (G,H,\Gamma ,W)$
be a model set. We define the r-slab as
$\Lambda (G,H,\Gamma ,W)$
be a model set. We define the r-slab as
Further, in the case where we are only interested in the displacements of a certain equivalence class, we define the r-slab of
![]() $\unicode{x3bb} $
as
$\unicode{x3bb} $
as
and
Remark 2.8. In the paper of Koivusalo and Walton, the sets
![]() $S_r(\unicode{x3bb} )$
and
$S_r(\unicode{x3bb} )$
and
![]() $S_r^{\mathrm {C}}(\unicode{x3bb} )$
are called
$S_r^{\mathrm {C}}(\unicode{x3bb} )$
are called
![]() $P_{in}$
and
$P_{in}$
and
![]() $P_{out}$
, but we think that our notation highlights the connection to the slab in a better way, whereas their notation highlights the connection to the patch P.
$P_{out}$
, but we think that our notation highlights the connection to the slab in a better way, whereas their notation highlights the connection to the patch P.
Lemma 2.9. For
![]() $\unicode{x3bb} , \mu \in \Lambda $
, we have that
$\unicode{x3bb} , \mu \in \Lambda $
, we have that
![]() $\unicode{x3bb} \sim _r \mu \Leftrightarrow {\mathcal {S}}_r(\unicode{x3bb} )={\mathcal {S}}_r(\mu )$
.
$\unicode{x3bb} \sim _r \mu \Leftrightarrow {\mathcal {S}}_r(\unicode{x3bb} )={\mathcal {S}}_r(\mu )$
.
Proof. Assume
![]() $\unicode{x3bb} \sim _r \mu $
, then
$\unicode{x3bb} \sim _r \mu $
, then
![]() $(B_r(\unicode{x3bb} ) \cap \Lambda )\unicode{x3bb} ^{-1}=(B_r(\mu ) \cap \Lambda )\mu ^{-1}$
. Let
$(B_r(\unicode{x3bb} ) \cap \Lambda )\unicode{x3bb} ^{-1}=(B_r(\mu ) \cap \Lambda )\mu ^{-1}$
. Let
![]() $x \in S_r(\unicode{x3bb} )$
, then there exists a
$x \in S_r(\unicode{x3bb} )$
, then there exists a
![]() $(\gamma , x)\in \Gamma $
such that
$(\gamma , x)\in \Gamma $
such that
 $$ \begin{align*} \gamma^{-1}\unicode{x3bb} &\in B_r(\unicode{x3bb}) \cap \Lambda\\ &\Leftrightarrow \gamma^{-1} \in (B_r(\unicode{x3bb}) \cap \Lambda)\unicode{x3bb}^{-1} = (B_r(\mu) \cap \Lambda)\mu^{-1}\\ &\Leftrightarrow \gamma^{-1}\mu \in B_r(\mu) \cap \Lambda. \end{align*} $$
$$ \begin{align*} \gamma^{-1}\unicode{x3bb} &\in B_r(\unicode{x3bb}) \cap \Lambda\\ &\Leftrightarrow \gamma^{-1} \in (B_r(\unicode{x3bb}) \cap \Lambda)\unicode{x3bb}^{-1} = (B_r(\mu) \cap \Lambda)\mu^{-1}\\ &\Leftrightarrow \gamma^{-1}\mu \in B_r(\mu) \cap \Lambda. \end{align*} $$
Therefore,
![]() $x \in S_r(\mu )$
.
$x \in S_r(\mu )$
.
Now assume
![]() ${\mathcal {S}}_r(\unicode{x3bb} )\kern1.4pt{=}\kern1.4pt{\mathcal {S}}_r(\mu )$
and let
${\mathcal {S}}_r(\unicode{x3bb} )\kern1.4pt{=}\kern1.4pt{\mathcal {S}}_r(\mu )$
and let
![]() $x \kern1.4pt{\in}\kern1.4pt (B_r(\unicode{x3bb} )\kern1.4pt{\cap}\kern1.4pt \Lambda )\unicode{x3bb} ^{-1}$
, then
$x \kern1.4pt{\in}\kern1.4pt (B_r(\unicode{x3bb} )\kern1.4pt{\cap}\kern1.4pt \Lambda )\unicode{x3bb} ^{-1}$
, then
![]() ${\tau (x^{-1}) \kern1.4pt{\in}\kern1.4pt {\mathcal {S}}_r(\unicode{x3bb} )\kern1.4pt{=}\kern1.4pt{\mathcal {S}}_r(\mu )}$
and this implies
${\tau (x^{-1}) \kern1.4pt{\in}\kern1.4pt {\mathcal {S}}_r(\unicode{x3bb} )\kern1.4pt{=}\kern1.4pt{\mathcal {S}}_r(\mu )}$
and this implies
![]() $x \in (B_r(\mu )\cap \Lambda )\mu ^{-1}$
.
$x \in (B_r(\mu )\cap \Lambda )\mu ^{-1}$
.
Proof of Theorem 2.2
Lemma 2.9 tells us that for all
![]() $\unicode{x3bb} \in A_r^G(\unicode{x3bb} )$
, the set
$\unicode{x3bb} \in A_r^G(\unicode{x3bb} )$
, the set
 $$ \begin{align*} W_r(\unicode{x3bb}):=\bigg(\bigcap_{\mu \in {\mathcal{S}}_r(\unicode{x3bb})}\mu \mathring{W}\bigg)\cap \bigg(\bigcap_{\mu \in {\mathcal{S}}_r(\unicode{x3bb})^{\mathrm{C}}} \mu W^{\mathrm{C}} \bigg) \end{align*} $$
$$ \begin{align*} W_r(\unicode{x3bb}):=\bigg(\bigcap_{\mu \in {\mathcal{S}}_r(\unicode{x3bb})}\mu \mathring{W}\bigg)\cap \bigg(\bigcap_{\mu \in {\mathcal{S}}_r(\unicode{x3bb})^{\mathrm{C}}} \mu W^{\mathrm{C}} \bigg) \end{align*} $$
is the same. So to prove equation (2.1), it is enough to show
![]() $\tau (\unicode{x3bb} )\in W_r(\unicode{x3bb} )$
. By the definition of the r-slab of
$\tau (\unicode{x3bb} )\in W_r(\unicode{x3bb} )$
. By the definition of the r-slab of
![]() $\unicode{x3bb} $
, we have for all
$\unicode{x3bb} $
, we have for all
![]() $\mu \in {\mathcal {S}}_r(\unicode{x3bb} )$
that there is a
$\mu \in {\mathcal {S}}_r(\unicode{x3bb} )$
that there is a
![]() $\mu _G \in \Gamma _G$
with
$\mu _G \in \Gamma _G$
with
![]() $\tau (\mu _G)=\mu $
and
$\tau (\mu _G)=\mu $
and
![]() $\mu _G^{-1}\unicode{x3bb} \in \Lambda $
. Further, Lemma 2.6 tells us that
$\mu _G^{-1}\unicode{x3bb} \in \Lambda $
. Further, Lemma 2.6 tells us that
![]() $\tau (\unicode{x3bb} ) \in \mu \mathring {W}$
. For
$\tau (\unicode{x3bb} ) \in \mu \mathring {W}$
. For
![]() $\mu \in {\mathcal {S}}_r^{\mathrm {C}}(\unicode{x3bb} )$
, Lemma 2.6 tells us that
$\mu \in {\mathcal {S}}_r^{\mathrm {C}}(\unicode{x3bb} )$
, Lemma 2.6 tells us that
![]() $\tau (\unicode{x3bb} ) \not \in \mu W$
, but this means that
$\tau (\unicode{x3bb} ) \not \in \mu W$
, but this means that
![]() $\tau (\unicode{x3bb} ) \in \mu W^{\mathrm {C}}$
. So it follows that
$\tau (\unicode{x3bb} ) \in \mu W^{\mathrm {C}}$
. So it follows that
![]() $\tau (\unicode{x3bb} )\in W_r(\unicode{x3bb} )$
.
$\tau (\unicode{x3bb} )\in W_r(\unicode{x3bb} )$
.
Now let
![]() $\unicode{x3bb} \not \sim _r \unicode{x3bb} '$
, so by Lemma 2.9,
$\unicode{x3bb} \not \sim _r \unicode{x3bb} '$
, so by Lemma 2.9,
![]() $S_r(\unicode{x3bb} ) \neq S_r(\mu )$
and the disjointness of
$S_r(\unicode{x3bb} ) \neq S_r(\mu )$
and the disjointness of
![]() $W_r(\unicode{x3bb} )$
and
$W_r(\unicode{x3bb} )$
and
![]() $W_r(\unicode{x3bb} ')$
follows by the same argument.
$W_r(\unicode{x3bb} ')$
follows by the same argument.
Finally, we show that the
![]() $W_r(\lambda)$
cover the closure of the window W. The inclusion
$W_r(\lambda)$
cover the closure of the window W. The inclusion
![]() ${\overline {W_r(\unicode{x3bb} )} \subseteq \overline {W}}$
is clear since
${\overline {W_r(\unicode{x3bb} )} \subseteq \overline {W}}$
is clear since
![]() $e_H \in {\mathcal {S}}_r(\unicode{x3bb} )$
for all
$e_H \in {\mathcal {S}}_r(\unicode{x3bb} )$
for all
![]() $\unicode{x3bb} \in \Lambda $
and all
$\unicode{x3bb} \in \Lambda $
and all
![]() $r>0$
. Since
$r>0$
. Since
![]() $\Gamma _H$
is dense in W and
$\Gamma _H$
is dense in W and
![]() $W_r(\unicode{x3bb} )$
is open, we know that
$W_r(\unicode{x3bb} )$
is open, we know that
![]() $\Gamma _H$
is dense in
$\Gamma _H$
is dense in
![]() $W_r(\unicode{x3bb} )$
. Since
$W_r(\unicode{x3bb} )$
. Since
![]() ${A_r^H(\unicode{x3bb} )=\Gamma _H \cap W_r(\unicode{x3bb} )}$
, we know that
${A_r^H(\unicode{x3bb} )=\Gamma _H \cap W_r(\unicode{x3bb} )}$
, we know that
![]() $A_r^H(\unicode{x3bb} )$
is dense in
$A_r^H(\unicode{x3bb} )$
is dense in
![]() $W_r(\unicode{x3bb} )$
. Therefore, the completion by sequences
$W_r(\unicode{x3bb} )$
. Therefore, the completion by sequences
![]() $\overline {A_r^H(\unicode{x3bb} )}^{\mathrm{seq}}$
is the topological closure
$\overline {A_r^H(\unicode{x3bb} )}^{\mathrm{seq}}$
is the topological closure
![]() $\overline {W_r(\unicode{x3bb} )}^{\mathrm{top}}$
. Further, since every
$\overline {W_r(\unicode{x3bb} )}^{\mathrm{top}}$
. Further, since every
![]() ${\gamma \in \Gamma _H \cap W}$
has to belong to some
${\gamma \in \Gamma _H \cap W}$
has to belong to some
![]() $W_r(\unicode{x3bb} )$
, we get that
$W_r(\unicode{x3bb} )$
, we get that
 $$ \begin{align*} W \cap \Gamma_H= \bigcup_{\unicode{x3bb} \in A_r^G} A_r^H(\unicode{x3bb}). \end{align*} $$
$$ \begin{align*} W \cap \Gamma_H= \bigcup_{\unicode{x3bb} \in A_r^G} A_r^H(\unicode{x3bb}). \end{align*} $$
Completion by sequences on both sides delivers
 $$ \begin{align*} \overline{W} = \bigcup_{\unicode{x3bb} \in A_r^G} \overline{A_r^H(\unicode{x3bb})}^{\mathrm{seq}} = \bigcup_{\unicode{x3bb} \in A_r^G} \overline{W_r(\unicode{x3bb})}^{\mathrm{top}}.\\[-50pt] \end{align*} $$
$$ \begin{align*} \overline{W} = \bigcup_{\unicode{x3bb} \in A_r^G} \overline{A_r^H(\unicode{x3bb})}^{\mathrm{seq}} = \bigcup_{\unicode{x3bb} \in A_r^G} \overline{W_r(\unicode{x3bb})}^{\mathrm{top}}.\\[-50pt] \end{align*} $$
Remark 2.10. Taking the closure of the window in the theorem does not make a big difference, since by
![]() $\Gamma $
-regularity, there are no projected lattice points on the boundary. This also holds for the shifted window, since if
$\Gamma $
-regularity, there are no projected lattice points on the boundary. This also holds for the shifted window, since if
![]() $\gamma _1, \gamma _2 \in \Gamma _H$
with
$\gamma _1, \gamma _2 \in \Gamma _H$
with
![]() $\gamma _1 \in \gamma _2 W$
, then
$\gamma _1 \in \gamma _2 W$
, then
![]() $\gamma _2^{-1}\gamma _1 \in W$
in contradiction to the
$\gamma _2^{-1}\gamma _1 \in W$
in contradiction to the
![]() $\Gamma $
-regularity of W. So for all acceptance domains,
$\Gamma $
-regularity of W. So for all acceptance domains,
![]() $\partial W_{r}(\unicode{x3bb} ) \cap \Gamma _H = \emptyset $
.
$\partial W_{r}(\unicode{x3bb} ) \cap \Gamma _H = \emptyset $
.
3. Lattice point counting
Before we begin with the actual proof of our main theorem, we will establish the growth lemma, Proposition 3.1. The growth lemma tells us how to count points in sets of the form
![]() $(B_r(e) \times A) \cap \Gamma $
. Notice that, in particular, the slab
$(B_r(e) \times A) \cap \Gamma $
. Notice that, in particular, the slab
![]() ${\mathcal {S}}_r=\pi _H((B_r(e)\times WW^{-1})\cap \Gamma )$
is of this form.
${\mathcal {S}}_r=\pi _H((B_r(e)\times WW^{-1})\cap \Gamma )$
is of this form.
Proposition 3.1. (Growth lemma)
Let G and H be lcsc groups. For a model set with a uniform lattice
![]() $\Gamma \subset G \times H$
and a bounded open set
$\Gamma \subset G \times H$
and a bounded open set
![]() ${\emptyset \neq A \subset H}$
, the asymptotic growth of the number of lattice points inside
${\emptyset \neq A \subset H}$
, the asymptotic growth of the number of lattice points inside
![]() $B^G_r(e) \times A$
is bounded by
$B^G_r(e) \times A$
is bounded by
for some constants
![]() $k_1,k_2>0$
as
$k_1,k_2>0$
as
![]() $r \to \infty $
.
$r \to \infty $
.
The proof consists of the following well-known proposition, see for example [Reference Baake and Grimm2, Lemma 7.4], and the two subsequent lemmas.
Proposition 3.2. Let G and H be lcsc groups and
![]() $\Gamma \subset G \times H$
a uniform lattice such that
$\Gamma \subset G \times H$
a uniform lattice such that
![]() $\pi _H(\Gamma )$
is dense in H. Further, let
$\pi _H(\Gamma )$
is dense in H. Further, let
![]() $U \subset H$
be an open non-empty set. Then there exists a compact set
$U \subset H$
be an open non-empty set. Then there exists a compact set
![]() $K \subset G$
such that
$K \subset G$
such that
Proof. Since
![]() $\Gamma $
is a uniform lattice in
$\Gamma $
is a uniform lattice in
![]() $G \times H$
, there exists a compact set C such that
$G \times H$
, there exists a compact set C such that
![]() $G \times H= C\Gamma $
. We can cover C by the bigger compact set
$G \times H= C\Gamma $
. We can cover C by the bigger compact set
![]() $\pi _G(C) \times \pi _H(C)$
, which implies
$\pi _G(C) \times \pi _H(C)$
, which implies
![]() $ G \times H = (C_G \times C_H)\Gamma $
. By density of
$ G \times H = (C_G \times C_H)\Gamma $
. By density of
![]() $\pi _H(\Gamma )$
in H, we get a covering
$\pi _H(\Gamma )$
in H, we get a covering
 $$ \begin{align*} \bigcup_{ \gamma \in \Gamma} U\pi_H(\gamma) = H \supset C_H. \end{align*} $$
$$ \begin{align*} \bigcup_{ \gamma \in \Gamma} U\pi_H(\gamma) = H \supset C_H. \end{align*} $$
Since
![]() $C_H$
is compact, we can choose a finite subcovering with finite
$C_H$
is compact, we can choose a finite subcovering with finite
![]() $F\subset \Gamma $
such that
$F\subset \Gamma $
such that
 $$ \begin{align*} \bigcup_{ \gamma \in F} U\pi_H(\gamma) \supset C_H. \end{align*} $$
$$ \begin{align*} \bigcup_{ \gamma \in F} U\pi_H(\gamma) \supset C_H. \end{align*} $$
Now let
![]() $z\in G \times H$
be arbitrary. By the choice of C, we find a
$z\in G \times H$
be arbitrary. By the choice of C, we find a
![]() $\gamma \in \Gamma $
such that
$\gamma \in \Gamma $
such that
![]() ${z \gamma ^{-1} \in C \subset C_G \times C_H}$
. By our covering argument, we find a
${z \gamma ^{-1} \in C \subset C_G \times C_H}$
. By our covering argument, we find a
![]() $f \in F$
such that
$f \in F$
such that
![]() $\pi _H(z \gamma ^{-1}) \in \ U \pi _H(f)$
and therefore
$\pi _H(z \gamma ^{-1}) \in \ U \pi _H(f)$
and therefore
![]() $\pi _H(z \gamma ^{-1} f^{-1}) \in U$
. If we project the same element to G, we get
$\pi _H(z \gamma ^{-1} f^{-1}) \in U$
. If we project the same element to G, we get
Now K is compact since
![]() $C_G$
is compact and
$C_G$
is compact and
![]() $\pi _G(F^{-1})$
is finite. Putting things together, we realise
$\pi _G(F^{-1})$
is finite. Putting things together, we realise
Lemma 3.3. Let G and H be lcsc groups. For a model set with a uniform lattice
![]() $\Gamma \subset G \times ~H$
and a bounded open set
$\Gamma \subset G \times ~H$
and a bounded open set
![]() ${\emptyset \neq A \subset H}$
, the growth of the lattice points inside
${\emptyset \neq A \subset H}$
, the growth of the lattice points inside
![]() $B^G_r(e) \times A$
is asymptotically bounded from above by
$B^G_r(e) \times A$
is asymptotically bounded from above by
where
![]() $k_2$
is some constant as
$k_2$
is some constant as
![]() $r \to \infty $
.
$r \to \infty $
.
Proof. Since
![]() $\Gamma $
is a lattice, it is uniformly discrete; therefore, we find a constant
$\Gamma $
is a lattice, it is uniformly discrete; therefore, we find a constant
![]() $c_1$
such that
$c_1$
such that
![]() $d(\gamma _1,\gamma _2)> c_1$
for all
$d(\gamma _1,\gamma _2)> c_1$
for all
![]() $\gamma _1 \neq \gamma _2 \in \Gamma $
. If we halve the constant, we get disjoint balls around the lattice points, that is,
$\gamma _1 \neq \gamma _2 \in \Gamma $
. If we halve the constant, we get disjoint balls around the lattice points, that is,
![]() $B^{G\times H}_{{c_1}/{2}}(\gamma _1) \cap B^{G\times H}_{{c_1}/{2}}(\gamma _2)=\emptyset $
.
$B^{G\times H}_{{c_1}/{2}}(\gamma _1) \cap B^{G\times H}_{{c_1}/{2}}(\gamma _2)=\emptyset $
.
Since A is bounded, we find a second constant
![]() $c_2$
such that
$c_2$
such that
![]() $A \subset B_{c_2}^H(e)$
and that
$A \subset B_{c_2}^H(e)$
and that
![]() $B_{c_1}^{G\times H}(x)\subset G \times B^H_{c_2}(e)$
for every
$B_{c_1}^{G\times H}(x)\subset G \times B^H_{c_2}(e)$
for every
![]() $x \in G\times A$
. The norm in the product is given by the maximum of the norms of the components.
$x \in G\times A$
. The norm in the product is given by the maximum of the norms of the components.
The idea is that we build a set that contains not only the points of
![]() $(B^G_r(e)\times A)\cap \Gamma $
, but also the balls around them. Then we can obtain an upper bound for the number of points in
$(B^G_r(e)\times A)\cap \Gamma $
, but also the balls around them. Then we can obtain an upper bound for the number of points in
![]() $(B^G_r(e)\times A) \cap \Gamma $
by estimating how often the thickened set of points could fit in this set via a volume estimate. Since by our choice of
$(B^G_r(e)\times A) \cap \Gamma $
by estimating how often the thickened set of points could fit in this set via a volume estimate. Since by our choice of
![]() ${c_1}/{2}$
the balls do not overlap, we obtain that
${c_1}/{2}$
the balls do not overlap, we obtain that
 $$ \begin{align*} \sum_{\gamma \in (B^G_r(e)\times A) \cap \Gamma} \mu_{G \times H}(B^{G \times H}_{{c_1}/{2}}(\gamma)) \leq \mu_{G\times H} (B^G_{r+c_1}(e) \times B^H_{c_2}(e)). \end{align*} $$
$$ \begin{align*} \sum_{\gamma \in (B^G_r(e)\times A) \cap \Gamma} \mu_{G \times H}(B^{G \times H}_{{c_1}/{2}}(\gamma)) \leq \mu_{G\times H} (B^G_{r+c_1}(e) \times B^H_{c_2}(e)). \end{align*} $$
We need the ‘
![]() $+c_1$
’ in the index so the set can also contain all the balls whose centres lie close to the border of
$+c_1$
’ in the index so the set can also contain all the balls whose centres lie close to the border of
![]() $B^G_r(e)$
. The volume of a ball is independent of its centre point since the metric and the Haar-measure are right-invariant. Therefore, we can write the inequality as
$B^G_r(e)$
. The volume of a ball is independent of its centre point since the metric and the Haar-measure are right-invariant. Therefore, we can write the inequality as
We will now divide this equation by
![]() $\mu _{G \times H}(B^{G\times H}_{{c_1}/{2}}(e))$
, which is just a constant dependent on
$\mu _{G \times H}(B^{G\times H}_{{c_1}/{2}}(e))$
, which is just a constant dependent on
![]() $c_1$
which we will denote by
$c_1$
which we will denote by
![]() $c_1'$
and the constant
$c_1'$
and the constant
![]() $\mu _{H}(B^H_{c_2}(e))$
will be denoted by
$\mu _{H}(B^H_{c_2}(e))$
will be denoted by
![]() $c_2'$
.
$c_2'$
.
 $$ \begin{align*} \vert(B^G_r(e)\times A) \cap \Gamma\vert &\leq \frac{\mu_{G \times H}(B^G_{r+c_1}(e) \times B^H_{c_2}(e))}{c_1'}\\ &=\frac{\mu_{G}(B^G_{r+c_1}(e)) \cdot \mu_{H}(B^H_{c_2}(e))}{c_1'} = \frac{c_2'}{c_1'} \mu_G(B^G_{r+c_1}(e)).\\[-45pt] \end{align*} $$
$$ \begin{align*} \vert(B^G_r(e)\times A) \cap \Gamma\vert &\leq \frac{\mu_{G \times H}(B^G_{r+c_1}(e) \times B^H_{c_2}(e))}{c_1'}\\ &=\frac{\mu_{G}(B^G_{r+c_1}(e)) \cdot \mu_{H}(B^H_{c_2}(e))}{c_1'} = \frac{c_2'}{c_1'} \mu_G(B^G_{r+c_1}(e)).\\[-45pt] \end{align*} $$
Lemma 3.4. Let G and H be lcsc groups. For a model set with a uniform lattice
![]() ${\Gamma \subset G \times H}$
and a bounded open set
${\Gamma \subset G \times H}$
and a bounded open set
![]() ${\emptyset \neq A \subset H}$
, the growth of the number of lattice points inside
${\emptyset \neq A \subset H}$
, the growth of the number of lattice points inside
![]() $B^G_r(e) \times A$
is asymptotically bounded from below by
$B^G_r(e) \times A$
is asymptotically bounded from below by
where
![]() $k_1$
is some constant as
$k_1$
is some constant as
![]() $r \to \infty $
.
$r \to \infty $
.
Proof. Let
![]() $\varepsilon>0$
be fixed. We choose an open ball
$\varepsilon>0$
be fixed. We choose an open ball
![]() $B^H_\varepsilon (\gamma _H) \subset A$
with
$B^H_\varepsilon (\gamma _H) \subset A$
with
![]() $\gamma _H \in \Gamma _H$
, this can be done since
$\gamma _H \in \Gamma _H$
, this can be done since
![]() $\Gamma _H$
is dense in H and A is open, and therefore
$\Gamma _H$
is dense in H and A is open, and therefore
![]() $\Gamma _H \cap A \subset A$
is dense.
$\Gamma _H \cap A \subset A$
is dense.
First, we assume that
![]() $\gamma _H = e$
. By Proposition 3.2, we find a compact set
$\gamma _H = e$
. By Proposition 3.2, we find a compact set
![]() ${K \subset G}$
such that
${K \subset G}$
such that
![]() $ G \times H = (K \times B^H_\varepsilon (e))\Gamma $
. Since K is compact, it is bounded, and we can consider
$ G \times H = (K \times B^H_\varepsilon (e))\Gamma $
. Since K is compact, it is bounded, and we can consider
![]() $\overline {B^G_{c_1}}(e)$
, with
$\overline {B^G_{c_1}}(e)$
, with
![]() $c_1$
large enough, instead. Then for all
$c_1$
large enough, instead. Then for all
![]() $z \in G \times H$
, we see
$z \in G \times H$
, we see
![]() $(B^G_{c_1}(e) \times B^H_\varepsilon (e)) z \cap \Gamma \neq \emptyset $
. This holds true since we can write
$(B^G_{c_1}(e) \times B^H_\varepsilon (e)) z \cap \Gamma \neq \emptyset $
. This holds true since we can write
![]() $z=(k_z,u_z)(\gamma _{zG},\gamma _{zH})$
with
$z=(k_z,u_z)(\gamma _{zG},\gamma _{zH})$
with
![]() $(\gamma _{zG},\gamma _{zH}) \in \Gamma $
,
$(\gamma _{zG},\gamma _{zH}) \in \Gamma $
,
![]() $k_z \in B^G_{c_1}(e)$
and
$k_z \in B^G_{c_1}(e)$
and
![]() $u_z \in B^H_\varepsilon (e)$
. However, then
$u_z \in B^H_\varepsilon (e)$
. However, then
since
![]() $k_z^{-1} \in B^G_{c_1}(e)$
and
$k_z^{-1} \in B^G_{c_1}(e)$
and
![]() $u_z^{-1} \in B^H_\varepsilon (e)$
.
$u_z^{-1} \in B^H_\varepsilon (e)$
.
We can find a lower bound of the growth if we can fit enough of the sets of type
![]() ${(B^G_{c_1}(e)\times B^H_\varepsilon (e)) z}$
into
${(B^G_{c_1}(e)\times B^H_\varepsilon (e)) z}$
into
![]() $B^G_r(e) \times A$
in a disjoint way. One should think of this as stacking these sets onto another with base
$B^G_r(e) \times A$
in a disjoint way. One should think of this as stacking these sets onto another with base
![]() $B^H_\varepsilon (e)$
. This comes down to
$B^H_\varepsilon (e)$
. This comes down to
 $$ \begin{align*} &\vert(B^G_r(e)\times A)\cap \Gamma \vert> \vert(B^G_r(e) \times B^H_\varepsilon (e))\cap \Gamma \vert\\ &\quad\geq \max \{ \vert X \vert \,|\, X \subset G,\text{ such that } \text{ for all } x \in X: B^G_{c_1}(x) \subset B^G_r(e) \\ &\quad\quad \quad \quad \text{ and } B^G_{c_1}(x)\cap B^G_{c_1}(y) = \emptyset \text{ for all } x \neq y \in X \}\\ &\quad\geq \max \{ \vert X \vert \,|\, X \subset B^G_{r-c_1}(e) \text{ and } X \text{ is } 2c_1\text{-uniformly discrete}\}. \end{align*} $$
$$ \begin{align*} &\vert(B^G_r(e)\times A)\cap \Gamma \vert> \vert(B^G_r(e) \times B^H_\varepsilon (e))\cap \Gamma \vert\\ &\quad\geq \max \{ \vert X \vert \,|\, X \subset G,\text{ such that } \text{ for all } x \in X: B^G_{c_1}(x) \subset B^G_r(e) \\ &\quad\quad \quad \quad \text{ and } B^G_{c_1}(x)\cap B^G_{c_1}(y) = \emptyset \text{ for all } x \neq y \in X \}\\ &\quad\geq \max \{ \vert X \vert \,|\, X \subset B^G_{r-c_1}(e) \text{ and } X \text{ is } 2c_1\text{-uniformly discrete}\}. \end{align*} $$
We can extend every
![]() $c_1$
-uniformly discrete set to a
$c_1$
-uniformly discrete set to a
![]() $(c_2,c_1)$
-Delone set for some constant
$(c_2,c_1)$
-Delone set for some constant
![]() $c_2$
[Reference Cornulier and de la Harpe11, Proposition 3.C.3]. Thus,
$c_2$
[Reference Cornulier and de la Harpe11, Proposition 3.C.3]. Thus,
 $$ \begin{align*} &\vert(B^G_r(e)\times A)\cap \Gamma \vert\\ &\quad> \max \{ \vert X \vert \,|\vert\, X \subset B^G_{r-c_1}(e) \text{ and } X \text{ is a } (c_2,2c_1)\text{-Delone subset of } B_r^G(e)\}. \end{align*} $$
$$ \begin{align*} &\vert(B^G_r(e)\times A)\cap \Gamma \vert\\ &\quad> \max \{ \vert X \vert \,|\vert\, X \subset B^G_{r-c_1}(e) \text{ and } X \text{ is a } (c_2,2c_1)\text{-Delone subset of } B_r^G(e)\}. \end{align*} $$
For every such Delone set, we can cover
![]() $B^G_{r-c_1}(e)$
with balls
$B^G_{r-c_1}(e)$
with balls
![]() $B^G_{c_2}(x)$
for
$B^G_{c_2}(x)$
for
![]() $x\in X$
, so that
$x\in X$
, so that
Since the metric and the Haar-measure are right-invariant, all of these balls have the same measure and we get
 $$ \begin{align*} \vert X \vert \cdot \mu_G(B^G_{c_2}(e)) \geq \mu_G(B^G_{r-c_1}(e)) \Leftrightarrow \vert X \vert \geq \frac{\mu_G(B^G_{r-c_1}(e))}{\mu_G(B^G_{c_2}(e))}. \end{align*} $$
$$ \begin{align*} \vert X \vert \cdot \mu_G(B^G_{c_2}(e)) \geq \mu_G(B^G_{r-c_1}(e)) \Leftrightarrow \vert X \vert \geq \frac{\mu_G(B^G_{r-c_1}(e))}{\mu_G(B^G_{c_2}(e))}. \end{align*} $$
Summing up, we have
 $$ \begin{align*} \vert(B^G_r(e)\times A)\cap \Gamma \vert> \frac{\mu_G(B^G_{r-c_1}(e))}{\mu_G(B^G_{c_2}(e))}.\\[-42pt] \end{align*} $$
$$ \begin{align*} \vert(B^G_r(e)\times A)\cap \Gamma \vert> \frac{\mu_G(B^G_{r-c_1}(e))}{\mu_G(B^G_{c_2}(e))}.\\[-42pt] \end{align*} $$
Definition 3.5. Let G be a locally compact group and let d be a right-invariant metric on G compatible with the topology on G. Then G is a group with exact polynomial growth of degree
![]() $\kappa $
with respect to d if there exists a constant
$\kappa $
with respect to d if there exists a constant
![]() $c>0$
such that
$c>0$
such that
Corollary 3.6. If G is a group with exact polynomial growth of degree
![]() $\kappa $
with respect to d, then
$\kappa $
with respect to d, then
4. Homogeneous Lie groups
In this section, we will review the basic concepts of homogeneous Lie groups, following the book by Fisher and Ruzhansky [Reference Fischer and Ruzhansky14]. In this context, we also recall an ergodic theorem, due to Gorodnik and Nevo [Reference Gorodnik and Nevo16, Reference Gorodnik and Nevo17, Reference Nevo40], which will be recalled later.
Definition 4.1. [Reference Fischer and Ruzhansky14, Definition 3.1.7]
-
(a) A family of dilations of a Lie algebra
 ${\mathfrak {g}}$
is a family of linear mappings
${\mathfrak {g}}$
is a family of linear mappings
 $\{D_r, r>0\}$
from
$\{D_r, r>0\}$
from
 ${\mathfrak {g}}$
to itself which satisfies:
${\mathfrak {g}}$
to itself which satisfies:-
(i) the mappings are of the form
where A is a diagonalizable linear operator on $$ \begin{align*} D_r=e^{(\ln(r) A)} = \sum_{l=0}^\infty \frac{1}{l !}(\ln(r)A)^l, \end{align*} $$
$$ \begin{align*} D_r=e^{(\ln(r) A)} = \sum_{l=0}^\infty \frac{1}{l !}(\ln(r)A)^l, \end{align*} $$
 ${\mathfrak {g}}$
with positive eigenvalues and
${\mathfrak {g}}$
with positive eigenvalues and
 $\ln (r)$
the natural logarithm of
$\ln (r)$
the natural logarithm of
 $r>0$
;
$r>0$
;
-
(ii) each
 $D_r$
is a morphism of the Lie algebra
$D_r$
is a morphism of the Lie algebra
 ${\mathfrak {g}}$
, that is, a linear mapping from
${\mathfrak {g}}$
, that is, a linear mapping from
 ${\mathfrak {g}}$
to itself which respects the Lie bracket, that is,
${\mathfrak {g}}$
to itself which respects the Lie bracket, that is,  $$ \begin{align*} \text{for all } X,Y \in {\mathfrak{g}}, r>0: [D_r X, D_r Y] = D_r[X,Y]. \end{align*} $$
$$ \begin{align*} \text{for all } X,Y \in {\mathfrak{g}}, r>0: [D_r X, D_r Y] = D_r[X,Y]. \end{align*} $$
-
-
(b) An homogeneous Lie group is a connected simply connected Lie group whose Lie algebra is equipped with a fixed family of dilations.
-
(c) We call the eigenvalues of A the dilations’ weights, and the sum of these weights is the homogeneous dimension of
 ${\mathfrak {g}}$
, denoted by
${\mathfrak {g}}$
, denoted by
 ${\mathrm {homdim}}({\mathfrak {g}})$
.
${\mathrm {homdim}}({\mathfrak {g}})$
.
Convention 4.2. From now on, we will always assume G and H to be homogeneous Lie groups.
Remark 4.3. Since every Lie algebra, which is equipped with dilations, is nilpotent, an homogeneous Lie group is nilpotent [Reference Fischer and Ruzhansky14, Proposition 3.1.10]. This together with the connectedness and the simply connectedness implies that the exponential map is a global diffeomorphism, see [Reference Fischer and Ruzhansky14, Proposition 1.6.6], which we use to identify the underlying sets of G and
![]() ${\mathfrak {g}}$
. On
${\mathfrak {g}}$
. On
![]() ${\mathfrak {g}}$
, the group multiplication takes the form
${\mathfrak {g}}$
, the group multiplication takes the form
The operation
![]() $\ast $
is called the Baker–Campbell–Hausdorff (BCH) multiplication, since to determine it, we can use the BCH formula. The explicit formula for multiplication then is
$\ast $
is called the Baker–Campbell–Hausdorff (BCH) multiplication, since to determine it, we can use the BCH formula. The explicit formula for multiplication then is
 $$ \begin{align*} X \ast Y = X + \sum_{\substack{k,m \geq 0 \\ p_i+q_i \geq 0\\ i \in \{0,\ldots ,k\}}} (-1)^k \frac{{{\mathrm{ad}}_X}^{p_1} \circ {{\mathrm{ad}}_Y}^{q_1} \circ \cdots \circ {{\mathrm{ad}}_X}^{p_k} \circ {{\mathrm{ad}}_Y}^{q_k} \circ {{\mathrm{ad}}_X}^m }{(k+1)(q_1+\cdots+q_k+1) \cdot p_1!\cdot q_1! \cdot \cdots \cdot p_k! \cdot q_k! \cdot m!}(Y). \end{align*} $$
$$ \begin{align*} X \ast Y = X + \sum_{\substack{k,m \geq 0 \\ p_i+q_i \geq 0\\ i \in \{0,\ldots ,k\}}} (-1)^k \frac{{{\mathrm{ad}}_X}^{p_1} \circ {{\mathrm{ad}}_Y}^{q_1} \circ \cdots \circ {{\mathrm{ad}}_X}^{p_k} \circ {{\mathrm{ad}}_Y}^{q_k} \circ {{\mathrm{ad}}_X}^m }{(k+1)(q_1+\cdots+q_k+1) \cdot p_1!\cdot q_1! \cdot \cdots \cdot p_k! \cdot q_k! \cdot m!}(Y). \end{align*} $$
In the case of an n-step nilpotent Lie group, this sum is finite since all terms there
![]() $m+\sum _i p_i + q_i \geq n$
are zero. The first few terms of the sum then look like
$m+\sum _i p_i + q_i \geq n$
are zero. The first few terms of the sum then look like
Observe that the inverse of X in terms of the action
![]() $\ast $
is given by the additive inverse of X in the Lie algebra, that is,
$\ast $
is given by the additive inverse of X in the Lie algebra, that is,
![]() $X^{-1}= -X$
.
$X^{-1}= -X$
.
In particular, the group law is a polynomial, see [Reference Fischer and Ruzhansky14, Proposition 1.6.6], which means that for
![]() $x=(x_1,\ldots ,x_n)$
and
$x=(x_1,\ldots ,x_n)$
and
![]() $y=(y_1,\ldots ,y_n)$
, we have
$y=(y_1,\ldots ,y_n)$
, we have
with
![]() $P_1,\ldots , P_n$
polynomials in
$P_1,\ldots , P_n$
polynomials in
![]() $2n$
variables. We will observe some restrictions for this polynomials in Appendix B.1.
$2n$
variables. We will observe some restrictions for this polynomials in Appendix B.1.
Observe that we can transport the dilations of the Lie algebra to the Lie group via the exponential map so that we also have a dilation structure on the Lie group itself. This results in a family of dilations of the form
![]() $D_r=\exp (A \ln (r))$
with a diagonalizable linear operator A. The eigenvalues of A are the weights we mentioned above. In accordance with [Reference Fischer and Ruzhansky14], we denote these weights by
$D_r=\exp (A \ln (r))$
with a diagonalizable linear operator A. The eigenvalues of A are the weights we mentioned above. In accordance with [Reference Fischer and Ruzhansky14], we denote these weights by
![]() $\nu _1,\ldots ,\nu _n$
. The trace of A gives us the homogeneous dimension of G. The properties listed below explain this terminology.
$\nu _1,\ldots ,\nu _n$
. The trace of A gives us the homogeneous dimension of G. The properties listed below explain this terminology.
Definition 4.4. [Reference Fischer and Ruzhansky14, Definition 3.1.33]
An homogeneous quasi-norm is a continuous non-negative function
![]() $G \to [0,\infty ), x \mapsto \vert x \vert $
satisfying:
$G \to [0,\infty ), x \mapsto \vert x \vert $
satisfying:
-
(i)
 $\vert x^{-1}\vert = \vert x \vert $
;
$\vert x^{-1}\vert = \vert x \vert $
; -
(ii)
 $\vert D_r( x )\vert = r \cdot \vert x \vert \text { for all } r>0$
;
$\vert D_r( x )\vert = r \cdot \vert x \vert \text { for all } r>0$
; -
(iii)
 $\vert x \vert =0$
if and only if
$\vert x \vert =0$
if and only if
 $x=e$
.
$x=e$
.
It is called an homogeneous norm if additionally:
-
(iv) for all
 $x,y \in G$
, it is
$x,y \in G$
, it is
 $\vert xy\vert \leq \vert x \vert + \vert y\vert $
.
$\vert xy\vert \leq \vert x \vert + \vert y\vert $
.
Lemma 4.5. [Reference Fischer and Ruzhansky14, Theorem 3.1.39]
If G is an homogeneous Lie group, then there exists an homogeneous norm
![]() $\vert \cdot \vert $
on G.
$\vert \cdot \vert $
on G.
Lemma 4.6. [Reference Fischer and Ruzhansky14, Proposition 3.1.35]
Any two homogeneous quasi-norms
![]() $\vert \cdot \vert $
and
$\vert \cdot \vert $
and
![]() $\vert \cdot \vert '$
on G are mutually equivalent, in the sense that there exists
$\vert \cdot \vert '$
on G are mutually equivalent, in the sense that there exists
![]() $a,b>0$
such that for all
$a,b>0$
such that for all
![]() $g \in G$
, it is
$g \in G$
, it is
![]() $a \vert x \vert ' \leq \vert x\vert \leq b \vert x\vert '$
.
$a \vert x \vert ' \leq \vert x\vert \leq b \vert x\vert '$
.
Remark 4.7. To such an homogeneous norm, we can associate the right invariant metric d given by
![]() $d(x,y):= \vert x y^{-1}\vert $
.
$d(x,y):= \vert x y^{-1}\vert $
.
Lemma 4.8. [Reference Fischer and Ruzhansky14, Proposition 3.1.37]
If
![]() $\vert \cdot \vert $
is a homogeneous quasi-norm on a homogeneous Lie group G of dimension n, then the topology induced by the quasi-norm coincides with the Euclidean topology on the underlying set
$\vert \cdot \vert $
is a homogeneous quasi-norm on a homogeneous Lie group G of dimension n, then the topology induced by the quasi-norm coincides with the Euclidean topology on the underlying set
![]() ${\mathbb {R}}^n$
.
${\mathbb {R}}^n$
.
Proposition 4.9. [Reference Fischer and Ruzhansky14, §§3.1.3 and 3.1.6]
Let G be an homogeneous Lie group and
![]() $\vert \cdot \vert $
an homogeneous norm on G with associated right invariant metric d, then for
$\vert \cdot \vert $
an homogeneous norm on G with associated right invariant metric d, then for
![]() $x,y \in G$
and
$x,y \in G$
and
![]() $r,s>0$
:
$r,s>0$
:
-
(i)
 $B_r(x) = \{y \in G \mid \vert y x^{-1}\vert < r\} = B_r(e) \cdot x$
;
$B_r(x) = \{y \in G \mid \vert y x^{-1}\vert < r\} = B_r(e) \cdot x$
; -
(ii)
 $D_r(x y) = D_r(x) D_r(y)$
;
$D_r(x y) = D_r(x) D_r(y)$
; -
(iii)
 $D_r(B_s(e)) = B_{r\cdot s}(e)$
;
$D_r(B_s(e)) = B_{r\cdot s}(e)$
; -
(iv)
 $D_r(B_s(x))=B_{r \cdot s}(D_r(x))$
;
$D_r(B_s(x))=B_{r \cdot s}(D_r(x))$
; -
(v)
 $\mu _{G}(B_r(x))= r^{{\mathrm {homdim}}(G)}\cdot \mu _{G}(B_1(e))$
.
$\mu _{G}(B_r(x))= r^{{\mathrm {homdim}}(G)}\cdot \mu _{G}(B_1(e))$
.
Remark 4.10. The fifth point of Proposition 4.9 tells us that an homogeneous Lie group has exact polynomial growth of degree
![]() ${\mathrm {homdim}}(G)$
. Since all homogeneous quasi-norms on G are mutually equivalent, the behaviour is independent from the choice of a metric.
${\mathrm {homdim}}(G)$
. Since all homogeneous quasi-norms on G are mutually equivalent, the behaviour is independent from the choice of a metric.
Definition 4.11. A hyperplane in an homogeneous Lie group G is the image of a hyperplane in the Lie algebra
![]() ${\mathfrak {g}}$
under the exponential map. The set of all hyperplanes in G is denoted by
${\mathfrak {g}}$
under the exponential map. The set of all hyperplanes in G is denoted by
![]() ${\mathcal {H}}(G)$
.
${\mathcal {H}}(G)$
.
A half-space in an homogeneous Lie group G is the image of a half-space in the Lie algebra
![]() ${\mathfrak {g}}$
under the exponential map.
${\mathfrak {g}}$
under the exponential map.
Definition 4.12. A group G is non-crooked if
![]() ${\mathcal {H}}(G) \subset {\mathcal {P}}(G)$
is G invariant.
${\mathcal {H}}(G) \subset {\mathcal {P}}(G)$
is G invariant.
Definition 4.13. A Lie group G is called locally k-step nilpotent if for all
![]() $X,Y \in {\mathfrak {g}}$
, we have
$X,Y \in {\mathfrak {g}}$
, we have
![]() ${\mathrm {ad}}_X^k(Y) = 0$
.
${\mathrm {ad}}_X^k(Y) = 0$
.
Theorem 4.14. Let G be an homogeneous Lie group, then the following are equivalent:
-
(a) G is non-crooked;
-
(b) G is
 $2$
-step nilpotent or abelian;
$2$
-step nilpotent or abelian; -
(c) G is locally
 $2$
-step nilpotent.
$2$
-step nilpotent.
For a proof of the theorem, see Appendix B.
Remark 4.15. The notion of locally k-step nilpotent and k-step nilpotent are only equivalent for
![]() $k=1$
and
$k=1$
and
![]() $k=2$
. For greater k, the notions are different.
$k=2$
. For greater k, the notions are different.
Definition 4.16. We call a window polytopal or of polytopal type if it is the intersection of finitely many half-spaces.
Convention 4.17. If W is polytopal, we can express W as
![]() $\bigcap _{i=1}^N P_i^+$
, where each
$\bigcap _{i=1}^N P_i^+$
, where each
![]() $P_i^+$
is a half-space with opposite half-space
$P_i^+$
is a half-space with opposite half-space
![]() $P_i^-$
and bounding hyperplane
$P_i^-$
and bounding hyperplane
![]() $P_i$
. This
$P_i$
. This
![]() $P_i$
can be chosen such that
$P_i$
can be chosen such that
![]() $P_i \cap W$
has the same dimension as
$P_i \cap W$
has the same dimension as
![]() $P_i$
.
$P_i$
.
Further, we denote the faces of W by
![]() $\partial _i W=W \cap P_i$
. In the rest of the paper, we will always use this notation for the half-spaces and hyperplanes associated to a window of polytopal type.
$\partial _i W=W \cap P_i$
. In the rest of the paper, we will always use this notation for the half-spaces and hyperplanes associated to a window of polytopal type.
We give a small example that the reader can keep in mind. We will now fix the basics of this example so the reader can follow the steps in the paper.
Example 4.18. We set
![]() $G=H={\mathbb {H}}$
, where
$G=H={\mathbb {H}}$
, where
![]() ${\mathbb {H}}$
denotes the Heisenberg group. We view the underlying set of
${\mathbb {H}}$
denotes the Heisenberg group. We view the underlying set of
![]() ${\mathbb {H}}$
as
${\mathbb {H}}$
as
![]() ${\mathbb {R}}^3$
. Further, we set
${\mathbb {R}}^3$
. Further, we set
and
![]() $W=[-\tfrac 12,\tfrac 12]\times [-\tfrac 12,\tfrac 12]\times [-\tfrac 12,\tfrac 12]$
, so it is clear that W is non-empty, pre-compact and
$W=[-\tfrac 12,\tfrac 12]\times [-\tfrac 12,\tfrac 12]\times [-\tfrac 12,\tfrac 12]$
, so it is clear that W is non-empty, pre-compact and
![]() $\Gamma $
-regular. Also, W is a polytope, in fact, it is a cube.
$\Gamma $
-regular. Also, W is a polytope, in fact, it is a cube.
A dilation structure on
![]() ${\mathbb {H}}$
is given by
${\mathbb {H}}$
is given by
![]() $D_r((x,y,z)) = (r \cdot x, r \cdot y , r^2 \cdot z)$
. Further, an homogeneous norm is given by the Korányi–Cygan norm
$D_r((x,y,z)) = (r \cdot x, r \cdot y , r^2 \cdot z)$
. Further, an homogeneous norm is given by the Korányi–Cygan norm
![]() $\vert (x,y,z)\vert _{{\mathbb {H}}} = ( (x^2+y^2)^2 + z^2 )^{1/4}$
.
$\vert (x,y,z)\vert _{{\mathbb {H}}} = ( (x^2+y^2)^2 + z^2 )^{1/4}$
.
4.1. Ergodic theorems for homogeneous Lie groups
In this section, we will learn about the growth of the number of lattice points in the slab under some extra conditions.
Definition 4.19. [Reference Gorodnik and Nevo17, Definition 1.1]
Let
![]() $O_\varepsilon $
,
$O_\varepsilon $
,
![]() $\varepsilon>0$
be a family of symmetric neighbourhoods of the identity in an lcsc group G, which are decreasing in
$\varepsilon>0$
be a family of symmetric neighbourhoods of the identity in an lcsc group G, which are decreasing in
![]() $\varepsilon $
. Then a family of bounded Borel subsets of finite Haar-measure
$\varepsilon $
. Then a family of bounded Borel subsets of finite Haar-measure
![]() $(B_t)_{t>0}$
is well rounded with respect to
$(B_t)_{t>0}$
is well rounded with respect to
![]() $O_\varepsilon $
if for every
$O_\varepsilon $
if for every
![]() $\delta>0$
, there exists
$\delta>0$
, there exists
![]() $\varepsilon , t_1>0$
such that for all
$\varepsilon , t_1>0$
such that for all
![]() $t \geq t_1$
,
$t \geq t_1$
,
 $$ \begin{align*} \mu_G(O_\varepsilon B_t O_\varepsilon ) \leq (1+\delta) \mu_G\bigg(\bigcap_{u,v \in O_\varepsilon }u B_t v\bigg). \end{align*} $$
$$ \begin{align*} \mu_G(O_\varepsilon B_t O_\varepsilon ) \leq (1+\delta) \mu_G\bigg(\bigcap_{u,v \in O_\varepsilon }u B_t v\bigg). \end{align*} $$
In our setup, we will always fix
![]() $O_\varepsilon $
as
$O_\varepsilon $
as
![]() $B_\varepsilon (e)$
, which does not make a difference by [Reference Horesh and Karasik25, Remark 2.3].
$B_\varepsilon (e)$
, which does not make a difference by [Reference Horesh and Karasik25, Remark 2.3].
Definition 4.20. [Reference Gorodnik and Nevo17, Definitions 1.4 and 1.5]
Let G be an lcsc group and
![]() $B_t$
a family of bounded Borel subsets of finite Haar-measure in X, where X is a space on which G acts. Additionally, let
$B_t$
a family of bounded Borel subsets of finite Haar-measure in X, where X is a space on which G acts. Additionally, let
![]() $\beta _{X,B_t}$
be the operator
$\beta _{X,B_t}$
be the operator
 $$ \begin{align*} \beta_{X,B_t}f(x) := \frac{1}{\mu_{X}(B_t)} \int_{B_t} f(g^{-1}x)\,d\mu_X(g) \end{align*} $$
$$ \begin{align*} \beta_{X,B_t}f(x) := \frac{1}{\mu_{X}(B_t)} \int_{B_t} f(g^{-1}x)\,d\mu_X(g) \end{align*} $$
for
![]() $f \in L^2(X)$
. We say that the mean ergodic theorem in
$f \in L^2(X)$
. We say that the mean ergodic theorem in
![]() $L^2(X)$
holds if
$L^2(X)$
holds if
 $$ \begin{align*} \bigg\| \beta_{X,B_t}f - \int_X f\,d\mu \bigg\|_{L^2(X)} \to 0 \quad\text{as } t \to \infty \end{align*} $$
$$ \begin{align*} \bigg\| \beta_{X,B_t}f - \int_X f\,d\mu \bigg\|_{L^2(X)} \to 0 \quad\text{as } t \to \infty \end{align*} $$
for all
![]() $f \in L^2(X)$
. We say that the stable mean ergodic theorem in
$f \in L^2(X)$
. We say that the stable mean ergodic theorem in
![]() $L^2(X)$
holds if the mean ergodic theorem in
$L^2(X)$
holds if the mean ergodic theorem in
![]() $L^2(X)$
holds for the sets
$L^2(X)$
holds for the sets
for all
![]() $\varepsilon \in (0, \varepsilon _1)$
with
$\varepsilon \in (0, \varepsilon _1)$
with
![]() $\varepsilon _1>0.$
$\varepsilon _1>0.$
Remark 4.21. From now on, we fix a Haar-measure
![]() $\mu _{G \times H}$
, which we assume to be normalized by
$\mu _{G \times H}$
, which we assume to be normalized by
![]() $\mu _{G \times H /\Gamma }(G \times H / \Gamma ) = 1$
.
$\mu _{G \times H /\Gamma }(G \times H / \Gamma ) = 1$
.
Theorem 4.22. [Reference Gorodnik and Nevo17, Theorem 1.7]
Let G be an lcsc group,
![]() $\Gamma \subset G$
a discrete lattice subgroup and
$\Gamma \subset G$
a discrete lattice subgroup and
![]() $(B_t)_{t>0}$
a well-rounded family of subsets of G. Assume that the averages
$(B_t)_{t>0}$
a well-rounded family of subsets of G. Assume that the averages
![]() $\beta _{G/\Gamma , B_t}$
satisfy the stable mean ergodic theorem in
$\beta _{G/\Gamma , B_t}$
satisfy the stable mean ergodic theorem in
![]() $L^2(G/\Gamma )$
. Then
$L^2(G/\Gamma )$
. Then
To apply this theorem, we have to show that the sets we consider are well rounded and that they satisfy the stable means ergodic theorem. We will give criteria which ensure this.
Lemma 4.23. Let G be an homogeneous Lie group and
![]() $(B_t(x))_{t>0}$
be the family of balls of radius t and centre x in G. Then this family is well rounded.
$(B_t(x))_{t>0}$
be the family of balls of radius t and centre x in G. Then this family is well rounded.
Proof. We have to show that for every
![]() $\delta>0$
, there exists some
$\delta>0$
, there exists some
![]() $\varepsilon , t_1>0$
such that for all
$\varepsilon , t_1>0$
such that for all
![]() $t \geq t_1$
,
$t \geq t_1$
,
 $$ \begin{align*} \mu_G(B_\varepsilon (e) B_t(x) B_\varepsilon (e)) \leq (1+\delta) \mu_G\bigg(\bigcap_{u,v \in B_\varepsilon (e)}u B_t(x) v\bigg) \end{align*} $$
$$ \begin{align*} \mu_G(B_\varepsilon (e) B_t(x) B_\varepsilon (e)) \leq (1+\delta) \mu_G\bigg(\bigcap_{u,v \in B_\varepsilon (e)}u B_t(x) v\bigg) \end{align*} $$
holds. We first show that we can choose
![]() $\varepsilon $
such that for a constant
$\varepsilon $
such that for a constant
![]() $k \in (0,t)$
, we have
$k \in (0,t)$
, we have
![]() $B_{t-k}(x) \subset \bigcap _{u,v \in B_\varepsilon (e)}u B_t(x) v$
. So let
$B_{t-k}(x) \subset \bigcap _{u,v \in B_\varepsilon (e)}u B_t(x) v$
. So let
![]() $g \in B_{t-k}(x)$
. Then we can write g as
$g \in B_{t-k}(x)$
. Then we can write g as
![]() $u u^{-1} g v^{-1} v$
with
$u u^{-1} g v^{-1} v$
with
![]() $u,v \in B_\varepsilon (e)$
and we have to show that
$u,v \in B_\varepsilon (e)$
and we have to show that
![]() $u^{-1} g v^{-1} \in B_t(x)$
.
$u^{-1} g v^{-1} \in B_t(x)$
.
 $$ \begin{align*} d(x, u^{-1}g v^{-1}) &= \vert x v g^{-1} u\vert_G = \vert x v x^{-1} x g^{-1} u\vert_G\\ &\leq \vert x v x^{-1}\vert_G + \vert xg^{-1} \vert_G + \vert u\vert_G \leq c_x(\varepsilon ) + t-k + \varepsilon. \end{align*} $$
$$ \begin{align*} d(x, u^{-1}g v^{-1}) &= \vert x v g^{-1} u\vert_G = \vert x v x^{-1} x g^{-1} u\vert_G\\ &\leq \vert x v x^{-1}\vert_G + \vert xg^{-1} \vert_G + \vert u\vert_G \leq c_x(\varepsilon ) + t-k + \varepsilon. \end{align*} $$
Here the last inequality holds by Lemma 5.11. Additionally, we have to choose
![]() $\varepsilon $
so small that
$\varepsilon $
so small that
![]() $k> \varepsilon + c_x(\varepsilon )$
, which is possible since
$k> \varepsilon + c_x(\varepsilon )$
, which is possible since
![]() $c(\varepsilon ) \to 0$
as
$c(\varepsilon ) \to 0$
as
![]() $\varepsilon \to 0$
.
$\varepsilon \to 0$
.
However,
![]() $B_\varepsilon (e)B_t(x)B_\varepsilon (e) \subset B_{\varepsilon + t}(x)B_\varepsilon (e)$
. Let
$B_\varepsilon (e)B_t(x)B_\varepsilon (e) \subset B_{\varepsilon + t}(x)B_\varepsilon (e)$
. Let
![]() $y \in B_{t+\varepsilon }(x)$
and
$y \in B_{t+\varepsilon }(x)$
and
![]() $u \in B_\varepsilon (e)$
, then
$u \in B_\varepsilon (e)$
, then
 $$ \begin{align*} d(x, yu) &= \vert x u^{-1} y^{-1}\vert_G = \vert x u^{-1} x^{-1} x y^{-1} \vert_G\\ &\leq \vert x u ^{-1} x^{-1}\vert_G + \vert x y^{-1} \vert_G \leq c_x(\varepsilon ) + \varepsilon + t. \end{align*} $$
$$ \begin{align*} d(x, yu) &= \vert x u^{-1} y^{-1}\vert_G = \vert x u^{-1} x^{-1} x y^{-1} \vert_G\\ &\leq \vert x u ^{-1} x^{-1}\vert_G + \vert x y^{-1} \vert_G \leq c_x(\varepsilon ) + \varepsilon + t. \end{align*} $$
Therefore,
![]() $B_\varepsilon (e)B_t(x)B_\varepsilon (e) \subset B_{\varepsilon + t + c_x(\varepsilon )}(x)$
. Hence, we can choose
$B_\varepsilon (e)B_t(x)B_\varepsilon (e) \subset B_{\varepsilon + t + c_x(\varepsilon )}(x)$
. Hence, we can choose
![]() $\varepsilon> 0$
and
$\varepsilon> 0$
and
![]() $k \in (0, t)$
such that
$k \in (0, t)$
such that
 $$ \begin{align*} B_\varepsilon (e) B_t(x) B_\varepsilon (e) \subset B_{\varepsilon + t + c_x(\varepsilon )}(x) \quad\text{and}\quad B_{t-k}(x) \subset \bigcap_{u,v \in B_\varepsilon (e)}u B_t(x) v \end{align*} $$
$$ \begin{align*} B_\varepsilon (e) B_t(x) B_\varepsilon (e) \subset B_{\varepsilon + t + c_x(\varepsilon )}(x) \quad\text{and}\quad B_{t-k}(x) \subset \bigcap_{u,v \in B_\varepsilon (e)}u B_t(x) v \end{align*} $$
hold simultaneously. Now we can use that we can calculate the measure of balls in homogeneous Lie groups by Proposition 4.9:
and
 $$ \begin{align*} (t-k)^{{\mathrm{homdim}}(G)} \mu_G(B_1(e)) \leq \mu_G(B_{t-k}(x)) \leq \mu_G\bigg(\bigcap_{u,v \in B_\varepsilon (e)}u B_t(x) v\bigg). \end{align*} $$
$$ \begin{align*} (t-k)^{{\mathrm{homdim}}(G)} \mu_G(B_1(e)) \leq \mu_G(B_{t-k}(x)) \leq \mu_G\bigg(\bigcap_{u,v \in B_\varepsilon (e)}u B_t(x) v\bigg). \end{align*} $$
Combining the arguments, we see that we have to choose
![]() $\varepsilon $
, k and
$\varepsilon $
, k and
![]() $t_1$
such that for all
$t_1$
such that for all
![]() $t> t_1$
,
$t> t_1$
,
 $$ \begin{align*} \bigg(\frac{(t+\varepsilon +c_x(\varepsilon ))}{(t-k)}\bigg)^{{\mathrm{homdim}}(G)} \leq (1+\delta).\\[-42pt] \end{align*} $$
$$ \begin{align*} \bigg(\frac{(t+\varepsilon +c_x(\varepsilon ))}{(t-k)}\bigg)^{{\mathrm{homdim}}(G)} \leq (1+\delta).\\[-42pt] \end{align*} $$
Lemma 4.24. Let G be an homogeneous Lie group and
![]() $(B_r(x))_{t>0}$
a constant family of balls in G. Then this family is well rounded.
$(B_r(x))_{t>0}$
a constant family of balls in G. Then this family is well rounded.
Proof. We have already seen in the proof of Lemma 4.23 that
![]() $\bigcap _{u,v \in B_\varepsilon (e)} u B_r(x) v$
contains a ball of the form
$\bigcap _{u,v \in B_\varepsilon (e)} u B_r(x) v$
contains a ball of the form
![]() $B_{r-k}(x)$
for any
$B_{r-k}(x)$
for any
![]() $k\in (0,t)$
if we choose
$k\in (0,t)$
if we choose
![]() $\varepsilon $
accordingly. However,
$\varepsilon $
accordingly. However,
![]() $B_\varepsilon (e)B_r(x)B_\varepsilon (e)$
is contained in a ball
$B_\varepsilon (e)B_r(x)B_\varepsilon (e)$
is contained in a ball
![]() $B_{r+\varepsilon +c_x(\varepsilon )}(x)$
and therefore has finite measure. Choosing
$B_{r+\varepsilon +c_x(\varepsilon )}(x)$
and therefore has finite measure. Choosing
![]() $\varepsilon $
accordingly, we are done.
$\varepsilon $
accordingly, we are done.
Now what is left to show is that the stable mean ergodic theorem holds for our families of sets. To do so, we use [Reference Glasner15, Theorem 3.33] which tells us that we have to check that our families are Følner sequences. Alternatively, see the work by Nevo [Reference Nevo40], especially, Step I in the proof of Theorem 5.1 is exactly what we need.
Definition 4.25. (Følner sequences)
Let G be an lcsc group acting on a measure space
![]() $(X,\mu )$
. A sequence
$(X,\mu )$
. A sequence
![]() $F_1, F_2, \ldots $
of subsets of finite, non-zero measure in X is called a (right) Følner sequence if for all
$F_1, F_2, \ldots $
of subsets of finite, non-zero measure in X is called a (right) Følner sequence if for all
![]() $g \in G$
,
$g \in G$
,
Lemma 4.26. Let
![]() $G \times H$
be a product of homogeneous Lie groups,
$G \times H$
be a product of homogeneous Lie groups,
![]() $\Gamma \subset G \times H$
a lattice,
$\Gamma \subset G \times H$
a lattice,
![]() $(B_t^G(e))_{t>0}$
a family of balls in G and
$(B_t^G(e))_{t>0}$
a family of balls in G and
![]() $(B_r^H(x))_{t>0}$
a constant family of balls in H. The family
$(B_r^H(x))_{t>0}$
a constant family of balls in H. The family
![]() $(B_t^G(e) \times B_r^H(x))_{t>0}/\Gamma $
is a Følner sequence for
$(B_t^G(e) \times B_r^H(x))_{t>0}/\Gamma $
is a Følner sequence for
![]() $G \times H$
acting on
$G \times H$
acting on
![]() $(G\times H)/ \Gamma $
.
$(G\times H)/ \Gamma $
.
Proof. We use Proposition 3.2, which tells us that for every
![]() $r>0$
and every
$r>0$
and every
![]() ${x \in H}$
, we find a compact
${x \in H}$
, we find a compact
![]() $K \subset G$
such that
$K \subset G$
such that
![]() $(K \times B_r^H(x))\Gamma = G \times H$
. Additionally, since every compact set K is contained in some
$(K \times B_r^H(x))\Gamma = G \times H$
. Additionally, since every compact set K is contained in some
![]() $B_t^G(e)$
, for t large enough, we get that
$B_t^G(e)$
, for t large enough, we get that
![]() $(B_t^G(e) \times B_r^H(x)) \Gamma = G \times H$
. This also holds if we consider balls
$(B_t^G(e) \times B_r^H(x)) \Gamma = G \times H$
. This also holds if we consider balls
![]() $B_t^G(g)$
instead of
$B_t^G(g)$
instead of
![]() $B_t^G(e)$
. Therefore, we have for every
$B_t^G(e)$
. Therefore, we have for every
![]() $(g,h) \in G \times H$
that there exists a
$(g,h) \in G \times H$
that there exists a
![]() $t_{g,h}>0$
such that
$t_{g,h}>0$
such that
![]() $(B_t^G(g) \times B_r^H(xh)) \Gamma = G \times H$
and so
$(B_t^G(g) \times B_r^H(xh)) \Gamma = G \times H$
and so
for all
![]() $(g,h) \in G \times H$
.
$(g,h) \in G \times H$
.
5. Growth of the complexity function
In this section, we prove our main theorem, modulo Theorem 6.1 which we will prove in §6.
Theorem 5.1. Let
![]() $\Lambda (G,H, \Gamma , W)$
be a model set, where G is an homogeneous Lie group and H is a non-crooked homogeneous Lie group. Further, let
$\Lambda (G,H, \Gamma , W)$
be a model set, where G is an homogeneous Lie group and H is a non-crooked homogeneous Lie group. Further, let
![]() $W \subset H$
be a non-empty, precompact window of polytopal type with bounding hyperplanes
$W \subset H$
be a non-empty, precompact window of polytopal type with bounding hyperplanes
![]() $P_1,\ldots , P_N$
such that
$P_1,\ldots , P_N$
such that
![]() $P_i$
has trivial stabilizer and that
$P_i$
has trivial stabilizer and that
![]() $P_i \cap \Gamma _H = \emptyset $
for all
$P_i \cap \Gamma _H = \emptyset $
for all
![]() $i \in \{1,\ldots , N\}$
. Then for the complexity function p of
$i \in \{1,\ldots , N\}$
. Then for the complexity function p of
![]() $\Lambda $
, we have
$\Lambda $
, we have
Notice that the condition of
![]() $\Gamma $
-regularity is hidden in the stronger condition that all the hyperplanes
$\Gamma $
-regularity is hidden in the stronger condition that all the hyperplanes
![]() $P_i$
do not intersect
$P_i$
do not intersect
![]() $\Gamma _H$
. The condition that the
$\Gamma _H$
. The condition that the
![]() $P_i$
have trivial stabilizer simplifies the problem since otherwise, we had to address the effects of the stabilizer. The effect of a non-trivial stabilizer is similar to the Euclidean case, for which we refer to [Reference Koivusalo and Walton28].
$P_i$
have trivial stabilizer simplifies the problem since otherwise, we had to address the effects of the stabilizer. The effect of a non-trivial stabilizer is similar to the Euclidean case, for which we refer to [Reference Koivusalo and Walton28].
The proof of Theorem 5.1 will be divided into establishing an upper bound and a lower bound. For the lower bound, we have to put in much more effort.
5.1. Upper bound of the growth
For an upper bound, we consider the decomposition of the window
![]() $W \setminus \bigcup _{x\in {\mathcal {S}}(r)} x\partial W$
. We will show that counting the connected components is an upper bound for the number of acceptance domains. Then we will use the theory of real hyperplane arrangements, which gives us an upper bound for our counting.
$W \setminus \bigcup _{x\in {\mathcal {S}}(r)} x\partial W$
. We will show that counting the connected components is an upper bound for the number of acceptance domains. Then we will use the theory of real hyperplane arrangements, which gives us an upper bound for our counting.
Lemma 5.2. For a model set
![]() $\Lambda (G,H,\Gamma ,W)$
, we have
$\Lambda (G,H,\Gamma ,W)$
, we have
 $$ \begin{align*} \vert A_r^H\vert \leq \#\pi_0 \bigg( W \setminus \bigcup_{\mu\in{\mathcal{S}}_r} \mu\partial W\bigg). \end{align*} $$
$$ \begin{align*} \vert A_r^H\vert \leq \#\pi_0 \bigg( W \setminus \bigcup_{\mu\in{\mathcal{S}}_r} \mu\partial W\bigg). \end{align*} $$
Proof. By Theorem 2.2, we know that the acceptance domains
![]() $W_r(\unicode{x3bb} )$
tile the window W and that they are disjoint. Further, for every
$W_r(\unicode{x3bb} )$
tile the window W and that they are disjoint. Further, for every
![]() $A_r(\unicode{x3bb} )$
, we know that
$A_r(\unicode{x3bb} )$
, we know that
So
 $$ \begin{align*} \partial W_r(\unicode{x3bb}) &= \partial \bigg( \bigg(\bigcap_{\mu \in {\mathcal{S}}_r(\unicode{x3bb})}\mu \mathring{W}\bigg)\cap \bigg(\bigcap_{\mu \in {\mathcal{S}}_r(\unicode{x3bb})^{\mathrm{C}}} \mu W^{\mathrm{C}} \bigg) \bigg)\\ &\subset \bigg(\bigcup_{\mu \in {\mathcal{S}}_r(\unicode{x3bb})}\mu \partial \mathring{W}\bigg) \cup \bigg(\bigcup_{\mu \in {\mathcal{S}}_r(\unicode{x3bb})^{\mathrm{C}}} \mu \partial W^{\mathrm{C}} \bigg) = \bigcup_{\mu \in S_r} \mu \partial W. \end{align*} $$
$$ \begin{align*} \partial W_r(\unicode{x3bb}) &= \partial \bigg( \bigg(\bigcap_{\mu \in {\mathcal{S}}_r(\unicode{x3bb})}\mu \mathring{W}\bigg)\cap \bigg(\bigcap_{\mu \in {\mathcal{S}}_r(\unicode{x3bb})^{\mathrm{C}}} \mu W^{\mathrm{C}} \bigg) \bigg)\\ &\subset \bigg(\bigcup_{\mu \in {\mathcal{S}}_r(\unicode{x3bb})}\mu \partial \mathring{W}\bigg) \cup \bigg(\bigcup_{\mu \in {\mathcal{S}}_r(\unicode{x3bb})^{\mathrm{C}}} \mu \partial W^{\mathrm{C}} \bigg) = \bigcup_{\mu \in S_r} \mu \partial W. \end{align*} $$
Therefore, every connected component of
![]() $ W \setminus \bigcup _{\mu \in {\mathcal {S}}_r} \mu \partial W$
is contained in some
$ W \setminus \bigcup _{\mu \in {\mathcal {S}}_r} \mu \partial W$
is contained in some
![]() $W_r(\unicode{x3bb} )$
, so
$W_r(\unicode{x3bb} )$
, so
 $$ \begin{align*} \vert A^H_r\vert = \vert W_r \vert \leq \#\pi_0 ( W \setminus \bigcup_{\mu\in{\mathcal{S}}_r} \mu\partial W).\\[-46pt] \end{align*} $$
$$ \begin{align*} \vert A^H_r\vert = \vert W_r \vert \leq \#\pi_0 ( W \setminus \bigcup_{\mu\in{\mathcal{S}}_r} \mu\partial W).\\[-46pt] \end{align*} $$
Lemma 5.3. For a model set
![]() $\Lambda (G,H,\Gamma , W)$
with polytopal window
$\Lambda (G,H,\Gamma , W)$
with polytopal window
![]() $W \subset H$
, we have
$W \subset H$
, we have
 $$ \begin{align*} \#\pi_0 \bigg( W \setminus \bigcup_{\mu\in{\mathcal{S}}_r} \mu\partial W\bigg) \leq \# \pi_0 \bigg( H \setminus \bigcup_{\mu\in{\mathcal{S}}_r} \bigcup_{i=1}^N \mu P_i\bigg). \end{align*} $$
$$ \begin{align*} \#\pi_0 \bigg( W \setminus \bigcup_{\mu\in{\mathcal{S}}_r} \mu\partial W\bigg) \leq \# \pi_0 \bigg( H \setminus \bigcup_{\mu\in{\mathcal{S}}_r} \bigcup_{i=1}^N \mu P_i\bigg). \end{align*} $$
Proof. Since
![]() $\bigcup _{\mu \in {\mathcal {S}}_r} \mu \partial W \subset \bigcup _{\mu \in {\mathcal {S}}_r} \bigcup _{i=1}^N \mu P_i$
, we have
$\bigcup _{\mu \in {\mathcal {S}}_r} \mu \partial W \subset \bigcup _{\mu \in {\mathcal {S}}_r} \bigcup _{i=1}^N \mu P_i$
, we have
 $$ \begin{align*} \#\pi_0 \bigg( W \setminus \bigcup_{\mu\in{\mathcal{S}}_r} \mu\partial W\bigg) \leq \# \pi_0 \bigg( W \setminus \bigcup_{\mu\in{\mathcal{S}}_r} \bigcup_{i=1}^N \mu P_i\bigg). \end{align*} $$
$$ \begin{align*} \#\pi_0 \bigg( W \setminus \bigcup_{\mu\in{\mathcal{S}}_r} \mu\partial W\bigg) \leq \# \pi_0 \bigg( W \setminus \bigcup_{\mu\in{\mathcal{S}}_r} \bigcup_{i=1}^N \mu P_i\bigg). \end{align*} $$
Since
![]() $e \in {\mathcal {S}}_r$
for all r, we have
$e \in {\mathcal {S}}_r$
for all r, we have
![]() $\partial W \subset \bigcup _{\mu \in S_r}\bigcup _{i=1}^N \mu P_i$
such that all regions inside W stay the same if we increase W to H. If we add the regions outside of W, we therefore get
$\partial W \subset \bigcup _{\mu \in S_r}\bigcup _{i=1}^N \mu P_i$
such that all regions inside W stay the same if we increase W to H. If we add the regions outside of W, we therefore get
 $$ \begin{align*} \#\pi_0 \bigg( W \setminus \bigcup_{\mu\in{\mathcal{S}}_r} \bigcup_{i=1}^N \mu P_i\bigg) \leq \# \pi_0 \bigg( H \setminus \bigcup_{\mu\in{\mathcal{S}}_r} \bigcup_{i=1}^N \mu P_i\bigg).\\[-46pt] \end{align*} $$
$$ \begin{align*} \#\pi_0 \bigg( W \setminus \bigcup_{\mu\in{\mathcal{S}}_r} \bigcup_{i=1}^N \mu P_i\bigg) \leq \# \pi_0 \bigg( H \setminus \bigcup_{\mu\in{\mathcal{S}}_r} \bigcup_{i=1}^N \mu P_i\bigg).\\[-46pt] \end{align*} $$
By Lemma 4.8, the topology on H is the same as on
![]() ${\mathbb {R}}^{\dim (H)}$
and we additionally assumed H to be non-crooked. So the problem of counting the connected components is a well-known problem from the theory of real hyperplane arrangements. A general upper bound for the number of connected components has been known for a long time and first appeared in [Reference Schläfli41] by Schläfli, see also [Reference Dimca12, Theorem 1.2]. For an arrangement
${\mathbb {R}}^{\dim (H)}$
and we additionally assumed H to be non-crooked. So the problem of counting the connected components is a well-known problem from the theory of real hyperplane arrangements. A general upper bound for the number of connected components has been known for a long time and first appeared in [Reference Schläfli41] by Schläfli, see also [Reference Dimca12, Theorem 1.2]. For an arrangement
![]() ${\mathcal {H}} \subset {\mathbb {R}}^n$
consisting of k different hyperplanes, we get the general upper bound
${\mathcal {H}} \subset {\mathbb {R}}^n$
consisting of k different hyperplanes, we get the general upper bound
 $$ \begin{align*} \sum_{i=0}^n \begin{pmatrix} k \\ i\end{pmatrix} \asymp k^n. \end{align*} $$
$$ \begin{align*} \sum_{i=0}^n \begin{pmatrix} k \\ i\end{pmatrix} \asymp k^n. \end{align*} $$
In our case,
![]() $n= \dim (H)$
and
$n= \dim (H)$
and
![]() $k= \vert {\mathcal {S}}(r)\vert $
. We know from Proposition 3.1 that
$k= \vert {\mathcal {S}}(r)\vert $
. We know from Proposition 3.1 that
![]() ${\vert {\mathcal {S}}(r)\vert \asymp r^{{\mathrm {homdim}}(G)}}$
. Combining these results yields
${\vert {\mathcal {S}}(r)\vert \asymp r^{{\mathrm {homdim}}(G)}}$
. Combining these results yields
 $$ \begin{align*} p(r) = \vert A_r^H\vert \leq \#\pi_0 \bigg( H \setminus \bigcup_{\mu\in{\mathcal{S}}(r)} \bigcup_{i=1}^N \mu P_i\bigg) \ll \vert {\mathcal{S}}(r)\vert^{\dim(H)} \asymp r^{{\mathrm{homdim}}(G) \cdot \dim (H)}. \end{align*} $$
$$ \begin{align*} p(r) = \vert A_r^H\vert \leq \#\pi_0 \bigg( H \setminus \bigcup_{\mu\in{\mathcal{S}}(r)} \bigcup_{i=1}^N \mu P_i\bigg) \ll \vert {\mathcal{S}}(r)\vert^{\dim(H)} \asymp r^{{\mathrm{homdim}}(G) \cdot \dim (H)}. \end{align*} $$
5.2. Lower bound of the growth
We fix some parameters of the window which will help us in proving Theorem 5.1.
Definition 5.4. For a given polytopal window W, we fix the following parameters:
-
(i) a centre of the window
 $c_W \in W$
such that
$c_W \in W$
such that
 $\inf \{r \in {\mathbb {R}} \mid B_r(c_W) \subset W \}$
is maximal;
$\inf \{r \in {\mathbb {R}} \mid B_r(c_W) \subset W \}$
is maximal; -
(ii) the inner radius of the window
 $I_W:=\sup \{r \in {\mathbb {R}} \mid B_r(c_W) \subset W\}$
;
$I_W:=\sup \{r \in {\mathbb {R}} \mid B_r(c_W) \subset W\}$
; -
(iii) the outer radius of the window
 $O_W:=\inf \{r \in {\mathbb {R}}\mid W \subset B_r(c_W)\}$
;
$O_W:=\inf \{r \in {\mathbb {R}}\mid W \subset B_r(c_W)\}$
; -
(iv) the size of
 $\partial _i W$
, respectively the inner radius of face i, and the minimum of all the sizes of the faces
$\partial _i W$
, respectively the inner radius of face i, and the minimum of all the sizes of the faces $$ \begin{align*} F_i:=\sup\{r \in {\mathbb{R}} \mid \text{there exists } p \in P_i: B_r(p)\cap \partial_i W = B_r(p) \cap P_i\} \end{align*} $$
$$ \begin{align*} F_i:=\sup\{r \in {\mathbb{R}} \mid \text{there exists } p \in P_i: B_r(p)\cap \partial_i W = B_r(p) \cap P_i\} \end{align*} $$
 $$ \begin{align*} F_W:=\min\{F_i \mid i \in \{1,\ldots ,N\}\}; \end{align*} $$
$$ \begin{align*} F_W:=\min\{F_i \mid i \in \{1,\ldots ,N\}\}; \end{align*} $$
-
(v) for each face
 $\partial _i W$
, a face centre
$\partial _i W$
, a face centre
 $p_i \in \partial _i W$
such that
$p_i \in \partial _i W$
such that
 $B_{F_W}(p_i)\cap \partial _i W= B_{F_W}(p_i)\cap P_i$
.
$B_{F_W}(p_i)\cap \partial _i W= B_{F_W}(p_i)\cap P_i$
.
We will use these parameters in our proof later. The centres may not be unique, but we fix a choice for the rest of the argument. Further, we need to widen the definition of parallel a little since we are only interested in intersections inside a bounded region.
Definition 5.5. Let
![]() $B \subset H$
be a bounded region and
$B \subset H$
be a bounded region and
![]() $P_1, P_2$
two hyperplanes in H. We call
$P_1, P_2$
two hyperplanes in H. We call
![]() $P_1$
and
$P_1$
and
![]() $P_2$
almost parallel with respect to B if
$P_2$
almost parallel with respect to B if
![]() $P_1\cap P_2 \cap B = \emptyset $
.
$P_1\cap P_2 \cap B = \emptyset $
.
The aim is now to find a region inside W for which it makes no difference if it is divided by a face
![]() $\partial _i W$
or by the whole hyperplane
$\partial _i W$
or by the whole hyperplane
![]() $P_i$
. Further, we wish to get a one-to-one correspondence between the connected components and the acceptance domains in this small region.
$P_i$
. Further, we wish to get a one-to-one correspondence between the connected components and the acceptance domains in this small region.
Definition 5.6. Let
![]() $B \subset H$
be a bounded region. For
$B \subset H$
be a bounded region. For
![]() $s \in H$
, we say
$s \in H$
, we say
![]() $s \partial _i W$
cuts B fully if
$s \partial _i W$
cuts B fully if
If additionally
we say
![]() $s \partial _i W$
cuts B all-round.
$s \partial _i W$
cuts B all-round.
Remark 5.7. An all-round cut is always a full cut, but the converse is false, see Figure 3.
Figure 3 On the left,
![]() $\partial _i W$
cuts B fully and all-round, and on the right,
$\partial _i W$
cuts B fully and all-round, and on the right,
![]() $\partial _i W$
cuts B fully but not all-round.
$\partial _i W$
cuts B fully but not all-round.
Additionally to decreasing the area of interest, we will decrease the set from which we operate on the window. Instead of considering all elements from
![]() ${\mathcal {S}}_r$
, we define for each face a subset
${\mathcal {S}}_r$
, we define for each face a subset
![]() $U_i(r) \subset {\mathcal {S}}_r$
. The
$U_i(r) \subset {\mathcal {S}}_r$
. The
![]() $U_i(r)$
will be defined such that we only obtain all-round cuts and get a one-to-one correspondence between the connected components and the acceptance domains.
$U_i(r)$
will be defined such that we only obtain all-round cuts and get a one-to-one correspondence between the connected components and the acceptance domains.
Definition 5.8. Let
![]() $(k,h) \in {\mathbb {R}}^2$
. The region we will consider is
$(k,h) \in {\mathbb {R}}^2$
. The region we will consider is
![]() $B_h(c_W)$
and the set from which we operate is
$B_h(c_W)$
and the set from which we operate is
![]() ${U_i:= B_k(c_W p_i^{-1})}$
for all
${U_i:= B_k(c_W p_i^{-1})}$
for all
![]() $i\in \{1,\ldots ,N\}$
. If the following conditions are fulfilled, we call
$i\in \{1,\ldots ,N\}$
. If the following conditions are fulfilled, we call
![]() $(k,h)$
a good pair:
$(k,h)$
a good pair:
-
(i)
 $0 < k <h$
;
$0 < k <h$
; -
(ii)
 $h < I_W$
, therefore,
$h < I_W$
, therefore,
 $B_h(c_W) \subset W$
;
$B_h(c_W) \subset W$
; -
(iii)
 $\text {for all } a\in B_{O_W}(e)$
,
$\text {for all } a\in B_{O_W}(e)$
,
 $x \in B_{2h}(e)$
:
$x \in B_{2h}(e)$
:
 $\vert a x a^{-1}\vert _H \leq F_W$
;
$\vert a x a^{-1}\vert _H \leq F_W$
; -
(iv)
 $\text {for all } i \in \{1,\ldots ,N\}$
,
$\text {for all } i \in \{1,\ldots ,N\}$
,
 $\text {for all } s \in U_i$
,
$\text {for all } s \in U_i$
,
 $(s P_i^+) \cap B_h(c_W) = (s W) \cap B_h(c_W)$
.
$(s P_i^+) \cap B_h(c_W) = (s W) \cap B_h(c_W)$
.
Remark 5.9. Observe that if
![]() $(k,h)$
is a good pair, then
$(k,h)$
is a good pair, then
![]() $(k',h)$
is a good pair for all
$(k',h)$
is a good pair for all
![]() ${0 < k' < k}$
.
${0 < k' < k}$
.
Proposition 5.10. A good pair exists.
For the proof, we need some preparation. It will begin after Corollary 5.19.
Lemma 5.11. Let G be an homogeneous Lie group and
![]() $x \in G$
fixed. Then for all
$x \in G$
fixed. Then for all
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $\delta (x)>0$
such that for
$\delta (x)>0$
such that for
![]() $u \in B_{\delta (x)}(e)$
,
$u \in B_{\delta (x)}(e)$
,
Further, if
![]() $\vert x \vert \leq k$
, then there exists a
$\vert x \vert \leq k$
, then there exists a
![]() $\delta '(k)>0$
such that for
$\delta '(k)>0$
such that for
![]() $u \in B_{\delta '(k)}(e)$
,
$u \in B_{\delta '(k)}(e)$
,
Proof. Using the Baker–Campbell–Hausdorff formula, we get
 $$ \begin{align*} x u x^{-1} &= (x + u + \tfrac{1}{2}[x,u]+\tfrac{1}{12}([x,[x,u]]-[u,[x,u]])-\cdots) x^{-1}\\ &= (x + u + \tfrac{1}{2}[x,u]+\tfrac{1}{12}([x,[x,u]]-[u,[x,u]])-\cdots)\\ &\quad - x + \tfrac{1}{2}[(x + u + \tfrac{1}{2}[x,u]+\tfrac{1}{12}([x,[x,u]]-[u[x,u]])-\cdots) ,x^{-1}]+\cdots\\ &= u +B(x,u), \end{align*} $$
$$ \begin{align*} x u x^{-1} &= (x + u + \tfrac{1}{2}[x,u]+\tfrac{1}{12}([x,[x,u]]-[u,[x,u]])-\cdots) x^{-1}\\ &= (x + u + \tfrac{1}{2}[x,u]+\tfrac{1}{12}([x,[x,u]]-[u,[x,u]])-\cdots)\\ &\quad - x + \tfrac{1}{2}[(x + u + \tfrac{1}{2}[x,u]+\tfrac{1}{12}([x,[x,u]]-[u[x,u]])-\cdots) ,x^{-1}]+\cdots\\ &= u +B(x,u), \end{align*} $$
where
![]() $B(x,u)$
only contains terms which include
$B(x,u)$
only contains terms which include
![]() $[u,x]$
. The continuity of the Lie bracket implies the claim. Be aware that we work in exponential coordinates here, as explained in §4, so formally, we should write
$[u,x]$
. The continuity of the Lie bracket implies the claim. Be aware that we work in exponential coordinates here, as explained in §4, so formally, we should write
![]() $\exp (x)$
and
$\exp (x)$
and
![]() $\exp (u)$
instead of x and u.
$\exp (u)$
instead of x and u.
Lemma 5.12. Let
![]() $(k,h)$
fulfil conditions (i) and (iii) of Definition 5.8, then for any
$(k,h)$
fulfil conditions (i) and (iii) of Definition 5.8, then for any
![]() ${i\in \{1,\ldots ,N\}}$
and for every
${i\in \{1,\ldots ,N\}}$
and for every
![]() $s \in U_i$
, it holds that
$s \in U_i$
, it holds that
![]() $s P_i $
cuts
$s P_i $
cuts
![]() $B_h(c_W)$
fully.
$B_h(c_W)$
fully.
Proof. First, we show that for all
![]() $s \in U_i$
, we get
$s \in U_i$
, we get
![]() $s P_i \cap B_h(c_W) \neq \emptyset $
. We can write
$s P_i \cap B_h(c_W) \neq \emptyset $
. We can write
![]() ${s=a \cdot c_W \cdot p_i^{-1}}$
with
${s=a \cdot c_W \cdot p_i^{-1}}$
with
![]() $a \in B_k(e)$
. Then
$a \in B_k(e)$
. Then
Now we need to show that
![]() $s \partial _i W \cap B_h(c_W) = s P_i \cap B_h(c_W)$
. This is equivalent to
$s \partial _i W \cap B_h(c_W) = s P_i \cap B_h(c_W)$
. This is equivalent to
The inclusion
![]() $\subseteq $
is obvious since
$\subseteq $
is obvious since
![]() $\partial _i W \subset P_i$
. We show that
$\partial _i W \subset P_i$
. We show that
![]() $s^{-1} B_h(c_W) \subseteq B_{F_W}(p_i)$
, then the claim follows from the definition of
$s^{-1} B_h(c_W) \subseteq B_{F_W}(p_i)$
, then the claim follows from the definition of
![]() $p_i$
and
$p_i$
and
![]() $F_W$
. Let
$F_W$
. Let
![]() $x \cdot c_W \in B_h(c_W)$
be an arbitrary element and
$x \cdot c_W \in B_h(c_W)$
be an arbitrary element and
![]() $s=a \cdot c_W \cdot p_i^{-1}$
as above.
$s=a \cdot c_W \cdot p_i^{-1}$
as above.
 $$ \begin{align*} d(s^{-1} x c_W, p_i)= \big\vert \hspace{-0.45cm}\underbrace{p_i c_W^{-1}}_{=: y \in B_{O_W}(e) } \cdot \underbrace{a^{-1} x_{}}_{\in B_{h + k}(e)} \cdot \underbrace{c_W p_i^{-1}}_{=y^{-1}}\big\vert \leq F_W. \end{align*} $$
$$ \begin{align*} d(s^{-1} x c_W, p_i)= \big\vert \hspace{-0.45cm}\underbrace{p_i c_W^{-1}}_{=: y \in B_{O_W}(e) } \cdot \underbrace{a^{-1} x_{}}_{\in B_{h + k}(e)} \cdot \underbrace{c_W p_i^{-1}}_{=y^{-1}}\big\vert \leq F_W. \end{align*} $$
The inequality follows by condition (iii) of Definition 5.8.
From the proof, we can extract the following corollary.
Corollary 5.13. Let
![]() $i\in \{1,\ldots ,N\}$
. For every
$i\in \{1,\ldots ,N\}$
. For every
![]() $s \in U_i$
, we have that
$s \in U_i$
, we have that
![]() $s P_i $
intersects
$s P_i $
intersects
![]() $B_k(c_W)$
non-trivially.
$B_k(c_W)$
non-trivially.
Corollary 5.14. Let
![]() $(k,h)$
fulfil conditions (i), (iii) and (iv) of Definition 5.8, then for any
$(k,h)$
fulfil conditions (i), (iii) and (iv) of Definition 5.8, then for any
![]() $i\in \{1,\ldots ,N\}$
and for every
$i\in \{1,\ldots ,N\}$
and for every
![]() $s \in U_i$
,
$s \in U_i$
,
![]() $s P_i $
cuts
$s P_i $
cuts
![]() $B_h(c_W)$
all-round holds.
$B_h(c_W)$
all-round holds.
We will also need the definition of an intersection angle between two hyperplanes since we will show that by acting with a small element, we can only rotate a plane a little.
Definition 5.15. The angle between two hyperplanes P and Q in
![]() ${\mathbb {R}}^d$
with normals
${\mathbb {R}}^d$
with normals
![]() $n_P$
and
$n_P$
and
![]() $n_Q$
, both normalized, is given by
$n_Q$
, both normalized, is given by
For
![]() $i,j \in \{1,\ldots ,N\}$
with
$i,j \in \{1,\ldots ,N\}$
with
![]() $i \neq j$
, we denote by
$i \neq j$
, we denote by
![]() $\alpha _{ij}$
the angle between
$\alpha _{ij}$
the angle between
![]() $c_Wp_i^{-1} P_i$
and
$c_Wp_i^{-1} P_i$
and
![]() $c_W p_j^{-1} P_j$
, that is,
$c_W p_j^{-1} P_j$
, that is,
Remark 5.16. In the definition, we use
![]() $c_W p_i^{-1} P_i$
instead of
$c_W p_i^{-1} P_i$
instead of
![]() $P_i$
. Since this plane is sort of the prototype for the family
$P_i$
. Since this plane is sort of the prototype for the family
![]() $U_i P_i$
, all the other planes from this family then result from an action with a small element. Here,
$U_i P_i$
, all the other planes from this family then result from an action with a small element. Here,
![]() $u \in U_i$
is of the form
$u \in U_i$
is of the form
![]() $a c_Wp_i^{-1}$
with
$a c_Wp_i^{-1}$
with
![]() $a\in B_k(e)$
.
$a\in B_k(e)$
.
Convention 5.17. We choose
![]() $i_1,\ldots , i_{\dim (H)}$
such that
$i_1,\ldots , i_{\dim (H)}$
such that
 $$ \begin{align*} \bigcap_{l=1}^{\dim(H)} c_W p_{i_l}^{-1} P_{i_l}= \{c_W\}. \end{align*} $$
$$ \begin{align*} \bigcap_{l=1}^{\dim(H)} c_W p_{i_l}^{-1} P_{i_l}= \{c_W\}. \end{align*} $$
So this is a set of hyperplanes in which each intersection of k hyperplanes has dimension
![]() $\dim (H)-k$
. From now on, we fix such a family and denote it by
$\dim (H)-k$
. From now on, we fix such a family and denote it by
![]() ${\mathcal {F}}$
. Without loss of generality,
${\mathcal {F}}$
. Without loss of generality,
![]() ${\mathcal {F}} = \{P_1,\ldots ,P_{\dim (H)}\}$
.
${\mathcal {F}} = \{P_1,\ldots ,P_{\dim (H)}\}$
.
Lemma 5.18. For all
![]() $r>0$
, there exists
$r>0$
, there exists
![]() $\beta (r)$
, with
$\beta (r)$
, with
![]() $\beta (r) \to 0$
for
$\beta (r) \to 0$
for
![]() $r \to 0$
, such that for all
$r \to 0$
, such that for all
![]() $x \in B_r(e) \subset H$
and any hyperplane P, we have
$x \in B_r(e) \subset H$
and any hyperplane P, we have
![]() $\sphericalangle (x P, P) \leq \beta (r)$
.
$\sphericalangle (x P, P) \leq \beta (r)$
.
Proof. Since H is a non-crooked homogeneous Lie group, we know that
![]() $xP$
is again a hyperplane. So let
$xP$
is again a hyperplane. So let
 $$ \begin{align*} P= \bigg\{a + \sum_{i=1}^n t_i v_i \mid t_i \in {\mathbb{R}}\bigg\}, \end{align*} $$
$$ \begin{align*} P= \bigg\{a + \sum_{i=1}^n t_i v_i \mid t_i \in {\mathbb{R}}\bigg\}, \end{align*} $$
where
![]() $a, v_i \in {\mathbb {R}}^n$
. By the form of the group action, which we discuss in Appendix B.1, we know that
$a, v_i \in {\mathbb {R}}^n$
. By the form of the group action, which we discuss in Appendix B.1, we know that
![]() $xP$
is of the form
$xP$
is of the form
with
![]() $f_i$
polynomials of a special form, namely
$f_i$
polynomials of a special form, namely
 $$ \begin{align*} f_i(x,P) = x_i + P_i +\sum_{k=1}^n\sum_{\substack{\alpha_1,\ldots ,\alpha_n \in {\mathbb{N}} \\ \sum \alpha_i \neq 0}} c_{k,\alpha_1,\ldots ,\alpha_n} P_k x_1^{\alpha_1}\cdots x_n^{\alpha_n}. \end{align*} $$
$$ \begin{align*} f_i(x,P) = x_i + P_i +\sum_{k=1}^n\sum_{\substack{\alpha_1,\ldots ,\alpha_n \in {\mathbb{N}} \\ \sum \alpha_i \neq 0}} c_{k,\alpha_1,\ldots ,\alpha_n} P_k x_1^{\alpha_1}\cdots x_n^{\alpha_n}. \end{align*} $$
The direction vectors are those from P plus some deviation which depends on x. If x gets smaller, the two planes are getting closer to being parallel.
Corollary 5.19. For all
![]() $r>0$
, there exists
$r>0$
, there exists
![]() $\beta (r)$
, with
$\beta (r)$
, with
![]() $\beta (r) \to 0$
for
$\beta (r) \to 0$
for
![]() $r \to 0$
, such that for all
$r \to 0$
, such that for all
![]() $x, y \in B_r(e) \subset H$
and any hyperplane P, we have
$x, y \in B_r(e) \subset H$
and any hyperplane P, we have
![]() $\sphericalangle (x P, y P) \leq 2\beta (r)$
.
$\sphericalangle (x P, y P) \leq 2\beta (r)$
.
Proof of Proposition 5.10
By Lemma 5.11, there exists an upper bound
![]() $b_1$
on h such that for all
$b_1$
on h such that for all
![]() $a\in B_{O_W}(e)$
,
$a\in B_{O_W}(e)$
,
![]() $x \in B_{2h}(e)$
:
$x \in B_{2h}(e)$
:
![]() $\vert a x a^{-1}\vert _H \leq F_W$
. Set
$\vert a x a^{-1}\vert _H \leq F_W$
. Set
![]() $h':=\min \{b_1, {I_W}/{2}\}$
and set
$h':=\min \{b_1, {I_W}/{2}\}$
and set
![]() $k':= {h'}/{2}$
, then conditions (i), (ii) and (iii) from Definition 5.8 are fulfilled.
$k':= {h'}/{2}$
, then conditions (i), (ii) and (iii) from Definition 5.8 are fulfilled.
By Lemma 5.12, for any
![]() $i \in \{1,\ldots ,N\}$
and all
$i \in \{1,\ldots ,N\}$
and all
![]() $s \in B_{k'}(c_Wp_i^{-1})$
, we have
$s \in B_{k'}(c_Wp_i^{-1})$
, we have
![]() $sP_i$
cuts
$sP_i$
cuts
![]() $B_{h'}(c_W)$
fully, this also holds for all
$B_{h'}(c_W)$
fully, this also holds for all
![]() $h \leq h'$
.
$h \leq h'$
.
Now assume that there is a cut that is full but not all-round; therefore,
To be more precise, we have
![]() $sW \cap B_{h'}(c_W) \subsetneq s P_i^+ \cap B_{h'}(c_W)$
since
$sW \cap B_{h'}(c_W) \subsetneq s P_i^+ \cap B_{h'}(c_W)$
since
![]() $sW \subset sP_i^+$
. Let
$sW \subset sP_i^+$
. Let
We see that
![]() $b_s^i \neq 0$
since
$b_s^i \neq 0$
since
![]() $sW$
is a polytope with non-empty interior. Now set
$sW$
is a polytope with non-empty interior. Now set
and
![]() $k={h}/{2}$
. The last thing to observe now is that the infimum over the
$k={h}/{2}$
. The last thing to observe now is that the infimum over the
![]() $b_s^i$
is not zero. If it were zero, this would mean that the polytope
$b_s^i$
is not zero. If it were zero, this would mean that the polytope
![]() $sW$
could become arbitrarily thin such that only an even smaller ball would fit in. However, this cannot be the case since we have seen that we can only rotate the bounding hyperplanes only by a small amount.
$sW$
could become arbitrarily thin such that only an even smaller ball would fit in. However, this cannot be the case since we have seen that we can only rotate the bounding hyperplanes only by a small amount.
Convention 5.20. From now on, let
![]() $(k,h)$
be a good pair.
$(k,h)$
be a good pair.
Observe that
![]() $U_i \subset WW^{-1}$
for all
$U_i \subset WW^{-1}$
for all
![]() $i\in \{1,\ldots ,N\}$
. Further, notice that we operate differently on the different hyperplanes that bound W. Te
$i\in \{1,\ldots ,N\}$
. Further, notice that we operate differently on the different hyperplanes that bound W. Te
![]() $U_i$
may overlap but they are not equal. Additionally, we have chosen
$U_i$
may overlap but they are not equal. Additionally, we have chosen
![]() $B_h(c_W)$
so that for each of the hyperplanes, it does not make a difference if we operate on the face
$B_h(c_W)$
so that for each of the hyperplanes, it does not make a difference if we operate on the face
![]() $\partial _i W$
or on the hyperplane
$\partial _i W$
or on the hyperplane
![]() $P_i$
.
$P_i$
.
Now we will reconsider the dependence of the growing parameter r and the lattice
![]() $\Gamma $
.
$\Gamma $
.
Definition 5.21. Set
![]() $U_i(r):= \pi _H((B_r^G(e) \times U_i)\cap \Gamma )$
which is a finite subset of
$U_i(r):= \pi _H((B_r^G(e) \times U_i)\cap \Gamma )$
which is a finite subset of
![]() $U_i$
.
$U_i$
.
Remark 5.22. Observe that
![]() $U_i(r)$
is a subset of the r-slab
$U_i(r)$
is a subset of the r-slab
![]() ${\mathcal {S}}_r$
since
${\mathcal {S}}_r$
since
![]() $U_i \subset WW^{-1}$
.
$U_i \subset WW^{-1}$
.
Proposition 5.23. The number of connected components of
 $ B_h(c_W) \setminus \bigcup _{i=1}^N \bigcup _{s \in U_i(r)} s \partial _i W$
is a lower bound of the number of acceptance domains
$ B_h(c_W) \setminus \bigcup _{i=1}^N \bigcup _{s \in U_i(r)} s \partial _i W$
is a lower bound of the number of acceptance domains
![]() $\vert A_r^H \vert $
, that is,
$\vert A_r^H \vert $
, that is,
 $$ \begin{align*} \# \pi_0 \bigg( B_h(c_W) \setminus \bigcup_{i=1}^N \bigcup_{s \in U_i(r)} s \partial_i W \bigg) \leq \vert A_r^H \vert. \end{align*} $$
$$ \begin{align*} \# \pi_0 \bigg( B_h(c_W) \setminus \bigcup_{i=1}^N \bigcup_{s \in U_i(r)} s \partial_i W \bigg) \leq \vert A_r^H \vert. \end{align*} $$
Proof. Recall that a pre-acceptance domain
![]() $A_r^H(\unicode{x3bb} )$
is contained in an acceptance domain
$A_r^H(\unicode{x3bb} )$
is contained in an acceptance domain
![]() $W_r(\unicode{x3bb} )$
. Let C be a connected component of
$W_r(\unicode{x3bb} )$
. Let C be a connected component of
![]() $B_h(c_W) \setminus \bigcup _{i=1}^N \bigcup _{s \in U_i(r)} s \partial _i W$
. By Lemma 5.12, we can replace the faces by the hyperplanes without changing the connected components in
$B_h(c_W) \setminus \bigcup _{i=1}^N \bigcup _{s \in U_i(r)} s \partial _i W$
. By Lemma 5.12, we can replace the faces by the hyperplanes without changing the connected components in
![]() $B_h(c_W)$
, so we consider
$B_h(c_W)$
, so we consider
![]() ${B_h(c_W) \setminus \bigcup _{i=1}^N \bigcup _{s \in U_i(r)} s P_i}$
.
${B_h(c_W) \setminus \bigcup _{i=1}^N \bigcup _{s \in U_i(r)} s P_i}$
.
We show that if an acceptance domain intersects a connected component of
![]() $B_h(c_W) \setminus \bigcup _{i=1}^N \bigcup _{s \in U_i(r)} s P_i$
, it is fully contained in it. Let
$B_h(c_W) \setminus \bigcup _{i=1}^N \bigcup _{s \in U_i(r)} s P_i$
, it is fully contained in it. Let
![]() $C'$
be another connected component of
$C'$
be another connected component of
![]() $B_h(c_W) \setminus \bigcup _{i=1}^N \bigcup _{s \in U_i(r)} s P_i$
and assume that
$B_h(c_W) \setminus \bigcup _{i=1}^N \bigcup _{s \in U_i(r)} s P_i$
and assume that
![]() $C \cap W_r(\unicode{x3bb} ) \neq \emptyset \neq C' \cap W_r(\unicode{x3bb} )$
. Between C and
$C \cap W_r(\unicode{x3bb} ) \neq \emptyset \neq C' \cap W_r(\unicode{x3bb} )$
. Between C and
![]() $C'$
is a hyperplane
$C'$
is a hyperplane
![]() $s P_i$
for some
$s P_i$
for some
![]() $i\in \{1,\ldots ,N\}$
and
$i\in \{1,\ldots ,N\}$
and
![]() $s \in U_i(r)$
. Therefore,
$s \in U_i(r)$
. Therefore,
![]() $C \subset s \mathring {P^+}$
and
$C \subset s \mathring {P^+}$
and
![]() $C'\subset s \mathring {P^-}$
, or the other way around. Additionally, since the cut
$C'\subset s \mathring {P^-}$
, or the other way around. Additionally, since the cut
![]() $s\partial _i W$
is all-round, we get that
$s\partial _i W$
is all-round, we get that
![]() $C \subset s \mathring {W}$
and
$C \subset s \mathring {W}$
and
![]() $C' \subset s W^{\mathrm {C}}$
, or the other way around. However, either
$C' \subset s W^{\mathrm {C}}$
, or the other way around. However, either
![]() $W_r(\unicode{x3bb} ) \subset s\mathring {W}$
or
$W_r(\unicode{x3bb} ) \subset s\mathring {W}$
or
![]() $W_r(\unicode{x3bb} ) \subset sW^{\mathrm {C}}$
, which is a contradiction.
$W_r(\unicode{x3bb} ) \subset sW^{\mathrm {C}}$
, which is a contradiction.
It remains to find a combinatorial argument for counting the connected components of
 $$ \begin{align*} B_h(c_W) \setminus \bigcup_{i=1}^N \bigcup_{s \in U_i} s \partial_i W=B_h(c_W) \setminus \bigcup_{i=1}^N \bigcup_{s \in U_i} s P_i, \end{align*} $$
$$ \begin{align*} B_h(c_W) \setminus \bigcup_{i=1}^N \bigcup_{s \in U_i} s \partial_i W=B_h(c_W) \setminus \bigcup_{i=1}^N \bigcup_{s \in U_i} s P_i, \end{align*} $$
which yields a lower bound by Proposition 5.23. This will be done in the next section.
In the rest of the section, we will prove the following proposition, which gives us the tools for the combinatorics in the next section.
Proposition 5.24. There exists a good pair
![]() $(k,h)$
such that:
$(k,h)$
such that:
-
(a) for all
 $I \subset \{1,\ldots ,N\}$
with
$I \subset \{1,\ldots ,N\}$
with
 $\vert I \vert = \dim (H)$
and all
$\vert I \vert = \dim (H)$
and all
 $u_{1} \in U_{i_1},\ldots ,u_{{\dim (H)}} \in U_{i_{\dim (H)}}$
, we get
$u_{1} \in U_{i_1},\ldots ,u_{{\dim (H)}} \in U_{i_{\dim (H)}}$
, we get  $$ \begin{align*} u_{1} P_{i_1} \cap \cdots \cap u_{{\dim(H)}} P_{i_{\dim(H)}} = \{s\}\quad\text{where } s \in B_h(c_W); \end{align*} $$
$$ \begin{align*} u_{1} P_{i_1} \cap \cdots \cap u_{{\dim(H)}} P_{i_{\dim(H)}} = \{s\}\quad\text{where } s \in B_h(c_W); \end{align*} $$
-
(b) for every constant
 $c>0$
and all
$c>0$
and all
 $s \in H$
, there is a
$s \in H$
, there is a
 $r_0$
such that for all
$r_0$
such that for all
 $r> r_0$
, we get that
$r> r_0$
, we get that  $$ \begin{align*} \vert \{u \in U_i(r) \mid s \in u P_i\}\vert \leq c \vert U_i(r) \vert. \end{align*} $$
$$ \begin{align*} \vert \{u \in U_i(r) \mid s \in u P_i\}\vert \leq c \vert U_i(r) \vert. \end{align*} $$
Lemma 5.25. For
![]() $i,j \in \{1,\ldots ,\dim (H)\}$
,
$i,j \in \{1,\ldots ,\dim (H)\}$
,
![]() $i \neq j$
, there exists a good pair
$i \neq j$
, there exists a good pair
![]() $(k,h)$
such that for all
$(k,h)$
such that for all
![]() $u \in U_i=B_k(c_Wp_i^{-1}), v \in U_j$
, we have
$u \in U_i=B_k(c_Wp_i^{-1}), v \in U_j$
, we have
![]() $u P_i$
and
$u P_i$
and
![]() $vP_j$
are not almost parallel with respect to
$vP_j$
are not almost parallel with respect to
![]() $B_h(c_W)$
.
$B_h(c_W)$
.
Proof. Fix some
![]() $i,j \in \{1,\ldots ,N\}$
with
$i,j \in \{1,\ldots ,N\}$
with
![]() $i \neq j$
. By Corollary 5.13, all the
$i \neq j$
. By Corollary 5.13, all the
![]() $u P_i$
,
$u P_i$
,
![]() $v P_j$
with
$v P_j$
with
![]() $u \in U_i$
,
$u \in U_i$
,
![]() $v \in U_j$
intersect
$v \in U_j$
intersect
![]() $B_k(c_W)$
.
$B_k(c_W)$
.
Further, we can control the angle between the two hyperplanes by Lemma 5.18 so that for all
![]() $ u \in U_i, v \in U_j $
,
$ u \in U_i, v \in U_j $
,
where
![]() $\beta (k)$
is from Lemma 5.18. We can choose k so small such that
$\beta (k)$
is from Lemma 5.18. We can choose k so small such that
![]() $0 < \alpha _{ij} - 2 \beta (k) < {\pi }/{2}$
, which means that the hyperplanes cannot be parallel so they intersect somewhere. For two hyperplanes that intersect the same ball of radius k and which intersect in at least a given angle, there is a bound for the intersection to the centre point of the ball:
$0 < \alpha _{ij} - 2 \beta (k) < {\pi }/{2}$
, which means that the hyperplanes cannot be parallel so they intersect somewhere. For two hyperplanes that intersect the same ball of radius k and which intersect in at least a given angle, there is a bound for the intersection to the centre point of the ball:
 $$ \begin{align*} c(k):= k \bigg( 1+\frac{1}{\tan(({\alpha_{ij}-2 \beta(k)})/{2})}\bigg). \end{align*} $$
$$ \begin{align*} c(k):= k \bigg( 1+\frac{1}{\tan(({\alpha_{ij}-2 \beta(k)})/{2})}\bigg). \end{align*} $$
The idea of how to establish this bound is to consider the space which is orthogonal to the intersection of
![]() $u P_i$
and
$u P_i$
and
![]() $v P_j$
, and contains
$v P_j$
, and contains
![]() $c_W$
. Then one can argue in a two-dimensional plane.
$c_W$
. Then one can argue in a two-dimensional plane.
The bound
![]() $c(k)$
goes to zero if k goes to zero, so we can choose k so small that
$c(k)$
goes to zero if k goes to zero, so we can choose k so small that
![]() $c(k) < h$
. Therefore, the two planes intersect inside
$c(k) < h$
. Therefore, the two planes intersect inside
![]() $B_h(c_W)$
.
$B_h(c_W)$
.
Corollary 5.26. There exists a good pair
![]() $(k,h)$
such that for all
$(k,h)$
such that for all
![]() $u_i \in U_{i}$
and
$u_i \in U_{i}$
and
![]() ${i \in \{1,\ldots ,\dim (H)\}}$
, we can find some
${i \in \{1,\ldots ,\dim (H)\}}$
, we can find some
![]() $x \in B_h(c_W)$
such that
$x \in B_h(c_W)$
such that
 $$ \begin{align*} \bigcap_{i=1}^{\dim(H)} u_i P_i = \{x\}. \end{align*} $$
$$ \begin{align*} \bigcap_{i=1}^{\dim(H)} u_i P_i = \{x\}. \end{align*} $$
Proof. By the choice of the family
![]() ${\mathcal {F}}$
, we know that
${\mathcal {F}}$
, we know that
![]() $\bigcap _{i=1}^{\dim (H)} c_W p_{i}^{-1} P_{i}= \{c_W\}$
. We will first show that there is a
$\bigcap _{i=1}^{\dim (H)} c_W p_{i}^{-1} P_{i}= \{c_W\}$
. We will first show that there is a
![]() $k_0$
such that for all
$k_0$
such that for all
![]() $0< k \leq k_0$
, we also get a zero-dimensional intersection inside
$0< k \leq k_0$
, we also get a zero-dimensional intersection inside
![]() $B_h(c_W)$
if we replace
$B_h(c_W)$
if we replace
![]() $c_W p_i^{-1}$
by
$c_W p_i^{-1}$
by
![]() $u_i \in U_i=B_k(c_Wp_i^{-1})$
.
$u_i \in U_i=B_k(c_Wp_i^{-1})$
.
This intersection behaviour means that if we choose some vector
![]() $v \parallel c_Wp_i^{-1}P_i$
, then
$v \parallel c_Wp_i^{-1}P_i$
, then
![]() $v \parallel c_Wp_j^{-1}P_j$
can maximally hold for all but one j since otherwise, the intersection of all hyperplanes would end up in a line instead of a point. We have to choose
$v \parallel c_Wp_j^{-1}P_j$
can maximally hold for all but one j since otherwise, the intersection of all hyperplanes would end up in a line instead of a point. We have to choose
![]() $k_0$
such that for all
$k_0$
such that for all
![]() $i\in \{1,\ldots ,\dim (H)\}$
and all
$i\in \{1,\ldots ,\dim (H)\}$
and all
![]() $v \parallel u_i P_i$
,
$v \parallel u_i P_i$
,
![]() $u_i \in U_i$
, there exists a
$u_i \in U_i$
, there exists a
![]() $j\in \{1,\ldots ,\dim (H)\}\setminus \{i\}$
and a
$j\in \{1,\ldots ,\dim (H)\}\setminus \{i\}$
and a
![]() $u_j \in U_j$
such that
$u_j \in U_j$
such that
![]() $v \nparallel u_jP_j$
. Since operating with an element from
$v \nparallel u_jP_j$
. Since operating with an element from
![]() $U_i$
only rotates the hyperplane a little, it is possible to find such a
$U_i$
only rotates the hyperplane a little, it is possible to find such a
![]() $k_0$
and then the property also holds for all k smaller than
$k_0$
and then the property also holds for all k smaller than
![]() $k_0$
.
$k_0$
.
Now we have to check that the intersection point also lies inside of
![]() $B_h(c_W)$
. We do this stepwise. It is clear that
$B_h(c_W)$
. We do this stepwise. It is clear that
![]() $\bigcap _{i=1}^{\dim (H)} c_W p_{i}^{-1} P_{i}= \{c_W\}$
and
$\bigcap _{i=1}^{\dim (H)} c_W p_{i}^{-1} P_{i}= \{c_W\}$
and
![]() $c_W \in B_h(c_W)$
. Now we change
$c_W \in B_h(c_W)$
. Now we change
![]() $c_W p_1^{-1}$
to some
$c_W p_1^{-1}$
to some
![]() $u_1 \in U_1$
and consider
$u_1 \in U_1$
and consider
![]() $u_1 P_1 \cap \bigcap _{i=2}^{\dim (H)} c_W p_{i}^{-1} P_{i} =\{x_1\}$
. We already know that
$u_1 P_1 \cap \bigcap _{i=2}^{\dim (H)} c_W p_{i}^{-1} P_{i} =\{x_1\}$
. We already know that
![]() $\bigcap _{i=2}^{\dim (H)} c_W p_{i}^{-1} P_{i}$
is a subspace of dimension
$\bigcap _{i=2}^{\dim (H)} c_W p_{i}^{-1} P_{i}$
is a subspace of dimension
![]() $1$
and that
$1$
and that
![]() $u_1 P_1$
intersects this subspace. Since
$u_1 P_1$
intersects this subspace. Since
![]() $u_1= a_1 c_W p_1^{-1}$
with
$u_1= a_1 c_W p_1^{-1}$
with
![]() $a_1\in B_k(e)$
, the plane
$a_1\in B_k(e)$
, the plane
![]() $u_1 P_1$
is just a small shift, which follows from the form of the group action that we explained in §4, and a small rotation away from
$u_1 P_1$
is just a small shift, which follows from the form of the group action that we explained in §4, and a small rotation away from
![]() $c_W p_1^{-1} P_1$
, which follows from Lemma 5.18. Therefore,
$c_W p_1^{-1} P_1$
, which follows from Lemma 5.18. Therefore,
![]() $d(x_1, c_W) < \varepsilon _1(k)$
, where
$d(x_1, c_W) < \varepsilon _1(k)$
, where
![]() $\varepsilon _1$
depends on k and goes to zero if k goes to zero. We can iterate this process and get a new solution on each step until we end at
$\varepsilon _1$
depends on k and goes to zero if k goes to zero. We can iterate this process and get a new solution on each step until we end at
![]() $x_d$
,
$x_d$
,
![]() $d=\dim (H)$
, where we have
$d=\dim (H)$
, where we have
 $$ \begin{align*} d(x_d,c_W)&< d(x_d, x_{d-1})+ d(x_{d-1},x_{d-2})+\cdots + d(x_2,x_1)+d(x_1,c_W)\\ & < \sum_{i=1}^d \varepsilon _i(k) =:\varepsilon (k). \end{align*} $$
$$ \begin{align*} d(x_d,c_W)&< d(x_d, x_{d-1})+ d(x_{d-1},x_{d-2})+\cdots + d(x_2,x_1)+d(x_1,c_W)\\ & < \sum_{i=1}^d \varepsilon _i(k) =:\varepsilon (k). \end{align*} $$
So by choosing k such that
![]() $\varepsilon (k)<h$
, we get the claim. This is possible since
$\varepsilon (k)<h$
, we get the claim. This is possible since
![]() $\varepsilon (k) \to 0$
for
$\varepsilon (k) \to 0$
for
![]() $k \to 0$
.
$k \to 0$
.
The corollary tells us that all intersections result in a single point in
![]() $B_h(c_W)$
, but it is not clear that different choices of
$B_h(c_W)$
, but it is not clear that different choices of
![]() $u_j$
result in different intersection points. This is a major difference to the Euclidean case since here, the action is just translation, so by acting on a hyperplane, we get a parallel hyperplane, which then either is still the same hyperplane or does not intersect the original hyperplane at all.
$u_j$
result in different intersection points. This is a major difference to the Euclidean case since here, the action is just translation, so by acting on a hyperplane, we get a parallel hyperplane, which then either is still the same hyperplane or does not intersect the original hyperplane at all.
To prove part (b) of Proposition 5.24, we need Theorem 4.22. We can use it by the discussion in §4.1.
Lemma 5.27. Consider a family
![]() $U_i(r) \cdot P_i$
. For any constant
$U_i(r) \cdot P_i$
. For any constant
![]() $c>0$
and all
$c>0$
and all
![]() $s \in H$
, there is an
$s \in H$
, there is an
![]() $r_0$
such that for all
$r_0$
such that for all
![]() $r \geq r_0$
, we get that
$r \geq r_0$
, we get that
Proof. Let
![]() $u \in U_i(r)$
such that
$u \in U_i(r)$
such that
![]() $s\in u P_i$
. This implies that
$s\in u P_i$
. This implies that
![]() $u^{-1} \in P_i s^{-1}$
, so
$u^{-1} \in P_i s^{-1}$
, so
![]() $u \in U_i(r) \cap (P_i s^{-1})^{-1}$
. So the question is how many elements are in
$u \in U_i(r) \cap (P_i s^{-1})^{-1}$
. So the question is how many elements are in
![]() $U_i(r) \cap (P_i s^{-1})^{-1}$
compared with the number of elements in
$U_i(r) \cap (P_i s^{-1})^{-1}$
compared with the number of elements in
![]() $U_i(r)$
. To get an estimate via the Haar measure, we have to thicken
$U_i(r)$
. To get an estimate via the Haar measure, we have to thicken
![]() $(P_i s^{-1})^{-1}$
since it is a subset of lower dimension. We consider an
$(P_i s^{-1})^{-1}$
since it is a subset of lower dimension. We consider an
![]() $\varepsilon $
-strip around the set, so we choose a finite set
$\varepsilon $
-strip around the set, so we choose a finite set
![]() $A(\varepsilon ) \subset (P_is^{-1})^{-1}\cap U_i$
such that
$A(\varepsilon ) \subset (P_is^{-1})^{-1}\cap U_i$
such that
 $$ \begin{align*} U_i \cap (P_i s^{-1})^{-1} \subset \bigcup_{p \in A(\varepsilon )}B_\varepsilon (p) \end{align*} $$
$$ \begin{align*} U_i \cap (P_i s^{-1})^{-1} \subset \bigcup_{p \in A(\varepsilon )}B_\varepsilon (p) \end{align*} $$
and further let
![]() $S_\varepsilon := U_i(r) \cap \bigcup _{p \in A(\varepsilon )} B_\varepsilon (p)$
. We have seen that we can use Theorem 4.22, so for every
$S_\varepsilon := U_i(r) \cap \bigcup _{p \in A(\varepsilon )} B_\varepsilon (p)$
. We have seen that we can use Theorem 4.22, so for every
![]() $\delta>0$
and r large enough,
$\delta>0$
and r large enough,
 $$ \begin{align*} \delta &\geq \vert \vert U_i(r)\vert - \mu_{G \times H}(B_r(e) \times U_i) \vert = \vert \vert U_i(r)\vert - \mu_{G}(B_r(e)) \mu_{H}(U_i) \vert\\ &= \vert \vert U_i(r)\vert - r^{{\mathrm{homdim}}(G)}\mu_{G}(B_1(e)) \mu_{H}(U_i)\vert. \end{align*} $$
$$ \begin{align*} \delta &\geq \vert \vert U_i(r)\vert - \mu_{G \times H}(B_r(e) \times U_i) \vert = \vert \vert U_i(r)\vert - \mu_{G}(B_r(e)) \mu_{H}(U_i) \vert\\ &= \vert \vert U_i(r)\vert - r^{{\mathrm{homdim}}(G)}\mu_{G}(B_1(e)) \mu_{H}(U_i)\vert. \end{align*} $$
Since
![]() $S_\varepsilon $
is a finite union of balls, we can use the same argument for all the balls simultaneously and get for
$S_\varepsilon $
is a finite union of balls, we can use the same argument for all the balls simultaneously and get for
![]() $\delta>0$
that
$\delta>0$
that
 $$ \begin{align*} \lim\limits_{r \to \infty} \frac{\vert U_i(r) \cap (P_i s^{-1})^{-1}\vert }{\vert U_i(r)\vert} &< \lim\limits_{r \to \infty}\frac{\vert S_\varepsilon \vert}{\vert U_i(r)\vert} = \frac{\sum_{p \in A(\varepsilon )} r^{{\mathrm{homdim}}(G)}\mu_{G}(B_1(e))\mu_{H}(B_\varepsilon (p))}{r^{{\mathrm{homdim}}(G)}\mu_{G}(B_1(e))\mu_{H}(U_i)}\\ &= \frac{\vert A(\varepsilon ) \vert \cdot \mu_{H}(B_\varepsilon (e))}{\mu_{H}(U_i)} \xrightarrow{\varepsilon \to 0} 0.\\[-42pt] \end{align*} $$
$$ \begin{align*} \lim\limits_{r \to \infty} \frac{\vert U_i(r) \cap (P_i s^{-1})^{-1}\vert }{\vert U_i(r)\vert} &< \lim\limits_{r \to \infty}\frac{\vert S_\varepsilon \vert}{\vert U_i(r)\vert} = \frac{\sum_{p \in A(\varepsilon )} r^{{\mathrm{homdim}}(G)}\mu_{G}(B_1(e))\mu_{H}(B_\varepsilon (p))}{r^{{\mathrm{homdim}}(G)}\mu_{G}(B_1(e))\mu_{H}(U_i)}\\ &= \frac{\vert A(\varepsilon ) \vert \cdot \mu_{H}(B_\varepsilon (e))}{\mu_{H}(U_i)} \xrightarrow{\varepsilon \to 0} 0.\\[-42pt] \end{align*} $$
6. Combinatorics
The aim of this section is to give a lower bound for the number of connected components of
 $$ \begin{align*} B_h(c_W) \setminus \bigcup_{i=1}^N \bigcup_{s \in U_i(r)} s P_i, \end{align*} $$
$$ \begin{align*} B_h(c_W) \setminus \bigcup_{i=1}^N \bigcup_{s \in U_i(r)} s P_i, \end{align*} $$
under some conditions on the family
![]() $s P_i$
. This will fill the gap we left in the last section. To do so, we will give a short introduction to the theory of hyperplane arrangements and fix the common notation for this setup. To do so, we will follow the lines of Dimca [Reference Dimca12] and Stanley [Reference Stanley46]. Furthermore, we will consider Beck’s theorem which was first proved in [Reference Beck6], but also follows from the Szémeredi–Trotter theorem [Reference Szemerédi and Trotter49]. An easier proof for the Szémeredi–Trotter theorem can be found in the paper by Szekely [Reference Székely48]. We leave it to the reader to see that the two versions are equivalent.
$s P_i$
. This will fill the gap we left in the last section. To do so, we will give a short introduction to the theory of hyperplane arrangements and fix the common notation for this setup. To do so, we will follow the lines of Dimca [Reference Dimca12] and Stanley [Reference Stanley46]. Furthermore, we will consider Beck’s theorem which was first proved in [Reference Beck6], but also follows from the Szémeredi–Trotter theorem [Reference Szemerédi and Trotter49]. An easier proof for the Szémeredi–Trotter theorem can be found in the paper by Szekely [Reference Székely48]. We leave it to the reader to see that the two versions are equivalent.
Theorem 6.1. (Higher dimensional local dual of Beck’s theorem)
Let
![]() ${\mathcal {H}}$
be a hyperplane arrangement in
${\mathcal {H}}$
be a hyperplane arrangement in
![]() ${\mathbb {R}}^d$
and let
${\mathbb {R}}^d$
and let
![]() $B \subset {\mathbb {R}}^d$
be convex. Further, let
$B \subset {\mathbb {R}}^d$
be convex. Further, let
![]() ${\mathcal {H}}$
consist of d families
${\mathcal {H}}$
consist of d families
![]() $F_1,\ldots ,F_d$
with
$F_1,\ldots ,F_d$
with
![]() $\vert F_i \vert = {n}/{d}$
and such that for all
$\vert F_i \vert = {n}/{d}$
and such that for all
![]() $(f_1,\ldots ,f_d) \in F_1 \times \cdots \times F_d$
, we have
$(f_1,\ldots ,f_d) \in F_1 \times \cdots \times F_d$
, we have
![]() $B \cap \bigcap _{i=1}^d f_i = \{p\}$
for some point
$B \cap \bigcap _{i=1}^d f_i = \{p\}$
for some point
![]() $p \in B$
. Moreover, assume that there is a constant
$p \in B$
. Moreover, assume that there is a constant
![]() $c< {1}/{100}$
such that at most
$c< {1}/{100}$
such that at most
![]() $c \cdot \vert F_i \vert $
hyperplanes from
$c \cdot \vert F_i \vert $
hyperplanes from
![]() $F_i$
can intersect in one point. Then there exists a constant
$F_i$
can intersect in one point. Then there exists a constant
![]() $c_d$
, depending on the dimension d, such that the number of intersection points in B exceeds
$c_d$
, depending on the dimension d, such that the number of intersection points in B exceeds
![]() $c_d \cdot n^d$
, that is,
$c_d \cdot n^d$
, that is,
![]() $\vert F_{0,B} \vert \geq c_d \cdot n^d$
.
$\vert F_{0,B} \vert \geq c_d \cdot n^d$
.
Corollary 6.2. In the situation of Theorem 5.1 and Proposition 5.24,
 $$ \begin{align*} \# \pi_0 \bigg( B_h(c_W) \setminus \bigcup_{i=1}^N \bigcup_{s \in U_i(r)} s P_i \bigg) \gg r^{{\mathrm{homdim}}(G) \cdot \dim(H)}. \end{align*} $$
$$ \begin{align*} \# \pi_0 \bigg( B_h(c_W) \setminus \bigcup_{i=1}^N \bigcup_{s \in U_i(r)} s P_i \bigg) \gg r^{{\mathrm{homdim}}(G) \cdot \dim(H)}. \end{align*} $$
This finishes the proof of the main theorem, Theorem 5.1. The rest of the section is devoted to prove Theorem 6.1.
Definition 6.3. A finite set of affine hyperplanes
![]() ${\mathcal {H}}=\{P_1,\ldots ,P_n\}$
in
${\mathcal {H}}=\{P_1,\ldots ,P_n\}$
in
![]() ${\mathbb {R}}^d$
is called a hyperplane arrangement.
${\mathbb {R}}^d$
is called a hyperplane arrangement.
Definition 6.4. Let
![]() ${\mathcal {H}}$
be a hyperplane arrangement in
${\mathcal {H}}$
be a hyperplane arrangement in
![]() ${\mathbb {R}}^d$
.
${\mathbb {R}}^d$
.
-
(i) A non-empty intersection of hyperplanes from
 ${\mathcal {H}}$
is called a flat of
${\mathcal {H}}$
is called a flat of
 ${\mathcal {H}}$
. The set of all flats is denoted by
${\mathcal {H}}$
. The set of all flats is denoted by
 $F({\mathcal {H}})$
. If we are only interested in flats of a certain dimension k, we denote this set by
$F({\mathcal {H}})$
. If we are only interested in flats of a certain dimension k, we denote this set by
 $F_k({\mathcal {H}})$
. Notice that the whole space is also a flat, as a result of the intersection over the empty set.
$F_k({\mathcal {H}})$
. Notice that the whole space is also a flat, as a result of the intersection over the empty set. -
(ii) The connected components of
are called regions of the arrangement. The set of all regions is denoted by $$ \begin{align*} {\mathbb{R}}^d \setminus \bigcup_{H \in {\mathcal{H}}} H \end{align*} $$
$$ \begin{align*} {\mathbb{R}}^d \setminus \bigcup_{H \in {\mathcal{H}}} H \end{align*} $$
 $f_d({\mathcal {H}})$
and the number of these regions is denoted by
$f_d({\mathcal {H}})$
and the number of these regions is denoted by
 $r({\mathcal {H}})$
.
$r({\mathcal {H}})$
.
-
(iii) Let
 $B\subset {\mathbb {R}}^d$
, then the connected components of are called regions of the arrangement with respect to B and the number of these regions is denoted by
$B\subset {\mathbb {R}}^d$
, then the connected components of are called regions of the arrangement with respect to B and the number of these regions is denoted by $$ \begin{align*} B \setminus \bigcup_{H \in {\mathcal{H}}} H \end{align*} $$
$$ \begin{align*} B \setminus \bigcup_{H \in {\mathcal{H}}} H \end{align*} $$
 $r_B({\mathcal {H}})$
.
$r_B({\mathcal {H}})$
.
-
(iv) Let
 $B\subset {\mathbb {R}}^d$
, then define the arrangement with respect to B as
$B\subset {\mathbb {R}}^d$
, then define the arrangement with respect to B as  $$ \begin{align*} {\mathcal{H}}_B := \{H \in {\mathcal{H}} \mid H \cap B \neq \emptyset\}. \end{align*} $$
$$ \begin{align*} {\mathcal{H}}_B := \{H \in {\mathcal{H}} \mid H \cap B \neq \emptyset\}. \end{align*} $$
-
(v) Let
 $B\subset {\mathbb {R}}^d$
, then a flat with respect to B is a flat of
$B\subset {\mathbb {R}}^d$
, then a flat with respect to B is a flat of
 ${\mathcal {H}}$
which intersects B. The set of these flats is denoted by
${\mathcal {H}}$
which intersects B. The set of these flats is denoted by
 $F_B({\mathcal {H}})$
and, again, if we only consider the flats of dimension k, we write
$F_B({\mathcal {H}})$
and, again, if we only consider the flats of dimension k, we write
 $F_{k,B}({\mathcal {H}})$
.
$F_{k,B}({\mathcal {H}})$
.
Remark 6.5. Obviously
![]() $r_B({\mathcal {H}})$
only depends on the hyperplanes which intersect B, so
$r_B({\mathcal {H}})$
only depends on the hyperplanes which intersect B, so
![]() $r_B({\mathcal {H}})=r_B({\mathcal {H}}_B)$
. Further, notice that in general,
$r_B({\mathcal {H}})=r_B({\mathcal {H}}_B)$
. Further, notice that in general,
![]() $r_B({\mathcal {H}}) \neq \vert \{ R \in f_d({\mathcal {H}}) \mid R \cap B \neq \emptyset \}\vert $
, but the following proposition will show that equality holds for convex B.
$r_B({\mathcal {H}}) \neq \vert \{ R \in f_d({\mathcal {H}}) \mid R \cap B \neq \emptyset \}\vert $
, but the following proposition will show that equality holds for convex B.
Proposition 6.6. Let
![]() ${\mathcal {H}}$
be a hyperplane arrangement in
${\mathcal {H}}$
be a hyperplane arrangement in
![]() ${\mathbb {R}}^d$
and
${\mathbb {R}}^d$
and
![]() $B \subset {\mathbb {R}}^d$
convex, then
$B \subset {\mathbb {R}}^d$
convex, then
Proof. The regions of a hyperplane arrangement are convex. Since B is also convex, we have for all
![]() $R \in f_d({\mathcal {H}})$
that
$R \in f_d({\mathcal {H}})$
that
![]() $R \cap B$
is convex and especially connected. So each region of the arrangement either intersects B and therefore contributes exactly one to
$R \cap B$
is convex and especially connected. So each region of the arrangement either intersects B and therefore contributes exactly one to
![]() $r_B({\mathcal {H}})$
, or it does not intersect at all.
$r_B({\mathcal {H}})$
, or it does not intersect at all.
Definition 6.7. An arrangement
![]() ${\mathcal {H}}$
in
${\mathcal {H}}$
in
![]() ${\mathbb {R}}^d$
is called:
${\mathbb {R}}^d$
is called:
-
(i) central if
 $\bigcap _{H \in {\mathcal {H}}} H \neq \emptyset $
(observe that the empty arrangement is central since the empty intersection is the whole space);
$\bigcap _{H \in {\mathcal {H}}} H \neq \emptyset $
(observe that the empty arrangement is central since the empty intersection is the whole space); -
(ii) central with respect to B, for some
 $B \subset {\mathbb {R}}^d$
, if
$B \subset {\mathbb {R}}^d$
, if
 $B \cap \bigcap _{H \in {\mathcal {H}}} H \neq \emptyset $
.
$B \cap \bigcap _{H \in {\mathcal {H}}} H \neq \emptyset $
.
We will now define the characteristic polynomial for the arrangement
![]() ${\mathcal {H}}$
which depends on
${\mathcal {H}}$
which depends on
![]() $B\subset {\mathbb {R}}^d$
. This idea is similar to the standard idea of considering the characteristic polynomial of the arrangement.
$B\subset {\mathbb {R}}^d$
. This idea is similar to the standard idea of considering the characteristic polynomial of the arrangement.
Definition 6.8. Let
![]() ${\mathcal {H}}$
be a hyperplane arrangement in
${\mathcal {H}}$
be a hyperplane arrangement in
![]() ${\mathbb {R}}^d$
. The characteristic polynomial with respect to B is defined by
${\mathbb {R}}^d$
. The characteristic polynomial with respect to B is defined by
 $$ \begin{align*} \chi_{{\mathcal{H}},B}(t):= \hspace{-0.5cm }\sum_{\substack{{\mathcal{A}} \subset {\mathcal{H}}\\ {\mathcal{A}} \text{ central with respect to } B}} \hspace{-0.5cm } (-1)^{\vert {\mathcal{A}} \vert} t^{\dim(\bigcap_{H \in {\mathcal{A}}} H)}. \end{align*} $$
$$ \begin{align*} \chi_{{\mathcal{H}},B}(t):= \hspace{-0.5cm }\sum_{\substack{{\mathcal{A}} \subset {\mathcal{H}}\\ {\mathcal{A}} \text{ central with respect to } B}} \hspace{-0.5cm } (-1)^{\vert {\mathcal{A}} \vert} t^{\dim(\bigcap_{H \in {\mathcal{A}}} H)}. \end{align*} $$
Following the argumentation in [Reference Dimca12] for the characteristic polynomial with respect to B instead of the characteristic polynomial, we can establish the following theorem. Since the argument is exactly the same, we will not prove the statement here.
Theorem 6.9. [Reference Dimca12, Theorem 2.8]
Let
![]() ${\mathcal {H}}$
be a hyperplane arrangement in
${\mathcal {H}}$
be a hyperplane arrangement in
![]() ${\mathbb {R}}^d$
and
${\mathbb {R}}^d$
and
![]() $B \subset {\mathbb {R}}^d$
convex, then
$B \subset {\mathbb {R}}^d$
convex, then
We can use this formula with the help of the following lemma, which we import from Stanley.
Lemma 6.10. [Reference Stanley46, Theorem 3.10]
Let
![]() $\chi (t)$
be a characteristic polynomial of a hyperplane arrangement
$\chi (t)$
be a characteristic polynomial of a hyperplane arrangement
![]() ${\mathcal {H}}$
in
${\mathcal {H}}$
in
![]() ${\mathbb {R}}^d$
, then
${\mathbb {R}}^d$
, then
 $$ \begin{align*} \chi(t) = \sum_{f \in F_B({\mathcal{H}})} a_f t^{\dim(f)} \end{align*} $$
$$ \begin{align*} \chi(t) = \sum_{f \in F_B({\mathcal{H}})} a_f t^{\dim(f)} \end{align*} $$
with
![]() $(-1)^{d-\dim (f)} a_f>0$
for
$(-1)^{d-\dim (f)} a_f>0$
for
![]() $f \in F_B({\mathcal {H}})$
.
$f \in F_B({\mathcal {H}})$
.
Corollary 6.11. Let
![]() ${\mathcal {H}}$
be a hyperplane arrangement in
${\mathcal {H}}$
be a hyperplane arrangement in
![]() ${\mathbb {R}}^d$
and
${\mathbb {R}}^d$
and
![]() $B \subset {\mathbb {R}}^d$
convex, then
$B \subset {\mathbb {R}}^d$
convex, then
This proposition means that to establish a lower bound of the regions, it is enough to count the number of intersection points. We will do this by following the idea of the proof of Beck’s theorem [Reference Beck6]. However, instead of considering the set of lines/hyperplanes spanned by a point set, we turn all the arguments around and consider the intersection points of a given arrangement. We will first handle the case of dimension two and then use induction to generalize the statement.
We first state the Szemerédi–Trotter theorem in two equivalent ways.
Theorem 6.12. (Szemerédi–Trotter theorem, [Reference Székely48, Reference Szemerédi and Trotter49])
Let
![]() $n,m \in {\mathbb {N}}$
. We set
$n,m \in {\mathbb {N}}$
. We set
where P denotes a set of points and L a set of lines in
![]() ${\mathbb {R}}^2$
.
${\mathbb {R}}^2$
.
-
(i) There exists a constant
 $c>0$
such that
$c>0$
such that
 $I(n,m) < c \cdot (n^{2/3}m^{2/3} + n + m)$
.
$I(n,m) < c \cdot (n^{2/3}m^{2/3} + n + m)$
. -
(ii) Let
 $\sqrt {n} \leq m \leq \begin {pmatrix} n \\ 2 \end {pmatrix}$
, then there exists a constant
$\sqrt {n} \leq m \leq \begin {pmatrix} n \\ 2 \end {pmatrix}$
, then there exists a constant
 $c>0$
such that
$c>0$
such that
 $I(n,m) < c \cdot (n^{2/3}m^{2/3})$
.
$I(n,m) < c \cdot (n^{2/3}m^{2/3})$
.
Remark 6.13. The constant for the growth in the Szemerédi–Trotter theorem is known to be less than
![]() $2.5$
but more than
$2.5$
but more than
![]() $0.4$
.
$0.4$
.
Definition 6.14. Let
![]() ${\mathcal {H}}$
be a hyperplane arrangement. Then for a flat
${\mathcal {H}}$
be a hyperplane arrangement. Then for a flat
![]() $f \in F({\mathcal {H}})$
, we define
$f \in F({\mathcal {H}})$
, we define
![]() $S(f):=\{H \in {\mathcal {H}} \mid f \subset H \}$
and further
$S(f):=\{H \in {\mathcal {H}} \mid f \subset H \}$
and further
![]() $a(f):=\vert S(f) \vert $
.
$a(f):=\vert S(f) \vert $
.
Definition 6.15. For a hyperplane arrangement
![]() ${\mathcal {H}}$
, let
${\mathcal {H}}$
, let
 $$ \begin{align*} t({\mathcal{H}},k) &:= \vert \{p \in F_0({\mathcal{H}}) \mid a(p) \geq k\}\vert, \\ t^\ast({\mathcal{H}},k) &:= \vert \{p \in F_0({\mathcal{H}}) \mid k \leq a(p) < 2k\}\vert. \end{align*} $$
$$ \begin{align*} t({\mathcal{H}},k) &:= \vert \{p \in F_0({\mathcal{H}}) \mid a(p) \geq k\}\vert, \\ t^\ast({\mathcal{H}},k) &:= \vert \{p \in F_0({\mathcal{H}}) \mid k \leq a(p) < 2k\}\vert. \end{align*} $$
Further, we consider the maximal value of the two terms:
 $$ \begin{align*} t(n,k) &:= \max_{\vert {\mathcal{H}} \vert = n } t({\mathcal{H}},k), \\ t^\ast(n,k) &:= \max_{\vert {\mathcal{H}} \vert = n } t^\ast({\mathcal{H}},k). \end{align*} $$
$$ \begin{align*} t(n,k) &:= \max_{\vert {\mathcal{H}} \vert = n } t({\mathcal{H}},k), \\ t^\ast(n,k) &:= \max_{\vert {\mathcal{H}} \vert = n } t^\ast({\mathcal{H}},k). \end{align*} $$
For our proof, we need some bounds on these terms. The first two are from the paper of Beck [Reference Beck6] and are easy to prove. The third is a corollary of the Szemerédi–Trotter theorem. Beck proves a similar inequality [Reference Beck6, Lemma 2.2], which is the main part of his argument. For us, it would also be possible in our setup to translate the proof of Beck, but this would require much effort. If the reader is interested, we challenge them to follow the proof, it certainly is illuminating to translate all the arguments.
Lemma 6.16. [Reference Beck6, Lemma 2.1]
For a hyperplane arrangement
![]() ${\mathcal {H}}$
in
${\mathcal {H}}$
in
![]() ${\mathbb {R}}^2$
, with
${\mathbb {R}}^2$
, with
![]() $\vert {\mathcal {H}} \vert = n$
, we have
$\vert {\mathcal {H}} \vert = n$
, we have
 $$ \begin{align*} t(n,k) \leq \frac{n(n-1)}{k(k-1)}\quad &\text{for all } 2 \leq k \leq n,\\ t(n,k) < \frac{2n}{k}\quad &\text{for all } \sqrt{2n} < k \leq n. \end{align*} $$
$$ \begin{align*} t(n,k) \leq \frac{n(n-1)}{k(k-1)}\quad &\text{for all } 2 \leq k \leq n,\\ t(n,k) < \frac{2n}{k}\quad &\text{for all } \sqrt{2n} < k \leq n. \end{align*} $$
Proof. For the first formula, we consider the number of pairs of lines. On the one hand, we consider all possible pairs and on the other hand, the pairs through points in which at least k lines intersect:
 $$ \begin{align*} t(n,k) \cdot \begin{pmatrix} k \\ 2 \end{pmatrix} \leq \begin{pmatrix} n \\ 2 \end{pmatrix}\hspace{-1.5pt}. \end{align*} $$
$$ \begin{align*} t(n,k) \cdot \begin{pmatrix} k \\ 2 \end{pmatrix} \leq \begin{pmatrix} n \\ 2 \end{pmatrix}\hspace{-1.5pt}. \end{align*} $$
For the second inequality, the points in which at least k lines intersect are denoted by
![]() $p_1,\ldots ,p_t$
. We assume that
$p_1,\ldots ,p_t$
. We assume that
![]() $t= (({2n +l})/{k}) \in {\mathbb {N}}$
, where
$t= (({2n +l})/{k}) \in {\mathbb {N}}$
, where
![]() $l \in \{0,\ldots ,k-1\}$
. Then
$l \in \{0,\ldots ,k-1\}$
. Then
![]() ${t < \sqrt {2n} + {l}/{k}}$
, since
${t < \sqrt {2n} + {l}/{k}}$
, since
![]() $\sqrt {2n} < k$
. Notice that
$\sqrt {2n} < k$
. Notice that
![]() $\vert S(p_i) \vert \geq k$
and
$\vert S(p_i) \vert \geq k$
and
![]() $\vert S(p_i) \cap S(p_j) \vert \leq 1$
for
$\vert S(p_i) \cap S(p_j) \vert \leq 1$
for
![]() $i \neq j$
, since two points are connected by exactly one line. Then
$i \neq j$
, since two points are connected by exactly one line. Then
 $$ \begin{align*} n &= \vert {\mathcal{H}} \vert \geq \bigg\vert \bigcup_{i=1}^t S(p_i) \bigg\vert \geq \sum_{i=1}^t \vert S(p_i)\vert - \sum_{1 \leq i < j \leq t} \vert S(p_i) \cap S(p_j)\vert\\ &\geq \sum_{i=1}^t k - \sum_{1 \leq i < j \leq t} 1 = tk - \frac{1}{2}t (t-1)> 2n+l - \frac{1}{2} \bigg(\sqrt{2n}+\frac{l}{k}\bigg) \bigg(\sqrt{2n}+\underbrace{\frac{l}{k}-1}_{<0}\bigg)\\ &> 2n+l - n - \sqrt{\frac{n}{2}} \frac{l}{k} = n+ l \bigg( 1 - \frac{\sqrt{n}}{\sqrt{2}k}\bigg) > n+l\bigg(1- \frac{1}{2}\bigg) \geq n. \end{align*} $$
$$ \begin{align*} n &= \vert {\mathcal{H}} \vert \geq \bigg\vert \bigcup_{i=1}^t S(p_i) \bigg\vert \geq \sum_{i=1}^t \vert S(p_i)\vert - \sum_{1 \leq i < j \leq t} \vert S(p_i) \cap S(p_j)\vert\\ &\geq \sum_{i=1}^t k - \sum_{1 \leq i < j \leq t} 1 = tk - \frac{1}{2}t (t-1)> 2n+l - \frac{1}{2} \bigg(\sqrt{2n}+\frac{l}{k}\bigg) \bigg(\sqrt{2n}+\underbrace{\frac{l}{k}-1}_{<0}\bigg)\\ &> 2n+l - n - \sqrt{\frac{n}{2}} \frac{l}{k} = n+ l \bigg( 1 - \frac{\sqrt{n}}{\sqrt{2}k}\bigg) > n+l\bigg(1- \frac{1}{2}\bigg) \geq n. \end{align*} $$
This is a contradiction, so
![]() $t=\lceil {2n}/{k}\rceil $
cannot hold and also
$t=\lceil {2n}/{k}\rceil $
cannot hold and also
![]() $t> {2n}/{k}$
is not possible since we can simply ignore some points to get the same contradiction.
$t> {2n}/{k}$
is not possible since we can simply ignore some points to get the same contradiction.
Corollary 6.17. (Corollary of Theorem 6.12, [Reference Szemerédi and Trotter49, Theorem 2])
For a hyperplane arrangement
![]() ${\mathcal {H}}$
in
${\mathcal {H}}$
in
![]() ${\mathbb {R}}^2$
, there is some constant
${\mathbb {R}}^2$
, there is some constant
![]() $\beta>0$
such that
$\beta>0$
such that
Proof. Assume there are
![]() $t= ({c^3n^2+l})/{k^3} \in {\mathbb {N}}$
, where
$t= ({c^3n^2+l})/{k^3} \in {\mathbb {N}}$
, where
![]() $l\in \{0,\ldots , k^3-1\}$
and
$l\in \{0,\ldots , k^3-1\}$
and
![]() ${c=2.5}$
, points with
${c=2.5}$
, points with
![]() $a(p)\geq k$
.
$a(p)\geq k$
.
Then
 $$ \begin{align*} \sqrt{t} = n \sqrt{\frac{c^3}{k^3} + \frac{l}{n^2 k^3}} \leq n \sqrt{\frac{c^3}{k^3} + \frac{k^3-1}{n^2k^3}} < n \sqrt{\frac{2.5^3}{3^3}+\frac{1}{n^2}} < n, \end{align*} $$
$$ \begin{align*} \sqrt{t} = n \sqrt{\frac{c^3}{k^3} + \frac{l}{n^2 k^3}} \leq n \sqrt{\frac{c^3}{k^3} + \frac{k^3-1}{n^2k^3}} < n \sqrt{\frac{2.5^3}{3^3}+\frac{1}{n^2}} < n, \end{align*} $$
since
![]() $n> 3$
. Further,
$n> 3$
. Further,
 $$ \begin{align*} \begin{pmatrix} t \\ 2 \end{pmatrix} &= \frac{1}{2} \frac{c^3 n^2+l}{k^3}\bigg(\frac{c^3 n^2+l}{k^3}-1 \bigg) \geq \frac{1}{2} \bigg(c^3 \sqrt{n}+ \frac{l}{n^{{3}/{2}}}\bigg) \bigg(c^3 \sqrt{n}+ \frac{l}{n^{{3}/{2}}}-1 \bigg)\\ &\geq \frac{1}{2} c^3 \sqrt{n}(c^3 \sqrt{n}-1)>n, \end{align*} $$
$$ \begin{align*} \begin{pmatrix} t \\ 2 \end{pmatrix} &= \frac{1}{2} \frac{c^3 n^2+l}{k^3}\bigg(\frac{c^3 n^2+l}{k^3}-1 \bigg) \geq \frac{1}{2} \bigg(c^3 \sqrt{n}+ \frac{l}{n^{{3}/{2}}}\bigg) \bigg(c^3 \sqrt{n}+ \frac{l}{n^{{3}/{2}}}-1 \bigg)\\ &\geq \frac{1}{2} c^3 \sqrt{n}(c^3 \sqrt{n}-1)>n, \end{align*} $$
since
![]() $c=2.5$
and
$c=2.5$
and
![]() $n>3$
. Therefore, we can use version (ii) of the Szemerédi–Trotter theorem: there is a constant c such that
$n>3$
. Therefore, we can use version (ii) of the Szemerédi–Trotter theorem: there is a constant c such that
![]() $I(n,m) < c n^{2/3}m^{2/3}$
and we know that
$I(n,m) < c n^{2/3}m^{2/3}$
and we know that
![]() $c=2.5$
works. The t point induces
$c=2.5$
works. The t point induces
![]() $t \cdot k$
incidences, but
$t \cdot k$
incidences, but
which is a contradiction to the theorem. Therefore,
![]() $t=\lceil {c^3n^2}/{k^3} \rceil $
is not possible and also
$t=\lceil {c^3n^2}/{k^3} \rceil $
is not possible and also
![]() $t> {c^3n^2}/{k^3}$
is not possible by the same argument if we ignore some points. We see that
$t> {c^3n^2}/{k^3}$
is not possible by the same argument if we ignore some points. We see that
![]() $\beta =2.5^3$
is a possible choice.
$\beta =2.5^3$
is a possible choice.
Theorem 6.18. (Local dual of Becks theorem)
Let
![]() ${\mathcal {H}}$
be a hyperplane arrangement in
${\mathcal {H}}$
be a hyperplane arrangement in
![]() ${\mathbb {R}}^2$
and
${\mathbb {R}}^2$
and
![]() $B \subset {\mathbb {R}}^2$
convex, where
$B \subset {\mathbb {R}}^2$
convex, where
![]() ${\mathcal {H}}$
consist of two disjoint families
${\mathcal {H}}$
consist of two disjoint families
![]() $F_1$
and
$F_1$
and
![]() $F_2$
of hyperplanes with
$F_2$
of hyperplanes with
![]() $\vert F_1 \vert = \vert F_2 \vert = {n}/{2}$
and such that for all
$\vert F_1 \vert = \vert F_2 \vert = {n}/{2}$
and such that for all
![]() $(f,g)\in F_1 \times F_2$
, we have
$(f,g)\in F_1 \times F_2$
, we have
![]() $B \cap f \cap g =\{p\}$
for some point
$B \cap f \cap g =\{p\}$
for some point
![]() $p \in B$
depending on f and g. Then there exists a constant
$p \in B$
depending on f and g. Then there exists a constant
![]() $c_2$
such that one of the following two cases holds.
$c_2$
such that one of the following two cases holds.
-
(a) There is a point
 $p \in B$
such that
$p \in B$
such that
 $a(p) \geq {n}/{100}$
.
$a(p) \geq {n}/{100}$
. -
(b) The number of intersection points in B exceeds
 $c_2 \cdot n^2$
, that is,
$c_2 \cdot n^2$
, that is,
 $\vert F_{0,B}({\mathcal {H}}) \vert \geq c\cdot n^2$
.
$\vert F_{0,B}({\mathcal {H}}) \vert \geq c\cdot n^2$
.
Proof. We count the number of pairs of lines, we get
 $$ \begin{align*} \begin{pmatrix} n \\ 2 \end{pmatrix} \geq \sum_{p \in F_{0,B}({\mathcal{H}})} \begin{pmatrix} a(p) \\ 2 \end{pmatrix} \geq \vert F_1 \vert \cdot \vert F_2 \vert = \frac{1}{4}n^2. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} n \\ 2 \end{pmatrix} \geq \sum_{p \in F_{0,B}({\mathcal{H}})} \begin{pmatrix} a(p) \\ 2 \end{pmatrix} \geq \vert F_1 \vert \cdot \vert F_2 \vert = \frac{1}{4}n^2. \end{align*} $$
On the left side, we counted all the possible options, in the middle, we counted the pairs that intersect inside B and on the right, we counted the pairs of lines from the two families since we know that they intersect in B. We will split the sum into three parts:
 $$ \begin{align*} S_1 &:= \sum_{\substack{p \in F_{0,B}({\mathcal{H}})\\ 2^k \leq a(p) < \sqrt{n}}} \begin{pmatrix} a(p) \\ 2\end{pmatrix}\hspace{-1.5pt},\\ S_2 &:= \sum_{\substack{p \in F_{0,B}({\mathcal{H}})\\ \sqrt{n} \leq a(p) < \frac{n}{100}}} \begin{pmatrix} a(p) \\ 2\end{pmatrix}\hspace{-1.5pt},\\ S_3 &:= \sum_{\substack{p \in F_{0,B}({\mathcal{H}})\\ 2 \leq a(p) < 2^k}} \begin{pmatrix} a(p) \\ 2\end{pmatrix} + \sum_{\substack{p \in F_{0,B}({\mathcal{H}})\\ \frac{n}{100} \leq a(p) \leq n}} \begin{pmatrix} a(p) \\ 2\end{pmatrix}\hspace{-1.5pt}, \end{align*} $$
$$ \begin{align*} S_1 &:= \sum_{\substack{p \in F_{0,B}({\mathcal{H}})\\ 2^k \leq a(p) < \sqrt{n}}} \begin{pmatrix} a(p) \\ 2\end{pmatrix}\hspace{-1.5pt},\\ S_2 &:= \sum_{\substack{p \in F_{0,B}({\mathcal{H}})\\ \sqrt{n} \leq a(p) < \frac{n}{100}}} \begin{pmatrix} a(p) \\ 2\end{pmatrix}\hspace{-1.5pt},\\ S_3 &:= \sum_{\substack{p \in F_{0,B}({\mathcal{H}})\\ 2 \leq a(p) < 2^k}} \begin{pmatrix} a(p) \\ 2\end{pmatrix} + \sum_{\substack{p \in F_{0,B}({\mathcal{H}})\\ \frac{n}{100} \leq a(p) \leq n}} \begin{pmatrix} a(p) \\ 2\end{pmatrix}\hspace{-1.5pt}, \end{align*} $$
where
![]() $k=10$
is constant. Now we will bound
$k=10$
is constant. Now we will bound
![]() $S_1$
and
$S_1$
and
![]() $S_2$
. We start with
$S_2$
. We start with
![]() $S_1$
using Corollary 6.17:
$S_1$
using Corollary 6.17:
 $$ \begin{align*} S_1 &= \sum_{l \geq k} \sum_{\substack{p \in F_{0,B}({\mathcal{H}}) \\ 2^l \leq a(p) < 2^{l+1} \\ a(p) < \sqrt{n}}} \begin{pmatrix} a(p) \\ 2 \end{pmatrix} \leq \sum_{\substack{l \geq k \\ 2^{l+1}<\sqrt{n}}} t^{\ast}(n,2^l) \begin{pmatrix} 2^{l+1} \\ 2 \end{pmatrix} \\ &= \sum_{\substack{l \geq k \\ 2^{l+1} < \sqrt{n}}} t^{\ast}(n,2^l) 2^l (2^{l+1}-1) \leq \sum_{\substack{l \geq k \\ 2^{l+1} < \sqrt{n}}} \beta \frac{n^2}{2^{3l}} 2^l (2^{l+1}-1)\\ &\leq 2 \beta n^2 \sum_{l \geq k} \frac{1}{2^l} = \frac{4 \beta}{2^k} n^2 \leq \frac{1}{8} \begin{pmatrix} n \\ 2\end{pmatrix}\hspace{-1.5pt}, \end{align*} $$
$$ \begin{align*} S_1 &= \sum_{l \geq k} \sum_{\substack{p \in F_{0,B}({\mathcal{H}}) \\ 2^l \leq a(p) < 2^{l+1} \\ a(p) < \sqrt{n}}} \begin{pmatrix} a(p) \\ 2 \end{pmatrix} \leq \sum_{\substack{l \geq k \\ 2^{l+1}<\sqrt{n}}} t^{\ast}(n,2^l) \begin{pmatrix} 2^{l+1} \\ 2 \end{pmatrix} \\ &= \sum_{\substack{l \geq k \\ 2^{l+1} < \sqrt{n}}} t^{\ast}(n,2^l) 2^l (2^{l+1}-1) \leq \sum_{\substack{l \geq k \\ 2^{l+1} < \sqrt{n}}} \beta \frac{n^2}{2^{3l}} 2^l (2^{l+1}-1)\\ &\leq 2 \beta n^2 \sum_{l \geq k} \frac{1}{2^l} = \frac{4 \beta}{2^k} n^2 \leq \frac{1}{8} \begin{pmatrix} n \\ 2\end{pmatrix}\hspace{-1.5pt}, \end{align*} $$
since
![]() $\beta = 2.5^3$
,
$\beta = 2.5^3$
,
![]() $k=10$
and
$k=10$
and
![]() $n\geq 2$
. For the next sum, we use Lemma 6.16 and Corollary 6.17:
$n\geq 2$
. For the next sum, we use Lemma 6.16 and Corollary 6.17:
 $$ \begin{align*} S_2 &= \sum_{l \geq0} \sum_{\substack{p \in F_{0,B}({\mathcal{H}}) \\ 2^l \sqrt{n} \leq a(p) < 2^{l+1} \sqrt{n} \\ a(p) < \frac{n}{100}}} \begin{pmatrix} a(p) \\ 2 \end{pmatrix} \leq \sum_{\substack{l \geq 0\\ 2^{l} \sqrt{n} < \frac{n}{100}}} t(n, 2^l \sqrt{n}) \begin{pmatrix} 2^{l+1} \sqrt{n} \\ 2 \end{pmatrix}\\ &= t(n, \sqrt{n}) \begin{pmatrix} 2 \sqrt{n} \\ 2 \end{pmatrix} +\sum_{\substack{l \geq 1\\ 2^{l} \sqrt{n} < \frac{n}{100}}} t(n,\underbrace{2^l \sqrt{n}}_{> \sqrt{2n}}) \begin{pmatrix} 2^{l+1} \sqrt{n} \\ 2 \end{pmatrix}\\&< \beta \frac{n^2}{n^{3/2}} \sqrt{n} (2 \sqrt{n}-1) + \sum_{\substack{l \geq 1\\ 2^{l} \sqrt{n} < \frac{n}{100}}} \frac{2n}{2^l \sqrt{n}} 2^l \sqrt{n} (2^{l+1} \sqrt{n}-1)\\ &< 2 \beta n^{3/2} + 4 n^{3/2} \sum_{\substack{l \geq 1 \\ 2^{l} < \frac{\sqrt{n}}{100}}} 2^l = 2 \beta n^{3/2} + 4 n^{3/2} \bigg( \frac{\sqrt{n}}{50}-2\bigg)\\ &= \frac{2}{25} n^2 + (2 \beta -8 )n^{3/2} \leq \frac{1}{4} \begin{pmatrix} n \\ 2\end{pmatrix}. \end{align*} $$
$$ \begin{align*} S_2 &= \sum_{l \geq0} \sum_{\substack{p \in F_{0,B}({\mathcal{H}}) \\ 2^l \sqrt{n} \leq a(p) < 2^{l+1} \sqrt{n} \\ a(p) < \frac{n}{100}}} \begin{pmatrix} a(p) \\ 2 \end{pmatrix} \leq \sum_{\substack{l \geq 0\\ 2^{l} \sqrt{n} < \frac{n}{100}}} t(n, 2^l \sqrt{n}) \begin{pmatrix} 2^{l+1} \sqrt{n} \\ 2 \end{pmatrix}\\ &= t(n, \sqrt{n}) \begin{pmatrix} 2 \sqrt{n} \\ 2 \end{pmatrix} +\sum_{\substack{l \geq 1\\ 2^{l} \sqrt{n} < \frac{n}{100}}} t(n,\underbrace{2^l \sqrt{n}}_{> \sqrt{2n}}) \begin{pmatrix} 2^{l+1} \sqrt{n} \\ 2 \end{pmatrix}\\&< \beta \frac{n^2}{n^{3/2}} \sqrt{n} (2 \sqrt{n}-1) + \sum_{\substack{l \geq 1\\ 2^{l} \sqrt{n} < \frac{n}{100}}} \frac{2n}{2^l \sqrt{n}} 2^l \sqrt{n} (2^{l+1} \sqrt{n}-1)\\ &< 2 \beta n^{3/2} + 4 n^{3/2} \sum_{\substack{l \geq 1 \\ 2^{l} < \frac{\sqrt{n}}{100}}} 2^l = 2 \beta n^{3/2} + 4 n^{3/2} \bigg( \frac{\sqrt{n}}{50}-2\bigg)\\ &= \frac{2}{25} n^2 + (2 \beta -8 )n^{3/2} \leq \frac{1}{4} \begin{pmatrix} n \\ 2\end{pmatrix}. \end{align*} $$
Combining the two results, we get a lower bound for
![]() $S_3$
:
$S_3$
:
 $$ \begin{align*} S_3 \geq \vert F_1 \vert \cdot \vert F_2 \vert - \frac{1}{4}\begin{pmatrix} n \\ 2 \end{pmatrix} - \frac{1}{8}\begin{pmatrix} n \\ 2 \end{pmatrix} \geq \frac{1}{16}n^2. \end{align*} $$
$$ \begin{align*} S_3 \geq \vert F_1 \vert \cdot \vert F_2 \vert - \frac{1}{4}\begin{pmatrix} n \\ 2 \end{pmatrix} - \frac{1}{8}\begin{pmatrix} n \\ 2 \end{pmatrix} \geq \frac{1}{16}n^2. \end{align*} $$
So now assume that condition (a) of the theorem does not hold, then
 $$ \begin{align*} \vert F_{0,B}({\mathcal{H}}) \vert \geq \sum_{\substack{p \in F_{0,B}\\ 2 \leq a(p) < 2^k}} 1 \geq \begin{pmatrix} 2^k \\ 2 \end{pmatrix}^{-1} \sum_{\substack{p \in F_{0,B}\\ 2 \leq a(p) < 2^k}} \begin{pmatrix} a(p) \\ 2 \end{pmatrix} \geq \begin{pmatrix} 2^k \\ 2 \end{pmatrix}^{-1} \frac{1}{16} n^2. \end{align*} $$
$$ \begin{align*} \vert F_{0,B}({\mathcal{H}}) \vert \geq \sum_{\substack{p \in F_{0,B}\\ 2 \leq a(p) < 2^k}} 1 \geq \begin{pmatrix} 2^k \\ 2 \end{pmatrix}^{-1} \sum_{\substack{p \in F_{0,B}\\ 2 \leq a(p) < 2^k}} \begin{pmatrix} a(p) \\ 2 \end{pmatrix} \geq \begin{pmatrix} 2^k \\ 2 \end{pmatrix}^{-1} \frac{1}{16} n^2. \end{align*} $$
Since we have seen that
![]() $k=10$
is a possible choice, the constant would be
$k=10$
is a possible choice, the constant would be
![]() $c={1}/{8 380416}$
.
$c={1}/{8 380416}$
.
Remark 6.19. In condition (a), the constant
![]() ${1}/{100}$
is by no means optimal, but since for us the constant plays an insignificant role, we stick to the original constant used by Beck.
${1}/{100}$
is by no means optimal, but since for us the constant plays an insignificant role, we stick to the original constant used by Beck.
Further notice that we have even proved a stronger theorem, namely that
if condition (a) does not hold.
Proof of Theorem 6.1
The idea of the proof is that for a family
![]() $F_i$
of hyperplanes, the other families induce a hyperplane arrangement in all
$F_i$
of hyperplanes, the other families induce a hyperplane arrangement in all
![]() $H \in F_i$
, thus we can conclude by induction. The case
$H \in F_i$
, thus we can conclude by induction. The case
![]() $d=2$
is already completed by Theorem 6.18, where we even proved the stronger statement that
$d=2$
is already completed by Theorem 6.18, where we even proved the stronger statement that
if for all
![]() $p \in B$
, we have
$p \in B$
, we have
![]() $a(p) < {n}/{100}$
. That
$a(p) < {n}/{100}$
. That
![]() $a(p) < {1}/{100} n$
is guaranteed by the assumption that at most
$a(p) < {1}/{100} n$
is guaranteed by the assumption that at most
![]() $c \cdot \vert F_i \vert $
hyperplanes from
$c \cdot \vert F_i \vert $
hyperplanes from
![]() $F_i$
can intersect in one point and
$F_i$
can intersect in one point and
![]() $c < {1}/{100}$
. So the initial case of the induction holds.
$c < {1}/{100}$
. So the initial case of the induction holds.
Now consider the family
![]() $F_1$
. We are interested in the
$F_1$
. We are interested in the
![]() $(d-1)$
-dimensional arrangement which is induced on the hyperplanes
$(d-1)$
-dimensional arrangement which is induced on the hyperplanes
![]() $H\in F_1$
. Notice that for
$H\in F_1$
. Notice that for
![]() $H_i \in F_i, H_j \in F_j$
and
$H_i \in F_i, H_j \in F_j$
and
![]() $H_k\in F_k$
,
$H_k\in F_k$
,
![]() $i \neq j \neq k$
, we have
$i \neq j \neq k$
, we have
![]() $H_i \cap H_j \neq H_i \cap H_k$
since otherwise, we get a contradiction to the assumption that
$H_i \cap H_j \neq H_i \cap H_k$
since otherwise, we get a contradiction to the assumption that
![]() $B \cap \bigcap _{i=1}^d f_i = \{p\}$
for all
$B \cap \bigcap _{i=1}^d f_i = \{p\}$
for all
![]() $(f_1,\ldots ,f_d) \in F_1 \times \cdots \times F_d$
. So the different families induce different
$(f_1,\ldots ,f_d) \in F_1 \times \cdots \times F_d$
. So the different families induce different
![]() $(d-2)$
-hyperplanes on the hyperplanes of
$(d-2)$
-hyperplanes on the hyperplanes of
![]() $F_1$
. Set
$F_1$
. Set
here
![]() $H \cap f \neq \emptyset $
holds for all f by the assumption on the intersection behaviour. Now we prove the following claim, which gives us the induction hypothesis.
$H \cap f \neq \emptyset $
holds for all f by the assumption on the intersection behaviour. Now we prove the following claim, which gives us the induction hypothesis.
Claim.
![]() $\vert {\mathcal {H}}^{H \ast } \vert> \delta \cdot n$
for some constant
$\vert {\mathcal {H}}^{H \ast } \vert> \delta \cdot n$
for some constant
![]() $\delta $
, and at least
$\delta $
, and at least
![]() $\varepsilon \cdot ({n}/{d})$
hyperplanes
$\varepsilon \cdot ({n}/{d})$
hyperplanes
![]() $H \in F_1$
for some constant
$H \in F_1$
for some constant
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
We prove the claim. We do this by considering two families and show that the one induces enough planes on the second one. To do so, let P be a generic two-dimensional plane in
![]() ${\mathbb {R}}^d$
, that is,
${\mathbb {R}}^d$
, that is,
![]() $P \cap H$
is one-dimensional for all
$P \cap H$
is one-dimensional for all
![]() $H \in F_1 \cup F_2$
and they are all distinct for different H. Additionally,
$H \in F_1 \cup F_2$
and they are all distinct for different H. Additionally,
![]() $P\cap f$
is a point for all
$P\cap f$
is a point for all
![]() $f=H \cap K$
with
$f=H \cap K$
with
![]() $H \in F_1$
,
$H \in F_1$
,
![]() $K \in F_2$
which are also distinct if the
$K \in F_2$
which are also distinct if the
![]() $K \cap H$
are distinct. So each hyperplane corresponds to a line and each
$K \cap H$
are distinct. So each hyperplane corresponds to a line and each
![]() $(d-2)$
-dimensional flat corresponds to a point. The intersection behaviour for the lines clearly fulfils the assumptions in Theorem 6.18. So we can apply the theorem and get
$(d-2)$
-dimensional flat corresponds to a point. The intersection behaviour for the lines clearly fulfils the assumptions in Theorem 6.18. So we can apply the theorem and get
![]() $c \cdot ({n}/{d})^2$
intersection points and therefore
$c \cdot ({n}/{d})^2$
intersection points and therefore
![]() $c \cdot ({n}/{d})^2$
induced flats. Since each hyperplane can carry at most
$c \cdot ({n}/{d})^2$
induced flats. Since each hyperplane can carry at most
![]() ${n}/{d}$
induced flats, we see that the flats have to spread out such that the claim holds.
${n}/{d}$
induced flats, we see that the flats have to spread out such that the claim holds.
Denote the set of hyperplanes from
![]() $F_1$
for which the claim holds by
$F_1$
for which the claim holds by
![]() $\tilde {F_1}$
. It is clear that the intersection behaviour of the different families also holds in the
$\tilde {F_1}$
. It is clear that the intersection behaviour of the different families also holds in the
![]() $(d-1)$
-dimensional arrangement induced on the hyperplanes in
$(d-1)$
-dimensional arrangement induced on the hyperplanes in
![]() $\tilde {F_1}$
. Also, assume that the stronger statement
$\tilde {F_1}$
. Also, assume that the stronger statement
is proved for all dimensions l up to
![]() $d-1$
, where k is a constant.
$d-1$
, where k is a constant.
Now we can do the induction step. We get the following inequality:
 $$ \begin{align*} \vert F_{0,B}({\mathcal{H}}) \vert \cdot \begin{pmatrix} d^k \\ d \end{pmatrix}> \sum_{\substack{p \in F_{0,B}({\mathcal{H}})\\ d \leq a(p) < d^{k}}} \begin{pmatrix} a(p) \\ d \end{pmatrix} \geq \sum_{H \in F_1} \sum_{\substack{p \in F_{0,B}({\mathcal{H}}^{H\ast})\\ d-1 \leq a_{{\mathcal{H}}^{H\ast}}(p) < (d-1)^k}} \begin{pmatrix} a_{{\mathcal{H}}^{H\ast}}(p) \\ d-1 \end{pmatrix}\hspace{-1.5pt}. \end{align*} $$
$$ \begin{align*} \vert F_{0,B}({\mathcal{H}}) \vert \cdot \begin{pmatrix} d^k \\ d \end{pmatrix}> \sum_{\substack{p \in F_{0,B}({\mathcal{H}})\\ d \leq a(p) < d^{k}}} \begin{pmatrix} a(p) \\ d \end{pmatrix} \geq \sum_{H \in F_1} \sum_{\substack{p \in F_{0,B}({\mathcal{H}}^{H\ast})\\ d-1 \leq a_{{\mathcal{H}}^{H\ast}}(p) < (d-1)^k}} \begin{pmatrix} a_{{\mathcal{H}}^{H\ast}}(p) \\ d-1 \end{pmatrix}\hspace{-1.5pt}. \end{align*} $$
For the last inequality, notice that
![]() $a_{{\mathcal {H}}^{H\ast }}(p)$
now only counts the hyperplanes in
$a_{{\mathcal {H}}^{H\ast }}(p)$
now only counts the hyperplanes in
![]() ${\mathcal {H}}^{H \ast }$
and we only have to take
${\mathcal {H}}^{H \ast }$
and we only have to take
![]() $d-1$
out of them since we fixed the choice
$d-1$
out of them since we fixed the choice
![]() $H \in F_1$
. Now further by the induction assumption,
$H \in F_1$
. Now further by the induction assumption,
 $$ \begin{align*} &\sum_{H \in F_1} \sum_{\substack{p \in F_{0,B}({\mathcal{H}}^{H\ast})\\ d-1 \leq a(p) < (d-1)^k}} \begin{pmatrix} a(p) \\ d-1 \end{pmatrix} \geq \sum_{H \in \tilde{F_1}} \sum_{\substack{p \in F_{0,B}({\mathcal{H}}^{H\ast})\\ d-1 \leq a(p) < (d-1)^k}} \begin{pmatrix} a(p) \\ d-1 \end{pmatrix}\\ &\quad\geq \sum_{H \in \tilde{F_1}} \vert \{ p \in F_{0,B}({\mathcal{H}}^{H\ast}) \mid d-1 \leq a(p) < (d-1)^k\}\vert\\ &\quad\geq \sum_{H \in \tilde{F_1}} c_{d-1} \cdot \delta^{d-1} n^{d-1} \geq \varepsilon \frac{n}{d} c_{d-1} \delta^{d-1} n^{d-1} = \frac{\varepsilon c_{d-1}}{d} \cdot \delta^{d-1} n^d.\\ \end{align*} $$
$$ \begin{align*} &\sum_{H \in F_1} \sum_{\substack{p \in F_{0,B}({\mathcal{H}}^{H\ast})\\ d-1 \leq a(p) < (d-1)^k}} \begin{pmatrix} a(p) \\ d-1 \end{pmatrix} \geq \sum_{H \in \tilde{F_1}} \sum_{\substack{p \in F_{0,B}({\mathcal{H}}^{H\ast})\\ d-1 \leq a(p) < (d-1)^k}} \begin{pmatrix} a(p) \\ d-1 \end{pmatrix}\\ &\quad\geq \sum_{H \in \tilde{F_1}} \vert \{ p \in F_{0,B}({\mathcal{H}}^{H\ast}) \mid d-1 \leq a(p) < (d-1)^k\}\vert\\ &\quad\geq \sum_{H \in \tilde{F_1}} c_{d-1} \cdot \delta^{d-1} n^{d-1} \geq \varepsilon \frac{n}{d} c_{d-1} \delta^{d-1} n^{d-1} = \frac{\varepsilon c_{d-1}}{d} \cdot \delta^{d-1} n^d.\\ \end{align*} $$
This finally yields
 $$ \begin{align*} \vert \{ F_{0,B}({\mathcal{H}}) \mid d \leq a(p) < d^k \} \vert \geq \begin{pmatrix} d^k \\ d \end{pmatrix}^{-1} \frac{\varepsilon c_{d-1}}{d} \cdot \delta^{d-1} n^d =: c_d n^d.\\[-42pt] \end{align*} $$
$$ \begin{align*} \vert \{ F_{0,B}({\mathcal{H}}) \mid d \leq a(p) < d^k \} \vert \geq \begin{pmatrix} d^k \\ d \end{pmatrix}^{-1} \frac{\varepsilon c_{d-1}}{d} \cdot \delta^{d-1} n^d =: c_d n^d.\\[-42pt] \end{align*} $$
A Appendix. FLC in non-abelian lcsc groups
This appendix is dedicated to giving some more information on sets with finite local complexity for lcsc groups and we will show that all model sets have FLC.
A locally finite subset
![]() $\Lambda \subset G$
which fulfils one and therefore all of the conditions in the following lemma has finite local complexity as defined in Definition 2.1. In the lemma, we only need that
$\Lambda \subset G$
which fulfils one and therefore all of the conditions in the following lemma has finite local complexity as defined in Definition 2.1. In the lemma, we only need that
![]() $\Lambda $
is locally finite, so we could also define the term of finite local complexity for this type of sets.
$\Lambda $
is locally finite, so we could also define the term of finite local complexity for this type of sets.
Lemma A.1. (Finite local complexity)
Let G be an lcsc group and
![]() $\Lambda \subset G$
a locally finite set, that is, for all bounded
$\Lambda \subset G$
a locally finite set, that is, for all bounded
![]() $B\subset G$
, we have that
$B\subset G$
, we have that
![]() $B \cap \Lambda $
is finite. Then the following are equivalent.
$B \cap \Lambda $
is finite. Then the following are equivalent.
-
(i) For all
 $B \subset G$
bounded, there exists a finite
$B \subset G$
bounded, there exists a finite
 $F_B \subset G$
such that
$F_B \subset G$
such that  $$ \begin{align*} \text{for all } g \kern1.4pt{\in}\kern1.4pt G, \text{ there exists } h \kern1.4pt{\in}\kern1.4pt \Lambda^{\kern-1.7pt-1}\Lambda \text{ there exists } f \kern1.4pt{\in}\kern1.4pt F_B: (B g^{\kern-1.5pt -1}\kern1.4pt{\cap}\kern1.4pt \Lambda)h\kern1.4pt{=}\kern1.4pt Bf^{-1}\kern1.4pt{\cap}\kern1.4pt \Lambda. \end{align*} $$
$$ \begin{align*} \text{for all } g \kern1.4pt{\in}\kern1.4pt G, \text{ there exists } h \kern1.4pt{\in}\kern1.4pt \Lambda^{\kern-1.7pt-1}\Lambda \text{ there exists } f \kern1.4pt{\in}\kern1.4pt F_B: (B g^{\kern-1.5pt -1}\kern1.4pt{\cap}\kern1.4pt \Lambda)h\kern1.4pt{=}\kern1.4pt Bf^{-1}\kern1.4pt{\cap}\kern1.4pt \Lambda. \end{align*} $$
-
(ii) For all
 $B \subset G$
bounded, there exists a finite
$B \subset G$
bounded, there exists a finite
 $F_B \subset G$
such that
$F_B \subset G$
such that  $$ \begin{align*} \text{for all } g \in G, \text{ there exists } h \in G \text{ there exists } f \in F_B: (B g^{-1}\cap \Lambda)h=Bf^{-1}\cap \Lambda. \end{align*} $$
$$ \begin{align*} \text{for all } g \in G, \text{ there exists } h \in G \text{ there exists } f \in F_B: (B g^{-1}\cap \Lambda)h=Bf^{-1}\cap \Lambda. \end{align*} $$
-
(iii)
 $\Lambda \Lambda ^{-1}$
is locally finite.
$\Lambda \Lambda ^{-1}$
is locally finite. -
(iv) For all
 $B \subset G$
bounded,
$B \subset G$
bounded,  $$ \begin{align*} \vert \{B \cap \Lambda \unicode{x3bb}^{-1}\mid \unicode{x3bb} \in \Lambda\}\vert< \infty. \end{align*} $$
$$ \begin{align*} \vert \{B \cap \Lambda \unicode{x3bb}^{-1}\mid \unicode{x3bb} \in \Lambda\}\vert< \infty. \end{align*} $$
-
(v) The complexity function
 $p(r)$
is finite for all
$p(r)$
is finite for all
 $r\geq 0$
.
$r\geq 0$
.
Proof. First, we will show the equivalence of items (i), (ii) and (iii). Afterwards, we will show the equivalence of items (iii) and (iv). Finally, the will show the equivalence of items (iv) and (v).
(i)
![]() $ \Rightarrow $
(ii): This step is obvious, since
$ \Rightarrow $
(ii): This step is obvious, since
![]() $\Lambda ^{-1}\Lambda \subset G$
.
$\Lambda ^{-1}\Lambda \subset G$
.
(ii)
![]() $ \Rightarrow $
(iii): Without loss of generality, we can assume that B is compact and contains the identity, otherwise, we just simply expand B and notice that this would just increase the number of elements in the intersection. For this B, we choose
$ \Rightarrow $
(iii): Without loss of generality, we can assume that B is compact and contains the identity, otherwise, we just simply expand B and notice that this would just increase the number of elements in the intersection. For this B, we choose
![]() $F_B$
such that item (ii) holds. Since
$F_B$
such that item (ii) holds. Since
![]() $F_B$
is finite and B is bounded, we see that
$F_B$
is finite and B is bounded, we see that
![]() $B':=BF_B^{-1}$
is also bounded, further we see, since
$B':=BF_B^{-1}$
is also bounded, further we see, since
![]() $\Lambda $
is locally finite, that
$\Lambda $
is locally finite, that
![]() $F:=B'\cap \Lambda $
is finite.
$F:=B'\cap \Lambda $
is finite.
Now let
![]() $\unicode{x3bb} _1, \unicode{x3bb} _2 \in \Lambda $
be arbitrary with
$\unicode{x3bb} _1, \unicode{x3bb} _2 \in \Lambda $
be arbitrary with
![]() $\unicode{x3bb} _1\unicode{x3bb} _2^{-1} \in B$
. We get
$\unicode{x3bb} _1\unicode{x3bb} _2^{-1} \in B$
. We get
![]() $\unicode{x3bb} _1 \in B\unicode{x3bb} _2 \cap \Lambda $
and since we assumed
$\unicode{x3bb} _1 \in B\unicode{x3bb} _2 \cap \Lambda $
and since we assumed
![]() $e \in B$
, we also get
$e \in B$
, we also get
![]() $\unicode{x3bb} _2 \in B \unicode{x3bb} _2 \cap \Lambda $
. With our assumption, we get that
$\unicode{x3bb} _2 \in B \unicode{x3bb} _2 \cap \Lambda $
. With our assumption, we get that
![]() $h_1 \in G$
and
$h_1 \in G$
and
![]() $f_1 \in F_B$
exist with
$f_1 \in F_B$
exist with
Putting the pieces together, we obtain
So
![]() $\unicode{x3bb} _1 \unicode{x3bb} _2^{-1} = (\unicode{x3bb} _1 h_1^{-1})(\unicode{x3bb} _2 h_1^{-1})^{-1}\in F F^{-1}$
and we get that
$\unicode{x3bb} _1 \unicode{x3bb} _2^{-1} = (\unicode{x3bb} _1 h_1^{-1})(\unicode{x3bb} _2 h_1^{-1})^{-1}\in F F^{-1}$
and we get that
![]() $\Lambda \Lambda ^{-1} \cap B \subset F F^{-1}$
is finite.
$\Lambda \Lambda ^{-1} \cap B \subset F F^{-1}$
is finite.
(iii)
![]() $ \Rightarrow $
(i): Let
$ \Rightarrow $
(i): Let
![]() $B \subset G$
be bounded. Without loss of generality, we can assume B to be symmetric, that is,
$B \subset G$
be bounded. Without loss of generality, we can assume B to be symmetric, that is,
![]() $B=B^{-1}$
. Since B is bounded,
$B=B^{-1}$
. Since B is bounded,
![]() $B^2$
is also bounded and
$B^2$
is also bounded and
![]() $B^2 \cap \Lambda \Lambda ^{-1}$
is finite by assumption. Then
$B^2 \cap \Lambda \Lambda ^{-1}$
is finite by assumption. Then
and since we know that this is finite, we conclude that
![]() $Bb \cap \Lambda \unicode{x3bb} ^{-1}$
can only have finitely many different forms. So we find
$Bb \cap \Lambda \unicode{x3bb} ^{-1}$
can only have finitely many different forms. So we find
![]() $b_1,\ldots ,b_s \in B$
and
$b_1,\ldots ,b_s \in B$
and
![]() $\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _t \in \Lambda $
such that for arbitrary
$\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _t \in \Lambda $
such that for arbitrary
![]() $b\in B$
and
$b\in B$
and
![]() $\unicode{x3bb} \in \Lambda $
, there exists an
$\unicode{x3bb} \in \Lambda $
, there exists an
![]() $n\in \{1,\ldots ,s\}$
and an
$n\in \{1,\ldots ,s\}$
and an
![]() $m\in \{1,\ldots ,t\}$
with
$m\in \{1,\ldots ,t\}$
with
Let
![]() $g\in G$
be arbitrary. Then the two following cases can appear.
$g\in G$
be arbitrary. Then the two following cases can appear.
Case 1:
![]() $B g^{-1} \cap \Lambda = \emptyset $
. To deal with this case, we simply set
$B g^{-1} \cap \Lambda = \emptyset $
. To deal with this case, we simply set
![]() $f_0 = g$
for one such g.
$f_0 = g$
for one such g.
Case 2:
![]() $B g^{-1} \cap \Lambda \neq \emptyset $
. Then there exists a
$B g^{-1} \cap \Lambda \neq \emptyset $
. Then there exists a
![]() $b'\in B$
such that
$b'\in B$
such that
![]() $b'g^{-1} = \unicode{x3bb} $
. Set
$b'g^{-1} = \unicode{x3bb} $
. Set
![]() ${b:=b^{\prime -1}}$
, then
${b:=b^{\prime -1}}$
, then
![]() $g^{-1}=b\unicode{x3bb} $
and, since B is symmetric,
$g^{-1}=b\unicode{x3bb} $
and, since B is symmetric,
![]() $b \in B$
. Now choose n and m such that
$b \in B$
. Now choose n and m such that
![]() $Bb \cap \Lambda \unicode{x3bb} ^{-1}=B b_n \cap \Lambda \unicode{x3bb} _n^{-1}$
and set
$Bb \cap \Lambda \unicode{x3bb} ^{-1}=B b_n \cap \Lambda \unicode{x3bb} _n^{-1}$
and set
![]() $h:=\unicode{x3bb} ^{-1}\unicode{x3bb} _n \in \Lambda ^{-1} \Lambda $
. Now we get
$h:=\unicode{x3bb} ^{-1}\unicode{x3bb} _n \in \Lambda ^{-1} \Lambda $
. Now we get

Finally, we set
![]() $F_B':=\{\unicode{x3bb} _m^{-1} b_n^{-1} \mid n \in \{1,\ldots ,s\}, m\in \{1,\ldots ,t\}\}$
, which is finite.
$F_B':=\{\unicode{x3bb} _m^{-1} b_n^{-1} \mid n \in \{1,\ldots ,s\}, m\in \{1,\ldots ,t\}\}$
, which is finite.
To combine both cases, define
![]() $F_B := F_B' \cup {f_0}$
.
$F_B := F_B' \cup {f_0}$
.
(iv)
![]() $ \Rightarrow $
(iii): Let
$ \Rightarrow $
(iii): Let
![]() $B\subset G$
be bounded. For
$B\subset G$
be bounded. For
![]() $\{B \cap \Lambda \unicode{x3bb} ^{-1} \mid \unicode{x3bb} \in \Lambda \}$
, we use our assumption to find finitely many representatives
$\{B \cap \Lambda \unicode{x3bb} ^{-1} \mid \unicode{x3bb} \in \Lambda \}$
, we use our assumption to find finitely many representatives
![]() $\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _k$
such that
$\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _k$
such that

We get

The sets
![]() $B \cap \Lambda \unicode{x3bb} _l^{-1} = (B \unicode{x3bb} _l \cap \Lambda )\unicode{x3bb} _l^{-1}$
are finite, since
$B \cap \Lambda \unicode{x3bb} _l^{-1} = (B \unicode{x3bb} _l \cap \Lambda )\unicode{x3bb} _l^{-1}$
are finite, since
![]() $\Lambda $
is locally finite.
$\Lambda $
is locally finite.
(iii)
![]() $ \Rightarrow $
(iv): Let
$ \Rightarrow $
(iv): Let
![]() $B \subset G$
be bounded, then by our assumption,
$B \subset G$
be bounded, then by our assumption,
![]() $B \cap \Lambda \Lambda ^{-1}$
is finite. Further,
$B \cap \Lambda \Lambda ^{-1}$
is finite. Further,
Since the left-hand side is finite, this also holds for the right-hand side. However, this means that there can only be finitely many combinations for the sets
![]() $B \cap \Lambda \unicode{x3bb} ^{-1}$
. So we get
$B \cap \Lambda \unicode{x3bb} ^{-1}$
. So we get
(iv)
![]() $ \Leftrightarrow $
(v): This is obvious since each ball
$ \Leftrightarrow $
(v): This is obvious since each ball
![]() $B_r(e)$
is a bounded set and, alternatively, for every bounded set B, we can find a
$B_r(e)$
is a bounded set and, alternatively, for every bounded set B, we can find a
![]() $r>0$
such that
$r>0$
such that
![]() $B \subset B_r(e)$
holds.
$B \subset B_r(e)$
holds.
The following proposition justifies our restriction to precompact windows with non-empty interior.
Proposition A.2. Let
![]() $(G,H, \Gamma )$
be a CPS,
$(G,H, \Gamma )$
be a CPS,
![]() $W\hspace{-1pt} \subset\hspace{-1pt} H$
a subset and
$W\hspace{-1pt} \subset\hspace{-1pt} H$
a subset and
![]() $\Lambda\hspace{-1pt} :=\hspace{-1pt} \pi _G((G\hspace{-1pt} \times\hspace{-1pt} W)\hspace{-1pt}\cap\hspace{-1pt} ~\Gamma )$
.
$\Lambda\hspace{-1pt} :=\hspace{-1pt} \pi _G((G\hspace{-1pt} \times\hspace{-1pt} W)\hspace{-1pt}\cap\hspace{-1pt} ~\Gamma )$
.
-
(i) If
 $W^\circ \neq \emptyset $
, then
$W^\circ \neq \emptyset $
, then
 $\Lambda $
is relatively dense.
$\Lambda $
is relatively dense. -
(ii) If W is relatively compact, then
 $\Lambda $
is uniformly discrete.
$\Lambda $
is uniformly discrete. -
(iii) If W is relatively compact and
 $W^\circ \neq \emptyset $
, then
$W^\circ \neq \emptyset $
, then
 $\Lambda $
has FLC.
$\Lambda $
has FLC.
Proof. (i) We are using Proposition 3.2. Since
![]() ${W^\circ \neq \emptyset }$
, this also holds for the inverse
${W^\circ \neq \emptyset }$
, this also holds for the inverse
![]() ${(W^{-1})^\circ \neq \emptyset }$
and we can choose an open subset
${(W^{-1})^\circ \neq \emptyset }$
and we can choose an open subset
![]() $\emptyset \neq U \subset W^{-1}$
. By Proposition 3.2, we find a compact set K such that
$\emptyset \neq U \subset W^{-1}$
. By Proposition 3.2, we find a compact set K such that
![]() $G\times H= (K \times U)\Gamma $
. Let
$G\times H= (K \times U)\Gamma $
. Let
![]() $g \in G$
be arbitrary. We can find
$g \in G$
be arbitrary. We can find
![]() $u \in U, k \in K$
and
$u \in U, k \in K$
and
![]() $\gamma \in \Gamma $
such that
$\gamma \in \Gamma $
such that
This tells us that
![]() $u \gamma _{H} = e_H$
and therefore
$u \gamma _{H} = e_H$
and therefore
![]() $\gamma _{H}=u^{-1} \in (W^{-1})^{-1}=W$
, so
$\gamma _{H}=u^{-1} \in (W^{-1})^{-1}=W$
, so
![]() ${\gamma _{G} \in \Lambda }$
. Therefore,
${\gamma _{G} \in \Lambda }$
. Therefore,
![]() $g = k \gamma _{G} \in K \Lambda $
. This shows the claim.
$g = k \gamma _{G} \in K \Lambda $
. This shows the claim.
(ii) Let us assume
![]() $\Lambda $
is not uniformly discrete, then for all
$\Lambda $
is not uniformly discrete, then for all
![]() $r>0$
, there exists
$r>0$
, there exists
![]() ${x,y \in \Lambda }$
such that
${x,y \in \Lambda }$
such that
![]() ${d(x,y)<r}$
. By the right-invariance of d, this is equivalent to
${d(x,y)<r}$
. By the right-invariance of d, this is equivalent to
![]() ${d(e, yx^{-1})<r}$
. We can lift x and y to elements in the product and get
${d(e, yx^{-1})<r}$
. We can lift x and y to elements in the product and get
Since
![]() $\Gamma $
and G are groups, we can deduce
$\Gamma $
and G are groups, we can deduce
Since we know that
![]() ${yx^{-1} \in B_r(x)}$
, we get
${yx^{-1} \in B_r(x)}$
, we get
Since W is relatively compact,
![]() $WW^{-1}$
is also relatively compact and therefore bounded. Moreover,
$WW^{-1}$
is also relatively compact and therefore bounded. Moreover,
![]() $B_r(e_G)$
is bounded so the product
$B_r(e_G)$
is bounded so the product
![]() ${B_r(e_G)\times WW^{-1}}$
is bounded. Thus, since
${B_r(e_G)\times WW^{-1}}$
is bounded. Thus, since
![]() $\Gamma $
is a lattice, we get that
$\Gamma $
is a lattice, we get that
![]() ${\Gamma \cap (B_r(e_G) \times WW^{-1})}$
is finite. By the injectivity of
${\Gamma \cap (B_r(e_G) \times WW^{-1})}$
is finite. By the injectivity of
![]() ${\pi _G}$
, we know that
${\pi _G}$
, we know that
![]() ${d(a_G,b_G) \neq 0}$
for
${d(a_G,b_G) \neq 0}$
for
![]() ${a \neq b \in \Gamma }$
, so we get that
${a \neq b \in \Gamma }$
, so we get that
![]() $d(a_G,b_G)> 0$
for
$d(a_G,b_G)> 0$
for
![]() $a,b \in \Gamma \cap (B_r(e_G) \times WW^{-1})$
and by finiteness, there is a minimal distance
$a,b \in \Gamma \cap (B_r(e_G) \times WW^{-1})$
and by finiteness, there is a minimal distance
![]() $\tilde {d}$
. Now set
$\tilde {d}$
. Now set
![]() $\tilde {r}< \tilde {d}$
and conclude
$\tilde {r}< \tilde {d}$
and conclude
![]() ${\Gamma \cap (B_{\tilde {r}}(e_G) \times WW^{-1})=\{(e_G,e_H)\}}$
. This is a contradiction to the assumption since we do not find two elements which are this close together. Therefore,
${\Gamma \cap (B_{\tilde {r}}(e_G) \times WW^{-1})=\{(e_G,e_H)\}}$
. This is a contradiction to the assumption since we do not find two elements which are this close together. Therefore,
![]() $\Lambda $
has to be uniformly discrete for
$\Lambda $
has to be uniformly discrete for
![]() $\tilde {r}$
.
$\tilde {r}$
.
(iii) By items (i) and (ii), we know that
![]() $\Lambda $
is a Delone set and therefore locally finite. We want to use the characterization in item (iii) of Lemma A.1, so we show that
$\Lambda $
is a Delone set and therefore locally finite. We want to use the characterization in item (iii) of Lemma A.1, so we show that
![]() $B \cap \Lambda \Lambda ^{-1}$
is finite for a bounded set
$B \cap \Lambda \Lambda ^{-1}$
is finite for a bounded set
![]() $B \subset H$
. It is enough to show that the preimage of this set is finite. Since taking the preimage and intersecting commutes, we get
$B \subset H$
. It is enough to show that the preimage of this set is finite. Since taking the preimage and intersecting commutes, we get
Now we can consider the two parts separately and then intersect them, so the preimage of B is obviously
![]() $\pi _G^{-1}(B)=B \times H$
.
$\pi _G^{-1}(B)=B \times H$
.
For the second part, we need to remember the definition of
![]() $\Lambda $
, which was given by
$\Lambda $
, which was given by
![]() ${\Lambda =\pi _G((G \times W)\cap \Gamma )}$
, so
${\Lambda =\pi _G((G \times W)\cap \Gamma )}$
, so
We want to show that this is a subset of
![]() $\Gamma \cap (G \times WW^{-1})$
. So let
$\Gamma \cap (G \times WW^{-1})$
. So let
![]() $\unicode{x3bb} _1, \unicode{x3bb} _2 \in \Lambda $
, then they are both in
$\unicode{x3bb} _1, \unicode{x3bb} _2 \in \Lambda $
, then they are both in
![]() $\Gamma _G$
, and therefore
$\Gamma _G$
, and therefore
![]() $\unicode{x3bb} _1 \unicode{x3bb} _2^{-1} \in \Gamma _G$
and there exists a unique preimage inside
$\unicode{x3bb} _1 \unicode{x3bb} _2^{-1} \in \Gamma _G$
and there exists a unique preimage inside
![]() $\Gamma $
which we name
$\Gamma $
which we name
![]() $(\unicode{x3bb} _1 \unicode{x3bb} _2^{-1},x)$
. However, the preimage of
$(\unicode{x3bb} _1 \unicode{x3bb} _2^{-1},x)$
. However, the preimage of
![]() $\unicode{x3bb} _i$
,
$\unicode{x3bb} _i$
,
![]() $i\in \{1,2\}$
, is
$i\in \{1,2\}$
, is
![]() $(\unicode{x3bb} _i, w_i) \in \Gamma \cap (G \times W)$
. Additionally,
$(\unicode{x3bb} _i, w_i) \in \Gamma \cap (G \times W)$
. Additionally,
Since the preimage was unique and we see that
we get that
![]() $\pi _G^{-1}(\unicode{x3bb} _1 \unicode{x3bb} _2^{-1}) \in \Gamma \cap (G \times WW^{-1})$
.
$\pi _G^{-1}(\unicode{x3bb} _1 \unicode{x3bb} _2^{-1}) \in \Gamma \cap (G \times WW^{-1})$
.
Combining the two arguments, we get
Since W is relatively compact, we get that
![]() $\overline {W}$
is compact. Since
$\overline {W}$
is compact. Since
![]() $W \subset \overline {W}$
, we see
$W \subset \overline {W}$
, we see
![]() $W \subset H$
is bounded. Hence, there exists a
$W \subset H$
is bounded. Hence, there exists a
![]() $r>0$
such that
$r>0$
such that
![]() $r>d(w_1, w_2)$
for all
$r>d(w_1, w_2)$
for all
![]() ${w_1,w_2 \in W}$
. Additionally, once more by right-invariance of the metric, we get
${w_1,w_2 \in W}$
. Additionally, once more by right-invariance of the metric, we get
![]() ${r>d(w_1w_2^{-1},e)}$
. This tells us that
${r>d(w_1w_2^{-1},e)}$
. This tells us that
![]() $WW^{-1} \subset B_r(e)$
and therefore it is bounded. Further,
$WW^{-1} \subset B_r(e)$
and therefore it is bounded. Further,
![]() $B \subset G$
was a bounded set. We see that
$B \subset G$
was a bounded set. We see that
![]() $B \times WW^{-1} \subset G \times H$
is bounded in the product. Since
$B \times WW^{-1} \subset G \times H$
is bounded in the product. Since
![]() $\Gamma $
is a lattice, it has FLC and therefore
$\Gamma $
is a lattice, it has FLC and therefore
![]() $(B \times WW^{-1}) \cap \Gamma $
is finite.
$(B \times WW^{-1}) \cap \Gamma $
is finite.
B Appendix. Homogeneous Lie groups
In the first part of this appendix, we are concerned with the proof of Theorem 4.14.
Proposition B.1. Every locally two-step nilpotent homogeneous Lie group is non-crooked.
Proof. This follows directly by considering the BCH formula and noticing that by using the assumption on locally two-step nilpotent Lie groups, for all
![]() $X,Y \in {\mathfrak {g}}$
,
$X,Y \in {\mathfrak {g}}$
,
So for a hyperplane
![]() $H =v_0 + \sum _{i=1}^d t_i v_i$
, with
$H =v_0 + \sum _{i=1}^d t_i v_i$
, with
![]() $t_i \in {\mathbb {R}}$
,
$t_i \in {\mathbb {R}}$
,
![]() $v_i \in {\mathbb {R}}^d$
and d the dimension of the Lie group, we get for all
$v_i \in {\mathbb {R}}^d$
and d the dimension of the Lie group, we get for all
![]() $X \in {\mathfrak {g}}$
,
$X \in {\mathfrak {g}}$
,
 $$ \begin{align*} X \ast H &= X + H + \frac{1}{2}[X,H] = v_0 +X +\sum_{i=1}^d t_i v_i + \frac{1}{2} [X, v_0] + \frac{1}{2} \sum_{i=1}^d t_i [X,v_i]\\ &= v_0 +X + \frac{1}{2} [X, v_0] +\sum_{i=1}^d t_i (v_i + [X,v_i]) =: \tilde{v_0} + \sum_{i=1}^d t_i \tilde{v_i}. \end{align*} $$
$$ \begin{align*} X \ast H &= X + H + \frac{1}{2}[X,H] = v_0 +X +\sum_{i=1}^d t_i v_i + \frac{1}{2} [X, v_0] + \frac{1}{2} \sum_{i=1}^d t_i [X,v_i]\\ &= v_0 +X + \frac{1}{2} [X, v_0] +\sum_{i=1}^d t_i (v_i + [X,v_i]) =: \tilde{v_0} + \sum_{i=1}^d t_i \tilde{v_i}. \end{align*} $$
This is again a hyperplane.
At first sight, the condition of locally two-step nilpotent seems weaker than the condition of being two-step nilpotent, but in fact, the two are equivalent by the following proposition.
Proposition B.2. Let G be a Lie group. If G is locally two-step nilpotent, then G is two-step nilpotent or abelian. If G is two-step nilpotent, it is locally two-step nilpotent.
Proof. The conclusion from two-step nilpotent to locally two-step nilpotent is trivial, so two-step nilpotent Lie groups are locally two-step nilpotent Lie groups.
So now assume that we have a locally two-step nilpotent Lie group and arbitrary
![]() $X,Y,Z \in {\mathfrak {g}}$
, then
$X,Y,Z \in {\mathfrak {g}}$
, then
 $$ \begin{align*} 0 &= [X+Y,[X+Y,Z] = [X,[X,Z]]+[X,[Y,Z]]+[Y,[X,Z]]+[Y,[Y,Z]]\\ &= [X,[Y,Z]]+[Y,[X,Z]]. \end{align*} $$
$$ \begin{align*} 0 &= [X+Y,[X+Y,Z] = [X,[X,Z]]+[X,[Y,Z]]+[Y,[X,Z]]+[Y,[Y,Z]]\\ &= [X,[Y,Z]]+[Y,[X,Z]]. \end{align*} $$
This means that
![]() $[X,[Y,Z]] =-[Y,[X,Z]] = [Y,[Z,X]]$
. By using Jacobi’s identity, we have
$[X,[Y,Z]] =-[Y,[X,Z]] = [Y,[Z,X]]$
. By using Jacobi’s identity, we have
Therefore, by using the equality we found before, we have
![]() $2[Y,[Z,X]]=[Z,[Y,X]]$
. Since X, Y and Z are arbitrary, we can switch the roles of Y and Z. Thus,
$2[Y,[Z,X]]=[Z,[Y,X]]$
. Since X, Y and Z are arbitrary, we can switch the roles of Y and Z. Thus,
![]() ${2[Z,[Y,X]]=[Y,[Z,X]]}$
. So in total, this means
${2[Z,[Y,X]]=[Y,[Z,X]]}$
. So in total, this means
and therefore
![]() $[Z,[Y,X]]=0$
. So G is two-step nilpotent or abelian.
$[Z,[Y,X]]=0$
. So G is two-step nilpotent or abelian.
We have seen that the class of non-crooked homogeneous Lie groups contains the abelian and the two-step nilpotent homogeneous Lie groups. We will now see that a higher nilpotency degree always implies crookedness.
Proposition B.3. A three-step homogeneous Lie group is crooked.
Proof. Let H be a hyperplane given by
![]() $H=v_0 + \sum _{i=1}^n t_i v_i$
, with
$H=v_0 + \sum _{i=1}^n t_i v_i$
, with
![]() $t_i \in {\mathbb {R}}$
,
$t_i \in {\mathbb {R}}$
,
![]() $v_i \in {\mathbb {R}}^d$
and d the dimension of the Lie group. We get for all
$v_i \in {\mathbb {R}}^d$
and d the dimension of the Lie group. We get for all
![]() $X \in {\mathfrak {g}}$
,
$X \in {\mathfrak {g}}$
,
 $$ \begin{align*} X \ast H &= X + H + \frac{1}{2}[X,H] + \frac{1}{12}([X,[X,H]]-[H,[X,H]])\\ &= X+ v_0 + \frac{1}{2}[X,v_0]+\frac{1}{12}([X,X,v_0]+[v_0,[X,v_0]])\\ &\quad + \sum_{i=1}^n t_i\cdot \bigg( v_i+\frac{1}{2} [X,v_i]+ \frac{1}{12}([X,[X,v_i]] - [v_0,[X,v_i]] - [v_i,[X,v_0]]) \bigg)\\ &\quad - \frac{1}{12} \sum_{i=1}^n \sum_{j=1}^n t_i t_j [v_i,[X,v_j]]. \end{align*} $$
$$ \begin{align*} X \ast H &= X + H + \frac{1}{2}[X,H] + \frac{1}{12}([X,[X,H]]-[H,[X,H]])\\ &= X+ v_0 + \frac{1}{2}[X,v_0]+\frac{1}{12}([X,X,v_0]+[v_0,[X,v_0]])\\ &\quad + \sum_{i=1}^n t_i\cdot \bigg( v_i+\frac{1}{2} [X,v_i]+ \frac{1}{12}([X,[X,v_i]] - [v_0,[X,v_i]] - [v_i,[X,v_0]]) \bigg)\\ &\quad - \frac{1}{12} \sum_{i=1}^n \sum_{j=1}^n t_i t_j [v_i,[X,v_j]]. \end{align*} $$
So for this to be non-crooked, the last sum has to disappear, that is,
 $$ \begin{align*} \sum_{i=1}^n \sum_{j=1}^n t_i t_j [v_i,[X,v_j]] = 0. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^n \sum_{j=1}^n t_i t_j [v_i,[X,v_j]] = 0. \end{align*} $$
However, since
![]() $t_i$
,
$t_i$
,
![]() $t_j$
are parameters, we can only compare the summands with the same coefficients, so for all
$t_j$
are parameters, we can only compare the summands with the same coefficients, so for all
![]() $i,j \in \{1,\ldots ,n\}$
,
$i,j \in \{1,\ldots ,n\}$
,
![]() $i\neq j$
,
$i\neq j$
,
and for the diagonal, that is,
![]() $i=j$
,
$i=j$
,
However, this last condition is the locally two-step nilpotency condition, which, as we have seen, implies two-step nilpotency.
Corollary B.4. All nilpotent homogeneous Lie groups, with nilpotency degree greater than two, are crooked.
B.1 Form of the polynomial action
We can find some restrictions on the form of the polynomials in the group law. Since we have a dilation structure, we get
 $$ \begin{align*} &(r^{\nu_1}P_1(x,y),\ldots,r^{\nu_n}P_n(x,y))=D_r( P_1(x,y),\ldots , P_n(x,y)) = D_r(xy)\\ &\quad= D_r(x) D_r(y) = ( P_1(D_r(x),D_r(y)),\ldots , P_n(D_r(x),D_r(y))). \end{align*} $$
$$ \begin{align*} &(r^{\nu_1}P_1(x,y),\ldots,r^{\nu_n}P_n(x,y))=D_r( P_1(x,y),\ldots , P_n(x,y)) = D_r(xy)\\ &\quad= D_r(x) D_r(y) = ( P_1(D_r(x),D_r(y)),\ldots , P_n(D_r(x),D_r(y))). \end{align*} $$
This means for the polynomials, we have
This gives us a restriction on the form of
![]() $P_i$
, namely if
$P_i$
, namely if
 $$ \begin{align*} P_i(x,y)= \sum_{\alpha_1,\ldots ,\alpha_n,\beta_1,\ldots ,\beta_n \in {\mathbb{N}}} c_{(\alpha_1,\ldots ,\alpha_n,\beta_1,\ldots ,\beta_n)} x_1^{\alpha_1}\cdots x_n^{\alpha_n} y_1^{\beta_1}\cdots y_n^{\beta_n}, \end{align*} $$
$$ \begin{align*} P_i(x,y)= \sum_{\alpha_1,\ldots ,\alpha_n,\beta_1,\ldots ,\beta_n \in {\mathbb{N}}} c_{(\alpha_1,\ldots ,\alpha_n,\beta_1,\ldots ,\beta_n)} x_1^{\alpha_1}\cdots x_n^{\alpha_n} y_1^{\beta_1}\cdots y_n^{\beta_n}, \end{align*} $$
then for all summands with
![]() $c\neq 0$
, it is
$c\neq 0$
, it is
![]() $\nu _i=\nu _1\alpha _1+\cdots +\nu _n\alpha _n+\nu _1\beta _1+\cdots +\nu _n\beta _n$
. Since we sorted the
$\nu _i=\nu _1\alpha _1+\cdots +\nu _n\alpha _n+\nu _1\beta _1+\cdots +\nu _n\beta _n$
. Since we sorted the
![]() $\nu _i$
by their size, we see that in the ith entry, all
$\nu _i$
by their size, we see that in the ith entry, all
![]() $\alpha _j$
and
$\alpha _j$
and
![]() $\beta _j$
have to be zero if
$\beta _j$
have to be zero if
![]() $\nu _j> \nu _i$
. This means that for the polynomial
$\nu _j> \nu _i$
. This means that for the polynomial
![]() $P_i$
, we have that it is only dependent on the first i entries of both x and y.
$P_i$
, we have that it is only dependent on the first i entries of both x and y.
Another restriction that can be seen from the BCH formula is that the polynomials are of a certain form, namely
 $$ \begin{align*} P_i(x,y) = x_i+y_i + \sum_{\substack{\alpha_1,\ldots ,\alpha_n,\beta_1,\ldots ,\beta_n \in {\mathbb{N}}\\\sum_i \alpha_i \neq 0, \sum_i \beta_i \neq 0 }} c_{(\alpha_1,\ldots ,\alpha_n,\beta_1,\ldots ,\beta_n)} x_1^{\alpha_1}\cdots x_{i-1}^{\alpha_{i-1}} y_1^{\beta_1}\cdots y_{i-1}^{\beta_{i-1}}. \end{align*} $$
$$ \begin{align*} P_i(x,y) = x_i+y_i + \sum_{\substack{\alpha_1,\ldots ,\alpha_n,\beta_1,\ldots ,\beta_n \in {\mathbb{N}}\\\sum_i \alpha_i \neq 0, \sum_i \beta_i \neq 0 }} c_{(\alpha_1,\ldots ,\alpha_n,\beta_1,\ldots ,\beta_n)} x_1^{\alpha_1}\cdots x_{i-1}^{\alpha_{i-1}} y_1^{\beta_1}\cdots y_{i-1}^{\beta_{i-1}}. \end{align*} $$
This means that in the polynomial, all summands except the two in front have entries from x and y.
Notice that in the non-crooked case, there can be no product of the
![]() $t_i$
, which means that we have either one of the
$t_i$
, which means that we have either one of the
![]() $\beta _j$
is one and all the overs are zero or all
$\beta _j$
is one and all the overs are zero or all
![]() $\beta _j$
are zero.
$\beta _j$
are zero.
To finish this appendix, we give one example of such a group. Consider the Heisenberg group
![]() ${\mathbb {H}}$
of upper triangular matrices with ones on the diagonal. The entries of the second diagonal have weight 1 and the third diagonal has weight 2. For two elements
${\mathbb {H}}$
of upper triangular matrices with ones on the diagonal. The entries of the second diagonal have weight 1 and the third diagonal has weight 2. For two elements
 $$ \begin{align*} \begin{pmatrix} 1 & a & c \\ 0 & 1 & b \\ 0 & 0 & 1 \end{pmatrix}\hspace{-1.5pt},\quad \begin{pmatrix} 1 & x & z \\ 0 & 1 & y \\ 0 & 0 & 1 \end{pmatrix}\hspace{-1.5pt}, \end{align*} $$
$$ \begin{align*} \begin{pmatrix} 1 & a & c \\ 0 & 1 & b \\ 0 & 0 & 1 \end{pmatrix}\hspace{-1.5pt},\quad \begin{pmatrix} 1 & x & z \\ 0 & 1 & y \\ 0 & 0 & 1 \end{pmatrix}\hspace{-1.5pt}, \end{align*} $$
the polynomials then are given by
 $$ \begin{align*} &P_1((a,b,c),(x,y,z))= a+x,\\ &P_2((a,b,c),(x,y,z))= b+y,\\ &P_3((a,b,c),(x,y,z))= c+z + ay. \end{align*} $$
$$ \begin{align*} &P_1((a,b,c),(x,y,z))= a+x,\\ &P_2((a,b,c),(x,y,z))= b+y,\\ &P_3((a,b,c),(x,y,z))= c+z + ay. \end{align*} $$
Additionally, we see that
![]() ${\mathbb {H}}$
is
${\mathbb {H}}$
is
![]() $2$
-step nilpotent and therefore non-crooked.
$2$
-step nilpotent and therefore non-crooked.