1. Introduction
The 2014 Farm Bill implemented the largest changes to commodity programs in recent decades by ending long-standing price supports and decoupled payments and, instead, focusing on mitigating risk faced by farmers (Campiche, Reference Campiche2014). This farm bill maintained the Loan Deficiency Payments (LDP) programFootnote 1 from previous farm bills and introduced the Price Loss Coverage (PLC) and Agriculture Risk Coverage (ARC) programs. With the passing of the Federal Crop Insurance Act of 1980, crop insurance gained momentum, though it was not the cornerstone of farm policies. However, in 2014, the existing farm-level individual revenue protection (RP) and yield protection (YP) crop insurance programs were expanded, and the county-level Supplemental Coverage Option (SCO)Footnote 2 crop insurance program was introduced.
LDP and PLC are price protection programs under which farmers receive payments when the market price falls below specified levels. ARC is a revenue support program, and farmers can select either the County (ARC-CO) or Individual Coverage (ARC-IC) revenue option.Footnote 3, Footnote 4 For a given crop, farmers can select either PLC or ARC, but not both. Common crop insurance options purchased by wheat farmers are RP and YP. However, nationally, RP is the most commonly selected individual crop insurance program with 76% of farmers electing RP in 2014 (U.S. Department of Agriculture, Risk Management Agency [USDA-RMA], 2015). Under RP, farmers receive indemnity payments if actual market revenues fall below the revenue guarantee. RP is a “deep loss” program because it can cover severe losses. By shifting some of the risk back to farmers, the deductible mitigates moral hazard. Farmers who enroll in individual crop insurance also have the option of selecting SCO.Footnote 5 The SCO policy is considered a “shallow loss” program because it is designed to potentially pay a portion of the farmers’ deductibles not covered by individual crop insurance, but payments are based on county-level outcomes and capped by the maximum payment rate, which is the difference between 86% and the coverage level. SCO takes the same form as individual insurance—that is, if the farmer selects RP, then SCO also protects again revenue losses, and if the farmer selects YP, then SCO protects against yield loss. Under both programs, private insurance companies charge farmers actuarially fair premiums (expected indemnity), which are then subsidized by the government. These policies are designed to influence farmers’ risk mitigating strategies over the life of the farm bill. Given the complex nature of the 2014 Farm Bill with many policy options, we examine the effects of both commodity programs and crop insurance policies on wheat producers’ optimal RP coverage levels.
Wheat is one of the leading crops grown in the United States. With the national area harvested and yield remaining stable at an average of 49.1 million acres and 43 bu./acre for the period 2000–2014, the real value of wheat production has also remained stable at an average of $13.5 billion (U.S. Department of Agriculture, National Agricultural Statistics Service [USDA-NASS], 2015b). With 25% of the total base acres and payments totaling $35.5 billion over the period 1995–2012, wheat is the second most subsidized commodity after corn (Environmental Working Group, 2012; Schnitkey and Zulauf, Reference Schnitkey and Zulauf2015). Kansas is the largest winter wheat producing state with about 8.8 million acres harvested and a total production of about 317 million bushels or 25% of the national production (USDA-NASS, 2015a). To study the impacts of the 2014 Farm Bill policies, we consider a representative dryland winter wheat farm from Mitchell County, Kansas. We focus the analysis on Mitchell Country because it is located in north-central Kansas, the heart of wheat production. Also, with an average of 152,788 harvested acres of winter wheat over the years 2013–2016 (USDA-NASS, 2017), it is one of the largest wheat producing counties in Kansas.
Since the implementation of the 2014 Farm Bill, studies have focused on the impact of the new policies on farmers’ attitude toward risk.Footnote 6 Hungerford, O’Donoghue, and Motamed (Reference Hungerford, O’Donoghue and Motamed2015) used price and yield simulation analyses and found that PLC, ARC, and SCO programs are effective in mitigating risk. Adhikari (Reference Adhikari2015) examined coverage levels of the 2014 Farm Bill crop insurance programs and showed that the optimal coverage level varies across counties and individual crop insurance, with SCO providing better protection. Just, Calvin, and Quiggin (Reference Just, Calvin and Quiggin1999) showed that, because of adverse selection in crop insurance, farmers enroll in crop insurance primarily to secure subsidies. Bocquého, Jacquet, and Reynaud (Reference Bocquého, Jacquet and Reynaud2013), using experimental data of French farmers, concluded prospect theory, not expected utility theory, more accurately models farmers’ choices and these farmers are more sensitive to losses than they are to gains. In contrast, expected utility theory posits that farmers should buy the highest level of coverage to receive the maximum subsidies. However, Du, Feng, and Hennessy (Reference Du, Feng and Hennessy2016) found no empirical support for this conclusion. Babcock (Reference Babcock2015), focusing on only RP, concluded that when farmers buy crop insurance as a stand-alone investment tool, then cumulative prospect theory predicts that the optimal choice of coverage level is lower than that by expected utility theory, which is consistent with the observed behavior of the farmer.
The specific objectives of this study are to (a) develop a theoretical model detailing the mathematical formulation of important commodity programs (PLC and ARC-CO) and crop insurance (RP and SCO) policies for a risk-averse wheat farmer; (b) model and nonparametrically estimate the bivariate wheat yield and price distribution; (c) calibrate the model to a representative Kansas wheat farm; and (d) simulate the effects of these policies on optimal RP coverage levels, commodity program payments, and crop insurance payments. Past studies have found that cumulative prospect theory predicted the optimal coverage level more accurately. Our study contributes to the literature by providing a detailed analysis of the impacts of the PLC and ARC-CO commodity programs and SCO crop insurance on farmers’ optimal RP coverage levels under cumulative prospect theory. Specifically, our findings show that inclusion of ARC-CO or PLC helps the farmer to select a higher coverage level. However, this effect is dampened if the loss aversion of the farmer decreases.
2. Model
We develop a model of a representative risk-averse dryland wheat farmer faced with uncertainty over both price and yield. The farmer’s per acre market revenue ![]() ${(\tilde R)}$ and expected revenue (ER) are, respectively,
${(\tilde R)}$ and expected revenue (ER) are, respectively,
 $$ER = \int\int {\tilde R}{( {\tilde \omega ,{{\tilde \varepsilon}_f}} )}\;d{G_{{\varepsilon _c}}}{( {\omega ,{\varepsilon _f}} )},$$(1b)
$$ER = \int\int {\tilde R}{( {\tilde \omega ,{{\tilde \varepsilon}_f}} )}\;d{G_{{\varepsilon _c}}}{( {\omega ,{\varepsilon _f}} )},$$(1b)
where ![]() $\tilde p = p + \tilde \omega $ is the random market price with average price p and random component
$\tilde p = p + \tilde \omega $ is the random market price with average price p and random component ![]() $\tilde \omega $;
$\tilde \omega $; ![]() $\tilde y = y + {\tilde \varepsilon _f}$ is the farm-level stochastic yield per acre with average yield y and
$\tilde y = y + {\tilde \varepsilon _f}$ is the farm-level stochastic yield per acre with average yield y and ![]() ${\tilde \varepsilon _f}$; G(ω, εc, εf) is the joint cumulative distribution function representing market price, county yield, and farm yield randomness; and thus
${\tilde \varepsilon _f}$; G(ω, εc, εf) is the joint cumulative distribution function representing market price, county yield, and farm yield randomness; and thus ![]() ${G_{{\varepsilon _c}}}{( {\omega ,{\varepsilon _f}} )}$ represents the marginal distribution of market price and farm yield.
${G_{{\varepsilon _c}}}{( {\omega ,{\varepsilon _f}} )}$ represents the marginal distribution of market price and farm yield.
2.1. Commodity programs
Under the 2014 Farm Bill, farmers make a one-time election of PLC or ARC for the life of the farm bill.Footnote 7 Farmers’ choice depends on their expectation of which program pays the largest government subsidies over the entire farm bill period. Nationally, 271,445 wheat farmers selected PLC for 27.0 million base acres (42%), and 527,343 signed up for ARC for 35.4 million base acres (58%) (U.S. Department of Agriculture, Farm Service Agency [USDA-FSA], 2015). Therefore, it is important to model both PLC and ARC separately.Footnote 8
The PLC program protects farmers against price shocks. PLC payments are based on a per payment acre (aP), which is equal to 85% of the base acre (aB): aP = 0.85aB. Per payment acre government subsidies ![]() $(\widetilde{PPLC})$ equal
$(\widetilde{PPLC})$ equal
where pR is the reference price established by the farm bill, and yP is the payment yield.Footnote 9 Thus, farmers receive payments when the effective price (the maximum of the market price or the loan rate) falls below the reference price. Payments equal the difference between the reference price and the effective price times the payment yield times the payment acre. Because this policy does not depend on current farm-level yield, farmers cannot augment payments by altering input use.Footnote 10 Expected PLC payments are
 $$EPLC = \int {\widetilde{PPLC}}({\tilde \omega}) d{G_{{\varepsilon _c},{\varepsilon _f}}}(\omega).$$
$$EPLC = \int {\widetilde{PPLC}}({\tilde \omega}) d{G_{{\varepsilon _c},{\varepsilon _f}}}(\omega).$$
We focus on ARC-CO only because no wheat farmers enrolled in ARC-IC (USDA-FSA, 2015). ARC-CO (henceforth ARC) insulates farmers from county-level revenue losses. Government support per payment acre ![]() $({\widetilde{PARC}^{CO}})$ under this program equals
$({\widetilde{PARC}^{CO}})$ under this program equals
where pO is the 5-year olympic averageFootnote 11 of the national market price; yOC is the 5-year olympic average county yield; and ![]() ${\tilde y^C}$ is the stochastic county yield, which equals the average county yield yC plus the random variable
${\tilde y^C}$ is the stochastic county yield, which equals the average county yield yC plus the random variable ![]() ${\tilde \varepsilon _c}: {\tilde y^C} = {y^C} + {\tilde \varepsilon _c}$. Under this program, farmers receive payments when per acre county market revenues (the higher of the market price or loan rate times the county yield:
${\tilde \varepsilon _c}: {\tilde y^C} = {y^C} + {\tilde \varepsilon _c}$. Under this program, farmers receive payments when per acre county market revenues (the higher of the market price or loan rate times the county yield: ![]() $\max [{\tilde p},{p^{LR}} ]{\tilde y}^C$) fall below the ARC per acre revenue guarantee (86% of the benchmark county revenue calculated as the product of the 5-year olympic national average market price and yield: 0.86pOyOC). Policy payments per payment acre are equal to the lower of the difference between the revenue guarantee and county market revenues or 10% of benchmark revenues. Because the coverage rate is 86% and the maximum payment cannot exceed 10% of the benchmark revenue, ARC covers only losses between 76% and 86% of the benchmark revenue. The ARC policy does not rely on farmer’s yield, and therefore, input decisions do not influence ARC payments. Expected ARC payments are
$\max [{\tilde p},{p^{LR}} ]{\tilde y}^C$) fall below the ARC per acre revenue guarantee (86% of the benchmark county revenue calculated as the product of the 5-year olympic national average market price and yield: 0.86pOyOC). Policy payments per payment acre are equal to the lower of the difference between the revenue guarantee and county market revenues or 10% of benchmark revenues. Because the coverage rate is 86% and the maximum payment cannot exceed 10% of the benchmark revenue, ARC covers only losses between 76% and 86% of the benchmark revenue. The ARC policy does not rely on farmer’s yield, and therefore, input decisions do not influence ARC payments. Expected ARC payments are
 $$EARC^{CO} = \int\int {\widetilde{PARC}}^{CO}(\tilde{\omega},\tilde{\varepsilon}_c) d{G_{\varepsilon_f}}(\omega,\varepsilon_c).$$
$$EARC^{CO} = \int\int {\widetilde{PARC}}^{CO}(\tilde{\omega},\tilde{\varepsilon}_c) d{G_{\varepsilon_f}}(\omega,\varepsilon_c).$$
2.2. Crop insurance programs
Farmers can also reduce risk from revenue volatility by participating in individual RP crop insurance and SCO insurance.Footnote 12 We consider RP because 86% of wheat farmers in Kansas signed up for RP in 2014 (USDA-RMA, 2015). Table 1 reports the coverage levels selected by Mitchell County wheat farmers for the period 2014–2017. As this table shows, the most opted coverage levels are 70% and 75%. In contrast, the least opted coverage levels include 50%, 55%, 60%, and 85%.
Table 1. Actual farmer RP coverage level decisions for Mitchell County, Kansas
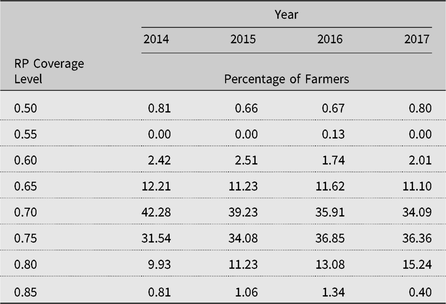
Note: RP, individual revenue protection insurance.
Source: USDA-RMA (2017).
Indemnity payments ![]() ${( {\widetilde {RPi}} )}$ per acre for individual RP insurance are
${( {\widetilde {RPi}} )}$ per acre for individual RP insurance are
where pF is the futures price, α is the coverage level chosen by the farmer, and yA is actual production history yield. Thus, farmers receive an indemnity payment if actual market revenues (![]() $\tilde{p} \tilde{y}$) fall below the revenue guarantee (which equals the higher of the market or futures price times the coverage level times the actual production history yield:
$\tilde{p} \tilde{y}$) fall below the revenue guarantee (which equals the higher of the market or futures price times the coverage level times the actual production history yield: ![]() $\max \left[ {\tilde p,{p^F}} \right]\alpha {y^A}$). The indemnity payment equals the difference between the revenue guarantee and market revenue. The actuarially fair premium rate (θRP) is defined as the expected indemnity payment:
$\max \left[ {\tilde p,{p^F}} \right]\alpha {y^A}$). The indemnity payment equals the difference between the revenue guarantee and market revenue. The actuarially fair premium rate (θRP) is defined as the expected indemnity payment:
 $$ {\theta^{RP}}{(\alpha)} = \int\int \widetilde {RPi}\;d{G_{{\varepsilon _c}}}{( {\omega ,{\varepsilon_f}} )}, $$(5)
$$ {\theta^{RP}}{(\alpha)} = \int\int \widetilde {RPi}\;d{G_{{\varepsilon _c}}}{( {\omega ,{\varepsilon_f}} )}, $$(5)
where ![]() ${G_{{\varepsilon _c}}}{( {\omega ,{\varepsilon _f}} )}$ represents the marginal distribution of market price and farm yield. The government subsidizes premiums for RP insurance policies. The premium subsidy σRP (α) received by the farmer depends on the selected coverage level α. The net benefit (PRP) from RP insurance is
${G_{{\varepsilon _c}}}{( {\omega ,{\varepsilon _f}} )}$ represents the marginal distribution of market price and farm yield. The government subsidizes premiums for RP insurance policies. The premium subsidy σRP (α) received by the farmer depends on the selected coverage level α. The net benefit (PRP) from RP insurance is
As noted in the introduction, farmers participating in RP have the option of selecting SCO coverage. Under individual RP coverage, the farmer chooses a coverage level ranging from 50%, by increments of 5%, to a top coverage level of 85%, implying the farmer’s deductible ranges from 50% to 15%. SCO was designed, based on county-level outcomes, to potentially insure against the farm-level RP deductible up to a maximum 86%, leaving producers responsible for 14% of the deductible. For example, if the farmer selects an individual RP coverage level at α = 0.65, SCO can cover between 65% and 86% of the farmer’s RP deductible. Because we consider only RP for the individual insurance policy, SCO coverage also protects against downside revenue risk. The SCO per acre indemnity payment is
 $$\widetilde{SCOi}(\alpha;\tilde{\omega},\tilde{\varepsilon}_c) = \min\left\{\max\left[\delta-{\tilde{p}\,\,\tilde{y}^C \over \max(\tilde{p},{p^F})y^C},0\right],(\delta-\alpha)\right\}{y^A}\max (\tilde{p},{p^F}).$$(7)
$$\widetilde{SCOi}(\alpha;\tilde{\omega},\tilde{\varepsilon}_c) = \min\left\{\max\left[\delta-{\tilde{p}\,\,\tilde{y}^C \over \max(\tilde{p},{p^F})y^C},0\right],(\delta-\alpha)\right\}{y^A}\max (\tilde{p},{p^F}).$$(7)
Under the SCO program, the farmer receives a payment if actual county revenue ![]() $\tilde{p}\tilde{y}^C$ is less than δ = 0.86 of average county revenues given by
$\tilde{p}\tilde{y}^C$ is less than δ = 0.86 of average county revenues given by ![]() $\max \left[ {\tilde p,{p^F}} \right]{y^C}$. The SCO indemnity per acre is the product of the payment rate and the liability. The payment rate, given by the min{·,·} function, is the lower of the revenue payment factor (the first term in the min function, i.e., the higher of the maximum deductible in excess of the percentage of county-revenue shortfallFootnote 13 or zero) or the maximum payment rate (δ − α). The liability is the actual production history yield times the payment price:
$\max \left[ {\tilde p,{p^F}} \right]{y^C}$. The SCO indemnity per acre is the product of the payment rate and the liability. The payment rate, given by the min{·,·} function, is the lower of the revenue payment factor (the first term in the min function, i.e., the higher of the maximum deductible in excess of the percentage of county-revenue shortfallFootnote 13 or zero) or the maximum payment rate (δ − α). The liability is the actual production history yield times the payment price: ![]() ${y^A}\max \left[ {\tilde p,{p^F}} \right]$. The actuarially fair premium rate (θSCO) is defined as the expected indemnity:
${y^A}\max \left[ {\tilde p,{p^F}} \right]$. The actuarially fair premium rate (θSCO) is defined as the expected indemnity:
 $$\theta^{SCO}(\alpha) = \int\int [\widetilde{SCOi}(\tilde{\omega},\tilde{\varepsilon}_c)] d{G_{\varepsilon_f}}(\tilde{\omega},\tilde{\varepsilon}_c).$$(8)
$$\theta^{SCO}(\alpha) = \int\int [\widetilde{SCOi}(\tilde{\omega},\tilde{\varepsilon}_c)] d{G_{\varepsilon_f}}(\tilde{\omega},\tilde{\varepsilon}_c).$$(8)
The government subsidizes the SCO premium at σSCO = 0.65. Thus, the net benefit of SCO payment per acre (PSCO) is
Because individual RP covers farm-level revenue losses up to the selected coverage level α and SCO covers county-level losses between α and the maximum coverage level of 0.86, the former is known as “deep loss” coverage, and the latter is known as “shallow loss” coverage.
Based on the previous discussion, the four policy combinations we examine are RP, RP & ARC, RP & PLC, and RP & PLC & SCO. This allows us to investigate the effects of the addition of the commodity programs ARC and PLC and the county-level insurance program SCO to RP on the RP coverage level.
2.3. Cumulative prospect theory
Bocquého, Jacquet, and Reynaud (Reference Bocquého, Jacquet and Reynaud2013) show that farmers are more sensitive to losses than to gains and focus more on unlikely extreme events. Consequently, as observed by Babcock (Reference Babcock2015), expected utility theory does not accurately predict farmers’ actual coverage-level decisions of revenue protection policy. In the cumulative prospect theory developed in Tversky and Kahneman (Reference Tversky and Kahneman1992), avoiding a loss can generate more value than a corresponding gain, which accurately reflects farmers’ behavior and explains why farmers choose to insure more against downside risk. Because crop insurance decision are made before the farmer realizes actual yield and price, the farmer values all possible risky prospects as the weighted average of n discrete gains and m discrete losses:
 $$V = \sum\limits_{i = - m}^n {v{( {{x_i}} )}\pi {( {{p_i}} )},} $$(9)
$$V = \sum\limits_{i = - m}^n {v{( {{x_i}} )}\pi {( {{p_i}} )},} $$(9)
where v(xi) is the value function of monetary gain or loss xi that is arranged in ascending order, π(pi) is the decision weight function, and pi is the probability of event xi occurring.
The value function is represented by the two-part power function:
 $$v{( {{x_i}} )} = \left\{ {\matrix {{{x_i^\phi }}\qquad\qquad {{\rm{if }}{\ x_i} \ge 0} \cr { - \eta {{{( { - {x_i}} )}}^\phi }}\quad {{\rm{if }}{\ x_i} < 0,} \cr } } \right.{\rm{ }}$$(10)
$$v{( {{x_i}} )} = \left\{ {\matrix {{{x_i^\phi }}\qquad\qquad {{\rm{if }}{\ x_i} \ge 0} \cr { - \eta {{{( { - {x_i}} )}}^\phi }}\quad {{\rm{if }}{\ x_i} < 0,} \cr } } \right.{\rm{ }}$$(10)
where ϕ is a shape parameter that specifies the curvature of the value function for gains and losses and η specifies the degree of loss aversion. The curvature of v(xi) is concave in gains, implying risk aversion, and convex in losses, indicating risk seeking. Furthermore, loss aversion plays a key role in the value function, and with η > 1, v(xi) is steeper in losses than in gains. Therefore, incurring a loss generates a greater negative value than a gain of equal magnitude; thus, farmers prefer to avoid a loss than to receive an equal gain.
Whether xi is a monetary gain or loss depends on the reference point, Γ, which is important in cumulative prospect theory. Based on Kőszegi and Rabin (Reference Kőszegi and Rabin2007) and Babcock (Reference Babcock2015), we utilize expected outcomes to define reference points. For all four policy combinations, we define three cases for the reference points on a per acre basis: (a) expected market revenue plus the subsidized premium/expected payment, (b) expected market revenue, and (c) subsidized premium/expected payment. The reference points and gain/loss function for each reference point case and policy combination are summarized in Table 2. The monetary gains/losses xi for cases 1 and 2 are realized farm revenue plus indemnity and/or commodity program payments minus the corresponding reference point. For these two cases, crop insurance minimizes the impacts of unforeseen adverse events on farm income. Thus, crop insurance in these two cases is a risk-management tool. For case 3, the values of xi are realized indemnity and/or commodity program payments minus the reference point. Under case 3, farmers consider crop insurance as an investment and make decisions based solely on the insurance gains or losses, without looking at its effects on income. In this case, crop insurance is treated as a lottery or simple investment. Note that in all four policy combinations in all three cases, the value of xi is the change in monetary returns from the reference points. Therefore, if realized returns equal the value of the reference point, then xi is zero.
Table 2. Reference points and gain/loss function
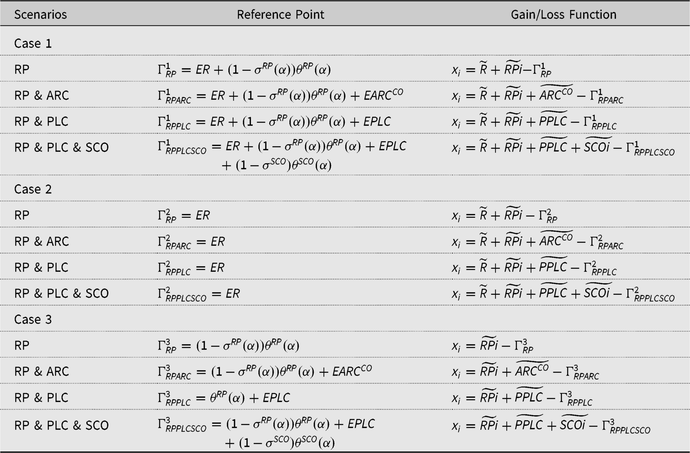
Notes: ARC, agriculture risk coverage; PLC, price loss coverage; RP, individual revenue protection insurance; SCO, supplemental coverage option.
Because of the risk-seeking behavior in losses, in addition to loss aversion η > 0, the probability (pi) of a monetary gain or loss is transformed into a decision weight. Tversky and Kahneman (Reference Tversky and Kahneman1992) formulate the decision weights to place less weight on high-probability events and more weight on low-probability events. Overweighting low-probability losses and the degree of loss aversion play a key role in incentivizing farmers to buy insurance against losses, despite the convexity (risk-seeking behavior in losses) of the value function.Footnote 14 The decision weights for gains (πg (pi)) and losses (πl (pi)) are computed as the difference between weighting functions for ranked outcomes:
 $$\eqalign{{\pi ^g}{( {{p_i}} )}={w^g}{( {{p_i} + \ldots + {p_n}} )} - {w^g}{( {{p_{i + 1}} + \ldots + {p_n}} )}\; {\rm{for}}\; 0 \le i \le n - 1 \cr{\pi^g}{( {{p_n}} )} = {w^g}{( {{p_n}} )} \cr {\pi ^l}{( {{p_i}} )} = {w^l}{( {{p_m} + \ldots + {p_i}} )} - {w^l}{( {{p_m} + \ldots + {p_{i - 1}}} )} \;{\rm{for}} \;1 - m \le i \le 0 \cr {\pi ^l}{( {{p_m}} )}= {w^l}{( {{p_m}} ).}}$$
$$\eqalign{{\pi ^g}{( {{p_i}} )}={w^g}{( {{p_i} + \ldots + {p_n}} )} - {w^g}{( {{p_{i + 1}} + \ldots + {p_n}} )}\; {\rm{for}}\; 0 \le i \le n - 1 \cr{\pi^g}{( {{p_n}} )} = {w^g}{( {{p_n}} )} \cr {\pi ^l}{( {{p_i}} )} = {w^l}{( {{p_m} + \ldots + {p_i}} )} - {w^l}{( {{p_m} + \ldots + {p_{i - 1}}} )} \;{\rm{for}} \;1 - m \le i \le 0 \cr {\pi ^l}{( {{p_m}} )}= {w^l}{( {{p_m}} ).}}$$
Thus, the decision weights π(pi) in equation (9) consist of π(pi) = πg (pi) for i ≥ 0 and π(pi) = πl (pi) for i < 0. π(pi) is interpreted as the marginal contribution of a monetary gain or loss. Here, the probability weighting functions for gains (wg (p)) and losses (wl (p)) are strictly increasing functions:
 $${w^g}{( p )} = {{{p^\lambda }} \over {{{{[ {{\,p^\lambda } + {{{( {1 - p} )}}^\lambda }} ]}}^{{1 \over \lambda }}}}},$$(11)
$${w^g}{( p )} = {{{p^\lambda }} \over {{{{[ {{\,p^\lambda } + {{{( {1 - p} )}}^\lambda }} ]}}^{{1 \over \lambda }}}}},$$(11)
 $$w^l(p) ={p^\rho \over [p^\rho + (1-p)^\rho]^{1 \over \rho}},$$(12)
$$w^l(p) ={p^\rho \over [p^\rho + (1-p)^\rho]^{1 \over \rho}},$$(12)
where p is a cumulative probability and λ and ρ are parameters.
Although the value function is ordinal, as in utility theory, V is not expected utility because the decision weights do not sum to 1. Consequently, V is translated into certainty equivalent
 $$CE = \left\{ {\matrix{ {{V^{{1 \over \phi }}}} \hfill \qquad\quad {{\rm{if}} V \ge 0} \hfill \cr { - {{{\Big( {{V \over { - \eta }}} \Big)}}^{{1 \over \phi }}}} \hfill \quad {{\rm{if}} V < 0} \hfill. \cr } } \right.$$(13)
$$CE = \left\{ {\matrix{ {{V^{{1 \over \phi }}}} \hfill \qquad\quad {{\rm{if}} V \ge 0} \hfill \cr { - {{{\Big( {{V \over { - \eta }}} \Big)}}^{{1 \over \phi }}}} \hfill \quad {{\rm{if}} V < 0} \hfill. \cr } } \right.$$(13)
3. Price and county yield distributions and idiosyncratic farm-level risk
This section estimates the bivariate price and yield distribution for Mitchell County using nonparametric methods and infers farm-level idiosyncratic risk. The state-level price ($/bu.) received by Kansas winter wheat farmers and yield (bu./acre) for Mitchell County were obtained from USDA-NASS (2015b) for the years 1949–2015. To detrend the nominal price data, the real price was calculated by dividing the nominal price data by the prices received index for food grains, which was obtained from USDA, Economic Research Service (2015). To detrend the county yield data, first, we run a spline regressionFootnote 15 of yield on a time trend to account for changes in the rate of technological advancements over time. Second, we compute the residuals by taking the difference between actual and predicted yields. Third, we obtain the detrended yield by adding the residuals to the 2015 yield level. Table 3 reports the summary statistics of the Kansas wheat price and Mitchell County yield. The mean and variance of the state-level real price in Kansas are 5.44 and 0.30. The distribution of price is left-skewed with a coefficient of −0.77 (also see Figure 1). The average yield in Mitchell county is 48.80 bu./acre with a variance of 59.74. The skewness coefficient of −0.20 indicates that, in contrast to price, the yield is skewed to the left (see Figure 1), reflecting the inverse relationship between price and yield. This relationship also captures the negative correlation coefficient between price and yield of −0.31.Footnote 16
Table 3. Summary statistics for detrended price and yield
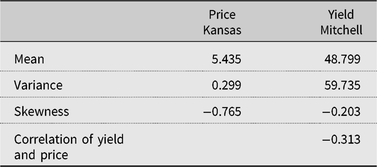

Figure 1. Marginal probability density function plots of real price and detrended county-level yield.
We normalize the detrended price by subtracting each observation by the average, which generates a normalized price with a mean of zero and is used to estimate the distribution for ![]() $\tilde \omega $. Similarly, we apply this normalization to the county-level yield data, which is used to generate the distribution for
$\tilde \omega $. Similarly, we apply this normalization to the county-level yield data, which is used to generate the distribution for ![]() ${\tilde \varepsilon _c}$. Precise estimates of the distribution of normalized price and county-level yield are key to accurately estimating certainty equivalents, actuarially fair premium rates for RP and SCO, and expected payments for ARC and PLC. To obtain accurate estimates of the normalized price and county-level yield distributions free of any parametric assumptions, we estimate the bivariate kernel density, which incorporates the correlation between price and yield. Consider normalized real price and detrended county yield data (ω, εc) of length n. The nonparametric estimation of the joint distribution g at points P and Yc is
${\tilde \varepsilon _c}$. Precise estimates of the distribution of normalized price and county-level yield are key to accurately estimating certainty equivalents, actuarially fair premium rates for RP and SCO, and expected payments for ARC and PLC. To obtain accurate estimates of the normalized price and county-level yield distributions free of any parametric assumptions, we estimate the bivariate kernel density, which incorporates the correlation between price and yield. Consider normalized real price and detrended county yield data (ω, εc) of length n. The nonparametric estimation of the joint distribution g at points P and Yc is
 $$\hat g{( {P,{Y_c}} )} = {1 \over n}\sum\limits_{i = 1}^n {{1 \over {{h_p}{h_{{y_c}}}}}} K{\bigg( {{{P - {\omega _i}} \over {{h_p}}}} \bigg)}K{\bigg( {{{{Y_c} - {\varepsilon _{c,i}}} \over {{h_c}}}} \bigg)},$$(14)
$$\hat g{( {P,{Y_c}} )} = {1 \over n}\sum\limits_{i = 1}^n {{1 \over {{h_p}{h_{{y_c}}}}}} K{\bigg( {{{P - {\omega _i}} \over {{h_p}}}} \bigg)}K{\bigg( {{{{Y_c} - {\varepsilon _{c,i}}} \over {{h_c}}}} \bigg)},$$(14)
where hp and ![]() ${h_{{y_c}}}$ are bandwidths calculated using adaptive bandwidths and K(·) is the Gaussian kernel. Figure 1 plots the marginal probability density functions (PDFs) of the normalized real price and county-level yield. The marginal price distribution displays a long upper tail as indicated by the positive skewness. The marginal PDF plot for yield illustrates the skewness toward the left.
${h_{{y_c}}}$ are bandwidths calculated using adaptive bandwidths and K(·) is the Gaussian kernel. Figure 1 plots the marginal probability density functions (PDFs) of the normalized real price and county-level yield. The marginal price distribution displays a long upper tail as indicated by the positive skewness. The marginal PDF plot for yield illustrates the skewness toward the left.
Because yields from all farmers in Mitchell County are averaged to obtain the county-level yield data, an individual farm is riskier than the county. We infer this risk using the RMA rating system for a representative farmer in Mitchell County. Following Miranda (Reference Miranda1991), the farm-level yield entering equation (1a) can be represented as
where ![]() ${\tilde y_f}$ is farm-level random yield, μf is expected farm yield,
${\tilde y_f}$ is farm-level random yield, μf is expected farm yield, ![]() ${\tilde y_c}$ is county-level random yield, μc is expected county yield, ψf measures the effect of county yield deviation from its mean
${\tilde y_c}$ is county-level random yield, μc is expected county yield, ψf measures the effect of county yield deviation from its mean ![]() ${( {{{\tilde y}_c} - {\mu _c} = {\varepsilon _c}} )}$ on farm yield, and
${( {{{\tilde y}_c} - {\mu _c} = {\varepsilon _c}} )}$ on farm yield, and ![]() ${\tilde \epsilon_f}$ measures idiosyncratic farm-level risk. Because county yield is an average of all farm yield within a county, ψ = 1 is the acreage weighted average of all ψf s for farmers within that county. Thus, equation (15) indicates that farm-level yield incorporates county-level and individual farm-level variabilities. Following Coble and Dismukes (Reference Coble and Dismukes2008), we assume that
${\tilde \epsilon_f}$ measures idiosyncratic farm-level risk. Because county yield is an average of all farm yield within a county, ψ = 1 is the acreage weighted average of all ψf s for farmers within that county. Thus, equation (15) indicates that farm-level yield incorporates county-level and individual farm-level variabilities. Following Coble and Dismukes (Reference Coble and Dismukes2008), we assume that ![]() ${\tilde \epsilon_f}$ follows the normal distribution with mean zero and standard deviation s.
${\tilde \epsilon_f}$ follows the normal distribution with mean zero and standard deviation s.
RMA determines a farmer’s premium rate based on their yield relative to the county average. Assuming that the average yield of a farmer (μf) is equal to their Actual Production History (APH) yield ![]() ${( {y_f^A} )}$ and average county yield (μc) is equal to the county reference yield
${( {y_f^A} )}$ and average county yield (μc) is equal to the county reference yield ![]() ${( {y_c^R} )}$,Footnote 17 the RMA base premium rate (BRf) for a farmer with a 65% coverage rate is (Coble et al., Reference Coble, Knight, Goodwin, Miller and Rejesus2010)
${( {y_c^R} )}$,Footnote 17 the RMA base premium rate (BRf) for a farmer with a 65% coverage rate is (Coble et al., Reference Coble, Knight, Goodwin, Miller and Rejesus2010)
 $$B{R_f}{( {y_f^A} )}\; = \;R{{\bigg( {{{y_f^A} \over {y_c^R}}} \bigg)}^\eta } + F{\rm{,}}$$(16)
$$B{R_f}{( {y_f^A} )}\; = \;R{{\bigg( {{{y_f^A} \over {y_c^R}}} \bigg)}^\eta } + F{\rm{,}}$$(16)
where R is the reference rate, η is an exponent, and F is the fixed rate. If the APH yield is equal to the county reference yield, then the base rate is simply the reference rate plus the fixed rate. RMA uses expected loss cost (ELC) data, which are equal to the expected indemnity divided by liability, and ![]() $y_f^A = y_c^R$ to derive the parameters (R and F) in calculating the base rate for an average farmer (Coble et al., Reference Coble, Knight, Goodwin, Miller and Rejesus2010). For a given farmer’s APH yield and corresponding base rate, we find the expected loss cost that matches the base rate by searching over farm-level standard deviations:
$y_f^A = y_c^R$ to derive the parameters (R and F) in calculating the base rate for an average farmer (Coble et al., Reference Coble, Knight, Goodwin, Miller and Rejesus2010). For a given farmer’s APH yield and corresponding base rate, we find the expected loss cost that matches the base rate by searching over farm-level standard deviations:
where the expected loss cost is defined as
 $$ELC{( {{s_f}} )} = {{\int\int {{p_g}} {( {\alpha {\mu _f} - {{\tilde y}_f}{( {{s_f}} )}} )}dH{( {{y_c}} )}dN{( {0,{s^2}} )}} \over {{p_g}\alpha {\mu _f}}},$$(18)
$$ELC{( {{s_f}} )} = {{\int\int {{p_g}} {( {\alpha {\mu _f} - {{\tilde y}_f}{( {{s_f}} )}} )}dH{( {{y_c}} )}dN{( {0,{s^2}} )}} \over {{p_g}\alpha {\mu _f}}},$$(18)
and pg is the price guarantee and H(yc) is the distribution of the detrended county yield.Footnote 18 Thus, ELC is the ratio of the expected indemnity over the liability for the coverage level α = 0.65. According to USDA-RMA (2016), for Mitchell County, Kansas, for 2017, ![]() $y_c^R = 45$, η = −1.044, R = 0.051, and F = 0.021. Given these RMA data, solving equation (17) yields sf = 21.73.
$y_c^R = 45$, η = −1.044, R = 0.051, and F = 0.021. Given these RMA data, solving equation (17) yields sf = 21.73.
4. Parameter specification of the model
We discuss the parameter specification of the model. For the value function (10), the shape parameter ϕ is 0.88, which comes from Tversky and Kahneman (Reference Tversky and Kahneman1992), and the degree of loss aversion is calibrated to η = 2.1 such that the farmer selects α = 0.70 under reference point RPRP for case 3, which is consistent with the actual RMA coverage level data reported in Table 1.Footnote 19 For the probability weighting function, we set λ = 0.61 and ρ = 0.69 (Babcock, Reference Babcock2015; Tversky and Kahneman, Reference Tversky and Kahneman1992).
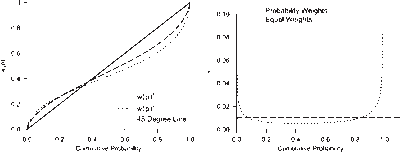
We use the abovementioned parameter specifications to plot the decision weighting function for gains and losses against a grid of cumulative probability values ranging from 0 to 1 (see the left panel of Figure 2). As expected, probabilities below about 0.38 are underweighted, generating lower values for wg and wl, and probabilities higher than 0.38 are overweighted, generating higher values for wg and wl. The right panel of Figure 2 graphs the decision weights against the cumulative probabilities. These decision weights are calculated as the slopes of the weighting function and highlights the overweighting tail probability events (p < 0.08 and p > 0.84) and underweighting events in between these probability ranges.

Figure 2. Cumulative probability and decision weights.
Next, we discuss parameters of the various government policies. The wheat reference price (pR = $5.50/bu.) and future price (pF = $5.37/bu.) are collected from Welch and Knapek (Reference Welch and Knapek2014). The wheat loan rate (pLR = $2.46/bu.) is obtained from USDA-FSA (2014b). We assume the representative farms harvested acreage a is 700 and the base acreage aB is 500. For Mitchell county, actual production history yieldFootnote 20 yA is 43.975, average yield over the period 2008–2012 y is 48.200, the detrended sample average yield yC is 43.409, and the olympic average yield yOC is 47.333. The olympic average price pO = $6.70/bu. comes from USDA-FSA (2015). The Federal Crop Insurance Act specifies premium subsidies for various RP coverage levels and the fixed premium subsidy of 0.65 for SCO (see Table 4).
Table 4. 2014 Farm Bill crop insurance premium subsidy levels

Notes: RP, individual revenue protection insurance; SCO, supplemental coverage option.
5. Simulation and results
For the simulation analysis, 5,000 random price and county-yield Monte Carlo draws were obtained from the nonparametric distribution ĝ(P, Yc). To generate random draws for idiosyncratic farm-yield variability ϵf, we obtain 5,000 random draws from normal distribution with mean zero and standard deviation s = 21.73 and add this noise to ϵc. Using these price and county and farm yield draws, we run four policy scenarios (RP, RP & ARC, RP & PLC, and RP & PLC & SCO) to analyze the farmers’ optimal RP coverage-level choice and how ARC, PLC, and PLC & SCO affect the optimal RP coverage level decision. We also compute the RP and SCO premiums and expected payments for RP, ARC, PLC, and SCO. Comparison of expected payments for the four policy scenarios allows us to determine which set of policies generates the highest payments for the farmer. For each RP coverage level and each of the three reference cases, we evaluate the gain or loss xi, then calculate the certainty equivalent based on equation (13).Footnote 21 For the three reference point cases, Tables 5–7, respectively, report the certainty equivalent for each RP coverage level for each of the four policy scenarios. Similarly, for the three reference point cases, Tables 8–10, respectively, present the premiums and expected payments for the optimal RP coverage rate for the four policy combinations.
Table 5. Certainty equivalents for case 1

Notes: ARC, agriculture risk coverage; PLC, price loss coverage; RP, individual revenue protection insurance; SCO, supplemental coverage.
Table 6. Certainty equivalents for case 2
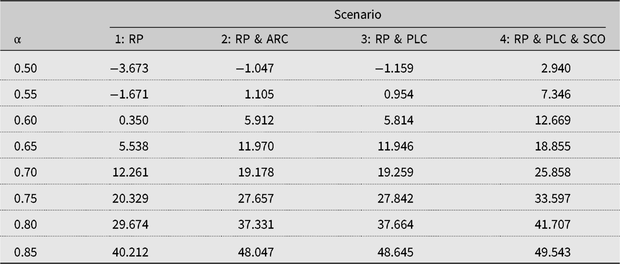
Notes: ARC, agriculture risk coverage; PLC, price loss coverage; RP, individual revenue protection insurance; SCO, supplemental coverage.
Table 7. Certainty equivalents for case 3
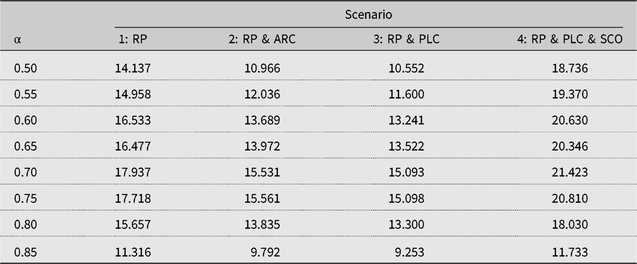
Notes: ARC, agriculture risk coverage; PLC, price loss coverage; RP, individual revenue protection insurance; SCO, supplemental coverage.
Table 8. Premiums and expected payments for case 1

Notes: ARC, agriculture risk coverage; PLC, price loss coverage; RP, individual revenue protection insurance; SCO, supplemental coverage.
Table 9. Premiums and expected payments for case 2

Notes: ARC, agriculture risk coverage; PLC, price loss coverage; RP, individual revenue protection insurance; SCO, supplemental coverage.
Table 10. Premiums and expected payments for case 3

Notes: ARC, agriculture risk coverage; PLC, price loss coverage; RP, individual revenue protection insurance; SCO, supplemental coverage.
5.1. Results
The RP reference points under cases 1 and 2 imply that the farmer buys RP crop insurance to manage risk, as farmers incur losses if market revenue plus indemnity payments fall below the reference point (see Table 2). For the RP scenario under reference points for cases 1 and 2 (the second column of Tables 5 and 6), comparison of the certainty equivalents across different coverage levels shows that the farmer would elect the 85% coverage level. These results, obtained using cumulative prospect theory, are similar to the optimal coverage levels estimated by other studies that used expected utility theory (Adhikari, Reference Adhikari2015; Devadoss and Luckstead, Reference Devadoss and Luckstead2018). However, according to USDA-RMA (2017), most farmers in Mitchell County, Kansas, opted for the 70%–75% coverage levels. Because the highest coverage levels under cases 1 and 2 are inconsistent with the observed farmers’ coverage decisions, these results suggest farmers do not purchase crop insurance to mitigate risk. For the risk management cases 1 and 2, higher coverage levels are optimal because they reduce the magnitude of losses, which is important to farmers when they are loss averse and view crop insurance as a risk management strategy. Furthermore, with the premium viewed as a sunk cost, the likelihood of a loss is also reduced in case 2. Thus, the farmer will likely prefer higher coverage levels more so under case 2 than under case 1.
For these two reference-point cases, adding ARC or PLC to RP policy does not affect the optimal RP coverage level, as it remains at 85%. When we include PLC & SCO to RP, the optimal coverage level drops to 80% for case 1 but remains at 85% for case 2. This result is in contrast to Devadoss and Luckstead (Reference Devadoss and Luckstead2018), who find that, under expected utility theory with endogenous input decisions, when a representative cotton farmer adds SCO to RP, the optimal RP coverage level drops to the lowest level of 50%. The reason for these differences in the results is that under cumulative prospect theory, in contrast to expected utility theory, the downside risk (losses) is overweighted through the probability weight function π(p) and the degree of loss aversion η, making the losses more pronounced relative to equivalent gains. As α declines, losses are more likely and η > 1 and π(p) magnify the value of losses v(x), leading to a decline in V and a smaller certainty equivalent. Consequently, low coverage levels are less preferable, and thus, farmers opt for the highest coverage level.
However, for RP reference points under case 3, the farmer views crop insurance, as a lottery or stand-alone investment and only cares about realized prices and yields as they determine the size of their indemnity payments without regard to market revenues. For this case, based on the calibration, the 70% coverage level yields the highest certainty equivalent. This coverage level is lower than those for cases 1 and 2 but reflects the observed coverage decisions by farmers. Thus, cumulative prospect theory predicts farmers’ actual coverage level choices better than the expected utility theory but only when insurance is framed as a lottery. For case 3, the probability of a loss is smaller at higher coverage levels; however, the average size of the loss is greater because farmers incur larger premiums. Consequently, increases in the coverage level do not benefit the farmer as much as avoiding a loss because of the trade-off between the probability of the losses and the size of the losses.
Interestingly, the certainty equivalent results show that adding ARC or PLC to RP results in the farmer selecting the next highest RP coverage level of 75%, while adding PLC & SCO causes the farmer to elect the 70% RP coverage level. With ARC and PLC, because the expected value of xi is equal to only the RP premium subsidy, the odds that total policy payments (indemnity plus ARC or PLC payments) cover the cost of the premium rise. As a result, higher coverage levels are more beneficial to farmers as the trade-off between the probability of a loss and the size of the loss is dampened. Conversely, with SCO, this trade-off is exacerbated because (a) the total (RP plus SCO) premium increases and (b) SCO is a county-level insurance policy with farm-level risk being imperfectly correlated with country-level risk, which offsets the ARC and PLC effects. Basis riskFootnote 22 increases the chance that a bad year for the farmer will not be covered if the county has an above average year, and SCO indemnity payments will not be triggered. This raises the odds that indemnities will not cover the total premium costs, and higher coverage levels with SCO are less beneficial than with RP alone.
For cases 1 and 2, with RP coverage rates ranging between 80% and 85%, the findings indicate that the RP premium rate is $32.673 and $38.058 per acre with an expected payment of $15.683 and $14.462 per acre. Similarly, the expected payments under ARC ($5.890) and PLC ($6.239) are the same for cases 1 and 2 because expected price and yield are constant. For SCO under case 1 with an 80% RP coverage level, the expected payments are $2.124 and premium rate is $3.267; but under case 2 with an 85% RP coverage level, the expected payments and premium rate fall to $0.439 and $0.675.
Because the RP coverage level in case 3 is lower than those for cases 1 and 2, the RP premium rate is smaller at $23.502 per acre under case 3 compared with $38.058 under cases 1 and 2. Because the coverage level, and thus the guaranteed payment, is smaller under case 3, the expected payment is slightly lower at $13.866 per acre. For case 3 under the policy combination RP & ARC, the RP coverage level, and thus the RP premium, are higher compared with those under the RP policy alone. Furthermore, the total expected payments under RP & ARC at the 75% coverage level are $21.194 ($15.304 + $5.890), which is higher than that for the RP policy alone, as farmers receive more net benefits by participating in ARC. For the policy combination RP & PLC, the coverage level, RP premium, and RP expected payments are the same as those under the policy combination RP & ARC; however, the expected PLC payments of $6.239 are more than the expected ARC payments of $5.89. For the policy combination RP & PLC & SCO, the lower RP coverage level at 70% leads to a lower RP premium ($23.502) and expected RP payments ($13.866) as per the crop insurance policy design. Furthermore, the actuarially fair SCO premium is $5.77, and the farmer receives expected payments of $3.751.
5.2. Sensitivity analyses
We conduct several sensitivity analyses for different values of the parameters to generalize our results for farmers with different characteristics.Footnote 23 Toward this goal, we focus on case 3 and examine the effects of changes in the degree of loss aversion (η), the shape parameter of the value function (ϕ), and parameters of the probability weighting functions (λ and ρ). The results from these sensitivity analyses are compared to the results reported in Section 5.1 for the base value parameterization: η = 2.1, ϕ = 0.88, λ = 0.61, and ρ = 0.69.
The sensitivity analysis shows that an increase in the value of η by 25%, while holding all other parameters at their base values, does not change the coverage level under RP but lowers to 70% for RP & ARC and RP & PLC policy and 60% for RP & PLC & SCO. These results occur because lower coverage levels decrease the average loss in a good market year, and a higher degree of loss aversion places a greater weight on losses, intensifying the effect of losses. Consequently, the farmer prefers lower coverage levels as η rises. However, when η is decreased by 25%, the coverage levels increase from 70% to 75% under RP, remain the same under RP & ARC and RP & PLC, and increase from 70% to 75% under RP & PLC & SCO. These results are in contrast to those under an increase in η. When loss aversion declines, the certainty equivalent for RP & ARC and RP & PLC rises whereas it falls for RP & PLC & SCO relative to the certainty equivalent for RP alone. This implies that we would expect enrollments in ARC and PLC to increase if farmers become less loss averse. The converse is true for an increase in loss aversion.
In the extreme case of no loss aversion (η = 1), the optimal RP coverage level for the RP, RP & ARC, and RP & PLC policy scenarios is 80%, while the optimal coverage for RP & PLC & SCO is 75%. Thus, except for the fourth policy scenario (RP & PLC & SCO), eliminating loss aversion generates results similar to expected utility theory.Footnote 24 These results provide strong evidence that loss aversion plays an important role in predicting the coverage levels observed in the RMA data summarized in Table 1.
Now we explore the sensitivity of the results to the curvature of the value function given by ϕ. Setting ϕ = 1, while maintaining all other parameter values at the base level, leads to a linear value function that increases the magnitude of gains and losses relative to the main results with ϕ = 0.88. As risk aversion in gains and risk seeking in losses diminish, higher coverage levels become more attractive to farmers, and the optimal RP coverage level of 75% under the RP policy scenario is still consistent with the observed data reported in Table 1. This suggests that the curvature does not play as large of a role in determining the optimal coverage levels as suggested in expected utility theory. For the RP & ARC, RP & PLC, and RP & PLC & SCO scenarios, the optimal coverage level remains the same as reported in Table 7.
Next, we analyze the impacts of changes in the value of the parameters in the decision weighing function. Specifically, we set the parameters λ = 1 and ρ = 1, while keeping the base parameterization for all other parameters. In doing so, the decision weighing functions turn into cumulative probabilities (see equations 11 and 12).
The sensitivity results show that the highest certainty equivalent is for the 60% coverage level, indicating a smaller coverage level is optimal policy for the farmer in case 3. The farmer incurs a smaller premium and receives lower indemnity payments. The rationale for this result is that, under case 3, indemnity payments in a bad year can be much larger than losses (which are capped at the subsidized premium level) in a good year. Setting λ = 1 and ρ = 1 eliminates the overweighting of extreme events, which has a larger impact on indemnity payments in a bad year than on subsidized premiums in a good year. Consequently, farmers choose a much lower coverage level.
When λ = 1 and ρ = 1, the inclusion of ARC to RP raises the optimal RP coverage level from 60% to 70%. When farmers participate in the ARC commodity program in addition to RP insurance, farmers do not incur any additional losses at the upper tail of the distribution because farmers do not incur any cost to participate in ARC; however, farmers will have larger total payments relative to RP alone at the lower tail of the distribution. Consequently, the positive gains at the lower-tail events dominate. Thus, ARC replicates the role of overweighting or mitigates the role of probabilities when λ = 1 and ρ = 1. As a result, the value of crop insurance is higher, causing farmers to buy crop insurance, and thus optimal coverage rises from 60% when only RP is considered to 70% with the addition of ARC to RP. Note that the RP & ARC policy combination lowers the optimal coverage level from 75% in the main results to 70% for this sensitivity analysis. This occurs because ARC payments do not fully compensate for the loss of overweighting the gains as ARC payments are based on county-level yield,Footnote 25 leading to a coverage level that is above 60% but less than 75%.
When PLC is added to RP, the change in the λ and ρ parameter values lowers optimal coverage level from 75% to 70%, which is similar to the results of adding ARC to RP. Adding SCO to RP & PLC lowers the optimal RP coverage level to 60% from 70% for the RP & PLC combination. This occurs for two reasons: First, because SCO is an insurance policy, its premium further increases the cost and losses to farmers. Second, basis risk occurs with SCO indemnity payments made on county-level outcomes. The combined effects make the higher coverage levels less attractive to farmers, leading to a lower coverage level under RP & PLC & SCO.
The abovementioned results from these sensitivity analyses can be generalized to farmers in other counties and states. For example, farmers with larger (smaller) loss aversion (η) will tend to choose lower (higher) cover level for RP insurance. Furthermore, changes in the shape parameter of the value function (ϕ) do not affect the choice of the coverage level. Additionally, when the parameters for the probability weighting functions (λ and ρ) approach 1 (i.e., putting less weight on extreme events), the value of crop insurance to farmers declines, which corroborates the findings of Babcock (Reference Babcock2015).
6. Discussion and conclusion
This study formulates a theoretical model using cumulative prospect theory and comprehensively examines the impact of ARC and PLC commodity programs and the SCO crop insurance policy on optimal RP coverage level decisions of a risk-averse wheat farmer. We model and nonparametrically estimate the bivariate wheat yield and price distribution for Mitchell County in Kansas. The model is calibrated to a representative wheat farm in this county and applies Monte Carlo simulation to analyze the effects of various policies on the optimal RP coverage level, certainty equivalent, commodity program payments, and crop insurance payments.
Cumulative prospect theory specifies risky outcomes as monetary gains or losses centered on a reference point. This theory treats the agent as risk averse in gains and risk seeking in losses; however, a weighting function disproportionately weights events in the tails of the distribution, and loss aversion makes negative outcomes have large values relative to positive outcome of equal size. The reference points play an important role, and we consider three cases: the first two cases frame RP crop insurance as a risk management strategy, whereas the third case views crop insurance as a stand-alone lottery.
The results show that the reference point is critical in accurately modeling farmers’ choice of coverage levels. Even with loss aversion, when the reference point is modeled as a risk management strategy (cases 1 and 2), the representative farmer optimally selects the 85% coverage level, which is largely consistent with expected utility theory but inconsistent with observed coverage decisions of the farmers. The addition of ARC and PLC commodity programs increase the average returns without exacerbating the average cost. Consequently, the farmer would be willing to incur a larger loss through a higher coverage level, but the coverage level cannot increase as the farmer has already selected the maximum allowable RP coverage level at 85%. In contrast, the optimal coverage level for case 3 is 70%, which is in line with the farmers’ observed coverage decisions. This result highlights that when insurance is framed as an investment, cumulative prospect theory predicts farmers’ coverage decisions accurately. When ARC and PLC programs are included with the RP policy, the coverage level rises to 75% because commodity programs result in higher average gains without changing the average cost. However, when PLC and SCO are added to the RP policy, the coverage level falls back to 70% because, while average gains increase, basis risk becomes a factor and average losses, which are given larger weight because of loss aversion, increase. Therefore, the results indicate the farmer is willing to take on more basis risk by relying more on the county-level SCO by decreasing the coverage level to reduce the average cost. Thus, the farmer lowers the RP coverage levels.
Key parameters for cumulative prospect theory—degree of loss aversion, the shape parameter of the value function, and parameters of the probability weighting functions—affect the farmer’s RP coverage decision. For instance, a marginal increase in loss aversion does not affect the optimal coverage level for case 3 for all the policy scenarios. In contrast, a marginal decrease in loss aversion leads to a small increase in the optimal coverage level. Furthermore, removing the curvature of the value function leads to small increases of the optimal coverage levels, which implies the shape of the value function plays a minor role in determining the optimal coverage levels.
Acknowledgements
This paper benefited greatly from the comments of two anonymous reviewers.
Financial support
The project was supported by the Economic Research Service of the U.S. Department of Agriculture under the Cooperative Agreement, Project Number 58-3000-4-0029.