Robust power line detection with particle-filter-based tracking in radar video

Abstract

In this paper, we propose a tracking algorithm to detect power lines from millimeter-wave radar video. We propose a general framework of cascaded particle filters which can naturally capture the temporal correlation of the power line objects, and the power-line-specific feature is embedded into the conditional likelihood measurement process of the particle filter. Because of the fusion of multiple information sources, power line detection is more effective than the previous approach. Both the accuracy and the recall of power line detection are improved from around 68% to over 92%.

I. INTRODUCTION

Power-line-strike accident is a substantial threat for helicopter flight safety. Recently, four Turkish soldiers died in such an accident when the helicopter hit power lines and crashed [1]. According to the report in [2], among the 934 registered helicopter accidents in the USA from 1996 through 2000, 50 of them are categorized as power-line-strike accidents. In these accidents, the helicopter was either destroyed or substantially damaged, and 15 of them resulted in fatality. Most of these accidents happened at night, thus an automatic power line detection and warning system for helicopters that can work anytime is highly desirable to ensure helicopter flight safety.

Radar is one of the object detection systems that can especially work at night. A few previous works have been developed for power line detection with radar. In [3], a passive millimeter-wave (PMMW) radar system is tested to detect power lines from a vehicle. In [4], an active millimeter-wave radar is mounted on a rescue helicopter to detect power lines together with an infra-red camera and a RGB camera. In [5], the radar cross-section model of power lines is developed, and the authors observe the so-called “Bragg-pattern” which is a distinguishing feature of power line due to its periodic surface structure. However, these works provide no automatic algorithm to detect the power lines from the radar reception signal.

In [6], a power line imaging system based on a 94 GHz active millimeter-wave radar is reported. Unlike previous radar systems, the system in [6] can synthesize the field-of-view scene containing the power lines from the intermediate frequency (IF) channel of the reception signal in real time at 10 fps (frames-per-second). Based on the synthesized field-of-view, the automatic detection of the power lines can be accomplished by an image-processing approach on the radar video. However, because of the strong ground return noise in the radar image, power line detection is still very challenging.

A heuristic algorithm for automatically detecting power lines from the radar video is proposed in our previous work [7]. The Hough Transform is employed to detect power line candidates, and a pre-trained support vector machine (SVM) classifier is used to differentiate power lines from noise lines based on the power-line-specific Bragg pattern. However, each frame is processed separately, and the important temporal correlation between power line objects is only imposed as a post-processing step using a heuristic algorithm. Thus, even though the frame-level detection accuracy (i.e. the accuracy of frame-level result as whether each frame contains power line or not) in [7] is impressive, the power-line-level accuracy (i.e. the accuracy of line-level result as whether each power line is correctly detected or not) is not as good.

In this paper, we observe that the temporal correlation of the power line objects can be captured using formal tracking methods such as particle filtering. Particle filtering offers a unified framework to represent and sequentially estimate the object state from the Bayesian probabilistic perspective. The object state probability distribution function (pdf) is represented by a group of weighted samples, or particles, and tracking is accomplished by a two-step process of prediction and update. The prediction step diffuses the particles from the last time instant by an object dynamic model, thus predicting the prior probability density of the object in the new time instant. The update step computes the likelihood of the diffused particles in the new time instant given new observations. The final tracking result is obtained from the posterior probability density combining the prior and the likelihood. Particle filtering has been applied to various tracking tasks such as tracking sports players [8], pedestrians [9], and surveillance applications.

In this paper, we demonstrate that the characteristics of the power lines can be embedded into the update step of particle filtering, by utilizing the detection algorithm developed in our previous work [7] to measure the likelihood of a power line object in the new frame. The temporal correlation between power line objects in neighboring frames is naturally captured by the particle filtering. Thus, the two distinguishing characteristics of the power line object, namely, the intrinsic characteristics or features of the object, and the temporal correlation of the object, are combined and both are effectively used. The successful usage of these two types of information is the key to the accurate and robust detection of the power line objects. Part of this work has been reported previously in [10], while this paper provides extensive results and more detailed analysis.

We also propose a cascaded particle filter tracking algorithm, and demonstrate its application for power line detection. To effectively represent the object probability density by a group of weighted samples, the number of samples often needs to be considerably large, which results in high computational load, especially when the evaluation of the measurement function for each sample is not trivial. In this paper, we show that when the tracking algorithm and the measurement function are carefully designed, tracking in the original state space can be accomplished by separating it into its sub-spaces. Then the original particle filter becomes a few simpler particle filters cascaded, and the original tracking problem is simplified to a few easier tracking problems in the smaller sub-spaces. Because of the dimensionality reduction, the number of particles needed in each sub-space is much smaller than that in the original state space. Thus, the computational cost is reduced, and higher robustness can be achieved. We also investigate the conditions under which such a factorization of a particle filter into smaller cascaded particle filters is possible.

In summary, in this paper we present a novel power line detection algorithm, which integrates both the intrinsic power line object characteristics and temporal correlation into particle filter tracking framework. We also demonstrated cascaded particle filters for dimensionality-reduced tracking of power lines, achieving higher robustness with lower computational cost. To the best of our knowledge, this is the first work to use particle filter tracking for power line detection from radar video.

The remaining part of this paper is organized as follows. In the next section, we review the background information including related works, the 94 GHz power line imaging system, and the previous power line detection algorithm in [7]. In Section III, we explain our proposed approach in details. We present the experimental results in Section IV, and conclude this paper in Section V.

II. BACKGROUND

A) Related works

A series of works have been developed in [11,12] to model and measure the backscattering characteristics of power lines in active millimeter-wave radar, which is utilized in [7] to develop a power line detection algorithm. PMMW imaging systems have gone through a growing stage [13]. In [3], a PMMW power line imaging system is evaluated in comparison with a RGB camera and an infra-red camera. The PMMW system can provide extra visibility of the power line objects, while the active millimeter-wave radar is even more effective at imaging them. In [4,14–16], a radar obstacle detection system is proposed, which also includes multiple information sources such as infra-red camera, RGB camera, and a millimeter-wave radar. However, none of these systems provide an automatic power line detection algorithm. Some power line inspection robots have been developed in [17–19], while the purpose of these works is to inspect the defects of power lines rather than to detect them.

The particle filter for object tracking is first proposed in [20]. Since then it has found tremendous successful applications in this field. A color-based particle filter for tracking is proposed in [21], which integrates color distribution into particle filtering for object tracking. In [22] an appearance-adaptive model is developed for simultaneous particle filter tracking and object recognition. The work in [9] places an object detector in the framework of particle filter tracking and achieves tracking-by-detection. However, the purpose of [9] is to use the confidence map provided by the object detector for object tracking, while our work is to use the object-tracking framework for robust object detection. A complete survey of the field of visual tracking is beyond the scope of this paper, and the reader is referred to [23] for a good review. Nonetheless, all these tracking works are applied to object tracking from the RGB video, while we investigate tracking from the radar video. For more works on particle filtering, the reader is referred to [24–29].

B) The millimeter-wave power line imaging system

The 94 GHz millimeter-wave power line imaging system used in this work is an evolution of the legacy hardware in [30]. For more information about the radar system and the imaging process the reader is referred to [6]. The front-end unit includes the millimeter-wave transmitter and receiver. The in-cabinet processing system receives the IF signal from the radar receiver and synthesizes the field-of-view scene from it, in which the power lines could be visible. We show an example frame of such a field-of-view in Fig. 1, and two zoom-in frames in Fig. 2. The synthesized radar image is a B-scope plot, i.e. range-versus-angle mapping of the scene from the sensor's perspective. One can think of such a plot as if a bird looking down onto the ground, with the only difference being that the B-scope plot is a polar plot. As Fig. 1 shows, different columns of the image refer to different sweeping angles of the sensor, or different azimuths; different rows refer to different distances, or ranges of the object from the radar sensor. A vertical stack of power lines appear as if one single power line in the image since they have roughly the same distance to the radar.

Fig. 1. B-scope image of a scene that contains power lines and their supporting towers. From [6], shown here for completeness.

Fig. 2. Zoom-in view of the power line images. The ground return noise is evident in the right image. From [6], shown here for completeness.

From Figs 1 and 2, a few characteristics of the power lines are evident. Firstly, they are all straight lines in the radar images. Though in these figures they appear as curves, it is just an artifact of the B-scope, i.e. polar coordinate view. They will appear as straight lines when the coordinate system is transformed to the Cartesian coordinate. The power lines have sagging effect due to gravity, yet it is not reflected in the radar images because the distance difference caused by sagging is negligible compared to the distance between the power lines and the radar sensor. Secondly, the power lines appear in parallel groups. Thirdly, the power lines have the so-called Bragg pattern, i.e. the periodic peak pattern. In the USA, all the high-voltage power lines consist of several wires twisting around each other, forming a periodic pattern on the surface of the power lines as shown in Fig. 3. When the millimeter-wave is diffracted by the power line surface, according to Bragg's Law of Diffraction, periodic peaks in the return signal will appear in the following angles [31]:

Fig. 3. Physical structure of the power line.

(1)$$\theta_n = \sin^{-1}\left( {n\lambda \over 2L} \right),$$

where λ is the wavelength and L is the period of the power line surface structure, i.e. the horizontal distance between two braiding strands of wires on the power line surface. Lastly, in Fig. 2 we find that when the noise is heavy, the power lines become not as visible. The noise is due to the ground return when the radar sensor pointing is low, so that the power line objects are surrounded by the strong return from the ground in the same range. The ground return noise brings extra difficulties to the power line detection algorithm.

C) Previous power line detection algorithm

In [7], we proposed an automatic power line detection algorithm for the millimeter-wave radar video. It adopts Hough Transform [32] to detect straight lines, which include both the true power lines and some noise lines. To make a differentiation between a power line and a noise line, a pre-trained SVM classifier [33] is further applied. A compact 14-dimensional feature set is extracted from the line data (i.e. all the pixel values on a line concatenated into a one-dimensional vector), in order to capture the distinguishing Bragg pattern and represent the line data efficiently. The feature vector includes features both in the spatial domain and the frequency domain. The power line detection algorithm for each frame is shown in Fig. 4. It outputs the detected power lines in one frame, with each line represented in two parameters, θ and ρ, corresponding to the orientation of the line and its distance from the origin. Based on the power line detection result in each frame, a heuristic adaptive algorithm is proposed to incorporate the inter-frame correlation and the parallel property of the power lines, and a final frame-level score is generated as an indicator of the probability for a frame to contain power lines, and a binary decision is made as to whether issue warning of containing power lines for this frame or not. The block diagram of this adaptive algorithm is shown in Fig. 5.

Fig. 4. Power line detection algorithm in [7] for a frame.

Fig. 5. Adaptive frame result generating algorithm in [7].

This algorithm can produce almost 100% accurate frame-level result, in terms that it can decide for each frame as containing power line or not almost perfectly. However, because the adaptive algorithm is rather ad hoc, important power line features, such as they are parallel and temporally correlated, are not effectively exploited in a systematic way. As a result, the algorithm has difficulties detecting power lines that are “occluded” by the ground return noise when the radar pointing is low. The result is that the algorithm performance in the line-level is not as good as the frame-level. In order to effectively utilize these important power-line-specific features, we propose to use a tracking-based approach to take care of the temporal correlation and incorporate the parallel property into the algorithm, which will be presented in the following section.

III. POWER LINE TRACKING WITH PARTICLE FILTERING

A) Object tracking with particle filtering

The problem of object tracking can be more generally modeled as the estimation of the hidden state of a system that changes over time using a sequence of noisy measurements that are made on the system. The system state includes the information about the object that is of interest, such as the position and velocity of the size of the object. The measurement is carried out in the image frames of the video. Mathematically, consider the evolution of the state sequence ${\bf x}_{k}, k \in {\open N}$ of a target object given by

(2)$${\bf x}_k = {\bf f}_k({\bf x}_{k - 1}, {\bf v}_{k - 1}),$$

where ${\bf x}_{k-1}$ is the state in the previous frame, ${\bf f}_{k}$ describes the system dynamics model which is a first-order Markov Chain, and $\{{\bf v}_{k-1}, k \in {\open N}\}$ is an i.i.d. process noise sequence. The measurement sequence ${\bf z}_{k}$ is generated from the state sequence ${\bf x}_{k}$ by the measurement process

(3)$${\bf z}_k = {\bf h}_k ({\bf x}_k, {\bf n}_k),$$

where ${\bf h}_{k}()$ is the measurement function, i.e. the mapping from the underlying state ${\bf x}_{k}$ to the observed quantity ${\bf z}_{k}$, and $\{{\bf n}_{k}, k \in {\open N} \}$ is an i.i.d. measurement noise sequence.

With the model and symbols defined, the tracking problem is to estimate $p\,({\bf x}_{k} \vert {\bf z}_{1:k})$, the posterior pdf of the state ${\bf x}_{k}$ given all the measurements ${\bf z}_{1:k}$ up to frame k from the Bayesian perspective. $p\,({\bf x}_{k} \vert {\bf z}_{1:k})$ may be obtained recursively in two steps: prediction and update. The prediction step is to obtain the prior pdf of ${\bf x}_{k}$, $p\,({\bf x}_{k} \vert {\bf z}_{1:k - 1})$, from the posterior $p\,({\bf x}_{k-1} \vert {\bf z}_{1:k-1})$ in the previous frame and the system model in equation (2) using the Chapman–Kolmogorov equation [34]

(4)$$p\,({\bf x}_k \vert {\bf z}_{1:k - 1}) = \int p\,({\bf x}_k \vert {\bf x}_{k - 1})\,p\,({\bf x}_{k - 1} \vert {\bf z}_{1:k - 1})\,{d}\,{\bf x}_{k - 1}.$$

In frame k, when a new measurement is available, the posterior pdf is obtained via Bayes’ rule

(5)$$p\,({\bf x}_k \vert {\bf z}_{1:k}) = {p\,({\bf z}_k \vert {\bf x}_k)p\,({\bf x}_k \vert {\bf z}_{1:k-1}) \over \int p\,({\bf z}_k \vert {\bf x}_k)p\,({\bf x}_k \vert {\bf z}_{1:k-1})\,{d}\,{\bf x}_k},$$

where $p\,({\bf z}_{k} \vert {\bf x}_{k})$ is the likelihood of the new measurement ${\bf z}_{k}$ given the predicted state ${\bf x}_{k}$.

The particle filter is a sequential importance sampling technique to approximate the posterior pdf $p\,({\bf x}_{k} \vert {\bf z}_{1:k})$ using a finite set of N weighted samples $\{{\bf x}_{k}^{i}, w_{k}^{i} \}_{i = 1,\ldots, N}$ by Monte Carlo simulation. When the number of samples N is large enough, the approximated posterior pdf becomes close to the true probability density and the approximate solution approaches the optimal Bayesian solution. The candidate particles $\tilde{{\bf x}}_{k}^{i}$ are sampled from an appropriate importance distribution $q\,({\bf x}_{k} \vert {\bf x}_{1:k-1}, {\bf z}_{1:k})$, and the weights of the samples are [35]

(6)$$w_k^i = w_{k - 1}^i {p\,({\bf z}_k \vert \tilde{{\bf x}}_k^i)p\,(\tilde{{\bf x}}_k^i \vert {\bf x}_{k-1}^i) \over q\,({\bf x}_k \vert {\bf x}_{1:k-1}, {\bf z}_{1:k})}.$$

In the case of bootstrap filter [36,37], the importance distribution $q\,({\bf x}_{k} \vert {\bf x}_{1:k-1}, {\bf z}_{1:k})$ is the same as the state transition density $p\,({\bf x}_{k} \vert {\bf x}_{k-1})$, and the weight $w_{k}^{i}$ for each particle i in frame k is then simplified as

(7)$$w_k^i = w_{k-1}^i \cdot p\,({\bf z}_k \vert \tilde{{\bf x}}_k^i).$$

Because a large number of these particles have negligible weights, the particles are re-sampled in each frame to avoid the degeneracy problem. For a fixed number of particles, $w_{k-1}^{i} = {1}/{N}$ is a constant and can be ignored. In the end, the importance weight in equation (6) is reduced to $p\,({\bf z}_{k} \vert \tilde{{\bf x}}_{k}^{i})$, the conditional likelihood of a new observation z_k given the particle $\tilde{{\bf x}}_{k}^{i}$. Note that the normalization term of the weights is omitted here for clarity.

B) Cascaded particle filters

The reason for the success of particle filter tracking is twofold. First, the theoretic framework of Bayesian estimation is a general and well-established model. The sequential Bayesian estimation model in equations (4) and (5) captures the nature of object tracking. Secondly, even though equations (4) and (5) are usually intractable except for a few special cases such as the linear dynamic model with Gaussian noise, Monte Carlo simulation can deal with any general distribution in a non-parametric way as long as the number of samples N is large enough.

However, when the dimensionality of the state space increases, the number of samples needed to effectively represent the probability density also increases, in an exponential rate – well-known as the “curse of dimensionality”. Although the computational cost for evaluating the likelihood function $p\,({\bf z}_{k} \vert \tilde{{\bf x}}_{k}^{i})$ for one sample is negligible, when the number of samples increases exponentially, the cost becomes huge. One could sacrifice the number of samples N for speed, but this will cause incomplete and problematic representation and estimation of the true probability density.

We thus propose to use cascaded particle filters to alleviate the curse of dimensionality. We observe that when the state vector incorporates more information and the dimensionality of the state space increases, often the state vector can be decomposed into a few un-correlated sub-states, and the state space can be decomposed into a few orthogonal sub-spaces. Let ${\bf x}_{k} = ({\bf u}_{k}, {\bf v}_{k})$, if we have $p\,({\bf x}_{k}) = p\,({\bf u}_{k}, {\bf v}_{k})=p\,({\bf u}_{k}) \cdot p\,({\bf v}_{k})$, $p\,({\bf x}_{k}, {\bf x}_{k - 1}) = p\,({\bf u}_{k}, {\bf u}_{k - 1}) \cdot p\,({\bf v}_{k}, {\bf v}_{k - 1})$, and $p\,({\bf x}_{k}, {\bf z}_{1:k}) = p\,({\bf u}_{k}, {\bf z}_{1:k})\cdot p\,({\bf v}_{k}, {\bf z}_{1:k})$, it can be easily shown that

(8)$$\eqalign{p\,({\bf x}_k \vert {\bf x}_{k-1}) &= p\,({\bf u}_k \vert {\bf u}_{k - 1}) \cdot p\,({\bf v}_k \vert {\bf v}_{k - 1}), \cr p\,({\bf x}_{k - 1} \vert {\bf z}_{1:k - 1}) &= p\,({\bf u}_{k - 1} \vert {\bf z}_{1:k - 1}) \cdot p\,({\bf v}_{k - 1} \vert {\bf z}_{1:k - 1}), \cr p\,({\bf z}_k \vert {\bf x}_k) &= p\,({\bf z}_k \vert {\bf u}_k)\cdot p\,({\bf z}_k \vert {\bf v}_k).}$$

So the prediction step in equation (4) becomes

(9)$$\eqalign{&p\,({\bf x}_k \vert {\bf z}_{1:k - 1})\cr &\quad = \int p\,({\bf x}_k \vert {\bf x}_{k - 1})\,p\,({\bf x}_{k - 1} \vert {\bf z}_{1:k - 1})\,{d}\,{\bf x}_{k - 1}\cr &\quad = \int p\,({\bf u}_k \vert {\bf u}_{k-1})\,p\,({\bf v}_{k} \vert {\bf v}_{k-1})\cr &\qquad \times p\,({\bf u}_{k - 1} \vert {\bf z}_{1:k - 1})\,p\,({\bf v}_{k - 1} \vert {\bf z}_{1:k - 1})\,{d}\,{\bf u}_{k - 1}\,{d}\,{\bf v}_{k - 1}\cr &\quad =\int p\,({\bf u}_k \vert {\bf u}_{k - 1})\,p\,({\bf u}_{k - 1} \vert {\bf z}_{1:k - 1})\,{d}\,{\bf u}_{k - 1} \cdot \cr &\qquad \times \int p\,({\bf v}_k \vert {\bf v}_{k - 1})\,p\,({\bf v}_{k - 1} \vert {\bf z}_{1:k - 1})\,{d}\,{\bf v}_{k - 1}\cr &\quad = p\,({\bf u}_k \vert {\bf z}_{1:k - 1}) \cdot p\,({\bf v}_k \vert {\bf z}_{1:k - 1}).}$$

And the update step in equation (5) becomes

(10)$$\eqalign{p\,({\bf x}_k \vert {\bf z}_{1:k}) &\propto p\,({\bf z}_k \vert {\bf x}_k)\,p\,({\bf x}_k \vert {\bf z}_{1:k - 1})\cr &\propto p\,({\bf z}_k \vert {\bf u}_k)\,p\,({\bf z}_k \vert {\bf v}_k) \cr &\quad \times p\,({\bf u}_k \vert {\bf z}_{1:k - 1})\,p\,({\bf v}_k \vert {\bf z}_{1:k - 1})\cr &\propto p\,({\bf z}_k \vert {\bf u}_k)\,p\,({\bf u}_k \vert {\bf z}_{1:k - 1}) \cr &\quad \times p\,({\bf z}_k \vert {\bf v}_k)\,p\,({\bf v}_k \vert {\bf z}_{1:k - 1})\cr &\propto p\,({\bf u}_k \vert {\bf z}_{1:k}) \cdot p\,({\bf v}_k \vert {\bf z}_{1:k}).}$$

It is clear from equations (9) and (10) that both the prediction and update steps can be factored into the prediction and update of u_k and v_k separately, so the estimation of u_k and v_k are independent of each other. Thus, the original tracking problem in a high-dimensional state space can be solved by some cascaded tracking in lower-dimensional sub-spaces, given that the state vector can be decomposed into some independent sub-space state vectors. The reduced dimensionality simplifies the problem, requires fewer samples to represent and estimate the probability density, and has a higher chance of success. The dynamic model to propagate the particles can be defined separately in the sub-spaces, and the measurement likelihood $p\,({\bf z}_{k} \vert \tilde{{\bf x}}_{k}^{i})$ is decomposed into individual measurement likelihood in the sub-spaces, i.e. $p\,({\bf z}_{k} \vert \tilde{{\bf u}}_{k}^{i})$ and $p\,({\bf z}_{k} \vert \tilde{{\bf v}}_{k}^{i})$. Similar idea of factorization has been successfully applied to face detection in [38].

C) Observation models

In this section, we define the observation models that embed the previous power line detection algorithm into the particle filter tracking framework. The power line is represented by two parameters, θ and ρ in the Hough Transform domain, and they are very much independent, i.e. the distance between the radar sensor and the power line is independent from the approaching angle of the helicopter. Another reason for separating θ and ρ is because in reality we find that all the power lines in the field-of-view captured by the radar are parallel, thus the θ value for all the power lines are the same. θ can be estimated first, then individual ρ values for individual power lines can be further estimated by individual ρ trackers along the estimated θ direction. Thus, according to the cascaded particle filters algorithm developed in the previous section, we consider two separate likelihood measurements, $p({\bf z}_{k} \vert \tilde{\theta}_{k}^{i})$ and $p({\bf z}_{k} \vert \tilde{\rho}_{k}^{i})$.

1) Observation model for θ, $p({\bf z}_{k} \vert \tilde{\theta}_{k}^{i})$

The purpose of θ tracking is to estimate the orientation of all the power lines in each frame. To compute the conditional likelihood of a particular θ sample $\tilde{\theta}_{k}^{i}$, we combine different sources of information, namely, a concentration measure based on the Hough Transform data, the strength of lines, and temporal smoothness:

(11)$$p({\bf z}_k \vert \tilde{\theta}_k^i) = \underbrace{c({\bf z}_k \vert \tilde{\theta}_k^i)}_{\rm concentration} \cdot \underbrace{s({\bf z}_k \vert \tilde{\theta}_k^i)}_{\rm line\ strength} \cdot \underbrace{g_\theta(\tilde{\theta}_k^i, \hat{\theta}_{k-1})}_{\rm temporal\ smoothness},$$

where k denotes current frame and k−1 denotes previous frame. Adopting the preprocessing algorithm including thresholding and coordinate transformation in [7], Hough Transform converts a frame z_k to Hough-domain data H _k (θ, ρ), and H _k(θ_i, ρ_j) represents the number of pixels (or line strength) for a particular line parameter combination (θ_i, ρ_j). From the definition of Hough Transform [32] it can be shown that the sum of all the Hough Transform domain data for any particular θ is constant, i.e. $\sum_{\rho} H_{k} (\theta_{1}, \rho) = \sum_{\rho} H_{k} (\theta_{2}, \rho)$, yet $H_{k} (\theta_{1}, \rho)$ and $H_{k} (\theta_{2}, \rho)$ have different distributions over ρ. For the true power line orientation, $H_{k} (\theta_{\rm true}, \rho)$ is more concentrated because a few power lines with large number of pixels will dominate. Taking the idea from Information Theory that the more concentrated a distribution is, the lower its uncertainty and its entropy, we define the “concentration” measure similar to the entropy:

(12)$$c \lpar {\bf z}_k \vert\tilde{\theta}_k^i \rpar = \sum_{\rho}H_k \lpar \tilde{\theta}_k^i, \rho \rpar \log\,\lpar H_k \lpar \tilde{\theta}_k^i, \rho \rpar \rpar \left\vert_{H_k(\tilde{\theta}_k^i, \rho) \gt 0}\right..$$

For the true power line orientation, there will be a few lines with significant strength, i.e. number of pixels. The line strength measure $s({\bf z}_{k} \vert \tilde{\theta}_{k}^{i})$ takes the sum of the top T values (in our simulations we use T=3) in $H_{k}(\tilde{\theta}_{k}^{i}, \rho)$. Lastly, the temporal smoothing term for θ is defined as:

(13)$$g_\theta(\tilde{\theta}_k^i, \hat{\theta}_{k - 1}) = \exp \left(-{(\tilde{\theta}_k^i - \hat{\theta}_{k - 1})^2 \over 2\sigma_{\theta}^2} \right),$$

where $\hat{\theta}_{k - 1}$ is the tracked θ in the previous frame and σ_θ is the standard deviation parameter of the Gaussian function.

2) Observation model for ρ, $p({\bf z}_{k} \vert \tilde{\rho}_{k}^{i})$

The ρ tracker is cascaded after the θ tracker and tracks for the ρ value of each individual power line along the orientation $\hat{\theta}_{k}$ tracked by the θ tracker. Similarly, different sources of information are combined to define the conditional likelihood of a particular ρ sample $\tilde{\rho}_{k}^{i}$:

(14)$$\eqalign{p({\bf z}_k \vert \tilde{\rho}_k^i) &= \underbrace{f({\bf z}_k \vert \tilde{\rho}_k^i)}_{\rm classifier confidence} \cdot \underbrace{a(\tilde{\rho}_k^i, \hat{\rho}_{k-1})}_{\rm association function} \cdot \cr &\quad \underbrace{g_{\rho} (\tilde{\rho}_k^i, \hat{\rho}_{k - 1})}_{\rm temporal smoothness}.}$$

The classifier confidence is directly inherited from the SVM-based power line detection algorithm in [7]. The algorithm retrieves the pixel data on a particular line specified by $(\hat{\theta}_{k}, \tilde{\rho}_{k}^{i})$, and outputs the SVM decision function value as the classifier confidence. Here we see the previous power line detection algorithm can fit nicely into the tracking framework by $f({\bf z}_{k} \vert \tilde{\rho}_{k}^{i})$. The association function measures the similarity of the Hough domain data in a local neighborhood between this sample $\tilde{\rho}_{k}^{i}$ and the tracked $\hat{\rho}_{k-1}$ in previous frame, based on the intuition that for the same power line, Hough domain data should be similar in local neighborhood for neighboring frames. It is defined as the normalized correlation:

(15)$$a(\tilde{\rho}_k^i, \hat{\rho}_{k - 1})= \matrix{\sum\nolimits_{l = - r}^{r}H_k(\hat{\theta}_k, \tilde{\rho}_k^i+l) \hfill \cr H_{k - 1}(\hat{\theta}_{k - 1}, \hat{\rho}_{k - 1}+l)} \over \matrix{\sqrt{\sum\nolimits_{l = -r}^{r} \lpar H_k(\hat{\theta}_k, \tilde{\rho}_k^i+l)\rpar ^2}\cr \cdot \sqrt{\sum\nolimits_{l=-r}^{r} \lpar H_{k-1}(\hat{\theta}_{k- 1}, \hat{\rho}_{k -1} + l) \rpar ^2}},$$

where r is a parameter specifying the size of the local neighborhood. Lastly, the temporal smoothing term for ρ is defined in the similar way as equation (13):

(16)$$g_{\rho} (\tilde{\rho}_k^i, \hat{\rho}_{k - 1}) = \exp \left(-{(\tilde{\rho}_k^i-\hat{\rho}_{k-1})^2 \over 2\sigma_{\rho}^2} \right).$$

D) Power line detection with tracking

To complete the particle filter tracking algorithm, we need to define the motion dynamic models that propagate the particles. Without any prior knowledge of the helicopter movement, we use a drifting model for both θ and ρ:

(17)$$\theta_k = \theta_{k - 1} + \varepsilon_{\theta},$$

(18)$$\rho_k =\rho_{k - 1} + \varepsilon_{\rho}.$$

The process noise $\varepsilon_{\theta}$ and $\varepsilon_{\rho}$ are drawn from zero-mean Gaussian distributions with standard deviations of σ_θ and σ_ρ, respectively.

With all the building blocks explained, now we can present the complete power line detection with tracking algorithm. For readability we first present the θ-tracking algorithm, the purpose of which is to estimate the orientation of all the parallel power lines in a frame given the orientation of the power lines in previous frame, in Algorithm 1.

Algorithm 1. The θ-tracking algorithm

Algorithm 2. The ρ-tracker processing algorithm

Algorithm 3. The power line detection with tracking algorithm

The re-sampling step is implemented in the same way as [20]. The algorithm for processing a ρ-tracker is presented in Algorithm 2.

Then we can present our complete power line detection with tracking algorithm in Algorithm 3. In this algorithm, T _ρ is a parameter that controls the association threshold for the ρ-tracker, and M _ρ defines the maximum number of ρ-trackers allowed in each frame. In the first frame, the ρ-trackers are initialized by searching for local maxima in Hough Transform data, which is the same way for detecting power lines in the previous algorithm [7]. If a line candidate (corresponding to a local maximum in Hough Transform data) is classified by the SVM as a power line, a ρ-tracker is initialized and it continues to track the position of this power line in future frames; otherwise it is ignored and no ρ-tracker is initialized. In the case of a false alarm power line, the tracker will most likely not be able to find any good association in future frames and this false alarm ρ-tracker will be terminated. We also deal with the situation of power line occlusion by ground return noise. When a power line is occluded by noise, the tracker could lose track of it. To re-capture it when the power line appears again, in each frame we also search for candidate power lines in the region that is not covered by any ρ-tracker and initialize new ρ-trackers. We immediately terminate the “lost-track” trackers rather than keeping them running and predicting because the purpose is to detect the power lines rather than to have an exact track of each single power line, and in simulation we find that such a strategy of immediate termination and re-initialization is more effective for detecting the power lines.

IV. EXPERIMENTS

A) Data collection

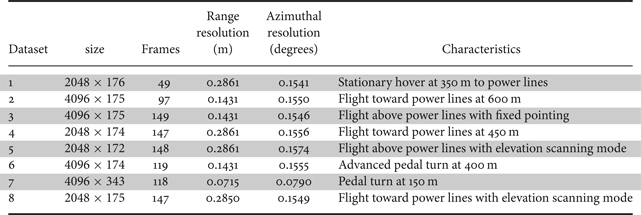
The helicopter flight test team has conducted a flight test in Everett, WA, and collected several datasets, each lasting from a few seconds to about 15 s. These datasets are collected under different flying conditions, such as hovering and flying toward the power lines, with the radar sensor either fixed or sweeping up-and-down, thus they have different characteristics and can represent most of the cases that happen in real-world situations. These datasets are further described in Table 1. The power lines in these datasets are clear in the radar video when they have a physical distance between about 200 m and 500 m to the sensor. The frame rate for all the videos are 10 fps, as constrained by the sensor in [6]. For more information regarding the collection of the radar video datasets, please refer to [6].

Table 1. Characteristics of the testing datasets.

B) Feature selection for the SVM classifier

In [7] we have proposed a 14-dimensional feature vector to represent the data on a candidate line. Though the dimensionality of the feature vector is not overwhelmingly high, it is desirable to select a more compact set from the feature vector for computational efficiency. Moreover, selecting the characterizing subset from the feature could often improve classification accuracy, since the “noisy” features can be removed by feature selection. It is also interesting to see which features are more important than others. We employ the feature selection algorithm proposed in [39]. The feature selection algorithm is applied to the same classifier training dataset as described in [7], and we progressively select a subset of the feature, and use the subset to get cross-validation results as classifier performance measurement. We do this for the subset feature size being 14 (i.e. the full feature set) to 3, as keeping only 1 and 2 features does not provide very meaningful classification results. The results are shown in Fig. 6¹. From the results we see consistent performance drop of the classifier when feature number is reduced. Even though the performance drop when 1 or 2 features being removed is not substantial, which could be an indication of some minor redundancy among the features, the full set of features still achieves the best overall performance. Thus, we keep the full set of 14 features for the SVM classifier in this paper.

Fig. 6. Feature selection results. For each sub-figure, horizontal axis is the size of the training set (as a portion of the entire classifier training set), and the vertical axis is the classification accuracy. (a) Cross-validation training accuracy for 14–9 features, (b) Cross-validation testing accuracy for 8–3 features.

C) Testing results

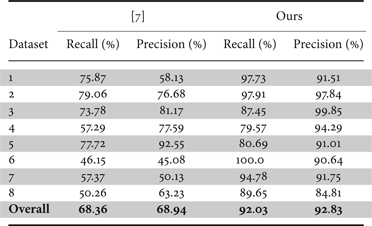
To show the effectiveness of the detection with tracking algorithm, we compare the line-level detection results in Table 2 with the previous power line detection algorithm in [7]. We manually inspect the result for each frame, and compute the line-level recall and precision for each dataset. Recall is the ratio of correctly detected power lines to all the existing power lines in the images, and precision is the ratio of correctly detected power lines to all the detected power lines returned by the algorithm. Conceptually, the higher the recall, the lower the false negatives; the higher the precision, the lower the false positives. We can see that with the cascaded particle filter tracking algorithm, both recall and precision are greatly improved, thus boosting the robustness of the power line detection algorithm significantly.

Table 2. Power-line-level recall and precision comparison with previous algorithm.

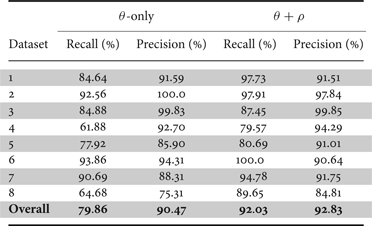
To validate the necessity for cascaded θ-tracking and ρ-tracking, in Table 3 we compare the line-level recall and precision with θ-only tracking algorithm. Only Algorithm 1 is activated in Algorithm 3 but not Algorithm 2 In each frame, the overall power line orientation is tracked, and the top M _ρ lines along that direction are classified by the SVM classifier as power lines or noise lines. We can see the performance with full θ+ρ tracking algorithm is superior to that of θ-only. We notice that the involvement of ρ-trackers particularly improves the recall, which means more true power lines can be detected. The reason is that without the ρ-trackers, power lines that are occluded by the ground return noise may not be correctly classified by the SVM, thus they are missed by the θ-only algorithm. But with the ρ-tracking algorithm, the strong association of these partially occluded power lines between neighboring frames can still be greater than T _ρ, thus the effective utilization of temporal correlation complements the “blind spots” of the SVM classifier. On the other hand, when the power lines are tracked through regular particle filter tracking algorithm in the (θ, ρ) state space instead of cascaded particle filter tracking, in simulation we found that the performance is not as good. The main reason is that the data on a line whose direction is not the direction of the real power lines and crossing multiple power lines looks just like a true power line, having multiple peaks corresponding to the crosses with the true power lines, thus bringing confusion. However with the cascaded particle filter, the confusion can be avoided.

Table 3. Power-line-level recall and precision comparison with θ-only tracking.

We show the visual results comparison in Fig. 7, where we list the original frames, the ground truth, the detection results in [7], and the results of the algorithm in this paper. It should be noted that these are all zoom-in views showing the power line regions, not the entire field-of-views of the radar. The radar images are displayed in pseudo-color, with a cooler color means lower intensity while a hotter color means higher intensity. The power lines are overlaid as red lines in the detection results. We can clearly see the superiority of the detection with tracking algorithm. Even when the ground return noise is strong and the power lines are occluded, the detection with tracking algorithm can still correctly detect most of them. The previous algorithm suffers from a lot of false alarm lines, while the new algorithm has a much cleaner result.

Fig. 7. Some example frames with power line detection results comparison. First column: original frames. Second column: ground truth power lines, as manually labeled. Third column: the detection results in [7]. Last column: the detection results in this paper. The reader is suggested to view this figure in color. Notice that in the first column many power lines are subtle and hard to recognize, while the detection with tracking algorithm can successfully detect them.

D) Performance and implementation

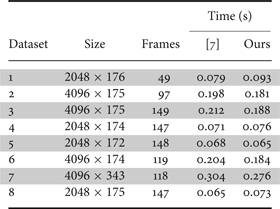
In Table 4, we present the speed performance comparison of the proposed algorithm with [7]. Both the algorithms are un-optimized, single-thread implementation in Section IV-C. The test is performed on a desktop PC with 3.40 GHz CPU. We can see the speed of the tracking algorithm is at the same level as the previous detection algorithm, while for some datasets the proposed algorithm performs even better. We see approximately there are three different resolutions for the radar videos in Table 1, 2048×176, 4096×175, and 4096×343. The resolution is a parameter controlled by the sensor, i.e. the power line imaging system. The resolution of 2048×176 is adequate for our target application, as we can see they can achieve the same detection results as those with other resolutions. For our current target application, we will use the videos with resolution of 2048×176, which can run in real-time. If a higher resolution is needed in the future, a faster PC, a multi-threaded implementation, or an field-programmable gate array (FPGA) implementation could be used to handle the required computation.

Table 4. Speed performance comparison, in terms of average processing time per frame.

The implementation of the algorithm requires few user-specified parameters. ε_θ, ε_ρ, and T _ρ are inherent to the nature of power line object dynamics and association, which can be optimally estimated from some training data. While the training requires manually labeling the track of each individual power line which is rather tedious, we adopt some sensible values for them. M _ρ specifies the maximum number of power lines in each frame, and we set it to 8 since in testing we find that is the maximum number of power lines to appear in the field-of-view. The other parameter needs to be set in the implementation is the number of particles. For the simulation results presented in this paper, we set N _θ=80 and N _ρ=20.

V. CONCLUSION

In this paper, we present a robust detection with particle filter tracking algorithm to automatically detect power lines from the video captured by a 94 GHz millimeter-wave radar. The particle filter framework captures both the power-line-inherent features and the important temporal correlation feature. The experimental results show that the algorithm has superior performance over a previous power line detection algorithm. The power line imaging radar and the detection algorithm in this paper is intended to provide a valuable assistance to helicopter pilots.

The power line detection and tracking could be a beginning of an image processing application platform with the 94 GHz millimeter-wave imaging radar developed in [30]. Future applications can include detection and tracking of other types of objects. Also, because the ground return noise has significant influence on the power line detection and possibly other applications, we would like to investigate the possibility of de-noising the radar video from an image-processing perspective.