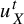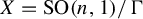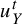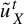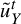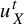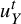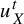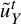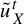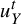Rigidity of joinings for time changes of unipotent flows on quotients of Lorentz groups

Abstract

Let $u_{X}^{t}$ be a unipotent flow on $X=\mathrm {SO}(n,1)/\Gamma $, $u_{Y}^{t}$ be a unipotent flow on $Y=G/\Gamma ^{\prime }$. Let $\tilde {u}_{X}^{t}$, $\tilde {u}_{Y}^{t}$ be time changes of $u_{X}^{t}$, $u_{Y}^{t}$, respectively. We show the disjointness (in the sense of Furstenberg) between $u_{X}^{t}$ and $\tilde {u}_{Y}^{t}$ (or $\tilde {u}_{X}^{t}$ and $u_{Y}^{t}$) in certain situations. Our method refines the works of Ratner’s shearing argument. The method also extends a recent work of Dong, Kanigowski, and Wei [Rigidity of joinings for some measure preserving systems. Ergod. Th. & Dynam. Sys. 42 (2022), 665–690].

1 Introduction

1.1 Main results

In this paper, we study the rigidity of joinings of time changes of unipotent flows. First, let:

• • $G_{X}=\mathrm {SO}(n_{X},1)$ , $G_{Y}$ be a semisimple Lie group with finite center and no compact factors and $\Gamma _{X}\subset G_{X}$ , $\Gamma _{Y}\subset G_{Y}$ be irreducible lattices;

• • $(X,m_{X})$ , $(Y,m_{Y})$ be the homogeneous spaces $X=G_{X}/\Gamma _{X}$ , $Y=G_{Y}/\Gamma _{Y}$ equipped with the Lebesgue measures $m_{X}$ , $m_{Y}$ respectively;

• • $u_{X}^{t}$ , $u_{Y}^{t}$ be unipotent flows on X and Y, respectively;

• • $\tau _{X}$ , $\tau _{Y}$ be positive functions with integral $m_{X}(\tau _{X})=m_{Y}(\tau _{Y})=1$ under certain regularity on X and Y, respectively;

• • $\tilde {u}^{t}_{X}$ , $\tilde {u}^{t}_{Y}$ be the time changes of $u^{t}_{X}$ , $u^{t}_{Y}$ induced by $\tau _{X}$ , $\tau _{Y}$ , respectively;

• • $d\mu =\tau _{X} dm_{X}$ , $d\nu =\tau _{Y} dm_{Y}$ be the $\tilde {u}_{X}$ -, $\tilde {u}_{Y}$ -invariant measures, respectively.

We shall verify the disjointness and so classify the joinings of $u_{X}^{t}$ and $\tilde {u}_{Y}^{t}$ (or $\tilde {u}_{X}^{t}$ and $u_{Y}^{t}$ ) in certain situations.

Recall that a joining of $\tilde {u}_{X}^{t}$ and $\tilde {u}_{Y}^{t}$ is a $(\tilde {u}_{X}^{t}\times \tilde {u}_{Y}^{t})$ -invariant probability measure on $X\times Y$ , whose marginals on X and Y are $\mu $ and $\nu $ , respectively. It was first introduced by Furstenberg in [Fur81], and is a natural generalization of measurable conjugacies. The classical results on classifying joinings under this context were established by Ratner [Rat82, Rat83, Rat86, Rat87, Rat90]. First, the celebrated Ratner’s theorem indicates that all joinings between $u_{X}^{t}$ and $u_{Y}^{t}$ have to be algebraic. In addition, for $G_{X}=\mathrm {SO}(2,1)$ , Ratner studied the H-property (or Ratner’s property) of horocycle flows $u_{X}^{t}$ , as well as their time changes $\tilde {u}_{X}^{t}$ , and then showed that any non-trivial (that is not the product measure $\mu \times \nu $ ) ergodic joining of $\tilde {u}_{X}^{t}$ and $\tilde {u}_{Y}^{t}$ is a finite extension of $\nu $ . (In fact, this is even true for any measure-preserving system on $(Y,\nu )$ .) Using this, Ratner was able to show that for $G_{X}=G_{Y}=\mathrm {SO}(2,1)$ , the existence of a non-trivial ergodic joining of $\tilde {u}_{X}^{t}$ and $\tilde {u}_{Y}^{t}$ implies that $\tau _{X}$ and $\tau _{Y}$ are algebraically cohomologous. In other words, whether $\tilde {u}_{X}^{t}$ and $\tilde {u}_{Y}^{t}$ are disjoint is determined by cohomological equations.

It is natural to ask if it is possible to extend the results to $G_{X}=\mathrm {SO}(n_{X},1)$ for $n_{X}\geq 3$ . The difficulty is that the time change $\tilde {u}^{t}_{X}$ needs not have the H-property. It is one of the main ingredients of unipotent flows. Roughly speaking, H-property states that the divergence of nearby unipotent orbits happens always along some direction from the centralizer $C_{G_{X}}(u_{X})$ of the flow $u^{t}_{X}$ . In particular, for $G_{X}=\mathrm {SO}(2,1)$ , the direction can only be the flow direction $u^{t}_{X}$ itself. Moreover, Ratner [Rat87] naturally extended this notion to the general measure-preserving systems and verified it for the time changes $\tilde {u}^{t}_{X}$ of horocycle flows. However, for $n_{X}\geq 3$ , it seems that there is no suitable way to describe the ‘centralizer’ of the time change $\tilde {u}^{t}_{X}$ . Thus, classifying joinings of $\tilde {u}_{X}^{t}$ and $\tilde {u}_{Y}^{t}$ for $n_{X}\geq 3$ becomes a difficult problem.

Recently, Dong, Kanigowski, and Wei [DKW22] considered the case when ${G_{X}=\mathrm {SO}(2,1)}$ , $G_{Y}$ is semisimple as above, and $\Gamma _{X}$ and $\Gamma _{Y}$ are cocompact lattices. After comparing the H-property of $\tilde {u}_{X}^{t}$ and $u_{Y}^{t}$ , they showed that $\tilde {u}_{X}^{t}$ and $u_{Y}^{t}$ are disjoint once the Lie algebra $\mathfrak {g}_{Y}$ of $G_{Y}$ contains at least one weight vector of weight at least $1$ other than the $\mathfrak {sl}_{2}$ -triples generated by $u_{Y}^{t}$ .

In this paper, we try to generalize the results stated above for $n_{X}\geq 3$ . First, we follow the idea of Ratner and study the H-property of $u_{X}^{t}$ and deduce the following theorem.

Theorem 1.1. Let $(Y,\nu ,S)$ be a measure-preserving system of some map $S:Y\rightarrow Y$ , and $\rho $ be an ergodic joining of $u_{X}^{1}$ and S. Then either $\rho =\mu \times \nu $ or $(u^{1}_{X}\times S,\rho )$ is a compact extension of $(S,\nu )$ . More precisely, if $\rho \neq \mu \times \nu $ , then there exists a compact subgroup $C^{\rho }\subset C_{G_{X}}(u_{X})$ , and $n>0$ such that, for $\nu $ -almost every (a.e.) $y\in Y$ , there exist $x_{1}^{y},\ldots ,x_{n}^{y}$ in the support of $\rho _{y}$ with

$$ \begin{align*}\rho_{y}(C^{\rho}x_{i}^{y})=\frac{1}{n}\end{align*} $$

for $i=1,\ldots ,n$ , where $ \rho =\int _{Y}\rho _{y}\,d\nu (y)$ is the disintegration along Y.

By Theorem 1.1, for any non-trivial ergodic joining $\rho $ of $u_{X}^{t}$ and $\tilde {u}_{Y}^{t}$ , there are measurable maps $\psi _{1},\ldots ,\psi _{n}:Y\rightarrow X$ such that

(1.1) $$ \begin{align} \rho(f)=\int_{Y} \int_{C^{\rho}}\frac{1}{n}\sum_{p=1}^{n}f(k\psi_{p}(y),y)\,dm(k)\,d\nu(y) \end{align} $$

for $f\in C(X\times Y)$ , where m is the Lebesgue measure of the compact group $C^{\rho }$ . Projecting $\rho $ to $(C^{\rho }\backslash X)\times Y$ , we get

$$ \begin{align*}\overline{\rho}(f)=\int_{Y} \frac{1}{n}\sum_{p=1}^{n}f(\overline{\psi}_{p}(y),y)\,d\nu(y)\end{align*} $$

for $f\in C((C^{\rho }\backslash X)\times Y)$ . Then, we can study the rigidity of $\rho $ by thinking about $\overline {\psi }_{1},\ldots ,\overline {\psi }_{n}$ . Also, $\overline {\rho }$ is a non-trivial ergodic joining of $u_{X}^{t}$ and $\tilde {u}^{t}_{Y}$ .

Then we can establish the rigidity of $\overline {\psi }_{p}$ by studying the shearing of $u_{X}^{t}$ . The idea comes from [Rat86, Tan22]. We require the time changes having the effective mixing property. Thus, let $\mathbf {K}(Y)$ be the set of all positive integrable functions $\tau $ on Y such that $\tau ,\tau ^{-1}$ are bounded and satisfies

$$ \begin{align*}\bigg|\int_{Y}\tau(y)\tau(u_{Y}^{t}y)\,d\nu(y)-\bigg(\int_{Y}\tau(y)\nu(y)\bigg)^{2}\bigg|\leq D_{\tau}|t|^{-\kappa_{\tau}}\end{align*} $$

for some $D_{\tau },\kappa _{\tau }>0$ . In other words, elements $\tau \in \mathbf {K}(Y)$ have polynomial decay of correlations. Let $\langle u_{X}, a_{X},\overline {u}_{X}\rangle $ , $\langle u_{Y}, a_{Y},\overline {u}_{Y}\rangle $ be $\mathfrak {sl}_{2}$ -triples of $G_{X}$ and $G_{Y}$ , respectively. Let $N_{G_{Y}}(u_{Y})$ be the normalizer of $u_{Y}$ . Then we obtain the following theorem.

Theorem 1.2. (Extra central invariance of $\rho $ )

Let $\tau _{Y}\in \mathbf {K}(Y)$ , $\tilde {u}^{t}_{Y}$ be the time change of $u^{t}_{Y}$ induced by $\tau _{Y}$ and $\rho $ be a non-trivial ergodic joining of $u_{X}^{t},\tilde {u}_{Y}^{t}$ . Then there exist maps $\alpha :N_{G_{Y}}(u_{Y})\times Y\rightarrow \mathbb {R}$ , $\beta :N_{G_{Y}}(u_{Y})\rightarrow C_{G_{Y}}(u_{Y})$ such that the following hold.

1. (1) Restricted to the centralizer $C_{G_{Y}}(u_{Y})$ , $\alpha :C_{G_{Y}}(u_{Y})\times Y\rightarrow \mathbb {R}$ is a cocycle, $\beta :C_{G_{Y}}(u_{Y})\rightarrow C_{G_{X}}(u_{X})$ is a homomorphism. In addition, $\tau _{Y}(cy)$ and $\tau _{Y}( y)$ are (measurably) cohomologous along $u_{Y}^{t}$ via the transfer function $\alpha (c,y)$ for all $c\in C_{G_{Y}}(u_{Y})$ ; in other words,

   $$ \begin{align*}\int_{0}^{T}\tau_{Y}(cu_{Y}^{t}y)-\tau_{Y}(u_{Y}^{t}y) \,dt=\alpha(c,u^{T}_{Y}y)-\alpha(c,y).\end{align*} $$

2. (2) There is a map $S:N_{G_{Y}}(u_{Y})\times X\times Y \rightarrow X\times Y$ that satisfies the following properties.

   • • For $c\in C_{G_{Y}}(u_{Y})$ , the map $S_{c}:X\times Y\rightarrow X\times Y$ defined by

     $$ \begin{align*}S_{c}:(x,y)\mapsto (\beta(c)x,\tilde{u}_{Y}^{-\alpha(c,y)}(cy))\end{align*} $$
     commutes with $u_{X}^{t}\times \widetilde {u}_{Y}^{\,t}$ , and is $\rho $ -invariant. In addition, $S_{c_{1}c_{2}}=S_{c_{1}}\circ S_{c_{2}}$ for any $c_{1},c_{2}\in C_{G_{Y}}(u_{Y})$ , and $S_{u_{Y}^{t}}=\operatorname {\mathrm {id}}$ for $t\in \mathbb {R}$ .

   • • For $r\in \mathbb {R}$ , the map $S_{a^{r}_{Y}}:X\times Y\rightarrow X\times Y$ defined by

     $$ \begin{align*}S_{a^{r}_{Y}}:(x,y)\mapsto (\beta(a^{r}_{Y})a^{r}_{X}x,\tilde{u}_{Y}^{-\alpha(a^{r}_{Y},y)}(a^{r}_{Y}y))\end{align*} $$
     satisfies
     $$ \begin{align*} S_{a^{r}_{Y}}\circ(u_{X}^{t}\times \widetilde{u}_{Y}^{\,t})=(u_{X}^{e^{-r}t}\times \widetilde{u}_{Y}^{\,e^{-r}t})\circ S_{a^{r}_{Y}}\end{align*} $$
     and is $\rho $ -invariant. In addition, $S_{a^{r_{1}+r_{2}}_{Y}}=S_{a^{r_{1}}_{Y}}S_{a^{r_{2}}_{Y}}$ for any $r_{1},r_{2}\in \mathbb {R}$ , and
     $$ \begin{align*}S_{a_{Y}}\circ S_{c}\circ S_{a_{Y}^{-1}}=S_{a_{Y}ca_{Y}^{-1}}\\[-16pt]\end{align*} $$
     for any $c\in C_{G_{Y}}(u_{Y})$ .

For the opposite unipotent direction $\overline {u}_{Y}$ , we cannot obtain the invariance for $\rho $ directly. However, we can fix it by making the ‘a-adjustment.’ Here, we further require that $\tau _{Y}$ be smooth and $\alpha (c,\cdot )$ be integrable. The idea comes from [Rat87]. Then, since $\overline {u}_{Y}$ and $C_{G_{Y}}(u_{Y})$ generate the whole group $G_{Y}$ , we are able to use Ratner’s theorem to get the rigidity of $\overline {\psi }_{1},\ldots ,\overline {\psi }_{n}$ .

Theorem 1.3. (Cohomological criterion)

Let $G_{X}=\mathrm {SO}(n_{X},1)$ , $G_{Y}$ be a semisimple Lie group with finite center and no compact factors and $\Gamma _{X}\subset G_{X}$ , $\Gamma _{Y}\subset G_{Y}$ be irreducible lattices. Let $U_{Y}\in \mathfrak {g}_{Y}$ be a nilpotent vector so that $C_{\mathfrak {g}_{Y}}(U_{Y})$ only contains vectors of weight at most $2$ , and let $u_{Y}=\exp (U_{Y})$ . Let $\tau _{Y}\in \mathbf {K}(Y)\cap C^{1}(Y)$ so that $\tau _{Y}(cy)$ and $\tau _{Y}(y)$ are $L^{1}$ -cohomologous along $u_{Y}^{t}$ for any $c=\exp (v)\in C_{G_{Y}}(u_{Y})$ with positive weight. If there is a non-trivial ergodic joining $\rho $ of $u_{X}^{t}$ and $\tilde {u}_{Y}^{t}$ , then $\tau _{X}\equiv 1$ and $\tau _{Y}$ are joint cohomologous (see Definition 2.2 for the precise definition).

Remark 1.4. When $\tau _{X}\equiv 1$ and $\tau _{Y}$ are joint cohomologous, one can deduce that $1$ (on Y) and $\tau _{Y}$ are (measurably) cohomologous over the flow $u^{t}_{Y}$ . See Proposition 2.14 for further discussion.

In [Tan22], we see that for $G_{Y}=\mathrm {SO}(n_{Y},1)$ , some cocompact lattice $\Gamma _{Y}$ , there exists a function $\tau _{Y}\in \mathbf {K}(Y)\cap C^{1}(Y)$ such that:

• • $\tau _{Y}$ and $1$ are not measurably cohomologous;

• • for any $c\in C_{G_{Y}}(u_{Y})$ , $\tau _{Y}(cy)$ and $\tau _{Y}(y)$ are not measurably cohomologous if they are not $L^{2}$ -cohomologous.

Applying Theorems 1.2(1) and 1.3 to $\tau _{Y}$ , we get the following corollary.

Corollary 1.5. (Existence of non-trivial time changes)

For $G_{Y}=\mathrm {SO}(n_{Y},1)$ , there exists a cocompact lattice $\Gamma _{Y}$ and a function $\tau _{Y}$ on $Y=G_{Y}/\Gamma _{Y}$ such that $u_{X}^{t}$ and $\tilde {u}_{Y}^{t}$ are disjoint (that is, the only joining of $u_{X}^{t}$ and $\tilde {u}_{Y}^{t}$ is the product measure $\mu \times \nu $ ).

In addition, the homomorphism $\beta |_{C_{G_{Y}}(u_{Y})}$ obtained by Theorem 1.2 also provides some information. Combining Ratner’s theorem, we conclude that the existence of non-trivial joinings requires the algebraic structure $G_{Y}$ to be similar to $G_{X}$ .

Theorem 1.6. (Algebraic criterion)

Let the notation and assumptions be as in Theorem 1.3. If there is a non-trivial ergodic joining $\rho $ of $u_{X}^{t}$ and $\tilde {u}_{Y}^{t}$ , then $\rho $ is a finite extension of $\nu $ (that is, the $C^{\rho }$ provided by Theorem 1.1 is trivial). In addition, consider the decomposition (see equation (2.7)):

$$ \begin{align*} C_{\mathfrak{g}_{Y}}(U_{Y})=\mathbb{R}U_{Y}\oplus V^{\perp}_{C_{Y}},\quad C_{\mathfrak{g}_{X}}(U_{X})=\mathbb{R}U_{X}\oplus V^{\perp}_{C_{X}}. \end{align*} $$

Then the derivative $d\beta |_{V^{\perp }_{C}}: V^{\perp }_{C_{Y}}\rightarrow V^{\perp }_{C_{X}}$ is an injective Lie algebra homomorphism.

Remark 1.7. Theorems 1.3 and 1.6 provide criteria for the disjointness of $u_{X}^{t}$ and $\tilde {u}_{Y}^{t}$ . However, they require that the functions $\tau _{Y}(cy)$ and $\tau _{Y}(y)$ are $L^{1}$ -cohomologous for all ${c\in C_{G_{Y}}(u_{Y})}$ with positive weight (Theorem 1.2(1) indicates that they are always measurably cohomologous whenever $u_{X}^{t}$ and $\tilde {u}_{Y}^{t}$ are not disjoint). This condition in general is not easy to verify.

However, when the time changes happen on quotients X of Lorentz groups, we no longer have Theorem 1.1, because of the lack of H-property. Nevertheless, if there exists a joining $\rho $ as in equation (1.1), we can follow the same idea as in Theorem 1.2 and obtain the rigidity in certain situations.

Theorem 1.8. Let $G_{X}=\mathrm {SO}(n_{X},1)$ , $G_{Y}$ be a semisimple Lie group with finite center and no compact factors, and $\Gamma _{X}\subset G_{X}$ , $\Gamma _{Y}\subset G_{Y}$ be irreducible lattices. Let $U_{Y}\in \mathfrak {g}_{Y}$ be nilpotent. Let $\tau _{Y}\equiv 1$ and $\tau _{X}\in \mathbf {K}(X)$ . Suppose that there exists an ergodic joining $\rho $ of $\tilde {u}^{t}_{X}$ and $u^{t}_{Y}$ that is a compact extension of $\nu $ , that is, satisfies equation (1.1). Then there exist maps $\alpha :N_{G_{Y}}(u_{Y})\times Y\rightarrow \mathbb {R}$ , $\beta :N_{G_{Y}}(u_{Y})\rightarrow C_{G_{Y}}(u_{Y})$ such that the following properties hold.

1. (1) Restricted to the centralizer $C_{G_{Y}}(u_{Y})$ , $\alpha :C_{G_{Y}}(u_{Y})\times Y\rightarrow \mathbb {R}$ is a cocycle, $\beta :C_{G_{Y}}(u_{Y})\rightarrow C_{G_{X}}(u_{X})$ is a homomorphism. In addition, $\tau _{X}(cx)$ and $\tau _{X}( x)$ are (measurably) cohomologous for all $c\in C_{G_{X}}(u_{X})$ .

2. (2) There is a map $\widetilde {S}:N_{G_{Y}}(u_{Y})\times X\times Y \rightarrow X\times Y$ that satisfies the following properties.

   • • For $c\in C_{G_{Y}}(u_{Y})$ , the map $\widetilde {S}_{c}:X\times Y\rightarrow X\times Y$ defined by

     $$ \begin{align*} \widetilde{S}_{c}:(x,y) \mapsto ( u_{X}^{\alpha(c,y)}\beta(c)x,cy) \end{align*} $$
     commutes with $\tilde {u}_{X}^{t}\times u_{Y}^{t}$ , and is $\rho $ -invariant. In addition, $\widetilde {S}_{c_{1}c_{2}}=\widetilde {S}_{c_{1}}\circ \widetilde {S}_{c_{2}}$ for any $c_{1},c_{2}\in C_{G_{Y}}(u_{Y})$ , and $\widetilde {S}_{u_{Y}^{t}}=\tilde {u}^{t}_{X}$ for $t\in \mathbb {R}$ .

   • • The map $S_{a_{Y}}:X\times Y\rightarrow X\times Y$ defined for $r\in \mathbb {R}$ by

     $$ \begin{align*}\widetilde{S}_{a^{r}_{Y}}:(x,y)\mapsto (u_{X}^{\alpha(a^{r}_{Y},y)}\beta(a^{r}_{Y})a^{r}_{X}x,a^{r}_{Y}y)\end{align*} $$
     is $\rho $ -invariant. In addition, $\widetilde {S}_{a^{r_{1}+r_{2}}_{Y}}=\widetilde {S}_{a^{r_{1}}_{Y}}\widetilde {S}_{a^{r_{2}}_{Y}}$ for any $r_{1},r_{2}\in \mathbb {R}$ , and
     $$ \begin{align*}\widetilde{S}_{a_{Y}}\circ \widetilde{S}_{c}\circ \widetilde{S}_{a_{Y}^{-1}}=\widetilde{S}_{a_{Y}ca_{Y}^{-1}}\end{align*} $$
     for any $c\in C_{G_{Y}}(u_{Y})$ .

Moreover, for any weight vector $v\in V^{\perp }_{C_{Y}}$ of positive weight, the derivative

(1.2) $$ \begin{align} d\beta|_{V^{\perp}_{C}}(v)\neq0. \end{align} $$

Remark 1.9. In other words, equation (1.2) asserts that $d\beta $ is injective on the nilpotent part of $V^{\perp }_{C_{Y}}$ . One direct consequence of equation (1.2) is that $C_{\mathfrak {g}_{Y}}(U_{Y})$ (under the assumptions of Theorem 1.8) does not contain any weight vector of weight $\neq 0, 2$ (see Lemma 6.5).

In particular, recall that [Rat87] showed that when $G_{X}=\mathrm {SO}(2,1)$ , any time change $\tilde {u}^{t}_{X}$ with $\tau _{X}\in \mathbf {K}(X)\cap C^{1}(X)$ has H-property. It meets all the requirements of Theorem 1.8. Then combining [Rat87], we obtain a slight extension of [DKW22].

Theorem 1.10. Let $G_{X}=\mathrm {SO}(2,1)$ , $G_{Y}$ be a semisimple Lie group with finite center and no compact factors and $\Gamma _{X}\subset G_{X}$ , $\Gamma _{Y}\subset G_{Y}$ be irreducible lattices. Let $\tau _{X}\in \mathbf {K}(X)\cap C^{1}(X)$ . If the Lie algebra $\mathfrak {g}_{Y}\ncong \mathfrak {sl}_{2}$ , then $\tilde {u}_{X}^{t}$ and $u_{Y}^{t}$ are disjoint.

1.2 Structure of the paper

In §2, we recall basic definitions, including some basic material on the Lie algebra $\mathfrak {so}(n,1)$ (in §§2.1 and 2.2), as well as time changes (§2.3) and coboundaries (§2.4). In §3, we make use of the H-property of unipotent flows and deduce Theorem 1.1. This requires studying the shearing property of $u_{X}^{t}$ for nearby points of the form $(x,y)$ and $(gx,y)$ . In §4, we state and prove a number of results which will be used as tools to prove the extra invariance of joinings $\rho $ (Theorem 1.2), in particular Proposition 4.16 which pulls the shearing phenomenon on the homogeneous space X back to the Lie group $G_{X}$ . We also give a quantitative estimate of the difference between two nearby points in terms of the length of the shearing (Lemma 4.11). In §5, we present the proof of Theorem 1.2 (§§5.1 and 5.2) and a technical result for the opposite unipotent direction (Theorem 5.15). The latter result also requires studying the H-property of unipotent flows. Finally, using the results we got and Ratner’s theorem, we present in §6 the proof of Theorems 1.3, 1.6 (in §6.1), 1.8 and 1.10 (in §6.2).

2 Preliminaries

2.1 Definitions

Let

be the set of $g\in SL_{n+1}(\mathbb {R})$ satisfying

$$ \begin{align*} \left[ \begin{array}{ccc} I_{n} & \\ & -1 \\ \end{array} \right]g^{T}\left[ \begin{array}{ccc} I_{n} & \\ & -1 \\ \end{array} \right]=g^{-1}, \end{align*} $$

where $I_{n}$ is the $n\times n$ identity matrix. The corresponding Lie algebra $\mathfrak {g}$ then consists of $v\in \mathfrak {sl}_{n+1}(\mathbb {R})$ satisfying

$$ \begin{align*}\left[ \begin{array}{ccc} I_{n} & \\ & -1 \\ \end{array} \right]v^{T}\left[ \begin{array}{ccc} I_{n} & \\ & -1 \\ \end{array} \right]=-v.\end{align*} $$

Then the Cartan decomposition can be given by

$$ \begin{align*}\mathfrak{g}=\mathfrak{l}\oplus\mathfrak{p}=\left\{\left[ \begin{array}{ccc} \mathbf{l} & \\ & 0 \\ \end{array} \right] :\mathbf{l}\in \mathfrak{so}(n) \right\}\oplus\left\{ \left[ \begin{array}{ccc} 0 & \mathbf{p} \\ \mathbf{p}^{T} & 0 \\ \end{array} \right]: \mathbf{p}\in\mathbb{R}^{n}\right\}\!.\end{align*} $$

Let $E_{ij}$ be the $(n\times n)$ -matrix with $1$ in the $(i,j)$ -entry and $0$ otherwise. Let $e_{k}\in \mathbb {R}^{n}$ be the kth standard basis (vertical) vector. Set

Then $Y_{i},\Theta _{ij}$ form a basis of $\mathfrak {g}=\mathfrak {so}(n,1)$ .

Let $\mathfrak {a}=\mathbb {R}Y_{n}\subset \mathfrak {p}$ be a maximal abelian subspace of $\mathfrak {p}$ . Then the root space decomposition of $\mathfrak {g}$ is given by

(2.1) $$ \begin{align} \mathfrak{g}=\mathfrak{g}_{-1}\oplus\mathfrak{m}\oplus\mathfrak{a}\oplus\mathfrak{g}_{1}. \end{align} $$

Denote by the sum of the positive root spaces. Let $\rho $ be the half sum of positive roots. We also adopt the convention by identifying $\mathfrak {a}^{\ast }$ with $\mathbb {C}$ via $\unicode{x3bb} \mapsto \unicode{x3bb} (Y_{n})$ . Thus, $\rho =\rho (Y_{n})=(n-1)/2$ .

Let $\Gamma \subset G$ be a lattice,

, $\mu $ be the Haar probability measure on X. Fix a nilpotent $U\in \mathfrak {g}_{-1}$ . On $G/\Gamma $ , denote by:

• • a geodesic flow;

• • a unipotent flow.

It is worth noting that

$$ \begin{align*}[Y_{n},U]=-U.\end{align*} $$

Then there exists $\overline {U}\in \mathfrak {g}$ such that $\{U,Y_{n},\overline {U}\}$ is an $\mathfrak {sl}_{2}$ -triple. Denote

For convenience, we choose

(2.2)

Then $\langle u^{t},a^{t},\overline {u}^{t}\rangle $ generates $\mathrm {SO}(2,1)\subset \mathrm {SO}(n,1)$ .

2.2 $\mathfrak {sl}_{2}$ -weight decomposition

First, consider an arbitrary Lie algebra $\mathfrak {g}$ as a $\mathfrak {sl}_{2}$ -representation via the adjoint map (after identifying an image of $\mathfrak {sl}_{2}$ by Jacobson– Morozov theorem), then by the complete reducibility of $\mathfrak {sl}_{2}$ , there is a decomposition of $\mathfrak {sl}_{2}$ -representations

(2.3) $$ \begin{align} \mathfrak{g}=\mathfrak{sl}_{2}\oplus V^{\perp}, \end{align} $$

where $V^{\perp }\subset \mathfrak {g}$ is the sum of $\mathfrak {sl}_{2}$ -irreducible representations other than $\mathfrak {sl}_{2}$ . In particular, for $\mathfrak {g}=\mathfrak {so}(n,1)$ , we have

(2.4) $$ \begin{align} V^{\perp}=\sum_{i} V_{i}^{0}\oplus\sum_{j} V_{j}^{2}, \end{align} $$

where $V_{i}^{0}$ and $V_{j}^{2}$ are $\mathfrak {sl}_{2}$ -irreducible representations with highest weights $0$ and $2$ . More precisely, we have the following lemma.

Lemma 2.1. By the weight decomposition, an irreducible $\mathfrak {sl}_{2}$ -representation $V^{\varsigma }$ is the direct sum of weight spaces, each of which is $1$ -dimensional. More precisely, there exists a basis $v_{0},\ldots ,v_{\varsigma }\in V^{\varsigma }$ such that

$$ \begin{align*}U.v_{i}=(i+1)v_{i+1},\quad Y_{n}.v_{i}= \frac{\varsigma-2i}{2}v_{i}.\end{align*} $$

Thus, if $V^{\varsigma }$ is an irreducible representation of $\mathfrak {sl}_{2}$ with the highest weight $\varsigma \leq 2$ , then for any $v=b_{0}v_{0}+\cdots +b_{\varsigma }v_{\varsigma }\in V^{\varsigma }$ , we have

(2.5) $$ \begin{align} \exp(tU).v=&\sum_{j=0}^{\varsigma}\sum_{i=0}^{j}b_{i}\binom{j}{i}t^{j-i}v_{j}, \; \end{align} $$

(2.6) $$ \begin{align} \hphantom{\hspace{-17pt}}\exp(\omega Y_{n}).v=& \sum_{j=0}^{\varsigma} b_{j}e^{ (\varsigma-2j)\omega /2} v_{j}. \; \end{align} $$

For elements $g\in \exp \mathfrak {g}$ close to identity, we decompose

$$ \begin{align*}g=h\exp(v),\quad h\in \mathrm{SO}_{0}(2,1),\quad v\in V^{\perp}\end{align*} $$

where $\mathrm {SO}_{0}(2,1)$ is the connected component of $\mathrm {SO}(2,1)$ . Moreover, it is convenient to think about $h\in \mathrm {SO}_{0}(2,1)$ as a $(2\times 2)$ -matrix with determinant $1$ . Thus, consider the two-to-one isogeny $\iota :SL_{2}(\mathbb {R})\rightarrow \mathrm {SO}(2,1)\subset G$ induced by ${\mathfrak {sl}_{2}(\mathbb {R})\rightarrow \operatorname {\mathrm {Span}}\{U,Y_{n},\bar {U}\} \subset \mathfrak {g}}$ . In the following, for $h\in \mathrm {SO}_{0}(2,1)$ and v in an irreducible representation, we write

$$ \begin{align*}h=\left[ \begin{array}{ccc} a & b \\ c & d\\ \end{array} \right]\!,\quad v=b_{0}v_{0}+\cdots+b_{\varsigma}v_{\varsigma}\end{align*} $$

where $v_{i}$ are weight vectors in $\mathfrak {g}$ of weight i. Notice that h should more appropriately be written as $\iota (h)$ . In addition, for notational simplicity, we shall usually assume that ${v\in V^{\perp }}$ lies in a single irreducible representation, since the proofs will mostly focus on the $\operatorname {\mathrm {Ad}} u^{t}$ -action and so the general case will be identical but tedious to write down.

For the centralizer $ C_{\mathfrak {g}}(U)$ (for an arbitrary Lie algebra $\mathfrak {g}$ ), we have the corresponding decomposition:

(2.7) $$ \begin{align} C_{\mathfrak{g}}(U)=\mathbb{R}U\oplus V^{\perp}_{C}, \end{align} $$

where $V^{\perp }_{C}\subset V^{\perp }$ consists of the highest weight vectors other than U. In particular, for $\mathfrak {g}=\mathfrak {so}(n,1)$ , under the setting of equation (2.2), one may calculate

(2.8) $$ \begin{align} C_{\mathfrak{g}}(U)&=\mathbb{R}U\oplus V^{\perp}_{C}=\mathbb{R}U\oplus \mathfrak{k}^{\perp}_{C}\oplus \mathfrak{n}^{\perp}_{C} \;\nonumber\\ &= \mathbb{R}U\oplus\left[ \begin{array}{ccc} \mathfrak{so}(n-2) & \\ & 0 \\ \end{array} \right] \oplus\left\{ \left[ \begin{array}{cccc} 0& 0 & \mathbf{u} & \mathbf{u} \\ 0& 0 & 0 & 0 \\ -\mathbf{u}^{T} & 0 & 0 & 0\\ \mathbf{u}^{T} &0 &0 & 0 \\ \end{array} \right]: \mathbf{u}\in\mathbb{R}^{n-2}\right\}\!. \; \end{align} $$

Note that $\mathfrak {k}^{\perp }_{C}$ consists of semisimple elements and $\mathfrak {n}^{\perp }_{C}$ consists of nilpotent elements, and they satisfy $[\mathfrak {k}^{\perp }_{C},\mathfrak {n}^{\perp }_{C}]=\mathfrak {n}^{\perp }_{C}$ .

2.3 Time changes

Let Y be a homogeneous space and U be a nilpotent. Let $\phi ^{U,\tau }_{t}$ be a time change for the unipotent flow $\phi ^{U}_{t}$ , $t\in \mathbb {R}$ . Thus, we assume that:

• • $\tau :Y\rightarrow \mathbb {R}^{+}$ is a integrable non-negative function on Y satisfying

  $$ \begin{align*}\int_{Y}\tau(y)\,dm_{Y}(y)=1; \end{align*} $$

• • $\xi :Y\times \mathbb {R}\rightarrow \mathbb {R}$ is the cocycle determined by

  $$ \begin{align*} t=\int_{0}^{\xi(y,t)}\tau(u^{s}y)\,ds=\int_{0}^{\xi(y,t)}\tau(\phi_{t}^{U} y)\,ds; \end{align*} $$

• • $\phi ^{U,\tau }_{t}:Y\rightarrow Y$ is given by the relation

  

Remark 2.2. Note that $\phi ^{U,1}_{t}=\phi ^{U}_{t}$ . In addition, one can check that $\phi ^{U,\tau }_{t}$ preserves the probability measure on Y defined by , where $m_{Y}$ is the Lebesgue measure on Y. However, if $\tau $ is smooth, then the time change $\phi _{t}^{U,\tau }$ is the flow on Y generated by the smooth vector field .

In practice, we define $z:Y\times \mathbb {R}\rightarrow \mathbb {R}$ by

$$ \begin{align*}z(y,t)=\int_{0}^{t}\tau(u^{s}y)\,ds.\end{align*} $$

It follows that

(2.9) $$ \begin{align} t=z(y,\xi(y,t)),\quad \phi^{U,\tau}_{z(y,t)}(x)=\phi^{U}_{t}(y)= u^{t}y. \end{align} $$

Let $\kappa>0$ and $\mathbf {K}_{\kappa }(Y)$ be the collection of all positive integrable functions $\tau $ on Y such that $\tau ,\tau ^{-1}$ are bounded and satisfy

(2.10) $$ \begin{align} \bigg|\int_{Y}\tau(y)\tau(u^{t}y)\,d\nu(y)-\bigg(\int_{Y}\tau(y)\nu(y)\bigg)^{2}\bigg|\leq D_{\tau}|t|^{-\kappa} \end{align} $$

for some $D_{\tau }>0$ . Let $\mathbf {K}(Y)=\bigcup _{\kappa>0}\mathbf {K}_{\kappa }(Y)$ . This is the effective mixing property of the unipotent flow $\phi _{t}^{U}$ . Note that [KM99] (see also [Ven10]) has shown that there is $\kappa>0$ such that

$$ \begin{align*}\bigg|\langle\phi^{U}_{t}(f),g\rangle-\bigg(\int_{Y}f(y)\nu(y)\bigg)\bigg(\int_{Y}g(y)\nu(y)\bigg)\bigg|\ll(1+|t|)^{-\kappa}\|f\|_{W^{s}}\|g\|_{W^{s}}\end{align*} $$

for $f,g\in C^{\infty }(X)$ , where $s\geq \dim (K)$ and $W^{s}$ denotes the Sobolev norm on $Y=G/\Gamma $ . According to Lemma 3.1 [Rat86], when $\tau \in \mathbf {K}_{\kappa }(Y)$ , we have the effective ergodicity: there is $K\subset Y$ with $\nu (K)>1-\sigma $ and $t_{K}>0$ such that

(2.11) $$ \begin{align} |t-z(y,t)|=O(t^{1-\kappa}) \end{align} $$

for all $t\geq t_{K}$ and $y\in K$ . Later on, we shall make use of the effective mixing/ergodicity to study the shearing property of unipotent flows (see §4 and equation (5.1)).

2.4 Cohomology

We first introduce the $1$ -coboundary of two functions.

Definition 2.1. (Cohomology)

We say that two functions $\tau _{1},\tau _{2}$ on Y are measurable (respectively $L^{2}$ , smooth, etc.) cohomologous over the flow $\phi _{t}$ if there exists a measurable (respectively $L^{2}$ , smooth, etc.) function f on Y, called the transfer function, such that

(2.12) $$ \begin{align} \int_{0}^{T}\tau_{1}(\phi_{t}y)-\tau_{2}(\phi_{t}y)\,dt=f(\phi_{T}y)-f(y). \end{align} $$

For $i\in \{1,2\}$ , let $(Y_{i},\mathcal {Y}_{i},\nu _{i},\phi _{t}^{(i)})$ be measure-preserving flows, and let $\tau _{i}:Y_{i}\rightarrow \mathbb {R}$ be measurable functions on $Y_{i}$ . In addition, we extend $\tau _{i}$ to $Y_{1}\times Y_{2}$ by setting

$$ \begin{align*}\tau_{i}: (y_{1},y_{2})\mapsto\tau_{i}(y_{i}),\quad i=1,2. \end{align*} $$

Definition 2.2. (Joint cohomology)

Let $\rho \in J(\phi _{t}^{(1)},\phi _{t}^{(2)})$ be a joining of $\phi _{t}^{(1)}$ and $\phi _{t}^{(2)}$ . We say that $\tau _{1}$ and $\tau _{2}$ are jointly cohomologous via $\rho $ if $\tau _{1}$ and $\tau _{2}$ (considered as functions on $Y_{1}\times Y_{2}$ ) are cohomologous over $\phi _{t}^{(1)}\times \phi _{t}^{(2)}$ on $(Y_{1}\times Y_{2},\rho )$ . More specifically, if $\tau _{1}$ and $\tau _{2}$ are cohomologous over $\phi _{t}^{(1)}\times \phi _{t}^{(2)}$ with a transfer function $f:Y_{1}\times Y_{2}\rightarrow \mathbb {R}$ , then we say that $\tau _{1}$ and $\tau _{2}$ are jointly cohomologous via $(\rho ,f)$ , and we have

(2.13) $$ \begin{align} \int_{0}^{T}(\tau_{1}-\tau_{2})(\phi^{(1)}_{t}y_{1}, \phi^{(2)}_{t}y_{2})\,dt= f(\phi^{(1)}_{T}y_{1}, \phi^{(2)}_{T}y_{2})-f(y_{1}, y_{2}) \end{align} $$

for $\rho $ -a.e. $(y_{1},y_{2})\in Y_{1}\times Y_{2}$ and all $T\in \mathbb {R}$ .

Let , . Then there is a unique family $\{\rho _{y_{1}}^{\mathcal {A}_{1}}:y_{1}\in Y_{1}\}$ of probability measure, called the conditional measures, on $Y_{2}$ such that

(2.14) $$ \begin{align} E^{\rho}(g|\mathcal{A}_{1})(y_{1})=\int_{Y_{2}}g(y_{1},y_{2})d\rho_{y_{1}}^{\mathcal{A}_{1}}(y_{2}),\quad \rho^{\mathcal{A}_{1}}_{\phi^{(1)}_{t}y_{1}}=(\phi^{(2)}_{t})_{\ast}\rho^{\mathcal{A}_{1}}_{y_{1}} \end{align} $$

for every $g\in L^{1}(Y_{1}\times Y_{2},\rho )$ , $t\in \mathbb {R}$ , and $\nu _{1}$ -a.e. $y_{1}\in Y_{1}$ . Taking the integration over $\rho _{y_{1}}^{\mathcal {A}_{1}}$ , the expressions of equations (2.13) and (2.14) show that if the transfer function $f(y_{1},\cdot )\in L^{1}(Y_{2},\rho ^{\mathcal {A}_{1}}_{y_{1}})$ for $\nu _{1}$ -a.e. $y_{1}\in Y_{1}$ , then $\tau _{1}$ and $E^{\rho }(\tau _{2}|\mathcal {A}_{1})$ are cohomologous along $\phi ^{(1)}_{t}$ via $E^{\rho }(f|\mathcal {A}_{1})$ . We have just proved the following proposition.

Proposition 2.3. Let $\tau _{i}:Y_{i}\rightarrow \mathbb {R}$ be measurable functions on $Y_{i}$ , $i=1,2$ . Suppose that $\tau _{1}$ and $\tau _{2}$ are jointly cohomologous via $(\rho ,f)$ with $f(y_{1},\cdot )\in L^{1}(Y_{2},\rho ^{\mathcal {A}_{1}}_{y_{1}})$ for $\mu _{1}$ -a.e. $y_{1}\in Y_{1}$ . Then $\tau _{1}$ and $E^{\rho }(\tau _{2}|\mathcal {A}_{1})$ are cohomologous over $\phi ^{(1)}_{t}$ via $E^{\rho }(f|\mathcal {A}_{1})$ .

3 Shearing property I, H-flow on one factor

3.1 Joinings

Let $G=\mathrm {SO}(n,1)$ , $\Gamma $ be a lattice of G, $(X,\mu )$ be the homogeneous space $X=G/\Gamma $ equipped with the Lebesgue measure $\mu $ , and let $\phi ^{U}_{t}$ be a unipotent flow on X. Let $(Y,\nu ,S)$ be a measure-preserving system. We want to study the joinings of $(X,\mu ,\phi _{1}^{U})$ and $(Y,\nu ,S)$ . Thus, let $\rho $ be an ergodic joining of $\phi _{1}^{U}$ and S, that is, $\rho $ is a probability measure on $X\times Y$ , whose marginals on X and Y are $\mu $ and $\nu $ , respectively, and which is $(\phi _{1}^{U}\times S)$ -ergodic.

Let $C(\phi _{1}^{U})$ be the commutant of $\phi _{1}^{U}$ , that is, the collection of all measure-preserving transformations on X that commute with $\phi _{1}^{U}$ . The following is a basic criterion for $\rho $ in terms of the commutant of $\phi _{1}^{U}$ .

Lemma 3.1. Let the notation and assumptions be as above. Assume further that $T\in C(\phi _{1}^{U})$ is ergodic on $(X,\mu )$ . Then

$$ \begin{align*} \text{either }(T\times\operatorname{\mathrm{id}})_{\ast}\rho\perp\rho\quad \text{or}\quad\rho=\mu\times\nu.\end{align*} $$

Proof. First, by the commutative property of T, we easily see that $(T\times \operatorname {\mathrm {id}})_{\ast }\rho $ is again $(\phi _{1}^{U}\times S)$ -ergodic on $X\times Y$ . It implies that either $(T\times \operatorname {\mathrm {id}})_{\ast }\rho \perp \rho $ or $(T\times \operatorname {\mathrm {id}})_{\ast }\rho =\rho $ . Now assume that $(T\times \operatorname {\mathrm {id}})_{\ast }\rho =\rho $ , that is, $\rho $ is $(T\times \operatorname {\mathrm {id}})$ -invariant. Then via disintegration, we know that $\rho _{y}$ is T-invariant on X for $\nu $ -a.e. $y\in Y$ , where

(3.1) $$ \begin{align} \rho=\int_{Y}\rho_{y}\,d\nu(y). \end{align} $$

Now assume for contradiction that there exists $B\subset Y$ with $\nu (B)>0$ such that $\rho _{y}\neq \mu $ for $y\in B$ . It follows that for $y\in B$ , there is $A_{y}\subset X$ with $\mu (A_{y})>0$ such that, for $x\in A_{y}$ , we have

(3.2) $$ \begin{align} (\rho_{y})_{x}^{\mathcal{E}}\neq\mu, \end{align} $$

where $(\rho _{y})_{x}^{\mathcal {E}}$ is given by the T-ergodic decomposition

$$ \begin{align*}\rho_{y}=\int_{X}(\rho_{y})_{x}^{\mathcal{E}}\,d\mu(x).\end{align*} $$

Notice that by the ergodicity, there is a $\mu $ -conull set $\Omega \subset X$ , namely the set of T-generic points of $\mu $ , such that $(\rho _{y})_{x}^{\mathcal {E}}(\Omega )=0$ for the measures $(\rho _{y})_{x}^{\mathcal {E}}$ in equation (3.2). Then by the assumption of joining, we have

$$ \begin{align*} \mu(\Omega)=\rho(\pi_{X}^{-1}(\Omega))&= \int_{Y}\rho_{y} (\Omega)\,d\nu(y)\;\nonumber\\ &= \int_{B}\rho_{y}(\Omega)\,d\nu(y)+\int_{Y\setminus B}\rho_{y}(\Omega)\,d\nu(y)\;\nonumber\\ &\leq \int_{B}\int_{X}(\rho_{y})_{x}^{\mathcal{E}}(\Omega)\,d\mu(x)\,d\nu(y)+ \nu(Y\setminus B)\;\nonumber\\ &= \int_{B}\int_{X\setminus A_{y}}(\rho_{y})_{x}^{\mathcal{E}}(\Omega)\,d\mu(x)\,d\nu(y)+ \nu(Y\setminus B)\;\nonumber\\ &\leq \int_{B} \mu(X\setminus A_{y})\,d\nu(y)+ \nu(Y\setminus B)\;\nonumber\\ &<\nu(B)+\nu(Y\setminus B)=1,\nonumber \end{align*} $$

which is a contradiction. Thus, we conclude that $\rho _{y}=\mu $ for $\nu $ -a.e. $y\in Y$ and so $\rho = \mu \times \nu $ .

By Moore’s ergodicity theorem, we deduce the following corollary.

Corollary 3.2. If $w\in C_{\mathfrak {g}}(U)$ so that $\langle \exp tw\rangle _{t\in \mathbb {R}}$ is not compact, then

$$ \begin{align*}\text{either }(\phi^{w}_{1}\times\operatorname{\mathrm{id}})_{\ast}\rho\perp\rho\quad\text{or}\quad \rho=\mu\times\nu.\end{align*} $$

3.2 H-property

In this section, we want to introduce the H-property (or Ratner property) to study the joining $\rho $ in terms of the unipotent flow $\phi ^{U}_{t}$ on X. The classic H-property can be formulated as the following theorem.

Theorem 3.3. (H-property, [Wit85])

Let u be a unipotent element of G. Given any neighborhood Q of e in $C_{G}(u)$ , there is a compact subset $\partial Q$ of $Q\setminus \{e\}$ such that, for any $\epsilon>0$ and $M>0$ , there are $\alpha =\alpha (u,Q,\epsilon )>0$ and $\delta =\delta (u,Q,\epsilon ,M)>0$ such that if $x_{1},x_{2}\in X$ with $d_{X}(x_{1},x_{2})<\delta $ , then one of the following holds:

• • $x_{2}=cx_{1}$ for some $c\in C_{G}(u)$ with $d_{G}(e,c)<\delta $ ;

• • there are $L>M/\alpha $ and $q\in \partial Q$ such that

  (3.3) $$ \begin{align} d_{X}(u^{n}x_{2},qu^{n}x_{1})<\epsilon \end{align} $$
  whenever $n\in [L,(1+\alpha )L]$ .

Remark 3.4. In fact, for $x_{2}=gx_{1}$ with $g=\exp (v)\in B^{G}_{\delta }$ , the element $q\in C_{\mathfrak {g}}(U)$ in Theorem 3.3 is chosen by

(3.4) $$ \begin{align} q=\pi_{C_{\mathfrak{g}}(U)}\exp(LU).v, \end{align} $$

where $\pi _{C_{\mathfrak {g}}(U)}: \mathfrak {g}\rightarrow C_{\mathfrak {g}}(U)$ is the natural projection and $\exp (LU).v$ is the adjoint representation (see equation (2.5)). We often call q as the fastest relative motion between $x_{1},x_{2}$ ; see [Mor05] for more discussion. In what follows, we choose $Q=B_{\unicode{x3bb} }^{C_{G}(u)}$ to be the ball of radius $\unicode{x3bb} $ of e in $C_{G}(u)$ for sufficiently small $\unicode{x3bb} $ (independent of $\epsilon $ ), and then $\partial Q$ is the sphere of radius $\unicode{x3bb} $ . Now by equations (2.3) and (2.4), we have the decomposition

$$ \begin{align*} v=v_{0}+v_{2}, \end{align*} $$

where $v_{0}\in \sum _{i} V_{i}^{0}$ and $v_{2}\in \mathfrak {sl}_{2}+\sum _{j} V_{j}^{2}$ . Thus, $\|v_{0}\|,\|v_{2}\|<\delta $ and

$$ \begin{align*} q=v_{0}+\pi_{C_{\mathfrak{g}}(U)}\exp(LU).v_{2}. \end{align*} $$

Since $\|q\|=\unicode{x3bb} $ , we see that $v_{0}$ is negligible. In other words, we can replace q by

(3.5)

and then Theorem 3.3 still holds. However, note that $q^{\prime }\in \mathfrak {n}= \mathbb {R}U+\mathfrak {n}_{C}^{\perp }$ (cf. equation (2.8)). Thus, the one-parameter group $\langle \exp (tq^{\prime })\rangle _{t\in \mathbb {R}}$ generated by $q^{\prime }$ is not compact.

In the following, we shall generalize the idea in [Rat83] and prove Theorem 1.1.

Theorem 3.5. Let the notation and assumptions be as above. Then either $\rho =\mu \times \nu $ or $(\phi ^{U}_{1}\times S,\rho )$ is a compact extension of $(S,\nu )$ . More precisely, if $\rho \neq \mu \times \nu $ , then there exists a $\nu $ -conull set $\Theta \subset Y$ , a compact subgroup $C^{\rho }\subset C_{G}(u)$ , and $n>0$ such that, for any $y\in \Theta $ , there exist $x_{1}^{y},\ldots ,x_{n}^{y}$ in the support of $\rho _{y}$ with

$$ \begin{align*}\rho_{y}(C^{\rho}x_{i}^{y})=\frac{1}{n}\end{align*} $$

for $i=1,\ldots ,n$ , where $ \rho =\int _{Y}\rho _{y}\,d\nu (y)$ is the disintegration along Y (cf. equation (3.1)).

Assume that $\rho \neq \mu \times \nu $ . Then by Corollary 3.2, there is a $\rho $ -conull set $\Omega \subset X\times Y$ , namely the set of $(\phi _{1}^{U}\times S)$ -generic points, such that $(\phi ^{w}_{1}\times \operatorname {\mathrm {id}}) (\Omega )\cap \Omega =\emptyset $ for all $w\in \mathfrak {n}$ . Given a sufficiently small $\unicode{x3bb}>0$ , we define the sphere of radius $\unicode{x3bb} $ of $0$ by

Then, one can find a compact subset $K_{1}\subset \Omega $ with $\mu (K_{1})>199/200$ . Then,

$$ \begin{align*} \bigcup_{w\in B^{\mathfrak{n}}_{\unicode{x3bb}}}(\phi^{w}_{1}\times \operatorname{\mathrm{id}})(K_{1}) \end{align*} $$

is compact. Thus, there are $\epsilon>0$ and $K_{2}\subset K_{1}$ with $\mu (K_{2})>99/100$ such that

$$ \begin{align*}d_{X\times Y}\bigg(K_{2},\bigcup_{w\in B^{\mathfrak{n}}_{\unicode{x3bb}}}(\phi^{w}_{1}\times \operatorname{\mathrm{id}})(K_{1}) \bigg)>\epsilon. \end{align*} $$

It follows that if $(x_{1},y),(x_{2},y)\in K_{2}$ then

(3.6) $$ \begin{align} d_{X}(x_{2},\phi^{w}_{1}x_{1})\geq\epsilon \end{align} $$

for all $w\in B^{\mathfrak {n}}_{\unicode{x3bb} }$ . Let $\alpha =\alpha (\epsilon )>0$ be as in Theorem 3.3. Comparing equation (3.6) with equation (3.3), we conclude the following lemma.

Lemma 3.6. Assume that $\rho \neq \mu \times \nu $ . There is a positive number $\delta =\delta (\epsilon )>0$ , a measurable set $K_{4}\subset \Omega $ with $\rho (K_{4})>0$ such that if $(x_{1},y),(x_{2},y)\in K_{4}$ and $d_{X}(x_{1},x_{2})<\delta $ , then $x_{2}\in C_{G}(u)x_{1}$ .

Proof. Suppose that M, $\delta $ , $K_{4}$ are given, and $x_{2}\not \in C_{G}(u)x_{1}$ with $d_{X}(x_{1},x_{2})<\delta $ . Then by the H-property of the unipotent flow (Theorem 3.3 and Remark 3.4), we know that there are $L>M/\alpha $ and $w\in B^{\mathfrak {n}}_{\unicode{x3bb} }$ such that

(3.7) $$ \begin{align} d_{X}(\phi^{U}_{n}x_{1},\phi^{w}_{1}\phi^{U}_{n}x_{2})<\epsilon \end{align} $$

for $n\in [L,(1+\alpha )L]$ . Next, we shall find some qualified $x_{1},x_{2}\in X$ such that the distance between $\phi ^{U}_{n}x_{1}$ and $\phi ^{w}_{1}\phi ^{U}_{n}x_{2}$ is at least $\epsilon $ . This will lead to a contradiction.

First, applying the ergodic theorem, there is a measurable set $K_{3}\subset \Omega $ with $\rho (K_{3})>1-\alpha /2(100+\alpha )$ , a number $M_{1}>0$ such that

(3.8) $$ \begin{align} \frac{1}{n}|\{k\in [0,n]:(\phi^{U}_{1}\times S)^{k}(x,y)\in K_{2}\}|> \frac{9}{10} \end{align} $$

for $(x,y)\in K_{3}$ and $n>M_{1}$ . Applying the ergodic theorem one more time, there is a measurable set $K_{4}\subset \Omega $ with $\rho (K_{4})>0$ , a number $M_{2}>0$ such that

(3.9) $$ \begin{align} \frac{1}{n}|\{k\in [0,n]:(\phi^{U}_{1}\times S)^{k}(x,y)\in K_{3}\}|> 1-\frac{\alpha}{10+\alpha} \end{align} $$

for $(x,y)\in K_{4}$ and $n>M_{2}$ .

Choose $M=\max \{M_{1},M_{2}\}$ and then $L>M/\alpha $ and $\delta =\delta (\epsilon ,M)>0$ as obtained from the H-property (Theorem 3.3). Let $(x_{1},y),(x_{2},y)\in K_{4}$ with $d_{X}(x_{1},x_{2})<\delta $ . Then replacing n by $(1+\alpha /10)L$ and applying equation (3.9), we know that

$$ \begin{align*}(\phi^{U}_{1}\times S)^{s}(x_{1},y),(\phi^{U}_{1}\times S)^{t}(x_{2},y)\in K_{3}\end{align*} $$

for some integers $s,t\in [L,(1+\alpha /10)L]$ . Further, replacing the interval $[0,n]$ by $[s,(1+\alpha )L]$ (respectively $[t,(1+\alpha )L]$ ) and applying equation (3.8), we know that

$$ \begin{align*}\frac{1}{(1+\alpha)L-s}|\{k\in [s,(1+\alpha)L]:(\phi^{U}_{1}\times S)^{k}(x_{1},y)\in K_{2}\}|> \frac{9}{10}, \end{align*} $$

$$ \begin{align*}\frac{1}{(1+\alpha)L-t}|\{k\in [t,(1+\alpha)L]:(\phi^{U}_{1}\times S)^{k}(x_{2},y)\in K_{2}\}|> \frac{9}{10}. \end{align*} $$

It follows that there exists $n\in [(1+\alpha /10)L,(1+\alpha )L]$ such that

$$ \begin{align*}(\phi^{U}_{1}\times S)^{n}(x_{1},y),\ (\phi^{U}_{1}\times S)^{n}(x_{2},y)\in K_{2}.\end{align*} $$

Then by equation (3.6), we have

$$ \begin{align*} d_{X}(\phi^{U}_{n}x_{1},\phi^{w}_{1}\phi^{U}_{n}x_{2})\geq\epsilon, \end{align*} $$

which contradicts equation (3.7).

Recall that via disintegration (cf. equation (3.1)), we have

$$ \begin{align*} \rho=\int_{Y}\rho_{y}\,d\nu(y). \end{align*} $$

Then by the ergodic theory, we have the following lemma.

Lemma 3.7. Assume that $\rho \neq \mu \times \nu $ . There exists a $\nu $ -conull set $\Theta \subset Y$ and $n>0$ such that, for any $y\in \Theta $ , there exist $x_{1}^{y},\ldots ,x_{n}^{y}$ in the support of $\rho _{y}$ with

$$ \begin{align*}\rho_{y}(C_{G}(u)x_{i}^{y})=\frac{1}{n} \end{align*} $$

for $i=1,\ldots ,n$ .

Proof. Let $f:Y\rightarrow \mathbb {R}$ be defined by

$$ \begin{align*} f:y\mapsto\sup_{x\in X}\rho_{y}(C_{G}(u)x). \end{align*} $$

By Lemma 3.6, we know that for , $f(y)>0$ . Note also that $\nu (K_{4}^{Y})>0$ and f is S-invariant. By the ergodicity, f is a positive constant, say $f\equiv c$ , on a $\nu $ -conull set $\Theta _{1}\subset Y$ .

Next, consider

Then D is $(\phi ^{U}_{1}\times S)$ -invariant and $\rho (D)>0$ . Thus, $\rho (D)=1$ . Next, define

Then $\Theta \subset Y$ is an S-invariant $\nu $ -conull set. Thus, for any $y\in \Theta $ , we have

$$ \begin{align*}\rho_{y}(C_{G}(u)x)\equiv c \end{align*} $$

for any $x\in X$ with $(x,y)\in D$ . It forces $n=1/c$ to be an integer. In addition, for any $y\in \Theta $ , there are only finitely many points $x_{1}^{y},\ldots ,x_{n}^{y}$ with

$$ \begin{align*} \rho_{y}(C_{G}(u)x_{i}^{y})=\frac{1}{n} \end{align*} $$

for $i=1,\ldots ,n$ .

Thus, by Lemma 3.7, we see that $\rho _{y}$ supports on $\bigsqcup _{i=1}^{n}C_{G}(u)x_{i}^{y}$ whenever $y\in \Theta $ . With a further effort, we observe that these $\rho _{y}$ must have a compact support.

Proof of Theorem 3.5

For a Borel measurable subset $A\subset C_{G}(u)$ , consider the map $f_{A}:X\times Y\rightarrow \mathbb {R}^{+}$ be defined by

$$ \begin{align*} f_{A}:(x,y)\mapsto \rho_{y}(Ax). \end{align*} $$

Note that since $\rho $ is $(\phi ^{U}_{1}\times S)$ -invariant, we have

$$ \begin{align*} (\phi^{U}_{1})_{\ast}\rho_{y}=\rho_{Sy}. \end{align*} $$

It follows that

$$ \begin{align*}f_{A}(x,y)=\rho_{y}(Ax)=\rho_{Sy}(\phi^{U}_{1}Ax)=\rho_{Sy}(A\phi^{U}_{1}x)=f_{A}(\phi^{U}_{1}x,Sy).\end{align*} $$

In other words, $f_{A}$ is $(\phi ^{U}_{1}\times S)$ -invariant and therefore is $\rho $ -almost everywhere a constant, say $m(A)$ . Thus, for any $A\in \mathcal {B}(C_{G}(u))$ , there exists a $\rho $ -conull set $\Omega _{A}\subset X\times Y$ , such that

(3.10) $$ \begin{align} \rho_{y}(Ax)\equiv m(A) \end{align} $$

for $(x,y)\in \Omega _{A}$ .

Next, we consider the fundamental domain, that is, a Borel subset $F\subset C_{G}(u)$ such that the natural map $F\rightarrow C_{G}(u)/(C_{G}(u)\cap \Gamma )$ defined by $g\mapsto g\Gamma $ is bijective. Then since $\mathcal {B}(F)$ is countably generated, by Carathéodory’s extension theorem, we know that $m:\mathcal {B}(F)\rightarrow \mathbb {R}^{+}$ is a measure. In addition, it follows from equation (3.10) that there exists a $\rho $ -conull set $\Omega \subset X\times Y$ , such that

(3.11) $$ \begin{align} \rho_{y}(Ax)\equiv m(A) \end{align} $$

for $(x,y)\in \Omega $ , $A\in \mathcal {B}(F)$ .

Now assume that equation (3.11) holds for $(x,y),(gx,y)\in \Omega $ and $g\in C_{G}(u)$ . Then,

$$ \begin{align*}m(A)=\rho_{y}(Agx)=m(Ag) \end{align*} $$

for $A\in \mathcal {B}(F)$ . In other words, m is g-(right) invariant and so is (right) Haar. Note that $C_{G}(u)$ is unimodular (since its Lie algebra $C_{\mathfrak {g}}(U)$ is a direct sum of a compact and a nilpotent Lie subalgebra). We conclude that m is also a (left) Haar measure, and therefore $\rho _{y}$ is (left) Haar on $C_{G}(u)x$ for $(x,y)\in \Omega $ .

Let $C^{\rho }$ be the stabilizer of m. Then the above result shows that $\rho $ is $(C^{\rho }\times \operatorname {\mathrm {id}})$ -invariant. Thus, according to Corollary 3.2, $C^{\rho }$ must be compact. This finishes the proof of Theorem 3.5.

Using Theorem 3.5, for any ergodic joining $\rho $ of $\phi _{1}^{U}$ and S on $X\times Y$ , we obtain an ergodic joining of $\phi _{1}^{U}$ and S on $C^{\rho }\backslash X\times Y$ under the natural projection $\pi : X\times Y\rightarrow C^{\rho }\backslash X\times Y$ . Moreover, when $\overline {\rho }\neq \overline {\mu }\times \nu $ is not the product measure, it is a finite extension of $\nu $ , that is, $\operatorname {\mathrm {supp}}\overline {\rho }_{y}$ consists of exactly n points $\overline {x}_{1}^{y},\ldots ,\overline {x}_{n}^{y}$ for $\nu $ -a.e. $y\in Y$ (without loss of generality, we shall assume that it holds for all $y\in Y$ ). Note that $y\mapsto \overline {x}_{i}^{y}$ need not be measurable. However, this can be resolved by using Kunugui’s theorem (see [Kal75, Kun40]).

Therefore, let , $\pi _{X}:X\times Y\rightarrow X$ , $\pi _{\overline {X}}:\overline {X}\times Y\rightarrow \overline {X}$ , $\pi _{Y}:\overline {X}\times Y\rightarrow Y$ be the natural projections. By Kunugui’s theorem, we are able to find $\hat {\psi }_{i}:Y\rightarrow \overline {X}\times Y$ for $i=1,\ldots ,n$ such that $\pi _{Y}\circ \hat {\psi }_{i}=\operatorname {\mathrm {id}}$ and $\hat {\psi }_{i}(Y)\cap \hat {\psi }_{j}(Y)=\emptyset $ whenever $i\neq j$ . Let

(3.12)

Then $\rho (\Omega _{i})=1/n$ , $ \bigcup \Omega _{i}=\operatorname {\mathrm {supp}}\overline {\rho }$ , and $\Omega \cap \operatorname {\mathrm {supp}}\overline {\rho }_{y}$ consists of exactly one point. Next, we can apply Kunugui’s theorem again and obtain $\psi _{i}:Y\rightarrow X$ so that $P_{X}\circ \psi _{i}=\overline {\psi }_{i}$ , where $P_{X}:X\rightarrow \overline {X}$ .

4 Shearing property II, time changes of unipotent flows

We continue to study the shearing property of unipotent flows. More precisely, we shall study the shearing in directions different from §3.2 and deduce the following Proposition 4.16. In fact, in §3.2, we study the shearing between points of the form $(x,y),(gx,y)\in X\times Y$ for some $g\in G_{X}$ sufficiently close to the identity. Thus, the information basically comes from the X-factor. However, in this section, we shall study the shearing between points of the form $(\psi (y),y),(\psi (gy),gy)\in C^{\rho }\backslash X \times Y$ , where $\psi :Y\rightarrow C^{\rho }\backslash X$ is a measurable map and $g\in G_{X}$ is sufficiently close to the identity. Thus, the time change on Y comes into play. The technique used in Proposition 4.16 generalizes the ideas in [Rat86, Tan22], and provides us with a quantitative estimate of a unipotent shearing on the double quotient space $C^{\rho }\backslash G_{X}/\Gamma _{X}$ . Roughly speaking, Proposition 4.16 helps us better understand the non-shifting time under a unipotent shearing.

4.1 Preliminaries

We start with a combinatorial result. Let I be an interval in $\mathbb {R}$ and let $J_{i},J_{j}$ be disjoint subintervals of $I,J_{i}=[x_{i},y_{i}]$ , $y_{i}<x_{j}$ if $i<j$ . Denote

For a collection $\beta $ of finitely many intervals, we define

In addition, for a collection $\beta $ of finitely many intervals, an interval I, let

Proposition 4.1. (Existence of large intervals, Solovay [Rat79])

Given $\eta \in (0,1)$ , $\zeta \in (0,1)$ , there is $\theta =\theta (\zeta ,\eta )\in (0,1)$ such that if I is an interval of length $\unicode{x3bb} \gg 1 $ and $\alpha =\{J_{1},\ldots ,J_{n}\}=\mathcal {G}\cup \mathcal {B}$ is a partition of I into good and bad intervals such that:

1. (1) for any two good intervals $J_{i},J_{j}\in \mathcal {G}$ , we have

   (4.1) $$ \begin{align} d(J_{i},J_{j})\geq[\min\{\operatorname{\mathrm{Leb}}(J_{i}),\operatorname{\mathrm{Leb}}(J_{j})\}]^{1+\eta}; \end{align} $$

2. (2) $ \operatorname {\mathrm {Leb}}(J)\leq \zeta \unicode{x3bb} $ for any good interval $J\in \mathcal {G}$ ;

3. (3) $ \operatorname {\mathrm {Leb}}(J)\geq 1$ for any bad interval $J\in \mathcal {B}$ ;

then the measure of bad intervals $\operatorname {\mathrm {Leb}}(\bigcup _{J\in \mathcal {B}}J)\geq \theta \unicode{x3bb} $ . More precisely, we can take

$$ \begin{align*} \theta=\theta(\zeta,\eta)= \prod_{n=0}^{\infty} (1+ C\zeta^{n\eta})^{-1} \end{align*} $$

for some constant $C>0$ (independent of $\zeta ,\eta $ ).

Proof. Assume that $\zeta ^{1-k} \leq \unicode{x3bb} \leq \zeta ^{-k}$ for some $k\geq 1$ . Let

, and $\mathcal {B}_{\leq n}$ be the collection of the remaining intervals forming $I\setminus \bigcup _{J\in \mathcal {G}_{\leq n}}J$ . Then for $n\in \mathbb {N}$ , $J\in \mathcal {B}_{\leq n}$ , by equation (4.1), we have

$$ \begin{align*} \frac{|\mathcal{B}_{\leq n+1}\cap J|}{\operatorname{\mathrm{Leb}}(J)}&=\frac{|\mathcal{B}_{\leq n+1}\cap J|}{|\mathcal{G}_{n+1}\cap J|+|\mathcal{B}_{\leq n+1}\cap J|}= \bigg(1+\frac{|\mathcal{G}_{n+1}\cap J|}{|\mathcal{B}_{\leq n+1}\cap J|}\bigg)^{-1} \;\nonumber\\ &\geq \bigg(1+\frac{l\zeta^{n+1}\unicode{x3bb}}{(l-1) \zeta^{(n+2)(1+\eta)}\unicode{x3bb}^{1+\eta}}\bigg)^{-1} = (1+ C\zeta^{(k-n)\eta})^{-1}, \; \nonumber \end{align*} $$

where $l\geq 2$ is the number of intervals in $\mathcal {G}_{n+1}\cap J$ , and $C>0$ is some constant depending on $\eta $ and $\zeta $ . One can also show that when $k=0,1$ , we have a similar relation. By summing over $J\in \mathcal {B}_{\leq n}$ , we obtain

$$ \begin{align*}\frac{|\mathcal{B}_{\leq n+1}|}{|\mathcal{B}_{\leq n}|}\geq(1+ C\zeta^{(k-n)\eta})^{-1}. \end{align*} $$

Note that by item (2), $|\mathcal {B}_{\leq 0}|=\unicode{x3bb} $ , and by item (3), $\mathcal {B}_{\leq n}=\mathcal {B}_{\leq n+1}$ for all $n\geq k$ . We calculate

$$ \begin{align*}|\mathcal{B}|=|\bigcap_{k\geq 0}\mathcal{B}_{\leq k}|=\lim_{k\rightarrow\infty}|\mathcal{B}_{\leq k}|=\prod_{n=0}^{\infty}\frac{|\mathcal{B}_{\leq n+1}|}{|\mathcal{B}_{\leq n}|}\cdot \unicode{x3bb}\geq \prod_{n=0}^{k} (1+ C\zeta^{(k-n)\eta})^{-1}\cdot \unicode{x3bb}.\end{align*} $$

Now note that

$$ \begin{align*}\theta(\zeta,\eta)=\prod_{n=0}^{\infty} (1+ C\zeta^{n\eta})^{-1}\leq\prod_{n=0}^{k} (1+ C\zeta^{(k-n)\eta})^{-1} \end{align*} $$

and the proposition follows.

In light of equation (4.1), we make the following definition.

Definition 4.1. (Effective gaps between intervals)

We say that two intervals $I,J\subset \mathbb {R}$ have an effective gap if

$$ \begin{align*} d(I,J)\geq[\min\{\operatorname{\mathrm{Leb}}(I),\operatorname{\mathrm{Leb}}(J)\}]^{1+\eta} \end{align*} $$

for some $\eta>0$ . Later, we shall obtain some quantitative results relative to the effective gap.

Remark 4.2. It is worth noting that if $\mathcal {A}$ and $\mathcal {B}$ are collections of intervals with effective gaps, then the intersections also have effective gaps. More generally, assume that $\mathcal {A}$ and $\mathcal {B}$ are collections of intervals with effective gaps. If $J_{1},J_{2}\in \mathcal {A}\cap \mathcal {B}$ have an effective gap, then there is a pair of intervals $I_{1},I_{2}$ , either in $\mathcal {A}$ or in $\mathcal {B}$ , such that $J_{1}\subset I_{1}$ , $J_{2}\subset I_{2}$ and $I_{1},I_{2}$ have an effective gap.

In the following, we shall use the asymptotic notation:

• • $A\ll B$ or $A=O(B)$ means there is a constant $C>0$ such that $A\leq CB$ (we also write $A\ll _{\kappa } B$ if the constant $C(\kappa )$ depends on some coefficient $\kappa $ );

• • $A=o(B)$ means that $A/B\rightarrow 0$ as $B\rightarrow 0$ ;

• • $A\asymp B$ means there is a constant $C>1$ such that $C^{-1}B\leq A\leq CB$ ;

• • $A\approx 0$ means $A\in (0,1)$ close to $0$ , and $A\approx 1$ means $A\in (0,1)$ close to $1$ .

Similar to [Tan22], we need to following quantitative property of polynomials.

Lemma 4.3. Fix numbers $R_{0}>0, \kappa \in (0,1]$ , a real polynomial $p(x)=v_{0}+v_{1}x+\cdots +v_{k}x^{k}\in \mathbb {R}[x]$ . Assume further that there exist intervals $[0,\overline {l}_{1}]\cup [l_{2},\overline {l}_{2}]\cup \cdots \cup [l_{m},\overline {l}_{m}]$ such that

(4.2) $$ \begin{align} |p(t)|\ll\max\{R_{0},t^{1-\kappa}\} \quad\text{if and only if}\, t\in[0,\overline{l}_{1}]\cup[l_{2},\overline{l}_{2}]\cup\cdots\cup[l_{m},\overline{l}_{m}]. \end{align} $$

Then $\overline {l}_{1}$ has the lower bound l depending on $\max _{i}|v_{i}|$ , $R_{0}$ , $\kappa $ , and the implicit constant such that $l\nearrow \infty $ as $\max _{i}|v_{i}|\searrow 0$ for fixed $R_{0},\kappa $ . In addition, $m\leq k$ and we have:

1. (1) $|v_{i}|\ll _{k,\kappa } R_{0}\overline {l}_{1}^{1-i-\kappa } $ for all $1\leq i\leq k$ ;

2. (2) fix $\eta \approx 0$ . Assume that for certain $1\leq j\leq m-1$ , sufficiently large $\overline {l}_{j}$ , the intervals $[0,\overline {l}_{j}]$ and $[l_{j+1},\overline {l}_{j+1}]$ do not have an effective gap:

   (4.3) $$ \begin{align} l_{j+1}-\overline{l}_{j}\leq \min\{\overline{l}_{j},\overline{l}_{j+1}-l_{j+1}\}^{1+\eta}. \end{align} $$
   Then there exists $1\approx \xi (\eta ,k)\in (0,1)$ with $\xi (\eta ,k)\rightarrow 1$ as $\eta \rightarrow 0$ such that
   $$ \begin{align*}|v_{i}|\ll_{k,\kappa} \overline{l}_{j}^{\xi(\eta,k)(1-i-\kappa)}\end{align*} $$
   for all $1\leq i\leq k$ .

Proof. The number m of intervals in equation (4.2) can be bounded by k via an elementary argument of polynomials.

(1) Let for $x\in [0,1]$ . Then we have

$$ \begin{align*}\left( \begin{array}{@{}c@{}} v_{1}\overline{l}_{1}^{\kappa} \\ v_{2}\overline{l}_{1}^{1+\kappa} \\ \vdots \\ v_{k}\overline{l}_{1}^{k-1+\kappa} \\ \end{array} \right)=\left[ \begin{array}{@{}cccc@{}} (1/k)^{\kappa}& (1/k)^{1+\kappa} & \cdots & (1/k)^{k-1+\kappa} \\ (2/k)^{\kappa}& (2/k)^{1+\kappa} & \cdots & (2/k)^{k-1+\kappa} \\ \vdots& \vdots & \ddots & \vdots \\ 1& 1 & \cdots & 1 \\ \end{array} \right]^{-1}\left( \begin{array}{@{}c@{}} F(1/k) \\ F(2/k) \\ \vdots \\ F(1) \\ \end{array} \right)\!.\end{align*} $$

By equation (4.2), we know that $|F (1/k)|,|F (2/k)|,\ldots ,|F(1)|\ll R_{0}$ . Thus, we obtain $|v_{i}|\ll _{k,\kappa } R_{0} \overline {l}_{1}^{1-i-\kappa } $ for all $1\leq i\leq k$ .

(2) This follows by induction. Assume that the statement holds for $j-1$ . For j, the only difficult situation is when $\overline {l}_{j}\leq l_{j+1}-\overline {l}_{j}$ and $\overline {l}_{j+1}-l_{j+1}\leq l_{j+1}-\overline {l}_{j}$ . If this is the case, then

$$ \begin{align*} \overline{l}_{j+1}= (\overline{l}_{j+1}-l_{j+1})+(l_{j+1}-\overline{l}_{j})+\overline{l}_{j}\leq 3\overline{l}_{j}^{1+\eta}. \end{align*} $$

Thus, by induction hypothesis, we get

$$ \begin{align*}|v_{i}|\ll \overline{l}_{j}^{\xi(\eta,j)(1-i-\kappa)}\ll \overline{l}_{j+1}^{{\xi(\eta,j)}/({1+\eta})(1-i-\kappa)} \end{align*} $$

for all $1\leq i\leq k$ .

4.2 Effective estimates of shearing phenomena

Now we begin to study the shearing between two nearby orbits of time changes of unipotent flows. Let $G=\mathrm {SO}(n,1)$ . First, since all maximal compact subgroups of $C_{G}(U)$ are conjugate, we can assume without loss of generality that $C^{\rho }$ is in the compact group generated by $\mathfrak {k}^{\perp }_{C}$ . Thus, via equations (2.3), (2.4), and (2.8), we consider the decomposition

$$ \begin{align*} \mathfrak{g}=\mathfrak{sl}_{2}\oplus V^{\perp\rho}\oplus\operatorname{\mathrm{Lie}}(C^{\rho}),\quad V^{\perp\rho}=\sum_{i} V_{i}^{0\perp\rho}\oplus\sum_{j} V_{j}^{2}, \end{align*} $$

$$ \begin{align*} \mathfrak{k}^{\perp}_{C}=\mathfrak{k}^{\perp\rho}_{C}\oplus\operatorname{\mathrm{Lie}}(C^{\rho}),\end{align*} $$

where $\operatorname {\mathrm {Lie}}(C^{\rho })$ denotes the Lie algebra of $C^{\rho }$ and note that $\operatorname {\mathrm {Lie}}(C^{\rho })$ consists of weight $0$ spaces. Since $C^{\rho }$ is compact, there is a G-right invariant metric $d_{C^{\rho }\backslash G}(\cdot ,\cdot )$ on $C^{\rho }\backslash G$ . Let $P:G\rightarrow C^{\rho }\backslash G$ be the natural projection

Then, for $g_{x},g_{y}\in G$ , we have

$$ \begin{align*}d_{C^{\rho}\backslash G}(\overline{g_{x}},\overline{g_{y}})=d_{C^{\rho}\backslash G}( C^{\rho}g_{x} ,C^{\rho}g_{y})=d_{C^{\rho}\backslash G}(C^{\rho}g_{x}g_{y}^{-1},C^{\rho})=d_{C^{\rho}\backslash G}(\overline{g_{x}g_{y}^{-1}},\overline{e}).\end{align*} $$

Moreover, $dP$ induces an isometry between $\mathfrak {sl}_{2}+ V^{\perp \rho }$ and $T_{\overline {e}}(C^{\rho }\backslash G)$ . See for example [GQ19] for more details.

Assume $\overline {g}\in B_{C^{\rho }\backslash G}(e,\epsilon )$ for sufficiently small $0<\epsilon $ . Since $C^{\rho }$ in fact commutes with $\mathrm {SO}_{0}(2,1)$ , we can identify

(4.4) $$ \begin{align} \overline{g}=C^{\rho}h\exp v \end{align} $$

for some $h\in B_{\mathrm {SO}_{0}(2,1)}(e,\epsilon )$ and $v\in B_{V^{\perp \rho }}(0,\epsilon )$ . In addition, for $h=[ \begin {smallmatrix} a& b \\ c& d\\ \end {smallmatrix} ]\in B_{\mathrm {SO}_{0}(2,1)}(e,\epsilon )$ , we must have $|b|,|c|<\epsilon $ , $1-\epsilon <|a|,|d|<1+\epsilon $ .

Next, let $t(s)\in \mathbb {R}^{+}$ be a function of $s\in \mathbb {R}^{+}$ . Then we want to study the difference $ u^{t}\overline {g}u^{-s}$ of two nearby orbits of time changes of unipotent flows. By equation (2.5), we have

(4.5) $$ \begin{align} u^{t}\overline{g}u^{-s} &=C^{\rho}u^{t}h\exp v u^{-s}=C^{\rho}(u^{t}hu^{-s})(u^{s}\exp(v)u^{-s}) \nonumber\\ & = C^{\rho}(u^{t}hu^{-s})\exp(\operatorname{\mathrm{Ad}} u^{s}.v) = C^{\rho}(u^{t}hu^{-s})\exp\bigg(\sum_{n=0}^{\varsigma}\sum_{i=0}^{n}b_{i}\binom{n}{i}s^{n-i}v_{n}\bigg). \end{align} $$

Then one may conclude that $u^{t}\overline {g}u^{-s}< \epsilon $ if and only if

(4.6) $$ \begin{align} u^{t}hu^{-s}\ll\epsilon,\quad \operatorname{\mathrm{Ad}} u^{s}.v=\sum_{n=0}^{\varsigma}\sum_{i=0}^{n}b_{i}\binom{n}{i}s^{n-i}v_{n}\ll\epsilon, \end{align} $$

where $\overline {g}\ll \epsilon $ for $g\in G$ means $d_{C^{\rho }\backslash G}(\overline {g},e)\ll \epsilon $ . Therefore, later on, we shall split the elements closing to the identity into two parts, say the $\mathrm {SO}(2,1)$ -part and the $V^{\perp \rho }$ -part.

As shown in equation (4.6), we consider the elements of the form $u^{t}hu^{-s}\in B_{\mathrm {SO}(2,1)}(e,\epsilon )$ . One may calculate

(4.7) $$ \begin{align} u^{t}hu^{-s}= &\left[ \begin{array}{@{}ccc@{}} 1& \\ t& 1\\ \end{array} \!\right]\left[ \begin{array}{@{}ccc@{}} a& b \\ c& d\\ \end{array} \!\right]\left[ \begin{array}{@{}ccc@{}} 1& \\ -s& 1\\ \end{array} \!\right]\;\nonumber\\ =& \left[ \begin{array}{@{}ccc@{}} a-bs& b \\ c+(a-d)s-bs^{2}+(t-s)(a-bs)& d+bt\\ \end{array} \!\right]\!. \; \end{align} $$

If we further impose the Hölder inequality $|s-t|\ll _{\kappa }\max \{R_{0},s^{1-\kappa }\}$ for some $R_{0}>\epsilon $ (see §2.3 or equation (4.33)), then we have the crude estimate

$$ \begin{align*} &|-bs^{2}+(a-d)s+c+(-bs+a)(t-s)|<\epsilon \;\nonumber\\ \Rightarrow\ & |-bs^{2}+(a-d)s|-|c|-|(-bs+a)(t-s)|<\epsilon\;\nonumber\\ \Rightarrow\ & |-bs^{2}+(a-d)s|<2\epsilon+2|t-s|\;\nonumber\\ \Rightarrow\ & |-bs^{2}+(a-d)s|\ll_{\kappa}\max\{R_{0},s^{1-\kappa}\}. \;\nonumber \end{align*} $$

By Lemma 4.3, we immediately obtain the following lemma.

Lemma 4.4. (Estimates for $\mathrm {SO}_{0}(2,1)$ -coefficients)

Given $\kappa \approx 0$ , $R_{0}>0$ , $\epsilon \approx 0$ , a matrix $h=[ \begin {smallmatrix} a& b \\ c& d\\ \end {smallmatrix} ]\in B_{\mathrm {SO}(2,1)}(e,\epsilon )$ , then the solutions $s\in [0,\infty )$ of the following inequality

(4.8) $$ \begin{align} |-bs^{2}+(a-d)s|\ll_{\kappa} \max\{R_{0},s^{1-\kappa}\} \end{align} $$

consist of at most two intervals, say $[0,\overline {l}_{1}(h)]\cup [l_{2}(h),\overline {l}_{2}(h)]$ , where $\overline {l}_{1}$ has the lower bound $l(\epsilon ,R_{0},\kappa )$ such that $l(\epsilon ,R_{0},\kappa )\nearrow \infty $ as $\epsilon \searrow 0$ for fixed $R_{0},\kappa $ . Moreover, we have:

1. (1) $|b|\ll _{\kappa } \overline {l}_{1}^{-1-\kappa }$ and $|a-d|\ll _{\kappa } \overline {l}_{1}^{-\kappa }$ ;

2. (2) if we further assume that the intervals $[0,\overline {l}_{1}]$ and $[l_{2},\overline {l}_{2}]$ do not have an effective gap as in equation (4.3), that is, $l_{2}-\overline {l}_{1}\leq \min \{\overline {l}_{1},\overline {l}_{2}-l_{2}\}^{1+\eta }$ for some $\eta \approx 0$ , then

   $$ \begin{align*}|b|\ll_{\kappa} \overline{l}_{2}^{\xi(\eta)(-1-\kappa)},\quad |a-d|\ll_{\kappa} \overline{l}_{2}^{\xi(\eta)(-\kappa)}.\end{align*} $$

Next, we study the situation when $\operatorname {\mathrm {Ad}} u^{s}.v\ll \epsilon $ . Again by Lemma 4.3, we have the following lemma.

Lemma 4.5. (Estimates for $V^{\perp \rho }$ -coefficients)

Fix $v=b_{0}v_{0}+\cdots +b_{\varsigma }v_{\varsigma }\in B_{V_{\varsigma }}(0,\epsilon )$ . Assume that

$$ \begin{align*} \operatorname{\mathrm{Ad}} u^{s}.v\ll \epsilon \quad\text{if and only if } s\in[0,\overline{l}_{1}(v)] \cup\cdots\cup[l_{m}(v),\overline{l}_{m}(v)], \end{align*} $$

where $\overline {l}_{1}$ has the lower bound $l(\epsilon ,R_{0},\kappa )$ such that $l(\epsilon ,R_{0},\kappa )\nearrow \infty $ as $\epsilon \searrow 0$ for fixed $R_{0},\kappa $ . Then $m=m(v)$ is bounded by a constant depending on $\varsigma $ . Moreover, for $1\leq j\leq \varsigma -1$ , the intervals $[0,\overline {l}_{j}]$ and $[l_{j+1},\overline {l}_{j+1}]$ do not have an effective gap as in equation (4.3), that is, $l_{j+1}-\overline {l}_{j}\leq \min \{\overline {l}_{j},\overline {l}_{j+1}-l_{j+1}\}^{1+\eta }$ , then we have

$$ \begin{align*} |b_{i}|\ll_{\varsigma,\kappa} \overline{l}_{j}^{\xi(\eta,\varsigma)(-\varsigma+i)}. \end{align*} $$

Next, we shall combine the results of Lemmas 4.4 and 4.5. The basic idea is to consider the intersection of the collections of intervals obtained from the above lemmas. For simplicity, we assume that the ‘ $V^{\perp \rho }$ -part’ consists of a single $\mathfrak {sl}_{2}$ -irreducible representation. For the general case, we can repeat the argument for each $\mathfrak {sl}_{2}$ -irreducible representation (cf. §2.2). First, for $\overline {g}=C^{\rho }h\exp (v)\in C^{\rho }\backslash G$ , we write as in Lemmas 4.4 and 4.5

$$ \begin{align*} u^{t}hu^{-s}\ll\epsilon &\text{ if and only if } s\in [0,\overline{l}_{1}(h)]\cup[l_{2}(h),\overline{l}_{2}(h)],\;\nonumber\\ Ad u^{s}.v\ll \epsilon &\text{ if and only if } s\in[0,\overline{l}_{1}(v)]\cup\cdots\cup[l_{m(v)}(v),\overline{l}_{m(v)}(v)].\; \nonumber \end{align*} $$

Write $l_{1}(h)=l_{1}(v)=0$ and we shall consider the family of intervals

(4.9)

where $\overline {l}_{k}(g)<l_{k+1}(g)$ for all k. Thus, in particular, $l_{1}(g)=0$ and $[0,\overline {l}_{1}(g)]=[0,\overline {l}_{1}(h)]\cap [0,\overline {l}_{1}(v)]$ .

Now assume that there exists k such that $[0,\overline {l}_{k}(g)]$ and $[l_{k+1}(g),\overline {l}_{k+1}(g)]$ do not have an effective gap as in equation (4.3), that is,

$$ \begin{align*} l_{k+1}(g)-\overline{l}_{k}(g)\leq \min\{\overline{l}_{k}(g),\overline{l}_{k+1}(g)-l_{k+1}(g)\}^{1+\eta}. \end{align*} $$

Then by Remark 4.2, the corresponding ‘ $\mathrm {SO}(2,1)$ -part’ and ‘ $V^{\perp \rho }$ -part’ should not have effective gaps either. More precisely, for the $\mathrm {SO}(2,1)$ -part, we define

Thus, we know

$$ \begin{align*}[0,\overline{l}_{k}(g)]\subset[0,\overline{l}_{i_{\geq k}}(h)],\quad [l_{k+1}(g),\overline{l}_{k+1}(g)]\subset[l_{i_{\leq k+1}}(h),\overline{l}_{i_{\leq k+1}}(h)] \end{align*} $$

and hence $[0,\overline {l}_{i_{\geq k}}(h)]$ and $[l_{i_{\leq k+1}}(h),\overline {l}_{i_{\leq k+1}}(h)] $ do not have an effective gap as in equation (4.3). Similarly, for the $V^{\perp \rho }$ -part, we define

Then we know

$$ \begin{align*}[0,\overline{l}_{k}(g)]\subset[0,\overline{l}_{j_{\geq k}}(v)],\quad [l_{k+1}(g),\overline{l}_{k+1}(g)]\subset[l_{j_{\leq k+1}}(v),\overline{l}_{j_{\leq k+1}}(v)] \end{align*} $$

and hence $[0,\overline {l}_{j_{\geq k}}(v)]$ and $[l_{j_{\leq k+1}}(v),\overline {l}_{j_{\leq k+1}}(v)] $ do not have an effective gap as in equation (4.3). Further, one observes

$$ \begin{align*} [0,\overline{l}_{k}(g)]&=[0,\overline{l}_{i_{\geq k}}(h)]\cap [0,\overline{l}_{j_{\geq k}}(v)],\;\nonumber\\ [l_{k+1}(g),\overline{l}_{k+1}(g)]&= [l_{i_{\leq k+1}}(h),\overline{l}_{i_{\leq k+1}}(h)]\cap [l_{j_{\leq k+1}}(v),\overline{l}_{j_{\leq k+1}}(v)].\; \nonumber \end{align*} $$

Now recall by the definition in equation (4.9) that the number of intervals in $\{[l_{k}(g),\overline {l}_{k}(g)]\}_{k}$ is bounded by a constant $c(\varsigma )>0$ because the numbers of intervals $\{[l_{i}(h),\overline {l}_{i}(h)]\}_{i}$ , $\{[l_{j}(v),\overline {l}_{j}(v)]\}_{j}$ are. Since $\varsigma \leq 2$ when $\mathfrak {g}=\mathfrak {so}(n,1)$ , we see that $c(\varsigma )$ is uniformly bounded for all $\varsigma $ . Thus, we conclude that the number of intervals in $\{[l_{k}(g),\overline {l}_{k}(g)]\}_{k}$ is uniformly bounded for all $g\in G$ . Then, combining Lemmas 4.5 and 4.4, we obtain the following lemma.

Lemma 4.6. (Estimates for $C^{\rho }\backslash G$ -coefficients)

Let $\kappa \approx 0$ , $R_{0}>0$ , $\epsilon \approx 0$ , $\overline {g}=C^{\rho }h\exp v\in B_{C^{\rho }\backslash G}(e,\epsilon )$ be as above, where

$$ \begin{align*}h=\left[ \begin{array}{@{}ccc@{}} a& b \\ c& d\\ \end{array} \!\!\right]\in \mathrm{SO}_{0}(2,1),\quad v=b_{0}v_{0}+\cdots+b_{\varsigma}v_{\varsigma}\in V_{\varsigma}.\end{align*} $$

Next, let $t(s)\in \mathbb {R}^{+}$ be a function of $s\in \mathbb {R}^{+}$ which satisfies the effectiveness

$$ \begin{align*}|s-t(s)|\ll_{\kappa}\max\{R_{0},s^{1-\kappa}\}.\end{align*} $$

Then there exist intervals $\{[l_{k}(g),\overline {l}_{k}(g)]\}_{k}$ such that

(4.10) $$ \begin{align} u^{t}\overline{g}u^{-s}<\epsilon, \quad\text{implies}\ s\in \bigcup_{k}[l_{k}(g),\overline{l}_{k}(g)], \end{align} $$

where $\overline {l}_{1}$ has the lower bound $l(\epsilon ,R_{0},\kappa )$ such that $l(\epsilon ,R_{0},\kappa )\nearrow \infty $ as $\epsilon \searrow 0$ for fixed $R_{0},\kappa $ . In addition, $k\leq c$ for some constant $c=c(\mathfrak {g})>0$ , and:

1. (1) $|b|\ll _{\kappa } \overline {l}_{1}(g)^{-1-\kappa }$ , $|a-d|\ll _{\kappa } \overline {l}_{1}(g)^{-\kappa }$ , $|b_{i}|\ll _{\varsigma ,\kappa } \overline {l}_{1}(g)^{-\varsigma +i}$ for all $0\leq i\leq \varsigma $ ;

2. (2) If we further assume that the intervals $[0,\overline {l}_{k}(g)]$ and $[l_{k+1}(g),\overline {l}_{k+1}(g)]$ do not have an effective gap as in equation (4.3), then there exists $1\approx \xi =\xi (\eta )\in (0,1)$ with $\xi \rightarrow 1$ as $\eta \rightarrow 0$ such that

   $$ \begin{align*}|b|\ll_{\kappa} \overline{l}_{k}(g)^{-\xi(1+\kappa)},\quad |a-d|\ll_{\kappa} \overline{l}_{k}(g)^{-\xi\kappa},\quad |b_{i}|\ll_{\varsigma,\kappa} \overline{l}_{k}(g)^{-\xi (\varsigma-i)}\end{align*} $$
   for all $1\leq i\leq \varsigma $ .

In practical use, we consider two strictly increasing functions $t(r),s(r)\in \mathbb {R}^{+}$ of $r\in \mathbb {R}^{+}$ satisfying the effective estimates

(4.11) $$ \begin{align} |r-t(r)|\ll_{\kappa}\max\{R_{0},r^{1-\kappa}\},\quad |r-s(r)|\ll_{\kappa}\max\{R_{0},r^{1-\kappa}\}. \end{align} $$

It follows that t is also an increasing function of s and satisfies

$$ \begin{align*}|t(r)-s(r)|\leq|t(r)-r|+|r-s(r)|\ll_{\kappa}\max\{R_{0},r^{1-\kappa}\}\ll_{\kappa}\max\{R_{0},s(r)^{1-\kappa}\}.\end{align*} $$

Then by Lemma 4.6 and the monotonic nature, we deduce the following corollary.

Corollary 4.7. (Change of variables)

Let $\kappa \approx 0$ , $R_{0}>0$ , $\epsilon \approx 0$ , $\overline {g}=C^{\rho }h\exp v\in B_{C^{\rho }\backslash G}(e,\epsilon )$ be as above, where

$$ \begin{align*}h=\left[ \begin{array}{@{}ccc@{}} a& b \\ c& d\\ \end{array} \!\!\right]\in \mathrm{SO}_{0}(2,1),\quad v=b_{0}v_{0}+\cdots+b_{\varsigma}v_{\varsigma}\in V_{\varsigma}.\end{align*} $$

Assume that we have equation (4.11). Then there exist intervals $\{[l_{k}(g),\overline {l}_{k}(g)]\}_{k}$ such that

(4.12) $$ \begin{align} u^{t(r)}\overline{g}u^{-s(r)}<\epsilon \quad\text{implies }\, r\in \bigcup_{k}[L_{k}(g),\overline{L}_{k}(g)], \end{align} $$

where $\overline {L}_{1}$ has the lower bound $L(\epsilon ,R_{0},\kappa )$ such that $L(\epsilon ,R_{0},\kappa )\nearrow \infty $ as $\epsilon \searrow 0$ for fixed $R_{0},\kappa $ . Then we have $k\leq c$ for some constant $c=c(\mathfrak {g})>0$ , and:

1. (1) $|b|\ll _{\kappa } \overline {L}_{1}(g)^{-1-\kappa }$ , $|a-d|\ll _{\kappa } \overline {L}_{1}(g)^{-\kappa }$ , $|b_{i}|\ll _{\varsigma ,\kappa } \overline {L}_{1}(g)^{-\varsigma +i}$ for all $0\leq i\leq \varsigma $ ;

2. (2) if we further assume that the intervals $[0,\overline {L}_{k}(g)]$ and $[L_{k+1}(g),\overline {L}_{k+1}(g)]$ do not have an effective gap, as in equation (4.3), then there exists $1\approx \xi =\xi (\eta )\in (0,1)$ with $\xi \rightarrow 1$ as $\eta \rightarrow 0$ such that

   $$ \begin{align*}|b|\ll_{\kappa} \overline{L}_{k}(g)^{-\xi(1+\kappa)},\quad |a-d|\ll_{\kappa} \overline{L}_{k}(g)^{-\xi\kappa},\quad |b_{i}|\ll_{\varsigma,\kappa} \overline{L}_{k}(g)^{-\xi (\varsigma-i)}\end{align*} $$
   for all $1\leq i\leq \varsigma $ .

4.3 $\epsilon $ -blocks and effective gaps

Let $x\in \overline {X}$ , $y\in B_{\overline {X}}(x,\epsilon )$ . We say that $(\overline {g_{x}},\overline {g_{y}})\in C^{\rho }\backslash G\times C^{\rho }\backslash G$ covers $(x,y)$ if $ d_{C^{\rho }\backslash G}(\overline {g_{x}},\overline {g_{y}})<\epsilon $ and $\overline {P}(\overline {g_{x}})=x$ , $\overline {P}(\overline {g_{y}})=y$ , where $\overline {P}:C^{\rho }\backslash G\rightarrow C^{\rho }\backslash G/\Gamma $ is the projection. Since $\operatorname {\mathrm {Lie}}(C^{\rho }\backslash G)\cong \mathfrak {sl}_{2}+ V^{\perp \rho }$ , given a representative $g_{x}$ of $\overline {g_{x}}$ , we may choose $g_{y}\in G$ such that $P(g_{y})=\overline {g_{y}}$ and

$$ \begin{align*} \log (g_{y}g_{x}^{-1})\in \mathfrak{sl}_{2}+ V^{\perp\rho}. \end{align*} $$

We shall always make such a choice if no further explanation.

Definition 4.2. ( $\epsilon $ -block)

Suppose that $x\in \overline {X}$ , $y\in B_{\overline {X}}(x,\epsilon )$ , $(\overline {g_{x}},\overline {g_{y}})$ covers $(x,y)$ , and $R\in (0,\infty ]$ satisfies

$$ \begin{align*} d_{C^{\rho}\backslash G}(u^{s(R)}\overline{g_{x}},u^{t(R)}\overline{g_{y}})<\epsilon. \end{align*} $$

Then we define the $\epsilon $ -block of $\overline {g_{x}},\overline {g_{y}}$ of length r by

Similarly, we define the $\epsilon $ -block of $x,y$ of length r by

In either case, we call $[0,R]$ the corresponding time interval and define the length $|\operatorname {\mathrm {BL}}|$ of $\operatorname {\mathrm {BL}}$ by

We also write

$$ \begin{align*}\operatorname{\mathrm{BL}}(x,y)=\{(x,y),(u^{s(R)}x ,u^{t(R)}y)\}=\{(x,y),(\overline{x},\overline{y})\}\end{align*} $$

emphasizing that $(x,y)$ is the first and $(\overline {x},\overline {y})$ is the last pair of the block $\operatorname {\mathrm {BL}}(x,y)$ .

For a pair of $\epsilon $ -blocks, a shifting problem may occur.

Definition 4.3. (Shifting)

Let $\overline {\operatorname {\mathrm {BL}}}^{\prime }=\{(x^{\prime },y^{\prime }),(\overline {x}^{\prime },\overline {y}^{\prime })\}$ , $\overline {\operatorname {\mathrm {BL}}}^{\prime \prime }=\{(x^{\prime \prime },y^{\prime \prime }),(\overline {x}^{\prime \prime },\overline {y}^{\prime \prime })\}$ be two $\epsilon $ -blocks. Then $x^{\prime \prime }= u^{s}g_{x^{\prime }}$ , $y^{\prime \prime }= u^{t}y^{\prime }$ for some $s,t>0$ . Further, there is a unique $\gamma \in \Gamma $ such that

(4.13) $$ \begin{align} d_{C^{\rho}\backslash G}(\overline{g_{x^{\prime\prime}}},\overline{g_{y^{\prime\prime}}}\gamma)<\epsilon, \end{align} $$

where , . We define:

• • (Shifting) $(x^{\prime },y^{\prime })\overset {\Gamma }{\sim }(x^{\prime \prime },y^{\prime \prime })$ if $\gamma \neq e$ in equation (4.13);

• • (Non-shifting) $(x^{\prime },y^{\prime })\overset {e}{\sim }(x^{\prime \prime },y^{\prime \prime })$ if $\gamma =e$ in equation (4.13).

The key observation here is that whenever the difference of $\overline {g_{x}},\overline {g_{y}}$ can be estimated by the length in an appropriate way, a shifting must lead to an effective gap between two $\epsilon $ -blocks. This follows from the natural renormalization of unipotent flows via diagonal flows.

Proposition 4.8. (Shiftings imply effective gaps)

There are quantities $\eta _{0}\approx 0$ , $\sigma _{0}\approx 0$ , $\epsilon _{0}\approx 0$ , $r_{0}>0$ determined orderly such that, for any

• • $\eta \in (0,\eta _{0})$ ,

• • $\sigma \in (0,\sigma _{0}(\eta ))$ ,

• • $\epsilon \in (0,\epsilon _{0}(\sigma ))$ ,

there exists a compact set $K\subset \overline {X}$ with $\overline {\mu }(K)>1-\sigma $ such that the following holds (see Figure 1).

Figure 1 The solid straight lines are the unipotent orbits in the $\overline {\operatorname {\mathrm {BL}}}^{\prime }$ and $\overline {\operatorname {\mathrm {BL}}}^{\prime \prime }$ , and the dashed lines are the rest of the unipotent orbits. The bent curves indicate the length defined by the letters.

Assume that there are two $\epsilon $ -blocks $\overline {\operatorname {\mathrm {BL}}}^{\prime }=\{(x^{\prime },y^{\prime }),(\overline {x}^{\prime },\overline {y}^{\prime })\}$ , $\overline {\operatorname {\mathrm {BL}}}^{\prime \prime }=\{(x^{\prime \prime },y^{\prime \prime }), (\overline {x}^{\prime \prime },\overline {y}^{\prime \prime })\}$ such that the y-endpoints lie in K (that is, $y^{\prime },\overline {y}^{\prime },y^{\prime \prime },\overline {y}^{\prime \prime } \in K$ ) and satisfy

(4.14) $$ \begin{align} g_{y^{\prime}}= h^{\prime}\exp(v^{\prime})g_{x^{\prime}},\quad g_{y^{\prime\prime}}= h^{\prime\prime}\exp(v^{\prime\prime})g_{x^{\prime\prime}}, \end{align} $$

where $h^{\prime }, h^{\prime \prime } \in \mathrm {SO}_{0}(2,1)$ , $v^{\prime }, v^{\prime \prime } \in V_{\varsigma }$ can be estimated by

(4.15) $$ \begin{align} h^{\prime} ,h^{\prime\prime}=\left[ \begin{array}{@{}ccc@{}} 1+O(r^{-2\eta}) & O(r^{-1-2\eta}) \\ O(\epsilon) & 1+O(r^{-2\eta})\\ \end{array} \!\!\right]\!,\quad v^{\prime}, v^{\prime\prime} =O(r^{-\xi\varsigma})v_{0}+\cdots+O(\epsilon)v_{\varsigma} \end{align} $$

for some $r> r_{0}(\sigma ,\epsilon _{0})$ , where $\xi =\xi (\eta )\approx 1$ is given by Corollary 4.7. Assume further that $x^{\prime \prime }=u^{s}\overline {x}^{\prime }$ , $y^{\prime \prime }=u^{t}\overline {y}^{\prime }$ , and $t\asymp s$ . If $\overline {\operatorname {\mathrm {BL}}}^{\prime }\overset {\Gamma }{\sim }\overline {\operatorname {\mathrm {BL}}}^{\prime \prime }$ , then

(4.16) $$ \begin{align} s,t> r^{1+\eta}. \end{align} $$

Proof. We only consider $\varsigma =2$ . Denote

(4.17) $$ \begin{align} g_{\overline{y}^{\prime}}= \overline{h}^{\prime}\exp(\overline{v}^{\prime})g_{\overline{x}^{\prime}} \end{align} $$

for $\overline {h}^{\prime } \in \mathrm {SO}_{0}(2,1)$ , $\overline {v}^{\prime } \in V_{2}$ . By Definition 4.2, we know that $g_{\overline {y}^{\prime }}, g_{\overline {x}^{\prime }}$ are obtained by the unipotent action on $g_{y^{\prime }}, g_{x^{\prime }}$ , and the difference of $g_{\overline {y}^{\prime }}, g_{\overline {x}^{\prime }}$ is controlled by $\epsilon $ . Combining equation (4.15), we get that

(4.18) $$ \begin{align} \overline{h}^{\prime} =\left[ \begin{array}{@{}ccc@{}} 1+O(\epsilon) & O(r^{-1-2\eta}) \\ O(\epsilon) & 1+O(\epsilon)\\ \end{array} \!\!\right]\!,\quad \overline{v}^{\prime} =O(r^{-2\xi })v_{0}+O(\epsilon)v_{1}+ O(\epsilon)v_{2}. \end{align} $$

Since $\overline {\operatorname {\mathrm {BL}}}^{\prime }\overset {\Gamma }{\sim }\overline {\operatorname {\mathrm {BL}}}^{\prime \prime }$ and $g_{x^{\prime \prime }}=u^{s}g_{\overline {x}^{\prime }}$ , we get that

(4.19) $$ \begin{align} g_{y^{\prime\prime}}= cu^{t}g_{\overline{y}^{\prime}}\gamma\quad \text{for some }e\neq \gamma\in\Gamma,\ c\in C^{\rho}. \end{align} $$

Then by equations (4.14), (4.17), and (4.19), we have

(4.20) $$ \begin{align} g_{\overline{y}^{\prime}}&= \overline{h}^{\prime}\exp (\overline{v}^{\prime}) u^{-s} g_{x^{\prime\prime}},\nonumber\\ g_{\overline{y}^{\prime}} \gamma &= c^{-1} u^{-t} h^{\prime\prime}\exp (v^{\prime\prime}) g_{x^{\prime\prime}}. \end{align} $$

Assume that one of $s,t$ is not greater than $r^{1+\eta }$ . Then since $s\asymp t$ , we know

(4.21) $$ \begin{align} 0<s,t\leq O(r^{1+\eta}). \end{align} $$

Next, we determine the quantities for the proposition.

• • (Choice of $\eta $ , $\delta $ (also $\eta _{0}$ )) Choose a small $\eta \approx 0$ that satisfies

  (4.22) $$ \begin{align} 1+2\delta<1+2\eta<2\xi(2\eta), \end{align} $$
  where $\xi (2\eta )$ was defined in Corollary 4.7, and . Here, $\eta _{0}\approx 0$ can be defined to be the maximal $\eta $ so that equation (4.22) holds.

• • (Choice of $\sigma $ ) Then $\sigma =\sigma (\eta )>0$ can be chosen as

  (4.23) $$ \begin{align} \sigma<\frac{3\eta}{4+6\eta}. \end{align} $$

• • (Choice of $\epsilon _{0}$ , $K_{1}$ ; injectivity radius) Since $\Gamma $ is discrete, there is a compact subset $K_{1}\subset \overline {X}$ , $\overline {\mu }(K_{1})>1- \tfrac 14\sigma $ and $ \epsilon _{0}>0$ such that for any $\overline {g_{y}}\in \overline {P}^{-1}(K_{1})$ satisfying

  (4.24) $$ \begin{align} d_{C^{\rho}\backslash G}( \overline{g_{y}}, \overline{g_{y}}\gamma)<O(\epsilon_{0}) \end{align} $$
  for some $\gamma \in \Gamma $ , then $\gamma =e$ . Here the constants hidden in $O(\epsilon _{0})$ will be determined after the estimate of equation (4.28) (see also equation (4.29)).

• • (Choice of $K_{2}$ , K, $T_{0}$ , $r_{0}$ ; ergodicity of $a^{T}$ ) Since the diagonal action $a^{T}$ is ergodic on $(\overline {X},\overline {\mu })$ , there is a compact subset $K_{2}\subset \overline {X}$ , $\overline {\mu }(K_{2})>1-\tfrac 14\sigma $ and $T_{0}=T_{0}(K_{2})>0$ such that the relative length measure $K_{2}$ on $[y,a^{T}y]$ (and $[a^{-T}y,y]$ ) is greater than $1-\sigma $ for any $y\in K_{2}$ , $|T|\geq T_{0}$ . Assume that

  (4.25)

  
  Note that $\overline {\mu }(K)>1-\sigma $ . The quantity $r_{0}$ will be even larger and determined by $\epsilon _{0}$ if necessary (see equation (4.29)).

Now we are in the position to apply the renomalization via the diagonal action $a^{w}$ . Since $r>r_{0}=e^{(1+2\delta )^{-1}T_{0}}$ , let and we know $\omega _{0}>T_{0}$ . Since $\overline {y}^{\prime }\in K\subset K_{2}$ , it follows from the choice of $K_{2}$ and $T_{0}$ that the relative length measure of K on $[\overline {y}^{\prime },a^{\omega _{0}}\overline {y}^{\prime }]$ is greater than $1-\sigma $ . This implies that there is $\omega $ satisfying

$$ \begin{align*} (1-\sigma)\omega_{0}<\omega\leq\omega_{0} \end{align*} $$

such that $a^{\omega }\overline {y}^{\prime }\in K$ and therefore

(4.26) $$ \begin{align} a^{\omega}\overline{g_{\overline{y}^{\prime}}}\in \overline{P}^{-1}(K). \end{align} $$

By equation (4.20), we have

(4.27) $$ \begin{align} a^{\omega} g_{\overline{y}^{\prime}} &= (a^{\omega} \overline{h}^{\prime} a^{-\omega})\exp (\operatorname{\mathrm{Ad}} a^{\omega}. \overline{v}^{\prime}) (a^{\omega}u^{-s}a^{-\omega}) a^{\omega} g_{x^{\prime\prime}},\nonumber\\ a^{\omega} g_{\overline{y}^{\prime}}\gamma &= c^{-1}(a^{\omega}u^{-t} a^{-\omega}) (a^{\omega} h^{\prime\prime} a^{-\omega})\exp (\operatorname{\mathrm{Ad}} a^{\omega}.v^{\prime\prime}) a^{\omega}g_{x^{\prime\prime}}. \end{align} $$

Then by equations (4.18), (4.15), and (4.21), we estimate

(4.28) $$ \begin{align} a^{w} \overline{h}^{\prime}a^{-w}&= \left[ \begin{array}{@{}ccc@{}} 1+O(\epsilon) & O(r^{2\delta-2\eta}) \\ O(\epsilon) & 1+O(\epsilon)\\ \end{array} \!\!\right]\! ,\nonumber\\[2pt] a^{w} \overline{h}^{\prime}a^{-w}&= \left[ \begin{array}{@{}ccc@{}} 1+O(r^{-2\eta}) & O(r^{2\delta-2\eta}) \\ O(\epsilon) & 1+O(r^{-2\eta})\\ \end{array} \!\!\right]\!,\nonumber\\[2pt] \operatorname{\mathrm{Ad}} a^{\omega}. \overline{v}^{\prime}&= O(r^{ -2\xi+1+2\delta })v_{0}+O(\epsilon)v_{1}+O(\epsilon)v_{2},\nonumber\\[2pt] \operatorname{\mathrm{Ad}} a^{\omega}. v^{\prime\prime}&= O(r^{ -2\xi+1+2\delta })v_{0}+O(\epsilon)v_{1}+O(r^{ - (1-\sigma)(1+2\delta) })v_{2} ,\\[2pt] a^{\omega}u^{-t}a^{-\omega}&= u^{-te^{-\omega}}= u^{O(r^{1+\eta}r^{-(1-\sigma)(1+2\delta)})},\nonumber\\[2pt] a^{\omega}u^{-s}a^{-\omega}&= u^{-se^{-\omega}}= u^{O(r^{1+\eta}r^{-(1-\sigma)(1+2\delta)})}. \nonumber \end{align} $$

Notice that by the choice of $\sigma ,\delta $ (see equations (4.22) and (4.23)), we have

$$ \begin{align*}1+\eta-(1-\sigma)(1+2\delta)=1+\eta-(1-\sigma)\big(1+\tfrac{3}{2}\eta\big)<-\tfrac{1}{4}\eta.\end{align*} $$

Also, by equation (4.22), we have

$$ \begin{align*}2\delta-2\eta<0, -2\xi+1+2\delta<0.\end{align*} $$

Thus, by enlarging $r_{0}$ if necessary, all terms of equation (4.28) can be quantitatively dominated by $O(\epsilon _{0})$ . Then by equation (4.27), we have

(4.29) $$ \begin{align} d_{C^{\rho}\backslash G}(\overline{a^{\omega} g_{\overline{y}^{\prime}}}\gamma,\overline{a^{\omega} g_{\overline{y}^{\prime}}})=d_{C^{\rho}\backslash G}(\overline{a^{\omega} g_{\overline{y}^{\prime}}}\gamma (a^{\omega} g_{x^{\prime\prime}})^{-1},\overline{a^{\omega} g_{\overline{y}^{\prime}}}(a^{\omega} g_{x^{\prime\prime}})^{-1})<O(\epsilon_{0}). \end{align} $$

Thus, by equation (4.24), we get $\gamma =e$ , which contradicts our assumptions.

4.4 Construction of $\epsilon $ -blocks

In light of Proposition 4.8, we try to construct a collection of $\epsilon $ -blocks based on the unipotent flows between two nearby points so that each pair of $\epsilon $ -blocks has an effective gap.

First, given $\eta _{0}\approx 0$ as in Proposition 4.8, we fix a sufficiently small $\kappa \in (0,2\eta _{0})$ , and then choose $\eta =\eta (\kappa )\approx 0$ such that

(4.30) $$ \begin{align} \frac{1+2\eta}{\xi(2\eta)}<1+\kappa<1+2\eta_{0}, \end{align} $$

where $\xi (2\eta )\approx 1$ is given by Corollary 4.7. Then, $\sigma _{0}=\sigma _{0}(\eta )\approx 0$ given in Proposition 4.8 has been determined. Next, assume that there exist:

• • $\sigma \in (0,\sigma _{0})$ ;

• • $R_{0}>1$ ;

• • $\epsilon _{0}=\epsilon _{0}(\sigma )\approx 0$ , $\epsilon =\epsilon (R_{0})\in (0,\epsilon _{0})$ so small that

  (4.31) $$ \begin{align} \overline{L}_{1}(g)\geq L(\epsilon,R_{0},\kappa)>\max\{r_{0}(\sigma,\epsilon_{0}),R_{0}\} \end{align} $$
  whenever $g\in B_{G}(e,\epsilon )$ , where $\overline {L}_{1},L$ are defined by Corollary 4.7,

such that, for $K\subset \overline {X}$ with $\overline {\mu }(K)>1-\sigma $ given by Proposition 4.8, $x,y\in \overline {X}$ , we have $A=A(x,y)\subset \mathbb {R}^{+}$ such that:

1. (1) if $r\in A$ , then

   (4.32) $$ \begin{align} u^{t(r)}y\in K\quad\text{and}\quad d_{\overline{X}}(u^{s(r)}x, u^{t(r)}y)<\epsilon \end{align} $$
   for continuous increasing functions $t,s:[0,\infty )\rightarrow [0,\infty )$ ;

2. (2) we have the Hölder inequalities:

   (4.33) $$ \begin{align} |(t(r^{\prime})-t(r))-(r^{\prime}-r)|\ll& |r^{\prime}-r|^{1-\kappa},\\ |(s(r^{\prime})-s(r))-(r^{\prime}-r)|\ll& |r^{\prime}-r|^{1-\kappa}, \nonumber \end{align} $$
   for all $r,r^{\prime }\in A$ with $r^{\prime }>r$ , $ r^{\prime }-r \geq R_{0}$ .

It is worth noting from equation (4.24) that points in K have injectivity radius at least $\epsilon _{0}$ . For simplicity, we shall assume that $0\in A$ in what follows.

Remark 4.9. For the conditions (i) and (ii), the quantities $s,t$ are symmetric. Thus, for instance, one can also consider s as an increasing function of t, and obtain similar Hölder inequalities. We have already made such a change of variables in §4.2 for notational simplicity

However, the assumptions in equations (4.32), (4.33) coincide with equations (4.11), (4.12). So Corollary 4.7 can apply.

4.4.1 Construction of $\beta _{1}$

For $\unicode{x3bb} \in A$ , denote

. Now we construct a collection $\beta _{1}(A_{\unicode{x3bb} })$ of $\epsilon $ -blocks. Let

,

. We follow the assumptions in equations (4.32) and (4.33). Suppose that $(\overline {g_{x_{1}}}, \overline {g_{y_{1}}})\in C^{\rho }\backslash G\times C^{\rho }\backslash G$ covers $(x_{1},y_{1})$ and

where $\overline {L}_{1}$ is defined by Corollary 4.7. Let $\operatorname {\mathrm {BL}}_{1}$ be the $\epsilon $ -block of $x_{1},y_{1}$ of length $\overline {r}_{1}$ , $\operatorname {\mathrm {BL}}_{1}=\{(x_{1},y_{1}),(\overline {x}_{1},\overline {y}_{1})\}$ . To define $\operatorname {\mathrm {BL}}_{2}$ , we take

and apply the above procedure to

(note that by equation (4.12), $r_{2}>\overline {r}_{1}$ ). This process defines a collection $\beta _{1}(A_{\unicode{x3bb} })=\{\operatorname {\mathrm {BL}}_{1},\ldots , \operatorname {\mathrm {BL}}_{n}\}$ of $\epsilon $ -blocks on the orbit intervals $[x_{1},u^{s(\unicode{x3bb} )}x_{1}]$ , $[y_{1},u^{t(\unicode{x3bb} )}y_{1}]$ (see Figure 2):

$$ \begin{align*}x_{i}= u^{s_{i}}x_{1},\quad \overline{x}_{i}=u^{\overline{s}_{i}}x_{1}, \quad y_{i}=u^{t_{i}} y_{1},\quad \overline{y}_{i}=u^{\overline{t}_{i}}y_{1},\end{align*} $$

$$ \begin{align*}s_{i}= s(r_{i}),\quad \overline{s}_{i}= s(\overline{r}_{i}), \quad t_{i}= t(r_{i}),\quad \overline{t}_{i}= t(\overline{r}_{i}).\end{align*} $$

Note also that by the assumption of A, we have $x_{i},\overline {x}_{i}\in K$ for all i, the corresponding time interval of $BL_{i}$ is $[r_{i},\overline {r}_{i}]$ , and the length $|\operatorname {\mathrm {BL}}_{i}|$ of $\operatorname {\mathrm {BL}}_{i}$ is

Figure 2 A collection of $\epsilon $ -blocks $\{\operatorname {\mathrm {BL}}_{1},\ldots ,\operatorname {\mathrm {BL}}_{n}\}$ . The solid straight lines are the unipotent orbits in the $\epsilon $ -blocks and the dashed lines are the rest of the unipotent orbits. The bent curves indicate the length defined by the letters.

Note that any $\operatorname {\mathrm {BL}}_{i}=\{(x_{i},y_{i}),(\overline {x}_{i},\overline {y}_{i})\}\in \beta _{1}(A_{\unicode{x3bb} })$ has length $|\operatorname {\mathrm {BL}}_{i}|\leq \overline {L}_{1}(g_{y_{i}}g_{x_{i}}^{-1})$ . By Corollary 4.7, we immediately obtain an estimate for the difference of $g_{x_{i}}$ and $g_{y_{i}}$ in terms of the length of $\epsilon $ -blocks.

Corollary 4.10. (Difference of $\beta _{1}(A_{\unicode{x3bb} })$ )

Assume that $\overline {g_{y_{i}}g_{x_{i}}^{-1}}=C^{\rho }h_{i}\exp (v_{i})$ , where

$$ \begin{align*}h_{i}=\left[ \begin{array}{@{}ccc@{}} a& b \\ c& d\\ \end{array} \!\!\right]\in \mathrm{SO}_{0}(2,1),\quad v_{i}=b_{0}v_{0}+\cdots+b_{\varsigma}v_{\varsigma}\in V_{\varsigma}.\end{align*} $$

Then we have

$$ \begin{align*}h_{i}=\left[ \begin{array}{@{}ccc@{}} 1+O(\mathbf{r}_{i}^{-\kappa}) & O(\mathbf{r}_{i}^{-1-\kappa}) \\ O(\epsilon) & 1+O(\mathbf{r}_{i}^{-\kappa})\\ \end{array} \!\!\right]\!,\quad v_{i}=O(\mathbf{r}_{i}^{-\varsigma})v_{0}+\cdots+O(\epsilon)v_{\varsigma}\end{align*} $$

for some $\mathbf {r}_{i}\geq \max \{r_{0},R_{0},|\!\operatorname {\mathrm {BL}}_{i}\!|\}$ .

We then immediately conclude from Proposition 4.8 that for any $\operatorname {\mathrm {BL}}^{\prime },\operatorname {\mathrm {BL}}^{\prime \prime }\in \beta _{1}(A_{\unicode{x3bb} })$ with $\operatorname {\mathrm {BL}}^{\prime }\overset {\Gamma }{\sim }\operatorname {\mathrm {BL}}^{\prime \prime }$ , there is an effective gap between them, that is,

$$ \begin{align*} d(\operatorname{\mathrm{BL}}^{\prime},\operatorname{\mathrm{BL}}^{\prime\prime})\geq[\min\{|\operatorname{\mathrm{BL}}^{\prime}\!|,|\operatorname{\mathrm{BL}}^{\prime\prime}\!|\}]^{1+\kappa/2}. \end{align*} $$

However, when $\operatorname {\mathrm {BL}}^{\prime }\overset {e}{\sim }\operatorname {\mathrm {BL}}^{\prime \prime }$ , they do not necessarily have an effective gap. This enlightens us to connect these $\epsilon $ -blocks and generate a new collection $\beta _{2}(A_{\unicode{x3bb} })$ .

4.4.2 Construction of $\beta _{2}$

Now we construct a new collection $\beta _{2}(A_{\unicode{x3bb} })=\{\overline {\operatorname {\mathrm {BL}}}_{1},\ldots ,\overline {\operatorname {\mathrm {BL}}}_{N}\}$ by the following procedure. The idea is to connect $\epsilon $ -blocks in $\beta _{1}(A_{\unicode{x3bb} })=\{\operatorname {\mathrm {BL}}_{1},\ldots ,\operatorname {\mathrm {BL}}_{n}\}$ so that each pair of new blocks must have an effective gap. Let $\operatorname {\mathrm {BL}}_{1}\in \beta _{1}(A_{\unicode{x3bb} })$ , $g_{y_{1}}=h\exp (v)g_{x_{1}}$ , and

$$ \begin{align*}h=\left[ \begin{array}{@{}ccc@{}} a& b \\ c& d\\ \end{array} \!\!\right]\in \mathrm{SO}(2,1),\quad v=b_{0}v_{0}+\cdots+b_{\varsigma}v_{\varsigma}\in V_{\varsigma}.\end{align*} $$

Then by Corollary 4.7, one can write $u^{t(r)}gu^{-s(r)}\in B_{G}(e,\epsilon )$ for

(4.34) $$ \begin{align} r\in \bigcup_{k}[L_{k}(g),\overline{L}_{k}(g)], \end{align} $$

where $k\leq c$ is uniformly bounded for all $g\in G$ . Then consider the following two cases.

1. (1) There is no $j\in \{2,\ldots ,n\}$ such that $(x_{1},y_{1})\overset {e}{\sim }(x_{j},y_{j})$ .

2. (2) There is $j\in \{2,\ldots ,n\}$ such that $(x_{1},y_{1})\overset {e}{\sim }(x_{j},y_{j})$ .

In case (i), we set $\overline {\operatorname {\mathrm {BL}}}_{1}=\operatorname {\mathrm {BL}}_{1}$ . Then by Corollary 4.10, we have

(4.35) $$ \begin{align} |b|\ll\overline{L}_{1}(g_{y_{1}}g_{x_{1}}^{-1})^{-1-\kappa},\quad |a-d|\leq \overline{L}_{1}(g_{y_{1}}g_{x_{1}}^{-1})^{-\kappa}. \end{align} $$

In case (ii), suppose that $g_{x_{j}}=u^{s_{j}}g_{x_{1}}$ , $g_{y_{j}}=u^{t_{j}}g_{y_{1}}$ . Clearly, by the construction, $\overline {r}_{j}>\overline {L}_{1}(g_{y_{1}}g_{x_{1}}^{-1})$ . However, by equation (4.34), we get

$$ \begin{align*}\overline{r}_{j}\in \bigcup_{k}[L_{k}(g_{y_{1}}g_{x_{1}}^{-1}),\overline{L}_{k}(g_{y_{1}}g_{x_{1}}^{-1})]\end{align*} $$

and $k\leq C$ is uniformly bounded for all $g\in G$ . Assume that $j_{\max }$ is the maximal j among $\overline {r}_{j}\in [L_{2}(g_{y_{1}}g_{x_{1}}^{-1}),\overline {L}_{2}(g_{y_{1}}g_{x_{1}}^{-1})]$ . Whether $[0,\overline {L}_{1}(g_{y_{1}}g_{x_{1}}^{-1})]$ and $[L_{2}(g_{y_{1}}g_{x_{1}}^{-1}),\overline {L}_{2}(g_{y_{1}}g_{x_{1}}^{-1})]$ have an effective gap leads to a dichotomy of choices:

$$ \begin{align*}\overline{\operatorname{\mathrm{BL}}}_{1}=\begin{cases} \text{remains unchanged}&\text{if } L_{2}(g_{y_{1}}g_{x_{1}}^{-1})-\overline{L}_{1}(g_{y_{1}}g_{x_{1}}^{-1})>\overline{L}_{1}(g_{y_{1}}g_{x_{1}}^{-1})^{1+2\eta},\\ \{(x_{1},y_{1}),(\overline{x}_{j_{\max}},\overline{y}_{j_{\max}})\}&\text{otherwise.} \end{cases}\end{align*} $$

If the first case occurs, we will not change $\overline {\operatorname {\mathrm {BL}}}_{1}$ anymore. If the second case occurs, that is, we redefine $\overline {\operatorname {\mathrm {BL}}}_{1}=\{(x_{1},y_{1}),(\overline {x}_{j_{\max }},\overline {y}_{j_{\max }})\}$ , then we repeat the construction for the new $\overline {\operatorname {\mathrm {BL}}}_{1}$ again.

1. (1) Suppose that there is $\overline {r}_{j}>\overline {L}_{2}(g_{y_{1}}g_{x_{1}}^{-1})$ . Then assume $j_{\max }$ to be the maximal j among $\overline {r}_{j}\in [L_{3}(g_{y_{1}}g_{x_{1}}^{-1}),\overline {L}_{3}(g_{y_{1}}g_{x_{1}}^{-1})]$ . Then again, we set

   $$ \begin{align*}\overline{\operatorname{\mathrm{BL}}}_{1}=\begin{cases} \text{remains unchanged}&\!\!\text{if } L_{3}(g_{y}g_{x}^{-1})-\overline{L}_{3}(g_{y_{1}}g_{x_{1}}^{-1})>\overline{L}_{2}(g_{y_{1}}g_{x_{1}}^{-1})^{1+2\eta},\\ \{(x_{1},y_{1}),(\overline{x}_{j_{\max}},\overline{y}_{j_{\max}})\}&\!\!\text{otherwise}, \end{cases} \end{align*} $$
   and so on.

The process will stop since the number of intervals is uniformly bounded for all $g\in G$ . Now $\overline {BL}_{1}\in \beta _{2}(A_{\unicode{x3bb} })$ has been constructed. By the choice of $\overline {\operatorname {\mathrm {BL}}}_{1}$ and Corollary 4.7, we conclude that

(4.36) $$ \begin{align} |b|\ll_{\kappa} |\operatorname{\mathrm{BL}}_{1}|^{-\xi(1+\kappa)},\quad |a-d|\ll_{\kappa} |\operatorname{\mathrm{BL}}_{1}|^{-\xi\kappa},\quad |b_{i}|\ll_{\varsigma,\kappa} |\operatorname{\mathrm{BL}}_{1}|^{-\xi (\varsigma-i)} \end{align} $$

for $\xi =\xi (2\eta )\approx 1$ and for all $1\leq i\leq \varsigma $ .

Next, we repeat the above argument to construct $\overline {\operatorname {\mathrm {BL}}}_{m+1}$ . More precisely, suppose that $ \overline {\operatorname {\mathrm {BL}}}_{m}=\{(x_{j_{m-1}+1},y_{j_{m-1}+1}),(\overline {x}_{j_{m}},\overline {y}_{j_{m}})\}\in \beta _{2}(A_{\unicode{x3bb} })$ has been constructed. To define $\overline {\operatorname {\mathrm {BL}}}_{m+1}$ , we repeat the above argument to $\operatorname {\mathrm {BL}}_{j_{m}+1}\in \beta _{1}(A_{\unicode{x3bb} })$ . Thus, $\beta _{2}(A_{\unicode{x3bb} })$ is completely defined. Further, one may conclude the difference of points of $\epsilon $ -blocks in $\beta _{2}(A_{\unicode{x3bb} })$ .

Lemma 4.11. (Difference of $\beta _{2}(A_{\unicode{x3bb} })$ )

For any $\overline {\operatorname {\mathrm {BL}}}_{i}=\{(x_{i}^{\prime },y_{i}^{\prime }),(\overline {x}_{i}^{\prime },\overline {y}_{i}^{\prime })\}$ in the collection $\beta _{2}(A_{\unicode{x3bb} })=\{\overline {\operatorname {\mathrm {BL}}}_{1},\ldots ,\overline {\operatorname {\mathrm {BL}}}_{N}\}$ of $\epsilon $ -blocks, we have

$$ \begin{align*} \overline{g_{y_{i}^{\prime}}g_{x_{i}^{\prime}}^{-1}}=C^{\rho}h_{i}\exp(v_{i}),\end{align*} $$

where

(4.37) $$ \begin{align} h_{i}=\left[ \begin{array}{@{}ccc@{}} 1+O(\mathbf{r}_{i}^{-2\eta}) & O(\mathbf{r}_{i}^{-1-2\eta}) \\ O(\epsilon) & 1+O(\mathbf{r}_{i}^{-2\eta})\\ \end{array} \!\!\right]\!,\quad v_{i}=O(\mathbf{r}_{i}^{-\xi\varsigma})v_{0}+\cdots+O(\epsilon)v_{\varsigma} \end{align} $$

for some $\mathbf {r}_{i}\geq \max \{r_{0},R_{0},|\overline {\operatorname {\mathrm {BL}}}_{i}|\}$ .

Proof. Equation (4.37) follows immediately from equations (4.35), (4.36), (4.30), and (4.31).

Then, recall that by the construction of $\beta _{2}(A_{\unicode{x3bb} })$ , for any $\overline {\operatorname {\mathrm {BL}}}^{\prime },\overline {\operatorname {\mathrm {BL}}}^{\prime \prime }\in \beta _{2}(A_{\unicode{x3bb} })$ with $\overline {\operatorname {\mathrm {BL}}}^{\prime }\overset {e}{\sim }\overline {\operatorname {\mathrm {BL}}}^{\prime \prime }$ , there is an effective gap between them, that is,

$$ \begin{align*}d(\overline{\operatorname{\mathrm{BL}}}^{\prime},\overline{\operatorname{\mathrm{BL}}}^{\prime\prime})\geq[\max\{r_{0},R_{0},\min\{|\overline{\operatorname{\mathrm{BL}}}^{\prime}|,|\overline{\operatorname{\mathrm{BL}}}^{\prime\prime}|\}\}]^{1+2\eta}.\end{align*} $$

However, when $\overline {\operatorname {\mathrm {BL}}}^{\prime }\overset {\Gamma }{\sim }\overline {\operatorname {\mathrm {BL}}}^{\prime \prime }$ , by Proposition 4.8 and Lemma 4.11, we have

$$ \begin{align*}d(\overline{\operatorname{\mathrm{BL}}}^{\prime},\overline{\operatorname{\mathrm{BL}}}^{\prime\prime})\geq[\max\{r_{0},R_{0},\min\{|\overline{\operatorname{\mathrm{BL}}}^{\prime}|,|\overline{\operatorname{\mathrm{BL}}}^{\prime\prime}|\}\}]^{1+\eta}.\end{align*} $$

Thus, we conclude from Proposition 4.1 the following proposition.

Proposition 4.12. (Effective gaps of $\beta _{2}(A_{\unicode{x3bb} })$ )

Let the notation and assumptions be as above. For any $\overline {\operatorname {\mathrm {BL}}}^{\prime },\overline {\operatorname {\mathrm {BL}}}^{\prime \prime }\in \beta _{2}(A_{\unicode{x3bb} })$ , we have

$$ \begin{align*} d(\overline{\operatorname{\mathrm{BL}}}^{\prime},\overline{\operatorname{\mathrm{BL}}}^{\prime\prime}) \geq[\max\{r_{0},R_{0},\min\{|\overline{\operatorname{\mathrm{BL}}}^{\prime}|,|\overline{\operatorname{\mathrm{BL}}}^{\prime\prime}|\}\}]^{1+\eta}. \end{align*} $$

Thus, for any $\zeta \in [0,1]$ , if

$$ \begin{align*} \frac{1}{\unicode{x3bb}}\operatorname{\mathrm{Leb}}( A_{\unicode{x3bb}})\geq \overline{\theta}_{\eta}(\zeta)=1-\theta(\eta,\zeta)= 1-\prod_{n=0}^{\infty} (1+ C\zeta^{n\eta})^{-1}, \end{align*} $$

then there is an $\epsilon $ -block $\overline {\operatorname {\mathrm {BL}}}\in \beta _{2}(A_{\unicode{x3bb} })$ that has

$$ \begin{align*} |\overline{\operatorname{\mathrm{BL}}}|\geq\zeta\unicode{x3bb}. \end{align*} $$

4.5 Non-shifting time

Now assume that for some $\unicode{x3bb} ,\zeta>0$ , we know that

$$ \begin{align*} \operatorname{\mathrm{Leb}}(A_{\unicode{x3bb}})\geq \overline{\theta}_{\eta}(\zeta)\unicode{x3bb}. \end{align*} $$

Then Proposition 4.12 provides us with an $\epsilon $ -block $\overline {\operatorname {\mathrm {BL}}}=\{(x^{\prime },y^{\prime }),(\overline {x}^{\prime },\overline {y}^{\prime })\}\in \beta _{2}(A_{\unicode{x3bb} })$ with $|\overline {\operatorname {\mathrm {BL}}}|\geq \zeta \unicode{x3bb} $ . In other words, if we write

(4.38) $$ \begin{align} x^{\prime}=u^{s(R_{1})}x,\quad \overline{x}^{\prime}=u^{s(R_{2})}x,\quad y^{\prime}=u^{t(R_{1})}y,\quad \overline{y}^{\prime}=u^{t(R_{2})}y, \end{align} $$

then we can find $R_{1},R_{2}>0$ with $R_{2}-R_{1}\geq \zeta \unicode{x3bb} $ such that

$$ \begin{align*}d_{C^{\rho}\backslash G}(u^{t(R_{1})}.\overline{g_{y}},u^{s(R_{1})}.\overline{g_{x}})<\epsilon,\quad d_{C^{\rho}\backslash G}(u^{t(R_{2})}.\overline{g_{y}},u^{s(R_{2})}.\overline{g_{x}})<\epsilon. \end{align*} $$

It is already quite surprising. However, it is still possible that

$$ \begin{align*}d_{C^{\rho}\backslash G}(u^{t(r)}.\overline{g_{y}},u^{s(r)}.\overline{g_{x}})>\epsilon\end{align*} $$

for some $r\in [R_{1},R_{2}]\cap A$ . Thus, define

and we want to show that $\operatorname {\mathrm {Leb}}(\overline {A}_{R_{1}R_{2}})/\unicode{x3bb} $ has a upper bound in certain situations.

Remark 4.13. By equation (4.37), we can estimate the difference between $x^{\prime },y^{\prime }$ ; more precisely, we have

$$ \begin{align*} \overline{g_{y^{\prime}}g_{x^{\prime}}^{-1}}=C^{\rho} h\exp(v), \end{align*} $$

where

$$ \begin{align*}h=\left[ \begin{array}{@{}ccc@{}} 1+O((\zeta\unicode{x3bb})^{-2\eta}) & O((\zeta\unicode{x3bb})^{-1-2\eta}) \\ O(\epsilon) & 1+O((\zeta\unicode{x3bb})^{-2\eta})\\ \end{array} \!\!\right]\!,\quad v=O((\zeta\unicode{x3bb})^{-\xi\varsigma})v_{0}+\cdots+O(\epsilon)v_{\varsigma}.\end{align*} $$

4.5.1 Construction of $\widetilde {\beta }_{1},\widetilde {\beta }_{2}$

Now we consider the shifting time of the $\epsilon $ -block $\overline {\operatorname {\mathrm {BL}}}=\{(x^{\prime },y^{\prime }),(\overline {x}^{\prime },\overline {y}^{\prime })\}\in \beta _{2}(A_{\unicode{x3bb} })$ . Define a collection $\widetilde {\beta }_{1}(\overline {A}_{R_{1}R_{2}})$ of $\epsilon $ -blocks on the orbit intervals $[x^{\prime },x^{\prime \prime }]$ , $[y^{\prime },y^{\prime \prime }]$ according to the following steps. Suppose that

and that $(\overline {g_{x_{1}}}, \overline {g_{y_{1}}})\in C^{\rho }\backslash G\times C^{\rho }\backslash G$ covers $(x_{1},y_{1})$ and

Let $\operatorname {\mathrm {BL}}_{1}\in \widetilde {\beta }_{1}(\overline {A}_{R_{1}R_{2}})$ be the $\epsilon $ -block of $x_{1},y_{1}$ of length $\overline {r}_{1}$ , and write $\operatorname {\mathrm {BL}}_{1}=\{(x_{1},y_{1}),(\overline {x}_{1},\overline {y}_{1})\}$ . To define $\operatorname {\mathrm {BL}}_{2}$ , we take

and apply the above procedure to

This process defines a collection $\widetilde {\beta }_{1}(\overline {A}_{R_{1}R_{2}})=\{\operatorname {\mathrm {BL}}_{1},\ldots , \operatorname {\mathrm {BL}}_{m}\}$ of $\epsilon $ -blocks on the orbit intervals $[u^{s(r_{1})}x^{\prime },u^{s(\overline {r}_{m})}x^{\prime }]$ , $[u^{t(r_{1})}y^{\prime },u^{t(\overline {r}_{m})}y^{\prime }]$ . Completely similar to $\beta _{1}$ , we can connect some of the $\epsilon $ -blocks in $\widetilde {\beta }_{1}(\overline {A}_{R_{1}R_{2}})$ and form a new collection $\widetilde {\beta }_{2}(\overline {A}_{R_{1}R_{2}})$ such that each pair of $\epsilon $ -blocks in $\widetilde {\beta }_{2}(\overline {A}_{R_{1}R_{2}})$ has an effective gap. Then, we conclude again from Proposition 4.1 the following lemma.

Lemma 4.14. (Difference and effective gaps of $\widetilde {\beta }_{2}(\overline {A}_{R_{1}R_{2}})$ )

For any $\widetilde {\operatorname {\mathrm {BL}}}_{i}=\{(\widetilde {x}_{i}^{\prime },\widetilde {y}_{i}^{\prime }), (\overline {\widetilde {x}}_{i}^{\prime },\overline {\widetilde {y}}_{i}^{\prime })\}$ in the collection $\widetilde {\beta }_{2}(\overline {A}_{R_{1}R_{2}})=\{\widetilde {\operatorname {\mathrm {BL}}}_{1},\ldots ,\widetilde {\operatorname {\mathrm {BL}}}_{M}\}$ of $\epsilon $ -blocks, we have

$$ \begin{align*} \overline{g_{\widetilde{y}_{i}^{\prime}}g_{\widetilde{x}_{i}^{\prime}}^{-1}}=C^{\rho}h_{i}\exp(v_{i}),\end{align*} $$

where

(4.39) $$ \begin{align} h_{i}=\left[ \begin{array}{@{}ccc@{}} 1+O(\mathbf{r}_{i}^{-2\eta}) & O(\mathbf{r}_{i}^{-1-2\eta}) \\ O(\epsilon) & 1+O(\mathbf{r}_{i}^{-2\eta})\\ \end{array} \!\!\right]\!,\quad v_{i}=O(\mathbf{r}_{i}^{-\xi\varsigma})v_{0}+\cdots+O(\epsilon)v_{\varsigma} \end{align} $$

for some $\mathbf {r}_{i}\geq \max \{r_{0},R_{0},|\widetilde {\operatorname {\mathrm {BL}}}_{i}|\}$ .

Moreover, for any $\widetilde {\operatorname {\mathrm {BL}}}^{\prime },\widetilde {\operatorname {\mathrm {BL}}}^{\prime \prime }\in \widetilde {\beta }_{2}(\overline {A}_{R_{1}R_{2}})$ , we have

$$ \begin{align*}d(\widetilde{\operatorname{\mathrm{BL}}}^{\prime},\widetilde{\operatorname{\mathrm{BL}}}^{\prime\prime})\geq[\max\{r_{0},R_{0},\min\{|\widetilde{\operatorname{\mathrm{BL}}}^{\prime}|,|\widetilde{\operatorname{\mathrm{BL}}}^{\prime\prime}|\}\}]^{1+\eta}.\end{align*} $$

Thus, for any $\widetilde {\zeta }\in [0,1]$ , if

$$ \begin{align*}\frac{1}{\unicode{x3bb}}\operatorname{\mathrm{Leb}}(\overline{A}_{R_{1}R_{2}})\geq \overline{\theta}_{\eta}(\widetilde{\zeta})= 1-\prod_{n=0}^{\infty} (1+ C\widetilde{\zeta}^{n\eta})^{-1},\end{align*} $$

then there is an $\epsilon $ -block $\widetilde {\operatorname {\mathrm {BL}}}\in \widetilde {\beta }_{2}(\overline {A}_{R_{1}R_{2}})$ that has

$$ \begin{align*}|\widetilde{\operatorname{\mathrm{BL}}}|\geq\widetilde{\zeta}\unicode{x3bb}.\end{align*} $$

Thus, given $\widetilde {\zeta }\in (0,\zeta )$ , we can apply Lemma 4.14 and obtain an $\epsilon $ -block $\widetilde {\operatorname {\mathrm {BL}}}=\{(\widetilde {x},\widetilde {y}),(\overline {\widetilde {x}},\overline {\widetilde {y}})\}\in \widetilde {\beta }_{2}(\overline {A}_{R_{1}R_{2}})$ that has length $|\widetilde {\operatorname {\mathrm {BL}}}|\geq \widetilde {\zeta }\unicode{x3bb} $ . Then by equation (4.39), we get that

$$ \begin{align*} \overline{g_{\widetilde{y}}g_{\widetilde{x}}^{-1}}=C^{\rho}\widetilde{h}\exp(\widetilde{v}\,),\end{align*} $$

where

$$ \begin{align*}\widetilde{h}=\left[ \begin{array}{@{}ccc@{}} 1+O((\widetilde{\zeta}\unicode{x3bb})^{-2\eta}) & O((\widetilde{\zeta}\unicode{x3bb})^{-1-2\eta}) \\ O(\epsilon) & 1+O((\widetilde{\zeta}\unicode{x3bb})^{-2\eta})\\ \end{array} \!\!\right]\!,\quad \widetilde{v}=O((\widetilde{\zeta}\unicode{x3bb})^{-\xi\varsigma})v_{0}+\cdots+O(\epsilon)v_{\varsigma}.\end{align*} $$

Then combining Remark 4.13 and Proposition 4.8, we conclude that

$$ \begin{align*}r_{1}>(\widetilde{\zeta}\unicode{x3bb})^{1+\eta}.\end{align*} $$

Since $r_{1}\in [R_{1},R_{2}]$ , we obtain $(\widetilde {\zeta }\unicode{x3bb} )^{1+\eta }\leq \zeta \unicode{x3bb} $ or

$$ \begin{align*}\widetilde{\zeta}\leq (\zeta\unicode{x3bb}^{-\eta})^{{1}/({1+\eta})}.\end{align*} $$

In other words, we obtain the following lemma.

Lemma 4.15. (Shifting is sparse in a big $\epsilon $ -block)

Given $\unicode{x3bb}>0,\zeta \in (0,1),\eta \approx 0$ , assume that

$$ \begin{align*}\operatorname{\mathrm{Leb}}(A_{\unicode{x3bb}})\geq \overline{\theta}_{\eta}(\zeta)\unicode{x3bb}.\end{align*} $$

Then there is an $\epsilon $ -block $\overline {\operatorname {\mathrm {BL}}}\in \beta _{2}(A_{\unicode{x3bb} })$ with the corresponding time interval $[R_{1},R_{2}]$ and $|\overline {\operatorname {\mathrm {BL}}}|=R_{2}-R_{1}\geq \zeta \unicode{x3bb} $ . In addition, denote the shifting time of $\overline {\operatorname {\mathrm {BL}}}$ by

Then we have

$$ \begin{align*}\operatorname{\mathrm{Leb}}(\overline{A}_{R_{1}R_{2}})/\unicode{x3bb}\leq \overline{\theta}_{\eta}((\zeta\unicode{x3bb}^{-\eta})^{{1}/({1+\eta})})= 1-\prod_{n=0}^{\infty} (1+ C(\zeta\unicode{x3bb}^{-\eta})^{{n\eta}/({1+\eta})})^{-1}.\end{align*} $$

In particular, $\operatorname {\mathrm {Leb}}(\overline {A}_{R_{1}R_{2}})/\unicode{x3bb} =o(\unicode{x3bb} )$ .

In the following, we present a key proposition below that will be used in the proof of Proposition 5.1. It basically says that non-shifting is always observable when the time scale is large.

Proposition 4.16. (Non-shifting time is not negligible)

Given an integer $n\geq 2$ , $\kappa \in (0,2\eta _{0})$ , there exist $\unicode{x3bb} _{0}>0$ , $\sigma _{0}\approx 0$ , $\vartheta \approx 0$ such that, for any

• • disjoint subsets $A^{1},\ldots ,A^{n}\subset [0,\infty )$ that satisfy equations (4.32) and (4.33),

• • $\unicode{x3bb}>\unicode{x3bb} _{0}$ ,

• • $\sigma \in (0,\sigma _{0})$ satisfying

  $$ \begin{align*}\operatorname{\mathrm{Leb}}\bigg(\coprod_{i=1}^{n}A^{i}\cap[0,\unicode{x3bb}]\bigg)>(1-2\sigma)\unicode{x3bb},\end{align*} $$

there exists one $A^{i(\unicode{x3bb} )}$ and $[R_{1}^{\prime }(\unicode{x3bb} ),R_{2}^{\prime }(\unicode{x3bb} )]\subset [0,\unicode{x3bb} ]$ such that there exists an $\epsilon $ -block $\overline {\operatorname {\mathrm {BL}}}\in \beta _{2}(A^{i(\unicode{x3bb} )}\cap [R_{1}^{\prime },R_{2}^{\prime }])$ with the corresponding time interval $[R_{1},R_{2}]$ such that

$$ \begin{align*}R_{2}-R_{1}>\vartheta\unicode{x3bb},\quad \operatorname{\mathrm{Leb}}(A^{i(\unicode{x3bb})}_{\epsilon}\cap [R_{1},R_{2}])>\vartheta\unicode{x3bb},\end{align*} $$

where is the non-shifting time of $A^{i(\unicode{x3bb} )}$ .

Proof. First, fix $\eta $ satisfying equation (4.30), $\zeta _{1}\in (0,1)$ so that $\overline {\theta }_{\eta }(\zeta _{1})=1/(n+1)$ and choose $\zeta _{2}\approx 0$ such that

(4.40) $$ \begin{align} \overline{\theta}_{\eta}(\zeta_{2})<\frac{\zeta_{1}^{-1}-1}{2(\zeta_{1}^{-n}-1)} \end{align} $$

and then $\unicode{x3bb} _{0}>0$ such that

(4.41) $$ \begin{align} \overline{\theta}_{\eta}(\zeta_{2})\zeta_{1}-\overline{\theta}_{\eta}((\zeta_{2}\unicode{x3bb}^{-\eta})^{{1}/({1+\eta})})>\tfrac{1}{2} \overline{\theta}_{\eta}(\zeta_{2})\zeta_{1} \end{align} $$

for $\unicode{x3bb}>\unicode{x3bb} _{0}$ . Then choose

(4.42) $$ \begin{align} \sigma_{0}&= \min\bigg\{\frac{1}{4}\zeta_{1}^{n},\frac{1}{2(n+1)}\bigg\}, \; \end{align} $$

(4.43) $$ \begin{align} \hphantom{\hspace{25pt}}\vartheta &= \frac{1}{2} \overline{\theta}_{\eta}(\zeta_{2})\zeta_{1}^{n}. \qquad\qquad\qquad\quad \end{align} $$

Given $\sigma \in (0,\sigma _{0})$ , $\unicode{x3bb}>\unicode{x3bb} _{0}$ , we write $[R_{1}^{(0)},R_{2}^{(0)}]=[0,\unicode{x3bb} ]$ , $b_{0}=2\sigma $ , and then apply the following algorithm on $ k=0,1,\ldots , n-1$ orderly.

First, assume that:

• • $i_{1},\ldots ,i_{k}\in \{1,\ldots ,n\}$ have been chosen without repetition;

• • $b_{0},\ldots ,b_{k}>0$ have been chosen;

and they satisfy

(4.44) $$ \begin{align} \operatorname{\mathrm{Leb}}\bigg(\coprod_{i\not\in\{i_{1},\ldots,i_{k}\}}A^{i}\cap[R_{1}^{(k)},R_{2}^{(k)}]\bigg)/\operatorname{\mathrm{Leb}}([R_{1}^{(k)},R_{2}^{(k)}])>1-b_{k}. \end{align} $$

(Note that by the choice of $\zeta _{1}$ and $\sigma _{0}$ , equation (4.44) is possible for $k=0$ .) Then there is one $A^{i_{k+1}}$ for some $i_{k+1}\not \in \{i_{1},\ldots ,i_{k}\}$ with

$$ \begin{align*}\operatorname{\mathrm{Leb}}(A^{i_{k+1}}\cap[R_{1}^{(k)},R_{2}^{(k)}])>\overline{\theta}(\zeta_{1}) \cdot\operatorname{\mathrm{Leb}}([R_{1}^{(k)},R_{2}^{(k)}]).\end{align*} $$

Applying Lemma 4.15 to $A^{i_{k+1}}$ , we obtain an $\epsilon $ -block $\overline {\operatorname {\mathrm {BL}}}_{k+1}$ with the corresponding time interval $[R_{1}^{(k+1)},R_{2}^{(k+1)}]\subset [R_{1}^{(k)},R_{2}^{(k)}]$ and

(4.45) $$ \begin{align} |\overline{\operatorname{\mathrm{BL}}}_{k+1}|=R_{2}^{(k+1)}-R_{1}^{(k+1)}\geq\zeta_{1}\cdot\operatorname{\mathrm{Leb}}([R_{1}^{(k)},R_{2}^{(k)}])\geq\zeta_{1}^{k+1}\unicode{x3bb}>\vartheta\unicode{x3bb}. \end{align} $$

It follows from equation (4.44) that

$$ \begin{align*} & \operatorname{\mathrm{Leb}}\bigg(\coprod_{i\not\in\{i_{1},\ldots,i_{k}\}}A^{i}\cap[R_{1}^{(k+1)},R_{2}^{(k+1)}]\bigg) \;\nonumber\\ &\quad= \operatorname{\mathrm{Leb}}([R_{1}^{(k+1)},R_{2}^{(k+1)}])- \operatorname{\mathrm{Leb}}\bigg(\bigg(\coprod_{i\not\in\{i_{1},\ldots,i_{k}\}}A^{i}\bigg)^{c}\cap[R_{1}^{(k+1)},R_{2}^{(k+1)}]\bigg) \;\nonumber\\ &\quad\geq \operatorname{\mathrm{Leb}}([R_{1}^{(k+1)},R_{2}^{(k+1)}])- \operatorname{\mathrm{Leb}}\bigg(\bigg(\coprod_{i\not\in\{i_{1},\ldots,i_{k}\}}A^{i}\bigg)^{c}\cap[R_{1}^{(k)},R_{2}^{(k)}]\bigg) \;\nonumber\\ &\quad> \operatorname{\mathrm{Leb}}([R_{1}^{(k+1)},R_{2}^{(k+1)}])- b_{k}\cdot\operatorname{\mathrm{Leb}}([R_{1}^{(k)},R_{2}^{(k)}]) \; \nonumber \end{align*} $$

and so by equation (4.45), we obtain

(4.46) $$ \begin{align} \operatorname{\mathrm{Leb}}\bigg(\coprod_{i\not\in\{i_{1},\ldots,i_{k}\}}A^{i}\cap[R_{1}^{(k+1)},R_{2}^{(k+1)}]\bigg)/\operatorname{\mathrm{Leb}}([R_{1}^{(k+1)},R_{2}^{(k+1)}])>1-b_{k}\zeta_{1}^{-1}. \end{align} $$

Then we face a dichotomy:

1. (1) $\operatorname {\mathrm {Leb}}(A^{i_{k+1}}\cap [R_{1}^{(k+1)},R_{2}^{(k+1)}])/\operatorname {\mathrm {Leb}}([R_{1}^{(k+1)},R_{2}^{(k+1)}])\geq \overline {\theta }_{\eta }(\zeta _{2})$ ;

2. (2) $\operatorname {\mathrm {Leb}}(A^{i_{k+1}}\cap [R_{1}^{(k+1)},R_{2}^{(k+1)}])/\operatorname {\mathrm {Leb}}([R_{1}^{(k+1)},R_{2}^{(k+1)}])<\overline {\theta }_{\eta }(\zeta _{2})$ .

In case (1), we take $i(\unicode{x3bb} )=i_{k+1}$ , $[R_{1}^{\prime }(\unicode{x3bb} ),R_{2}^{\prime }(\unicode{x3bb} )]=[R_{1}^{(k)},R_{2}^{(k)}]$ , $\overline {\operatorname {\mathrm {BL}}}=\overline {\operatorname {\mathrm {BL}}}_{k+1}$ . By equations (4.41), (4.43), and (4.45), we have

(4.47) $$ \begin{align} & \operatorname{\mathrm{Leb}}(A_{\epsilon}^{i(\unicode{x3bb})}\cap[R_{1}^{(k+1)},R_{2}^{(k+1)}])\;\nonumber\\ &\quad= \operatorname{\mathrm{Leb}}(A^{i(\unicode{x3bb})}\cap[R_{1}^{(k+1)},R_{2}^{(k+1)}])-\operatorname{\mathrm{Leb}}((A^{i(\unicode{x3bb})}_{\epsilon})^{c}\cap A^{i(\unicode{x3bb})}\cap[R_{1}^{(k+1)},R_{2}^{(k+1)}])\;\nonumber\\ &\quad\geq \overline{\theta}_{\eta}(\zeta_{2})\cdot\operatorname{\mathrm{Leb}}([R_{1}^{(k+1)},R_{2}^{(k+1)}])-\overline{\theta}_{\eta}((\zeta_{2}\unicode{x3bb}^{-\eta})^{{1}/({1+\eta})})\cdot\operatorname{\mathrm{Leb}}([R_{1}^{(k)},R_{2}^{(k)}]) \;\nonumber\\ &\quad\geq (\overline{\theta}_{\eta}(\zeta_{2})\zeta_{1} -\overline{\theta}_{\eta}((\zeta_{2}\unicode{x3bb}^{-\eta})^{{1}/({1+\eta})}))\cdot\operatorname{\mathrm{Leb}}([R_{1}^{(k)},R_{2}^{(k)}])\;\nonumber \\ &\quad> \frac{1}{2} \overline{\theta}_{\eta}(\zeta_{2})\zeta_{1}\cdot\zeta_{1}^{k}\unicode{x3bb} \geq \vartheta\unicode{x3bb}\; \end{align} $$

and the consequence of Proposition 4.16 follows. In case (2), by equation (4.46), we have

(4.48) $$ \begin{align} \operatorname{\mathrm{Leb}}\bigg(\coprod_{i\not\in\{i_{1},\ldots,i_{k+1}\}}A^{i}\cap[R_{1}^{(k+1)},R_{2}^{(k+1)}]\bigg)\big/\operatorname{\mathrm{Leb}}([R_{1}^{(k+1)},R_{2}^{(k+1)}])>1-b_{k}\zeta_{1}^{-1}-\overline{\theta}_{\eta}(\zeta_{2}). \end{align} $$

Now note that:

• • $i_{k+1}\not \in \{i_{1},\ldots ,i_{k}\}$ has been chosen;

• • choose $b_{k+1}=b_{k}\zeta _{1}^{-1}+\overline {\theta }_{\eta }(\zeta _{2})$ ;

and then equation (4.48) coincides with equation (4.44) by replacing k by $k+1$ . Thus, we can apply the algorithm again by replacing k by $k+1$ .

After applying the algorithm, we either stop in the middle and finish the proof, or we determine:

• • $i_{1},\ldots ,i_{n-1}\in \{1,\ldots ,n\}$ without repetition;

• • a sequence $\{b_{k}\}_{k=0}^{n-1}$ of positive numbers with $b_{0}=2\sigma $ and

  (4.49) $$ \begin{align} b_{k+1}=b_{k}\zeta_{1}^{-1}+\overline{\theta}_{\eta}(\zeta_{2}). \end{align} $$

Let $i(\unicode{x3bb} )$ be the only element in $\{1,\ldots ,n\}\setminus \{i_{1},\ldots ,i_{n-1}\}$ . Let $[R_{1}^{\prime }(\unicode{x3bb} ),R_{2}^{\prime }(\unicode{x3bb} )]=[R_{1}^{(n-1)},R_{2}^{(n-1)}]$ . In addition, by equation (4.49), we calculate

$$ \begin{align*}b_{n-1}=2\sigma\zeta_{1}^{-(n-1)}+\overline{\theta}_{\eta}(\zeta_{2})\frac{\zeta_{1}^{-(n-1)}-1}{\zeta_{1}^{-1}-1}.\end{align*} $$

Now we try to do the algorithm one more time. Thus, we apply again Lemma 4.15 to $A^{i(\unicode{x3bb} )}$ , and then we obtain an $\epsilon $ -block $\overline {\operatorname {\mathrm {BL}}}=\overline {\operatorname {\mathrm {BL}}}_{n}$ with the corresponding time interval $[R_{1}^{(n)},R_{2}^{(n)}]\subset [R_{1}^{(n-1)},R_{2}^{(n-1)}]$ satisfying equations (4.45) and (4.46), that is,

(4.50) $$ \begin{align} |\overline{\operatorname{\mathrm{BL}}}_{n}|=\operatorname{\mathrm{Leb}}([R_{1}^{(n)},R_{2}^{(n)}])\geq\zeta_{1}\cdot\operatorname{\mathrm{Leb}}([R_{1}^{(n-1)},R_{2}^{(n-1)}])\geq \zeta_{1}^{n}\unicode{x3bb}>\vartheta\unicode{x3bb}, \end{align} $$

(4.51) $$ \begin{align} &\operatorname{\mathrm{Leb}}(A^{i(\unicode{x3bb})}\cap[R_{1}^{(n)},R_{2}^{(n)}])/\operatorname{\mathrm{Leb}}([R_{1}^{(n)},R_{2}^{(n)}])\nonumber\\ &\quad>1-b_{n-1}\zeta_{1}^{-1}=1-2\sigma\zeta_{1}^{-n}-\overline{\theta}_{\eta}(\zeta_{2})\frac{\zeta_{1}^{-n}-\zeta_{1}^{-1}}{\zeta_{1}^{-1}-1}\geq\overline{\theta}_{\eta}(\zeta_{2}), \end{align} $$

where the last inequality of equation (4.51) follows from equations (4.40) and (4.42). Then, as in equation (4.47), we calculate

$$ \begin{align*} &\operatorname{\mathrm{Leb}}(A_{\epsilon}^{i(\unicode{x3bb})}\cap[R_{1}^{(n)},R_{2}^{(n)}])\\ &\quad\geq (\overline{\theta}_{\eta}(\zeta_{2})\zeta_{1} -\overline{\theta}_{\eta}((\zeta_{2}\unicode{x3bb}^{-\eta})^{{1}/({1+\eta})}))\cdot\operatorname{\mathrm{Leb}}([R_{1}^{(n-1)},R_{2}^{(n-1)}])> \vartheta\unicode{x3bb},\end{align*} $$

where the last inequality follows from equations (4.41), (4.43), and (4.50).

5 Invariance

Let $G_{X}=\mathrm {SO}(n_{X},1)$ and $\Gamma _{X}\subset G_{X}$ be a lattice. Let $(X,\mu )$ be the homogeneous space $X=G_{X}/\Gamma _{X}$ equipped with the Lebesgue measure $\mu $ , and let $\phi ^{U_{X}}_{t}=u_{X}^{t}$ be a unipotent flow on X as before. In addition, let $G_{Y}$ be a Lie group and $\Gamma _{Y}\subset G_{Y}$ be a lattice. Let $(Y,m_{Y})$ be the homogeneous space $Y=G_{Y}/\Gamma _{Y}$ equipped with the Lebesgue measure $m_{Y}$ and let $\phi ^{U_{Y}}_{t}=u^{t}_{Y}$ be a unipotent flow on Y. Next, choose $\tau _{Y}\in \mathbf {K}_{\kappa }(Y)$ a positive integrable function $\tau _{Y}$ on Y such that $\tau _{Y},\tau _{Y}^{-1}$ are bounded and satisfies equation (2.10). Then define the measure and so the time-change flow $\phi ^{U_{Y},\tau _{Y}}_{t}=\widetilde {u}_{Y}^{\,t}$ preserves the measure $\nu $ by Remark 2.2. Also recall from equation (2.9) that

$$ \begin{align*} u^{t}_{Y}y=\phi^{U_{Y},\tau_{Y}}_{z(y,t)}(y)=\widetilde{u}_{Y}^{\,z(y,t)}(y). \end{align*} $$

We shall to study the joinings of $(X,\mu ,u_{X}^{t})$ and $(Y,\nu ,\widetilde {u}_{Y}^{\,t})$ . Let $\rho $ be an ergodic joining of $u_{X}^{t}$ and $\widetilde {u}_{Y}^{\,t}$ , that is, $\rho $ is a probability measure on $X\times Y$ , whose marginals on X and Y are $\mu $ and $\nu $ , respectively, and which is $(u_{X}^{t}\times \widetilde {u}_{Y}^{\,t})$ -ergodic. As indicated at the end of §3, when $\rho $ is not the product measure $\mu \times \nu $ , we apply Theorem 3.5 and then obtain a compact subgroup $C^{\rho }\subset C_{G_{X}}(U_{X})$ such that is an ergodic joining $u_{X}^{t}$ and $\widetilde {u}_{Y}^{\,t}$ on $C^{\rho }\backslash X\times Y$ under the natural projection $\pi : X\times Y\rightarrow C^{\rho }\backslash X\times Y$ . In addition, it is a finite extension of $\nu $ , that is, $\operatorname {\mathrm {supp}}\overline {\rho }_{y}$ consists of exactly n points $\overline {\psi }_{1}(y),\ldots ,\overline {\psi }_{n}(y)$ for $\nu $ -a.e. $y\in Y$ (without loss of generality, we shall assume that it holds for all $y\in Y$ ). By Kunugui’s theorem, we obtain $\psi _{i}:Y\rightarrow X$ so that $P_{X}\circ \psi _{i}=\overline {\psi }_{i}$ , where $P_{X}:X\rightarrow C^{\rho }\backslash X$ .

5.1 Central direction

We want to study the behavior of $\overline {\psi }_{p}$ along the central direction $C_{G_{Y}}(U_{Y})$ of $U_{Y}$ . In the following, assume that $\rho $ is a $(u_{X}^{t}\times \widetilde {u}_{Y}^{\,t})$ -joining. Then by equation (3.12), we get that

$$ \begin{align*}\overline{\psi}_{p}(u^{t}_{Y}y)=\overline{\psi}_{p}(\widetilde{u}_{Y}^{\,z(y,t)}(y))=u_{X}^{z(y,t)}\overline{\psi}_{i_{p}}(y),\end{align*} $$

where the index $i_{p}=i_{p}(y,t)\in \{1,\ldots ,n\}$ is determined by

$$ \begin{align*}(u_{X}^{-z(y,t)}\times \widetilde{u}_{Y}^{\,-z(y,t)} )(\overline{\psi}_{p}(\widetilde{u}_{Y}^{\,z(y,t)}(y)),\widetilde{u}_{Y}^{\,z(y,t)}(y))\in\hat{\psi}_{i_{p}}(Y).\end{align*} $$

Now we orderly fix the following data so that the propositions in §4 can be used:

• • fix $\kappa \in (0,2\eta _{0})$ satisfying equation (2.10), where $\eta _{0}>0$ comes from Proposition 4.8;

• • fix $\sigma \in (0,\sigma _{0})$ , where $\sigma _{0}\approx 0$ comes from both Propositions 4.8 and 4.16;

• • fix $\epsilon \in (0,\epsilon _{0})$ as in equation (4.31);

such that the following holds.

• • (Effective ergodicity) By equation (2.11), there is $K_{1}\subset Y$ with $\nu (K_{1})>1-\sigma /6$ and $t_{K_{1}}>0$ such that

  (5.1) $$ \begin{align} |t-z(y,t)|=O(t^{1-\kappa}) \end{align} $$
  for all $t\geq t_{K_{1}}$ and $y\in K_{1}$ . Note that using ergodic theorem, we have
  (5.2) $$ \begin{align} |t-z(y,t)|=o(t) \end{align} $$
  for $\nu $ -almost all $y\in Y$ .

• • (Distinguishing $\overline {\psi }_{p},\overline {\psi }_{q}$ ) There is $K_{2}\subset Y$ with $\nu (K_{2})>1-\sigma /6$ such that

  (5.3) $$ \begin{align} d(\overline{\psi}_{p}(y),\overline{\psi}_{q}(y))>100\epsilon \end{align} $$
  for $y\in K_{2}$ , $1\leq p< q\leq n$ .

• • (Lusin’s theorem) There is $K_{3}\subset Y$ such that $\nu (K_{3})>1-\sigma /6$ and $\overline {\psi }_{p}|_{K_{3}}$ is uniformly continuous for all $p\in \{1,\ldots ,n\}$ . Thus, there is $\delta>0$ such that

  (5.4) $$ \begin{align} d_{\overline{X}}(\overline{\psi}_{p}(y_{1}),\overline{\psi}_{p}(y_{2}))<\epsilon \end{align} $$
  for $p\in \{1,\ldots ,n\}$ , $d_{Y}(y_{1},y_{2})<\delta $ , and $y_{1},y_{2}\in K_{3}$ .

Given $K\subset \overline {X}$ by Proposition 4.8, let

(5.5)

Here we choose $\overline {\mu }(K)$ being so large that $m_{Y}(K^{0})>1-\sigma /2$ .

Fix $c\in C_{G_{Y}}(U_{Y})\cap B_{G_{Y}}(e,\delta )$ . We choose arbitrarily a representative $g_{\overline {\psi }_{p}(y)}\in G_{X}$ of $\overline {\psi }_{p}(y)$ . Then there is a representative $g_{\overline {\psi }_{p}(cy)}\in G_{X}$ so that:

• • $\overline {g_{\overline {\psi }_{p}(y)}}$ and $\overline {g_{\overline {\psi }_{p}(cy)}}$ lie in the same fundamental domain;

• • the difference $g(y)=g_{\overline {\psi }_{p}(cy)}g_{\overline {\psi }_{p}(y)}^{-1}=h^{(p)}(y)\exp (v^{(p)}(y))$ , where

  (5.6) $$ \begin{align} h^{(p)}(y)&=\left[ \begin{array}{@{}ccc@{}} a^{(p)}(y)& b^{(p)}(y) \\ c^{(p)}(y)& d^{(p)}(y)\\ \end{array} \!\!\right]\in \mathrm{SO}_{0}(2,1),\nonumber\\ v^{(p)}&=b_{0}^{(p)}(y)v_{0}+\cdots+b_{\varsigma}^{(p)}(y)v_{\varsigma}\in V_{\varsigma}. \end{align} $$

Further, applying the effectiveness of the unipotent flow, we shall show that the difference $g(y)$ has to lie in the centralizer $C_{G_{X}}(U_{X})$ .

Proposition 5.1. Let the notation and assumptions be as above. For the quantities in equation (5.6), there is a measurable set $S(c)\subset Y$ with $\nu (S(c))>0$ such that

$$ \begin{align*} b^{(p)}(y)=0,\quad a^{(p)}(y)=d^{(p)}(y)=1,\quad b^{(p)}_{0}(y)=\cdots=b^{(p)}_{\varsigma-1}(y)=0 \end{align*} $$

for $y\in S(c)$ , $p\in \{1,\ldots ,n\}$ .

Proof. Consider the measure of the set

for $l\in \mathbb {Z}^{+}$ . We shall show that

satisfies the requirement. By ergodic theorem, we have

(5.7) $$ \begin{align} m_{Y}(Y_{l}(c))=\lim_{\unicode{x3bb}\rightarrow\infty}\frac{1}{\unicode{x3bb}}\int_{0}^{\unicode{x3bb}}\mathbf{1}_{Y_{l}(c)}(u^{r}_{Y}y)\,dr \end{align} $$

for $m_{Y}$ -a.e. $y\in Y$ , where $m_{Y}$ denotes the Lebesgue measure on Y.

However, by ergodic theorem, for $m_{Y}$ -a.e. $y\in Y$ , there is $A_{c,y}\subset \mathbb {R}^{+}$ and $\unicode{x3bb} _{0}(y)>0$ such that:

• • for $r\in A_{c,y}$ , we have

  $$ \begin{align*} u^{r}_{Y}y ,u^{r}_{Y}cy\in K^{0}; \end{align*} $$

• • $\operatorname {\mathrm {Leb}}(A_{c,y}\cap [0,\unicode{x3bb} ])\geq (1-2\sigma )\unicode{x3bb} $ whenever $\unicode{x3bb} \geq \unicode{x3bb} _{0}(y)$ .

Then, by the assumptions, we have

(5.8) $$ \begin{align} A_{c,y} \subset \{r\in[0,\infty):d_{\overline{X}}(\overline{\psi}_{p}(u^{r}_{Y}y),\overline{\psi}_{p}(u^{r}_{Y}cy))<\epsilon,\ p\in\{1,\ldots,n\}\}. \end{align} $$

It follows that for $r\in A_{c,y}$ , we have

(5.9) $$ \begin{align} d_{\overline{X}}(u_{X}^{z(y,r)}\overline{\psi}_{i_{p}(y,r)}(y),u_{X}^{z(cy ,r)}\overline{\psi}_{i_{p}(cy,r)}(cy))<\epsilon \end{align} $$

for any $p\in \{1,\ldots ,n\}$ . Now we restrict our attention on $A_{c,y}\cap [0,\unicode{x3bb} ]$ with $\unicode{x3bb} \geq \unicode{x3bb} _{0}(y)$ . For simplicity, we assume that $0\in A_{c,y}$ . Let $I=((p_{1},p_{2}),\ldots , (p_{2n-1},p_{2n}))\in \{1,\ldots ,n\}^{2n}$ be a sequence of indexes and

(5.10)

Then $A=A_{c,y}^{I}$ , $R_{0}=t_{K_{1}}$ , $t(r)=z(cy ,r)$ , $s(r)=z(y ,r)$ satisfy equations (4.32) and (4.33) for points

$$ \begin{align*} \overline{\psi}_{p_{2k-1}}(y),\overline{\psi}_{p_{2k}}(cy)\in K \end{align*} $$

for all $k\in \{1,\ldots ,n\}$ .

Since $A_{c,y}=\coprod _{I\in \{1,\ldots ,n\}^{2n}}A^{I}_{c,y}$ (is a disjoint union because of equation (5.3)), by Proposition 4.16, for any $\unicode{x3bb} \geq \unicode{x3bb} _{0}$ , there exists one $A_{c,y}^{I(\unicode{x3bb} )}$ and $[R_{1}^{\prime },R_{2}^{\prime }]\subset [0,\unicode{x3bb} ]$ such that there exists an $\epsilon $ -block $\overline {\operatorname {\mathrm {BL}}}=\{(x^{\prime },y^{\prime }),(x^{\prime \prime },y^{\prime \prime })\}\in \beta _{2}(A_{c,y}^{I(\unicode{x3bb} )}\cap [R_{1}^{\prime },R_{2}^{\prime }])$ with the corresponding time interval $[R_{1},R_{2}]$ such that

$$ \begin{align*} R_{2}-R_{1}>\vartheta\unicode{x3bb},\quad \operatorname{\mathrm{Leb}}(A^{I(\unicode{x3bb})}_{\epsilon}\cap [R_{1},R_{2}])>\vartheta\unicode{x3bb}, \end{align*} $$

where $A^{I(\unicode{x3bb} )}_{\epsilon }$ is the non-shifting time of $A_{c,y}^{I(\unicode{x3bb} )}$ . Then by the definition of $A^{I(\unicode{x3bb} )}_{\epsilon }$ , we know that

$$ \begin{align*}d_{C^{\rho}\backslash G}(u_{X}^{z(cy,r)}.\overline{g_{\overline{\psi}_{i_{p}(cy,r)}(cy)}},u_{X}^{z(y,r)}.\overline{g_{\overline{\psi}_{i_{p}(y,r)}(y)}})<\epsilon\end{align*} $$

for $r\in A^{I(\unicode{x3bb} )}_{\epsilon }$ , $p\in \{1,\ldots ,n\}$ . Recall from equation (4.24) that points in K have injectivity radius at least $\epsilon _{0}$ . Thus, for $r\in A^{I(\unicode{x3bb} )}_{\epsilon }$ ,

$$ \begin{align*}u_{X}^{z(y,r)}.\overline{g_{\overline{\psi}_{i_{p}(y,r)}(y)}}\quad \text{and} \quad u_{X}^{z(cy,r)}.\overline{g_{\overline{\psi}_{i_{p}(cy,r)}(cy)}}\end{align*} $$

lie in the same fundamental domain. Thus, if $r\in A^{I(\unicode{x3bb} )}_{\epsilon }$ and

$$ \begin{align*}\overline{g_{\overline{\psi}_{p}(u^{r}_{Y}y)}}=u_{X}^{z(y,r)}.\overline{g_{\overline{\psi}_{i_{p}(y,r)}(y)}},\end{align*} $$

then we get

$$ \begin{align*}\overline{g_{\overline{\psi}_{p}(u^{r}_{Y}cy)}}=u_{X}^{z(cy,r)}.\overline{g_{\overline{\psi}_{i_{p}(cy,r)}(cy)}}.\end{align*} $$

Recall that the difference of $u_{X}^{z(y,r)}.\overline {g_{\overline {\psi }_{i_{p}(y,r)}(y)}}$ , $u_{X}^{z(cy,r)}.\overline {g_{\overline {\psi }_{i_{p}(cy,r)}(cy)}}$ for $r\in A^{i(\unicode{x3bb} )}_{\epsilon }\cap [R_{1},R_{2}]$ was estimated by equation (4.37) (see also equations (4.5), (4.6), and (4.7)). In particular, for $r\in A^{i(\unicode{x3bb} )}_{\epsilon }\cap [R_{1},R_{2}]$ , the quantities of

$$ \begin{align*}g(u^{r}_{Y}y)=g_{\overline{\psi}_{p}(cu^{r}_{Y}y)}g_{\overline{\psi}_{p}(u^{r}_{Y}y)}^{-1}=u_{X}^{z(cy,r)}g_{\overline{\psi}_{i_{p}(cy,r)}(cy)}(u_{X}^{z(y,r)}g_{\overline{\psi}_{i_{p}(y,r)}(y)})^{-1}\end{align*} $$

that need to be estimated in $Y_{l}(c)$ are all decreasing as $\unicode{x3bb} \rightarrow \infty $ . Then given $l\in \mathbb {Z}^{+}$ , there is a sufficiently large $\unicode{x3bb} $ such that

$$ \begin{align*} \int_{0}^{\unicode{x3bb}}\mathbf{1}_{Y_{l}(c)}(u^{r}_{Y}y)\,dr \geq\operatorname{\mathrm{Leb}}(A^{i(\unicode{x3bb})}_{\epsilon}\cap [R_{1},R_{2}])>\vartheta\unicode{x3bb}.\end{align*} $$

Thus, by equation (5.7), we have $m_{Y}(Y_{l}(c))>\vartheta $ . Now letting $\unicode{x3bb} \rightarrow \infty $ and then $l\rightarrow \infty $ , we see that $m_{Y}(\bigcap _{l}Y_{l}(c))>\vartheta $ . Finally, by Remark 2.2 and $\tau _{Y}\in \mathbf {K}_{\kappa }(Y)$ , we obtain $\nu (\bigcap _{l}Y_{l}(c))>0$ .

Using Proposition 5.1, we immediately obtain the following corollary.

Corollary 5.2. There is a measurable map $\varpi :C_{G_{Y}}(U_{Y})\times X\times Y\rightarrow C_{G_{X}}(U_{X})$ that induces a map $\widetilde {S}_{c}:\operatorname {\mathrm {supp}} (\rho )\rightarrow \operatorname {\mathrm {supp}} (\rho )$ by

(5.11) $$ \begin{align} \widetilde{S}_{c}: (x,y) \mapsto (\varpi(c,x,y)x,cy) \end{align} $$

for all $c\in C_{G_{Y}}(U_{Y})$ , $\rho $ -a.e. $(x,y)\in X\times Y$ . Moreover, we have

(5.12) $$ \begin{align} \varpi(c,x,y)= \ & u_{X}^{-z(cy,t)}\varpi(c,(u_{X}^{z(y,t)}\times \widetilde{u}_{Y}^{\,z(y,t)}).(x,y))u_{X}^{z(y,t)}, \end{align} $$

(5.13) $$ \begin{align} \varpi(c_{1}c_{2},x,y) =\ & \varpi(c_{1},\varpi(c_{2},x,y)x,c_{2}y)\varpi(c_{2},x,y)\; \end{align} $$

for $c,c_{1},c_{2}\in C_{G_{Y}}(U_{Y})$ , $\rho $ -a.e. $(x,y)\in X\times Y$ , $t\in \mathbb {R}$ .

Remark 5.3. Note that when $c\in \exp (\mathbb {R}U_{Y})$ , $\varpi $ reduces to an element in $\exp (\mathbb {R}U_{X})$ ; in fact, we have

$$ \begin{align*}\varpi(u^{t}_{Y},x,y)=u_{X}^{z(y,r)}=\exp(z(y,t)U_{X})\end{align*} $$

for all $t\in \mathbb {R}$ .

However, for distinct $q_{1},q_{2}\in \{1,\ldots ,n\}$ , any $c\in C_{G_{Y}}(U_{Y})$ , we have

(5.14) $$ \begin{align} w(c,\psi_{q_{1}}(y),y)\psi_{q_{1}}(y)\in C^{\rho}\psi_{p_{1}}(y), \quad w(c,\psi_{q_{2}}(y),y)\psi_{q_{2}}(y)\in C^{\rho}\psi_{p_{2}}(y) \end{align} $$

for distinct $p_{1},p_{2}\in \{1,\ldots ,n\}$ ; for otherwise it would lead to $\psi _{q_{2}}(y)\in C_{G_{X}}(U_{X})\psi _{q_{1}}(y)$ , which contradicts the definition of $\psi $ (cf. §3.2).

Proof of Corollary 5.2

Fix $c\in C_{G_{Y}}(U_{Y})\cap B(e,\delta )$ . Proposition 5.1 provides us a subset $S(c)\subset Y$ with $\nu (S(c))>0$ such that

(5.15) $$ \begin{align} \psi_{p}(cy)=w_{p}(c,y)\psi_{p}(y) \end{align} $$

for $y\in S(c)$ , $w_{p}(c,y)\in C_{G_{X}}(U_{X})$ . In addition, for $y,u^{r}_{Y}y\in S(c)$ , we know that

$$ \begin{align*}w_{p}(c,u^{r}_{Y}y)u_{X}^{z(y,r)}\psi_{i_{p}(y,r)}(y)=\psi_{p}(u^{r}_{Y}cy)=u_{X}^{z(cy,r)}w_{i_{p}(cy,r)}(c,y)\psi_{i_{p}(cy,r)}(y).\end{align*} $$

Thus, $\psi _{i_{p}(y,r)}(y)\in C_{G_{X}}(U_{X})\psi _{i_{p}(cy,r)}(y)$ and so $i_{p}(y,r)=i_{p}(cy,r)$ . It follows that

(5.16) $$ \begin{align} w_{p}(c,u^{r}_{Y}y)u_{X}^{z(y,r)}=u_{X}^{z(cy,r)}w_{i_{p}(cy,r)}(c,y)=u_{X}^{z(cy,r)}w_{i_{p}(y,r)}(c,y) \end{align} $$

for $y,u^{r}_{Y}y\in S(c)$ .

Thus, for $y\in S(c)$ , we define

Let $\pi _{Y}:\operatorname {\mathrm {supp}}(\rho )\rightarrow Y$ be the natural projection. Then for $(x,y)\in \pi ^{-1}_{Y}(S(c))$ , we know that $C^{\rho }x= C^{\rho }\psi _{p_{x}}(y)$ for some $p_{x}\in \{1,\ldots ,n\}$ . Thus, given $\psi _{p_{x}}(y)=k^{\rho }_{x}x$ for some $k^{\rho }_{x}\in C^{\rho }$ , we define

(5.17)

Thus, we successfully define $\varpi (c,\cdot ,\cdot )$ for $\pi ^{-1}_{Y}(S(c))$ . Then the $(u_{X}^{t}\times \tilde {u}_{Y}^{t})$ -flow helps us to define $\varpi (c,\cdot ,\cdot )$ for all $\rho $ -a.e. $(x,y)\in X\times Y$ . More precisely, for $(x,y)\in X\times Y$ (in a $\rho $ -conull set), we can choose $t=t(x,y)\in \mathbb {R}$ such that $(u_{X}^{z(y,t)}x,u_{Y}^{t}y)\in \pi _{Y}^{-1}(S(c))$ . Then define

(5.18)

(Note that equation (5.16) tells us that equation (5.18) holds true for $y,u_{Y}^{t}y\in S(c)$ and thus $\varpi $ is well defined.) Finally, for general $c\in C_{G_{Y}}(U_{Y})$ , choose $k\in C_{G_{Y}}(U_{Y})\cap B(e,\delta )$ such that $k^{m}=c$ , and then define iteratively

and finally reach $c=k^{m}$ . Then the map of equation (5.11) is well defined on $\operatorname {\mathrm {supp}}(\rho )$ .

In light of Corollary 5.2, we consider the decomposition in equation (2.7) and write

(5.19) $$ \begin{align} \varpi(c,x,y)=u_{X}^{\alpha(c,x,y)} \beta(c,x,y), \end{align} $$

where $\alpha (c,x,y)\in \mathbb {R}$ and $\beta (c,x,y)\in \exp V^{\perp }_{C_{X}}$ . Then by equation (5.12), we have

(5.20) $$ \begin{align} z(cy,t)+\alpha(c,x,y)=\ & \alpha(c,(u^{z(y,t)}\times \widetilde{u}^{z(y,t)}).(x,y))+z(y,t),\; \end{align} $$

(5.21) $$ \begin{align} \beta(c,x,y)=\ & \beta(c,(u^{z(y,t)}\times \widetilde{u}^{z(y,t)}).(x,y))\; \end{align} $$

for all $t\in \mathbb {R}$ .

First consider $\alpha $ . Recall that for fixed $y\in Y$ , $\operatorname {\mathrm {supp}}(\rho _{y})=\bigsqcup _{p=1}^{n}C^{\rho }\psi _{p}(y)$ . Then by equation (5.20), for $\nu $ -a.e. $y\in Y$ , $x\in \operatorname {\mathrm {supp}}(\rho _{y})$ , we have

(5.22) $$ \begin{align} \alpha(c,x,y)-\alpha(c,(u^{z(y,t)}\times \widetilde{u}^{z(y,t)}).(x,y))=z(y,t)-z(cy,t) \end{align} $$

for all $r\in \mathbb {R}$ . In addition, by equation (5.17), we have

(5.23) $$ \begin{align} \alpha(c,x,y)=\alpha(c,kx,y) \end{align} $$

for all $x\in \operatorname {\mathrm {supp}}(\rho _{y})$ , $k\in C^{\rho }$ . By equation (5.20), for any $(x_{1},y),(x_{2},y)\in \operatorname {\mathrm {supp}}(\rho )$ , we have

(5.24) $$ \begin{align} \alpha(c,x_{1},y)-\alpha(c,x_{2},y)= \alpha(c,(u^{t}\times \widetilde{u}^{t}).(x_{1},y))-\alpha(c,(u^{t}\times \widetilde{u}^{t}).(x_{2},y)). \end{align} $$

Define $\alpha _{\max }:C_{G_{Y}}(U_{Y})\times X\times Y\rightarrow \mathbb {R}$ by

$$ \begin{align*} \alpha_{\max}:(c,x,y)\mapsto\max\{r\in\mathbb{R}:\rho_{y}\{x^{\prime}\in X:\alpha(c,x^{\prime},y)-\alpha(c,x,y)=r\}>0\}. \end{align*} $$

Then by equation (5.24), we have

$$ \begin{align*} \alpha_{\max}(c,(x,y))=\alpha_{\max}(c,(u_{X}^{t}\times \widetilde{u}_{Y}^{\,t}).(x,y)) \end{align*} $$

for any $t\in \mathbb {R}$ , $\rho $ -a.e. $(x,y)\in X\times Y$ . Thus, $\alpha _{\max }(c,x,y)\equiv \alpha _{\max }(c)$ . Now if $\alpha _{\max }(c)>0$ , then for $\rho $ -a.e. $(x,y)$ , there is $x^{\prime }\in X$ such that $\alpha (c,x^{\prime },y)=\alpha (c,x,y)+\alpha _{\max }(c)$ , which contradicts the fact that $\alpha _{\max }(c,x,y)$ take at most finitely many different values for fixed y (by equation (5.23)). Thus, we conclude that $\alpha _{\max }(c)\equiv 0$ and so

$$ \begin{align*} \alpha(c,x,y)\equiv \alpha(c,y) \end{align*} $$

for all $c\in C_{G_{Y}}(U_{Y})$ , $\rho $ -a.e. $(x,y)\in X\times Y$ .

However, via the ergodicity of the flow $u_{X}^{t}\times \widetilde {u}_{Y}^{\,t}$ , we conclude from equation (5.21) that

$$ \begin{align*} \beta(c,x,y)\equiv\beta(c) \end{align*} $$

for all $c\in C_{G_{Y}}(U_{Y})$ . In particular, we have

$$ \begin{align*} \varpi(c,x,y)=\varpi(c,y)=u_{X}^{\alpha(c,y)}\beta(y) \end{align*} $$

for all $c\in C_{G_{Y}}(U_{Y})$ , $\rho $ -a.e. $(x,y)\in X\times Y$ . In addition, we know from equation (5.13) that $\beta (c_{1} c_{2})=\beta (c_{1})\beta (c_{2})$ via the definition of $\beta $ . Further, we always have $d\beta (U_{Y})\equiv 0$ . Therefore, we can restrict our attention to $V^{\perp }_{C}$ and conclude that $d\beta |_{V^{\perp }_{C}}: V^{\perp }_{C_{Y}}\rightarrow V^{\perp }_{C_{X}}$ is a Lie algebra homomorphism.

In sum, we obtain Theorem 1.2 for the centralizer $C_{G_{Y}}(U_{Y})$ .

Theorem 5.4. (Extra central invariance of $\rho $ )

For any $c\in C_{G_{Y}}(U_{Y})$ , the map $S_{c}:X\times Y\rightarrow X\times Y$ defined by

$$ \begin{align*} S_{c}:(x,y)\mapsto (\beta(c)x,\tilde{u}_{Y}^{-\alpha(c,y)}(cy)) \end{align*} $$

commutes with $u_{X}^{t}\times \widetilde {u}_{Y}^{\,t}$ , and is $\rho $ -invariant. In addition, $S_{c_{1}c_{2}}=S_{c_{1}}\circ S_{c_{2}}$ for any $c_{1},c_{2}\in C_{G_{Y}}(U_{Y})$ , and $S_{u_{Y}^{t}}=\operatorname {\mathrm {id}}$ for $t\in \mathbb {R}$ .

Proof. Clearly, $S_{c}$ is well defined:

(5.25) $$ \begin{align} S_{c}(x,y)=(u_{X}^{-\alpha(c,y)}\times \widetilde{u}_{Y}^{\,-\alpha(c,y)}).\widetilde{S}_{c}(x,y)\in\operatorname{\mathrm{supp}}(\rho) \end{align} $$

whenever $(x,y)\in \operatorname {\mathrm {supp}}(\rho )$ . Also, one may check that $S_{c_{1}c_{2}}=S_{c_{1}}S_{c_{2}}$ for any $c_{1},c_{2}\in C_{G_{Y}}(U_{Y})$ , and $S_{u_{Y}^{t}}=\operatorname {\mathrm {id}}$ for $t\in \mathbb {R}$ . Next, by equation (5.20), one verifies

$$ \begin{align*}(u_{X}^{z(y,r)}\times \widetilde{u}_{Y}^{\,z(y,r)}).S_{c}(x,y)=S_{c}(u_{X}^{z(y,r)}\times \widetilde{u}_{Y}^{\,z(y,r)}).(x,y) \end{align*} $$

for any $r\in \mathbb {R}$ , $(x,y)\in \operatorname {\mathrm {supp}}(\rho )$ . That is, $(u_{X}^{t}\times \widetilde {u}_{Y}^{\,t})\circ S_{c}=S_{c}\circ (u_{X}^{t}\times \widetilde {u}_{Y}^{\,t})$ .

Finally, let $\Omega $ be the set of $(u_{X}^{t}\times \widetilde {u}_{Y}^{\,t})$ -generic points, and we want to show that there is a point $(x_{0},y_{0})\in \Omega \cap S_{c}^{-1}\Omega $ . By equation (5.25), it suffices to show that there is a point $(x_{0},y_{0})\in \Omega \cap \widetilde {S}_{c}^{-1}\Omega $ . Fix $c\in C_{G_{Y}}(U_{Y})\cap B(e,\delta )$ . Recall that

$$ \begin{align*}1=\rho(\Omega)=\int_{Y}\int_{C^{\rho}}\frac{1}{n} \sum_{p=1}^{n}\mathbf{1}_{\Omega}(k\psi_{p}(y),y)\,dm(k)\,d\nu(y).\end{align*} $$

Thus, there is $\Omega _{Y}\subset Y$ with $\nu (\Omega _{Y})=1$ such that

(5.26) $$ \begin{align} \int_{C^{\rho}} \frac{1}{n} \sum_{p=1}^{n}\mathbf{1}_{\Omega}(k\psi_{p}(y),y)\,dm(k)=1 \end{align} $$

for $y\in \Omega _{Y}$ . Since $\nu $ and $m_{Y}$ are equivalent, and $\Omega _{Y}\cap k^{-1}\Omega _{Y}$ is $m_{Y}$ -conull, we get that $\Omega _{Y}\cap c^{-1}\Omega _{Y}$ is $\nu $ -conull. Choose $y_{0}\in \Omega _{Y}\cap c^{-1}\Omega _{Y}\cap S(c)$ , where $S(c)$ is given by Proposition 5.1 (cf. equation (5.15)). Then equation (5.26) leads to

$$ \begin{align*} \int_{C^{\rho}} \mathbf{1}_{\Omega}(k\psi_{1}(y_{0}),y_{0})\,dm(k)=1,\quad \int_{C^{\rho}} \mathbf{1}_{\Omega}(k\psi_{1}(cy_{0}),cy_{0})\,dm(k)=1.\end{align*} $$

Then we can choose $k_{0}\in C^{\rho }$ such that $(k_{0}\psi _{1}(y_{0}),y_{0}),(k_{0}\psi _{1}(cy_{0}),cy_{0})\in \Omega $ . Let . Then by equations (5.15) and (5.17), we have

$$ \begin{align*}\widetilde{S}_{c}(x_{0},y_{0})= (\varpi(c,y_{0})x_{0},cy_{0})=(k_{0}w_{p}(c,y_{0})k_{0}^{-1}k_{0}\psi_{1}(y_{0}),cy_{0})=(k_{0}\psi_{1}(cy_{0}),cy_{0}).\end{align*} $$

Thus, $(x_{0},y_{0})\in \Omega \cap \widetilde {S}_{c}^{-1}\Omega $ .

Hence, since $u_{X}^{t}\times \widetilde {u}_{Y}^{\,t}$ is $\rho $ -ergodic, by ergodic theorem, for any bounded continuous function f, we have

$$ \begin{align*} \int f d\rho &=\lim_{T\rightarrow\infty}\frac{1}{T}\int_{0}^{T} f((u_{X}^{t}\times\tilde{u}_{Y}^{t}).S_{c}(x_{0},y_{0}))\,dt \\ &=\lim_{T\rightarrow\infty}\frac{1}{T}\int_{0}^{T} f(S_{c}(u_{X}^{t}x_{0},\tilde{u}_{Y}^{t}y_{0}))\,dt= \int f\circ S_{c} d\rho \nonumber \end{align*} $$

and so $\rho =(S_{c})_{\ast }\rho $ .

In particular, we obtain the following corollary.

Corollary 5.5. (Extra central invariance of $\nu $ )

For any $c\in C_{G_{Y}}(U_{Y})$ , the map $S^{Y}_{c}:Y\rightarrow Y$ defined by

$$ \begin{align*}S_{c}^{Y}:y\mapsto \tilde{u}_{Y}^{-\alpha(c,y)}(cy)\end{align*} $$

commutes with $\widetilde {u}^{t}$ , and is $\nu $ -invariant. In addition, $S^{Y}_{c_{1}c_{2}}=S^{Y}_{c_{1}}S^{Y}_{c_{2}}$ for any $c_{1},c_{2}\in C_{G_{Y}}(U_{Y})$ , and $S^{Y}_{u_{Y}^{t}}=\operatorname {\mathrm {id}}$ for $t\in \mathbb {R}$ .

It is worth noting that equation (5.11) can be interpreted through the language of cohomology. More precisely, equation (5.11) implies the time change $\tau _{Y}$ and $\tau _{Y}\circ c$ are measurably cohomologous.

Theorem 5.6. Let $\tau _{Y}\in \mathbf {K}_{\kappa }(Y)$ . Suppose that there is a non-trivial ergodic joining $\rho \in J(u_{X}^{t},\phi _{t}^{U_{Y},\tau _{Y}})$ . Then $\tau _{Y}(y)$ and $\tau _{Y}( cy)$ are (measurably) cohomologous along $u_{Y}^{t}$ for all $c\in C_{G_{Y}}(U_{Y})$ . More precisely, the transfer function can be taken to be

$$ \begin{align*}F_{c}(y)= \alpha(c,y).\end{align*} $$

Proof. By equation (5.20), for $m_{Y}$ -a.e. $y\in Y$ , $x\in \operatorname {\mathrm {supp}}(\rho _{y})$ , we have

$$ \begin{align*} &\int_{0}^{t}\tau_{Y}(u_{Y}^{s}y)-\tau_{Y}(u_{Y}^{s}cy)\,ds\;\nonumber\\ &\quad=\int_{0}^{t}\tau_{Y}(u_{Y}^{s}y)\,ds-\int_{0}^{t}\tau_{Y}(u_{Y}^{s}cy)\,ds\;\nonumber\\ &\quad= z(y,t)-z(cy,t)\;\nonumber\\ &\quad=\alpha(c,y)- \alpha(c,u_{Y}^{t}y). \; \nonumber \end{align*} $$

Thus, we can take the transfer function as

Then $\tau _{Y}(y)$ and $\tau _{Y}( cy)$ are (measurably) cohomologous for all $c\in C_{G_{Y}}(U_{Y})$ .

If $\tau _{Y}(y)$ and $\tau _{Y}(cy)$ are cohomologous with an $L^{1}$ transfer function, then we are able to do more via the ergodic theorem.

Lemma 5.7. Given $c\in C_{G_{Y}}(U_{Y})$ , if:

• • c is $m_{Y}$ -ergodic (as a left action on Y);

• • $\tau _{Y}(y)$ and $\tau _{Y}(cy)$ are cohomologous with a $L^{1}$ transfer function $F_{c}(y)$ ;

then for $m_{Y}$ -a.e. $y\in Y$ , we have

$$ \begin{align*}\lim_{t\rightarrow\infty}\frac{1}{t}\alpha(c^{t},y)=\int \alpha(c,y)\,dm_{Y}(y).\end{align*} $$

Proof. By equations (5.13) and (5.14), for $c_{1},c_{2}\in C_{G_{Y}}(U_{Y})$ , $m_{Y}$ -a.e. $y\in Y$ , we have the cocycle identity

$$ \begin{align*} \alpha(c_{1}c_{2},y)= \alpha(c_{1},c_{2}y)+\alpha(c_{2},y) .\end{align*} $$

Thus, if $F_{c}(\cdot )\in L^{1}(Y)$ , then by the ergodicity, we get

(5.27) $$ \begin{align} \lim_{k\rightarrow\infty}\frac{1}{k} \alpha(c^{k},y)=\lim_{k\rightarrow\infty}\frac{1}{k}\sum_{i=0}^{k}\alpha(c^{i},y)=\int \alpha(c,y)\,dm_{Y}(y).\\[-25pt]\nonumber \end{align} $$

Remark 5.8. The results obtained in §5.1 also hold true for $\rho $ being a finite extension of $\nu $ , when $(X,\phi ^{U_{X},\tau _{X}}_{t})$ is a time change of the unipotent flow on $X=\mathrm {SO}(n_{X},1)/\Gamma _{X}$ . For example, we consider the case when $n_{X}=2$ , $\tau _{X}\in C^{1}(X)$ , $\tau _{Y}\equiv 1$ (in other words, $\phi ^{U_{Y},\tau _{Y}}_{t}=\phi ^{U_{Y}}_{t}=u_{Y}^{t}$ is the usual unipotent flow, and $\nu =m_{Y}$ ). First, [Rat87] shows that $(X,\phi ^{U_{X},\tau _{X}}_{t})$ has H-property. In particular, suppose that $\rho \in J(\phi ^{U_{X},\tau _{X}}_{t},\phi ^{U_{Y}}_{t})$ is not the product measure $\mu \times \nu $ . Then H-property of deduces that $\rho $ is a finite extension of $\nu $ (see Theorem 3, [Rat83]):

$$ \begin{align*} \int f(x,y)d\rho(x,y)=\int\frac{1}{n} \sum_{p=1}^{n}f(\psi_{p}(y),y)\,d\nu(y). \end{align*} $$

However, since $V^{\perp }_{C_{X}}=0$ , by Corollary 5.2 (and equation (5.19)), we again have a map $ \widetilde {S}_{c}: \operatorname {\mathrm {supp}} (\rho )\rightarrow \operatorname {\mathrm {supp}} (\rho )$ given by

(5.28) $$ \begin{align} \widetilde{S}_{c}:(x,y) \mapsto ( u_{X}^{\alpha(c,y)}x,cy). \end{align} $$

In contrast to Theorem 5.4, $\widetilde {S}_{c}$ is $\rho $ -invariant in this situation. We can further specify $\alpha (c,x,y)$ in certain situation as follows.

First, under the current setting, equation (5.20) changes to

$$ \begin{align*}\xi(\psi_{p}(cy),t)+\alpha(c,y)= \alpha(c,u_{Y}^{t}y)+\xi(\psi_{p}(y),t)\end{align*} $$

for $t\in \mathbb {R}$ . It follows that

$$ \begin{align*} 0&=\int_{0}^{\xi(\psi_{p}(y),t)}\tau(u_{X}^{s}\psi_{p}(y))-\tau(u_{X}^{s}\psi_{p}(y))\,ds\;\nonumber\\ &=\int_{0}^{\xi(\psi_{p}(cy),t)}\tau(u_{X}^{s}\psi_{p}(cy))\,ds-\int_{0}^{\xi(\psi_{p}(y),t)}\tau(u_{X}^{s}\psi_{p}(y))\,ds\;\nonumber\\ &=\int_{0}^{\xi(\psi_{p}(cy),t)}\tau(u_{X}^{\alpha(c,y)+s}\psi_{p}(y))\,ds-\int_{0}^{\xi(\psi_{p}(y),t)}\tau(u_{X}^{s}\psi_{p}(y))\,ds\;\nonumber\\ &=\int_{0}^{\alpha(c,y)+\xi(\psi_{p}(cy),t)}\tau(u_{X}^{s}\psi_{p}(y))\,ds-\int_{0}^{\alpha(c,y)}\tau(u_{X}^{s}\psi_{p}(y))\,ds\\ &\quad-\int_{0}^{\xi(\psi_{p}(y),t)}\tau(u_{X}^{s}\psi_{p}(y))\,ds\;\nonumber\\ &=\int_{0}^{\alpha(c,u_{Y}^{t}y)+\xi(\psi_{p}(y),t)}\tau(u_{X}^{s}\psi_{p}(y))\,ds-\int_{0}^{\xi(\psi_{p}(y),t)}\tau(u_{X}^{s}\psi_{p}(y))\,ds\\ &\quad-\int_{0}^{\alpha(c,y)}\tau(u_{X}^{s}\psi_{p}(y))\,ds\;\nonumber\\ &=\int_{0}^{\alpha(c,u_{Y}^{t}y)}\tau(u_{X}^{s}\tilde{u}_{X}^{t}(\psi_{p}(y)))\,ds-\int_{0}^{\alpha(c,y)}\tau(u_{X}^{s}\psi_{p}(y))\,ds. \; \nonumber \end{align*} $$

In other words, we have

$$ \begin{align*}\int_{0}^{\alpha(c, u_{Y}^{t}y)}\tau(u_{X}^{s}\tilde{u}_{X}^{t}(x))\,ds=\int_{0}^{\alpha(c,y)}\tau(u_{X}^{s}x)\,ds \end{align*} $$

for $\rho $ -a.e. $(x,y)\in X\times Y$ and therefore

$$ \begin{align*}\int_{0}^{\alpha(c,y)}\tau(u_{X}^{s}x)\,ds\equiv r_{c} \end{align*} $$

for some $r_{c}\in \mathbb {R}$ . It follows that

(5.29) $$ \begin{align} \alpha(c,y)=\xi(x,r_{c}) \end{align} $$

for $\rho $ -a.e. $(x,y)\in X\times Y$ . Moreover, we apply $\tilde {u}_{X}^{-r_{c}}\times u_{Y}^{-r_{c}}$ to equation (5.28), and get that

(5.30) $$ \begin{align} (x,y) \mapsto ( u_{X}^{\alpha(c,y)}x,cy)\mapsto ( x,u_{Y}^{-r_{c}}cy) \end{align} $$

is $\rho $ -invariant. In particular, suppose that $G_{Y}$ is a semisimple Lie group with finite center and no compact factors and $\Gamma _{Y}\subset G_{Y}$ is a irreducible lattice. Suppose the $\mathfrak {sl}_{2}$ -weight decomposition $\mathfrak {g}_{Y}=\mathfrak {sl}_{2}+V^{\perp }$ of $\mathfrak {g}_{Y}$ (see equation (2.3)) contains at least one $\mathfrak {sl}_{2}$ -irreducible representation $V_{\varsigma }\subset V^{\perp }$ with a positive highest weight $\varsigma>0$ . Choosing $c=\exp (v_{\varsigma })$ , by Moore’s ergodicity theorem, we must have $\rho =\mu \times \nu $ (cf. Lemma 3.1). Note that this coincides with the result obtained in [DKW22]. In addition, even if the highest weight of $V_{\varsigma }$ is $\varsigma =0$ for any $V_{\varsigma }\subset V^{\perp }$ , the only possible situation for $\rho \neq \mu \times \nu $ is that $\alpha (\exp v,y)\equiv 0$ for all $v\in V^{\perp }$ . Thus, by equation (5.30), we conclude that $\rho $ is $(\operatorname {\mathrm {id}}\times \exp (v))$ -invariant for any $v\in V^{\perp }$ . In §6.2, we shall see that $\langle \exp (v)\rangle \subset G_{Y}$ is a normal subgroup, which leads to a contradiction. Thus, we conclude that $V^{\perp }=0$ and so $\mathfrak {g}_{Y}=\mathfrak {sl}_{2}$ .

5.2 Normal direction

Applying a similar argument in §5.1, we can study the behavior of $\overline {\psi }_{p}$ along the normal direction $N_{G_{Y}}(U_{Y})$ of $U_{Y}$ as well. Here we only study the diagonal action provided by the $\mathfrak {sl}_{2}$ -triple. Thus, let

$$ \begin{align*}\operatorname{\mathrm{Span}}\{U_{Y},A_{Y},\overline{U}_{Y}\}\subset\mathfrak{g}_{Y},\quad \operatorname{\mathrm{Span}}\{U_{X},Y_{n},\overline{U}_{X}\}\subset\mathfrak{g}_{X}\end{align*} $$

be $\mathfrak {sl}_{2}$ -triples in $\mathfrak {g}_{Y}$ , $\mathfrak {g}_{X}$ , respectively, where $Y_{n}$ is given in §2.1. Denote

We adopt the same notation and orderly fix the data as in §5.1; thus, $\sigma ,\epsilon ,t_{K_{1}},\delta ,K,K^{0}$ are chosen so that equations (5.1), (5.3), and (5.4) hold. (Here we further assume $\delta <\epsilon $ .) Fix $|t_{0}|<\delta $ , $a_{Y}=a_{Y}^{t_{0}}$ , and $a_{X}=a_{X}^{t_{0}}$ . By ergodic theorem, there is $A_{a_{Y},y}\subset \mathbb {R}^{+}$ and $\unicode{x3bb} _{0}>0$ such that:

• • for $r\in A_{a_{Y},y}$ , we have

  $$ \begin{align*} u^{r}_{Y}y ,a_{Y}u^{r}_{Y}y\in K^{0};\end{align*} $$

• • $\operatorname {\mathrm {Leb}}(A_{a_{Y},y}\cap [\unicode{x3bb} ^{\prime },\unicode{x3bb} ^{\prime \prime }])\geq (1-2\sigma )(\unicode{x3bb} ^{\prime \prime }-\unicode{x3bb} ^{\prime })$ whenever $\unicode{x3bb} ^{\prime \prime }-\unicode{x3bb} ^{\prime }\geq \unicode{x3bb} _{0}$ and $\unicode{x3bb} ^{\prime }\in A_{a_{Y},y}$ .

Then by the assumptions, we have

(5.31) $$ \begin{align} A_{a_{Y},y} \subset \{r\in[0,\infty):d_{\overline{X}}(a_{X}\overline{\psi}_{p}(u^{r}_{Y}y),\overline{\psi}_{p}(a_{Y}u^{r}_{Y}y))<2\epsilon,\ p\in\{1,\ldots,n\}\}. \end{align} $$

It follows that for $r\in A_{a_{Y},y}$ , we have

$$ \begin{align*} 2\epsilon&>d_{\overline{X}}(a_{X}\overline{\psi}_{p}(u^{r}_{Y}y),\overline{\psi}_{p}(a_{Y}u^{r}_{Y}y))\;\nonumber\\ &=d_{\overline{X}}(a_{X}\overline{\psi}_{p}(u^{r}_{Y}y),\overline{\psi}_{p}(u^{e^{-t_{0}}r}_{Y}a_{Y}y))\;\nonumber\\ &=d_{\overline{X}}(a_{X}u_{X}^{z(y,r)}\overline{\psi}_{i_{p}(y,r)}(y),u_{X}^{z(a_{Y}y ,e^{-t_{0}}r)}\overline{\psi}_{i_{p}(a_{Y}y,e^{-t_{0}}r)}(a_{Y}y))\;\nonumber\\ &=d_{\overline{X}}(u_{X}^{e^{-t_{0}}z(y,r)}a_{X}\overline{\psi}_{i_{p}(y,r)}(y),u_{X}^{z(a_{Y}y ,e^{-t_{0}}r)}\overline{\psi}_{i_{p}(a_{Y}y,e^{-t_{0}}r)}(a_{Y}y)) \; \nonumber \end{align*} $$

for any $p\in \{1,\ldots ,n\}$ (cf. equation (5.9)).

Assume that $0\in A_{a_{Y},y}$ . Let $I=((p_{1},p_{2}),\ldots , (p_{2n-1},p_{2n}))\in \{1,\ldots ,n\}^{2n}$ be a sequence of indexes and

Then, $A= A_{a_{Y},y}^{I}$ , $R_{0}=t_{K_{1}}$ , $s(r)=e^{-t_{0}}z(y,r)$ , $t(r)=z(a_{Y}y ,e^{-t_{0}}r)$ satisfy equations (4.32) and (4.33) for points

$$ \begin{align*} a_{X}\overline{\psi}_{p_{2k-1}}(y)\in \overline{X},\quad \overline{\psi}_{p_{2k}}(a_{Y}y)\in K \end{align*} $$

for all $k\in \{1,\ldots ,n\}$ . We can then apply Proposition 4.16 to $A_{a_{Y},y}=\coprod _{I\in \{1,\ldots ,n\}^{2n}}A^{I}_{a_{Y},y}$ for any $\unicode{x3bb} \geq \unicode{x3bb} _{0}$ . Then we follow the same argument as in Proposition 5.1 (see also Corollary 5.2), and obtain the following proposition.

Proposition 5.9. There is a measurable map $\varpi :\exp (\mathbb {R}A_{Y})\times X\times Y\rightarrow C_{G_{X}}(U_{X})$ that induces a map $\widetilde {S}_{a^{r}_{Y}}:\operatorname {\mathrm {supp}} (\rho )\rightarrow \operatorname {\mathrm {supp}} (\rho )$ by

(5.32) $$ \begin{align} \widetilde{S}_{a^{r}_{Y}}: (x,y) \mapsto (\varpi(a^{r}_{Y},x,y)a^{r}_{X}x,a^{r}_{Y}y) \end{align} $$

for all $r\in \mathbb {R}$ , $\rho $ -a.e. $(x,y)\in X\times Y$ . Moreover, we have

(5.33) $$ \begin{align} \qquad\varpi(a_{Y}^{r},x,y)= \ & u_{X}^{-z(a_{Y}y,t)}\varpi(a_{Y}^{r},(u_{X}^{z(y,e^{r}t)}\times \widetilde{u}_{Y}^{\,z(y,e^{r}t)}).(x,y))u_{X}^{e^{-r}z(y,e^{r}t)}, \end{align} $$

(5.34) $$ \begin{align} \hphantom{\hspace{-9pt}}\varpi(a_{Y}^{r_{1}+r_{2}},x,y) =\ & \varpi(a_{Y}^{r_{1}},\varpi(a_{Y}^{r_{2}},x,y)a_{X}^{r_{2}}x,a_{Y}^{r_{2}}y)a_{X}^{r_{1}}\varpi(a_{Y}^{r_{2}},x,y)a_{X}^{-r_{1}}\; \end{align} $$

for $r,r_{1},r_{2}\in \mathbb {R}$ , $\rho $ -a.e. $(x,y)\in X\times Y$ , $t\in \mathbb {R}$ .

Similar to the discussion after Corollary 5.2, we consider the decomposition in equation (2.7) and write

(5.35) $$ \begin{align} \varpi(a_{Y}^{r},x,y)=u_{X}^{\alpha(a_{Y}^{r},x,y)} \beta(a_{Y}^{r},x,y), \end{align} $$

where $\alpha (a_{Y}^{r},x,y)\in \mathbb {R}$ and $\beta (a_{Y}^{r},x,y)\in \exp V^{\perp }_{C_{X}}$ . Then by equation (5.33), we have

(5.36) $$ \begin{align} z(a^{r}_{Y}y,t)+\alpha(a^{r}_{Y},x,y)=\ & \alpha(a^{r}_{Y},(u_{X}^{z(y,e^{r}t)}\times \widetilde{u}_{Y}^{\,z(y,e^{r}t)}).(x,y))+e^{-r}z(y,e^{r}t),\; \end{align} $$

(5.37) $$ \begin{align} \hphantom{\hspace{-39pt}}\beta(a^{r}_{Y},x,y)\equiv\ & \beta(a^{r}_{Y},(u_{X}^{z(y,e^{r}t)}\times \widetilde{u}_{Y}^{\,z(y,e^{r}t)}).(x,y))\; \end{align} $$

for all $r,t\in \mathbb {R}$ . The same argument then shows that

$$ \begin{align*} \alpha(a^{r}_{Y},x,y)\equiv\alpha(a^{r}_{Y},y),\quad \beta(a^{r}_{Y},x,y)\equiv\beta(a_{Y}^{r}) \end{align*} $$

for all $r\in \mathbb {R}$ , $\rho $ -a.e. $(x,y)\in X\times Y$ . In addition, following the same lines as in Theorem 5.4, we obtain Theorem 1.2.

Theorem 5.10. (Extra normal invariance of $\rho $ )

For any $a_{Y}\in \exp (\mathbb {R}A_{Y})$ , the map $S_{a_{Y}}:X\times Y\rightarrow X\times Y$ defined by

$$ \begin{align*} S_{a_{Y}}:(x,y)\mapsto (\beta(a_{Y})a_{X}x,\tilde{u}_{Y}^{-\alpha(a_{Y},y)}(a_{Y}y)) \end{align*} $$

satisfies

$$ \begin{align*} S_{a^{r}_{Y}}\circ(u_{X}^{t}\times \widetilde{u}_{Y}^{\,t})=(u_{X}^{e^{-r}t}\times \widetilde{u}_{Y}^{\,e^{-r}t})\circ S_{a^{r}_{Y}} \end{align*} $$

and is $\rho $ -invariant. In addition, $S_{a^{r_{1}+r_{2}}_{Y}}=S_{a^{r_{1}}_{Y}}S_{a^{r_{2}}_{Y}}$ for any $r_{1},r_{2}\in \mathbb {R}$ . Also, we have

$$ \begin{align*} S_{a_{Y}}\circ S_{c}\circ S_{a_{Y}^{-1}}=S_{a_{Y}ca_{Y}^{-1}} \end{align*} $$

for any $a_{Y}\in \exp (\mathbb {R}A_{Y})$ , $c\in C_{G_{Y}}(U_{Y})$ .

Corollary 5.11. (Extra normal invariance of $\nu $ )

For any $a_{Y}\in \exp (\mathbb {R}A_{Y})$ , the map $S^{Y}_{a_{Y}}:Y\rightarrow Y$ defined by

$$ \begin{align*} S_{a_{Y}}^{Y}:y\mapsto \tilde{u}_{Y}^{-\alpha(a_{Y},y)}(a_{Y}y) \end{align*} $$

satisfies

$$ \begin{align*} S^{Y}_{a^{r}_{Y}}\circ \widetilde{u}_{Y}^{\,t} = \widetilde{u}_{Y}^{\,e^{-r}t} \circ S^{Y}_{a^{r}_{Y}} \end{align*} $$

and is $\nu $ -invariant. In addition, $S^{Y}_{a^{r_{1}+r_{2}}_{Y}}=S^{Y}_{a^{r_{1}}_{Y}}S^{Y}_{a^{r_{2}}_{Y}}$ for any $r_{1},r_{2}\in \mathbb {R}$ . Also, we have

$$ \begin{align*}S^{Y}_{a_{Y}}\circ S^{Y}_{c}\circ S^{Y}_{a_{Y}^{-1}}=S^{Y}_{a_{Y}ca_{Y}^{-1}} \end{align*} $$

for any $a_{Y}\in \exp (\mathbb {R}A_{Y})$ , $c\in C_{G_{Y}}(U_{Y})$ .

Theorem 5.12. Let $\tau _{Y}\in \mathbf {K}_{\kappa }(Y)$ . Suppose that there is an ergodic joining $\rho \in J(u_{X}^{t},\phi _{t}^{U_{Y},\tau _{Y}})$ . Then $\tau _{Y}(y)$ and $\tau _{Y}(a_{Y}y)$ are (measurably) cohomologous along $u_{Y}^{t}$ for all $a^{r}_{Y}\in \exp (\mathbb {R}A_{Y})$ . More precisely, the transfer function can be taken to be

$$ \begin{align*} F_{a^{r}_{Y}}(y)= e^{r} \alpha(a_{Y}^{r},y). \end{align*} $$

Proof. By equation (5.20), for $m_{Y}$ -a.e. $y\in Y$ , $x\in \operatorname {\mathrm {supp}}(\rho _{y})$ , we have

$$ \begin{align*} &e^{-r}\int_{0}^{e^{r}t}\tau(u_{Y}^{s}y)-\tau(a^{r}_{Y}u_{Y}^{s}y)\,ds\;\nonumber\\ &\quad=e^{-r}\int_{0}^{e^{r}t}\tau(u_{Y}^{s}y)\,ds-\int_{0}^{t}\tau(u_{Y}^{s}a_{Y}y)\,ds\;\nonumber\\ &\quad= e^{-r}z(y,e^{r}t)-z(a^{r}_{Y}y,t)\;\nonumber\\ &\quad= \alpha(a^{r}_{Y},y) - \alpha(a^{r}_{Y},\widetilde{u}^{z(y,e^{r}t)}(y))\;\nonumber\\ &\quad=\alpha(a_{Y}^{r},y)- \alpha(a_{Y}^{r},u_{Y}^{e^{r}t}y). \; \nonumber \end{align*} $$

Thus, we can take the transfer function as

Then $\tau (y)$ and $\tau (a_{Y}y)$ are (measurably) cohomologous for all $a_{Y}\in \exp (\mathbb {R}A_{Y})$ .

5.3 Opposite unipotent direction

Now we shall study the opposite unipotent direction $\overline {u}_{Y}^{r}=\exp (r\overline {U}_{Y})$ , $\overline {u}_{X}^{r}=\exp (r\overline {U}_{X})$ . Unlike previous sections, we cannot directly obtain $\rho $ is invariant under the opposite unipotent direction. However, we compensate for it by making the ‘a-adjustment.’ More precisely, by choosing appropriate coefficients $\unicode{x3bb} _{k}>0$ , set

for a.e. $y\in Y$ . Then we shall show that (see Theorem 5.15)

$$ \begin{align*}\lim_{n\rightarrow\infty}d_{\overline{X}}(\Psi_{k,p}(\overline{u}_{Y}^{r}y), \overline{u}_{X}^{r}\Psi_{k,p}(y))=0.\end{align*} $$

Here we adopt the argument given by Ratner [Rat87] and make a slight generalization. It is again convenient to consider $u,a,\overline {u}\in SL(2,\mathbb {R})$ as $(2\times 2)$ -matrices. We first introduce a basic lemma by Ratner that estimates the time difference of the $\phi ^{U_{Y},\tau }_{t}$ -flow under the $\overline {u}_{Y}^{r}$ -direction.

First of all, one directly calculates

(5.38) $$ \begin{align} &u^{t}_{Y}\overline{u}_{Y}^{r} =\left[ \begin{array}{ccc} 1 & 0\\ t& 1\\ \end{array} \right]\left[ \begin{array}{ccc} 1 & r\\ 0& 1\\ \end{array} \right]=\left[ \begin{array}{ccc} 1 & r\\ t& 1+rt\\ \end{array} \right] \notag \\ &=\left[\! \begin{array}{ccc} 1 & \dfrac{r}{1+rt}\\ 0& 1\\ \end{array} \!\right]\!\left[\! \begin{array}{ccc} \dfrac{1}{1+rt} & \\ & 1+rt \\ \end{array} \!\right]\!\left[\! \begin{array}{ccc} 1 & 0\\ \dfrac{t}{1+rt}& 1\\ \end{array} \!\right]=\overline{u}_{Y}^{{r}/({1+rt})}a_{Y}^{-2\log(1+rt)}u_{Y}^{{t}/({1+rt})}. \end{align} $$

We are interested in the fastest relative motion of $u_{Y}^{t}$ -shearing

(5.39)

Lemma 5.13. [Rat87, Lemma 1.2]

Assume $\tau _{Y}\in C^{1}(Y)$ . Then given sufficiently small $\epsilon>0$ , there are:

• • $\delta =\delta (\epsilon )\approx 0$ ;

• • $l=l(\epsilon )>0$ ;

• • $E=E(\epsilon )\subset Y$ with $\mu (E)>1-\epsilon $

such that if $y,\overline {u}^{r}_{Y}y\in E$ for some $|r|\leq \delta /l$ , then

(5.40) $$ \begin{align} |\Delta^{\tau_{Y}}_{r}(y,t)-\Delta_{r}(t)|\leq O(\epsilon)|\Delta_{r}(t)| \end{align} $$

for all $t\in [l,\delta |r|^{-1}]$ .

Proof. Denote

$$ \begin{align*}\tau_{a}(y)=\lim_{t\rightarrow0}\frac{\tau_{Y}(a_{Y}^{t}y)-\tau_{Y}(y)}{t},\quad \tau_{\overline{u}}(y)=\lim_{t\rightarrow0}\frac{\tau_{Y}(\overline{u}^{t}_{Y}y)-\tau_{Y}(y)}{t}.\end{align*} $$

The functions $\tau _{g},\tau _{k}$ are continuous on Y and

(5.41) $$ \begin{align} |\tau_{Y}(y)|,|\tau_{a}(y)|,|\tau_{\overline{u}}(y)|\leq \|\tau_{Y}\|_{C^{1}(Y)} \end{align} $$

for all $y\in Y$ . In addition, we have

$$ \begin{align*} \int_{Y}\tau_{a}(y)\,dm_{Y}(y)=\int_{Y}\tau_{\overline{u}}(y)\,dm_{Y}(y)=0. \end{align*} $$

Given $\epsilon>0$ , we fix the data as follows.

• • Let $K\subset Y$ be an open subset of Y such that $\overline {K}$ is compact and

  $$ \begin{align*} m_{Y}(K)>1-\epsilon,\quad m_{Y}(\partial K)=0, \end{align*} $$
  where $\partial K$ denotes the boundary of K.

• • Fix a sufficiently small $\delta ^{\prime }=\delta ^{\prime }(\epsilon )\approx 0$ such that:

  1. (1) $\mu (B(\partial K,\delta ^{\prime }))\leq \epsilon $ , where $B(\partial K,\delta ^{\prime })$ denotes the $\delta ^{\prime }$ -neighborhood of $\partial K$ (it follows that $\mu (K\setminus B(\partial K,\delta ^{\prime }))\geq 1-2\epsilon $ );

  2. (2) if $y_{1},y_{2}\in \overline {K}$ , $d_{Y}(y_{1},y_{2})\leq \delta ^{\prime }$ , then

     (5.42) $$ \begin{align} |\tau_{a}(y_{1})-\tau_{a}(y_{2})|\leq\epsilon. \end{align} $$

• • Fix $\delta \in (0,({1}/{100}) \delta ^{\prime })$ such that if $|rt|\leq \delta $ , then for all $s\in [0,t]$ ,

  (5.43)

  

• • Fix $t_{1}=t_{1}(\epsilon )>0$ and a subset $E=E(\epsilon )\subset Y$ with $m_{Y}(E)>1-\epsilon $ such that if ${y\in E}$ , $t\in [ t_{1},\infty )$ , then the relative length measure of $K\setminus B(\partial K,\delta ^{\prime })$ on the orbit interval $[y,u_{Y}^{t}y]$ is at least $1-3\epsilon $ and $|\epsilon _{2}(t)|\leq \epsilon $ , $|\epsilon _{3}(t)|\leq \epsilon $ , where

  (5.44)

  

• • Fix $l=l(\epsilon )>t_{1}$ such that

  (5.45) $$ \begin{align} t_{1}/l\leq\epsilon. \end{align} $$

We shall show that if $y,\overline {u}_{Y}^{r}y\in E$ for some $|r|\leq \delta /l$ , and $ t\in [l,\delta |r|^{-1}]$ , then equation (5.40) holds if $\epsilon $ is sufficiently small.

Now let us estimate $\Delta ^{\tau _{Y}}_{r}(y,t)$ . Recall that

$$ \begin{align*} \Delta^{\tau_{Y}}_{r}(y,t) = \int_{0}^{t}\tau_{Y}(u_{Y}^{s}\overline{u}^{r}_{Y}y)\,ds-\int_{0}^{{t}/({1+rt})}\tau_{Y}(u_{Y}^{s}y)\,ds. \end{align*} $$

Then by equation (5.38) and the mean value theorem, we have

$$ \begin{align*} \int_{0}^{{t}/({1+rt})}\tau_{Y}(u_{Y}^{s}y)\,ds&= \int_{0}^{t}\tau_{Y}(u_{Y}^{{s}/({1+rs})}y)\cdot\frac{ds}{(1+rs)^{2}} \;\nonumber\\ &= \int_{0}^{t}\tau_{Y}(a_{Y}^{2\log(1+rs)}\overline{u}_{Y}^{-{r}/({1+rs})}u^{s}_{Y}\overline{u}^{r}_{Y}y)\cdot\frac{ds}{(1+rs)^{2}} \;\nonumber\\ &= \int_{0}^{t}\tau_{Y}(u^{s}_{Y}\overline{u}^{r}_{Y}y)\cdot\frac{ds}{(1+rs)^{2}}\;\nonumber\\ &\quad -\int_{0}^{t}\frac{r}{1+rs}\tau_{\overline{u}}(\overline{u}_{Y}^{k_{s}}u^{s}_{Y}\overline{u}^{r}_{Y}y) \cdot\frac{ds}{(1+rs)^{2}}\;\nonumber\\ &\quad +\int_{0}^{t}2\log(1+rs) \tau_{a}(a_{Y}^{g_{s}}\overline{u}_{Y}^{-{r}/({1+rs})}u^{s}_{Y}\overline{u}^{r}_{Y}y) \cdot\frac{ds}{(1+rs)^{2}}, \; \nonumber \end{align*} $$

where $k_{s}\in [-{r}/({1+rs}),0]$ and $g_{s}\in [0,2\log (1+rs)]$ . This implies

$$ \begin{align*} \Delta^{\tau_{Y}}_{r}(y,t)&= \int_{0}^{t}\tau_{Y}(u_{Y}^{s}\overline{u}^{r}_{Y}y) \bigg(1- \frac{1}{(1+rs)^{2}}\bigg)\,ds\;\nonumber\\ &\quad +\int_{0}^{t}\frac{r}{1+rs}\tau_{\overline{u}}(\overline{u}_{Y}^{k_{s}}u^{s}_{Y}\overline{u}^{r}_{Y}y) \cdot\frac{ds}{(1+rs)^{2}}\;\nonumber\\ & \quad-\int_{0}^{t}2\log(1+rs) \tau_{a}(a_{Y}^{g_{s}}\overline{u}_{Y}^{-{r}/({1+rs})}u^{s}_{Y}\overline{u}^{r}_{Y}y) \cdot\frac{ds}{(1+rs)^{2}} \;\nonumber\\ &= J_{1}+ J_{2}+J_{3}. \; \nonumber \end{align*} $$

We estimate the integrals $J_{1},J_{2},J_{3}$ separately.

(1) Using equations (5.43) and (5.44), we have

$$ \begin{align*} J_{1}&= 2\Delta_{r}(t)\frac{1}{t^{2}}\int_{0}^{t}s\tau_{Y}(u_{Y}^{s}\overline{u}^{r}_{Y}y)\,ds+ \Delta_{r}(t)\frac{1}{t}\int_{0}^{t}\epsilon_{1,t}(s)\tau_{Y}(u_{Y}^{s}\overline{u}^{r}_{Y}y)\,ds\;\nonumber\\ &= 2\Delta_{r}(t)\frac{1}{t^{2}}\int_{0}^{t}s\tau_{Y}(u_{Y}^{s}\overline{u}^{r}_{Y}y)\,ds +\Delta_{r}(t) O(\epsilon) , \; \nonumber \end{align*} $$

since $\overline {u}^{r}_{Y}y\in E$ . Now by the integration by parts and equations (5.44), (5.41), and (5.45), we have

$$ \begin{align*} & \frac{1}{t^{2}}\int_{0}^{t}s\tau_{Y}(u_{Y}^{s}\overline{u}^{r}_{Y}y)\,ds \;\nonumber\\ &\quad= \frac{1}{t} \int_{0}^{t}\tau_{Y}(u_{Y}^{s}\overline{u}^{r}_{Y}y) \,ds-\frac{1}{t^{2}} \int_{0}^{t}\bigg(\int_{0}^{s}\tau_{Y}(u_{Y}^{p}\overline{u}^{r}_{Y}y) \,dp\bigg)\, ds \;\nonumber\\ &\quad= 1+\epsilon_{2}(t)-\frac{1}{t^{2}}\bigg[\int_{t_{1}}^{t} +\int_{0}^{t_{1}}\bigg]\bigg(\int_{0}^{s}\tau_{Y}(u_{Y}^{p}\overline{u}^{r}_{Y}y) \,dp\bigg)\,ds \;\nonumber\\ &\quad= 1+\epsilon_{2}(t)-\frac{1}{t^{2}}\int_{t_{1}}^{t}s( 1+\epsilon_{2}(s))\,ds +O(\epsilon)= \frac{1}{2} +O(\epsilon).\; \nonumber \end{align*} $$

It follows that

$$ \begin{align*} \bigg|\frac{J_{1}}{\Delta_{r}(t)}-1\bigg|\leq O(\epsilon). \end{align*} $$

(2) For $J_{2}$ , by equation (5.45), we have

$$ \begin{align*}|J_{2}|= \bigg|\int_{0}^{t}\frac{r}{1+rs}\tau_{\overline{u}}(\overline{u}_{Y}^{k_{s}}u^{s}_{Y}\overline{u}^{r}_{Y}y) \cdot\frac{ds}{(1+rs)^{2}}\bigg|\leq O\bigg(\frac{|\Delta_{r}(t)|}{t}\bigg)\leq O(\epsilon)|\Delta_{r}(t)|. \end{align*} $$

(3) Note that since $d_{Y}(a_{Y}^{g_{s}}\overline {u}_{Y}^{-{r}/({1+rs})}u^{s}_{Y}\overline {u}^{r}_{Y}y ,u^{s}_{Y}\overline {u}^{r}_{Y}y)<\delta ^{\prime }$ , we know $a_{Y}^{g_{s}}\overline {u}_{Y}^{-{r}/({1+rs})}u^{s}_{Y}\overline {u}^{r}_{Y} y \in \overline {K}$ if $u^{s}_{Y}\overline {u}^{r}_{Y}y\in K\setminus B(\partial K,\delta ^{\prime })$ . Now set

Then by equation (5.44), one has $\operatorname {\mathrm {Leb}}(I_{y}^{c})<3\epsilon t$ . Then for $J_{3}$ , using equations (5.41) and (5.42), we have

$$ \begin{align*} & \bigg|J_{3}- \bigg(-\int_{0}^{t}2\log(1+rs) \tau_{a}(u^{s}_{Y}\overline{u}^{r}_{Y}y) \cdot\frac{ds}{(1+rs)^{2}}\bigg)\bigg|\;\nonumber\\ &\quad\ll | \log(1+rt)|\bigg[\int_{I_{y}}\bigg|\tau_{a}(a_{Y}^{g_{s}}\overline{u}_{Y}^{-{r}/({1+rs})}u^{s}_{Y}\overline{u}^{r}_{Y}y) -\tau_{a}(u^{s}_{Y}\overline{u}^{r}_{Y}y) \bigg|\,ds+ \epsilon t\|\tau_{Y}\|_{C^{1}(Y)}\bigg]\;\nonumber\\ &\quad\leq t| \log(1+rt)|(\epsilon+\epsilon \|\tau_{Y}\|_{C^{1}(Y)})\ll O(\epsilon)| \Delta_{r}(t)|.\; \nonumber \end{align*} $$

We also have

$$ \begin{align*} & \bigg| \int_{0}^{t}2\log(1+rs) \tau_{a}(u^{s}_{Y}\overline{u}^{r}_{Y}y) \cdot\frac{ds}{(1+rs)^{2}} - \int_{0}^{t}2\log(1+rs) \tau_{a}(u^{s}_{Y}\overline{u}^{r}_{Y}y) \,ds \bigg|\;\nonumber\\ &\quad = \bigg| \int_{0}^{t}2\log(1+rs) \tau_{a}(u^{s}_{Y}\overline{u}^{r}_{Y}y) \cdot\bigg(\frac{1}{(1+rs)^{2}} -1\bigg) \,ds\bigg|\;\nonumber\\ &\quad\ll |\Delta_{r}(t)|\|\tau_{Y}\|_{C^{1}(Y)} \delta\ll O(\epsilon)|\Delta_{r}(t)|. \; \nonumber \end{align*} $$

Finally, by using the integration by parts, we get

$$ \begin{align*} & \bigg|\int_{0}^{t} \log(1+rs) \tau_{a}(u^{s}_{Y}\overline{u}^{r}_{Y}y) \,ds\bigg|\;\nonumber\\ &\quad= \bigg|\log(1+rt) \int_{0}^{t} \tau_{a}(u^{s}_{Y}\overline{u}^{r}_{Y}y)\,ds -\int_{0}^{t} \bigg(\int_{0}^{s}\tau_{a}(u^{p}_{Y}\overline{u}^{r}_{Y}y)\, dp\bigg)\frac{r}{1+rs} \,ds\bigg|\;\nonumber\\ &\quad\ll \frac{|\Delta_{r}(t)|}{t}\bigg| \int_{0}^{t} \tau_{a}(u^{s}_{Y}\overline{u}^{r}_{Y}y)\,ds \bigg|+ \frac{|\Delta_{r}(t)|}{t^{2}}\bigg|\int_{0}^{t} \bigg(\int_{0}^{s}\tau_{a}(u^{p}_{Y}\overline{u}^{r}_{Y}y)\,dp\bigg)\,ds\bigg|\;\nonumber\\ &\quad= \epsilon_{3}(t) |\Delta_{r}(t)| +\frac{|\Delta_{r}(t)|}{t^{2}} \bigg|\bigg[\int_{0}^{t_{1}} +\int_{t_{1}}^{t} \bigg] \bigg(\int_{0}^{s}\tau_{a}(u^{p}_{Y}\overline{u}^{r}_{Y}y)\,dp\bigg)\,ds\bigg|\;\nonumber\\ &\quad\ll \epsilon_{3}(t) |\Delta_{r}(t)| +\frac{|\Delta_{r}(t)|}{t^{2}}\bigg| t_{1}^{2}\|\tau_{Y}\|_{C^{1}(Y)} +\int_{t_{1}}^{t} s\epsilon_{3}(s) \,ds \bigg|\ll O(\epsilon)|\Delta_{r}(t)| .\; \nonumber \end{align*} $$

Thus, we conclude that $|J_{3}|\leq O(\epsilon )|\Delta _{r}(t)|$ .

Therefore, combining the above estimates, we have

$$ \begin{align*}|\Delta^{\tau_{Y}}_{r}(y,t)-\Delta_{r}(t)|\leq O(\epsilon)\Delta_{r}(t).\end{align*} $$

This completes the proof of the lemma.

The following lemma tells us that we only need to know the fastest relative motion at finitely many different time points to determine the difference of two nearby points.

Lemma 5.14. (Shearing comparison)

Given $\epsilon>0$ , let $x,y,z\in \overline {X}$ be three $\epsilon $ -nearby points such that the fastest relative motions between the pairs $(x,z)$ and $(y,z)$ at time $t>0$ are $q_{1}(t)$ and $q_{2}(t)$ , respectively. Assume that there are $s_{1},s_{2}>0$ with $s_{1}\in [\tfrac 13s_{2},\tfrac 23s_{2}]$ such that

$$ \begin{align*} d_{\overline{X}}(u_{X}^{s_{i}}x,u_{X}^{s_{i}}q_{1}(s_{i})z)<\epsilon,\quad d_{\overline{X}}(u_{X}^{s_{i}}y,u_{X}^{s_{i}}q_{2}(s_{i})z)<\epsilon,\quad d_{G_{X}}(q_{1}(s_{i}),q_{2}(s_{i}))<\epsilon \end{align*} $$

for $i\in \{1,2\}$ . Then we have

(5.46) $$ \begin{align} d_{\overline{X}}(u_{X}^{t}x,u_{X}^{t}y)<O(\epsilon) \end{align} $$

for $t\in [0,s_{2}]$ .

Proof. This is a direct consequence of Lemma 4.3. Assume that $x=gy$ , $x=h_{1}z$ , $y=h_{2}z$ for some $g,h_{1},h_{2}\in G_{X}$ . Then by the definition in equation (3.4), there are $\delta _{1}(t)$ , $\delta _{2}(t)\in G_{X}$ with $d_{G_{X}}(\delta _{1}(t),e)<\epsilon $ , $d_{G_{X}}(\delta _{2}(t),e)<\epsilon $ such that

$$ \begin{align*}u_{X}^{t}h_{1}u_{X}^{-t}=\delta_{1}(t)q_{1}(t),\quad u_{X}^{t}h_{2}u_{X}^{-t}=\delta_{2}(t)q_{2}(t) \end{align*} $$

for $t\in [0,s]$ . By the assumption, we have

(5.47) $$ \begin{align} u_{X}^{t}gu_{X}^{-t}=u_{X}^{t}h_{1}h_{2}^{-1}u_{X}^{-t}=\delta_{1}(t)q_{1}(t)q_{2}(t)^{-1}\delta_{2}(t)^{-1} \end{align} $$

and

(5.48) $$ \begin{align} q_{1}(s_{1})q_{2}(s_{1})^{-1}<\epsilon,\quad q_{1}(s_{2})q_{2}(s_{2})^{-1}<\epsilon. \end{align} $$

Note that $q_{1}(t)q_{2}(t)^{-1}\in C_{G_{X}}(U_{X})$ and so their corresponding vectors in the Lie algebra are polynomials of t with the degree at most $2$ (see equations (2.5) and (3.4)). Thus, we can write

$$ \begin{align*} h_{1}h_{2}^{-1}=\exp\bigg(\sum_{j} \sum_{i=0}^{\varsigma(j)}b_{j}^{i}v_{j}^{i}\bigg),\quad q_{1}(t)q_{2}(t)^{-1}=\exp\bigg(\sum_{j} p_{j}(t)v_{j}^{\varsigma(j)}\bigg), \end{align*} $$

where $p_{j}(t)=\sum ^{\varsigma (j)}_{i=0}b_{j}^{\varsigma (j)-i}\binom {\varsigma (j)}{i}t^{i}$ is a polynomial having the degree at most $2$ , $|b_{i}|<\epsilon $ , and $v_{j}^{i}\in V_{j}$ is the ith weight vector of the $\mathfrak {sl}_{2}$ -irreducible representation $V_{j}$ . Then equation (5.48) and the proof of Lemma 4.3(1) with $\kappa =1$ imply that

(5.49) $$ \begin{align} |b_{j}^{\varsigma(j)-i}|<O(\epsilon)s_{2}^{-i}. \end{align} $$

It follows that for $t\in [0,s_{2}]$ ,

$$ \begin{align*} |p_{j}(t)|<O(\epsilon)\quad \text{and so}\quad q_{1}(t)q_{2}(t)^{-1}<O(\epsilon). \end{align*} $$

Then by equation (5.47), we obtain equation (5.46).

Next, we shall prove Theorem 5.15. The idea is to consider the fastest relative motion of the pairs $(\Psi _{k,p}(\overline {u}_{Y}^{r}y), \Psi _{k,p}(y))$ and $(\overline {u}_{X}^{r}\Psi _{k,p}(y),\Psi _{k,p}(y))$ at finitely many time points, and then apply Lemma 5.14. First, we orderly fix the following data.

• • (Injectivity radius) Since $\Gamma _{X}$ is discrete, there is a compact $K_{1}\subset \overline {X}$ with $\nu (\overline {\psi }_{p}^{-1}(K_{1}))>{999}/{1000}$ and $D_{1}=D_{1}(K_{1})>0$ such that if $\overline {g}\in \overline {P}^{-1}(K_{1})$ , then $D_{1}$ is an isometry on the ball $B_{C^{\rho }\backslash G_{X}}(\overline {g},D_{1})$ of radius $D_{1}$ centered at $\overline {g}$ . Here, $\overline {P}:C^{\rho }\backslash G_{X}\rightarrow C^{\rho }\backslash G_{X}/\Gamma _{X}=\overline {X}$ is the projection

  $$ \begin{align*}\overline{P}:C^{\rho} g\mapsto C^{\rho} g\Gamma_{X}.\end{align*} $$

• • (Distinguishing $\overline {\psi }_{p},\overline {\psi }_{q}$ ) There is $K_{2}\subset Y$ with $\nu (K_{2})>{999}/{1000}$ such that

  (5.50) $$ \begin{align} d_{\overline{X}}(\overline{\psi}_{p}(y),\overline{\psi}_{q}(y))>D_{2} \end{align} $$
  for $y\in K_{2}$ , $1\leq p< q\leq n$ .

• • Define $D=\min \{D_{1},D_{2},1\}$ .

• • (Lemma 5.13) Let $\delta _{k}=\min \{\delta (({1}/{10})2^{-k}D), ({1}/{10})2^{-k}D\}$ , $l_{k}=l(({1}/{10})2^{-k}D)$ and $E_{k}=E(({1}/{10})2^{-k}D)\subset Y$ be as in Lemma 5.13 for $\tau _{Y}$ .

• • (Lusin’s theorem) There is $K^{\prime }_{k}\subset Y$ such that $\nu (K^{\prime }_{k})>1-({1}/{10})2^{-k}$ and $\overline {\psi }_{p}|_{K^{\prime }_{k}}$ is uniformly continuous for all $p\in \{1,\ldots ,n\}$ . Thus, for any $\epsilon>0$ , there is $\delta ^{\prime }(\epsilon )>0$ such that, for $p\in \{1,\ldots ,n\}$ , $d_{Y}(y_{1},y_{2})<\delta ^{\prime }(\epsilon )$ and $y_{1},y_{2}\in K^{\prime }_{k}$ , we have

  (5.51) $$ \begin{align} d_{\overline{X}}(\overline{\psi}_{p}(y_{1}),\overline{\psi}_{p}(y_{2}))<\epsilon. \end{align} $$
  Let $\delta ^{\prime }_{k}=\min \{\delta ^{\prime }(({1}/{10})2^{-k} D), ({1}/{10})2^{-k}D\}$ .

• • (Ergodicity) Fix $\tau _{Y}\in C^{1}(Y)$ . By the ergodicity of unipotent flows, there are $T_{k}\geq \max \{l_{k},20\delta _{k}^{-1},20\delta _{k}^{\prime -1}\}$ and subsets $K^{\prime \prime }_{k}\subset Y$ with $\nu (K^{\prime \prime }_{k})>1-({1}/{10})2^{-k}$ such that if $y\in K^{\prime \prime }_{k}$ , $t\geq T_{k}$ , then:

  1. (1) the relative length measure of $K^{\prime }_{k}\cap E_{k}\cap K_{2} \cap \bigcap _{p}\overline {\psi }_{p}^{-1}(K_{1})$ on the orbit interval $[y,u^{t}_{Y}y]$ is at least ${998}/{1000}$ ;

  2. (2) we have, by the ergodic theorem,

     (5.52) $$ \begin{align} \bigg|\frac{1}{t}z(y,t)-1\bigg|=\bigg|\frac{1}{t}\int_{0}^{t}\tau_{Y}(u_{Y}^{s}y)\,ds-1\bigg|\leq\frac{1}{10}2^{-k}D. \end{align} $$

• • (Fastest relative motion)

  1. (1) For $r\in \mathbb {R}$ , let $L_{1}^{i}(r)$ denote the first $t>0$ with $\Delta _{r}(t)=i^{2}D/10$ for $i\in \{1,2\}$ , where $\Delta _{r}(t)$ is defined in equation (5.39). Note that for sufficiently small r, one may calculate that

     (5.53) $$ \begin{align} L_{1}^{1}(r)\in\bigg[\frac{9}{20}L_{1}^{2}(r),\frac{11}{20}L_{1}^{2}(r)\bigg]. \end{align} $$

  2. (2) As in equation (4.4), for $\overline {x_{1}},\overline {x_{2}}\in \overline {X}$ close enough, we can write $\overline {x_{1}}=\overline {gx_{2}}$ , where $g=\exp (v)$ for $v\in \mathfrak {sl}_{2}+V^{\rho \perp }$ . Then the H-property (Remark 3.4) tells us that at time $t\in \mathbb {R}$ , the fastest relative motion is given by

     $$ \begin{align*} q(\overline{x_{1}},\overline{x_{2}},t)=\pi_{C_{\mathfrak{g}_{\overline{X}}}(U_{X})} \operatorname{\mathrm{Ad}}(u_{X}^{t}).v.\end{align*} $$
     Then let $L^{i}_{2}(\overline {x_{1}},\overline {x_{2}})$ denote the first $t>0$ with $\|q(\overline {x_{1}},\overline {x_{2}},t)\|=i^{2}D/10$ .

  For $y\in Y$ , $i\in \{1,2\}$ , let

  (5.54)

  
  By applying Theorem 3.3 to $Q=B_{C_{G_{Y}}(U_{Y})}(e,i^{2}D/10)$ and $\epsilon =({1}/{10})2^{-k}$ , we can choose small $0<\omega _{k}\leq \min \{\delta _{k},\delta ^{\prime }_{k}\}$ such that if $|r|\leq \omega _{k}$ , $y,\overline {u}^{r}y\in K^{\prime }_{k}$ , $i\in \{1,2\}$ , then we have
  (5.55) $$ \begin{align} L^{i}=L^{i}(y,r)\geq\max\bigg\{10T_{k},\frac{10i^{2}D}{\delta^{\prime}_{k}}\bigg\} \end{align} $$
  and for all $p\in \{1,\ldots , p\}$ ,
  (5.56) $$ \begin{align} \| q^{i}_{p}\|\leq \frac{i^{2}D}{10},\quad d_{\overline{X}}(u_{X}^{L}\overline{\psi}_{p}(\overline{u}^{r}y),u_{X}^{L}\overline{q^{i}_{p}(L)\psi_{p}(y)})\leq\frac{1}{10}2^{-k}D, \end{align} $$
  where $q^{i}_{p}=q(\overline {\psi }_{p}(\overline {u}^{r}y),\overline {\psi }_{p}(y),L^{i})$ .

Now let

(5.57)

It follows that $\nu (K_{k}^{0})>1- 2^{-k}$ . Let

(5.58)

It follows that $\nu (\Omega )>1$ .

Theorem 5.15. Let the notation and assumption be as above. Then for $r\in \mathbb {R}$ , $y\in \Omega $ , we have

$$ \begin{align*}\lim_{n\rightarrow\infty}d_{\overline{X}}(\Psi_{k,p}(\overline{u}_{Y}^{r}y), \overline{u}_{X}^{r}\Psi_{k,p}(y))=0.\end{align*} $$

Proof. Suppose that $y,\overline {u}_{Y}^{r}y\in \bigcup _{l\geq 1}\bigcap _{k\geq l}a^{\unicode{x3bb} _{k}}_{Y}(K_{k}^{0})$ . Then $y,\overline {u}_{Y}^{r}y\in a^{\unicode{x3bb} _{k}}_{Y}(K_{k}^{0})$ for sufficiently large k. For $r\in \mathbb {R}$ , let $r_{k}=e^{-\unicode{x3bb} _{k}}r$ . Then for sufficiently large k,

$$ \begin{align*} a_{Y}^{-\unicode{x3bb}_{k}}\overline{u}_{Y}^{r}y=\overline{u}_{Y}^{r_{k}}a_{Y}^{-\unicode{x3bb}_{k}}y\quad\text{and} \quad |r_{k}|\leq |r|\omega_{k}^{2}\leq \omega_{k}. \end{align*} $$

Thus, equation (5.55) holds true for $L^{i}(y,r_{k})$ for any sufficiently large k, $i\in \{1,2\}$ . In the following, we fix $i=1$ (for the case $i=2$ is similar).

Next, since by equation (5.55) $L^{1}(y,r_{k})>10T_{k}$ , there exists $t_{k}\in [({98}/{100})L^{1}(y,r_{k}),({99}/{100})L^{1} (y,r_{k})]$ such that

(5.59) $$ \begin{align} u_{Y}^{t_{k}}a_{Y}^{-\unicode{x3bb}_{k}}\overline{u}_{Y}^{r}y,\quad u_{Y}^{t^{\prime}_{k}}a_{Y}^{-\unicode{x3bb}_{k}}y\in K^{\prime}_{k}\cap K_{2} \cap \bigcap_{p}\overline{\psi}_{p}^{-1}(K_{1}), \end{align} $$

where . Then by equation (5.38), we get

(5.60) $$ \begin{align} &d_{Y}(u_{Y}^{t_{k}}a_{Y}^{-\unicode{x3bb}_{k}}\overline{u}_{Y}^{r}y,u_{Y}^{t^{\prime}_{k}}a_{Y}^{-\unicode{x3bb}_{k}}y)=d_{Y}(u_{Y}^{t_{k}} \overline{u}_{Y}^{r_{k}}a_{Y}^{-\unicode{x3bb}_{k}}y,u_{Y}^{t^{\prime}_{k}}a_{Y}^{-\unicode{x3bb}_{k}}y)\nonumber\\ &\quad=d_{Y}\left( \left[ \begin{array}{@{}cc@{}} \dfrac{1}{1+r_{k}t_{k}} & r_{k} \\[4pt] 0 & 1+r_{k}t_{k}\\ \end{array} \right]u_{Y}^{t_{k}^{\prime}}a_{Y}^{-\unicode{x3bb}_{k}}y,u_{Y}^{t_{k}^{\prime}}a_{Y}^{-\unicode{x3bb}_{k}}y\right)\leq\min\{\delta_{k},\delta_{k}^{\prime}\}, \end{align} $$

where the last inequality follows from equation (5.39):

(5.61) $$ \begin{align} |r_{k}t_{k}|\leq 2\frac{\Delta_{r_{k}}(t_{k})}{t_{k}}\leq 4 \frac{\Delta_{r_{k}}(L^{1}(y,r_{k}))}{T_{k}}\leq 4\frac{D}{10}\cdot \frac{\min\{\delta_{k},\delta_{k}^{\prime}\}}{20}\leq \min\{\delta_{k},\delta_{k}^{\prime}\}. \end{align} $$

This implies via Lemma 5.13 that

(5.62) $$ \begin{align} |\Delta^{\tau_{Y}}_{r_{k}}(a_{Y}^{-\unicode{x3bb}_{k}}y,t_{k})-\Delta_{r_{k}}(t_{k})|\leq \frac{1}{10}2^{-k} D \end{align} $$

since $a_{Y}^{-\unicode{x3bb} _{k}}y,\overline {u}_{Y}^{r_{k}}a_{Y}^{-\unicode{x3bb} _{k}}y\in E_{k}$ and $t_{k}\in [T_{k},\delta _{k} |r_{k}|^{-1}]\subset [l_{k},\delta _{k} |r_{k}|^{-1}]$ .

Next, consider

$$ \begin{align*} u_{X}^{s_{k}}\overline{\psi}_{p}(a_{Y}^{-\unicode{x3bb}_{k}}\overline{u}_{Y}^{r}y)=\overline{\psi}_{i(p,k)}(u_{Y}^{t_{k}}a_{Y}^{-\unicode{x3bb}_{k}}\overline{u}_{Y}^{r}y),\quad u_{X}^{h^{\prime}_{k}}\overline{\psi}_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y)=\overline{\psi}_{j(p,k)}(u_{Y}^{t^{\prime}_{k}}a_{Y}^{-\unicode{x3bb}_{k}}y),\end{align*} $$

where $s_{k}$ and $h^{\prime }_{k}$ are defined by

(5.63) $$ \begin{align} z(a_{Y,k}^{-1}\overline{u}^{r}y,t_{k})= s_{k},\quad z(a_{Y,k}^{-1}y,t_{k}^{\prime}) = h^{\prime}_{k}. \end{align} $$

Then $\Delta ^{\tau _{Y}}_{r_{k}}(a_{Y,k}^{-1}y,t_{k})=s_{k}-h_{k}^{\prime }$ and by equation (5.52), we have $s_{k}\in [({97}/{100})L^{1}(y,r_{k}),({995}/{1000}) L^{1}(y,r_{k})]$ .

Claim 5.16. For $p\in \{1,\ldots ,n\}$ ,

$$ \begin{align*}d_{G}(q_{p}(s_{k}),u_{X}^{h^{\prime}_{k}-s_{k}})\leq \frac{2}{10}2^{-k}D, \end{align*} $$

where $q_{p}(s_{k})=q(\overline {\psi }_{p}(\overline {u}^{r_{k}}a_{Y}^{-\unicode{x3bb} _{k}}y),\overline {\psi }_{p}(a_{Y}^{-\unicode{x3bb} _{k}}y),s_{k})$ .

Proof. Since $|r_{k}|\leq \omega _{k}$ and $a^{-\unicode{x3bb} _{k}}_{Y}y,\overline {u}_{Y}^{r_{k}}a^{-\unicode{x3bb} _{k}}_{Y}y\in K_{k}^{0}$ , by equation (5.54) and Lemma 5.13, we know that

(5.64) $$ \begin{align} |\Delta^{\tau_{Y}}_{r_{k}}(a_{Y,k}^{-1}y,t_{k})|\leq \frac{11}{10}|\Delta_{r_{k}}(t_{k})|\leq\frac{11}{100}D. \end{align} $$

It follows that

(5.65) $$ \begin{align} d_{\overline{X}}(u_{X}^{s_{k}}\overline{\psi}_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y),u_{X}^{h^{\prime}_{k}}\overline{\psi}_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y))<\tfrac{1}{3}D. \end{align} $$

However, by equation (5.56), we have

(5.66) $$ \begin{align} \| q_{p}(s_{k})\|\leq \frac{D}{10},\quad d_{\overline{X}}(u_{X}^{s_{k}}\overline{\psi}_{p}(\overline{u}^{r_{k}}a_{Y}^{-\unicode{x3bb}_{k}}y),u_{X}^{s_{k}}\overline{q_{p}(s_{k})\psi_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y)})\leq\frac{1}{10}2^{-k}D. \end{align} $$

It follows that

(5.67) $$ \begin{align} d_{\overline{X}}(u_{X}^{s_{k}}\overline{\psi}_{p}(\overline{u}^{r_{k}}a_{Y}^{-\unicode{x3bb}_{k}}y),u_{X}^{s_{k}}\overline{\psi}_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y))<\tfrac{1}{3}D \end{align} $$

for $p\in \{1,\ldots ,p\}$ . Therefore, equations (5.65) and (5.67) tell us that

$$ \begin{align*} & d_{\overline{X}}(\overline{\psi}_{i(p,k)}(u_{Y}^{t_{k}}a_{Y}^{-\unicode{x3bb}_{k}}\overline{u}_{Y}^{r}y), \overline{\psi}_{j(p,k)}(u_{Y}^{t^{\prime}_{k}}a_{Y}^{-\unicode{x3bb}_{k}}y))\;\nonumber\\ &\quad= d_{\overline{X}}(u_{X}^{s_{k}}\overline{\psi}_{p}(\overline{u}_{Y}^{r_{k}}a_{Y}^{-\unicode{x3bb}_{k}}y),u_{X}^{h^{\prime}_{k}}\overline{\psi}_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y))< D.\; \nonumber \end{align*} $$

Then by equation (5.50), we must have $i(p,k)=j(p,k)$ . Then by Lusin theorem equations (5.51) and (5.60), we further obtain

(5.68) $$ \begin{align} &d_{\overline{X}}(u_{X}^{s_{k}}\overline{\psi}_{p}(\overline{u}_{Y}^{r_{k}}a_{Y}^{-\unicode{x3bb}_{k}}y),u_{X}^{h^{\prime}_{k}}\overline{\psi}_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y))\;\\ &\quad= d_{\overline{X}}(\overline{\psi}_{i(p,k)}(u_{Y}^{t_{k}}a_{Y}^{-\unicode{x3bb}_{k}}\overline{u}_{Y}^{r}y), \overline{\psi}_{i(p,k)}(u_{Y}^{t^{\prime}_{k}}a_{Y}^{-\unicode{x3bb}_{k}}y))\leq \frac{1}{10}2^{-k}D.\; \nonumber \end{align} $$

Combining equation (5.66), we get

$$ \begin{align*} &d_{\overline{X}}(\overline{q_{p}(s_{k})\cdot u_{X}^{s_{k}}\psi_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y)},\overline{u_{X}^{h^{\prime}_{k}-s_{k}}\cdot u_{X}^{s_{k}}\psi_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y)})\;\nonumber\\ &\quad= d_{\overline{X}}(u_{X}^{s_{k}}\overline{q_{p}(s_{k})\psi_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y)},u_{X}^{h^{\prime}_{k}}\overline{\psi}_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y))\leq \frac{2}{10}2^{-k}D.\; \nonumber \end{align*} $$

Since by equation (5.59), $u_{X}^{h^{\prime }_{k}}\overline {\psi }_{p}(a_{Y}^{-\unicode{x3bb} _{k}}y)\in K_{1}$ , $\|q_{p}(s_{k})\|\leq ({1}/{10})D$ , $|s_{k}-h^{\prime }_{k}|=|\Delta ^{\tau _{Y}}_{r_{k}}(a_{Y,k}^{-1}y,t_{k})|\leq ({11}/{100})D$ , we conclude that

$$ \begin{align*}d_{G}(q_{p}(s_{k}),u_{X}^{h^{\prime}_{k}-s_{k}})\leq \frac{2}{10}2^{-k}D\end{align*} $$

for any $p\in \{1,\ldots ,n\}$ .

It then follows from the definition of $L^{1}(y,r_{k})$ in equation (5.54) that

(5.69) $$ \begin{align} \|q^{1}_{p}(s_{k})\|\geq\frac{9}{100}D ,\quad |h^{\prime}_{k}-s_{k}|\geq\frac{9}{100}D \end{align} $$

for any $p\in \{1,\ldots ,n\}$ .

However, denote $h_{k}={h^{\prime }_{k}}/({1-r_{k}h^{\prime }_{k}})$ .

Claim 5.17. We have

$$ \begin{align*} |h_{k}-s_{k}|<2^{1-k}D. \end{align*} $$

Proof. One can calculate via equation (5.62)

(5.70) $$ \begin{align} |h_{k}-s_{k}|&= |h_{k}-h^{\prime}_{k}-(s_{k}-h^{\prime}_{k})| \;\nonumber\\ &= |\Delta_{r_{k}} ( h_{k})-\Delta^{\tau_{Y}}_{r_{k}}(a_{Y}^{-\unicode{x3bb}_{k}}y,t_{k})|\;\nonumber\\ &\leq |\Delta_{r_{k}} ( h_{k})-\Delta_{r_{k}} (t_{k})|+|\Delta_{r_{k}} ( t_{k})-\Delta^{\tau_{Y}}_{r_{k}}(a_{Y}^{-\unicode{x3bb}_{k}}y,t_{k})|\;\nonumber\\ &\leq |\Delta_{r_{k}} ( h_{k})-\Delta_{r_{k}} (t_{k})|+ \frac{1}{10}2^{-k} D. \end{align} $$

However, by the ergodicity equations (5.63) and (5.52), we have

$$ \begin{align*}|h_{k}^{\prime}-t_{k}^{\prime}|\leq \frac{1}{10}2^{-k}D\cdot t_{k}^{\prime}\leq \frac{2}{10}2^{-k}D\cdot t_{k}. \end{align*} $$

Then by equation (5.61) and $|\Delta _{r_{k}}(t_{k})|\leq D/10$ , we have

$$ \begin{align*}|h_{k}-t_{k}|= \bigg|\frac{h^{\prime}_{k}}{1-r_{k}h^{\prime}_{k}}-\frac{t^{\prime}_{k}}{1-r_{k}t^{\prime}_{k}}\bigg| =\bigg|\frac{h^{\prime}_{k}-t^{\prime}_{k}}{(1-r_{k}h^{\prime}_{k})(1-r_{k}t^{\prime}_{k})}\bigg| \leq \frac{4}{10}2^{-k}D\cdot t_{k}.\end{align*} $$

It follows that

$$ \begin{align*} |\Delta_{r_{k}} ( h_{k})-\Delta_{r_{k}} (t_{k})|&= |r_{k}h_{k}h^{\prime}_{k}-r_{k}t_{k}t^{\prime}_{k}| \;\nonumber\\ &\leq |r_{k}h_{k}(h^{\prime}_{k}-t^{\prime}_{k})|+|r_{k}t^{\prime}_{k}(h_{k}-t_{k})| \;\nonumber\\ &\leq \frac{2}{10}2^{-k}D\cdot |r_{k}h_{k}t_{k}|+\frac{4}{10}2^{-k}D\cdot |r_{k}t_{k}^{\prime}t_{k}|\;\nonumber\\ &\leq \frac{4}{10}2^{-k}D\cdot |\Delta(t_{k})|+\frac{8}{10}2^{-k}D\cdot |\Delta(t_{k})|\leq\frac{12}{10}2^{-k}D. \nonumber \end{align*} $$

Then equation (5.70) is clearly not greater than $2^{1-k}D$ .

Now Claims 5.16 and 5.17 imply that $h_{k}\in [({96}/{100})L^{1}(y,r_{k}),({999}/{1000})L^{1}(y,r_{k})]$ , $|h^{\prime }_{k}-h_{k}|\in [({9}/{100})D,({11}/{100})D]$ , and

$$ \begin{align*} d_{\overline{X}}(u_{X}^{h_{k}}\overline{\psi}_{p}(\overline{u}_{Y}^{r_{k}}a_{Y}^{-\unicode{x3bb}_{k}}y),u_{X}^{h^{\prime}_{k}}\overline{\psi}_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y))&\leq \frac{2}{10}2^{1-k}D,\;\nonumber\\ d_{\overline{X}}(u_{X}^{h_{k}}\overline{u}_{X}^{r_{k}}\overline{\psi}_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y),u_{X}^{h^{\prime}_{k}}\overline{\psi}_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y))&\leq \frac{2}{10}2^{1-k}D, \;\nonumber\\ d_{G_{X}}(q_{p}(h_{k}),u_{X}^{h^{\prime}_{k}-h_{k}})&\leq \frac{2}{10}2^{1-k}D,\; \nonumber \end{align*} $$

for $p\in \{1,\ldots ,n\}$ .

Similarly, for $i=2$ , there exists $h_{k,2}\in [({96}/{100})L^{2}(y,r_{k}),({999}/{1000})L^{2}(y,r_{k})]$ and $h^{\prime }_{k,2}\in \mathbb {R}$ with $|h^{\prime }_{k,2}-h_{k,2}|\in [({9}/{100})2^{2}D,({11}/{100})2^{2}D]$ such that

$$ \begin{align*} d_{\overline{X}}(u_{X}^{h_{k,2}}\overline{\psi}_{p}(\overline{u}_{Y}^{r_{k}}a_{Y}^{-\unicode{x3bb}_{k}}y),u_{X}^{h^{\prime}_{k,2}}\overline{\psi}_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y))&\leq \frac{2}{10}2^{1-k}D,\;\nonumber\\ d_{\overline{X}}(u_{X}^{h_{k,2}}\overline{u}_{X}^{r_{k}}\overline{\psi}_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y),u_{X}^{h^{\prime}_{k,2}}\overline{\psi}_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y))&\leq \frac{2}{10}2^{1-k}D, \;\nonumber\\ d_{G_{X}}(q_{p}^{2}(h_{k,2}),u_{X}^{h^{\prime}_{k,2}-h_{k,2}})&\leq \frac{2}{10}2^{1-k}D,\; \nonumber \end{align*} $$

for $p\in \{1,\ldots ,n\}$ . Note that by equation (5.53), we have $h_{k}\in [\tfrac 13h_{k,2},\tfrac 23h_{k,2}]$ . Thus, we have met the requirement of Lemma 5.14 with pairs

$$ \begin{align*} (\overline{\psi}_{p}(\overline{u}_{Y}^{r_{k}}a_{Y}^{-\unicode{x3bb}_{k}}y),\overline{\psi}_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y))\quad\text{and}\quad (\overline{u}_{X}^{r_{k}}\overline{\psi}_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y),\overline{\psi}_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y))\end{align*} $$

at time $t=h_{k},h_{k,2}$ . Then Lemma 5.14 implies that

$$ \begin{align*} d_{\overline{X}}(u_{X}^{t}\overline{\psi}_{p}(\overline{u}^{r_{k}}a_{Y}^{-\unicode{x3bb}_{k}}y),u_{X}^{t}\overline{u}^{r_{k}}_{X}\overline{\psi}_{p}(a_{Y}^{-\unicode{x3bb}_{k}}y))\leq O\bigg(\frac{2}{10}2^{1-k}D\bigg)=O(2^{-k}) \end{align*} $$

for $t\in [0,h_{k,2}]$ . Moreover, if we write $\overline {\psi }_{p}(\overline {u}_{Y}^{r_{k}}a_{Y}^{-\unicode{x3bb} _{k}}y) =g_{p,k}\overline {u}_{X}^{r_{k}}\overline {\psi }_{p}(a_{Y}^{-\unicode{x3bb} _{k}}y)$ and

$$ \begin{align*} g_{p,k}=\exp\bigg(\sum_{j} \sum_{i=0}^{\varsigma(j)}b_{j}^{i}v_{j}^{i}\bigg), \end{align*} $$

where $v^{i}_{j}$ are the weight vectors of the $\mathfrak {sl}_{2}$ -irreducible representation $V_{j}$ , then by equation (5.49), we deduce

$$ \begin{align*} |b_{j}^{\varsigma(j)-i}|<O(2^{-k})h_{k,2}^{-i}. \end{align*} $$

Finally, one calculates via equations (2.6), (5.55), and (5.58)

$$ \begin{align*} a_{X}^{\unicode{x3bb}_{k}}g_{p,k}a_{X}^{-\unicode{x3bb}_{k}}\leq&\exp\bigg(\sum_{j} \sum_{i=0}^{\varsigma(j)}O(2^{-k})h_{k,2}^{\varsigma(j)-2i}\cdot h_{k,2}^{i-\varsigma(j)}v_{j}^{i}\bigg)\;\nonumber\\ =& \exp\bigg(\sum_{j} \sum_{i=0}^{\varsigma(j)}O(2^{-k})h_{k,2}^{-i}v_{j}^{i}\bigg)\leq O(2^{-k}).\; \nonumber \end{align*} $$

Therefore, we conclude that

$$ \begin{align*}d_{\overline{X}}(\Psi_{k,p}(\overline{u}_{Y}^{r}y), \overline{u}_{X}^{r}\Psi_{k,p}(y))\leq O(2^{-k})\end{align*} $$

for $p\in \{1,\ldots ,n\}$ . The theorem follows.

Remark 5.18. Similar to Remark 5.8, Theorem 5.15 also holds true for $\rho $ being a finite extension of $\nu $ when $(X,\phi ^{U_{X},\tau _{X}}_{t})$ is a time change of the unipotent flow on $X=\mathrm {SO}(n_{X},1)/\Gamma _{X}$ : if for $f\in C(X\times Y)$ ,

$$ \begin{align*} \int f(x,y)d\rho(x,y)=\int \frac{1}{n}\sum_{p=1}^{n}f(\psi_{p}(y),y)\,d\nu(y), \end{align*} $$

then we still have

$$ \begin{align*} \lim_{n\rightarrow\infty}d_{X}(\Psi_{k,p}(\overline{u}_{Y}^{r}y), \overline{u}_{X}^{r}\Psi_{k,p}(y))=0 \end{align*} $$

for $p\in \{1,\ldots , n\}$ and a.e. $y\in Y$ .

6 Applications

In the previous sections, we considered the measure of the form

$$ \begin{align*} \int fd\rho=\int\frac{1}{n}\sum_{p=1}^{n}f(\overline{\psi}_{p}(y),y)\,d\nu(y) \end{align*} $$

for some measurable functions $\overline {\psi }_{p}$ . In addition, we studied the equivariant properties of $\overline {\psi }_{p}$ . In this section, we use these results to develop the rigidity of $\rho $ .

6.1 Unipotent flows of $\mathrm {SO}(n,1)$ versus time changes of unipotent flows

In this section, we shall prove Theorems 1.3 and 1.6. Let $G_{X}=\mathrm {SO}(n_{X},1)$ , $G_{Y}$ be a semisimple Lie group with finite center and no compact factors, and $\Gamma _{X}\subset G_{X}$ , $\Gamma _{Y}\subset G_{Y}$ be irreducible lattices. Let $(X,\mu )$ be the homogeneous space $X=G_{X}/\Gamma _{X}$ equipped with the Lebesgue measure $\mu $ , and let $\phi ^{U_{X}}_{t}=u_{X}^{t}$ be a unipotent flow on X. Suppose that:

• • Y is the homogeneous space $Y=G_{Y}/\Gamma _{Y}$ ;

• • $m_{Y}$ is the Lebesgue measure on Y;

• • $u_{Y}\in G_{Y}$ is a unipotent element that $C_{\mathfrak {g}_{Y}}(u_{Y})$ only contains vectors of weight at most $2$ ;

• • $\tau _{Y}\in \mathbf {K}_{\kappa }(Y)\cap C^{1}(Y)$ is a positive integrable and $C^{1}$ function on Y such that $\tau _{Y},\tau _{Y}^{-1}$ are bounded and satisfy equation (2.10);

• • $\tilde {u}_{Y}^{t}=\phi ^{U_{Y},\tau _{Y}}_{t}$ of the unipotent flow $u_{Y}$ ;

• • $\nu $ is a $\tilde {u}_{Y}^{t}$ -invariant measure on Y;

• • $\rho \in J(u_{X}^{t},\phi _{t}^{U_{Y},\tau _{Y}})$ is a non-trivial (that is, not the product $\mu \times \nu $ ) ergodic joining.

Proposition 6.1. $\tau _{Y}(y)$ and $\tau _{Y}( cy)$ are (measurably) cohomologous along $u_{Y}^{t}$ for all $c\in C_{G_{Y}}(U_{Y})$ . Further, if $\tau _{Y}(y)$ and $\tau _{Y}(cy)$ are $L^{1}$ -cohomologous, then after passing a subsequence if necessary,

exists for $\nu $ -a.e. $y\in Y$ , where

and $\Psi _{k,p}(y)$ is given by equation (5.58).

Proof. The first consequence follows from Theorem 5.6. For the second one, we first apply Lemma 5.7 and obtain

$$ \begin{align*}\lim_{t\rightarrow\infty}\frac{1}{t}\alpha(c^{t},y)=\int \alpha(c,y)\,dm_{Y}(y)\end{align*} $$

for m-a.e. $y\in Y$ whenever c is $m_{Y}$ -ergodic. Note that $d\beta :C_{\mathfrak {g}_{Y}}(U_{Y})\rightarrow V_{C_{X}}^{\perp }$ sends nilpotent elements to nilpotent elements. Thus, for weight vector $v\in C_{\mathfrak {g}_{Y}}(U_{Y})$ of weight $\varsigma \leq 2$ , $\nu $ -almost all $y\in Y$ , we have

$$ \begin{align*} \Psi^{\ast}_{k}(\exp(v)y)= \begin{cases} u_{X}^{e^{-\unicode{x3bb}_{k}}\alpha(\exp(e^{\varsigma\unicode{x3bb}_{k}/2}v),y)}\beta(\exp(e^{\varsigma\unicode{x3bb}_{k}/2}v))^{e^{-\unicode{x3bb}_{k}}}\Psi^{\ast}_{k}(y) &\text{for } \varsigma\geq 1,\\[4pt] u_{X}^{e^{-\unicode{x3bb}_{k}}\alpha(\exp(v),y)}a_{X}^{\unicode{x3bb}_{k}}\beta(\exp(v))a_{X}^{-\unicode{x3bb}_{k}}\Psi^{\ast}_{k}(y) &\text{for } \varsigma=0. \end{cases} \end{align*} $$

Thus, after passing to a subsequence if necessary, we have

(6.1) $$ \begin{align} \lim_{k\rightarrow\infty}\Psi^{\ast}_{k}(\exp(v)y)= \begin{cases} u_{X}^{\int\alpha(\exp(v),\cdot)}\beta(\exp(v))\lim_{k\rightarrow\infty}\Psi^{\ast}_{k}(y) &\text{for } \varsigma= 2,\\ \lim_{k\rightarrow\infty}\Psi^{\ast}_{k}(y), &\text{for } \varsigma= 1\\ \exp(v_{0})\lim_{k\rightarrow\infty}\Psi^{\ast}_{k}(y) &\text{for } \varsigma=0, \end{cases} \end{align} $$

where $\beta (\exp (v))=\exp (v_{0}+v_{2})$ for $v_{0},v_{2}\in V_{C_{X}}^{\perp }$ of weight $0$ and $2$ , respectively. In particular, $\lim _{k\rightarrow \infty }\Psi ^{\ast }_{k}(\exp (v)y)$ exists whenever $\lim _{k\rightarrow \infty }\Psi ^{\ast }_{k}(y)$ exists. In addition, by Theorem 5.15, we have

$$ \begin{align*} \lim_{n\rightarrow\infty}d_{\overline{X}}(\Psi^{\ast}_{k}(\overline{u}_{Y}^{r}y), \overline{u}_{X}^{r}\Psi^{\ast}_{k}(y))=0 \end{align*} $$

for $r\in \mathbb {R}$ , $\nu $ -a.e. $y\in Y$ .

It remains to show that for $\nu $ -almost all $y\in Y$ , there exists a subsequence $\{k(y,l)\}_{l\in \mathbb {N}}\subset \mathbb {N}$ and $\Psi _{p}(y)\in \overline {X}$ such that

(6.2) $$ \begin{align} \lim_{l\rightarrow\infty}\Psi_{k(y,l),p}(y)= \Psi_{p}(y). \end{align} $$

To do this, write $\overline {X}= \bigcup _{i=1}K_{i}$ , where $K_{i}$ are compact and $\overline {\mu }( K_{i})\nearrow 1$ as $i\rightarrow \infty $ . Let

Claim 6.2. $\nu (\Omega )=1$ .

Proof. From a direct calculation (recall that ), we know

$$ \begin{align*} m_{Y}\bigg(\bigcup_{i\geq1}\bigcap_{k\geq1}\bigcup_{j\geq k}\bigcap_{p=1}^{n}\Psi_{j,p}^{-1}(K_{i})\bigg)&\geq m_{Y}\bigg( \bigcap_{k\geq1}\bigcup_{j\geq k}\bigcap_{p=1}^{n}\Psi_{j,p}^{-1}(K_{i})\bigg) \\ &=\lim_{k\rightarrow\infty} m_{Y}\bigg( \bigcup_{j\geq k}\bigcap_{p=1}^{n}\Psi_{j,p}^{-1}(K_{i})\bigg) \geq m_{Y}(\psi_{p}^{-1}a^{-\unicode{x3bb}_{j}} K_{i})\nonumber \end{align*} $$

for any p, j, and i. As $\overline {\mu }(K_{i})\nearrow 1$ as $i\rightarrow \infty $ , the claim follows.

Then by Claim 6.2 for $y\in \Omega $ , there exists $i\geq 1$ such that $ \Psi _{j,p}(y)\in K_{i}$ for infinitely many j. Thus, we proved equation (6.2). Therefore, since the opposite unipotent and central directions generate the whole group $\langle \overline {u}^{r}_{Y},C_{G_{Y}}(U_{Y})\rangle =G_{Y}$ , we conclude that after passing a subsequence if necessary,

$$ \begin{align*}\lim_{n\rightarrow\infty} \Psi_{k,p}(y) \end{align*} $$

exists for $\nu $ -a.e. $y\in Y$ .

Then, define a measure $\widetilde {\rho }$ on $\overline {X}\times Y$ by

for $f\in C(\overline {X}\times Y)$ , where $\Psi ^{\ast }(y)=\{\Psi _{1}(y),\ldots ,\Psi _{n}(y)\}$ . Then $\widetilde {\rho }$ is a non-trivial $(u^{t}_{X}\times u^{t}_{Y})$ -invariant measure on $\overline {X}\times Y$ such that $(\pi _{\overline {X}})_{\ast }\widetilde {\rho }=\overline {\mu }$ and $(\pi _{Y})_{\ast }\widetilde {\rho }=m_{Y}$ . Then, Ratner’s theorem [Rat90] asserts that $C^{\rho }=\{e\}$ and

$$ \begin{align*} \widetilde{\rho}(\operatorname{\mathrm{stab}}(\widetilde{\rho}\,).(x_{0},y_{0}))=1 \end{align*} $$

for some $(x_{0},y_{0})\in X\times Y$ , where

. Then let:

• • (note that $\operatorname {\mathrm {stab}}_{Y}(\widetilde {\rho }\,)\lhd G_{Y}$ is a normal subgroup of $G_{Y}$ );

• • for $g\in G_{X}$ .

Then Ratner’s theorem [Rat90] further asserts that there is $g_{0}\in G_{Y}$ and a continuous surjective homomorphism $\Phi :G_{Y}\rightarrow G_{X}$ with kernel $\operatorname {\mathrm {stab}}_{Y}(\widetilde {\rho }\,)$ , $\Phi (g)=g$ for $g\in SL_{2}$ such that

(6.3) $$ \begin{align} \{\Psi_{1}(h\Gamma_{Y}),\ldots,\Psi_{n}(h\Gamma_{Y})\}=\{\Phi(h)\gamma_{1}g_{0}\Gamma_{X},\ldots,\Phi(h)\gamma_{n}g_{0}\Gamma_{X}\} \end{align} $$

for all $h\in G_{Y}$ , where the intersection

is of finite index in $\Phi (\Gamma _{Y})$ and in $\Gamma _{X}^{g_{0}}$ , $n=|\alpha (\Gamma _{Y})/\Gamma _{0}|$ and $\Phi (\Gamma _{Y})=\{\gamma _{p}\Gamma _{0}:p\in \{1,\ldots ,n\}\}$ .

Next, by using Proposition 6.1 and equation (6.3), for any $\sigma>0 \epsilon >0$ , there exists a subset $K\subset Y$ with $\nu (K)>1-\sigma $ and $k_{0}>0$ such that

$$ \begin{align*} \max_{p}\min_{q}d_{X}(\Psi_{k,p}(h\Gamma_{Y}),\Phi(h)\gamma_{q}g_{0}\Gamma_{X})<\epsilon \end{align*} $$

for $h\Gamma _{Y}\in K$ , $k\geq k_{0}$ . In particular, by the ergodic theorem, we know that for $\nu $ -a.e. $y\in Y$ , there is $A_{y}\subset \mathbb {R}^{+}$ and $\unicode{x3bb} _{0}(y)>0$ such that:

• • for $r\in A_{y}$ , we have $u^{r}_{Y}y \in K$ ;

• • $\operatorname {\mathrm {Leb}}(A_{y}\cap [0,\unicode{x3bb} ])\geq (1-2\sigma )\unicode{x3bb} $ whenever $\unicode{x3bb} \geq \unicode{x3bb} _{0}(y)$ .

Therefore, one can repeat the same argument as in §5.1, and then conclude that there exists $c^{\prime }(h\Gamma _{Y})\in C_{G_{Y}}(U_{Y})$ , $q^{\prime }(p,h\Gamma _{Y})\in \{1,\ldots ,n\}$ such that

$$ \begin{align*} \Psi_{k,p}(h\Gamma_{Y})=c^{\prime}(h\Gamma_{Y})\Phi(h)\gamma_{q^{\prime}(p,h\Gamma_{Y})}g_{0}\Gamma_{X} \end{align*} $$

for $\nu $ -a.e. $h\Gamma _{Y}\in Y$ . We can then write

$$ \begin{align*}\psi_{p}(h\Gamma_{Y})=c(h\Gamma_{Y})\Phi(h)\gamma_{q(p,h\Gamma_{Y})}g_{0}\Gamma_{X} \end{align*} $$

for some $c(h\Gamma _{Y})\in C_{G_{Y}}(U_{Y})$ , $q(p,h\Gamma _{Y})\in \{1,\ldots ,n\}$ , $\nu $ -a.e. $h\Gamma _{Y}\in Y$ . Thus, let $I=(q_{1},q_{2},\ldots ,q_{n})$ be a permutation of $\{1,\ldots ,n\}$ ,

and let

Then $\widetilde {\psi }_{p}(y)$ plays the same role as $\psi _{p}(y)$ and satisfies

(6.4) $$ \begin{align} \widetilde{\psi}_{p}(h\Gamma_{Y})=c(h\Gamma_{Y})\Phi(h)\gamma_{p}g_{0}\Gamma_{X} \end{align} $$

for $\nu $ -a.e. $h\Gamma _{Y}\in Y$ . Thus, without loss of generality, we assume that $\psi _{p}$ satisfies equation (6.4). It follows that the map $\Upsilon :\operatorname {\mathrm {supp}}(\rho )\rightarrow X\times Y$ defined by

$$ \begin{align*}\Upsilon:(\psi_{p}(h\Gamma_{Y}),h\Gamma_{Y})\mapsto(\Phi(h)\gamma_{p}g_{0}\Gamma_{X},h\Gamma_{Y})\quad \text{for } p\in\{1,\ldots,n\}\end{align*} $$

is bijective and satisfies

(6.5) $$ \begin{align} \Upsilon(u_{X}^{t}x,\tilde{u}_{Y}^{t}(y))=(u_{X}^{\xi(y,t)}\times u_{Y}^{\xi(y,t)}).\Upsilon(x,y) \end{align} $$

for $\rho $ -a.e. $(x,y)$ and $t\in \mathbb {R}$ . Equivalently, we obtain the following proposition.

Proposition 6.3. Assume that $\tau _{Y}(y)$ and $\tau _{Y}( cy)$ are $L^{1}$ -cohomologous for all $c\in C_{G_{Y}}(U_{Y})$ . Then, $\tau _{X}\equiv 1$ and $\tau _{Y}$ are joint cohomologous.

Proof. By equation (6.5), we can write down the decomposition in equation (2.7) for $c(y)$ as

$$ \begin{align*} c(y)=u_{X}^{a(y)}b \end{align*} $$

and

$$ \begin{align*}a(y)+t=\xi(y,t)+a(u_{Y}^{\xi(y,t)}y).\end{align*} $$

It follows that

$$ \begin{align*}\int_{0}^{\xi(y,t)}\tau_{Y}(u_{Y}^{s}y)-1 ds= t-\xi(y,t)= a(u_{Y}^{\xi(y,t)}y)-a(y).\end{align*} $$

Thus, $1$ and $\tau _{Y}$ are joint cohomologous via $(\tilde {\rho },a)$ .

Recall from equation (6.1) that when a weight vector $v\in C_{\mathfrak {g}_{Y}}(U_{Y})$ of weight $\varsigma \geq 1$ , we know that $\widetilde {\rho }$ is invariant under

(6.6) $$ \begin{align} \begin{cases} u_{X}^{\int\alpha(\exp(v),\cdot)}\beta(\exp(v))\times \exp(v) &\text{for } \varsigma= 2,\\ \operatorname{\mathrm{id}}\times \exp(v) &\text{for } \varsigma= 1,\\ \exp(v_{0})\times \exp(v) &\text{for } \varsigma= 0, \end{cases} \end{align} $$

where $\beta (\exp (v))=\exp (v_{0}+v_{2})$ . Since $\widetilde {\rho }$ is also $(u_{X}^{t}\times u^{t}_{Y})$ -invariant, if $\beta (\exp (v))=e$ , then Moore’s ergodicity theorem and Lemma 3.1 imply that $\langle \exp (v)\rangle \subset \ker \Phi $ is a compact normal subgroup of $G_{Y}$ . It is a contradiction. Thus, we make the following conclusion.

Proposition 6.4. The map $d\beta |_{V^{\perp }_{C}}: V^{\perp }_{C_{Y}}\rightarrow V^{\perp }_{C_{X}}$ is an injective Lie algebra homomorphism.

6.2 Time changes of unipotent flows of $\mathrm {SO}(n,1)$ vs. unipotent flows

In this section, we shall prove Theorem 1.8. Let $G_{X}=\mathrm {SO}(n_{X},1)$ , $G_{Y}$ be a semisimple Lie group with finite center and no compact factors and $\Gamma _{X}\subset G_{X}$ , $\Gamma _{Y}\subset G_{Y}$ be irreducible lattices. Let $(Y,\nu )$ be the homogeneous space $Y=G_{Y}/\Gamma _{Y}$ equipped with the Lebesgue measure $\nu $ , and let $\phi ^{U_{Y}}_{t}=u_{Y}^{t}$ be a unipotent flow on Y. Suppose that:

• • X is the homogeneous space $X=G_{X}/\Gamma _{X}$ ;

• • $u_{X}\in G_{X}$ is a unipotent element;

• • $\tau _{X}\in \mathbf {K}_{\kappa }(X)$ is a positive integrable and $C^{1}$ function on Y such that $\tau _{X},\tau _{X}^{-1}$ are bounded and satisfies equation (2.10);

• • $\tilde {u}_{X}^{t}=\phi ^{U_{X},\tau }_{t}$ of the unipotent flow $u_{X}$ ;

• • $\mu $ is a $\tilde {u}_{X}^{t}$ -invariant measure on X;

• • $\rho \in J(\tilde {u}_{X}^{t},u_{Y}^{t})$ is an ergodic joining that is a compact extension of $\nu $ , that is, has the form

  $$ \begin{align*} \rho(f)=\int_{Y} \int_{C^{\rho}}\frac{1}{n}\sum_{p=1}^{n}f(k\psi_{p}(y),y)\,dm(k)\,d\nu(y)\end{align*} $$
  for $f\in C(X\times Y)$ and compact $C^{\rho }\in C_{G_{X}}(U_{X})$ .

Recall that in Remark 5.8, for $c\in C_{G_{Y}}(U_{Y})$ , we know that $\rho $ is invariant under the map

$$ \begin{align*}\widetilde{S}_{c}:(x,y) \mapsto ( u_{X}^{\alpha(c,y)}\beta(c)x,cy)\end{align*} $$

(cf. equation (5.28)). In addition, $\alpha ,\beta $ satisfy

$$ \begin{align*}\xi(\psi_{p}(cy),t)+\alpha(c,y)= \alpha(c,u_{Y}^{t}y)+\xi(\psi_{p}(y),t),\end{align*} $$

(6.7) $$ \begin{align} \alpha(c_{1}c_{2},y)=\alpha(c_{1},c_{2}y)+\alpha(c_{2},y),\quad \beta(c_{1}c_{2})=\beta(c_{1})\beta(c_{2}), \end{align} $$

where

$$ \begin{align*}t=\int_{0}^{\xi(x,t)}\tau_{X}(u_{X}^{s}x)\,ds.\end{align*} $$

Moreover, if $\beta (c)=e$ for some $c\in C_{G_{Y}}(U_{Y})$ , then we have equation (5.29):

(6.8) $$ \begin{align} \alpha(c,y)=\xi(x,r_{c}) \end{align} $$

for some $r_{c}\in \mathbb {R}$ . Note that equation (6.8) implies that

$$ \begin{align*} (x,y) \mapsto ( u_{X}^{\alpha(c,y)}x,cy)\mapsto ( x,u_{Y}^{-r_{c}}cy)\end{align*} $$

is $\rho $ -invariant. Thus, Moore’s ergodicity theorem and Lemma 3.1 force

(6.9) $$ \begin{align} \alpha(\exp (v),y)\equiv 0\quad \text{and} \quad \langle\exp(v)\rangle\subset G_{Y} \end{align} $$

is compact. In particular, we obtain equation (1.2):

$$ \begin{align*} d\beta|_{V^{\perp}_{C}}(v)\neq0 \end{align*} $$

for any weight vector $v\in V^{\perp }_{C_{Y}}$ of positive weight. Inspired by this, we deduce the following lemma.

Lemma 6.5. For weight vectors $v\in C_{\mathfrak {g}_{Y}}(U_{Y})$ of weight $\varsigma \neq 0, 2$ , we must have

$$ \begin{align*} d\beta(v)=0. \end{align*} $$

Proof. Similar to Theorem 5.10, one can deduce that for $r\in \mathbb {R}$ ,

$$ \begin{align*} \widetilde{S}_{a^{r}_{Y}}:(x,y)\mapsto (u_{X}^{\alpha(a^{r}_{Y},y)}\beta(a^{r}_{Y})a^{r}_{X}x,a^{r}_{Y}y) \end{align*} $$

is $\rho $ -invariant. Also, we have

$$ \begin{align*} \widetilde{S}_{a_{Y}}\circ \widetilde{S}_{c}\circ \widetilde{S}_{a_{Y}^{-1}}=\widetilde{S}_{a_{Y}ca_{Y}^{-1}} \end{align*} $$

for any $a_{Y}\in \exp (\mathbb {R}A_{Y})$ , $c\in C_{G_{Y}}(U_{Y})$ . In particular, one deduces

$$ \begin{align*} \beta(a_{Y}^{r})a_{X}^{r}\beta(a_{Y}^{-r})a_{X}^{-r}=e,\quad \beta(a_{Y}^{r})a_{X}^{r}\beta(c)\beta(a_{Y}^{-r})a_{X}^{-r}=\beta(a_{Y}^{r}ca_{Y}^{-r}). \end{align*} $$

Thus, suppose that $v\in C_{\mathfrak {g}_{Y}}(U_{Y})$ is a weight vector of weight $\varsigma \neq 0, 2$ . Then,

(6.10) $$ \begin{align} \beta(\exp(v))^{e^{r\varsigma/2}}&=\beta(\exp(e^{r\varsigma/2}v))= \beta(a_{Y}^{r}\exp(v)a_{Y}^{-r}) \nonumber\\ &=\beta(a_{Y}^{r})a_{X}^{r}\beta(\exp(v))\beta(a_{Y}^{-r})a_{X}^{-r} =\beta(a_{Y}^{r})a_{X}^{r}\beta(\exp(v))a_{X}^{-r}\beta(a_{Y}^{r})^{-1}. \end{align} $$

Assume that $\beta (\exp (v))=\exp (w)$ for some $w\in C_{\mathfrak {g}_{X}}(U_{X})$ . By the assumption, w has to be nilpotent and so

(6.11) $$ \begin{align} a_{X}^{r}\beta(\exp(v))a_{X}^{-r}=a_{X}^{r}\exp(w)a_{X}^{-r}=\exp(e^{r}w). \end{align} $$

Combining equations (6.10) and (6.11), we get

$$ \begin{align*}e^{r\varsigma/2}\|w\|=\|e^{r\varsigma/2}w\|= \|\operatorname{\mathrm{Ad}} \beta(a_{Y}^{r}).e^{r}w\|= \|e^{r}w\|= e^{r}\|w\|,\end{align*} $$

which leads to a contradiction.

Then by Moore’s ergodicity theorem and Lemma 3.1 (cf. Remark 5.8), we make the following conclusion.

Corollary 6.6. If $C_{\mathfrak {g}_{Y}}(U_{Y})$ contains a weight vector of weight $\varsigma \neq 0, 2$ , then

$$ \begin{align*} \rho=\mu\times\nu. \end{align*} $$

Now we focus on the case $n_{X}=2$ and $\tau _{X}\in \mathbf {K}(X)\cap C^{1}(X)$ . Note that in this case, Ratner [Rat87] showed that $\tilde {u}^{t}_{X}$ also has H-property. Thus, we can repeat the same idea as in §6.1 to discuss the case when $C_{\mathfrak {g}_{Y}}(U_{Y})$ consists only of weight vectors of weight $\varsigma =0, 2$ . Note that since $\beta \equiv 0$ , by equation (6.8), we must have $\alpha (c,\cdot )\in L^{\infty }(Y)$ for any $c\in C_{G_{Y}}(U_{Y})$ . Then, similar to Proposition 6.1, we have the following proposition.

Proposition 6.7. Assume that $C_{\mathfrak {g}_{Y}}(U_{Y})$ consists only of weight vectors of weight $\varsigma =0, 2$ . Then after passing a subsequence if necessary,

(6.12)

exists for $\nu $ -a.e. $y\in Y$ , where and $\Psi _{k,p}(y)$ is given by equation (5.58).

Remark 6.8. One non-trivial step of Proposition 6.7 is to obtain a similar version of Theorem 5.15. This requires that the time change $\tilde {u}^{t}_{X}$ also has H-property. See [Rat87] Lemma 3.1 for further details.

Then by Ratner’s theorem (cf. equation (6.4)), there exists $c(h\Gamma _{Y})\in C_{G_{X}}(U_{X})=\exp (\mathbb {R}U_{X})$ , a homomorphism $\Phi (h)$ , $\gamma _{p},g_{0}\in G_{X}$ such that $\psi _{p}$ can be written as

(6.13) $$ \begin{align} \psi_{p}(h\Gamma_{Y})=c(h\Gamma_{Y})\Phi(h)\gamma_{p}g_{0}\Gamma_{X} \end{align} $$

for $h\Gamma _{Y}\in Y$ . Then as in Proposition 6.3, we get the following proposition.

Proposition 6.9. $\tau _{X}$ and $\tau _{Y}\equiv 1$ are joint cohomologous.

Finally, consider $\rho $ is non-trivial $v\in C_{G_{Y}}(U_{Y})$ . Since $\beta (\exp (v))=e$ , equation (6.9) asserts that

$$ \begin{align*} \alpha(\exp (v),y)\equiv 0\quad \text{and} \quad \langle\exp(v)\rangle\subset G_{Y}\end{align*} $$

is compact. However, Ratner’s theorem implies that $\langle \exp (v)\rangle \subset \ker \Phi $ is a normal subgroup of $G_{Y}$ . It is a contradiction. Thus, we conclude

$$ \begin{align*} V^{\perp}_{C_{Y}}=0. \end{align*} $$

Therefore, we have proved Theorem 1.10.