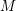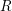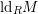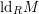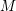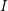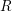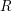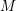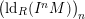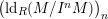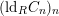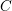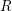1 Introduction
This paper concerns the asymptotic behavior of the powers of an ideal in a Noetherian local ring
![]() $R$
. A paradigm for our results is the statement, due to Hilbert, and to Samuel, that for any ideal
$R$
. A paradigm for our results is the statement, due to Hilbert, and to Samuel, that for any ideal
![]() $I$
that is primary to the maximal ideal of
$I$
that is primary to the maximal ideal of
![]() $R$
, the sequence
$R$
, the sequence
![]() $(\text{length}_{R}(R/I^{n}))_{n}$
is eventually given by a polynomial in
$(\text{length}_{R}(R/I^{n}))_{n}$
is eventually given by a polynomial in
![]() $n$
. Another example, due to Brodmann [Reference Brodmann3], is that for any ideal
$n$
. Another example, due to Brodmann [Reference Brodmann3], is that for any ideal
![]() $I$
, the sequence
$I$
, the sequence
![]() $(\text{depth}_{R}(R/I^{n}))_{n}$
is eventually constant. We are also interested in the value of
$(\text{depth}_{R}(R/I^{n}))_{n}$
is eventually constant. We are also interested in the value of
![]() $n$
beyond which the asymptotic behavior sets in, and the asymptotic value of the relevant invariants. The papers [Reference Chardin5, Reference Herzog and Hibi13] and their references discuss various aspects of similar asymptotic results.
$n$
beyond which the asymptotic behavior sets in, and the asymptotic value of the relevant invariants. The papers [Reference Chardin5, Reference Herzog and Hibi13] and their references discuss various aspects of similar asymptotic results.
In this paper, we study the linearity defect introduced by Herzog and Iyengar [Reference Herzog and Iyengar15] (see Section 2). One of the motivations for studying the linearity defect is the research on the linear part of minimal free resolutions over the exterior algebras in [Reference Eisenbud, Fløystad and Schreyer9]. The finiteness of the linearity defect has strong consequences on the structure of a module: if
![]() $\text{ld}_{R}M$
is finite, then the Poincaré series of
$\text{ld}_{R}M$
is finite, then the Poincaré series of
![]() $M$
is rational with denominator depending only on
$M$
is rational with denominator depending only on
![]() $R$
(see [Reference Herzog and Iyengar15, Proposition 1.8]). However, there remain many open questions on the finiteness of the linearity defect (see [Reference Ahangari Maleki and Rossi1, Reference Conca, Iyengar, Nguyen and Römer6, Reference Şega23] for details).
$R$
(see [Reference Herzog and Iyengar15, Proposition 1.8]). However, there remain many open questions on the finiteness of the linearity defect (see [Reference Ahangari Maleki and Rossi1, Reference Conca, Iyengar, Nguyen and Römer6, Reference Şega23] for details).
The linearity defect was studied by many authors (see e.g., [Reference Ahangari Maleki and Rossi1, Reference Conca, Iyengar, Nguyen and Römer6, Reference Herzog and Iyengar15, Reference Iyengar and Römer19, Reference Okazaki and Yanagawa21, Reference Şega23, Reference Yanagawa24]). Nevertheless, it is still an elusive invariant. The problem is highly nontrivial as to bound efficiently the linearity defect even for familiar classes of ideals like monomial ideals. Beyond componentwise linear ideals [Reference Herzog and Hibi12] (which have linearity defect zero), there are few interesting and large enough classes of ideals whose linearity defect is known. In this paper, the above remarks notwithstanding, we show that the linearity defect behaves in a pleasant way asymptotically. Let
![]() $\text{gl}\,\text{ld}\,R$
be the supremum of the numbers
$\text{gl}\,\text{ld}\,R$
be the supremum of the numbers
![]() $\text{ld}_{R}M$
, where
$\text{ld}_{R}M$
, where
![]() $M$
runs through all the finitely generated
$M$
runs through all the finitely generated
![]() $R$
-modules (see Section 2). The main result of this paper is
$R$
-modules (see Section 2). The main result of this paper is
Theorem 1.1. Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring such that
$(R,\mathfrak{m})$
be a Noetherian local ring such that
![]() $\text{gl}\,\text{ld}\,R$
is finite. For any ideal
$\text{gl}\,\text{ld}\,R$
is finite. For any ideal
![]() $I\subseteq \mathfrak{m}$
and finitely generated
$I\subseteq \mathfrak{m}$
and finitely generated
![]() $R$
-module
$R$
-module
![]() $M$
, the sequences
$M$
, the sequences
![]() $(\text{ld}_{R}(I^{n}M))_{n}$
,
$(\text{ld}_{R}(I^{n}M))_{n}$
,
![]() $(\text{ld}_{R}(I^{n}M/I^{n+1}M))_{n}$
, and
$(\text{ld}_{R}(I^{n}M/I^{n+1}M))_{n}$
, and
![]() $(\text{ld}_{R}(M/I^{n}M))_{n}$
are eventually constant.
$(\text{ld}_{R}(M/I^{n}M))_{n}$
are eventually constant.
We obtain the assertion concerning the linearity defect of the sequences
![]() $(I^{n}M)_{n}$
and
$(I^{n}M)_{n}$
and
![]() $(I^{n}M/I^{n+1}M)_{n}$
as a corollary of Theorem 1.2 below, whose proof makes crucial use of work of Şega [Reference Şega23], and the theory of Rees algebras. The assertion involving
$(I^{n}M/I^{n+1}M)_{n}$
as a corollary of Theorem 1.2 below, whose proof makes crucial use of work of Şega [Reference Şega23], and the theory of Rees algebras. The assertion involving
![]() $(M/I^{n}M)_{n}$
uses, in addition, a result of Avramov [Reference Avramov2] concerning small homomorphisms of modules. Below, recall that
$(M/I^{n}M)_{n}$
uses, in addition, a result of Avramov [Reference Avramov2] concerning small homomorphisms of modules. Below, recall that
![]() $S$
is called a standard graded algebra over
$S$
is called a standard graded algebra over
![]() $R$
if it is an
$R$
if it is an
![]() $\mathbb{N}$
-graded ring with
$\mathbb{N}$
-graded ring with
![]() $S_{0}=R$
and
$S_{0}=R$
and
![]() $S$
is generated over
$S$
is generated over
![]() $R$
by finitely many elements of
$R$
by finitely many elements of
![]() $S_{1}$
.
$S_{1}$
.
Theorem 1.2. Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring such that
$(R,\mathfrak{m})$
be a Noetherian local ring such that
![]() $\text{gl}\,\text{ld}\,R<\infty$
. Let
$\text{gl}\,\text{ld}\,R<\infty$
. Let
![]() $S$
be a standard graded algebra over
$S$
be a standard graded algebra over
![]() $R$
, and let
$R$
, and let
![]() $C$
be a finitely generated graded
$C$
be a finitely generated graded
![]() $S$
-module. Then the sequence
$S$
-module. Then the sequence
![]() $(\text{ld}_{R}C_{n})_{n}$
is eventually constant.
$(\text{ld}_{R}C_{n})_{n}$
is eventually constant.
This result is motivated by previous work of Herzog and Hibi [Reference Herzog and Hibi13, Theorem 1.1] on depth. In the last part of Section 4, particularly Remark 4.3, we discuss variations of Theorem 1.2.
We do not know how to bound effectively the asymptotic values of the sequences in Theorem 1.1. A rare result in this direction is [Reference Herzog, Hibi and Ohsugi14, Theorem 2.4]. There the authors establish a necessary and sufficient condition for all the powers of a polynomial ideal to have linearity defect zero, using the theory of
![]() $d$
-sequences [Reference Huneke17]. It would be interesting to study possible generalizations and analogues of this result.
$d$
-sequences [Reference Huneke17]. It would be interesting to study possible generalizations and analogues of this result.
We use [Reference Bruns and Herzog4, Reference Eisenbud8] as our reference for standard concepts and facts in commutative algebra.
2 Linearity defect
Let
![]() $(R,\mathfrak{m})$
be a commutative Noetherian local ring with residue field
$(R,\mathfrak{m})$
be a commutative Noetherian local ring with residue field
![]() $k$
. Let
$k$
. Let
![]() $I$
be a proper ideal of
$I$
be a proper ideal of
![]() $R$
. Let
$R$
. Let
![]() $M$
be a finitely generated
$M$
be a finitely generated
![]() $R$
-module. We call
$R$
-module. We call
the associated graded module of
![]() $M$
with respect to
$M$
with respect to
![]() $I$
.
$I$
.
Let
![]() $F$
be the minimal free resolution of
$F$
be the minimal free resolution of
![]() $M$
:
$M$
:
Since
![]() $\unicode[STIX]{x2202}(F)\subseteq \mathfrak{m}F$
the graded submodule
$\unicode[STIX]{x2202}(F)\subseteq \mathfrak{m}F$
the graded submodule
of
![]() $F$
is stable under the differential; said otherwise,
$F$
is stable under the differential; said otherwise,
![]() ${\mathcal{F}}^{i}F$
is a subcomplex of
${\mathcal{F}}^{i}F$
is a subcomplex of
![]() $F$
. The linear part of
$F$
. The linear part of
![]() $F$
is the associated graded complex
$F$
is the associated graded complex
Note that
![]() $\text{lin}^{R}F$
is a complex of graded modules over
$\text{lin}^{R}F$
is a complex of graded modules over
![]() $\text{gr}_{\mathfrak{m}}R$
, and
$\text{gr}_{\mathfrak{m}}R$
, and
![]() $(\text{lin}^{R}F)_{i}=(\text{gr}_{\mathfrak{m}}F_{i})(-i)$
for every
$(\text{lin}^{R}F)_{i}=(\text{gr}_{\mathfrak{m}}F_{i})(-i)$
for every
![]() $i\geqslant 0$
. Following [Reference Herzog and Iyengar15], the linearity defect of
$i\geqslant 0$
. Following [Reference Herzog and Iyengar15], the linearity defect of
![]() $M$
is defined by
$M$
is defined by
If
![]() $M\cong 0$
, we set
$M\cong 0$
, we set
![]() $\text{ld}_{R}M=0$
. This convention guarantees that the maximal ideal
$\text{ld}_{R}M=0$
. This convention guarantees that the maximal ideal
![]() $(0)$
of the field
$(0)$
of the field
![]() $k$
has linearity defect zero.
$k$
has linearity defect zero.
In order to establish our main results, we use the following characterization of the linearity defect due to Şega [Reference Şega23, Theorem 2.2].
Theorem 2.1. Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring,
$(R,\mathfrak{m})$
be a Noetherian local ring,
![]() $M$
be a finitely generated
$M$
be a finitely generated
![]() $R$
-module, and
$R$
-module, and
![]() $d\geqslant 0$
be an integer. The following statements are equivalent:
$d\geqslant 0$
be an integer. The following statements are equivalent:
(i)
 $\text{ld}_{R}M\leqslant d$
;
$\text{ld}_{R}M\leqslant d$
;(ii) the natural morphism
 $\text{Tor}_{i}^{R}(R/\mathfrak{m}^{q+1},M)\longrightarrow \text{Tor}_{i}^{R}(R/\mathfrak{m}^{q},M)$
is the zero map for every
$\text{Tor}_{i}^{R}(R/\mathfrak{m}^{q+1},M)\longrightarrow \text{Tor}_{i}^{R}(R/\mathfrak{m}^{q},M)$
is the zero map for every
 $i>d$
and every
$i>d$
and every
 $q\geqslant 0$
.
$q\geqslant 0$
.
The following result is useful to study the sequence
![]() $(\text{ld}_{R}(M/I^{n}M))_{n}$
in Theorem 1.1.
$(\text{ld}_{R}(M/I^{n}M))_{n}$
in Theorem 1.1.
Lemma 2.2. Let
![]() $0\longrightarrow M\longrightarrow P\longrightarrow N\longrightarrow 0$
be an exact sequence of nonzero, finitely generated
$0\longrightarrow M\longrightarrow P\longrightarrow N\longrightarrow 0$
be an exact sequence of nonzero, finitely generated
![]() $R$
-modules. Let
$R$
-modules. Let
![]() $F$
and
$F$
and
![]() $G$
be the minimal free resolutions of
$G$
be the minimal free resolutions of
![]() $M$
and
$M$
and
![]() $P$
, respectively. Assume that there is a lifting
$P$
, respectively. Assume that there is a lifting
![]() $\unicode[STIX]{x1D711}:F\longrightarrow G$
of
$\unicode[STIX]{x1D711}:F\longrightarrow G$
of
![]() $M\rightarrow P$
such that
$M\rightarrow P$
such that
![]() $\unicode[STIX]{x1D711}(F)\subseteq \mathfrak{m}^{2}G$
. Then there is an equality
$\unicode[STIX]{x1D711}(F)\subseteq \mathfrak{m}^{2}G$
. Then there is an equality
Proof. Since
![]() $\unicode[STIX]{x1D711}(F)\subseteq \mathfrak{m}^{2}G$
, the mapping cone, say
$\unicode[STIX]{x1D711}(F)\subseteq \mathfrak{m}^{2}G$
, the mapping cone, say
![]() $W$
, of
$W$
, of
![]() $\unicode[STIX]{x1D711}$
, is a minimal free resolution of
$\unicode[STIX]{x1D711}$
, is a minimal free resolution of
![]() $N$
. By simple computations, we get a direct sum decomposition
$N$
. By simple computations, we get a direct sum decomposition
Hence by accounting,
![]() $\text{ld}_{R}N=\max \{\text{ld}_{R}P,\text{ld}_{R}M+1\},$
as desired.◻
$\text{ld}_{R}N=\max \{\text{ld}_{R}P,\text{ld}_{R}M+1\},$
as desired.◻
Our results require the finiteness of the global linearity defect of
![]() $R$
, which is defined by
$R$
, which is defined by
There is an ample supply of rings with finite global linearity defect: regular rings, or more generally local rings which are both Koszul and Golod (see [Reference Herzog and Iyengar15, Corollary 6.2]).
3 Asymptotic behavior of the linearity defect
Let
![]() $R$
be a Noetherian local ring with
$R$
be a Noetherian local ring with
![]() $\text{gl}\,\text{ld}\,R<\infty$
. Assuming that
$\text{gl}\,\text{ld}\,R<\infty$
. Assuming that
![]() $S$
is a standard graded polynomial ring over
$S$
is a standard graded polynomial ring over
![]() $R$
, we can make Theorem 1.2 more precise by giving an upper bound for the smallest integer from which the sequence
$R$
, we can make Theorem 1.2 more precise by giving an upper bound for the smallest integer from which the sequence
![]() $(\text{ld}_{R}C_{n})_{n}$
becomes constant. This requires certain information about the minimal graded free resolution of
$(\text{ld}_{R}C_{n})_{n}$
becomes constant. This requires certain information about the minimal graded free resolution of
![]() $C$
as an
$C$
as an
![]() $S$
-module.
$S$
-module.
Definition 3.1. Let
![]() $S=R[y_{1},\ldots ,y_{m}]$
be a polynomial extension of
$S=R[y_{1},\ldots ,y_{m}]$
be a polynomial extension of
![]() $R$
, where
$R$
, where
![]() $m\geqslant 0$
, each variable
$m\geqslant 0$
, each variable
![]() $y_{i}$
has degree 1. For each finitely generated graded
$y_{i}$
has degree 1. For each finitely generated graded
![]() $S$
-module
$S$
-module
![]() $C$
, let
$C$
, let
![]() $\text{pdeg}_{S}(C)$
be the minimal number such that
$\text{pdeg}_{S}(C)$
be the minimal number such that
![]() $C_{i}=0$
for all
$C_{i}=0$
for all
![]() $i\geqslant \text{pdeg}_{S}(C)$
or
$i\geqslant \text{pdeg}_{S}(C)$
or
![]() $C_{i}\neq 0$
for all
$C_{i}\neq 0$
for all
![]() $i\geqslant \text{pdeg}_{S}(C)$
. If
$i\geqslant \text{pdeg}_{S}(C)$
. If
![]() $C=0$
, we set
$C=0$
, we set
![]() $\text{pdeg}_{S}(0)=-\infty$
. Note that
$\text{pdeg}_{S}(0)=-\infty$
. Note that
![]() $\text{pdeg}_{S}(C)$
is well defined since
$\text{pdeg}_{S}(C)$
is well defined since
![]() $S$
is standard graded.
$S$
is standard graded.
We can compute the number
![]() $\text{pdeg}_{S}(C)$
effectively, using two simple facts:
$\text{pdeg}_{S}(C)$
effectively, using two simple facts:
(i)
 $\text{pdeg}_{S}(C)=\text{pdeg}_{S/\mathfrak{m}S}(C/\mathfrak{m}C)$
. This is by Nakayama’s lemma.
$\text{pdeg}_{S}(C)=\text{pdeg}_{S/\mathfrak{m}S}(C/\mathfrak{m}C)$
. This is by Nakayama’s lemma.(ii)
 $\text{pdeg}_{S/\mathfrak{m}S}(C/\mathfrak{m}C)$
is bounded above by one plus the postulation number of
$\text{pdeg}_{S/\mathfrak{m}S}(C/\mathfrak{m}C)$
is bounded above by one plus the postulation number of
 $C/\mathfrak{m}C$
, viewed as a module over
$C/\mathfrak{m}C$
, viewed as a module over
 $S/\mathfrak{m}S=k[y_{1},\ldots ,y_{m}]$
. The latter number is given, for example, in [Reference Bruns and Herzog4, Proposition 4.12].
$S/\mathfrak{m}S=k[y_{1},\ldots ,y_{m}]$
. The latter number is given, for example, in [Reference Bruns and Herzog4, Proposition 4.12].
Definition 3.2. Given a finitely generated graded
![]() $S$
-module
$S$
-module
![]() $C$
, define the constant
$C$
, define the constant
![]() $N(C)$
as follows. For
$N(C)$
as follows. For
![]() $i=0$
, denote
$i=0$
, denote
![]() $n(0)=\text{pdeg}_{S}(C)$
. For
$n(0)=\text{pdeg}_{S}(C)$
. For
![]() $1\leqslant i\leqslant \min \{\text{gl}\,\text{ld}\,R,\text{pd}_{S}C\}$
, let
$1\leqslant i\leqslant \min \{\text{gl}\,\text{ld}\,R,\text{pd}_{S}C\}$
, let
![]() $c(i,q):=\text{pdeg}_{S}\left(\text{Im}\,\unicode[STIX]{x1D707}^{i,q}\right)$
, where
$c(i,q):=\text{pdeg}_{S}\left(\text{Im}\,\unicode[STIX]{x1D707}^{i,q}\right)$
, where
![]() $\unicode[STIX]{x1D707}^{i,q}$
denotes the map
$\unicode[STIX]{x1D707}^{i,q}$
denotes the map
Let
be the minimal graded free resolution of
![]() $C$
over
$C$
over
![]() $S$
(see [Reference Bruns and Herzog4, Section 1.5]).
$S$
(see [Reference Bruns and Herzog4, Section 1.5]).
Set
![]() $M_{i}=\text{Im}\,(F_{i}\rightarrow F_{i-1})$
and let
$M_{i}=\text{Im}\,(F_{i}\rightarrow F_{i-1})$
and let
Note that
![]() $T(i)$
is finite, by the Artin–Rees lemma. Denote
$T(i)$
is finite, by the Artin–Rees lemma. Denote
Finally, define
![]() $N(C):=\max \{n(0),n(1),\ldots ,n(\min \{\text{gl}\,\text{ld}\,R,\text{pd}_{S}C\})\}$
.
$N(C):=\max \{n(0),n(1),\ldots ,n(\min \{\text{gl}\,\text{ld}\,R,\text{pd}_{S}C\})\}$
.
Since
![]() $\text{gl}\,\text{ld}\,R$
is a finite number,
$\text{gl}\,\text{ld}\,R$
is a finite number,
![]() $N(C)$
is also finite.
$N(C)$
is also finite.
Remark 3.3. In principal, the numbers
![]() $T(i)$
in the definition of
$T(i)$
in the definition of
![]() $N(C)$
should not be difficult to compute. Indeed, consider the graded ring
$N(C)$
should not be difficult to compute. Indeed, consider the graded ring
![]() $\text{gr}_{\mathfrak{m}S}S$
and the ideal
$\text{gr}_{\mathfrak{m}S}S$
and the ideal
![]() $\mathfrak{n}=\bigoplus _{j\geqslant 1}\left(\mathfrak{m}^{j}S/\mathfrak{m}^{j+1}S\right)$
. Denote by
$\mathfrak{n}=\bigoplus _{j\geqslant 1}\left(\mathfrak{m}^{j}S/\mathfrak{m}^{j+1}S\right)$
. Denote by
![]() $K_{i}$
the kernel of the natural surjective map
$K_{i}$
the kernel of the natural surjective map
![]() $\text{gr}_{\mathfrak{m}S}(F_{i-1})\rightarrow \text{gr}_{\mathfrak{m}S}(F_{i-1}/M_{i})$
. Then there is an equality
$\text{gr}_{\mathfrak{m}S}(F_{i-1})\rightarrow \text{gr}_{\mathfrak{m}S}(F_{i-1}/M_{i})$
. Then there is an equality
The proof is straightforward (see [Reference Herzog, Welker and Yassemi16, Proposition 2.1] for an analogous statement).
The main technical result of this paper is as follows.
Theorem 3.4. Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring with
$(R,\mathfrak{m})$
be a Noetherian local ring with
![]() $\text{gl}\,\text{ld}\,R<\infty$
. Let
$\text{gl}\,\text{ld}\,R<\infty$
. Let
![]() $S$
be a standard graded polynomial ring over
$S$
be a standard graded polynomial ring over
![]() $R$
, and let
$R$
, and let
![]() $C$
be a finitely generated graded
$C$
be a finitely generated graded
![]() $S$
-module. Then for all
$S$
-module. Then for all
![]() $n\geqslant N(C)$
, there is an equality
$n\geqslant N(C)$
, there is an equality
![]() $\text{ld}_{R}C_{n}=\text{ld}_{R}C_{N(C)}$
.
$\text{ld}_{R}C_{n}=\text{ld}_{R}C_{N(C)}$
.
Proof. Since
![]() $S$
is a flat
$S$
is a flat
![]() $R$
-algebra, there is an isomorphism of
$R$
-algebra, there is an isomorphism of
![]() $R$
-modules
$R$
-modules
for all
![]() $i,q\geqslant 0,n\in \mathbb{Z}$
.
$i,q\geqslant 0,n\in \mathbb{Z}$
.
Let
![]() $N=N(C)$
and
$N=N(C)$
and
![]() $e=\sup \{\text{ld}_{R}C_{n}:n\geqslant N\}\leqslant \text{gl}\,\text{ld}\,R<\infty$
. We prove that
$e=\sup \{\text{ld}_{R}C_{n}:n\geqslant N\}\leqslant \text{gl}\,\text{ld}\,R<\infty$
. We prove that
![]() $\text{ld}_{R}C_{n}=e$
for any
$\text{ld}_{R}C_{n}=e$
for any
![]() $n\geqslant N$
. There is nothing to do if
$n\geqslant N$
. There is nothing to do if
![]() $e=0$
, so we assume that
$e=0$
, so we assume that
![]() $e\geqslant 1$
. Note that, since
$e\geqslant 1$
. Note that, since
![]() $\text{Tor}_{i}^{S}(S/\mathfrak{m}^{q}S,C)=0$
for
$\text{Tor}_{i}^{S}(S/\mathfrak{m}^{q}S,C)=0$
for
![]() $i>\text{pd}_{S}C$
, Isomorphism (3.1) yields
$i>\text{pd}_{S}C$
, Isomorphism (3.1) yields
![]() $e\leqslant \min \{\text{gl}\,\text{ld}\,R,\text{pd}_{S}C\}$
.
$e\leqslant \min \{\text{gl}\,\text{ld}\,R,\text{pd}_{S}C\}$
.
Denote by
![]() $\unicode[STIX]{x1D707}_{n}^{e,q}$
the following map
$\unicode[STIX]{x1D707}_{n}^{e,q}$
the following map
Choose
![]() $m\geqslant N$
such that
$m\geqslant N$
such that
![]() $\text{ld}_{R}C_{m}=e$
. Since
$\text{ld}_{R}C_{m}=e$
. Since
![]() $\text{ld}_{R}C_{m}=e>e-1$
, Theorem 2.1 implies that
$\text{ld}_{R}C_{m}=e>e-1$
, Theorem 2.1 implies that
![]() $\unicode[STIX]{x1D707}_{m}^{e,\overline{q}}\neq 0$
for some
$\unicode[STIX]{x1D707}_{m}^{e,\overline{q}}\neq 0$
for some
![]() $\overline{q}\geqslant 0$
. To prove the inequality
$\overline{q}\geqslant 0$
. To prove the inequality
![]() $\text{ld}_{R}C_{n}\geqslant e$
, also by Theorem 2.1, it suffices to show that
$\text{ld}_{R}C_{n}\geqslant e$
, also by Theorem 2.1, it suffices to show that
![]() $\unicode[STIX]{x1D707}_{n}^{e,q}\neq 0$
for some
$\unicode[STIX]{x1D707}_{n}^{e,q}\neq 0$
for some
![]() $q\geqslant 0$
.
$q\geqslant 0$
.
Firstly, consider the case
![]() $\overline{q}<T(e)$
. Since
$\overline{q}<T(e)$
. Since
![]() $n,m\geqslant N\geqslant c(e,\overline{q})$
, the definition of
$n,m\geqslant N\geqslant c(e,\overline{q})$
, the definition of
![]() $c(e,\overline{q})$
implies that
$c(e,\overline{q})$
implies that
![]() $\unicode[STIX]{x1D707}_{n}^{e,\overline{q}}$
and
$\unicode[STIX]{x1D707}_{n}^{e,\overline{q}}$
and
![]() $\unicode[STIX]{x1D707}_{m}^{e,\overline{q}}$
are both zero or both nonzero. This implies that
$\unicode[STIX]{x1D707}_{m}^{e,\overline{q}}$
are both zero or both nonzero. This implies that
![]() $\unicode[STIX]{x1D707}_{n}^{e,\overline{q}}\neq 0$
, as desired.
$\unicode[STIX]{x1D707}_{n}^{e,\overline{q}}\neq 0$
, as desired.
Secondly, consider the case
![]() $\overline{q}\geqslant T(e)$
. Denote
$\overline{q}\geqslant T(e)$
. Denote
![]() $T=T(e)$
, we claim that
$T=T(e)$
, we claim that
![]() $\unicode[STIX]{x1D707}_{n}^{e,T}\neq 0$
. As
$\unicode[STIX]{x1D707}_{n}^{e,T}\neq 0$
. As
![]() $m,n\geqslant c(e,T)$
,
$m,n\geqslant c(e,T)$
,
![]() $\unicode[STIX]{x1D707}_{m}^{e,T}$
and
$\unicode[STIX]{x1D707}_{m}^{e,T}$
and
![]() $\unicode[STIX]{x1D707}_{n}^{e,T}$
are both zero or both nonzero, so it suffices to prove that
$\unicode[STIX]{x1D707}_{n}^{e,T}$
are both zero or both nonzero, so it suffices to prove that
![]() $\unicode[STIX]{x1D707}_{m}^{e,T}\neq 0$
. Assume the contrary, so
$\unicode[STIX]{x1D707}_{m}^{e,T}\neq 0$
. Assume the contrary, so
![]() $\unicode[STIX]{x1D707}_{m}^{e,T}=0$
. Let
$\unicode[STIX]{x1D707}_{m}^{e,T}=0$
. Let
![]() $F$
be the minimal graded free resolution of
$F$
be the minimal graded free resolution of
![]() $C$
over
$C$
over
![]() $S$
. Denote
$S$
. Denote
![]() $M_{i}=\text{Im}\,(F_{i}\rightarrow F_{i-1})$
, the
$M_{i}=\text{Im}\,(F_{i}\rightarrow F_{i-1})$
, the
![]() $i$
th syzygy of
$i$
th syzygy of
![]() $C$
as an
$C$
as an
![]() $S$
-module if
$S$
-module if
![]() $i\geqslant 1$
and
$i\geqslant 1$
and
![]() $M_{0}=C$
. Denote
$M_{0}=C$
. Denote
![]() $M=M_{e}$
and
$M=M_{e}$
and
![]() $P=F_{e-1}$
. Clearly
$P=F_{e-1}$
. Clearly
 $$\begin{eqnarray}\displaystyle & \displaystyle \text{Tor}_{e}^{S}(S/\mathfrak{m}^{q}S,C)\cong \text{Tor}_{1}^{S}(S/\mathfrak{m}^{q}S,M_{e-1})\cong \frac{\mathfrak{m}^{q}P\cap M}{\mathfrak{m}^{q}M}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{Im}\,\unicode[STIX]{x1D707}^{e,q}\cong \frac{\mathfrak{m}^{q+1}P\cap M+\mathfrak{m}^{q}M}{\mathfrak{m}^{q}M}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{Tor}_{e}^{S}(S/\mathfrak{m}^{q}S,C)\cong \text{Tor}_{1}^{S}(S/\mathfrak{m}^{q}S,M_{e-1})\cong \frac{\mathfrak{m}^{q}P\cap M}{\mathfrak{m}^{q}M}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{Im}\,\unicode[STIX]{x1D707}^{e,q}\cong \frac{\mathfrak{m}^{q+1}P\cap M+\mathfrak{m}^{q}M}{\mathfrak{m}^{q}M}. & \displaystyle \nonumber\end{eqnarray}$$
The equality
![]() $\unicode[STIX]{x1D707}_{m}^{e,T}=0$
then yields
$\unicode[STIX]{x1D707}_{m}^{e,T}=0$
then yields
We show that
![]() $\unicode[STIX]{x1D707}_{m}^{e,\overline{q}}=0$
. Indeed,
$\unicode[STIX]{x1D707}_{m}^{e,\overline{q}}=0$
. Indeed,
 $$\begin{eqnarray}\displaystyle \left(\mathfrak{m}^{\overline{q}+1}P\cap M+\mathfrak{m}^{\overline{q}}M\right)_{m} & = & \displaystyle (\mathfrak{m}^{\overline{q}-T}(\mathfrak{m}^{T+1}P\cap M+\mathfrak{m}^{T}M))_{m}\nonumber\\ \displaystyle & = & \displaystyle \mathfrak{m}^{\overline{q}-T}\left(\mathfrak{m}^{T+1}P\cap M+\mathfrak{m}^{T}M\right)_{m}\nonumber\\ \displaystyle & = & \displaystyle \mathfrak{m}^{\overline{q}-T}(\mathfrak{m}^{T}M)_{m}=(\mathfrak{m}^{\overline{q}}M)_{m}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\mathfrak{m}^{\overline{q}+1}P\cap M+\mathfrak{m}^{\overline{q}}M\right)_{m} & = & \displaystyle (\mathfrak{m}^{\overline{q}-T}(\mathfrak{m}^{T+1}P\cap M+\mathfrak{m}^{T}M))_{m}\nonumber\\ \displaystyle & = & \displaystyle \mathfrak{m}^{\overline{q}-T}\left(\mathfrak{m}^{T+1}P\cap M+\mathfrak{m}^{T}M\right)_{m}\nonumber\\ \displaystyle & = & \displaystyle \mathfrak{m}^{\overline{q}-T}(\mathfrak{m}^{T}M)_{m}=(\mathfrak{m}^{\overline{q}}M)_{m}.\nonumber\end{eqnarray}$$
In the above string, the first equality holds because of the inequality
![]() $\overline{q}\geqslant T=T(e)$
and the definition of
$\overline{q}\geqslant T=T(e)$
and the definition of
![]() $T(e)$
, the second and fourth because
$T(e)$
, the second and fourth because
![]() $\mathfrak{m}\subseteq S_{0}$
, the third because of (3.2).
$\mathfrak{m}\subseteq S_{0}$
, the third because of (3.2).
Therefore,
![]() $\unicode[STIX]{x1D707}_{m}^{e,\overline{q}}=0$
. But this is a contradiction, so the proof of the theorem is finished.◻
$\unicode[STIX]{x1D707}_{m}^{e,\overline{q}}=0$
. But this is a contradiction, so the proof of the theorem is finished.◻
From Theorem 3.4, it is easy to deduce the
Proof of Theorem 1.2.
Let
![]() $Q$
be a standard graded polynomial ring over
$Q$
be a standard graded polynomial ring over
![]() $R$
which surjects onto
$R$
which surjects onto
![]() $S$
, then by scalar restriction,
$S$
, then by scalar restriction,
![]() $C$
is a finitely generated graded
$C$
is a finitely generated graded
![]() $Q$
-module. The conclusion follows by applying Theorem 3.4.◻
$Q$
-module. The conclusion follows by applying Theorem 3.4.◻
Now we present the proof of Theorem 1.1. Recall that
![]() $\text{Rees}\,(I)=R\oplus I\oplus I^{2}\oplus \cdots \,$
denotes the Rees algebra of
$\text{Rees}\,(I)=R\oplus I\oplus I^{2}\oplus \cdots \,$
denotes the Rees algebra of
![]() $I$
, whose grading is given by
$I$
, whose grading is given by
![]() $\deg I^{n}=n$
. Since
$\deg I^{n}=n$
. Since
![]() $R$
is Noetherian,
$R$
is Noetherian,
![]() $\text{Rees}\,(I)$
is a standard graded
$\text{Rees}\,(I)$
is a standard graded
![]() $R$
-algebra.
$R$
-algebra.
Proof of Theorem 1.1.
Clearly
![]() $\bigoplus _{n\geqslant 0}I^{n}M$
and
$\bigoplus _{n\geqslant 0}I^{n}M$
and
![]() $\bigoplus _{n\geqslant 0}I^{n}M/I^{n+1}M$
are finitely generated graded modules over
$\bigoplus _{n\geqslant 0}I^{n}M/I^{n+1}M$
are finitely generated graded modules over
![]() $\text{Rees}\,(I)$
. By Theorem 1.2, we see that each of the sequences
$\text{Rees}\,(I)$
. By Theorem 1.2, we see that each of the sequences
![]() $(\text{ld}_{R}I^{n}M)_{n}$
and
$(\text{ld}_{R}I^{n}M)_{n}$
and
![]() $(\text{ld}_{R}I^{n}M/I^{n+1}M)_{n}$
is eventually constant.
$(\text{ld}_{R}I^{n}M/I^{n+1}M)_{n}$
is eventually constant.
Next, we prove the eventual constancy of the sequence
![]() $(\text{ld}_{R}(M/I^{n}M))_{n}$
. If
$(\text{ld}_{R}(M/I^{n}M))_{n}$
. If
![]() $I^{n}M=0$
then so is
$I^{n}M=0$
then so is
![]() $I^{n+1}M$
, hence below, we assume that
$I^{n+1}M$
, hence below, we assume that
![]() $I^{n}M\neq 0$
for all
$I^{n}M\neq 0$
for all
![]() $n\geqslant 0$
.
$n\geqslant 0$
.
Applying [Reference Avramov2, Corollary A.4] for
![]() $M$
, there exists
$M$
, there exists
![]() $d\geqslant 1$
such that for any
$d\geqslant 1$
such that for any
![]() $P\subseteq \mathfrak{m}^{d}M$
, the map
$P\subseteq \mathfrak{m}^{d}M$
, the map
is zero for all
![]() $i\geqslant 0$
. Applying the same result for
$i\geqslant 0$
. Applying the same result for
![]() $\mathfrak{m}^{d}M$
, there exists
$\mathfrak{m}^{d}M$
, there exists
![]() $e\geqslant 1$
such that for any
$e\geqslant 1$
such that for any
![]() $P\subseteq \mathfrak{m}^{d+e}M$
, the map
$P\subseteq \mathfrak{m}^{d+e}M$
, the map
is zero for all
![]() $i\geqslant 0$
.
$i\geqslant 0$
.
Take
![]() $n\geqslant \max \{N,d+e\}$
. Then the maps
$n\geqslant \max \{N,d+e\}$
. Then the maps
![]() $\text{Tor}_{i}^{R}(k,I^{n}M)\rightarrow \text{Tor}_{i}^{R}(k,I^{d}M)$
and
$\text{Tor}_{i}^{R}(k,I^{n}M)\rightarrow \text{Tor}_{i}^{R}(k,I^{d}M)$
and
![]() $\text{Tor}_{i}^{R}(k,I^{d}M)\rightarrow \text{Tor}_{i}^{R}(k,M)$
are zero for all
$\text{Tor}_{i}^{R}(k,I^{d}M)\rightarrow \text{Tor}_{i}^{R}(k,M)$
are zero for all
![]() $i\geqslant 0$
. Let
$i\geqslant 0$
. Let
![]() $F,G,H$
be the minimal free resolution of
$F,G,H$
be the minimal free resolution of
![]() $I^{n}M,I^{d}M,M$
, respectively. Take any lifting
$I^{n}M,I^{d}M,M$
, respectively. Take any lifting
![]() $\unicode[STIX]{x1D706}:F\rightarrow G$
of the map
$\unicode[STIX]{x1D706}:F\rightarrow G$
of the map
![]() $I^{n}M\rightarrow I^{d}M$
, then
$I^{n}M\rightarrow I^{d}M$
, then
![]() $\unicode[STIX]{x1D706}(F)\subseteq \mathfrak{m}G$
. Similarly, for any lifting
$\unicode[STIX]{x1D706}(F)\subseteq \mathfrak{m}G$
. Similarly, for any lifting
![]() $\unicode[STIX]{x1D713}:G\rightarrow H$
of the map
$\unicode[STIX]{x1D713}:G\rightarrow H$
of the map
![]() $I^{d}M\rightarrow M$
, we have
$I^{d}M\rightarrow M$
, we have
![]() $\unicode[STIX]{x1D713}(G)\subseteq \mathfrak{m}H$
. Therefore, we obtain a lifting
$\unicode[STIX]{x1D713}(G)\subseteq \mathfrak{m}H$
. Therefore, we obtain a lifting
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D706}:F\rightarrow H$
on the level of minimal free resolutions of the map
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D706}:F\rightarrow H$
on the level of minimal free resolutions of the map
![]() $I^{n}M\rightarrow M$
which satisfies
$I^{n}M\rightarrow M$
which satisfies
![]() $\unicode[STIX]{x1D719}(F)\subseteq \mathfrak{m}^{2}G$
.
$\unicode[STIX]{x1D719}(F)\subseteq \mathfrak{m}^{2}G$
.
By Lemma 2.2, we have for any
![]() $n\geqslant \max \{N,d+e\}$
the equality
$n\geqslant \max \{N,d+e\}$
the equality
As explained above, for
![]() $n$
large enough,
$n$
large enough,
![]() $\text{ld}_{R}(I^{n}M)$
is a constant independent of
$\text{ld}_{R}(I^{n}M)$
is a constant independent of
![]() $n$
. Hence the same is true for
$n$
. Hence the same is true for
![]() $\text{ld}_{R}(M/I^{n}M)$
. This concludes the proof.◻
$\text{ld}_{R}(M/I^{n}M)$
. This concludes the proof.◻
Theorem 3.4 has the following consequence on the linearity defect of the integral closure of powers (see [Reference Huneke and Swanson18] for the definition of the integral closure
![]() $\overline{I}$
of an ideal
$\overline{I}$
of an ideal
![]() $I$
).
$I$
).
Corollary 3.5. Let
![]() $(R,\mathfrak{m})$
be a regular local ring, and let
$(R,\mathfrak{m})$
be a regular local ring, and let
![]() $I\subseteq \mathfrak{m}$
be an ideal. Then the sequence
$I\subseteq \mathfrak{m}$
be an ideal. Then the sequence
![]() $(\text{ld}_{R}\overline{I^{n}})_{n}$
is eventually constant.
$(\text{ld}_{R}\overline{I^{n}})_{n}$
is eventually constant.
Proof. Denote
![]() $C=R\oplus \overline{I}\oplus \overline{I^{2}}\oplus \cdots \,,$
then
$C=R\oplus \overline{I}\oplus \overline{I^{2}}\oplus \cdots \,,$
then
![]() $C$
is a graded module over
$C$
is a graded module over
![]() $\text{Rees}\,(I)$
with
$\text{Rees}\,(I)$
with
![]() $\deg \overline{I^{n}}=n$
. By [Reference Huneke and Swanson18, Proposition 5.3.4],
$\deg \overline{I^{n}}=n$
. By [Reference Huneke and Swanson18, Proposition 5.3.4],
![]() $C$
is a finitely generated
$C$
is a finitely generated
![]() $\text{Rees}\,(I)$
-module. An application of Theorem 1.2 yields the desired conclusion.◻
$\text{Rees}\,(I)$
-module. An application of Theorem 1.2 yields the desired conclusion.◻
4 Examples and remarks
The following example illustrates how
![]() $N(C)$
can be computed using Macaulay2 [Reference Grayson and Stillman10].
$N(C)$
can be computed using Macaulay2 [Reference Grayson and Stillman10].
Example 4.1. Let
![]() $R=\mathbb{Q}[x,y,z]$
be a polynomial ring of dimension
$R=\mathbb{Q}[x,y,z]$
be a polynomial ring of dimension
![]() $3$
, and let
$3$
, and let
![]() $I=(x^{2},xy,z^{2})$
. Denote
$I=(x^{2},xy,z^{2})$
. Denote
![]() $S=R[w_{0},w_{1},w_{2}]$
a standard graded polynomial extension of
$S=R[w_{0},w_{1},w_{2}]$
a standard graded polynomial extension of
![]() $R$
which surjects onto the Rees algebra
$R$
which surjects onto the Rees algebra
![]() $E=\text{Rees}\,(I)$
by mapping
$E=\text{Rees}\,(I)$
by mapping
![]() $w_{0}\mapsto x^{2},w_{1}\mapsto xy,w_{2}\mapsto z^{2}$
. The ring
$w_{0}\mapsto x^{2},w_{1}\mapsto xy,w_{2}\mapsto z^{2}$
. The ring
![]() $E$
has the following presentation
$E$
has the following presentation
where
![]() $p_{1}=w_{0}y-w_{1}x$
,
$p_{1}=w_{0}y-w_{1}x$
,
![]() $p_{2}=w_{0}z^{2}-w_{2}x^{2}$
,
$p_{2}=w_{0}z^{2}-w_{2}x^{2}$
,
![]() $p_{3}=w_{1}z^{2}-w_{2}xy$
.
$p_{3}=w_{1}z^{2}-w_{2}xy$
.
The minimal graded free resolution of
![]() $E$
over
$E$
over
![]() $S$
is as follows
$S$
is as follows
 $$\begin{eqnarray}F:0\longrightarrow \begin{array}{@{}c@{}}S(-2)\\ \bigoplus \\ S(-1)\end{array}\xrightarrow[{}]{\left(\begin{array}{@{}cc@{}}w_{2}x & -z^{2}\\ -w_{1} & y\\ w_{0} & -x\end{array}\right)}S(-1)^{3}\xrightarrow[{}]{\left(\begin{array}{@{}ccc@{}}p_{1} & p_{2} & p_{3}\end{array}\right)}S\longrightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}F:0\longrightarrow \begin{array}{@{}c@{}}S(-2)\\ \bigoplus \\ S(-1)\end{array}\xrightarrow[{}]{\left(\begin{array}{@{}cc@{}}w_{2}x & -z^{2}\\ -w_{1} & y\\ w_{0} & -x\end{array}\right)}S(-1)^{3}\xrightarrow[{}]{\left(\begin{array}{@{}ccc@{}}p_{1} & p_{2} & p_{3}\end{array}\right)}S\longrightarrow 0.\end{eqnarray}$$
Using the notation of the proof of Theorem 3.4, we show that
![]() $N=1$
, namely all the powers of
$N=1$
, namely all the powers of
![]() $I$
have the same linearity defect, which turns out to be
$I$
have the same linearity defect, which turns out to be
![]() $1$
. Since
$1$
. Since
![]() $\text{pd}_{S}E=2<\text{gl}\,\text{ld}\,R=3$
,
$\text{pd}_{S}E=2<\text{gl}\,\text{ld}\,R=3$
,
![]() $N=\max \{n(0),n(1),n(2)\}$
. The graded structure of
$N=\max \{n(0),n(1),n(2)\}$
. The graded structure of
![]() $E$
tells us that
$E$
tells us that
![]() $n(0)=\text{pdeg}_{S}(E)=0$
.
$n(0)=\text{pdeg}_{S}(E)=0$
.
Let
![]() $J\subseteq S,M_{2}\subseteq G$
be the first and second syzygies of
$J\subseteq S,M_{2}\subseteq G$
be the first and second syzygies of
![]() $E$
, where
$E$
, where
![]() $G$
denotes the module
$G$
denotes the module
![]() $F_{1}=S(-1)^{3}$
. We claim that
$F_{1}=S(-1)^{3}$
. We claim that
![]() $T(1)=2$
and
$T(1)=2$
and
![]() $T(2)=1$
, namely,
$T(2)=1$
, namely,
For (4.1): one sees immediately that both sides are equal to
![]() $\mathfrak{m}^{q-1}(w_{0}y-w_{1}x)S+\mathfrak{m}^{q-2}(w_{0}z^{2}-w_{2}x^{2},w_{1}z^{2}-w_{2}xy)S$
.
$\mathfrak{m}^{q-1}(w_{0}y-w_{1}x)S+\mathfrak{m}^{q-2}(w_{0}z^{2}-w_{2}x^{2},w_{1}z^{2}-w_{2}xy)S$
.
For (4.2): we have
![]() $M_{2}=(w_{2}xe_{1}-w_{1}e_{2}+w_{0}e_{3},-z^{2}e_{1}+ye_{2}-xe_{3})$
, where
$M_{2}=(w_{2}xe_{1}-w_{1}e_{2}+w_{0}e_{3},-z^{2}e_{1}+ye_{2}-xe_{3})$
, where
![]() $e_{1},e_{2},e_{3}$
is the standard basis of
$e_{1},e_{2},e_{3}$
is the standard basis of
![]() $G$
sitting in degree
$G$
sitting in degree
![]() $1$
. It is not hard to check that both sides of (4.2) are equal to
$1$
. It is not hard to check that both sides of (4.2) are equal to
The above arguments yield
![]() $n(1)=\max \{c(1,1),c(1,2)\}$
and
$n(1)=\max \{c(1,1),c(1,2)\}$
and
![]() $n(2)=c(2,1)$
. We prove that
$n(2)=c(2,1)$
. We prove that
![]() $n(1)=1$
and
$n(1)=1$
and
![]() $n(2)=-\infty$
.
$n(2)=-\infty$
.
For each
![]() $q\geqslant 1$
,
$q\geqslant 1$
,
![]() $\text{Tor}_{1}^{S}(S/\mathfrak{m}^{q}S,E)=\text{Tor}_{1}^{S}(S/\mathfrak{m}^{q}S,S/J)=(J\cap \mathfrak{m}^{q}S)/$
$\text{Tor}_{1}^{S}(S/\mathfrak{m}^{q}S,E)=\text{Tor}_{1}^{S}(S/\mathfrak{m}^{q}S,S/J)=(J\cap \mathfrak{m}^{q}S)/$
![]() $(J\mathfrak{m}^{q}S)$
. Therefore, the image of
$(J\mathfrak{m}^{q}S)$
. Therefore, the image of
![]() $\text{Tor}_{1}^{S}(S/\mathfrak{m}^{q+1}S,E)\rightarrow \text{Tor}_{1}^{S}(S/\mathfrak{m}^{q}S,E)$
is
$\text{Tor}_{1}^{S}(S/\mathfrak{m}^{q+1}S,E)\rightarrow \text{Tor}_{1}^{S}(S/\mathfrak{m}^{q}S,E)$
is
![]() $\text{Im}\,\unicode[STIX]{x1D707}^{1,q}=(J\cap \mathfrak{m}^{q+1}S+J\mathfrak{m}^{q}S)/(J\mathfrak{m}^{q}S)$
. Computations show that
$\text{Im}\,\unicode[STIX]{x1D707}^{1,q}=(J\cap \mathfrak{m}^{q+1}S+J\mathfrak{m}^{q}S)/(J\mathfrak{m}^{q}S)$
. Computations show that
where
![]() $e_{1}^{1},e_{2}^{1}$
is a basis for
$e_{1}^{1},e_{2}^{1}$
is a basis for
![]() $S^{2}$
, both of degree
$S^{2}$
, both of degree
![]() $1$
, and
$1$
, and
where
![]() $e_{1}^{2},\ldots ,e_{5}^{2}$
are a basis for
$e_{1}^{2},\ldots ,e_{5}^{2}$
are a basis for
![]() $S^{5}$
, all of them of degree
$S^{5}$
, all of them of degree
![]() $1$
. Thanks to routine Gröbner basis arguments, the residue classes
$1$
. Thanks to routine Gröbner basis arguments, the residue classes
![]() $\overline{w_{0}^{i}e_{2}^{1}}\in \text{Im}\,\unicode[STIX]{x1D707}^{1,1}$
and
$\overline{w_{0}^{i}e_{2}^{1}}\in \text{Im}\,\unicode[STIX]{x1D707}^{1,1}$
and
![]() $\overline{w_{0}^{i}e_{2}^{2}}\in \text{Im}\,\unicode[STIX]{x1D707}^{1,2}$
are always nonzero for every
$\overline{w_{0}^{i}e_{2}^{2}}\in \text{Im}\,\unicode[STIX]{x1D707}^{1,2}$
are always nonzero for every
![]() $i\geqslant 0$
. Hence
$i\geqslant 0$
. Hence
![]() $c(1,1)=c(1,2)=1$
, and thus
$c(1,1)=c(1,2)=1$
, and thus
![]() $n(1)=1$
.
$n(1)=1$
.
Denote by
![]() $f_{1},f_{2}$
the standard basis of
$f_{1},f_{2}$
the standard basis of
![]() $F_{2}$
where
$F_{2}$
where
![]() $\deg f_{1}=2,\deg f_{2}=1$
. Since
$\deg f_{1}=2,\deg f_{2}=1$
. Since
![]() $\text{Tor}_{2}^{S}(S/\mathfrak{m}^{2}S,E)=H_{2}(F\otimes _{S}S/\mathfrak{m}^{2}S)$
, computations show that
$\text{Tor}_{2}^{S}(S/\mathfrak{m}^{2}S,E)=H_{2}(F\otimes _{S}S/\mathfrak{m}^{2}S)$
, computations show that
(i)
 $\text{Tor}_{2}^{S}(S/\mathfrak{m}^{2}S,E)$
is generated by
$\text{Tor}_{2}^{S}(S/\mathfrak{m}^{2}S,E)$
is generated by
 $\overline{xf_{2}},\overline{yf_{2}},\overline{zf_{2}}\in F_{2}\otimes (S/\mathfrak{m}^{2}S)$
;
$\overline{xf_{2}},\overline{yf_{2}},\overline{zf_{2}}\in F_{2}\otimes (S/\mathfrak{m}^{2}S)$
;(ii)
 $\text{Tor}_{2}^{S}(S/\mathfrak{m}S,E)$
is generated by
$\text{Tor}_{2}^{S}(S/\mathfrak{m}S,E)$
is generated by
 $\overline{f_{2}}\in F_{2}\otimes (S/\mathfrak{m}S)$
.
$\overline{f_{2}}\in F_{2}\otimes (S/\mathfrak{m}S)$
.
As
![]() $\text{Tor}_{2}^{S}(S/\mathfrak{m}S,E)$
is killed by
$\text{Tor}_{2}^{S}(S/\mathfrak{m}S,E)$
is killed by
![]() $\mathfrak{m}S$
, the map
$\mathfrak{m}S$
, the map
![]() $\text{Tor}_{2}^{S}(S/\mathfrak{m}^{2}S,E)\rightarrow \text{Tor}_{2}^{S}(S/\mathfrak{m}S,E)$
is zero; this yields
$\text{Tor}_{2}^{S}(S/\mathfrak{m}^{2}S,E)\rightarrow \text{Tor}_{2}^{S}(S/\mathfrak{m}S,E)$
is zero; this yields
![]() $n(2)=c(2,1)=-\infty$
.
$n(2)=c(2,1)=-\infty$
.
Putting everything together,
![]() $N=\max \{n(0),n(1),n(2)\}=\max \!\{\!0,1,$
$N=\max \{n(0),n(1),n(2)\}=\max \!\{\!0,1,$
![]() $-\infty \!\}=1$
.
$-\infty \!\}=1$
.
Recall that the saturation of
![]() $I$
is
$I$
is
![]() $\widetilde{I}=\{x\in R:x\mathfrak{m}^{d}\subseteq I\text{ for some }d\geqslant 1\}$
. The next example shows that the (graded) analog of Corollary 3.5 for saturation of powers does not hold.
$\widetilde{I}=\{x\in R:x\mathfrak{m}^{d}\subseteq I\text{ for some }d\geqslant 1\}$
. The next example shows that the (graded) analog of Corollary 3.5 for saturation of powers does not hold.
Example 4.2. Consider the ideal
![]() $I=(x(y^{3}-z^{3}),y(x^{3}-z^{3}),z(x^{3}-y^{3}))\subseteq R=\mathbb{C}[x,y,z]$
. The ideal
$I=(x(y^{3}-z^{3}),y(x^{3}-z^{3}),z(x^{3}-y^{3}))\subseteq R=\mathbb{C}[x,y,z]$
. The ideal
![]() $I$
defines a reduced set of
$I$
defines a reduced set of
![]() $12$
points in
$12$
points in
![]() $\mathbb{P}^{2}$
, the so-called Fermat configuration (see the proof of [Reference Harbourne and Seceleanu11, Proposition 2.1]). We show that the saturation ideals
$\mathbb{P}^{2}$
, the so-called Fermat configuration (see the proof of [Reference Harbourne and Seceleanu11, Proposition 2.1]). We show that the saturation ideals
![]() $\widetilde{I^{s}}$
do not have eventually constant linearity defect.
$\widetilde{I^{s}}$
do not have eventually constant linearity defect.
For
![]() $s\geqslant 1$
, denote by
$s\geqslant 1$
, denote by
![]() $I^{(s)}=R\cap \bigcap _{P\in \text{Ass}\,(I)}I^{s}R_{P}$
the
$I^{(s)}=R\cap \bigcap _{P\in \text{Ass}\,(I)}I^{s}R_{P}$
the
![]() $s$
th symbolic power of
$s$
th symbolic power of
![]() $I$
. Since
$I$
. Since
![]() $I$
is the defining ideal of a reduced set of points, we get that
$I$
is the defining ideal of a reduced set of points, we get that
![]() $\widetilde{I^{s}}=I^{(s)}$
. From [Reference Harbourne and Seceleanu11, Proposition 1.1], we deduce that
$\widetilde{I^{s}}=I^{(s)}$
. From [Reference Harbourne and Seceleanu11, Proposition 1.1], we deduce that
![]() $\widetilde{I^{3s}}=(\widetilde{I^{3}})^{s}$
. By [Reference Herzog, Hibi and Ohsugi14, Theorem 2.4],
$\widetilde{I^{3s}}=(\widetilde{I^{3}})^{s}$
. By [Reference Herzog, Hibi and Ohsugi14, Theorem 2.4],
![]() $\text{ld}_{R}\widetilde{I^{3s}}=0$
for all
$\text{ld}_{R}\widetilde{I^{3s}}=0$
for all
![]() $s\geqslant 1$
. Indeed, computations with Macaulay2 [Reference Grayson and Stillman10] show that
$s\geqslant 1$
. Indeed, computations with Macaulay2 [Reference Grayson and Stillman10] show that
![]() $x,y+z,z$
is a
$x,y+z,z$
is a
![]() $d$
-sequence with respect to
$d$
-sequence with respect to
![]() $\text{Rees}\,(\widetilde{I^{3}})$
.
$\text{Rees}\,(\widetilde{I^{3}})$
.
Now we show that
![]() $\text{ld}_{R}\widetilde{I^{3s+1}}=1$
for all
$\text{ld}_{R}\widetilde{I^{3s+1}}=1$
for all
![]() $s\geqslant 1$
. First, since
$s\geqslant 1$
. First, since
![]() $\text{depth}\,R/\widetilde{I^{3s+1}}\geqslant 1$
, by [Reference Conca, Iyengar, Nguyen and Römer6, Proposition 6.3],
$\text{depth}\,R/\widetilde{I^{3s+1}}\geqslant 1$
, by [Reference Conca, Iyengar, Nguyen and Römer6, Proposition 6.3],
![]() $\text{ld}_{R}R/\widetilde{I^{3s+1}}\leqslant \dim R-1=2$
. Hence
$\text{ld}_{R}R/\widetilde{I^{3s+1}}\leqslant \dim R-1=2$
. Hence
![]() $\text{ld}_{R}\widetilde{I^{3s+1}}\leqslant 1$
.
$\text{ld}_{R}\widetilde{I^{3s+1}}\leqslant 1$
.
Let
![]() $H=(x^{3}-y^{3})(y^{3}-z^{3})(z^{3}-x^{3})$
. We show that the minimal nonzero component of
$H=(x^{3}-y^{3})(y^{3}-z^{3})(z^{3}-x^{3})$
. We show that the minimal nonzero component of
![]() $\widetilde{I^{3s+1}}=I^{(3s+1)}$
is of degree
$\widetilde{I^{3s+1}}=I^{(3s+1)}$
is of degree
![]() $9s+4$
and
$9s+4$
and
If this is the case, then
![]() $\widetilde{I^{3s+1}}_{\left\langle 9s+4\right\rangle }$
has linearity defect at least 1, as
$\widetilde{I^{3s+1}}_{\left\langle 9s+4\right\rangle }$
has linearity defect at least 1, as
![]() $I$
does. (For the inequality
$I$
does. (For the inequality
![]() $\text{ld}_{R}I\geqslant 1$
, use Römer’s theorem [Reference Römer22, Theorem 3.2.8] and the fact that
$\text{ld}_{R}I\geqslant 1$
, use Römer’s theorem [Reference Römer22, Theorem 3.2.8] and the fact that
![]() $I$
is generated in degree
$I$
is generated in degree
![]() $4$
but does not have
$4$
but does not have
![]() $4$
-linear resolution.) Hence
$4$
-linear resolution.) Hence
![]() $\text{ld}_{R}\widetilde{I^{3s+1}}\geqslant 1$
for every
$\text{ld}_{R}\widetilde{I^{3s+1}}\geqslant 1$
for every
![]() $s\geqslant 1$
. All in all, we obtain
$s\geqslant 1$
. All in all, we obtain
![]() $\text{ld}_{R}\widetilde{I^{3s+1}}=1$
for every
$\text{ld}_{R}\widetilde{I^{3s+1}}=1$
for every
![]() $s\geqslant 1$
.
$s\geqslant 1$
.
Now for our purpose, it suffices to prove the following claim:
holds for all
![]() $d\leqslant 9s+4$
. We are grateful to Alexandra Seceleanu for providing us the following nice argument.
$d\leqslant 9s+4$
. We are grateful to Alexandra Seceleanu for providing us the following nice argument.
We proceed by induction on
![]() $s$
; the starting case
$s$
; the starting case
![]() $s$
= 0 is trivial. Assume that
$s$
= 0 is trivial. Assume that
![]() $s>0$
.
$s>0$
.
Let
![]() $G$
be a homogeneous element of
$G$
be a homogeneous element of
![]() $I^{(3s+1)}$
of degree
$I^{(3s+1)}$
of degree
![]() $d$
. Here the geometry of the Fermat configuration comes into play. We have a decomposition
$d$
. Here the geometry of the Fermat configuration comes into play. We have a decomposition
![]() $H=\prod _{i=1}^{9}h_{i}$
, where each
$H=\prod _{i=1}^{9}h_{i}$
, where each
![]() $h_{i}$
is a linear form and no two of them are proportional. According to [Reference Harbourne and Seceleanu11, Section 1.1], for each
$h_{i}$
is a linear form and no two of them are proportional. According to [Reference Harbourne and Seceleanu11, Section 1.1], for each
![]() $i$
,
$i$
,
![]() $h_{i}$
passes through exactly
$h_{i}$
passes through exactly
![]() $4$
points (among the
$4$
points (among the
![]() $12$
points of the configuration). Moreover, each point of the configuration lies on
$12$
points of the configuration). Moreover, each point of the configuration lies on
![]() $3$
of the
$3$
of the
![]() $9$
lines defined by the
$9$
lines defined by the
![]() $h_{i}$
s.
$h_{i}$
s.
Now as
![]() $G$
lies in
$G$
lies in
![]() $I^{(3s+1)}$
,
$I^{(3s+1)}$
,
![]() $G$
passes through each point of the configuration with multiplicity at least
$G$
passes through each point of the configuration with multiplicity at least
![]() $3s+1$
. Thus the curves
$3s+1$
. Thus the curves
![]() $(G)$
and
$(G)$
and
![]() $(h_{i})$
intersect with multiplicity at least
$(h_{i})$
intersect with multiplicity at least
![]() $4(3s+1)$
, which is strictly larger than
$4(3s+1)$
, which is strictly larger than
![]() $d=(\deg G)\cdot (\deg h_{i})$
. From that, Bezout’s theorem forces
$d=(\deg G)\cdot (\deg h_{i})$
. From that, Bezout’s theorem forces
![]() $G$
to be divisible by
$G$
to be divisible by
![]() $h_{i}$
for all
$h_{i}$
for all
![]() $1\leqslant i\leqslant 9$
. In particular,
$1\leqslant i\leqslant 9$
. In particular,
![]() $G$
is divisible by
$G$
is divisible by
![]() $H$
. Writing
$H$
. Writing
![]() $G=HG^{\prime }$
, then as
$G=HG^{\prime }$
, then as
![]() $H$
vanishes exactly
$H$
vanishes exactly
![]() $3$
times at each of the points, we must have
$3$
times at each of the points, we must have
![]() $G^{\prime }\in I_{\left\langle d-9\right\rangle }^{(3s+1-3)}=I_{\left\langle d-9\right\rangle }^{(3(s-1)+1)}$
. Finally, the induction hypothesis gives us the claim.
$G^{\prime }\in I_{\left\langle d-9\right\rangle }^{(3s+1-3)}=I_{\left\langle d-9\right\rangle }^{(3(s-1)+1)}$
. Finally, the induction hypothesis gives us the claim.
So we conclude that the sequence
![]() $\text{ld}_{R}\widetilde{I^{s}}$
is not eventually constant when
$\text{ld}_{R}\widetilde{I^{s}}$
is not eventually constant when
![]() $s$
goes to infinity.
$s$
goes to infinity.
Remark 4.3. More generally than Theorem 1.2, one can prove the following: if
![]() $S$
is a Noetherian
$S$
is a Noetherian
![]() $R$
-algebra which is generated by elements of positive degrees, and
$R$
-algebra which is generated by elements of positive degrees, and
![]() $C$
is a finitely generated graded
$C$
is a finitely generated graded
![]() $S$
-module, then the sequence
$S$
-module, then the sequence
![]() $(\text{ld}_{R}C_{n})_{n}$
is quasiperiodic, namely there exist a number
$(\text{ld}_{R}C_{n})_{n}$
is quasiperiodic, namely there exist a number
![]() $p\geqslant 1$
and integral constants
$p\geqslant 1$
and integral constants
![]() $\ell _{0},\ldots ,\ell _{p-1}$
such that for all
$\ell _{0},\ldots ,\ell _{p-1}$
such that for all
![]() $n\gg 0$
, we have
$n\gg 0$
, we have
![]() $\text{ld}_{R}\widetilde{C_{n}}=\ell _{i}$
if
$\text{ld}_{R}\widetilde{C_{n}}=\ell _{i}$
if
![]() $n$
is congruent to
$n$
is congruent to
![]() $i\in \{0,\ldots ,p-1\}$
modulo
$i\in \{0,\ldots ,p-1\}$
modulo
![]() $p$
.
$p$
.
The proof uses the fact that any high enough Veronese subring of
![]() $S$
is standard graded (after normalizing the grading), and Theorem 1.2. We leave the details to the interested reader (see an analogous statement in [Reference Cutkosky, Herzog and Trung7, Theorem 4.3]).
$S$
is standard graded (after normalizing the grading), and Theorem 1.2. We leave the details to the interested reader (see an analogous statement in [Reference Cutkosky, Herzog and Trung7, Theorem 4.3]).
By [Reference Nagel and Seceleanu20, Theorem 4.3], for the ideal
![]() $I$
in Example 4.2, the graded
$I$
in Example 4.2, the graded
![]() $R$
-algebra
$R$
-algebra
![]() $R\oplus \widetilde{I}\oplus \widetilde{I^{2}}\oplus \cdots \,$
is finitely generated. This fact and the above general version of Theorem 1.2 guarantee the quasiperiodic behavior of the sequence
$R\oplus \widetilde{I}\oplus \widetilde{I^{2}}\oplus \cdots \,$
is finitely generated. This fact and the above general version of Theorem 1.2 guarantee the quasiperiodic behavior of the sequence
![]() $(\text{ld}_{R}\widetilde{I^{n}})_{n}$
in the example.
$(\text{ld}_{R}\widetilde{I^{n}})_{n}$
in the example.
We do not know any example where the sequence
![]() $(\text{ld}_{R}\widetilde{I^{n}})_{n}$
is not quasiperiodic. In view of [Reference Cutkosky, Herzog and Trung7, Example 4.4] on bad behavior of regularity for saturations of powers, it is desirable to seek for one.
$(\text{ld}_{R}\widetilde{I^{n}})_{n}$
is not quasiperiodic. In view of [Reference Cutkosky, Herzog and Trung7, Example 4.4] on bad behavior of regularity for saturations of powers, it is desirable to seek for one.
Remark 4.4. The theory in Section 2 (the linear part, linearity defect) works also for standard graded algebras and finitely generated graded modules over them. Furthermore, there are obvious analogues of our results in that setting.
Acknowledgments
The content of this paper has been worked out when Hop D. Nguyen was visiting the Department of Mathematics, University of Nebraska-Lincoln (UNL) in March 2015. The authors are grateful to Luchezar Avramov, Dale Cutkosky, Hailong Dao, Thomas Marley and Alexandra Seceleanu for inspiring comments and useful suggestions. Hop D. Nguyen would like to thank the colleagues at Department of Mathematics of the UNL, among them Luchezar Avramov, Roger and Sylvia Wiegand for their hospitality and warm support. Finally, both authors are grateful to the anonymous referee for her/his careful reading of the manuscript and many thoughtful comments which greatly improve the presentation.