Materials for energy harvesting: At the forefront of a new wave

Abstract

The rapid increase and dependency on mobile electronic devices and burgeoning importance of sensor network systems and Internet of Things (IoT) to sustain an aging society indicates the strong need to develop battery-less and mobile power sources. Materials for energy harvesting from environmental sources, including mechanical vibrations, magnetic field, heat, and light have become highly relevant for implementation of the IoT vision that requires self-powered wireless sensor networks for sustainable deployment. The articles in this issue cover piezoelectric materials, magnetoelectrics, and thermoelectrics and provide a summary of state-of-the-art energy-harvesting approaches, various material design strategies being targeted by the community, and fundamental challenges in finding an optimum solution and future roadmap. Flexibility of energy harvesters is also emphasized, given the huge potential for wearables. Photovoltaics are briefly covered with respect to wearables and textiles.

Introduction

Society in the future will require materials and methodologies for energy harvesting to enable smart systems and embedded automation. As the Internet of Things (IoT) becomes a reality, there will be a need for trillions of sensors¹ to enable artificial intelligence (AI) applications, for example, to automate caretaking for aging populations. There is also a need to effectively power increasingly ubiquitous mobile personal devices that are already an integral part of everyday life. Changing batteries for a trillion sensors is not feasible; even recharging batteries of everyday mobile devices is quite a challenge currently.

It is thus vital to develop energy-harvesting materials and technologies that can dynamically harvest energy from the surroundings to generate electrical power for sensors and devices. Energy harvesting can target a variety of environmental resources (e.g., the utilization of mechanical vibrations and motion, magnetic field, and heat). Figure 1 shows examples of energy-harvesting devices demonstrated in the literature.² The performance of energy-harvesting devices capturing such broadband low-amplitude energy from the environment is critically dependent upon the figure of merit of the material. Further increases in the efficiency of these devices will be realized by improving material performance, which in many cases remains magnitudes behind the desired values. In this issue of the MRS Bulletin, we feature six articles describing the progress and challenges at the forefront of developing cutting-edge energy-harvesting devices, as illustrated in Figure 2.³ Given the increasing relevance of wearables in our lives, some of the articles also focus on the flexibility of energy harvesters compatible with textiles, wearables, and the human body.

Figure 1. (a) Piezoelectric spiral energy harvester and (b) perovskite flexible solar module.² (c) Thermoelectric wearable module.

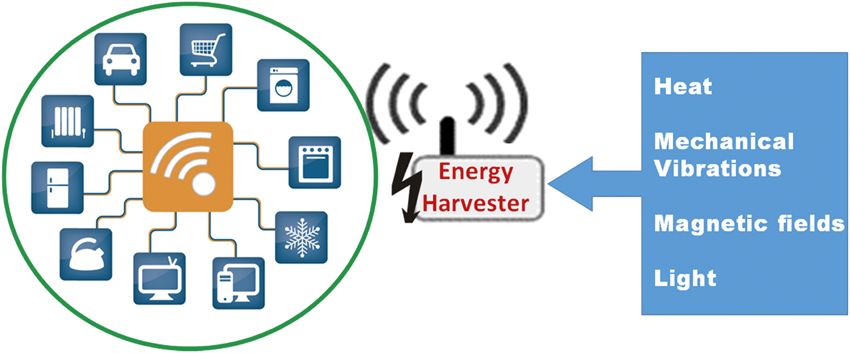
Figure 2. Vision for energy harvesters for powering a variety of wireless sensors and devices.³

Energy harvesting from heat

It is well known that out of the primary energy that we consume, only one-third is effectively used, and the majority of energy is lost as waste heat (Figure 3).⁴ In the 20th century, humankind learned to achieve unprecedented control over charge carriers (electrons), spins, and photons, however, advanced control over phonons and thermal energy is still not satisfactory and remains one of the important scientific challenges for the 21st century. The majority of waste heat is estimated to have temperatures below 150°C,⁵ and thermoelectrics, which can compactly convert heat to electricity through solid-state devices using the Seebeck effect without scaling, are quite promising. The Seebeck effect is the phenomenon where electrical voltage is generated by the diffusion of charge carriers when a temperature difference is applied to a material (Figure 3). With wearable thermoelectrics, generating electricity by utilizing human body heat is another attractive application.

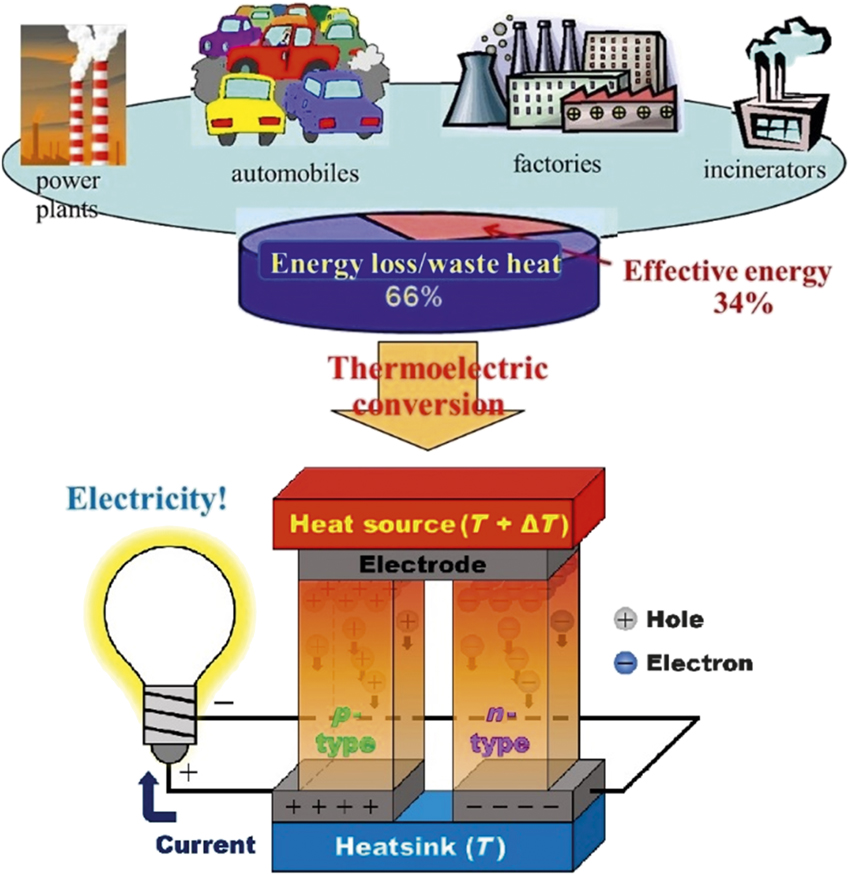
Figure 3. Waste heat and thermoelectric power generation, where carrier diffusion to the lower temperature side generates electricity. Note: T, temperature.

One difficulty in achieving high conversion efficiency in thermoelectric materials is that the figure of merit ZT = (S ²σT)/κ comprises of competing requirements in physical properties, namely, optimally designing a material with a large Seebeck coefficient (S), as an insulator, but with high electrical conductivity (σ), like a metal, yet simultaneously with low thermal conductivity (κ); T is temperature.^6,7 Therefore, to achieve high thermoelectric performance, it is necessary to find property enhancement principles and materials that can overcome these traditional paradoxes.^8–10 The articles by Liu et al.,¹¹ Gooth et al.,¹² and Tian et al.¹³ lay out different important directions and materials research strategies that may enable the first widespread applications of thermoelectric power generation.

To overcome the paradox of conducting electricity while blocking heat transport as much as possible, selective scattering of phonons has been shown to be an effective strategy to achieve high ZT.^14–16 The thermal conductivity is composed of heat transport by the electrical carriers, κ_el, and that carried by the lattice, κ_lat, where κ = κ_el + κ_lat. According to the Wiedemann–Franz Law,¹⁷ κ_el is proportional to the electrical conductivity: κ_el∝σ. Since high σ is desirable, it is necessary to find ways to lower κ_lat without overly harming the electrical conductivity. This can be strategically carried out by utilizing the fact that for the range of materials suitable for thermoelectrics, the phonon mean free path (MFP) is typically longer than the carrier MFP. If materials can be modified such that phonons are selectively scattered, this can enhance the ZT.

The Liu et al. article in this issue addresses phonon engineering through nano-microstructural control.¹¹ In general, phonons have a wide range of MFPs in solids. Therefore, designing multiscale nano-microstructures, ranging from point defects to volume defects, which have different phonon scattering behaviors, can be effective at reducing κ_lat. The article lays out this strategy, detailing the formation of various nano-microstructures and their phonon scattering mechanisms.¹¹ Point defects have a frequency (ω) dependence of the scattering rate (the inverse of the phonon relaxation time), of τ_PD^–1∝ω⁴, meaning they are particularly effective in scattering high-frequency phonons. They also show that line defects have relaxation time dependencies of τ_DS^–1∝ω¹ and τ_DC^–1∝ω³ for dislocation strain fields and dislocation cores, respectively, and therefore scatter mid-frequency phonons well. Two-dimensional defects, such as grain boundaries, are typically frequency independent with τ_GB^–1∝ω⁰ and scatter low-frequency phonons. Volume defects can have τ_NP^–1 ∼ ω⁰ + ω⁴, and therefore can scatter phonons over a wide range.¹¹ Strategic nano-microstructural control can thus lead to large enhancement of ZT. Looking toward the future, improved calculation and simulation methods are necessary for the rational design of even more effective nano-microstructures, and the authors discuss necessary conditions for developing such tools.¹¹

While such nano-microstructuring with phonon selective scattering has led to significant enhancements in ZT for a wide range of materials, finding new broadly applicable principles to enhance the power factor, S ²σ, the denominator of ZT, has been more elusive. Various principles such as utilizing resonance levels,¹⁸ band convergence,¹⁹ modulation doping,²⁰ and magnetism²¹ have been proposed. The Gooth et al. article in this issue discusses the potential of so-called quantum materials that may overcome the traditional bounds of conventional materials.¹² Dresselhaus et al.²² first predicted quantum-sized effects in semiconductor nanostructures, such as quantum-well structures, superlattices, nanowires, and quantum dots, as a potential way to significantly enhance the power factor through modification of the band structure. Gooth et al. analyzed the case of Bi₂Te₃ nanowires and pointed out that a two-channel model considering both surface and bulk states can explain the lack of large power factor enhancement experimentally found to date.¹² As interesting quantum systems with particular surface states, topological insulators (TIs)²³ have embodied many high-performance thermoelectric systems such as Bi₂Te₃, Bi₂Se₃, Sb₂Te₃, Sn-doped PbTe, and PbSe. TIs possess a bulk bandgap and highly conductive gapless surface states that are protected by time-reversal symmetry and therefore do not backscatter, and they possess high mobility charge carriers. Nanograin materials with different grain-size distributions were pointed out as a way to tune the contribution of the topological states and thereby tune the thermoelectric properties.¹²

Gooth et al. also review Dirac and Weyl semimetals, such as TaAs, NbP, or CdAs, which are three-dimensional topological materials possessing exotic states. Application of a magnetic field parallel to the electrical current breaks the chirality of these states at the quantum level, leading to an additional topological current and enhancement of S and σ. They posit that the utilization of the exotic states in these quantum materials, which are just being explored in the context of thermoelectrics, may help overcome the classical limits.¹²

A large challenge for thermoelectrics has been achieving widespread power-generation applications. The article by Tian et al. presents perspectives on applications of flexible materials such as organic and hybrid materials to enable wearable thermoelectric applications.¹³ While not as extensively investigated compared to their inorganic counterparts, organic thermoelectric materials were developed from a relatively early time by, for example, Toshima.²⁴ In 2011, Crispin et al. achieved a large enhancement in performance through carrier tuning of PEDOT:Tos (poly(3,4-ethylenedioxythiophene):tosylate anion),²⁵ and this created intense interest in these materials. Organic materials have an advantage over inorganic materials in the general low cost of materials and scalable processing, as well as their lightweight and flexible nature, which enables wearable applications. Their relatively low temperature stability is also not as critical an issue when dealing with wearable or moderate temperature applications below 150°C, where the majority of unutilized (waste) thermal energy exists. However, the general long-range structural disorder in organic materials largely hinders electrical conduction, typically outweighing the benefit gained from their low thermal conductivity.¹³ Therefore, it is necessary to realize a significant improvement in their thermoelectric figure of merit to make them suitable for applicable devices. Tian et al. overview and discuss recent advancements in thermoelectric performance made in organic materials and hybrid materials, where researchers attempt to utilize the respective advantages of organic and inorganic materials.¹³ Namely, the flexibility and low thermal conductivity of organic materials and the good electrical properties, that is, high power factor, of inorganic materials. This may also be a solution to the difficulty in finding n-type organic thermoelectric materials with good thermoelectric performance. Tian et al. review inorganic–organic hybrid composites that have reportedly exhibited high power factor, such as ∼900 μW/mK² for a TiS₂/organic superlattice material.¹³ The overall design and advanced synthesis techniques of organic and hybrid materials are reviewed in this article, and optimization strategies to achieve high ZT are laid out, together with examples of industrial module design and fabrication.¹³

Energy harvesting from mechanical vibrations and magnetic fields

Both piezoelectric and magnetoelectric (ME) energy harvesting have recently gained momentum due to the simplicity of their implementation in converting mechanical vibrations and magnetic fields into electricity, respectively. In a magnetoelectric composite, piezoelectric and magnetostrictive materials are coupled together through elastic strain to convert an electric field into a magnetic field or vice-versa. The direct ME (DME) and converse ME (CME) effects in the laminate composites consisting of a piezoelectric layer and a magnetostrictive layer.²⁶

The DME effect involves the conversion of an applied magnetic field to an electric field. The magnetic field (H) applied onto the magnetic layer is converted into mechanical stress (X), which is then applied onto the piezoelectric layer that converts it into electric field (E). The CME effect converts an electric field into a magnetic field. The electric field applied to the piezoelectric layer is converted into mechanical strain, which is then applied to the piezomagnetic layer that converts it into a magnetic field. In the off-resonance condition, the ME coefficient (α_E) in the composites is given as:²⁷

(1)$${\alpha _{E,31}} = {{d{E_3}} \over {d{H_1}}} = {{n{q_{11}}g_{31}^ * } \over {nS_{11}^E\left {1 - k_{31}^2} \right + \left {1 - n} \rightS_{11}^H}}, $$

(2)$$where\,g_{31}^ * = {g_{31}}{1 \over {\left( {\tan{{\delta ^\prime}} = \tan{{\theta ^\prime}} + {{C - {C_f}} \over {{C_f}}}} \right)}},$$

where H ₁ is the longitudinally applied magnetic field along 1-axis (Cartesian coordinate system with axes 1-2-3), E ₃ is the generated electric field perpendicular to the direction of H ₁ (along the 3-axis), n is the volume fraction of the magnetostrictive layer (n = V _magnetic/(V _{piezoelectric} + V _magnetic)); V _{piezoelectric} is the volume of the piezoelectric layer and V _magnetic is the volume of the magnetostrictive layer, q ₁₁ is the piezomagnetic coefficient, g ₃₁ is the piezoelectric voltage coefficient, k ₃₁ is the electromechanical coupling coefficient, piezoelectric loss is shown as tanθ′, dielectric loss is shown as tanδ′, C is the capacitance at a given frequency, C _f is the capacitance at 1 kHz, and $s_{11}^{\rm{E}}$ and $s_{11}^{\rm{H}}$ are the elastic compliances of the piezoelectric and magnetostrictive layers, respectively. The angles θ′ and δ′ represent the phase difference between the real and imaginary components of the respective properties.

In general, under a constant applied AC (alternating current) magnetic field, the ME coupling coefficient shows a peak in its response to a varying DC (direct current) magnetic bias field. The peak is caused by the dependence of the ME coefficient on the piezomagnetic coefficient (q = dλ/dH, λ:magnetostriction) with respect to the DC magnetic field, delineating the requirement of optimizing the magnitude of DC magnetic bias (H _opt) to obtain the maximum ME voltage output. Traditionally, one needs to use a permanent magnet or a solenoid to provide the external magnetic bias H _bias, which in turn results in the problem of large device size, electromagnetic interference, and potentially additional noise sources. Thus, a novel laminate architecture is desired where one can achieve ME coupling with large tunability in the absence of a DC magnetic field. This allows the development of energy harvesters and AC magnetic field sensors for a variety of environments. Magnetoelectric composites with large nonzero α _E in the absence of a DC magnetic field, namely with a “self-biased ME effect,” have been developed in various configurations using different strategies.²⁸ These self-biased ME composites are discussed in the article by Chu et al. in this issue,²⁹ and their use for energy harvesting is illustrated. Further, using these ME composites, dual-mode energy harvesting can be accomplished, where both magnetic field and vibration can be simultaneously converted into electricity. Chu et al. highlight the key materials and requirements for the magnetovibration dual-mode energy harvesting.²⁹ Research has demonstrated high power densities under resonance condition using oriented single-crystal fiber-composite-based ME laminates.

The general principle for conversion of low-frequency mechanical stress into electrical energy using the direct piezoelectric effect has been widely investigated.³⁰ There are three primary steps in power generation through a piezoelectric transducer: (1) trapping the mechanical AC stress from the available source (mechanical structure), (2) converting the mechanical energy into electrical energy by direct piezoelectric transduction, and (3) processing and storing the generated electrical energy. Depending upon the frequency and amplitude of the mechanical stress, piezoelectric transducers are designed to meet the requirements for flexibility, dimensions, and operating conditions. The power density of a harvesting system is dependent upon the strategies that maximize the trapping of energy and reduce the losses occurring at each step, namely, mechanical loss due to mismatch in mechanical impedance, and electromechanical loss depending upon the magnitude of the coupling factor.^2,31

Piezoelectric materials used for energy harvesting require maximizing the dimensionless figure of merit (DFOM). Using a simple spring mass–damper model, the total available power in the vibrating system can be shown to be the sum of the mechanical power dissipated and the electrical power generated as:³⁰

(3)$${P_T}(\omega ) = {P_m}(\omega ) + {P_e}(\omega ) = {{m{\zeta _m}{Y^2}{\omega _n}^3} \over {4{{\left( {{\zeta _m} + {\zeta _e}} \right)}^2}}} + {{m{\zeta _e}{Y^2}{\omega _n}^3} \over {4{{\left( {{\zeta _m} + {\zeta _e}} \right)}^2}}},$$

where the electrical power generated is equal to P _e(ω), the mechanical power dissipated is given by P _m(ω), Y is the amplitude of displacement, ω is the source frequency, ω_n is the natural frequency, and ζ_e and ζ_m are the electrical and mechanical damping ratios, respectively, of the harvester. The maximum power that can be generated by the electrical power takeoff system (rise in the output electrical power) occurs when the electrical damping is equal to the mechanical damping (ζ_m = ζ_e). The electrical damping factor is related to the dielectric loss factor (tanδ′), which should be minimized.

A more precise FOM for piezoelectric energy harvesters can be derived by considering the power response of the piezoelectric transducer. Recently, Priya conducted detailed modeling of piezoelectric energy harvesting, and proposed a DFOM for the piezoelectric transducer material in energy-harvesting application as:^32,33

(4)$$DOFM = {\left( {{{k_{31}^2 \cdot {Q_m}} \over {s_{11}^E}}} \right)_{on - resonance}}{\left( {{{{d_{31}} \cdot {g_{31}}} \over {\tan \delta }}} \right)_{off - resonance}},$$

where k ₃₁ is the transversal electromechanical coupling factor, Q_m is the mechanical quality factor, s ₁₁^E is the elastic compliance at the constant field condition, d ₃₁ is the transversal piezoelectric strain constant, g ₃₁ is the transversal constant, and tanδ is the loss factor.^27,28 By comparing DFOMs for the various piezoelectric compositions, one can identify the better material system suitable for energy harvesting applications.

In addition to composition, material parameters can be optimized through synthesis techniques that exploit the anisotropy through epitaxial growth and grain texturing. Roundy and Trolier-McKinstry in their article in this issue discuss the FOM for piezoelectric thin films and methodology for maximizing it in transducers.³⁴ Torah et al. in their article discuss the FOM for piezoelectric fiber and polymer-based structures and describe the methodology for their synthesis.³⁵ Particle/granule spray deposition techniques such as aerosol deposition (AD) and granule spray in vacuum (GSV) are being investigated to synthesize the mesoscale structures with desired microstructure in a rapid manner. The AD/GSV deposition technique is briefly mentioned in the article by Chu et al.²⁹

The articles by Roundy and Trolier-McKinstry and Torah et al.^34,35 both address the energy-harvester requirements for the human body in the form of smart fabrics and textiles and also as wearables. There are several constraints in implementing flexible harvesters using films and fibers, which need to conform to curved surfaces, stretch, and be comfortable to the user. In addition to mechanical vibrations, energy harvesting from thermal gradients between the body and external environment and sunlight is also briefly discussed. Inertial structures are described by Roundy and Trolier-McKinstry that utilize human motion directly to create relative displacement and transduction.³⁴ Together, these two articles summarize the current state of the art of smart fabrics and provide a list of challenges that needs to be addressed by the community.

Summary

We believe that energy harvesting will become increasingly important with time to address the emerging revolution in connectivity, data analytics, IoT, wireless sensors, and personal mobile devices. We hope that the articles in this issue will serve the role of informing the community on the current status of energy harvesting from heat, vibrations, and magnetic fields. Further, we hope that the discussions provided on integration of energy-harvesting function with smart fabrics, textiles, and wearables will assist the research community to continue to resolve the scientific and technological challenges in their deployment. We anticipate that this issue will strengthen the design and development of materials that can meet the practical requirements of energy harvesters, which are expected to play a vital role in future society.