Introduction
Snow cover in Asian cold deserts is highly variable both spatially and temporally. Thin, discontinuous sheets of snow can occur year-round (Reference Zheng, Zhang and WuZheng and others, 2000). Extreme cold-weather events, in which prolonged low temperatures following snowstorms prevent snowmelt, are also common and can cause extensive damage to humans, livestock and the economy (Reference MillerMiller, 1998; Reference Zheng, Zhang and WuZheng and others, 2000). Remote-sensing and in situ observations indicate rapid changes in the cryosphere in China since the 1960s, with a 5.5% decline in glacier area, large inter-annual variation in snow depth with a small increasing trend (Reference Qin, Liu and LiQin and others, 2006; Reference Che, Li, Jin, Armstrong and ZhangChe and others, 2008; Reference LiLi and others, 2008) and significant permafrost degradation (Reference LiLi and others, 2008).
The presence of snow cover plays a key role in the cold-desert ecosystem by affecting the hydrology, ecology and climate. Snowpack affects soil temperature, moisture, permeability, microbial activity and potentially carbon sequestration (Reference MonsonMonson and others, 2006; Reference Isard, Schaetzl and AndresenIsard and others, 2007). The presence of snow acts as an insulator to soils, preventing freezing and decreasing evaporation/sublimation, while increasing the surface albedo and reinforcing atmospheric stability. Deep snowpack prevents grazing and increases infiltration of water into the soils, revitalizing grasslands in the coming spring (Reference MillerMiller, 1998).
In the absence of snow, soils are more vulnerable to freezing and potentially decreased rates of transpiration by microbes in the soil, which may alter the soil’s ability to sequester carbon (Reference MonsonMonson and others, 2006). Freezing of the soil decreases permeability and infiltration rates, thus promoting runoff and vulnerability to soil erosion. Soil freezing can also thereby alter rates of groundwater recharge and the availability of water for vegetation.
Cold deserts differ from hot deserts primarily in that the dominant form of precipitation in cold deserts is snowfall. The Tibetan Plateau is the largest non-polar cold desert in the world, with an average elevation above 4000 m (Fig. 1). Snow disasters are common in the Tibetan Plateau, and variability in snow cover has been linked to local and global climate (Reference Barnett, Dümenil, Schlese, Roeckner and LatifBarnett and others, 1989; Reference Vernekar, Zhou and ShuklaVernekar and others, 1995; Reference Wu and QianWu and Qian, 2003).

Fig. 1. True-color mosaic image of h24 and h25v05 MODIS tiles for 22 April 2001 spanning the majority of the Tibetan Plateau. Red outlines mark the location of the two Landsat scenes used for validation: path 147 row 36 to the west and path 139 row 35 to the east. People’s Republic of China provinces are overlain in yellow. Meteorological stations are shown as blue dots.
Temperature and precipitation decrease northwestward across the Tibetan Plateau, with annual precipitation decreasing from about 400 to 200 mm (WWF, http://www.worldlife.org/wildworld/profiles/terrestrial_pa.html). The amount of precipitation that falls as snow increases with latitude, so snow is also an important water resource for vegetation, especially in higher latitudes on gentle slopes where radiation intensity is less and conditions are more conducive for vegetation growth (L.R. Verma and others, http://www.fao.org/docrep/x5672e/x5672e00.htm).
Due to the remoteness and topographic complexity of the Tibetan Plateau, remote sensing offers the most practical tool for monitoring snow-cover dynamics in Asian cold deserts. For the past few decades, microwave and optical sensors have been applied to global snow-cover mapping (Reference Armstrong and BrodzikArmstrong and Brodzik, 2002; Reference Hall, Riggs, Salomonson, DiGirolamo and BayrHall and others, 2002; Reference Dozier and PainterDozier and Painter, 2004), with microwave sensors having the added capacity to infer snow depth and snow water equivalent. However, evaluation of microwave-derived estimates of snow on the Tibetan Plateau with ground-truth data revealed that snow is often overestimated in the Tibetan Plateau (Reference Chang, Foster, Hall, Robinson, Li and CaoChang and others, 1992; Reference Basist, Garrett, Ferraro, Grody and MitchellBasist and others, 1996; Reference Bo and FengBo and Feng, 2000; Reference Che, Li, Jin, Armstrong and ZhangChe and others, 2008).
Snow grain size and density (Reference Che, Li, Jin, Armstrong and ZhangChe and others, 2008), snow wetness, similarity in the scattering properties of snow, ice and permafrost (Reference Tait, Hall, Foster and ArmstrongTait and others, 2000) and the presence of vegetation (Reference Ghedira, Arevalo, Lakhankar, Azar, Khanbilvardi and RomanovGhedira and others, 2006; Reference Che, Li, Jin, Armstrong and ZhangChe and others, 2008) are variables affecting passive microwave estimates of snow cover, snow depth and snow water equivalent. Additionally, the shallowness (<3 cm) and discontinuity of snow cover (common for snow on the Tibetan Plateau (Reference Bo and FengBo and Feng, 2000)) may be a source of error in passive microwave estimates (Reference Tait, Hall, Foster and ArmstrongTait and others, 2000). Recent modifications to passive microwave remote-sensing data correct for snow grain size and density and consider the effects of vegetation and snow wetness; however, the low resolution of the passive microwave products (25 km) makes validation of snow-cover extent difficult because observations at some sites cannot represent regional information within a single large pixel (625 km2) (Reference Che, Li, Jin, Armstrong and ZhangChe and others, 2008). Higher-resolution datasets such as MODIS (moderate-resolution imaging spectroradiometer) can be applied to achieve regional-scale measures of snow extent.
Snow grain size also affects estimation of snow cover in the reflected solar spectrum; however, measurable grain-size effects on snow reflectance can also yield valuable information on snow properties necessary for snow hydrologic and energy-balance models (Reference Painter, Roberts, Green and DozierPainter and others, 1998, Reference Painter, Dozier, Roberts, Davis and Green2003; Reference Nolin and DozierNolin and Dozier, 2000). Higher-resolution optically derived snow indices which consider the effects of snow grain size on optical reflectance may provide more accurate estimates of snow cover for the Tibetan Plateau than lower-resolution passive microwave estimates.
Band ratio and spectral mixture analysis (SMA) techniques are commonly applied for monitoring snow cover using remotely sensed optical data (Reference Hall, Riggs and SalomonsonHall and others, 1995, Reference Hall, Riggs, Salomonson, DiGirolamo and Bayr2002; Reference Painter, Roberts, Green and DozierPainter and others, 1998, Reference Painter, Dozier, Roberts, Davis and Green2003, Reference Painter, Rittger, McKenzie, Slaughter, Davis and Dozier2009; Reference OkinOkin, 2007). The most common band threshold approach, the normalized-difference snow index (NDSI; Reference Crane and AndersonCrane and Anderson, 1984; Reference DozierDozier, 1984; Reference Hall, Riggs and SalomonsonHall and others, 1995, Reference Hall, Riggs, Salomonson, DiGirolamo and Bayr2002), is used to generate snow maps on a global scale using MODIS data. Until recently, MODIS snow products were binary (e.g. they classified a pixel as either ‘snow’ or ‘not snow’). Binary products, though computationally efficient, are not accurate enough for many hydrologic and energy-balance models.
More recent MODIS products (MOD10A1) provide fractional snow cover using the regression equation of Reference Salomonson and AppelSalomonson and Appel (2004). This approach utilized higher-resolution Landsat data for three sites typifying diverse snow conditions in Alaska, Canada and Russia. Independent tests suggest that these relationships are robust, stable and an improvement upon earlier methods of mapping fractional snow cover (e.g. Reference Barton, Hall and RiggsBarton and others, 2000). However, a similar regression approach applied using MODIS NDSI data in the Tibetan Plateau using higher-resolution Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) data suggested regression relationships were sensitive to local conditions (Reference Xu, Shi, Zhang and WuXu and others, 2005). The scatter in the data used for the regression suggests a large range of fractional snow-covered area solutions for a given NDSI, as would be expected with changes in grain size and optical properties of the non-snow constituent.
Modifications to SMA have been used to retrieve sub-pixel snow-covered area using Airborne Visible/Infrared Imaging Spectrometer (AVIRIS; Reference Painter, Roberts, Green and DozierPainter and others, 1998, Reference Painter, Dozier, Roberts, Davis and Green2003, Reference Painter, Rittger, McKenzie, Slaughter, Davis and Dozier2009) and MODIS datasets (Reference OkinOkin, 2007). Topographic conditions influence the morphology (grain size) of snow and hence the spectral reflectance (Reference Painter, Roberts, Green and DozierPainter and others, 1998). Multiple Endmember Spectral Mixture Analysis (MESMA; Reference Painter, Roberts, Green and DozierPainter and others, 1998, Reference Painter, Dozier, Roberts, Davis and Green2003; Reference Roberts, Gardner, Church, Ustin, Scheer and GreenRoberts and others, 1998), a variant of SMA which allows for spectral variation caused by grain-size effects, may have the potential to retrieve snow-covered area in Asian cold deserts more accurately than band ratio products and provide fractional snow cover in the absence of a regression approach.
The purpose of this study is to introduce a new MESMA snow index, Relative Multiple Endmember Spectral Mixture Analysis (RMESMA), and compare its performance in mapping fractional snow cover in the western Tibetan Plateau with a more computationally comprehensive MESMA variant, MODIS Snow Covered Area and Grain Size (MODSCAG); a less computationally expensive single end-member SMA technique, Relative Spectral Mixture Analysis (RSMA); and a band ratio technique, NDSI. The MODIS dataset, although it does not encompass the extreme winter of 1998 in the Tibetan Plateau, provides a realistic scale for monitoring snow cover in the Tibetan Plateau and allows comparison of several different snow indices. Classified Landsat Enhanced Thematic Plus (ETM+) sensor data are used to validate the MODIS snow results (classification described below).
Methods
Datasets and geographic location of study site
Two tiles of the MODIS nadir bidirectional reflectance distribution function (BRDF) adjusted reflectance (NBAR) data with 1 km spatial and 16 day temporal resolution (MOD43B4 v004) were used (Fig. 1) reprojected to the geographic coordinate system. Together, these tiles cover nearly the entire Tibetan Plateau. Dates for the MODIS images were 16 October 2000 and 10 November 2000. These dates represent the final day of the 16 day composite period in which data were collected.
Landsat ETM+ path 139 row 35 (NASA Landsat Program, 2000, Landsat ETM+ scene L7CPF20001001_20001231_07, SLC-off, US Geological Survey (USGS), Sioux Falls, SD, 16 October 2000) and path 147 row 36 (NASA Landsat Program, 2000, Landsat ETM+ scene L7CPF20001001_20001231_07, SLC-off, USGS, Sioux Falls, 1 November 2000) were used to produce a validation dataset for the MODIS-derived snow indices. The location of these two scenes reprojected to the geographic coordinate system is shown in red in Figure 1.
Snow index descriptions
MODSCAG
MODSCAG (Reference Painter, Rittger, McKenzie, Slaughter, Davis and DozierPainter and others, 2009) uses MESMA (Reference Roberts, Gardner, Church, Ustin, Scheer and GreenRoberts and others, 1998) to simultaneously solve for sub-pixel snow-covered area and grain size of the fractional snow cover. MODSCAG estimates the fraction of each pixel that is covered by snow and its grain size using SMA and a radiative transfer model for snow directional reflectance. Non-snow end-members include rock and vegetation and were collected in the field at nadir. The dominant form of vegetation in the Tibetan Plateau is classified as Montane Grassland (WWF, http://www.worldlife.org/wildworld/profiles/terrestrial_pa.html). Vegetation structure in the Tibetan Plateau is very flat, i.e. has a low structure, and can be considered a Lambertian surface. In the absence of highly structured vegetation such as forest, treating non-snow end-members as a Lambertian surface is an adequate approximation. End-members are constrained to sum to 1. The best end-member is selected within a sub-model run based first on whether it meets modeling constraints on root mean square (RMS), fractions and consecutive residuals. There are 30 model subsets used to partition the spectral library permutations sensibly, and within each of these an optimal scene is produced. The 30 scenes are then merged into a final suite using RMS error (RMSE) as the metric for fit quality.
RSMA and RMESMA
RSMA (Reference OkinOkin, 2007) uses SMA to quantify changes in vegetation and snow cover in a pixel through time. The first step in RSMA is to generate a ‘baseline spectrum’ for each pixel in an image. The baseline spectrum is the apparent surface reflectance of a pixel at a reference time, t 0. The baseline spectrum for a pixel is typically selected at a time with the least amount of snow and vegetation cover. At time, ti , other than the reference time, RSMA indices quantify change in ground-cover components (GV (green vegetation), NPV (non-photosynthetic vegetation)/litter, and snow) relative to the reference time. RSMA indices are calculated by modeling the pixel reflectance at ti as a linear combination of four end-members: the baseline spectrum and reference end-members for GV, NPV/litter and snow. The least-squares bestfit coefficients of the GV, NPV/litter and snow reference end-members to the pixel spectrum are the RSMA indices X GV, X NPV/litter and X Snow respectively. The fourth RSMA index, X B, is equal to the best-fit coefficient for the baseline spectrum minus one. The four RSMA indices must sum to zero.
RSMA does not prohibit the coefficients of the linear mixture model from being negative, as is often the case in other SMA approaches (e.g. Reference Roberts, Gardner, Church, Ustin, Scheer and GreenRoberts and others, 1998). Positive values in RSMA indices reflect an increase in the ground-cover component with respect to the baseline spectrum, while negative values reflect a decrease in the ground-cover component. When the fractional cover of any ground cover in the baseline spectrum is zero, the RSMA index for that ground cover is equal to the fractional cover of that ground cover. Since the baseline spectra are generally chosen at snow-free times, the fractional cover of snow in the baseline spectrum is often zero. In these cases, which represent the majority of cases in an image, the value of X Snow is equal to the actual fractional cover of snow in a pixel. In cases where there is snow present in the baseline spectrum, X Snow must be less than the fractional cover of snow.
RMESMA, which is presented here for the first time and is a new technique developed by the authors, is a multiple end-member implementation of RSMA (Reference OkinOkin, 2007) in which multiple spectra of GV, NPV/litter and snow are combined into multiple mixture models with the baseline spectrum as the fourth end-member. The RSMA indices of the model with the lowest RMSE are chosen as the best-fit index values for each pixel. GV and NPV/litter spectra were obtained by convolving field spectra to MODIS bands. Snow end-members were obtained from the MODSCAG snow spectral library (Reference Painter, Rittger, McKenzie, Slaughter, Davis and DozierPainter and others, 2009). Preliminary results showed the best-fit snow end-members were of varying grain size and predominately solar zenith angle of 30°, so these end-members were retained for the modeling. Up to ten input reference spectra for each ground-cover component (e.g. GV, NPV/litter, snow) were included.
NDSI
NDSI is a band ratio index of snow cover utilizing the shortwave infrared and red bands (Reference Hall, Riggs and SalomonsonHall and others, 1995). The global criteria for characterizing a pixel as snow in the MODIS snow-cover products include an NDSI value greater than 0.4 and additional threshold values in bands 2 and 4 of ≥0.11 and 0.1 respectively, to mask out water bodies. In addition, a criterion test is applied using the normalized-difference vegetation index (NDVI) for areas of dense vegetation (after Reference Riggs, Hall, Salomonson and SteinRiggs and others, 1994). NDSI and NDVI were calculated for this study directly from MODIS NBAR data (after Reference Hall, Riggs and SalomonsonHall and others, 1995, Reference Hall, Riggs, Salomonson, DiGirolamo and Bayr2002):
and
The fractional NDSI product (MOD10A1) was not used in this study, due to discrepancies in both the temporal resolution between ETM+ scenes used and the available MOD10A1 scenes and the spatial resolution of the MODIS snow indices used (1 km vs 500 m).
Creation of a validation snow-cover dataset using ETM+
Snow was classified in the ETM+ scenes using the ENVI (ITT VIS, Inc., Boulder, CO, USA) Sequential Maximum Angle Convex Cone (SMACC) spectral tool to extract spectral end-members and their abundance. SMACC uses a convex cone model (also known as Residual Minimization) to identify image end-member spectra. We used a six end-member limit, a 0.25 (25%) RMSE tolerance and a constraint that end-member abundances sum to unity. Redundant end-members were coalesced so that snow abundances were merged into a single band of total snow cover.
The snow-classified ETM+ scenes were then degraded to the MODIS NBAR pixel size. The resulting image gave fractional snow cover at the same resolution as the MODIS snow-cover indices. MODIS snow indices were spatially and temporally subset to match the resampled ETM+ scenes. A 5 × 5 moving average box filter was applied to both the degraded ETM+ derived snow cover and the subset MODIS snow-cover index images to decrease noise in the images.
Statistical tests
We compared 2500 randomly selected pixels with >20% snow cover in the ETM+ snow classifications, and subset MODIS scenes using linear least-squares regression and Pearson correlation. Pixels without snow were excluded from the analysis to avoid weighting the dataset near the origin and distorting the regression relationship. Five iterations were repeated, and final regression and correlation results were calculated as the average regress and correlation results for all five runs. RMSE was also calculated between SMACC and MODIS snow-index values for pixels containing snow.
Results
Linear least-squares regressions showed that the MODSCAG index had the best agreement with the validation datasets, with slope values close to 1 and y-intercept values close to 0 (Table 1). The 95% confidence intervals in the regression analysis for slope and y-intercept were [0.98, 1.06] and [−0.02, 0.06] for the eastern scene and [0.94, 1.02] and [−0.01, 0.07] for the western scene. Therefore, at a 95% confidence level, the slope and y-intercept values were not significantly different from 1.0 and 0.0, and MODSCAG had accuracy comparable to the Landsat validation scenes.
Table 1. Linear regression coefficients (ETM+ = Slope × Index + y-intercept) and Pearson correlation values. All Pearson r values were significant at p = 0.01. Second line values for RMESMA and RSMA denote values calculated with a correction for snowy pixels in the baseline image

RMESMA, RSMA and NDSI underestimated snow in comparison to the validation datasets (Table 1), with the 95% confidence of slope and y-intercept for regression analysis of [0.77, 0.89; 0.75, 0.81; 0.66, 0.72] and [0.03, 0.15; −0.02, 0.04; −0.04, 0.02] for the eastern scene and [0.76, 0.84; 0.71, 0.79; 0.80, 0.86] and [−0.03, 0.05; 0.0, 0.08; 0.07, 0.13] for the western scene.
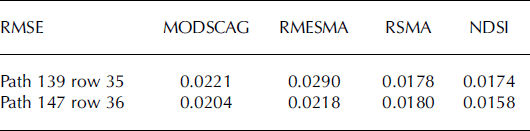
Pearson correlation coefficients were significant (p = 0.01) and positively correlated for all snow-index comparisons and were higher for the western scene (≥0.75) vs the eastern scene (≥0.52) (Table 1). The RMSE (Table 2) ranged from a minimum of 0.0158 for NDSI (1.6%) in the western scene to a maximum of 0.0290 (2.9%) for RMESMA in the eastern scene.
Table 2. RMSE results for both validation scenes
Discussion
Absolute value comparisons
The underestimation of snow by RSMA and RMESMA in comparison to the validation datasets can be attributed largely to the presence of snow in the baseline image. Snowy pixels in the baseline image exhibit reduced snow-covered area at later times (t > t 0) in a manner proportional to the fraction of snow at time t 0. To verify that snow cover in the baseline image caused the original underestimation of snow cover by RSMA and RMESMA, snow was classified in the baseline images for the h24v05 and h25v05 tiles using the ENVI SMACC algorithm. Pixels identified with ≥25% snow in the SMACC classification of the baseline image were screened out from the random pixel selection for the linear regression and Pearson correlation calculations. In regression analysis of these data (Table 1), the 95% confidence intervals for slope and y-intercept were [0.93, 0.99; 0.93, 1.0] and [−0.03, 0.08; −0.05, 0.03] for RMESMA in the eastern and western scenes respectively and [0.83, 0.89; 0.98, 1.06] and [0.06, 0.12; −0.02, 0.06] for RSMA. Therefore, at the 95% confidence interval, RMESMA was not significantly different from 1.0 and 0.0 for the western scene, indicating that RMESMA has comparable accuracy to the Landsat validation scenes when snowy pixels are identified in the baseline image. For the eastern scene, the RMESMA slope was slightly less than 1.0 according to the 95% confidence interval, but the y-intercept was not significantly different from 0.0.
Pearson r-values between NDSI and the validation datasets, which measure the spread or scatter of the data, were significant and positively correlated for both scenes, indicating a linear relationship between NDSI and the validation data. The slope values, which reflect the actual fit to the linear regression and can be thought of as the calibration coefficient for NDSI, were <1 for both scenes and varied significantly between scenes. These results suggest that NDSI, while providing a reasonable index of the total snow cover within a scene, is sensitive to local conditions. The results of this study are consistent with Reference Xu, Shi, Zhang and WuXu and others’ (2005) study, which suggests that the calibration coefficient for NDSI fractional snow cover is sensitive to local conditions (e.g. variables such as snow grain size, vegetation and soil types, and snow impurities) and therefore is not suitable for quantifying snow cover in the complex terrain of the Tibetan Plateau.
Influence of terrain and spatial distribution of snow
In general, the spatial distribution of snow was better maintained by all snow indices for the western scene than the eastern scene (Fig. 2). Visual inspection of the scenes suggests that glacial moraines, which contaminate snow with dust and debris, and a greater percentage of shadowing due to the physical structure of the glaciers, were more prevalent in the eastern scene (Fig. 3 shows enlarged regions of this scene). Snow cover in the western scene (Fig. 4) was more spatially coherent (e.g. larger patches), and thus more easily identifiable.

Fig. 2. True-color image of (a) path 139 row 35; (b) SMACC (validation); (c) MODSCAG snow index; (d) RMESMA snow index; (e) RSMA snow index; and (f) NDSI.

Fig. 3. Enlarged true-color images of smaller, less continuous snowy regions in the path 139 row 35 scene. Red-outlined area is enlarged as (a) and yellow-outlined area as (b). MODSCAG, RMESMA and RSMA did a better job detecting snow in these regions where SMACC did not (Fig. 2).

Fig. 4. True-color image of (a) path 147 row 36; (b) SMACC (validation); (c) MODSCAG snow index; (d) RMESMA snow index; (e) RSMA snow index; and (f) NDSI.
By selecting scenes that varied both in topographic and snow-cover conditions, this analysis was more representative of the complex topographic conditions and highly variable nature of snow cover in the Tibetan Plateau. Our results suggest that the MESMA snow indices, especially MODSCAG, are insensitive to terrain effects since both had accuracy comparable to validation scenes.
Limitations associated with Landsat sensor characteristics and end-member selection
The visible bands of the Landsat sensor, which were designed for the analysis of vegetation, soils and open water, are often saturated by the upwelling radiance over snow and clouds (Reference DozierDozier, 1984; Reference Painter, Dozier, Roberts, Davis and GreenPainter and others, 2003). This saturation can reduce the ability to separate snow from other surfaces in mixture analysis because the complete spectrum of snow is not represented. Saturation of Landsat bands could result in underestimation of the amount of snow cover in the validation scene.
Technique-specific limitations
Techniques that utilize the entire spectrum of a sensor, rather than specific absorption features, are more sensitive to grain-size effects (Reference Painter, Dozier, Roberts, Davis and GreenPainter and others, 2003). In this study MODSCAG, RSMESMA, RSMA and SMACC algorithms utilize end-members that span the full range of the sensor spectrum, but end-member selection varies for each of these techniques. RSMA, the single end-member variant, does not account for spectral variation within the same material. Therefore, we did not expect this index to quantify snow cover as accurately as the MESMA techniques, and this was supported by the results. MODSCAG and RMESMA, the two MESMA variants, address this issue by allowing end-members and the number of end-members to vary on a per-pixel basis (Reference Roberts, Gardner, Church, Ustin, Scheer and GreenRoberts and others, 1998). In contrast to the SMA and MESMA techniques, which rely on uniform end-members input from a spectral library, SMACC extracts end-members directly from the image. Figure 3 shows two enlarged regions of the eastern scene with small, intermittent patches of snow. Pixels containing these snowpatches are more likely to be contaminated by other ground-cover components and misclassified. Visual comparison between Figures 2 and 3 suggests that MODSCAG and RMESMA quantify snow with these spatial characteristics better than the SMACC algorithm. This could explain the slightly higher RMSE values for MODSCAG and RMESMA. However, further work that compares SMACC and MESMA is required before this conclusion can be drawn.
Similar to MESMA, SMACC is sensitive to the number of end-members selected for a scene (Reference Gruninger, Ratkowski and HokeGruninger and others, 2004). While the literature is robust both for optimizing end-member selection for MESMA techniques (Reference Dennison and RobertsDennison and Roberts, 2003a,Reference Dennison and Robertsb) and quantifying fractional snow cover using MESMA across sensors (Reference Painter, Roberts, Green and DozierPainter and others, 1998, Reference Painter, Dozier, Roberts, Davis and Green2003, Reference Painter, Rittger, McKenzie, Slaughter, Davis and Dozier2009; Reference OkinOkin, 2007), literature for the SMACC algorithm is less abundant, and unavailable pertaining specifically to snow mapping. However, preliminary work for this study, comparing validation scenes generated using multiple unsupervised and supervised classification techniques, suggested the SMACC was more accurate in classifying snow cover from ETM+ than other techniques. In addition, at the time of writing, the MODSCAG algorithm is being implemented for ETM+ and Thematic Mapper (TM) data, and preliminary results indicate RMSE <5% for fractional snow cover in complex terrain.
Accuracy assessments are unavailable for snow-cover mapping using ETM+ data at the global scale. However, studies have shown that both the MODIS (Reference Hall, Riggs and SalomonsonHall and others, 1995, Reference Hall, Riggs, Salomonson, DiGirolamo and Bayr2002; Reference Xiao, Shen and QinXiao and others, 2001; Reference Wang and LiWang and Li, 2003) and Landsat sensors (Reference DozierDozier, 1984; Reference Boresjö Bronge and BrongeBoresjö Bronge and Bronge, 1999; Reference Sidjak and WheateSidjak and Wheate, 1999) are suitable for mapping snow cover in alpine and glacial environments and in regional studies of the Tibetan Plateau (Reference Xiao, Shen and QinXiao and others, 2001; Reference Wang and LiWang and Li, 2003).
Application of optical indices for quantifying spatial and temporal patterns in snow cover
Snow cover is highly variable both spatially and temporally in the Tibetan Plateau, with the greatest concentration of snow cover and snow depth occurring along the primary mountain ranges (Reference Wu and QianWu and Qian, 2003; Reference Qin, Liu and LiQin and others, 2006; Reference Che, Li, Jin, Armstrong and ZhangChe and others, 2008). Figure 5 shows the average winter (December–February) snow cover from 2000 to 2005 using the RMESMA snow index. The winters of 2001 and 2005 showed a higher concentration of snow cover near the Kunlun Shan (∼35–36° N, 78–88° E). Winter 2001 also showed a higher average snow cover in the inner plateau, and the winter of 2002/03 showed greater snow-covered area along the eastern border of the plateau in comparison with other years. Figure 6 shows the 6 year winter average fractional snow cover using the RMESMA snow index and emphasizes that the greatest concentration of snow cover occurs primarily along the mountain ranges in the Tibetan Plateau. These results are in agreement with literature estimations of the spatial locations of regions of greatest snow cover in the Tibetan Plateau (Reference Wu and QianWu and Qian, 2003; Reference Qin, Liu and LiQin and others, 2006; Reference Che, Li, Jin, Armstrong and ZhangChe and others, 2008). The lower-elevation region to the southwest of the Himalaya (∼28–34° N, 78–90° E) in northern India received little to no winter snow cover, while the Himalaya and Kunlun Shan to the west, Nyainqêntanglha Shan and Tanggula Shan (∼30–32° N, 90–100° E) in the south and southeast, and Bayan Har Shan, A’nyêmaqên Shan (∼34–35° N, 95–100° E) and Qilian Shan (∼36–37° N, 95–97° E) in the northeast region received the greatest snow cover. These results briefly demonstrate the potential of optical snow indices to enhance our understanding of the spatial and temporal patterns of snow cover for the Tibetan Plateau.

Fig. 5. Yearly winter (December–February) average fractional snow cover: (a) 2000; (b) 2001; (c) 2002; (d) 2003; (e) 2004; (f) 2005.

Fig. 6. Average winter (December–February) fractional snow cover 2000–05. Percentage of spatial coverage of each class is shown in parentheses.
Conclusions
This study compares four optically derived snow indices, three variants of spectral mixture analysis (MODSCAG, RSMA, RMESMA) and continuous NDSI using Landsatderived validation data for two diverse snow-cover and topographic conditions. The results show that the MESMA variants of SMA, particularly MODSCAG, compared exceptionally well to the validation datasets. RSMA and RMESMA underestimated snow cover due to the presence of snow in the baseline image where this was the case. This highlights the importance of choosing a baseline image with minimum snow cover. RSMA, the single end-member relative SMA technique, underestimated snow cover in the lower snow-validation scene. NDSI performed as well as other indices as an index of snow cover, but our results suggest that the linear calibration coefficient to convert NDSI values to fractional snow cover is not constant in space or time.
Taken together, the regression, correlation and RMSE results for MODSCAG, RMESMA and RSMA in both low-snow and high-snow conditions with differing topographies suggest that the SMA approach, particularly the MESMA variants, is suitable for quantifying snow cover in the Tibetan Plateau.
RMESMA and RSMA provide simultaneous indices of GV, NPV/litter and snow, parameters necessary for biophysical studies on vegetation productivity and energy balance as it pertains to both vegetative cover/litter decomposition and snow cover. RMESMA, which had accuracy comparable to validation scenes once persistently snowy pixels in the baseline spectrum were accounted for, is more sensitive to lower fractional snow-cover conditions compared to MODSCAG because it does not have the 20% snow-cover threshold constraint. Low-snow conditions on the Tibetan Plateau are common (Reference Zheng, Zhang and WuZheng and others, 2000) and may play an important role in vegetation productivity through insulating soils and providing a water resource.
MODSCAG outputs of grain size, albedo and fractional snow cover can greatly enhance our understanding of the seasonal evolution of these variables and improve upon the current generation of climate and snowmelt models which rely largely on empirical aging functions to predict snow albedo (Reference Molotch and BalesMolotch and Bales, 2006; Reference Dozier, Painter, Rittger and FrewDozier and others, 2008). Though snow cover in the Tibetan Plateau has been linked to climate change, much uncertainty remains regarding the magnitude and mechanisms, largely because monitoring of snow cover is insufficient (e.g. still based on binary products or low-resolution microwave datasets).
Recent advances in sensor resolution and adjustments to variables affecting estimates of snow extent have improved passive-microwave derived estimates of snow cover (Reference Che, Li and ArmstrongChe and others, 2004, Reference Che, Li, Jin, Armstrong and Zhang2008; Reference Armstrong and BrunArmstrong and Brun, 2008), but the low resolution constrains regional snow-cover estimates. Fractional snow-covered area derived using optical snow indices at the 1 km scale would provide additional information about where snow water equivalent is distributed within a 25 km microwave pixel. Application of RMESMA, RSMA or MODSCAG to quantifying fractional snow cover in the Tibetan Plateau has the potential to further our understanding of cryospheric changes in this climatically sensitive region.










