Hostname: page-component-6587cd75c8-2cm9h Total loading time: 0 Render date: 2025-04-23T15:01:04.844Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE DIVISIBILITY OF SUMS OF q-SUPER CATALAN NUMBERS

Part of: Sequences and sets Combinatorics Elementary number theory

Published online by Cambridge University Press:  15 May 2023

JI-CAI LIU Open the ORCID record for JI-CAI LIU [Opens in a new window]  and
YAN-NI LI
JI-CAI LIU*
Affiliation:
Department of Mathematics, Wenzhou University, Wenzhou 325035, PR China
YAN-NI LI
Affiliation:
Department of Mathematics, Wenzhou University, Wenzhou 325035, PR China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The integrality of the numbers 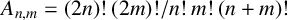$A_{n,m}={(2n)!(2m)!}/{n!m!(n+m)!}$ was observed by Catalan as early as 1874 and Gessel named 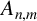$A_{n,m}$ the super Catalan numbers. The positivity of the q-super Catalan numbers (q-analogue of the super Catalan numbers) was investigated by Warnaar and Zudilin [‘A q-rious positivity’, Aequationes Math. 81 (2011), 177–183]. We prove the divisibility of sums of q-super Catalan numbers, which establishes a q-analogue of Apagodu’s congruence involving super Catalan numbers.

Keywords

Catalan numberq-super Catalan numbercyclotomic polynomial

MSC classification

Primary: 11B65: Binomial coefficients; factorials; $q$-identities
Secondary: 05A10: Factorials, binomial coefficients, combinatorial functions 11A07: Congruences; primitive roots; residue systems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 109 , Issue 2 , April 2024 , pp. 215 - 224
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The first author was supported by the National Natural Science Foundation of China (grant 12171370).

References

Allen, E. and Gheorghiciuc, I., ‘A weighted interpretation for the super Catalan numbers’, J. Integer Seq. 17 (2014), Article no. 14.10.7.Google Scholar
Apagodu, M., ‘Elementary proof of congruences involving sum of binomial coefficients’, Int. J. Number Theory 14 (2018), 1547–1557.CrossRefGoogle Scholar
Catalan, E., ‘Question 1135’, Nouv. Ann. Math. 13 (1874), 207.Google Scholar
Chen, X. and Wang, J., ‘The super Catalan numbers $S\left(m,m+s\right)$ for $s\le 4$ ’, Preprint, 2012, arXiv:1208.4196.Google Scholar
Gasper, G. and Rahman, M., Basic Hypergeometric Series, 2nd edn, Encyclopedia of Mathematics and Its Applications, 96 (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Gessel, I., ‘Super ballot numbers’, J. Symbolic Comput. 14 (1992), 179–194.CrossRefGoogle Scholar
Guo, V. J. W., Jouhet, F. and Zeng, J., ‘Factors of alternating sums of products of binomial and $q$ -binomial coefficients’, Acta Arith. 127 (2007), 17–31.CrossRefGoogle Scholar
Liu, J.-C., ‘Congruences on sums of super Catalan numbers’, Results Math. 73 (2018), Article no. 140.CrossRefGoogle Scholar
Liu, J.-C., ‘On a congruence involving $q$ -Catalan numbers’, C. R. Math. Acad. Sci. Paris 358 (2020), 211–215.CrossRefGoogle Scholar
Petkovšek, M., Wilf, H. S. and Zeilberger, D., $A=B$ (A.K. Peters, Wellesley, MA, 1996).Google Scholar
Pippenger, N. and Schleich, K., ‘Topological characteristics of random triangulated surfaces’, Random Structures Algorithms 28 (2006), 247–288.CrossRefGoogle Scholar
Stanley, R. P., Enumerative Combinatorics, Vol. 2 (Cambridge University Press, Cambridge, 1999).CrossRefGoogle Scholar
Sun, Z.-W. and Tauraso, R., ‘On some new congruences for binomial coefficients’, Int. J. Number Theory 7 (2011), 645–662.CrossRefGoogle Scholar
Tauraso, R., ‘ $q$ -Analogs of some congruences involving Catalan numbers’, Adv. Appl. Math. 48 (2012), 603–614.CrossRefGoogle Scholar
Von Szily, K., ‘Üeber die Quadratsummen der Binomialcoefficienten’, Ungar. Ber. 12 (1894), 84–91.Google Scholar
Warnaar, S. O. and Zudilin, W., ‘A $q$ -rious positivity’, Aequationes Math. 81 (2011), 177–183.CrossRefGoogle Scholar