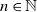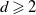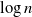1. Introduction
We consider a tree of n levels, where
![]() $n \in \mathbb{N}$
. We assume that the root node of this tree has d children, who in turn each have d children, and so on, till generation n, which are leaf nodes. Here we assume that
$n \in \mathbb{N}$
. We assume that the root node of this tree has d children, who in turn each have d children, and so on, till generation n, which are leaf nodes. Here we assume that
![]() $d \in \mathbb{N}$
, with
$d \in \mathbb{N}$
, with
![]() $d\geqslant 2$
, since the case
$d\geqslant 2$
, since the case
![]() $d=1$
is really trivial. This is a d-ary tree, and we refer to it as
$d=1$
is really trivial. This is a d-ary tree, and we refer to it as
![]() $T^n$
. We refer to the subset of all the leaf nodes of this tree as
$T^n$
. We refer to the subset of all the leaf nodes of this tree as
![]() $T_n$
. So
$T_n$
. So
![]() $| T_n | = d^n$
.
$| T_n | = d^n$
.
We consider a particle starting from
![]() $0 \in \mathbb{R}$
, which dies at time 1, and splits into d children. Each of these children travels a distance given by independent standard Gaussian random variables. Then, at time 2, each of these children die and give rise to d children, which in turn follow the same process, the displacements at each step being independent of the displacements at the previous time points. At time n we have
$0 \in \mathbb{R}$
, which dies at time 1, and splits into d children. Each of these children travels a distance given by independent standard Gaussian random variables. Then, at time 2, each of these children die and give rise to d children, which in turn follow the same process, the displacements at each step being independent of the displacements at the previous time points. At time n we have
![]() $d^n$
particles, each having a displacement. The positions of these particles are collectively called a branching random walk at time n. We can equivalently define a branching random walk (BRW) as a Gaussian process on
$d^n$
particles, each having a displacement. The positions of these particles are collectively called a branching random walk at time n. We can equivalently define a branching random walk (BRW) as a Gaussian process on
![]() $T^n$
. The origin stands for the root, and the displacements at each step are attached to the edges. So the d displacements at the first generation are attached to the edges between the root and its d children. To each vertex we attach a quantity equal to the sum of the Gaussian variables that we encounter while looking at the shortest path between itself and the root. The collection of displacements of the
$T^n$
. The origin stands for the root, and the displacements at each step are attached to the edges. So the d displacements at the first generation are attached to the edges between the root and its d children. To each vertex we attach a quantity equal to the sum of the Gaussian variables that we encounter while looking at the shortest path between itself and the root. The collection of displacements of the
![]() $d^n$
particles at time n is given by the Gaussian variables attached to all the vertices in
$d^n$
particles at time n is given by the Gaussian variables attached to all the vertices in
![]() $T_n$
. We denote it by
$T_n$
. We denote it by
![]() $\{ \phi_v^n \colon v \in T_n \}$
. This is the branching random walk at time n. Two particles at time n having the last common ancestor at time k
$\{ \phi_v^n \colon v \in T_n \}$
. This is the branching random walk at time n. Two particles at time n having the last common ancestor at time k
![]() $(k \leq n)$
are equivalent to two leaf nodes that have branched out from the same vertex at level k of the tree. Each of these displacements is a sum of n independent standard Gaussian random variables. Figure 1 gives a pictorial representation of the branching random walk for the case
$(k \leq n)$
are equivalent to two leaf nodes that have branched out from the same vertex at level k of the tree. Each of these displacements is a sum of n independent standard Gaussian random variables. Figure 1 gives a pictorial representation of the branching random walk for the case
![]() $d=2$
, i.e. on a binary tree. The collection
$d=2$
, i.e. on a binary tree. The collection
represents independent displacements, and these are independent and identically distributed (i.i.d.) standard Gaussian random variables. There are
![]() $d^n$
leaf nodes in the tree, and we can fix an ordering of the vertices from 1 to
$d^n$
leaf nodes in the tree, and we can fix an ordering of the vertices from 1 to
![]() $d^n$
. For any
$d^n$
. For any
![]() $v \in T_n$
, i.e.
$v \in T_n$
, i.e.
![]() $v \in \{1,2,\ldots, d^n \}$
, we define
$v \in \{1,2,\ldots, d^n \}$
, we define
![]() $a_i(v)=\lceil {v}/{d^{n-i}}\rceil$
for
$a_i(v)=\lceil {v}/{d^{n-i}}\rceil$
for
![]() $i=1,2,\ldots, n$
. Then we can define
$i=1,2,\ldots, n$
. Then we can define
![]() $\phi_n^v=\sum_{j=1}^n X_{j,a_j(v)}$
. This is another way of constructing the BRW.
$\phi_n^v=\sum_{j=1}^n X_{j,a_j(v)}$
. This is another way of constructing the BRW.

Figure 1. Branching random walk on a binary tree.
The covariance structure of this Gaussian process is given by
 \begin{equation}\begin{aligned}{\textrm{Var}} (\phi_v^n) &= n \quad \text{for all $ v \in T_n$,} \\{\textrm{Cov}}(\phi_u^n, \phi^n_v) &= n - \dfrac{1}{2}d_T(u,v) \quad \text{for all $u \neq v \in T_n$.}\end{aligned}\end{equation}
\begin{equation}\begin{aligned}{\textrm{Var}} (\phi_v^n) &= n \quad \text{for all $ v \in T_n$,} \\{\textrm{Cov}}(\phi_u^n, \phi^n_v) &= n - \dfrac{1}{2}d_T(u,v) \quad \text{for all $u \neq v \in T_n$.}\end{aligned}\end{equation}
where
![]() $d_T$
denotes the graph distance. So essentially the BRW is a multivariate normal distribution of dimension
$d_T$
denotes the graph distance. So essentially the BRW is a multivariate normal distribution of dimension
![]() $d^n$
, with all means 0, and variances and covariances given by (1.1). We call the corresponding probability measure
$d^n$
, with all means 0, and variances and covariances given by (1.1). We call the corresponding probability measure
![]() $\mathbb{P}(\cdot)$
.
$\mathbb{P}(\cdot)$
.
We wish to find bounds on the order of the probability of a branching random walk being positive at the leaf nodes (
![]() $v \in T_n$
). This is also the event that all the particles are on the right of the starting point of the first particle. We also wish to find the expected value of the field at a typical vertex in generation n, under the condition that the BRW is positive at all the leaf nodes. The behaviour we consider is that of entropic repulsion for this Gaussian field, which is its phenomenon of drifting away when pressed against a hard wall so as to have enough room for local fluctuations, as is referred to by Lebowitz and Maes [Reference Lebowitz and Maes15]. The phenomenon of entropic repulsion for the Gaussian free field (GFF) has been studied in the literature for some time now. The entropic repulsion for an infinite GFF on
$v \in T_n$
). This is also the event that all the particles are on the right of the starting point of the first particle. We also wish to find the expected value of the field at a typical vertex in generation n, under the condition that the BRW is positive at all the leaf nodes. The behaviour we consider is that of entropic repulsion for this Gaussian field, which is its phenomenon of drifting away when pressed against a hard wall so as to have enough room for local fluctuations, as is referred to by Lebowitz and Maes [Reference Lebowitz and Maes15]. The phenomenon of entropic repulsion for the Gaussian free field (GFF) has been studied in the literature for some time now. The entropic repulsion for an infinite GFF on
![]() $\mathbb{Z}^d$
,
$\mathbb{Z}^d$
,
![]() $d\geq 3$
, was studied by Bolthausen, Deuschel, and Zeitouni [Reference Bolthausen, Deuschel and Zeitouni3]. As a continuation, Deuschel [Reference Deuschel9] studied the GFF on a finite box with Dirichlet boundary conditions, for dimension 3 or more. For the GFF on a finite box, the positivity was looked at from two different angles, one involving the interior only, while the other considered the whole box. Both looked at the phenomenon of positivity of the field in a box of size N. Although the typical behaviour of a vertex was similar, the order was not, when positivity for the entire box was considered. But on removing the positivity condition for a layer near the box, the order was the same as in [Reference Bolthausen, Deuschel and Zeitouni3]. Further, Bolthausen, Deuschel, and Giacomin [Reference Bolthausen, Deuschel and Giacomin2] stated that the probability of positivity for a GFF in a box of dimension 2 decays exponentially, and this is really a boundary phenomenon. So in order to look into the long-range correlations and local fluctuations, the boundary effect has to be removed. This approach was taken in [Reference Bolthausen, Deuschel and Giacomin2] to look into the behaviour of a typical vertex when pressed against this hard wall for a GFF.
$d\geq 3$
, was studied by Bolthausen, Deuschel, and Zeitouni [Reference Bolthausen, Deuschel and Zeitouni3]. As a continuation, Deuschel [Reference Deuschel9] studied the GFF on a finite box with Dirichlet boundary conditions, for dimension 3 or more. For the GFF on a finite box, the positivity was looked at from two different angles, one involving the interior only, while the other considered the whole box. Both looked at the phenomenon of positivity of the field in a box of size N. Although the typical behaviour of a vertex was similar, the order was not, when positivity for the entire box was considered. But on removing the positivity condition for a layer near the box, the order was the same as in [Reference Bolthausen, Deuschel and Zeitouni3]. Further, Bolthausen, Deuschel, and Giacomin [Reference Bolthausen, Deuschel and Giacomin2] stated that the probability of positivity for a GFF in a box of dimension 2 decays exponentially, and this is really a boundary phenomenon. So in order to look into the long-range correlations and local fluctuations, the boundary effect has to be removed. This approach was taken in [Reference Bolthausen, Deuschel and Giacomin2] to look into the behaviour of a typical vertex when pressed against this hard wall for a GFF.
Studies of a GFF in a box of size n in dimension 2 since Bolthausen, Deuschel, and Giacomin [Reference Bolthausen, Deuschel and Giacomin2] have utilised the covariance of a GFF in the interior of the box. The connection between the covariance structure of a 2D-GFF and a BRW was made by Bramson and Zeitouni [Reference Bramson and Zeitouni4] to show tightness for the maximum of the GFF. It was observed to be log-correlated. To further refine the results on entropic repulsion of the GFF in dimension 2, it is imperative to consider similar behaviour for the BRW on a tree. Our calculations heavily rely on the tail behaviour of a BRW, as shown in Section 2. The connection between the tail behaviours of a 2D-GFF and a BRW have already been mentioned above. The multi-scale analysis, hinting towards the tree structure, is used extensively to study the extremal properties of a GFF in dimension 2, as shown by Bramson et al. [Reference Bramson and Zeitouni4–Reference Bramson, Ding and Zeitouni6]. Similar strategies were used by Kurt [Reference Kurt14] to study the entropic repulsion of the Gaussian membrane model for the critical dimension 4. Roy [Reference Roy16] and Schweiger [Reference Schweiger17] worked out that the Gaussian membrane model in the critical dimension is log-correlated. The work of Ding, Roy, and Zeitouni [Reference Ding, Roy and Zeitouni13] further exhibits strong relations between the BRW and log-correlated Gaussian fields, the branching number varying according to the dimension of the box.
In the context of these studies, we consider the behaviour at a typical vertex of a branching random walk on a d-ary tree. This is especially relevant bearing in mind the covariance structure of the BRW and that of the GFF in dimension 2, in the interior.
Entropic repulsion for a GFF on Sierpinski carpet graphs has been covered by Chen and Ugurcan [Reference Chen and Ugurcan8]. More recently, Caputo et al. [Reference Caputo, Martinelli and Toninelli7] considered entropic repulsion in
![]() $|\nabla \phi|^p$
surfaces.
$|\nabla \phi|^p$
surfaces.
We are interested in
![]() ${\mathbb{P}} ( \phi_v^n \geq 0 \ \forall\, v \in T_n)$
as well as
${\mathbb{P}} ( \phi_v^n \geq 0 \ \forall\, v \in T_n)$
as well as
![]() ${\mathbb E}( \phi_u^n \mid \phi_v^n \ge 0 \ \forall\, v \in T_n )$
. We are essentially interested in the conditional distribution of a BRW at a typical vertex under the condition of positivity at all vertices of level n. The computation of the expectation is the first step in that direction.
${\mathbb E}( \phi_u^n \mid \phi_v^n \ge 0 \ \forall\, v \in T_n )$
. We are essentially interested in the conditional distribution of a BRW at a typical vertex under the condition of positivity at all vertices of level n. The computation of the expectation is the first step in that direction.
In regard to the behaviour of the branching random walk in the presence of a hard wall, we recall similar results for other Gaussian processes, such as [Reference Bolthausen, Deuschel and Giacomin2], [Reference Caputo, Martinelli and Toninelli7], [Reference Chen and Ugurcan8], [Reference Deuschel and Giacomin10], [Reference Deuschel and Giacomin11], and [Reference Kurt14]. The leading-order term in the exponent of the probability of positivity is estimated, while we estimate both the leading-order term and the second leading term in the exponent. This also helps us to find the second-order term in the expected value of a typical vertex, under the hard wall condition.
We know from [Reference Zeitouni19, Theorem 4] that
![]() ${\mathbb E}(\max_{v \in T_n} {\phi}_v)$
is of the form
${\mathbb E}(\max_{v \in T_n} {\phi}_v)$
is of the form
![]() $c_1 n - c_2 \log n + {{\textrm{O}}}(1)$
. We define
$c_1 n - c_2 \log n + {{\textrm{O}}}(1)$
. We define
![]() $m_n =c_1 n - c_2 \log n$
, and
$m_n =c_1 n - c_2 \log n$
, and
![]() $\sigma_{d,n}^2 = {(1-d^{-n})}/{d-1}$
. In fact we have explicit values of
$\sigma_{d,n}^2 = {(1-d^{-n})}/{d-1}$
. In fact we have explicit values of
![]() $c_1$
and
$c_1$
and
![]() $c_2$
as
$c_2$
as
![]() $\sqrt{2 \log d}$
and
$\sqrt{2 \log d}$
and
![]() ${3}/{(2\sqrt{2 \log d})}$
respectively.
${3}/{(2\sqrt{2 \log d})}$
respectively.
The main result of this paper, in regard to the probability of positivity, is as follows.
Theorem 1.1. (Positivity probability.) There exists
![]() $\lambda'={\sqrt{2}\log n}/{\sqrt{\log d}}+{{\textrm{O}}}(1)$
, such that for n sufficiently large we have, for
$\lambda'={\sqrt{2}\log n}/{\sqrt{\log d}}+{{\textrm{O}}}(1)$
, such that for n sufficiently large we have, for
![]() $K_1, K_2, K_3 > 0$
independent of n, and
$K_1, K_2, K_3 > 0$
independent of n, and
![]() $K_4 = {1}/{(c\sigma^2_{d,n}\log d)}$
,
$K_4 = {1}/{(c\sigma^2_{d,n}\log d)}$
,
 \begin{align} & K_1 \exp\biggl({-\frac{1}{2\sigma^2_{d,n}}(m_n - \lambda')^2- K_3(m_{n} - \lambda') }\biggr) \notag \\ & \quad \le {\mathbb{P}}( \phi_v^n \geq 0\ \forall\, v \in T_n ) \notag \\ & \quad \le K_2 \exp\biggl({-\frac{1}{2\sigma^2_{d,n}}(m_{n} - \lambda')^2 - K_4 (m_{n} - \lambda')}\biggr).\end{align}
\begin{align} & K_1 \exp\biggl({-\frac{1}{2\sigma^2_{d,n}}(m_n - \lambda')^2- K_3(m_{n} - \lambda') }\biggr) \notag \\ & \quad \le {\mathbb{P}}( \phi_v^n \geq 0\ \forall\, v \in T_n ) \notag \\ & \quad \le K_2 \exp\biggl({-\frac{1}{2\sigma^2_{d,n}}(m_{n} - \lambda')^2 - K_4 (m_{n} - \lambda')}\biggr).\end{align}
Bolthausen, Deuschel, and Giacomin [Reference Bolthausen, Deuschel and Giacomin2] showed that the conditional expectation under positivity is roughly close to the expected maximum for the discrete GFF in two dimensions. Similarly, for the membrane model in dimension
![]() $d=4$
, Kurt [Reference Kurt14] computed that a lower bound on the conditional expectation of a typical vertex under positivity is close to the expected maximum. Here, however, we show that for a branching random walk the conditional expectation is at least a constant times
$d=4$
, Kurt [Reference Kurt14] computed that a lower bound on the conditional expectation of a typical vertex under positivity is close to the expected maximum. Here, however, we show that for a branching random walk the conditional expectation is at least a constant times
![]() $\log n$
less than the expected maximum. The second main result of this paper is as follows.
$\log n$
less than the expected maximum. The second main result of this paper is as follows.
Theorem 1.2. (Expected value.) We have for
![]() $u \in T_n$
, and n sufficiently large,
$u \in T_n$
, and n sufficiently large,
The approach we take to prove this is that we raise the average value of the Gaussian process and then multiply by a compensation probability. We optimise this average value so as to maximise the probability of positivity. The value at which this probability is maximised should ideally be the required conditional expectation.
In order to prove this in detail, we invoke a model called the switching-sign branching random walk, which is similar in structure to the original branching random walk. The model is motivated by a similar model introduced in [Reference Ding and Goswami12] for a BRW on the lattice
![]() $\mathbb{Z}^2$
, which was effectively a construction on a 4-ary tree. We have provided a more general construction of this on a d-ary tree in Section 3. We begin our calculations with a preliminary upper bound on the left tail of the maximum of the BRW in Section 2. Section 3 contains the definition of the new model of the switching-sign branching random walk, followed by a comparison of positivity for the branching random walk with this model using Slepian’s lemma. A left tail computation for the maximum of this model gives us the ingredients for the proof of Theorem 1.1, which is in the concluding part of Section 4. Section 5 contains the proof of Theorem 1.2. The upper bound follows from Section 3, while for the lower bound we also have to invoke Bayes’ rule and tail estimates to arrive at our result.
$\mathbb{Z}^2$
, which was effectively a construction on a 4-ary tree. We have provided a more general construction of this on a d-ary tree in Section 3. We begin our calculations with a preliminary upper bound on the left tail of the maximum of the BRW in Section 2. Section 3 contains the definition of the new model of the switching-sign branching random walk, followed by a comparison of positivity for the branching random walk with this model using Slepian’s lemma. A left tail computation for the maximum of this model gives us the ingredients for the proof of Theorem 1.1, which is in the concluding part of Section 4. Section 5 contains the proof of Theorem 1.2. The upper bound follows from Section 3, while for the lower bound we also have to invoke Bayes’ rule and tail estimates to arrive at our result.
Notation. We let
![]() $\Lambda^+_n$
denote the event
$\Lambda^+_n$
denote the event
![]() $\{ \phi_v^n \ge 0 \ \forall\, v \in T_n\}$
. We also let
$\{ \phi_v^n \ge 0 \ \forall\, v \in T_n\}$
. We also let
![]() $S_n$
be the sum of all the Gaussian variables at the level n. In mathematical terms
$S_n$
be the sum of all the Gaussian variables at the level n. In mathematical terms
![]() $S_n = \sum_{v \colon v \in T_n} \phi_v^n,$
where the sum contains
$S_n = \sum_{v \colon v \in T_n} \phi_v^n,$
where the sum contains
![]() $d^n$
terms.
$d^n$
terms.
Remark 1.1. The representation of the BRW as a sum of two Gaussian fields, in the setting of entropic repulsion, is a key point of the article. The constant part, which represents the typical value of the field, helps us to obtain the height under entropic repulsion, while the covariance fluctuations are kept unchanged in the remaining part. This representation helps us to optimise over the set of possible values for the typical height of the field under positivity.
Remark 1.2. Future directions along the line of this work include firstly the distributional behaviour and convergence of the branching random walk under positivity. Deuschel and Giacomin [Reference Deuschel and Giacomin10] have shown that the infinite GFF for
![]() $d\ge 3$
under positivity, on removing the conditioned height, converges weakly to the lattice free field. It is worth considering whether a similar phenomenon can be observed for the BRW.
$d\ge 3$
under positivity, on removing the conditioned height, converges weakly to the lattice free field. It is worth considering whether a similar phenomenon can be observed for the BRW.
Remark 1.3. Continuing our work, we can also consider the similar phenomenon for general log-correlated Gaussian fields. The splitting of the covariance matrix into two parts, one involving a constant Gaussian field, is not immediate for log-correlated Gaussian fields as in the form considered in [Reference Ding, Roy and Zeitouni13].
2. Left tail of maximum of BRW
This section is dedicated to proving an exponential upper bound on the left tail of the maximum of a BRW. We first begin with a comparison lemma by Slepian [Reference Slepian18] for Gaussian processes.
Lemma 2.1. Let
![]() $\mathcal{A}$
be an arbitrary finite index set and let
$\mathcal{A}$
be an arbitrary finite index set and let
![]() $\{ X_a \colon a \in \mathcal{A}\}$
and
$\{ X_a \colon a \in \mathcal{A}\}$
and
![]() $\{ Y_a \colon a \in \mathcal{A}\}$
be two centred Gaussian processes such that
$\{ Y_a \colon a \in \mathcal{A}\}$
be two centred Gaussian processes such that
![]() ${\mathbb E}(X_a - X_b)^2 \ge {\mathbb E}(Y_a - Y_b)^2$
for all
${\mathbb E}(X_a - X_b)^2 \ge {\mathbb E}(Y_a - Y_b)^2$
for all
![]() $a,b \in \mathcal{A}$
and
$a,b \in \mathcal{A}$
and
![]() ${\textrm{Var}}(X_a) = {\textrm{Var}} (Y_a)$
for all
${\textrm{Var}}(X_a) = {\textrm{Var}} (Y_a)$
for all
![]() $a \in \mathcal{A}$
. Then
$a \in \mathcal{A}$
. Then
![]() ${\mathbb{P}}(\max_{a \in \mathcal{A}} X_a \ge \lambda) \ge {\mathbb{P}}(\max_{a \in \mathcal{A}} Y_a \ge \lambda)$
for all
${\mathbb{P}}(\max_{a \in \mathcal{A}} X_a \ge \lambda) \ge {\mathbb{P}}(\max_{a \in \mathcal{A}} Y_a \ge \lambda)$
for all
![]() $\lambda \in \mathbb{R}$
.
$\lambda \in \mathbb{R}$
.
The main result of the section is as follows.
Lemma 2.2.
There exist constants
![]() $\bar{C} , c^* >0$
such that, for all
$\bar{C} , c^* >0$
such that, for all
![]() $n \in \mathbb{N}$
and
$n \in \mathbb{N}$
and
![]() $0 \le \lambda \le ( n)^{2/3}$
,
$0 \le \lambda \le ( n)^{2/3}$
,
Proof. From [Reference Zeitouni19, Section 2.5] we have tightness for
![]() $\{ \max_{v \in T_n} \phi^n_v - m_n \}_{n \in \mathbb{N}} $
, where
$\{ \max_{v \in T_n} \phi^n_v - m_n \}_{n \in \mathbb{N}} $
, where
So there exists
![]() $ \beta > 0$
such that for all
$ \beta > 0$
such that for all
![]() $n\ge 2$
$n\ge 2$
Further, we also have that, for some
![]() $\kappa > 0$
and for all
$\kappa > 0$
and for all
![]() $ n \geq n' \geq 2$
,
$ n \geq n' \geq 2$
,
Now we fix
![]() $\lambda' = \lambda/2$
, and
$\lambda' = \lambda/2$
, and
where
![]() $\lambda'$
satisfies
$\lambda'$
satisfies
![]() $\lambda' \geqslant \beta + \kappa+\sqrt{2 \log d}$
. From (2.3) it then follows that
$\lambda' \geqslant \beta + \kappa+\sqrt{2 \log d}$
. From (2.3) it then follows that
![]() $m_n - m_{n'} \leqslant \lambda' - \beta$
. We consider a tree of height n rooted at 0. We consider all subtrees rooted at vertices
$m_n - m_{n'} \leqslant \lambda' - \beta$
. We consider a tree of height n rooted at 0. We consider all subtrees rooted at vertices
![]() $v \in T^n$
such that
$v \in T^n$
such that
![]() $d_T(0,v)=n-n'$
. They are individually trees of height nʹ. The total number of such subtrees we have is
$d_T(0,v)=n-n'$
. They are individually trees of height nʹ. The total number of such subtrees we have is
![]() $d^{n-n'}$
. We call their leaf nodes
$d^{n-n'}$
. We call their leaf nodes
Now, for all
![]() $v \in T_n$
, we define
$v \in T_n$
, we define
where
![]() $(g_v^{n'})_{v \in T_n}$
are the BRWs obtained by adding the Gaussians for the edges only in the subtrees of height nʹ, and
$(g_v^{n'})_{v \in T_n}$
are the BRWs obtained by adding the Gaussians for the edges only in the subtrees of height nʹ, and
![]() $\phi$
is an independent Gaussian of mean 0 and variance
$\phi$
is an independent Gaussian of mean 0 and variance
![]() $n-n'$
. Clearly
$n-n'$
. Clearly
So by Lemma 2.1, we have
Using (2.2) and (2.3), we have for all
![]() $i \in \{1, 2, \ldots, d^{n-n'} \}$
$i \in \{1, 2, \ldots, d^{n-n'} \}$
 \begin{align*}{\mathbb{P}}\biggl(\sup_{v \in T_{n'}^{(i)}} g_v^{n'} \geq m_n - \lambda' \biggr) &= {\mathbb{P}}\biggl(\sup_{v \in T_{n'}^{(i)}} g_v^{n'} \geq m_{n'}+ m_n - m_{n'} - \lambda' \biggr) \\&\ge {\mathbb{P}}\biggl(\sup_{v \in T_{n'}^{(i)}} g_v^{n'} \geq m_{n'} - \beta \biggr) \\&\ge \frac12\end{align*}
\begin{align*}{\mathbb{P}}\biggl(\sup_{v \in T_{n'}^{(i)}} g_v^{n'} \geq m_n - \lambda' \biggr) &= {\mathbb{P}}\biggl(\sup_{v \in T_{n'}^{(i)}} g_v^{n'} \geq m_{n'}+ m_n - m_{n'} - \lambda' \biggr) \\&\ge {\mathbb{P}}\biggl(\sup_{v \in T_{n'}^{(i)}} g_v^{n'} \geq m_{n'} - \beta \biggr) \\&\ge \frac12\end{align*}
and thus
 \[{\mathbb{P}}\Bigl(\sup_{v \in T_n} g_v^{n'} < m_n - \lambda' \Bigr) \leq\biggl(\frac{1}{2}\biggr)^{d^{n-n'}}.\]
\[{\mathbb{P}}\Bigl(\sup_{v \in T_n} g_v^{n'} < m_n - \lambda' \Bigr) \leq\biggl(\frac{1}{2}\biggr)^{d^{n-n'}}.\]
Therefore
for some
![]() $\bar{C} , c^* > 0$
. Now, in conjunction with (2.4), the lemma is proved. Note that we choose
$\bar{C} , c^* > 0$
. Now, in conjunction with (2.4), the lemma is proved. Note that we choose
![]() $\bar{C} , c^* > 0$
such that the inequality holds for
$\bar{C} , c^* > 0$
such that the inequality holds for
![]() $\lambda \geqslant 2(\beta +\kappa+\sqrt{2 \log d})$
as well as
$\lambda \geqslant 2(\beta +\kappa+\sqrt{2 \log d})$
as well as
![]() $\lambda < 2(\beta +\kappa+\sqrt{2 \log d})$
.
$\lambda < 2(\beta +\kappa+\sqrt{2 \log d})$
.
3. Switching-sign branching random walk
At this juncture we define a new Gaussian process on the tree, which we call the switching-sign branching random walk. This was used to approximate the branching random walk in [Reference Ding and Goswami12] for a 4-ary tree. We have generalised the process for a d-ary tree. The switching-sign branching random walk consists of two parts: one that varies across vertices and another that is fixed over vertices. The first part of the process, which is not fixed over vertices, is different from the normal branching random walk in the sense that, instead of the d edges coming out of it being associated with independent normal random variables, they are associated with linear combinations of
![]() $d-1$
independent Gaussians, such that the covariance between any two of them is the same, and all of them add up to zero. The existence of this is guaranteed by the following lemma.
$d-1$
independent Gaussians, such that the covariance between any two of them is the same, and all of them add up to zero. The existence of this is guaranteed by the following lemma.
Lemma 3.1.
There exists
![]() $A \in \mathbb{R}^{(d-1)\times(d-1)}$
such that for
$A \in \mathbb{R}^{(d-1)\times(d-1)}$
such that for
![]() $W \sim N(0, \sigma^2 I_{(d-1) \times (d-1)})$
, the covariance matrix of
$W \sim N(0, \sigma^2 I_{(d-1) \times (d-1)})$
, the covariance matrix of
![]() $\tilde{Y}=(Y_1, Y_2, \cdots, Y_{d-1})^{\top}=AW$
has diagonal entries equal to
$\tilde{Y}=(Y_1, Y_2, \cdots, Y_{d-1})^{\top}=AW$
has diagonal entries equal to
![]() $\sigma^2$
and all its off-diagonal entries equal (say
$\sigma^2$
and all its off-diagonal entries equal (say
![]() $\eta$
). Further,
$\eta$
). Further,
![]() ${\textrm{Var}}({{\bf 1}}^{\top} AW)=\sigma^2$
and
${\textrm{Var}}({{\bf 1}}^{\top} AW)=\sigma^2$
and
![]() ${\textrm{Cov}}(-{{\bf 1}}^{\top}AW, (AW)_i)=\eta$
for all
${\textrm{Cov}}(-{{\bf 1}}^{\top}AW, (AW)_i)=\eta$
for all
![]() $i \in \{1, 2, \ldots, d-1\}$
. Here
$i \in \{1, 2, \ldots, d-1\}$
. Here
![]() ${{\bf 1}}$
denotes the column vector of size
${{\bf 1}}$
denotes the column vector of size
![]() $d-1$
with all entries equal to 1, and
$d-1$
with all entries equal to 1, and
![]() ${{\bf 1}}^{\top}$
is its transpose.
${{\bf 1}}^{\top}$
is its transpose.
Proof. We know that the covariance matrix for
![]() $\tilde{Y}$
is
$\tilde{Y}$
is
![]() $\sigma^2 AA^{\top}$
. Further, from the condition that
$\sigma^2 AA^{\top}$
. Further, from the condition that
![]() ${\textrm{Var}}({{\bf 1}}^{\top} AW)=\sigma^2$
, we get
${\textrm{Var}}({{\bf 1}}^{\top} AW)=\sigma^2$
, we get
![]() $\eta=-{\sigma^2}/{(d-1)}$
. So in order for A to exist we must have
$\eta=-{\sigma^2}/{(d-1)}$
. So in order for A to exist we must have
 \[AA^{\top}= \begin{bmatrix}1 & -\frac{1}{d-1} & -\frac{1}{d-1} & \dots & -\frac{1}{d-1} \\-\frac{1}{d-1} & 1 & -\frac{1}{d-1} & \dots & -\frac{1}{d-1} \\\vdots & \vdots & \vdots & \ddots & \vdots \\-\frac{1}{d-1} & -\frac{1}{d-1} & -\frac{1}{d-1} & \dots & 1\end{bmatrix} {\in \mathbb{R}^{(d-1) \times (d-1)}}\]
\[AA^{\top}= \begin{bmatrix}1 & -\frac{1}{d-1} & -\frac{1}{d-1} & \dots & -\frac{1}{d-1} \\-\frac{1}{d-1} & 1 & -\frac{1}{d-1} & \dots & -\frac{1}{d-1} \\\vdots & \vdots & \vdots & \ddots & \vdots \\-\frac{1}{d-1} & -\frac{1}{d-1} & -\frac{1}{d-1} & \dots & 1\end{bmatrix} {\in \mathbb{R}^{(d-1) \times (d-1)}}\]
Since the matrix on the right-hand side is a symmetric matrix with non-negative eigenvalues, by Cholesky decomposition we obtain the existence of such an A. In particular, we have a specific choice of
where
![]() $J_{k\times k}$
is the square matrix of order k with all entries equal to 1.
$J_{k\times k}$
is the square matrix of order k with all entries equal to 1.
We now define
![]() $Y_d=-{{\bf 1}}^{\top}\tilde{Y}$
, and
$Y_d=-{{\bf 1}}^{\top}\tilde{Y}$
, and
![]() $Y=(Y_1, Y_2, \ldots, Y_{d})^{\top}$
. This Y is a degenerate multivariate normal, with variance–covariance matrix given as follows:
$Y=(Y_1, Y_2, \ldots, Y_{d})^{\top}$
. This Y is a degenerate multivariate normal, with variance–covariance matrix given as follows:
 \begin{equation}\begin{aligned}{\textrm{Var}} (Y_i) &= \sigma^2 \quad \text{for all } i \in \{1,2,\ldots, d\}, \\{\textrm{Cov}}(Y_i, Y_j) &= - \dfrac{\sigma^2}{d-1} \quad \text{ for all }i \neq j \in \{1,2,\ldots, d\} \,.\end{aligned}\end{equation}
\begin{equation}\begin{aligned}{\textrm{Var}} (Y_i) &= \sigma^2 \quad \text{for all } i \in \{1,2,\ldots, d\}, \\{\textrm{Cov}}(Y_i, Y_j) &= - \dfrac{\sigma^2}{d-1} \quad \text{ for all }i \neq j \in \{1,2,\ldots, d\} \,.\end{aligned}\end{equation}
A pictorial representation of a node for the SSBRW process is given in Figure 2.

Figure 2. Node of the varying part of a switching-sign branching random walk.
We now provide a few heuristic descriptions of the SSBRW, followed by a formal definition.
We consider a particle starting from a random point
![]() $X \in \mathbb{R}$
, which dies at time 1 and splits into d children. The joint distribution of the distances travelled by these children is given by (3.1), with a choice of
$X \in \mathbb{R}$
, which dies at time 1 and splits into d children. The joint distribution of the distances travelled by these children is given by (3.1), with a choice of
![]() $\sigma^2=1-d^{-n}$
. Then, at time 2, each of these children die and give rise to d children, which in turn follow the same process, the displacements at each step being independent of the displacements in the previous time points, except for the variances and covariances at level l being
$\sigma^2=1-d^{-n}$
. Then, at time 2, each of these children die and give rise to d children, which in turn follow the same process, the displacements at each step being independent of the displacements in the previous time points, except for the variances and covariances at level l being
![]() $1-d^{-(n-l+1)}$
and
$1-d^{-(n-l+1)}$
and
![]() $-{(1-d^{-(n-l+1)})}/{(d-1)}$
respectively. At time n we have
$-{(1-d^{-(n-l+1)})}/{(d-1)}$
respectively. At time n we have
![]() $d^n$
particles, each having a displacement. The displacements of the collection of these particles are called a switching-sign branching random walk at time n. The random term X is normally distributed, with mean 0 and variance
$d^n$
particles, each having a displacement. The displacements of the collection of these particles are called a switching-sign branching random walk at time n. The random term X is normally distributed, with mean 0 and variance
![]() ${(1- d^{-n})}/{(d-1)}$
, and is independent of everything else.
${(1- d^{-n})}/{(d-1)}$
, and is independent of everything else.
We can equivalently define a switching-sign branching random walk as a Gaussian process on
![]() $T^n$
. The root is fixed at a random point X, and the displacements at each step are attached to the edges. So the first d displacements are attached to the edges between the root and its d children. To each vertex we attach a quantity equal to the sum of the Gaussians that we encounter while looking at the shortest path between itself and the root, plus the random variable attached to the root. Then the collection of the displacements of the
$T^n$
. The root is fixed at a random point X, and the displacements at each step are attached to the edges. So the first d displacements are attached to the edges between the root and its d children. To each vertex we attach a quantity equal to the sum of the Gaussians that we encounter while looking at the shortest path between itself and the root, plus the random variable attached to the root. Then the collection of the displacements of the
![]() $d^n$
particles at time n is given by the Gaussians attached to all the vertices in
$d^n$
particles at time n is given by the Gaussians attached to all the vertices in
![]() $T_n$
. We denote it by
$T_n$
. We denote it by
![]() $\{ \xi_v^n \colon v \in T_n \}$
. This is the switching-sign branching random walk at time n. Two particles at time n descended from the same ancestor at time k
$\{ \xi_v^n \colon v \in T_n \}$
. This is the switching-sign branching random walk at time n. Two particles at time n descended from the same ancestor at time k
![]() $(k \leq n)$
are equivalent to two leaf nodes that have branched out from the same vertex at level k of the tree. Each of these displacements is a sum of n independent Gaussians, plus the random term X which is independent of everything else.
$(k \leq n)$
are equivalent to two leaf nodes that have branched out from the same vertex at level k of the tree. Each of these displacements is a sum of n independent Gaussians, plus the random term X which is independent of everything else.
We now provide a formal definition of the SSBRW.
Definition 3.1. The collection
![]() $\{ Y_{i,j}\colon j=1,2,\ldots, d^i, i =1,2,\ldots, n \}$
represents displacements, and consists of Gaussian random variables. But unlike the BRW, we have
$\{ Y_{i,j}\colon j=1,2,\ldots, d^i, i =1,2,\ldots, n \}$
represents displacements, and consists of Gaussian random variables. But unlike the BRW, we have
![]() ${\textrm{Var}}(Y_{i,j})=1-d^{-(n-i+1)}$
. Also, the collection of
${\textrm{Var}}(Y_{i,j})=1-d^{-(n-i+1)}$
. Also, the collection of
![]() $\{Y_{i,j} \colon j=1,2,\ldots, d^i, i =1,2,\ldots, n \}$
does not represent a collection of independent random variables. Rather, we have
$\{Y_{i,j} \colon j=1,2,\ldots, d^i, i =1,2,\ldots, n \}$
does not represent a collection of independent random variables. Rather, we have
![]() $\sum_{j'=1}^d Y_{i,md+j'}=0$
, for all
$\sum_{j'=1}^d Y_{i,md+j'}=0$
, for all
![]() $m=\{0,1,\ldots, d^{i-1}-1\},$
$m=\{0,1,\ldots, d^{i-1}-1\},$
![]() $ i=\{1,2,\ldots, n\}$
. However, we do still have that
$ i=\{1,2,\ldots, n\}$
. However, we do still have that
![]() $Y_{i_1,j_1}$
and
$Y_{i_1,j_1}$
and
![]() $Y_{i_2, j_2}$
are independent if
$Y_{i_2, j_2}$
are independent if
![]() $i_1\neq i_2$
. Also,
$i_1\neq i_2$
. Also,
![]() $Y_{i,j_1}$
and
$Y_{i,j_1}$
and
![]() $Y_{i, j_2}$
are independent if
$Y_{i, j_2}$
are independent if
![]() $\lceil j_1/d \rceil \neq \lceil j_2/d \rceil$
. Otherwise, if
$\lceil j_1/d \rceil \neq \lceil j_2/d \rceil$
. Otherwise, if
![]() $\lceil j_1/d \rceil =\lceil j_2/d \rceil$
, then
$\lceil j_1/d \rceil =\lceil j_2/d \rceil$
, then
![]() $Y_{i,j_1}$
and
$Y_{i,j_1}$
and
![]() $Y_{i, j_2}$
are not independent, and
$Y_{i, j_2}$
are not independent, and
There are
![]() $d^n$
leaf nodes in the tree, and we can fix an ordering of the vertices from 1 to
$d^n$
leaf nodes in the tree, and we can fix an ordering of the vertices from 1 to
![]() $d^n$
. For any
$d^n$
. For any
![]() $v \in T_n$
, i.e.
$v \in T_n$
, i.e.
![]() $v \in \{1,2,\ldots, d^n \}$
, we define
$v \in \{1,2,\ldots, d^n \}$
, we define
![]() $a_i(v)=\lceil {v}/{(d^{n-i})}\rceil$
for
$a_i(v)=\lceil {v}/{(d^{n-i})}\rceil$
for
![]() $i=1,2,\ldots, n$
. Then we can define
$i=1,2,\ldots, n$
. Then we can define
![]() $\tilde{\phi}_v^n=\sum_{j=1}^n Y_{j,a_j(v)}$
. The switching-sign branching random walk is given by
$\tilde{\phi}_v^n=\sum_{j=1}^n Y_{j,a_j(v)}$
. The switching-sign branching random walk is given by
where X is an independent Gaussian variable with mean zero and variance
![]() ${(1- d^{-n})}/{(d-1)}$
.
${(1- d^{-n})}/{(d-1)}$
.
Figure 3 gives a pictorial representation of the switching-sign branching random walk for the case
![]() $d=2$
, i.e. on a binary tree. All the
$d=2$
, i.e. on a binary tree. All the
![]() $Y_{i,j}$
represent displacements and are distributed as Gaussian. In this figure we show the dependence described in the paragraph above by replacing one of the dependent random variables with the relevant function of the others with which it correlates.
$Y_{i,j}$
represent displacements and are distributed as Gaussian. In this figure we show the dependence described in the paragraph above by replacing one of the dependent random variables with the relevant function of the others with which it correlates.

Figure 3. Switching-sign branching random walk on a binary tree.
In this construction, unlike the BRW, we have a different variance for each level l (
![]() $1\le l \le n$
). Here, level 1 denotes the edge connecting the root to its children and level n denotes the edges joining the leaf nodes to their parents. We denote this switching-sign branching random walk on the leaf nodes
$1\le l \le n$
). Here, level 1 denotes the edge connecting the root to its children and level n denotes the edges joining the leaf nodes to their parents. We denote this switching-sign branching random walk on the leaf nodes
![]() $T_n$
as
$T_n$
as
![]() $\{ \xi_v^n \colon v \in T_n \}$
. For
$\{ \xi_v^n \colon v \in T_n \}$
. For
![]() $v \in T_n$
we let
$v \in T_n$
we let
![]() $Y_{l,a_l(v)}$
, as defined earlier, denote the Gaussian variable that is added on level l, on the path connecting v to the root. We have
$Y_{l,a_l(v)}$
, as defined earlier, denote the Gaussian variable that is added on level l, on the path connecting v to the root. We have
![]() ${\textrm{Var}}( Y_{l,a_l(v)})= 1 - d^{-(n-l+1)}$
as stated in the formal definition. The switching-sign branching random walk will consist of two parts, the first coming from the contribution at different levels in the tree, which is
${\textrm{Var}}( Y_{l,a_l(v)})= 1 - d^{-(n-l+1)}$
as stated in the formal definition. The switching-sign branching random walk will consist of two parts, the first coming from the contribution at different levels in the tree, which is
![]() $\tilde{\phi}_v^n \overset{\textrm{def}}{=} \sum_{l=1}^n Y_{l,a_l(v)}$
. The second part is the random variable X, which is an independent Gaussian variable with mean zero and variance
$\tilde{\phi}_v^n \overset{\textrm{def}}{=} \sum_{l=1}^n Y_{l,a_l(v)}$
. The second part is the random variable X, which is an independent Gaussian variable with mean zero and variance
![]() ${(1- d^{-n})}/{(d-1)}$
. The two parts are summed together to get
${(1- d^{-n})}/{(d-1)}$
. The two parts are summed together to get
![]() $\xi_v^n$
.
$\xi_v^n$
.
The covariance structure for this new model closely resembles that of the branching random walk. The following lemma deals with this comparison.
Lemma 3.2.
The Gaussian fields
![]() $\{ \xi^n_v\colon v \in T_n \}$
and
$\{ \xi^n_v\colon v \in T_n \}$
and
![]() $\{ \phi_v^n \colon v \in T_n \}$
are identically distributed.
$\{ \phi_v^n \colon v \in T_n \}$
are identically distributed.
Proof. First we show that the variances are identical for the two processes. To this end, we begin by computing the variance of
![]() $\xi^n_v$
as follows:
$\xi^n_v$
as follows:
 \begin{align*}{\textrm{Var}}(\xi^n_v) &= 1 - d^{-1}+ 1 - d^{-2}+ \cdots + 1 - d^{-n} + \dfrac{1- d^{-n}}{d-1}\\&= n - \dfrac{1- d^{-n}}{d-1}+ \dfrac{1- d^{-n}}{d-1}\\&= n.\end{align*}
\begin{align*}{\textrm{Var}}(\xi^n_v) &= 1 - d^{-1}+ 1 - d^{-2}+ \cdots + 1 - d^{-n} + \dfrac{1- d^{-n}}{d-1}\\&= n - \dfrac{1- d^{-n}}{d-1}+ \dfrac{1- d^{-n}}{d-1}\\&= n.\end{align*}
Next, for the covariances we consider
![]() $u, v \in T_n$
,
$u, v \in T_n$
,
![]() $u \neq v$
, such that they have the last common ancestor at generation
$u \neq v$
, such that they have the last common ancestor at generation
![]() $n-k$
, i.e.
$n-k$
, i.e.
![]() ${\textrm{Cov}}(\phi^n_u, \phi^n_v)=n-k$
. Then we have
${\textrm{Cov}}(\phi^n_u, \phi^n_v)=n-k$
. Then we have
 \begin{equation}\begin{aligned}a_i (u) &= a_i (v) \quad \text{for $ 1\leq i \leq n- k$,} \\a_i (u)& \neq a_i (v) \quad \text{for $ n-k+1\leq i \leq n$,} \\\lceil a_{n-k+1}(u)/d \rceil &= \lceil a_{n-k+1}(v)/d \rceil, \\\lceil a_{j}(u)/d \rceil &\neq \lceil a_{j}(v)/d \rceil \quad \text{for $ n-k+2\leq i \leq n$.}\end{aligned}\end{equation}
\begin{equation}\begin{aligned}a_i (u) &= a_i (v) \quad \text{for $ 1\leq i \leq n- k$,} \\a_i (u)& \neq a_i (v) \quad \text{for $ n-k+1\leq i \leq n$,} \\\lceil a_{n-k+1}(u)/d \rceil &= \lceil a_{n-k+1}(v)/d \rceil, \\\lceil a_{j}(u)/d \rceil &\neq \lceil a_{j}(v)/d \rceil \quad \text{for $ n-k+2\leq i \leq n$.}\end{aligned}\end{equation}
We know that
from the fact that
![]() $Y_{i_1,j_1}$
and
$Y_{i_1,j_1}$
and
![]() $Y_{i_2, j_2}$
are independent if
$Y_{i_2, j_2}$
are independent if
![]() $i_1\neq i_2$
. From (3.2) we have
$i_1\neq i_2$
. From (3.2) we have
 \begin{equation*}{\textrm{Cov}}( \tilde{\phi}_u^n, \tilde{\phi}_v^n)= \sum_{i=1}^{n-k} {\textrm{Var}}(Y_{i, a_i(u)})+ {\textrm{Cov}}(Y_{n-k+1, a_{n-k+1}(u)}, Y_{n-k+1, a_{n-k+1}(v)}).\end{equation*}
\begin{equation*}{\textrm{Cov}}( \tilde{\phi}_u^n, \tilde{\phi}_v^n)= \sum_{i=1}^{n-k} {\textrm{Var}}(Y_{i, a_i(u)})+ {\textrm{Cov}}(Y_{n-k+1, a_{n-k+1}(u)}, Y_{n-k+1, a_{n-k+1}(v)}).\end{equation*}
Plugging in the values, we get
Hence
So the covariance structures for the fields
![]() $\xi$
and
$\xi$
and
![]() $\phi$
match, and hence they are identically distributed.
$\phi$
match, and hence they are identically distributed.
A simple corollary of Lemma 3.2 is the following, based on the fact that the two processes have identical distributions.
Corollary 3.1. We have the following equality:
Corollary 3.2. From [Reference Zeitouni19, Theorem 4] we have
Therefore
Corollary 3.3.
There exist constants
![]() $\bar{C}' , c^* >0$
such that, for all
$\bar{C}' , c^* >0$
such that, for all
![]() $n \in \mathbb{N}$
and
$n \in \mathbb{N}$
and
![]() $0 \le \lambda \le ( n)^{2/3}$
,
$0 \le \lambda \le ( n)^{2/3}$
,
Proof.
Now, using (2.1) and with
![]() $\bar{C}'= 2\bar{C}$
, we arrive at (3.4).
$\bar{C}'= 2\bar{C}$
, we arrive at (3.4).
4. Estimates on left tail and positivity
From equation (3.3) we understand that the probability of positivity for the branching random walk can be computed using bounds on the left tail of the maximum of
![]() $\tilde{\phi}^n_.$
, a part of the switching-sign branching random walk, as the left tail is heavily concentrated around the maximum. This motivates the following computations on the left tail of the maximum.
$\tilde{\phi}^n_.$
, a part of the switching-sign branching random walk, as the left tail is heavily concentrated around the maximum. This motivates the following computations on the left tail of the maximum.
Lemma 4.1.
We let
![]() $c=1/\sqrt{2 \log d}$
, where
$c=1/\sqrt{2 \log d}$
, where
denote the constant such that
![]() $|m_{n-c\lambda }- m_n+\lambda|\rightarrow 0$
as
$|m_{n-c\lambda }- m_n+\lambda|\rightarrow 0$
as
![]() $n\rightarrow \infty$
, where
$n\rightarrow \infty$
, where
![]() $\lambda=\lambda(n)={{\textrm{o}}}(n)$
is positive. Then there exist constants Cʹ, Cʹʹ, Kʹ, Kʹʹ independent of n such that for sufficiently large n we have
$\lambda=\lambda(n)={{\textrm{o}}}(n)$
is positive. Then there exist constants Cʹ, Cʹʹ, Kʹ, Kʹʹ independent of n such that for sufficiently large n we have
Proof. We work with
![]() ${\mathbb{P}}(\max_{v \in T_n} \tilde{\phi}_v \le m_{n - c\lambda})$
, as due to our definition of c, for sufficiently large n this probability is close to
${\mathbb{P}}(\max_{v \in T_n} \tilde{\phi}_v \le m_{n - c\lambda})$
, as due to our definition of c, for sufficiently large n this probability is close to
![]() ${\mathbb{P}}(\max_{v \in T_n} \tilde{\phi}_v \le m_n - \lambda )$
. From [Reference Bramson, Ding and Zeitouni6] and [Reference Ding, Roy and Zeitouni13] we can see that
${\mathbb{P}}(\max_{v \in T_n} \tilde{\phi}_v \le m_n - \lambda )$
. From [Reference Bramson, Ding and Zeitouni6] and [Reference Ding, Roy and Zeitouni13] we can see that
![]() $\{ \max_{v \in T_n} \tilde{\phi}_v - m_n \}$
converges in distribution, as it is equivalent in distribution to a BRW, after adding the same independent Gaussian to all points. Hence
$\{ \max_{v \in T_n} \tilde{\phi}_v - m_n \}$
converges in distribution, as it is equivalent in distribution to a BRW, after adding the same independent Gaussian to all points. Hence
![]() ${\mathbb{P}}(\max_{v \in T_n} \tilde{\phi}_v \le m_{n - c\lambda})$
and
${\mathbb{P}}(\max_{v \in T_n} \tilde{\phi}_v \le m_{n - c\lambda})$
and
![]() ${\mathbb{P}}(\max_{v \in T_n} \tilde{\phi}_v \le m_n - \lambda )$
converge to the same point. We know that the BRW is a Gaussian field obtained by adding the same Gaussian to all vertices of an SSBRW. This helps us find bounds on lower and upper tails of the maximum of an SSBRW using results on convergence of the maximum of a BRW, as proved in [Reference Aïdékon1] and [Reference Bramson, Ding and Zeitouni6], etc.
${\mathbb{P}}(\max_{v \in T_n} \tilde{\phi}_v \le m_n - \lambda )$
converge to the same point. We know that the BRW is a Gaussian field obtained by adding the same Gaussian to all vertices of an SSBRW. This helps us find bounds on lower and upper tails of the maximum of an SSBRW using results on convergence of the maximum of a BRW, as proved in [Reference Aïdékon1] and [Reference Bramson, Ding and Zeitouni6], etc.
We also force
![]() $\lambda$
to be such that
$\lambda$
to be such that
![]() $c\lambda$
is an integer. For other values of
$c\lambda$
is an integer. For other values of
![]() $\lambda$
, we can adjust for the constants by looking at
$\lambda$
, we can adjust for the constants by looking at
![]() $\lceil c\lambda \rceil$
and
$\lceil c\lambda \rceil$
and
![]() $\lfloor c \lambda \rfloor$
. We first consider the tree only up to the level
$\lfloor c \lambda \rfloor$
. We first consider the tree only up to the level
![]() $c\lambda$
and consider the cumulative sum of the Gaussian variables at these vertices till the level
$c\lambda$
and consider the cumulative sum of the Gaussian variables at these vertices till the level
![]() $c\lambda$
. We rename all these Gaussian variables at level
$c\lambda$
. We rename all these Gaussian variables at level
![]() $c\lambda$
of this new tree to be
$c\lambda$
of this new tree to be
![]() $A_1, A_2, \ldots, A_{d^{c\lambda}}$
. Then each
$A_1, A_2, \ldots, A_{d^{c\lambda}}$
. Then each
![]() $A_i$
is essentially of the form
$A_i$
is essentially of the form
![]() $\sum_{j=1}^{c\lambda} Y_{j,a_j(v)}$
for some
$\sum_{j=1}^{c\lambda} Y_{j,a_j(v)}$
for some
![]() $v\in T_n$
. We know that the definition in Section 3 of the SSBRW model guarantees
$v\in T_n$
. We know that the definition in Section 3 of the SSBRW model guarantees
![]() $\sum_{i=1}^{d^{c\lambda}} A_i = 0$
. We consider the subtrees rooted at the vertex which has values
$\sum_{i=1}^{d^{c\lambda}} A_i = 0$
. We consider the subtrees rooted at the vertex which has values
![]() $A_i$
and call its maximum
$A_i$
and call its maximum
![]() $M_i$
. These are trees of height
$M_i$
. These are trees of height
![]() $n-c\lambda$
, and hence we have
$n-c\lambda$
, and hence we have
We want to obtain bounds for the probability
![]() ${\mathbb{P}}(\max_{v \in T_n} \tilde{\phi}_v \leq m_{n-c\lambda})$
. We condition on the values of
${\mathbb{P}}(\max_{v \in T_n} \tilde{\phi}_v \leq m_{n-c\lambda})$
. We condition on the values of
![]() $A_1, A_2, \ldots, A_{d^{c\lambda}}$
, which in turn breaks down the required probability in a product form since the maxima for the
$A_1, A_2, \ldots, A_{d^{c\lambda}}$
, which in turn breaks down the required probability in a product form since the maxima for the
![]() $d^{c \lambda}$
subtrees are independent and have identical distributions. We have the following:
$d^{c \lambda}$
subtrees are independent and have identical distributions. We have the following:
This can be further broken down from independence as
 \begin{align}{\mathbb{P}}\Bigl(\max_{i=1}^{d^{c\lambda}} (M_i + A_i) \leq m_{n-c\lambda} \mid A_1, A_2, \ldots, A_{d^{c\lambda}} \Bigr)=\prod_{i=1}^{d^{c\lambda}} {\mathbb{P}}(M_i + A_i \leq m_{n-c\lambda} \mid A_i ).\end{align}
\begin{align}{\mathbb{P}}\Bigl(\max_{i=1}^{d^{c\lambda}} (M_i + A_i) \leq m_{n-c\lambda} \mid A_1, A_2, \ldots, A_{d^{c\lambda}} \Bigr)=\prod_{i=1}^{d^{c\lambda}} {\mathbb{P}}(M_i + A_i \leq m_{n-c\lambda} \mid A_i ).\end{align}
The right-hand side of (4.2) satisfies the following inequality:
 \[\prod_{i=1}^{d^{c\lambda}} {\mathbb{P}}(M_i + A_i \leq m_{n-c\lambda} \mid A_i ) \leq \prod_{i\colon A_i > 0}^{d^{c\lambda}} {\mathbb{P}}(M_i \leq m_{n-c\lambda}-A_i \mid A_i ),\]
\[\prod_{i=1}^{d^{c\lambda}} {\mathbb{P}}(M_i + A_i \leq m_{n-c\lambda} \mid A_i ) \leq \prod_{i\colon A_i > 0}^{d^{c\lambda}} {\mathbb{P}}(M_i \leq m_{n-c\lambda}-A_i \mid A_i ),\]
which happens since for the cases where
![]() $A_i < 0$
we bound the terms in the product by 1. The right-hand side of the last inequality is further bounded by
$A_i < 0$
we bound the terms in the product by 1. The right-hand side of the last inequality is further bounded by
 \begin{equation}(\bar{C'}\vee1)^{d^{c\lambda}} \exp\Biggl(-c^* \sum_{i=1}^{d^{c\lambda}}A_i^+\Biggr) = \exp\Biggl({d^{c\lambda}} \log (\bar{C'}\vee1) -c^* \sum_{i=1}^{d^{c\lambda}}A_i^-\Biggr) .\end{equation}
\begin{equation}(\bar{C'}\vee1)^{d^{c\lambda}} \exp\Biggl(-c^* \sum_{i=1}^{d^{c\lambda}}A_i^+\Biggr) = \exp\Biggl({d^{c\lambda}} \log (\bar{C'}\vee1) -c^* \sum_{i=1}^{d^{c\lambda}}A_i^-\Biggr) .\end{equation}
In the final two steps we first make use of (3.4), followed by the fact that
![]() $\sum_i A_i =0$
. We consider two different cases:
$\sum_i A_i =0$
. We consider two different cases:
-
(1)
 $A_i^- \leq 2\bar{A}$
for at least
$A_i^- \leq 2\bar{A}$
for at least
 $d^{c\lambda}/2$
many i, where
$d^{c\lambda}/2$
many i, where
 $\bar{A}$
is a positive constant to be chosen later on;
$\bar{A}$
is a positive constant to be chosen later on; -
(2) case (1) does not happen and thus
 $\sum_{i=1}^{d^{c\lambda}} A_i^- \geq \bar{A} d^{c\lambda}$
.
$\sum_{i=1}^{d^{c\lambda}} A_i^- \geq \bar{A} d^{c\lambda}$
.
Even for case (1) we break it down into two parts according to whether or not
![]() $\sum_{i=1}^{d^{c\lambda}} A_i^- \geq \bar{A} d^{c\lambda}$
.
$\sum_{i=1}^{d^{c\lambda}} A_i^- \geq \bar{A} d^{c\lambda}$
.
When (2) holds then clearly (4.3) is bounded by
![]() $\exp(- (c^* \bar{A} - \log (\bar{C'}\vee1)) d^{c\lambda})$
, and now on choosing
$\exp(- (c^* \bar{A} - \log (\bar{C'}\vee1)) d^{c\lambda})$
, and now on choosing
![]() $\bar{A}$
such that
$\bar{A}$
such that
![]() $c^* \bar{A} - \log (\bar{C'}\vee1)> 0$
, we have
$c^* \bar{A} - \log (\bar{C'}\vee1)> 0$
, we have
![]() $c^{**}>0$
such that our required term is bounded by
$c^{**}>0$
such that our required term is bounded by
![]() $\exp(- c^{**} d^{c\lambda})$
.
$\exp(- c^{**} d^{c\lambda})$
.
In the other case also
for those i for which
![]() $A_i^- \leq 2\bar{A}$
. From the lower bound on the right tail of the maximum of a branching random walk (see [Reference Zeitouni19, eq.(2.5.11)]), we can find p, independent of n, where
$A_i^- \leq 2\bar{A}$
. From the lower bound on the right tail of the maximum of a branching random walk (see [Reference Zeitouni19, eq.(2.5.11)]), we can find p, independent of n, where
![]() $0<p<1$
such that
$0<p<1$
such that
![]() ${\mathbb{P}}(M_i \leq m_{n-c\lambda}+2\bar{A})<p$
for all sufficiently large n and so the probability
${\mathbb{P}}(M_i \leq m_{n-c\lambda}+2\bar{A})<p$
for all sufficiently large n and so the probability
 \[\prod_{i=1}^{d^{c\lambda}} {\mathbb{P}}(M_i + A_i \leq m_{n-c\lambda} \mid A_i )\]
\[\prod_{i=1}^{d^{c\lambda}} {\mathbb{P}}(M_i + A_i \leq m_{n-c\lambda} \mid A_i )\]
is bounded by
![]() $\exp(-\bar{c}d^{c\lambda})$
. Now, from this
$\exp(-\bar{c}d^{c\lambda})$
. Now, from this
![]() $\bar{c}$
and
$\bar{c}$
and
![]() $c^{**}$
we select one unified Cʹ, Cʹʹ so that
$c^{**}$
we select one unified Cʹ, Cʹʹ so that
Again for the lower bound we have
 \begin{align*}{\mathbb{P}}\Bigl(\max_{v \in T_n} \tilde{\phi}_v \le m_{n - c\lambda} \Bigr) &= \int_{\mathbb{R}^{d^{c\lambda}}} \prod_{i=1}^{d^{c\lambda}} {\mathbb{P}}(M_i \leq m_{n-c\lambda}- A_i ) \,{{\textrm{d}}} P_{A_1,\ldots, A_{d^{c\lambda}}} \\&\ge (\bar{p})^{d^{c\lambda}} \int_{[-1,1]^{d^{c\lambda}}} \,{{\textrm{d}}} P_{A_1,\ldots, A_{d^{c\lambda}}},\end{align*}
\begin{align*}{\mathbb{P}}\Bigl(\max_{v \in T_n} \tilde{\phi}_v \le m_{n - c\lambda} \Bigr) &= \int_{\mathbb{R}^{d^{c\lambda}}} \prod_{i=1}^{d^{c\lambda}} {\mathbb{P}}(M_i \leq m_{n-c\lambda}- A_i ) \,{{\textrm{d}}} P_{A_1,\ldots, A_{d^{c\lambda}}} \\&\ge (\bar{p})^{d^{c\lambda}} \int_{[-1,1]^{d^{c\lambda}}} \,{{\textrm{d}}} P_{A_1,\ldots, A_{d^{c\lambda}}},\end{align*}
where
![]() $\bar{p}$
is chosen to be a lower bound on
$\bar{p}$
is chosen to be a lower bound on
![]() ${\mathbb{P}}(M_i \leq m_{n-c\lambda}-1)$
for all sufficiently large n, which can be obtained from using convergence results on the maximum of the branching random walk. Now
${\mathbb{P}}(M_i \leq m_{n-c\lambda}-1)$
for all sufficiently large n, which can be obtained from using convergence results on the maximum of the branching random walk. Now
![]() $\{A_1, A_2, \ldots, A_{d^{c\lambda}}\}$
are obtained by linear combinations of
$\{A_1, A_2, \ldots, A_{d^{c\lambda}}\}$
are obtained by linear combinations of
![]() $c\lambda$
independent Gaussian random variables
$c\lambda$
independent Gaussian random variables
One way to force all the
![]() $A_i$
to be in the range
$A_i$
to be in the range
![]() $[{-}1,1]$
is to take the absolute value of the contribution at the jth level (i.e.
$[{-}1,1]$
is to take the absolute value of the contribution at the jth level (i.e.
![]() $Y_{j,a_v(j)}$
) to be bounded by
$Y_{j,a_v(j)}$
) to be bounded by
![]() ${1}/{(10(c\lambda+1-j)^2)}$
, for
${1}/{(10(c\lambda+1-j)^2)}$
, for
![]() $j=1, 2, \ldots, c\lambda$
. Each of these
$j=1, 2, \ldots, c\lambda$
. Each of these
![]() $Y_{j,a_v(j)}$
comes from translation of independent standard Gaussians, which we bounded. So the independent standard Gaussians for level j are bounded by
$Y_{j,a_v(j)}$
comes from translation of independent standard Gaussians, which we bounded. So the independent standard Gaussians for level j are bounded by
![]() ${1}/{(10 \sqrt{d}(c \lambda +1-j)^2)}$
. For some constant
${1}/{(10 \sqrt{d}(c \lambda +1-j)^2)}$
. For some constant
![]() $K>0$
, this gives
$K>0$
, this gives
 \begin{equation*}{\mathbb{P}}\Bigl(\max_{v \in T_n} \tilde{\phi}_v \le m_{n - c\lambda} \Bigr)\ge (\bar{p})^{d^{c\lambda}} \prod_{j=1}^{c\lambda} \biggl( \dfrac{1}{10 K \sqrt{d}(c \lambda +1-j)^2} \biggr)^{(d-1)d^{j-1}} .\end{equation*}
\begin{equation*}{\mathbb{P}}\Bigl(\max_{v \in T_n} \tilde{\phi}_v \le m_{n - c\lambda} \Bigr)\ge (\bar{p})^{d^{c\lambda}} \prod_{j=1}^{c\lambda} \biggl( \dfrac{1}{10 K \sqrt{d}(c \lambda +1-j)^2} \biggr)^{(d-1)d^{j-1}} .\end{equation*}
We take a logarithm of this term above, which leads to a sum. Approximation of the sum, as shown below in Lemma 4.2, proves (4.1).
Lemma 4.2.
![]() $\sum_{j=1}^{n} (\log |n+1-j|) d^j$
is of order
$\sum_{j=1}^{n} (\log |n+1-j|) d^j$
is of order
![]() $\Theta(d^n)$
.
$\Theta(d^n)$
.
Proof. We begin with an upper bound on the sum. We use a trivial bound of
![]() $\log |x| \le |x|$
for
$\log |x| \le |x|$
for
![]() $|x| \geq 1$
, followed by a few series summations:
$|x| \geq 1$
, followed by a few series summations:
 \begin{align*}\sum_{j=1}^{n} (\!\log |n+1-j|) d^j &\le \sum_{j=1}^{n} ( |n+1-j|) d^j \\&= (n+1) \sum_{j=1}^{n} d^j - \sum_{j=1}^{n} j d^j \\&= (n+1) \dfrac{d^{n+1}-d}{d-1} - \dfrac{nd^{n+2}- (n+1)d^{n+1} +d}{(d-1)^2} \\&= \dfrac{d^{n+2}- (n+1)d^{2} +nd}{(d-1)^2} .\end{align*}
\begin{align*}\sum_{j=1}^{n} (\!\log |n+1-j|) d^j &\le \sum_{j=1}^{n} ( |n+1-j|) d^j \\&= (n+1) \sum_{j=1}^{n} d^j - \sum_{j=1}^{n} j d^j \\&= (n+1) \dfrac{d^{n+1}-d}{d-1} - \dfrac{nd^{n+2}- (n+1)d^{n+1} +d}{(d-1)^2} \\&= \dfrac{d^{n+2}- (n+1)d^{2} +nd}{(d-1)^2} .\end{align*}
This gives an upper bound of order
![]() $d^n$
. The lower bound follows easily.
$d^n$
. The lower bound follows easily.
We now return to our question of the branching random walk being positive at all vertices. We know that the maximum of the BRW is heavily concentrated around the expected maximum. Using this fact, in a neighbourhood around the maximum, we further try to maximise the probability of the maximum being there. The point where this occurs will also roughly be the typical value of a vertex. This motivates the proof of Theorem 1.1.
Proof of Theorem 1.1. Upper bound. From (3.3) we have an upper bound on the probability of positivity based on the switching-sign branching random walk. We optimise this bound by first raising the mean to a level and look at the corresponding compensation we have to apply. We optimise over these two to obtain our bound. We use a similar strategy to obtain the lower bound as well. We recall (3.3) at this juncture along with X, and the variance of X to be
![]() $\sigma_{d,n}^2 = {(1-d^{-n})}/{(d-1)}$
. Let us recall the event
$\sigma_{d,n}^2 = {(1-d^{-n})}/{(d-1)}$
. Let us recall the event
![]() $\Lambda_n^+$
defined before as
$\Lambda_n^+$
defined before as
![]() $\{ \phi_v^n \ge 0 \ \forall\, v \in T_n\}$
. In (3.3) we condition on the value of X to obtain the following:
$\{ \phi_v^n \ge 0 \ \forall\, v \in T_n\}$
. In (3.3) we condition on the value of X to obtain the following:
Instead of integrating over x we may as well replace x with
![]() $m_{n} - \lambda$
, and then integrate over
$m_{n} - \lambda$
, and then integrate over
![]() $\lambda$
. We split the integral into three parts, the first with
$\lambda$
. We split the integral into three parts, the first with
![]() $\{ -\infty < \lambda \le 0\} $
, the second
$\{ -\infty < \lambda \le 0\} $
, the second
![]() $\{{3}{c}^{-1}\log_d n \le \lambda < \infty \}$
, and the third
$\{{3}{c}^{-1}\log_d n \le \lambda < \infty \}$
, and the third
![]() $\{0 < \lambda \leq 3 c^{-1}\log_d n\}$
. From tail estimates of a Gaussian, the first part is bounded by
$\{0 < \lambda \leq 3 c^{-1}\log_d n\}$
. From tail estimates of a Gaussian, the first part is bounded by
From (4.1), we know that the second part is bounded by
![]() $C' \exp(-C''n^3)$
. The remaining part has the upper bound
$C' \exp(-C''n^3)$
. The remaining part has the upper bound
 \begin{equation}\dfrac{C'}{\sigma_{d,n}\sqrt{2\pi}} \int_{0}^{{{3}{c}^{-1}}\log_d n } \exp({-}C''d^{c\lambda})\exp({-(m_{n} - \lambda)^2/2\sigma^2_{d,n}})\,{{\textrm{d}}}\lambda.\end{equation}
\begin{equation}\dfrac{C'}{\sigma_{d,n}\sqrt{2\pi}} \int_{0}^{{{3}{c}^{-1}}\log_d n } \exp({-}C''d^{c\lambda})\exp({-(m_{n} - \lambda)^2/2\sigma^2_{d,n}})\,{{\textrm{d}}}\lambda.\end{equation}
We maximise the integrand in (4.4), over the range of the integral, to obtain an optimal
![]() $\lambda$
, say
$\lambda$
, say
![]() $\lambda'$
, which is of order
$\lambda'$
, which is of order
![]() $\log n$
. It satisfies the equation
$\log n$
. It satisfies the equation
Recalling from Lemma 4 that
we can see that
This implies that
Substituting, we obtain an upper bound as in (1.2).
Lower bound. Again recalling (4.1), we obtain that
The integrand here is in fact a decreasing function of
![]() $\lambda$
in the range
$\lambda$
in the range
![]() $\lambda \in [\lambda' , \lambda' + 1 ]$
, where
$\lambda \in [\lambda' , \lambda' + 1 ]$
, where
![]() $\lambda'$
is from the first part of the proof. This gives a lower bound of
$\lambda'$
is from the first part of the proof. This gives a lower bound of
So we obtain the required lower bound in (1.2).
5. Expected value of a typical vertex under positivity
Proof of Theorem 1.2.We want to compute
Due to Lemma 3.2, this is equivalent to computing
The conditioning events
![]() $\{ \xi^n_u \ge 0 \ \forall\, u \in T_n\}$
and
$\{ \xi^n_u \ge 0 \ \forall\, u \in T_n\}$
and
![]() $\{ \max_{ v \in T_n} \tilde{\phi}_v^n \le X\}$
are equivalent, since
$\{ \max_{ v \in T_n} \tilde{\phi}_v^n \le X\}$
are equivalent, since
![]() $(\tilde{\phi}_v^n)_{v \in T_n}$
is symmetric around 0. Also,
$(\tilde{\phi}_v^n)_{v \in T_n}$
is symmetric around 0. Also,
![]() ${\sum_{v=1}^{d^n} \xi_v^n}/{d^n}$
equals X since
${\sum_{v=1}^{d^n} \xi_v^n}/{d^n}$
equals X since
![]() $\sum_{v=1}^{d^n} \tilde{\phi}_v^n=0$
. So the above equality holds.
$\sum_{v=1}^{d^n} \tilde{\phi}_v^n=0$
. So the above equality holds.
Upper bound. We first split the expectation into two parts: one concerning the contribution of the right tail in the integral, and the remainder. We aim to show that the contribution of the right tail is negligible, thereby implying that the main contribution is from the remainder, which gives an upper bound on the expectation. The tail here is motivated by the maximiser in Theorem 1.1. Thus
 \begin{align*}{\mathbb E}\Bigl(X \mid \max_{ v \in T_n} \tilde{\phi}_v^n \le X \Bigr) &= \dfrac{1}{\sqrt{2\pi}\sigma_{d,n}}\int_{-\infty}^{\infty} x {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le x\bigr)}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x \\&= \dfrac{1}{\sqrt{2\pi}\sigma_{d,n}}\int_{-\infty}^{m_n-a\log n } x {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le x\bigr)}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x \\&\quad + \dfrac{1}{\sqrt{2\pi}\sigma_{d,n}}\int_{m_n-a\log n }^{\infty} x {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le x\bigr)}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x.\end{align*}
\begin{align*}{\mathbb E}\Bigl(X \mid \max_{ v \in T_n} \tilde{\phi}_v^n \le X \Bigr) &= \dfrac{1}{\sqrt{2\pi}\sigma_{d,n}}\int_{-\infty}^{\infty} x {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le x\bigr)}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x \\&= \dfrac{1}{\sqrt{2\pi}\sigma_{d,n}}\int_{-\infty}^{m_n-a\log n } x {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le x\bigr)}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x \\&\quad + \dfrac{1}{\sqrt{2\pi}\sigma_{d,n}}\int_{m_n-a\log n }^{\infty} x {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le x\bigr)}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x.\end{align*}
We denote the first term by
![]() $J_1$
and the next one by
$J_1$
and the next one by
![]() $J_2$
. We first want to show that the contribution of
$J_2$
. We first want to show that the contribution of
![]() $J_2$
in the conditional expectation is negligible. We use a trivial upper bound on the tail probability in the numerator. Then we compute the integral, which is the tail expectation of a normal random variable, that is,
$J_2$
in the conditional expectation is negligible. We use a trivial upper bound on the tail probability in the numerator. Then we compute the integral, which is the tail expectation of a normal random variable, that is,
 \begin{align*}J_2 &\le \dfrac{1}{\sqrt{2\pi}\sigma_{d,n}}\int_{m_n-a\log n }^{\infty} x {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{1}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x \\&= \dfrac{1}{\sqrt{2\pi}\sigma_{d,n}{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)}\int_{m_n-a\log n }^{\infty} x {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \,{{\textrm{d}}} x \\&= \dfrac{\sigma_{d,n}{{\textrm{e}}}^{-(m_n-a\log n)^2/2\sigma^2_{d,n}}}{\sqrt{2\pi}{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} .\end{align*}
\begin{align*}J_2 &\le \dfrac{1}{\sqrt{2\pi}\sigma_{d,n}}\int_{m_n-a\log n }^{\infty} x {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{1}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x \\&= \dfrac{1}{\sqrt{2\pi}\sigma_{d,n}{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)}\int_{m_n-a\log n }^{\infty} x {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \,{{\textrm{d}}} x \\&= \dfrac{\sigma_{d,n}{{\textrm{e}}}^{-(m_n-a\log n)^2/2\sigma^2_{d,n}}}{\sqrt{2\pi}{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} .\end{align*}
So we end up showing that the contribution from the right tail is negligible. We now move on to the remainder and obtain an upper bound for it. We use a general upper bound on x from the range of the integral, which we can do since the integral exists and is finite by the fact that absolute expectation of a normal exists. Thus
 \begin{align*}J_1 &\le \dfrac{m_n-a\log n }{\sqrt{2\pi}\sigma_{d,n}}\int^{m_n-a\log n }_{-\infty} {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le x\bigr)}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x \\&\le \dfrac{m_n-a\log n }{\sqrt{2\pi}\sigma_{d,n}}\int^{\infty }_{-\infty} {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le x\bigr)}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x \\&= m_n-a\log n.\end{align*}
\begin{align*}J_1 &\le \dfrac{m_n-a\log n }{\sqrt{2\pi}\sigma_{d,n}}\int^{m_n-a\log n }_{-\infty} {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le x\bigr)}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x \\&\le \dfrac{m_n-a\log n }{\sqrt{2\pi}\sigma_{d,n}}\int^{\infty }_{-\infty} {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le x\bigr)}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x \\&= m_n-a\log n.\end{align*}
From (1.2) it is clear that on choosing a such that
![]() $a\log n \le \lambda'$
, the upper bound on the conditional expectation is
$a\log n \le \lambda'$
, the upper bound on the conditional expectation is
![]() $m_n - a \log n$
. Hence we can choose
$m_n - a \log n$
. Hence we can choose
![]() $a={\sqrt{2}}/{\sqrt{\log d}}$
.
$a={\sqrt{2}}/{\sqrt{\log d}}$
.
Lower bound. We apply a technique similar to that for the upper bound, the only difference being that we look at the left tail instead, motivated by the left tail of the maximum of the Gaussian process. Thus
 \begin{align*}{\mathbb E}\Bigl(X \mid \max_{ v \in T_n} \tilde{\phi}_v^n \le X \Bigr) &= \dfrac{1}{\sqrt{2\pi}\sigma_{d,n}}\int_{-\infty}^{\infty} x {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le x\bigr)}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x \\&= \dfrac{1}{\sqrt{2\pi}\sigma_{d,n}}\int_{-\infty}^{m_n-{{3}{c}^{-1}}\log_d n} x {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le x\bigr)}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x \\&\quad + \dfrac{1}{\sqrt{2\pi}\sigma_{d,n}}\int_{m_n-{{3}{c}^{-1}}\log_d n}^{\infty} x {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le x\bigr)}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x .\end{align*}
\begin{align*}{\mathbb E}\Bigl(X \mid \max_{ v \in T_n} \tilde{\phi}_v^n \le X \Bigr) &= \dfrac{1}{\sqrt{2\pi}\sigma_{d,n}}\int_{-\infty}^{\infty} x {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le x\bigr)}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x \\&= \dfrac{1}{\sqrt{2\pi}\sigma_{d,n}}\int_{-\infty}^{m_n-{{3}{c}^{-1}}\log_d n} x {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le x\bigr)}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x \\&\quad + \dfrac{1}{\sqrt{2\pi}\sigma_{d,n}}\int_{m_n-{{3}{c}^{-1}}\log_d n}^{\infty} x {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le x\bigr)}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x .\end{align*}
We denote the first term by
![]() $I_1$
and the second by
$I_1$
and the second by
![]() $I_2$
.
$I_2$
.
When
![]() $x \in (-\infty, m_n-{{3}{c}^{-1}}\log_d n]$
, then
$x \in (-\infty, m_n-{{3}{c}^{-1}}\log_d n]$
, then
following (4.1). Also, we have a lower bound on the probability of positivity, which gives the following bounds on
![]() $I_1$
and
$I_1$
and
![]() $I_2$
:
$I_2$
:
where
![]() $\underset{\sim}{C}>0$
is a constant not depending on n. This shows that this term is negligible. Further,
$\underset{\sim}{C}>0$
is a constant not depending on n. This shows that this term is negligible. Further,
 \begin{align*}I_2 &\ge \biggl(m_n-\dfrac{3}{c}\log_d n \biggr)\dfrac{1}{\sqrt{2\pi}\sigma_{d,n}}\int_{m_n-{{3}{c}^{-1}}\log_d n}^{\infty} {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le x\bigr)}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x \\&= \biggl(m_n-\dfrac{3}{c}\log_d n \biggr)\dfrac{1}{\sqrt{2\pi}\sigma_{d,n}}\int_{-\infty}^{\infty} {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le x\bigr)}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x - {{\textrm{o}}}(1) \\&= m_n-\dfrac{3\sqrt{2}}{\sqrt{\log d}}\log n - {{\textrm{o}}}(1).\end{align*}
\begin{align*}I_2 &\ge \biggl(m_n-\dfrac{3}{c}\log_d n \biggr)\dfrac{1}{\sqrt{2\pi}\sigma_{d,n}}\int_{m_n-{{3}{c}^{-1}}\log_d n}^{\infty} {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le x\bigr)}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x \\&= \biggl(m_n-\dfrac{3}{c}\log_d n \biggr)\dfrac{1}{\sqrt{2\pi}\sigma_{d,n}}\int_{-\infty}^{\infty} {{\textrm{e}}}^{-x^2/2\sigma^2_{d,n}} \dfrac{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le x\bigr)}{{\mathbb{P}}\bigl(\max_{v \in T_n} \tilde{\phi}_v^n \le X\bigr)} \,{{\textrm{d}}} x - {{\textrm{o}}}(1) \\&= m_n-\dfrac{3\sqrt{2}}{\sqrt{\log d}}\log n - {{\textrm{o}}}(1).\end{align*}
In the last step we used the value of
![]() $c={1}/{\sqrt{2 \log d}}$
, as fixed earlier in Lemma 4.1.
$c={1}/{\sqrt{2 \log d}}$
, as fixed earlier in Lemma 4.1.
Acknowledgement
The author would like to thank their graduate advisor Professor Jian Ding for suggesting the problem and for many helpful discussions on the same.
Funding information
There are no funding bodies to thank relating to the creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.