Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-12-01T00:01:57.406Z Has data issue: false hasContentIssue false
  • English
  • Français

KERNEL FUNCTIONS OF THE TWISTED SYMMETRIC SQUARE OF ELLIPTIC MODULAR FORMS

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  07 February 2018

Hayato Kohama  and
Yoshinori Mizuno
Hayato Kohama
Affiliation:
Graduate School of Technology, Industrial and Social Sciences, Tokushima University, 2-1, Minami-josanjima-cho, Tokushima, 770-8506, Japan email [email protected]
Yoshinori Mizuno
Affiliation:
Graduate School of Technology, Industrial and Social Sciences, Tokushima University, 2-1, Minami-josanjima-cho, Tokushima, 770-8506, Japan email [email protected]
Get access

Abstract

We study a kernel function of the twisted symmetric square 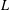$L$-function of elliptic modular forms. As an application, several exact special values of the 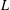$L$-function are computed.

MSC classification

Primary: 11F67: Special values of automorphic $L$-series, periods of modular forms, cohomology, modular symbols
Secondary: 11F50: Jacobi forms
Type
Research Article
Information
Mathematika , Volume 64 , Issue 1 , 2018 , pp. 184 - 210
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arakawa, T., Real analytic Eisenstein series for the Jacobi group. Abh. Math. Semin. Univ. Hambg. 60 1990, 131–148.Google Scholar
Choie, Y. and Lim, S., Eichler integrals, period relations and Jacobi forms. Math. Z. 271(3–4) 2012, 639–661.Google Scholar
Cohen, H., Sums involving the values at negative integers of L-functions of quadratic characters. Math. Ann. 217(3) 1975, 271–285.Google Scholar
Diamantis, N. and O’sullivan, C., Kernels of L-functions of cusp forms. Math. Ann. 346 2010, 897–929.Google Scholar
Diamantis, N. and O’sullivan, C., Kernels for products of L-functions. Algebra Number Theory 7 2013, 1883–1917.Google Scholar
Doi, K., Hida, H. and Ishii, H., Discriminant of Hecke fields and twisted adjoint L-values for GL(2). Invent. Math. 134(3) 1998, 547–577.Google Scholar
Eichler, M. and Zagier, D., The Theory of Jacobi Forms (Progress in Mathematics 55 ), Birkhäuser Boston, Inc. (Boston, MA, 1985).Google Scholar
Erdelyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G., Higher Transcendental Functions, Vol. I (Based, in part, on notes left by Harry Bateman), McGraw-Hill Book Company, Inc. (New York–Toronto–London, 1953).Google Scholar
Erdelyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G., Tables of Integral Transforms, Vol. I (Based, in part, on notes left by Harry Bateman), McGraw-Hill Book Company, Inc. (New York–Toronto–London, 1954).Google Scholar
Goldfeld, D. and Zhang, S., The holomorphic kernel of the Rankin–Selberg convolution. Asian J. Math. 3 1999, 729–748.Google Scholar
Goto, K., A twisted adjoint L-value of an elliptic modular form. J. Number Theory 73(1) 1998, 34–46.Google Scholar
Gradshteyn, I. S. and Ryzhik, I. M., Table of integrals, series, and products. Translated from the Russian. In With one CD-ROM (Windows, Macintosh and UNIX), 7th edn., Elsevier/Academic Press (2007) Translation edited and with a preface by Alan Jeffrey and Daniel Zwillinger.Google Scholar
Guerzhoy, P., Jacobi forms and a two–variable p-adic L-function. Fundam. Prikl. Mat. 6(4) 2000, 1007–1021, translated at: http://www.math.hawaii.edu/∼pavel/publications/list.html (in Russian).Google Scholar
Guerzhoy, P., Jacobi–Eisenstein series and p-adic interpolation of symmetric squares of cusp forms. Ann. Inst. Fourier (Grenoble) 45(3) 2003, 451–464.Google Scholar
Hashim, A. and Ram Murty, M., On Zagier’s cusp form and the Ramanujan 𝜏 function. Proc. Indian Acad. Sci. Math. Sci. 104(1) 1994, 93–98.CrossRefGoogle Scholar
Heim, B., Analytic Jacobi Eisenstein series and the Shimura method. J. Math. Kyoto Univ. 43(3) 2003, 451–464.Google Scholar
Hiraoka, Y., Numerical calculation of twisted adjoint L-values attached to modular forms. Experiment. Math. 9(1) 2000, 67–73.Google Scholar
Katsurada, H., Special values of the standard zeta functions for elliptic modular forms. Experiment. Math. 14(1) 2005, 27–45.Google Scholar
Katsurada, H., Special values of the standard zeta functions for elliptic modular forms II. Preprint.Google Scholar
Knopp, M., Some new results on the Eichler cohomology of automorphic forms. Bull. Amer. Math. Soc. (N.S.) 80 1974, 607–632.Google Scholar
Kohnen, W. and Sengupta, J., Nonvanishing of symmetric square L-functions of cusp forms inside the critical strip. Proc. Amer. Math. Soc. 128(6) 2000, 1641–1646.Google Scholar
Kohnen, W. and Sengupta, J., On the average of central values of symmetric square L-functions in weight aspect. Nagoya Math. J. 167 2002, 95–100.Google Scholar
Lebedev, N., Special functions and their applications. In Unabridged and Corrected Republication, Dover Publications, Inc. (New York, 1972) Revised edition, translated from the Russian and edited by Richard A. Silverman.Google Scholar
Luo, W., Central values of the symmetric square L-functions. Proc. Amer. Math. Soc. 140(10) 2012, 3313–3322.Google Scholar
Miyake, T., Modular Forms, Springer (Berlin, 1989) Translated from the Japanese by Yoshitaka Maeda.Google Scholar
Mizumoto, S., On the second L-functions attached to Hilbert modular forms. Math. Ann. 269(2) 1984, 191–216.Google Scholar
Nelson, P., Stable averages of central values of Rankin–Selberg L-functions: some new variants. J. Number Theory 133 2013, 2588–2615.CrossRefGoogle Scholar
Panchishkin, A., Symmetric squares of Hecke series and their values at lattice points. Mat. Sb. 108(150)(3) 1979, 393–417, 478.Google Scholar
Rademacher, H., On the Phragmen-Lindelöf theorem and some applications. Math. Z. 72(3) 1959/1960, 192–204.Google Scholar
Shimura, G., On the holomorphy of certain Dirichlet series. Proc. Lond. Math. Soc. (3) 31(1) 1975, 79–98.Google Scholar
Shimura, G., Elementary Dirichlet Series and Modular Forms (Springer Monographs in Mathematics), Springer (New York, 2007).Google Scholar
Small, C., Arithmetic of Finite Fields (Monographs and Textbooks in Pure and Applied Mathematics 148 ), Marcel Dekker, Inc. (New York, 1991).Google Scholar
Stopple, J., Special values of twisted symmetric square L-functions and the trace formula. Compositio Math. 104(1) 1996, 65–76.Google Scholar
Sturm, J., Projections of C ∞ automorphic forms. Bull. Amer. Math. Soc. (N.S.) 2(3) 1980, 435–439.Google Scholar
Sturm, J., Special values of zeta functions, and Eisenstein series of half integral weight. Amer. J. Math. 102(2) 1980, 219–240.CrossRefGoogle Scholar
Sturm, J., Evaluation of the symmetric square at the near center point. Amer. J. Math. 111(4) 1989, 585–598.Google Scholar
Takase, K., On the trace formula of the Hecke operators and the special values of the second L-functions attached to the Hilbert modular forms. Manuscripta Math. 55(2) 1986, 137–170.Google Scholar
Temme, N., Special Functions: An Introduction to the Classical Functions of Mathematical Physics, John Wiley & Sons (Hoboken, NJ, 1996), 374.Google Scholar
Zagier, D., Modular forms whose Fourier coefficients involve zeta-functions of quadratic fields. In Modular Functions of One Variable, VI (Proc. Second Internat. Conf., Univ. Bonn, Bonn, 1976) (Lecture Notes in Mathematics 627 ), Springer (Berlin, 1977), 105–169.Google Scholar
Zagier, D., Introduction to Modular Forms. From Number Theory to Physics (Les Houches, 1989), Springer (Berlin, 1992), 238–291.Google Scholar