1. Introduction
Phenotypic stability is the genotype's tendency to exhibit a constant phenotypic expression in different environments (Lynch & Walsh, Reference Lynch and Walsh1998). The stability or sensitivity of each genotype to macro-environmental changes can be estimated as the variance of the genotype over the set of macro-environments where it was grown and the stability of each genotype to micro-environmental change can be estimated as the variance of the genotype within each macro-environment (developmental stability). Differences among genotypes in stability will be exhibited as heterogeneity among genotypes in micro- or macro-environmental variance. It is likely that the genetic factors contributing to stability to macro- and to micro-environmental changes may not be the same factors as those which influence the stability to micro-environmental changes, although little work has been done on the subject.
Evidence for the existence of genetic heterogeneity of micro-environmental variance (V E) can come from selection experiments, for theory predicts that environmental variance would decrease with stabilizing selection and increase with disruptive selection (Mulder et al., Reference Mulder, Bijma and Hill2007). Accordingly, Kaufman et al. (Reference Kaufman, Enfield and Comstock1977) observed a decrease in V E with stabilizing selection and Scharloo et al. (Reference Scharloo, Zweep, Schuitema and Wijnstra1972) observed an increase with disruptive selection. Some experiments using directional selection by truncation have shown that phenotypic variance increased with the generations of selection (Clayton & Robertson, Reference Clayton and Robertson1957; Mackay et al., Reference Mackay, Fry, Lyman and Nuzhdin1994). One explanation for these data is that there is genetic variance in V E because more variable genotypes are more likely to have extreme phenotypes and thus to be selected when selection intensity is high (Hill & Zhang, Reference Hill and Zhang2004).
Genetic differences in V E have been quantified in analyses of field data in domestic animals by Van Vleck (Reference Van Vleck1968) and Clay et al. (Reference Clay, Vinson and White1979) in dairy cattle, SanCristobal-Gaudy et al. (Reference SanCristobal-Gaudy, Bodin, Elsen and Chevalet2001) in sheep, Sorensen & Waagepetersen (Reference Sorensen and Waagepetersen2003) and Ibáñez-Escriche et al. (Reference Ibáñez-Escriche, Varona, Sorensen and Noguera2008) in pigs and Rowe et al. (Reference Rowe, White, Avendano and Hill2006) in chicken. Other authors have found genetic heterogeneity of V E in model species including mice (Gutierrez et al., Reference Gutierrez, Nieto, Piqueras, Ibanez and Salgado2006) and Drosophila melanogaster (Whitlock & Fowler, Reference Whitlock and Fowler1999; Mackay & Lyman, Reference Mackay and Lyman2005) and in the snail Helix aspersa (Ros et al., Reference Ros, Sorensen, Waagepetersen, Dupont-Nivet, SanCristobal, Bonnet and Mallard2004).
Although some of the previous analyses of field data and selection experiments show evidence for genetic heterogeneity in V E, estimates could be due to or biased by statistical artefacts, e.g. confounding of genetic and environmental effects on variance or violation of the infinitesimal model assumption (Mulder et al., Reference Mulder, Bijma and Hill2007).
In plant breeding, there is a vast body of literature documenting research on the statistical modelling of genotype×macro-environment interaction and on assessing stability in the context of multi-environment trials (Cotes et al., Reference Cotes, Crossa, Sanches and Cornelius2006). However, until recently researchers have not paid attention to the heterogeneity of V E or the error variance, and then only with the objective of reducing the error of estimating genotype×macro-environment interaction variances (Edwards & Jannink, Reference Edwards and Jannink2006). The heterogeneity of V E or the error variance due to genetic causes does, however, give useful information about the genetic component of the developmental stability.
At the molecular level, there is limited experimental information about the genetic basis of V E. In D. melanogaster, genetic determinants for differences in the mean and variance of bristle number and yield of progeny have been located to one or more chromosomes (Caligari & Mather, Reference Caligari and Mather1975). In an interspecific cross between Lycopersicon esculentun and Lycopersicon pimpinellifolium, marker-associated effects on variance were found for several traits using six morphological and four electrophoretic markers (Weller et al., Reference Weller, Soller and Brody1988). In Arabidopsis thaliana, Stratton (Reference Stratton1998) has found two QTLs affecting flowering time and rosette leaf number and with significant effects on the linear and quadratic components of the reaction norm function. Mackay & Lyman (Reference Mackay and Lyman2005) have found that molecular polymorphisms at Dopa decarboxylase (Ddc) are associated with variation in environmental variance in abdominal bristle number of D. melanogaster.
Experimental data on the distribution of QTLs affecting environmental variance or environmental stability, particularly the V E or stability (developmental stability) along the genome, or the effects of such QTLs are, therefore, needed. Such information could, for example, be helpful in understanding how levels of phenotypic variance evolve to take the values they do (Zhang & Hill, Reference Zhang and Hill2005). Also, in livestock and plant breeding, information about QTLs affecting V E is useful because the uniformity of end product is an important topic.
The availability of thousands of polymorphic molecular markers and the development of appropriate statistical tools enable the use of QTL mapping experiments to identify many genomic regions affecting the mean of different traits in many plant and animal species. As far as we know, however, this technology has had little or no application in locating genomic regions or QTLs affecting V E and the environmental correlation between traits. Therefore, the present study, using a population of maize recombinant inbred lines (RIL) and simple sequence repeat (SSR) polymorphic markers, aims at the following:
1. To quantify the genetic component of the V E or developmental stability for four traits in maize and the environmental correlation between these traits.
2. To identify and quantify the effects of QTLs on the V E of these traits and on the environmental correlations between them.
2. Material and methods
(i) Experimental material, phenotypic evaluation and marker loci
A total of 129 unselected F6 lines were developed from the cross EP42×EP39 by single-seed descent. Line EP42 was obtained from a local open pollinated variety from North-Western Spain (humid Spain), whereas EP39 was obtained from the race ‘Fino’ from Central Spain (dry Spain). The RILs were multiplied the same year and in the same location to have homogeneous seed. The 129 RILs were grown in a randomized complete block design with five replications in Pontevedra (humid Spain) in 2006. Each plot consisted of one row, with 13 plants per plot of the same line distributed in 13 hills. The distance between rows was 0·80 m and between plants 0·21 m for a planting density of approximately 60 000 plants/ha. The average number of plants that survived per RIL was 49·5, ranging from 12 to 65. The following data were taken on individual plants: plant and ear height, tassel length and days to pollen first shedding.
DNA of ten plants picked at random from each RIL was extracted according to Liu & Whittier (Reference Liu and Whittier1994) with modifications. SSR amplifications were performed as described by Butron et al. (Reference Butron, Tarrio, Revilla, Malvar and Ordas2003). SSR products were separated after amplification by electrophoresis using 1×TBE on a 6% non-denaturing acrylamide gel (approximately 250 V for 3 h) (Wang et al., Reference Wang, Shi, Carlson, Cregan, Ward and Diers2003). A total of 85 SSR polymorphic primer pairs distributed along the genome were genotyped in the RILs (locations tabulated in the Appendix).
(ii) Statistical analysis
In this paper, we use the term ‘micro-environment’ to refer to the environment of a single plant growing at the same time and nearly at the same place as another plant, specifically that of plants in the same row.
(a) Basic analysis assuming homogeneity of variances and environmental correlations (model 1)
Under the first model, the phenotype (P) of a plant is the sum of the effects due to the genotypic value or RIL (G), the replication or block (R), the interaction between genotype and replication (I) and a random error (e). The model may be written as
i=1, 129, j=1, 5, and k=1, n ij; where μ is the overall mean and is a fixed effect, the other effects are random with mean zero and variances V G, V R, V I and V E, respectively, and n ij is the number of plants in RIL i and replication j.
The variance components associated with each source of variation were estimated by restricted maximum likelihood (REML) using the VARCOMP procedure of SAS (SAS Institute, 2003).
The residual variance, V E, estimates the variation between plants within the same row. V E is mainly micro-environmental variability, but also includes any genetic variability remaining after four generations of selfing due to segregation within the F6 families (which is, on average, 1/16 of the genetic variance in the F2 generation assuming no epistasis). Under model 1, V E is assumed to be the same for all genotypes and thus that there is no genetic heterogeneity of micro-environmental variability and also that the remaining genetic variance is identical for all families as predicted from the infinitesimal genetic model.
The estimated additive variance (V A) of plant height and ear height is 6 and 14 times the dominance variance (V D), respectively, in maize open-pollinated populations, whereas the estimated dominance variance for days to first flowering is 0 (Table 5.1 in Hallauer & Miranda, Reference Hallauer and Miranda Filho1988). Although there is no information available about the genetic variance of tassel length, we assume that its components are similar to those for plant height and therefore that V D is much lower than V A. Under continuous selfing and assuming no selection, the expected value of the genetic variance between F6 lines is 1·875V A+0·0586V D, where V A and V D refer to the F2 generation (Kearsey & Pooni, Reference Kearsey and Pooni1996). Therefore, because the dominance variance is expected to be low in the F2 generation and is greatly reduced by the F6, the contribution of V D to the variance between F6 families is assumed to be negligible. Therefore, we estimated the additive variance (![]() ) in the F2 generation as
) in the F2 generation as ![]() , where
, where ![]() is the estimated variance component between RILs of the F6 generation. The contribution of V D to the variance within families was assumed to be negligible and the residual genetic variance within families (
is the estimated variance component between RILs of the F6 generation. The contribution of V D to the variance within families was assumed to be negligible and the residual genetic variance within families (![]() ) was therefore estimated as
) was therefore estimated as ![]() .
.
The error sum of squares and error cross products obtained from the multivariate REML were used to calculate the residual correlation between traits. These correlation coefficients are mainly environmental correlations, averaged over all genotypes because there is assumed to be little genetic variance within lines.
(b) Estimation of heterogeneity of environmental variances and correlations between RILs (model 2)
Under the infinitesimal model, the residual genetic variability is the same for all RIL, and therefore heterogeneity in the residual variance between the RILs is due only to variation in V E. In our experiment, the blocks were relatively homogeneous, although due to their size some environmental heterogeneity could exist within them. However, because we had five blocks and the RILs were randomized within each block, we assumed that the environmental effects were on average similar for all RILs. Therefore any differences in residual variance between the RILs can be ascribed to differences between them in sensitivity to the micro-environmental conditions.
We had a variable number of plants per row because some of the plants did not grow. The difference in the number of plants could induce an environmental bias affecting the error variance. To examine the effect of the number of plants on the residual variance, we carried out a linear regression of the residual variance of the combination RIL×replication against the number of plants surviving and also a linear regression of the pooled residual variance of each RIL against the number of plants surviving per RIL. The variation in the residual variance explained by the variation in the number of plants was negligible (r 2⩽0·02) and therefore we conclude that the differences in residual variance between the RIL could not be due to differences between them in the number of surviving plants.
To test whether the residual variances of the RILs differ significantly, a random one-fold nested multivariate analysis of variance (ANOVA) was undertaken on each of the 129 RIL and V E
i (the residual variance of RIL i) was estimated from the mean squares. The sources of variation were replications and plants within replication and the mean squares corresponding to these sources of variation were designated ![]() and
and ![]() , respectively, such that
, respectively, such that ![]() is an estimate of V Ei. A test of homogeneity of the residual variances of the RILs was made using the criterion due to Barlett,
is an estimate of V Ei. A test of homogeneity of the residual variances of the RILs was made using the criterion due to Barlett, ![]() (Steel et al., Reference Steel, Torrie and Dickey1997), where
(Steel et al., Reference Steel, Torrie and Dickey1997), where ![]() . Bartlett's test statistic M is chi-square distributed under the null hypothesis of homogeneous V Ei if observations are normally distributed. However, instead of assuming that M is chi-square distributed under the null hypothesis which requires the normality assumption, we estimated the distribution of M under the null hypothesis using a randomization procedure which does not require such an assumption. The values of the residual variances and its degrees of freedom were randomly allocated to the RILs within each replication, and pooled residual variances together with its degrees of freedom were calculated for each RIL. We randomized the residual variances together with their degrees of freedom to take into account the imbalance of the experiment. Using the pooled residual variances and the degrees of freedom, M was calculated as previously described and the value was recorded. This random sampling was repeated 1000 times to obtain the distribution of M under the null hypothesis of homogeneity of variances as a basis for testing the significance of the observed M.
. Bartlett's test statistic M is chi-square distributed under the null hypothesis of homogeneous V Ei if observations are normally distributed. However, instead of assuming that M is chi-square distributed under the null hypothesis which requires the normality assumption, we estimated the distribution of M under the null hypothesis using a randomization procedure which does not require such an assumption. The values of the residual variances and its degrees of freedom were randomly allocated to the RILs within each replication, and pooled residual variances together with its degrees of freedom were calculated for each RIL. We randomized the residual variances together with their degrees of freedom to take into account the imbalance of the experiment. Using the pooled residual variances and the degrees of freedom, M was calculated as previously described and the value was recorded. This random sampling was repeated 1000 times to obtain the distribution of M under the null hypothesis of homogeneity of variances as a basis for testing the significance of the observed M.
To quantify the genetic heterogeneity in the environmental variance, the variances of the plants within each row (![]() ), that is, the residual variances for each combination of RIL×replication, were estimated. We assumed that the residual variance (V E) of each RIL×replication is the sum of an average residual variance, a deviation due to a RIL effect, a replication effect and a random effect. The model may be written as
), that is, the residual variances for each combination of RIL×replication, were estimated. We assumed that the residual variance (V E) of each RIL×replication is the sum of an average residual variance, a deviation due to a RIL effect, a replication effect and a random effect. The model may be written as
i=1, 129, j=1, 5, where ![]() is the average residual variance and
is the average residual variance and ![]() is a random effect with mean 0 and variance
is a random effect with mean 0 and variance ![]() . The sources of variation, namely RIL, replication and the interaction RIL×replication (error), were estimated by REML using the VARCOMP procedure of SAS (SAS Institute, 2003). We undertook the analysis using both untransformed residual variances obtained for each RIL×replication combination and natural logarithms of those values. The untransformed values were used to show most clearly the magnitude of the variances; and the log transformed values to obtain more homogeneous errors.
. The sources of variation, namely RIL, replication and the interaction RIL×replication (error), were estimated by REML using the VARCOMP procedure of SAS (SAS Institute, 2003). We undertook the analysis using both untransformed residual variances obtained for each RIL×replication combination and natural logarithms of those values. The untransformed values were used to show most clearly the magnitude of the variances; and the log transformed values to obtain more homogeneous errors.
In the analysis of the untransformed variances, the variance component associated with RILs (![]() ) was used to estimate the variance among the residual variances of the RILs,
) was used to estimate the variance among the residual variances of the RILs, ![]() (model 1, Table 2) to estimate the mean of the residual variance of the RILs (
(model 1, Table 2) to estimate the mean of the residual variance of the RILs (![]() , and
, and ![]() was estimated as
was estimated as ![]() . In the analysis of the log transformed variances, which measure variation in squared coefficient of variation (Rowe et al., Reference Rowe, White, Avendano and Hill2006),
. In the analysis of the log transformed variances, which measure variation in squared coefficient of variation (Rowe et al., Reference Rowe, White, Avendano and Hill2006), ![]() was estimated directly as the square root of
was estimated directly as the square root of ![]() the variance component associated with RILs. Assuming additivity such that the expected genetic variance in the environmental variance increased with generations of inbreeding to 1·875 times that in the F2, the genetic coefficient of variation for environmental variance (
the variance component associated with RILs. Assuming additivity such that the expected genetic variance in the environmental variance increased with generations of inbreeding to 1·875 times that in the F2, the genetic coefficient of variation for environmental variance (![]() ) was estimated as
) was estimated as ![]() .
.
To examine the influence of the imbalance of numbers of plants on the estimates, we repeated the same analysis twice: with only those rows with 6 plants or more and with only those rows with 9 plants or more. In both cases, we found similar estimates to those obtained when we used the whole dataset, indicating that the impact of the imbalance is not important.
For each RIL, the error sum of squares and cross products between pairs of traits obtained from the multivariate ANOVA were used to calculate the coefficient of correlation between all pairs of traits as ![]() . For each pair of traits, we tested the homogeneity of the correlation coefficients for within replicate components of the RILs by computing, for each RIL, the transformation
. For each pair of traits, we tested the homogeneity of the correlation coefficients for within replicate components of the RILs by computing, for each RIL, the transformation ![]() which is approximately normally distributed with variance
which is approximately normally distributed with variance ![]() , where d i are the error degrees of freedom from the multivariate ANOVA (Steel et al., Reference Steel, Torrie and Dickey1997). The test criterion is C=
, where d i are the error degrees of freedom from the multivariate ANOVA (Steel et al., Reference Steel, Torrie and Dickey1997). The test criterion is C=![]() , where
, where ![]() This criterion is distributed as chi-square with 128 degrees of freedom if the Z i are homogeneous and normally distributed; but to allow for non-normality, the distribution of the test criterion (C) was estimated by a randomization procedure equivalent to that for the test of homogeneity of variances.
This criterion is distributed as chi-square with 128 degrees of freedom if the Z i are homogeneous and normally distributed; but to allow for non-normality, the distribution of the test criterion (C) was estimated by a randomization procedure equivalent to that for the test of homogeneity of variances.
(c) Location of QTLs related to environmental variances and correlations (model 3)
The aim with model 3 is to locate QTLs that have some effect on the environmental variance and/or the environmental correlation and quantify their effects. At each marker, approximately one-half of the RILs are homozygous for the allele from EP39 (allele A) and the other half homozygous for the allele from EP42 (allele B). At each marker, model 1 was applied separately to each of the two sets of RILs, and from each, within replication variance and the environmental correlations between pairs of traits were estimated. Therefore, at each marker, we estimated V E for the RILs with the allele A and V E for the RILs with allele B. The larger of these values was divided by the smaller to obtain an F statistic. The probability of a value equal to or higher than the observed F was obtained by a permutation procedure (Churchill & Doerge, Reference Churchill and Doerge1994), rather than by relying on normality of observations. The permutation procedure was also used because the markers are linked and the tests involving linked markers are not independent. The phenotypes of RILs were randomly shuffled over genotypes, keeping the genotypes constant, generating a sample with the original marker information but with trait values randomly assigned over genotypes. We calculated the F value for each marker and recorded the maximum value of F over all markers, and repeated the process 1000 times. Thus, we obtained a distribution of this F statistic that allows us to estimate the experimentwise probability of the observed values.
For each marker, the error sums of squares and cross products between pairs of traits obtained from the multivariate ANOVA were used to calculate the coefficient of correlation between all pairs of traits as ![]() for the RILs with allele A and the same for those with allele B. To test the hypothesis that the two estimated correlations are from the same population, they were transformed to Z values as above, and a test criterion
for the RILs with allele A and the same for those with allele B. To test the hypothesis that the two estimated correlations are from the same population, they were transformed to Z values as above, and a test criterion ![]() was calculated. The probability of a value equal to or higher than the observed T was obtained by a permutation procedure equivalent to that above.
was calculated. The probability of a value equal to or higher than the observed T was obtained by a permutation procedure equivalent to that above.
(d) Location of QTLs associated with the mean of the traits (model 4)
Detecting QTLs associated with the mean of the traits was undertaken by a Single Factor ANOVA (Soller et al., Reference Soller, Brody and Genizi1976). Each marker locus was subjected to ANOVA with the following sources of variation: replication, allele, replication×allele, RIL (allele) and RIL (allele)×replication and the error due to individual plants. Replication, replication×allele, RIL (allele) and RIL (allele)×replication were considered random factors, whereas allele was considered fixed.
The ANOVA, including the F statistics to test the allele effects, was computed with the Mixed procedure of SAS (SAS Institute, 2003) based on principles of generalized least squares to estimate and test fixed effects (Littell et al., Reference Littell, Stroup and Freund2002). A permutation test similar to that used for the variances and correlations was used to estimate the experimentwise threshold.
3. Results
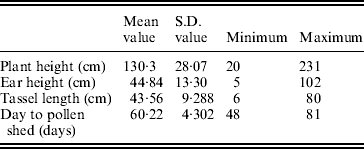
The mean, S.D. and extreme values of the traits in the population of RILs are shown in Table 1.
Table 1. Mean, S.D., maximum and minimum values for plant height, ear height, tassel length and days to pollen shed
(i) Basic analysis assuming homogeneity of variances and environmental correlations (model 1)
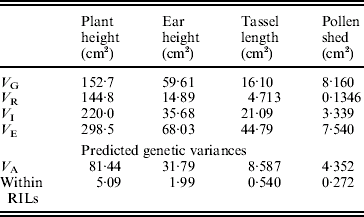
The estimates of variance components are shown in Table 2. For all traits, the estimated variance ![]() was significantly higher than 0 (F test, P<0·05, data not shown), but the predicted genetic variances within RILs are nevertheless negligible compared with the magnitudes of
was significantly higher than 0 (F test, P<0·05, data not shown), but the predicted genetic variances within RILs are nevertheless negligible compared with the magnitudes of ![]() (Table 2).
(Table 2).
Table 2. Estimates of variance components associated with replication (VR), genotypes or RILs (VG), replication×genotypes interaction (VI) and error (VE). The predicted additive genetic (VA=VG/1·875) and residual genetic variance within RILs (VA/16) are also shown
The environmental correlations were positive between plant height, ear height and tassel length and negative between each of these and days to flowering (Table 3). The magnitudes of the genetic correlations were similar to those of the environmental correlations, except for the correlations of plant and ear height with days to pollen shed.
Table 3. Estimates of genetic correlations (rG) and environmental correlations (rE) (±S.E.) between pairs of traits

(ii) Estimation of heterogeneity of environmental variances and correlations between RILs (model 2)
For plant height, ear height, tassel length and days to pollen shedding, the correlation coefficients between the number of heterozygous markers, as indicative of residual genetic variance, and the V E of the RILs were −0·05, 0·21, −0·02 and −0·08, respectively (not statistically significant at P=0·05).
For each of the four traits, the estimate of residual variance (![]() ) varied widely between the RILs (Fig. 1). In agreement with this visual observation, the hypothesis of homogeneity of variances was rejected for all traits (P<0·01, randomization test, Table 4). The estimated
) varied widely between the RILs (Fig. 1). In agreement with this visual observation, the hypothesis of homogeneity of variances was rejected for all traits (P<0·01, randomization test, Table 4). The estimated ![]() were similar when obtained with transformed and untransformed variances and ranged from 0·14 to 0·25 (Table 4).
were similar when obtained with transformed and untransformed variances and ranged from 0·14 to 0·25 (Table 4).
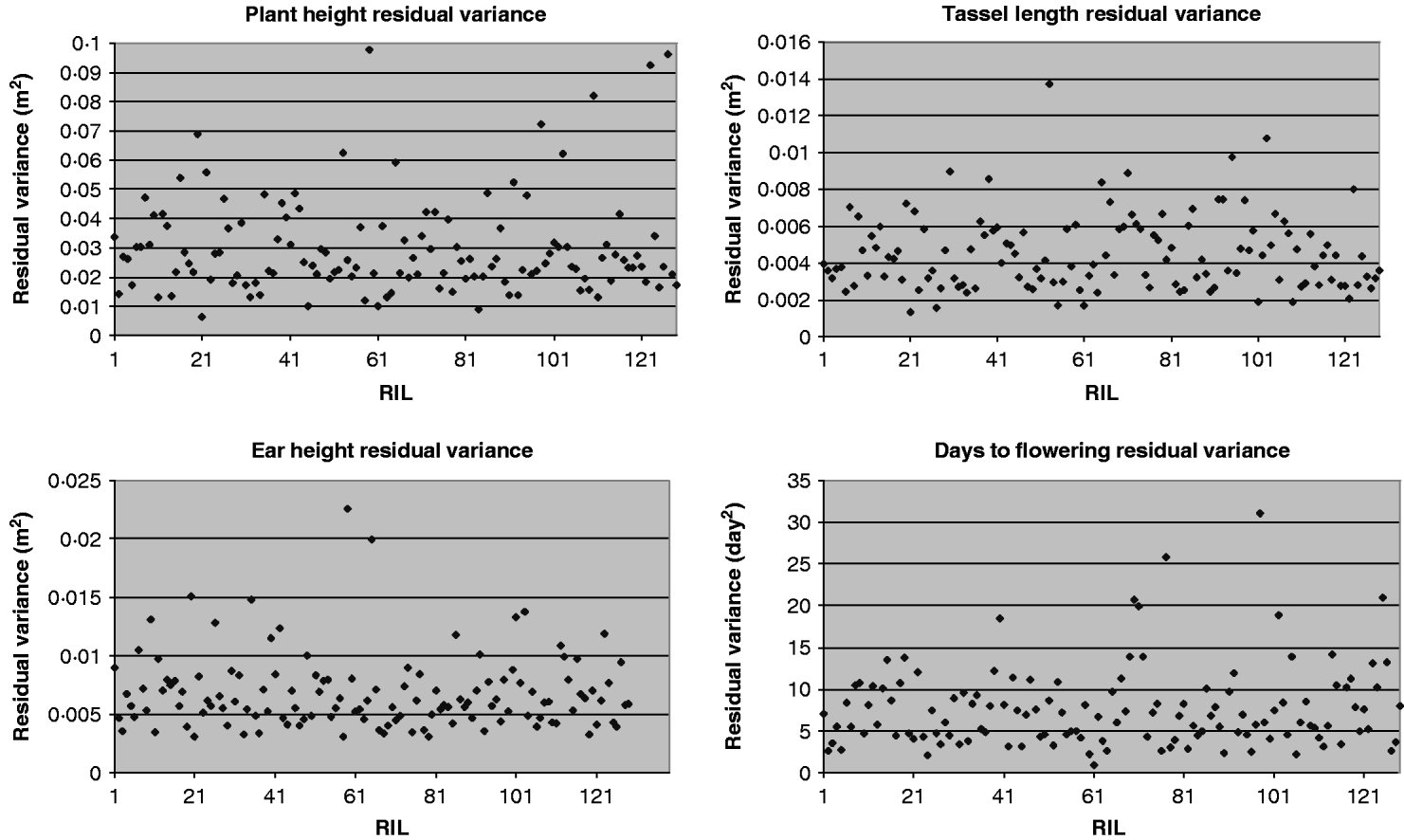
Fig. 1. Residual variance of the 129 RILs for plant height, ear height, tassel length and days to flowering.
Table 4. Variance of the residual variance of the RILs (![]() ), coefficient of variation of the residual variance (
), coefficient of variation of the residual variance (![]() ) and
) and ![]() calculated with the untransformed values,
calculated with the untransformed values, ![]() calculated with the transformed values (
calculated with the transformed values (![]() ), and observed value of the test criterion
), and observed value of the test criterion ![]() for testing the homogeneity of the residual variances and probability of obtaining by chance a value of M equal to or higher than observed in randomizations
for testing the homogeneity of the residual variances and probability of obtaining by chance a value of M equal to or higher than observed in randomizations

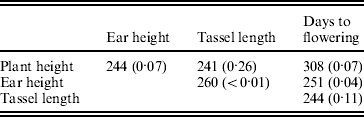
The environmental correlations also varied widely between the RILs (supplementary Figure FS1). They departed significantly from homogeneity (P<0·05) for ear height with tassel length and with days to flowering (Table 5).
Table 5. Test criterion ![]() for testing the homogeneity of the environmental correlations and probability of obtaining by chance a value of M equal to or higher than observed in randomizations (within brackets)
for testing the homogeneity of the environmental correlations and probability of obtaining by chance a value of M equal to or higher than observed in randomizations (within brackets)
(iii) Location of QTLs related to environmental variances and correlations (model 3)
For each marker, the mean and the estimated residual variance (![]() ) of the RILs that carry the allele from EP39 (A) and those that carry the allele from EP42 (B) are shown in supplementary Table TS1.
) of the RILs that carry the allele from EP39 (A) and those that carry the allele from EP42 (B) are shown in supplementary Table TS1.
QTLs associated with the micro-environmental stability were detected at a significance level of 4, 8, 8 and 13% for days to flowering, plant height, ear height and tassel length, respectively (Fig. 2). The QTLs detected for plant and ear height were located in the same region (chromosome 10), but those for tassel length and days to flowering were located on different chromosomes. To quantify the difference between variances, for the significant markers we generated the difference in residual variance between alleles as a percentage of the average residual variance. This ratio was close to 30% for umc1113 (for plant and ear height) and umc1394 (for tassel length), and to 40% for bnlg1346 (for days to flowering).
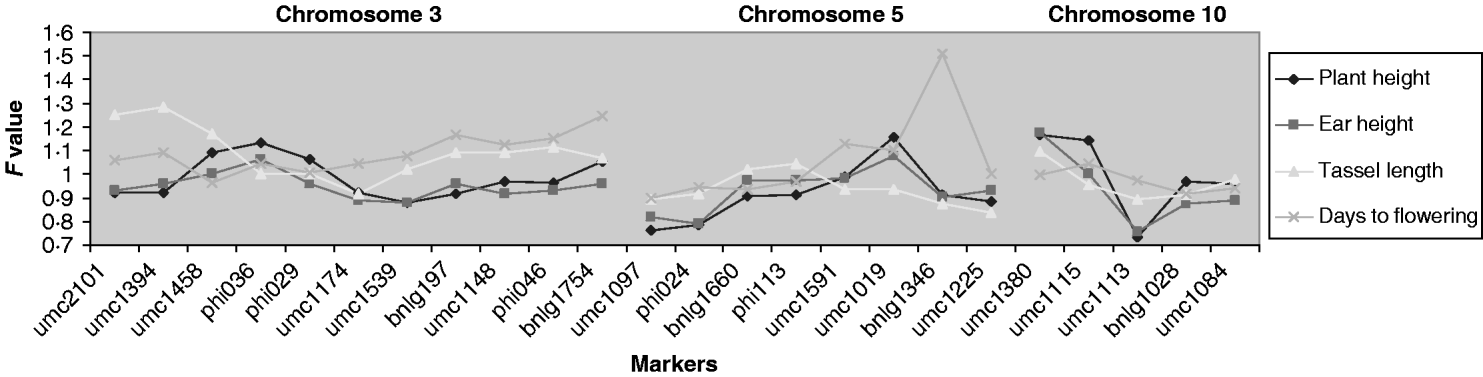
Fig. 2. Ratio of variances (the variance of allele A divided by the variance of allele B) for each marker for those chromosomes in which significant effects were detected. For F>1, the F experimentwise critical values at α=0·05 are 1·375, 1·322, 1·310 and 1·491 and at α=0·25 are 1·324, 1·279, 1·268 and 1·397 for plant height, ear height, tassel length and days to flowering, respectively. For these traits, when F is lower than 1, the F experimentwise critical values at α=0·05 are 0·7275, 0·7563, 0·7632 and 0·6706 and at α=0·25 are 0·7551, 0·7819, 0·7885 and 0·7158, respectively.
A weakly significantly (P<0·10) QTL associated with the environmental correlation between ear height and days to pollen shed was detected on chromosome 3 (Fig. 3). For markers umc2101 and umc1394 at this region, the difference in the coefficient of correlation between alleles was 0·12, which is 50% of the average environmental correlation. No QTLs were detected for the other pairs of traits.
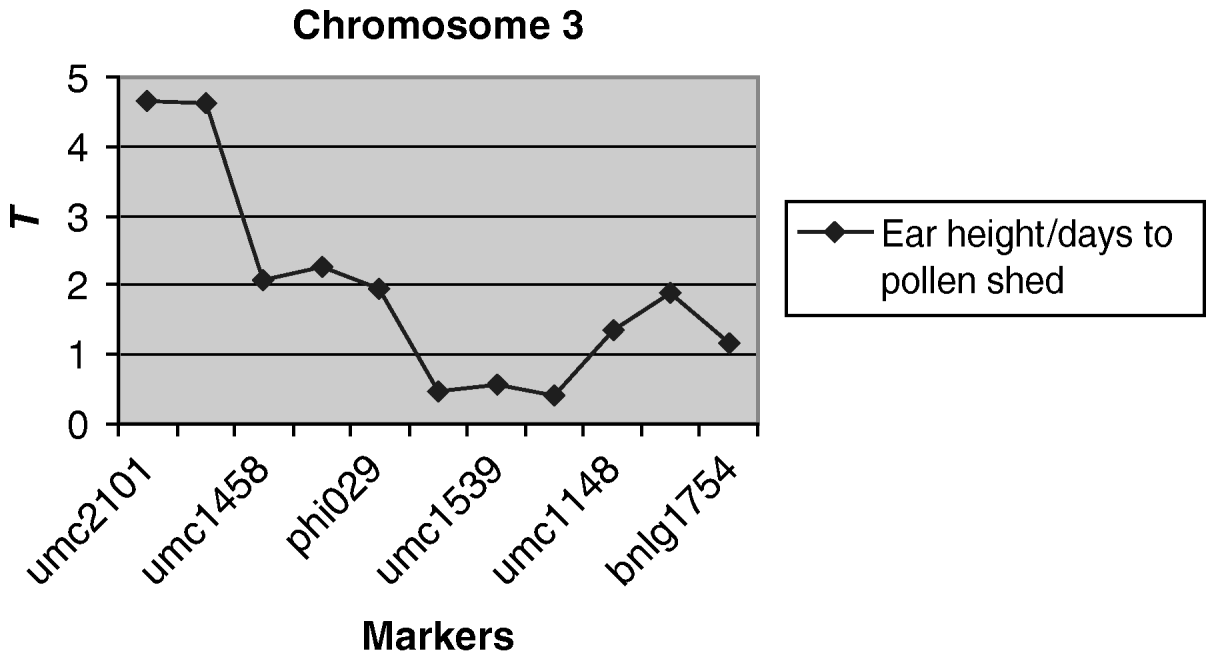
Fig. 3. Observed value of the test criterion ![]() for the markers of chromosome 3. The T experimentwise critical values are 4·935 and 4·236 at α=0·05 and α=0·25, respectively.
for the markers of chromosome 3. The T experimentwise critical values are 4·935 and 4·236 at α=0·05 and α=0·25, respectively.
(iv) Location of QTLs associated with the mean of the traits (model 4)
At least one putative QTL related to the mean traits was detected at a significance level of 10% or lower for ear height, tassel length and days to flowering. Those QTLs are located on chromosomes 2, 3 and 8 (Fig. 4). The QTLs associated with the mean and with the V E of the traits are not located in the same regions. Each QTL explains between about 2 and 4% of the total variation, except the one for ear height on chromosome 3 that explains 6%.
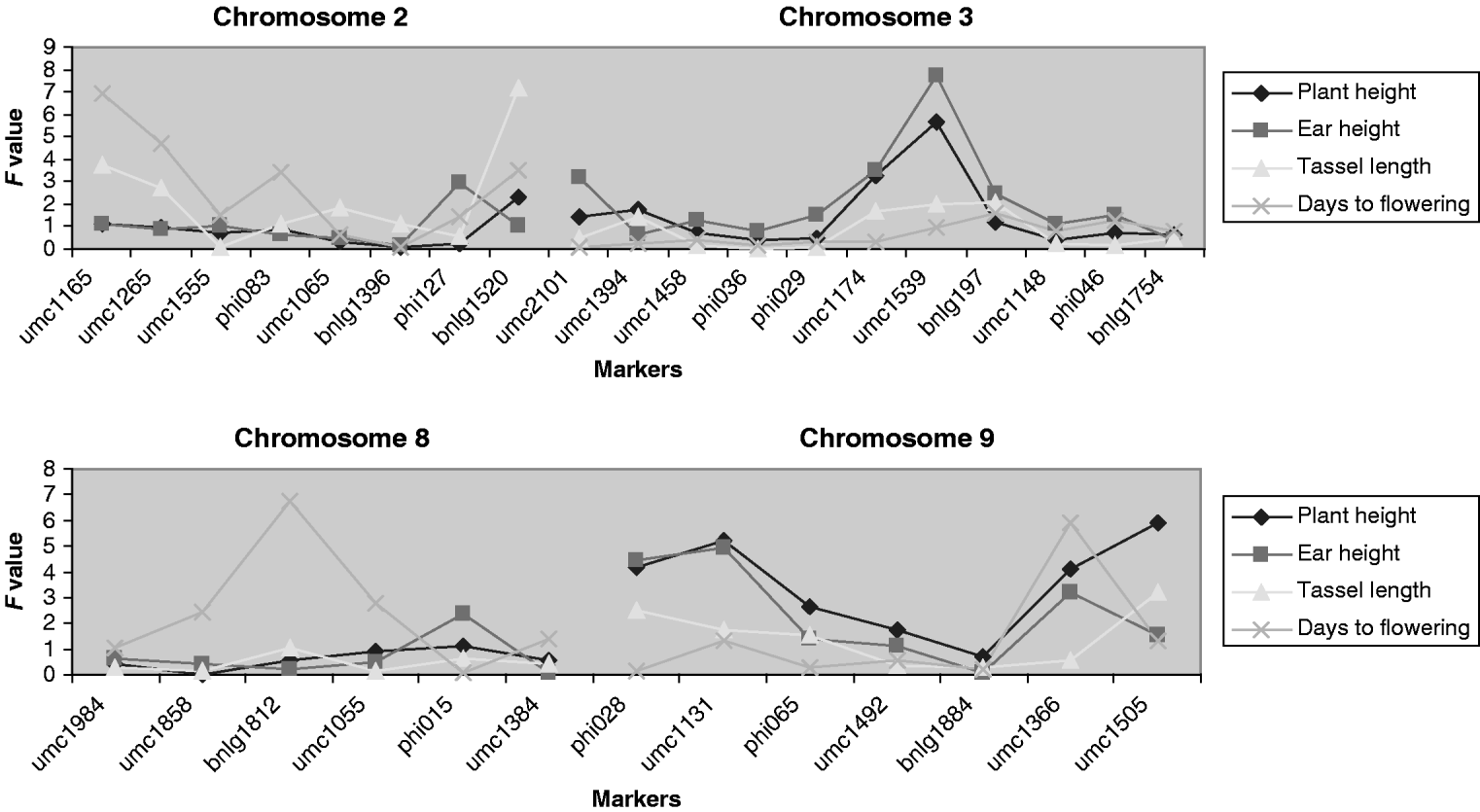
Fig. 4. F statistic obtained for detecting QTLs associated with the means of the traits. The F experimentwise critical values at α=0·05 are 7·57, 7·69, 7·75 and 7·51 and at α=0·25 are 5·61, 5·59, 5·82 and 5·84 for plant height, ear height, tassel length and days to flowering.
4. Discussion
In this study, we have used an analysis of RILs of maize to investigate the presence of genetic variation in the magnitude of the environmental variance (V E) and in the correlation between traits and to identify QTLs that influence these quantities. We have shown that there is considerable genetic variance in V E, in support of studies in other species. We have also shown, we believe for the first time, evidence of genetic variation in the environmental correlation between traits and of QTLs affecting the magnitudes of the environmental variance and the environmental correlation.
(i) The effect of non-normality on significance and estimates
We first review some statistical aspects important in the analysis. When tests assuming normality were used for testing the homogeneity of variances and correlations, both among RILs and for QTL detection, the significance levels were much lower than those obtained from randomization tests. For example, for the comparison of variances for umc1113 and plant height and for bnlg1346 and days to flowering, the observed F ratios were 1·363 and 1·512, respectively, and the probability of a higher value according to F tables is 10−12 or less after Bonferroni's correction. The probabilities according to the permutation test were 0·078 and 0·037, respectively. In contrast, for the comparison of means the significance levels of the tests were relatively similar. For example, for days to pollen shed and markers umc1512, umc1774 and umc1725, the probabilities with the normality test were, respectively, 0·90, 0·12 and 0·34, whereas with the permutation test, they were 0·90, 0·05 and 0·26, respectively.
Tests of heterogeneity of variance such as Barlett's are more sensitive to non-normality than is the use of F test for comparing means in the ANOVA, such that the tests of homogeneity of variances may detect non-normality rather than heterogeneity of variance (Steel et al., Reference Steel, Torrie and Dickey1997; Manly, Reference Manly2007). Our results suggest the need to use permutation or other non-parametric methods for testing homogeneity of variances and correlations because they require fewer model assumptions and provide protection against failures of such assumptions (Churchill & Doerge, Reference Churchill and Doerge1994).
To consider the effect of non-normality on estimates of variation in V E, we used Monte Carlo simulations to generate samples from 130 generalized Lambda distributions (Fan et al., Reference Fan, Felsovalyi, Sivo and Keenan2001), with different values of variances, but with a fixed value of ![]() , for example 0·22. We generated 5 samples of 13 individuals from each of the 130 populations, a similar structure to that of our experiment, and obtained the sampling distribution of
, for example 0·22. We generated 5 samples of 13 individuals from each of the 130 populations, a similar structure to that of our experiment, and obtained the sampling distribution of ![]() estimated both by the procedure described in the Material and Methods (method M) and by the procedure used by Rowe et al. (Reference Rowe, White, Avendano and Hill2006) (method N). In our method M, an ANOVA of the residual variances is used to estimate their sampling variance. In method N, the observations for each RIL are assumed to be normally distributed such that an estimate of variance is proportional to a chi-square variate. The variance between RILs in within line variance is then compared against the pooled error and will be biased by non-normality of the observations such that the chi-square assumption fails.
estimated both by the procedure described in the Material and Methods (method M) and by the procedure used by Rowe et al. (Reference Rowe, White, Avendano and Hill2006) (method N). In our method M, an ANOVA of the residual variances is used to estimate their sampling variance. In method N, the observations for each RIL are assumed to be normally distributed such that an estimate of variance is proportional to a chi-square variate. The variance between RILs in within line variance is then compared against the pooled error and will be biased by non-normality of the observations such that the chi-square assumption fails.
We found using simulation that the estimate of ![]() using method M is unbiased and unaffected by departures from normality while that using method N is biased upwards, increasingly as the distribution becomes skewed or more kurtotic than the normal. For example, when the original distributions have skew −0·35 and kurtosis 0·60 (similar to the average values per replication×RIL found in our data) and the true value of
using method M is unbiased and unaffected by departures from normality while that using method N is biased upwards, increasingly as the distribution becomes skewed or more kurtotic than the normal. For example, when the original distributions have skew −0·35 and kurtosis 0·60 (similar to the average values per replication×RIL found in our data) and the true value of ![]() was 0·22, the estimates from the averages of 1000 simulations using methods M and N were 0·22 and 0·30, respectively. In general, other authors who used different estimation procedures from that of Rowe et al. (Reference Rowe, White, Avendano and Hill2006) also assume normally distributed errors (conditional on genotype), so it would be worthwhile to check the effect of departures from normality in their estimates (e.g. SanCristobal-Gaudy et al., Reference SanCristobal-Gaudy, Bodin, Elsen and Chevalet2001; Sorensen & Waagepetersen, Reference Sorensen and Waagepetersen2003).
was 0·22, the estimates from the averages of 1000 simulations using methods M and N were 0·22 and 0·30, respectively. In general, other authors who used different estimation procedures from that of Rowe et al. (Reference Rowe, White, Avendano and Hill2006) also assume normally distributed errors (conditional on genotype), so it would be worthwhile to check the effect of departures from normality in their estimates (e.g. SanCristobal-Gaudy et al., Reference SanCristobal-Gaudy, Bodin, Elsen and Chevalet2001; Sorensen & Waagepetersen, Reference Sorensen and Waagepetersen2003).
(ii) Magnitude of environmental variances and correlations
The analysis using model 1 shows that there is substantial genetic variance among the means of the RILs. As these were highly inbred, however, the genetic variance within RILs is predicted to be sufficiently small that the residual variance (V E) is due mainly to micro-environmental factors. The environmental correlations among the vegetative traits, plant height, ear height and tassel length, were all positive, indicating similar environmental influences. The correlations between these vegetative traits and time to pollen shed were negative, indicating that any stress that affected the growth of the plant and therefore reduced its size also increased the time that the stressed plant spent in the vegetative phase.
(iii) Genetic variance in environmental variances and correlations
The evident variation in V E between the RILs is an indication of genetic heterogeneity of the V E, that is, EP39 and EP42 have different alleles at loci affecting V E. This conforms with the results of other authors for different species, particularly, those for bristle number in D. melanogaster (Whitlock & Fowler, Reference Whitlock and Fowler1999; Mackay & Lyman, Reference Mackay and Lyman2005). The variation in the environmental correlation coefficients for some of the traits among RILs indicates that there is also a genetic component to the environmental correlations. The magnitude of ![]() of about 20% indicates that there is substantial opportunity for genetic change in the residual variance or, equivalently, the uniformity of vegetative traits of maize.
of about 20% indicates that there is substantial opportunity for genetic change in the residual variance or, equivalently, the uniformity of vegetative traits of maize.
The estimated magnitudes of ![]() of about 20% are lower than those obtained by other authors, which range from 30 to 50% approximately (for a review, see Table 9 in Mulder et al., Reference Mulder, Bijma and Hill2007). However, as already noted, departures from normality could have caused upward bias in some of the estimates. Thus, when we estimated
of about 20% are lower than those obtained by other authors, which range from 30 to 50% approximately (for a review, see Table 9 in Mulder et al., Reference Mulder, Bijma and Hill2007). However, as already noted, departures from normality could have caused upward bias in some of the estimates. Thus, when we estimated ![]() from our data with the method of Rowe et al. (Reference Rowe, White, Avendano and Hill2006), we also obtained values around 30%.
from our data with the method of Rowe et al. (Reference Rowe, White, Avendano and Hill2006), we also obtained values around 30%.
(iv) QTL analyses
QTLs associated with the trait means were observed, as expected from previous analyses in maize. Of these QTLs, those for flowering time at bins 8·05 and 9·06 are located within or close to a consensus region of major effect (Chardon et al., Reference Chardon, Virlon, Moreau, Falque, Joets, Decousset, Murigneux and Charcosset2004).
In accordance with the genetic heterogeneity of V E found among the RILs, QTLs associated with V E were found for all traits. Except for plant and ear height, the QTLs for different traits were detected in different regions. Furthermore, the sign of the difference in the variance for alleles A and B generally varied between traits. We detected several genomic regions involved in the stability of one trait, or two in the case of plant and ear height which have a strong genetic relationship, but did not find any involved in the developmental stability of several traits. This result is in agreement with the very small correlation of the fluctuating asymmetry of different traits found by many authors (see Whitlock, Reference Whitlock1996), although Whitlock & Fowler (Reference Whitlock and Fowler1999) found a weak correlation of environmental variance across some traits.
The QTLs associated with V E and means were not detected in the same regions. This indicates the presence of genomic regions specifically involved in developmental stability but without an important function on the mean of the trait. If genetic heterogeneity between RILs and QTLs for developmental stability were detected for all the traits that we analysed, it is not unreasonable to think that genes associated with developmental stability could exist for several of the traits. Thus, a comprehensive understanding of the genetic architecture of any quantitative trait would include knowledge not only of QTLs or genes associated with means, but also with the stability of the trait.
From a practical perspective, some of the QTLs from V E could be incorporated into breeding programmes with the aim of improving homogeneity of market product or lessening environmental sensitivity. For example, in some special types of maize such as sweet corn, the homogeneity of flowering time is crucial to the final quality of the product. Notably, alleles at the significant (P<0·05) QTL for flowering time at bin 5·07 differed in residual variance by 40%, although the estimated size of the effect could be biased upwards due to the Beavis effect (Beavis, Reference Beavis1994).
For the environmental correlation between ear height and days to pollen shed, genetic heterogeneity between RILs was detected and, in accordance with that, a QTL associated with this environmental correlation was located on chromosome 3. In that region, no QTLs related to either the mean or the variance of ear height and days to pollen shed were detected, suggesting that this region could be specifically involved in environmental correlations. For some combinations of traits, we detected genetic heterogeneity, but not genomic regions associated with the environmental correlations, suggesting the presence of genes with effects too small to detect in our experiment.
In conclusion: firstly, for all traits there is a genetic basis for the differences between the means, the developmental stability (V E) and the environmental correlations between traits; secondly, genomic regions associated with developmental stability and environmental correlations were detected and they were not located in the genomic regions associated with the mean of the traits; thirdly, for estimating variances and correlations and testing their homogeneity, methods that are not highly dependent on model assumptions, such as normality, are necessary.
We thank Pedro Revilla, Anna Wolc, Hans Mulder and Ian White for valuable comments on earlier versions of the manuscript and Ana Butron for developing and genotyping the RILs. The National Plan for Research and Development of Spain (project code AGL2006-13140) is acknowledged for financial support. B. Ordas acknowledges a contract from the Spanish National Research Council (I3P Program).
Appendix. SSR loci used to genotype the inbred lines
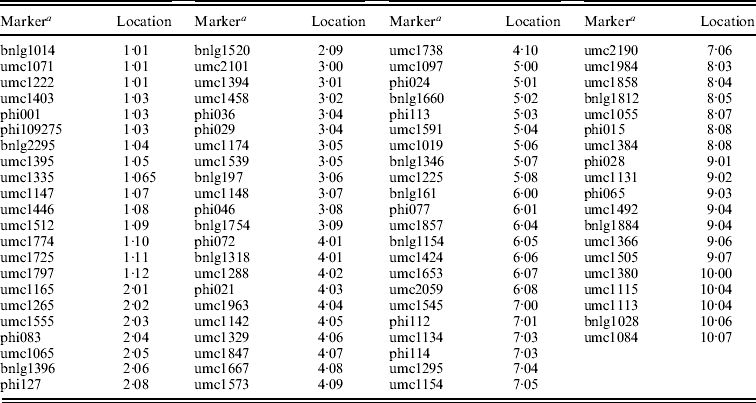
a Marker details can be obtained from the maize database at http://www.maizegdb.org.


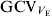 ) was estimated to be 20%, which is lower than estimates obtained for other species. A few genomic regions involved in the stability of one trait or two traits were detected, and these did not have an important influence on the mean of the trait. One region that could be associated with the environmental correlations between traits was also detected.
) was estimated to be 20%, which is lower than estimates obtained for other species. A few genomic regions involved in the stability of one trait or two traits were detected, and these did not have an important influence on the mean of the trait. One region that could be associated with the environmental correlations between traits was also detected.









