Introduction
The cryosphere is one of the most important subsystems of the Earth’s climate. In the Southern Hemisphere, the Antarctic ice sheet, ice shelves, icebergs and sea ice are closely related to the Southern Ocean system. Ice sheets were first formed on the Antarctic continent ∼34 x 106 years ago (Reference Zachos, Pagani, Sloan, Thomas and BillupsZachos and others, 2001). Since then, they have advanced and retreated repeatedly over long timescales. Ice shelves are the floating outer margins of grounded ice sheets and are in contact with the relatively warm ocean at their base, leading to basal melt. Changes in ice-shelf shape by collapse or basal melt can alter the stress distribution of the ice shelf, and the effects can be rapidly transmitted to the ice-sheet interior through ice-sheet dynamics (Reference SchoofSchoof, 2007; Reference RignotRignot and others, 2008; Reference Pritchard and ArthernPritchard and others, 2009). Sea ice is frozen sea water, which is formed by strong oceanic heat loss to the atmosphere. Sea ice plays an important role in the global climate system as an insulating layer at the ocean surface and has high albedo relative to that of open ocean (with the effects amplified by presence of a snow cover). Within these cryospheric processes, sea ice and ice shelves in particular are strongly affected by Southern Ocean climate change.
The mass balance of the Antarctic ice sheet (including ice shelves) is roughly explained by precipitation on ice sheets, calving of icebergs and basal melt of ice shelves. A recent ice-shelf-ice-sheet modelling study (Reference PollardPollard and DeConto, 2009) suggested that basal melt of ice shelves has a pronounced influence on the long-term fluctuations of the Antarctic ice sheet. In present ice-sheet modelling, constant values or simple parameterizations are often used for the basal melt of ice shelves. The model parameterization for basal melt is basically inferred and formulated from present-day ice-shelf conditions. However, the basal melt should be determined by solving the interaction between the ice-shelf base and the ocean (Reference Holland and JenkinsHolland and Jenkins, 1999). It is still unclear how much basal melt of Antarctic ice shelves changes under different climate conditions. Thus, the treatment of ice-shelf basal melt is one of the major problems in current ice-sheet modelling.
In recent years, coupled ice-shelf–sea-ice–ocean models have often been used to better understand Antarctic and Southern Ocean climate change over the past few decades and in the future (Reference Hellmer, Kauker, Timmermann, Determann and RaeHellmer and others, 2012; Reference Timmermann and WangTimmermann and others, 2012; Reference Kusahara and HasumiKusahara and Hasumi, 2013; Reference TimmermannTimmermann and Hellmer, 2013). These models can diagnose the interaction between ice-shelf bases and the ocean. Such modelling applied to past climates will provide us with useful information about ice-shelf basal melt.
The purpose of this study is to investigate sea-ice and Antarctic ice-shelf basal melt in the Last Glacial Maximum (LGM) using a coupled ice-shelf–sea-ice–ocean model (Reference Kusahara and HasumiKusahara and Hasumi, 2013). The LGM is the latest full glacial period and occurred between 26.5 and 19 ka ago (Reference ClarkClark and others, 2009), when the Antarctic ice-sheet/ice-shelf configuration was different from today. It is the best-studied period of past climate, and its environmental conditions have been actively reconstructed. In particular, sea-ice extent and seasonality at the LGM have been reconstructed well from sea-floor sedimentary records. We use the sea-ice reconstruction to validate the numerical simulation under the LGM climate. Subsequently, we investigate the basal melt of the Antarctic ice shelf under present-day and LGM conditions, and explore the differences in the basal melt features.
Numerical Model and Experiments
Coupled ice-shelf-sea-ice-ocean model
We use a sea-ice-ocean model (‘COCO’; Reference Hasumi and EmoriHasumi, 2006 ) with an ice-shelf component. The coupled model is the same as in Reference Kusahara and HasumiKusahara and Hasumi (2013), so only a brief outline of the model set-up is presented here. The model domain is taken to be the Southern Ocean, and the artificial northern boundary is placed at ∼35°S. We use an orthogonal, curvilinear, horizontal coordinate system. The singular points are placed on East Antarctica (82° S, 45° E) and the north pole. The horizontal grid spacing over Antarctic coastal regions is between 10 and 20 km; thus, we represent almost all the Antarctic ice shelves in a single model (Fig. 1). Time steps for the ocean baroclinic and brotropic modes are 180 s and 1.5 s, respectively. The present-day bathymetry and ice-shelf draft are calculated from the RTopo-1 dataset (Reference TimmermannTimmermann and others, 2010). This relatively high horizontal resolution enables us to simulate high sea-ice production in Antarctic coastal margins and dense-water formation (Reference Marsland and BindoffMarsland and others, 2004; Reference Kusahara, Hasumi and TamuraKusahara and others, 2010, Reference Kusahara and Hasumi2011).

Fig. 1. Bottom topography (colour and contour) and ice-shelf draft (colour) for the LGM configuration. Thick and thin red (black) lines indicate the present-day (LGM) grounding line and ice front line, respectively.
We performed a 25 year simulation driven by present-day climate conditions (‘PRESENT’ case). Initial values for temperature and salinity fields in the PRESENT case are derived from Polar Science Center Hydrographic Climatology (PHC; Reference Steele, Morley and ErmoldSteele and others, 2001), and the ocean velocity is set to zero over the model domain. In the northern six grids, temperature and salinity are restored to the PHC monthly climatology throughout the water column. Surface boundary conditions on the open ocean and sea ice are wind stresses, wind speed, air temperature, specific humidity, downward shortwave radiation, downward longwave radiation and freshwater flux. These boundary conditions for the PRESENT case are calculated from the atmospheric surface dataset of Röske (2006), and are used for the background surface boundary conditions of the LGM simulation, as explained below.
There are three main differences in the model configuration for the LGM simulation (‘LGM’ case): the shape of the ice shelves, the ocean conditions (temperature and salinity) and the surface boundary conditions. In the following subsections, we describe our treatment of these components for the LGM case. A 25 year simulation is also performed for the LGM case.
Antarctic ice-sheet-ice-shelf configuration during the LGM
During glacial periods, Antarctic grounding lines advance to close to shelf-break regions (Reference Anderson, Shipp and LoweAnderson and others, 2002; Reference Denton and HughesDenton and Hughes, 2002), and the floating ice shelves are considered to overhang the continental slopes (Reference PollardPollard and DeConto, 2009). There are reconstructions of Antarctic ice sheets and ice shelves in the Paleoclimate Modeling Inter-comparison Project (PMIP)/Coupled Model Intercomparison Phase 5 (CMIP5), which were obtained by averaging three different estimates (Reference BraconnotBraconnot and others, 2012; https://wiki.lsce.ipsl.fr/pmip3/doku.php/pmip3.design:pi:final:icesheet). However, the horizontal resolution is coarse (1.0°) and the data provide only positions of grounding and ice-front lines. At present, no data are available for ice-shelf draft in the LGM. In this study, we use the shape of ice shelves in the LGM case simulated by a coupled ice-sheet-ice-shelf model. The ice-sheet model is the SImulation COde for POLy-thermal Ice Sheets (SICOPOLIS) (Reference GreveGreve, 1997a,b), including an ice-shelf component (Reference Sato and GreveSato and Greve, 2012). The ice-sheet model has been used for previous palaeoclimate studies (Reference Calov, Ganopolski, Petoukhov, Claussen and GreveCalov and others, 2002; Reference Forsström, Sallasmaa, Greve and ZwingerForsström and others, 2003; Reference Forsström and GreveForsström and Greve, 2004). The set-up of our palaeo-climatic run from 125 ka BP until 20 ka BP (LGM) is essentially the same as that of the palaeoclimatic spin-up, as described in section 3.1 of Reference Sato and GreveSato and Greve (2012), which was also used for the Sea-level Response to Ice Sheet Evolution (SeaRISE) experiments with SICOPOLIS (Reference BindschadlerBindschadler and others, 2013; Reference NowickiNowicki and others, 2013). However, here we allow the topography (ice surface, ice base, grounding line and calving front) to evolve freely. ALBMAP version 1 (Reference Le Brocq, Payne and VieliLe Brocq and others, 2010) is used for the Antarctic bed elevation. The standard conversion of the deuterium record to temperature from the Vostok ice core (Reference PetitPetit and others, 1999) and its relationship with surface temperature is applied to one glacial cycle calculation. The horizontal resolution of the ice-sheet model is 20 km.
Figure 1 shows the position and draft of the ice shelves in the LGM case. The ice shelves in the LGM are placed more northward than in the present day. In particular, the ice shelves in the Weddell, Ross and Amundsen-Bellingshausen seas are different from the present-day configuration. The position of ice shelves in the LGM case is roughly consistent with that in the blended product of the ice sheets in PMIP/ CMIP5. The draft of the ice shelves ranges from 200 m in the ice front regions to 1000 m near the grounding line.
LGM surface boundary and initial conditions for the ice-shelf-sea-ice-ocean model
The surface boundary conditions for the LGM case are calculated from the results for the present-day and LGM simulations using the climate model (MIROC: Model for Interdisciplinary Research On Climate; Reference Hasumi and EmoriHasumi and Emori, 2004), which are listed in PMIP2 (Reference WeberWeber and others, 2007). We use model results from the medium-resolution version of MIROC (atmospheric resolution T42L20; sea-ice and oceanic resolutions ∼1 °). Note that COCO is the sea-ice and ocean component of MIROC.
In this study, to produce surface boundary conditions in the LGM, the LGM anomalies of surface atmospheric variables are superimposed on the present-day surface boundary conditions. This treatment is conducted to minimize model biases that are inherent to MIROC simulations. Appendix A shows sea-ice representation in the LGM and present-day MIROC simulations. Monthly anomalies of surface boundary conditions (LGM–present) are calculated from the present-day and LGM simulations by MIROC. The monthly values are averaged over 100 years in the present-day and LGM simulations to better represent the climatological surface conditions for each climate simulation. The surface air temperature in the LGM is lower than that in the present day over the Southern Ocean (Fig. 2a). Moreover, there are eastward wind stress anomalies in offshore regions, westward wind stress anomalies near coastal regions and lower specific humidity and precipitation over most regions south of 40° S (Fig. 2b–d).

Fig. 2. Annual mean anomalies (LGM–PRESENT) of (a) surface air temperature, (b) wind stress vectors with eastward wind stress (colour), (c) specific humidity and (d) precipitation.
Ocean temperature and salinity in the LGM are also different from those in the present day. As our model domain is limited to the Southern Ocean and the numerical integration is only several tens of years, we could not obtain LGM oceanic conditions solely by changing surface boundary conditions. Therefore, in addition to surface boundary conditions, we superimpose anomalies of temperature and salinity (LGM-present) on the present-day initial and northern boundary conditions to represent long-term model integration by the LGM surface boundary conditions. Reference Oka, Hasumi and OuchiOka and others (2012) performed present-day and LGM simulations using the sea-ice-ocean model (COCO) to investigate the behaviour of the Atlantic meridional overturning circulation. Their model was integrated by the surface boundary conditions from the MIROC simulations, and they obtained quasi-steady states of ocean circulation in both climate states. We use their steady oceanic states of the present-day and LGM simulations. In addition to surface boundary conditions, monthly temperature and salinity fields averaged over 100 years are used to calculate the LGM anomalies. Figure 3 shows the spatial anomaly of surface temperature and the vertical profile of zonal average temperature. Ocean temperature in the surface and intermediate layers in the LGM is lower on average by ∼2°C than in the present day.

Fig. 3. Annual mean anomaly (LGM–PRESENT) of (a) ocean surface temperature and (b) zonal average ocean temperature.
Results and Discussion
In this section, we compare the results for the LGM case with those for the PRESENT case and the literature for sea-ice fields and basal melt of Antarctic ice shelves. In both the PRESENT and LGM cases and after about a 15 year integration, the modelled sea ice and basal melt of Antarctic ice shelves show quasi-steady states. Figure 4 shows the time evolution of sea-ice production in coastal areas and the total basal melt of ice shelves. We use the monthly values averaged over the last 3 years (23rd-25th) for the following analyses. In Appendix B, we compare the simulated meridional overturning circulation in the two cases because the thermohaline circulation is important for global climate and is one of the key topics in palaeoceanography.
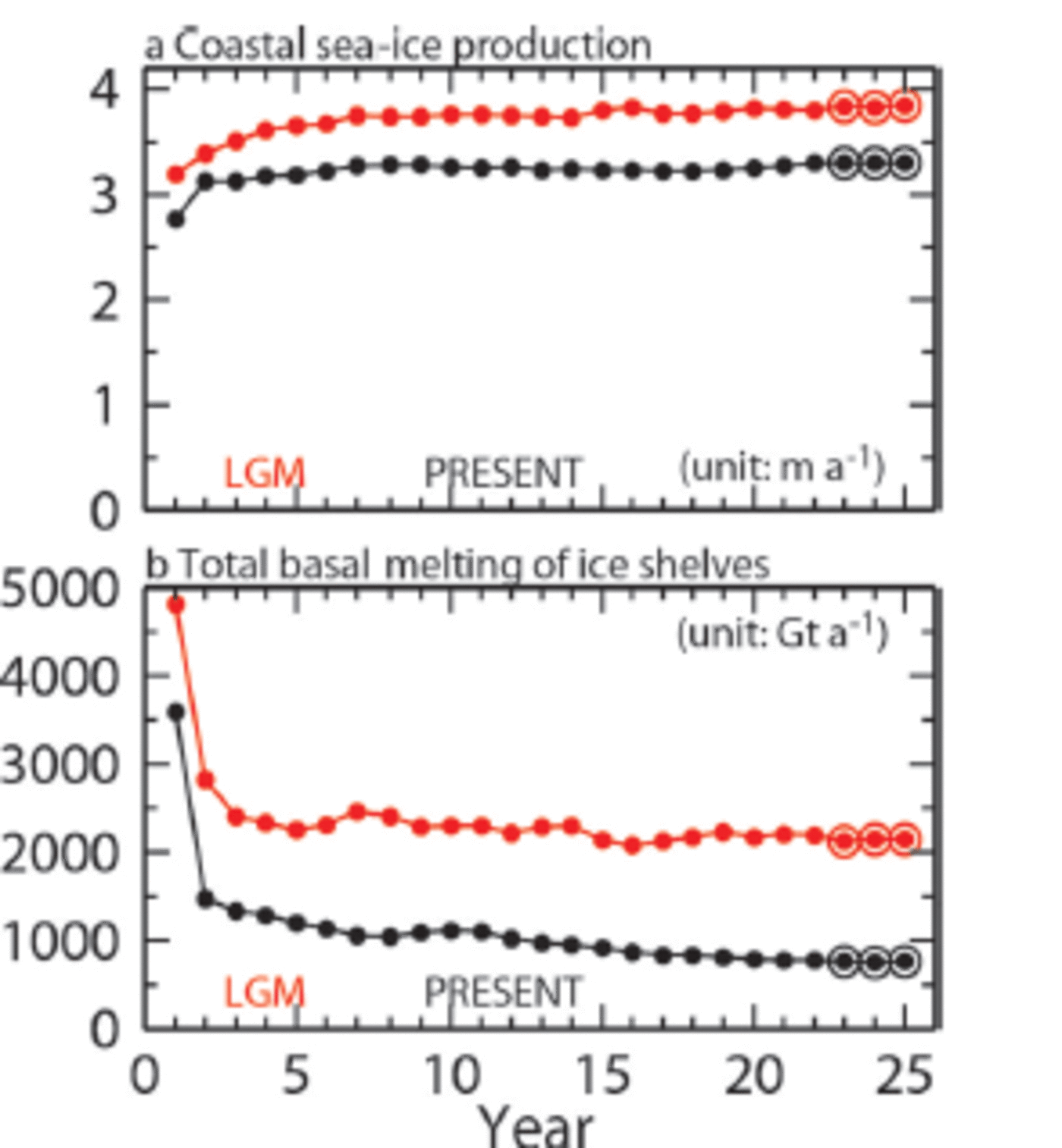
Fig. 4. Time series of (a) mean coastal sea-ice production and (b) total basal melt of Antarctic ice shelves. The red and black symbols and lines indicate results for the LGM and PRESENT cases, respectively. The last 3 years are fringed by the circles to show the averaging period used for the analyses.
Sea-ice extent
It is known that sea-ice coverage was more extensive in the LGM. Microfossils of diatoms and radiolarians in sea-floor sediment cores are used as a proxy for past sea-ice extent (Reference Gersonde, Crosta, Abelmann and ArmandGersonde and others 2005), and the reconstructed sea-ice information is useful for validating the sea-ice model in the LGM simulation. In this subsection, we show the distribution and seasonal change of sea ice in the LGM case (Fig. 5), and show that the modelled sea-ice fields are largely consistent with those estimated from sea-floor sedimentary records.

Fig. 5. Maps of sea-ice concentration ((a) September, (b) February) and seasonal variation of sea-ice extent. The colours in (a) and (b) indicate sea-ice concentration in the LGM case, and the black curves in the two panels show sea-ice edges in the PRESENT case, which is defined by a sea-ice concentration of 15%. Blue lines indicate the sea-ice edge reconstructed by Reference Gersonde, Crosta, Abelmann and ArmandGersonde and others (2005). Grey areas indicate the extended ice sheet/shelf at the LGM.
The modelled winter maximum sea-ice edge (defined by 15% sea-ice concentration) in the LGM case is located at a latitude of ∼50°S in the Atlantic and western Indian sectors (45°W-90°E, Fig. 5a). In the other sectors, the sea-ice edge is in the latitudinal range 60-55°S. At all longitudes, the winter ice edge in the LGM case is located to the north of the PRESENT case (black line in Fig. 5a), by 3-7° in latitude. The winter ice edge in this model is broadly consistent with that estimated by Reference Gersonde, Crosta, Abelmann and ArmandGersonde and others (2005) (blue line in Fig. 5a), although the model tends to underestimate the winter ice extent near 15°W and 150°E.
Extensive summer sea-ice coverage in the LGM case is found only in the Atlantic Ocean sector, with little sea ice in the Indian and Pacific Ocean sectors (Fig. 5b). Although the summer sea-ice edges reconstructed by Reference Gersonde, Crosta, Abelmann and ArmandGersonde and others (2005) are sparse in space, except in central longitudes in the Atlantic and Indian Ocean sectors, the modelled sea-ice edge in summer agrees well with their estimate. Reference Gersonde, Crosta, Abelmann and ArmandGersonde and others (2005) noted that the summer sea-ice extent reconstructed from the sediment cores is an indicator of sporadic occurrence of sea-ice existence in the LGM period.
Seasonal variations of the Southern Ocean sea-ice extent between PRESENT and LGM cases (Fig. 5) exhibit clear difference. In the PRESENT case, the sea ice reaches its maximum extent between August and October and has its minimum between February and March. In the LGM case, the sea ice reaches its maximum extent between September and November and has its minimum between February and March. The amplitude of seasonal variation in sea-ice extent is greater in the LGM case than in the PRESENT case. Sea-ice distribution responds to surface ocean and atmospheric boundary conditions, hence we conclude that the model’s LGM results and surface boundary conditions are within acceptable ranges. Note that in Appendix A, we show the representation of sea ice in the LGM and present-day simulations using MIROC. The climate model tends to underestimate the sea-ice extent in the LGM summer and the present-day winter.
Sea-ice production
Along the Antarctic continental margin (edges of ice shelves and fast ice), rapid sea-ice formation occurs during the freezing period in persistent and recurrent coastal polynyas that are maintained by wind and/or ocean currents (Reference Massom and HarrisMassom and others, 1998; Reference Morales and MaquedaMorales Maqueda and others, 2004; Reference Tamura and NihashiTamura and others, 2008; Reference KernKern, 2009). With high sea-ice production, vast amounts of salt rejected from growing sea ice lead to densification of the water column. Therefore, Antarctic coastal polynyas are known to be active dense-water formation sites. The sinking of the dense waters into the deep Southern Ocean along continental slopes constitutes the lower limb of the global thermohaline circulation in the Southern Hemisphere (Reference OrsiOrsi and others, 1999). The dense waters formed in coastal polynyas typically have temperatures near the surface freezing point. At some locations, the dense waters are transported into ice-shelf cavities. As the freezing temperature of sea water decreases with depth, these dense waters at near-surface freezing point can melt the ice-shelf base (Reference Jacobs, Hellmer and JenkinsJacobs and others, 1992). As described here, sea-ice production is important not only to sea ice but also to the basal melt of Antarctic ice shelves and the Southern Ocean circulation; therefore we describe here the modelled sea-ice production in the LGM and PRESENT cases.
Figure 6 shows the spatial distributions of annual sea-ice production in the LGM and PRESENT cases. The model reproduces the present-day Antarctic coastal polynyas and high levels of sea-ice production (Reference Kusahara and HasumiKusahara and others, 2010), consistent with an estimate based on heat flux calculation and satellite data (Reference Tamura and NihashiTamura and others, 2008). In the PRESENT case, high sea-ice production areas occur in the Ross and Weddell Seas and along the East Antarctic coast. Consistent with lower atmospheric surface temperatures, the LGM case shows more active sea-ice formation than the PRESENT case. Circumpolar-averaged sea-ice production in coastal areas (areas within 120km of the coastline or ice-sheet margin) in the LGM and PRESENT cases is 3.84 and 3.30 m a–1respectively. The typical horizontal scale of high sea-ice production in coastal areas (i.e. coastal polynyas) is <100 km. We use the wider distance of 120 km for calculating the sea-ice production to avoid a dependency on the selected distance. In the LGM case, high sea-ice production areas are found extensively in the Ross Sea and along the East Antarctic coast. Moreover, in the LGM case, there are moderate (>2 ma–1) though extensive sea-ice production areas in offshore regions. In the Weddell Sea, sea-ice production in the LGM case is smaller overall than in the PRESENT case because of the large amount of sea ice throughout the year (Fig. 5), but there is high sea-ice formation along the Antarctic Peninsula.
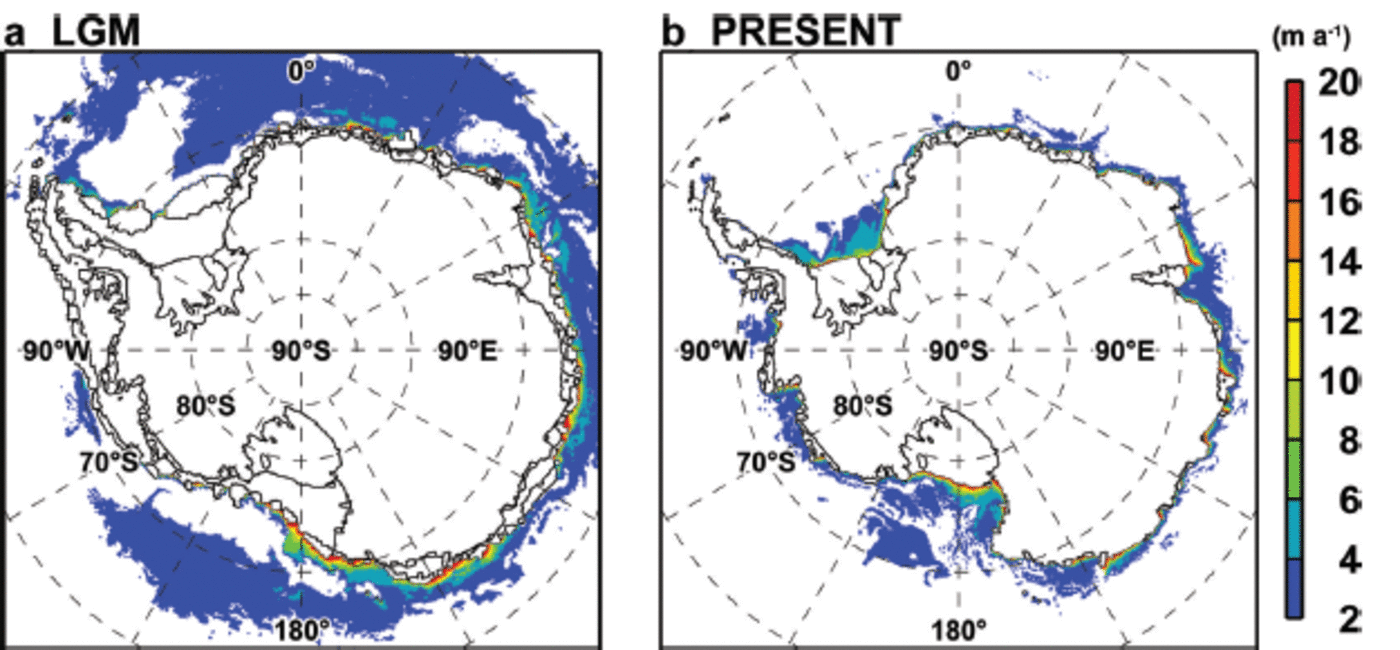
Fig. 6. Maps of sea-ice production (ma–1) for (a) LGM and (b) PRESENT. Areas in which ice production is <2m are masked out.
Basal melt of Antarctic ice shelves
Before comparing ice-shelf basal melt in the different epochs, we assess the model performance in simulating present-day basal melt. The total amount of basal melt is 762 Gta–1 in the PRESENT case (Table 1). Cumulative ice flux across from the Antarctic ice sheet to the Southern Ocean across current grounding lines is currently estimated to be 2000–2500Gt a–1 (Reference RignotRignot and others, 2008, 2011). Other studies have estimated that basal melt of ice shelves accounts for 20–40% of the ice flux from the Antarctic ice sheet (Reference Jacobs, Hellmer and JenkinsJacobs and others, 1992, Reference Jacobs and Jenkins1996; Reference Hooke RLeHooke, 2005). As our estimate in the PRESENT case is within this range, we consider that the model can approximately reproduce general basal melt of Antarctic ice shelves in the present day (Reference Kusahara and HasumiKusahara and Hasumi, 2013). However, we note that recent high-resolution satellite-based studies by Reference DepoorterDepoorter and others (2013) and Reference Rignot, Jacobs, Mouginot and ScheuchlRignot and others (2013) have reported basal melt rates of Antarctic ice shelves ranging from 1325 to 1454 Gta–1. These estimates are larger than our model estimate in the PRESENT case. There are two major reasons for the difference. First, our model tends to underestimate the basal melt of some ice shelves (see also the appendix of Reference Kusahara and HasumiKusahara and Hasumi (2013) for a detailed comparison of the basal melt of all Antarctic ice shelves). In particular, the model fails to reproduce the high basal melt for ice shelves in the Amundsen Sea, because the horizontal resolution in the model (∼20km there) is not sufficient to resolve bathymetrically guided, local-scale intrusions of relatively warm Circumpolar Deep Water onto the continental shelf (Fig. 10b further below). Consequently, in numerical simulations the absence of the Circumpolar Deep Water may lead to small basal melt at these ice shelves (Reference Timmermann and WangTimmermann and others, 2012; Reference Kusahara and HasumiKusahara and Hasumi, 2013). Second, recent observational estimates (Reference Rignot, Jacobs, Mouginot and ScheuchlRignot and others, 2013) have indicated that basal melt is more important than previously thought, and/or that basal melt has tended to increase in recent decades.
Table 1. Amount of basal melt and mean melt rate of Antarctic ice shelves in the LGM and PRESENT cases
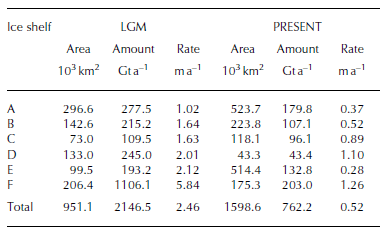
For convenience, we categorize the Antarctic ice shelves into six groups (A-F) based on their locations. Figure 7 shows the spatial distribution of the basal melt/freeze of Antarctic ice shelves in the LGM and PRESENT cases. For all the categorized ice shelves, amounts and rates of basal melt are much higher in the LGM case than in the PRESENT case (Table 1). The mean basal melt rate in the LGM case is 4.7 times that in the PRESENT case. The mean melt rate of ice shelf F in the Amundsen-Bellingshausen Sea is 5.8 m a–1and there are regions where the local melt rate exceeds 10 m a–1. Even though the areal extent of Antarctic ice shelves in the LGM is 59% of the present-day ice-shelf area, the total amount of basal melt in the LGM case is 2147 Gta–1i.e. 2.8 times that of the PRESENT case.
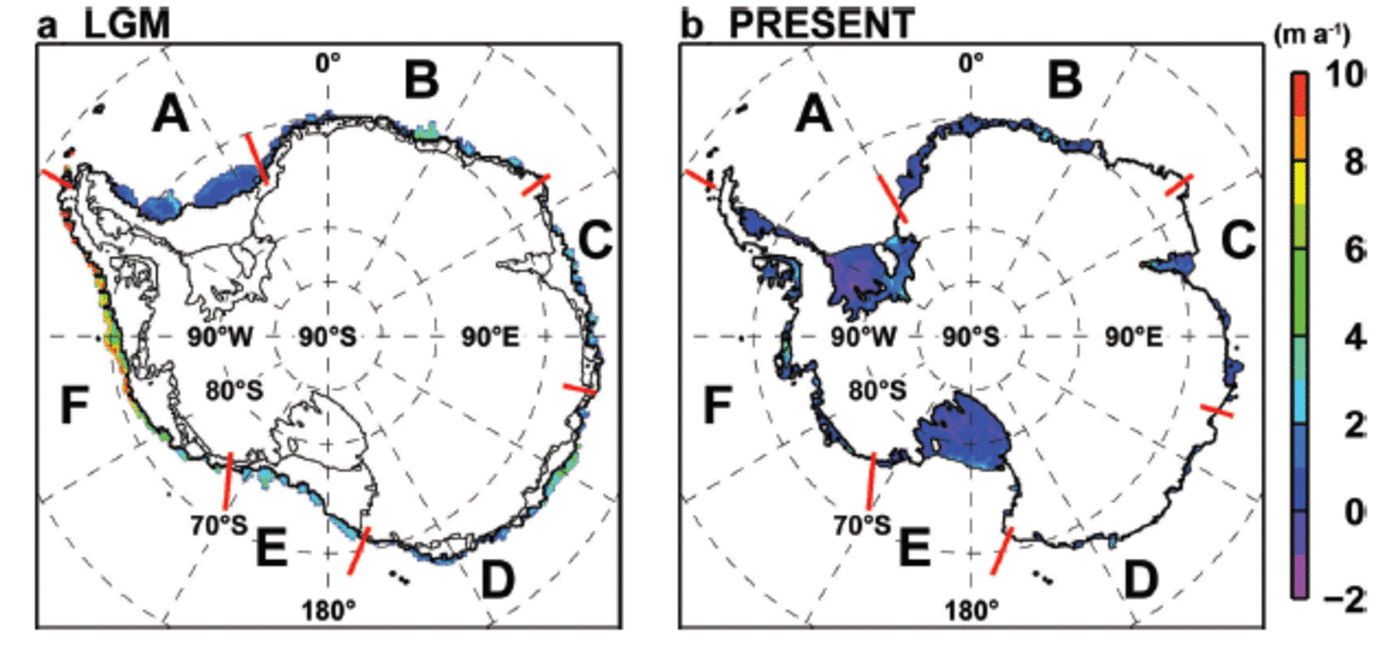
Fig. 7. Maps of basal melt/freezing rate (m a–1) for (a) LGM and (b) PRESENT. Positive values indicate melting. Labels A–F are referred to in Figure 9.
Heat source for basal melt of ice shelves
At the base, ice shelves melt due to thermal energy from the ocean. In this model, basal melt at an ice shelf is calculated by a three-equation scheme (Reference HellmerHellmer and Olbers, 1989; Reference Holland and JenkinsHolland and Jenkins, 1999) with constant coefficients for thermal and salinity exchange velocities (γt 1.0 x 10– 4 ms–1, γs 1 . 0 x 1 0 4 m s–1; Reference HellmerHellmer and Olbers, 1989). Therefore, the basal melt of an ice shelf is dominated by changes in the heat content of ocean inflow into the ice-shelf cavity (temperature and volume transport). As shown above, the basal melt features are different between the LGM and PRESENT cases (Fig. 7; Table 1). Here we assess the ocean inflow volume into ice shelves across the ice fronts and its properties (in particular ocean temperature) to understand the causes of high ice-shelf basal melt in the LGM case. Figure 8 shows the inflow and outflow transport in the temperature–salinity space with bin intervals of 0.1 °C and 0.05 psu in the LGM and PRESENT cases. For convenience, the boundaries of present-day water masses defined by temperature and salinity are superimposed (Reference Kusahara and HasumiKusahara and Hasumi, 2013).

Fig. 8. Water exchange across ice front in the temperature–salinity space in the LGM (left) and PRESENT (right) cases. Bin intervals for potential temperature (vertical axis) and salinity (horizontal axis) are 0.1°C and 0.05 psu respectively. Blue and red indicate outflow from the cavity and inflow into the cavity, respectively. The pink lines indicate the boundaries of present-day water masses (Reference Kusahara and HasumiKusahara and Hasumi, 2013). The abbreviations of the water masses are AASW (Antarctic Surface Water), MCDW (Modified Circumpolar Deep Water), MSW (Modified Shelf Water), LSSW (Low Salinity Shelf Water), HSSW (High Salinity Shelf Water) and ISW (Ice Shelf Water). The grey line indicates the surface freezing temperatures. The dashed contours with labels show the potential density anomaly.
Reference Jacobs, Hellmer and JenkinsJacobs and others (1992) pointed out that three heat sources contribute to the basal melt of Antarctic ice shelves. The first is Shelf Water (SW), which originates from brine drainage by sea-ice formation in winter and has near-surface freezing temperatures; SW is divided into Low Salinity Shelf Water (LSSW) and High Salinity Shelf Water (HSSW) by salinity. The second is Circumpolar Deep Water (CDW) or modified CDW (MCDW). MCDW is formed by the mixing of CDW with ambient waters over continental shelves, and mixing of MCDW and SW forms Modified Shelf Water (MSW). The third is warm Antarctic Surface Water (AASW), which is formed by sea-ice melt and is characterized by low salinity. During the summer sea-ice-free period, AASW is warmed by surface heating, and the warm AASW is transported to ice-shelf cavities by tides and/or seasonally variable coastal currents. Note that ocean eddies also play a role in ocean heat transport into ice-shelf cavities (Hatter-mann and others, 2012). The model can reproduce the three main heat sources of basal melt (PRESENT case in Fig. 8; Reference Kusahara and HasumiKusahara and Hasumi, 2013). However, we could not evaluate the impact of eddies and tides on the basal melt of ice shelves in this model, because the model is a non-eddy-resolving and non-tidal one.
Figure 9 shows the ratios of temperature and total volume transport of inflowing water masses into each ice-shelf cavity (A-F in Fig. 7). In both cases, the water properties and temperature profiles of inflowing water into the cavities are largely different among ice shelves. Figure 10 shows the spatial distribution of annual mean temperature at the sea floor. Here we show that in the LGM case, the relatively warm water is transported much more into the cavities than in the PRESENT case. In all the ice shelves, the total volume transported into the cavities is larger in the LGM case than in the PRESENT case. In the PRESENT case, waters near the surface freezing point (θ<-1.6°C, SW and cold MSW) dominate the inflows into ice shelves A-E. The cold waters originate from brine rejection over the continental shelf regions (Fig. 10). At ice shelf F, there are intrusions of relatively warm waters (-1.6°C< θ<0.0°C, MCDW and warm MSW) in the PRESENT case (Fig. 9 and 10). For ice shelves A, B, C, E and F, the ratio of the inflowing warm waters in the LGM case is higher than that in the PRESENT case. Although the ratio of the warm waters at ice shelf D is lower than in the PRESENT case, the total transport of the warm waters is larger in the LGM case than in the PRESENT case.
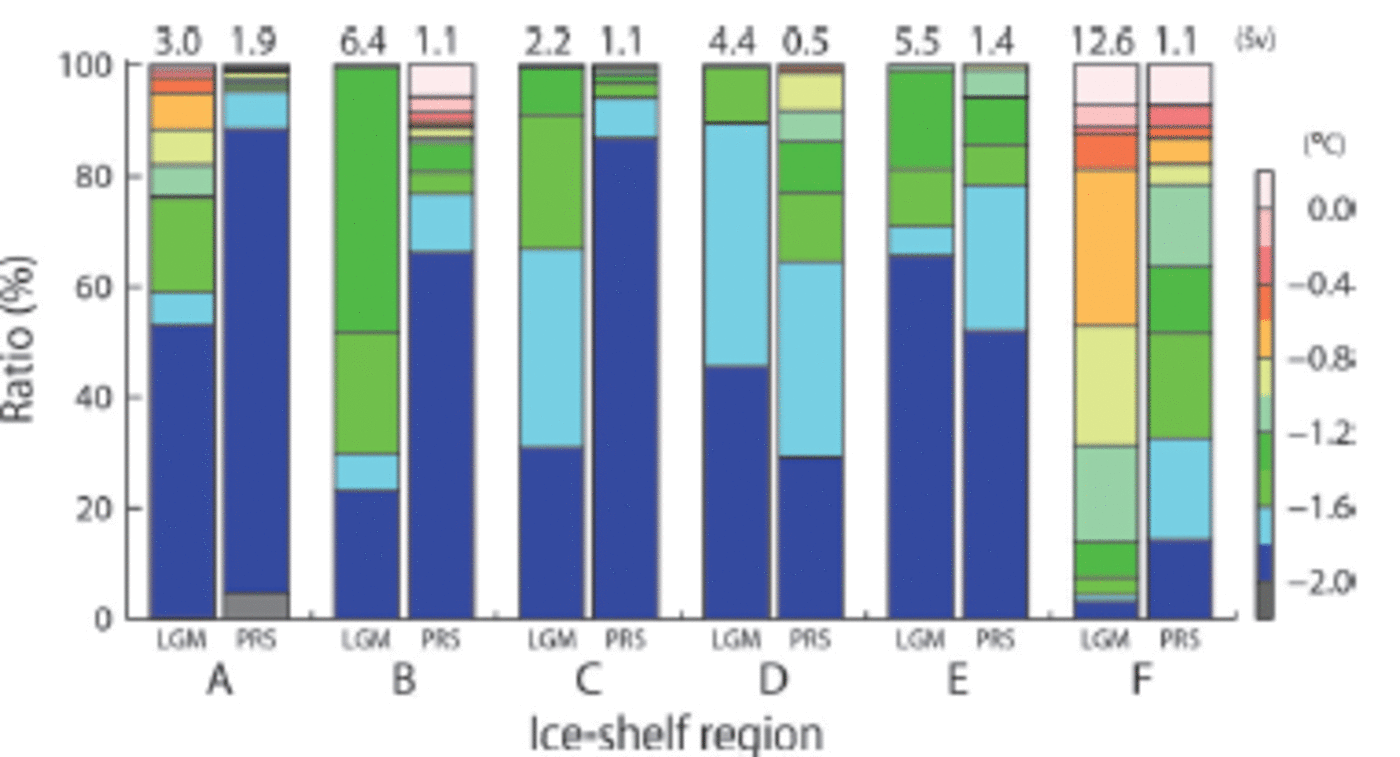
Fig. 9. Ratio of temperature of inflowing water into each ice-shelf cavity. Numbers on each bar indicate the volume transport of the inflow to each ice-shelf cavity (1 Sv = 1 x 106m3s–1). See Figure 7 for the locations of ice shelves A-F. The left and right bars in each ice shelf show the LGM and PRESENT cases, respectively.
As Antarctic ice shelves in the LGM overhang continental shelf regions and are close to the warm (modified) CDW, high basal melt of ice shelves occurs in the LGM case. Even though sea-ice production is higher in the LGM case than in the PRESENT case, the water column in the regions of active ice formation is much thicker than in the PRESENT case (Fig. 1); therefore, ice production in the LGM case is not sufficient to decrease the temperature of the inflows to the near-surface freezing point. In contrast, and as there are wide and shallow continental shelves in the present day, the waters inflowing into ice-shelf cavities can easily reach the near-surface freezing point in front of most ice shelves (Fig. 10).
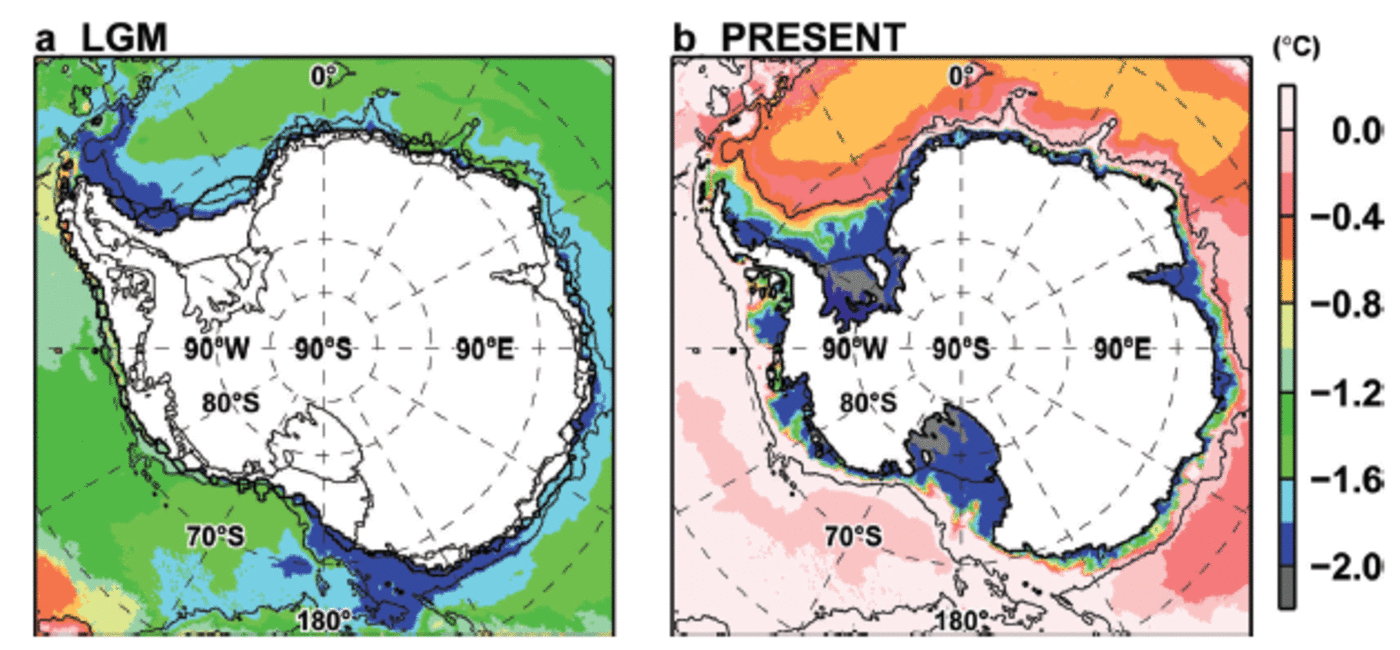
Fig. 10. Spatial distribution of annual mean bottom temperature in the LGM and PRESENT cases. Black contours indicate the 3000 m depth.
Conclusion
We investigated the sea-ice extent and basal melt of Antarctic ice shelves in the LGM using a coupled ice-shelf-sea-ice-ocean model, which can approximately reproduce these features at the present day (Fig. 5 and 7). We change the shapes of ice shelves, ocean conditions and surface boundary conditions to produce the LGM configuration for the Southern Ocean regional model (Fig. 1-3). The winter maximum sea-ice edge in the LGM is located ∼3-7° of latitude further north compared to the present day. In summer, extensive sea ice is found in the Atlantic Ocean sector but little sea ice in the other sectors. The modelled seasonal variations in sea-ice extent (Fig. 5) are consistent with the reconstruction of sea-ice extent from sea-floor sedimentary records over the Southern Ocean (Reference Gersonde, Crosta, Abelmann and ArmandGersonde and others, 2005).
The total basal melt amount of Antarctic ice shelves is estimated at 2147Gta–1 in the LGM case, which is about three times larger than the PRESENT case (Fig. 4; Table 1). The mean melt rate at ice-shelf bases in the LGM case increases about fivefold in the PRESENT case (Fig. 7; Table 1). As the full glacial Antarctic grounding line is close to the shelf break and the ice shelves overhang the continental slopes, relatively warm waters originating from the CDW can readily access the ice-shelf cavities (Fig. 8-10).
Basal melt of the Antarctic ice shelves, i.e. interaction between the Antarctic ice sheet and the Southern Ocean, is an important process in long-term fluctuations of the ice sheet (Reference PollardPollard and DeConto, 2009). At present, a constant value or simple parameterization is used for basal melt in ice-sheet models. Ice-sheet models often adopt lower ice-shelf basal melt rates in glacial periods, which may be inferred from cold atmospheric and ocean conditions. However, in this study, we suggest that there is active basal melt of ice shelves during the glacial period. We consider that the basal melt of Antarctic ice shelves estimated in this study (Fig. 7; Table 1) can be used for ice-shelf basal melt in ice-sheet models instead of the previous parameterization. We are currently planning to run an ice-sheet model (Reference Sato and GreveSato and Greve, 2012) with this strategy to understand the Antarctic climate system better.
Acknowledgements
Numerical simulations were performed on a Fujitsu FX10 at the Information Technology Center, University of Tokyo. K.K. was supported by Grants-in-Aid for Scientific Research A (No. 26247080), B (No. 23340138) and Research Activity Start-up (No. 25887001) from the Japan Society for the Promotion of Science (JSPS) and by The Canon Foundation. H.H. was supported by Grants-in-Aid for Scientific Research A (No. 26247080) and B (No. 23340138) from the JSPS. T.S. and R.G. were supported by a Grant-in-Aid for Scientific Research A (No. 22244058) from the JSPS. A.A.-O., A.O., R.G. and H.H. were supported by a Grant-in-Aid for Scientific Research A (No. 25241005) from the JSPS. We are grateful to the chief editor P. Heil, the scientific editor R.A. Massom and two anonymous reviewers for their careful reading and constructive comments on the manuscript.
Appendix A: Representation of Sea Ice in the Climate Model (MIROC)
In this study, we use the LGM anomaly, which is calculated from the output of the LGM and present-day simulations using MIROC, and the LGM surface boundary conditions for the LGM case are produced by adding the LGM anomaly on the present-day surface boundary conditions of Röske (2006). In polar oceans, sea ice acts as a thermal insulator between the ocean and atmosphere, so the presence of sea ice significantly affects lower atmospheric and upper oceanic properties. This is also the case in climate models, so the representation of sea ice is very important for regulating atmospheric and oceanic surface boundary conditions. Thus, we briefly describe the representation of sea ice in the MIROC simulations in this appendix.
Figure 11 shows the spatial distributions of sea-ice concentrations in September and February in the original MIROC simulations. The LGM winter sea ice in MIROC extends northward of the present-day sea-ice edge, as well as that estimated by Reference Gersonde, Crosta, Abelmann and ArmandGersonde and others (2005). In the LGM summer and present-day winter, MIROC simulations underestimate the extent of sea ice in the Atlantic sector. This misrepresentation of sea ice leads to model biases in atmospheric and oceanic surface variables in the coupled system.
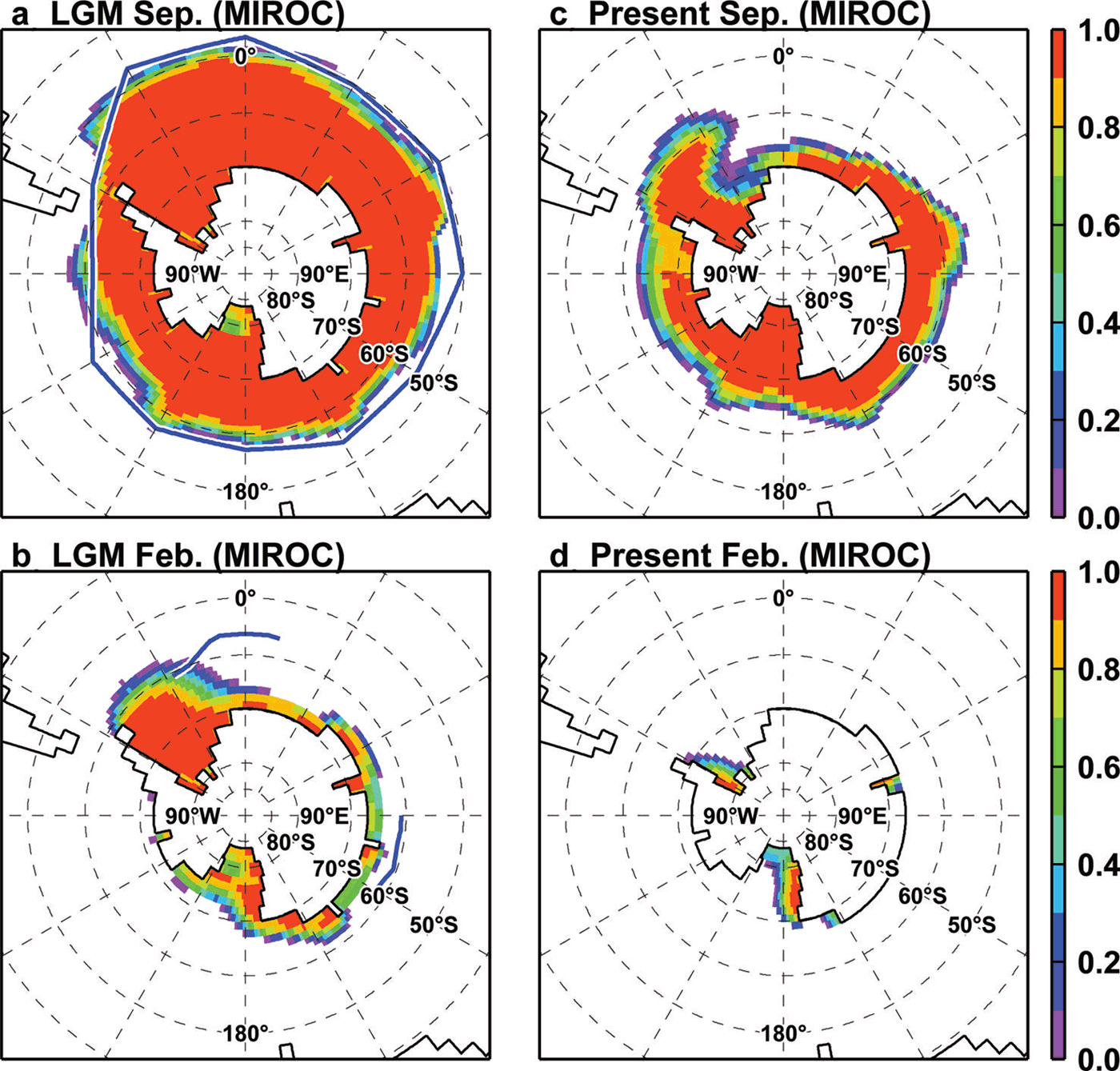
Fig. 11. Maps of sea-ice concentration in MIROC simulations. Upper (lower) panels show the concentration in September (February), and left (right) panels show results under LGM (present-day) conditions. Blue lines in left panels indicate the sea-ice edge reconstructed by Gersonde and others (2005).
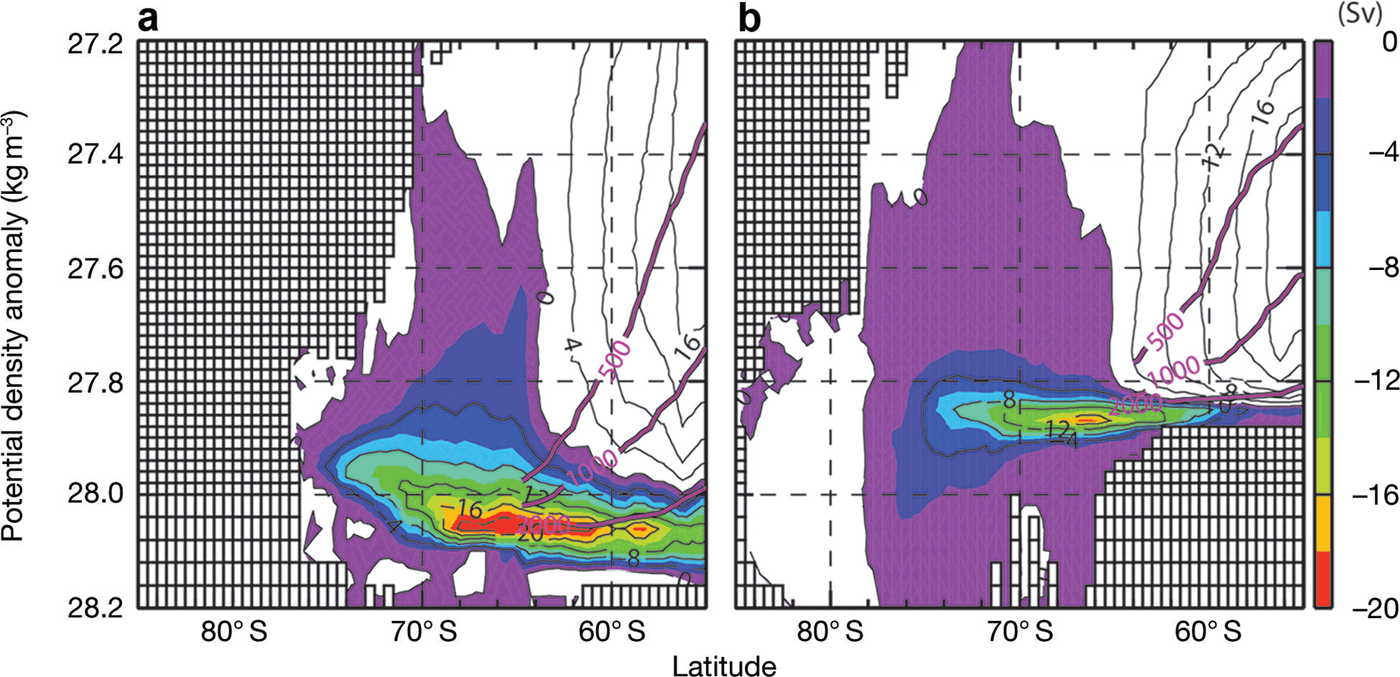
Fig. 12. Stream function of zonally integrated, annual mean meridional overturning circulation in the latitude-density domain (1 Sv = 1 x106m3s–1; (a) LGM, (b) PRESENT). Positive contours indicate clockwise circulation. Negative shades indicate anticlockwise circulation. The vertical axis indicates potential density anomaly referenced to the surface. Purple lines with labels indicate zonal-averaged depth.
Appendix B: Southern Ocean Meridional Overturning Circulation
In the main text, we have shown that sea-ice production and the basal melt of ice shelves in the LGM case are different from those in the PRESENT case. The salt and freshwater inputs into the Southern Ocean profoundly affect the thermohaline circulation (Reference HellmerHellmer, 2004; Reference Kusahara and HasumiKusahara and Hasumi, 2013). Here we discuss the simulated meridional overturning circulation in the LGM case, with a comparison with the PRESENT case. Evidently, the integration period of 25 years is very short to obtain a steady state for the thermohaline circulation, and our regional modelling study is not suitable for examining the global thermohaline circulation. However, we consider that numerical modelling results under the two different configurations still inform investigation of the behaviour of the thermohaline circulation in the Southern Ocean.
Figure 12 shows the stream functions of zonally integrated, annual-mean meridional overturning circulation in the latitude-density domain in the two cases. In both cases, there is a deep cell in the lower layers, which is related to dense water formation in Antarctic coastal regions. The absolute maximum value of the cell in the LGM is 23.6 Sv, which is larger than 18.9 Sv in the PRESENT case. The central density of the cell in the LGM case is denser by 0.18kg m –3 than in the PRESENT case. From additional numerical experiments in which the present-day surface boundary conditions or initial condition is switched back to the LGM case, it is found that the intensification of the deep cell in the LGM is due to the LGM surface boundary conditions, and the deepening of the cell is due to the combination of surface boundary and initial conditions (not shown). Geological evidence suggests shoaling of the North Atlantic Deep Water and a northward extension of the Antarctic Bottom Water in the Atlantic Ocean at the LGM (Reference Curry and OppoCurry and Oppo, 2005; Reference Lynch-StieglitzLynch-Stieglitz and others, 2007). Our Southern Ocean regional model result of the stronger deep cell does not conflict with the geological evidence.















