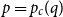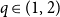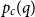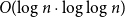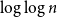1. Introduction
The random-cluster model generalises classical random graph and spin system models, providing a unifying framework for their study [Reference Fortuin and Kasteleyn14]. It plays an indispensable role in the design of efficient Markov Chain Monte Carlo (MCMC) sampling algorithms for the ferromagnetic Ising/Potts model [Reference Ullrich31, Reference Blanca and Sinclair8, Reference Guo and Jerrum20] and has become a fundamental tool in the study of phase transitions [Reference Beffara and Duminil-Copin2, Reference Duminil-Copin, Sidoravicius and Tassion12, Reference Duminil-Copin, Gagnebin, Harel, Manolescu and Tassion11].
The random-cluster model is defined on a finite graph
![]() $G=(V,E)$
with an edge probability parameter
$G=(V,E)$
with an edge probability parameter
![]() $p\in(0,1)$
and a cluster weight
$p\in(0,1)$
and a cluster weight
![]() $q>0$
. The set of configurations of the model is the set of all subsets of edges
$q>0$
. The set of configurations of the model is the set of all subsets of edges
![]() $A \subseteq E$
. The probability of each configuration A is given by the Gibbs distribution:
$A \subseteq E$
. The probability of each configuration A is given by the Gibbs distribution:
where c(A) is the number of connected components in (V, A) and
![]() $Z\,:\!=\,Z(G,p,q)$
is the normalising factor called the partition function.
$Z\,:\!=\,Z(G,p,q)$
is the normalising factor called the partition function.
The special case when
![]() $q=1$
corresponds to the independent bond percolation model, where each edge of the graph G appears independently with probability p. Independent bond percolation is also known as the Erdös–Rényi random graph model when G is the complete graph.
$q=1$
corresponds to the independent bond percolation model, where each edge of the graph G appears independently with probability p. Independent bond percolation is also known as the Erdös–Rényi random graph model when G is the complete graph.
For integer
![]() $q \ge 2$
, the random-cluster model is closely related to the ferromagnetic q-state Potts model. Configurations in the q-state Potts model are the assignments of spin values
$q \ge 2$
, the random-cluster model is closely related to the ferromagnetic q-state Potts model. Configurations in the q-state Potts model are the assignments of spin values
![]() $\{1,\dots,q\}$
to the vertices of G; the
$\{1,\dots,q\}$
to the vertices of G; the
![]() $q=2$
case corresponds to the Ising model. A sample
$q=2$
case corresponds to the Ising model. A sample
![]() $A \subseteq E$
from the random-cluster distribution can be easily transformed into one for the Ising/Potts model by independently assigning a random spin from
$A \subseteq E$
from the random-cluster distribution can be easily transformed into one for the Ising/Potts model by independently assigning a random spin from
![]() $\{1,\dots,q\}$
to each connected component of (V, A). Random-cluster based sampling algorithms, which include the widely studied Swendsen–Wang dynamics [Reference Swendsen and Wang30], are an attractive alternative to Ising/Potts Markov chains since they are often efficient at ‘low-temperatures’ (large p). In this parameter regime, several standard Ising/Potts Markov chains are known to converge slowly.
$\{1,\dots,q\}$
to each connected component of (V, A). Random-cluster based sampling algorithms, which include the widely studied Swendsen–Wang dynamics [Reference Swendsen and Wang30], are an attractive alternative to Ising/Potts Markov chains since they are often efficient at ‘low-temperatures’ (large p). In this parameter regime, several standard Ising/Potts Markov chains are known to converge slowly.
In this paper we investigate the Chayes–Machta (CM) dynamics [Reference Chayes and Machta10], a natural Markov chain on random-cluster configurations that converges to the random-cluster measure. The CM dynamics is a generalisation to non-integer values of q of the widely studied Swendsen–Wang dynamics [Reference Swendsen and Wang30]. As with all applications of the MCMC method, the primary object of study is the mixing time, that is, the number of steps until the dynamics is close to its stationary distribution, starting from the worst possible initial configuration. We are interested in understanding how the mixing time of the CM dynamics grows as the size of the graph G increases, and in particular how it relates to the phase transition of the model.
Given a random-cluster configuration (V, A), one step of the CM dynamics is defined as follows:
-
i. activate each connected component of (V, A) independently with probability
 $1/q$
;
$1/q$
; -
ii. remove all edges connecting active vertices;
-
iii. add each edge between active vertices independently with probability p, leaving the rest of the configuration unchanged.
We call (i) the activation sub-step, and (ii) and (iii) combined the percolation sub-step. It is easy to check that this dynamics is reversible with respect to the Gibbs distribution (1) and thus converges to it [Reference Chayes and Machta10]. For integer q, the CM dynamics may be viewed as a variant of the Swendsen–Wang dynamics. In the Swendsen–Wang dynamics, each connected component of (V, A) receives a random colour from
![]() $\{1,\dots,q\}$
, and the edges are updated within each colour class as in (ii) and (iii) above; in contrast, the CM dynamics updates the edges of exactly one colour class. However, note that the Swendsen–Wang dynamics is only well defined for integer q, while the CM dynamics is feasible for any real
$\{1,\dots,q\}$
, and the edges are updated within each colour class as in (ii) and (iii) above; in contrast, the CM dynamics updates the edges of exactly one colour class. However, note that the Swendsen–Wang dynamics is only well defined for integer q, while the CM dynamics is feasible for any real
![]() $q > 1$
. Indeed, the CM dynamics was introduced precisely to allow this generalisation.
$q > 1$
. Indeed, the CM dynamics was introduced precisely to allow this generalisation.
The study of the interplay between phase transitions and the mixing time of Markov chains goes back to pioneering work in mathematical physics in the late 1980s. This connection for the specific case of the CM dynamics on the complete n-vertex graph, known as the mean-field model, has received some attention in recent years (see [Reference Blanca and Sinclair7, Reference Galanis, Štefankovič and Vigoda15, Reference Gheissari, Lubetzky and Peres18]) and is the focus of this paper. As we shall see, the mean-field case is already quite non-trivial and has historically proven to be a useful starting point in understanding various types of dynamics on more general graphs. We note that, so far, the mean-field is the only setting in which there are tight mixing time bounds for the CM dynamics; all other known bounds are deduced indirectly via comparison with other Markov chains, thus incurring significant overhead [Reference Blanca and Sinclair8, Reference Blanca, Gheissari and Vigoda6, Reference Gheissari and Lubetzky17, Reference Blanca and Gheissari5, Reference Ullrich31, Reference Blanca and Sinclair7].
The phase transition for the mean-field random-cluster model is fairly well understood [Reference Bollobás, Grimmett and Janson9, Reference Luczak and Luczak25]. In this setting, it is natural to re-parameterise by setting
![]() $p=\zeta/n$
; the phase transition then occurs at the critical value
$p=\zeta/n$
; the phase transition then occurs at the critical value
![]() $\zeta = \zeta_{\text{CR}}(q)$
, where
$\zeta = \zeta_{\text{CR}}(q)$
, where
![]() $\zeta_{\text{CR}}(q)=q$
when
$\zeta_{\text{CR}}(q)=q$
when
![]() $q \in (0,2]$
and
$q \in (0,2]$
and
![]() $\zeta_{\text{CR}}(q)=2\Big(\frac{q-1}{q-2}\Big)\log(q-1)$
for
$\zeta_{\text{CR}}(q)=2\Big(\frac{q-1}{q-2}\Big)\log(q-1)$
for
![]() $q>2$
. For
$q>2$
. For
![]() $\zeta <\zeta_{\text{CR}}(q)$
all components are of size
$\zeta <\zeta_{\text{CR}}(q)$
all components are of size
![]() $O({\log}\ n)$
with high probability (w.h.p.); that is, with probability tending to 1 as
$O({\log}\ n)$
with high probability (w.h.p.); that is, with probability tending to 1 as
![]() $n \rightarrow \infty$
. This regime is known as the disordered phase. On the other hand, for
$n \rightarrow \infty$
. This regime is known as the disordered phase. On the other hand, for
![]() $\zeta>\zeta_{\text{CR}}(q)$
there is a unique giant component of size
$\zeta>\zeta_{\text{CR}}(q)$
there is a unique giant component of size
![]() $\approx \theta n$
, where
$\approx \theta n$
, where
![]() $\theta = \theta(\zeta,q)$
; this regime of parameters is known as the ordered phase. The phase transition is thus analogous to that in G(n, p) corresponding to the emergence of a giant component.
$\theta = \theta(\zeta,q)$
; this regime of parameters is known as the ordered phase. The phase transition is thus analogous to that in G(n, p) corresponding to the emergence of a giant component.
The phase structure of the mean-field random-cluster model, however, is more subtle and depends crucially on the second parameter q. In particular, when
![]() $q>2$
the model exhibits phase coexistence at the critical threshold
$q>2$
the model exhibits phase coexistence at the critical threshold
![]() $\zeta = \zeta_{\text{CR}}(q)$
. Roughly speaking, this means that when
$\zeta = \zeta_{\text{CR}}(q)$
. Roughly speaking, this means that when
![]() $\zeta = \zeta_{\text{CR}}(q)$
, the set of configurations with all connected components of size
$\zeta = \zeta_{\text{CR}}(q)$
, the set of configurations with all connected components of size
![]() $O({\log}\ n)$
, and set of configurations with a unique giant component, contribute each a constant fraction of the probability mass. For
$O({\log}\ n)$
, and set of configurations with a unique giant component, contribute each a constant fraction of the probability mass. For
![]() $q \le 2$
, on the other hand, there is no phase coexistence. These subtleties are illustrated in Figure 1.
$q \le 2$
, on the other hand, there is no phase coexistence. These subtleties are illustrated in Figure 1.

Figure 1. (a): phase structure when
![]() $q>2$
. (b): phase structure when
$q>2$
. (b): phase structure when
![]() $q\in(1,2]$
.
$q\in(1,2]$
.
Phase coexistence at
![]() $\zeta =\zeta_{\text{CR}}(q)$
when
$\zeta =\zeta_{\text{CR}}(q)$
when
![]() $q > 2$
has significant implications for the speed of convergence of Markov chains, including the CM dynamics. The following detailed connection between the phase structure of the model and the mixing time
$q > 2$
has significant implications for the speed of convergence of Markov chains, including the CM dynamics. The following detailed connection between the phase structure of the model and the mixing time
![]() $\tau_{\textrm{mix}}^{\textrm{CM}}$
of the CM dynamics was recently established in [Reference Blanca and Sinclair7, Reference Blanca4, Reference Gheissari, Lubetzky and Peres18]. When
$\tau_{\textrm{mix}}^{\textrm{CM}}$
of the CM dynamics was recently established in [Reference Blanca and Sinclair7, Reference Blanca4, Reference Gheissari, Lubetzky and Peres18]. When
![]() $q > 2$
, we have:
$q > 2$
, we have:
 \begin{equation} \tau_{\textrm{mix}}^{\textrm{CM}} = \begin{cases} \Theta({\log}\ n) & \textrm{if}\ \zeta \not\in [\zeta_{\text{L}},\zeta_{\text{R}}); \\[4pt] \Theta\!\left(n^{1/3}\right) & \textrm{if}\ \zeta = \zeta_{\text{L}}; \\[4pt] e^{\Omega({n})} & \textrm{if}\ \zeta \in (\zeta_{\text{L}},\zeta_{\text{R}}), \end{cases}\end{equation}
\begin{equation} \tau_{\textrm{mix}}^{\textrm{CM}} = \begin{cases} \Theta({\log}\ n) & \textrm{if}\ \zeta \not\in [\zeta_{\text{L}},\zeta_{\text{R}}); \\[4pt] \Theta\!\left(n^{1/3}\right) & \textrm{if}\ \zeta = \zeta_{\text{L}}; \\[4pt] e^{\Omega({n})} & \textrm{if}\ \zeta \in (\zeta_{\text{L}},\zeta_{\text{R}}), \end{cases}\end{equation}
where
![]() $(\zeta_{\text{L}},\zeta_{\text{R}})$
is the so-called metastability window. It is known that
$(\zeta_{\text{L}},\zeta_{\text{R}})$
is the so-called metastability window. It is known that
![]() $\zeta_{\text{R}} = q$
, but
$\zeta_{\text{R}} = q$
, but
![]() $\zeta_{\text{L}}$
does not have a closed form; see [Reference Blanca and Sinclair7, Reference Luczak and Luczak25]; we note that
$\zeta_{\text{L}}$
does not have a closed form; see [Reference Blanca and Sinclair7, Reference Luczak and Luczak25]; we note that
![]() $\zeta_{\text{CR}}(q) \in (\zeta_{\text{L}},\zeta_{\text{R}})$
for
$\zeta_{\text{CR}}(q) \in (\zeta_{\text{L}},\zeta_{\text{R}})$
for
![]() $q > 2$
.
$q > 2$
.
When
![]() $q \in (1,2]$
, there is no metastability window, and the mixing time of the mean-field CM dynamics is
$q \in (1,2]$
, there is no metastability window, and the mixing time of the mean-field CM dynamics is
![]() $\Theta({\log}\ n)$
for all
$\Theta({\log}\ n)$
for all
![]() $\zeta \neq \zeta_{\text{CR}}(q)$
. In view of these results, the only case remaining open is when
$\zeta \neq \zeta_{\text{CR}}(q)$
. In view of these results, the only case remaining open is when
![]() $q \in (1,2]$
and
$q \in (1,2]$
and
![]() $\zeta = \zeta_{\text{CR}}(q)$
. Our main result shown below concerns precisely this regime, which is particularly delicate and had resisted analysis until now for reasons we explain in our proof overview.
$\zeta = \zeta_{\text{CR}}(q)$
. Our main result shown below concerns precisely this regime, which is particularly delicate and had resisted analysis until now for reasons we explain in our proof overview.
Theorem 1.1. The mixing time of the CM dynamics on the complete n-vertex graph when
![]() $\zeta=\zeta_{\text{CR}}(q) = q$
and
$\zeta=\zeta_{\text{CR}}(q) = q$
and
![]() $q \in (1,2)$
is
$q \in (1,2)$
is
![]() $O({\log}\ n \cdot \log \log n)$
.
$O({\log}\ n \cdot \log \log n)$
.
A
![]() $\Omega({\log}\ n)$
lower bound is known for the mixing time of the mean-field CM dynamics that holds for all
$\Omega({\log}\ n)$
lower bound is known for the mixing time of the mean-field CM dynamics that holds for all
![]() $p \in (0,1)$
and
$p \in (0,1)$
and
![]() $q > 1$
[Reference Blanca and Sinclair7]. Therefore, our result is tight up to the lower order
$q > 1$
[Reference Blanca and Sinclair7]. Therefore, our result is tight up to the lower order
![]() $O({\log} \log n)$
factor, and in fact even better as we explain in Remark 2.14. The conjectured tight bound when
$O({\log} \log n)$
factor, and in fact even better as we explain in Remark 2.14. The conjectured tight bound when
![]() $\zeta=\zeta_{\text{CR}}(q)$
and
$\zeta=\zeta_{\text{CR}}(q)$
and
![]() $q \in (1,2)$
is
$q \in (1,2)$
is
![]() $\Theta({\log}\ n)$
. We mention that the
$\Theta({\log}\ n)$
. We mention that the
![]() $\zeta=\zeta_{\text{CR}}(q)$
and
$\zeta=\zeta_{\text{CR}}(q)$
and
![]() $q=2$
case, which is quite different and not covered by Theorem 1.1, was considered earlier in [Reference Long, Nachmias, Ning and Peres24] for the closely related Swendsen–Wang dynamics, and a tight
$q=2$
case, which is quite different and not covered by Theorem 1.1, was considered earlier in [Reference Long, Nachmias, Ning and Peres24] for the closely related Swendsen–Wang dynamics, and a tight
![]() $\Theta(n^{1/4})$
bound was established for its mixing time. The same mixing time bound is expected for the CM dynamics in this regime.
$\Theta(n^{1/4})$
bound was established for its mixing time. The same mixing time bound is expected for the CM dynamics in this regime.
Our result establishes a striking behaviour for random-cluster dynamics when
![]() $q \in (1,2)$
. Namely, there is no slowdown (exponential or power law) in this regime at the critical threshold
$q \in (1,2)$
. Namely, there is no slowdown (exponential or power law) in this regime at the critical threshold
![]() $\zeta=\zeta_{\text{CR}}(q)$
. Note that for
$\zeta=\zeta_{\text{CR}}(q)$
. Note that for
![]() $q > 2$
, as described in (2) above, the mixing time of the dynamics undergoes an exponential slowdown, transitioning from
$q > 2$
, as described in (2) above, the mixing time of the dynamics undergoes an exponential slowdown, transitioning from
![]() $\Theta({\log}\ n)$
when
$\Theta({\log}\ n)$
when
![]() $\zeta < \zeta_{\text{L}}$
, to a power law at
$\zeta < \zeta_{\text{L}}$
, to a power law at
![]() $\zeta = \zeta_{\text{L}}$
, and to exponential in n when
$\zeta = \zeta_{\text{L}}$
, and to exponential in n when
![]() $\zeta \in (\zeta_{\text{L}},\zeta_{\text{R}})$
. The absence of a critical slowdown for
$\zeta \in (\zeta_{\text{L}},\zeta_{\text{R}})$
. The absence of a critical slowdown for
![]() $q \in (1,2)$
was in fact predicted by the statistical physics community [Reference Garoni16], and our result provides the first rigorous proof of this phenomenon. See Remark 2.5 for further comments.
$q \in (1,2)$
was in fact predicted by the statistical physics community [Reference Garoni16], and our result provides the first rigorous proof of this phenomenon. See Remark 2.5 for further comments.
Our second result concerns the local Glauber dynamics for the random-cluster model. In each step, the Glauber dynamics updates a single edge of the current configuration chosen uniformly at random; a precise definition of this Markov chain is given in Section 6. In [Reference Blanca and Sinclair7], it was established that any upper bound on the mixing time
![]() $\tau_{\textrm{mix}}^{\textrm{CM}}$
of the CM dynamics can be translated to one for the mixing time
$\tau_{\textrm{mix}}^{\textrm{CM}}$
of the CM dynamics can be translated to one for the mixing time
![]() $\tau_{\textrm{mix}}^{\textrm{GD}}$
of the Glauber dynamics, at the expense of a
$\tau_{\textrm{mix}}^{\textrm{GD}}$
of the Glauber dynamics, at the expense of a
![]() $\tilde{O}(n^4)$
factor; the
$\tilde{O}(n^4)$
factor; the
![]() $\tilde{O}$
notation hides polylogarithmic factors. In particular, it was proved in [Reference Blanca and Sinclair7] that
$\tilde{O}$
notation hides polylogarithmic factors. In particular, it was proved in [Reference Blanca and Sinclair7] that
![]() $\tau_{\textrm{mix}}^{\textrm{GD}} \le \tau_{\textrm{mix}}^{\textrm{CM}} \cdot \tilde{O}(n^4).$
We provide here an improvement of this comparison inequality.
$\tau_{\textrm{mix}}^{\textrm{GD}} \le \tau_{\textrm{mix}}^{\textrm{CM}} \cdot \tilde{O}(n^4).$
We provide here an improvement of this comparison inequality.
Theorem 1.2. For all
![]() $q > 1$
and all
$q > 1$
and all
![]() $\zeta = O(1)$
,
$\zeta = O(1)$
,
![]() $ \tau_{\textrm{mix}}^{\textrm{GD}} \le \tau_{\text{mix}}^{\text{CM}} \cdot {O}\!\left(n^3 ({\log}\ n)^2\right). $
$ \tau_{\textrm{mix}}^{\textrm{GD}} \le \tau_{\text{mix}}^{\text{CM}} \cdot {O}\!\left(n^3 ({\log}\ n)^2\right). $
To prove this theorem, we establish a general comparison inequality that holds for any graph, any
![]() $q \ge 1$
and any
$q \ge 1$
and any
![]() $p \in (0,1)$
; see Theorem 6.1 for a precise statement. When combined with the known mixing time bounds for the CM dynamics on the complete graph, Theorem 1.2 yields that the random-cluster Glauber dynamics mixes in
$p \in (0,1)$
; see Theorem 6.1 for a precise statement. When combined with the known mixing time bounds for the CM dynamics on the complete graph, Theorem 1.2 yields that the random-cluster Glauber dynamics mixes in
![]() $\tilde{O}(n^3)$
steps when
$\tilde{O}(n^3)$
steps when
![]() $q > 2$
and
$q > 2$
and
![]() $\zeta \not\in(\zeta_{\text{L}},\zeta_{\text{R}})$
, or when
$\zeta \not\in(\zeta_{\text{L}},\zeta_{\text{R}})$
, or when
![]() $q \in (1,2)$
and
$q \in (1,2)$
and
![]() $\zeta = O(1)$
. In these regimes, the mixing time of the Glauber dynamics was previously known to be
$\zeta = O(1)$
. In these regimes, the mixing time of the Glauber dynamics was previously known to be
![]() $\tilde{O}(n^4)$
and is conjectured to be
$\tilde{O}(n^4)$
and is conjectured to be
![]() $\tilde{O}(n^2)$
; the improved comparison inequality in Theorem 1.2 gets us closer to this conjectured tight bound. We note, however, that even if one showed the conjectured optimal bound for the mixing time of the Glauber dynamics, the CM is faster, even if we take into account the computational cost associated to implementing its steps.
$\tilde{O}(n^2)$
; the improved comparison inequality in Theorem 1.2 gets us closer to this conjectured tight bound. We note, however, that even if one showed the conjectured optimal bound for the mixing time of the Glauber dynamics, the CM is faster, even if we take into account the computational cost associated to implementing its steps.
We conclude this introduction with some brief remarks about our analysis techniques, which combine several key ingredients in a non-trivial way. Our bound on the mixing time uses the well-known technique of coupling: in order to show that the mixing time is
![]() $O({\log}\ n \cdot \log \log n)$
, it suffices to couple the evolutions of two copies of the dynamics, starting from two arbitrary configurations, in such a way that they arrive at the same configuration after
$O({\log}\ n \cdot \log \log n)$
, it suffices to couple the evolutions of two copies of the dynamics, starting from two arbitrary configurations, in such a way that they arrive at the same configuration after
![]() $O({\log}\ n )$
steps with probability
$O({\log}\ n )$
steps with probability
![]() $\Omega(1/ \log \log n)$
. (The moves of the two copies can be correlated any way we choose, provided that each copy, viewed in isolation, is a valid realisation of the dynamics.) Because of the delicate nature of the phase transition in the random-cluster model, combined with the fact that the percolation sub-step of the CM dynamics is critical when
$\Omega(1/ \log \log n)$
. (The moves of the two copies can be correlated any way we choose, provided that each copy, viewed in isolation, is a valid realisation of the dynamics.) Because of the delicate nature of the phase transition in the random-cluster model, combined with the fact that the percolation sub-step of the CM dynamics is critical when
![]() $\zeta = q$
, our coupling is somewhat elaborate and proceeds in multiple phases. The first phase consists of a burn-in period, where the two copies of the chain are run independently and the evolution of their largest components is observed until they have shrunk to their ‘typical’ sizes. This part of the analysis is inspired by similar arguments in earlier work [Reference Blanca and Sinclair7, Reference Long, Nachmias, Ning and Peres24, Reference Galanis, Štefankovič and Vigoda15].
$\zeta = q$
, our coupling is somewhat elaborate and proceeds in multiple phases. The first phase consists of a burn-in period, where the two copies of the chain are run independently and the evolution of their largest components is observed until they have shrunk to their ‘typical’ sizes. This part of the analysis is inspired by similar arguments in earlier work [Reference Blanca and Sinclair7, Reference Long, Nachmias, Ning and Peres24, Reference Galanis, Štefankovič and Vigoda15].
In the second phase, we design a coupling of the activation of the connected components of the two copies which uses: (i) a local limit theorem, which can be thought of as a stronger version of a central limit theorem; (ii) a precise understanding of the distribution of the maximum of symmetric random walks on
![]() $\mathbb{Z}$
with varying step sizes; and (iii) precise estimates for the component structure of random graphs. We develop tailored versions of these probabilistic tools for our setting and combine them to guarantee that the same number of vertices from each copy are activated in each step w.h.p. for sufficiently many steps. This phase of the coupling is the main novelty in our analysis and allows us to quickly converge to the same configuration. We give a more detailed overview of our proof in the following section.
$\mathbb{Z}$
with varying step sizes; and (iii) precise estimates for the component structure of random graphs. We develop tailored versions of these probabilistic tools for our setting and combine them to guarantee that the same number of vertices from each copy are activated in each step w.h.p. for sufficiently many steps. This phase of the coupling is the main novelty in our analysis and allows us to quickly converge to the same configuration. We give a more detailed overview of our proof in the following section.
2. Proof sketch and techniques
We now give a detailed sketch of the multi-phased coupling argument for proving Theorem 1.1. We start by formally defining the notions of mixing and coupling times. Let
![]() $\Omega_{\text{RC}}$
be the set of random-cluster configurations of a graph G; let
$\Omega_{\text{RC}}$
be the set of random-cluster configurations of a graph G; let
![]() $\mathcal{M}$
be the transition matrix of a random-cluster Markov chain with stationary distribution
$\mathcal{M}$
be the transition matrix of a random-cluster Markov chain with stationary distribution
![]() $\mu = \mu_{G,p,q}$
, and let
$\mu = \mu_{G,p,q}$
, and let
![]() $\mathcal{M}^t(X_0,\cdot)$
be the distribution of the chain after t steps starting from
$\mathcal{M}^t(X_0,\cdot)$
be the distribution of the chain after t steps starting from
![]() $X_0 \in \Omega_{\text{RC}}$
. The
$X_0 \in \Omega_{\text{RC}}$
. The
![]() $\varepsilon$
-mixing time of
$\varepsilon$
-mixing time of
![]() $\mathcal{M}$
is given by
$\mathcal{M}$
is given by
where
![]() $||{\cdot}||_{\text{TV}}$
denotes total variation distance. In particular, the mixing time of
$||{\cdot}||_{\text{TV}}$
denotes total variation distance. In particular, the mixing time of
![]() $\mathcal{M}$
is
$\mathcal{M}$
is
![]() $\tau_{\textrm{mix}}^{\mathcal{M}} \,:\!=\, \tau_{\textrm{mix}}^{\mathcal{M}}(1/4)$
.
$\tau_{\textrm{mix}}^{\mathcal{M}} \,:\!=\, \tau_{\textrm{mix}}^{\mathcal{M}}(1/4)$
.
A (one-step) coupling of the Markov chain
![]() $\mathcal{M}$
specifies, for every pair of states
$\mathcal{M}$
specifies, for every pair of states
![]() $(X_t, Y_t) \in \Omega_{\text{RC}} \times \Omega_{\text{RC}}$
, a probability distribution over
$(X_t, Y_t) \in \Omega_{\text{RC}} \times \Omega_{\text{RC}}$
, a probability distribution over
![]() $(X_{t+1}, Y_{t+1})$
such that the processes
$(X_{t+1}, Y_{t+1})$
such that the processes
![]() $\{X_t\}$
and
$\{X_t\}$
and
![]() $\{Y_t\}$
are valid realisations of
$\{Y_t\}$
are valid realisations of
![]() $\mathcal{M}$
, and if
$\mathcal{M}$
, and if
![]() $X_t=Y_t$
then
$X_t=Y_t$
then
![]() $X_{t+1}=Y_{t+1}$
. The coupling time, denoted
$X_{t+1}=Y_{t+1}$
. The coupling time, denoted
![]() $T_{\textrm{coup}}$
, is the minimum T such that
$T_{\textrm{coup}}$
, is the minimum T such that
![]() ${\mathbb{P}}[X_T \neq Y_T] \le 1/4$
, starting from the worst possible pair of configurations in
${\mathbb{P}}[X_T \neq Y_T] \le 1/4$
, starting from the worst possible pair of configurations in
![]() $\Omega_{\text{RC}}$
. It is a standard fact that
$\Omega_{\text{RC}}$
. It is a standard fact that
![]() $\tau_{\textrm{mix}}^{\mathcal{M}} \le T_{\textrm{coup}}$
; moreover, when
$\tau_{\textrm{mix}}^{\mathcal{M}} \le T_{\textrm{coup}}$
; moreover, when
![]() ${\mathbb{P}}[X_T = Y_T] \ge \delta$
for some coupling, then
${\mathbb{P}}[X_T = Y_T] \ge \delta$
for some coupling, then
![]() $\tau_{\textrm{mix}}^{\mathcal{M}} = O(T \delta^{-1})$
(see, e.g., [Reference Levin and Peres22]).
$\tau_{\textrm{mix}}^{\mathcal{M}} = O(T \delta^{-1})$
(see, e.g., [Reference Levin and Peres22]).
We provide first a high level description of our coupling for the CM dynamics. For this, we require the following notation. For a random-cluster configuration X, let
![]() $L_i(X)$
denote the size of the i-th largest connected component in (V, X), and let
$L_i(X)$
denote the size of the i-th largest connected component in (V, X), and let
![]() $\mathcal{R}_i(X)\,:\!=\,\sum_{j \ge i} L_j(X)^2$
; in particular,
$\mathcal{R}_i(X)\,:\!=\,\sum_{j \ge i} L_j(X)^2$
; in particular,
![]() $\mathcal{R}_1(X)$
is the sum of the squares of the sizes of all the components of (V, X). Our coupling has three main phases:
$\mathcal{R}_1(X)$
is the sum of the squares of the sizes of all the components of (V, X). Our coupling has three main phases:
-
1. Burn-in period: run two copies
 $\{X_t\}$
,
$\{X_t\}$
,
 $\{Y_t\}$
independently, starting from a pair of arbitrary initial configurations, until
$\{Y_t\}$
independently, starting from a pair of arbitrary initial configurations, until
 $\mathcal{R}_1(X_T) = O\!\left(n^{4/3}\right)$
and
$\mathcal{R}_1(X_T) = O\!\left(n^{4/3}\right)$
and
 $\mathcal{R}_1(Y_T) = O\!\left(n^{4/3}\right)$
.
$\mathcal{R}_1(Y_T) = O\!\left(n^{4/3}\right)$
. -
2. Coupling to the same component structure: starting from
 $X_T$
and
$X_T$
and
 $Y_T$
such that
$Y_T$
such that
 $\mathcal{R}_1(X_T) = O\!\left(n^{4/3}\right)$
and
$\mathcal{R}_1(X_T) = O\!\left(n^{4/3}\right)$
and
 $\mathcal{R}_1(Y_T) = O\!\left(n^{4/3}\right)$
, we design a two-phased coupling that reaches two configurations with the same component structure as follows:
$\mathcal{R}_1(Y_T) = O\!\left(n^{4/3}\right)$
, we design a two-phased coupling that reaches two configurations with the same component structure as follows:-
2a. A two-step coupling after which the two configurations agree on all ‘large components’;
-
2b. A coupling that after
 $O({\log}\ n)$
additional steps reaches two configurations that will also have the same ‘small component’ structure.
$O({\log}\ n)$
additional steps reaches two configurations that will also have the same ‘small component’ structure.
-
-
3. Coupling to the same configuration: starting from two configurations with the same component structure, there is a straightforward coupling that couples the two configurations in
 $O({\log}\ n)$
steps w.h.p.
$O({\log}\ n)$
steps w.h.p.
We proceed to describe each of these phases in detail.
2.1 The burn-in period
During the initial phase, two copies of the dynamics evolve independently. This is called a burn-in period and in our case consists of three sub-phases.
In the first sub-phase of the burn-in period the goal is to reach a configuration X such that
![]() $\mathcal{R}_2(X) = O\!\left(n^{4/3}\right)$
. For this, we use a lemma from [Reference Blanca4], which shows that after
$\mathcal{R}_2(X) = O\!\left(n^{4/3}\right)$
. For this, we use a lemma from [Reference Blanca4], which shows that after
![]() $T = O({\log}\ n)$
steps of the CM dynamics
$T = O({\log}\ n)$
steps of the CM dynamics
![]() $\mathcal{R}_2(X_T) = O\!\left(n^{4/3}\right)$
with at least constant probability; this holds when
$\mathcal{R}_2(X_T) = O\!\left(n^{4/3}\right)$
with at least constant probability; this holds when
![]() $\zeta=q$
for any initial configuration
$\zeta=q$
for any initial configuration
![]() $X_0$
and any
$X_0$
and any
![]() $q > 1$
.
$q > 1$
.
Lemma 2.1 ([Reference Blanca4], Lemma 3.42). Let
![]() $q>1$
and
$q>1$
and
![]() $\zeta=q$
, and let
$\zeta=q$
, and let
![]() $X_0$
be an arbitrary random-cluster configuration. Then, for any constant
$X_0$
be an arbitrary random-cluster configuration. Then, for any constant
![]() $C \geq 0$
, after
$C \geq 0$
, after
![]() $T=O({\log}\ n)$
steps
$T=O({\log}\ n)$
steps
![]() $\mathcal{R}_2(X_T) = O\!\left(n^{4/3}\right)$
and
$\mathcal{R}_2(X_T) = O\!\left(n^{4/3}\right)$
and
![]() $L_1(X_T) > Cn^{2/3}$
with probability
$L_1(X_T) > Cn^{2/3}$
with probability
![]() $\Omega(1)$
.
$\Omega(1)$
.
In the second and third sub-phases of the burn-in period, we use the fact that when
![]() $\mathcal{R}_2(X_t) = O\!\left(n^{4/3}\right)$
, the number of activated vertices is well concentrated around
$\mathcal{R}_2(X_t) = O\!\left(n^{4/3}\right)$
, the number of activated vertices is well concentrated around
![]() $n/q$
(its expectation). This is used to show that the size of the largest component contracts at a constant rate for
$n/q$
(its expectation). This is used to show that the size of the largest component contracts at a constant rate for
![]() $T=O({\log}\ n)$
steps until a configuration
$T=O({\log}\ n)$
steps until a configuration
![]() $X_T$
is reached such that
$X_T$
is reached such that
![]() $\mathcal{R}_1(X_T) = O\!\left(n^{4/3}\right)$
. This part of the analysis is split into two sub-phases because the contraction for
$\mathcal{R}_1(X_T) = O\!\left(n^{4/3}\right)$
. This part of the analysis is split into two sub-phases because the contraction for
![]() $L_1(X_t)$
requires a more delicate analysis when
$L_1(X_t)$
requires a more delicate analysis when
![]() $L_1(X_t) = o(n)$
; this is captured in the following two lemmas.
$L_1(X_t) = o(n)$
; this is captured in the following two lemmas.
Lemma 2.2. Let
![]() $\zeta=q$
and
$\zeta=q$
and
![]() $q \in (1,2)$
. Suppose
$q \in (1,2)$
. Suppose
![]() $\mathcal{R}_2(X_0) = O\!\left(n^{4/3}\right)$
. Then, for any constant
$\mathcal{R}_2(X_0) = O\!\left(n^{4/3}\right)$
. Then, for any constant
![]() $\delta > 0$
, there exists
$\delta > 0$
, there exists
![]() $T = T(\delta) = O(1)$
such that
$T = T(\delta) = O(1)$
such that
![]() $\mathcal{R}_2(X_T) = O\!\left(n^{4/3}\right)$
and
$\mathcal{R}_2(X_T) = O\!\left(n^{4/3}\right)$
and
![]() ${L_1}(X_T) \leq \delta n$
with probability
${L_1}(X_T) \leq \delta n$
with probability
![]() $\Omega(1)$
.
$\Omega(1)$
.
Lemma 2.3. Let
![]() $\zeta=q$
and
$\zeta=q$
and
![]() $q \in (1,2)$
. Suppose
$q \in (1,2)$
. Suppose
![]() $\mathcal{R}_2(X_{0}) = O\!\left(n^{4/3}\right)$
and that
$\mathcal{R}_2(X_{0}) = O\!\left(n^{4/3}\right)$
and that
![]() $L_1(X_{0}) \leq \delta n$
for a sufficiently small constant
$L_1(X_{0}) \leq \delta n$
for a sufficiently small constant
![]() $\delta$
. Then, with probability
$\delta$
. Then, with probability
![]() $\Omega(1)$
, after
$\Omega(1)$
, after
![]() $T=O({\log}\ n)$
steps
$T=O({\log}\ n)$
steps
![]() $\mathcal{R}_1(X_T) = O\!\left(n^{4/3}\right)$
.
$\mathcal{R}_1(X_T) = O\!\left(n^{4/3}\right)$
.
Lemmas 2.2 and 2.3 are proved in Section 4. Combining them with Lemma 2.1 immediately yields the following theorem.
Theorem 2.4. Let
![]() $\zeta=q$
,
$\zeta=q$
,
![]() $q \in (1,2)$
and let
$q \in (1,2)$
and let
![]() $X_0$
be an arbitrary random-cluster configuration of the complete n-vertex graph. Then, with probability
$X_0$
be an arbitrary random-cluster configuration of the complete n-vertex graph. Then, with probability
![]() $\Omega(1)$
, after
$\Omega(1)$
, after
![]() $T=O({\log}\ n)$
steps
$T=O({\log}\ n)$
steps
![]() $\mathcal{R}_1(X_T) = O\!\left(n^{4/3}\right)$
.
$\mathcal{R}_1(X_T) = O\!\left(n^{4/3}\right)$
.
Remark 2.5. The contraction of
![]() $L_1(X_t)$
established by Lemmas 2.2 and 2.3 only occurs when
$L_1(X_t)$
established by Lemmas 2.2 and 2.3 only occurs when
![]() $q \in (1,2)$
; when
$q \in (1,2)$
; when
![]() $q > 2$
the quantity
$q > 2$
the quantity
![]() $L_1(X_t)$
may increase in expectation, whereas for
$L_1(X_t)$
may increase in expectation, whereas for
![]() $q=2$
we have
$q=2$
we have
![]() ${\mathbb{E}}[L_1(X_{t+1}) \mid X_t] \approx L_1(X_t)$
, and the contraction of the size of the largest component is due instead to fluctuations caused by a large second moment. (This is what causes the power law slowdown when
${\mathbb{E}}[L_1(X_{t+1}) \mid X_t] \approx L_1(X_t)$
, and the contraction of the size of the largest component is due instead to fluctuations caused by a large second moment. (This is what causes the power law slowdown when
![]() $\zeta=q=2$
.)
$\zeta=q=2$
.)
Remark 2.6. Sub-steps (ii) and (iii) of the CM dynamics are equivalent to replacing the active portion of the configuration by a
![]() $G(m,q/n)$
random graph, where m is the number of active vertices. Since
$G(m,q/n)$
random graph, where m is the number of active vertices. Since
![]() ${\mathbb{E}}[m] = n/q$
, one key challenge in the proofs of Lemmas 2.2 and 2.3, and in fact in the entirety of our analysis, is that the random graph
${\mathbb{E}}[m] = n/q$
, one key challenge in the proofs of Lemmas 2.2 and 2.3, and in fact in the entirety of our analysis, is that the random graph
![]() $G(m,q/n)$
is critical or almost critical w.h.p. since
$G(m,q/n)$
is critical or almost critical w.h.p. since
![]() $m \cdot q/n \approx 1$
; consequently its structural properties are not well concentrated and cannot be maintained for the required
$m \cdot q/n \approx 1$
; consequently its structural properties are not well concentrated and cannot be maintained for the required
![]() $O({\log}\ n)$
steps of the coupling. This is one of the key reasons why the
$O({\log}\ n)$
steps of the coupling. This is one of the key reasons why the
![]() $\zeta = \zeta_{\text{CR}}(q) =q$
regime is quite delicate.
$\zeta = \zeta_{\text{CR}}(q) =q$
regime is quite delicate.
2.2 Coupling to the same component structure
For the second phase of the coupling, we assume that we start from a pair of configurations
![]() $X_0$
,
$X_0$
,
![]() $Y_0$
such that
$Y_0$
such that
![]() $\mathcal{R}_1(X_0) = O\!\left(n^{4/3}\right)$
,
$\mathcal{R}_1(X_0) = O\!\left(n^{4/3}\right)$
,
![]() $\mathcal{R}_1(Y_0) = O\!\left(n^{4/3}\right)$
. The goal is to show that after
$\mathcal{R}_1(Y_0) = O\!\left(n^{4/3}\right)$
. The goal is to show that after
![]() $T = O({\log}\ n)$
steps, with probability
$T = O({\log}\ n)$
steps, with probability
![]() $\Omega(1/\log \log n)$
, we reach two configurations
$\Omega(1/\log \log n)$
, we reach two configurations
![]() $X_T$
and
$X_T$
and
![]() $Y_T$
with the same component structure, that is,
$Y_T$
with the same component structure, that is,
![]() $L_j(X_T) = L_j(Y_T)$
for all
$L_j(X_T) = L_j(Y_T)$
for all
![]() $j \ge 1$
. In particular, we prove the following.
$j \ge 1$
. In particular, we prove the following.
Theorem 2.7. Let
![]() $\zeta=q$
,
$\zeta=q$
,
![]() $q \in (1,2)$
and suppose
$q \in (1,2)$
and suppose
![]() $X_0, Y_0$
are random-cluster configurations such that
$X_0, Y_0$
are random-cluster configurations such that
![]() $\mathcal{R}_1(X_0) = O\!\left(n^{4/3}\right)$
and
$\mathcal{R}_1(X_0) = O\!\left(n^{4/3}\right)$
and
![]() $\mathcal{R}_1(Y_0) = O\!\left(n^{4/3}\right)$
. Then, there exists a coupling of the CM steps such that after
$\mathcal{R}_1(Y_0) = O\!\left(n^{4/3}\right)$
. Then, there exists a coupling of the CM steps such that after
![]() $T=O({\log}\ n)$
steps
$T=O({\log}\ n)$
steps
![]() $X_T$
and
$X_T$
and
![]() $Y_T$
have the same component structure with probability
$Y_T$
have the same component structure with probability
![]() $\Omega\!\left( ({\log} \log n)^{-1} \right)$
.
$\Omega\!\left( ({\log} \log n)^{-1} \right)$
.
Our coupling construction for proving Theorem 2.7 has two main sub-phases. The first is a two-step coupling after which the two configurations agree on all the components of size above a certain threshold
![]() $B_\omega = {n^{2/3}}/{\omega (n)}$
, where
$B_\omega = {n^{2/3}}/{\omega (n)}$
, where
![]() $\omega (n)$
is a slowly increasing function. For convenience and definiteness we set
$\omega (n)$
is a slowly increasing function. For convenience and definiteness we set
![]() $\omega (n) = \log \log \log \log n$
. In the second sub-phase we take care of matching the small component structures.
$\omega (n) = \log \log \log \log n$
. In the second sub-phase we take care of matching the small component structures.
We note that when the same number of vertices are activated from each copy of the chain, we can easily couple the percolation sub-step (with an arbitrary bijection between the activated vertices) and replace the configuration on the active vertices in both chains with the same random sub-graph; consequently, the component structure in the updated sub-graph would be identical. Our goal is thus to design a coupling of the activation of the components that activates the same number of vertices in both copies in every step.
In order for the initial two-step coupling to succeed, certain (additional) properties of the configurations are required. These properties are achieved with a continuation of the initial burn-in phase for a small number of
![]() $O({\log} \omega (n))$
steps. For a random-cluster configuration X, let
$O({\log} \omega (n))$
steps. For a random-cluster configuration X, let
![]() $\widetilde{\mathcal{R}}_\omega(X) = \sum_{j\,:\, L_j(X) \le B_\omega} L_j(X)^2$
and let I(X) denote the number of isolated vertices of X. Our extension of the burn-in period is captured by the following lemma.
$\widetilde{\mathcal{R}}_\omega(X) = \sum_{j\,:\, L_j(X) \le B_\omega} L_j(X)^2$
and let I(X) denote the number of isolated vertices of X. Our extension of the burn-in period is captured by the following lemma.
Lemma 2.8. Let
![]() $\zeta=q$
,
$\zeta=q$
,
![]() $q \in (1,2)$
and suppose
$q \in (1,2)$
and suppose
![]() $X_0$
is such that
$X_0$
is such that
![]() $\mathcal{R}_1(X_0) = O\!\left(n^{4/3}\right)$
. Then, there exists
$\mathcal{R}_1(X_0) = O\!\left(n^{4/3}\right)$
. Then, there exists
![]() $T=O({\log} \omega (n))$
and a constant
$T=O({\log} \omega (n))$
and a constant
![]() $\beta > 0$
such that
$\beta > 0$
such that
![]() $ \widetilde{\mathcal{R}}_\omega(X_T) = O\big(n^{4/3}{\omega (n)}^{-1/2}\big)$
,
$ \widetilde{\mathcal{R}}_\omega(X_T) = O\big(n^{4/3}{\omega (n)}^{-1/2}\big)$
,
![]() $\mathcal{R}_1(X_T) = O\!\left(n^{4/3}\right)$
and
$\mathcal{R}_1(X_T) = O\!\left(n^{4/3}\right)$
and
![]() $I(X_T) = \Omega(n)$
with probability
$I(X_T) = \Omega(n)$
with probability
![]() $\Omega(\omega (n)^{-\beta})$
.
$\Omega(\omega (n)^{-\beta})$
.
The proof of Lemma 2.8 is provided in Section 5.1.
With these bounds on
![]() $\widetilde{\mathcal{R}}_\omega(X_T)$
,
$\widetilde{\mathcal{R}}_\omega(X_T)$
,
![]() $\widetilde{\mathcal{R}}_\omega(Y_T)$
,
$\widetilde{\mathcal{R}}_\omega(Y_T)$
,
![]() $I(X_T)$
and
$I(X_T)$
and
![]() $I(Y_T)$
, we construct the two-step coupling for matching the large component structure. The construction crucially relies on a new local limit theorem (Theorem 5.1). In particular, under our assumptions, when
$I(Y_T)$
, we construct the two-step coupling for matching the large component structure. The construction crucially relies on a new local limit theorem (Theorem 5.1). In particular, under our assumptions, when
![]() $\omega (n)$
is small enough, there are few components with sizes above
$\omega (n)$
is small enough, there are few components with sizes above
![]() $B_\omega$
. Hence, we can condition on the event that all of them are activated simultaneously. The difference in the number of active vertices generated by the activation of these large components can then be ‘corrected’ by a coupling of the activation of the smaller components; for this we use our new local limit theorem.
$B_\omega$
. Hence, we can condition on the event that all of them are activated simultaneously. The difference in the number of active vertices generated by the activation of these large components can then be ‘corrected’ by a coupling of the activation of the smaller components; for this we use our new local limit theorem.
Specifically, our local limit theorem applies to the random variables corresponding to the number of activated vertices from the small components of each copy. We prove it using a result of Mukhin [Reference Mukhin28] and the fact that, among the small components, there are (roughly speaking) many components of many different sizes. To establish the latter we require a refinement of known random graph estimates (see Lemma 3.11).
To formally state our result we introduce some additional notation. Let
![]() $\mathcal{S}_{\omega}(X)$
be the set of connected components of X with sizes greater than
$\mathcal{S}_{\omega}(X)$
be the set of connected components of X with sizes greater than
![]() $B_\omega$
. At step t, the activation of the components of two random-cluster configurations
$B_\omega$
. At step t, the activation of the components of two random-cluster configurations
![]() $X_t$
and
$X_t$
and
![]() $Y_t$
is done using a maximal matching
$Y_t$
is done using a maximal matching
![]() $W_t$
between the components of
$W_t$
between the components of
![]() $X_t$
and
$X_t$
and
![]() $Y_t$
, with the restriction that only components of equal size are matched to each other. For an increasing positive function g and each integer
$Y_t$
, with the restriction that only components of equal size are matched to each other. For an increasing positive function g and each integer
![]() $k \ge 0$
, define
$k \ge 0$
, define
![]() $\hat{N}_k(t, g) \,:\!=\, \hat{N}_k(X_t,Y_t, g)$
as the number of matched pairs in
$\hat{N}_k(t, g) \,:\!=\, \hat{N}_k(X_t,Y_t, g)$
as the number of matched pairs in
![]() $W_t$
whose component sizes are in the interval
$W_t$
whose component sizes are in the interval
 \begin{equation*}\mathcal{I}_{k}(g) = \left[\frac{\vartheta n^{2/3}}{2g(n)^{2^k}},\frac{\vartheta n^{2/3}}{g(n)^{2^k}}\right],\end{equation*}
\begin{equation*}\mathcal{I}_{k}(g) = \left[\frac{\vartheta n^{2/3}}{2g(n)^{2^k}},\frac{\vartheta n^{2/3}}{g(n)^{2^k}}\right],\end{equation*}
where
![]() $\vartheta>0$
is a fixed large constant (independent of n).
$\vartheta>0$
is a fixed large constant (independent of n).
Lemma 2.9. Let
![]() $\zeta=q$
,
$\zeta=q$
,
![]() $q \in (1,2)$
and suppose
$q \in (1,2)$
and suppose
![]() $X_0, Y_0$
are random-cluster configurations such that
$X_0, Y_0$
are random-cluster configurations such that
![]() $\mathcal{R}_1(X_0) = O\!\left(n^{4/3}\right)$
,
$\mathcal{R}_1(X_0) = O\!\left(n^{4/3}\right)$
,
![]() $\widetilde{\mathcal{R}}_\omega(X_0) = O\big(n^{4/3}{\omega (n)}^{-1/2}\big)$
,
$\widetilde{\mathcal{R}}_\omega(X_0) = O\big(n^{4/3}{\omega (n)}^{-1/2}\big)$
,
![]() $I(X_0)=\Omega(n)$
and similarly for
$I(X_0)=\Omega(n)$
and similarly for
![]() $Y_0$
. Then, there exists a two-step coupling of the CM dynamics such that
$Y_0$
. Then, there exists a two-step coupling of the CM dynamics such that
![]() $\mathcal{S}_{\omega}(X_2) = \mathcal{S}_{\omega}(Y_2)$
with probability
$\mathcal{S}_{\omega}(X_2) = \mathcal{S}_{\omega}(Y_2)$
with probability
![]() $\exp\!\left({-}O\big(\omega (n)^9\big)\right)$
.
$\exp\!\left({-}O\big(\omega (n)^9\big)\right)$
.
Moreover,
![]() $L_1(X_2) = O\big(n^{2/3} \omega (n)\big)$
,
$L_1(X_2) = O\big(n^{2/3} \omega (n)\big)$
,
![]() $\mathcal{R}_2(X_2) = O\!\left(n^{4/3}\right)$
,
$\mathcal{R}_2(X_2) = O\!\left(n^{4/3}\right)$
,
![]() $\widetilde{\mathcal{R}}_\omega(X_2) = O\big(n^{4/3}{\omega (n)}^{-1/2}\big)$
,
$\widetilde{\mathcal{R}}_\omega(X_2) = O\big(n^{4/3}{\omega (n)}^{-1/2}\big)$
,
![]() $I(X_2)=\Omega(n)$
,
$I(X_2)=\Omega(n)$
,
![]() $\hat{N}_k(2,\omega (n)) = \Omega\Big({\omega (n)}^{3 \cdot 2^{k-1}}\Big)$
for all
$\hat{N}_k(2,\omega (n)) = \Omega\Big({\omega (n)}^{3 \cdot 2^{k-1}}\Big)$
for all
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $n^{2/3}\omega (n)^{-2^{k-1}}\rightarrow \infty$
, and similarly for
$n^{2/3}\omega (n)^{-2^{k-1}}\rightarrow \infty$
, and similarly for
![]() $Y_2$
.
$Y_2$
.
From the first part of the lemma we obtain two configurations that agree on all of their large components, as desired, while the second part guarantees additional structural properties for the resulting configurations so that the next sub-phase of the coupling can also succeed with the required probability. The proof of Lemma 2.9 is given in Section 5.2.
In the second sub-phase, after the large component are matched, we can design a coupling that activates exactly the same number of vertices from each copy of the chain. To analyze this coupling we use a precise estimate on the distribution of the maximum of symmetric random walks over integers (with steps of different sizes). We are first required to run the chains coupled for
![]() $T=O({\log} \omega (n))$
steps, so that certain additional structural properties appear. Let
$T=O({\log} \omega (n))$
steps, so that certain additional structural properties appear. Let
![]() $M (X_t)$
and
$M (X_t)$
and
![]() $M(Y_t)$
be the components in the matching
$M(Y_t)$
be the components in the matching
![]() $W_t$
that belong to
$W_t$
that belong to
![]() $X_t$
and
$X_t$
and
![]() $Y_t$
, respectively, and let
$Y_t$
, respectively, and let
![]() $D(X_t)$
and
$D(X_t)$
and
![]() $D(Y_t)$
be the complements of
$D(Y_t)$
be the complements of
![]() $M (X_t )$
and
$M (X_t )$
and
![]() $M (Y_t)$
. Let
$M (Y_t)$
. Let
Lemma 2.10. Let
![]() $\zeta=q$
,
$\zeta=q$
,
![]() $q \in (1,2)$
. Suppose
$q \in (1,2)$
. Suppose
![]() $X_0$
and
$X_0$
and
![]() $Y_0$
are random-cluster configurations such that
$Y_0$
are random-cluster configurations such that
![]() $\mathcal{S}_{\omega}(X_0) = \mathcal{S}_{\omega}(Y_0)$
, and
$\mathcal{S}_{\omega}(X_0) = \mathcal{S}_{\omega}(Y_0)$
, and
![]() $\hat{N}_k(0, \omega (n)) = \Omega\Big({\omega (n)}^{3 \cdot 2^{k-1}}\Big)$
for all
$\hat{N}_k(0, \omega (n)) = \Omega\Big({\omega (n)}^{3 \cdot 2^{k-1}}\Big)$
for all
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $n^{2/3}\omega (n)^{-2^{k-1}}\rightarrow \infty$
. Suppose also that
$n^{2/3}\omega (n)^{-2^{k-1}}\rightarrow \infty$
. Suppose also that
![]() $L_1(X_0) = O\!\left(n^{2/3} \omega (n)\right)$
,
$L_1(X_0) = O\!\left(n^{2/3} \omega (n)\right)$
,
![]() $\mathcal{R}_2(X_0) = O\!\left(n^{4/3}\right)$
,
$\mathcal{R}_2(X_0) = O\!\left(n^{4/3}\right)$
,
![]() $\widetilde{\mathcal{R}}_\omega(X_0) = O\!\left(n^{4/3}{\omega (n)}^{-1/2}\right)$
,
$\widetilde{\mathcal{R}}_\omega(X_0) = O\!\left(n^{4/3}{\omega (n)}^{-1/2}\right)$
,
![]() $I(X_0)=\Omega(n)$
, and similarly for
$I(X_0)=\Omega(n)$
, and similarly for
![]() $Y_0$
.
$Y_0$
.
Then, there exists a coupling of the CM steps such that with probability
![]() $\exp\!\left({-}O \!\left( \left({\log} \omega (n)\right)^2\right)\right)$
after
$\exp\!\left({-}O \!\left( \left({\log} \omega (n)\right)^2\right)\right)$
after
![]() $T=O({\log} \omega (n))$
steps:
$T=O({\log} \omega (n))$
steps:
![]() $\mathcal{S}_{\omega}(X_T) = \mathcal{S}_{\omega}(Y_T)$
,
$\mathcal{S}_{\omega}(X_T) = \mathcal{S}_{\omega}(Y_T)$
,
![]() $Z_T = O\!\left(n^{4/3}{\omega (n)}^{-1/2}\right)$
,
$Z_T = O\!\left(n^{4/3}{\omega (n)}^{-1/2}\right)$
,
![]() $\hat{N}_k\!\left(T, \omega (n)^{1/2}\right)= \Omega\!\left({\omega (n)}^{3 \cdot 2^{k-2}}\right)$
for all
$\hat{N}_k\!\left(T, \omega (n)^{1/2}\right)= \Omega\!\left({\omega (n)}^{3 \cdot 2^{k-2}}\right)$
for all
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $n^{2/3}\omega (n)^{-2^{k-1}}\rightarrow \infty$
,
$n^{2/3}\omega (n)^{-2^{k-1}}\rightarrow \infty$
,
![]() $\mathcal{R}_1(X_T) = O\!\left(n^{4/3}\right)$
,
$\mathcal{R}_1(X_T) = O\!\left(n^{4/3}\right)$
,
![]() $I(X_T) = \Omega(n)$
, and similarly for
$I(X_T) = \Omega(n)$
, and similarly for
![]() $Y_T$
.
$Y_T$
.
The proof of Lemma 2.10 also uses our local limit theorem (Theorem 5.1) and is provided in Section 5.3.
The final step of our construction is a coupling of the activation of the components of size less than
![]() $B_\omega$
, so that exactly the same number of vertices are activated from each copy in each step w.h.p.
$B_\omega$
, so that exactly the same number of vertices are activated from each copy in each step w.h.p.
Lemma 2.11. Let
![]() $\zeta=q$
,
$\zeta=q$
,
![]() $q \in (1,2)$
and suppose
$q \in (1,2)$
and suppose
![]() $X_0$
and
$X_0$
and
![]() $Y_0$
are random-cluster configurations such that
$Y_0$
are random-cluster configurations such that
![]() $\mathcal{S}_{\omega}(X_0) = \mathcal{S}_{\omega}(Y_0)$
,
$\mathcal{S}_{\omega}(X_0) = \mathcal{S}_{\omega}(Y_0)$
,
![]() $Z_0 = O\!\left(n^{4/3}{\omega (n)}^{-1/2}\right)$
, and
$Z_0 = O\!\left(n^{4/3}{\omega (n)}^{-1/2}\right)$
, and
![]() $\hat{N}_k\!\left(0, \omega (n)^{1/2}\right)= \Omega\!\left({\omega (n)}^{3 \cdot 2^{k-2}}\right)$
for all
$\hat{N}_k\!\left(0, \omega (n)^{1/2}\right)= \Omega\!\left({\omega (n)}^{3 \cdot 2^{k-2}}\right)$
for all
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $n^{2/3}\omega (n)^{-2^{k-1}}\rightarrow \infty$
. Suppose also that
$n^{2/3}\omega (n)^{-2^{k-1}}\rightarrow \infty$
. Suppose also that
![]() $\mathcal{R}_1(X_0) = O\!\left(n^{4/3}\right)$
,
$\mathcal{R}_1(X_0) = O\!\left(n^{4/3}\right)$
,
![]() $I(X_0) = \Omega(n)$
and similarly for
$I(X_0) = \Omega(n)$
and similarly for
![]() $Y_0$
. Then, there exist a coupling of the CM steps and a constant
$Y_0$
. Then, there exist a coupling of the CM steps and a constant
![]() $\beta > 0$
such that after
$\beta > 0$
such that after
![]() $T=O({\log}\ n)$
steps,
$T=O({\log}\ n)$
steps,
![]() $X_T$
and
$X_T$
and
![]() $Y_T$
have the same component structure with probability
$Y_T$
have the same component structure with probability
![]() $\Omega \!\left( ({\log} \log \log n)^{-\beta} \right)$
.
$\Omega \!\left( ({\log} \log \log n)^{-\beta} \right)$
.
We comment briefly on how we prove this lemma. Our starting point is two configurations with the same ‘large’ component structure, that is,
![]() $\mathcal{S}_{\omega}(X_0) = \mathcal{S}_{\omega}(Y_0)$
. We use the maximal matching
$\mathcal{S}_{\omega}(X_0) = \mathcal{S}_{\omega}(Y_0)$
. We use the maximal matching
![]() $W_0$
to couple the activation of the large components in
$W_0$
to couple the activation of the large components in
![]() $X_0$
and
$X_0$
and
![]() $Y_0$
. The small components not matched by
$Y_0$
. The small components not matched by
![]() $W_0$
, that is, those counted in
$W_0$
, that is, those counted in
![]() $Z_0$
, are then activated independently. This creates a discrepancy
$Z_0$
, are then activated independently. This creates a discrepancy
![]() $\mathcal{D}_0$
between the number of active vertices from each copy. Since
$\mathcal{D}_0$
between the number of active vertices from each copy. Since
![]() ${\mathbb{E}}[\mathcal{D}_0] = 0$
and
${\mathbb{E}}[\mathcal{D}_0] = 0$
and
![]() ${\textrm{Var}}(\mathcal{D}_0) = \Theta(Z_0) = \Theta({n^{4/3}}{\omega (n)^{-1/2}})$
, it follows from Hoeffding’s inequality that
${\textrm{Var}}(\mathcal{D}_0) = \Theta(Z_0) = \Theta({n^{4/3}}{\omega (n)^{-1/2}})$
, it follows from Hoeffding’s inequality that
![]() $\mathcal{D}_0 \le {n^{2/3}}{\omega (n)^{-1/4}}$
w.h.p. To fix this discrepancy, we use the small components matched by
$\mathcal{D}_0 \le {n^{2/3}}{\omega (n)^{-1/4}}$
w.h.p. To fix this discrepancy, we use the small components matched by
![]() $W_0$
. Specifically, under the assumptions in Lemma 2.11, we can construct a coupling of the activation of the small components so that the difference in the number of activated vertices from the small components from each copy is exactly
$W_0$
. Specifically, under the assumptions in Lemma 2.11, we can construct a coupling of the activation of the small components so that the difference in the number of activated vertices from the small components from each copy is exactly
![]() $\mathcal{D}_0$
with probability
$\mathcal{D}_0$
with probability
![]() $\Omega(1)$
. This part of the construction utilises random walks over the integers; in particular, we use a lower bound for the maximum of such a random walk.
$\Omega(1)$
. This part of the construction utilises random walks over the integers; in particular, we use a lower bound for the maximum of such a random walk.
We need to repeat this process until
![]() $Z_t = 0$
; this takes
$Z_t = 0$
; this takes
![]() $O({\log}\ n)$
steps since
$O({\log}\ n)$
steps since
![]() $Z_t \approx (1-1/q)^t Z_0$
. However, there are a few complications. First, the initial assumptions on the component structure of the configurations are not preserved for this many steps w.h.p., so we need to relax the requirements as the process evolves. This is in turn possible because the discrepancy
$Z_t \approx (1-1/q)^t Z_0$
. However, there are a few complications. First, the initial assumptions on the component structure of the configurations are not preserved for this many steps w.h.p., so we need to relax the requirements as the process evolves. This is in turn possible because the discrepancy
![]() $\mathcal{D}_t$
decreases with each step, which implies that the probability of success of the coupling increases at each step. See Section 5.4 for the detailed proof.
$\mathcal{D}_t$
decreases with each step, which implies that the probability of success of the coupling increases at each step. See Section 5.4 for the detailed proof.
We now indicate how these lemmas lead to a proof of Theorem 2.7 stated earlier.
Proof of Theorem 2.7. Suppose
![]() $\mathcal{R}_1(X_{0}) = O\!\left(n^{4/3}\right)$
and
$\mathcal{R}_1(X_{0}) = O\!\left(n^{4/3}\right)$
and
![]() $\mathcal{R}_1(Y_{0}) = O\!\left(n^{4/3}\right)$
. It follows from Lemmas 2.8, 2.9, 2.10 and 2.11 that there exists a coupling of the CM steps such that after
$\mathcal{R}_1(Y_{0}) = O\!\left(n^{4/3}\right)$
. It follows from Lemmas 2.8, 2.9, 2.10 and 2.11 that there exists a coupling of the CM steps such that after
![]() $T = O({\log}\ n)$
steps,
$T = O({\log}\ n)$
steps,
![]() $X_{T}$
and
$X_{T}$
and
![]() $Y_{T}$
could have the same component structure. This coupling succeeds with probability at least
$Y_{T}$
could have the same component structure. This coupling succeeds with probability at least
where
![]() $\beta_1, \beta_2 > 0$
are constants. Thus,
$\beta_1, \beta_2 > 0$
are constants. Thus,
![]() $\rho = \Omega\big( ({\log} \log n)^{-1} \big)$
, since
$\rho = \Omega\big( ({\log} \log n)^{-1} \big)$
, since
![]() $\omega (n) = \log \log \log \log n$
.
$\omega (n) = \log \log \log \log n$
.
Remark 2.12. We pause to mention that this delicate coupling for the activation of the components is not required when
![]() $\zeta=q$
and
$\zeta=q$
and
![]() $q > 2$
. In that regime, the random-cluster model is super-critical, so after the first
$q > 2$
. In that regime, the random-cluster model is super-critical, so after the first
![]() $O({\log}\ n)$
steps, the component structure is much simpler, with exactly one large component. On the other hand, when
$O({\log}\ n)$
steps, the component structure is much simpler, with exactly one large component. On the other hand, when
![]() $\zeta=q$
and
$\zeta=q$
and
![]() $q \in (1,2]$
the model is critical, which, combined with the fact mentioned earlier that the percolation sub-step of the dynamics is also critical when
$q \in (1,2]$
the model is critical, which, combined with the fact mentioned earlier that the percolation sub-step of the dynamics is also critical when
![]() $\zeta=q$
, makes the analysis of the CM dynamics in this regime quite subtle.
$\zeta=q$
, makes the analysis of the CM dynamics in this regime quite subtle.
2.3 Coupling to the same configuration
In the last phase of the coupling, suppose we start with two configurations
![]() $X_0$
,
$X_0$
,
![]() $Y_0$
with the same component structure. We are still required to bound the number of steps until the same configuration is reached. The following lemma from [Reference Blanca and Sinclair7] supplies the desired bound.
$Y_0$
with the same component structure. We are still required to bound the number of steps until the same configuration is reached. The following lemma from [Reference Blanca and Sinclair7] supplies the desired bound.
Lemma 2.13. ([Reference Blanca and Sinclair7], Lemma 24). Let
![]() $q>1$
,
$q>1$
,
![]() $\zeta >0$
and let
$\zeta >0$
and let
![]() $X_0$
,
$X_0$
,
![]() $Y_0$
be two random-cluster configurations with the same component structure. Then, there exists a coupling of the CM steps such that after
$Y_0$
be two random-cluster configurations with the same component structure. Then, there exists a coupling of the CM steps such that after
![]() $T=O({\log}\ n)$
steps,
$T=O({\log}\ n)$
steps,
![]() $X_T = Y_T$
w.h.p.
$X_T = Y_T$
w.h.p.
Combining the results for each of the phases of the coupling, we now prove Theorem 1.1.
Proof of Theorem 1.1. By Theorem 2.4, after
![]() $t_0 = O({\log}\ n)$
steps, with probability
$t_0 = O({\log}\ n)$
steps, with probability
![]() $\Omega(1)$
, we have
$\Omega(1)$
, we have
![]() $\mathcal{R}_1(X_{t_0}) = O\!\left(n^{4/3}\right)$
and
$\mathcal{R}_1(X_{t_0}) = O\!\left(n^{4/3}\right)$
and
![]() $\mathcal{R}_1(Y_{t_0}) = O\!\left(n^{4/3}\right)$
. If this is the case, Theorem 2.7 and Lemma 2.13 imply that there exists a coupling of the CM steps such that with probability
$\mathcal{R}_1(Y_{t_0}) = O\!\left(n^{4/3}\right)$
. If this is the case, Theorem 2.7 and Lemma 2.13 imply that there exists a coupling of the CM steps such that with probability
![]() $\Omega\!\left( ({\log} \log n)^{-1} \right)$
after an additional
$\Omega\!\left( ({\log} \log n)^{-1} \right)$
after an additional
![]() $t_1 = O({\log}\ n)$
steps,
$t_1 = O({\log}\ n)$
steps,
![]() $X_{t_0 + t_1} = Y_{t_0 + t_1}$
. Consequently, we obtain that
$X_{t_0 + t_1} = Y_{t_0 + t_1}$
. Consequently, we obtain that
![]() $\tau_{\textrm{mix}}^{\textrm{CM}} = O({\log}\ n \cdot \log \log n)$
as claimed.
$\tau_{\textrm{mix}}^{\textrm{CM}} = O({\log}\ n \cdot \log \log n)$
as claimed.
Remark 2.14. The probability of success in Theorem 2.7, which governs the lower order term
![]() $O({\log} \log n)$
in our mixing time bound, is controlled by our choice of the function
$O({\log} \log n)$
in our mixing time bound, is controlled by our choice of the function
![]() $\omega (n)$
for the definition of ‘large components’. By choosing
$\omega (n)$
for the definition of ‘large components’. By choosing
![]() $\omega (n) $
that goes to
$\omega (n) $
that goes to
![]() $ \infty$
more slowly, we could improve our mixing time bound to
$ \infty$
more slowly, we could improve our mixing time bound to
![]() $O({\log}\ n \cdot g(n))$
where g(n) is any function that tends to infinity arbitrarily slowly. However, it seems that new ideas are required to obtain a bound of
$O({\log}\ n \cdot g(n))$
where g(n) is any function that tends to infinity arbitrarily slowly. However, it seems that new ideas are required to obtain a bound of
![]() $O({\log}\ n)$
(matching the known lower bound). In particular, the fact that
$O({\log}\ n)$
(matching the known lower bound). In particular, the fact that
![]() $\omega (n) \rightarrow \infty$
is crucially used in some of our proofs. Our specific choice of
$\omega (n) \rightarrow \infty$
is crucially used in some of our proofs. Our specific choice of
![]() $\omega (n)$
yields the
$\omega (n)$
yields the
![]() $O({\log}\ n \cdot \log \log n)$
bound and makes our analysis cleaner.
$O({\log}\ n \cdot \log \log n)$
bound and makes our analysis cleaner.
3. Random graph estimates
In this section, we compile a number of standard facts about the G(n, p) random graph model which will be useful in our proofs. We use
![]() $G \sim G(n,p)$
to denote a random graph G sampled from the standard G(n, p) model, in which every edge appears independently with probability p. A G(n, p) random graph is said to be sub-critical when
$G \sim G(n,p)$
to denote a random graph G sampled from the standard G(n, p) model, in which every edge appears independently with probability p. A G(n, p) random graph is said to be sub-critical when
![]() $n p < 1$
. It is called super-critical when
$n p < 1$
. It is called super-critical when
![]() $n p > 1$
and critical when
$n p > 1$
and critical when
![]() $np=1$
. For a graph G, with a slight abuse of notation, let
$np=1$
. For a graph G, with a slight abuse of notation, let
![]() $L_i(G)$
denote the size of the i-th largest connected component in G, and let
$L_i(G)$
denote the size of the i-th largest connected component in G, and let
![]() $\mathcal{R}_i(G)\,:\!=\,\sum_{j \ge i} L_j(G)^2$
; note that the same notation is used for the components of a random-cluster configuration, but it will always be clear from context which case is meant.
$\mathcal{R}_i(G)\,:\!=\,\sum_{j \ge i} L_j(G)^2$
; note that the same notation is used for the components of a random-cluster configuration, but it will always be clear from context which case is meant.
Fact 3.1. Given
![]() $0 < N_1 < N_2$
and
$0 < N_1 < N_2$
and
![]() $p \in [0, 1]$
. Let
$p \in [0, 1]$
. Let
![]() $G_1 \sim G(N_1, p)$
and
$G_1 \sim G(N_1, p)$
and
![]() $G_2 \sim G(N_2, p)$
. For any
$G_2 \sim G(N_2, p)$
. For any
![]() $K > 0$
,
$K > 0$
,
![]() ${\mathbb{P}}[L_1(G_1) > K] \leq {\mathbb{P}}[L_1(G_2) > K]$
.
${\mathbb{P}}[L_1(G_1) > K] \leq {\mathbb{P}}[L_1(G_2) > K]$
.
Proof. Consider the coupling of
![]() $(G_1, G_2)$
such that
$(G_1, G_2)$
such that
![]() $G_1$
is a subgraph of
$G_1$
is a subgraph of
![]() $G_2$
.
$G_2$
.
![]() $L_1(G_1) \le L_1(G_2)$
with probability 1. Proposition just follows from Strassen’s theorem (see, e.g., Theorem 22.6 in [Reference Levin and Peres22]).
$L_1(G_1) \le L_1(G_2)$
with probability 1. Proposition just follows from Strassen’s theorem (see, e.g., Theorem 22.6 in [Reference Levin and Peres22]).
Lemma 3.2. ([Reference Long, Nachmias, Ning and Peres24], Lemma 5.7). Let I(G) denote the number of isolated vertices in G. If
![]() $np = O (1)$
, then there exists a constant
$np = O (1)$
, then there exists a constant
![]() $C > 0$
such that
$C > 0$
such that
Consider the equation
and let
![]() $\beta(d)$
be defined as its unique positive root. Observe that
$\beta(d)$
be defined as its unique positive root. Observe that
![]() $\beta$
is well defined for
$\beta$
is well defined for
![]() $d > 1$
.
$d > 1$
.
Lemma 3.3 ([Reference Blanca4], Lemma 2.7). Let
![]() $G\sim G(n + m, d_n /n)$
random graph where
$G\sim G(n + m, d_n /n)$
random graph where
![]() $|m| = o(n)$
and
$|m| = o(n)$
and
![]() $\lim_{n\rightarrow \infty} d_n = d$
. Assume
$\lim_{n\rightarrow \infty} d_n = d$
. Assume
![]() $1 < d_n = O(1)$
and
$1 < d_n = O(1)$
and
![]() $d_n$
is bounded away from 1 for all
$d_n$
is bounded away from 1 for all
![]() $n\in \mathbb{N} $
. Then, For
$n\in \mathbb{N} $
. Then, For
![]() $A = o({\log}\ n)$
and sufficiently large n, there exists a constant
$A = o({\log}\ n)$
and sufficiently large n, there exists a constant
![]() $c > 0$
such that
$c > 0$
such that
Lemma 3.4 ([Reference Blanca4], Lemma 2.16). For
![]() $np>0$
, we have
$np>0$
, we have
![]() ${\mathbb{E}}\left[\mathcal{R}_2(G)\right] = O\!\left(n^{4/3}\right)$
.
${\mathbb{E}}\left[\mathcal{R}_2(G)\right] = O\!\left(n^{4/3}\right)$
.
Consider the near-critical random graph
![]() $G\!\left(n, \frac{1 + \varepsilon}{n}\right)$
with
$G\!\left(n, \frac{1 + \varepsilon}{n}\right)$
with
![]() $\varepsilon = \varepsilon(n) = o(1)$
.
$\varepsilon = \varepsilon(n) = o(1)$
.
Lemma 3.5 ([Reference Long, Nachmias, Ning and Peres24], Theorem 5.9). Assume
![]() $\varepsilon^3n \geq 1$
, then for any A satisfying
$\varepsilon^3n \geq 1$
, then for any A satisfying
![]() $2 \leq A \leq \sqrt{\varepsilon^3n}/10$
, there exists some constant
$2 \leq A \leq \sqrt{\varepsilon^3n}/10$
, there exists some constant
![]() $c > 0$
such that
$c > 0$
such that
Corollary 3.6. Let
![]() $G\sim G\!\left(n, \frac{1 + \varepsilon}{n}\right)$
with
$G\sim G\!\left(n, \frac{1 + \varepsilon}{n}\right)$
with
![]() $\varepsilon = o(1)$
. For any positive constant
$\varepsilon = o(1)$
. For any positive constant
![]() $\rho \le 1/10$
, there exist constants
$\rho \le 1/10$
, there exist constants
![]() $C \ge 1$
and
$C \ge 1$
and
![]() $c > 0$
such that if
$c > 0$
such that if
![]() $\varepsilon^3 n \ge C$
, then
$\varepsilon^3 n \ge C$
, then
Lemma 3.7 ([Reference Long, Nachmias, Ning and Peres24], Theorem 5.12). Let
![]() $\varepsilon < 0$
, then
$\varepsilon < 0$
, then
![]() ${\mathbb{E}}[\mathcal{R}_1(G)] = O\!\left(n/|\varepsilon|\right).$
${\mathbb{E}}[\mathcal{R}_1(G)] = O\!\left(n/|\varepsilon|\right).$
Lemma 3.8 ([Reference Long, Nachmias, Ning and Peres24], Theorem 5.13). Let
![]() $\varepsilon > 0$
and
$\varepsilon > 0$
and
![]() $\varepsilon^3 n \geq 1$
for large n, then
$\varepsilon^3 n \geq 1$
for large n, then
![]() ${\mathbb{E}}[\mathcal{R}_2(G)] = O\!\left(n/\varepsilon \right)$
.
${\mathbb{E}}[\mathcal{R}_2(G)] = O\!\left(n/\varepsilon \right)$
.
For the next results, suppose that
![]() $G \sim G\big(n,\frac{1+\lambda n^{-1/3}}{n}\big)$
, where
$G \sim G\big(n,\frac{1+\lambda n^{-1/3}}{n}\big)$
, where
![]() $\lambda = \lambda(n)$
may depend on n.
$\lambda = \lambda(n)$
may depend on n.
Lemma 3.9. If
![]() $|\lambda| = O(1)$
, then
$|\lambda| = O(1)$
, then
![]() ${\mathbb{E}}\left[\mathcal{R}_1(G)\right] = O\!\left(n^{4/3}\right)$
.
${\mathbb{E}}\left[\mathcal{R}_1(G)\right] = O\!\left(n^{4/3}\right)$
.
Proof. Follows from Lemmas 2.13, 2.15 and 2.16 in [Reference Blanca4].
All the random graph facts stated so far can be either found in the literature, or follow directly from well-known results. The following lemmas are slightly more refined versions of similar results in the literature.
Lemma 3.10. Suppose
![]() $|\lambda| = O(h(n))$
and let
$|\lambda| = O(h(n))$
and let
![]() $B_h = {n^{2/3}}{h(n)^{-1}}$
, where
$B_h = {n^{2/3}}{h(n)^{-1}}$
, where
![]() $h\,:\,\mathbb{N} \rightarrow \mathbb{R}$
is a positive increasing function such that
$h\,:\,\mathbb{N} \rightarrow \mathbb{R}$
is a positive increasing function such that
![]() $h(n)=o({\log}\ n)$
. Then, for any
$h(n)=o({\log}\ n)$
. Then, for any
![]() $\alpha \in (0,1)$
there exists a constant
$\alpha \in (0,1)$
there exists a constant
![]() $C = C(\alpha) > 0$
such that, with probability at least
$C = C(\alpha) > 0$
such that, with probability at least
![]() $\alpha$
,
$\alpha$
,
Lemma 3.11. Let
![]() $S_B = \{j\,:\, B \le L_j(G) \le 2B\}$
and suppose there exists a positive increasing function g such that
$S_B = \{j\,:\, B \le L_j(G) \le 2B\}$
and suppose there exists a positive increasing function g such that
![]() $g(n) \rightarrow \infty$
,
$g(n) \rightarrow \infty$
,
![]() $g(n) = o\!\left(n^{1/3}\right)$
,
$g(n) = o\!\left(n^{1/3}\right)$
,
![]() $|\lambda| \le g(n)$
and
$|\lambda| \le g(n)$
and
![]() $B \le \frac{n^{2/3}}{g(n)^2}$
. If
$B \le \frac{n^{2/3}}{g(n)^2}$
. If
![]() $B \rightarrow \infty$
, then there exists constants
$B \rightarrow \infty$
, then there exists constants
![]() $\delta_1,\delta_2 > 0$
independent of n such that
$\delta_1,\delta_2 > 0$
independent of n such that
The proofs of Lemmas 3.10 and 3.11 are provided in Appendix C. Finally, the following corollary of Lemma 3.11 will also be useful. For a graph H, let
![]() ${N}_k(H, g)$
be the number of components of H whose sizes are in the interval
${N}_k(H, g)$
be the number of components of H whose sizes are in the interval
![]() $\mathcal{I}_k(g)$
. We note that with a slight abuse of notation, for a random-cluster configuration X, we also use
$\mathcal{I}_k(g)$
. We note that with a slight abuse of notation, for a random-cluster configuration X, we also use
![]() ${N}_k(X, g)$
for the number of connected components of X in
${N}_k(X, g)$
for the number of connected components of X in
![]() $\mathcal{I}_k(g)$
.
$\mathcal{I}_k(g)$
.
Corollary 3.12. Let
![]() $m \in (n/2q,n]$
and let g be an increasing positive function that such that
$m \in (n/2q,n]$
and let g be an increasing positive function that such that
![]() $g(n)=o\!\left(m^{1/3}\right)$
,
$g(n)=o\!\left(m^{1/3}\right)$
,
![]() $g(n) \rightarrow \infty$
and
$g(n) \rightarrow \infty$
and
![]() $|\lambda| \le g(m)$
. If
$|\lambda| \le g(m)$
. If
![]() $H \sim G\Big(m, \frac{1 + \lambda m^{-1/3}}{m}\Big)$
, there exists a constant
$H \sim G\Big(m, \frac{1 + \lambda m^{-1/3}}{m}\Big)$
, there exists a constant
![]() $b > 0$
such that, with probability at least
$b > 0$
such that, with probability at least
![]() $1-O\!\left(g(n)^{-3}\right)$
,
$1-O\!\left(g(n)^{-3}\right)$
,
![]() $N_{k}(H,g) \ge b g(n)^{3 \cdot 2^{k-1}}$
for all
$N_{k}(H,g) \ge b g(n)^{3 \cdot 2^{k-1}}$
for all
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $n^{2/3}g(n)^{-2^k}\rightarrow \infty$
.
$n^{2/3}g(n)^{-2^k}\rightarrow \infty$
.
4. The burn-in period: proofs
In this section we will provide proofs for Lemmas 2.2 and 2.3.
4.1 A drift function
Consider the mean-field random-cluster model with parameters
![]() $q \ge 1$
and
$q \ge 1$
and
![]() $p = \zeta/n$
. In this subsection, we introduce a drift function captures the rate of decay of the size of the largest component in a configuration under steps of the CM dynamics which will be helpful for proving Lemma 2.2; this function was first studied in [Reference Blanca and Sinclair7].
$p = \zeta/n$
. In this subsection, we introduce a drift function captures the rate of decay of the size of the largest component in a configuration under steps of the CM dynamics which will be helpful for proving Lemma 2.2; this function was first studied in [Reference Blanca and Sinclair7].
Given
![]() $\theta \in (0,1]$
, consider the equation
$\theta \in (0,1]$
, consider the equation
and let
![]() $\phi(\theta, \zeta, q)$
be defined as the largest positive root of (4). We shall see that
$\phi(\theta, \zeta, q)$
be defined as the largest positive root of (4). We shall see that
![]() $\phi$
is not defined for all q and
$\phi$
is not defined for all q and
![]() $\zeta$
since there may not be a positive root. When
$\zeta$
since there may not be a positive root. When
![]() $ \zeta$
and q are clear from the context we use
$ \zeta$
and q are clear from the context we use
![]() $\phi(\theta)=\phi(\theta, \zeta, q)$
. Note that
$\phi(\theta)=\phi(\theta, \zeta, q)$
. Note that
![]() $\beta(\zeta)$
defined by equation (3) is the special case of (4) when
$\beta(\zeta)$
defined by equation (3) is the special case of (4) when
![]() $q=1$
; observe that
$q=1$
; observe that
![]() $\beta$
is only well defined when
$\beta$
is only well defined when
![]() $\zeta > 1$
.
$\zeta > 1$
.
We let
![]() $k(\theta, q)\,:\!=\,(1+(q-1)\theta)/q$
so that
$k(\theta, q)\,:\!=\,(1+(q-1)\theta)/q$
so that
![]() $\phi(\theta, \zeta, q)=\beta(\zeta \cdot k(\theta, q)) \cdot k(\theta, q).$
Hence,
$\phi(\theta, \zeta, q)=\beta(\zeta \cdot k(\theta, q)) \cdot k(\theta, q).$
Hence,
![]() $\phi(\theta, \zeta, q)$
is only defined when
$\phi(\theta, \zeta, q)$
is only defined when
![]() $\zeta \cdot k(\theta, q)>1$
; that is,
$\zeta \cdot k(\theta, q)>1$
; that is,
![]() $\theta \in (\theta_{\min}, 1]$
, where
$\theta \in (\theta_{\min}, 1]$
, where
![]() $\theta_{\min}=\frac{q-\zeta}{\zeta(q-1)}$
. Note that when
$\theta_{\min}=\frac{q-\zeta}{\zeta(q-1)}$
. Note that when
![]() $\zeta = q$
,
$\zeta = q$
,
![]() $\phi(\theta)$
is defined for every
$\phi(\theta)$
is defined for every
![]() $\theta \in (0, 1]$
.
$\theta \in (0, 1]$
.
For fixed
![]() $\zeta$
and q, we call
$\zeta$
and q, we call
![]() $f(\theta)\,:\!=\,\theta - \phi(\theta)$
the drift function. which is defined on
$f(\theta)\,:\!=\,\theta - \phi(\theta)$
the drift function. which is defined on
![]() $({\max}\{\theta_{\min}, 0\}, 1]$
.
$({\max}\{\theta_{\min}, 0\}, 1]$
.
Lemma 4.1. When
![]() $q = \zeta < 2$
, the drift function f is non-negative for any
$q = \zeta < 2$
, the drift function f is non-negative for any
![]() $\theta \in [\xi, 1]$
, where
$\theta \in [\xi, 1]$
, where
![]() $\xi$
is an arbitrarily small positive constant.
$\xi$
is an arbitrarily small positive constant.
Proof. When
![]() $\zeta = q < 2$
, the drift function f does not have a positive root, it is continuous in (0,1], and
$\zeta = q < 2$
, the drift function f does not have a positive root, it is continuous in (0,1], and
![]() $f(1)>0$
; see Lemma 2.5 in [Reference Bollobás, Grimmett and Janson9] and Fact 3.5 in [Reference Blanca4]. Since
$f(1)>0$
; see Lemma 2.5 in [Reference Bollobás, Grimmett and Janson9] and Fact 3.5 in [Reference Blanca4]. Since
![]() $\lim_{\theta \rightarrow 0}f(\theta) = 0$
, the result follows.
$\lim_{\theta \rightarrow 0}f(\theta) = 0$
, the result follows.
4.2 Shrinking a large component: proof of Lemma 2.2
The proof of Lemma 2.2 uses the following lemma, which follows directly from standard random graph estimates and Hoeffding’s inequality. To simplify the notation, we let
![]() $\hat{L}(X) \,:\!=\, L_1(X)/n^{2/3}$
. We use A(X) to denote the number of vertices activated by the step CM dynamics from configuration X. Let
$\hat{L}(X) \,:\!=\, L_1(X)/n^{2/3}$
. We use A(X) to denote the number of vertices activated by the step CM dynamics from configuration X. Let
![]() $\Lambda_t$
denote the event that the largest component of the configuration is activated in step t.
$\Lambda_t$
denote the event that the largest component of the configuration is activated in step t.
Lemma 4.2 ([Reference Blanca4], Claim 3.45). Suppose
![]() $ \mathcal{R}_2(X_t) = O\!\left(n^{4/3}\right)$
and
$ \mathcal{R}_2(X_t) = O\!\left(n^{4/3}\right)$
and
![]() $\hat{L}(X_t) \geq B$
for a large constant B, and let C be a fixed large constant. Then
$\hat{L}(X_t) \geq B$
for a large constant B, and let C be a fixed large constant. Then
-
1.
 ${\mathbb{P}}\left[\mathcal{R}_2(X_{t+1}) < \mathcal{R}_2(X_t) + \frac{Cn^{4/3}}{\sqrt{\hat{L}(X_t)}} \ \middle|\ X_t, \Lambda_t \right] = 1 - O\!\left(\hat{L}(X_{t})^{-1/2} \right)$
.
${\mathbb{P}}\left[\mathcal{R}_2(X_{t+1}) < \mathcal{R}_2(X_t) + \frac{Cn^{4/3}}{\sqrt{\hat{L}(X_t)}} \ \middle|\ X_t, \Lambda_t \right] = 1 - O\!\left(\hat{L}(X_{t})^{-1/2} \right)$
. -
2.
 ${\mathbb{P}}\left[\mathcal{R}_2(X_{t+1}) < \mathcal{R}_2(X_t) + \frac{Cn^{4/3}}{\sqrt{\hat{L}(X_t)}} \ \middle|\ X_t, \neg\Lambda_t \right] = 1 - O\!\left(\hat{L}(X_{t})^{-1/2} \right)$
.
${\mathbb{P}}\left[\mathcal{R}_2(X_{t+1}) < \mathcal{R}_2(X_t) + \frac{Cn^{4/3}}{\sqrt{\hat{L}(X_t)}} \ \middle|\ X_t, \neg\Lambda_t \right] = 1 - O\!\left(\hat{L}(X_{t})^{-1/2} \right)$
.
Proof of Lemma 2.2. Let
![]() $\hat{T}$
be the first time t when
$\hat{T}$
be the first time t when
![]() $\hat{L}(X_t) \leq \delta n^{1/3}$
, let T
′ be a large constant we choose later; we set
$\hat{L}(X_t) \leq \delta n^{1/3}$
, let T
′ be a large constant we choose later; we set
![]() $T \,:\!=\, \min\{\hat{T}, T^{\prime}\}$
. Observe that with constant probability the largest component in the configuration is activated by the CM dynamics for every
$T \,:\!=\, \min\{\hat{T}, T^{\prime}\}$
. Observe that with constant probability the largest component in the configuration is activated by the CM dynamics for every
![]() $t \le T^{\prime}$
, that is, the event
$t \le T^{\prime}$
, that is, the event
![]() $\Lambda_t$
occurs for every
$\Lambda_t$
occurs for every
![]() $t \le T^{\prime}$
. Let us assume this is the case and fix
$t \le T^{\prime}$
. Let us assume this is the case and fix
![]() $t < T$
. Suppose
$t < T$
. Suppose
![]() $\mathcal{R}_2(X_t) \leq \mathcal{R}_2(X_0) + t \cdot \frac{C}{\sqrt{\delta}} n^{\frac{7}{6}}$
where C is the positive constant from Lemma 4.2. We show that with high probability:
$\mathcal{R}_2(X_t) \leq \mathcal{R}_2(X_0) + t \cdot \frac{C}{\sqrt{\delta}} n^{\frac{7}{6}}$
where C is the positive constant from Lemma 4.2. We show that with high probability:
-
i.
 $\mathcal{R}_2(X_{t+1}) \leq \mathcal{R}_2(X_0) + t \cdot \frac{C}{\sqrt{\delta}} n^{\frac{7}{6}}$
; and
$\mathcal{R}_2(X_{t+1}) \leq \mathcal{R}_2(X_0) + t \cdot \frac{C}{\sqrt{\delta}} n^{\frac{7}{6}}$
; and -
ii.
 $L_1(X_{t+1}) \le L_1(X_t) - \xi n$
where
$L_1(X_{t+1}) \le L_1(X_t) - \xi n$
where
 $\xi$
is a positive constant independent of t and n.
$\xi$
is a positive constant independent of t and n.
In particular, it suffices to set
![]() $T^{\prime} = (1-\delta)/\xi$
for the lemma to hold.
$T^{\prime} = (1-\delta)/\xi$
for the lemma to hold.
First, we show that
![]() $A(X_t)$
is concentrated around its mean. Let
$A(X_t)$
is concentrated around its mean. Let
![]() $L_1(X_t) \,:\!=\, \theta_t n$
and
$L_1(X_t) \,:\!=\, \theta_t n$
and
![]() $L_1(X_{t+1}) \,:\!=\, \theta_{t+1} n$
. Let
$L_1(X_{t+1}) \,:\!=\, \theta_{t+1} n$
. Let
![]() ${\mathbb{E}}[A(X_t) \mid \Lambda_t] = \mu_t = \frac{n}{q}+ \left(1-\frac{1}{q}\right)\cdot\theta_t n$
,
${\mathbb{E}}[A(X_t) \mid \Lambda_t] = \mu_t = \frac{n}{q}+ \left(1-\frac{1}{q}\right)\cdot\theta_t n$
,
![]() $\gamma\,:\!=\,n^{5/6}$
, and
$\gamma\,:\!=\,n^{5/6}$
, and
![]() $J_t\,:\!=\,[\mu_t - \gamma, \mu_t + \gamma]$
. Hoeffding’s inequality implies
$J_t\,:\!=\,[\mu_t - \gamma, \mu_t + \gamma]$
. Hoeffding’s inequality implies
If
![]() $A(X_t) \in J_t$
, then the random graph
$A(X_t) \in J_t$
, then the random graph
![]() $G(A(X_t), p)$
is super-critical since
$G(A(X_t), p)$
is super-critical since
Next, for a super-critical random graph, Lemma 3.3 provides a concentration bound for the size of largest new component, provided
![]() $A(X_t) \in J_t$
. To see this, we write
$A(X_t) \in J_t$
. To see this, we write
![]() $G(A(X_t), \zeta/n)$
as
$G(A(X_t), \zeta/n)$
as
where
![]() $m\,:\!=\,A(X_t)-\mu_t$
; notice that
$m\,:\!=\,A(X_t)-\mu_t$
; notice that
![]() $|m| \leq \gamma = o(n)$
. Let
$|m| \leq \gamma = o(n)$
. Let
![]() $H \sim G \!\left(\mu_t + m, k(\theta_t, q)\cdot q/\mu_t \right)$
. Since
$H \sim G \!\left(\mu_t + m, k(\theta_t, q)\cdot q/\mu_t \right)$
. Since
holds regardless of n, Lemma 3.3 implies that for
![]() $\phi(\theta_t) > 0$
defined in Section 4.1, with high probability
$\phi(\theta_t) > 0$
defined in Section 4.1, with high probability
Note that
![]() $L_1(H) = \Omega(n)$
w.h.p.; hence, since
$L_1(H) = \Omega(n)$
w.h.p.; hence, since
![]() $L_2(X_t) = O\big(n^{2/3}\big)$
we have
$L_2(X_t) = O\big(n^{2/3}\big)$
we have
![]() $L_1(X_{t+1}) = L_1(H)$
w.h.p. We have shown that w.h.p.
$L_1(X_{t+1}) = L_1(H)$
w.h.p. We have shown that w.h.p.
where f is the drift function defined in Section 4.1. By Lemma 4.1, we know
![]() $f(\theta_t) > \xi_1 > 0$
for sufficiently small constant
$f(\theta_t) > \xi_1 > 0$
for sufficiently small constant
![]() $\xi_1$
(independent of n and t). Hence, w.h.p. for sufficiently large n
$\xi_1$
(independent of n and t). Hence, w.h.p. for sufficiently large n
this establishes (ii) from above.
For (i), note that for
![]() $t < T$
we have
$t < T$
we have
![]() $\hat{L}(X_t) > \delta n^{1/3}$
, so Lemma 4.2 implies,
$\hat{L}(X_t) > \delta n^{1/3}$
, so Lemma 4.2 implies,
A union bound implies that these two events occur simultaneously w.h.p. and the result follows.
4.3 Shrinking a medium size component: proof of Lemma 2.3
In the third sub-phase of the burn-in period, we show that
![]() ${L_1}(X_t)$
contracts at a constant rate; the precise description of this phenomenon is captured in the following lemma.
${L_1}(X_t)$
contracts at a constant rate; the precise description of this phenomenon is captured in the following lemma.
Lemma 4.3. Suppose
![]() $\mathcal{R}_2(X_{t}) = O\!\left(n^{4/3}\right)$
,
$\mathcal{R}_2(X_{t}) = O\!\left(n^{4/3}\right)$
,
![]() $\delta n^{1/3} \geq \hat{L}(X_{t}) \geq B$
for a large constant
$\delta n^{1/3} \geq \hat{L}(X_{t}) \geq B$
for a large constant
![]() $B \,:\!=\, B(q)$
, and a small constant
$B \,:\!=\, B(q)$
, and a small constant
![]() $\delta(q, B)$
. Then:
$\delta(q, B)$
. Then:
-
1. There exists a constant
 $\alpha \,:\!=\,\alpha(B, q, \delta) < 1$
such that
$\alpha \,:\!=\,\alpha(B, q, \delta) < 1$
such that  \begin{equation*}{\mathbb{P}}\left[L_1(X_{t+1}) \leq \max \{\alpha L_1(X_t) ,L_2(X_t)\} \mid X_t, \Lambda_t\right]\geq 1 - \exp\!\left({-}\Omega\!\left(\hat{L}(X_{t})\right)\right);\end{equation*}
\begin{equation*}{\mathbb{P}}\left[L_1(X_{t+1}) \leq \max \{\alpha L_1(X_t) ,L_2(X_t)\} \mid X_t, \Lambda_t\right]\geq 1 - \exp\!\left({-}\Omega\!\left(\hat{L}(X_{t})\right)\right);\end{equation*}
-
2.
 ${\mathbb{P}}\left[L_1(X_{t+1}) = L_1(X_t) | X_t, \neg\Lambda_t\right] \geq 1 - O\!\left(\hat{L}(X_{t})^{-3} \right).$
${\mathbb{P}}\left[L_1(X_{t+1}) = L_1(X_t) | X_t, \neg\Lambda_t\right] \geq 1 - O\!\left(\hat{L}(X_{t})^{-3} \right).$
Since Lemmas 4.2 suggests
![]() $\mathcal{R}_2(X_{t}) = O\!\left(n^{4/3}\right)$
with reasonably high probability throughout the execution of the sub-phase, Lemmas 4.3 and 4.2 can be combined to derive the following more accurate contraction estimate which will be crucial in the proof Lemma 2.3.
$\mathcal{R}_2(X_{t}) = O\!\left(n^{4/3}\right)$
with reasonably high probability throughout the execution of the sub-phase, Lemmas 4.3 and 4.2 can be combined to derive the following more accurate contraction estimate which will be crucial in the proof Lemma 2.3.
Lemma 4.4. Suppose g(n) is an arbitrary function with range in the interval
![]() $\left[B^6, \delta n^{1/3}\right]$
where B is a large enough constant such that for
$\left[B^6, \delta n^{1/3}\right]$
where B is a large enough constant such that for
![]() $x \ge B^6$
we have
$x \ge B^6$
we have
![]() $x \geq B ({\log} x)^8$
, and
$x \geq B ({\log} x)^8$
, and
![]() $\delta \,:\!=\, \delta(q, B)$
is a small constant.
$\delta \,:\!=\, \delta(q, B)$
is a small constant.
Suppose
![]() $X_0$
is such that
$X_0$
is such that
![]() $g(n) \geq \hat{L}(X_0) \geq B \big({\log} g(n)\big)^8$
and
$g(n) \geq \hat{L}(X_0) \geq B \big({\log} g(n)\big)^8$
and
![]() $\mathcal{R}_2(X_0) = O\!\left(n^{4/3}\right)$
, then there exists a constant D and
$\mathcal{R}_2(X_0) = O\!\left(n^{4/3}\right)$
, then there exists a constant D and
![]() $T = O\big({\log} g(n)\big)$
such that at time T,
$T = O\big({\log} g(n)\big)$
such that at time T,
![]() $ \hat{L}(X_T) \leq \max\{ B \big({\log} g(n)\big)^8 , D\}$
and
$ \hat{L}(X_T) \leq \max\{ B \big({\log} g(n)\big)^8 , D\}$
and
![]() $\mathcal{R}_2(X_T) \leq \mathcal{R}_2(X_0) + O\!\left(\frac{n^{4/3}}{\log g(n)}\right)$
with probability at least
$\mathcal{R}_2(X_T) \leq \mathcal{R}_2(X_0) + O\!\left(\frac{n^{4/3}}{\log g(n)}\right)$
with probability at least
![]() $1 - O\!\left({\log}^{-1} g(n) \right)$
.
$1 - O\!\left({\log}^{-1} g(n) \right)$
.
We first provide a proof for Lemma 2.3 that recursively uses the contraction estimate of Lemma 4.4.
Proof of Lemma 2.3. Let B be a constant large enough so that
![]() $\forall x \geq B^6$
, we have
$\forall x \geq B^6$
, we have
![]() $x \geq ({\log} x)^{48}$
. Suppose
$x \geq ({\log} x)^{48}$
. Suppose
![]() $\hat{L}(X_{0}) \leq \delta n^{1/3}$
and
$\hat{L}(X_{0}) \leq \delta n^{1/3}$
and
![]() $\mathcal{R}_2(X_{0}) = O\!\left(n^{4/3}\right)$
for the constant
$\mathcal{R}_2(X_{0}) = O\!\left(n^{4/3}\right)$
for the constant
![]() $\delta = \delta(q,B)$
from Lemma 4.4. Suppose also
$\delta = \delta(q,B)$
from Lemma 4.4. Suppose also
![]() $ \hat{L}(X_{0}) \geq B^6$
; otherwise there is nothing to prove.
$ \hat{L}(X_{0}) \geq B^6$
; otherwise there is nothing to prove.
Let
![]() $g_0(n)\,:\!=\,\delta n^{1/3}$
and
$g_0(n)\,:\!=\,\delta n^{1/3}$
and
![]() $g_{i+1}(n)\,:\!=\, B ({\log} g_i(n))^8$
for all
$g_{i+1}(n)\,:\!=\, B ({\log} g_i(n))^8$
for all
![]() $i \geq 0$
. Let K be defined as the minimum natural number such that
$i \geq 0$
. Let K be defined as the minimum natural number such that
![]() $g_K(n) \leq B^6$
. Note that
$g_K(n) \leq B^6$
. Note that
![]() $K = O({\log}^* n)$
. Assume at time
$K = O({\log}^* n)$
. Assume at time
![]() $t \ge 0$
, there exists an integer
$t \ge 0$
, there exists an integer
![]() $j \ge 0$
such that
$j \ge 0$
such that
![]() $X_{t}$
satisfies:
$X_{t}$
satisfies:
-
1.
 $g_{j+1}(n) \leq \hat{L}(X_{t}) \leq g_j(n)$
, and
$g_{j+1}(n) \leq \hat{L}(X_{t}) \leq g_j(n)$
, and -
2.
 $\mathcal{R}_2(X_{t}) = O\!\left(n^{4/3}\right) + O\!\left(\sum_{k=0}^{j-1} \frac{n^{4/3}}{\log g_{k}(n)}\right)$
.
$\mathcal{R}_2(X_{t}) = O\!\left(n^{4/3}\right) + O\!\left(\sum_{k=0}^{j-1} \frac{n^{4/3}}{\log g_{k}(n)}\right)$
.
We show there exists time
![]() $t^{\prime} > t$
such that properties 1 and 2 hold for
$t^{\prime} > t$
such that properties 1 and 2 hold for
![]() $X_{t^{\prime}}$
for a different index
$X_{t^{\prime}}$
for a different index
![]() $j^{\prime} > j$
. The following bounds on sums and products involving the
$j^{\prime} > j$
. The following bounds on sums and products involving the
![]() $g_i$
’s will be useful; the proof is elementary and delayed to the end of this section.
$g_i$
’s will be useful; the proof is elementary and delayed to the end of this section.
Claim 4.5. Let K be defined as above.
![]() $ \forall j < K,$
$ \forall j < K,$
-
i. For any positive constant c, we have
 $\prod_{i=0}^{j} \!\left( 1 - \frac{c}{\log g_{i}(n)} \right) \geq 1 - \frac{1.5 c}{\log g_j(n)}$
$\prod_{i=0}^{j} \!\left( 1 - \frac{c}{\log g_{i}(n)} \right) \geq 1 - \frac{1.5 c}{\log g_j(n)}$
-
ii.
 $\sum_{i=0}^{j} \frac{1}{\log g_i(n)} \leq \frac{1.5}{\log g_j(n)} $
$\sum_{i=0}^{j} \frac{1}{\log g_i(n)} \leq \frac{1.5}{\log g_j(n)} $
By part (ii) of this claim, note that
 \begin{equation*}O\!\left(\sum_{k=0}^{j-1} \frac{n^{4/3}}{\log g_{k}(n)}\right) =O\!\left(\frac{n^{4/3}}{\log g_{j-1}(n)}\right) = O\!\left(n^{4/3}\right).\end{equation*}
\begin{equation*}O\!\left(\sum_{k=0}^{j-1} \frac{n^{4/3}}{\log g_{k}(n)}\right) =O\!\left(\frac{n^{4/3}}{\log g_{j-1}(n)}\right) = O\!\left(n^{4/3}\right).\end{equation*}
Hence, Lemma 4.4 implies that with probability
![]() $1 - O\!\left(\left({\log} g_j(n)\right)^{-1} \right)$
there exist a time
$1 - O\!\left(\left({\log} g_j(n)\right)^{-1} \right)$
there exist a time
![]() $t^{\prime} \leq t + O( \log g_j(n) )$
and a large constant D such that
$t^{\prime} \leq t + O( \log g_j(n) )$
and a large constant D such that
![]() $ \hat{L}\!\left(X_{t^{\prime}}\right) \leq \max\left\{B\!\left({\log} g_j(n)\right)^8, D\right\}$
and
$ \hat{L}\!\left(X_{t^{\prime}}\right) \leq \max\left\{B\!\left({\log} g_j(n)\right)^8, D\right\}$
and
![]() $\mathcal{R}_2\!\left(X_{t^{\prime}}\right) \leq \mathcal{R}_2(X_{t}) + O\!\left(\frac{n^{4/3}}{\log g_j(n)}\right).$
If
$\mathcal{R}_2\!\left(X_{t^{\prime}}\right) \leq \mathcal{R}_2(X_{t}) + O\!\left(\frac{n^{4/3}}{\log g_j(n)}\right).$
If
![]() $\hat{L}\!\left(X_{t^{\prime}}\right) \le \max \left\{D, B^6\right\}$
we are done. Hence, suppose otherwise that
$\hat{L}\!\left(X_{t^{\prime}}\right) \le \max \left\{D, B^6\right\}$
we are done. Hence, suppose otherwise that
![]() $\hat{L}\!\left(X_{t^{\prime}}\right) \in \left(B^6, \log g_{j+1}(n)\right]$
. Since the interval
$\hat{L}\!\left(X_{t^{\prime}}\right) \in \left(B^6, \log g_{j+1}(n)\right]$
. Since the interval
![]() $(B^6, \log g_{j+1}(n)]$
is completely covered by the union of the intervals
$(B^6, \log g_{j+1}(n)]$
is completely covered by the union of the intervals
![]() $[g_{j+2}, g_{j+1}]$
, …,
$[g_{j+2}, g_{j+1}]$
, …,
![]() $[g_{K}, g_{K-1}]$
, there must be an integer
$[g_{K}, g_{K-1}]$
, there must be an integer
![]() $j^{\prime}\ge j+1$
such that
$j^{\prime}\ge j+1$
such that
![]() $g_{j^{\prime}+1}(n) \leq \hat{L}\!\left(X_{t^{\prime}}\right) \leq g_{j^{\prime}}(n)$
. Also, notice
$g_{j^{\prime}+1}(n) \leq \hat{L}\!\left(X_{t^{\prime}}\right) \leq g_{j^{\prime}}(n)$
. Also, notice
 \begin{align*} \mathcal{R}_2\!\left(X_{t^{\prime}}\right) & \le \mathcal{R}_2(X_{t}) + O\!\left(\frac{n^{4/3}}{\log g_j(n)}\right) = O\!\left(n^{4/3}\right) + O\!\left(\sum_{k=0}^{j-1} \frac{n^{4/3}}{\log g_{k}(n)}\right) + O\!\left(\frac{n^{4/3}}{\log g_j(n)}\right) \\ &= O\!\left(n^{4/3}\right) + O\!\left(\sum_{k=0}^{j} \frac{n^{4/3}}{\log g_{k}(n)}\right) = O\!\left(n^{4/3}\right) + O\!\left(\sum_{k=0}^{j^{\prime}-1} \frac{n^{4/3}}{\log g_{k}(n)}\right). \end{align*}
\begin{align*} \mathcal{R}_2\!\left(X_{t^{\prime}}\right) & \le \mathcal{R}_2(X_{t}) + O\!\left(\frac{n^{4/3}}{\log g_j(n)}\right) = O\!\left(n^{4/3}\right) + O\!\left(\sum_{k=0}^{j-1} \frac{n^{4/3}}{\log g_{k}(n)}\right) + O\!\left(\frac{n^{4/3}}{\log g_j(n)}\right) \\ &= O\!\left(n^{4/3}\right) + O\!\left(\sum_{k=0}^{j} \frac{n^{4/3}}{\log g_{k}(n)}\right) = O\!\left(n^{4/3}\right) + O\!\left(\sum_{k=0}^{j^{\prime}-1} \frac{n^{4/3}}{\log g_{k}(n)}\right). \end{align*}
By taking at most K steps of induction, we obtain that there exist constants C and c such that with probability at least
![]() $\rho \,:\!=\, \prod_{i=0}^{K-1} \left(1 - \frac{c}{\log g_{i}(n)}\right),$
there exists a time
$\rho \,:\!=\, \prod_{i=0}^{K-1} \left(1 - \frac{c}{\log g_{i}(n)}\right),$
there exists a time
 \begin{equation*}t_{K} \leq \sum_{i=0}^{K-1} C \log g_i(n)\end{equation*}
\begin{equation*}t_{K} \leq \sum_{i=0}^{K-1} C \log g_i(n)\end{equation*}
that satisfies
![]() $ \hat{L}(X_{t_{K}}) \leq g_{K}(n) \leq B^6 $
and
$ \hat{L}(X_{t_{K}}) \leq g_{K}(n) \leq B^6 $
and
![]() $\mathcal{R}_2(X_{t_{K}}) = O\!\left(n^{4/3}\right)$
. Observe that
$\mathcal{R}_2(X_{t_{K}}) = O\!\left(n^{4/3}\right)$
. Observe that
![]() $t_{K}$
is a time when our goal has been achieved, so it only remains to show that
$t_{K}$
is a time when our goal has been achieved, so it only remains to show that
![]() $\rho = \Omega(1)$
and
$\rho = \Omega(1)$
and
![]() $t_{K} = O({\log}\ n)$
. The lower bound on
$t_{K} = O({\log}\ n)$
. The lower bound on
![]() $\rho$
follows from part (i) of Claim 4.5:
$\rho$
follows from part (i) of Claim 4.5:
 \begin{align*} \prod_{i=0}^{K-1} 1 - \frac{c}{\log g_{i}(n)} & \geq 1 - \frac{1.5 c}{\log g_{K-1}(n)} > 1 - \frac{1.5 c}{\log B^6} = \Omega(1). \end{align*}
\begin{align*} \prod_{i=0}^{K-1} 1 - \frac{c}{\log g_{i}(n)} & \geq 1 - \frac{1.5 c}{\log g_{K-1}(n)} > 1 - \frac{1.5 c}{\log B^6} = \Omega(1). \end{align*}
By noting that
![]() $K = O({\log}^*n)$
, we can also bound
$K = O({\log}^*n)$
, we can also bound
![]() $t_{K}$
since
$t_{K}$
since
![]() $ \sum_{i=0}^{K-1} C \log g_i(n)$
is at most
$ \sum_{i=0}^{K-1} C \log g_i(n)$
is at most
![]() $\log g_0(n) + (K-1)\log g_1(n) = O({\log}\ n)$
.
$\log g_0(n) + (K-1)\log g_1(n) = O({\log}\ n)$
.
Before proving Lemma 4.4 we provide the proof of Lemma 4.3.
Proof of Lemma 4.3. We start with part 1. Let
![]() $\mu_t \,:\!=\, {\mathbb{E}}[A(X_t) | \Lambda_t, X_t]$
,
$\mu_t \,:\!=\, {\mathbb{E}}[A(X_t) | \Lambda_t, X_t]$
,
![]() $\gamma_t\,:\!=\,\sqrt{\hat{L}(X_{t})} \cdot n^{2/3}$
, and
$\gamma_t\,:\!=\,\sqrt{\hat{L}(X_{t})} \cdot n^{2/3}$
, and
![]() $J_t\,:\!=\,[\mu_t - \gamma_t, \mu_t + \gamma_t]$
. Hoeffding’s inequality implies that
$J_t\,:\!=\,[\mu_t - \gamma_t, \mu_t + \gamma_t]$
. Hoeffding’s inequality implies that
Let
![]() $m \,:\!=\, \mu_t +\gamma_t$
,
$m \,:\!=\, \mu_t +\gamma_t$
,
![]() $G \sim G\!\left(m, \frac{q}{n}\right)$
and
$G \sim G\!\left(m, \frac{q}{n}\right)$
and
![]() $\hat{G} \sim G(A(X_t), p)$
. Then, the monotonicity of the largest component in a random graph implies that for any
$\hat{G} \sim G(A(X_t), p)$
. Then, the monotonicity of the largest component in a random graph implies that for any
![]() $\ell > 0$
$\ell > 0$
 \begin{align*} & {\mathbb{P}}\left[L_1(\hat{G}) > \ell \mid A(X_t) \in J_t\right] \\ & = \sum_{a \in J_t} {\mathbb{P}}\left[L_1(\hat{G}) > \ell\mid A(X_t) = a\right]{\mathbb{P}}\left[A(X_t) = a \mid A(X_t) \in J_t\right] \\ & \leq \sum_{a \in J_t} {\mathbb{P}}\left[L_1(\hat{G}) > \ell\mid A(X_t) = m\right] {\mathbb{P}}\left[A(X_t) = a \mid A(X_t) \in J_t\right] \\ & = {\mathbb{P}}[L_1(G) > \ell] \sum_{a \in J_t} {\mathbb{P}}[A(X_t) = a \mid A(X_t) \in J_t] \\ & = {\mathbb{P}}[L_1(G) > \ell]. \end{align*}
\begin{align*} & {\mathbb{P}}\left[L_1(\hat{G}) > \ell \mid A(X_t) \in J_t\right] \\ & = \sum_{a \in J_t} {\mathbb{P}}\left[L_1(\hat{G}) > \ell\mid A(X_t) = a\right]{\mathbb{P}}\left[A(X_t) = a \mid A(X_t) \in J_t\right] \\ & \leq \sum_{a \in J_t} {\mathbb{P}}\left[L_1(\hat{G}) > \ell\mid A(X_t) = m\right] {\mathbb{P}}\left[A(X_t) = a \mid A(X_t) \in J_t\right] \\ & = {\mathbb{P}}[L_1(G) > \ell] \sum_{a \in J_t} {\mathbb{P}}[A(X_t) = a \mid A(X_t) \in J_t] \\ & = {\mathbb{P}}[L_1(G) > \ell]. \end{align*}
We bound next
![]() ${\mathbb{P}}[L_1(G) > \ell]$
. For this, we rewrite
${\mathbb{P}}[L_1(G) > \ell]$
. For this, we rewrite
![]() $G\!\left(m, \frac{q}{n}\right)$
as
$G\!\left(m, \frac{q}{n}\right)$
as
![]() $G\!\left(m, \frac{1+\varepsilon}{m}\right)$
; since
$G\!\left(m, \frac{1+\varepsilon}{m}\right)$
; since
we have
 \begin{equation*}\varepsilon = m\cdot \frac{q}{n} - 1 = \left(q - 1 + \frac{q}{\sqrt{\hat{L}(X_{t})}}\right) \frac{\hat{L}(X_{t})}{n^{1/3}}.\end{equation*}
\begin{equation*}\varepsilon = m\cdot \frac{q}{n} - 1 = \left(q - 1 + \frac{q}{\sqrt{\hat{L}(X_{t})}}\right) \frac{\hat{L}(X_{t})}{n^{1/3}}.\end{equation*}
Thus,
 \begin{align*} \varepsilon^3\cdot m &= \left(q - 1 + \frac{q}{\sqrt{\hat{L}(X_{t})}}\right)^3 \frac{ \hat{L}(X_{t})^3}{n} \left(\hat{L}(X_{t}) n^{2/3} + \frac{n- \hat{L}(X_{t}) n^{2/3}}{q} + \sqrt{\hat{L}(X_{t})}n^{2/3}\right) \\ & \geq \left(q - 1 + \frac{q}{\sqrt{\hat{L}(X_{t})}}\right)^3 \cdot \frac{\hat{L}(X_{t})^3}{n} \cdot \frac{n}{q} \\ & \geq \frac{1}{q}\cdot \left((q-1)^3 \hat{L}(X_{t})^3 + q^3\sqrt{\hat{L}(X_{t})}^3\right)\\ & \geq q^2 \hat{L}(X_{t})^{3/2} \geq 100 \hat{L}(X_{t}), \end{align*}
\begin{align*} \varepsilon^3\cdot m &= \left(q - 1 + \frac{q}{\sqrt{\hat{L}(X_{t})}}\right)^3 \frac{ \hat{L}(X_{t})^3}{n} \left(\hat{L}(X_{t}) n^{2/3} + \frac{n- \hat{L}(X_{t}) n^{2/3}}{q} + \sqrt{\hat{L}(X_{t})}n^{2/3}\right) \\ & \geq \left(q - 1 + \frac{q}{\sqrt{\hat{L}(X_{t})}}\right)^3 \cdot \frac{\hat{L}(X_{t})^3}{n} \cdot \frac{n}{q} \\ & \geq \frac{1}{q}\cdot \left((q-1)^3 \hat{L}(X_{t})^3 + q^3\sqrt{\hat{L}(X_{t})}^3\right)\\ & \geq q^2 \hat{L}(X_{t})^{3/2} \geq 100 \hat{L}(X_{t}), \end{align*}
where the last inequality follows from the fact that
![]() $\hat{L}(X_{t}) > B$
, where
$\hat{L}(X_{t}) > B$
, where
![]() $B=B(q)$
is a sufficiently large constant.
$B=B(q)$
is a sufficiently large constant.
Since
![]() $\varepsilon^3\cdot m\geq1$
, Lemma 3.5 implies
$\varepsilon^3\cdot m\geq1$
, Lemma 3.5 implies
Let
![]() $c_1=2\sqrt{\frac{1+(q-1)\delta}{q(q-1)}}$
. The upper tail bound implies
$c_1=2\sqrt{\frac{1+(q-1)\delta}{q(q-1)}}$
. The upper tail bound implies
We show next that
![]() $2\varepsilon m + c_1 n^{2/3} \le \alpha L_1(X_t)$
for some
$2\varepsilon m + c_1 n^{2/3} \le \alpha L_1(X_t)$
for some
![]() $\alpha \in (0,1)$
.
$\alpha \in (0,1)$
.
 \begin{align*} &2\varepsilon m + c_1 n^{2/3} \\ = & 2\!\left(q - 1 + \frac{q}{\sqrt{\hat{L}(X_{t})}}\right) \frac{\hat{L}(X_{t})}{n^{1/3}} \left(\hat{L}(X_{t}) n^{2/3} + \frac{n-\hat{L}(X_{t}) n^{2/3}}{q} + \sqrt{\hat{L}(X_{t})}n^{2/3}\right) + c_1 n^{2/3}\\ = & \frac{2}{q} \left(q - 1 + \frac{q}{\sqrt{\hat{L}(X_{t})}}\right) \frac{\hat{L}(X_{t})}{n^{1/3}} \left[ n + \left( q - 1 + \frac{q}{\sqrt{\hat{L}(X_{t})}}\right) \hat{L}(X_{t}) n^{2/3} \right] + c_1 n^{2/3} \\ = & \frac{2}{q} \left(q - 1 + \frac{q}{\sqrt{\hat{L}(X_{t})}} + \frac{c_1q}{\hat{L}(X_{t})}\right) \hat{L}(X_{t}) n^{2/3} + \frac{2}{q} \left(q - 1 + \frac{q}{\sqrt{\hat{L}(X_{t})}}\right)^2 \hat{L}(X_{t})^2 n^{1/3} \\ \leq & \frac{2}{q} \left[ \delta\!\left(q - 1 + O\!\left(\hat{L}(X_{t})^{-1/2}\right) \right)^2 + \left(q - 1 + O\!\left(\hat{L}(X_{t})^{-1/2} \right)\right)\right] \hat{L}(X_{t}) n^{2/3}, \end{align*}
\begin{align*} &2\varepsilon m + c_1 n^{2/3} \\ = & 2\!\left(q - 1 + \frac{q}{\sqrt{\hat{L}(X_{t})}}\right) \frac{\hat{L}(X_{t})}{n^{1/3}} \left(\hat{L}(X_{t}) n^{2/3} + \frac{n-\hat{L}(X_{t}) n^{2/3}}{q} + \sqrt{\hat{L}(X_{t})}n^{2/3}\right) + c_1 n^{2/3}\\ = & \frac{2}{q} \left(q - 1 + \frac{q}{\sqrt{\hat{L}(X_{t})}}\right) \frac{\hat{L}(X_{t})}{n^{1/3}} \left[ n + \left( q - 1 + \frac{q}{\sqrt{\hat{L}(X_{t})}}\right) \hat{L}(X_{t}) n^{2/3} \right] + c_1 n^{2/3} \\ = & \frac{2}{q} \left(q - 1 + \frac{q}{\sqrt{\hat{L}(X_{t})}} + \frac{c_1q}{\hat{L}(X_{t})}\right) \hat{L}(X_{t}) n^{2/3} + \frac{2}{q} \left(q - 1 + \frac{q}{\sqrt{\hat{L}(X_{t})}}\right)^2 \hat{L}(X_{t})^2 n^{1/3} \\ \leq & \frac{2}{q} \left[ \delta\!\left(q - 1 + O\!\left(\hat{L}(X_{t})^{-1/2}\right) \right)^2 + \left(q - 1 + O\!\left(\hat{L}(X_{t})^{-1/2} \right)\right)\right] \hat{L}(X_{t}) n^{2/3}, \end{align*}
where in the last inequality we use the assumption that
![]() $\delta n^{1/3} \geq \hat{L}(X_{t})$
. For sufficiently small
$\delta n^{1/3} \geq \hat{L}(X_{t})$
. For sufficiently small
![]() $\delta$
and sufficiently large B,
$\delta$
and sufficiently large B,
![]() $\exists \ \alpha < 1$
such that
$\exists \ \alpha < 1$
such that
 \begin{equation*}\alpha > \frac{2}{q}\left[ \delta\!\left(q - 1 + \frac{2q}{B^{1/2}}\right)^2 + \left(q - 1 + \frac{2q}{B^{1/2}}\right)\right].\end{equation*}
\begin{equation*}\alpha > \frac{2}{q}\left[ \delta\!\left(q - 1 + \frac{2q}{B^{1/2}}\right)^2 + \left(q - 1 + \frac{2q}{B^{1/2}}\right)\right].\end{equation*}
Consequently,
![]() $ L_1\!\left(G\right) \leq 2\varepsilon m + c_1 n^{2/3} \leq \alpha L_1(X_t)$
with probability
$ L_1\!\left(G\right) \leq 2\varepsilon m + c_1 n^{2/3} \leq \alpha L_1(X_t)$
with probability
![]() $1 - \exp\big({-}\Omega\big(\hat{L}(X_{t}\big)\big)$
. If that is the case,
$1 - \exp\big({-}\Omega\big(\hat{L}(X_{t}\big)\big)$
. If that is the case,
![]() $L_1(X_{t+1}) \leq \max\left\{\alpha L_1(X_t), L_2(X_t)\right\} \,=\!:\, L^+$
. Therefore,
$L_1(X_{t+1}) \leq \max\left\{\alpha L_1(X_t), L_2(X_t)\right\} \,=\!:\, L^+$
. Therefore,
 \begin{align*} & {\mathbb{P}}\left[L_1(X_{t+1}) \leq L^+ \mid X_t, \Lambda_t\right] \\[3pt] & \geq {\mathbb{P}}\left[L_1(X_{t+1}) \leq L^+ \mid X_t, \Lambda_t , A(X_t) \in J_t\right] \cdot {\mathbb{P}}\left[A(X_t) \in J_t \mid X_t, \Lambda_t \right] \\[3pt] & \geq 1 - \exp\big({-}\Omega\big(\hat{L}(X_{t})\big)\big), \end{align*}
\begin{align*} & {\mathbb{P}}\left[L_1(X_{t+1}) \leq L^+ \mid X_t, \Lambda_t\right] \\[3pt] & \geq {\mathbb{P}}\left[L_1(X_{t+1}) \leq L^+ \mid X_t, \Lambda_t , A(X_t) \in J_t\right] \cdot {\mathbb{P}}\left[A(X_t) \in J_t \mid X_t, \Lambda_t \right] \\[3pt] & \geq 1 - \exp\big({-}\Omega\big(\hat{L}(X_{t})\big)\big), \end{align*}
which concludes the proof of part 1.
For part 2, note first that when the largest component is inactive, we have
![]() $L_1(X_{t+1}) \geq L_1(X_t)$
; hence, it is sufficient to show that
$L_1(X_{t+1}) \geq L_1(X_t)$
; hence, it is sufficient to show that
![]() $L_1(X_{t+1}) \leq L_1(X_t)$
with the desired probability.
$L_1(X_{t+1}) \leq L_1(X_t)$
with the desired probability.
Let
![]() $\mu^{\prime}_t \,:\!=\, {\mathbb{E}}\left[A(X_t) \mid \neg \Lambda_t, X_t\right] = \big(n- \hat{L}(X_{t}) n^{2/3} \big)q^{-1}$
,
$\mu^{\prime}_t \,:\!=\, {\mathbb{E}}\left[A(X_t) \mid \neg \Lambda_t, X_t\right] = \big(n- \hat{L}(X_{t}) n^{2/3} \big)q^{-1}$
,
![]() $\gamma^{\prime}_t\,:\!=\,\sqrt{\hat{L}(X_{t})} \cdot n^{2/3}$
, and
$\gamma^{\prime}_t\,:\!=\,\sqrt{\hat{L}(X_{t})} \cdot n^{2/3}$
, and
![]() $J^{\prime}_t \,:\!=\, [\mu^{\prime}_t - \gamma^{\prime}_t, \mu^{\prime}_t + \gamma^{\prime}_t]$
. By Hoeffding’s inequality,
$J^{\prime}_t \,:\!=\, [\mu^{\prime}_t - \gamma^{\prime}_t, \mu^{\prime}_t + \gamma^{\prime}_t]$
. By Hoeffding’s inequality,
Let
![]() $G\sim G(A(X_t), p)$
,
$G\sim G(A(X_t), p)$
,
![]() $m = \mu^{\prime}_t + \gamma^{\prime}_t$
and let
$m = \mu^{\prime}_t + \gamma^{\prime}_t$
and let
![]() $G^+ \sim G\!\left(\mu^{\prime}_t + \gamma^{\prime}_t, p\right) $
, By monotonicity of the largest component in a random graph,
$G^+ \sim G\!\left(\mu^{\prime}_t + \gamma^{\prime}_t, p\right) $
, By monotonicity of the largest component in a random graph,
Rewrite
![]() $G\!\left(\mu^{\prime}_t + \gamma^{\prime}_t, p\right)$
as
$G\!\left(\mu^{\prime}_t + \gamma^{\prime}_t, p\right)$
as
![]() $G\!\left(m, \frac{1 + \varepsilon}{m}\right)$
, where
$G\!\left(m, \frac{1 + \varepsilon}{m}\right)$
, where
 \begin{equation*}\varepsilon = \left(\frac{n - \hat{L}(X_{t}) n^{2/3}}{q} + \sqrt{\hat{L}(X_{t})} n^{2/3} \right) \cdot \frac{q}{n} - 1 = \left(\sqrt{\hat{L}(X_{t})}q -\hat{L}(X_{t}) \right) n^{-1/3}. \end{equation*}
\begin{equation*}\varepsilon = \left(\frac{n - \hat{L}(X_{t}) n^{2/3}}{q} + \sqrt{\hat{L}(X_{t})} n^{2/3} \right) \cdot \frac{q}{n} - 1 = \left(\sqrt{\hat{L}(X_{t})}q -\hat{L}(X_{t}) \right) n^{-1/3}. \end{equation*}
From this bound, applying Lemma 3.7 to
![]() $G^+$
, we obtain
$G^+$
, we obtain
Hence,
![]() ${\mathbb{E}}\left[L_1(G^+)^2\right] = O\!\left(n^{4/3}/\hat{L}(X_{t})\right)$
and by Markov’s inequality
${\mathbb{E}}\left[L_1(G^+)^2\right] = O\!\left(n^{4/3}/\hat{L}(X_{t})\right)$
and by Markov’s inequality
To conclude, we observe that
 \begin{align*} & {\mathbb{P}}[L_1(X_{t+1}) \leq L_1(X_t) \mid X_t, \neg\Lambda_t] \\ & \geq {\mathbb{P}}\left[L_1(G) \leq L_1(X_t) \mid X_t, \neg\Lambda_t, A(X_t) \in J^{\prime}_t\right] {\mathbb{P}}\left[A(X_t) \in J^{\prime}_t \mid X_t, \neg\Lambda_t\right] \\ & \geq \left(1 - e^{- \Omega\left( \hat{L}(X_{t}) \right) }\right) \left(1 - O\!\left(\frac{1}{\hat{L}(X_{t})^3} \right)\right) = 1 - O\!\left(\frac{1}{\hat{L}(X_{t})^3} \right), \end{align*}
\begin{align*} & {\mathbb{P}}[L_1(X_{t+1}) \leq L_1(X_t) \mid X_t, \neg\Lambda_t] \\ & \geq {\mathbb{P}}\left[L_1(G) \leq L_1(X_t) \mid X_t, \neg\Lambda_t, A(X_t) \in J^{\prime}_t\right] {\mathbb{P}}\left[A(X_t) \in J^{\prime}_t \mid X_t, \neg\Lambda_t\right] \\ & \geq \left(1 - e^{- \Omega\left( \hat{L}(X_{t}) \right) }\right) \left(1 - O\!\left(\frac{1}{\hat{L}(X_{t})^3} \right)\right) = 1 - O\!\left(\frac{1}{\hat{L}(X_{t})^3} \right), \end{align*}
as desired.
We are now ready to prove Lemma 4.4.
Proof of Lemma 4.4. Suppose
![]() $\mathcal{R}_2(X_0) \le D_1^2n^{4/3}$
for a constant
$\mathcal{R}_2(X_0) \le D_1^2n^{4/3}$
for a constant
![]() $D_1$
. Let
$D_1$
. Let
![]() $T^{\prime}\,:\!=\,B^{\prime}\log g(n)$
, where B
′ is a constant such that
$T^{\prime}\,:\!=\,B^{\prime}\log g(n)$
, where B
′ is a constant such that
 $B^{\prime} \log g(n)= 2q \log_{1/\alpha}\left(\frac{ g(n)}{B \big({\log} g(n)\big)^8}\right)$
and
$B^{\prime} \log g(n)= 2q \log_{1/\alpha}\left(\frac{ g(n)}{B \big({\log} g(n)\big)^8}\right)$
and
![]() $\alpha \,:\!=\, \alpha(B, q, \delta)$
is the constant from Lemma 4.3. Let
$\alpha \,:\!=\, \alpha(B, q, \delta)$
is the constant from Lemma 4.3. Let
![]() $\hat{T}$
be the first time
$\hat{T}$
be the first time
where D is a large constant we choose later. Let
![]() $T\,:\!=\,T^{\prime}\wedge \hat{T}$
, where the operator
$T\,:\!=\,T^{\prime}\wedge \hat{T}$
, where the operator
![]() $\wedge$
takes the minimum of the two numbers. Define e(t) as the number of steps up to time t in which the largest component of the configuration is activated.
$\wedge$
takes the minimum of the two numbers. Define e(t) as the number of steps up to time t in which the largest component of the configuration is activated.
To facilitate the notation, we define the following events. (The constants C and
![]() $\alpha$
are those from Lemmas 4.3 and 4.2, respectively).
$\alpha$
are those from Lemmas 4.3 and 4.2, respectively).
-
1. Let
 $H_i $
denote
$H_i $
denote
 $\hat{L}(X_{i}) > \max\big\{ B \big({\log} g(n)\big)^8, D\big\}$
;
$\hat{L}(X_{i}) > \max\big\{ B \big({\log} g(n)\big)^8, D\big\}$
; -
2. Let
 $F_i $
denote
$F_i $
denote
 $\mathcal{R}_2(X_{i}) \leq \mathcal{R}_2(X_{i-1}) + C n^{4/3}\hat{L}(X_{i-1})^{-1/2}$
; let us assume
$\mathcal{R}_2(X_{i}) \leq \mathcal{R}_2(X_{i-1}) + C n^{4/3}\hat{L}(X_{i-1})^{-1/2}$
; let us assume
 $F_0$
occurs;
$F_0$
occurs; -
3. Let
 $F^{\prime}_i$
denote
$F^{\prime}_i$
denote
 $\mathcal{R}_2(X_{i}) \leq \mathcal{R}_2(X_{i-1}) + C n^{4/3} \big({\log} g(n)\big)^{-4} B^{-1/2}$
; again, we assume
$\mathcal{R}_2(X_{i}) \leq \mathcal{R}_2(X_{i-1}) + C n^{4/3} \big({\log} g(n)\big)^{-4} B^{-1/2}$
; again, we assume
 $F^{\prime}_0$
occurs;
$F^{\prime}_0$
occurs; -
4. Let
 $Q_i$
denote
$Q_i$
denote
 $\hat{L}(X_{i}) \leq \max\big\{\alpha^{e(i)}\hat{L}(X_{0}), D \big\}$
;
$\hat{L}(X_{i}) \leq \max\big\{\alpha^{e(i)}\hat{L}(X_{0}), D \big\}$
; -
5. Let
 $Base_i$
be the intersection of
$Base_i$
be the intersection of
 $\big\{F^{\prime}_0, Q_0, H_0\big\}, ..., \big\{F^{\prime}_{i-1}, Q_{i-1}, H_{i-1}\big\},$
and
$\big\{F^{\prime}_0, Q_0, H_0\big\}, ..., \big\{F^{\prime}_{i-1}, Q_{i-1}, H_{i-1}\big\},$
and
 $ \big\{F^{\prime}_i, Q_i\big\}$
.
$ \big\{F^{\prime}_i, Q_i\big\}$
.
By induction, we find a lower bound for the probability of
![]() $Base_T$
. For the base case, note that
$Base_T$
. For the base case, note that
![]() ${\mathbb{P}}[Base_0] $
${\mathbb{P}}[Base_0] $
![]() $= 1$
by assumption. Next we show
$= 1$
by assumption. Next we show
If
![]() $T \leq i$
, then
$T \leq i$
, then
![]() $Base_{i\wedge T} = Base_{ T} = Base_{i+1\wedge T}$
, so the induction holds. If
$Base_{i\wedge T} = Base_{ T} = Base_{i+1\wedge T}$
, so the induction holds. If
![]() $T > i$
, then we have
$T > i$
, then we have
![]() $H_i$
.
$H_i$
.
By the induction hypothesis
![]() $F^{\prime}_1, F^{\prime}_2, ..., F^{\prime}_{i-1}$
,
$F^{\prime}_1, F^{\prime}_2, ..., F^{\prime}_{i-1}$
,
Moreover, since
![]() $i < T \leq T^{\prime} = B^{\prime} \log g(n)$
and
$i < T \leq T^{\prime} = B^{\prime} \log g(n)$
and
![]() $\mathcal{R}_2(X_0) \le D_1^2n^{4/3}$
, we have
$\mathcal{R}_2(X_0) \le D_1^2n^{4/3}$
, we have
Given
![]() $\mathcal{R}_2(X_{i}) = O\!\left(n^{4/3}\right)$
and
$\mathcal{R}_2(X_{i}) = O\!\left(n^{4/3}\right)$
and
![]() $H_i$
, Lemma 4.2 implies that
$H_i$
, Lemma 4.2 implies that
![]() $F_{i+1}$
occurs with probability
$F_{i+1}$
occurs with probability
In addition, note that
![]() $F_{i+1} \cup H_i $
leads to
$F_{i+1} \cup H_i $
leads to
![]() $F^{\prime}_{i+1}$
. Let
$F^{\prime}_{i+1}$
. Let
![]() $\unicode{x1D7D9}(\Lambda_t)$
be the indicator function for the event
$\unicode{x1D7D9}(\Lambda_t)$
be the indicator function for the event
![]() $\Lambda_t$
. Given
$\Lambda_t$
. Given
![]() $H_i, Q_i$
and
$H_i, Q_i$
and
![]() $\mathcal{R}_2(X_{i}) = O\!\left(n^{4/3}\right)$
, Lemma 4.3 implies
$\mathcal{R}_2(X_{i}) = O\!\left(n^{4/3}\right)$
, Lemma 4.3 implies
with probability at least
![]() $1 - O\big(\hat{L}(X_{t})^{-3}\big) = 1 - O\!\left( \big({\log} g(n)\big)^{-24} \right)$
.
$1 - O\big(\hat{L}(X_{t})^{-3}\big) = 1 - O\!\left( \big({\log} g(n)\big)^{-24} \right)$
.
Dividing equation (5) by
![]() $n^{2/3}$
, we obtain
$n^{2/3}$
, we obtain
![]() $Q_{i+1}$
for large enough D. In particular, we can choose D to be
$Q_{i+1}$
for large enough D. In particular, we can choose D to be
![]() $D_1 + 2$
. A union bound then implies
$D_1 + 2$
. A union bound then implies
The probability for
![]() $Base_{T}$
can then be bounded as follows:
$Base_{T}$
can then be bounded as follows:
 \begin{equation*}{\mathbb{P}}[Base_{T}] \geq \prod_{i=0}^{T-1} {\mathbb{P}}\big[Base_{i+1 \wedge T} \mid Base_{i \wedge T}\big]= \prod_{i=0}^{T-1} 1 - O\!\left( \big({\log} g(n)\big)^{-4} \right)= 1 - O\Big( \big({\log} g(n)\big)^{-3} \Big).\end{equation*}
\begin{equation*}{\mathbb{P}}[Base_{T}] \geq \prod_{i=0}^{T-1} {\mathbb{P}}\big[Base_{i+1 \wedge T} \mid Base_{i \wedge T}\big]= \prod_{i=0}^{T-1} 1 - O\!\left( \big({\log} g(n)\big)^{-4} \right)= 1 - O\Big( \big({\log} g(n)\big)^{-3} \Big).\end{equation*}
Next, let us assume
![]() $Base_T$
. Then we have
$Base_T$
. Then we have
Notice that if
![]() $T = \hat{T}$
then the proof is complete. Consequently, it suffices to show
$T = \hat{T}$
then the proof is complete. Consequently, it suffices to show
![]() $\hat{T} \le T^{\prime}$
with probability at least
$\hat{T} \le T^{\prime}$
with probability at least
![]() $1 - g(n)^{-\Omega(1)}$
.
$1 - g(n)^{-\Omega(1)}$
.
Observe that
![]() $K \,:\!=\, e(T^{\prime})$
is a binomial random variable
$K \,:\!=\, e(T^{\prime})$
is a binomial random variable
![]() $Bin\!\left(T^{\prime}, 1/q\right)$
, whose expectation is
$Bin\!\left(T^{\prime}, 1/q\right)$
, whose expectation is
![]() $\frac{T^{\prime}}{q} = \frac{B^{\prime}}{q} \log g(n)$
. By Chernoff bound
$\frac{T^{\prime}}{q} = \frac{B^{\prime}}{q} \log g(n)$
. By Chernoff bound
If indeed
![]() $T = T^{\prime}$
and
$T = T^{\prime}$
and
![]() $ K \geq \frac{B^{\prime}}{2q} \log g(n)$
, then the event
$ K \geq \frac{B^{\prime}}{2q} \log g(n)$
, then the event
![]() $Q_T$
implies
$Q_T$
implies
 \begin{equation*}\hat{L}(X_{T}) < \alpha^{e(T)} \hat{L}(X_{0}) \leq \alpha^{\log_{\alpha}\left(\frac{B \big({\log} g(n)\big)^8}{g(n)}\right)} \hat{L}(X_{0})= \frac{B \big({\log} g(n)\big)^8}{g(n)} \hat{L}(X_{0}) \leq B \big({\log} g(n)\big)^8,\end{equation*}
\begin{equation*}\hat{L}(X_{T}) < \alpha^{e(T)} \hat{L}(X_{0}) \leq \alpha^{\log_{\alpha}\left(\frac{B \big({\log} g(n)\big)^8}{g(n)}\right)} \hat{L}(X_{0})= \frac{B \big({\log} g(n)\big)^8}{g(n)} \hat{L}(X_{0}) \leq B \big({\log} g(n)\big)^8,\end{equation*}
which leads to
![]() $\hat{T} \le T$
. Therefore,
$\hat{T} \le T$
. Therefore,
as desired.
Proof of Claim 4.5. We first show the following inequality:
Note that by direction computation
From the definition of K, we know that
![]() $g_j(n) > B^6$
for all
$g_j(n) > B^6$
for all
![]() $j < K$
. Hence,
$j < K$
. Hence,
![]() $\log B < \log g_j(n)^{1/6}$
. In addition, recall that B is such that
$\log B < \log g_j(n)^{1/6}$
. In addition, recall that B is such that
![]() $\forall\,x \geq B^6$
, we have
$\forall\,x \geq B^6$
, we have
![]() $x \geq ({\log} x)^{48}$
; therefore,
$x \geq ({\log} x)^{48}$
; therefore,
![]() $g_j(n) \geq \big({\log} g_j(n)\big)^{48}$
. Then,
$g_j(n) \geq \big({\log} g_j(n)\big)^{48}$
. Then,
![]() $\log \big({\log} g_j(n)\big)^8 \le \log g_j(n)^{1/6}$
. Putting all these together,
$\log \big({\log} g_j(n)\big)^8 \le \log g_j(n)^{1/6}$
. Putting all these together,
 \begin{equation*} \begin{split} \frac{1.5 \big({\log} B + \log \big({\log} g_j(n)\big)^8\big) + \log g_j(n)}{\log g_j(n) \log g_{j+1}(n)} & \leq \frac{1.5 \big(\frac{1}{6}\log g_j(n) + \frac{1}{6} \log g_j(n)\big) + \log g_j(n)}{\log g_j(n) \log g_{j+1}(n)} \\ & = \frac{ 1.5 \log g_j(n)}{\log g_j(n) \log g_{j+1}(n)} = \frac{ 1.5 }{ \log g_{j+1}(n)} \end{split} \end{equation*}
\begin{equation*} \begin{split} \frac{1.5 \big({\log} B + \log \big({\log} g_j(n)\big)^8\big) + \log g_j(n)}{\log g_j(n) \log g_{j+1}(n)} & \leq \frac{1.5 \big(\frac{1}{6}\log g_j(n) + \frac{1}{6} \log g_j(n)\big) + \log g_j(n)}{\log g_j(n) \log g_{j+1}(n)} \\ & = \frac{ 1.5 \log g_j(n)}{\log g_j(n) \log g_{j+1}(n)} = \frac{ 1.5 }{ \log g_{j+1}(n)} \end{split} \end{equation*}
The proof of part (i) is inductive. The base case (
![]() $i=0$
) holds trivially. For the inductive step note that
$i=0$
) holds trivially. For the inductive step note that
 \begin{equation*} \begin{split} \prod_{i=0}^{j+1} \left(1 - \frac{c}{\log g_{i}(n)}\right) & = \left(1 - \frac{c}{\log g_{j+1}(n)}\right) \prod_{i=0}^{j} \left(1 - \frac{c}{\log g_{i}(n)}\right) \\[3pt] & \geq \left(1 - \frac{c}{\log g_{j+1}(n)}\right) \left(1 - \frac{1.5 c}{\log g_j(n)} \right) \\[3pt] & \geq 1 - c\!\left(\frac{1.5}{\log g_j(n)} + \frac{1}{\log g_{j+1}(n)}\right) \\[3pt] & \geq 1 - \frac{ 1.5 c }{ \log g_{j+1}(n)}, \end{split} \end{equation*}
\begin{equation*} \begin{split} \prod_{i=0}^{j+1} \left(1 - \frac{c}{\log g_{i}(n)}\right) & = \left(1 - \frac{c}{\log g_{j+1}(n)}\right) \prod_{i=0}^{j} \left(1 - \frac{c}{\log g_{i}(n)}\right) \\[3pt] & \geq \left(1 - \frac{c}{\log g_{j+1}(n)}\right) \left(1 - \frac{1.5 c}{\log g_j(n)} \right) \\[3pt] & \geq 1 - c\!\left(\frac{1.5}{\log g_j(n)} + \frac{1}{\log g_{j+1}(n)}\right) \\[3pt] & \geq 1 - \frac{ 1.5 c }{ \log g_{j+1}(n)}, \end{split} \end{equation*}
where the last inequality follows from (6).
For part (ii) we also use induction. The base case (
![]() $i=0$
) can be checked straightforwardly. For the inductive step,
$i=0$
) can be checked straightforwardly. For the inductive step,
 \begin{equation*} \begin{split} \sum_{i=0}^{j+1} \frac{1}{\log g_i(n)} & \leq \frac{1}{\log g_{j+1}(n)} + \sum_{i=0}^{j} \frac{1}{\log g_i(n)} \leq \frac{1}{\log g_{j+1}(n)} + \frac{1.5}{\log g_j(n)} \leq \frac{1.5}{\log g_i(n)}, \end{split} \end{equation*}
\begin{equation*} \begin{split} \sum_{i=0}^{j+1} \frac{1}{\log g_i(n)} & \leq \frac{1}{\log g_{j+1}(n)} + \sum_{i=0}^{j} \frac{1}{\log g_i(n)} \leq \frac{1}{\log g_{j+1}(n)} + \frac{1.5}{\log g_j(n)} \leq \frac{1.5}{\log g_i(n)}, \end{split} \end{equation*}
where the last inequality follows from (6).
5. Coupling to the same component structure: proofs
In this section we provide the proofs of Lemmas 2.8, 2.9, 2.10 and 2.11.
5.1 Continuation of the burn-in phase: proof of Lemma 2.8
Recall that for a random-cluster configuration X, let A(X) denote the random variable corresponding to the number of vertices activated by step (i) of the CM dynamics from X.
Proof of Lemma 2.8. We show that there exist suitable constants C,
![]() $D > 0$
and
$D > 0$
and
![]() $\alpha \in (0,1)$
such that if
$\alpha \in (0,1)$
such that if
![]() $\mathcal{R}_1(X_t)\le C n^{4/3}$
and
$\mathcal{R}_1(X_t)\le C n^{4/3}$
and
![]() $\widetilde{\mathcal{R}}_\omega(X_t) > Dn^{4/3}\omega (n)^{-1/2}$
, then
$\widetilde{\mathcal{R}}_\omega(X_t) > Dn^{4/3}\omega (n)^{-1/2}$
, then
with probability
![]() $\rho = \Omega(1)$
. This implies that we can maintain (7)–(8) for T steps with probability
$\rho = \Omega(1)$
. This implies that we can maintain (7)–(8) for T steps with probability
![]() $\rho^T$
. Precisely, if we let
$\rho^T$
. Precisely, if we let
 \begin{align*} \tau_1 &= \min \left\{t > 0\,:\, \mathcal{R}_1(X_{t}) > C n^{4/3}\right\}, \\ \tau_2 &= \min \left\{t > 0\,:\,\widetilde{\mathcal{R}}_\omega(X_{t}) > (1-\alpha) \widetilde{\mathcal{R}}_\omega(X_{t-1})\right\}, \\ T &= \min \left\{ \tau_1,\tau_2,c\log \omega (n)\right\}, \end{align*}
\begin{align*} \tau_1 &= \min \left\{t > 0\,:\, \mathcal{R}_1(X_{t}) > C n^{4/3}\right\}, \\ \tau_2 &= \min \left\{t > 0\,:\,\widetilde{\mathcal{R}}_\omega(X_{t}) > (1-\alpha) \widetilde{\mathcal{R}}_\omega(X_{t-1})\right\}, \\ T &= \min \left\{ \tau_1,\tau_2,c\log \omega (n)\right\}, \end{align*}
where the constant
![]() $c>0$
is chosen such that
$c>0$
is chosen such that
![]() $(1-\alpha)^{c\log \omega (n)} = O(\omega (n)^{-1/2})$
, then
$(1-\alpha)^{c\log \omega (n)} = O(\omega (n)^{-1/2})$
, then
![]() $T = c\log \omega (n)$
with probability
$T = c\log \omega (n)$
with probability
![]() $\rho^{c \log \omega (n)}$
. (Note that
$\rho^{c \log \omega (n)}$
. (Note that
![]() $\rho^{c \log \omega (n)}= {\omega (n)}^{-\beta}$
for a suitable constant
$\rho^{c \log \omega (n)}= {\omega (n)}^{-\beta}$
for a suitable constant
![]() $\beta > 0$
.) Hence,
$\beta > 0$
.) Hence,
![]() $\mathcal{R}_1(X_T) = O\!\left(n^{4/3}\right)$
and
$\mathcal{R}_1(X_T) = O\!\left(n^{4/3}\right)$
and
The lemma then follows from the fact that
![]() $I(X_T) = \Omega(n)$
with probability
$I(X_T) = \Omega(n)$
with probability
![]() $1-o(1)$
by Lemma 3.2 and a union bound.
$1-o(1)$
by Lemma 3.2 and a union bound.
To establish (7)–(8), let
![]() $\mathcal{H}^1_t$
be the event that
$\mathcal{H}^1_t$
be the event that
![]() $A(X_t) \in \left[n/q - \delta n^{2/3},n/q + \delta n^{2/3}\right]$
, where
$A(X_t) \in \left[n/q - \delta n^{2/3},n/q + \delta n^{2/3}\right]$
, where
![]() $\delta > 0$
is a constant. By Hoeffding’s inequality, for a suitable
$\delta > 0$
is a constant. By Hoeffding’s inequality, for a suitable
![]() $\delta > 0$
,
$\delta > 0$
,
![]() ${\mathbb{P}}[\mathcal{H}^1_t] \ge 1 - \frac{1}{8q^2}$
since
${\mathbb{P}}[\mathcal{H}^1_t] \ge 1 - \frac{1}{8q^2}$
since
![]() $\mathcal{R}_1(X_t) = O\!\left(n^{4/3}\right)$
. Let
$\mathcal{R}_1(X_t) = O\!\left(n^{4/3}\right)$
. Let
![]() $K_t$
denote the subgraph induced on the inactivated vertices at the step t. Observe that
$K_t$
denote the subgraph induced on the inactivated vertices at the step t. Observe that
![]() ${\mathbb{E}}\big[\widetilde{\mathcal{R}}_\omega(K_t)\big] = \left(1-\frac{1}{q}\right)\widetilde{\mathcal{R}}_\omega(X_{t})$
. Similarly,
${\mathbb{E}}\big[\widetilde{\mathcal{R}}_\omega(K_t)\big] = \left(1-\frac{1}{q}\right)\widetilde{\mathcal{R}}_\omega(X_{t})$
. Similarly,
![]() ${\mathbb{E}}\big[\mathcal{R}_1(K_t) - \widetilde{\mathcal{R}}_\omega(K_t)\big] = \left(1-\frac{1}{q}\right) \big(\mathcal{R}_1(X_{t}) - \widetilde{\mathcal{R}}_\omega(X_{t+1})\big)$
. Hence, by Markov’s inequality and independence between activation of each component, with probability at least
${\mathbb{E}}\big[\mathcal{R}_1(K_t) - \widetilde{\mathcal{R}}_\omega(K_t)\big] = \left(1-\frac{1}{q}\right) \big(\mathcal{R}_1(X_{t}) - \widetilde{\mathcal{R}}_\omega(X_{t+1})\big)$
. Hence, by Markov’s inequality and independence between activation of each component, with probability at least
![]() $1/4q^2$
, the activation sub-step is such that
$1/4q^2$
, the activation sub-step is such that
![]() $G_u$
satisfies
$G_u$
satisfies
and
We denote this event by
![]() $\mathcal{H}^2_t$
. It follows by a union bound that
$\mathcal{H}^2_t$
. It follows by a union bound that
![]() $\mathcal{H}^1_t$
and
$\mathcal{H}^1_t$
and
![]() $\mathcal{H}^2_t$
happen simultaneously with probability at least
$\mathcal{H}^2_t$
happen simultaneously with probability at least
![]() $1/8q^2$
. We assume that this is indeed the case and proceed to discuss the percolation sub-step.
$1/8q^2$
. We assume that this is indeed the case and proceed to discuss the percolation sub-step.
Lemma 3.10 implies that there exists
![]() $C_1 > 0$
such that with probability
$C_1 > 0$
such that with probability
![]() $99/100$
,
$99/100$
,
Hence,
where the last inequality holds for a suitable constant
![]() $\alpha \in (0,1)$
and a sufficiently large D since
$\alpha \in (0,1)$
and a sufficiently large D since
![]() $\widetilde{\mathcal{R}}_\omega(X_t) > Dn^{4/3}\omega (n)^{-1/2}$
.
$\widetilde{\mathcal{R}}_\omega(X_t) > Dn^{4/3}\omega (n)^{-1/2}$
.
On the other hand, Lemma 3.9 implies
![]() ${\mathbb{E}}\left[\mathcal{R}_1\left(G\!\left(A(X_t), \frac{q}{n}\right)\right)\right] = O\!\left(n^{4/3}\right)$
. By Markov’s inequality, there exists
${\mathbb{E}}\left[\mathcal{R}_1\left(G\!\left(A(X_t), \frac{q}{n}\right)\right)\right] = O\!\left(n^{4/3}\right)$
. By Markov’s inequality, there exists
![]() $C_2$
such that, with probability
$C_2$
such that, with probability
![]() $99/100$
,
$99/100$
,
For large enough C,
 \begin{align*} \mathcal{R}_1(X_{t+1}) &\le \mathcal{R}_1(K_t) + \mathcal{R}_1\left(G\!\left(A(X_t), \frac{q}{n}\right)\right) \le \left( 1- \frac{1}{2q} \right)\mathcal{R}_1(X_{t}) + \mathcal{R}_1\left(G\!\left(A(X_t), \frac{q}{n}\right)\right) \\ &\le \left( 1- \frac{1}{2q} \right) Cn^{4/3} + C_2n^{4/3} \le Cn^{4/3} \end{align*}
\begin{align*} \mathcal{R}_1(X_{t+1}) &\le \mathcal{R}_1(K_t) + \mathcal{R}_1\left(G\!\left(A(X_t), \frac{q}{n}\right)\right) \le \left( 1- \frac{1}{2q} \right)\mathcal{R}_1(X_{t}) + \mathcal{R}_1\left(G\!\left(A(X_t), \frac{q}{n}\right)\right) \\ &\le \left( 1- \frac{1}{2q} \right) Cn^{4/3} + C_2n^{4/3} \le Cn^{4/3} \end{align*}
Finally, it follows from a union bound that (7) and (8) hold simultaneously with probability at least
![]() $\frac{98}{100\cdot 8q^2}$
.
$\frac{98}{100\cdot 8q^2}$
.
5.2 Coupling to the same large component structure: proof of Lemma 2.9
To prove Lemma 2.9, we use a local limit theorem to construct a two-step coupling of the CM dynamics that reaches two configurations with the same large component structure. The construction of Markov chain couplings using local limit theorems is not common (see [Reference Long, Nachmias, Ning and Peres24] for another example), but it appears to be a powerful technique that may have other interesting applications. We provide next a brief introduction to local limit theorems.
Local limit theorem. Let m be an integer. Let
![]() $c_1 \le \dots \le c_m$
be integers and for
$c_1 \le \dots \le c_m$
be integers and for
![]() $i=1,\dots,m$
, let
$i=1,\dots,m$
, let
![]() $X_i$
be the random variable that is equal to
$X_i$
be the random variable that is equal to
![]() $c_i$
with probability
$c_i$
with probability
![]() $r \in (0,1)$
, and it is zero otherwise. Let us assume that
$r \in (0,1)$
, and it is zero otherwise. Let us assume that
![]() $X_1, \dots, X_m$
are independent random variables. Let
$X_1, \dots, X_m$
are independent random variables. Let
![]() $S_m = \sum_{i=1}^m X_i$
,
$S_m = \sum_{i=1}^m X_i$
,
![]() $\mu_m = {\mathbb{E}}[S_m]$
and
$\mu_m = {\mathbb{E}}[S_m]$
and
![]() $\sigma_m^2 = {\textrm{Var}}(S_m)$
. We say that a local limit theorem holds for
$\sigma_m^2 = {\textrm{Var}}(S_m)$
. We say that a local limit theorem holds for
![]() $S_m$
if for every integer
$S_m$
if for every integer
![]() $a \in \mathbb{Z}$
:
$a \in \mathbb{Z}$
:
We prove, under some conditions, a local limit theorem that applies to the random variables corresponding to the number of active vertices from small components. Recall that for an increasing positive function g and each integer
![]() $k \ge 0$
, we defined the intervals
$k \ge 0$
, we defined the intervals
 \begin{equation*}\mathcal{I}_k = \left[\frac{\vartheta m^{2/3}}{2 g(m)^{2^k}},\frac{\vartheta m^{2/3}}{g(m)^{2^k}}\right],\end{equation*}
\begin{equation*}\mathcal{I}_k = \left[\frac{\vartheta m^{2/3}}{2 g(m)^{2^k}},\frac{\vartheta m^{2/3}}{g(m)^{2^k}}\right],\end{equation*}
where
![]() $\vartheta>0$
is a fixed large constant.
$\vartheta>0$
is a fixed large constant.
Theorem 5.1. Let m be an integer. Let
![]() $c_1 \le \dots \le c_m$
be integers, and suppose
$c_1 \le \dots \le c_m$
be integers, and suppose
![]() $X_1, ..., X_m$
are independent random variables such that
$X_1, ..., X_m$
are independent random variables such that
![]() $X_i$
is equal to
$X_i$
is equal to
![]() $c_i$
with probability
$c_i$
with probability
![]() $r \in (0,1)$
, and
$r \in (0,1)$
, and
![]() $X_i$
is zero otherwise. Let
$X_i$
is zero otherwise. Let
![]() $g\,:\,\mathbb{N} \rightarrow \mathbb{R}$
be an increasing positive function such that
$g\,:\,\mathbb{N} \rightarrow \mathbb{R}$
be an increasing positive function such that
![]() $g(m) \rightarrow \infty$
and
$g(m) \rightarrow \infty$
and
![]() $g(m)=o({\log} m)$
. Suppose
$g(m)=o({\log} m)$
. Suppose
![]() $c_m = O\!\left(m^{2/3}g(m)^{-1}\right)$
,
$c_m = O\!\left(m^{2/3}g(m)^{-1}\right)$
,
![]() $\sum_{i=1}^m c_i^2 = O\!\left(m^{4/3}g(m)^{-1/2}\right)$
and
$\sum_{i=1}^m c_i^2 = O\!\left(m^{4/3}g(m)^{-1/2}\right)$
and
![]() $c_i = 1$
for all
$c_i = 1$
for all
![]() $i \le \rho m$
, where
$i \le \rho m$
, where
![]() $\rho \in (0,1)$
is independent of m. Let
$\rho \in (0,1)$
is independent of m. Let
![]() $\ell = \ell(m, g) > 0$
be the smallest integer such that
$\ell = \ell(m, g) > 0$
be the smallest integer such that
![]() $m^{2/3}g(m)^{-2^\ell} = o\!\left(m^{1/4}\right)$
. If for all
$m^{2/3}g(m)^{-2^\ell} = o\!\left(m^{1/4}\right)$
. If for all
![]() $1\le k \le \ell$
, we have
$1\le k \le \ell$
, we have
![]() $\left|\left\{i\,:\,c_i \in \mathcal{I}_k(g )\right\}\right| = \Omega\!\left(g(m)^{3\cdot2^{k-1}}\right)$
, then a local limit theorem holds for
$\left|\left\{i\,:\,c_i \in \mathcal{I}_k(g )\right\}\right| = \Omega\!\left(g(m)^{3\cdot2^{k-1}}\right)$
, then a local limit theorem holds for
![]() $S_m = \sum_{i=1}^m X_i$
.
$S_m = \sum_{i=1}^m X_i$
.
Theorem 5.1 follows from a general local limit theorem proved in [Reference Mukhin28]; a proof is given in Appendix A. We provide next the proof of Lemma 2.9.
Proof of Lemma 2.9. First, both
![]() $\{X_t\}$
,
$\{X_t\}$
,
![]() $\{Y_t\}$
perform one independent CM step from the initial configurations
$\{Y_t\}$
perform one independent CM step from the initial configurations
![]() $X_0$
,
$X_0$
,
![]() $Y_0$
. We start by establishing that
$Y_0$
. We start by establishing that
![]() $X_1$
and
$X_1$
and
![]() $Y_1$
preserve the structural properties assumed for
$Y_1$
preserve the structural properties assumed for
![]() $X_0$
and
$X_0$
and
![]() $Y_0$
.
$Y_0$
.
By assumption
![]() $\mathcal{R}_1(X_{0}) = O\!\left(n^{4/3}\right)$
, so Hoeffding’s inequality implies that the number of activated vertices from
$\mathcal{R}_1(X_{0}) = O\!\left(n^{4/3}\right)$
, so Hoeffding’s inequality implies that the number of activated vertices from
![]() $X_0$
is such that
$X_0$
is such that
with probability
![]() $\Omega(1)$
. Then, the percolation step is distributed as a
$\Omega(1)$
. Then, the percolation step is distributed as a
random graph, with
![]() $|\lambda| = O(1)$
with probability
$|\lambda| = O(1)$
with probability
![]() $\Omega(1)$
. Conditioning on this event, from Lemma 3.2 we obtain that
$\Omega(1)$
. Conditioning on this event, from Lemma 3.2 we obtain that
![]() $I(X_1)=\Omega(n)$
w.h.p. Moreover, from Lemma 3.9 and Markov’s inequality we obtain that
$I(X_1)=\Omega(n)$
w.h.p. Moreover, from Lemma 3.9 and Markov’s inequality we obtain that
![]() $\mathcal{R}_1(X_1) = O\!\left(n^{4/3}\right)$
with probability at least
$\mathcal{R}_1(X_1) = O\!\left(n^{4/3}\right)$
with probability at least
![]() $99/100$
and from Lemma 3.10 that
$99/100$
and from Lemma 3.10 that
![]() $\widetilde{\mathcal{R}}_\omega(X_1) = O\big(n^{4/3}{\omega (n)}^{-1/2}\big)$
also with probability at least
$\widetilde{\mathcal{R}}_\omega(X_1) = O\big(n^{4/3}{\omega (n)}^{-1/2}\big)$
also with probability at least
![]() $99/100$
.
$99/100$
.
We show next that
![]() $X_1$
and
$X_1$
and
![]() $Y_1$
, in addition to preserving the structural properties of
$Y_1$
, in addition to preserving the structural properties of
![]() $X_0$
and
$X_0$
and
![]() $Y_0$
, also have many connected components with sizes in certain carefully chosen intervals. This fact will be crucial in the design of our coupling. When
$Y_0$
, also have many connected components with sizes in certain carefully chosen intervals. This fact will be crucial in the design of our coupling. When
![]() $A(X_0) \in I$
, by Lemmas 3.11 and 3.12 and a union bound, for all integer
$A(X_0) \in I$
, by Lemmas 3.11 and 3.12 and a union bound, for all integer
![]() $k \ge 0$
such that
$k \ge 0$
such that
![]() $n^{2/3}\omega (n)^{-2^k} \rightarrow \infty$
,
$n^{2/3}\omega (n)^{-2^k} \rightarrow \infty$
,
![]() $N_{k}(X_1, \omega) = \Omega(\omega (n)^{3 \cdot 2^{k-1}})$
w.h.p. (Recall, that
$N_{k}(X_1, \omega) = \Omega(\omega (n)^{3 \cdot 2^{k-1}})$
w.h.p. (Recall, that
![]() $N_{k}(X_1, \omega)$
denotes the number of connected components of
$N_{k}(X_1, \omega)$
denotes the number of connected components of
![]() $X_1$
with sizes in the interval
$X_1$
with sizes in the interval
![]() $\mathcal I_k(\omega)$
.) We will also require a bound for the number of components with sizes in the interval
$\mathcal I_k(\omega)$
.) We will also require a bound for the number of components with sizes in the interval
where
![]() $c > 0$
is a constant such that J does not intersect any of the
$c > 0$
is a constant such that J does not intersect any of the
![]() $\mathcal I_k(\omega)$
’s intervals. Let
$\mathcal I_k(\omega)$
’s intervals. Let
![]() $W_X$
(resp.,
$W_X$
(resp.,
![]() $W_Y$
) be the set of components of
$W_Y$
) be the set of components of
![]() $X_1$
(resp.,
$X_1$
(resp.,
![]() $Y_1$
) with sizes in the interval J. Lemma 3.11 then implies that for some positive constants
$Y_1$
) with sizes in the interval J. Lemma 3.11 then implies that for some positive constants
![]() $\delta_1, \delta_2$
independent of n,
$\delta_1, \delta_2$
independent of n,
 \begin{equation*} {\mathbb{P}}\left[|W_X|\ge \delta_1n \left(\frac{\omega (n)^{6}}{cn^{2/3}}\right)^{3/2} \right] \ge 1- \frac{\delta_2}{n} \left(\frac{cn^{2/3}}{\omega (n)^{6}}\right)^{3/2} = 1 - O\!\left(\omega (n)^{-9}\right). \end{equation*}
\begin{equation*} {\mathbb{P}}\left[|W_X|\ge \delta_1n \left(\frac{\omega (n)^{6}}{cn^{2/3}}\right)^{3/2} \right] \ge 1- \frac{\delta_2}{n} \left(\frac{cn^{2/3}}{\omega (n)^{6}}\right)^{3/2} = 1 - O\!\left(\omega (n)^{-9}\right). \end{equation*}
All the bounds above apply also to the analogous quantities for
![]() $Y_1$
with the same respective probabilities. Therefore, by a union bound, all these properties hold simultaneously for both
$Y_1$
with the same respective probabilities. Therefore, by a union bound, all these properties hold simultaneously for both
![]() $X_1$
and
$X_1$
and
![]() $Y_1$
with probability
$Y_1$
with probability
![]() $\Omega(1)$
. We assume that this is indeed the case and proceed to describe the second step of the coupling, in which we shall use each of the established properties for
$\Omega(1)$
. We assume that this is indeed the case and proceed to describe the second step of the coupling, in which we shall use each of the established properties for
![]() $X_1$
and
$X_1$
and
![]() $Y_1$
.
$Y_1$
.
Recall
![]() $\mathcal{S}_{\omega}(X_1)$
and
$\mathcal{S}_{\omega}(X_1)$
and
![]() $\mathcal{S}_{\omega}(Y_1)$
denote the sets of connected components in
$\mathcal{S}_{\omega}(Y_1)$
denote the sets of connected components in
![]() $X_1$
and
$X_1$
and
![]() $Y_1$
, respectively, with sizes larger than
$Y_1$
, respectively, with sizes larger than
![]() $B_\omega$
. (Recall that
$B_\omega$
. (Recall that
![]() $B_\omega = n^{2/3} \omega (n)^{-1}$
, where
$B_\omega = n^{2/3} \omega (n)^{-1}$
, where
![]() $\omega (n) = \log \log \log \log n$
.) Since
$\omega (n) = \log \log \log \log n$
.) Since
![]() $\mathcal{R}_1(X_1) = O\!\left(n^{4/3}\right)$
, the total number of components in
$\mathcal{R}_1(X_1) = O\!\left(n^{4/3}\right)$
, the total number of components in
![]() $\mathcal{S}_{\omega}(X_1)$
is
$\mathcal{S}_{\omega}(X_1)$
is
![]() $O\big(\omega (n)^2\big)$
; moreover, it follows from the Cauchy–Schwarz inequality that the total number of vertices in the components in
$O\big(\omega (n)^2\big)$
; moreover, it follows from the Cauchy–Schwarz inequality that the total number of vertices in the components in
![]() $\mathcal{S}_{\omega}(X_1)$
, denoted
$\mathcal{S}_{\omega}(X_1)$
, denoted
![]() $\|\mathcal{S}_{\omega}(X_1)\|$
, is
$\|\mathcal{S}_{\omega}(X_1)\|$
, is
![]() $O\big(n^{2/3}\omega (n)\big)$
; the same holds for
$O\big(n^{2/3}\omega (n)\big)$
; the same holds for
![]() $\mathcal{S}_{\omega}(Y_1)$
. Without loss of generality, let us assume that
$\mathcal{S}_{\omega}(Y_1)$
. Without loss of generality, let us assume that
![]() $\|\mathcal{S}_{\omega}(X_1)\| \ge \|\mathcal{S}_{\omega}(Y_1)\|$
. Let
$\|\mathcal{S}_{\omega}(X_1)\| \ge \|\mathcal{S}_{\omega}(Y_1)\|$
. Let
and let
![]() $C_{\textrm{min}} = \arg \min_{C \in \varGamma} \|\mathcal{S}_{\omega}(Y_1) \cup C\|$
. In words,
$C_{\textrm{min}} = \arg \min_{C \in \varGamma} \|\mathcal{S}_{\omega}(Y_1) \cup C\|$
. In words,
![]() $C_{\textrm{min}}$
is the smallest subset C of components of
$C_{\textrm{min}}$
is the smallest subset C of components of
![]() $W_Y$
so that the number of vertices in the union of
$W_Y$
so that the number of vertices in the union of
![]() $\mathcal{S}_{\omega}(Y_1)$
and C is greater than that in
$\mathcal{S}_{\omega}(Y_1)$
and C is greater than that in
![]() $\mathcal{S}_{\omega}(X_1)$
. Since every component in
$\mathcal{S}_{\omega}(X_1)$
. Since every component in
![]() $W_Y$
has size at least
$W_Y$
has size at least
![]() $cn^{2/3}\omega (n)^{-6}$
and
$cn^{2/3}\omega (n)^{-6}$
and
![]() $|W_Y| = \Omega\big(\omega (n)^9\big)$
, the number of vertices in
$|W_Y| = \Omega\big(\omega (n)^9\big)$
, the number of vertices in
![]() $W_Y$
is
$W_Y$
is
![]() $\Omega\big(n^{2/3}\omega (n)^3\big)$
and so
$\Omega\big(n^{2/3}\omega (n)^3\big)$
and so
![]() $\varGamma \neq \emptyset$
. In addition, the number of components in
$\varGamma \neq \emptyset$
. In addition, the number of components in
![]() $C_{\textrm{min}}$
is
$C_{\textrm{min}}$
is
![]() $O\big(\omega (n)^9\big)$
. Let
$O\big(\omega (n)^9\big)$
. Let
![]() $\mathcal{S}^{\prime}_{\omega}(Y_1) = \mathcal{S}_{\omega}(Y_1) \cup C_{\textrm{min}}$
and observe that the number of components in
$\mathcal{S}^{\prime}_{\omega}(Y_1) = \mathcal{S}_{\omega}(Y_1) \cup C_{\textrm{min}}$
and observe that the number of components in
![]() $\mathcal{S}^{\prime}_{\omega}(Y_1)$
is also
$\mathcal{S}^{\prime}_{\omega}(Y_1)$
is also
![]() $O\big(\omega (n)^9\big)$
and that
$O\big(\omega (n)^9\big)$
and that
Note that
![]() $\|\mathcal{S}_{\omega}(X_1)\| - \|\mathcal{S}_{\omega}(Y_1)\|$
may be
$\|\mathcal{S}_{\omega}(X_1)\| - \|\mathcal{S}_{\omega}(Y_1)\|$
may be
![]() $\Omega\big(n^{2/3}\omega (n)\big)$
(i.e., much larger than
$\Omega\big(n^{2/3}\omega (n)\big)$
(i.e., much larger than
![]() $ \|\mathcal{S}^{\prime}_{\omega}(Y_1)\| - \|\mathcal{S}_{\omega}(X_1)\| $
). Hence, if all the components from
$ \|\mathcal{S}^{\prime}_{\omega}(Y_1)\| - \|\mathcal{S}_{\omega}(X_1)\| $
). Hence, if all the components from
![]() $\mathcal{S}_{\omega}(Y_1)$
and
$\mathcal{S}_{\omega}(Y_1)$
and
![]() $\mathcal{S}_{\omega}(X_1)$
were activated, the difference in the number of active vertices could be
$\mathcal{S}_{\omega}(X_1)$
were activated, the difference in the number of active vertices could be
![]() $\Omega\big(n^{2/3}\omega (n)\big)$
. This difference cannot be corrected by our coupling for the activation of the small components. We shall require instead that all the components from
$\Omega\big(n^{2/3}\omega (n)\big)$
. This difference cannot be corrected by our coupling for the activation of the small components. We shall require instead that all the components from
![]() $\mathcal{S}^{\prime}_{\omega}(Y_1)$
and
$\mathcal{S}^{\prime}_{\omega}(Y_1)$
and
![]() $\mathcal{S}_{\omega}(X_1)$
are activated so that the difference is
$\mathcal{S}_{\omega}(X_1)$
are activated so that the difference is
![]() $O\big(n^{2/3}\omega (n)^{-6}\big)$
instead.
$O\big(n^{2/3}\omega (n)^{-6}\big)$
instead.
We now describe a coupling of the activation sub-step for the second step of the CM dynamics. As mentioned, our goal is to design a coupling in which the same number of vertices are activated from each copy. If indeed
![]() $A(X_1) = A(Y_1)$
, then we can choose an arbitrary bijective map
$A(X_1) = A(Y_1)$
, then we can choose an arbitrary bijective map
![]() $\varphi$
between the activated vertices of
$\varphi$
between the activated vertices of
![]() $X_1$
and the activated vertices of
$X_1$
and the activated vertices of
![]() $Y_1$
and use
$Y_1$
and use
![]() $\varphi$
to couple the percolation sub-step. Specifically, if u and v were activated in
$\varphi$
to couple the percolation sub-step. Specifically, if u and v were activated in
![]() $X_1$
, the state of the edges
$X_1$
, the state of the edges
![]() $\{u,v\}$
in
$\{u,v\}$
in
![]() $X_2$
and
$X_2$
and
![]() $\{\varphi(u),\varphi(v)\}$
in
$\{\varphi(u),\varphi(v)\}$
in
![]() $Y_2$
would be the same. This yields a coupling of the percolation sub-step such that
$Y_2$
would be the same. This yields a coupling of the percolation sub-step such that
![]() $X_2$
and
$X_2$
and
![]() $Y_2$
agree on the subgraph update at time 1.
$Y_2$
agree on the subgraph update at time 1.
Suppose then that in the second CM step all the components in
![]() $\mathcal{S}_{\omega}(X_1)$
and
$\mathcal{S}_{\omega}(X_1)$
and
![]() $\mathcal{S}^{\prime}_{\omega}(Y_1)$
are activated simultaneously. If this is the case, then the difference in the number of activated vertices is
$\mathcal{S}^{\prime}_{\omega}(Y_1)$
are activated simultaneously. If this is the case, then the difference in the number of activated vertices is
![]() $d \le 2c n^{2/3}\omega (n)^{-6}$
. We will use a local limit theorem (i.e., Theorem 5.1) to argue that there is a coupling of the activation of the remaining components in
$d \le 2c n^{2/3}\omega (n)^{-6}$
. We will use a local limit theorem (i.e., Theorem 5.1) to argue that there is a coupling of the activation of the remaining components in
![]() $X_1$
and
$X_1$
and
![]() $Y_1$
such that the total number of active vertices in both copies is the same with probability
$Y_1$
such that the total number of active vertices in both copies is the same with probability
![]() $\Omega(1)$
. Since all the components in
$\Omega(1)$
. Since all the components in
![]() $\mathcal{S}_{\omega}(X_1)$
and
$\mathcal{S}_{\omega}(X_1)$
and
![]() $\mathcal{S}^{\prime}_{\omega}(Y_1)$
are activated with probability
$\mathcal{S}^{\prime}_{\omega}(Y_1)$
are activated with probability
![]() $\exp\big({-}O\big(\omega (n)^9\big)\big)$
, the overall success probability of the coupling will be
$\exp\big({-}O\big(\omega (n)^9\big)\big)$
, the overall success probability of the coupling will be
![]() $\exp\big({-}O\big(\omega (n)^9\big)\big)$
.
$\exp\big({-}O\big(\omega (n)^9\big)\big)$
.
Now, let
![]() $x_1,x_2,\dots,x_m$
be the sizes of the components of
$x_1,x_2,\dots,x_m$
be the sizes of the components of
![]() $X_1$
that are not in
$X_1$
that are not in
![]() $\mathcal{S}_{\omega}(X_1)$
(in increasing order). Let
$\mathcal{S}_{\omega}(X_1)$
(in increasing order). Let
![]() $\hat{A}(X_1)$
be the random variable corresponding to the number of active vertices from these components. Observe that
$\hat{A}(X_1)$
be the random variable corresponding to the number of active vertices from these components. Observe that
![]() $\hat{A}(X_1)$
is the sum of m independent random variables, where the j-th variable in the sum is equal to
$\hat{A}(X_1)$
is the sum of m independent random variables, where the j-th variable in the sum is equal to
![]() $x_j$
with probability
$x_j$
with probability
![]() $1/q$
, and it is 0 otherwise. We claim that sequence
$1/q$
, and it is 0 otherwise. We claim that sequence
![]() $x_1,x_2,\dots,x_m$
satisfies all the conditions in Theorem 5.1.
$x_1,x_2,\dots,x_m$
satisfies all the conditions in Theorem 5.1.
First, note that since the number of isolated vertices in
![]() $X_1$
is
$X_1$
is
![]() $\Omega(n)$
,
$\Omega(n)$
,
![]() $m = \Theta(n)$
and consequently
$m = \Theta(n)$
and consequently
![]() $x_m = O\big(m^{2/3}\omega(m)^{-1}\big)$
,
$x_m = O\big(m^{2/3}\omega(m)^{-1}\big)$
,
![]() $\sum_{i=1}^m x_i^2 = \tilde{R}_\omega(X_1) = O\big(m^{4/3}\omega(m)^{-1/2}\big)$
and
$\sum_{i=1}^m x_i^2 = \tilde{R}_\omega(X_1) = O\big(m^{4/3}\omega(m)^{-1/2}\big)$
and
![]() $x_i=1$
for all
$x_i=1$
for all
![]() $i \le \rho m$
, where
$i \le \rho m$
, where
![]() $\rho \in (0,1)$
is independent of m. Moreover, since
$\rho \in (0,1)$
is independent of m. Moreover, since
![]() $N_{k}(X_1, \omega) = \Omega\Big(\omega (n)^{3 \cdot 2^{k-1}}\Big)$
for all
$N_{k}(X_1, \omega) = \Omega\Big(\omega (n)^{3 \cdot 2^{k-1}}\Big)$
for all
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $n^{2/3}\omega (n)^{-2^k} \rightarrow \infty$
,
$n^{2/3}\omega (n)^{-2^k} \rightarrow \infty$
,
Since
![]() $N_0(X_1,\omega) = \Omega\!\left( \omega (n)^{3/2}\right) $
, we also have
$N_0(X_1,\omega) = \Omega\!\left( \omega (n)^{3/2}\right) $
, we also have
Let
![]() $\mu_X = {\mathbb{E}}\big[\hat{A}(X_1)\big] = q^{-1}\sum_{i=1}^m x_i$
and let
$\mu_X = {\mathbb{E}}\big[\hat{A}(X_1)\big] = q^{-1}\sum_{i=1}^m x_i$
and let
Hence, Theorem 5.1 implies that
![]() ${\mathbb{P}} \big[\hat{A}(X_1) = a\big] = \Omega\!\left(\sigma_X^{-1}\right)$
for any
${\mathbb{P}} \big[\hat{A}(X_1) = a\big] = \Omega\!\left(\sigma_X^{-1}\right)$
for any
![]() $a \in [\mu_X-\sigma_X,\mu_X+\sigma_X]$
. Similarly, we get
$a \in [\mu_X-\sigma_X,\mu_X+\sigma_X]$
. Similarly, we get
![]() ${\mathbb{P}} \big[\hat{A}(Y_1) = a \big] = \Omega\big(\sigma_Y^{-1}\big)$
for any
${\mathbb{P}} \big[\hat{A}(Y_1) = a \big] = \Omega\big(\sigma_Y^{-1}\big)$
for any
![]() $a \in [\mu_Y-\sigma_Y,\mu_Y+\sigma_Y]$
, with
$a \in [\mu_Y-\sigma_Y,\mu_Y+\sigma_Y]$
, with
![]() $\hat{A}(Y_1)$
,
$\hat{A}(Y_1)$
,
![]() $\mu_Y$
and
$\mu_Y$
and
![]() $\sigma_Y$
defined analogously for
$\sigma_Y$
defined analogously for
![]() $Y_1$
. Note that
$Y_1$
. Note that
![]() $\mu_X - \mu_Y = O\big(n^{2/3}\omega (n)^{-6}\big)$
and
$\mu_X - \mu_Y = O\big(n^{2/3}\omega (n)^{-6}\big)$
and
![]() $\sigma_X , \sigma_Y= \Theta\big(n^{2/3} \omega (n)^{-1/4}\big)$
. Without loss of generality, suppose
$\sigma_X , \sigma_Y= \Theta\big(n^{2/3} \omega (n)^{-1/4}\big)$
. Without loss of generality, suppose
![]() $\sigma_X < \sigma_Y$
. Then for any
$\sigma_X < \sigma_Y$
. Then for any
![]() $a \in [\mu_X-\sigma_X /2,\mu_Y+\sigma_X /2]$
and
$a \in [\mu_X-\sigma_X /2,\mu_Y+\sigma_X /2]$
and
![]() $d = O\big(n^{2/3}\omega (n)^{-6}\big)$
, we have
$d = O\big(n^{2/3}\omega (n)^{-6}\big)$
, we have
Hence, there exists a coupling
![]() $\mathbb P$
of
$\mathbb P$
of
![]() $\hat{A}(X_1)$
and
$\hat{A}(X_1)$
and
![]() $\hat{A}(Y_1)$
so that
$\hat{A}(Y_1)$
so that
![]() $\mathbb P\big[\hat{A}(X_1) = a, \hat{A}(Y_1) = a - d\big] = \Omega\big(\sigma_Y^{-1}\big)$
for all
$\mathbb P\big[\hat{A}(X_1) = a, \hat{A}(Y_1) = a - d\big] = \Omega\big(\sigma_Y^{-1}\big)$
for all
![]() $a \in \left[\mu_X-\sigma_X /2,\mu_Y+\sigma_X /2\right]$
. Therefore, there is a coupling of
$a \in \left[\mu_X-\sigma_X /2,\mu_Y+\sigma_X /2\right]$
. Therefore, there is a coupling of
![]() $\hat{A}(X_1)$
and
$\hat{A}(X_1)$
and
![]() $\hat{A}(Y_1)$
such that
$\hat{A}(Y_1)$
such that
Putting all these together, we deduce that
![]() $A(X_1) = A(Y_1)$
with probability
$A(X_1) = A(Y_1)$
with probability
![]() $\exp\big({-}O\big(\omega (n)^{9}\big)\big)$
. If this is the case, the edge re-sampling step is coupled bijectively (as described above) so that
$\exp\big({-}O\big(\omega (n)^{9}\big)\big)$
. If this is the case, the edge re-sampling step is coupled bijectively (as described above) so that
![]() $\mathcal{S}_{\omega}(X_2) = \mathcal{S}_{\omega}(Y_2)$
.
$\mathcal{S}_{\omega}(X_2) = \mathcal{S}_{\omega}(Y_2)$
.
It remains for us to guarantee the additional desired structural properties of
![]() $X_2$
and
$X_2$
and
![]() $Y_2$
, which follow straightforwardly from the random graph estimates stated in Section 3. First note that by Hoeffding’s inequality, with probability
$Y_2$
, which follow straightforwardly from the random graph estimates stated in Section 3. First note that by Hoeffding’s inequality, with probability
![]() $\Omega(1)$
,
$\Omega(1)$
,
Hence, in the percolation sub-step the active subgraph is replaced by
![]() $F \sim G\!\left(A(X_1), \frac{1 + \lambda A(X_1)^{-1/3}}{A(X_1)}\right)$
, where
$F \sim G\!\left(A(X_1), \frac{1 + \lambda A(X_1)^{-1/3}}{A(X_1)}\right)$
, where
![]() $|\lambda| = O(\omega (n))$
with probability
$|\lambda| = O(\omega (n))$
with probability
![]() $\Omega(1)$
since
$\Omega(1)$
since
![]() $\|\mathcal{S}_{\omega}(X_1)\| = O\big(n^{2/3}\omega (n)\big)$
. Conditioning on this event, since the components of F contribute to both
$\|\mathcal{S}_{\omega}(X_1)\| = O\big(n^{2/3}\omega (n)\big)$
. Conditioning on this event, since the components of F contribute to both
![]() $X_2$
and
$X_2$
and
![]() $Y_2$
, Corollary 3.12 implies that w.h.p.
$Y_2$
, Corollary 3.12 implies that w.h.p.
![]() $\hat{N}_k(2, \omega (n)) $
$\hat{N}_k(2, \omega (n)) $
![]() $ = \Omega\big( \omega (n)^{3 \cdot 2^{k-1}} \big)$
for all
$ = \Omega\big( \omega (n)^{3 \cdot 2^{k-1}} \big)$
for all
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $n^{2/3}\omega (n)^{-2^k}\rightarrow \infty$
. Moreover, from Lemma 3.2 we obtain that
$n^{2/3}\omega (n)^{-2^k}\rightarrow \infty$
. Moreover, from Lemma 3.2 we obtain that
![]() $I(X_2)=\Omega(n)$
w.h.p. From Lemma 3.4 and Markov’s inequality, we obtain that
$I(X_2)=\Omega(n)$
w.h.p. From Lemma 3.4 and Markov’s inequality, we obtain that
![]() $\mathcal{R}_2(X_2) = O\!\left(n^{4/3}\right)$
with probability at least
$\mathcal{R}_2(X_2) = O\!\left(n^{4/3}\right)$
with probability at least
![]() $99/100$
and from Lemma 3.10 that
$99/100$
and from Lemma 3.10 that
![]() $\widetilde{\mathcal{R}}_\omega(X_2) = O\big(n^{4/3}{\omega (n)}^{-1/2}\big)$
also with probability at least
$\widetilde{\mathcal{R}}_\omega(X_2) = O\big(n^{4/3}{\omega (n)}^{-1/2}\big)$
also with probability at least
![]() $99/100$
. All these bounds apply also to the analogous quantities for
$99/100$
. All these bounds apply also to the analogous quantities for
![]() $Y_2$
with the same respective probabilities.
$Y_2$
with the same respective probabilities.
Finally, we derive the bound for
![]() $L_1(X_2)$
and
$L_1(X_2)$
and
![]() $L_1(Y_2)$
. First, notice
$L_1(Y_2)$
. First, notice
![]() $L_1(F)$
is stochastically dominated by
$L_1(F)$
is stochastically dominated by
![]() $L_1(F^{\prime})$
, where
$L_1(F^{\prime})$
, where
![]() $F^{\prime}\sim G\Big(A(X_1), \frac{1 + |\lambda| A(X_1)^{-1/3}}{A(X_1)}\Big)$
. Under the assumption that
$F^{\prime}\sim G\Big(A(X_1), \frac{1 + |\lambda| A(X_1)^{-1/3}}{A(X_1)}\Big)$
. Under the assumption that
![]() $|\lambda| = O(\omega (n))$
, if
$|\lambda| = O(\omega (n))$
, if
![]() $|\lambda| \rightarrow \infty$
, then Corollary 3.6 implies that
$|\lambda| \rightarrow \infty$
, then Corollary 3.6 implies that
![]() $L_1(F^{\prime}) = O(|\lambda| A(X_1)^{2/3}) = O\big(n^{2/3} \omega (n)\big)$
w.h.p.; otherwise,
$L_1(F^{\prime}) = O(|\lambda| A(X_1)^{2/3}) = O\big(n^{2/3} \omega (n)\big)$
w.h.p.; otherwise,
![]() $|\lambda| = O(1)$
and by Lemma 3.9 and Markov’s inequality,
$|\lambda| = O(1)$
and by Lemma 3.9 and Markov’s inequality,
![]() $L_1(F^{\prime}) = O\big(n^{2/3}\big)$
with probability at least
$L_1(F^{\prime}) = O\big(n^{2/3}\big)$
with probability at least
![]() $99/100$
. Thus,
$99/100$
. Thus,
![]() $L_1(F) = O\big(n^{2/3}\omega (n)\big)$
with probability at least
$L_1(F) = O\big(n^{2/3}\omega (n)\big)$
with probability at least
![]() $99/100$
. We also know that the largest inactivated component in
$99/100$
. We also know that the largest inactivated component in
![]() $X_1$
has size less than
$X_1$
has size less than
![]() $n^{2/3}\omega (n)^{-1}$
, so
$n^{2/3}\omega (n)^{-1}$
, so
![]() $L_1(X_2) = O\big(n^{2/3} \omega (n)\big)$
with probability at least
$L_1(X_2) = O\big(n^{2/3} \omega (n)\big)$
with probability at least
![]() $99/100$
. The same holds for
$99/100$
. The same holds for
![]() $Y_2$
. Therefore, by a union bound, all these properties hold simultaneously for both
$Y_2$
. Therefore, by a union bound, all these properties hold simultaneously for both
![]() $X_2$
and
$X_2$
and
![]() $Y_2$
with probability
$Y_2$
with probability
![]() $\Omega(1)$
, as claimed.
$\Omega(1)$
, as claimed.
5.3 Re-contracting largest component: proof of Lemma 2.10
In Section 5.2, we designed a coupling argument to ensure that the largest components of both configurations have the same size. For this, we needed to relax our constraint on the size of the largest component of the configurations. In this section we prove Lemma 2.10, which ensures that after
![]() $O({\log} \omega (n))$
steps the largest components of each configuration have size
$O({\log} \omega (n))$
steps the largest components of each configuration have size
![]() $O\big(n^{2/3}\big)$
again.
$O\big(n^{2/3}\big)$
again.
The following lemma is the core of the proof Lemma 2.10 and it may be viewed as a generalisation of the coupling from the proof of Lemma 2.9 using the local limit theorem from Section 5.2.
We recall some notation from the proof sketch. Given two random-cluster configurations
![]() $X_t$
and
$X_t$
and
![]() $Y_t$
,
$Y_t$
,
![]() $W_t$
is maximal matching between the components of
$W_t$
is maximal matching between the components of
![]() $X_t$
and
$X_t$
and
![]() $Y_t$
that only matches components of equal size to each other. We use
$Y_t$
that only matches components of equal size to each other. We use
![]() $M (X_t)$
,
$M (X_t)$
,
![]() $M(Y_t)$
for the components in
$M(Y_t)$
for the components in
![]() $W_t$
from
$W_t$
from
![]() $X_t$
,
$X_t$
,
![]() $Y_t$
, respectively,
$Y_t$
, respectively,
![]() $D(X_t)$
,
$D(X_t)$
,
![]() $D(Y_t)$
for the complements of
$D(Y_t)$
for the complements of
![]() $M (X_t )$
,
$M (X_t )$
,
![]() $M (Y_t)$
, and
$M (Y_t)$
, and
![]() $ Z_t = \sum_{\mathcal{C} \in D(X_t) \cup D(Y_t)} |\mathcal{C}|^2. $
For an increasing positive function g and each integer
$ Z_t = \sum_{\mathcal{C} \in D(X_t) \cup D(Y_t)} |\mathcal{C}|^2. $
For an increasing positive function g and each integer
![]() $k \ge 1$
, define
$k \ge 1$
, define
![]() $\hat{N}_k(t, g) \,:\!=\, \hat{N}_k(X_t,Y_t, g)$
as the number of matched pairs in
$\hat{N}_k(t, g) \,:\!=\, \hat{N}_k(X_t,Y_t, g)$
as the number of matched pairs in
![]() $W_t$
whose component sizes are in the interval
$W_t$
whose component sizes are in the interval
 \begin{equation*}\mathcal{I}_{k}(g) = \left[\frac{\vartheta n^{2/3}}{2g(n)^{2^k}},\frac{\vartheta n^{2/3}}{g(n)^{2^k}}\right],\end{equation*}
\begin{equation*}\mathcal{I}_{k}(g) = \left[\frac{\vartheta n^{2/3}}{2g(n)^{2^k}},\frac{\vartheta n^{2/3}}{g(n)^{2^k}}\right],\end{equation*}
where
![]() $\vartheta>0$
is a fixed large constant (independent of n).
$\vartheta>0$
is a fixed large constant (independent of n).
Lemma 5.2. There exists a coupling of the activation sub-step of the CM dynamics such that
![]() $A(X_t) = A(Y_t)$
with at least
$A(X_t) = A(Y_t)$
with at least
![]() $\Omega \!\left(\frac{1}{\omega (n)} \right)$
probability, provided
$\Omega \!\left(\frac{1}{\omega (n)} \right)$
probability, provided
![]() $X_t$
and
$X_t$
and
![]() $Y_t$
are random-cluster configurations satisfying
$Y_t$
are random-cluster configurations satisfying
-
1.
 $\mathcal{S}_{\omega}(X_t) = \mathcal{S}_{\omega}(Y_t)$
;
$\mathcal{S}_{\omega}(X_t) = \mathcal{S}_{\omega}(Y_t)$
; -
2.
 $Z_t = O\!\left(\frac{n^{4/3}}{\omega (n)^{1/2}}\right)$
;
$Z_t = O\!\left(\frac{n^{4/3}}{\omega (n)^{1/2}}\right)$
; -
3.
 $\hat{N}_k(X_t, Y_t, \omega (n)) = \Omega\!\left(\omega (n) ^ {3 \cdot 2 ^{k-1}}\right)$
for all
$\hat{N}_k(X_t, Y_t, \omega (n)) = \Omega\!\left(\omega (n) ^ {3 \cdot 2 ^{k-1}}\right)$
for all
 $k \ge 1$
such that
$k \ge 1$
such that
 $n^{2/3}\omega (n)^{-2^k}\rightarrow \infty$
;
$n^{2/3}\omega (n)^{-2^k}\rightarrow \infty$
; -
4.
 $I(X_t), I(Y_t) = \Omega(n)$
.
$I(X_t), I(Y_t) = \Omega(n)$
.
Proof. The activation coupling has two parts. First we use the maximal matching
![]() $W_t$
to couple the activation of a subset of the components in
$W_t$
to couple the activation of a subset of the components in
![]() $M(X_t)$
and
$M(X_t)$
and
![]() $M(Y_t)$
. Specifically, let
$M(Y_t)$
. Specifically, let
![]() $\ell$
be defined as in Theorem 5.1; for all
$\ell$
be defined as in Theorem 5.1; for all
![]() $k \in [1, \ell]$
, we exclude
$k \in [1, \ell]$
, we exclude
![]() $\Theta\big(\omega (n) ^ {3 \cdot 2 ^{k-1}}\big)$
pairs of components of size in the interval
$\Theta\big(\omega (n) ^ {3 \cdot 2 ^{k-1}}\big)$
pairs of components of size in the interval
![]() $\mathcal{I}_k(\omega)$
and we exclude
$\mathcal{I}_k(\omega)$
and we exclude
![]() $\Theta(n)$
pairs of matched isolated vertices. (These components exist by Assumptions 3 and 4.) All other pairs of components matched by
$\Theta(n)$
pairs of matched isolated vertices. (These components exist by Assumptions 3 and 4.) All other pairs of components matched by
![]() $W_t$
are jointly activated (or not). Hence, the number of vertices activated from
$W_t$
are jointly activated (or not). Hence, the number of vertices activated from
![]() $X_t$
in this first part of the coupling is the same as that from
$X_t$
in this first part of the coupling is the same as that from
![]() $Y_t$
.
$Y_t$
.
Let
![]() $\mathcal{C}(X_t)$
and
$\mathcal{C}(X_t)$
and
![]() $\mathcal{C}(Y_t)$
denote the sets containing the components in
$\mathcal{C}(Y_t)$
denote the sets containing the components in
![]() $X_t$
and components in
$X_t$
and components in
![]() $Y_t$
not considered to be activated in the first step of the coupling. This includes all the components from
$Y_t$
not considered to be activated in the first step of the coupling. This includes all the components from
![]() $D(X_t)$
and
$D(X_t)$
and
![]() $D(Y_t)$
, and all the components from
$D(Y_t)$
, and all the components from
![]() $M(X_t)$
and
$M(X_t)$
and
![]() $M(Y_t)$
excluded in the first part of the coupling. Let
$M(Y_t)$
excluded in the first part of the coupling. Let
![]() $A^{\prime}(X_t)$
and
$A^{\prime}(X_t)$
and
![]() $A^{\prime}(Y_t)$
denote the number of activated vertices from
$A^{\prime}(Y_t)$
denote the number of activated vertices from
![]() $\mathcal{C}(X_t)$
and
$\mathcal{C}(X_t)$
and
![]() $\mathcal{C}(Y_t)$
respectively. The second part is a coupling of the activation sub-step in a way such that
$\mathcal{C}(Y_t)$
respectively. The second part is a coupling of the activation sub-step in a way such that
Let
![]() $m_x \,:\!=\, |\mathcal{C}(X_t)| = \Theta(n)$
, and similarly for
$m_x \,:\!=\, |\mathcal{C}(X_t)| = \Theta(n)$
, and similarly for
![]() $m_y\,:\!=\,|\mathcal{C}(Y_t)|$
. Let
$m_y\,:\!=\,|\mathcal{C}(Y_t)|$
. Let
![]() $\mathcal{C}_1 \le \dots \le \mathcal{C}_{m_x}$
(resp.,
$\mathcal{C}_1 \le \dots \le \mathcal{C}_{m_x}$
(resp.,
![]() ${\mathcal{C}^{\prime}}_1 \le \dots \le {\mathcal{C}^{\prime}}_{m_y}$
) be sizes of components in
${\mathcal{C}^{\prime}}_1 \le \dots \le {\mathcal{C}^{\prime}}_{m_y}$
) be sizes of components in
![]() $\mathcal{C}(X_t)$
(resp.,
$\mathcal{C}(X_t)$
(resp.,
![]() $\mathcal{C}(Y_t)$
) in ascending order. For all
$\mathcal{C}(Y_t)$
) in ascending order. For all
![]() $i\le m_x$
, let
$i\le m_x$
, let
![]() $\mathcal{X}_i$
be a random variable that equals to
$\mathcal{X}_i$
be a random variable that equals to
![]() $\mathcal{C}_i$
with probability
$\mathcal{C}_i$
with probability
![]() $1/q$
and 0 otherwise, which corresponds to the number of activated vertices from ith component in
$1/q$
and 0 otherwise, which corresponds to the number of activated vertices from ith component in
![]() $\mathcal{C}(X_t)$
. Note that
$\mathcal{C}(X_t)$
. Note that
![]() $\mathcal{X}_1, \dots, \mathcal{X}_{m_x}$
are independent. We check that
$\mathcal{X}_1, \dots, \mathcal{X}_{m_x}$
are independent. We check that
![]() $\mathcal{X}_1, \dots, \mathcal{X}_{m_x}$
satisfy all other conditions of Theorem 5.1.
$\mathcal{X}_1, \dots, \mathcal{X}_{m_x}$
satisfy all other conditions of Theorem 5.1.
Assumption
![]() $\mathcal{S}_{\omega}(X_t) = \mathcal{S}_{\omega}(Y_t)$
and the first part of the activation ensure that
$\mathcal{S}_{\omega}(X_t) = \mathcal{S}_{\omega}(Y_t)$
and the first part of the activation ensure that
Observe also that there exists a constant
![]() $\rho$
such that
$\rho$
such that
![]() $\mathcal{C}_i = 1$
for
$\mathcal{C}_i = 1$
for
![]() $i \le \rho m_x$
and
$i \le \rho m_x$
and
![]() $\lvert\{i \,:\, \mathcal{C}_i \in \mathcal{I}_k(\omega)\}\rvert = \Theta\!\left(\omega (n) ^ {3 \cdot 2 ^{k-1}}\right)$
for
$\lvert\{i \,:\, \mathcal{C}_i \in \mathcal{I}_k(\omega)\}\rvert = \Theta\!\left(\omega (n) ^ {3 \cdot 2 ^{k-1}}\right)$
for
![]() $ 1 \le k \le \ell$
; lastly, from assumption
$ 1 \le k \le \ell$
; lastly, from assumption
![]() $Z_t = O\!\left(\frac{n^{4/3}}{\omega (n)^{1/2}}\right)$
, we obtain
$Z_t = O\!\left(\frac{n^{4/3}}{\omega (n)^{1/2}}\right)$
, we obtain
 \begin{align} \sum_{i = 1}^{m_x} \mathcal{C}_i^2 & \le Z_t + O(\rho m_x) + \sum_{k=1}^{\ell} \frac{\vartheta n^{4/3}}{\omega(n)^{2^{k+1}}} \cdot O\!\left(\omega (n)^{3\cdot 2^{k-1}} \right) \nonumber \\ & = O\!\left(\frac{m_x^{4/3}}{\sqrt{\omega(m_x)}}\right) + O\!\left( \sum_{k=1}^{\ell} \frac{m_x^{4/3}}{\omega(m_x)^{2^{k-1}}} \right) \nonumber \\ & = O\!\left(\frac{m_x^{4/3}}{\sqrt{\omega(m_x)}}\right) + O\!\left( \sum_{k=1}^{\ell} \frac{m_x^{4/3}}{\omega(m_x)^{k}} \right) \nonumber \\ & = O\!\left(\frac{m_x^{4/3}}{\sqrt{\omega(m_x)}}\right) + O\!\left(\frac{m_x^{4/3}}{\omega(m_x)}\right) = O\!\left(\frac{m_x^{4/3}}{\sqrt{\omega(m_x)}}\right) . \end{align}
\begin{align} \sum_{i = 1}^{m_x} \mathcal{C}_i^2 & \le Z_t + O(\rho m_x) + \sum_{k=1}^{\ell} \frac{\vartheta n^{4/3}}{\omega(n)^{2^{k+1}}} \cdot O\!\left(\omega (n)^{3\cdot 2^{k-1}} \right) \nonumber \\ & = O\!\left(\frac{m_x^{4/3}}{\sqrt{\omega(m_x)}}\right) + O\!\left( \sum_{k=1}^{\ell} \frac{m_x^{4/3}}{\omega(m_x)^{2^{k-1}}} \right) \nonumber \\ & = O\!\left(\frac{m_x^{4/3}}{\sqrt{\omega(m_x)}}\right) + O\!\left( \sum_{k=1}^{\ell} \frac{m_x^{4/3}}{\omega(m_x)^{k}} \right) \nonumber \\ & = O\!\left(\frac{m_x^{4/3}}{\sqrt{\omega(m_x)}}\right) + O\!\left(\frac{m_x^{4/3}}{\omega(m_x)}\right) = O\!\left(\frac{m_x^{4/3}}{\sqrt{\omega(m_x)}}\right) . \end{align}
Therefore, if
![]() $\mu_x = {\mathbb{E}} \left[ \sum_{i=1}^{m_x} \mathcal{X}_i \right] $
and
$\mu_x = {\mathbb{E}} \left[ \sum_{i=1}^{m_x} \mathcal{X}_i \right] $
and
![]() $\sigma_x^2 = Var\!\left( \sum_{i=1}^{m_x} \mathcal{X}_i \right)$
, Theorem 5.1 implies that for any
$\sigma_x^2 = Var\!\left( \sum_{i=1}^{m_x} \mathcal{X}_i \right)$
, Theorem 5.1 implies that for any
![]() $x \in [\mu_x - \sigma_x, \mu_x + \sigma_x]$
,
$x \in [\mu_x - \sigma_x, \mu_x + \sigma_x]$
,
 \begin{equation*}{\mathbb{P}} \left[A^{\prime}(X_t) = x\right] = {\mathbb{P}} \left[\sum_{i=1}^{m_x} \mathcal{X}_i = x\right] = \frac{1}{\sqrt{2\pi} \sigma_x} \exp\!\left({-}\frac{(x-\mu_x)^2}{2\sigma_x^2}\right) + o\!\left(\frac{1}{\sigma_x}\right) = \Omega \!\left( \frac{1}{\sigma_x}\right) .\end{equation*}
\begin{equation*}{\mathbb{P}} \left[A^{\prime}(X_t) = x\right] = {\mathbb{P}} \left[\sum_{i=1}^{m_x} \mathcal{X}_i = x\right] = \frac{1}{\sqrt{2\pi} \sigma_x} \exp\!\left({-}\frac{(x-\mu_x)^2}{2\sigma_x^2}\right) + o\!\left(\frac{1}{\sigma_x}\right) = \Omega \!\left( \frac{1}{\sigma_x}\right) .\end{equation*}
Similarly, we get that
![]() ${\mathbb{P}} \left[A^{\prime}(Y_t) = y\right] = \Omega (\sigma_y^{-1})$
for any
${\mathbb{P}} \left[A^{\prime}(Y_t) = y\right] = \Omega (\sigma_y^{-1})$
for any
![]() $y \in [\mu_y - \sigma_y, \mu_y + \sigma_y]$
, with
$y \in [\mu_y - \sigma_y, \mu_y + \sigma_y]$
, with
![]() $\mu_y$
and
$\mu_y$
and
![]() $\sigma_y$
defined analogously. Without loss of generality, suppose
$\sigma_y$
defined analogously. Without loss of generality, suppose
![]() $\sigma_y \le \sigma_x$
. Since
$\sigma_y \le \sigma_x$
. Since
![]() $\mu_x = \mu_y$
, for
$\mu_x = \mu_y$
, for
![]() $x \in \left[\mu_x - \sigma_y, \mu_x + \sigma_y\right]$
, we obtain
$x \in \left[\mu_x - \sigma_y, \mu_x + \sigma_y\right]$
, we obtain
Hence, we can couple
![]() $(A^{\prime}(X_t), A^{\prime}(Y_t))$
so that
$(A^{\prime}(X_t), A^{\prime}(Y_t))$
so that
![]() ${\mathbb{P}} [A^{\prime}(X_t) = A^{\prime}(Y_t) = x] = \Omega(\sigma_x^{-1})$
for all
${\mathbb{P}} [A^{\prime}(X_t) = A^{\prime}(Y_t) = x] = \Omega(\sigma_x^{-1})$
for all
![]() $x \in [\mu_x - \sigma_y, \mu_x + \sigma_y]$
. Consequently, under this coupling,
$x \in [\mu_x - \sigma_y, \mu_x + \sigma_y]$
. Consequently, under this coupling,
Since
![]() $\mathcal{X}_1, \dots, \mathcal{X}_{m_x}$
are independent,
$\mathcal{X}_1, \dots, \mathcal{X}_{m_x}$
are independent,
![]() $\sigma_x^2 = \Theta \!\left(\sum_{i = 1}^{m_x} \mathcal{C}_i^2\right)$
, and similarly
$\sigma_x^2 = \Theta \!\left(\sum_{i = 1}^{m_x} \mathcal{C}_i^2\right)$
, and similarly
![]() $\sigma_y^2 = \Theta \!\left(\sum_{i = 1}^{m_y} {\mathcal{C}^{\prime}}_i^2\right)$
. Hence, inequality (10) gives an upper bound for
$\sigma_y^2 = \Theta \!\left(\sum_{i = 1}^{m_y} {\mathcal{C}^{\prime}}_i^2\right)$
. Hence, inequality (10) gives an upper bound for
![]() $\sigma_x^2$
; meanwhile, a lower bound for
$\sigma_x^2$
; meanwhile, a lower bound for
![]() $\sigma_y^2$
can be obtained by counting components in the largest interval:
$\sigma_y^2$
can be obtained by counting components in the largest interval:
 \begin{equation*} \sum_{i = 1}^{m_y} {\mathcal{C}^{\prime}}_i^2 \ge \sum_{i\,:\, {\mathcal{C}^{\prime}}_i \in \mathcal{I}_1(\omega)} {\mathcal{C}^{\prime}}_i^2 \ge \frac{Bn^{4/3}}{\omega(n)^{4}} \cdot \Theta\!\left(\omega (n)^{3} \right) = \Omega\!\left(\frac{n^{4/3}}{\omega(n)} \right). \end{equation*}
\begin{equation*} \sum_{i = 1}^{m_y} {\mathcal{C}^{\prime}}_i^2 \ge \sum_{i\,:\, {\mathcal{C}^{\prime}}_i \in \mathcal{I}_1(\omega)} {\mathcal{C}^{\prime}}_i^2 \ge \frac{Bn^{4/3}}{\omega(n)^{4}} \cdot \Theta\!\left(\omega (n)^{3} \right) = \Omega\!\left(\frac{n^{4/3}}{\omega(n)} \right). \end{equation*}
Therefore,
 \begin{equation*} {\mathbb{P}} \left[ A^{\prime}(X_t) = A^{\prime}(Y_t) \right] = \Omega\!\left(\frac{n^{2/3}}{\omega (n)^{1/2}} \cdot \frac{\omega(m_x)^{1/4} }{m_x^{2/3}}\right) = \Omega \!\left( \frac{1}{\omega (n)}\right), \end{equation*}
\begin{equation*} {\mathbb{P}} \left[ A^{\prime}(X_t) = A^{\prime}(Y_t) \right] = \Omega\!\left(\frac{n^{2/3}}{\omega (n)^{1/2}} \cdot \frac{\omega(m_x)^{1/4} }{m_x^{2/3}}\right) = \Omega \!\left( \frac{1}{\omega (n)}\right), \end{equation*}
as desired.
We are now ready to prove Lemma 2.10.
Proof of Lemma 2.10. Let
![]() $C_1$
be a suitable constant that we choose later. We wish to maintain the following properties for all
$C_1$
be a suitable constant that we choose later. We wish to maintain the following properties for all
![]() $t \le T \,:\!=\, C_1 \log \omega (n)$
:
$t \le T \,:\!=\, C_1 \log \omega (n)$
:
-
1.
 $\mathcal{S}_{\omega}(X_t) = \mathcal{S}_{\omega}(Y_t)$
;
$\mathcal{S}_{\omega}(X_t) = \mathcal{S}_{\omega}(Y_t)$
; -
2.
 $Z_t = O\!\left(\frac{n^{4/3}}{\omega (n)^{1/2}}\right)$
;
$Z_t = O\!\left(\frac{n^{4/3}}{\omega (n)^{1/2}}\right)$
; -
3.
 $\hat{N}_k(X_t, Y_t, \omega (n)) = \Omega\!\left(\omega (n) ^ {3 \cdot 2 ^{k-1}}\right)$
for all
$\hat{N}_k(X_t, Y_t, \omega (n)) = \Omega\!\left(\omega (n) ^ {3 \cdot 2 ^{k-1}}\right)$
for all
 $k \ge 1$
such that
$k \ge 1$
such that
 $n^{2/3}\omega (n)^{-2^k}\rightarrow \infty$
;
$n^{2/3}\omega (n)^{-2^k}\rightarrow \infty$
; -
4.
 $I(X_t), I(Y_t) = \Omega(n)$
;
$I(X_t), I(Y_t) = \Omega(n)$
; -
5.
 $\mathcal{R}_2(X_t), \mathcal{R}_2(Y_t) = O\!\left(n^{4/3}\right)$
;
$\mathcal{R}_2(X_t), \mathcal{R}_2(Y_t) = O\!\left(n^{4/3}\right)$
; -
6.
 $L_1 (X_t) \le \alpha^t L_1(X_0), L_1 (Y_t) \le \alpha^t L_1(Y_0)$
for some constant
$L_1 (X_t) \le \alpha^t L_1(X_0), L_1 (Y_t) \le \alpha^t L_1(Y_0)$
for some constant
 $\alpha$
independent of t.
$\alpha$
independent of t.
By assumption,
![]() $X_0$
and
$X_0$
and
![]() $Y_0$
satisfy these properties. Suppose that
$Y_0$
satisfy these properties. Suppose that
![]() $X_t$
and
$X_t$
and
![]() $Y_t$
satisfy these properties at step
$Y_t$
satisfy these properties at step
![]() $t \le T$
. We show that there exists a one-step coupling of the CM dynamics such that
$t \le T$
. We show that there exists a one-step coupling of the CM dynamics such that
![]() $X_{t+1}$
and
$X_{t+1}$
and
![]() $Y_{t+1}$
preserve all six properties with probability
$Y_{t+1}$
preserve all six properties with probability
![]() $\Omega \!\left(\omega (n)^{-1} \right)$
.
$\Omega \!\left(\omega (n)^{-1} \right)$
.
We provide the high-level ideas of the proof first. We will crucially exploit the coupling from Lemma 5.2. Assuming
![]() $A(X_t) = A(Y_t)$
, properties 1 and 2 hold immediately at
$A(X_t) = A(Y_t)$
, properties 1 and 2 hold immediately at
![]() $t + 1$
, and properties 3 and 4 can be shown by a ‘standard’ approach used throughout the paper. In addition, we reuse simple arguments from previous stages to guarantee properties 5 and 6.
$t + 1$
, and properties 3 and 4 can be shown by a ‘standard’ approach used throughout the paper. In addition, we reuse simple arguments from previous stages to guarantee properties 5 and 6.
Consider first the activation sub-step. By Lemma 5.2,
![]() $A(X_t) = A(Y_t)$
with probability at least
$A(X_t) = A(Y_t)$
with probability at least
![]() $\Omega(\omega (n)^{-1})$
. If the number of vertices in the percolation is the same in both copies, we can couple the edge re-sampling so that the updated part of the configuration is identical in both copies. In other words, all new components created in this step are automatically contained in the component matching
$\Omega(\omega (n)^{-1})$
. If the number of vertices in the percolation is the same in both copies, we can couple the edge re-sampling so that the updated part of the configuration is identical in both copies. In other words, all new components created in this step are automatically contained in the component matching
![]() $W_{t+1}$
; this includes all new components whose sizes are greater than
$W_{t+1}$
; this includes all new components whose sizes are greater than
![]() $B_\omega$
. Since none of the new components contributes to
$B_\omega$
. Since none of the new components contributes to
![]() $Z_{t+1}$
, we obtain
$Z_{t+1}$
, we obtain
![]() $Z_{t+1} \le Z_t = O\!\left(\frac{n^{4/3}}{\omega (n)^{1/2}}\right)$
. Therefore,
$Z_{t+1} \le Z_t = O\!\left(\frac{n^{4/3}}{\omega (n)^{1/2}}\right)$
. Therefore,
![]() $A(X_t) = A(Y_t)$
immediately implies properties 1 and 2 at time
$A(X_t) = A(Y_t)$
immediately implies properties 1 and 2 at time
![]() $t+1$
.
$t+1$
.
With probability
![]() $1/q$
, the largest components of
$1/q$
, the largest components of
![]() $X_t$
and
$X_t$
and
![]() $Y_t$
are activated simultaneously. Suppose that this is the case. By Hoeffding’s inequality, for constant
$Y_t$
are activated simultaneously. Suppose that this is the case. By Hoeffding’s inequality, for constant
![]() $K>0$
, we have
$K>0$
, we have
Property 5 and the observation that
![]() ${\mathbb{E}}\left[A(X_t)\right] = L_1(X_t) + \frac{n - L_1(X_t)}{q}$
imply that
${\mathbb{E}}\left[A(X_t)\right] = L_1(X_t) + \frac{n - L_1(X_t)}{q}$
imply that
By noting that
![]() $L_1(Y_0), L_1(X_0) \le n^{2/3} \omega (n)$
, property 6 implies that
$L_1(Y_0), L_1(X_0) \le n^{2/3} \omega (n)$
, property 6 implies that
We denote
![]() $A(X_t) = A(Y_t)$
by m. By inequality (11), with at least constant probability, the random graph for both chains is
$A(X_t) = A(Y_t)$
by m. By inequality (11), with at least constant probability, the random graph for both chains is
![]() $H \sim G\!\left(m, \frac{1 + \lambda m^{-1/3}}{m}\right)$
, where
$H \sim G\!\left(m, \frac{1 + \lambda m^{-1/3}}{m}\right)$
, where
![]() $\lambda \le \omega(m)$
. Let us assume that is the case. Corollary 3.12 ensures that there exists a constant
$\lambda \le \omega(m)$
. Let us assume that is the case. Corollary 3.12 ensures that there exists a constant
![]() $b > 0$
such that, with probability at least
$b > 0$
such that, with probability at least
![]() $1- O\big(\omega (n)^{-3}\big)$
,
$1- O\big(\omega (n)^{-3}\big)$
,
![]() $N_{k}(H,\omega (n)) \ge b \omega (n)^{3 \cdot 2^{k-1}}$
for all
$N_{k}(H,\omega (n)) \ge b \omega (n)^{3 \cdot 2^{k-1}}$
for all
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $n^{2/3}\omega (n)^{-2^k}\rightarrow \infty$
. Since components in H are simultaneously added to both
$n^{2/3}\omega (n)^{-2^k}\rightarrow \infty$
. Since components in H are simultaneously added to both
![]() $X_{t+1}$
and
$X_{t+1}$
and
![]() $Y_{t+1}$
, property 3 is satisfied. Moreover, Lemma 3.2 implies that with high probability
$Y_{t+1}$
, property 3 is satisfied. Moreover, Lemma 3.2 implies that with high probability
![]() $\Omega(n)$
isolated vertices are added to
$\Omega(n)$
isolated vertices are added to
![]() $X_{t+1}$
and
$X_{t+1}$
and
![]() $Y_{t+1}$
, and thus property 4 is satisfied at time
$Y_{t+1}$
, and thus property 4 is satisfied at time
![]() $t+1$
.
$t+1$
.
In addition, Lemma 3.4 and Markov’s inequality imply that there exists a constant
![]() $C_2$
such that
$C_2$
such that
By Lemma 4.3, there exists
![]() $\alpha < 1$
such that with at least probability
$\alpha < 1$
such that with at least probability
![]() $99/100$
$99/100$
where
![]() $\alpha$
is independent of t and n. Potentially, property 6 may not hold when
$\alpha$
is independent of t and n. Potentially, property 6 may not hold when
![]() $\alpha L_1(X_t) < L_1(X_{t+1}) \le L_2(X_t) = O\big(n^{2/3}\big)$
, but then we stop at this point. (We will argue that in this case all the desired properties are also established shortly.) Hence, we suppose otherwise and establish properties 5 and 6 for
$\alpha L_1(X_t) < L_1(X_{t+1}) \le L_2(X_t) = O\big(n^{2/3}\big)$
, but then we stop at this point. (We will argue that in this case all the desired properties are also established shortly.) Hence, we suppose otherwise and establish properties 5 and 6 for
![]() $X_{t+1}$
. Similar bounds hold for
$X_{t+1}$
. Similar bounds hold for
![]() $Y_{t+1}$
.
$Y_{t+1}$
.
By a union bound,
![]() $X_{t+1}$
and
$X_{t+1}$
and
![]() $Y_{t+1}$
have all six properties with probability at least
$Y_{t+1}$
have all six properties with probability at least
![]() $92/100$
, assuming the activation sub-step satisfies all the desired properties, and thus overall with probability
$92/100$
, assuming the activation sub-step satisfies all the desired properties, and thus overall with probability
![]() $\Omega \!\left(\omega (n)^{-1} \right)$
. Inductively, the probability that
$\Omega \!\left(\omega (n)^{-1} \right)$
. Inductively, the probability that
![]() $X_T$
and
$X_T$
and
![]() $Y_T$
satisfy the six properties is
$Y_T$
satisfy the six properties is
Suppose
![]() $X_T$
and
$X_T$
and
![]() $Y_T$
have the six properties. By choosing
$Y_T$
have the six properties. By choosing
![]() $C_1 > 1 / \log \frac{1}{\alpha}$
, properties 5 and 6 imply
$C_1 > 1 / \log \frac{1}{\alpha}$
, properties 5 and 6 imply
and
![]() $\mathcal{R}_1(Y_T) = O\!\left(n^{4/3}\right)$
. While the lemma almost follows from these properties, notice that property 3 does not match the desired bounds on the components in the lemma statement. To fix this issue, we perform one additional step of the coupling.
$\mathcal{R}_1(Y_T) = O\!\left(n^{4/3}\right)$
. While the lemma almost follows from these properties, notice that property 3 does not match the desired bounds on the components in the lemma statement. To fix this issue, we perform one additional step of the coupling.
Consider the activation sub-step at T. Assume again
![]() $A(X_T) = A(Y_T) \,=\!:\, m^{\prime}$
. By Hoeffding’s inequality, for some constant K
′, we obtain
$A(X_T) = A(Y_T) \,=\!:\, m^{\prime}$
. By Hoeffding’s inequality, for some constant K
′, we obtain
 \begin{equation} {\mathbb{P}}\left[ \left| m^{\prime} \cdot \frac{q}{n} - 1 \right| > \frac{K^{\prime}}{n^{1/3}} \right] ={\mathbb{P}}\left[ \left| m^{\prime} - \frac{n}{q} \right| > K^{\prime}n^{2/3} \right] \le \exp\!\left( \frac{-{K^{\prime}}^2 n^{4/3}}{\mathcal{R}_1(X_T)}\right) = O(1). \end{equation}
\begin{equation} {\mathbb{P}}\left[ \left| m^{\prime} \cdot \frac{q}{n} - 1 \right| > \frac{K^{\prime}}{n^{1/3}} \right] ={\mathbb{P}}\left[ \left| m^{\prime} - \frac{n}{q} \right| > K^{\prime}n^{2/3} \right] \le \exp\!\left( \frac{-{K^{\prime}}^2 n^{4/3}}{\mathcal{R}_1(X_T)}\right) = O(1). \end{equation}
Let
![]() $\lambda^{\prime} \,:\!=\, (m^{\prime}qn^{-1} - 1)\cdot m^{\prime 1/3}$
. Inequality (12) implies with at least constant probability the random graph in the percolation step is
$\lambda^{\prime} \,:\!=\, (m^{\prime}qn^{-1} - 1)\cdot m^{\prime 1/3}$
. Inequality (12) implies with at least constant probability the random graph in the percolation step is
![]() $H^{\prime} \sim G\!\left(m^{\prime}, \frac{1 + \lambda^{\prime} m^{\prime-1/3}}{m^{\prime}}\right)$
, where
$H^{\prime} \sim G\!\left(m^{\prime}, \frac{1 + \lambda^{\prime} m^{\prime-1/3}}{m^{\prime}}\right)$
, where
![]() $\lambda^{\prime} \le K^{\prime}$
and
$\lambda^{\prime} \le K^{\prime}$
and
![]() $m^{\prime} \in (n/2q,n)$
. If so, Corollary 3.12 ensures with high probability
$m^{\prime} \in (n/2q,n)$
. If so, Corollary 3.12 ensures with high probability
![]() $\hat{N}_k(X_{T+1}, Y_{T+1}, \omega (n)^{1/2})= \Omega\Big({\omega (n)}^{3 \cdot 2^{k-2}}\Big)$
for all
$\hat{N}_k(X_{T+1}, Y_{T+1}, \omega (n)^{1/2})= \Omega\Big({\omega (n)}^{3 \cdot 2^{k-2}}\Big)$
for all
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $n^{2/3}\omega (n)^{-2^{k-1}}\rightarrow \infty$
.
$n^{2/3}\omega (n)^{-2^{k-1}}\rightarrow \infty$
.
By the preceding argument, with
![]() $\Omega(\omega (n)^{-1})$
probability, the six properties are still valid at step
$\Omega(\omega (n)^{-1})$
probability, the six properties are still valid at step
![]() $T+1$
, so the proof is complete. We note that if we had to stop earlier because property 6 did not hold, we perform one extra step (as above) to ensure that
$T+1$
, so the proof is complete. We note that if we had to stop earlier because property 6 did not hold, we perform one extra step (as above) to ensure that
![]() $\hat{N}_k\big(X_{T+1}, Y_{T+1}, \omega (n)^{1/2}\big)= \Omega\Big({\omega (n)}^{3 \cdot 2^{k-2}}\Big)$
for all
$\hat{N}_k\big(X_{T+1}, Y_{T+1}, \omega (n)^{1/2}\big)= \Omega\Big({\omega (n)}^{3 \cdot 2^{k-2}}\Big)$
for all
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $n^{2/3}\omega (n)^{-2^{k-1}}\rightarrow \infty$
.
$n^{2/3}\omega (n)^{-2^{k-1}}\rightarrow \infty$
.
5.4 A four-phase analysis using random walks couplings: proof of Lemma 2.11
We introduce first some notation that will be useful in the proof of Lemma 2.11. Let
![]() $S(X_0) = \emptyset$
, and given
$S(X_0) = \emptyset$
, and given
![]() $S(X_t)$
,
$S(X_t)$
,
![]() $S(X_{t+1})$
is obtained as follows:
$S(X_{t+1})$
is obtained as follows:
-
i.
 $S(X_{t+1})= S(X_{t})$
;
$S(X_{t+1})= S(X_{t})$
; -
ii. every component in
 $S(X_{t})$
activated by the CM dynamics at time t is removed from
$S(X_{t})$
activated by the CM dynamics at time t is removed from
 $S(X_{t+1})$
; and
$S(X_{t+1})$
; and -
iii. the largest new component (breaking ties arbitrarily) is added to
 $S(X_{t+1})$
.
$S(X_{t+1})$
.
Let
![]() $\mathcal{C}(X_t)$
denote the set of connected components of
$\mathcal{C}(X_t)$
denote the set of connected components of
![]() $X_t$
and note that
$X_t$
and note that
![]() $S(X_t)$
is a subset of
$S(X_t)$
is a subset of
![]() $\mathcal{C}(X_t)$
; we use
$\mathcal{C}(X_t)$
; we use
![]() $|S(X_t)|$
to denote the total number of vertices of the components in
$|S(X_t)|$
to denote the total number of vertices of the components in
![]() $S(X_t)$
. Finally, let
$S(X_t)$
. Finally, let
In the proof of Lemma 2.11, we use the following lemmas.
Lemma 5.3. Let r be an increasing positive function such that
![]() $r(n) = o(n^{1/15})$
and let
$r(n) = o(n^{1/15})$
and let
![]() $c > 0$
be a sufficiently large constant. Suppose
$c > 0$
be a sufficiently large constant. Suppose
![]() $|S(X_t)| \le c t n^{2/3} r(n)$
,
$|S(X_t)| \le c t n^{2/3} r(n)$
,
![]() $Q(X_t) \le t n^{4/3} r(n) + O\!\left(n^{4/3}\right)$
and
$Q(X_t) \le t n^{4/3} r(n) + O\!\left(n^{4/3}\right)$
and
![]() $t \le r(n)/\log r(n)$
. Then, with probability at least
$t \le r(n)/\log r(n)$
. Then, with probability at least
![]() $1 - O\!\left(r(n)^{-1}\right)$
,
$1 - O\!\left(r(n)^{-1}\right)$
,
![]() $|S(X_{t+1})| \le c(t+1) n^{2/3} r(n)$
and
$|S(X_{t+1})| \le c(t+1) n^{2/3} r(n)$
and
![]() $Q(X_{t+1}) \le (t+1) n^{4/3} r(n) + O\!\left(n^{4/3}\right)$
.
$Q(X_{t+1}) \le (t+1) n^{4/3} r(n) + O\!\left(n^{4/3}\right)$
.
Lemma 5.4. Let f be a positive function such that
![]() $f(n)=o\!\left(n^{1/3}\right)$
. Suppose a configuration
$f(n)=o\!\left(n^{1/3}\right)$
. Suppose a configuration
![]() $X_t$
satisfies
$X_t$
satisfies
![]() $\mathcal{R}_1(X_t) = O\!\left(n^{4/3} f(n)^2 ({\log} f(n))^{-1}\right)$
. Let m denote the number of activated vertices in this step, and
$\mathcal{R}_1(X_t) = O\!\left(n^{4/3} f(n)^2 ({\log} f(n))^{-1}\right)$
. Let m denote the number of activated vertices in this step, and
![]() $\lambda\,:\!=\,(mq/n - 1)\cdot m^{1/3}$
. With probability
$\lambda\,:\!=\,(mq/n - 1)\cdot m^{1/3}$
. With probability
![]() $1-O\!\left(f(n)^{-1}\right)$
,
$1-O\!\left(f(n)^{-1}\right)$
,
![]() $m \in (n/2q,n)$
and
$m \in (n/2q,n)$
and
![]() $|\lambda| \le f(n)$
.
$|\lambda| \le f(n)$
.
Lemma 5.5. Let g and h be two increasing positive functions of n. Assume
![]() $g(n) = o(n^{1/6})$
. Let
$g(n) = o(n^{1/6})$
. Let
![]() $X_t$
and
$X_t$
and
![]() $Y_t$
be two random-cluster configuration such that
$Y_t$
be two random-cluster configuration such that
![]() $\hat{N}_{k}(X_t, Y_t, g) \ge b g(n)^{3 \cdot 2^{k-1}}$
for some fixed constant
$\hat{N}_{k}(X_t, Y_t, g) \ge b g(n)^{3 \cdot 2^{k-1}}$
for some fixed constant
![]() $b>0$
independent of n and for all
$b>0$
independent of n and for all
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $n^{2/3}g(n)^{-2^k}\rightarrow \infty$
. Assume also that
$n^{2/3}g(n)^{-2^k}\rightarrow \infty$
. Assume also that
![]() $Z_t \le C n^{4/3}h(n)^{-1}$
for some constant
$Z_t \le C n^{4/3}h(n)^{-1}$
for some constant
![]() $C>0$
. Lastly, assume
$C>0$
. Lastly, assume
![]() $I(X_t), I(Y_t) = \Omega(n)$
. Then for every positive function
$I(X_t), I(Y_t) = \Omega(n)$
. Then for every positive function
![]() $\eta$
there exists a coupling for the activation sub-step of the components of
$\eta$
there exists a coupling for the activation sub-step of the components of
![]() $X_t$
and
$X_t$
and
![]() $Y_t$
such that
$Y_t$
such that
 \begin{equation*}{\mathbb{P}}[A(X_t) = A(Y_t)] \ge 1- 4e^{-2\eta(n)}- \sqrt{\frac{g(n)\eta(n)}{h(n)}} - \frac{\delta}{g(n)},\end{equation*}
\begin{equation*}{\mathbb{P}}[A(X_t) = A(Y_t)] \ge 1- 4e^{-2\eta(n)}- \sqrt{\frac{g(n)\eta(n)}{h(n)}} - \frac{\delta}{g(n)},\end{equation*}
for some constant
![]() $\delta > 0$
independent of n.
$\delta > 0$
independent of n.
The proofs of these lemmas are given in Section 5.4.1. In particular, as mentioned, to prove Lemma 5.5 we use a precise estimate on the maximum of a random walk on
![]() $\mathbb{Z}$
with steps of different sizes (see Theorem 5.7).
$\mathbb{Z}$
with steps of different sizes (see Theorem 5.7).
Proof of Lemma 2.11. The coupling has four phases: in phase 1 we will consider
![]() $O({\log} \log \log \log n)$
steps of the coupling,
$O({\log} \log \log \log n)$
steps of the coupling,
![]() $O({\log} \log \log n)$
steps in phase 2,
$O({\log} \log \log n)$
steps in phase 2,
![]() $O({\log} \log n)$
steps in phase 3 and phase 4 consists of
$O({\log} \log n)$
steps in phase 3 and phase 4 consists of
![]() $O({\log}\ n)$
steps.
$O({\log}\ n)$
steps.
We will keep track of the random variables
![]() $ \mathcal{R}_1(X_t), \mathcal{R}_1(Y_t), I(X_t), I(Y_t), Z_t$
and
$ \mathcal{R}_1(X_t), \mathcal{R}_1(Y_t), I(X_t), I(Y_t), Z_t$
and
![]() $\hat{N}_{k}(t, g)$
for a function g we shall carefully choose for each phase, and use these random variables to derive bounds on the probability of various events.
$\hat{N}_{k}(t, g)$
for a function g we shall carefully choose for each phase, and use these random variables to derive bounds on the probability of various events.
Phase 1. We set
![]() $g_1(n) =\omega (n)^{1/2}$
and
$g_1(n) =\omega (n)^{1/2}$
and
![]() $h_1(n) = K^2\omega (n)^{1/2}$
where
$h_1(n) = K^2\omega (n)^{1/2}$
where
![]() $K>0$
is a constant we choose. Let
$K>0$
is a constant we choose. Let
![]() $a_1 \,:\!=\, 1 - \frac{1}{2q}$
and let
$a_1 \,:\!=\, 1 - \frac{1}{2q}$
and let
![]() $T_1\,:\!=\,-12\log_{a_1} ({\log} \log \log n)$
, and we fix
$T_1\,:\!=\,-12\log_{a_1} ({\log} \log \log n)$
, and we fix
![]() $t < T_1$
. Suppose we have
$t < T_1$
. Suppose we have
![]() $\mathcal{R}_1(X_t) + \mathcal{R}_1(Y_t) \le C_1 n^{4/3}$
,
$\mathcal{R}_1(X_t) + \mathcal{R}_1(Y_t) \le C_1 n^{4/3}$
,
![]() $I(X_t), I(Y_t) = \Omega(n)$
, and
$I(X_t), I(Y_t) = \Omega(n)$
, and
![]() $\hat{N}_{k}(t, g_1) = \Omega\Big(g_1(n)^{3 \cdot 2^{k-1} }\Big)$
for all
$\hat{N}_{k}(t, g_1) = \Omega\Big(g_1(n)^{3 \cdot 2^{k-1} }\Big)$
for all
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $n^{2/3}g_1(n)^{-2^k}\rightarrow \infty$
, where
$n^{2/3}g_1(n)^{-2^k}\rightarrow \infty$
, where
![]() $C_1 > 0$
is a large constant that we choose later.
$C_1 > 0$
is a large constant that we choose later.
By Lemma 5.5, for a sufficiently large constant
![]() $K>0$
, we obtain a coupling for the activation of
$K>0$
, we obtain a coupling for the activation of
![]() $X_t$
and
$X_t$
and
![]() $Y_t$
such that the same number of vertices are activated in
$Y_t$
such that the same number of vertices are activated in
![]() $X_t$
and
$X_t$
and
![]() $Y_t$
, with probability at least
$Y_t$
, with probability at least
 \begin{equation*}1- 4e^{-2K}- \sqrt{\frac{K\omega (n)^{1/2}}{K^2\omega (n)^{1/2}}} - \frac{\delta}{\omega (n)^{1/2}} \ge 1 - \frac{1}{16q^2}.\end{equation*}
\begin{equation*}1- 4e^{-2K}- \sqrt{\frac{K\omega (n)^{1/2}}{K^2\omega (n)^{1/2}}} - \frac{\delta}{\omega (n)^{1/2}} \ge 1 - \frac{1}{16q^2}.\end{equation*}
By Lemma 5.4,
![]() $A(X_t) \in (n/2q,n)$
and
$A(X_t) \in (n/2q,n)$
and
![]() $\lambda \,:\!=\, (A(X_t)q/n - 1)\cdot A(X_t)^{1/3} = O(1)$
with probability at least
$\lambda \,:\!=\, (A(X_t)q/n - 1)\cdot A(X_t)^{1/3} = O(1)$
with probability at least
![]() $ 1 - \frac{1}{16q^2}$
. It follows a union bound that
$ 1 - \frac{1}{16q^2}$
. It follows a union bound that
![]() $A(X_t) = A(Y_t)$
,
$A(X_t) = A(Y_t)$
,
![]() $A(X_t) \in (n/2q,n)$
and
$A(X_t) \in (n/2q,n)$
and
![]() $\lambda = O(1)$
with probability
$\lambda = O(1)$
with probability
![]() $1 - \frac{1}{8q^2}$
. We call this event
$1 - \frac{1}{8q^2}$
. We call this event
![]() $\mathcal{H}^1_t$
.
$\mathcal{H}^1_t$
.
Let
![]() $D^{\prime}_t$
denote the inactivated components in
$D^{\prime}_t$
denote the inactivated components in
![]() $D(X_t) \cup D(Y_t)$
at the step t, and
$D(X_t) \cup D(Y_t)$
at the step t, and
![]() $M^{\prime}_t$
the inactivated components in
$M^{\prime}_t$
the inactivated components in
![]() $M(X_t) \cup M(X_t)$
. Observe that
$M(X_t) \cup M(X_t)$
. Observe that
Similarly,
Hence, by Markov’s inequality and independence between activation of components in
![]() $D^{\prime}_t$
and components in
$D^{\prime}_t$
and components in
![]() $M^{\prime}_t$
, with probability at least
$M^{\prime}_t$
, with probability at least
![]() $1/4q^2$
, the activation sub-step is such that
$1/4q^2$
, the activation sub-step is such that
and
We denote this event by
![]() $\mathcal{H}^2_t$
. By a union bound,
$\mathcal{H}^2_t$
. By a union bound,
![]() $\mathcal{H}^1_t$
and
$\mathcal{H}^1_t$
and
![]() $\mathcal{H}^2_t$
happen simultaneously with probability
$\mathcal{H}^2_t$
happen simultaneously with probability
![]() $1/8q^2$
.
$1/8q^2$
.
Suppose all these events indeed happen; then we couple the percolation step so that the components newly generated in both copies are exactly identical, and we claim that all of the following holds with at least constant probability:
-
1.
 $\mathcal{R}_1(X_{t+1}) + \mathcal{R}_1(Y_{t+1}) \le C_1 n^{4/3}$
;
$\mathcal{R}_1(X_{t+1}) + \mathcal{R}_1(Y_{t+1}) \le C_1 n^{4/3}$
; -
2.
 $Z_{t+1} \le a_1 Z_t$
;
$Z_{t+1} \le a_1 Z_t$
; -
3.
 $I(X_{t+1}), I(Y_{t+1}) = \Omega(n)$
;
$I(X_{t+1}), I(Y_{t+1}) = \Omega(n)$
; -
4.
 $\hat{N}_{k}(t + 1, g_1) = \Omega\Big(g_1(n)^{3 \cdot 2^{k-1}}\Big)$
for all
$\hat{N}_{k}(t + 1, g_1) = \Omega\Big(g_1(n)^{3 \cdot 2^{k-1}}\Big)$
for all
 $k \ge 1$
such that
$k \ge 1$
such that
 $n^{2/3}g_1(n)^{-2^k}\rightarrow \infty$
.
$n^{2/3}g_1(n)^{-2^k}\rightarrow \infty$
.
First, note that
![]() $Z_{t+1}$
can not possibly increase because the matching
$Z_{t+1}$
can not possibly increase because the matching
![]() $W_{t+1}$
can only grow under the coupling if indeed
$W_{t+1}$
can only grow under the coupling if indeed
![]() $A(X_t) = A(Y_t)$
. Observe that only the inactivated components in
$A(X_t) = A(Y_t)$
. Observe that only the inactivated components in
![]() $X_t$
and
$X_t$
and
![]() $Y_t$
would contribute to
$Y_t$
would contribute to
![]() $Z_{t+1}$
, so
$Z_{t+1}$
, so
Next, we establish the properties 3 and 4. For this, notice that the percolation step is distributed as a
![]() $H \sim $
$H \sim $
![]() $G\!\left(A(X_t), \frac{1 + \lambda A(X_t)^{-1/3}}{A(X_t)}\right)$
random graph. Corollary 3.12 implies
$G\!\left(A(X_t), \frac{1 + \lambda A(X_t)^{-1/3}}{A(X_t)}\right)$
random graph. Corollary 3.12 implies
![]() $N_{k}(H, g_1) = \Omega\Big( g_1(n)^{3 \cdot 2^{k-1}}\Big)$
for all
$N_{k}(H, g_1) = \Omega\Big( g_1(n)^{3 \cdot 2^{k-1}}\Big)$
for all
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $n^{2/3}g_1(n)^{-2^k}\rightarrow \infty$
, with probability at least
$n^{2/3}g_1(n)^{-2^k}\rightarrow \infty$
, with probability at least
![]() $1 - O\!\left(g_1(n)^{-3}\right) $
. Moreover, Lemma 3.2 implies that with high probability
$1 - O\!\left(g_1(n)^{-3}\right) $
. Moreover, Lemma 3.2 implies that with high probability
![]() $I(H) = \Omega(n)$
. Since the percolation step is coupled, this implies that both
$I(H) = \Omega(n)$
. Since the percolation step is coupled, this implies that both
![]() $X_{t+1}$
and
$X_{t+1}$
and
![]() $Y_{t+1}$
will have all the components in H, so we have
$Y_{t+1}$
will have all the components in H, so we have
![]() $\hat{N}_{k}(t+1, g_1) = \Omega\Big(g_1(n)^{3 \cdot 2^{k-1}}\Big)$
for all
$\hat{N}_{k}(t+1, g_1) = \Omega\Big(g_1(n)^{3 \cdot 2^{k-1}}\Big)$
for all
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $n^{2/3}g_1(n)^{-2^k}\rightarrow \infty$
, and
$n^{2/3}g_1(n)^{-2^k}\rightarrow \infty$
, and
![]() $I(X_{t+1}), I(Y_{t+1}) = \Omega(n)$
, w.h.p.
$I(X_{t+1}), I(Y_{t+1}) = \Omega(n)$
, w.h.p.
Finally, assuming that
![]() $|\lambda| = O(1)$
, by Lemma 3.9 and Markov’s inequality, there exists
$|\lambda| = O(1)$
, by Lemma 3.9 and Markov’s inequality, there exists
![]() $C_2 > 0$
such that
$C_2 > 0$
such that
![]() ${\mathbb{E}} \left[\mathcal{R}_1(H) \right] = C_2n^{4/3}$
with probability at least
${\mathbb{E}} \left[\mathcal{R}_1(H) \right] = C_2n^{4/3}$
with probability at least
![]() $99/100$
. Then
$99/100$
. Then
 \begin{align*} \mathcal{R}_1(X_{t+1}) + \mathcal{R}_1(Y_{t+1}) &= \sum\nolimits_{\mathcal{C} \in D^{\prime}_t} |\mathcal{C}|^2 + \sum\nolimits_{\mathcal{C} \in M^{\prime}_t} |\mathcal{C}|^2 + \mathcal{R}_1(H) \\ & \le a_1 \left(\mathcal{R}_1(X_{t}) + \mathcal{R}_1(Y_{t})\right) + C_2n^{4/3} \le a_1 C_1 n^{4/3} + C_2n^{4/3} \le C_1 n^{4/3}, \end{align*}
\begin{align*} \mathcal{R}_1(X_{t+1}) + \mathcal{R}_1(Y_{t+1}) &= \sum\nolimits_{\mathcal{C} \in D^{\prime}_t} |\mathcal{C}|^2 + \sum\nolimits_{\mathcal{C} \in M^{\prime}_t} |\mathcal{C}|^2 + \mathcal{R}_1(H) \\ & \le a_1 \left(\mathcal{R}_1(X_{t}) + \mathcal{R}_1(Y_{t})\right) + C_2n^{4/3} \le a_1 C_1 n^{4/3} + C_2n^{4/3} \le C_1 n^{4/3}, \end{align*}
for large enough
![]() $C_1$
. A union bound implies that all four properties hold with at least constant probability
$C_1$
. A union bound implies that all four properties hold with at least constant probability
![]() $\varrho > 0$
.
$\varrho > 0$
.
Thus, the probability that at each step of update all four properties can be maintained throughout Phase 1 is at least
If property 2 holds at the end of Phase 1, we have
To facilitate discussions in Phase 2, we show that the two copies of chains satisfy one additional property at the end of Phase 1. In particular, there exist a lower bound for the number of components in a different set of intervals. We consider the last percolation step in Phase 1. Then, Corollary 3.12 with
![]() $g_2(n) \,:\!=\, \left( \log\log\log n \cdot \log\log\log\log n \right)^2$
implies
$g_2(n) \,:\!=\, \left( \log\log\log n \cdot \log\log\log\log n \right)^2$
implies
![]() $\hat{N}_{k}(T_1, g_2) = \Omega\Big(g_2(n)^{3 \cdot 2^{k-1}}\Big)$
for all
$\hat{N}_{k}(T_1, g_2) = \Omega\Big(g_2(n)^{3 \cdot 2^{k-1}}\Big)$
for all
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $n^{2/3}g_2(n)^{-2^k}\rightarrow \infty$
, with high probability.
$n^{2/3}g_2(n)^{-2^k}\rightarrow \infty$
, with high probability.
Recall S(X) and Q(X) defined at the beginning of Section 5.4. In Phase 2, 3 and 4, a new element of the argument is to also control the behaviour
![]() $S(X_t)$
and
$S(X_t)$
and
![]() $Q(X_t)$
. We provide a general result that will be used in the analysis of the three phases:
$Q(X_t)$
. We provide a general result that will be used in the analysis of the three phases:
Claim 5.6. Given positive increasing functions T, g, h and r that tend to infinity and satisfy
-
1.
 $g(n) = o(n^{1/6})$
;
$g(n) = o(n^{1/6})$
; -
2.
 $T = o(g)$
;
$T = o(g)$
; -
3.
 $r(n) = o(n^{1/15})$
;
$r(n) = o(n^{1/15})$
; -
4.
 $T(n)^2 \cdot r(n)^2 \leq g(n)^2/\log g(n)$
;
$T(n)^2 \cdot r(n)^2 \leq g(n)^2/\log g(n)$
; -
5.
 $T(n) \leq r(n) / \log r(n)$
;
$T(n) \leq r(n) / \log r(n)$
; -
6.
 $ g(n) \log g(n) \leq h(n)^{1/3}$
.
$ g(n) \log g(n) \leq h(n)^{1/3}$
.
and random-cluster configurations
![]() $X_0, Y_0$
satisfying
$X_0, Y_0$
satisfying
-
1.
 $Z_0 = O\!\left( \frac{n^{4/3}}{h(n)} \right)$
;
$Z_0 = O\!\left( \frac{n^{4/3}}{h(n)} \right)$
; -
2.
 $|S(X_0)|, |S(Y_0)| \le n^{2/3} r(n) $
;
$|S(X_0)|, |S(Y_0)| \le n^{2/3} r(n) $
; -
3.
 $Q(X_0), Q(Y_0) = O(n^{4/3}r(n)) $
;
$Q(X_0), Q(Y_0) = O(n^{4/3}r(n)) $
; -
4.
 $I(X_{0}), I(Y_{0}) = \Omega(n)$
;
$I(X_{0}), I(Y_{0}) = \Omega(n)$
; -
5.
 $\hat{N}_{k}(0, g) = \Omega\!\left( g(n)^{3 \cdot 2^{k-1}}\right)$
for all
$\hat{N}_{k}(0, g) = \Omega\!\left( g(n)^{3 \cdot 2^{k-1}}\right)$
for all
 $k \ge 1$
such that
$k \ge 1$
such that
 $n^{2/3}g(n)^{-2^k}\rightarrow \infty$
.
$n^{2/3}g(n)^{-2^k}\rightarrow \infty$
.
There exists a coupling of CM steps such that after
![]() $T=T(n)$
steps, with
$T=T(n)$
steps, with
![]() $\Omega(1)$
probability,
$\Omega(1)$
probability,
-
1.
 $Z_T = O\!\left( \frac{n^{4/3}}{a^{T(n)}} \right)$
;
$Z_T = O\!\left( \frac{n^{4/3}}{a^{T(n)}} \right)$
; -
2.
 $|S(X_T)|, |S(Y_T)| = O(n^{2/3} r(n) T(n)) $
;
$|S(X_T)|, |S(Y_T)| = O(n^{2/3} r(n) T(n)) $
; -
3.
 $Q(X_T), Q(Y_T) = O(n^{4/3}r(n)T(n)) $
;
$Q(X_T), Q(Y_T) = O(n^{4/3}r(n)T(n)) $
; -
4.
 $I(X_{T}), I(Y_{T}) = \Omega(n)$
;
$I(X_{T}), I(Y_{T}) = \Omega(n)$
; -
5. If a function g ′ satisfies
 $g^{\prime}\geq g$
and
$g^{\prime}\geq g$
and
 $g^{\prime}(n) = o\!\left(n^{1/3}\right)$
, then
$g^{\prime}(n) = o\!\left(n^{1/3}\right)$
, then
 $\hat{N}_{k}(T, g^{\prime}) = \Omega\!\left( g^{\prime}(n)^{3 \cdot 2^{k-1}}\right)$
for all
$\hat{N}_{k}(T, g^{\prime}) = \Omega\!\left( g^{\prime}(n)^{3 \cdot 2^{k-1}}\right)$
for all
 $k \ge 1$
such that
$k \ge 1$
such that
 $n^{2/3}g^{\prime}(n)^{-2^k}\rightarrow \infty$
.
$n^{2/3}g^{\prime}(n)^{-2^k}\rightarrow \infty$
.
Proof of this claim is provided later in Section 5.4.1.
Phase 2. Let
![]() $a= q/(q-1)$
. For Phase 2, we set
$a= q/(q-1)$
. For Phase 2, we set
![]() $g_2(n) = \left( \log\log\log n \cdot \log\log\log\log n \right)^2$
,
$g_2(n) = \left( \log\log\log n \cdot \log\log\log\log n \right)^2$
,
![]() $g_3(n) = ({\log}\log n \cdot \log \log \log n )^2$
,
$g_3(n) = ({\log}\log n \cdot \log \log \log n )^2$
,
![]() $h_2(n) = \left({\log} \log \log n\right)^{12} $
,
$h_2(n) = \left({\log} \log \log n\right)^{12} $
,
![]() $r_2(n) = 13 \log_a \log \log n \cdot \log \log_a \log \log n$
and
$r_2(n) = 13 \log_a \log \log n \cdot \log \log_a \log \log n$
and
![]() $T_2 = T_1 + 12 \log_a \log \log n$
. Notice these functions satisfy the conditions of Claim 5.6:
$T_2 = T_1 + 12 \log_a \log \log n$
. Notice these functions satisfy the conditions of Claim 5.6:
-
1.
 $g_2(n) = o(n^{1/6})$
;
$g_2(n) = o(n^{1/6})$
; -
2.
 $T_2 - T_1 = o(g_2(n))$
;
$T_2 - T_1 = o(g_2(n))$
; -
3.
 $r_2(n) = o(n^{1/15})$
;
$r_2(n) = o(n^{1/15})$
; -
4.
 $(T_2 - T_1)^2 r_2(n)^2 \le 10^6({\log}_a \log \log n)^4 ( \log \log_a \log \log n)^2 \le g_2(n)^2/\log g_2(n)$
;
$(T_2 - T_1)^2 r_2(n)^2 \le 10^6({\log}_a \log \log n)^4 ( \log \log_a \log \log n)^2 \le g_2(n)^2/\log g_2(n)$
; -
5.
 $T_2 - T_1 = 12 \log_a \log \log n \le r_2(n)/\log r_2(n)$
;
$T_2 - T_1 = 12 \log_a \log \log n \le r_2(n)/\log r_2(n)$
; -
6.
 $g_2(n)/\log g_2(n) \le \left({\log} \log \log n\right)^{4} = h_2(n)^{1/3}$
.
$g_2(n)/\log g_2(n) \le \left({\log} \log \log n\right)^{4} = h_2(n)^{1/3}$
.
Suppose that we have all the desired properties from Phase 1, so at the beginning of Phase 2 we have:
-
1.
 $Z_{T_1} = O\!\left( \frac{n^{4/3}}{({\log} \log \log n)^{12}} \right) = O\!\left( \frac{n^{4/3}}{h_2(n)}\right)$
;
$Z_{T_1} = O\!\left( \frac{n^{4/3}}{({\log} \log \log n)^{12}} \right) = O\!\left( \frac{n^{4/3}}{h_2(n)}\right)$
; -
2.
 $S(X_{T_1}) \le \sqrt{ R_1(X_{T_1})} \le n^{2/3}r_2(n)$
,
$S(X_{T_1}) \le \sqrt{ R_1(X_{T_1})} \le n^{2/3}r_2(n)$
,
 $S(Y_{T_1}) = \sqrt{ R_1(Y_{T_1})} \le n^{2/3}r_2(n)$
;
$S(Y_{T_1}) = \sqrt{ R_1(Y_{T_1})} \le n^{2/3}r_2(n)$
; -
3.
 $I(X_{T_1}) = \Omega(n), I(Y_{T_1}) = \Omega(n)$
;
$I(X_{T_1}) = \Omega(n), I(Y_{T_1}) = \Omega(n)$
; -
4.
 $ Q(X_{T_1}) \le R_1(X_{T_1}) = O\!\left(n^{4/3}\right)$
,
$ Q(X_{T_1}) \le R_1(X_{T_1}) = O\!\left(n^{4/3}\right)$
,
 $Q(Y_{T_1}) \le R_1(Y_{T_1}) = O\!\left(n^{4/3}\right)$
;
$Q(Y_{T_1}) \le R_1(Y_{T_1}) = O\!\left(n^{4/3}\right)$
; -
5.
 $\hat{N}_{k}(T_1, g_2) =\Omega\!\left( g_2(n)^{3 \cdot 2^{k-1}}\right)$
for all
$\hat{N}_{k}(T_1, g_2) =\Omega\!\left( g_2(n)^{3 \cdot 2^{k-1}}\right)$
for all
 $k \ge 1$
such that
$k \ge 1$
such that
 $n^{2/3}g_2(n)^{-2^k}\rightarrow \infty$
.
$n^{2/3}g_2(n)^{-2^k}\rightarrow \infty$
.
Claim 5.6 implies there exists a coupling such that with
![]() $\Omega(1)$
probability
$\Omega(1)$
probability
-
1.
 $Z_{T_2} = O\!\left( \frac{n^{4/3}}{({\log} \log n)^{12}}\right)$
;
$Z_{T_2} = O\!\left( \frac{n^{4/3}}{({\log} \log n)^{12}}\right)$
; -
2.
 $\lvert S(X_{T_2}) \rvert \le n^{2/3} r_2(n) \log_a \log \log n$
,
$\lvert S(X_{T_2}) \rvert \le n^{2/3} r_2(n) \log_a \log \log n$
,
 $\lvert S(Y_{T_2}) \rvert \le n^{2/3} r_2(n) \log_a \log \log n$
;
$\lvert S(Y_{T_2}) \rvert \le n^{2/3} r_2(n) \log_a \log \log n$
; -
3.
 $ Q(Y_{T_2}) = O(n^{4/3} r_2(n) \log_a \log \log n)$
,
$ Q(Y_{T_2}) = O(n^{4/3} r_2(n) \log_a \log \log n)$
,
 $Q(X_{T_2}) = O(n^{4/3} r_2(n) \log_a \log \log n)$
;
$Q(X_{T_2}) = O(n^{4/3} r_2(n) \log_a \log \log n)$
; -
4.
 $I(X_{T_2}) = \Omega(n), I(Y_{T_2}) = \Omega(n)$
;
$I(X_{T_2}) = \Omega(n), I(Y_{T_2}) = \Omega(n)$
; -
5.
 $\hat{N}_{k}(T_2, g_3) = \Omega( g_3(n)^{3 \cdot 2^{k-1}})$
for all
$\hat{N}_{k}(T_2, g_3) = \Omega( g_3(n)^{3 \cdot 2^{k-1}})$
for all
 $k \ge 1$
such that
$k \ge 1$
such that
 $n^{2/3}g_3(n)^{-2^k}\rightarrow \infty$
.
$n^{2/3}g_3(n)^{-2^k}\rightarrow \infty$
.
Phase 3. Suppose the coupling in Phase 2 succeeds.
For Phase 3, we set the functions as
![]() $g_3(n) = \left( \log\log n \cdot \log\log\log n \right)^2$
,
$g_3(n) = \left( \log\log n \cdot \log\log\log n \right)^2$
,
![]() $g_4(n) = ({\log}\ n \cdot \log \log n )^2$
,
$g_4(n) = ({\log}\ n \cdot \log \log n )^2$
,
![]() $h_3(n) = \left({\log} \log n\right)^{12} $
,
$h_3(n) = \left({\log} \log n\right)^{12} $
,
![]() $r_3(n) = 20\log_a \log n \cdot \log \log_a \log n$
and
$r_3(n) = 20\log_a \log n \cdot \log \log_a \log n$
and
![]() $T_3 = T_2 + 10 \log_a \log n$
. Claim 5.6 implies there exists a coupling such that with
$T_3 = T_2 + 10 \log_a \log n$
. Claim 5.6 implies there exists a coupling such that with
![]() $\Omega(1)$
probability
$\Omega(1)$
probability
-
1.
 $Z_{T_3} = O\!\left( \frac{n^{4/3}}{({\log}\ n)^{10}}\right)$
;
$Z_{T_3} = O\!\left( \frac{n^{4/3}}{({\log}\ n)^{10}}\right)$
; -
2.
 $|S(X_{T_3})| = O(n^{2/3} r_3(n) \log_a \log n ), |S(Y_{T_3})| = O(n^{2/3} r_3(n) \log_a \log n)$
;
$|S(X_{T_3})| = O(n^{2/3} r_3(n) \log_a \log n ), |S(Y_{T_3})| = O(n^{2/3} r_3(n) \log_a \log n)$
; -
3.
 $Q(X_{T_3}) = O(n^{4/3} r_3(n) \log_a \log n)$
,
$Q(X_{T_3}) = O(n^{4/3} r_3(n) \log_a \log n)$
,
 $ Q(Y_{T_3}) = O(n^{2/3} r_3(n) \log_a \log n)$
;
$ Q(Y_{T_3}) = O(n^{2/3} r_3(n) \log_a \log n)$
; -
4.
 $I(X_{T_3}) = \Omega(n), I(Y_{T_3}) = \Omega(n)$
,
$I(X_{T_3}) = \Omega(n), I(Y_{T_3}) = \Omega(n)$
, -
5.
 $\hat{N}_{k}(T_3, g_4) = \Omega( g_4(n)^{3 \cdot 2^{k-1}})$
for all
$\hat{N}_{k}(T_3, g_4) = \Omega( g_4(n)^{3 \cdot 2^{k-1}})$
for all
 $k \ge 1$
such that
$k \ge 1$
such that
 $n^{2/3}g_4(n)^{-2^k}\rightarrow \infty$
.
$n^{2/3}g_4(n)^{-2^k}\rightarrow \infty$
.
Phase 4. Suppose the coupling in Phase 3 succeeds. Let
![]() $C_2$
be a constant greater than
$C_2$
be a constant greater than
![]() $4/3$
. We set
$4/3$
. We set
![]() $g_4(n) = \left( \log n \cdot \log\log n \right)^2$
,
$g_4(n) = \left( \log n \cdot \log\log n \right)^2$
,
![]() $h_4(n) = \left({\log}\ n\right)^{10} $
,
$h_4(n) = \left({\log}\ n\right)^{10} $
,
![]() $r_4(n) = 2C_2 \log_a n \cdot \log \log_a n$
and
$r_4(n) = 2C_2 \log_a n \cdot \log \log_a n$
and
![]() $T_4 = T_3 + C_2 \log_a n$
. Claim 5.6 implies there exists a coupling such that with
$T_4 = T_3 + C_2 \log_a n$
. Claim 5.6 implies there exists a coupling such that with
![]() $\Omega(1)$
probability
$\Omega(1)$
probability
![]() $Z_{T_4} < 1$
. Since
$Z_{T_4} < 1$
. Since
![]() $Z_{T_4}$
is a non-negative integer value random variable,
$Z_{T_4}$
is a non-negative integer value random variable,
![]() ${\mathbb{P}}[Z_{T_4} < 1] = {\mathbb{P}}[Z_{T_4} = 0]$
. When
${\mathbb{P}}[Z_{T_4} < 1] = {\mathbb{P}}[Z_{T_4} = 0]$
. When
![]() $Z_{T_4} = 0$
,
$Z_{T_4} = 0$
,
![]() $X_{T_4}$
and
$X_{T_4}$
and
![]() $Y_{T_4}$
have the same component structure.
$Y_{T_4}$
have the same component structure.
Therefore, if the coupling in every phase succeeds,
![]() $X_{T_4}$
and
$X_{T_4}$
and
![]() $Y_{T_4}$
have the same component structure. The probability that coupling in Phase 1 succeeds is
$Y_{T_4}$
have the same component structure. The probability that coupling in Phase 1 succeeds is
![]() $\left({\log} \log \log n\right)^{- O({\log}_\varrho (1/a_1))}$
. Conditional on the success of their previous phases, couplings in Phase 2, 3 and 4 succeed respectively with at least constant probability. Thus, the entire coupling succeeds with probability
$\left({\log} \log \log n\right)^{- O({\log}_\varrho (1/a_1))}$
. Conditional on the success of their previous phases, couplings in Phase 2, 3 and 4 succeed respectively with at least constant probability. Thus, the entire coupling succeeds with probability
where
![]() $\beta$
is a positive constant.
$\beta$
is a positive constant.
5.4.1 Proof of lemmas used in Section 5.4
Proof of Claim 5.6. We will show that given the following properties at any time
![]() $t \le T(n)$
, we can maintain them at time
$t \le T(n)$
, we can maintain them at time
![]() $t+1$
with probability at least
$t+1$
with probability at least
![]() $1 - O(g(n)^{-1}) - O(r(n)^{-1})$
:
$1 - O(g(n)^{-1}) - O(r(n)^{-1})$
:
-
1.
 $Z_t = O\!\left( \frac{n^{4/3}}{h(n)} \right)$
;
$Z_t = O\!\left( \frac{n^{4/3}}{h(n)} \right)$
; -
2.
 $|S(X_t)|, |S(Y_t)| \le C_3 t n^{2/3} r(n) $
for a constant
$|S(X_t)|, |S(Y_t)| \le C_3 t n^{2/3} r(n) $
for a constant
 $C_3 > 0$
;
$C_3 > 0$
; -
3.
 $Q(X_t), Q(Y_t) \le t n^{4/3}r(n) + O\!\left(n^{4/3}\right)$
;
$Q(X_t), Q(Y_t) \le t n^{4/3}r(n) + O\!\left(n^{4/3}\right)$
; -
4.
 $I(X_{t}), I(Y_{t}) = \Omega(n)$
;
$I(X_{t}), I(Y_{t}) = \Omega(n)$
; -
5.
 $\hat{N}_{k}(t, g) = \Omega( g(n)^{3 \cdot 2^{k-1}})$
for all
$\hat{N}_{k}(t, g) = \Omega( g(n)^{3 \cdot 2^{k-1}})$
for all
 $k \ge 1$
such that
$k \ge 1$
such that
 $n^{2/3}g(n)^{-2^k}\rightarrow \infty$
.
$n^{2/3}g(n)^{-2^k}\rightarrow \infty$
.
By assumption,
![]() $t \le T(n) \le r(n)/\log r(n)$
. According to Lemma 5.3,
$t \le T(n) \le r(n)/\log r(n)$
. According to Lemma 5.3,
![]() $X_{t+1}$
and
$X_{t+1}$
and
![]() $Y_{t+1}$
retain properties 2 and 3 with probability at least
$Y_{t+1}$
retain properties 2 and 3 with probability at least
![]() $1 - O(r(n)^{-1})$
.
$1 - O(r(n)^{-1})$
.
Given properties 1, 4 and 5, Lemma 5.5 (with
![]() $\eta = \log g(n)/2$
) implies that there exist a constant
$\eta = \log g(n)/2$
) implies that there exist a constant
![]() $\delta > 0$
and a coupling for the activation sub-step of
$\delta > 0$
and a coupling for the activation sub-step of
![]() $X_t$
and
$X_t$
and
![]() $Y_t$
$Y_t$
 \begin{align*} {\mathbb{P}} \left[A(X_t) = A(Y_t) \right] & \ge 1- 4e^{-\log g(n)}- \sqrt{\frac{g(n)\log g(n)}{2h(n)}} - \frac{\delta}{g(n)} \\ & = 1 - O\!\left(\frac{1}{h(n)^{1/3}} \right) - O\!\left(\frac{1}{g(n)}\right) = 1 - O\!\left(\frac{1}{g(n)}\right). \end{align*}
\begin{align*} {\mathbb{P}} \left[A(X_t) = A(Y_t) \right] & \ge 1- 4e^{-\log g(n)}- \sqrt{\frac{g(n)\log g(n)}{2h(n)}} - \frac{\delta}{g(n)} \\ & = 1 - O\!\left(\frac{1}{h(n)^{1/3}} \right) - O\!\left(\frac{1}{g(n)}\right) = 1 - O\!\left(\frac{1}{g(n)}\right). \end{align*}
Note that condition
![]() $ g(n) \log g(n) \leq h(n)^{1/3}$
is used to deduce the inequality above. Suppose
$ g(n) \log g(n) \leq h(n)^{1/3}$
is used to deduce the inequality above. Suppose
![]() $A(X_t)=A(Y_t)$
; we couple components generated in the percolation step and preclude the growth of
$A(X_t)=A(Y_t)$
; we couple components generated in the percolation step and preclude the growth of
![]() $Z_t$
. Hence,
$Z_t$
. Hence,
![]() $Z_{t+1} \le Z_t = O\!\left( \frac{n^{4/3}}{h(n)} \right)$
, and property 1 holds immediately.
$Z_{t+1} \le Z_t = O\!\left( \frac{n^{4/3}}{h(n)} \right)$
, and property 1 holds immediately.
Recall that
![]() $\mathcal{R}_1(X) = Q(X) + \lvert S(X) \rvert^2$
. Properties 2 and 3 imply that
$\mathcal{R}_1(X) = Q(X) + \lvert S(X) \rvert^2$
. Properties 2 and 3 imply that
![]() $\mathcal{R}_1(X_t) = O(t^2 n^{4/3} r(n)^2)$
and
$\mathcal{R}_1(X_t) = O(t^2 n^{4/3} r(n)^2)$
and
![]() $\mathcal{R}_1(Y_t) = O(t^2 n^{4/3} r(n)^2)$
. Since
$\mathcal{R}_1(Y_t) = O(t^2 n^{4/3} r(n)^2)$
. Since
![]() $t < T(n)$
and
$t < T(n)$
and
![]() $T(n)^2 \cdot r(n)^2 \leq g(n)^2/\log g(n)$
, we can upper bound
$T(n)^2 \cdot r(n)^2 \leq g(n)^2/\log g(n)$
, we can upper bound
![]() $\mathcal{R}_1(X_t)$
and
$\mathcal{R}_1(X_t)$
and
![]() $\mathcal{R}_1(Y_t) $
by
$\mathcal{R}_1(Y_t) $
by
We establish properties 4 and 5 with a similar argument as the one used in Phase 1.
Let
![]() $H_t\sim G(A(X_t), n/q)$
. Due to Lemma 5.4 (with
$H_t\sim G(A(X_t), n/q)$
. Due to Lemma 5.4 (with
![]() $f = g$
) and Corollary 3.12 with probability at least
$f = g$
) and Corollary 3.12 with probability at least
![]() $1 - O(g(n)^{-1})$
,
$1 - O(g(n)^{-1})$
,
![]() $N_{k}(H_t,g) = \Omega( g(n)^{3 \cdot 2^{k-1}})$
for all
$N_{k}(H_t,g) = \Omega( g(n)^{3 \cdot 2^{k-1}})$
for all
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $n^{2/3}g(n)^{-2^k}\rightarrow \infty$
. In addition,
$n^{2/3}g(n)^{-2^k}\rightarrow \infty$
. In addition,
![]() $I(H_t)=\Omega(n)$
with probability
$I(H_t)=\Omega(n)$
with probability
![]() $1-O(n^{-1})$
by Lemma 3.2. Since the coupling adds components in
$1-O(n^{-1})$
by Lemma 3.2. Since the coupling adds components in
![]() $H_t$
to both
$H_t$
to both
![]() $X_{t+1}$
and
$X_{t+1}$
and
![]() $Y_{t+1}$
, properties 4 and 5 are maintained at time
$Y_{t+1}$
, properties 4 and 5 are maintained at time
![]() $t+1$
, with probability at least
$t+1$
, with probability at least
![]() $1 - O(g(n)^{-1})$
.
$1 - O(g(n)^{-1})$
.
A union bound concludes that at time
![]() $t+1$
we can maintain all five properties with probability at least
$t+1$
we can maintain all five properties with probability at least
![]() $1 - O(g(n)^{-1})- O(r(n)^{-1})$
. Hence, the probability that
$1 - O(g(n)^{-1})- O(r(n)^{-1})$
. Hence, the probability that
![]() $X_{T(n)}$
and
$X_{T(n)}$
and
![]() $Y_{T(n)}$
still satisfy the listed 5 properties above is
$Y_{T(n)}$
still satisfy the listed 5 properties above is
It remains for us to show the bound for
![]() $Z_T$
and that for a given function g
′ satisfying
$Z_T$
and that for a given function g
′ satisfying
![]() $g^{\prime}\geq g$
and
$g^{\prime}\geq g$
and
![]() $g^{\prime}(n) = o\!\left(n^{1/3}\right)$
, then
$g^{\prime}(n) = o\!\left(n^{1/3}\right)$
, then
![]() $\hat{N}_{k}(T, g^{\prime}) = \Omega\!\left( g^{\prime}(n)^{3 \cdot 2^{k-1}}\right)$
for all
$\hat{N}_{k}(T, g^{\prime}) = \Omega\!\left( g^{\prime}(n)^{3 \cdot 2^{k-1}}\right)$
for all
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $n^{2/3}g^{\prime}(n)^{-2^k}\rightarrow \infty$
.
$n^{2/3}g^{\prime}(n)^{-2^k}\rightarrow \infty$
.
Conditioned on
![]() $A(X_t) = A(Y_t)$
for every activation sub-step in this phase, a bound for
$A(X_t) = A(Y_t)$
for every activation sub-step in this phase, a bound for
![]() $Z_{T}$
can be obtained through a first moment method. On expectation
$Z_{T}$
can be obtained through a first moment method. On expectation
![]() $Z_t$
contract by a factor of
$Z_t$
contract by a factor of
![]() $\frac{1}{a} = 1 - \frac{1}{q}$
each step. Thus, we can recursively compute the expectation of
$\frac{1}{a} = 1 - \frac{1}{q}$
each step. Thus, we can recursively compute the expectation of
![]() ${\mathbb{E}}[Z_{T}]$
:
${\mathbb{E}}[Z_{T}]$
:
 \begin{align} {\mathbb{E}}[Z_{T}] &= {\mathbb{E}}[{\mathbb{E}}[Z_{T} \mid Z_{T - 1}]] = \frac{1}{a} \cdot {\mathbb{E}}[Z_{T - 1} ] = ...= \left( \frac{1}{a}\right)^{T} {\mathbb{E}}[Z_0] = O\!\left(\left( \frac{1}{a}\right)^{T} \cdot \frac{n^{4/3}}{h(n)} \right). \end{align}
\begin{align} {\mathbb{E}}[Z_{T}] &= {\mathbb{E}}[{\mathbb{E}}[Z_{T} \mid Z_{T - 1}]] = \frac{1}{a} \cdot {\mathbb{E}}[Z_{T - 1} ] = ...= \left( \frac{1}{a}\right)^{T} {\mathbb{E}}[Z_0] = O\!\left(\left( \frac{1}{a}\right)^{T} \cdot \frac{n^{4/3}}{h(n)} \right). \end{align}
It follows from Markov’s inequality that with at least constant probability
Finally, in the last percolation step in this phase, Corollary 3.12 guarantees that with high probability
![]() $\hat{N}_{k}(T, g^{\prime}) $
$\hat{N}_{k}(T, g^{\prime}) $
![]() $ =\Omega( g^{\prime}(n)^{3 \cdot 2^{k-1}})$
for all
$ =\Omega( g^{\prime}(n)^{3 \cdot 2^{k-1}})$
for all
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $n^{2/3}g^{\prime}(n)^{-2^k}\rightarrow \infty$
. The claim follows from a union bound.
$n^{2/3}g^{\prime}(n)^{-2^k}\rightarrow \infty$
. The claim follows from a union bound.
Proof of Lemma 5.3. We establish first the bound for
![]() $|S(X_{t+1})|$
. Suppose s vertices are activated from
$|S(X_{t+1})|$
. Suppose s vertices are activated from
![]() $S(X_t)$
. By assumption
$S(X_t)$
. By assumption
for sufficiently large n. Hence, Hoeffding’s inequality implies that
with probability at least
![]() $1-O(r(n)^{-1})$
.
$1-O(r(n)^{-1})$
.
We consider two cases. First suppose that
![]() $ \delta(q-1)s/q \ge n^{2/3} r(n)$
, where
$ \delta(q-1)s/q \ge n^{2/3} r(n)$
, where
![]() $\delta > 0$
is a sufficiently small constant we choose later. Then,
$\delta > 0$
is a sufficiently small constant we choose later. Then,
The largest new component corresponds to the largest component of a
![]() $G(A(X_t),q/n)$
random graph. Let N be the size of that component, and let
$G(A(X_t),q/n)$
random graph. Let N be the size of that component, and let
![]() $N_M$
be the size of the largest component of a
$N_M$
be the size of the largest component of a
![]() $G\!\left(M,\frac{1+\varepsilon}{M}\right)$
random graph, where
$G\!\left(M,\frac{1+\varepsilon}{M}\right)$
random graph, where
![]() $\varepsilon = qM/n - 1$
. By Fact 3.1, N is stochastically dominated by
$\varepsilon = qM/n - 1$
. By Fact 3.1, N is stochastically dominated by
![]() $N_M$
. Then by Corollary 3.6 there exists a constant
$N_M$
. Then by Corollary 3.6 there exists a constant
![]() $c>0$
such that
$c>0$
such that
for any
![]() $\rho < 1/10$
. Now,
$\rho < 1/10$
. Now,
 \begin{align} \varepsilon M &= \frac{(1+\delta)(q-1)s}{n} \left(\frac{n}{q} +\frac{(1+\delta)(q-1)s}{q}\right) \notag \\ &= \frac{(1+\delta)(q-1)s}{q} + O\!\left(\frac{s^2}{n}\right) \notag \\ &\le \frac{(1+\delta)(q-1)s}{q} + O(n^{1/3}r(n)^4), \notag \\ &\le \frac{(1+2\delta)(q-1)s}{q} , \end{align}
\begin{align} \varepsilon M &= \frac{(1+\delta)(q-1)s}{n} \left(\frac{n}{q} +\frac{(1+\delta)(q-1)s}{q}\right) \notag \\ &= \frac{(1+\delta)(q-1)s}{q} + O\!\left(\frac{s^2}{n}\right) \notag \\ &\le \frac{(1+\delta)(q-1)s}{q} + O(n^{1/3}r(n)^4), \notag \\ &\le \frac{(1+2\delta)(q-1)s}{q} , \end{align}
where for the second to last inequality we use that
![]() $s \le |S(X_t)| = O(n^{2/3}r(n)^2)$
, and the last inequality follows from the assumptions
$s \le |S(X_t)| = O(n^{2/3}r(n)^2)$
, and the last inequality follows from the assumptions
![]() $\frac{\delta(q-1)s}{q} \ge n^{2/3} r(n)$
and
$\frac{\delta(q-1)s}{q} \ge n^{2/3} r(n)$
and
![]() $r(n) = o\!\left(n^{1/15}\right)$
. Also, since
$r(n) = o\!\left(n^{1/15}\right)$
. Also, since
![]() $s = O(n^{2/3}r(n)^2)$
and
$s = O(n^{2/3}r(n)^2)$
and
![]() $r(n) = o\!\left(n^{1/15}\right)$
,
$r(n) = o\!\left(n^{1/15}\right)$
,
Hence, (14), (15) and (16) imply
Since
![]() $q < 2$
, for sufficiently small
$q < 2$
, for sufficiently small
![]() $\rho$
and
$\rho$
and
![]() $\delta$
$\delta$
Therefore,
![]() $N \le s$
with probability
$N \le s$
with probability
![]() $1 - \exp({-}\Omega(r(n)^3))$
. If this is the case, then
$1 - \exp({-}\Omega(r(n)^3))$
. If this is the case, then
![]() $|S(X_{t+1})| \le |S(X_{t})|$
and so by a union bound
$|S(X_{t+1})| \le |S(X_{t})|$
and so by a union bound
![]() $|S(X_{t+1})| \le c(t+1) n^{2/3} r(n)$
with probability at least
$|S(X_{t+1})| \le c(t+1) n^{2/3} r(n)$
with probability at least
![]() $1-O(r(n)^{-1})$
.
$1-O(r(n)^{-1})$
.
For the second case we assume
![]() $ \frac{\delta(q-1)s}{q} < n^{2/3} r(n)$
and proceed in similar fashion. In this case, Hoeffding’s inequality implies with probability at least
$ \frac{\delta(q-1)s}{q} < n^{2/3} r(n)$
and proceed in similar fashion. In this case, Hoeffding’s inequality implies with probability at least
![]() $1-O(r(n)^{-1})$
,
$1-O(r(n)^{-1})$
,
The size of the largest new component, denoted N
′, is stochastically dominated by the size of the largest component of a
![]() $G(M^{\prime},\frac{1+\varepsilon^{\prime}}{M^{\prime}})$
random graph, with
$G(M^{\prime},\frac{1+\varepsilon^{\prime}}{M^{\prime}})$
random graph, with
![]() $\varepsilon^{\prime} = qM^{\prime}/n - 1$
. Now, since we assume
$\varepsilon^{\prime} = qM^{\prime}/n - 1$
. Now, since we assume
![]() $r(n) = o\!\left(n^{1/15}\right)$
,
$r(n) = o\!\left(n^{1/15}\right)$
,
 \begin{align*} \varepsilon^{\prime} M^{\prime} &\le \frac{q(1+1/\delta)r(n)}{n^{1/3}}\left[\frac{n}{q} +(1+1/\delta)n^{2/3} r(n)\right] \\ &= (1+1/\delta) n^{2/3} r(n) + O(n^{1/3}r(n)^2) \le \frac{c}{3} n^{2/3} r(n), \end{align*}
\begin{align*} \varepsilon^{\prime} M^{\prime} &\le \frac{q(1+1/\delta)r(n)}{n^{1/3}}\left[\frac{n}{q} +(1+1/\delta)n^{2/3} r(n)\right] \\ &= (1+1/\delta) n^{2/3} r(n) + O(n^{1/3}r(n)^2) \le \frac{c}{3} n^{2/3} r(n), \end{align*}
where the last inequality holds for large n and a sufficiently large constant c. Moreover,
Hence,
where
![]() $\rho < 1/10$
, and by Corollary 3.6
$\rho < 1/10$
, and by Corollary 3.6
Since,
![]() $|S(X_{t+1})| \le |S(X_t)| + N^{\prime}$
, a union bound implies that
$|S(X_{t+1})| \le |S(X_t)| + N^{\prime}$
, a union bound implies that
![]() $|S(X_{t+1})| \le c(t+1)n^{2/3} r(n)$
with probability at least
$|S(X_{t+1})| \le c(t+1)n^{2/3} r(n)$
with probability at least
![]() $1-O(r(n)^{-1})$
as desired.
$1-O(r(n)^{-1})$
as desired.
Finally, to bound
![]() $Q(X_{t+1})$
we observe that if
$Q(X_{t+1})$
we observe that if
![]() $C_1,\dots,C_k$
are all the new components in order of their sizes, then by Lemma 3.4 and Markov’s inequality:
$C_1,\dots,C_k$
are all the new components in order of their sizes, then by Lemma 3.4 and Markov’s inequality:
 \begin{equation*} {\mathbb{P}}\left[\sum_{j \ge 2} |C_j|^2 \ge n^{4/3} r(n)\right] = O(r(n)^{-1}). \end{equation*}
\begin{equation*} {\mathbb{P}}\left[\sum_{j \ge 2} |C_j|^2 \ge n^{4/3} r(n)\right] = O(r(n)^{-1}). \end{equation*}
Thus,
![]() $Q(X_{t+1}) \le Q(X_t) + n^{4/3} r(n) \le (t+1)n^{4/3} r(n)$
with probability at least
$Q(X_{t+1}) \le Q(X_t) + n^{4/3} r(n) \le (t+1)n^{4/3} r(n)$
with probability at least
![]() $1-O(r(n)^{-1})$
as claimed. The lemma follows from a union bound.
$1-O(r(n)^{-1})$
as claimed. The lemma follows from a union bound.
Proof of Lemma 5.4. Since
![]() $\mathcal{R}_1(X_t) = O\!\left(n^{4/3} f(n)^2 ({\log} f(n))^{-1}\right)$
, by Hoeffding’s inequality
$\mathcal{R}_1(X_t) = O\!\left(n^{4/3} f(n)^2 ({\log} f(n))^{-1}\right)$
, by Hoeffding’s inequality
with probability at least
![]() $1 - O(f(n)^{-1})$
. The new connected components in
$1 - O(f(n)^{-1})$
. The new connected components in
![]() $X_{t+1}$
correspond to those of a
$X_{t+1}$
correspond to those of a
![]() $G(A(X_t),\frac{1+\varepsilon}{A(X_t)})$
random graph, where
$G(A(X_t),\frac{1+\varepsilon}{A(X_t)})$
random graph, where
![]() $\varepsilon = A(X_t) q/n -1$
. If
$\varepsilon = A(X_t) q/n -1$
. If
![]() $A(X_t) \in J$
, then
$A(X_t) \in J$
, then
Since
![]() $A(X_t) \in J$
we can also define
$A(X_t) \in J$
we can also define
![]() $m \,:\!=\, A(X_t) = \theta n$
for
$m \,:\!=\, A(X_t) = \theta n$
for
![]() $\theta \in (1/2q,1)$
, and
$\theta \in (1/2q,1)$
, and
![]() $\lambda \,:\!=\, \varepsilon m^{1/3}$
, so we may rewrite (16) as
$\lambda \,:\!=\, \varepsilon m^{1/3}$
, so we may rewrite (16) as
and the lemma follows.
An important tool used in the proof of Lemma 5.5 is the following coupling on a (lazy) symmetric random walk on
![]() $\mathbb{Z}$
; its proof is given in Appendix B.
$\mathbb{Z}$
; its proof is given in Appendix B.
Theorem 5.7. Let
![]() $A > 0$
and let
$A > 0$
and let
![]() $A \le c_1,c_2,\dots,c_m \le 2A$
be positive integers. Let
$A \le c_1,c_2,\dots,c_m \le 2A$
be positive integers. Let
![]() $r \in (0,1/2]$
and consider the sequences of random variables
$r \in (0,1/2]$
and consider the sequences of random variables
![]() $X_1,\dots,X_m$
and
$X_1,\dots,X_m$
and
![]() $Y_1,\dots,Y_m$
where for each
$Y_1,\dots,Y_m$
where for each
![]() $i = 1,\dots,m$
:
$i = 1,\dots,m$
:
![]() $X_i = c_i$
with probability r;
$X_i = c_i$
with probability r;
![]() $X_i = -c_i$
with probability r;
$X_i = -c_i$
with probability r;
![]() $X_i = 0$
otherwise and
$X_i = 0$
otherwise and
![]() $Y_i$
has the same distribution as
$Y_i$
has the same distribution as
![]() $X_i$
. Let
$X_i$
. Let
![]() $X = \sum_{i=1}^m X_i$
and
$X = \sum_{i=1}^m X_i$
and
![]() $Y = \sum_{i=1}^mY_i$
. Then for any
$Y = \sum_{i=1}^mY_i$
. Then for any
![]() $d > 0$
, there exist a constant
$d > 0$
, there exist a constant
![]() $\delta \,:\!=\, \delta(r) > 0$
and a coupling of X and Y such that
$\delta \,:\!=\, \delta(r) > 0$
and a coupling of X and Y such that
We note that Theorem 5.7 is a generalisation of the following more standard fact which will also be useful to us.
Lemma 5.8 ([Reference Blanca4], Lemma 2.18). Let X and Y be binomial random variables with parameters m and r, where
![]() $r \in (0,1)$
is a constant. Then, for any integer
$r \in (0,1)$
is a constant. Then, for any integer
![]() $ y>0$
, there exists a coupling (X, Y) such that for a suitable constant
$ y>0$
, there exists a coupling (X, Y) such that for a suitable constant
![]() $\gamma = \gamma(r) > 0$
,
$\gamma = \gamma(r) > 0$
,
Proof of Lemma 5.5. For ease of notation let
![]() $\mathcal{I}_k = \mathcal{I}_{k}(g)$
and
$\mathcal{I}_k = \mathcal{I}_{k}(g)$
and
![]() $\hat{N}_{k} = \hat{N}_{k}(t,g)$
for each
$\hat{N}_{k} = \hat{N}_{k}(t,g)$
for each
![]() $k \ge 1$
. Also recall the notations
$k \ge 1$
. Also recall the notations
![]() $W_t$
, M(X) and D(X) defined in Section 2.2. Let
$W_t$
, M(X) and D(X) defined in Section 2.2. Let
![]() $\hat{I} (X_t)$
and
$\hat{I} (X_t)$
and
![]() $\hat{I} (Y_t)$
be the isolated vertices in
$\hat{I} (Y_t)$
be the isolated vertices in
![]() $W_t$
from
$W_t$
from
![]() $X_t$
and
$X_t$
and
![]() $Y_t$
, respectively.
$Y_t$
, respectively.
Let
![]() $k^* \,:\!=\, \min_k \{ k \in \mathbb{Z} : g(n)^{2^{k}} \ge \vartheta n^{1/3} \}$
. The activation of the non-trivial components in
$k^* \,:\!=\, \min_k \{ k \in \mathbb{Z} : g(n)^{2^{k}} \ge \vartheta n^{1/3} \}$
. The activation of the non-trivial components in
![]() $M(X_t)$
and
$M(X_t)$
and
![]() $M(Y_t)$
whose sizes are not in
$M(Y_t)$
whose sizes are not in
![]() $\{1\} \cup \mathcal{I}_1 \cup \dots \cup \mathcal{I}_{k^*} $
is coupled using the matching
$\{1\} \cup \mathcal{I}_1 \cup \dots \cup \mathcal{I}_{k^*} $
is coupled using the matching
![]() $W_t$
. That is,
$W_t$
. That is,
![]() $c \in M(X_t)$
and
$c \in M(X_t)$
and
![]() $W_t(c) \in M(Y_t)$
are activated simultaneously with probability
$W_t(c) \in M(Y_t)$
are activated simultaneously with probability
![]() $1/q$
. The components in
$1/q$
. The components in
![]() $D(X_t)$
and
$D(X_t)$
and
![]() $D(Y_t)$
are activated independently. After independently activating these components, the number of active vertices from each copy is not necessarily the same. The idea is to couple the activation of the remaining components in
$D(Y_t)$
are activated independently. After independently activating these components, the number of active vertices from each copy is not necessarily the same. The idea is to couple the activation of the remaining components in
![]() $M(X_t)$
and
$M(X_t)$
and
![]() $M(Y_t)$
in way that corrects this difference.
$M(Y_t)$
in way that corrects this difference.
Let
![]() $A_0(X_t)$
and
$A_0(X_t)$
and
![]() $A_0(Y_t)$
be number of active vertices from
$A_0(Y_t)$
be number of active vertices from
![]() $X_t$
and
$X_t$
and
![]() $Y_t$
, respectively, after the activation of the components from
$Y_t$
, respectively, after the activation of the components from
![]() $D(X_t)$
and
$D(X_t)$
and
![]() $D(Y_t)$
. Observe that
$D(Y_t)$
. Observe that
![]() ${\mathbb{E}}[A_0(X_t)] = {\mathbb{E}}[A_0(Y_t)] \,=\!:\, \mu$
and that by Hoeffding’s inequality, for any
${\mathbb{E}}[A_0(X_t)] = {\mathbb{E}}[A_0(Y_t)] \,=\!:\, \mu$
and that by Hoeffding’s inequality, for any
![]() $\eta(n) > 0$
$\eta(n) > 0$
Recall
![]() $Z_t \le \frac{C n^{4/3}}{h(n)}$
. Hence, with probability at least
$Z_t \le \frac{C n^{4/3}}{h(n)}$
. Hence, with probability at least
![]() $1 - 4\exp\!\left({-}2\eta(n)\right)$
,
$1 - 4\exp\!\left({-}2\eta(n)\right)$
,
We first couple the activation of the components in
![]() $\mathcal{I}_1$
, then in
$\mathcal{I}_1$
, then in
![]() $\mathcal{I}_2$
and so on up to
$\mathcal{I}_2$
and so on up to
![]() $\mathcal{I}_{k^*}$
. Without loss of generality, suppose that
$\mathcal{I}_{k^*}$
. Without loss of generality, suppose that
![]() $d_0 = A_0(Y_t) - A_0(X_t)$
. If
$d_0 = A_0(Y_t) - A_0(X_t)$
. If
![]() $d_0 \le \frac{\vartheta n^{2/3}}{g(n)^2}$
, we simply couple the components with sizes in
$d_0 \le \frac{\vartheta n^{2/3}}{g(n)^2}$
, we simply couple the components with sizes in
![]() $\mathcal{I}_1$
using the matching
$\mathcal{I}_1$
using the matching
![]() $W_t$
. Suppose otherwise that
$W_t$
. Suppose otherwise that
![]() $ d_0 > \frac{\vartheta n^{2/3}}{g(n)^2}$
. Let
$ d_0 > \frac{\vartheta n^{2/3}}{g(n)^2}$
. Let
![]() $A_1(X_t)$
and
$A_1(X_t)$
and
![]() $A_1(Y_t)$
be random variables corresponding to the numbers of active vertices from
$A_1(Y_t)$
be random variables corresponding to the numbers of active vertices from
![]() $M(X_t)$
and
$M(X_t)$
and
![]() $M(Y_t)$
with sizes in
$M(Y_t)$
with sizes in
![]() $\mathcal{I}_1$
respectively. By assumption
$\mathcal{I}_1$
respectively. By assumption
![]() $\hat{N}_1 \ge b g(n)^{3}$
. Hence, Theorem 5.7 implies that for
$\hat{N}_1 \ge b g(n)^{3}$
. Hence, Theorem 5.7 implies that for
![]() $\delta = \delta(q) > 0$
, there exists a coupling for the activation of the components in
$\delta = \delta(q) > 0$
, there exists a coupling for the activation of the components in
![]() $M(X_t)$
and
$M(X_t)$
and
![]() $M(Y_t)$
with sizes in
$M(Y_t)$
with sizes in
![]() $\mathcal{I}_1$
such that
$\mathcal{I}_1$
such that
with probability at least
 \begin{equation*}1 - \frac{\delta \!\left( d_0 - \frac{\vartheta n^{2/3}}{2g(n)^2}\right)}{\frac{\vartheta n^{2/3}}{2g(n)^2} \sqrt{b g(n)^{3}}} \ge 1 - \frac{\delta d_0}{\frac{\vartheta n^{2/3}}{2g(n)^2} \sqrt{b g(n)^{3}}} \ge 1 - \frac{4\delta \sqrt{C \eta(n) g(n)} }{\vartheta \sqrt{b h(n)} } \ge 1 - \sqrt{\frac{\eta(n)g(n)}{ h(n)}} ,\end{equation*}
\begin{equation*}1 - \frac{\delta \!\left( d_0 - \frac{\vartheta n^{2/3}}{2g(n)^2}\right)}{\frac{\vartheta n^{2/3}}{2g(n)^2} \sqrt{b g(n)^{3}}} \ge 1 - \frac{\delta d_0}{\frac{\vartheta n^{2/3}}{2g(n)^2} \sqrt{b g(n)^{3}}} \ge 1 - \frac{4\delta \sqrt{C \eta(n) g(n)} }{\vartheta \sqrt{b h(n)} } \ge 1 - \sqrt{\frac{\eta(n)g(n)}{ h(n)}} ,\end{equation*}
where the last inequality holds for
![]() $\vartheta $
large enough. Let
$\vartheta $
large enough. Let
![]() $d_1 \,:\!=\, \left(A_0(Y_t) - A_0(X_t)\right) + \left(A_1(Y_t) - A_1(X_t)\right)$
. If the coupling succeeds, we have
$d_1 \,:\!=\, \left(A_0(Y_t) - A_0(X_t)\right) + \left(A_1(Y_t) - A_1(X_t)\right)$
. If the coupling succeeds, we have
![]() $0 \le d_1 \le \frac{\vartheta n^{2/3}}{g(n)^2}$
. Thus, we have shown that
$0 \le d_1 \le \frac{\vartheta n^{2/3}}{g(n)^2}$
. Thus, we have shown that
![]() $d_1 \le \frac{\vartheta n^{2/3}}{g(n)^2}$
with probability at least
$d_1 \le \frac{\vartheta n^{2/3}}{g(n)^2}$
with probability at least
 \begin{equation*}\left(1 - 4e^{-2\eta(n)}\right)\left(1 - \sqrt{\frac{\eta(n)g(n)}{ h(n)}}\right) \ge 1 - 4e^{-2\eta(n)} - \sqrt{\frac{\eta(n)g(n)}{ h(n)}}.\end{equation*}
\begin{equation*}\left(1 - 4e^{-2\eta(n)}\right)\left(1 - \sqrt{\frac{\eta(n)g(n)}{ h(n)}}\right) \ge 1 - 4e^{-2\eta(n)} - \sqrt{\frac{\eta(n)g(n)}{ h(n)}}.\end{equation*}
Now, let
![]() $d_k$
be the difference in the number of active vertices after activating the components in
$d_k$
be the difference in the number of active vertices after activating the components in
![]() $\mathcal{I}_k$
. Suppose that
$\mathcal{I}_k$
. Suppose that
![]() $d_k \le \frac{\vartheta n^{2/3}}{g(n)^{2^{k}}}$
, for
$d_k \le \frac{\vartheta n^{2/3}}{g(n)^{2^{k}}}$
, for
![]() $k \le k^*$
. By assumption,
$k \le k^*$
. By assumption,
![]() $\hat{N}_{k+1} \ge b g(n)^{3 \cdot 2^{k}}$
. Thus, using Theorem 5.7 again we get that there exists a coupling for the activation of the components in
$\hat{N}_{k+1} \ge b g(n)^{3 \cdot 2^{k}}$
. Thus, using Theorem 5.7 again we get that there exists a coupling for the activation of the components in
![]() $\mathcal{I}_{k+1}$
such that
$\mathcal{I}_{k+1}$
such that
 \begin{equation*}{\mathbb{P}}\left[d_{k+1} \le \frac{\vartheta n^{2/3}}{g(n)^{2^{k+1}}} \,\middle\vert\, d_k \le \frac{\vartheta n^{2/3}}{g(n)^{2^{k}}} \right] \ge 1 - \frac{\delta d_k}{\frac{\vartheta n^{2/3}}{2g(n)^{2^{k+1}}} \sqrt{b g(n)^{3 \cdot 2^{k}}}} \ge 1 - \frac{2\delta}{\sqrt{b}g(n)^{2^{k-1}}}.\end{equation*}
\begin{equation*}{\mathbb{P}}\left[d_{k+1} \le \frac{\vartheta n^{2/3}}{g(n)^{2^{k+1}}} \,\middle\vert\, d_k \le \frac{\vartheta n^{2/3}}{g(n)^{2^{k}}} \right] \ge 1 - \frac{\delta d_k}{\frac{\vartheta n^{2/3}}{2g(n)^{2^{k+1}}} \sqrt{b g(n)^{3 \cdot 2^{k}}}} \ge 1 - \frac{2\delta}{\sqrt{b}g(n)^{2^{k-1}}}.\end{equation*}
Therefore, there is a coupling of the activation components in
![]() $\mathcal{I}_2, \mathcal{I}_3, \dots, \mathcal{I}_{k^*}$
such that
$\mathcal{I}_2, \mathcal{I}_3, \dots, \mathcal{I}_{k^*}$
such that
 \begin{equation*}{\mathbb{P}}\left[ d_{k^*} \le n^{1/3} \,\middle\vert\, d_1 \le \frac{\vartheta n^{2/3}}{g(n)^2} \right] \ge \prod_{k = 2}^{k^*} \left(1 - \frac{\delta^{\prime}}{g(n)^{2^{k-1}}} \right),\end{equation*}
\begin{equation*}{\mathbb{P}}\left[ d_{k^*} \le n^{1/3} \,\middle\vert\, d_1 \le \frac{\vartheta n^{2/3}}{g(n)^2} \right] \ge \prod_{k = 2}^{k^*} \left(1 - \frac{\delta^{\prime}}{g(n)^{2^{k-1}}} \right),\end{equation*}
where
![]() $\delta^{\prime} = 2\delta/\sqrt{b}$
. Note that for a suitable constant
$\delta^{\prime} = 2\delta/\sqrt{b}$
. Note that for a suitable constant
![]() $\delta^{\prime\prime} > 0$
, we have
$\delta^{\prime\prime} > 0$
, we have
 \begin{equation} \prod_{k \ge 2}^{k^*} \left(1 - \frac{\delta^{\prime}}{g(n)^{2^{k-1}}} \right) = \exp\!\left( \sum_{k \ge 1}^{k^*} \ln\!\left(1 - \frac{\delta^{\prime}}{g(n)^{2^{k}}}\right)\right) \ge \exp\!\left({-}\delta^{\prime\prime} \sum_{k \ge 1}^{k^*} \frac{1}{g(n)^{2^{k}}}\right), \notag \end{equation}
\begin{equation} \prod_{k \ge 2}^{k^*} \left(1 - \frac{\delta^{\prime}}{g(n)^{2^{k-1}}} \right) = \exp\!\left( \sum_{k \ge 1}^{k^*} \ln\!\left(1 - \frac{\delta^{\prime}}{g(n)^{2^{k}}}\right)\right) \ge \exp\!\left({-}\delta^{\prime\prime} \sum_{k \ge 1}^{k^*} \frac{1}{g(n)^{2^{k}}}\right), \notag \end{equation}
and since
 \begin{equation*}\sum_{k \ge 1}^{k^*} \frac{1}{g(n)^{2^{k}}} \le \sum_{k \ge 1}^\infty \frac{1}{g(n)^{2^{k}}} \le \sum_{k \ge 1}^\infty \frac{1}{g(n)^{{k}}} \le \frac{1}{g(n)^2-g(n)}, \end{equation*}
\begin{equation*}\sum_{k \ge 1}^{k^*} \frac{1}{g(n)^{2^{k}}} \le \sum_{k \ge 1}^\infty \frac{1}{g(n)^{2^{k}}} \le \sum_{k \ge 1}^\infty \frac{1}{g(n)^{{k}}} \le \frac{1}{g(n)^2-g(n)}, \end{equation*}
we get
 \begin{equation*}\prod_{k = 2}^{k^*} \left(1 - \frac{\delta^{\prime}}{g(n)^{2^{k-1}}} \right) \ge \exp\!\left({-}\frac{\delta^{\prime\prime}}{g(n)^2-g(n)} \right) \ge 1 - \frac{\delta^{\prime\prime}}{g(n)^2-g(n)}.\end{equation*}
\begin{equation*}\prod_{k = 2}^{k^*} \left(1 - \frac{\delta^{\prime}}{g(n)^{2^{k-1}}} \right) \ge \exp\!\left({-}\frac{\delta^{\prime\prime}}{g(n)^2-g(n)} \right) \ge 1 - \frac{\delta^{\prime\prime}}{g(n)^2-g(n)}.\end{equation*}
Finally, we couple
![]() $\hat{I}(X_t)$
and
$\hat{I}(X_t)$
and
![]() $\hat{I}(Y_t)$
to fix
$\hat{I}(Y_t)$
to fix
![]() $d_{k^*}$
. By assumption
$d_{k^*}$
. By assumption
![]() $I(X_t), I(Y_t) = \Omega(n)$
, so
$I(X_t), I(Y_t) = \Omega(n)$
, so
![]() $m \,:\!=\, |\hat{I}(X_t)| = |\hat{I}(Y_t)| = \Omega(n)$
. Let
$m \,:\!=\, |\hat{I}(X_t)| = |\hat{I}(Y_t)| = \Omega(n)$
. Let
![]() $A_I(X_t)$
and
$A_I(X_t)$
and
![]() $A_I(Y_t)$
denote the total number of activated isolated vertices from
$A_I(Y_t)$
denote the total number of activated isolated vertices from
![]() $\hat{I}(X_t)$
and
$\hat{I}(X_t)$
and
![]() $\hat{I}(Y_t)$
respectively. We activate all isolated vertices independently, so
$\hat{I}(Y_t)$
respectively. We activate all isolated vertices independently, so
![]() $A_I(X_t)$
and
$A_I(X_t)$
and
![]() $A_I(Y_t)$
can be seen as two binomial random variables with the same parameters m and
$A_I(Y_t)$
can be seen as two binomial random variables with the same parameters m and
![]() $1/q$
. Lemma 5.8 gives a coupling for binomial random variables such that for
$1/q$
. Lemma 5.8 gives a coupling for binomial random variables such that for
![]() $r \le n^{1/3}$
,
$r \le n^{1/3}$
,
Therefore,
 \begin{equation*}{\mathbb{P}} \left[A(X_t) = A(Y_t)\right] \ge 1 - 4e^{-2\eta(n)} - \sqrt{\frac{\eta(n)g(n)}{ h(n)}} - O\!\left(\frac{1}{g(n)}\right),\end{equation*}
\begin{equation*}{\mathbb{P}} \left[A(X_t) = A(Y_t)\right] \ge 1 - 4e^{-2\eta(n)} - \sqrt{\frac{\eta(n)g(n)}{ h(n)}} - O\!\left(\frac{1}{g(n)}\right),\end{equation*}
as claimed.
6. New mixing time for the Glauber dynamics via comparison
In this section, we establish a comparison inequality between the mixing times of the CM dynamics and of the heat-bath Glauber dynamics for the random-cluster model for a general graph
![]() $G = (V,E)$
. The Glauber dynamics is defined as follows. Given a random-cluster configuration
$G = (V,E)$
. The Glauber dynamics is defined as follows. Given a random-cluster configuration
![]() $A_t$
, one step of this chain is given by:
$A_t$
, one step of this chain is given by:
-
i. pick an edge
 $e \in E$
uniformly at random;
$e \in E$
uniformly at random; -
ii. replace the current configuration
 $A_t$
by
$A_t$
by
 $A_t\cup \{e\}$
with probability
$A_t\cup \{e\}$
with probability  \begin{equation*} \frac{ \mu_{G,p,q} (A_t \cup \{e\}) } { \mu_{G,p,q} (A_t \cup \{e\}) + \mu_{G,p,q} (A_t \setminus \{e\}) }; \end{equation*}
\begin{equation*} \frac{ \mu_{G,p,q} (A_t \cup \{e\}) } { \mu_{G,p,q} (A_t \cup \{e\}) + \mu_{G,p,q} (A_t \setminus \{e\}) }; \end{equation*}
-
iii. else replace
 $A_t$
by
$A_t$
by
 $A_t \setminus \{e\}$
.
$A_t \setminus \{e\}$
.
It is immediate from its definition this chain is reversible with respect to
![]() $\mu = \mu_{G,p,q}$
and thus converges to it.
$\mu = \mu_{G,p,q}$
and thus converges to it.
The following comparison inequality was proved in [Reference Blanca and Sinclair7]:
where m denotes the number of edges in G, and
![]() $\textrm{gap}(\textrm{CM})$
,
$\textrm{gap}(\textrm{CM})$
,
![]() $\textrm{gap}(\textrm{GD})$
the spectral gaps of the transition matrices of the CM and Glauber dynamics, respectively. The standard connection between the spectral gap and the mixing time (see, e.g., Theorem 12.3 in [Reference Levin, Peres and Wilmer23]) yields
$\textrm{gap}(\textrm{GD})$
the spectral gaps of the transition matrices of the CM and Glauber dynamics, respectively. The standard connection between the spectral gap and the mixing time (see, e.g., Theorem 12.3 in [Reference Levin, Peres and Wilmer23]) yields
where
![]() $\mu_{\textrm{min}} = \min_{A \in \Omega} \mu(A)$
with
$\mu_{\textrm{min}} = \min_{A \in \Omega} \mu(A)$
with
![]() $\Omega$
denoting the set of random-cluster configurations on G. In some cases, such as in the mean-field model with
$\Omega$
denoting the set of random-cluster configurations on G. In some cases, such as in the mean-field model with
![]() $p = \Theta(n^{-1})$
,
$p = \Theta(n^{-1})$
,
![]() $\log \mu_{\textrm{min}}^{-1} = \Omega(m \log m)$
, and a factor of
$\log \mu_{\textrm{min}}^{-1} = \Omega(m \log m)$
, and a factor of
![]() $O(m^2 ({\log} m)^2)$
is thus lost in the comparison. We provide here an improved version of this inequality.
$O(m^2 ({\log} m)^2)$
is thus lost in the comparison. We provide here an improved version of this inequality.
Theorem 6.1. For any
![]() $q > 1$
and any
$q > 1$
and any
![]() $p\in (0,1)$
, the mixing time of Glauber dynamics for the random-cluster model on a graph G with n vertices and m edges satisfies
$p\in (0,1)$
, the mixing time of Glauber dynamics for the random-cluster model on a graph G with n vertices and m edges satisfies
We note that in the mean-field model, where
![]() $m = \Theta(n^2)$
and we take
$m = \Theta(n^2)$
and we take
![]() $p = \zeta/n$
with
$p = \zeta/n$
with
![]() $\zeta = O(1)$
, this theorem yields that
$\zeta = O(1)$
, this theorem yields that
![]() $\tau_{\textrm{mix}}^{\textrm{GD}} = O(n^3 ({\log}\ n)^2) \cdot \tau_{\textrm{mix}}^{\textrm{CM}}$
, which establishes Theorem 1.2 from the introduction and improves by a factor of O(n) the best previously known bound for the Glauber dynamics on the complete graph.
$\tau_{\textrm{mix}}^{\textrm{GD}} = O(n^3 ({\log}\ n)^2) \cdot \tau_{\textrm{mix}}^{\textrm{CM}}$
, which establishes Theorem 1.2 from the introduction and improves by a factor of O(n) the best previously known bound for the Glauber dynamics on the complete graph.
To prove Theorem 6.1 we use the following standard fact.
Theorem 6.2. Let P be a Markov chain on state space
![]() $\Gamma$
with stationary distribution
$\Gamma$
with stationary distribution
![]() $\pi$
. Suppose there exist a subset of states
$\pi$
. Suppose there exist a subset of states
![]() $\Gamma_0 \subseteq \Gamma$
and a time T, such that for any
$\Gamma_0 \subseteq \Gamma$
and a time T, such that for any
![]() $t\ge T$
and any
$t\ge T$
and any
![]() $x \in \Gamma$
we have
$x \in \Gamma$
we have
![]() $ P^t(x, \Gamma\setminus\Gamma_0) \le \frac{1}{16}. $
Then
$ P^t(x, \Gamma\setminus\Gamma_0) \le \frac{1}{16}. $
Then
where
![]() $\pi_0 \,:\!=\, \min_{\omega\in \Gamma_0} \pi(\omega)$
.
$\pi_0 \,:\!=\, \min_{\omega\in \Gamma_0} \pi(\omega)$
.
Note that
![]() $\pi_0$
is the minimum probability of any configuration on
$\pi_0$
is the minimum probability of any configuration on
![]() $\Gamma_0$
. Without the additional assumptions in the theorem, the best possible bound involves a factor of
$\Gamma_0$
. Without the additional assumptions in the theorem, the best possible bound involves a factor of
![]() $\pi_{\textrm{min}} = \min_{A\in \Gamma} \pi(A)$
instead. We remark that there are related conditions under which (20) holds; we choose the condition that
$\pi_{\textrm{min}} = \min_{A\in \Gamma} \pi(A)$
instead. We remark that there are related conditions under which (20) holds; we choose the condition that
![]() $P^t(x, \Gamma\setminus\Gamma_0) \le \frac{1}{16}$
for every x and every
$P^t(x, \Gamma\setminus\Gamma_0) \le \frac{1}{16}$
for every x and every
![]() $t \ge T$
for convenience.
$t \ge T$
for convenience.
We can now provide the proof of Theorem 6.1.
Proof of Theorem 6.1. First note that if
![]() $p=\Omega(1)$
, it suffices to prove that
$p=\Omega(1)$
, it suffices to prove that
This follows from (19) and the fact that
since the partition function for the random-cluster model on G satisfies
![]() $Z_{G} \le q^n$
(see, e.g., Theorem 3.60 in [Reference Grimmett19]).
$Z_{G} \le q^n$
(see, e.g., Theorem 3.60 in [Reference Grimmett19]).
Thus, we may assume
![]() $p \le 1/100$
. From (18) and the standard relationship between the spectral gap and the mixing time (see, e.g., Theorem 12.4 in [Reference Levin, Peres and Wilmer23]) we obtain:
$p \le 1/100$
. From (18) and the standard relationship between the spectral gap and the mixing time (see, e.g., Theorem 12.4 in [Reference Levin, Peres and Wilmer23]) we obtain:
Let P denote the transition matrix of the Glauber dynamics. In order to apply Theorem 6.2, we have to find a suitable subset of states
![]() $\Omega_0 \subseteq \Omega$
and a suitable time T so that
$\Omega_0 \subseteq \Omega$
and a suitable time T so that
![]() $P^t(A, \Omega\setminus\Omega_0) \le \frac{1}{16}$
, for every
$P^t(A, \Omega\setminus\Omega_0) \le \frac{1}{16}$
, for every
![]() $A \in \Omega$
and every
$A \in \Omega$
and every
![]() $t \ge T$
.
$t \ge T$
.
We let
![]() $\Omega_0 = \{A \subseteq E: |A| \le 100mp\}$
and
$\Omega_0 = \{A \subseteq E: |A| \le 100mp\}$
and
![]() $T = C m \log m$
for a sufficiently large constant
$T = C m \log m$
for a sufficiently large constant
![]() $C > 0$
. When an edge is selected for update by the Glauber dynamics, it is set to be open with probability
$C > 0$
. When an edge is selected for update by the Glauber dynamics, it is set to be open with probability
![]() $p/(p+q(1-p))$
if it is a ‘cut edge’ or with probability p if it is not; recall that we say an edge e is open if the edge is present in the random-cluster configuration. Therefore, since
$p/(p+q(1-p))$
if it is a ‘cut edge’ or with probability p if it is not; recall that we say an edge e is open if the edge is present in the random-cluster configuration. Therefore, since
![]() $p \ge p/(p+q(1-p))$
when
$p \ge p/(p+q(1-p))$
when
![]() $q > 1$
, after every edge has been updated at least once the number of open edges in any configuration is stochastically dominated by the number of edges in a G(n, p) random graph. By the coupon collector bound, every edge has been updated at least once at time T w.h.p. for large enough C. Moreover, if all edges are indeed updated by time T, the number of open edges in
$q > 1$
, after every edge has been updated at least once the number of open edges in any configuration is stochastically dominated by the number of edges in a G(n, p) random graph. By the coupon collector bound, every edge has been updated at least once at time T w.h.p. for large enough C. Moreover, if all edges are indeed updated by time T, the number of open edges in
![]() $X_t$
at any time
$X_t$
at any time
![]() $t \ge T$
is at most 100 m p with probability at least
$t \ge T$
is at most 100 m p with probability at least
![]() $19/20$
by Markov’s inequality. Therefore, the Glauber dynamics satisfies condition in Theorem 6.2 for these choices of T and
$19/20$
by Markov’s inequality. Therefore, the Glauber dynamics satisfies condition in Theorem 6.2 for these choices of T and
![]() $\Omega_0$
.
$\Omega_0$
.
It remains for us to estimate
![]() $\pi_0$
. Let
$\pi_0$
. Let
![]() $\pi_{m}$
denote the probability of the configuration where all the edges are open; then,
$\pi_{m}$
denote the probability of the configuration where all the edges are open; then,
where the inequality follows from the fact that
![]() $Z_G \le q^n$
. Moreover, since
$Z_G \le q^n$
. Moreover, since
![]() $1-p>p$
when
$1-p>p$
when
![]() $p \le 1/100$
, then
$p \le 1/100$
, then
![]() $\pi_0 \ge qp^{100mp}(1-p)^{m-100mp}/Z_{G}$
and so
$\pi_0 \ge qp^{100mp}(1-p)^{m-100mp}/Z_{G}$
and so
Using (22), (23) and the fact that
![]() $p \le 1/100$
, we obtain:
$p \le 1/100$
, we obtain:
 \begin{align*} \log \frac{1}{\pi_0} &= \log\frac{1}{\pi_m} + \log\frac{\pi_m}{\pi_0} \le (n - 1)\log q + m \log p^{-1} - (m - 100mp) \log \frac{1-p}{p} \\ & = 100mp\log p^{-1} + m(1- 100p)\log \frac{1}{1-p} + O(n)\\ &\le 100mp\log p^{-1} + \frac{mp(1-100p)}{1-p} + O(n) = O\big(n + mp\big({\log} p^{-1}\big)\big). \end{align*}
\begin{align*} \log \frac{1}{\pi_0} &= \log\frac{1}{\pi_m} + \log\frac{\pi_m}{\pi_0} \le (n - 1)\log q + m \log p^{-1} - (m - 100mp) \log \frac{1-p}{p} \\ & = 100mp\log p^{-1} + m(1- 100p)\log \frac{1}{1-p} + O(n)\\ &\le 100mp\log p^{-1} + \frac{mp(1-100p)}{1-p} + O(n) = O\big(n + mp\big({\log} p^{-1}\big)\big). \end{align*}
Therefore, from (21) and Theorem 6.2 we obtain:
 \begin{align*}\tau_{\textrm{mix}}^{\textrm{GD}} & \le O(m\log m) + \tau_{\textrm{mix}}^{\textrm{CM}} \cdot O( m\log n) \cdot O(n + mp\big({\log} p^{-1}\big)) \\[3pt]& = O(m \log n \cdot(n+mp\log p^{-1})) \cdot \tau_{\textrm{mix}}^{\textrm{CM}}, \end{align*}
\begin{align*}\tau_{\textrm{mix}}^{\textrm{GD}} & \le O(m\log m) + \tau_{\textrm{mix}}^{\textrm{CM}} \cdot O( m\log n) \cdot O(n + mp\big({\log} p^{-1}\big)) \\[3pt]& = O(m \log n \cdot(n+mp\log p^{-1})) \cdot \tau_{\textrm{mix}}^{\textrm{CM}}, \end{align*}
as claimed.
For the sake of completeness, we conclude this section with a proof of Theorem 6.2.
Proof of Theorem 6.2. For
![]() $x \in \Gamma$
and
$x \in \Gamma$
and
![]() $t \ge T$
, we have
$t \ge T$
, we have
 \begin{align*} {\|P^t(x,\cdot)-\pi({\cdot})\|}_{\text{TV}} &= \sum_{y\in \Gamma: P^t(x,y) > \pi(y)} P^t(x,y) -\pi(y) \\ &\le \sum_{y \in\Gamma_0: P^t(x,y) > \pi(y)} \pi(y) \left|1 - \frac{P^t(x,y)}{\pi(y)} \right| +\sum_{y \notin \Gamma_0: P^t(x,y) > \pi(y)} P^t(x,y) \left|1 - \frac{\pi(y)}{P^t(x,y)} \right| \\ &\le \pi(\Gamma_0) \max_{y\in \Gamma_0}\left|1 - \frac{P^t(x,y)}{\pi(y)} \right| + P^t(x, \Gamma \setminus \Gamma_0) \\ &\le \max_{y\in \Gamma_0}\left|1 - \frac{P^t(x,y)}{\pi(y)} \right| + \frac{1}{16}, \end{align*}
\begin{align*} {\|P^t(x,\cdot)-\pi({\cdot})\|}_{\text{TV}} &= \sum_{y\in \Gamma: P^t(x,y) > \pi(y)} P^t(x,y) -\pi(y) \\ &\le \sum_{y \in\Gamma_0: P^t(x,y) > \pi(y)} \pi(y) \left|1 - \frac{P^t(x,y)}{\pi(y)} \right| +\sum_{y \notin \Gamma_0: P^t(x,y) > \pi(y)} P^t(x,y) \left|1 - \frac{\pi(y)}{P^t(x,y)} \right| \\ &\le \pi(\Gamma_0) \max_{y\in \Gamma_0}\left|1 - \frac{P^t(x,y)}{\pi(y)} \right| + P^t(x, \Gamma \setminus \Gamma_0) \\ &\le \max_{y\in \Gamma_0}\left|1 - \frac{P^t(x,y)}{\pi(y)} \right| + \frac{1}{16}, \end{align*}
where the last inequality follows from the theorem assumption for
![]() $t \ge T$
.
$t \ge T$
.
For any
![]() $y \in \Gamma$
, we have
$y \in \Gamma$
, we have
see inequality (12.11) in [Reference Levin, Peres and Wilmer23]. Hence, for any
![]() $x \in \Gamma_0$
we have
$x \in \Gamma_0$
we have
Letting
![]() $\tau_{\textrm{mix}}^P(x) = \min \left\{{t \ge 0 : \|P^t(x,\cdot)-\pi({\cdot})\|}_{\text{TV}} \le 1/4 \right\}$
, we deduce from (24) that for
$\tau_{\textrm{mix}}^P(x) = \min \left\{{t \ge 0 : \|P^t(x,\cdot)-\pi({\cdot})\|}_{\text{TV}} \le 1/4 \right\}$
, we deduce from (24) that for
![]() $x \in \Gamma_0$
$x \in \Gamma_0$
Since
![]() $\tau_{\textrm{mix}}^P = \max_{x \in \Gamma} \tau_{\textrm{mix}}(x)$
, it remains for us to provide a bound for
$\tau_{\textrm{mix}}^P = \max_{x \in \Gamma} \tau_{\textrm{mix}}(x)$
, it remains for us to provide a bound for
![]() $\tau_{\textrm{mix}}(x)$
when
$\tau_{\textrm{mix}}(x)$
when
![]() $x \in \Gamma\setminus\Gamma_0$
. Consider two copies
$x \in \Gamma\setminus\Gamma_0$
. Consider two copies
![]() $\{X_t\}$
,
$\{X_t\}$
,
![]() $\{Y_t\}$
of the chain P. For
$\{Y_t\}$
of the chain P. For
![]() $t>T$
let
$t>T$
let
![]() $\mathbb P$
be the coupling of
$\mathbb P$
be the coupling of
![]() $X_t$
,
$X_t$
,
![]() $Y_t$
such that the two copies evolve independently up to time T and if
$Y_t$
such that the two copies evolve independently up to time T and if
![]() $ X_T = x^{\prime}$
and
$ X_T = x^{\prime}$
and
![]() $Y_T = y^{\prime}$
for some
$Y_T = y^{\prime}$
for some
![]() $x^{\prime}, y^{\prime}\in \Gamma_0$
then the optimal coupling is used so that
$x^{\prime}, y^{\prime}\in \Gamma_0$
then the optimal coupling is used so that
recall that the existence of an optimal coupling is guaranteed by the coupling lemma (see, e.g., Proposition 4.7 in [Reference Levin, Peres and Wilmer23]). Then, for any
![]() $x,y \in \Gamma$
$x,y \in \Gamma$
 \begin{align*} \mathbb P[X_t \neq Y_t &\mid X_0 = x, Y_0 = y ] \\&\le \mathbb P[X_T \notin \Gamma_0 \mid X_0=x] + \mathbb P[Y_T \notin \Gamma_0\mid Y_0=y] + \max_{x^{\prime},y^{\prime}\in \Gamma_0} \mathbb P[X_t \neq Y_t \mid X_T = x^{\prime}, Y_T = y^{\prime}] \\ &\le \max_{x^{\prime},y^{\prime}\in \Gamma_0} \mathbb P[X_t \neq Y_t \mid X_T = x^{\prime}, Y_T = y^{\prime}] + \frac{1}{8}\\ &\le \max_{x^{\prime},y^{\prime}\in \Gamma_0}{\|P^{t-T}(x^{\prime},\cdot)-P^{t-T}(y^{\prime},\cdot)\|}_{\text{TV}} + \frac{1}{8}\\ &\le 2 \max_{x^{\prime} \in \Gamma_0}{\|P^{t-T}(x^{\prime},\cdot)-\pi({\cdot})\|}_{\text{TV}} + \frac{1}{8}, \end{align*}
\begin{align*} \mathbb P[X_t \neq Y_t &\mid X_0 = x, Y_0 = y ] \\&\le \mathbb P[X_T \notin \Gamma_0 \mid X_0=x] + \mathbb P[Y_T \notin \Gamma_0\mid Y_0=y] + \max_{x^{\prime},y^{\prime}\in \Gamma_0} \mathbb P[X_t \neq Y_t \mid X_T = x^{\prime}, Y_T = y^{\prime}] \\ &\le \max_{x^{\prime},y^{\prime}\in \Gamma_0} \mathbb P[X_t \neq Y_t \mid X_T = x^{\prime}, Y_T = y^{\prime}] + \frac{1}{8}\\ &\le \max_{x^{\prime},y^{\prime}\in \Gamma_0}{\|P^{t-T}(x^{\prime},\cdot)-P^{t-T}(y^{\prime},\cdot)\|}_{\text{TV}} + \frac{1}{8}\\ &\le 2 \max_{x^{\prime} \in \Gamma_0}{\|P^{t-T}(x^{\prime},\cdot)-\pi({\cdot})\|}_{\text{TV}} + \frac{1}{8}, \end{align*}
where the last inequality follows from the triangle inequality. Now,
 \begin{align*} & \max_{x \in \Gamma} {\|P^{t}(x,\cdot) -\pi({\cdot})\|}_{\text{TV}} &\le \max_{x,y \in \Gamma} \mathbb P [X_t \neq Y_t \mid X_0 = x, Y_0 = y] \le 2 \max_{x^{\prime} \in \Gamma_0}\|P^{t-T}(x^{\prime},\cdot)\\& -\pi({\cdot})\|_{\text{TV}} + \frac{1}{8} \le \frac 58. \end{align*}
\begin{align*} & \max_{x \in \Gamma} {\|P^{t}(x,\cdot) -\pi({\cdot})\|}_{\text{TV}} &\le \max_{x,y \in \Gamma} \mathbb P [X_t \neq Y_t \mid X_0 = x, Y_0 = y] \le 2 \max_{x^{\prime} \in \Gamma_0}\|P^{t-T}(x^{\prime},\cdot)\\& -\pi({\cdot})\|_{\text{TV}} + \frac{1}{8} \le \frac 58. \end{align*}
provided
![]() $t \ge T + \max_{z \in \Gamma_0} \tau_{\textrm{mix}}^P(z)$
. Using a standard boosting argument (see (4.36) in [Reference Levin, Peres and Wilmer23]) and (25) we deduce that
$t \ge T + \max_{z \in \Gamma_0} \tau_{\textrm{mix}}^P(z)$
. Using a standard boosting argument (see (4.36) in [Reference Levin, Peres and Wilmer23]) and (25) we deduce that
![]() $\tau_{\textrm{mix}}^P = O\Big(T + \textrm{gap}^{-1}(P) \log \frac{8}{\pi_0}\Big)$
as claimed.
$\tau_{\textrm{mix}}^P = O\Big(T + \textrm{gap}^{-1}(P) \log \frac{8}{\pi_0}\Big)$
as claimed.
Appendix A. Proof of the local limit theorem
In this appendix, we prove Theorem 5.1. First, we introduce some notation. For a random variable X and
![]() $d \in \mathbb{R}$
, let
$d \in \mathbb{R}$
, let
![]() $H(X,d) = {\mathbb{E}}[\langle X^* d \rangle^2]$
, where
$H(X,d) = {\mathbb{E}}[\langle X^* d \rangle^2]$
, where
![]() $\langle \cdot \rangle$
denotes distance to the closest integer and
$\langle \cdot \rangle$
denotes distance to the closest integer and
![]() $X^*$
is a symmetrised version of X, that is,
$X^*$
is a symmetrised version of X, that is,
![]() $X^*= X - X^{\prime}$
where X
′ is an i.i.d. copy of X. Let
$X^*= X - X^{\prime}$
where X
′ is an i.i.d. copy of X. Let
![]() $H_m = \inf_{d \in [\frac{1}{4},\frac{1}{2}]} \,\, \sum_{i=1}^m H(X_i,d)$
. The following local limit theorem is due to Mukhin [Reference Mukhin28] (all limits are taken as
$H_m = \inf_{d \in [\frac{1}{4},\frac{1}{2}]} \,\, \sum_{i=1}^m H(X_i,d)$
. The following local limit theorem is due to Mukhin [Reference Mukhin28] (all limits are taken as
![]() $m \rightarrow \infty$
).
$m \rightarrow \infty$
).
Theorem A.1 ([Reference Mukhin28], Theorem 1). Suppose that the sequence
![]() $\frac{S_m-\mu_m}{\sigma_m}$
converges in distribution to a standard normal random variable and that
$\frac{S_m-\mu_m}{\sigma_m}$
converges in distribution to a standard normal random variable and that
![]() $\sigma_m \rightarrow \infty$
. If
$\sigma_m \rightarrow \infty$
. If
![]() $H_m \rightarrow \infty$
and there exists
$H_m \rightarrow \infty$
and there exists
![]() $\alpha > 0$
such that
$\alpha > 0$
such that
![]() $\forall u \in \big[H_m^{1/4},\sigma_m\big]$
we have
$\forall u \in \big[H_m^{1/4},\sigma_m\big]$
we have
![]() $\sum_{i:c_i \le u} c_i^2 \ge \alpha u \sigma_m ,$
then the local limit theorem holds.
$\sum_{i:c_i \le u} c_i^2 \ge \alpha u \sigma_m ,$
then the local limit theorem holds.
Next, we show how to derive Theorem 5.1 from Theorem A.1. The proof involves the following two lemmas.
Lemma A.2. For the random variables satisfying the conditions from Theorem 5.1,
![]() $\sigma_m \rightarrow \infty$
and
$\sigma_m \rightarrow \infty$
and
![]() $\frac{S_m-\mu_m}{\sigma_m}$
converges in distribution to a standard normal random variable.
$\frac{S_m-\mu_m}{\sigma_m}$
converges in distribution to a standard normal random variable.
Proof. Observe that
 \begin{equation*}\sigma_m^2 = r(1-r) \sum_{i=1}^m c_i^2 \ge r(1-r) \sum_{i: c_i \in I_1} c_i^2 = \Omega\!\left(\frac{m^{4/3}}{g(m)^4} \cdot g(m)^3\right) = \Omega\!\left(\frac{m^{4/3}}{g(m)}\right) \rightarrow \infty,\end{equation*}
\begin{equation*}\sigma_m^2 = r(1-r) \sum_{i=1}^m c_i^2 \ge r(1-r) \sum_{i: c_i \in I_1} c_i^2 = \Omega\!\left(\frac{m^{4/3}}{g(m)^4} \cdot g(m)^3\right) = \Omega\!\left(\frac{m^{4/3}}{g(m)}\right) \rightarrow \infty,\end{equation*}
and also
 \begin{align*} \frac{1}{\sigma_m^3} \sum_{i=1}^m {\mathbb{E}}[|X_i - {\mathbb{E}}[X_i]|^3] &= \frac{1}{\sigma_m^3} \sum_{i=1}^m r(1-r) c_i^3 \le \frac{\sigma^2_m c_m}{\sigma^3_m} = O\!\left(\frac{c_m}{\sigma_m}\right) \\ &= O\!\left( \frac{m^{2/3}g(m)^{-1}}{m^{2/3}g(m)^{-1/2}} \right) = O\!\left(g(m)^{-1/2}\right) \rightarrow 0. \end{align*}
\begin{align*} \frac{1}{\sigma_m^3} \sum_{i=1}^m {\mathbb{E}}[|X_i - {\mathbb{E}}[X_i]|^3] &= \frac{1}{\sigma_m^3} \sum_{i=1}^m r(1-r) c_i^3 \le \frac{\sigma^2_m c_m}{\sigma^3_m} = O\!\left(\frac{c_m}{\sigma_m}\right) \\ &= O\!\left( \frac{m^{2/3}g(m)^{-1}}{m^{2/3}g(m)^{-1/2}} \right) = O\!\left(g(m)^{-1/2}\right) \rightarrow 0. \end{align*}
Hence, the random variables
![]() $\{X_i\}$
satisfy Lyapunov’s central limit theorem conditions (see, e.g., [13]), and so
$\{X_i\}$
satisfy Lyapunov’s central limit theorem conditions (see, e.g., [13]), and so
![]() $\frac{S_m-\mu_m}{\sigma_m}$
converges in distribution to a standard normal random variable.
$\frac{S_m-\mu_m}{\sigma_m}$
converges in distribution to a standard normal random variable.
Lemma A.3. Suppose
![]() $c_1, \dots, c_m$
satisfy the conditions from Theorem 5.1. For any u satisfying
$c_1, \dots, c_m$
satisfy the conditions from Theorem 5.1. For any u satisfying
![]() $\sigma_m \ge u\ge 1$
,
$\sigma_m \ge u\ge 1$
,
![]() $\sum_{j:c_j \le u} c_j^2 \ge u \sigma_m / r(1-r)$
.
$\sum_{j:c_j \le u} c_j^2 \ge u \sigma_m / r(1-r)$
.
Proof. We have
![]() $\sigma_m^2 = r(1-r)\sum_{i=1}^m c_i^2 = O\!\left( \frac{m^{4/3}}{\sqrt{g(m)}} \right).$
We consider three cases. First, if
$\sigma_m^2 = r(1-r)\sum_{i=1}^m c_i^2 = O\!\left( \frac{m^{4/3}}{\sqrt{g(m)}} \right).$
We consider three cases. First, if
![]() $m^{1/4} \le u \le c_m = O\!\left(m^{2/3}g(m)^{-1}\right)$
, there exists a largest integer
$m^{1/4} \le u \le c_m = O\!\left(m^{2/3}g(m)^{-1}\right)$
, there exists a largest integer
![]() $k \in [0, \ell)$
such that
$k \in [0, \ell)$
such that
![]() $u = O\!\left( \frac{ \vartheta m^{2/3}}{g(m)^{2^k}} \right)$
, where
$u = O\!\left( \frac{ \vartheta m^{2/3}}{g(m)^{2^k}} \right)$
, where
![]() $\ell > 0$
is the smallest integer such that
$\ell > 0$
is the smallest integer such that
![]() $ m^{2/3}g(m)^{-2^\ell} = o\!\left(m^{1/4}\right)$
. Then,
$ m^{2/3}g(m)^{-2^\ell} = o\!\left(m^{1/4}\right)$
. Then,
 \begin{equation*}\sum_{i:c_i \le u} c_i^2 \ge \sum_{i:c_i \in I_{k+1}} c_i^2 \ge \frac{\vartheta^2 m^{4/3}}{4 g(m)^{2^{k+2}}} g(m)^{3\cdot 2^{k}} = \frac{\vartheta^2 m^{4/3}}{4 g(m)^{2^{k}}} \gg u \sigma_m;\end{equation*}
\begin{equation*}\sum_{i:c_i \le u} c_i^2 \ge \sum_{i:c_i \in I_{k+1}} c_i^2 \ge \frac{\vartheta^2 m^{4/3}}{4 g(m)^{2^{k+2}}} g(m)^{3\cdot 2^{k}} = \frac{\vartheta^2 m^{4/3}}{4 g(m)^{2^{k}}} \gg u \sigma_m;\end{equation*}
by
![]() $\gg$
we mean that
$\gg$
we mean that
![]() $u \sigma_m$
is of lower order with respect to
$u \sigma_m$
is of lower order with respect to
![]() $\frac{\vartheta^2 m^{4/3}}{4 g(m)^{2^{k}}}$
. Now, when
$\frac{\vartheta^2 m^{4/3}}{4 g(m)^{2^{k}}}$
. Now, when
![]() $\sigma_m \ge u \ge c_m$
, we have
$\sigma_m \ge u \ge c_m$
, we have
 \begin{equation*}\sum_{i:c_i \le u} c_i^2 = \sum_{i=1}^m c_i^2 = \frac{\sigma_m^2}{r(1-r)} \ge \frac{u \sigma_m}{r(1-r)}.\end{equation*}
\begin{equation*}\sum_{i:c_i \le u} c_i^2 = \sum_{i=1}^m c_i^2 = \frac{\sigma_m^2}{r(1-r)} \ge \frac{u \sigma_m}{r(1-r)}.\end{equation*}
Finally, if
![]() $1 \le u \le m^{1/4}$
,
$1 \le u \le m^{1/4}$
,
![]() $u\sigma_m$
is sublinear and so
$u\sigma_m$
is sublinear and so
 \begin{equation*} \sum_{i:c_i \le u} c_i^2 \ge \sum_{i=1}^{\rho m} c_i^2 = \rho m \gg m^{1/4} \sigma_m \ge u\sigma_m, \end{equation*}
\begin{equation*} \sum_{i:c_i \le u} c_i^2 \ge \sum_{i=1}^{\rho m} c_i^2 = \rho m \gg m^{1/4} \sigma_m \ge u\sigma_m, \end{equation*}
as claimed.
Proof of Theorem 5.1. We check that the
![]() $X_i$
’s satisfy the conditions from Theorem A.1. Lemma A.2 implies
$X_i$
’s satisfy the conditions from Theorem A.1. Lemma A.2 implies
![]() $\sigma_m \rightarrow \infty$
and
$\sigma_m \rightarrow \infty$
and
![]() $\frac{S_m - \mu_m}{\sigma_m} \rightarrow N(0,1)$
; by Lemma A.3 we also have that for any u satisfying
$\frac{S_m - \mu_m}{\sigma_m} \rightarrow N(0,1)$
; by Lemma A.3 we also have that for any u satisfying
![]() $\sigma_m \ge u\ge 1$
,
$\sigma_m \ge u\ge 1$
,
![]() $\sum_{j:c_j \le u} c_j^2 \ge u \sigma_m / r(1-r)$
. It remains to show that
$\sum_{j:c_j \le u} c_j^2 \ge u \sigma_m / r(1-r)$
. It remains to show that
![]() $H_m \rightarrow \infty$
.
$H_m \rightarrow \infty$
.
Now, for
![]() $i \le \rho m$
, observe that the value of
$i \le \rho m$
, observe that the value of
![]() $X^*_i$
equals to 1 with probability
$X^*_i$
equals to 1 with probability
![]() $r(1-r)$
, equals to
$r(1-r)$
, equals to
![]() $-1$
with probability
$-1$
with probability
![]() $r(1-r)$
and equals to 0 otherwise. Then for
$r(1-r)$
and equals to 0 otherwise. Then for
![]() $1/4 \le d \le 1/2$
,
$1/4 \le d \le 1/2$
,
![]() $\langle X_i^* d \rangle^2$
evaluates to
$\langle X_i^* d \rangle^2$
evaluates to
![]() $d^2$
with probability
$d^2$
with probability
![]() $2r(1-r)$
, and 0 otherwise. Therefore, for
$2r(1-r)$
, and 0 otherwise. Therefore, for
![]() $i \le \rho m$
and
$i \le \rho m$
and
![]() $1/4 \le d \le 1/2$
we have that
$1/4 \le d \le 1/2$
we have that
![]() $ {\mathbb{E}}[\langle X_i^* d \rangle^2] = 2 r(1-r)d^2. $
Thus,
$ {\mathbb{E}}[\langle X_i^* d \rangle^2] = 2 r(1-r)d^2. $
Thus,
 \begin{equation*}H_m = \inf_{\frac{1}{4} \le d \le\frac{1}{2}} \sum_{i=1}^{m} H(X_i,d) \ge \inf_{\frac{1}{4} \le d \le\frac{1}{2}} \sum_{i=1}^{\lfloor\rho m \rfloor} H(X_i,d) = \inf_{\frac{1}{4} \le d \le\frac{1}{2}} \sum_{i=1}^{\lfloor\rho m \rfloor} 2r(1-r)d^2 = \Omega(m) \rightarrow \infty.\end{equation*}
\begin{equation*}H_m = \inf_{\frac{1}{4} \le d \le\frac{1}{2}} \sum_{i=1}^{m} H(X_i,d) \ge \inf_{\frac{1}{4} \le d \le\frac{1}{2}} \sum_{i=1}^{\lfloor\rho m \rfloor} H(X_i,d) = \inf_{\frac{1}{4} \le d \le\frac{1}{2}} \sum_{i=1}^{\lfloor\rho m \rfloor} 2r(1-r)d^2 = \Omega(m) \rightarrow \infty.\end{equation*}
Since we have shown that the
![]() $X_i$
’s satisfy all the conditions from Theorem A.1, the result follows.
$X_i$
’s satisfy all the conditions from Theorem A.1, the result follows.
For completeness, we also derive Theorem 5.1 from first principles (i.e., without using Mukhin’s result [Reference Mukhin28]) in Appendix D.
Appendix B. Proofs of random walk couplings
Another important tool in our proofs are couplings based on the evolutions of certain random walks. In this section we consider a (lazy) symmetric random walk
![]() $(S_k)$
on
$(S_k)$
on
![]() $\mathbb{Z}$
with bounded step size, and the first result we present is an estimate on
$\mathbb{Z}$
with bounded step size, and the first result we present is an estimate on
![]() $M_k = \max\{S_1, \dots, S_k\}$
which is based on the well-known reflection principle (see, e.g., Chapter 2.7 in [Reference Levin and Peres22]).
$M_k = \max\{S_1, \dots, S_k\}$
which is based on the well-known reflection principle (see, e.g., Chapter 2.7 in [Reference Levin and Peres22]).
Lemma B.1. Let
![]() $A > 0$
and let
$A > 0$
and let
![]() $A \le c_1,c_2,\dots,c_n \le 4A$
be positive integers. Let
$A \le c_1,c_2,\dots,c_n \le 4A$
be positive integers. Let
![]() $r \in (0,1/2]$
and consider the sequence of random variables
$r \in (0,1/2]$
and consider the sequence of random variables
![]() $X_1,\dots,X_n$
where for each
$X_1,\dots,X_n$
where for each
![]() $i = 1,\dots,n$
:
$i = 1,\dots,n$
:
![]() $X_i = c_i$
with probability r;
$X_i = c_i$
with probability r;
![]() $X_i = -c_i$
with probability r; and
$X_i = -c_i$
with probability r; and
![]() $X_i = 0$
otherwise. Let
$X_i = 0$
otherwise. Let
![]() $S_k = \sum_{i=1}^k X_i $
and
$S_k = \sum_{i=1}^k X_i $
and
![]() $M_k = \max\{S_1,\dots,S_k\}$
. Then, for any
$M_k = \max\{S_1,\dots,S_k\}$
. Then, for any
![]() $y \ge 0$
$y \ge 0$
Proof. First, note that
 \begin{align} {\mathbb{P}}[M_n \ge y] &= \sum_{k=y}^{4An} {\mathbb{P}}[M_n \ge y,S_n=k] + \sum_{k=-4An}^{y-1} {\mathbb{P}}[M_n \ge y,S_n=k] \notag\\ &= {\mathbb{P}}[S_n \ge y] + \sum_{k=-4An}^{y-1} {\mathbb{P}}[M_n \ge y,S_n=k]. \end{align}
\begin{align} {\mathbb{P}}[M_n \ge y] &= \sum_{k=y}^{4An} {\mathbb{P}}[M_n \ge y,S_n=k] + \sum_{k=-4An}^{y-1} {\mathbb{P}}[M_n \ge y,S_n=k] \notag\\ &= {\mathbb{P}}[S_n \ge y] + \sum_{k=-4An}^{y-1} {\mathbb{P}}[M_n \ge y,S_n=k]. \end{align}
If
![]() $M_n \ge y$
, let
$M_n \ge y$
, let
![]() $W_n$
be the value of the random walk
$W_n$
be the value of the random walk
![]() $\{S_i\}$
the first time its value was at least y. Then,
$\{S_i\}$
the first time its value was at least y. Then,
 \begin{align} {\mathbb{P}}[M_n \ge y,S_n=k] &= \sum_{b = y}^{y+4A-1} {\mathbb{P}}[M_n \ge y,S_n=k,W_n=b] \notag\\ &= \sum_{b = y}^{y+4A-1} {\mathbb{P}}[M_n \ge y,S_n=2b-k,W_n=b] \notag\\ &= \sum_{b = y}^{y+4A-1} {\mathbb{P}}[S_n=2b-k,W_n=b],\notag \end{align}
\begin{align} {\mathbb{P}}[M_n \ge y,S_n=k] &= \sum_{b = y}^{y+4A-1} {\mathbb{P}}[M_n \ge y,S_n=k,W_n=b] \notag\\ &= \sum_{b = y}^{y+4A-1} {\mathbb{P}}[M_n \ge y,S_n=2b-k,W_n=b] \notag\\ &= \sum_{b = y}^{y+4A-1} {\mathbb{P}}[S_n=2b-k,W_n=b],\notag \end{align}
where in the second equality we used the fact that the random walk is symmetric and the last one follows from the fact that
![]() $2b - k \ge y$
. Plugging this into (B.1), we get
$2b - k \ge y$
. Plugging this into (B.1), we get
 \begin{align} {\mathbb{P}}[M_n \ge y] &= {\mathbb{P}}[S_n \ge y] + \sum_{b = y}^{y+4A-1}\sum_{k=-4An}^{y-1} {\mathbb{P}}[S_n=2b-k,W_n=b] \notag\\ &= {\mathbb{P}}[S_n \ge y] + \sum_{b = y}^{y+4A-1}\sum_{k=2b-y+1}^{4An} {\mathbb{P}}[S_n = k,W_n=b] \notag\\ &= {\mathbb{P}}[S_n \ge y] + \sum_{b = y}^{y+4A-1} {\mathbb{P}}[S_n \ge 2b-y+1,W_n=b] \notag\\ &\ge {\mathbb{P}}[S_n \ge y] + \sum_{b = y}^{y+4A-1} {\mathbb{P}}[S_n \ge y+8A+1,W_n=b] \notag, \end{align}
\begin{align} {\mathbb{P}}[M_n \ge y] &= {\mathbb{P}}[S_n \ge y] + \sum_{b = y}^{y+4A-1}\sum_{k=-4An}^{y-1} {\mathbb{P}}[S_n=2b-k,W_n=b] \notag\\ &= {\mathbb{P}}[S_n \ge y] + \sum_{b = y}^{y+4A-1}\sum_{k=2b-y+1}^{4An} {\mathbb{P}}[S_n = k,W_n=b] \notag\\ &= {\mathbb{P}}[S_n \ge y] + \sum_{b = y}^{y+4A-1} {\mathbb{P}}[S_n \ge 2b-y+1,W_n=b] \notag\\ &\ge {\mathbb{P}}[S_n \ge y] + \sum_{b = y}^{y+4A-1} {\mathbb{P}}[S_n \ge y+8A+1,W_n=b] \notag, \end{align}
since
![]() $b < y + 4A$
. Finally, observe that
$b < y + 4A$
. Finally, observe that
 \begin{equation*}\sum_{b = y}^{y+4A-1} {\mathbb{P}}[S_n \ge y+8A+1,W_n=b] = {\mathbb{P}}[S_n \ge y+8A+1]\end{equation*}
\begin{equation*}\sum_{b = y}^{y+4A-1} {\mathbb{P}}[S_n \ge y+8A+1,W_n=b] = {\mathbb{P}}[S_n \ge y+8A+1]\end{equation*}
and so
as desired.
We can now prove Theorem 5.7.
Proof of Theorem 5.7. Set
![]() $\delta = \frac{10}{\sqrt{r}}$
. Let
$\delta = \frac{10}{\sqrt{r}}$
. Let
![]() $D_k = \sum_{i=1}^k (X_i - Y_i)$
for each
$D_k = \sum_{i=1}^k (X_i - Y_i)$
for each
![]() $k \in \{1,\dots,m\}$
. We construct a coupling for (X, Y) by coupling each
$k \in \{1,\dots,m\}$
. We construct a coupling for (X, Y) by coupling each
![]() $\big(X_k,Y_k\big)$
as follows:
$\big(X_k,Y_k\big)$
as follows:
-
1. If
 $D_k < d$
, sample
$D_k < d$
, sample
 $X_{k+1}$
and
$X_{k+1}$
and
 $Y_{k+1}$
independently.
$Y_{k+1}$
independently. -
2. If
 $D_k \ge d$
, set
$D_k \ge d$
, set
 $X_{k+1} = Y_{k+1}$
.
$X_{k+1} = Y_{k+1}$
.
Observe that if
![]() $D_k \ge d$
for any
$D_k \ge d$
for any
![]() $k \le m$
, then
$k \le m$
, then
![]() $d + 2A \ge X - Y \ge d$
. Therefore,
$d + 2A \ge X - Y \ge d$
. Therefore,
where
![]() $M_m = \max\{D_0,...,D_m\}$
. Note that
$M_m = \max\{D_0,...,D_m\}$
. Note that
![]() $\{D_k\}$
behaves like a (lazy) symmetric random walk until the first time
$\{D_k\}$
behaves like a (lazy) symmetric random walk until the first time
![]() $\tau$
it is at least d; after that
$\tau$
it is at least d; after that
![]() $\{D_k\}$
stays put.
$\{D_k\}$
stays put.
Let
![]() $\big\{D^{\prime}_k\big\}$
denote such random walk which does not stop after
$\big\{D^{\prime}_k\big\}$
denote such random walk which does not stop after
![]() $\tau$
, and
$\tau$
, and
![]() $M^{\prime}_m\,:\!=\,\max\big\{D^{\prime}_0,...,D^{\prime}_m\big\}$
. Notice
$M^{\prime}_m\,:\!=\,\max\big\{D^{\prime}_0,...,D^{\prime}_m\big\}$
. Notice
Since the step size of
![]() $\big\{D^{\prime}_k\big\}$
is at least A and at most 4A, by Lemma B.1 for any
$\big\{D^{\prime}_k\big\}$
is at least A and at most 4A, by Lemma B.1 for any
![]() $d \ge 0$
$d \ge 0$
Let
![]() $\sigma^2 = \sum_{i=1}^m {\mathbb{E}}[(X_i-Y_i)^2] = 4r\sum_{i=1}^m c_i^2$
and
$\sigma^2 = \sum_{i=1}^m {\mathbb{E}}[(X_i-Y_i)^2] = 4r\sum_{i=1}^m c_i^2$
and
![]() $\rho = \sum_{i=1}^m {\mathbb{E}}[|X_i - Y_i|^3] = 4r(1+2r)\sum_{i=1}^m c_i^3$
. By the Berry–Esséen theorem for independent (but not necessarily identical) random variables (see, e.g., [Reference Berry3]), we get that for any
$\rho = \sum_{i=1}^m {\mathbb{E}}[|X_i - Y_i|^3] = 4r(1+2r)\sum_{i=1}^m c_i^3$
. By the Berry–Esséen theorem for independent (but not necessarily identical) random variables (see, e.g., [Reference Berry3]), we get that for any
![]() $y \in \mathbb{R}$
$y \in \mathbb{R}$
where N is a standard normal random variable, and
![]() $c\in [0.4, 0.6]$
is an absolute constant. Then,
$c\in [0.4, 0.6]$
is an absolute constant. Then,
Notice
![]() $\sigma \ge 2A \sqrt{rm}$
. If
$\sigma \ge 2A \sqrt{rm}$
. If
![]() $d + 8A \ge \sigma$
, the theorem holds vacuously since
$d + 8A \ge \sigma$
, the theorem holds vacuously since
If
![]() $d + 8A < \sigma$
, since it can be checked via a Taylor’s expansion that
$d + 8A < \sigma$
, since it can be checked via a Taylor’s expansion that
![]() $2 {\mathbb{P}}[N > y] \ge 1 - \sqrt{\frac{2}{\pi}}y$
for
$2 {\mathbb{P}}[N > y] \ge 1 - \sqrt{\frac{2}{\pi}}y$
for
![]() $y < 1$
, we get from (B.2)
$y < 1$
, we get from (B.2)
 \begin{align} {\mathbb{P}}[M_m \ge d] \ge 2 {\mathbb{P}}\big[D^{\prime}_m > d + 8A\big] & \ge 2{\mathbb{P}}\left[N>\frac{d + 8A}{\sigma}\right] - \frac{4cA}{\sigma} \notag\\ & \ge 1 - \frac{\sqrt{2/\pi}(d+8A)}{\sigma} - \frac{4cA}{\sigma} \notag\\ &\ge 1 - \frac{9 (d+A)}{\sigma} \notag \\ & \ge 1- \frac{\delta (d+A)}{A\sqrt{m}}, \notag \end{align}
\begin{align} {\mathbb{P}}[M_m \ge d] \ge 2 {\mathbb{P}}\big[D^{\prime}_m > d + 8A\big] & \ge 2{\mathbb{P}}\left[N>\frac{d + 8A}{\sigma}\right] - \frac{4cA}{\sigma} \notag\\ & \ge 1 - \frac{\sqrt{2/\pi}(d+8A)}{\sigma} - \frac{4cA}{\sigma} \notag\\ &\ge 1 - \frac{9 (d+A)}{\sigma} \notag \\ & \ge 1- \frac{\delta (d+A)}{A\sqrt{m}}, \notag \end{align}
as claimed.
Appendix C. Random graphs estimates
In this section, we provide proofs of lemmas which do not appear in the literature.
Recall
![]() $G \sim G\Big(n,\frac{1+\lambda n^{-1/3}}{n}\Big)$
, where
$G \sim G\Big(n,\frac{1+\lambda n^{-1/3}}{n}\Big)$
, where
![]() $\lambda = \lambda(n)$
may depend on n. Both of Lemmas 3.10 and 3.11 are proved using the following precise estimates on the moments of the number of trees of a given size in G. We note that similar estimates can be found in the literature (see, e.g., [Reference Pittel29, Reference Alon and Spencer1]); a proof is included for completeness.
$\lambda = \lambda(n)$
may depend on n. Both of Lemmas 3.10 and 3.11 are proved using the following precise estimates on the moments of the number of trees of a given size in G. We note that similar estimates can be found in the literature (see, e.g., [Reference Pittel29, Reference Alon and Spencer1]); a proof is included for completeness.
Claim C.1. Let
![]() $t_k$
be the number of trees of size k in G. Suppose there exists a positive increasing function g such that
$t_k$
be the number of trees of size k in G. Suppose there exists a positive increasing function g such that
![]() $g(n) \rightarrow \infty$
,
$g(n) \rightarrow \infty$
,
![]() $|\lambda| \le g(n)$
and
$|\lambda| \le g(n)$
and
![]() $i,j,k \le \frac{n^{2/3}}{g(n)^2}$
. If
$i,j,k \le \frac{n^{2/3}}{g(n)^2}$
. If
![]() $i,j,k\rightarrow \infty$
as
$i,j,k\rightarrow \infty$
as
![]() $n \rightarrow \infty$
, then:
$n \rightarrow \infty$
, then:
-
i.
 ${\mathbb{E}}[t_k] = \Theta\!\left(\frac{n}{k^{5/2}}\right)$
;
${\mathbb{E}}[t_k] = \Theta\!\left(\frac{n}{k^{5/2}}\right)$
; -
ii.
 ${\textrm{Var}}(t_k) \le {\mathbb{E}}[t_k] + \frac{(1+o(1)) \lambda n^{2/3}}{2\pi k^{3}}$
;
${\textrm{Var}}(t_k) \le {\mathbb{E}}[t_k] + \frac{(1+o(1)) \lambda n^{2/3}}{2\pi k^{3}}$
; -
iii. For
 $i \neq j$
,
$i \neq j$
,
 ${\textrm{Cov}}(t_i,t_j) \le \frac{(1+o(1))\lambda n^{2/3}}{2\pi i^{3/2} j^{3/2}}$
.
${\textrm{Cov}}(t_i,t_j) \le \frac{(1+o(1))\lambda n^{2/3}}{2\pi i^{3/2} j^{3/2}}$
.
To prove Lemma 3.10, we also use the following result.
Lemma C.2. Suppose
![]() $\varepsilon^3 n \rightarrow \infty$
and
$\varepsilon^3 n \rightarrow \infty$
and
![]() $\varepsilon = o(1)$
. Then w.h.p. the largest component of
$\varepsilon = o(1)$
. Then w.h.p. the largest component of
![]() $G \sim G\!\left(n, \frac{1 + \varepsilon}{n}\right)$
is the only component of G which contains more than one cycle. Also, w.h.p. the number of vertices contained in the unicyclic components of G is less than
$G \sim G\!\left(n, \frac{1 + \varepsilon}{n}\right)$
is the only component of G which contains more than one cycle. Also, w.h.p. the number of vertices contained in the unicyclic components of G is less than
![]() $g(n) \varepsilon^{-2}$
for any function
$g(n) \varepsilon^{-2}$
for any function
![]() $g(n) \rightarrow \infty$
.
$g(n) \rightarrow \infty$
.
Proof. An equivalent result was established in [Reference Luczak26] for the G(n, M) model, in which exactly M edges are chosen independently at random from the set of all
![]() $\binom{n}{2}$
possible edges (see Theorem 7 in [Reference Luczak26]). The result follows from the asymptotic equivalence between the G(n, p) and G(n, M) models when
$\binom{n}{2}$
possible edges (see Theorem 7 in [Reference Luczak26]). The result follows from the asymptotic equivalence between the G(n, p) and G(n, M) models when
![]() $M = \binom{n}{2} p$
(see, e.g., Proposition 1.12 in [Reference Janson, Łuczak and RuciŃski21]).
$M = \binom{n}{2} p$
(see, e.g., Proposition 1.12 in [Reference Janson, Łuczak and RuciŃski21]).
Proof of Lemma 3.10. Let us fix
![]() $\alpha > 0$
and consider first the case when
$\alpha > 0$
and consider first the case when
![]() $|\lambda|$
is large. If
$|\lambda|$
is large. If
![]() $\lambda < 0$
and
$\lambda < 0$
and
![]() $|\lambda| = \Omega\big(h(n)^{1/2}\big)$
, then Lemma 3.7 implies that
$|\lambda| = \Omega\big(h(n)^{1/2}\big)$
, then Lemma 3.7 implies that
Similarly, if
![]() $\lambda > 0$
and
$\lambda > 0$
and
![]() $\lambda = \Omega\big(h(n)^{1/2}\big)$
, then Lemma 3.8 implies that
$\lambda = \Omega\big(h(n)^{1/2}\big)$
, then Lemma 3.8 implies that
![]() ${\mathbb{E}}[\mathcal{R}_2(G)] = O\big(n^{4/3}h(n)^{-1/2}\big)$
. We may assume
${\mathbb{E}}[\mathcal{R}_2(G)] = O\big(n^{4/3}h(n)^{-1/2}\big)$
. We may assume
![]() $L_1(G) \le B_h$
since otherwise the size of the largest component does not contribute to the sum. Then,
$L_1(G) \le B_h$
since otherwise the size of the largest component does not contribute to the sum. Then,
Hence, if
![]() $|\lambda| = \Omega\big(h(n)^{-1/2}\big)$
, the result follows from Markov’s inequality.
$|\lambda| = \Omega\big(h(n)^{-1/2}\big)$
, the result follows from Markov’s inequality.
Suppose next
![]() $|\lambda| \le \sqrt{h(n)}$
. Let
$|\lambda| \le \sqrt{h(n)}$
. Let
![]() $t_k$
be the number of trees of size k in G and let
$t_k$
be the number of trees of size k in G and let
![]() $\mathcal{T}_{B_h}$
be the set of trees of size at most
$\mathcal{T}_{B_h}$
be the set of trees of size at most
![]() $B_h$
in G. By Claim C.1.i,
$B_h$
in G. By Claim C.1.i,
 \begin{align} {\mathbb{E}}\left[\sum\nolimits_{\tau \in \mathcal{T}_{B_h}} |\tau|^2\right] &= \sum_{k=1}^{B_h} k^2{\mathbb{E}}[t_k] = O\big(n h(n)^2\big) + \sum_{k=\lfloor h(n) \rfloor}^{B_h} k^2{\mathbb{E}}[t_k] \notag\\ &= O\big(n h(n)^2\big) + O(n) \sum_{k=\lfloor h(n) \rfloor}^{B_h} \frac{1}{k^{1/2}} = O\!\left(\frac{n^{4/3}}{h(n)^{1/2}}\right). \end{align}
\begin{align} {\mathbb{E}}\left[\sum\nolimits_{\tau \in \mathcal{T}_{B_h}} |\tau|^2\right] &= \sum_{k=1}^{B_h} k^2{\mathbb{E}}[t_k] = O\big(n h(n)^2\big) + \sum_{k=\lfloor h(n) \rfloor}^{B_h} k^2{\mathbb{E}}[t_k] \notag\\ &= O\big(n h(n)^2\big) + O(n) \sum_{k=\lfloor h(n) \rfloor}^{B_h} \frac{1}{k^{1/2}} = O\!\left(\frac{n^{4/3}}{h(n)^{1/2}}\right). \end{align}
By Markov’s inequality, we get that
![]() $\sum\nolimits_{\tau \in \mathcal{T}_{B_h}} |\tau|^2 \le An^{4/3}h(n)^{-1/2}$
with probability at least
$\sum\nolimits_{\tau \in \mathcal{T}_{B_h}} |\tau|^2 \le An^{4/3}h(n)^{-1/2}$
with probability at least
![]() $\gamma$
, for any desired
$\gamma$
, for any desired
![]() $\gamma > 0$
for a suitable constant
$\gamma > 0$
for a suitable constant
![]() $A = A(\gamma) > 0$
.
$A = A(\gamma) > 0$
.
All that is left to prove is that the contribution from complex (non-tree) components is small. When
![]() $|\lambda| = O(1)$
, this follows immediately from the fact that the expected number of complex components is O(1) (see, e.g., Lemma 2.1 in [Reference Łuczak, Pittel and Wierman27]). Then, if
$|\lambda| = O(1)$
, this follows immediately from the fact that the expected number of complex components is O(1) (see, e.g., Lemma 2.1 in [Reference Łuczak, Pittel and Wierman27]). Then, if
![]() $\mathcal{C}_{B_h}$
is the set of complex components in G of size at most
$\mathcal{C}_{B_h}$
is the set of complex components in G of size at most
![]() $B_h$
, we have
$B_h$
, we have
and the result follows again from Markov’s inequality and a union bound.
Finally, when
![]() $\sqrt{h(n)} \ge |\lambda| \rightarrow \infty$
, Lemma C.2 implies that w.h.p. there is no multicyclic component except the largest component and that the number of vertices in unicyclic components is bounded by
$\sqrt{h(n)} \ge |\lambda| \rightarrow \infty$
, Lemma C.2 implies that w.h.p. there is no multicyclic component except the largest component and that the number of vertices in unicyclic components is bounded by
![]() $n^{2/3} g(n)/\lambda^2$
, for any function
$n^{2/3} g(n)/\lambda^2$
, for any function
![]() $g(n) \rightarrow \infty$
. Hence, w.h.p.,
$g(n) \rightarrow \infty$
. Hence, w.h.p.,
Setting
![]() $g(n)=\lambda^2$
, it follows that w.h.p.
$g(n)=\lambda^2$
, it follows that w.h.p.
This, combined with (C.1), Markov’s inequality and a union bound yields the result.
Proof of Lemma 3.11. Let
![]() $T_B$
be number of trees in G with size in the interval [B,2B]; then
$T_B$
be number of trees in G with size in the interval [B,2B]; then
![]() $|S_B| \ge T_B$
. By Chebyshev’s inequality for
$|S_B| \ge T_B$
. By Chebyshev’s inequality for
![]() $a>0$
:
$a>0$
:
where
![]() $\sigma^2 = {\textrm{Var}}(T_B)$
. By Claim C.1.i,
$\sigma^2 = {\textrm{Var}}(T_B)$
. By Claim C.1.i,
 \begin{equation*}{\mathbb{E}}[T_B] = \sum_{k=B}^{2B} {\mathbb{E}}[T_k] \ge \frac{c_1 n}{B^{3/2}}\end{equation*}
\begin{equation*}{\mathbb{E}}[T_B] = \sum_{k=B}^{2B} {\mathbb{E}}[T_k] \ge \frac{c_1 n}{B^{3/2}}\end{equation*}
for a suitable constant
![]() $c_1 > 0$
. Now,
$c_1 > 0$
. Now,
 \begin{equation*}{\textrm{Var}}(T_B) = \sum_{k=B}^{2B} {\textrm{Var}}(t_k) + \sum_{j \neq i: j,i \in [B,2B]} {\textrm{Cov}}(t_i,t_j).\end{equation*}
\begin{equation*}{\textrm{Var}}(T_B) = \sum_{k=B}^{2B} {\textrm{Var}}(t_k) + \sum_{j \neq i: j,i \in [B,2B]} {\textrm{Cov}}(t_i,t_j).\end{equation*}
 \begin{equation*}\sum_{k=B}^{2B} {\textrm{Var}}(t_k) \le \sum_{k=B}^{2B} {\mathbb{E}}[t_k] + \sum_{k=B}^{2B} \frac{(1+o(1)) \lambda n^{2/3}}{2\pi k^{3}} = O\!\left(\frac{n}{B^{3/2}}\right) + O\!\left(\frac{|\lambda| n^{2/3}}{B^2}\right) = O\!\left(\frac{n}{B^{3/2}}\right),\end{equation*}
\begin{equation*}\sum_{k=B}^{2B} {\textrm{Var}}(t_k) \le \sum_{k=B}^{2B} {\mathbb{E}}[t_k] + \sum_{k=B}^{2B} \frac{(1+o(1)) \lambda n^{2/3}}{2\pi k^{3}} = O\!\left(\frac{n}{B^{3/2}}\right) + O\!\left(\frac{|\lambda| n^{2/3}}{B^2}\right) = O\!\left(\frac{n}{B^{3/2}}\right),\end{equation*}
where in the last equality we used the assumption that
![]() $\lambda = o\!\left(n^{1/3}\right)$
. Similarly, by Claim C.1.iii
$\lambda = o\!\left(n^{1/3}\right)$
. Similarly, by Claim C.1.iii
 \begin{equation*}\sum_{j \neq i: j,i \in [B,2B]} {\textrm{Cov}}(t_i,t_j) \le \sum_{j \neq i: j,i \in [B,2B]} \frac{(1+o(1))\lambda n^{2/3}}{2\pi i^{3/2} j^{3/2}} \le \frac{(1+o(1))|\lambda| n^{2/3}}{2\pi B} = O\!\left(\frac{n}{B^{3/2}}\right),\end{equation*}
\begin{equation*}\sum_{j \neq i: j,i \in [B,2B]} {\textrm{Cov}}(t_i,t_j) \le \sum_{j \neq i: j,i \in [B,2B]} \frac{(1+o(1))\lambda n^{2/3}}{2\pi i^{3/2} j^{3/2}} \le \frac{(1+o(1))|\lambda| n^{2/3}}{2\pi B} = O\!\left(\frac{n}{B^{3/2}}\right),\end{equation*}
where the last inequality follows from the assumption that
![]() $B \le \frac{n^{2/3}}{g(n)^2}$
. Hence, for a suitable constant
$B \le \frac{n^{2/3}}{g(n)^2}$
. Hence, for a suitable constant
![]() $c_2 > 0$
$c_2 > 0$
and taking
![]() $a = \frac{c_1 n}{2 B^{3/2} \sigma}$
we get
$a = \frac{c_1 n}{2 B^{3/2} \sigma}$
we get
as desired.
Proof Corollary 3.12. Lemma 3.11 implies that for a suitable constant
![]() $b>0$
$b>0$
for any
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $g(n)^{2^k} = o(m^{2/3})$
. Observe that
$g(n)^{2^k} = o(m^{2/3})$
. Observe that
Hence, a union bound over k, that is, over the intervals
![]() $\mathcal{I}_k(g)$
, implies that, with probability at least
$\mathcal{I}_k(g)$
, implies that, with probability at least
![]() $1-O\big(g(n)^{-3}\big)$
,
$1-O\big(g(n)^{-3}\big)$
,
![]() $N_{k}(X_{t+1},g) \ge b g(n)^{3 \cdot 2^{k-1}}$
for all
$N_{k}(X_{t+1},g) \ge b g(n)^{3 \cdot 2^{k-1}}$
for all
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $n^{2/3}g(n)^{-2^k}\rightarrow \infty$
, as claimed.
$n^{2/3}g(n)^{-2^k}\rightarrow \infty$
, as claimed.
Proof of Claim C.1. Let
![]() $c = 1+\lambda n^{-1/3}$
. The following combinatorial identity follows immediately from the fact that there are exactly
$c = 1+\lambda n^{-1/3}$
. The following combinatorial identity follows immediately from the fact that there are exactly
![]() $k^{k-2}$
trees of size k.
$k^{k-2}$
trees of size k.
Using the Taylor expansion for
![]() $\ln(1-x)$
and the fact that
$\ln(1-x)$
and the fact that
![]() $k = o\big(n^{2/3}\big)$
, we get
$k = o\big(n^{2/3}\big)$
, we get
 \begin{align} \frac{n!}{(n-k)!} &= n^k \, \prod_{i=1}^{k-1} \left(1-\frac{i}{n}\right) =n^k \exp\!\left({-}\frac{k^2}{2n}-\frac{k^3}{6n^2}+o(1)\right). \end{align}
\begin{align} \frac{n!}{(n-k)!} &= n^k \, \prod_{i=1}^{k-1} \left(1-\frac{i}{n}\right) =n^k \exp\!\left({-}\frac{k^2}{2n}-\frac{k^3}{6n^2}+o(1)\right). \end{align}
Similarly,
 \begin{align} \left(\frac{c}{n}\right)^{k-1} &= \frac{1}{n^{k-1}} \exp\!\left(\frac{\lambda k}{n^{1/3}} - \frac{\lambda^2 k}{2 n^{2/3}}+o(1)\right), \notag\\ \left(1-\frac{c}{n}\right)^{k(n-k)+ \binom{k}{2}-k+1} &= \exp\!\left({-}k-\frac{\lambda k}{n^{1/3}}+\frac{k^2}{2n}+\frac{\lambda k^2}{2n^{4/3}}+o(1)\right).\notag \end{align}
\begin{align} \left(\frac{c}{n}\right)^{k-1} &= \frac{1}{n^{k-1}} \exp\!\left(\frac{\lambda k}{n^{1/3}} - \frac{\lambda^2 k}{2 n^{2/3}}+o(1)\right), \notag\\ \left(1-\frac{c}{n}\right)^{k(n-k)+ \binom{k}{2}-k+1} &= \exp\!\left({-}k-\frac{\lambda k}{n^{1/3}}+\frac{k^2}{2n}+\frac{\lambda k^2}{2n^{4/3}}+o(1)\right).\notag \end{align}
Since
![]() $k \rightarrow \infty$
, Stirling’s approximation gives
$k \rightarrow \infty$
, Stirling’s approximation gives
Putting all these bounds together, we get
where in the last inequality we used the assumptions that
![]() $|\lambda| \le g(n)$
and
$|\lambda| \le g(n)$
and
![]() $k \le \frac{n^{2/3}}{g(n)^2}$
. This establishes part (i).
$k \le \frac{n^{2/3}}{g(n)^2}$
. This establishes part (i).
For part (ii) we proceed in similar fashion, starting instead from the following combinatorial identity:
where
![]() $m = 2\binom{k}{2}-2(k-1)+k^2+2k(n-2k)$
(see, e.g., [Reference Pittel29]). Using the Taylor expansion for
$m = 2\binom{k}{2}-2(k-1)+k^2+2k(n-2k)$
(see, e.g., [Reference Pittel29]). Using the Taylor expansion for
![]() $\ln (1-x)$
, we get
$\ln (1-x)$
, we get
 \begin{align} \frac{n!}{(n-2k)!} &= n^{2k} \exp\!\left({-}\frac{2k^2}{n}-\frac{4k^3}{3n^2}+o(1)\right), \notag\\ \left(\frac{c}{n}\right)^{2k-2} &= \frac{1}{n^{2k-2}} \exp\!\left(\frac{2\lambda k}{n^{1/3}}-\frac{\lambda^2 k}{n^{2/3}}+o(1)\right),\notag\\ \left(1-\frac{c}{n}\right)^{m} &= \exp\!\left({-}2k+\frac{2k^2}{n}-\frac{2\lambda k}{n^{1/3}}+\frac{2\lambda k^2}{n^{4/3}}+o(1)\right).\notag \end{align}
\begin{align} \frac{n!}{(n-2k)!} &= n^{2k} \exp\!\left({-}\frac{2k^2}{n}-\frac{4k^3}{3n^2}+o(1)\right), \notag\\ \left(\frac{c}{n}\right)^{2k-2} &= \frac{1}{n^{2k-2}} \exp\!\left(\frac{2\lambda k}{n^{1/3}}-\frac{\lambda^2 k}{n^{2/3}}+o(1)\right),\notag\\ \left(1-\frac{c}{n}\right)^{m} &= \exp\!\left({-}2k+\frac{2k^2}{n}-\frac{2\lambda k}{n^{1/3}}+\frac{2\lambda k^2}{n^{4/3}}+o(1)\right).\notag \end{align}
These three bounds together with (C.3) imply
From (C.4), we get
Hence,
 \begin{align} {\textrm{Var}}(t_k) &= {\mathbb{E}}[t_k]+\frac{(1+o(1))n^2}{2\pi k^5} \exp\!\left({-}\frac{\lambda^2 k}{n^{2/3}} + \frac{\lambda k^2}{n^{4/3}} - \frac{k^3}{3n^2}\right) \left[\exp\!\left(\frac{\lambda k^2}{n^{4/3}}-\frac{k^3}{n^2}\right) - 1\right] \notag\\ &= {\mathbb{E}}[t_k]+\frac{(1+o(1))n^2}{2\pi k^5}\left[\exp\!\left(\frac{\lambda k^2}{n^{4/3}}-\frac{k^3}{n^2}\right) - 1\right] \notag\\ &\le {\mathbb{E}}[t_k]+\frac{(1+o(1))n^2}{2\pi k^5}\left[\exp\!\left(\frac{\lambda k^2}{n^{4/3}}\right) - 1\right] \notag\\ &\le {\mathbb{E}}[t_k]+\frac{(1+o(1)) \lambda n^{2/3}}{2\pi k^3}, \notag \end{align}
\begin{align} {\textrm{Var}}(t_k) &= {\mathbb{E}}[t_k]+\frac{(1+o(1))n^2}{2\pi k^5} \exp\!\left({-}\frac{\lambda^2 k}{n^{2/3}} + \frac{\lambda k^2}{n^{4/3}} - \frac{k^3}{3n^2}\right) \left[\exp\!\left(\frac{\lambda k^2}{n^{4/3}}-\frac{k^3}{n^2}\right) - 1\right] \notag\\ &= {\mathbb{E}}[t_k]+\frac{(1+o(1))n^2}{2\pi k^5}\left[\exp\!\left(\frac{\lambda k^2}{n^{4/3}}-\frac{k^3}{n^2}\right) - 1\right] \notag\\ &\le {\mathbb{E}}[t_k]+\frac{(1+o(1))n^2}{2\pi k^5}\left[\exp\!\left(\frac{\lambda k^2}{n^{4/3}}\right) - 1\right] \notag\\ &\le {\mathbb{E}}[t_k]+\frac{(1+o(1)) \lambda n^{2/3}}{2\pi k^3}, \notag \end{align}
where in the second equality we used the assumptions that
![]() $|\lambda| \le g(n)$
and
$|\lambda| \le g(n)$
and
![]() $k \le \frac{n^{2/3}}{g(n)^2}$
and for the last inequality we used the Taylor expansion for
$k \le \frac{n^{2/3}}{g(n)^2}$
and for the last inequality we used the Taylor expansion for
![]() $e^x$
. This completes the proof of part (ii).
$e^x$
. This completes the proof of part (ii).
For part (iii), let
![]() $\ell = i+j$
. When
$\ell = i+j$
. When
![]() $i \neq j$
we have the following combinatorial identity (see, e.g., [Reference Pittel29]):
$i \neq j$
we have the following combinatorial identity (see, e.g., [Reference Pittel29]):
where
![]() $m^{\prime} = \binom{i}{2}-(i-1)+\binom{j}{2}-(j-1)+ij+\ell(n-\ell)$
. Using Taylor expansions and Stirling’s approximation as in the previous two parts, we get
$m^{\prime} = \binom{i}{2}-(i-1)+\binom{j}{2}-(j-1)+ij+\ell(n-\ell)$
. Using Taylor expansions and Stirling’s approximation as in the previous two parts, we get
Moreover, from (C.4) we have
 \begin{equation*}{\mathbb{E}}[t_i]{\mathbb{E}}[t_j] = \frac{(1+o(1))n^2}{2\pi i^{5/2} j^{5/2}} \exp\!\left({-}\frac{\lambda^2 \ell}{2n^{2/3}} + \frac{\lambda \big(i^2+j^2\big)}{2n^{4/3}} - \frac{i^3+j^3}{6n^2} + o(1)\right),\end{equation*}
\begin{equation*}{\mathbb{E}}[t_i]{\mathbb{E}}[t_j] = \frac{(1+o(1))n^2}{2\pi i^{5/2} j^{5/2}} \exp\!\left({-}\frac{\lambda^2 \ell}{2n^{2/3}} + \frac{\lambda \big(i^2+j^2\big)}{2n^{4/3}} - \frac{i^3+j^3}{6n^2} + o(1)\right),\end{equation*}
and so
 \begin{align} {\textrm{Cov}}(t_i,t_j) &= {\mathbb{E}}[t_it_j]-{\mathbb{E}}[t_i]{\mathbb{E}}[t_j] \notag\\ &= \frac{(1+o(1))n^2}{2\pi i^{5/2} j^{5/2}} \exp\!\left({-}\frac{\ell^3}{6n^2}-\frac{\lambda^2 \ell}{2n^{2/3}} + \frac{\lambda \ell^2}{2 n^{4/3}}\right) \left[1-\exp\!\left({-}\frac{\lambda ij}{n^{4/3}}+\frac{ij\ell}{2n^2}\right)\right] \notag\\ &= \frac{(1+o(1))n^2}{2\pi i^{5/2} j^{5/2}} \left[1-\exp\!\left({-}\frac{\lambda ij}{n^{4/3}}+\frac{ij(i+j)}{2n^2}\right)\right] \notag\\ &\le \frac{(1+o(1)) \lambda n^{2/3}}{2\pi i^{3/2} j^{3/2}}, \notag \end{align}
\begin{align} {\textrm{Cov}}(t_i,t_j) &= {\mathbb{E}}[t_it_j]-{\mathbb{E}}[t_i]{\mathbb{E}}[t_j] \notag\\ &= \frac{(1+o(1))n^2}{2\pi i^{5/2} j^{5/2}} \exp\!\left({-}\frac{\ell^3}{6n^2}-\frac{\lambda^2 \ell}{2n^{2/3}} + \frac{\lambda \ell^2}{2 n^{4/3}}\right) \left[1-\exp\!\left({-}\frac{\lambda ij}{n^{4/3}}+\frac{ij\ell}{2n^2}\right)\right] \notag\\ &= \frac{(1+o(1))n^2}{2\pi i^{5/2} j^{5/2}} \left[1-\exp\!\left({-}\frac{\lambda ij}{n^{4/3}}+\frac{ij(i+j)}{2n^2}\right)\right] \notag\\ &\le \frac{(1+o(1)) \lambda n^{2/3}}{2\pi i^{3/2} j^{3/2}}, \notag \end{align}
where in the third equality we used the assumptions that
![]() $|\lambda| \le g(n)$
and
$|\lambda| \le g(n)$
and
![]() $i,j \le \frac{n^{2/3}}{g(n)^2}$
and the last inequality follows from the Taylor expansion for
$i,j \le \frac{n^{2/3}}{g(n)^2}$
and the last inequality follows from the Taylor expansion for
![]() $e^x$
.
$e^x$
.
Appendix D. The second proof of the local limit theorem
In this appendix, we provide an alternative proof of Theorem 5.1 that does not use Theorem A.1.
Proof of Theorem 5.1. Let
![]() $\Phi({\cdot})$
denote the probability density function of a standard normal distribution. We will show for any fixed
$\Phi({\cdot})$
denote the probability density function of a standard normal distribution. We will show for any fixed
![]() $a \in \mathbb{R}$
,
$a \in \mathbb{R}$
,
which is equivalent to (9).
Let
![]() $\phi(t)$
denote the characteristic function for the random variable
$\phi(t)$
denote the characteristic function for the random variable
![]() $(S_m - \mu_m )/\sigma_m$
. By applying the inversion formula (see Theorem 3.3.14 and Exercise 3.3.2 in [Reference Durrett13]),
$(S_m - \mu_m )/\sigma_m$
. By applying the inversion formula (see Theorem 3.3.14 and Exercise 3.3.2 in [Reference Durrett13]),
and
Hence, the left hand side of (D.1) can be bounded from above by
Since
![]() $|e^{-ita}| \le 1$
, it suffices to show that for all
$|e^{-ita}| \le 1$
, it suffices to show that for all
![]() $\varepsilon > 0$
there exists
$\varepsilon > 0$
there exists
![]() $M>0$
such that if
$M>0$
such that if
![]() $m >M$
then
$m >M$
then
We can bound from above the left hand side of (D.2) by:
The division depends on some constant A that we will choose soon. We proceed to bound integral terms in (D.3) independently.
Lemma A.2 implies that
![]() $\frac{S_m-\mu_m}{\sigma_m}$
converges in distribution to a standard normal. Combined with the continuity theorem (see Theorem 3.3.17 in [Reference Durrett13]), we get that
$\frac{S_m-\mu_m}{\sigma_m}$
converges in distribution to a standard normal. Combined with the continuity theorem (see Theorem 3.3.17 in [Reference Durrett13]), we get that
![]() $\phi(t) \rightarrow e^{-\frac{t^2}{2}}$
as
$\phi(t) \rightarrow e^{-\frac{t^2}{2}}$
as
![]() $m \rightarrow \infty$
. The dominated convergence theorem (see Theorem 1.5.8 in [Reference Durrett13]) hence implies that for any
$m \rightarrow \infty$
. The dominated convergence theorem (see Theorem 1.5.8 in [Reference Durrett13]) hence implies that for any
![]() $A < \infty$
the first integral of (D.3) converges to 0. We select M large enough so that the integral is less than
$A < \infty$
the first integral of (D.3) converges to 0. We select M large enough so that the integral is less than
![]() $\varepsilon/4$
.
$\varepsilon/4$
.
The last integral of (D.3) is the standard normal tail that goes to 0 exponentially fast as A increases (see e.g., Proposition 2.1.2 in [Reference Vershynin32]). Therefore, we are able to select A large enough so that each tail has probability mass less than
![]() $\varepsilon/8$
.
$\varepsilon/8$
.
To bound the remaining two terms we use the properties of the characteristic function
![]() $\phi(t)$
. By definition and the independence between
$\phi(t)$
. By definition and the independence between
![]() $X_i$
’s,
$X_i$
’s,
 \begin{equation*}\phi(t) = {\mathbb{E}} \left[\exp\!\left(it\cdot \frac{S_m - \mu_m}{\sigma_m}\right)\right] = \exp\!\left({-} \frac{it\mu_m}{\sigma_m}\right) \prod_{j=1}^m \phi_j(t),\end{equation*}
\begin{equation*}\phi(t) = {\mathbb{E}} \left[\exp\!\left(it\cdot \frac{S_m - \mu_m}{\sigma_m}\right)\right] = \exp\!\left({-} \frac{it\mu_m}{\sigma_m}\right) \prod_{j=1}^m \phi_j(t),\end{equation*}
where
![]() $\phi_j(t)$
denotes the characteristic function of
$\phi_j(t)$
denotes the characteristic function of
![]() $X_j/\sigma_m$
. Since
$X_j/\sigma_m$
. Since
![]() $\exp\big({-}\frac{it \mu_m}{\sigma_m}\big) $
always has modulo 1,
$\exp\big({-}\frac{it \mu_m}{\sigma_m}\big) $
always has modulo 1,
![]() $\lvert \phi(t) \rvert \le \prod_{j=1}^m \lvert \phi_j(t)\rvert $
.
$\lvert \phi(t) \rvert \le \prod_{j=1}^m \lvert \phi_j(t)\rvert $
.
We proceed to bound the third integral of (D.3). Note that
![]() $\lvert \phi_j(t)\rvert \le 1$
for all j and t. Therefore,
$\lvert \phi_j(t)\rvert \le 1$
for all j and t. Therefore,
 \begin{equation*} \lvert \phi(t) \rvert \le \prod_{j=1}^m |\phi_j(t)| \le \prod_{j\le\rho m} |\phi_j(t)|. \end{equation*}
\begin{equation*} \lvert \phi(t) \rvert \le \prod_{j=1}^m |\phi_j(t)| \le \prod_{j\le\rho m} |\phi_j(t)|. \end{equation*}
Notice that the
![]() $X_j$
’s for
$X_j$
’s for
![]() $j \le \rho m$
are Bernoulli random variables. By periodicity (see Theorem 3.5.2 in [Reference Durrett13]),
$j \le \rho m$
are Bernoulli random variables. By periodicity (see Theorem 3.5.2 in [Reference Durrett13]),
![]() $|\phi_j(t)|$
equals to 1 only when t equals to the multiples of
$|\phi_j(t)|$
equals to 1 only when t equals to the multiples of
![]() $2\pi \sigma_m$
. For
$2\pi \sigma_m$
. For
![]() $t \in [\sigma_m/2, \sigma_m\pi]$
,
$t \in [\sigma_m/2, \sigma_m\pi]$
,
![]() $|\phi_j(t)|$
is bounded away from 1, and there exists a constant
$|\phi_j(t)|$
is bounded away from 1, and there exists a constant
![]() $\eta<1$
such that
$\eta<1$
such that
![]() $\lvert \phi_j(t) \rvert \le \eta$
. Hence,
$\lvert \phi_j(t) \rvert \le \eta$
. Hence,
![]() $\lvert \phi(t) \rvert \le \eta^{\rho m}$
. By choosing M to be sufficiently large, we may bound the integral for
$\lvert \phi(t) \rvert \le \eta^{\rho m}$
. By choosing M to be sufficiently large, we may bound the integral for
![]() $m > M$
:
$m > M$
:
Finally, we bound the second integral of (D.3). By the definition of
![]() $X_j$
, we have
$X_j$
, we have
where the last identity uses Euler’ formula. Take the modulo of both sides,
 \begin{align*} \lvert \phi_j(t) \rvert &= \sqrt{r^2 \sin^2 \frac{c_j t}{\sigma_m} + \left(r \frac{c_j t}{\sigma_m} + 1 -r \right)^2}\\ &= \sqrt{r^2 \sin^2 \frac{c_j t}{\sigma_m} + r^2 \cos^2 \frac{c_j t}{\sigma_m} + (1-r)^2 + 2r(1-r) \cos \frac{c_j t}{\sigma_m}}\\ &= \sqrt{r^2 + (1-r)^2 + 2r(1-r) \cos \frac{c_j t}{\sigma_m}} \\ & = \sqrt{1 - 2r(1-r)\left(1-\cos \frac{c_j t}{\sigma_m}\right)} \\ & = 1 - r(1-r)\left(1-\cos \frac{c_j t}{\sigma_m}\right) - \frac{1}{2}r^2(1-r)^2\left(1-\cos \frac{c_j t}{\sigma_m}\right)^2 - \dots, \end{align*}
\begin{align*} \lvert \phi_j(t) \rvert &= \sqrt{r^2 \sin^2 \frac{c_j t}{\sigma_m} + \left(r \frac{c_j t}{\sigma_m} + 1 -r \right)^2}\\ &= \sqrt{r^2 \sin^2 \frac{c_j t}{\sigma_m} + r^2 \cos^2 \frac{c_j t}{\sigma_m} + (1-r)^2 + 2r(1-r) \cos \frac{c_j t}{\sigma_m}}\\ &= \sqrt{r^2 + (1-r)^2 + 2r(1-r) \cos \frac{c_j t}{\sigma_m}} \\ & = \sqrt{1 - 2r(1-r)\left(1-\cos \frac{c_j t}{\sigma_m}\right)} \\ & = 1 - r(1-r)\left(1-\cos \frac{c_j t}{\sigma_m}\right) - \frac{1}{2}r^2(1-r)^2\left(1-\cos \frac{c_j t}{\sigma_m}\right)^2 - \dots, \end{align*}
where the last equality corresponds to the Taylor expansion for
![]() $\sqrt{1+y}$
when
$\sqrt{1+y}$
when
![]() $\lvert y \rvert \le 1$
. We can also Taylor expand
$\lvert y \rvert \le 1$
. We can also Taylor expand
![]() $\cos \frac{c_j t}{\sigma_m}$
as
$\cos \frac{c_j t}{\sigma_m}$
as
Observe that if
![]() $\frac{c_j t}{\sigma_m} < 1$
, then we can bound
$\frac{c_j t}{\sigma_m} < 1$
, then we can bound
![]() $\cos \frac{c_j t}{\sigma_m}$
from above by
$\cos \frac{c_j t}{\sigma_m}$
from above by
![]() $1 - \frac{c_j^2 t^2}{4\sigma_m^2}$
. Furthermore, if we keep only the first order term from the expansion for
$1 - \frac{c_j^2 t^2}{4\sigma_m^2}$
. Furthermore, if we keep only the first order term from the expansion for
![]() $\lvert \phi_j(t) \rvert$
, we have
$\lvert \phi_j(t) \rvert$
, we have
 \begin{equation} \lvert \phi_j(t) \rvert \le 1 - r(1-r) \frac{c_j^2 t^2}{4\sigma_m^2} \le \exp \!\left({-} r(1-r) \frac{c_j^2 t^2}{4\sigma_m^2} \right). \end{equation}
\begin{equation} \lvert \phi_j(t) \rvert \le 1 - r(1-r) \frac{c_j^2 t^2}{4\sigma_m^2} \le \exp \!\left({-} r(1-r) \frac{c_j^2 t^2}{4\sigma_m^2} \right). \end{equation}
Note that (D.4) only holds if
![]() $c_j t< \sigma_m$
. However, if we fix
$c_j t< \sigma_m$
. However, if we fix
![]() $\sigma_m$
then for every
$\sigma_m$
then for every
![]() $t \in [A, \sigma_m/2]$
, there always exists a real number
$t \in [A, \sigma_m/2]$
, there always exists a real number
![]() $u(t)\ge 1$
such that
$u(t)\ge 1$
such that
![]() $u(t) t < \sigma_m \le 2u(t)t$
, which implies for all
$u(t) t < \sigma_m \le 2u(t)t$
, which implies for all
![]() $c_j \le u(t)$
, (D.4) can be established. Now we aggregate all
$c_j \le u(t)$
, (D.4) can be established. Now we aggregate all
![]() $\lvert \phi_j(t) \rvert$
for which we could claim (D.4).
$\lvert \phi_j(t) \rvert$
for which we could claim (D.4).
 \begin{equation} \lvert \phi(t) \rvert \le \prod_{j:c_j \le u(t)} \lvert \phi_j(t) \rvert \le \exp \!\left({-} r(1-r) \sum_{j:c_j \le u(t)} \frac{c_j^2 t^2}{4\sigma_m^2} \right). \end{equation}
\begin{equation} \lvert \phi(t) \rvert \le \prod_{j:c_j \le u(t)} \lvert \phi_j(t) \rvert \le \exp \!\left({-} r(1-r) \sum_{j:c_j \le u(t)} \frac{c_j^2 t^2}{4\sigma_m^2} \right). \end{equation}
Without loss of generality, we assume
![]() $A>1$
. Consequently,
$A>1$
. Consequently,
![]() $u(t) \le \sigma_m$
. Lemma A.3 implies for
$u(t) \le \sigma_m$
. Lemma A.3 implies for
![]() $\sigma_m\ge u(t) \ge 1$
,
$\sigma_m\ge u(t) \ge 1$
,
![]() $\sum_{j:c_j \le u(t)} c_j^2 \ge u(t) \sigma_m / r(1-r)$
. Plugging this inequality into (D.5), we obtain
$\sum_{j:c_j \le u(t)} c_j^2 \ge u(t) \sigma_m / r(1-r)$
. Plugging this inequality into (D.5), we obtain
Therefore, for sufficiently large A,
Thus we established (D.2) and the proof is complete.