DISCUSSION POINTS
• How much energy is used in delivering small packages by a drone?
• How does the energy used to move a given mass compare for an electrically powered drone, a helicopter, an airplane, and a delivery truck?
• Does a drone that has vertical take-off and landing capabilities use more energy than a conventional airplane?
• Could the package delivery drone be solar powered?
• Is such a drone less efficient than a helicopter?
• Could a passenger-carrying air taxi, capable of vertical take-off and landing, be powered by batteries?
There has been much excitement recently on the possibility of using drones instead of trucks for parcel delivery. As a consequence of the widespread growth of online retailing as pioneered by Amazon, many people would find it appealing to have something that they ordered dropped directly to their backyard, rather than wait for a truck to show up sometime late in the day. Given the congestion on the roads in major urban areas, many city dwellers dream of summoning an air taxi that would whisk them to their destination above the chaos in the streets below. Not only would these innovations benefit the affluent city dweller, in principle they could bring substantial economic benefits to people who live in isolated areas of developing nations where there are no roads. However, the growing concerns about anthropogenic carbon dioxide emissions leading to irreversible climate change mean it is appropriate to consider their energy use. Is there a way for drones or air taxis to use renewable energy, presumably solar?
Vehicles that move along the ground use energy to overcome rolling resistance and air resistance.Reference Rez1 Since the rolling resistance does not depend on velocity, but the air resistance varies as the square of the velocity, the energy use increases as the vehicle goes faster. Ships have to overcome hydrodynamic resistance, which again scales as the square of the velocity. Aircraft are fundamentally different. As MacKay so eloquently said in his book,Reference Mackay2 half the energy used by an aircraft is used for staying “up”.
In cruise flight, the lift generated by the wings is equal to the weight of the aircraft, and the thrust is equal to the drag. Both the lift, L, and the profile drag, D p, (the drag due to the shape of the aircraft and friction of the air) are proportional to the square of the airspeed, v, and the density of air, ρ.
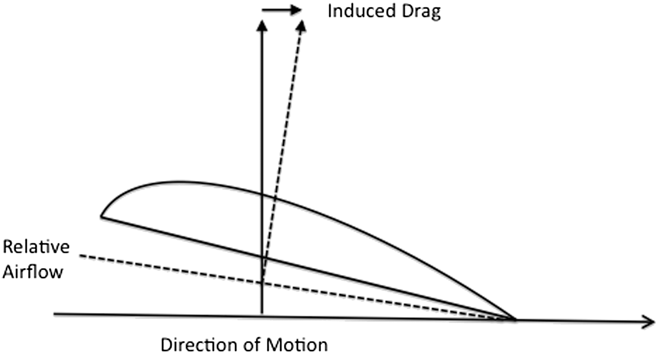
where A is the wing area, c L is the lift coefficient, A p is the profile area, and c D is the drag coefficient. The lift increases as the angle relative to the airflow, the angle of attack, increases. Eventually a point is reached where the airflow over the upper surface of the wing becomes turbulent and the lift abruptly decreases, the wing is then said to be stalled. As the angle of attack and the lift increases, the lift vector is no longer vertically opposed to the weight, and the drag component, called the induced drag, increases as shown in Fig. 1.
Figure 1. Diagram showing how induced drag arises as a result of deviation of the angle of relative airflow from the direction of motion.
The induced drag, D I, a consequence of generating lift, is
where
where e is a parameter called the ellipticity, which is about 0.9 for most wings, and a is the aspect ratio, the ratio of the wing span to its width or chord. It is important to note that the induced drag decreases as the wing area and the aspect ratio increase, and increases as the air speed decreases. Adding the two sources of drag together, the total drag is
which is plotted in Fig. 2.
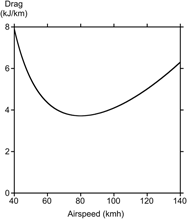
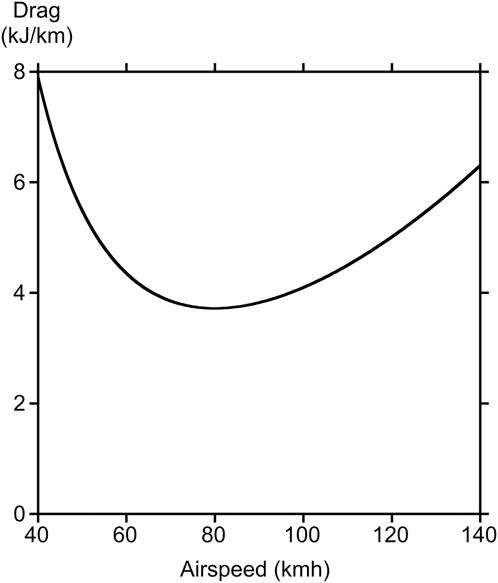
Figure 2. Drag for solar-powered 25-kg airplane for possible home-delivery of packages.
There is clearly an airspeed that minimizes the drag, or minimum energy used to fly a certain distance. If the energy available is fixed, it therefore maximizes the distance that the aircraft can fly. This speed is lower for an aircraft with a larger wing area and a higher aspect ratio, like a glider. Aircraft with short, stubby wings like a fighter plane will necessarily operate at higher airspeeds. At the maximum range airspeed, or minimum drag airspeed, the induced drag is equal to the profile drag, given as Eq. (2). The total drag is
The power required is the drag multiplied by the airspeed, v.
By this, it is possible to power the Amazon drone, mass 25 kg, airspeed 80 km/h or 22.2 m/s, using PV cells covering the wing surface. We will assume a normal solar intensity of I Watts/m2 and an overall efficiency η, which could also incorporate the efficiency of the electric motor and the propeller.
If the electric motor is 90% efficient and the propeller is 80% efficient, the overall efficiency would be about 11% for a 15% efficient PV panel. We will assume an aspect ratio of 20, about the same as the Solar Impulse 2 or a high performance glider, and a normal incidence of 400 W/m2, achievable for much of the day in sunny parts of the world. Equation (8) can then be rearranged and solved for the wing area, A.
The wing of the proposed drone has a chord of 31 cm and a span of 6.13 m, large but not totally impractical. A 150 W electric motor should be adequate. This is a lower estimate as excess power would be needed for a short climb. To reach flying speed, it would be best to launch from a catapult, like on an aircraft carrier, and recover it with a net or some type of arresting system. The package would have to be dropped while the drone is still flying, and thus would need a parachute, both to assure a gentle landing and slow it down.
However this is not what Amazon has in mind with their package delivery drone. The drone shown in published images3 is capable of vertical take-off and landing. Half the energy used by an airplane that flies at the airspeed that gives the maximum range is used to keep the airplane in the air. For an aircraft, such as a helicopter, that is capable of vertical take-off and landing most of the energy is used in keeping it in the air. For forward motion, the rotor disk is tilted so that a small part of the lift vector provides a forward thrust. This should also be evident from the fact that the engine in a helicopter is 1.5 times more powerful than that of an airplane of comparable mass (Robinson R44 compared to Cessna 172, Bell 206 compared to Beech Bonzanza).Reference Taylor4,5
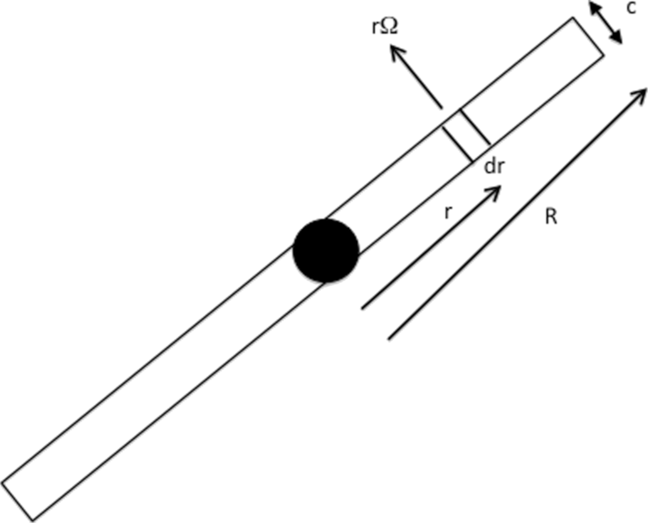
A drone like the proposed Amazon package delivery drone,3 or the popular Parrot AR4,6 is in many ways similar to a helicopter, the only difference being that they use propellers rather than a rotor to generate the lift needed to keep them in the air. A rotor is a rotating wing; it has a high aspect ratio, about 30, to minimise the induced drag. The lift and drag can be calculated by considering the forces on an element of extent dr as shown in Fig. 3. The rotor is rotating at angular velocity ω so that the air is moving at rω with respect to the element of the rotor.Reference Seddon and Newman7 Integrating along the rotor blade radius, the lift that has to balance the weight for a helicopter with N rotors each with n blades, radius R, is
Figure 3. Helicopter rotor.
To overcome the drag, a torque T has to be applied to turn the rotor
The first term is the induced drag, assuming that the velocity induced by the rotor is constant across the rotor disk. This requires an input power, P,
Helicopters are limited by the tip speed of the rotor. When added in quadrature with the forward speed of the helicopter, it becomes a significant fraction of the speed of sound.
This leads to extra drag from air compressibility effects. In fact for most helicopters, the rotor tip speed is about 220 m/s. To generate more lift, it is necessary to increase the number of blades, increase the number of rotors, or both. Increasing the number of blades on the rotor can lower the overall efficiency of the rotor, just as increasing the number of rotor blades in a wind turbine decreases the maximum output with respect to the theoretical maximum output as given by Betz’s law.Reference Hermans8 The tip speed, v t, is
Equation (10) can then be used to give the tip speed in terms of the mass of the helicopter and the dimensions and number of rotor blades
The power required, Eq. (12) can be expressed in terms of the rotor tip speed
and by substituting Eq. (14) for v t, the power can be directly related to the rotor dimensions c and r, the number blades per rotor, n, the number or rotors, N, and the mass of the helicopter.
The power scales as, 
${m^{{3 \over 2}}}$, and inversely as ${\left( {nNcr} \right)^{{1 \over 2}}}$, the square root of an area. A similar derivation can be based on momentum theory, where the thrust is proportional to the propeller swept area.Reference Seddon and Newman7,Reference Allain9,Reference Allain10
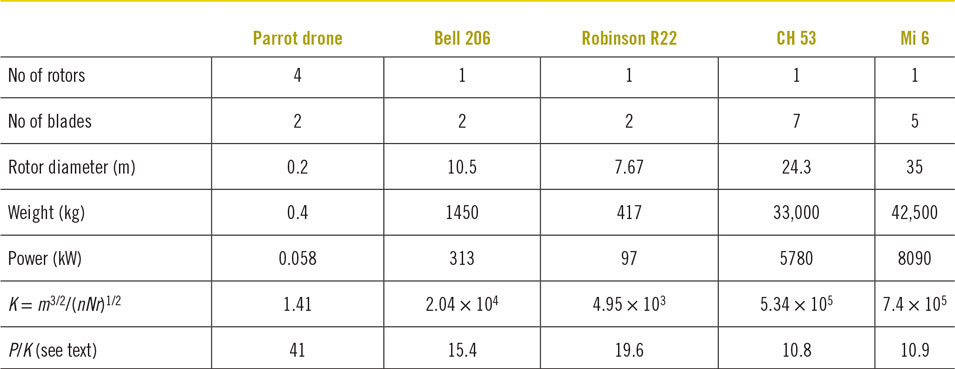
What is important are not the exact numbers but the scaling relationship. In Table 1, the parameter $K = {m^{{3 \over 2}}}{\left( {cRnN} \right)^{ - {1 \over 2}}}$ and the power divided by K is given for a number of helicopters and the Parrot drone. P/K is a measure of the total power available for the aircraft, compared to what is required for a specific helicopter or drone, to hover. In a sense, P/K is a measure of the efficiency, the higher P/K the less efficient the aircraft. Note that on this measure, the Robinson R22, a very small 2-seat helicopter, is less efficient than the large heavy-lift helicopters such as the CH53 and the Mi6 that have a mass of several thousand kg. This would not be the case if the rotor disk areas, rather than the actual areas of the blades were used in Eqs. (10)–(16). Another complication is that on the CH53, part of the lift is provided by the tilted tail rotor. Even so the Parrot drone is using twice as much power relative even to the small helicopters. That is because the drone is using propellers rather than optimized rotor blades to provide lift. The aspect ratio is lower, about 10, which means that there is more induced drag [see Fig. 1 and eqn. (3)], and the propeller is not operating at an advance ratio (the ratio of distance traveled, to product of diameter and angular velocity, dω) that gives optimum efficiency. Optimistically, the efficiency is about 70%. Another factor to consider is that forward motion of a helicopter is achieved by tilting the rotor disk using a mechanical system that varies the pitch of the individual rotor blades as the rotor rotates. The body of the helicopter is aligned with the direction of motion and the drag is minimized. For a drone, forward motion is achieved by varying the output of the motors driving individual propellers and the body of the aircraft is tilted, increasing the projected frontal area and hence the drag.
Table 1. Summary of specifications for the Parrot drone and various helicopters.
Amazon does not give the power used by their drone, although they do give the mass as 25 kg. From the images shown, it is believed that the Amazon drone has 8 two-bladed propellers of diameter 0.24 m (two different configurations have been shown in video images). There is also another propeller that provides thrust for forward motion. We will assume that P/K is the same for the Robinson light helicopter since the Amazon drone does not have to tilt in the direction of flight. This gives a power of 8 kW, or 1 kW per motor, a number that is reasonable for a high performance electric motor used in a drone. Not knowing the profile area and drag coefficient, it is hard to estimate the power from the published speed of 80 km/h, so we will assume that it is also 1 kW.Footnote * A drone that uses multiple propellers to provide lift is less efficient than a helicopter with a large rotor blade. The advantage of the drone is that it can easily be steered by varying the output of the different electric motors.
The time to deliver a package and return to the distribution center is 0.4 h so that a battery capacity of 3.6 kW h is needed that would imply a high discharge rate of 2.5 C, (C is the full battery charge), which would not be good for the life of the battery. Li batteries have a gravimetric density of about 0.2 kW h/kgReference Rez1 so the mass of the battery is 18 kg that accounts for the low value of the payload, only 2.5 kg, which leaves about 4.5 kg for the mass of the drone. Interestingly the ratio of mass of the payload to mass of the aircraft, approximately 10%, is about the same as that for a fully loaded Boeing 747-400. However about 40% of the mass of a fully loaded Boeing 747-400 is the fuel needed for journeys of up to 12 h. In the case of the drone, if our estimate is correct, 64% of the mass is the battery or “fuel”. This is a graphic illustration of the low endurance of a battery-powered aerial vehicle capable of vertical take-off and landing, as opposed to a conventional airplane powered by engines running on a liquid hydrocarbon that has 50 times the energy density of the Li batteries.Reference Rez1
RezReference Rez1 used the energy in MJ per tonne per km as a measure of the energy used to move freight. Delivering the package to a site 10 miles (16 km) away is equivalent to 324 MJ/t/km. This compares very unfavourably to deliver by a small delivery truck, which is about 2.5 MJ/tonne/km. The solar-powered conventional airplane described above, if powered by batteries, would use an energy of 7.2 MJ/t/km. Flying objects in vehicles that are capable of vertical take off is inherently inefficient.
Is it environmentally friendly? We will assume that when the drone returns to the delivery center it is recharged with electricity from solar panels. If the battery is to last then it should not be charged faster than 1–1.5 h. For an average solar intensity of 400 W/m2 and with PV that is 15% efficient, an area of 80 m2 is needed for the solar panel. Needless to say the drone spends more time recharging than delivering packages.
We can assess if air taxis are practical from the performance of existing small helicopters like the four-seat Robinson R44. They are able to do trips of about 2.5 h with a tank of 50 gallons (190 L). The energy per unit mass of a battery is about 50 times worse than gasoline or jet fuel. If an electric motor were driving the rotor, it would be 3 times as efficient as a gas turbine, or an internal combustion engine operating in an optimal manner at peak operating temperature and rpm. Replacing the fuel with a battery would reduce the time for a journey to 10 min before a recharging is necessary. If more of the mass were devoted to fuel or battery then there would be less available for passengers (it is already a tight squeeze). The poor energy density of batteries compared to liquid hydrocarbons limits both the journey time and the range of an electrically powered helicopter or drone. Furthermore, as with the electric car, more time will be spent on charging the battery than actually making a journey.
DISCUSSION POINTS
• How much energy is used in delivering small packages by a drone?
• How does the energy used to move a given mass compare for an electrically powered drone, a helicopter, an airplane, and a delivery truck?
• Does a drone that has vertical take-off and landing capabilities use more energy than a conventional airplane?
• Could the package delivery drone be solar powered?
• Is such a drone less efficient than a helicopter?
• Could a passenger-carrying air taxi, capable of vertical take-off and landing, be powered by batteries?
There has been much excitement recently on the possibility of using drones instead of trucks for parcel delivery. As a consequence of the widespread growth of online retailing as pioneered by Amazon, many people would find it appealing to have something that they ordered dropped directly to their backyard, rather than wait for a truck to show up sometime late in the day. Given the congestion on the roads in major urban areas, many city dwellers dream of summoning an air taxi that would whisk them to their destination above the chaos in the streets below. Not only would these innovations benefit the affluent city dweller, in principle they could bring substantial economic benefits to people who live in isolated areas of developing nations where there are no roads. However, the growing concerns about anthropogenic carbon dioxide emissions leading to irreversible climate change mean it is appropriate to consider their energy use. Is there a way for drones or air taxis to use renewable energy, presumably solar?
Vehicles that move along the ground use energy to overcome rolling resistance and air resistance.Reference Rez1 Since the rolling resistance does not depend on velocity, but the air resistance varies as the square of the velocity, the energy use increases as the vehicle goes faster. Ships have to overcome hydrodynamic resistance, which again scales as the square of the velocity. Aircraft are fundamentally different. As MacKay so eloquently said in his book,Reference Mackay2 half the energy used by an aircraft is used for staying “up”.
In cruise flight, the lift generated by the wings is equal to the weight of the aircraft, and the thrust is equal to the drag. Both the lift, L, and the profile drag, D p, (the drag due to the shape of the aircraft and friction of the air) are proportional to the square of the airspeed, v, and the density of air, ρ.
where A is the wing area, c L is the lift coefficient, A p is the profile area, and c D is the drag coefficient. The lift increases as the angle relative to the airflow, the angle of attack, increases. Eventually a point is reached where the airflow over the upper surface of the wing becomes turbulent and the lift abruptly decreases, the wing is then said to be stalled. As the angle of attack and the lift increases, the lift vector is no longer vertically opposed to the weight, and the drag component, called the induced drag, increases as shown in Fig. 1.
Figure 1. Diagram showing how induced drag arises as a result of deviation of the angle of relative airflow from the direction of motion.
The induced drag, D I, a consequence of generating lift, is
where
where e is a parameter called the ellipticity, which is about 0.9 for most wings, and a is the aspect ratio, the ratio of the wing span to its width or chord. It is important to note that the induced drag decreases as the wing area and the aspect ratio increase, and increases as the air speed decreases. Adding the two sources of drag together, the total drag is
which is plotted in Fig. 2.
Figure 2. Drag for solar-powered 25-kg airplane for possible home-delivery of packages.
There is clearly an airspeed that minimizes the drag, or minimum energy used to fly a certain distance. If the energy available is fixed, it therefore maximizes the distance that the aircraft can fly. This speed is lower for an aircraft with a larger wing area and a higher aspect ratio, like a glider. Aircraft with short, stubby wings like a fighter plane will necessarily operate at higher airspeeds. At the maximum range airspeed, or minimum drag airspeed, the induced drag is equal to the profile drag, given as Eq. (2). The total drag is
The power required is the drag multiplied by the airspeed, v.
By this, it is possible to power the Amazon drone, mass 25 kg, airspeed 80 km/h or 22.2 m/s, using PV cells covering the wing surface. We will assume a normal solar intensity of I Watts/m2 and an overall efficiency η, which could also incorporate the efficiency of the electric motor and the propeller.
If the electric motor is 90% efficient and the propeller is 80% efficient, the overall efficiency would be about 11% for a 15% efficient PV panel. We will assume an aspect ratio of 20, about the same as the Solar Impulse 2 or a high performance glider, and a normal incidence of 400 W/m2, achievable for much of the day in sunny parts of the world. Equation (8) can then be rearranged and solved for the wing area, A.
The wing of the proposed drone has a chord of 31 cm and a span of 6.13 m, large but not totally impractical. A 150 W electric motor should be adequate. This is a lower estimate as excess power would be needed for a short climb. To reach flying speed, it would be best to launch from a catapult, like on an aircraft carrier, and recover it with a net or some type of arresting system. The package would have to be dropped while the drone is still flying, and thus would need a parachute, both to assure a gentle landing and slow it down.
However this is not what Amazon has in mind with their package delivery drone. The drone shown in published images3 is capable of vertical take-off and landing. Half the energy used by an airplane that flies at the airspeed that gives the maximum range is used to keep the airplane in the air. For an aircraft, such as a helicopter, that is capable of vertical take-off and landing most of the energy is used in keeping it in the air. For forward motion, the rotor disk is tilted so that a small part of the lift vector provides a forward thrust. This should also be evident from the fact that the engine in a helicopter is 1.5 times more powerful than that of an airplane of comparable mass (Robinson R44 compared to Cessna 172, Bell 206 compared to Beech Bonzanza).Reference Taylor4,5
A drone like the proposed Amazon package delivery drone,3 or the popular Parrot AR4,6 is in many ways similar to a helicopter, the only difference being that they use propellers rather than a rotor to generate the lift needed to keep them in the air. A rotor is a rotating wing; it has a high aspect ratio, about 30, to minimise the induced drag. The lift and drag can be calculated by considering the forces on an element of extent dr as shown in Fig. 3. The rotor is rotating at angular velocity ω so that the air is moving at rω with respect to the element of the rotor.Reference Seddon and Newman7 Integrating along the rotor blade radius, the lift that has to balance the weight for a helicopter with N rotors each with n blades, radius R, is
Figure 3. Helicopter rotor.
To overcome the drag, a torque T has to be applied to turn the rotor
The first term is the induced drag, assuming that the velocity induced by the rotor is constant across the rotor disk. This requires an input power, P,
Helicopters are limited by the tip speed of the rotor. When added in quadrature with the forward speed of the helicopter, it becomes a significant fraction of the speed of sound.
This leads to extra drag from air compressibility effects. In fact for most helicopters, the rotor tip speed is about 220 m/s. To generate more lift, it is necessary to increase the number of blades, increase the number of rotors, or both. Increasing the number of blades on the rotor can lower the overall efficiency of the rotor, just as increasing the number of rotor blades in a wind turbine decreases the maximum output with respect to the theoretical maximum output as given by Betz’s law.Reference Hermans8 The tip speed, v t, is
Equation (10) can then be used to give the tip speed in terms of the mass of the helicopter and the dimensions and number of rotor blades
The power required, Eq. (12) can be expressed in terms of the rotor tip speed
and by substituting Eq. (14) for v t, the power can be directly related to the rotor dimensions c and r, the number blades per rotor, n, the number or rotors, N, and the mass of the helicopter.
The power scales as,
${m^{{3 \over 2}}}$, and inversely as 
${\left( {nNcr} \right)^{{1 \over 2}}}$, the square root of an area. A similar derivation can be based on momentum theory, where the thrust is proportional to the propeller swept area.Reference Seddon and Newman7,Reference Allain9,Reference Allain10
What is important are not the exact numbers but the scaling relationship. In Table 1, the parameter
$K = {m^{{3 \over 2}}}{\left( {cRnN} \right)^{ - {1 \over 2}}}$ and the power divided by K is given for a number of helicopters and the Parrot drone. P/K is a measure of the total power available for the aircraft, compared to what is required for a specific helicopter or drone, to hover. In a sense, P/K is a measure of the efficiency, the higher P/K the less efficient the aircraft. Note that on this measure, the Robinson R22, a very small 2-seat helicopter, is less efficient than the large heavy-lift helicopters such as the CH53 and the Mi6 that have a mass of several thousand kg. This would not be the case if the rotor disk areas, rather than the actual areas of the blades were used in Eqs. (10)–(16). Another complication is that on the CH53, part of the lift is provided by the tilted tail rotor. Even so the Parrot drone is using twice as much power relative even to the small helicopters. That is because the drone is using propellers rather than optimized rotor blades to provide lift. The aspect ratio is lower, about 10, which means that there is more induced drag [see Fig. 1 and eqn. (3)], and the propeller is not operating at an advance ratio (the ratio of distance traveled, to product of diameter and angular velocity, dω) that gives optimum efficiency. Optimistically, the efficiency is about 70%. Another factor to consider is that forward motion of a helicopter is achieved by tilting the rotor disk using a mechanical system that varies the pitch of the individual rotor blades as the rotor rotates. The body of the helicopter is aligned with the direction of motion and the drag is minimized. For a drone, forward motion is achieved by varying the output of the motors driving individual propellers and the body of the aircraft is tilted, increasing the projected frontal area and hence the drag.
Table 1. Summary of specifications for the Parrot drone and various helicopters.
Amazon does not give the power used by their drone, although they do give the mass as 25 kg. From the images shown, it is believed that the Amazon drone has 8 two-bladed propellers of diameter 0.24 m (two different configurations have been shown in video images). There is also another propeller that provides thrust for forward motion. We will assume that P/K is the same for the Robinson light helicopter since the Amazon drone does not have to tilt in the direction of flight. This gives a power of 8 kW, or 1 kW per motor, a number that is reasonable for a high performance electric motor used in a drone. Not knowing the profile area and drag coefficient, it is hard to estimate the power from the published speed of 80 km/h, so we will assume that it is also 1 kW.Footnote * A drone that uses multiple propellers to provide lift is less efficient than a helicopter with a large rotor blade. The advantage of the drone is that it can easily be steered by varying the output of the different electric motors.
The time to deliver a package and return to the distribution center is 0.4 h so that a battery capacity of 3.6 kW h is needed that would imply a high discharge rate of 2.5 C, (C is the full battery charge), which would not be good for the life of the battery. Li batteries have a gravimetric density of about 0.2 kW h/kgReference Rez1 so the mass of the battery is 18 kg that accounts for the low value of the payload, only 2.5 kg, which leaves about 4.5 kg for the mass of the drone. Interestingly the ratio of mass of the payload to mass of the aircraft, approximately 10%, is about the same as that for a fully loaded Boeing 747-400. However about 40% of the mass of a fully loaded Boeing 747-400 is the fuel needed for journeys of up to 12 h. In the case of the drone, if our estimate is correct, 64% of the mass is the battery or “fuel”. This is a graphic illustration of the low endurance of a battery-powered aerial vehicle capable of vertical take-off and landing, as opposed to a conventional airplane powered by engines running on a liquid hydrocarbon that has 50 times the energy density of the Li batteries.Reference Rez1
RezReference Rez1 used the energy in MJ per tonne per km as a measure of the energy used to move freight. Delivering the package to a site 10 miles (16 km) away is equivalent to 324 MJ/t/km. This compares very unfavourably to deliver by a small delivery truck, which is about 2.5 MJ/tonne/km. The solar-powered conventional airplane described above, if powered by batteries, would use an energy of 7.2 MJ/t/km. Flying objects in vehicles that are capable of vertical take off is inherently inefficient.
Is it environmentally friendly? We will assume that when the drone returns to the delivery center it is recharged with electricity from solar panels. If the battery is to last then it should not be charged faster than 1–1.5 h. For an average solar intensity of 400 W/m2 and with PV that is 15% efficient, an area of 80 m2 is needed for the solar panel. Needless to say the drone spends more time recharging than delivering packages.
We can assess if air taxis are practical from the performance of existing small helicopters like the four-seat Robinson R44. They are able to do trips of about 2.5 h with a tank of 50 gallons (190 L). The energy per unit mass of a battery is about 50 times worse than gasoline or jet fuel. If an electric motor were driving the rotor, it would be 3 times as efficient as a gas turbine, or an internal combustion engine operating in an optimal manner at peak operating temperature and rpm. Replacing the fuel with a battery would reduce the time for a journey to 10 min before a recharging is necessary. If more of the mass were devoted to fuel or battery then there would be less available for passengers (it is already a tight squeeze). The poor energy density of batteries compared to liquid hydrocarbons limits both the journey time and the range of an electrically powered helicopter or drone. Furthermore, as with the electric car, more time will be spent on charging the battery than actually making a journey.