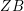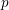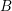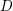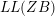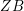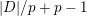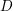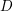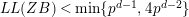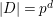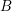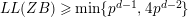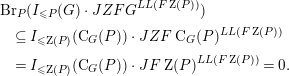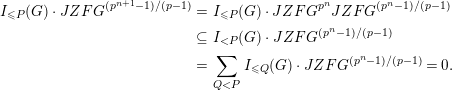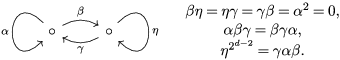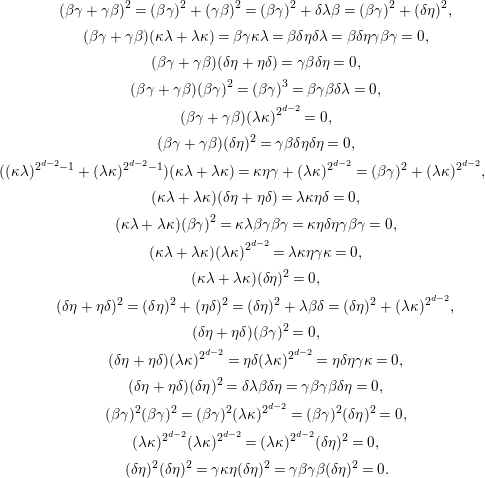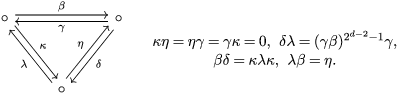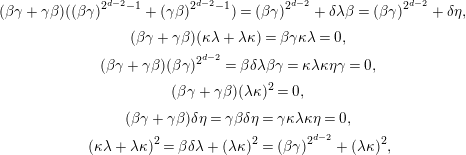1 Introduction
The aim of this paper is to extend some results on Loewy lengths of centers of blocks obtained in [Reference Külshammer and Sambale9, Reference Otokita12]. In the following we will reuse some of the notation introduced in [Reference Külshammer and Sambale9]. In particular,
![]() $B$
is a block of a finite group
$B$
is a block of a finite group
![]() $G$
with respect to an algebraically closed field
$G$
with respect to an algebraically closed field
![]() $F$
of characteristic
$F$
of characteristic
![]() $p>0$
. Moreover, let
$p>0$
. Moreover, let
![]() $D$
be a defect group of
$D$
be a defect group of
![]() $B$
. The second author has shown in [Reference Otokita12, Corollary 3.3] that the Loewy length of the center of
$B$
. The second author has shown in [Reference Otokita12, Corollary 3.3] that the Loewy length of the center of
![]() $B$
is bounded by
$B$
is bounded by
where
![]() $\exp (D)$
is the exponent of
$\exp (D)$
is the exponent of
![]() $D$
. It was already known to Okuyama [Reference Okuyama10] that this bound is best possible if
$D$
. It was already known to Okuyama [Reference Okuyama10] that this bound is best possible if
![]() $D$
is cyclic. The first and the third author have given in [Reference Külshammer and Sambale9, Theorem 1] the optimal bound
$D$
is cyclic. The first and the third author have given in [Reference Külshammer and Sambale9, Theorem 1] the optimal bound
![]() $LL(ZB)\leqslant LL(FD)$
for blocks with abelian defect groups. Our main result of the present paper establishes the following bound for blocks with nonabelian defect groups:
$LL(ZB)\leqslant LL(FD)$
for blocks with abelian defect groups. Our main result of the present paper establishes the following bound for blocks with nonabelian defect groups:
where
![]() $|D|=p^{d}$
. As a consequence we obtain
$|D|=p^{d}$
. As a consequence we obtain
for all blocks with noncyclic defect groups. It can be seen that this bound is achieved whenever
![]() $B$
is nilpotent and
$B$
is nilpotent and
![]() $D\cong C_{p^{d-1}}\times C_{p}$
.
$D\cong C_{p^{d-1}}\times C_{p}$
.
In the second part of the paper we show that
![]() $LL(ZB)$
depends more on
$LL(ZB)$
depends more on
![]() $\exp (D)$
than on
$\exp (D)$
than on
![]() $|D|$
. We prove for instance that
$|D|$
. We prove for instance that
![]() $LL(ZB)\leqslant d^{2}\exp (D)$
unless
$LL(ZB)\leqslant d^{2}\exp (D)$
unless
![]() $d=0$
. Finally, we use the opportunity to improve a result of Willems [Reference Willems15] about blocks with uniserial center.
$d=0$
. Finally, we use the opportunity to improve a result of Willems [Reference Willems15] about blocks with uniserial center.
In addition to the notation used in the papers cited above, we introduce the following objects. Let
![]() $\operatorname{Cl}(G)$
be the set of conjugacy classes of
$\operatorname{Cl}(G)$
be the set of conjugacy classes of
![]() $G$
. A
$G$
. A
![]() $p$
-subgroup
$p$
-subgroup
![]() $P\leqslant G$
is called a defect group of
$P\leqslant G$
is called a defect group of
![]() $K\in \operatorname{Cl}(G)$
if
$K\in \operatorname{Cl}(G)$
if
![]() $P$
is a Sylow
$P$
is a Sylow
![]() $p$
-subgroup of
$p$
-subgroup of
![]() $\operatorname{C}_{G}(x)$
for some
$\operatorname{C}_{G}(x)$
for some
![]() $x\in K$
. Let
$x\in K$
. Let
![]() $\operatorname{Cl}_{P}(G)$
be the set of conjugacy classes with defect group
$\operatorname{Cl}_{P}(G)$
be the set of conjugacy classes with defect group
![]() $P$
. Let
$P$
. Let
![]() $K^{+}:=\sum _{x\in K}x\in FG$
and
$K^{+}:=\sum _{x\in K}x\in FG$
and
 $$\begin{eqnarray}\displaystyle I_{P}(G) & := & \displaystyle \langle K^{+}:K\in \operatorname{Cl}_{P}(G)\rangle \subseteq ZFG,\nonumber\\ \displaystyle I_{{\leqslant}P}(G) & := & \displaystyle \mathop{\sum }_{Q\leqslant P}I_{Q}(G)\unlhd ZFG,\nonumber\\ \displaystyle I_{{<}P}(G) & := & \displaystyle \mathop{\sum }_{Q<P}I_{Q}(G)\unlhd ZFG\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{P}(G) & := & \displaystyle \langle K^{+}:K\in \operatorname{Cl}_{P}(G)\rangle \subseteq ZFG,\nonumber\\ \displaystyle I_{{\leqslant}P}(G) & := & \displaystyle \mathop{\sum }_{Q\leqslant P}I_{Q}(G)\unlhd ZFG,\nonumber\\ \displaystyle I_{{<}P}(G) & := & \displaystyle \mathop{\sum }_{Q<P}I_{Q}(G)\unlhd ZFG\nonumber\end{eqnarray}$$
(here
![]() $\unlhd$
means that the subsets are ideals).
$\unlhd$
means that the subsets are ideals).
2 Results
We begin by restating a lemma of Passman [Reference Passman13, Lemma 2]. For the convenience of the reader we provide a (slightly easier) proof.
Lemma 1. Let
![]() $P$
be a central
$P$
be a central
![]() $p$
-subgroup of
$p$
-subgroup of
![]() $G$
. Then
$G$
. Then
![]() $I_{{\leqslant}P}(G)\cdot JZFG=I_{{\leqslant}P}(G)\cdot JFP$
.
$I_{{\leqslant}P}(G)\cdot JZFG=I_{{\leqslant}P}(G)\cdot JFP$
.
Proof. Let
![]() $K$
be a conjugacy class of
$K$
be a conjugacy class of
![]() $G$
with defect group
$G$
with defect group
![]() $P$
, and let
$P$
, and let
![]() $x\in K$
. Then
$x\in K$
. Then
![]() $P$
is the only Sylow
$P$
is the only Sylow
![]() $p$
-subgroup of
$p$
-subgroup of
![]() $\operatorname{C}_{G}(x)$
, and the
$\operatorname{C}_{G}(x)$
, and the
![]() $p$
-factor
$p$
-factor
![]() $u$
of
$u$
of
![]() $x$
centralizes
$x$
centralizes
![]() $x$
. Thus
$x$
. Thus
![]() $u\in P$
. Hence
$u\in P$
. Hence
![]() $u$
is the
$u$
is the
![]() $p$
-factor of every element in
$p$
-factor of every element in
![]() $K$
, and
$K$
, and
![]() $K=uK^{\prime }$
where
$K=uK^{\prime }$
where
![]() $K^{\prime }$
is a
$K^{\prime }$
is a
![]() $p$
-regular conjugacy class of
$p$
-regular conjugacy class of
![]() $G$
with defect group
$G$
with defect group
![]() $P$
. This shows that
$P$
. This shows that
![]() $I:=I_{{\leqslant}P}(G)$
is a free
$I:=I_{{\leqslant}P}(G)$
is a free
![]() $FP$
-module with the
$FP$
-module with the
![]() $p$
-regular class sums with defect group
$p$
-regular class sums with defect group
![]() $P$
as an
$P$
as an
![]() $FP$
-basis. The canonical epimorphism
$FP$
-basis. The canonical epimorphism
![]() $\unicode[STIX]{x1D708}:FG\rightarrow F[G/P]$
maps
$\unicode[STIX]{x1D708}:FG\rightarrow F[G/P]$
maps
![]() $I$
into
$I$
into
![]() $I_{1}(G/P)\subseteq SF[G/P]$
(recall that
$I_{1}(G/P)\subseteq SF[G/P]$
(recall that
![]() $SF[G/P]$
is the socle of
$SF[G/P]$
is the socle of
![]() $F[G/P]$
). Thus
$F[G/P]$
). Thus
![]() $\unicode[STIX]{x1D708}(I\cdot JZFG)\subseteq SF[G/P]\cdot JZF[G/P]=0$
. Hence
$\unicode[STIX]{x1D708}(I\cdot JZFG)\subseteq SF[G/P]\cdot JZF[G/P]=0$
. Hence
![]() $I\cdot JZFG\subseteq I\cdot JFP$
. The other inclusion is trivial.◻
$I\cdot JZFG\subseteq I\cdot JFP$
. The other inclusion is trivial.◻
Lemma 2. Let
![]() $P\leqslant G$
be a
$P\leqslant G$
be a
![]() $p$
-subgroup of order
$p$
-subgroup of order
![]() $p^{n}$
. Then
$p^{n}$
. Then
(i)
 $I_{{\leqslant}P}(G)\cdot JZFG^{LL(F\operatorname{Z}(P))}\subseteq I_{{<}P}(G)$
.
$I_{{\leqslant}P}(G)\cdot JZFG^{LL(F\operatorname{Z}(P))}\subseteq I_{{<}P}(G)$
.(ii)
 $I_{{\leqslant}P}(G)\cdot JZFG^{(p^{n+1}-1)/(p-1)}=0$
.
$I_{{\leqslant}P}(G)\cdot JZFG^{(p^{n+1}-1)/(p-1)}=0$
.
Proof.
(i) Let
 $\operatorname{Br}_{P}:ZFG\rightarrow ZF\operatorname{C}_{G}(P)$
be the Brauer homomorphism. Since
$\operatorname{Br}_{P}:ZFG\rightarrow ZF\operatorname{C}_{G}(P)$
be the Brauer homomorphism. Since
 $\operatorname{Ker}(\operatorname{Br}_{P})\cap I_{{\leqslant}P}(G)=I_{{<}P}(G)$
, we need to show that
$\operatorname{Ker}(\operatorname{Br}_{P})\cap I_{{\leqslant}P}(G)=I_{{<}P}(G)$
, we need to show that
 $\operatorname{Br}_{P}(I_{{\leqslant}P}(G)\cdot JZFG^{LL(F\operatorname{Z}(P))})=0$
. By Lemma 1 we have
$\operatorname{Br}_{P}(I_{{\leqslant}P}(G)\cdot JZFG^{LL(F\operatorname{Z}(P))})=0$
. By Lemma 1 we have  $$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{Br}_{P}(I_{{\leqslant}P}(G)\cdot JZFG^{LL(F\operatorname{Z}(P))})\nonumber\\ \displaystyle & & \displaystyle \quad \subseteq I_{{\leqslant}\operatorname{Z}(P)}(\operatorname{C}_{G}(P))\cdot JZF\operatorname{C}_{G}(P)^{LL(F\operatorname{Z}(P))}\nonumber\\ \displaystyle & & \displaystyle \quad =I_{{\leqslant}\operatorname{Z}(P)}(\operatorname{C}_{G}(P))\cdot JF\operatorname{Z}(P)^{LL(F\operatorname{Z}(P))}=0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{Br}_{P}(I_{{\leqslant}P}(G)\cdot JZFG^{LL(F\operatorname{Z}(P))})\nonumber\\ \displaystyle & & \displaystyle \quad \subseteq I_{{\leqslant}\operatorname{Z}(P)}(\operatorname{C}_{G}(P))\cdot JZF\operatorname{C}_{G}(P)^{LL(F\operatorname{Z}(P))}\nonumber\\ \displaystyle & & \displaystyle \quad =I_{{\leqslant}\operatorname{Z}(P)}(\operatorname{C}_{G}(P))\cdot JF\operatorname{Z}(P)^{LL(F\operatorname{Z}(P))}=0.\nonumber\end{eqnarray}$$
(ii) We argue by induction on
 $n$
. The case
$n$
. The case
 $n=1$
follows from
$n=1$
follows from
 $I_{1}(G)\subseteq SFG$
. Now suppose that the claim holds for
$I_{1}(G)\subseteq SFG$
. Now suppose that the claim holds for
 $n-1$
. Since
$n-1$
. Since
 $LL(F\operatorname{Z}(P))\leqslant |P|=p^{n}$
, (i) implies
$LL(F\operatorname{Z}(P))\leqslant |P|=p^{n}$
, (i) implies  $$\begin{eqnarray}\displaystyle I_{{\leqslant}P}(G)\cdot JZFG^{(p^{n+1}-1)/(p-1)} & = & \displaystyle I_{{\leqslant}P}(G)\cdot JZFG^{p^{n}}JZFG^{(p^{n}-1)/(p-1)}\nonumber\\ \displaystyle & \subseteq & \displaystyle I_{{<}P}(G)\cdot JZFG^{(p^{n}-1)/(p-1)}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{Q<P}I_{{\leqslant}Q}(G)\cdot JZFG^{(p^{n}-1)/(p-1)}=0.\qquad \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{{\leqslant}P}(G)\cdot JZFG^{(p^{n+1}-1)/(p-1)} & = & \displaystyle I_{{\leqslant}P}(G)\cdot JZFG^{p^{n}}JZFG^{(p^{n}-1)/(p-1)}\nonumber\\ \displaystyle & \subseteq & \displaystyle I_{{<}P}(G)\cdot JZFG^{(p^{n}-1)/(p-1)}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{Q<P}I_{{\leqslant}Q}(G)\cdot JZFG^{(p^{n}-1)/(p-1)}=0.\qquad \nonumber\end{eqnarray}$$
Recall from [Reference Külshammer and Sambale9, Lemma 9] the following group
Note that
![]() $W_{p^{d}}$
is a central product of
$W_{p^{d}}$
is a central product of
![]() $C_{p^{d-2}}$
and an extraspecial group of order
$C_{p^{d-2}}$
and an extraspecial group of order
![]() $p^{3}$
. Now we prove our main theorem which improves [Reference Külshammer and Sambale9, Theorem 12].
$p^{3}$
. Now we prove our main theorem which improves [Reference Külshammer and Sambale9, Theorem 12].
Theorem 3. Let
![]() $B$
be a block of
$B$
be a block of
![]() $FG$
with nonabelian defect group
$FG$
with nonabelian defect group
![]() $D$
of order
$D$
of order
![]() $p^{d}$
. Then (at least) one of the following holds
$p^{d}$
. Then (at least) one of the following holds
(i)
 $LL(ZB)<3p^{d-2}$
.
$LL(ZB)<3p^{d-2}$
.(ii)
 $p\geqslant 5$
,
$p\geqslant 5$
,
 $D\cong W_{p^{d}}$
and
$D\cong W_{p^{d}}$
and
 $LL(ZB)<4p^{d-2}$
.
$LL(ZB)<4p^{d-2}$
.
In any case we have
Proof. By [Reference Külshammer and Sambale9, Proposition 15], we may assume that
![]() $p>2$
. Since
$p>2$
. Since
![]() $D$
is nonabelian,
$D$
is nonabelian,
![]() $|D:\operatorname{Z}(D)|\geqslant p^{2}$
and
$|D:\operatorname{Z}(D)|\geqslant p^{2}$
and
![]() $LL(F\operatorname{Z}(D))\leqslant p^{d-2}$
. Let
$LL(F\operatorname{Z}(D))\leqslant p^{d-2}$
. Let
![]() $Q$
be a maximal subgroup of
$Q$
be a maximal subgroup of
![]() $D$
. If
$D$
. If
![]() $Q$
is cyclic, then
$Q$
is cyclic, then
![]() $D\cong M_{p^{n}}$
(see [Reference Gorenstein4, Theorem 5.4.4]) and the claim follows from [Reference Külshammer and Sambale9, Proposition 10]. Hence, we may assume that
$D\cong M_{p^{n}}$
(see [Reference Gorenstein4, Theorem 5.4.4]) and the claim follows from [Reference Külshammer and Sambale9, Proposition 10]. Hence, we may assume that
![]() $Q$
is not cyclic. Then
$Q$
is not cyclic. Then
![]() $LL(F\operatorname{Z}(Q))\leqslant p^{d-2}+p-1$
. Now setting
$LL(F\operatorname{Z}(Q))\leqslant p^{d-2}+p-1$
. Now setting
![]() $\unicode[STIX]{x1D706}:=(p^{d-1}-1)/(p-1)$
it follows from Lemma 2 that
$\unicode[STIX]{x1D706}:=(p^{d-1}-1)/(p-1)$
it follows from Lemma 2 that
 $$\begin{eqnarray}\displaystyle JZB^{2p^{d-2}+p-1+\unicode[STIX]{x1D706}} & \subseteq & \displaystyle 1_{B}JZFG^{2p^{d-2}+p-1+\unicode[STIX]{x1D706}}\subseteq I_{{\leqslant}D}(G)\cdot JZFG^{2p^{d-2}+p-1+\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & \subseteq & \displaystyle I_{{<}D}(G)\cdot JZFG^{p^{d-2}+p-1+\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{Q<D}I_{{\leqslant}Q}(G)\cdot JZFG^{p^{d-2}+p-1+\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & \subseteq & \displaystyle \mathop{\sum }_{Q<D}I_{{<}Q}(G)\cdot JZFG^{\unicode[STIX]{x1D706}}=0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle JZB^{2p^{d-2}+p-1+\unicode[STIX]{x1D706}} & \subseteq & \displaystyle 1_{B}JZFG^{2p^{d-2}+p-1+\unicode[STIX]{x1D706}}\subseteq I_{{\leqslant}D}(G)\cdot JZFG^{2p^{d-2}+p-1+\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & \subseteq & \displaystyle I_{{<}D}(G)\cdot JZFG^{p^{d-2}+p-1+\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{Q<D}I_{{\leqslant}Q}(G)\cdot JZFG^{p^{d-2}+p-1+\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & \subseteq & \displaystyle \mathop{\sum }_{Q<D}I_{{<}Q}(G)\cdot JZFG^{\unicode[STIX]{x1D706}}=0.\nonumber\end{eqnarray}$$
Since
![]() $2p^{d-2}+p-1+\unicode[STIX]{x1D706}\leqslant 4p^{d-2}$
, we are done in case
$2p^{d-2}+p-1+\unicode[STIX]{x1D706}\leqslant 4p^{d-2}$
, we are done in case
![]() $p\geqslant 5$
and
$p\geqslant 5$
and
![]() $D\cong W_{p^{d}}$
. If
$D\cong W_{p^{d}}$
. If
![]() $p=3$
and
$p=3$
and
![]() $D\cong W_{p^{d}}$
, then the claim follows from [Reference Külshammer and Sambale9, Lemma 11]. Now suppose that
$D\cong W_{p^{d}}$
, then the claim follows from [Reference Külshammer and Sambale9, Lemma 11]. Now suppose that
![]() $D\not \cong W_{p^{d}}$
. If
$D\not \cong W_{p^{d}}$
. If
![]() $\operatorname{Z}(D)$
is cyclic of order
$\operatorname{Z}(D)$
is cyclic of order
![]() $p^{d-2}$
, then the claim follows from [Reference Külshammer and Sambale9, Lemma 9 and Proposition 10]. Hence, suppose that
$p^{d-2}$
, then the claim follows from [Reference Külshammer and Sambale9, Lemma 9 and Proposition 10]. Hence, suppose that
![]() $\operatorname{Z}(D)$
is noncyclic or
$\operatorname{Z}(D)$
is noncyclic or
![]() $|\operatorname{Z}(D)|<p^{d-2}$
. Then
$|\operatorname{Z}(D)|<p^{d-2}$
. Then
![]() $d\geqslant 4$
and
$d\geqslant 4$
and
![]() $LL(F\operatorname{Z}(D))\leqslant p^{d-3}+p-1$
. The arguments above give
$LL(F\operatorname{Z}(D))\leqslant p^{d-3}+p-1$
. The arguments above give
![]() $LL(ZB)\leqslant p^{d-2}+p^{d-3}+2p-2+\unicode[STIX]{x1D706}$
, hence we are done whenever
$LL(ZB)\leqslant p^{d-2}+p^{d-3}+2p-2+\unicode[STIX]{x1D706}$
, hence we are done whenever
![]() $p>3$
.
$p>3$
.
In the following we assume that
![]() $p=3$
. Here we have
$p=3$
. Here we have
![]() $LL(ZB)\leqslant 3^{d-2}+3^{d-3}+4+\frac{1}{2}(3^{d-1}-1)$
and it suffices to handle the case
$LL(ZB)\leqslant 3^{d-2}+3^{d-3}+4+\frac{1}{2}(3^{d-1}-1)$
and it suffices to handle the case
![]() $d=4$
. By [Reference Otokita12, Theorem 3.2], there exists a nontrivial
$d=4$
. By [Reference Otokita12, Theorem 3.2], there exists a nontrivial
![]() $B$
-subsection
$B$
-subsection
![]() $(u,b)$
such that
$(u,b)$
such that
where
![]() $\overline{b}$
is the unique block of
$\overline{b}$
is the unique block of
![]() $F\operatorname{C}_{G}(u)/\langle u\rangle$
dominated by
$F\operatorname{C}_{G}(u)/\langle u\rangle$
dominated by
![]() $b$
. We may assume that
$b$
. We may assume that
![]() $\overline{b}$
has defect group
$\overline{b}$
has defect group
![]() $\operatorname{C}_{D}(u)/\langle u\rangle$
(see [Reference Sambale14, Lemma 1.34]). If
$\operatorname{C}_{D}(u)/\langle u\rangle$
(see [Reference Sambale14, Lemma 1.34]). If
![]() $u\notin \operatorname{Z}(D)$
, we obtain
$u\notin \operatorname{Z}(D)$
, we obtain
![]() $LL(ZB)<|\!\operatorname{C}_{D}(u)|\leqslant 27$
as desired. Hence, let
$LL(ZB)<|\!\operatorname{C}_{D}(u)|\leqslant 27$
as desired. Hence, let
![]() $u\in \operatorname{Z}(D)$
. Then
$u\in \operatorname{Z}(D)$
. Then
![]() $D/\langle u\rangle$
is not cyclic. Moreover, by our assumption on
$D/\langle u\rangle$
is not cyclic. Moreover, by our assumption on
![]() $\operatorname{Z}(D)$
, we have
$\operatorname{Z}(D)$
, we have
![]() $|\langle u\rangle |=3$
. Now it follows from [Reference Külshammer and Sambale9, Theorem 1, Proposition 10 and Lemma 11] applied to
$|\langle u\rangle |=3$
. Now it follows from [Reference Külshammer and Sambale9, Theorem 1, Proposition 10 and Lemma 11] applied to
![]() $\overline{b}$
that
$\overline{b}$
that
We do not expect that the bounds in Theorem 3 are sharp. In fact, we do not know if there are
![]() $p$
-blocks
$p$
-blocks
![]() $B$
with nonabelian defect groups of order
$B$
with nonabelian defect groups of order
![]() $p^{d}$
such that
$p^{d}$
such that
![]() $p>2$
and
$p>2$
and
![]() $LL(ZB)>p^{d-2}$
. See also Proposition 7 below.
$LL(ZB)>p^{d-2}$
. See also Proposition 7 below.
Corollary 4. Let
![]() $B$
be a block of
$B$
be a block of
![]() $FG$
with noncyclic defect group of order
$FG$
with noncyclic defect group of order
![]() $p^{d}$
. Then
$p^{d}$
. Then
Proof. By Theorem 3, we may assume that
![]() $B$
has abelian defect group
$B$
has abelian defect group
![]() $D$
. Then [Reference Külshammer and Sambale9, Theorem 1] implies
$D$
. Then [Reference Külshammer and Sambale9, Theorem 1] implies
![]() $LL(ZB)\leqslant LL(FD)\leqslant p^{d-1}+p-1$
.◻
$LL(ZB)\leqslant LL(FD)\leqslant p^{d-1}+p-1$
.◻
We are now in a position to generalize [Reference Külshammer and Sambale9, Corollary 16].
Corollary 5. Let
![]() $B$
be a block of
$B$
be a block of
![]() $FG$
with defect group
$FG$
with defect group
![]() $D$
of order
$D$
of order
![]() $p^{d}$
such that
$p^{d}$
such that
![]() $LL(ZB)\geqslant \min \{p^{d-1},4p^{d-2}\}$
. Then one of the following holds
$LL(ZB)\geqslant \min \{p^{d-1},4p^{d-2}\}$
. Then one of the following holds
(i)
 $D$
is cyclic.
$D$
is cyclic.(ii)
 $D\cong C_{p^{d-1}}\times C_{p}$
.
$D\cong C_{p^{d-1}}\times C_{p}$
.(iii)
 $D\cong C_{2}\times C_{2}\times C_{2}$
and
$D\cong C_{2}\times C_{2}\times C_{2}$
and
 $B$
is nilpotent.
$B$
is nilpotent.
Proof. Again by Theorem 3 we may assume that
![]() $D$
is abelian. By [Reference Külshammer and Sambale9, Corollary 16], we may assume that
$D$
is abelian. By [Reference Külshammer and Sambale9, Corollary 16], we may assume that
![]() $p>2$
. Suppose that
$p>2$
. Suppose that
![]() $D$
is of type
$D$
is of type
![]() $(p^{a_{1}},\ldots ,p^{a_{s}})$
such that
$(p^{a_{1}},\ldots ,p^{a_{s}})$
such that
![]() $s\geqslant 3$
. Then
$s\geqslant 3$
. Then
This clearly leads to a contradiction. Therefore,
![]() $s\leqslant 2$
and the claim follows.◻
$s\leqslant 2$
and the claim follows.◻
In case (i) of Corollary 5 it is known conversely that
![]() $LL(ZB)=(p^{d}-1)/l(B)+1>p^{d-1}$
(see [Reference Koshitani, Külshammer and Sambale7, Corollary 2.8]).
$LL(ZB)=(p^{d}-1)/l(B)+1>p^{d-1}$
(see [Reference Koshitani, Külshammer and Sambale7, Corollary 2.8]).
Our next result gives a more precise bound by invoking the exponent of a defect group.
Theorem 6. Let
![]() $B$
be a block of
$B$
be a block of
![]() $FG$
with defect group
$FG$
with defect group
![]() $D$
of order
$D$
of order
![]() $p^{d}>1$
and exponent
$p^{d}>1$
and exponent
![]() $p^{e}$
. Then
$p^{e}$
. Then
In particular,
![]() $LL(ZB)\leqslant d^{2}p^{e}$
.
$LL(ZB)\leqslant d^{2}p^{e}$
.
Proof. Let
![]() $\unicode[STIX]{x1D6FC}:=\lfloor d/e\rfloor$
. Let
$\unicode[STIX]{x1D6FC}:=\lfloor d/e\rfloor$
. Let
![]() $P\leqslant D$
be abelian of order
$P\leqslant D$
be abelian of order
![]() $p^{ie+j}$
with
$p^{ie+j}$
with
![]() $0\leqslant i\leqslant \unicode[STIX]{x1D6FC}$
and
$0\leqslant i\leqslant \unicode[STIX]{x1D6FC}$
and
![]() $0\leqslant j<e$
. If
$0\leqslant j<e$
. If
![]() $P$
has type
$P$
has type
![]() $(p^{a_{1}},\ldots ,p^{a_{r}})$
, then
$(p^{a_{1}},\ldots ,p^{a_{r}})$
, then
![]() $a_{i}\leqslant e$
for
$a_{i}\leqslant e$
for
![]() $i=1,\ldots ,r$
and
$i=1,\ldots ,r$
and
Arguing as in Theorem 3, we obtain
 $$\begin{eqnarray}\displaystyle LL(ZB) & {\leqslant} & \displaystyle \mathop{\sum }_{i=0}^{\unicode[STIX]{x1D6FC}}\mathop{\sum }_{j=0}^{e-1}i(p^{e}-1)+p^{j}=e(p^{e}-1)\biggl(\mathop{\sum }_{i=0}^{\unicode[STIX]{x1D6FC}}i\biggr)+(\unicode[STIX]{x1D6FC}+1)\frac{p^{e}-1}{p-1}\nonumber\\ \displaystyle & = & \displaystyle e(p^{e}-1)\frac{\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FC}+1)}{2}+(\unicode[STIX]{x1D6FC}+1)\frac{p^{e}-1}{p-1}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \biggl(\frac{d}{e}+1\biggr)\biggl(\frac{d}{2}+\frac{1}{p-1}\biggr)(p^{e}-1).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle LL(ZB) & {\leqslant} & \displaystyle \mathop{\sum }_{i=0}^{\unicode[STIX]{x1D6FC}}\mathop{\sum }_{j=0}^{e-1}i(p^{e}-1)+p^{j}=e(p^{e}-1)\biggl(\mathop{\sum }_{i=0}^{\unicode[STIX]{x1D6FC}}i\biggr)+(\unicode[STIX]{x1D6FC}+1)\frac{p^{e}-1}{p-1}\nonumber\\ \displaystyle & = & \displaystyle e(p^{e}-1)\frac{\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FC}+1)}{2}+(\unicode[STIX]{x1D6FC}+1)\frac{p^{e}-1}{p-1}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \biggl(\frac{d}{e}+1\biggr)\biggl(\frac{d}{2}+\frac{1}{p-1}\biggr)(p^{e}-1).\nonumber\end{eqnarray}$$
This proves the first claim. For the second claim we note that
unless
![]() $d\leqslant 3$
. In these small cases the claim follows from Theorem 3 and Corollary 4.◻
$d\leqslant 3$
. In these small cases the claim follows from Theorem 3 and Corollary 4.◻
If
![]() $2e>d$
and
$2e>d$
and
![]() $p$
is large, then the bound in Theorem 6 is approximately
$p$
is large, then the bound in Theorem 6 is approximately
![]() $dp^{e}$
. The groups of the form
$dp^{e}$
. The groups of the form
![]() $G=D=C_{p^{e}}\times \cdots \times C_{p^{e}}$
show that there is no bound of the form
$G=D=C_{p^{e}}\times \cdots \times C_{p^{e}}$
show that there is no bound of the form
![]() $LL(ZB)\leqslant Cp^{e}$
where
$LL(ZB)\leqslant Cp^{e}$
where
![]() $C$
is an absolute constant. A more careful argumentation in the proof above gives the stronger (but opaque) bound
$C$
is an absolute constant. A more careful argumentation in the proof above gives the stronger (but opaque) bound
 $$\begin{eqnarray}\displaystyle LL(ZB) & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FC}(p^{e}-1)\biggl(\frac{e(\unicode[STIX]{x1D6FC}-1)}{2}+\frac{1}{p-1}+d-\unicode[STIX]{x1D6FC}e\biggr)+\unicode[STIX]{x1D6FD}(p^{e}-1)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{p^{d-\unicode[STIX]{x1D6FC}e}-1}{p-1}+p^{d-2-\unicode[STIX]{x1D6FD}e}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle LL(ZB) & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FC}(p^{e}-1)\biggl(\frac{e(\unicode[STIX]{x1D6FC}-1)}{2}+\frac{1}{p-1}+d-\unicode[STIX]{x1D6FC}e\biggr)+\unicode[STIX]{x1D6FD}(p^{e}-1)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{p^{d-\unicode[STIX]{x1D6FC}e}-1}{p-1}+p^{d-2-\unicode[STIX]{x1D6FD}e}\nonumber\end{eqnarray}$$
for nonabelian defect groups where
![]() $\unicode[STIX]{x1D6FC}:=\lfloor (d-1)/e\rfloor$
and
$\unicode[STIX]{x1D6FC}:=\lfloor (d-1)/e\rfloor$
and
![]() $\unicode[STIX]{x1D6FD}:=\lfloor (d-2)/e\rfloor$
. We omit the details.
$\unicode[STIX]{x1D6FD}:=\lfloor (d-2)/e\rfloor$
. We omit the details.
In the next result we compute the Loewy length for
![]() $d=e+1$
.
$d=e+1$
.
Proposition 7. Let
![]() $B$
be a block of
$B$
be a block of
![]() $FG$
with nonabelian defect group of order
$FG$
with nonabelian defect group of order
![]() $p^{d}$
and exponent
$p^{d}$
and exponent
![]() $p^{d-1}$
. Then
$p^{d-1}$
. Then
and both bounds are optimal for every
![]() $d\geqslant 3$
.
$d\geqslant 3$
.
Proof. Let
![]() $D$
be a defect group of
$D$
be a defect group of
![]() $B$
. If
$B$
. If
![]() $p>2$
, then
$p>2$
, then
![]() $D\cong M_{p^{d}}$
(see [Reference Gorenstein4, Theorem 5.4.4]) and we have shown
$D\cong M_{p^{d}}$
(see [Reference Gorenstein4, Theorem 5.4.4]) and we have shown
![]() $LL(ZB)\leqslant p^{d-2}$
in [Reference Külshammer and Sambale9, Proposition 10]. Equality holds if and only if
$LL(ZB)\leqslant p^{d-2}$
in [Reference Külshammer and Sambale9, Proposition 10]. Equality holds if and only if
![]() $B$
is nilpotent.
$B$
is nilpotent.
Therefore, we may assume
![]() $p=2$
in the following. The modular groups
$p=2$
in the following. The modular groups
![]() $M_{2^{d}}$
are still handled by [Reference Külshammer and Sambale9, Proposition 10]. Hence, it remains to consider the defect groups of maximal nilpotency class, i. e.,
$M_{2^{d}}$
are still handled by [Reference Külshammer and Sambale9, Proposition 10]. Hence, it remains to consider the defect groups of maximal nilpotency class, i. e.,
![]() $D\in \{D_{2^{d}},Q_{2^{d}},SD_{2^{d}}\}$
. By [Reference Külshammer and Sambale9, Proposition 10], we may assume that
$D\in \{D_{2^{d}},Q_{2^{d}},SD_{2^{d}}\}$
. By [Reference Külshammer and Sambale9, Proposition 10], we may assume that
![]() $d\geqslant 4$
. The isomorphism type of
$d\geqslant 4$
. The isomorphism type of
![]() $ZB$
is uniquely determined by
$ZB$
is uniquely determined by
![]() $D$
and the fusion system of
$D$
and the fusion system of
![]() $B$
(see [Reference Cabanes and Picaronny2]). The possible cases are listed in [Reference Sambale14, Theorem 8.1]. If
$B$
(see [Reference Cabanes and Picaronny2]). The possible cases are listed in [Reference Sambale14, Theorem 8.1]. If
![]() $B$
is nilpotent, [Reference Külshammer and Sambale9, Proposition 8] gives
$B$
is nilpotent, [Reference Külshammer and Sambale9, Proposition 8] gives
![]() $LL(ZB)=LL(ZFD)\leqslant LL(FD^{\prime })=2^{d-2}$
. Moreover, in the case
$LL(ZB)=LL(ZFD)\leqslant LL(FD^{\prime })=2^{d-2}$
. Moreover, in the case
![]() $D\cong D_{2^{d}}$
and
$D\cong D_{2^{d}}$
and
![]() $l(B)=3$
we have
$l(B)=3$
we have
![]() $LL(ZB)\leqslant k(B)-l(B)+1=2^{d-2}+1$
by [Reference Otokita12, Proposition 2.2]. In the remaining cases we present
$LL(ZB)\leqslant k(B)-l(B)+1=2^{d-2}+1$
by [Reference Otokita12, Proposition 2.2]. In the remaining cases we present
![]() $B$
by quivers with relations which were constructed originally by Erdmann [Reference Erdmann3]. We refer to [Reference Holm5, Appendix B]. Keep in mind that we need to consider only one quiver for each fusion system.
$B$
by quivers with relations which were constructed originally by Erdmann [Reference Erdmann3]. We refer to [Reference Holm5, Appendix B]. Keep in mind that we need to consider only one quiver for each fusion system.
(i)
 $D\cong D_{2^{d}}$
,
$D\cong D_{2^{d}}$
,
 $l(B)=2$
:By [Reference Holm5, Lemma 2.3.3], we have
$l(B)=2$
:By [Reference Holm5, Lemma 2.3.3], we have It follows that
It follows that $$\begin{eqnarray}ZB=\operatorname{span}\{1,\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D702}^{i}:i=1,\ldots ,2^{d-2}\}.\end{eqnarray}$$
$$\begin{eqnarray}ZB=\operatorname{span}\{1,\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D702}^{i}:i=1,\ldots ,2^{d-2}\}.\end{eqnarray}$$
 $JZB^{2}=\langle \unicode[STIX]{x1D702}^{2}\rangle$
and
$JZB^{2}=\langle \unicode[STIX]{x1D702}^{2}\rangle$
and
 $LL(ZB)=2^{d-2}+1$
.
$LL(ZB)=2^{d-2}+1$
.(ii)
 $D\cong Q_{2^{d}}$
,
$D\cong Q_{2^{d}}$
,
 $l(B)=2$
: Here [Reference Zimmermann16, Lemma 6] gives the isomorphism type of
$l(B)=2$
: Here [Reference Zimmermann16, Lemma 6] gives the isomorphism type of
 $ZB$
directly as a quotient of a polynomial ring It follows that
$ZB$
directly as a quotient of a polynomial ring It follows that $$\begin{eqnarray}\displaystyle ZB & \cong & \displaystyle F[U,Y,S,T]/\!(Y^{2^{d-2}+1},U^{2}-Y^{2^{d-2}},S^{2},T^{2},SY,\nonumber\\ \displaystyle & & \displaystyle SU,ST,UY,UT,YT)\!.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle ZB & \cong & \displaystyle F[U,Y,S,T]/\!(Y^{2^{d-2}+1},U^{2}-Y^{2^{d-2}},S^{2},T^{2},SY,\nonumber\\ \displaystyle & & \displaystyle SU,ST,UY,UT,YT)\!.\nonumber\end{eqnarray}$$
 $JZB^{2}=(Y^{2})$
and again
$JZB^{2}=(Y^{2})$
and again
 $LL(ZB)=2^{d-2}+1$
.
$LL(ZB)=2^{d-2}+1$
.(iii)
 $D\cong Q_{2^{d}}$
,
$D\cong Q_{2^{d}}$
,
 $l(B)=3$
:By [Reference Holm5, Lemma 2.5.15],
$l(B)=3$
:By [Reference Holm5, Lemma 2.5.15], We compute
We compute $$\begin{eqnarray}\displaystyle ZB & = & \displaystyle \operatorname{span}\{\!1,\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD},(\unicode[STIX]{x1D705}\unicode[STIX]{x1D706})^{i}+(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{i},\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF},(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2},(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}},\nonumber\\ \displaystyle & & \displaystyle (\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}:i=1,\ldots ,2^{d-2}-1\!\}\!.\nonumber\end{eqnarray}$$
Hence,
$$\begin{eqnarray}\displaystyle ZB & = & \displaystyle \operatorname{span}\{\!1,\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD},(\unicode[STIX]{x1D705}\unicode[STIX]{x1D706})^{i}+(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{i},\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF},(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2},(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}},\nonumber\\ \displaystyle & & \displaystyle (\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}:i=1,\ldots ,2^{d-2}-1\!\}\!.\nonumber\end{eqnarray}$$
Hence, $$\begin{eqnarray}\displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})^{2}=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}+(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})^{2}=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}+(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{3}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \!\!\!\!\!\!\!\!((\unicode[STIX]{x1D705}\unicode[STIX]{x1D706})^{2^{d-2}-1}+(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}-1})(\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})=\unicode[STIX]{x1D705}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}+(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}+(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D706}\unicode[STIX]{x1D705}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}=\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D705}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D705}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D705}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF})^{2}=(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}+(\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF})^{2}=(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}=(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}+(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF})(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF})(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}=\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}=\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D705}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF})(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}=\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}=(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D705}\unicode[STIX]{x1D702}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}=0. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})^{2}=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}+(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})^{2}=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}+(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{3}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \!\!\!\!\!\!\!\!((\unicode[STIX]{x1D705}\unicode[STIX]{x1D706})^{2^{d-2}-1}+(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}-1})(\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})=\unicode[STIX]{x1D705}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}+(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}+(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D706}\unicode[STIX]{x1D705}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}=\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D705}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D705}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D705}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF})^{2}=(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}+(\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF})^{2}=(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}=(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}+(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF})(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF})(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}=\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}=\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D705}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FF})(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}=\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}=(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2^{d-2}}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D705}\unicode[STIX]{x1D702}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}=0. & \displaystyle \nonumber\end{eqnarray}$$
 $JZB^{2}=\langle (\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2}+(\unicode[STIX]{x1D705}\unicode[STIX]{x1D706})^{2},(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}+(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}\rangle$
and
$JZB^{2}=\langle (\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2}+(\unicode[STIX]{x1D705}\unicode[STIX]{x1D706})^{2},(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}+(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}\rangle$
and
 $JZB^{3}=\langle (\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{3}+(\unicode[STIX]{x1D705}\unicode[STIX]{x1D706})^{3}\rangle$
. This implies
$JZB^{3}=\langle (\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{3}+(\unicode[STIX]{x1D705}\unicode[STIX]{x1D706})^{3}\rangle$
. This implies
 $LL(ZB)=2^{d-2}+1$
.
$LL(ZB)=2^{d-2}+1$
.(iv)
 $D\cong SD_{2^{d}}$
,
$D\cong SD_{2^{d}}$
,
 $k(B)=2^{d-2}+3$
and
$k(B)=2^{d-2}+3$
and
 $l(B)=2$
:By [Reference Holm and Zimmermann6, Section 5.1], we have
$l(B)=2$
:By [Reference Holm and Zimmermann6, Section 5.1], we have As in (i) we obtain
As in (i) we obtain $$\begin{eqnarray}ZB=\operatorname{span}\{1,\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D702}^{i}:i=1,\ldots ,2^{d-2}\}.\end{eqnarray}$$
$$\begin{eqnarray}ZB=\operatorname{span}\{1,\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D702}^{i}:i=1,\ldots ,2^{d-2}\}.\end{eqnarray}$$
 $JZB^{2}=\langle \unicode[STIX]{x1D702}^{2}\rangle$
and
$JZB^{2}=\langle \unicode[STIX]{x1D702}^{2}\rangle$
and
 $LL(ZB)=2^{d-2}+1$
.
$LL(ZB)=2^{d-2}+1$
.(v)
 $D\cong SD_{2^{d}}$
,
$D\cong SD_{2^{d}}$
,
 $k(B)=2^{d-2}+4$
and
$k(B)=2^{d-2}+4$
and
 $l(B)=2$
:By [Reference Holm and Zimmermann6, Section 5.2.2], we have
$l(B)=2$
:By [Reference Holm and Zimmermann6, Section 5.2.2], we have Since
Since $$\begin{eqnarray}\displaystyle ZB & = & \displaystyle \operatorname{span}\{\!1,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE},(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2},\unicode[STIX]{x1D702}^{i},\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D702}+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}:i=2,\ldots ,2^{d-2}\!\}\!.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle ZB & = & \displaystyle \operatorname{span}\{\!1,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE},(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2},\unicode[STIX]{x1D702}^{i},\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D702}+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}:i=2,\ldots ,2^{d-2}\!\}\!.\nonumber\end{eqnarray}$$
 $(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC})^{2}$
and
$(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC})^{2}$
and
 $(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})^{2}=\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D702}^{2^{d-2}}$
, it follows that Similarly,
$(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})^{2}=\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D702}^{2^{d-2}}$
, it follows that Similarly, $$\begin{eqnarray}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})^{2}=(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}+(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC})^{2}+(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})^{2}=\unicode[STIX]{x1D702}^{2^{d-2}}.\end{eqnarray}$$
Consequently,
$$\begin{eqnarray}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})^{2}=(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}+(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC})^{2}+(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})^{2}=\unicode[STIX]{x1D702}^{2^{d-2}}.\end{eqnarray}$$
Consequently, $$\begin{eqnarray}\displaystyle & \displaystyle (\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D702}^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D702}+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC})=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D702}^{2}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D702}^{2}\unicode[STIX]{x1D6FE}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D702}+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}\unicode[STIX]{x1D6FC}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}\unicode[STIX]{x1D702}^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}(\unicode[STIX]{x1D702}+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC})=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D702}^{2}(\unicode[STIX]{x1D702}+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D702}^{3}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D702}+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC})^{2}=\unicode[STIX]{x1D702}^{2}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D702}^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D702}+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC})=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D702}^{2}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D702}^{2}\unicode[STIX]{x1D6FE}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D702}+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}\unicode[STIX]{x1D6FC}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}\unicode[STIX]{x1D702}^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}(\unicode[STIX]{x1D702}+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC})=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D702}^{2}(\unicode[STIX]{x1D702}+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D702}^{3}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D702}+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC})^{2}=\unicode[STIX]{x1D702}^{2}. & \displaystyle \nonumber\end{eqnarray}$$
 $JZB^{2}=\langle \unicode[STIX]{x1D702}^{2}\rangle$
and
$JZB^{2}=\langle \unicode[STIX]{x1D702}^{2}\rangle$
and
 $LL(ZB)=2^{d-2}+1$
.
$LL(ZB)=2^{d-2}+1$
.(vi)
 $D\cong SD_{2^{d}}$
,
$D\cong SD_{2^{d}}$
,
 $l(B)=3$
:From [Reference Holm5, Lemma 2.4.16] we get
$l(B)=3$
:From [Reference Holm5, Lemma 2.4.16] we get We compute
We compute $$\begin{eqnarray}\displaystyle ZB & = & \displaystyle \operatorname{span}\{\!1,(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{i}+(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})^{i},\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705},(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}},(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2},\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}:i=1,\ldots ,2^{d-2}-1\!\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle ZB & = & \displaystyle \operatorname{span}\{\!1,(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{i}+(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})^{i},\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705},(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}},(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2},\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}:i=1,\ldots ,2^{d-2}-1\!\}.\nonumber\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \!\!\!(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})((\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}-1}+(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})^{2^{d-2}-1})=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}\unicode[STIX]{x1D705}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}\unicode[STIX]{x1D705}\unicode[STIX]{x1D702}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}+(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2}=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}}+(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2}, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \!\!\!(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})((\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}-1}+(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})^{2^{d-2}-1})=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}\unicode[STIX]{x1D705}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}\unicode[STIX]{x1D705}\unicode[STIX]{x1D702}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}+(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2}=(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}}+(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2}, & \displaystyle \nonumber\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}} & = & \displaystyle \unicode[STIX]{x1D705}\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}-1}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D705}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}-1}=0,\nonumber\\ \displaystyle (\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2} & = & \displaystyle \unicode[STIX]{x1D706}(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}}\unicode[STIX]{x1D705}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}-1}\unicode[STIX]{x1D705}=0,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}} & = & \displaystyle \unicode[STIX]{x1D705}\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}-1}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D705}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}-1}=0,\nonumber\\ \displaystyle (\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2} & = & \displaystyle \unicode[STIX]{x1D706}(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}}\unicode[STIX]{x1D705}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}-1}\unicode[STIX]{x1D705}=0,\nonumber\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}=0, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}=0, & & \displaystyle \nonumber\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}}(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}} & = & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}}(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2}\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}=0,\nonumber\end{eqnarray}$$
Hence,
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}}(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}} & = & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}}(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2}\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2^{d-2}}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}=0,\nonumber\end{eqnarray}$$
Hence, $$\begin{eqnarray}\displaystyle & \displaystyle (\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2}(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2}=(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}=\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}\unicode[STIX]{x1D705}\unicode[STIX]{x1D702}=0. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2}(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2}=(\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})^{2}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})^{2}=\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}\unicode[STIX]{x1D705}\unicode[STIX]{x1D706}\unicode[STIX]{x1D705}\unicode[STIX]{x1D702}=0. & \displaystyle \nonumber\end{eqnarray}$$
 $JZB^{2}=\langle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}+(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})^{2},(\unicode[STIX]{x1D705}\unicode[STIX]{x1D706})^{2}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}\rangle$
and
$JZB^{2}=\langle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{2}+(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})^{2},(\unicode[STIX]{x1D705}\unicode[STIX]{x1D706})^{2}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}\rangle$
and
 $JZB^{3}=\langle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{3}+(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})^{3}\rangle$
. This implies
$JZB^{3}=\langle (\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE})^{3}+(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})^{3}\rangle$
. This implies
 $LL(ZB)=2^{d-2}+1$
. ◻
$LL(ZB)=2^{d-2}+1$
. ◻
It is interesting to note the difference between even and odd primes in Proposition 7. For
![]() $p=2$
, non-nilpotent blocks give larger Loewy lengths while for
$p=2$
, non-nilpotent blocks give larger Loewy lengths while for
![]() $p>2$
the maximal Loewy length is only attained for nilpotent blocks.
$p>2$
the maximal Loewy length is only attained for nilpotent blocks.
Recall that a lower defect group of a block
![]() $B$
of
$B$
of
![]() $FG$
is a
$FG$
is a
![]() $p$
-subgroup
$p$
-subgroup
![]() $Q\leqslant G$
such that
$Q\leqslant G$
such that
In this case
![]() $Q$
is conjugate to a subgroup of a defect group
$Q$
is conjugate to a subgroup of a defect group
![]() $D$
of
$D$
of
![]() $B$
and conversely
$B$
and conversely
![]() $D$
is also a lower defect group since
$D$
is also a lower defect group since
![]() $1_{B}\in I_{{\leqslant}D}(G)\setminus I_{{<}D}(G)$
. It is clear that in the proofs of Theorems 3 and 6 it suffices to sum over the lower defect groups of
$1_{B}\in I_{{\leqslant}D}(G)\setminus I_{{<}D}(G)$
. It is clear that in the proofs of Theorems 3 and 6 it suffices to sum over the lower defect groups of
![]() $B$
. In particular there exists a chain of lower defect groups
$B$
. In particular there exists a chain of lower defect groups
![]() $Q_{1}<\cdots <Q_{n}=D$
such that
$Q_{1}<\cdots <Q_{n}=D$
such that
![]() $LL(ZB)\leqslant \sum _{i=1}^{n}LL(F\operatorname{Z}(Q_{i}))$
. Unfortunately, it is hard to compute the lower defect groups of a given block.
$LL(ZB)\leqslant \sum _{i=1}^{n}LL(F\operatorname{Z}(Q_{i}))$
. Unfortunately, it is hard to compute the lower defect groups of a given block.
The following proposition generalizes [Reference Willems15, Theorem 1.5].
Proposition 8. Let
![]() $B$
be a block of
$B$
be a block of
![]() $FG$
. Then
$FG$
. Then
![]() $ZB$
is uniserial if and only if
$ZB$
is uniserial if and only if
![]() $B$
is nilpotent with cyclic defect groups.
$B$
is nilpotent with cyclic defect groups.
Proof. Suppose first that
![]() $ZB$
is uniserial. Then
$ZB$
is uniserial. Then
![]() $ZB\cong F[X]/(X^{n})$
for some
$ZB\cong F[X]/(X^{n})$
for some
![]() $n\in \mathbb{N}$
; in particular,
$n\in \mathbb{N}$
; in particular,
![]() $ZB$
is a symmetric
$ZB$
is a symmetric
![]() $F$
-algebra. Then [Reference Okuyama and Tsushima11, Theorems 3 and 5] implies that
$F$
-algebra. Then [Reference Okuyama and Tsushima11, Theorems 3 and 5] implies that
![]() $B$
is nilpotent with abelian defect group
$B$
is nilpotent with abelian defect group
![]() $D$
. Thus, by a result of Broué and Puig [Reference Broué and Puig1] (see also [Reference Külshammer8]),
$D$
. Thus, by a result of Broué and Puig [Reference Broué and Puig1] (see also [Reference Külshammer8]),
![]() $B$
is Morita equivalent to
$B$
is Morita equivalent to
![]() $FD$
; in particular,
$FD$
; in particular,
![]() $FD$
is also uniserial. Thus
$FD$
is also uniserial. Thus
![]() $D$
is cyclic.
$D$
is cyclic.
Conversely, suppose that
![]() $B$
is nilpotent with cyclic defect group
$B$
is nilpotent with cyclic defect group
![]() $D$
. Then the Broué–Puig result mentioned above implies that
$D$
. Then the Broué–Puig result mentioned above implies that
![]() $B$
is Morita equivalent of
$B$
is Morita equivalent of
![]() $FD$
. Thus
$FD$
. Thus
![]() $ZB\cong ZFD=FD$
. Since
$ZB\cong ZFD=FD$
. Since
![]() $FD$
is uniserial, the result follows.◻
$FD$
is uniserial, the result follows.◻
A similar proof shows that
![]() $ZB$
is isomorphic to the group algebra of the Klein four group over an algebraically closed field of characteristic
$ZB$
is isomorphic to the group algebra of the Klein four group over an algebraically closed field of characteristic
![]() $2$
if and only if
$2$
if and only if
![]() $B$
is nilpotent with Klein four defect groups.
$B$
is nilpotent with Klein four defect groups.