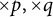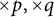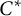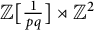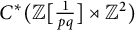1 Introduction
Let
![]() $p,q\geq 2$
be two multiplicatively independent integers, in the sense that there are no
$p,q\geq 2$
be two multiplicatively independent integers, in the sense that there are no
![]() $r,s\in \mathbb {Z}_{>0}$
such that
$r,s\in \mathbb {Z}_{>0}$
such that
![]() $p^r=q^s$
. In [Reference FurstenbergFur67], Furstenberg showed that the only infinite closed
$p^r=q^s$
. In [Reference FurstenbergFur67], Furstenberg showed that the only infinite closed
![]() $\times p,\times q$
-invariant subset of
$\times p,\times q$
-invariant subset of
![]() $\frac {\mathbb {R}}{\mathbb {Z}}\simeq \mathbb {T}$
is the whole circle. The measure-theoretic analog of this result is now one of the most fundamental open problems in ergodic theory (for a survey on this problem, see, for example, [Reference Laca and WarrenLin05]). It can be formulated precisely as follows.
$\frac {\mathbb {R}}{\mathbb {Z}}\simeq \mathbb {T}$
is the whole circle. The measure-theoretic analog of this result is now one of the most fundamental open problems in ergodic theory (for a survey on this problem, see, for example, [Reference Laca and WarrenLin05]). It can be formulated precisely as follows.
Conjecture 1 (Furstenberg’s
 $\times p,\times q$
conjecture)
$\times p,\times q$
conjecture)
The only ergodic
![]() $\times p,\times q$
-invariant probability measure on
$\times p,\times q$
-invariant probability measure on
![]() $\mathbb {T}$
with infinite (hence full) support is the Lebesgue measure.
$\mathbb {T}$
with infinite (hence full) support is the Lebesgue measure.
There have already been two connections between the above conjecture and
![]() $C^*$
-algebra theory. Following an idea from Cuntz, Huang and Wu in [Reference Huang and WuHW17] gave a characterization of Furstenberg’s conjecture in terms of irreducible representations of the group
$C^*$
-algebra theory. Following an idea from Cuntz, Huang and Wu in [Reference Huang and WuHW17] gave a characterization of Furstenberg’s conjecture in terms of irreducible representations of the group
![]() $\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2$
. In [Reference ScarparoSca20], Furstenberg’s theorem on closed
$\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2$
. In [Reference ScarparoSca20], Furstenberg’s theorem on closed
![]() $\times p,\times q$
-invariant subsets of
$\times p,\times q$
-invariant subsets of
![]() $\mathbb {T}$
was used to show that every nonzero ideal
$\mathbb {T}$
was used to show that every nonzero ideal
![]() $I\unlhd C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
intersects
$I\unlhd C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
intersects
![]() $\mathbb {C}[\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2]$
nontrivially. Since there is a nontrivial, but well-understood, relationship between
$\mathbb {C}[\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2]$
nontrivially. Since there is a nontrivial, but well-understood, relationship between
![]() $C^*$
-simplicity of a group (that is, simplicity of the reduced group
$C^*$
-simplicity of a group (that is, simplicity of the reduced group
![]() $C^*$
-algebra) and uniqueness of the canonical tracial state on the reduced group
$C^*$
-algebra) and uniqueness of the canonical tracial state on the reduced group
![]() $C^*$
-algebra [Reference BerendBKKO17], it is, in light of [Reference ScarparoSca20], natural to ask if Furstenberg’s
$C^*$
-algebra [Reference BerendBKKO17], it is, in light of [Reference ScarparoSca20], natural to ask if Furstenberg’s
![]() $\times p,\times q$
conjecture has a
$\times p,\times q$
conjecture has a
![]() $C^*$
-algebraic manifestation in terms of tracial states on
$C^*$
-algebraic manifestation in terms of tracial states on
![]() $C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
. In this work, we show that this is indeed the case: We present a characterization of the conjecture in terms of the set of tracial states on
$C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
. In this work, we show that this is indeed the case: We present a characterization of the conjecture in terms of the set of tracial states on
![]() $C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
(see Corollary 3.7).
$C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
(see Corollary 3.7).
Since
![]() $C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
can be realized as a crossed product
$C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
can be realized as a crossed product
![]() $C^*$
-algebra for a certain almost minimal action of
$C^*$
-algebra for a certain almost minimal action of
![]() $\mathbb {Z}^2$
, we begin with several general results on tracial states and primitive ideals for crossed products arising from such actions. Recall that an action of a group
$\mathbb {Z}^2$
, we begin with several general results on tracial states and primitive ideals for crossed products arising from such actions. Recall that an action of a group
![]() $\Gamma $
on a compact space X is said to be almost minimal if every invariant closed set
$\Gamma $
on a compact space X is said to be almost minimal if every invariant closed set
![]() $F\subsetneq X$
is finite. Almost minimality is also known in the literature as irreducibility or as the ID property (see, for example, [Reference SchmidtSch95, Section 29] for an account of this property).
$F\subsetneq X$
is finite. Almost minimality is also known in the literature as irreducibility or as the ID property (see, for example, [Reference SchmidtSch95, Section 29] for an account of this property).
In Section 2, we compute the primitive ideal space and the set of extreme tracial states of the crossed product associated with an almost minimal action of an abelian group. Along the way, we fix a mistake in the literature concerning the computation of the primitive ideal spaces of a special class of such crossed products (see Remark 2.5).
In Section 3, we apply the results of the previous section for computing the primitive ideal space and the set of extreme tracial states on
![]() $C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
. As an application, we show that Furstenberg’s
$C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
. As an application, we show that Furstenberg’s
![]() $\times p,\times q$
conjecture holds if and only if the canonical trace is the only faithful extreme tracial state on
$\times p,\times q$
conjecture holds if and only if the canonical trace is the only faithful extreme tracial state on
![]() $C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
. We also compute the K-theory of
$C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
. We also compute the K-theory of
![]() $C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
.
$C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
.
Finally, in Section 4, we pose a few questions that arise naturally in light of our results.
2 Almost minimal actions
2.1 Preliminaries
Throughout this paper,
![]() $\Gamma \!\curvearrowright \! X$
denotes an action of a group
$\Gamma \!\curvearrowright \! X$
denotes an action of a group
![]() $\Gamma $
on a compact Hausdorff space X by homeomorphisms. Given
$\Gamma $
on a compact Hausdorff space X by homeomorphisms. Given
![]() $x\in X$
, we let
$x\in X$
, we let
![]() $\Gamma _x:=\{g\in \Gamma :gx=x\}$
be the stabilizer of x, and
$\Gamma _x:=\{g\in \Gamma :gx=x\}$
be the stabilizer of x, and
![]() $[x]:=\{gx:g\in \Gamma \}$
be the orbit of x.
$[x]:=\{gx:g\in \Gamma \}$
be the orbit of x.
Given
![]() $g\in \Gamma $
, let
$g\in \Gamma $
, let
![]() $\operatorname {Fix}_g:=\{x\in X:gx=x\}$
. We say that the action is faithful if
$\operatorname {Fix}_g:=\{x\in X:gx=x\}$
. We say that the action is faithful if
![]() $\operatorname {Fix}_g\subsetneq X$
for any
$\operatorname {Fix}_g\subsetneq X$
for any
![]() $g\in \Gamma \backslash \{e\}$
. The action is said to be topologically free if, for every
$g\in \Gamma \backslash \{e\}$
. The action is said to be topologically free if, for every
![]() $g\in \Gamma \backslash \{e\}$
,
$g\in \Gamma \backslash \{e\}$
,
![]() $\operatorname {\mathrm {int}}\operatorname {Fix}_g=\emptyset $
. If
$\operatorname {\mathrm {int}}\operatorname {Fix}_g=\emptyset $
. If
![]() $\Gamma $
is countable, then topological freeness is equivalent to the set
$\Gamma $
is countable, then topological freeness is equivalent to the set
![]() $\{x\in X:\Gamma _x=\{e\}\}$
being dense in X by a Baire category argument.
$\{x\in X:\Gamma _x=\{e\}\}$
being dense in X by a Baire category argument.
Let
![]() $\mathcal {P}_{\Gamma} (X)$
be the space of
$\mathcal {P}_{\Gamma} (X)$
be the space of
![]() $\Gamma $
-invariant regular probability measures on X. We say that
$\Gamma $
-invariant regular probability measures on X. We say that
![]() $\mu \in \mathcal {P}_{\Gamma} (X)$
is essentially free if, for any
$\mu \in \mathcal {P}_{\Gamma} (X)$
is essentially free if, for any
![]() $g\in \Gamma \backslash \{e\}$
,
$g\in \Gamma \backslash \{e\}$
,
![]() $\mu (\operatorname {Fix}_g)=0$
. If
$\mu (\operatorname {Fix}_g)=0$
. If
![]() $\Gamma $
is countable, then
$\Gamma $
is countable, then
![]() $\mu $
is essentially free if and only if
$\mu $
is essentially free if and only if
![]() $\mu (\{x\in X:\Gamma _x=\{e\}\})=1$
.
$\mu (\{x\in X:\Gamma _x=\{e\}\})=1$
.
The action is said to be almost minimal if every invariant closed set
![]() $F\subsetneq X$
is finite. If
$F\subsetneq X$
is finite. If
![]() $\Gamma \!\curvearrowright \! X$
is almost minimal, then any infinite orbit is dense in X.
$\Gamma \!\curvearrowright \! X$
is almost minimal, then any infinite orbit is dense in X.
Example 2.1 Let
![]() $\alpha $
be an action by homeomorphisms on a noncompact, locally compact Hausdorff space X. If
$\alpha $
be an action by homeomorphisms on a noncompact, locally compact Hausdorff space X. If
![]() $\alpha $
is minimal (that is, every orbit is dense), then the extension of
$\alpha $
is minimal (that is, every orbit is dense), then the extension of
![]() $\alpha $
to the one-point compactification of X is almost minimal.
$\alpha $
to the one-point compactification of X is almost minimal.
Certain almost minimal algebraic actions were studied by Berend [Reference Bekka and de la HarpeBer83; Reference BerendBer84] and by Laca and Warren [Reference LindenstraussLW20]. We also refer the reader to Schmidt’s book [Reference SchmidtSch95, Section 29] for further discussions of examples from algebraic actions.
Any action on a finite space is almost minimal, but if
![]() $\Gamma \!\curvearrowright \! X$
is an almost minimal action and X is infinite, then
$\Gamma \!\curvearrowright \! X$
is an almost minimal action and X is infinite, then
![]() $\Gamma $
is infinite.
$\Gamma $
is infinite.
Proposition 2.2 Let X be an infinite compact space, and let
![]() $\Gamma \!\curvearrowright \! X$
be an almost minimal action. Then
$\Gamma \!\curvearrowright \! X$
be an almost minimal action. Then
![]() $\Gamma $
is infinite.
$\Gamma $
is infinite.
Proof Suppose
![]() $\Gamma $
is finite. Take
$\Gamma $
is finite. Take
![]() $x,y\in X$
such that
$x,y\in X$
such that
![]() $[x]\cap [y]=\emptyset $
. We will show that there are disjoint
$[x]\cap [y]=\emptyset $
. We will show that there are disjoint
![]() $\Gamma $
-invariant open neighborhoods
$\Gamma $
-invariant open neighborhoods
![]() $W_x$
and
$W_x$
and
![]() $W_y$
of
$W_y$
of
![]() $[x]$
and
$[x]$
and
![]() $[y]$
, respectively. This suffices to prove the result by the following argument: Since
$[y]$
, respectively. This suffices to prove the result by the following argument: Since
![]() $W_x^c\cup W_y^ c= X$
, we have that either
$W_x^c\cup W_y^ c= X$
, we have that either
![]() $W_x^c$
or
$W_x^c$
or
![]() $W_y^c$
is infinite, hence equal to X, thus contradicting that
$W_y^c$
is infinite, hence equal to X, thus contradicting that
![]() $W_x$
and
$W_x$
and
![]() $W_y$
are not empty.
$W_y$
are not empty.
Now, let us construct such
![]() $W_x$
and
$W_x$
and
![]() $W_y$
. Given an open neighborhood U of x, the set
$W_y$
. Given an open neighborhood U of x, the set
![]() $V:=\bigcap _{g\in \Gamma _x}gU$
is a
$V:=\bigcap _{g\in \Gamma _x}gU$
is a
![]() $\Gamma _x$
-invariant open neighborhood of x. Let
$\Gamma _x$
-invariant open neighborhood of x. Let
![]() $g_1,\dots ,g_n$
be left coset representatives for
$g_1,\dots ,g_n$
be left coset representatives for
![]() $\Gamma /\Gamma _x$
. By taking U smaller, we may assume that
$\Gamma /\Gamma _x$
. By taking U smaller, we may assume that
![]() $g_1 V,\dots ,g_n V$
are disjoint sets. Then
$g_1 V,\dots ,g_n V$
are disjoint sets. Then
![]() $W_x:=\bigcup _{i=1}^n g_i V$
is a
$W_x:=\bigcup _{i=1}^n g_i V$
is a
![]() $\Gamma $
-invariant open neighborhood of
$\Gamma $
-invariant open neighborhood of
![]() $[x]$
. Moreover, by taking U smaller, we can assume that
$[x]$
. Moreover, by taking U smaller, we can assume that
![]() $\overline {W_x}\cap [y]=\emptyset $
. By constructing a neighborhood
$\overline {W_x}\cap [y]=\emptyset $
. By constructing a neighborhood
![]() $W_y$
of
$W_y$
of
![]() $[y]$
in an analogous way, such that
$[y]$
in an analogous way, such that
![]() $W_y\subseteq \overline {W_x}^c$
, we obtain the open sets with the desired properties.
$W_y\subseteq \overline {W_x}^c$
, we obtain the open sets with the desired properties.
For the proof of the next result, notice that, if h is a homeomorphism on a space X, then, given
![]() $Y\subset X$
, we have that
$Y\subset X$
, we have that
![]() $h((\operatorname {\mathrm {int}} Y)^c)=(h(\operatorname {\mathrm {int}} Y))^c=(\operatorname {\mathrm {int}} h(Y))^c$
. In particular, if
$h((\operatorname {\mathrm {int}} Y)^c)=(h(\operatorname {\mathrm {int}} Y))^c=(\operatorname {\mathrm {int}} h(Y))^c$
. In particular, if
![]() $h(Y)=Y$
, then
$h(Y)=Y$
, then
![]() $h((\operatorname {\mathrm {int}} Y)^c)=(\operatorname {\mathrm {int}} Y)^c$
as well.
$h((\operatorname {\mathrm {int}} Y)^c)=(\operatorname {\mathrm {int}} Y)^c$
as well.
Proposition 2.3 Let
![]() $\Gamma $
be a countable abelian group, X an infinite compact space, and
$\Gamma $
be a countable abelian group, X an infinite compact space, and
![]() $\Gamma \!\curvearrowright \! X$
a faithful almost minimal action. Then the action
$\Gamma \!\curvearrowright \! X$
a faithful almost minimal action. Then the action
![]() $\Gamma \!\curvearrowright \! X$
is topologically free, and the set of points that have finite orbits is countable and has empty interior.
$\Gamma \!\curvearrowright \! X$
is topologically free, and the set of points that have finite orbits is countable and has empty interior.
Proof Given
![]() $g\in \Gamma \backslash \{e\}$
, we have that
$g\in \Gamma \backslash \{e\}$
, we have that
![]() $\operatorname {Fix}_g\subsetneq X$
is closed and invariant, hence finite. Since
$\operatorname {Fix}_g\subsetneq X$
is closed and invariant, hence finite. Since
![]() $(\operatorname {\mathrm {int}}\operatorname {Fix}_g)^c$
is closed, infinite, and invariant, it follows that
$(\operatorname {\mathrm {int}}\operatorname {Fix}_g)^c$
is closed, infinite, and invariant, it follows that
![]() $(\operatorname {\mathrm {int}}\operatorname {Fix}_g)^c=X$
, hence
$(\operatorname {\mathrm {int}}\operatorname {Fix}_g)^c=X$
, hence
![]() $\operatorname {\mathrm {int}}\operatorname {Fix}_g=\emptyset $
. Therefore, the action is topologically free.
$\operatorname {\mathrm {int}}\operatorname {Fix}_g=\emptyset $
. Therefore, the action is topologically free.
Suppose
![]() $x\in X$
has finite orbit. Since
$x\in X$
has finite orbit. Since
![]() $\Gamma $
is infinite by Proposition 2.2, we have that
$\Gamma $
is infinite by Proposition 2.2, we have that
![]() $x\in \operatorname {Fix}_g$
for some
$x\in \operatorname {Fix}_g$
for some
![]() $g\in \Gamma \backslash \{e\}$
. Since
$g\in \Gamma \backslash \{e\}$
. Since
![]() $\operatorname {Fix}_g$
is finite and has empty interior for any
$\operatorname {Fix}_g$
is finite and has empty interior for any
![]() $g\in \Gamma \backslash \{e\}$
, the result follows from the Baire category theorem.
$g\in \Gamma \backslash \{e\}$
, the result follows from the Baire category theorem.
2.2 Primitive ideals
Recall that an ideal I of a
![]() $C^*$
-algebra A is said to be primitive if there exists a nonzero irreducible representation
$C^*$
-algebra A is said to be primitive if there exists a nonzero irreducible representation
![]() $\varphi \colon A \to B(H)$
such that
$\varphi \colon A \to B(H)$
such that
![]() $I=\ker (\varphi )$
. The primitive ideal space of A, denoted by
$I=\ker (\varphi )$
. The primitive ideal space of A, denoted by
![]() $\mathrm {Prim}(A)$
, is the set of primitive ideals endowed with the hull-kernel topology (see, for instance, [Reference MurphyMur90, Section 5.4]).
$\mathrm {Prim}(A)$
, is the set of primitive ideals endowed with the hull-kernel topology (see, for instance, [Reference MurphyMur90, Section 5.4]).
In the proof of the next result, we use a description from [Reference WilliamsWil81] of the primitive ideal space of the crossed product associated with an action of an abelian group. We also use some ideas from [Reference LindenstraussLW20, Section 5] (beware that there is an issue with the description of convergent nets in [Reference LindenstraussLW20, Theorem 5.2]; see Remark 2.5). For an alternative approach to describing the primitive ideal space, see the proof of [Reference Becker, Lubotzky and ThomBdlH20, Theorem 9.D.1].
Theorem 2.4 Let
![]() $\Gamma $
be a countable abelian group, X an infinite, second countable compact space, and
$\Gamma $
be a countable abelian group, X an infinite, second countable compact space, and
![]() $\Gamma \!\curvearrowright \! X$
a faithful and almost minimal action. Then the set
$\Gamma \!\curvearrowright \! X$
a faithful and almost minimal action. Then the set
![]() $\mathcal {C}$
of finite orbits is countable, and
$\mathcal {C}$
of finite orbits is countable, and
![]() $\mathrm {Prim}(C(X)\rtimes \Gamma )$
is homeomorphic to
$\mathrm {Prim}(C(X)\rtimes \Gamma )$
is homeomorphic to
 $$ \begin{align*}P:=\left(\bigsqcup_{[x]\in \mathcal{C}}\{[x]\}\times\widehat{\Gamma_x}\right)\sqcup\{\infty\},\end{align*} $$
$$ \begin{align*}P:=\left(\bigsqcup_{[x]\in \mathcal{C}}\{[x]\}\times\widehat{\Gamma_x}\right)\sqcup\{\infty\},\end{align*} $$
where the topology on P is defined as follows: the closed subsets of P are P and finite unions of elements from the collection
![]() $\{\{[x]\}\times F:[x]\in \mathcal {C}, F\text { a closed subset of}\ \widehat {\Gamma _x}\}$
.
$\{\{[x]\}\times F:[x]\in \mathcal {C}, F\text { a closed subset of}\ \widehat {\Gamma _x}\}$
.
Proof By Proposition 2.3,
![]() $\Gamma \!\curvearrowright \! X$
is topologically free, and
$\Gamma \!\curvearrowright \! X$
is topologically free, and
![]() $\mathcal {C}$
is countable.
$\mathcal {C}$
is countable.
Consider the equivalence relation on
![]() $X\times \widehat {\Gamma }$
defined by
$X\times \widehat {\Gamma }$
defined by
![]() $(x,\eta )\sim (y,\chi )$
if
$(x,\eta )\sim (y,\chi )$
if
![]() $\overline {[x]}=\overline {[y]}$
and
$\overline {[x]}=\overline {[y]}$
and
![]() $\eta |_{\Gamma _x}=\chi |_{\Gamma _x}$
(note that, since
$\eta |_{\Gamma _x}=\chi |_{\Gamma _x}$
(note that, since
![]() $\Gamma $
is abelian,
$\Gamma $
is abelian,
![]() $\overline {[x]}=\overline {[y]}$
implies that
$\overline {[x]}=\overline {[y]}$
implies that
![]() $\Gamma _x=\Gamma _y$
). By [Reference WilliamsWil81, Theorem 5.3],
$\Gamma _x=\Gamma _y$
). By [Reference WilliamsWil81, Theorem 5.3],
![]() $\mathrm {Prim}(C(X)\rtimes \Gamma )$
is homeomorphic to the quotient space
$\mathrm {Prim}(C(X)\rtimes \Gamma )$
is homeomorphic to the quotient space
![]() $\frac {X\times \widehat {\Gamma }}{\sim }$
.
$\frac {X\times \widehat {\Gamma }}{\sim }$
.
Given
![]() $x\in X$
such that
$x\in X$
such that
![]() $[x]\notin \mathcal {C}$
, it follows from almost minimality and topological freeness of the action that
$[x]\notin \mathcal {C}$
, it follows from almost minimality and topological freeness of the action that
![]() $\overline {[x]}=X$
and
$\overline {[x]}=X$
and
![]() $\Gamma _x=\{e\}$
. Let
$\Gamma _x=\{e\}$
. Let
![]() $f\colon \frac {X\times \widehat {\Gamma }}{\sim }\to P$
be given by
$f\colon \frac {X\times \widehat {\Gamma }}{\sim }\to P$
be given by
![]() $f([x,\chi ]):=([x],\chi |_{\Gamma _x})$
if
$f([x,\chi ]):=([x],\chi |_{\Gamma _x})$
if
![]() $[x]\in \mathcal {C}$
, and
$[x]\in \mathcal {C}$
, and
![]() $f([x,\chi ]):=\infty $
otherwise. Given
$f([x,\chi ]):=\infty $
otherwise. Given
![]() $x\in X$
, let
$x\in X$
, let
![]() $r_x\colon \widehat {\Gamma }\to \widehat {\Gamma _x}$
be the restriction map. It is not difficult to see that f is bijective (surjectivity follows from surjectivity of each
$r_x\colon \widehat {\Gamma }\to \widehat {\Gamma _x}$
be the restriction map. It is not difficult to see that f is bijective (surjectivity follows from surjectivity of each
![]() $r_x$
).
$r_x$
).
Let
![]() $\pi \colon X\times \widehat {\Gamma }\to \frac {X\times \widehat {\Gamma }}{\sim }$
be the quotient map. We will show that f is continuous. For this, it suffices to show that
$\pi \colon X\times \widehat {\Gamma }\to \frac {X\times \widehat {\Gamma }}{\sim }$
be the quotient map. We will show that f is continuous. For this, it suffices to show that
![]() $f\circ \pi $
is continuous. Given
$f\circ \pi $
is continuous. Given
![]() $[x]\in \mathcal {C}$
and
$[x]\in \mathcal {C}$
and
![]() $F\subseteq \widehat {\Gamma _x}$
closed, we have that
$F\subseteq \widehat {\Gamma _x}$
closed, we have that
![]() $(f\circ \pi )^{-1}(\{[x]\}\times F)=[x]\times r_x^{-1}(F)$
is closed in
$(f\circ \pi )^{-1}(\{[x]\}\times F)=[x]\times r_x^{-1}(F)$
is closed in
![]() $X\times \widehat {\Gamma }$
. Therefore,
$X\times \widehat {\Gamma }$
. Therefore,
![]() $f\circ \pi $
is continuous.
$f\circ \pi $
is continuous.
Let us now show that
![]() $f^{-1}$
is continuous, that is, that f is a closed map. Let
$f^{-1}$
is continuous, that is, that f is a closed map. Let
![]() $A\subseteq \frac {X\times \widehat {\Gamma }}{\sim }$
be a closed subset. We will show that
$A\subseteq \frac {X\times \widehat {\Gamma }}{\sim }$
be a closed subset. We will show that
![]() $f(A)$
is closed in P.
$f(A)$
is closed in P.
Case
![]() $\infty \in f(A)$
: In this case,
$\infty \in f(A)$
: In this case,
![]() $\{x\in X:[x]\notin \mathcal {C}\}\times \widehat {\Gamma }\subseteq \pi ^{-1}(A)$
. Since the set of points with infinite orbit is dense in X by Proposition 2.3, it follows that
$\{x\in X:[x]\notin \mathcal {C}\}\times \widehat {\Gamma }\subseteq \pi ^{-1}(A)$
. Since the set of points with infinite orbit is dense in X by Proposition 2.3, it follows that
![]() $\pi ^{-1}(A)=X\times \widehat {\Gamma }$
, hence
$\pi ^{-1}(A)=X\times \widehat {\Gamma }$
, hence
![]() $f(A)=f(\pi (\pi ^{-1}(A)))=P$
.
$f(A)=f(\pi (\pi ^{-1}(A)))=P$
.
Case
![]() $I_A:=\{[x]\in \mathcal {C}:f(A)\cap (\{[x]\}\times \widehat {\Gamma _x})\neq \emptyset \}$
is infinite: Since
$I_A:=\{[x]\in \mathcal {C}:f(A)\cap (\{[x]\}\times \widehat {\Gamma _x})\neq \emptyset \}$
is infinite: Since
![]() $U:=\bigcup I_A$
is
$U:=\bigcup I_A$
is
![]() $\Gamma $
-invariant and infinite, it follows from almost minimality that U is dense in X. This implies that
$\Gamma $
-invariant and infinite, it follows from almost minimality that U is dense in X. This implies that
![]() $\{x : \exists \chi \in \widehat {\Gamma } \text { with } (x,\chi )\in \pi ^{-1}(A)\}=X$
. Hence, there exists
$\{x : \exists \chi \in \widehat {\Gamma } \text { with } (x,\chi )\in \pi ^{-1}(A)\}=X$
. Hence, there exists
![]() $(x,\chi )\in \pi ^{-1}(A)$
such that
$(x,\chi )\in \pi ^{-1}(A)$
such that
![]() $[x]\notin \mathcal {C}$
. In particular,
$[x]\notin \mathcal {C}$
. In particular,
![]() $\infty \in f(A)$
and
$\infty \in f(A)$
and
![]() $f(A)=P$
by the previous case.
$f(A)=P$
by the previous case.
Finally, assume that
![]() $I_A$
is finite and
$I_A$
is finite and
![]() $\infty \notin f(A)$
. In this case, there exists a family
$\infty \notin f(A)$
. In this case, there exists a family
![]() $(B_{[x]})_{[x]\in I_A}$
such that each
$(B_{[x]})_{[x]\in I_A}$
such that each
![]() $B_{[x]}$
is a subset of
$B_{[x]}$
is a subset of
![]() $\widehat {\Gamma _x}$
, and
$\widehat {\Gamma _x}$
, and
![]() $f(A)=\bigsqcup _{[x]\in I_A}\{[x]\}\times B_{[x]}$
. In order to conclude that
$f(A)=\bigsqcup _{[x]\in I_A}\{[x]\}\times B_{[x]}$
. In order to conclude that
![]() $f(A)$
is closed, we have to show that each
$f(A)$
is closed, we have to show that each
![]() $B_{[x]}$
is closed in
$B_{[x]}$
is closed in
![]() $\widehat {\Gamma _x}$
. We have that
$\widehat {\Gamma _x}$
. We have that
![]() $\pi ^{-1}(A)=\bigsqcup _{[x]\in I_A}[x]\times r_x^{-1}(B_{[x]})$
. Given
$\pi ^{-1}(A)=\bigsqcup _{[x]\in I_A}[x]\times r_x^{-1}(B_{[x]})$
. Given
![]() $[x]\in I_A$
, since
$[x]\in I_A$
, since
![]() $\pi ^{-1}(A)$
is closed in
$\pi ^{-1}(A)$
is closed in
![]() $X\times \widehat {\Gamma }$
, it follows that
$X\times \widehat {\Gamma }$
, it follows that
![]() $r_x^{-1}(B_{[x]})$
is closed in
$r_x^{-1}(B_{[x]})$
is closed in
![]() $\widehat {\Gamma }$
. Since
$\widehat {\Gamma }$
. Since
![]() $r_x$
is a quotient map (being a surjective continuous map between compact spaces), we conclude that
$r_x$
is a quotient map (being a surjective continuous map between compact spaces), we conclude that
![]() $B_{[x]}$
is closed in
$B_{[x]}$
is closed in
![]() $\widehat {\Gamma _x}$
.
$\widehat {\Gamma _x}$
.
Remark 2.5 Given
![]() $\Gamma \!\curvearrowright \! X$
and P as in Theorem 2.4, we have that
$\Gamma \!\curvearrowright \! X$
and P as in Theorem 2.4, we have that
![]() $\infty $
is a dense point in P (this corresponds to the fact that the ideal
$\infty $
is a dense point in P (this corresponds to the fact that the ideal
![]() $\{0\}$
is a dense point in
$\{0\}$
is a dense point in
![]() $\mathrm {Prim}(C(X)\rtimes \Gamma )$
). Moreover, given a net
$\mathrm {Prim}(C(X)\rtimes \Gamma )$
). Moreover, given a net
![]() $([x_i],\chi _i)$
in
$([x_i],\chi _i)$
in
![]() $P\backslash \{\infty \}$
, we have:
$P\backslash \{\infty \}$
, we have:
-
(a) if for every finite set
 $F\subseteq \mathcal {C}$
, the net
$F\subseteq \mathcal {C}$
, the net
 $[x_i]$
is eventually outside F, then
$[x_i]$
is eventually outside F, then
 $([x_i],\chi _i)$
converges to every point in P;
$([x_i],\chi _i)$
converges to every point in P; -
(b) if
 $[x_i]$
is eventually constant,
$[x_i]$
is eventually constant,
 $[x_i]=[x]$
for all
$[x_i]=[x]$
for all
 $i\geq j$
say, then
$i\geq j$
say, then
 $([x_i],\chi _i)$
converges to
$([x_i],\chi _i)$
converges to
 $([y],\chi )$
if and only if
$([y],\chi )$
if and only if
 $[y]=[x]$
and
$[y]=[x]$
and
 $\chi =\lim _{i\geq j}\chi _i$
.
$\chi =\lim _{i\geq j}\chi _i$
.
The paper [Reference LindenstraussLW20] considers a special class of algebraic actions coming from algebraic number theory. Theorem 2.4 corrects an error in [Reference LindenstraussLW20, Section 5]: Convergent nets as in (a) above are not accounted for in the description of the topology on the primitive ideal space stated in [Reference LindenstraussLW20, Theorem 5.2]. Note that the class of actions considered in [Reference LindenstraussLW20, Theorem 5.2] satisfy the hypothesis of Theorem 2.4 by [Reference LindenstraussLW20, Theorem 4.3].
2.3 Tracial states
Given a group
![]() $\Gamma $
, let
$\Gamma $
, let
![]() $\operatorname {Sub}(\Gamma )$
be the set of subgroups of
$\operatorname {Sub}(\Gamma )$
be the set of subgroups of
![]() $\Gamma $
, endowed with the Chabauty topology; this is the restriction to
$\Gamma $
, endowed with the Chabauty topology; this is the restriction to
![]() $\operatorname {Sub}(\Gamma )$
of the product topology on
$\operatorname {Sub}(\Gamma )$
of the product topology on
![]() $\{0,1\}^{\Gamma} $
, where every
$\{0,1\}^{\Gamma} $
, where every
![]() $\Lambda \in \operatorname {Sub}(\Gamma )$
is identified with its characteristic function
$\Lambda \in \operatorname {Sub}(\Gamma )$
is identified with its characteristic function
![]() $1_\Lambda \in \{0,1\}^{\Gamma} $
. We also endow
$1_\Lambda \in \{0,1\}^{\Gamma} $
. We also endow
![]() $\operatorname {Sub}(\Gamma )$
with the action of
$\operatorname {Sub}(\Gamma )$
with the action of
![]() $\Gamma $
given by conjugation.
$\Gamma $
given by conjugation.
Given a convex set K, let
![]() $\partial K$
be the set of extreme points of K.
$\partial K$
be the set of extreme points of K.
Proposition 2.6 Let
![]() $\Gamma $
be a countable abelian group and
$\Gamma $
be a countable abelian group and
![]() $\Gamma \!\curvearrowright \! X$
a topologically free action on a compact space X. Given
$\Gamma \!\curvearrowright \! X$
a topologically free action on a compact space X. Given
![]() $\mu \in \partial \mathcal {P}_{\Gamma} (X)$
with full support, we have that
$\mu \in \partial \mathcal {P}_{\Gamma} (X)$
with full support, we have that
![]() $\mu $
is essentially free.
$\mu $
is essentially free.
Proof Suppose that
![]() $\mu (\{x\in X:\Gamma _x\neq \{e\}\})>0$
. The map
$\mu (\{x\in X:\Gamma _x\neq \{e\}\})>0$
. The map
 $$ \begin{align*} S\colon X&\to\operatorname{Sub}(\Gamma)\\ x&\mapsto \Gamma_x \end{align*} $$
$$ \begin{align*} S\colon X&\to\operatorname{Sub}(\Gamma)\\ x&\mapsto \Gamma_x \end{align*} $$
is
![]() $\Gamma $
-invariant and Borel measurable. Since
$\Gamma $
-invariant and Borel measurable. Since
![]() $\Gamma $
is abelian, the action
$\Gamma $
is abelian, the action
![]() $\Gamma \!\curvearrowright \!\operatorname {Sub}(\Gamma )$
is trivial. Given any Borel measurable set
$\Gamma \!\curvearrowright \!\operatorname {Sub}(\Gamma )$
is trivial. Given any Borel measurable set
![]() $U\subseteq \operatorname {Sub}(\Gamma )$
, by ergodicity of
$U\subseteq \operatorname {Sub}(\Gamma )$
, by ergodicity of
![]() $\mu $
we have that
$\mu $
we have that
![]() $S_*\mu (U)=\mu (S^{-1}(U))\in \{0,1\}$
. Thus, there exists
$S_*\mu (U)=\mu (S^{-1}(U))\in \{0,1\}$
. Thus, there exists
![]() $\{e\}\lneq \Lambda \leq \Gamma $
such that
$\{e\}\lneq \Lambda \leq \Gamma $
such that
![]() $S_*\mu =\delta _\Lambda $
, the point-mass measure concentrated at
$S_*\mu =\delta _\Lambda $
, the point-mass measure concentrated at
![]() $\Lambda $
. It follows that
$\Lambda $
. It follows that
![]() $\mu (\{x\in X:\Gamma _x=\Lambda \})=1$
. Since
$\mu (\{x\in X:\Gamma _x=\Lambda \})=1$
. Since
![]() $\mu $
has full support, we have that
$\mu $
has full support, we have that
![]() $\{x\in X:\Gamma _x=\Lambda \}$
is dense. This implies that, for any
$\{x\in X:\Gamma _x=\Lambda \}$
is dense. This implies that, for any
![]() $x\in X$
, it holds that
$x\in X$
, it holds that
![]() $\Lambda \leq \Gamma _x$
. But by topological freeness, there exists
$\Lambda \leq \Gamma _x$
. But by topological freeness, there exists
![]() $x\in X$
such that
$x\in X$
such that
![]() $\Gamma _{x}=\{e\}$
, which gives a contradiction.
$\Gamma _{x}=\{e\}$
, which gives a contradiction.
Given a
![]() $C^*$
-algebra A, we denote by
$C^*$
-algebra A, we denote by
![]() $T(A)$
the set of tracial states on A. We say that
$T(A)$
the set of tracial states on A. We say that
![]() $\tau \in T(A)$
is faithful if, for any
$\tau \in T(A)$
is faithful if, for any
![]() $a\in A\backslash \{0\}$
, we have that
$a\in A\backslash \{0\}$
, we have that
![]() $\tau (a^*a)>0$
.
$\tau (a^*a)>0$
.
Let
![]() $\Gamma $
be an abelian group acting on a compact space X. Given
$\Gamma $
be an abelian group acting on a compact space X. Given
![]() $x\in X$
with finite orbit and
$x\in X$
with finite orbit and
![]() $\chi \in \widehat {\Gamma _x}$
, let
$\chi \in \widehat {\Gamma _x}$
, let
![]() $\tau _{x,\chi }$
be the state on
$\tau _{x,\chi }$
be the state on
![]() $C(X)\rtimes \Gamma $
such that, given
$C(X)\rtimes \Gamma $
such that, given
![]() $f\in C(X)$
and
$f\in C(X)$
and
![]() $g\in \Gamma $
,
$g\in \Gamma $
,
 $$ \begin{align} \tau_{x,\chi}(fu_g)= \begin{cases} \frac{\chi(g)}{|\Gamma x|}\sum_{y\in[x]} f(y), &\text{ if}\ g\in\Gamma_x,\\ 0, &\text{ otherwise.} \end{cases} \end{align} $$
$$ \begin{align} \tau_{x,\chi}(fu_g)= \begin{cases} \frac{\chi(g)}{|\Gamma x|}\sum_{y\in[x]} f(y), &\text{ if}\ g\in\Gamma_x,\\ 0, &\text{ otherwise.} \end{cases} \end{align} $$
The fact that
![]() $\tau _{x,\chi }$
is well defined follows, for example, from [Reference Brown and OzawaBO08, Corollary 2.5.12 and Exercise 4.1.4]. Here, and throughout this paper, we use
$\tau _{x,\chi }$
is well defined follows, for example, from [Reference Brown and OzawaBO08, Corollary 2.5.12 and Exercise 4.1.4]. Here, and throughout this paper, we use
![]() $u_g$
to denote both the canonical unitary in the group C*-algebra
$u_g$
to denote both the canonical unitary in the group C*-algebra
![]() $C_r^*(\Gamma )$
and the canonical unitary in the crossed product
$C_r^*(\Gamma )$
and the canonical unitary in the crossed product
![]() $C(X)\rtimes _r\Gamma $
corresponding to an element
$C(X)\rtimes _r\Gamma $
corresponding to an element
![]() $g\in \Gamma $
.
$g\in \Gamma $
.
Given
![]() $\mu \in \mathcal {P}_{\Gamma} (X)$
, let
$\mu \in \mathcal {P}_{\Gamma} (X)$
, let
![]() $\tau _\mu $
be the state on
$\tau _\mu $
be the state on
![]() $C(X)\rtimes \Gamma $
such that, given
$C(X)\rtimes \Gamma $
such that, given
![]() $f\in C(X)$
and
$f\in C(X)$
and
![]() $g\in \Gamma $
,
$g\in \Gamma $
,
 $$ \begin{align} \tau_\mu(fu_g)= \begin{cases} \int_X f\,d\mu, &\text{if}\ g=e,\\ 0, &\text{otherwise.} \end{cases} \end{align} $$
$$ \begin{align} \tau_\mu(fu_g)= \begin{cases} \int_X f\,d\mu, &\text{if}\ g=e,\\ 0, &\text{otherwise.} \end{cases} \end{align} $$
The following result is an immediate consequence of Propositions 2.3 and 2.6, together with [Reference NeshveyevNes13, Corollary 2.4] (for an alternative approach to Neshveyev’s result, see [Reference Kawamura, Takemoto and TomiyamaKTT90, Theorem 2.7] and the proof of [Reference Becker, Lubotzky and ThomBdlH20, Theorem 12.D.1]).
Proposition 2.7 Let
![]() $\Gamma $
be a countable abelian group, X an infinite, second countable compact space, and
$\Gamma $
be a countable abelian group, X an infinite, second countable compact space, and
![]() $\Gamma \!\curvearrowright \! X$
a faithful and almost minimal action. Then the set
$\Gamma \!\curvearrowright \! X$
a faithful and almost minimal action. Then the set
![]() $\mathcal {C}$
of finite orbits is countable, and there is a bijective correspondence between
$\mathcal {C}$
of finite orbits is countable, and there is a bijective correspondence between
 $$ \begin{align*}\left(\bigsqcup_{ [x]\in \mathcal{C}}\{[x]\}\times\widehat{\Gamma_x}\right)\sqcup\{\mu\in\partial\mathcal{P}_{\Gamma}(X):\mu\text{ has full support}\}\end{align*} $$
$$ \begin{align*}\left(\bigsqcup_{ [x]\in \mathcal{C}}\{[x]\}\times\widehat{\Gamma_x}\right)\sqcup\{\mu\in\partial\mathcal{P}_{\Gamma}(X):\mu\text{ has full support}\}\end{align*} $$
and
![]() $\partial T(C(X)\rtimes \Gamma )$
, which maps
$\partial T(C(X)\rtimes \Gamma )$
, which maps
![]() $\mu \in \partial \mathcal {P}_{\Gamma} (X)$
with full support to
$\mu \in \partial \mathcal {P}_{\Gamma} (X)$
with full support to
![]() $\tau _\mu $
as in (2.2), and, given
$\tau _\mu $
as in (2.2), and, given
![]() $[x]\in \mathcal {C}$
, maps
$[x]\in \mathcal {C}$
, maps
![]() $([x],\chi )\in \{[x]\}\times \widehat {\Gamma _x}$
to
$([x],\chi )\in \{[x]\}\times \widehat {\Gamma _x}$
to
![]() $\tau _{x,\chi }$
as in (2.1).
$\tau _{x,\chi }$
as in (2.1).
3 Some observations on
 $C^*(\mathbb {Z}[1/pq]\rtimes \mathbb {Z}^2)$
$C^*(\mathbb {Z}[1/pq]\rtimes \mathbb {Z}^2)$
3.1 Preliminaries
Fix integers
![]() $p,q\geq 2$
, and let
$p,q\geq 2$
, and let
![]() $\alpha $
be the action of
$\alpha $
be the action of
![]() $\mathbb {Z}^2$
on
$\mathbb {Z}^2$
on
![]() $\mathbb {Z}[\frac {1}{pq}]$
given by
$\mathbb {Z}[\frac {1}{pq}]$
given by
![]() $\alpha _{(n,m)}(x):=p^nq^mx$
, for
$\alpha _{(n,m)}(x):=p^nq^mx$
, for
![]() $n,m\in \mathbb {Z}$
, and
$n,m\in \mathbb {Z}$
, and
![]() $x\in \mathbb {Z}[\frac {1}{pq}]$
. Also, let
$x\in \mathbb {Z}[\frac {1}{pq}]$
. Also, let
and consider the compact abelian group
 $$ \begin{align*} X:=\varprojlim(\mathbb{T},\varphi)=\left\{(x_n)_{n\in\mathbb{Z}_{\geq 0}}\in\prod_{n\in\mathbb{Z}_{\geq 0}}\mathbb{T}:\text{ for all } n\in\mathbb{Z}_{\geq0},x_n=\varphi(x_{n+1})\right\}. \end{align*} $$
$$ \begin{align*} X:=\varprojlim(\mathbb{T},\varphi)=\left\{(x_n)_{n\in\mathbb{Z}_{\geq 0}}\in\prod_{n\in\mathbb{Z}_{\geq 0}}\mathbb{T}:\text{ for all } n\in\mathbb{Z}_{\geq0},x_n=\varphi(x_{n+1})\right\}. \end{align*} $$
There is a homeomorphism (which is also a group isomorphism)
![]() $H\colon \widehat {\mathbb {Z}[\frac {1}{pq}]}\to X$
given by
$H\colon \widehat {\mathbb {Z}[\frac {1}{pq}]}\to X$
given by
 $$ \begin{align} H(\tau):=\left(\tau\left(\frac{1}{(pq)^n}\right)\right)_{n\in\mathbb{Z}_{\geq 0}}, \end{align} $$
$$ \begin{align} H(\tau):=\left(\tau\left(\frac{1}{(pq)^n}\right)\right)_{n\in\mathbb{Z}_{\geq 0}}, \end{align} $$
for
![]() $\tau \in \widehat {\mathbb {Z}[\frac {1}{pq}]}$
(see, for example, the proof of [Reference ScarparoSca20, Lemma 2.3]).
$\tau \in \widehat {\mathbb {Z}[\frac {1}{pq}]}$
(see, for example, the proof of [Reference ScarparoSca20, Lemma 2.3]).
Let
![]() $S\colon X\to X$
be the left shift map and
$S\colon X\to X$
be the left shift map and
![]() $T_p,T_q\colon X\to X$
be the maps given by
$T_p,T_q\colon X\to X$
be the maps given by
![]() $T_p(x):=x^p$
and
$T_p(x):=x^p$
and
![]() $T_q(x):=x^q$
, for
$T_q(x):=x^q$
, for
![]() $x\in X$
. Then
$x\in X$
. Then
![]() $T_p$
and
$T_p$
and
![]() $T_q$
are the continuous group automorphisms of X associated with the multiplication-by-p and the multiplication-by-q automorphisms of
$T_q$
are the continuous group automorphisms of X associated with the multiplication-by-p and the multiplication-by-q automorphisms of
![]() $\mathbb {Z}[\frac {1}{pq}]$
via the homeomorphism H. Moreover,
$\mathbb {Z}[\frac {1}{pq}]$
via the homeomorphism H. Moreover,
![]() $T_p$
and
$T_p$
and
![]() $T_q$
satisfy
$T_q$
satisfy
![]() $T_p^{-1}=ST_q$
and
$T_p^{-1}=ST_q$
and
![]() $T_q^{-1}=ST_p$
. Let
$T_q^{-1}=ST_p$
. Let
![]() $\beta :\mathbb {Z}^2\!\curvearrowright \! X$
be given by
$\beta :\mathbb {Z}^2\!\curvearrowright \! X$
be given by
for
![]() $(r,s)\in \mathbb {Z}^2$
. In particular,
$(r,s)\in \mathbb {Z}^2$
. In particular,
![]() $\beta _{(1,1)}=S$
.
$\beta _{(1,1)}=S$
.
Furthermore, one can easily check that H conjugates
![]() $\widehat {\alpha }\colon \mathbb {Z}^2\!\curvearrowright \! \widehat {\mathbb {Z}[\frac {1}{pq}]}$
with
$\widehat {\alpha }\colon \mathbb {Z}^2\!\curvearrowright \! \widehat {\mathbb {Z}[\frac {1}{pq}]}$
with
![]() $\beta $
, where
$\beta $
, where
![]() $\widehat {\alpha }\colon \mathbb {Z}^2\curvearrowright \widehat {\mathbb {Z}[\frac {1}{pq}]}$
is the action
$\widehat {\alpha }\colon \mathbb {Z}^2\curvearrowright \widehat {\mathbb {Z}[\frac {1}{pq}]}$
is the action
![]() $\widehat {\alpha }_{(r,s)}(\chi ):=\chi \circ \alpha _{(-r,-s)}$
for all
$\widehat {\alpha }_{(r,s)}(\chi ):=\chi \circ \alpha _{(-r,-s)}$
for all
![]() $(r,s)\in \mathbb {Z}^2$
and
$(r,s)\in \mathbb {Z}^2$
and
![]() $\chi \in \widehat {\mathbb {Z}[\frac {1}{pq}]}$
. Hence,
$\chi \in \widehat {\mathbb {Z}[\frac {1}{pq}]}$
. Hence,
![]() $C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)\simeq C(X)\rtimes \mathbb {Z}^2$
.
$C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)\simeq C(X)\rtimes \mathbb {Z}^2$
.
Let
![]() $\varphi _p,\varphi _q\colon \mathbb {T}\to \mathbb {T}$
be given by
$\varphi _p,\varphi _q\colon \mathbb {T}\to \mathbb {T}$
be given by
![]() $\varphi _p(z):=z^p$
and
$\varphi _p(z):=z^p$
and
![]() $\varphi _q(z):=z^q$
, for
$\varphi _q(z):=z^q$
, for
![]() $z\in \mathbb {T}$
, and
$z\in \mathbb {T}$
, and
Given
![]() $i\in \mathbb {Z}_{\geq 0}$
, let
$i\in \mathbb {Z}_{\geq 0}$
, let
![]() $\pi _i\colon X\to \mathbb {T}$
be defined by
$\pi _i\colon X\to \mathbb {T}$
be defined by
![]() $\pi _i((x_n)):=x_i$
, for
$\pi _i((x_n)):=x_i$
, for
![]() $(x_n)\in X$
.
$(x_n)\in X$
.
Proposition 3.1 There is a bijection between closed
![]() $\mathbb {Z}^2$
-invariant subsets
$\mathbb {Z}^2$
-invariant subsets
![]() $F\subseteq X$
and closed sets
$F\subseteq X$
and closed sets
![]() $B\in \mathcal {I}$
, which maps F into
$B\in \mathcal {I}$
, which maps F into
![]() $\pi _0(F)$
. Moreover, a
$\pi _0(F)$
. Moreover, a
![]() $\mathbb {Z}^2$
-invariant subset
$\mathbb {Z}^2$
-invariant subset
![]() $F\subset X$
is finite if and only if
$F\subset X$
is finite if and only if
![]() $\pi _0(F)$
is finite.
$\pi _0(F)$
is finite.
Proof Given
![]() $F\subset X$
closed and
$F\subset X$
closed and
![]() $\mathbb {Z}^2$
-invariant, it follows from the definition of the
$\mathbb {Z}^2$
-invariant, it follows from the definition of the
![]() $\mathbb {Z}^2$
-action in (3.2) that
$\mathbb {Z}^2$
-action in (3.2) that
![]() $\pi _0(F)\in \mathcal {I}$
. Since F is shift-invariant (recall that
$\pi _0(F)\in \mathcal {I}$
. Since F is shift-invariant (recall that
![]() $S=T_p^{-1}T_q^{-1}$
), we also have that
$S=T_p^{-1}T_q^{-1}$
), we also have that
![]() $\pi _0(F)=\pi _n(F)$
for every
$\pi _0(F)=\pi _n(F)$
for every
![]() $n\geq 0$
.
$n\geq 0$
.
We claim that
![]() $F=\left (\prod _{n\geq 0}\pi _n(F)\right )\cap X$
. Clearly,
$F=\left (\prod _{n\geq 0}\pi _n(F)\right )\cap X$
. Clearly,
![]() $F\subset \left (\prod _{n\geq 0}\pi _n(F)\right )\cap X$
. Conversely, given
$F\subset \left (\prod _{n\geq 0}\pi _n(F)\right )\cap X$
. Conversely, given
![]() $x\in \left (\prod _{n\geq 0}\pi _n(F)\right )\cap X$
, for each
$x\in \left (\prod _{n\geq 0}\pi _n(F)\right )\cap X$
, for each
![]() $m\in \mathbb {Z}_{\geq 0}$
there is
$m\in \mathbb {Z}_{\geq 0}$
there is
![]() $y\in F$
such that
$y\in F$
such that
![]() $\pi _n(x)=\pi _n(y)$
for
$\pi _n(x)=\pi _n(y)$
for
![]() $n\leq m$
. Since F is closed, we conclude that
$n\leq m$
. Since F is closed, we conclude that
![]() $x\in F$
, thus showing the claim. In particular,
$x\in F$
, thus showing the claim. In particular,
![]() $F=\left (\prod _{n\geq 0}\pi _0(F)\right )\cap X$
.
$F=\left (\prod _{n\geq 0}\pi _0(F)\right )\cap X$
.
Given
![]() $B\in \mathcal {I}$
, we have that
$B\in \mathcal {I}$
, we have that
![]() $F:=\left (\prod _{n\geq 0}B\right )\cap X$
is closed,
$F:=\left (\prod _{n\geq 0}B\right )\cap X$
is closed,
![]() $\mathbb {Z}^2$
-invariant and
$\mathbb {Z}^2$
-invariant and
![]() $\pi _0(F)=B$
. This concludes the proof of the first claim.
$\pi _0(F)=B$
. This concludes the proof of the first claim.
Suppose
![]() $B:=\pi _0(F)$
is finite. Given
$B:=\pi _0(F)$
is finite. Given
![]() $z\in B$
, since
$z\in B$
, since
![]() $B=B^{pq}$
and B is finite, there is a unique
$B=B^{pq}$
and B is finite, there is a unique
![]() $w\in B$
such that
$w\in B$
such that
![]() $w^{pq}=z$
. This shows that any
$w^{pq}=z$
. This shows that any
![]() $x\in F$
is uniquely determined by
$x\in F$
is uniquely determined by
![]() $\pi _0(x)$
. Therefore,
$\pi _0(x)$
. Therefore,
![]() $|B|=|F|$
.
$|B|=|F|$
.
Recall that integers
![]() $p,q\geq 2$
are said to be multiplicatively independent if
$p,q\geq 2$
are said to be multiplicatively independent if
![]() $p^r\neq q^s$
for all
$p^r\neq q^s$
for all
![]() $r,s\in \mathbb {Z}_{>0}$
. Furstenberg’s theorem [Reference FurstenbergFur67, Part IV] and Proposition 3.1 imply that
$r,s\in \mathbb {Z}_{>0}$
. Furstenberg’s theorem [Reference FurstenbergFur67, Part IV] and Proposition 3.1 imply that
![]() $\mathbb {Z}^2\!\curvearrowright \! X$
is almost minimal. By [Reference ScarparoSca20, Lemma 2.2] (or Proposition 2.3),
$\mathbb {Z}^2\!\curvearrowright \! X$
is almost minimal. By [Reference ScarparoSca20, Lemma 2.2] (or Proposition 2.3),
![]() $\mathbb {Z}^2\!\curvearrowright \! X$
is topologically free. For future reference, let us record these facts in the following result.
$\mathbb {Z}^2\!\curvearrowright \! X$
is topologically free. For future reference, let us record these facts in the following result.
Lemma 3.2 Let
![]() $p,q\geq 2$
be multiplicatively independent integers. Then
$p,q\geq 2$
be multiplicatively independent integers. Then
![]() $\mathbb {Z}^2\!\curvearrowright \! X$
is almost minimal and topologically free.
$\mathbb {Z}^2\!\curvearrowright \! X$
is almost minimal and topologically free.
Let
![]() $\mathcal {O}$
be the set of finite minimal (among the nonempty sets) elements of
$\mathcal {O}$
be the set of finite minimal (among the nonempty sets) elements of
![]() $\mathcal {I}$
. Notice that
$\mathcal {I}$
. Notice that
![]() $\mathcal {O}$
is in one-to-one correspondence with the set of finite orbits of
$\mathcal {O}$
is in one-to-one correspondence with the set of finite orbits of
![]() $\mathbb {Z}^2\!\curvearrowright \! X$
. For any
$\mathbb {Z}^2\!\curvearrowright \! X$
. For any
![]() $r\in \mathbb {Z}_{>0}$
coprime with p and q, we have that
$r\in \mathbb {Z}_{>0}$
coprime with p and q, we have that
![]() $\{e^{\frac {2\pi i}{r}}:1\leq i<r\}\in \mathcal {I}$
. In particular,
$\{e^{\frac {2\pi i}{r}}:1\leq i<r\}\in \mathcal {I}$
. In particular,
![]() $\mathcal {O}$
is infinite. The following is an immediate consequence of Lemma 3.2, Theorem 2.4, and the isomorphism
$\mathcal {O}$
is infinite. The following is an immediate consequence of Lemma 3.2, Theorem 2.4, and the isomorphism
![]() $C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)\simeq C(X)\rtimes \mathbb {Z}^2$
. Note that if a point of X has finite
$C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)\simeq C(X)\rtimes \mathbb {Z}^2$
. Note that if a point of X has finite
![]() $\mathbb {Z}^2$
-orbit, then its stabilizer subgroup is of finite index in
$\mathbb {Z}^2$
-orbit, then its stabilizer subgroup is of finite index in
![]() $\mathbb {Z}^2$
and is thus isomorphic to
$\mathbb {Z}^2$
and is thus isomorphic to
![]() $\mathbb {Z}^2$
.
$\mathbb {Z}^2$
.
Theorem 3.3 Let
![]() $p ,q\geq 2$
be multiplicatively independent integers. Then the primitive ideal space of
$p ,q\geq 2$
be multiplicatively independent integers. Then the primitive ideal space of
![]() $C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
is homeomorphic to
$C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
is homeomorphic to
where the closed subsets of P are P and finite unions of elements of the collection
![]() $\{\{B\}\times F:B\in \mathcal {O},\ F\text { a closed subset of}\ \mathbb {T}^2\}$
.
$\{\{B\}\times F:B\in \mathcal {O},\ F\text { a closed subset of}\ \mathbb {T}^2\}$
.
Let
![]() $\mathcal {P}_{p,q}(\mathbb {T})$
be the set of regular probability measures
$\mathcal {P}_{p,q}(\mathbb {T})$
be the set of regular probability measures
![]() $\mu $
on
$\mu $
on
![]() $\mathbb {T}$
such that
$\mathbb {T}$
such that
![]() $(\varphi _p)_*\mu =(\varphi _q)_*\mu =\mu $
. Since
$(\varphi _p)_*\mu =(\varphi _q)_*\mu =\mu $
. Since
![]() $\varphi _{p}\circ \pi _0=\pi _0\circ T_p$
and
$\varphi _{p}\circ \pi _0=\pi _0\circ T_p$
and
![]() $\varphi _q\circ \pi _0=\pi _0\circ T_q$
, it follows that
$\varphi _q\circ \pi _0=\pi _0\circ T_q$
, it follows that
![]() $(\pi _0)_*\colon \mathcal {P}_{\mathbb {Z}^2}(X)\to \mathcal {P}_{p,q}(\mathbb {T})$
is a well-defined affine map. The following result is known (see [Reference Huang and WuHW17, Proposition 4.1]), but for the reader’s convenience, we provide a different proof.
$(\pi _0)_*\colon \mathcal {P}_{\mathbb {Z}^2}(X)\to \mathcal {P}_{p,q}(\mathbb {T})$
is a well-defined affine map. The following result is known (see [Reference Huang and WuHW17, Proposition 4.1]), but for the reader’s convenience, we provide a different proof.
Lemma 3.4 The map
![]() $(\pi _0)_*\colon \mathcal {P}_{\mathbb {Z}^2}(X)\to \mathcal {P}_{p,q}(\mathbb {T})$
is an affine isomorphism.
$(\pi _0)_*\colon \mathcal {P}_{\mathbb {Z}^2}(X)\to \mathcal {P}_{p,q}(\mathbb {T})$
is an affine isomorphism.
Proof We will show that
![]() $(\pi _0)_*$
is bijective by constructing an inverse. Given
$(\pi _0)_*$
is bijective by constructing an inverse. Given
![]() $n\in \mathbb {Z}_{\geq 0}$
, let
$n\in \mathbb {Z}_{\geq 0}$
, let
![]() $\pi _n^*\colon C(\mathbb {T})\to C(X)$
be the adjoint map given by
$\pi _n^*\colon C(\mathbb {T})\to C(X)$
be the adjoint map given by
![]() $\pi _n^*(f):=f\circ \pi _n$
for
$\pi _n^*(f):=f\circ \pi _n$
for
![]() $f\in C(\mathbb {T})$
, and
$f\in C(\mathbb {T})$
, and
![]() $A_n:=\pi _n^*(C(\mathbb {T}))$
. Notice that
$A_n:=\pi _n^*(C(\mathbb {T}))$
. Notice that
![]() $\pi _n^*$
is injective. For every
$\pi _n^*$
is injective. For every
![]() $n\in \mathbb {Z}_{\geq 0}$
, we have that
$n\in \mathbb {Z}_{\geq 0}$
, we have that
In particular,
![]() $A_n\subseteq A_{n+1}$
.
$A_n\subseteq A_{n+1}$
.
Fix
![]() $\mu \in \mathcal {P}_{p,q}(\mathbb {T})$
. By (3.3) and the invariance of
$\mu \in \mathcal {P}_{p,q}(\mathbb {T})$
. By (3.3) and the invariance of
![]() $\mu $
, there exists a bounded, positive, and unital linear functional
$\mu $
, there exists a bounded, positive, and unital linear functional
![]() $\sigma $
on
$\sigma $
on
![]() $\bigcup _{n\in \mathbb {Z}_{\geq 0}}A_n$
such that, for
$\bigcup _{n\in \mathbb {Z}_{\geq 0}}A_n$
such that, for
![]() $f\in C(\mathbb {T})$
and
$f\in C(\mathbb {T})$
and
![]() $n\in \mathbb {Z}_{\geq 0}$
, we have that
$n\in \mathbb {Z}_{\geq 0}$
, we have that
![]() $\sigma (\pi _n^*(f))=\int f\,d\mu $
. Since
$\sigma (\pi _n^*(f))=\int f\,d\mu $
. Since
![]() $C(X)=\overline {\bigcup _{n\in \mathbb {Z}_{\geq 0}}A_n}$
, we can extend
$C(X)=\overline {\bigcup _{n\in \mathbb {Z}_{\geq 0}}A_n}$
, we can extend
![]() $\sigma $
to a state on
$\sigma $
to a state on
![]() $C(X)$
. Let
$C(X)$
. Let
![]() $\psi (\mu )\in \mathcal {P}(X)$
be the measure corresponding to
$\psi (\mu )\in \mathcal {P}(X)$
be the measure corresponding to
![]() $\sigma $
. By
$\sigma $
. By
![]() $\times p,\times q$
-invariance of
$\times p,\times q$
-invariance of
![]() $\mu $
, we have that
$\mu $
, we have that
![]() $\psi (\mu )$
is
$\psi (\mu )$
is
![]() $\mathbb {Z}^2$
-invariant.
$\mathbb {Z}^2$
-invariant.
By
![]() $T_p,T_q$
-invariance, we have that
$T_p,T_q$
-invariance, we have that
![]() $(\pi _n)_*|_{\mathcal {P}_{\mathbb {Z}^2}(X)}=(\pi _0)_*|_{\mathcal {P}_{\mathbb {Z}^2}(X)}$
for any
$(\pi _n)_*|_{\mathcal {P}_{\mathbb {Z}^2}(X)}=(\pi _0)_*|_{\mathcal {P}_{\mathbb {Z}^2}(X)}$
for any
![]() $n\geq 0$
. This shows that any
$n\geq 0$
. This shows that any
![]() $\nu \in \mathcal {P}_{\mathbb {Z}^2}$
is uniquely determined by its restriction to
$\nu \in \mathcal {P}_{\mathbb {Z}^2}$
is uniquely determined by its restriction to
![]() $A_0$
. Using this fact, it is easy to check that
$A_0$
. Using this fact, it is easy to check that
![]() $\psi \colon \mathcal {P}_{p,q}(\mathbb {T})\to \mathcal {P}_{\mathbb {Z}^2}(X) $
is an inverse for
$\psi \colon \mathcal {P}_{p,q}(\mathbb {T})\to \mathcal {P}_{\mathbb {Z}^2}(X) $
is an inverse for
![]() $(\pi _0)_*|_{\mathcal {P}_{\mathbb {Z}^2}(X)}$
.
$(\pi _0)_*|_{\mathcal {P}_{\mathbb {Z}^2}(X)}$
.
Let
![]() $\mathrm {Ev}\colon C^*(\mathbb {Z}[\frac {1}{pq}])\to C(\widehat {\mathbb {Z}[\frac {1}{pq}]})$
be the isomorphism given by point evaluation, that is, given
$\mathrm {Ev}\colon C^*(\mathbb {Z}[\frac {1}{pq}])\to C(\widehat {\mathbb {Z}[\frac {1}{pq}]})$
be the isomorphism given by point evaluation, that is, given
![]() $g\in \mathbb {Z}[\frac {1}{pq}]$
and
$g\in \mathbb {Z}[\frac {1}{pq}]$
and
![]() $\chi \in \widehat {\mathbb {Z}[\frac {1}{pq}]}$
, we have that
$\chi \in \widehat {\mathbb {Z}[\frac {1}{pq}]}$
, we have that
![]() $\mathrm {Ev}(u_g)(\chi )=\chi (g)$
. One can easily check that
$\mathrm {Ev}(u_g)(\chi )=\chi (g)$
. One can easily check that
![]() $\mathrm {Ev}$
conjugates the canonical actions
$\mathrm {Ev}$
conjugates the canonical actions
![]() $\mathbb {Z}^2\!\curvearrowright \! C^*(\mathbb {Z}[\frac {1}{pq}])$
and
$\mathbb {Z}^2\!\curvearrowright \! C^*(\mathbb {Z}[\frac {1}{pq}])$
and
![]() $\mathbb {Z}^2\!\curvearrowright \! C(\widehat {\mathbb {Z}[\frac {1}{pq}]})$
.
$\mathbb {Z}^2\!\curvearrowright \! C(\widehat {\mathbb {Z}[\frac {1}{pq}]})$
.
Proposition 3.5 Let
![]() $p ,q\geq 2$
be multiplicatively independent integers. Then there is a bijection between
$p ,q\geq 2$
be multiplicatively independent integers. Then there is a bijection between
![]() $\partial T(C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2))$
and
$\partial T(C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2))$
and
as in Proposition 2.7. This bijection takes the non-faithful tracial states into
![]() $\mathcal {O}\times \mathbb {T}^2$
, and takes each faithful tracial state
$\mathcal {O}\times \mathbb {T}^2$
, and takes each faithful tracial state
![]() $\tau $
to
$\tau $
to
![]() $\mu \in \partial \mathcal {P}_{p,q}(\mathbb {T})$
with full support such that, for
$\mu \in \partial \mathcal {P}_{p,q}(\mathbb {T})$
with full support such that, for
![]() $n\in \mathbb {Z},$
$n\in \mathbb {Z},$
Proof Identify
![]() $C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
with
$C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
with
![]() $C(X)\rtimes \mathbb {Z}^2$
. Notice that the tracial states in (2.1) are not faithful, whereas, given
$C(X)\rtimes \mathbb {Z}^2$
. Notice that the tracial states in (2.1) are not faithful, whereas, given
![]() $\mu \in \mathcal {P}_{\mathbb {Z}^2}(X)$
with full support, the tracial states as in (2.2) are faithful. Together with Proposition 2.7, this shows the first claims.
$\mu \in \mathcal {P}_{\mathbb {Z}^2}(X)$
with full support, the tracial states as in (2.2) are faithful. Together with Proposition 2.7, this shows the first claims.
Let us prove (3.4). Identify
![]() $C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
with
$C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
with
![]() $C^*(\mathbb {Z}[\frac {1}{pq}])\rtimes \mathbb {Z}^2$
. By Proposition 2.7, there exists
$C^*(\mathbb {Z}[\frac {1}{pq}])\rtimes \mathbb {Z}^2$
. By Proposition 2.7, there exists
![]() $\nu \in \partial \mathcal {P}_{\mathbb {Z}^2}(X)$
with full support such that
$\nu \in \partial \mathcal {P}_{\mathbb {Z}^2}(X)$
with full support such that
for any
![]() $f\in C(X)$
. Let
$f\in C(X)$
. Let
![]() $\mu :=(\pi _0)_*(\nu )$
. Given
$\mu :=(\pi _0)_*(\nu )$
. Given
![]() $n\in \mathbb {Z}$
, we have that
$n\in \mathbb {Z}$
, we have that
Given
![]() $\chi \in \widehat {\mathbb {Z}[\frac {1}{pq}]}$
, we also have that
$\chi \in \widehat {\mathbb {Z}[\frac {1}{pq}]}$
, we also have that
![]() $H(\chi )_0^n=\chi (n)=\mathrm {Ev}(u_n)(\chi )$
(here, H is the isomorphism defined in (3.1)). Together with (3.5) and (3.6), this concludes the proof of (3.4).
$H(\chi )_0^n=\chi (n)=\mathrm {Ev}(u_n)(\chi )$
(here, H is the isomorphism defined in (3.1)). Together with (3.5) and (3.6), this concludes the proof of (3.4).
3.2 Tracial states
A group
![]() $\Gamma $
is said to be icc if the conjugacy class of any
$\Gamma $
is said to be icc if the conjugacy class of any
![]() $g\in \Gamma \backslash \{e\}$
is infinite. Here, icc stands for infinite conjugacy classes.
$g\in \Gamma \backslash \{e\}$
is infinite. Here, icc stands for infinite conjugacy classes.
The canonical trace on
![]() $C^*_r(\Gamma )$
is the faithful tracial state
$C^*_r(\Gamma )$
is the faithful tracial state
![]() $\tau $
on
$\tau $
on
![]() $C^*_r(\Gamma )$
which satisfies
$C^*_r(\Gamma )$
which satisfies
![]() $\tau (u_g)=0$
for all
$\tau (u_g)=0$
for all
![]() $g\in \Gamma \backslash \{e\}$
. Recall that
$g\in \Gamma \backslash \{e\}$
. Recall that
![]() $\Gamma $
is icc if and only if the canonical trace is an extreme tracial state on
$\Gamma $
is icc if and only if the canonical trace is an extreme tracial state on
![]() $C^*_r(\Gamma )$
[Reference Becker, Lubotzky and ThomBdlH20, Propositions 7.A.1 and 11.C.3].
$C^*_r(\Gamma )$
[Reference Becker, Lubotzky and ThomBdlH20, Propositions 7.A.1 and 11.C.3].
Lemma 3.6 Let
![]() $p,q\geq 2$
be multiplicatively independent integers. Then
$p,q\geq 2$
be multiplicatively independent integers. Then
![]() $\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2$
is icc.
$\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2$
is icc.
Proof Given
![]() $x\in \mathbb {Z}[\frac {1}{pq}]\backslash \{0\}$
,
$x\in \mathbb {Z}[\frac {1}{pq}]\backslash \{0\}$
,
![]() $y\in \mathbb {Z}^2$
and
$y\in \mathbb {Z}^2$
and
![]() $n\in \mathbb {Z}$
, we have that
$n\in \mathbb {Z}$
, we have that
Therefore, the conjugacy class of
![]() $(x,y)$
is infinite.
$(x,y)$
is infinite.
Given
![]() $(m,n)\in \mathbb {Z}^2\backslash \{0,0\}$
and
$(m,n)\in \mathbb {Z}^2\backslash \{0,0\}$
and
![]() $x\in \mathbb {Z}[\frac {1}{pq}]$
, we have that
$x\in \mathbb {Z}[\frac {1}{pq}]$
, we have that
From multiplicative independence of p and q, we conclude that the conjugacy class of
![]() $(0,m,n)$
is infinite as well.
$(0,m,n)$
is infinite as well.
Since the canonical trace corresponds to the Lebesgue measure on
![]() $\mathbb {T}$
under the bijection of Proposition 3.5, the following holds.
$\mathbb {T}$
under the bijection of Proposition 3.5, the following holds.
Corollary 3.7 Let
![]() $p,q\geq 2$
be multiplicatively independent integers. Then the canonical trace is the only faithful extreme tracial state on
$p,q\geq 2$
be multiplicatively independent integers. Then the canonical trace is the only faithful extreme tracial state on
![]() $C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
if and only if Furstenberg’s
$C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$
if and only if Furstenberg’s
![]() $\times p,\times q$
conjecture holds.
$\times p,\times q$
conjecture holds.
For the purpose of the following discussion, let us say that an icc group
![]() $\Gamma $
has the weak unique trace property if the canonical trace is the only faithful extreme tracial state on
$\Gamma $
has the weak unique trace property if the canonical trace is the only faithful extreme tracial state on
![]() $C^*_r(\Gamma )$
and is weakly
$C^*_r(\Gamma )$
and is weakly
![]() $C^*$
-simple if every nonzero ideal
$C^*$
-simple if every nonzero ideal
![]() $I\unlhd C^*_r(\Gamma )$
intersects
$I\unlhd C^*_r(\Gamma )$
intersects
![]() $\mathbb {C}\Gamma $
non-trivially. In [Reference ScarparoSca20], it was shown that, for
$\mathbb {C}\Gamma $
non-trivially. In [Reference ScarparoSca20], it was shown that, for
![]() $p,q\geq 2$
multiplicatively independent integers,
$p,q\geq 2$
multiplicatively independent integers,
![]() $\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2$
is weakly
$\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2$
is weakly
![]() $C^*$
-simple. Furthermore, Corollary 3.7 can be rephrased as saying that Furstenberg’s
$C^*$
-simple. Furthermore, Corollary 3.7 can be rephrased as saying that Furstenberg’s
![]() $\times p,\times q$
conjecture holds if and only if
$\times p,\times q$
conjecture holds if and only if
![]() $\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2$
has the weak unique trace property.
$\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2$
has the weak unique trace property.
Since
![]() $C^*$
-simplicity implies the unique trace property by [Reference BerendBKKO17, Corollary 4.3], one could naively wonder whether weak
$C^*$
-simplicity implies the unique trace property by [Reference BerendBKKO17, Corollary 4.3], one could naively wonder whether weak
![]() $C^*$
-simplicity implies the weak unique trace property (by the above, if this were true, it would imply Furstenberg’s conjecture). Unfortunately, this does not hold in general, as the following example shows.
$C^*$
-simplicity implies the weak unique trace property (by the above, if this were true, it would imply Furstenberg’s conjecture). Unfortunately, this does not hold in general, as the following example shows.
Example 3.8 It was observed by Ozawa that the lamplighter group
![]() $\mathbb {Z}_2\wr \mathbb {Z}$
is weakly
$\mathbb {Z}_2\wr \mathbb {Z}$
is weakly
![]() $C^*$
-simple [Reference AlekseevAle19]. We claim that
$C^*$
-simple [Reference AlekseevAle19]. We claim that
![]() $\mathbb {Z}_2\wr \mathbb {Z}$
does not have the weak unique trace property. Given
$\mathbb {Z}_2\wr \mathbb {Z}$
does not have the weak unique trace property. Given
![]() $t\in (0,1)$
, let
$t\in (0,1)$
, let
![]() $\mu _t:=\prod _{\mathbb {Z}}(t\delta _0+(1-t)\delta _1)\in \partial \mathcal {P}_{\mathbb {Z}}(\{0,1\}^{\mathbb {Z}})$
. Since
$\mu _t:=\prod _{\mathbb {Z}}(t\delta _0+(1-t)\delta _1)\in \partial \mathcal {P}_{\mathbb {Z}}(\{0,1\}^{\mathbb {Z}})$
. Since
![]() $\mu _t$
has full support, it follows from [Reference NeshveyevNes13, Corollary 2.4] that
$\mu _t$
has full support, it follows from [Reference NeshveyevNes13, Corollary 2.4] that
![]() $\mu _t$
gives rise to a faithful extreme tracial state on
$\mu _t$
gives rise to a faithful extreme tracial state on
![]() $C^*(\mathbb {Z}_2\wr \mathbb {Z})\simeq C(\{0,1\}^{\mathbb {Z}})\rtimes \mathbb {Z}$
(this has been observed independently by Vaes in [Reference VaesVae]).
$C^*(\mathbb {Z}_2\wr \mathbb {Z})\simeq C(\{0,1\}^{\mathbb {Z}})\rtimes \mathbb {Z}$
(this has been observed independently by Vaes in [Reference VaesVae]).
3.3 K-theory
Given an automorphism
![]() $\alpha $
on a
$\alpha $
on a
![]() $C^*$
-algebra A, let
$C^*$
-algebra A, let
![]() $\iota \colon A\to A\rtimes \mathbb {Z}$
be the canonical embedding. The Pimsner–Voiculescu sequence is the following exact sequence (see, for instance, [Reference Pooya and ValettePV80]):
$\iota \colon A\to A\rtimes \mathbb {Z}$
be the canonical embedding. The Pimsner–Voiculescu sequence is the following exact sequence (see, for instance, [Reference Pooya and ValettePV80]):

We provide the proof of the following simple lemma for the reader’s convenience.
Lemma 3.9 Let
![]() $m\leq n$
be positive integers and
$m\leq n$
be positive integers and
![]() $\psi $
be the endomorphism on
$\psi $
be the endomorphism on
![]() $\frac {\mathbb {Z}}{n\mathbb {Z}}$
given by
$\frac {\mathbb {Z}}{n\mathbb {Z}}$
given by
![]() $\psi (x):=mx$
, for
$\psi (x):=mx$
, for
![]() $x\in \frac {\mathbb {Z}}{n\mathbb {Z}}$
. Then
$x\in \frac {\mathbb {Z}}{n\mathbb {Z}}$
. Then
![]() $\ker (\psi )\simeq \frac {\frac {\mathbb {Z}}{n\mathbb {Z}}}{\operatorname {\mathrm {im}}\psi }\simeq \frac {\mathbb {Z}}{\gcd (m,n)\mathbb {Z}}$
.
$\ker (\psi )\simeq \frac {\frac {\mathbb {Z}}{n\mathbb {Z}}}{\operatorname {\mathrm {im}}\psi }\simeq \frac {\mathbb {Z}}{\gcd (m,n)\mathbb {Z}}$
.
Proof Clearly,
![]() $\operatorname {\mathrm {im}}\psi =\gcd (m,n)\frac {\mathbb {Z}}{n\mathbb {Z}}\simeq \frac {\mathbb {Z}}{\frac {n}{gcd(m,n)}\mathbb {Z}}.$
The result then follows from cardinality arguments.
$\operatorname {\mathrm {im}}\psi =\gcd (m,n)\frac {\mathbb {Z}}{n\mathbb {Z}}\simeq \frac {\mathbb {Z}}{\frac {n}{gcd(m,n)}\mathbb {Z}}.$
The result then follows from cardinality arguments.
Theorem 3.10 Let
![]() $p,q\geq 2$
be integers. For
$p,q\geq 2$
be integers. For
![]() $i=0,1$
, we have
$i=0,1$
, we have
 $$ \begin{align*}K_i(C^*(\mathbb{Z}[1/pq]\rtimes\mathbb{Z}^2))\simeq\mathbb{Z}^2\oplus\frac{\mathbb{Z}}{\gcd(p-1,q-1)\mathbb{Z}}.\end{align*} $$
$$ \begin{align*}K_i(C^*(\mathbb{Z}[1/pq]\rtimes\mathbb{Z}^2))\simeq\mathbb{Z}^2\oplus\frac{\mathbb{Z}}{\gcd(p-1,q-1)\mathbb{Z}}.\end{align*} $$
Proof Let
![]() $\eta \colon \mathbb {Z}\!\curvearrowright \!\mathbb {Z}[\frac {1}{pq}]$
be given by multiplication by
$\eta \colon \mathbb {Z}\!\curvearrowright \!\mathbb {Z}[\frac {1}{pq}]$
be given by multiplication by
![]() $pq$
and
$pq$
and
![]() $\gamma \colon \mathbb {Z}\!\curvearrowright \!\mathbb {Z}[\frac {1}{pq}]\rtimes _\eta \mathbb {Z}$
be given by
$\gamma \colon \mathbb {Z}\!\curvearrowright \!\mathbb {Z}[\frac {1}{pq}]\rtimes _\eta \mathbb {Z}$
be given by
![]() $\gamma _n(x,z):=(p^nx,z)$
, for
$\gamma _n(x,z):=(p^nx,z)$
, for
![]() $(x,z)\in \mathbb {Z}[\frac {1}{pq}]\rtimes _\eta \mathbb {Z}$
. Notice that
$(x,z)\in \mathbb {Z}[\frac {1}{pq}]\rtimes _\eta \mathbb {Z}$
. Notice that
 $$ \begin{align*} \mathbb{Z}[1/pq]\rtimes\mathbb{Z}^2&\to(\mathbb{Z}[1/pq]\rtimes_\eta\mathbb{Z})\rtimes_\gamma\mathbb{Z}\\ (x,m,n)&\mapsto(x,n,m-n) \end{align*} $$
$$ \begin{align*} \mathbb{Z}[1/pq]\rtimes\mathbb{Z}^2&\to(\mathbb{Z}[1/pq]\rtimes_\eta\mathbb{Z})\rtimes_\gamma\mathbb{Z}\\ (x,m,n)&\mapsto(x,n,m-n) \end{align*} $$
is an isomorphism.
Let
![]() $A:=C^*(\mathbb {Z}[1/pq]\rtimes _\eta \mathbb {Z})$
. Using the fact that
$A:=C^*(\mathbb {Z}[1/pq]\rtimes _\eta \mathbb {Z})$
. Using the fact that
![]() $\mathbb {Z}[1/pq]\rtimes _\eta \mathbb {Z}$
is isomorphic to the Baumslag–Solitar group
$\mathbb {Z}[1/pq]\rtimes _\eta \mathbb {Z}$
is isomorphic to the Baumslag–Solitar group
![]() $BS(1,pq)$
, it follows from [Reference Pimsner and VoiculescuPV18, Theorem 1] that
$BS(1,pq)$
, it follows from [Reference Pimsner and VoiculescuPV18, Theorem 1] that
![]() $K_0(A)=\mathbb {Z}[1_A]$
(an infinite cyclic group generated by
$K_0(A)=\mathbb {Z}[1_A]$
(an infinite cyclic group generated by
![]() $[1_A]$
), and
$[1_A]$
), and
![]() $K_1(A)=\mathbb {Z}\oplus \frac {\mathbb {Z}}{(pq-1)\mathbb {Z}}$
, with generators
$K_1(A)=\mathbb {Z}\oplus \frac {\mathbb {Z}}{(pq-1)\mathbb {Z}}$
, with generators
![]() $[u_{(0,1)}]_1$
of infinite order and
$[u_{(0,1)}]_1$
of infinite order and
![]() $[u_{(1,0)}]_1$
of order
$[u_{(1,0)}]_1$
of order
![]() $pq-1$
.
$pq-1$
.
Consider the Pimsner–Voiculescu sequence associated with
![]() $\tilde {\gamma }\colon \mathbb {Z}\!\curvearrowright \! A$
, where
$\tilde {\gamma }\colon \mathbb {Z}\!\curvearrowright \! A$
, where
![]() $\tilde {\gamma }$
is the action induced by
$\tilde {\gamma }$
is the action induced by
![]() $\gamma $
. Surjectivity of
$\gamma $
. Surjectivity of
![]() $\partial _1$
follows from [Reference Pimsner and VoiculescuPV18, Lemma 2]. Moreover,
$\partial _1$
follows from [Reference Pimsner and VoiculescuPV18, Lemma 2]. Moreover,
![]() $\mathrm {id}-\tilde {\gamma }_*\colon K_0(A)\to K_0(A)$
is
$\mathrm {id}-\tilde {\gamma }_*\colon K_0(A)\to K_0(A)$
is
![]() $0$
. Therefore, the following sequence is exact:
$0$
. Therefore, the following sequence is exact:

For
![]() $(x,y)\in \mathbb {Z}\oplus \frac {\mathbb {Z}}{(1-pq)\mathbb {Z}}$
, we have that
$(x,y)\in \mathbb {Z}\oplus \frac {\mathbb {Z}}{(1-pq)\mathbb {Z}}$
, we have that
![]() $(\tilde {\gamma }_*-\mathrm {id})(x,y)=(0,(p-1)y)$
. In particular, by Lemma 3.9, we have that
$(\tilde {\gamma }_*-\mathrm {id})(x,y)=(0,(p-1)y)$
. In particular, by Lemma 3.9, we have that
 $$ \begin{align*}\frac{\mathbb{Z}\oplus\frac{\mathbb{Z}}{(1-pq)\mathbb{Z}}}{\operatorname{\mathrm{im}}(\mathrm{id}-\tilde{\gamma}_*)}\simeq\mathbb{Z}\oplus\frac{\mathbb{Z}}{\gcd(1-pq,p-1)\mathbb{Z}}=\mathbb{Z}\oplus\frac{\mathbb{Z}}{\gcd(p-1,q-1)\mathbb{Z}}.\end{align*} $$
$$ \begin{align*}\frac{\mathbb{Z}\oplus\frac{\mathbb{Z}}{(1-pq)\mathbb{Z}}}{\operatorname{\mathrm{im}}(\mathrm{id}-\tilde{\gamma}_*)}\simeq\mathbb{Z}\oplus\frac{\mathbb{Z}}{\gcd(1-pq,p-1)\mathbb{Z}}=\mathbb{Z}\oplus\frac{\mathbb{Z}}{\gcd(p-1,q-1)\mathbb{Z}}.\end{align*} $$
This finishes the computation of
![]() $K_1(C^*(\mathbb {Z}[1/pq]\rtimes \mathbb {Z}^2))$
.
$K_1(C^*(\mathbb {Z}[1/pq]\rtimes \mathbb {Z}^2))$
.
By Lemma 3.9 again, we also have that
![]() $\ker (\mathrm {id}-\tilde {\gamma }_*)\simeq \mathbb {Z}\oplus \frac {\mathbb {Z}}{\gcd (p-1,q-1)\mathbb {Z}}$
.
$\ker (\mathrm {id}-\tilde {\gamma }_*)\simeq \mathbb {Z}\oplus \frac {\mathbb {Z}}{\gcd (p-1,q-1)\mathbb {Z}}$
.
Let
![]() $\tau \colon A\rtimes _{\tilde {\gamma }}\mathbb {Z}\cong C^*(\mathbb {Z}[1/pq]\rtimes \mathbb {Z}^2)\to \mathbb {C}$
be the unital
$\tau \colon A\rtimes _{\tilde {\gamma }}\mathbb {Z}\cong C^*(\mathbb {Z}[1/pq]\rtimes \mathbb {Z}^2)\to \mathbb {C}$
be the unital
![]() $*$
-homomorphism associated with the trivial representation of
$*$
-homomorphism associated with the trivial representation of
![]() $\mathbb {Z}[1/pq]\rtimes \mathbb {Z}^2$
. By identifying
$\mathbb {Z}[1/pq]\rtimes \mathbb {Z}^2$
. By identifying
![]() $K_0(\mathbb {C})$
with
$K_0(\mathbb {C})$
with
![]() $\mathbb {Z}$
, we obtain that
$\mathbb {Z}$
, we obtain that
![]() $K_0(\tau )\circ \iota _*=\mathrm {id}_{\mathbb {Z}}$
, and the short exact sequence
$K_0(\tau )\circ \iota _*=\mathrm {id}_{\mathbb {Z}}$
, and the short exact sequence
left splits. This concludes the proof.
Example 3.11 Given integers
![]() $p,q\geq 2$
, let
$p,q\geq 2$
, let
![]() $\alpha ^{p,q}\colon \mathbb {Z}^2\!\curvearrowright \!\mathbb {Z}[\frac {1}{pq}]$
be given by multiplication by p and q. For
$\alpha ^{p,q}\colon \mathbb {Z}^2\!\curvearrowright \!\mathbb {Z}[\frac {1}{pq}]$
be given by multiplication by p and q. For
![]() $i=0,1$
, we have
$i=0,1$
, we have
 $$ \begin{align*} K_i(C^*(\mathbb{Z}[1/6]\rtimes_{\alpha^{2,3}}\mathbb{Z}^2))&\simeq\mathbb{Z}^2,\\ K_i(C^*(\mathbb{Z}[1/15]\rtimes_{\alpha^{3,5}}\mathbb{Z}^2))&\simeq\mathbb{Z}^2\oplus\mathbb{Z}_2. \end{align*} $$
$$ \begin{align*} K_i(C^*(\mathbb{Z}[1/6]\rtimes_{\alpha^{2,3}}\mathbb{Z}^2))&\simeq\mathbb{Z}^2,\\ K_i(C^*(\mathbb{Z}[1/15]\rtimes_{\alpha^{3,5}}\mathbb{Z}^2))&\simeq\mathbb{Z}^2\oplus\mathbb{Z}_2. \end{align*} $$
4 Questions
Let us conclude by posing a few questions that arise naturally in light of our results.
Given multiplicatively independent integers
![]() $p,q\geq 2$
, we know that the group
$p,q\geq 2$
, we know that the group
![]() $\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2$
is weakly
$\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2$
is weakly
![]() $C^*$
-simple by [Reference ScarparoSca20], and that it has the weak unique trace property if and only if Furstenberg’s conjecture is true by Corollary 3.7 (this terminology is defined in the discussion following Corollary 3.7). We have also seen in Example 3.8 that
$C^*$
-simple by [Reference ScarparoSca20], and that it has the weak unique trace property if and only if Furstenberg’s conjecture is true by Corollary 3.7 (this terminology is defined in the discussion following Corollary 3.7). We have also seen in Example 3.8 that
![]() $\mathbb {Z}_2\wr \mathbb {Z}$
is weakly
$\mathbb {Z}_2\wr \mathbb {Z}$
is weakly
![]() $C^*$
-simple without having the weak unique trace property.
$C^*$
-simple without having the weak unique trace property.
It follows from [Reference BerendBKKO17, Theorem 6.11] that, for groups with countably many subgroups,
![]() $C^*$
-simplicity is equivalent to the unique trace property. On the other hand,
$C^*$
-simplicity is equivalent to the unique trace property. On the other hand,
![]() $\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2$
has countably many subgroups by the argument in [Reference Breuillard, Kalantar, Kennedy and OzawaBLT19, Corollary 8.4] (whereas
$\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2$
has countably many subgroups by the argument in [Reference Breuillard, Kalantar, Kennedy and OzawaBLT19, Corollary 8.4] (whereas
![]() $\mathbb {Z}_2\wr \mathbb {Z}$
has uncountably many subgroups).
$\mathbb {Z}_2\wr \mathbb {Z}$
has uncountably many subgroups).
Question 4.1 Is there an icc group with countably many subgroups that is weakly
![]() $C^*$
-simple but does not have the weak unique trace property?
$C^*$
-simple but does not have the weak unique trace property?
Given a faithful, almost minimal action
![]() $\Gamma \curvearrowright X$
as in Theorem 2.4, the crossed product
$\Gamma \curvearrowright X$
as in Theorem 2.4, the crossed product
![]() $C(X)\rtimes \Gamma $
has the property that any of its irreducible representations are either faithful or have finite-dimensional image.
$C(X)\rtimes \Gamma $
has the property that any of its irreducible representations are either faithful or have finite-dimensional image.
Question 4.2 Can (some of) the theory of just-infinite
![]() $C^*$
-algebras from [Reference Grigorchuk, Musat and RørdamGMR18] be extended to the class of
$C^*$
-algebras from [Reference Grigorchuk, Musat and RørdamGMR18] be extended to the class of
![]() $C^*$
-algebras for which any irreducible representation is either faithful or has finite-dimensional image?
$C^*$
-algebras for which any irreducible representation is either faithful or has finite-dimensional image?
In [Reference RørdamRør19], it was shown that each infinite-dimensional metrizable Choquet simplex arises as the trace simplex of a residually finite-dimensional just-infinite AF-algebra. A
![]() $C^*$
-algebra is said to be subhomogeneous if it is isomorphic to a sub-
$C^*$
-algebra is said to be subhomogeneous if it is isomorphic to a sub-
![]() $C^*$
-algebra of
$C^*$
-algebra of
![]() $M_n(C_ 0(X))$
for some
$M_n(C_ 0(X))$
for some
![]() $n\in \mathbb {Z}_{>0}$
and X locally compact Hausdorff space. A
$n\in \mathbb {Z}_{>0}$
and X locally compact Hausdorff space. A
![]() $C^*$
-algebra is said to be approximately subhomogeneous (ASH-algebra) if it is the inductive limit of a sequence of subhomogeneous
$C^*$
-algebra is said to be approximately subhomogeneous (ASH-algebra) if it is the inductive limit of a sequence of subhomogeneous
![]() $C^*$
-algebras.
$C^*$
-algebras.
Question 4.3 Let
![]() $p,q\geq 2$
be multiplicatively independent integers. Is there a unital ASH-algebra A with the property that any of its irreducible representations are either faithful or have finite-dimensional image, and such that A has the same K-theory and primitive ideal space of
$p,q\geq 2$
be multiplicatively independent integers. Is there a unital ASH-algebra A with the property that any of its irreducible representations are either faithful or have finite-dimensional image, and such that A has the same K-theory and primitive ideal space of
![]() $C^*(\mathbb {Z}[1/pq]\rtimes \mathbb {Z}^2)$
? If yes, can one compute the trace simplex of A?
$C^*(\mathbb {Z}[1/pq]\rtimes \mathbb {Z}^2)$
? If yes, can one compute the trace simplex of A?
Acknowledgment
We thank the referee for several useful suggestions and for pointing out a gap in the original argument of Theorem 3.10.