Impact of fertility transmission and other sociodemographic factors on reproductive success and coalescent trees

Summary

Fertility transmission (FT) is a phenomenon with a cultural and/or genetic basis, whereby a positive correlation exists between the number of offspring of an individual and that of his/her parents. Theoretical studies using a haploid individual-based model have shown that FT increases the variance and intergenerational correlation in reproductive success and results in an imbalance in the coalescent tree of sampled genes. This phenomenon has been documented in several demographic studies conducted on the correlation in fertility between generations, or through the reconstruction of the genealogical trees of mitochondrial DNA sequences. However, as mtDNA is a single locus, potentially subject to other forces (e.g. natural selection), it is of interest to extend the theory of FT to nuclear loci. We show that because random mating between individuals leads to a mixing of their fertility profiles, FT in these cases will have less influence on the variance and intergenerational correlation of reproductive success. This, in turn, results in less impact on the shape of the coalescent trees. Nevertheless, in the presence of FT, high heterogeneity in reproductive success and homogamy for family size will increase the imbalance in the coalescent tree. Thus, FT should be easier to detect when occurring in conjunction with these other factors. We also show the utility of analysing different kinds of loci (X-linked, Y-linked, mitochondrial and autosomal) to assess whether FT is matrilineal, patrilineal or biparental. Finally, we demonstrate that the shape of the coalescent tree depends upon population size, in contrast to the classical Kingman's model.

1. Introduction

A positive correlation between the fertility of children and their parents has been observed in many populations of humans and in several other species (Heyer et al., 2005). This phenomenon of fertility transmission (FT) is highly variable, with significant differences found among populations, at different time periods and between sexes (Murphy, 1999). As fertility is one of the major life-history traits, the relative contribution of genetic, social and environmental factors on fertility has been a subject of considerable debate for over a century among geneticists, demographers and economists (see e.g. Kohler et al., 1999). In particular, FT is known to reduce effective population size and to increase inbreeding (Robertson, 1961; Nei & Murata, 1966; Wray & Thompson, 1990) and to have a strong impact on the frequency of genetic diseases in some human populations (Austerlitz & Heyer, 1998).

FT can be caused by genetic or cultural factors. An example of the cultural transmission of fertility (CTF) comes from the Saguenay–Lac Saint Jean (SLSJ) population in Quebec, where intergenerational correlations in effective family size (EFS) are much higher than correlations in census family size (CFS), which was interpreted as evidence of a cultural rather than genetic basis for FT (Austerlitz & Heyer, 1998). Indeed, EFS only considers individuals who reproduced at least once in their native population and is thought to be strongly influenced by cultural factors, such as transmission of wealth or migration behaviour.

In other human populations, evidence of CTF is identified through the simultaneous observation of specific allelic frequencies distributions and of transmission of cultural traits linked to fertility. For instance, the transmission of female social ranks observed in Maoris was proposed to explain the peculiar frequency distribution of mitochondrial DNA (mtDNA) haplotypes (Murray-McIntosh et al., 1998). Similarly, cultural transmission of higher male social status initiated by Genghis Khan and his relatives was suggested to explain the increase in gene frequency of some closely related Y-chromosome haplotypes in modern Asia (Zerjal et al., 2003; Dulik et al., 2011). Thus, CTF is observed in several human populations, even though it is not a general phenomenon (Lansing et al., 2008). Finally, note that CTF was also observed in non-human species, such as matrilineal whales (Whitehead, 1998) and cheetahs (Kelly, 2001), where migration strategy, foraging techniques and vigilance against potential predators are culturally transmitted through the generations.

Contrary to the above studies, which emphasize the role of social and cultural determinants, other research has instead advocated a significant genetic basis for FT. The intergenerational correlations in sibship size observed in Huterrites, for example, probably results, in part, from genetic factors, because of the high social and environmental homogeneity of this population (Pluzhnikov et al., 2007; Kosova et al., 2010). Similarly, a Danish study of twins found moderate genetic heritability for fertility (Rodgers et al., 2001). Actually, any pattern of selection on a quantitative trait occurring during several generations will lead to FT in any species (e.g. in wheat, Goldringer et al., 2001). Note that in all cases, this genetic FT is not linked to selection at a single locus but on a quantitative trait coded by many loci located throughout the genome. Finally, FT may even be linked to both genetic and social factors in some cases (Frère et al., 2010).

The impact of FT on neutral genetic diversity can be theoretically studied using a parametric model simulating the transmission of various degrees of reproductive success. Using haploid models without recombination, Sibert et al. (2002) and Blum et al. (2006) showed that, for neutral genes, coalescent trees under FT are expected to differ substantially from standard coalescent trees (Kingman, 1982) in the following ways: (i) the time to the most recent common ancestor (TMRCA) is reduced, resulting in lower genetic diversity; (ii) the ratio between external and internal branch lengths is increased, yielding more star-like trees; (iii) coalescent trees tend to be highly imbalanced, i.e. for a given binary node, the distribution of tips is not balanced between the two sub-trees.

While a star-like tree can also be observed in cases of population expansion (Slatkin & Hudson, 1991), tree imbalance for neutral sequences is much more specific of FT (Sibert et al., 2002; Blum et al., 2006). Estimating the imbalance of coalescence trees reconstructed from samples of neutral DNA sequences, therefore, constitutes an unambiguous method by which to infer FT (Blum et al., 2006). This is quite helpful because genealogical data of sufficient depth are rarely available, while current population genetics data can be obtained more easily. Using mitochondrial HV1 sequences, Blum et al. (2006) could thus show that matrilineal FT is more frequent in hunter-gatherer populations (HGPs) than in food-producer populations (FPPs).

This approach requires the absence of recombination, restricting the application of the model to the uniparentally inherited non-recombining sections of the Y-chromosome, and the mitochondrial genome. While these haploid markers provide information on a unique gene history, using several independent markers increases the ability to detect genome-wide processes (Nielsen, 2001). Another limitation of non-recombining uniparentally transmitted loci is the difficulty to discriminate between FT and selection at a single locus. This is important, because non-neutral evolution is common for mitochondrial DNA (Elson et al., 2004; Ruiz-Pesini et al., 2004; Bazin et al., 2006; Stewart et al., 2008; Balloux et al., 2009). Maia et al. (2004) demonstrated theoretically that purifying selection also leads to tree imbalance at the locus under selection. Interestingly, Kivisild et al. (2006) suggested a purifying selection process that would differ between populations with a diet based on grains or not. This may be a part of the explanation of the more imbalanced genealogical trees inferred in HGPs (Blum et al., 2006). Analysing many independent autosomal neutral markers is obviously a more powerful strategy to infer FT than one that relies on a unique gene history, possibly affected by selection.

A further limitation of previous theoretical studies on FT is that they do not distinguish between sexes. Yet, empirical data show that fertility can be transmitted by the mother alone (matrilineal FT) as in the British (Pearson et al., 1899; Murphy, 2006) and Icelandic populations (Helgason et al., 2003), by the father alone (patrilineal FT) as suspected for the Mongols (Zerjal et al., 2003) or by both parents (biparental FT) as in the French Canadian (Austerlitz & Heyer, 1998), Hutterite (Pluzhnikov et al., 2007) and Danish populations (Rodgers et al., 2001). A joint analysis of biparentally and uniparentally inherited markers (autosomal, X-linked, mitochondrial and Y-linked markers) should help to differentiate the sex-specific contributions to FT, in the same manner as sex differences were found for other demographic forces such as migration (Ségurel et al., 2008).

Moreover, other demographic phenomena may occur simultaneously with FT. One such factor is an increased heterogeneity in family size among couples relative to expectations under the Wright–Fisher model. Such heterogeneity may stem from socioeconomic conditions and behavioural characteristics of the parents (Ronsmans, 1995; Sastry, 1997) or from other sources of heterogeneity such as individuals’ ‘frailty’ at birth (Vaupel et al., 1979). In the SLSJ population in Quebec the observed high frequencies of severe genetic disorders can only be explained by the conjunction of FT and heterogeneity in family size (Austerlitz & Heyer, 1998).

Finally, one may question whether spouses tend to marry more often with partners from families with sizes similar to their own family. Mate choice is generally not random and may depend on social factors such as material resources, cultural factors (e.g. religion) and biological factors (e.g. indicators of good genes in the context of sexual selection) (Geary et al., 2004). As social factors may affect both mate choice and number of siblings, homogamy in sibship size is a possible consequence of assortative mating practices, and has been observed in several human populations (Imaizumi et al., 1970; Bocquet-Appel & Jakobi, 1993; Murphy, 2006).

In this paper, we study the joint impact of all these factors on demographic features and on the shape of gene trees inside populations. For this purpose, we simulated a population of diploid individuals with separate sexes, carrying genes belonging to the four genomic compartments: autosomal genes; X-linked genes; Y-linked genes; and mitochondrial genes. These loci have biparental, maternally biased, paternal or maternal inheritance, respectively. We investigated the joint impact of the level of FT, heterogeneity in family size, homogamy in sibship size, and the population size, on the variance in reproductive success among individuals in a given generation together with the correlation of this reproductive success between parents and offspring.

We next investigated how these phenomena jointly affect the level of imbalance of coalescent trees, as measured by an index that we modified from Fusco and Cronk (1995) to allow for non-binary nodes. This enabled us to establish the differences between our diploid model and the haploid model previously studied by Sibert et al. (2002) and Blum et al. (2006), and to assess the conditions that resulted in a maximal level of imbalance. We also evaluated the impact of FT on the different genomic compartments (autosomal, X-linked, Y-linked and mitochondrial), under biparental, matrilineal and patrilineal transmission, and determined the amount of independent nuclear loci that would be necessary to detect FT as a function of the intensity of this phenomenon.

2. Materials and methods

(i) Simulations

Populations were simulated using a forward individual-based approach where the pairing rules of individuals and the Mendelian rules of gene transmission from parents to children were explicitly implemented. This allowed us to incorporate a flexible model of FT into the classical Wright–Fisher framework. All simulations were performed assuming non-overlapping generations and a constant-size population of N individuals. In order to study the properties of the resulting coalescent trees, we stored the genealogical links that were progressively built between gene copies in each simulation. In other words, we did not directly simulate coalescent trees with a backward algorithm, but we considered the gene trees that resulted from our forward-in-time simulation procedure. For each simulation, we randomly sampled n=100 gene copies in the last simulated generation and we extracted their coalescence tree.

We performed first a set of simulations in a haploid model as in Sibert et al. (2002) and Blum et al. (2006). In this model, each child had a single parent, which was drawn randomly among the individuals of the previous generation according to a probability distribution modelling FT. As in Sibert et al. (2002), the probability p_i for a given individual i to be chosen as parent was

(1)

where M was the number of individuals (M=N), s_i the sibship size of individual i (i.e. the progeny size of its own parent), α the intensity of FT, and γ _i (a) was a random deviate drawn independently for each individual i from a gamma distribution with shape parameter a and mean 1. We considered a wide range of intensities of FT, from no FT (α=0) to very high FT (α=2). The a-parameter is a way to control the variance in reproductive success among individuals, as this variance increases when a decreases. As in Sibert et al. (2002), we only considered the cases (a=∞) and (a=1), which correspond respectively to a Poisson-like and a geometric-like distribution of the offspring number, the latter having a higher variance.

Then we modified this model to consider a population of diploid individuals with separate sexes assuming a constant 1:1 sex-ratio and simulated the transmission of autosomal, mitochondrial, X-linked and Y-linked genes. We assumed that each individual produced offspring with one partner only (strict monogamy). In each generation, couples were formed either randomly or under a model of homogamy for sibship size adapted from McKusick et al. (1990) . In this latter case, we first ranked the individuals according to their sibship size. An individual coming from a family of rank k (i.e. with k-offspring) randomly chose a mate among the individuals coming from families of rank between (k−s/2) and (k+s/2) (s thus being the ‘homogamy window size’). Therefore, the choice of mates was limited to individuals with similar sibship sizes. When such mates were not available, the actual mate was chosen among families with the nearest rank. Unlike in McKusick et al. (1990), the ranking was not circularized in order to avoid mating between individuals with opposite rankings (an additional set of simulations confirmed that results were not sensitive to this hypothesis, results not shown). This parametric pairing rule allowed us to quantitatively model homogamy for sibship size; i.e. the level of correlation between sibship sizes increased as the homogamy window size (s) decreased (Fig. 1).

Fig. 1. Impact of homogamy window size s on the Pearson correlation coefficient r between the mother's sibship and the father's sibship sizes without FT and without heterogeneity in reproductive success.

Once the couples were formed, we then drew from them the parents for each individual in the next generation. The probability p_i for a given couple i to be chosen as parents was computed with eqn (1) except that M was the number of couples (M=N/2) and s_i was either the mean sibship size of the two parents, the sibship size of the mother or the sibship size of the father; chosen in order to simulate biparental, matrilineal or patrilineal FT, respectively. As in the haploid model, the parameter α controlled the level of FT and the parameter a controlled the level of heterogeneity in family size.

In order to be consistent, we performed the comparisons between haploid and diploid models for the same number of gene copies (N _c). In the haploid model, we have N _c=N, since each individual carries one allele for each locus. However, in the diploid model, the number of gene copies for a given locus in a population of N individuals varies according to the compartment: N _c=2N for autosomal loci whereas, because we assumed a 1:1 sex-ratio; N _c=N/2 for Y-linked and mitochondrial loci; N _c=3N/2 for X-linked loci. For each simulation, we recorded the variance in reproductive success, the intergenerational correlation in this reproductive success, and the level of imbalance of the coalescent tree, as described below.

(ii) Variance and correlation in reproductive success

Comparing the reproductive success in haploid and diploid models is not trivial, as in the first case the number of offspring of an individual is the same as the number of copies for which a gene of this individual will be found in the population in the next generation, whereas in a diploid model a gene of a given individual is transmitted on average to only half of its offspring. In order to make valid comparisons between haploid and diploid models, we considered in all cases the ‘gene reproductive success’ (GRS), defined for each gene in a given generation as the number of copies of this gene occurring in the next generation. For all simulations, we computed the variance in GRS among genes in the final generation and the correlation between the GRS of a gene in the final generation and the GRS of its parent. In diploid models, we computed these values for each genomic compartment (mtDNA, X-linked, Y-linked and autosomal). As variances and correlations stabilize rapidly, each simulation was run until the 100th generation and we computed the mean values of variance and correlation in GRS over 1000 replicates for each set of parameters.

(iii) Tree imbalance analysis

FT reduces the height of coalescent trees (Sibert et al., 2002) and thus increases the frequency of polytomies (i.e. when a node has more than two direct sub-nodes). Therefore, in order to measure tree imbalance in this context, we developed a modified version of the imbalance index I of Fusco and Cronk (1995) used in its unbiased form (I′) in Blum et al. (2006), as this index does not permit the analysis of non-binary nodes and is biased for nodes with an even number of tips (Purvis et al., 2002). For each node in a tree, this modified index (I _nb) was computed as:

where k is the number of direct sub-nodes of the studied node (e.g. 2 for a binary node, 3 for a tertiary node, etc.); t is its number of tips; B is the maximum number of tips across all its sub-nodes; D=t–k+1 is the maximal possible value for B; m_{k ,t} was a correction factor allowing the expected value of I _nb to be 0·5 in a standard population (without FT). It is computed as m_{k ,t} =2 B_{k,t ,coal}–D, where B_{k,t ,coal} is the expected value of B in a standard population (without FT). B_{k ,t,coal} was obtained in practice by performing repeated simulations of a random Kingman's coalescent for t tips that was stopped when only k nodes remained in the genealogy. In each simulation, we recorded the B-value as the number of tips of the node with the highest number of tips among these k nodes. B_{k ,t,coal} was obtained by averaging the B-values over 1000 independent simulations. To handle polytomies, we only considered the nodes with a minimum of t=k+1 tips (Supplementary Fig. S1, available at http://journals.cambridge.org/grh). As for Fusco and Cronk's (1995)I index, the expected value of I _nb was 0·5 for each node in the coalescent for a standard population, whereas it was greater than 0·5 when the nodes were imbalanced, as for instance under FT. The imbalance measure of the whole tree was simply the mean of I _nb across all its nodes on which it could be computed, only removing the most terminal nodes (i.e. the nodes occurring less than four generations before the present), as a preliminary study had shown us that using these nodes was biasing downward the I _nb value of the tree (result not shown). Each retained node was given an equal weight in the final measure of total tree imbalance, as in Blum et al. (2006).

Finally, we estimated the expected value of I _nb for each set of parameters by averaging 500 independent replicates.

(iv) Impact of the number of loci on the possibility to detect FT

We also studied the number of independent loci necessary to detect FT for a given level of transmission (α). In order to do so, we performed sets of simulations in which we simulated a given number (x) of independent loci and computed the mean I _nb value over these xloci; for x=1, 2, 5, 20 and 40. We performed 500 replicates for each value of x and α and computed the 10th percentile of the mean imbalance statistics as a function of the intensity of FT α. This allowed us to obtain for each value of x, the minimal value of α for which at least 90% of the replicates showed an I _nb greater than 0·5.

3. Results

(i) Haploid model

Considering first the haploid model without heterogeneity in family size (a=∞), the variance in GRS and the level of correlation in GRS between parents and offspring increased with the level of FT (α), whatever the assumed population size (N). Starting from a value of 1·0 as expected in the standard Wright– Fisher model (Fig. 2 a), variance increased at first slowly with α for values up to 1·2, but then increased more rapidly to reach values of about 3·0 for α=2. The strength of correlation showed the opposite pattern (Fig. 2 b); starting from the expected null value for α=0, it increased first rapidly until α=1·2, but much more slowly afterwards. Starting from the expected value of 0·5 for α=0, the level of imbalance I _nb increased with α according to a sigmoid shape with an inflexion point for α=1·0 (Fig. 2 c).

Fig. 2. Impact of the intensity of FT (α) on the variance in GRS (a), the intergenerational correlation in GRS (b) and the tree imbalance index I _nb (c) for five population sizes (N=500, 1000, 2000, 4000, 8000), and a low level of heterogeneity (a=∞), in a haploid model, for a sample size n=100.

Regarding the impact of population size (N), for α<0·8, the levels of variance and correlation were similar for all N values (Figs 2 a and b). Nevertheless, for higher values of α, variance increased substantially with N, whereas the correlation slightly decreased with N. The pattern was more complex for I _nb; the higher the population size N, the steeper the slope at the inflexion point (Fig. 2 c). The initial increase of I _nb was thus delayed for high N, while the opposite pattern was observed after the inflexion point. The final pattern also was complex as I _nb reached a plateau for the highest N, whereas it kept increasing for the lowest N. These parameters were also affected by the level of heterogeneity in family size (Fig. 3). Variance in GRS was larger when heterogeneity in family size was higher (a=1) than when it was lower (a=∞), especially for high α–values (Fig. 3 a); the ratio between the variances obtained in these two cases increased from 2·0 for α=0 to 3·3 for α=2. Conversely, the correlation in GRS between generations was lower for a=1 than for a=∞ (Fig. 3 b). Finally, I _nb was higher for a=1 than for a=∞ as a result of a left-shift of the curve in the case of high heterogeneity in family size (Fig. 3 c). The difference was particularly noticeable for small values of α: for instance for α=0·8, I _nb was only ~0·53 when a=∞, whereas it was ~0·64 when a=1.

Fig. 3. Impact of the intensity of FT (α) on the variance in GRS (a), the intergenerational correlation in GRS (b) and the tree imbalance index I _nb (c), for two levels of heterogeneity in reproductive success (a=1 and a=∞), in a haploid model, assuming a population size N=4000 and a sample size n=100.

(ii) Diploid model

We then investigated whether the levels of variance and correlation in GRS were different between the haploid and the diploid models (Fig. 4). The levels of variance and correlation in GRS were much lower for the diploid model with biparental transmission than they were for the haploid one (Figs 4 a and b). Regarding I _nb, it increased rapidly in the haploid model, until it reached a plateau, whereas it increased slowly but continuously in the diploid model (Fig. 4 c). In this diploid model, we found no differences among the different genetic compartments (autosomes, X-linked, Y-linked and mtDNA) in their levels of variance and correlation, as long as FT was biparental (Figs 4 a and b). Nevertheless, we observed that I _nb values were slightly higher for the haploid compartments (mitochondrial and Y-linked) than for the autosomal and X-linked compartments (Fig. 4 c).

Fig. 4. Impact of the intensity of FT (α) on the variance in GRS (a), the intergenerational correlation in GRS (b) and the tree imbalance index I _nb (c) for haploid and diploid models, considering for the latter autosomal loci with biparental transmission and no homogamy in family size (s=0), assuming a number of gene copies N _c=4000 for the haploid and diploid models (N=2000 for the diploid model) and a sample size n=100.

When considering matrilineal transmission, the level of variance in GRS increased substantially with α in a similar manner for all four compartments, even for the strictly paternally transmitted Y-chromosomes (Fig. 5 a). This contrasted with the patterns observed for the correlation (Fig. 5 b) and I _nb (Fig. 5 c), which were very strong for mitochondrial genes, but reached lower values for X-linked genes, even lower values for autosomal genes and null for Y-linked genes. A symmetric pattern was observed for patrilineal transmission: variance was the same for all compartments (Supplementary Fig. S2 a, available at http://journals.cambridge.org/grh), whereas the correlation and I _nb values were the highest for Y-linked genes and then were lower for autosomal genes, even lower for X-linked genes and null for mitochondrial genes (Figs S2b and c). Finally, as in the haploid model, variances in GRS and imbalance I _nb were higher in the diploid model with high heterogeneity in family size (a=1) than in the standard diploid model (a=∞), while intergenerational correlations in GRS were lower in the former than in the latter (Supplementary Figs S3–S5, available at http://journals.cambridge.org/grh).

Fig. 5. Impact of the intensity of FT (α) on the variance in GRS (a), the intergenerational correlation in GRS (b) and the tree imbalance index I _nb (c) for different genomic compartments (autosomal, mitochondrial, X-linked and Y-linked) in a diploid model without homogamy in family size (s=0) using a matrilineal transmission of fertility and without heterogeneity in reproductive success (a=∞), assuming a population size N=2000 and a sample size n=100.

(iii) Homogamy in family size

We observed that both the correlation and the variance in GRS increased as the level of homogamy increased (i.e. as s decreased, Supplementary Figs S6a and b, available at http://journals.cambridge.org/grh). Regarding I _nb, we observed no difference for low α values (α<0·6) between the situations with or without homogamy (Fig. 6). For intermediate α values (0·6<α<1·4), the addition of homogamy yielded an increase in I _nb, which increased as s decreased. However, for large α-values (α>1·4), I _nb was larger without homogamy and decreased as the level of homogamy increased.

Fig. 6. Impact of the intensity of FT (α) and homogamy windows size (s) on the tree imbalance index I _nb for autosomal genes in a diploid model using a biparental transmission of fertility and without heterogeneity in reproductive success (a=∞), assuming a population size N=2000 and a sample size n=100.

(iv) Impact of the number of loci used on the possibility of detecting FT

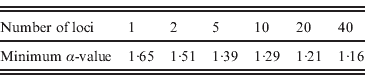
We studied the impact of increasing the number of loci on the power of detecting FT in populations. We observed that the threshold value for α above which at least 90% of the I _nb values are larger than 0·5 decreased with the number of loci used, from 1·65 with one locus to 1·16 with 40 loci (Table 1).

Table 1. Minimum levels of FT (α) for which 90% of the imbalance index values (I _nb) are higher than 0·5 as a function of the number of loci used to compute this index. We assumed autosomal loci in a diploid model without homogamy in family size (s=0) under biparental transmission of fertility and without heterogeneity in reproductive success (a=∞), assuming a population size N=2000 and a sample size n=100.

4. Discussion

(i) Interaction between parameters in the haploid model

Using an individual-based model of FT, our simulations have provided a theoretical framework to detect and understand FT and its impact on the demographic patterns of the population (namely the variance and correlation between parents and offspring in reproductive success) and on the level of imbalance of genealogical trees, as measured by our new index (I _nb) that can account for polytomies in the tree. When demographic data are available, FT can be directly measured through the correlation between parents and offspring in reproductive success. In most cases, however, demographic data are not available; so FT cannot be inferred directly. Therefore, Blum et al. (2006) developed a method to detect FT from genealogical tree imbalance. We showed here with our simulation study that the imbalance index (I _nb) increases in a population submitted to FT.

This index, however, is affected by other parameters, in particular population size (N) and heterogeneity in family size (a). Regarding the latter parameter, I _nb increased when heterogeneity increased (Fig. 3), which is a consequence of the increased variance in GRS. By definition, a genealogical tree can be imbalanced only if some of its nodes have more tips than others, and this is only possible if some individuals have a larger reproductive success than others. Thus, an increased level of heterogeneity in progeny size will increase the potential to observe tree imbalance, but this imbalance will only occur in the presence of FT, because the nodes with more direct sub-nodes will always occur in the same part of the tree. In other words, variance is the prerequisite for the creation of imbalance in the genealogical tree, but this imbalance can only be maintained in subsequent generations when GRS is correlated between generations.

It is interesting however to note that increasing the level of heterogeneity in progeny size resulted in reductions in the level of correlation for a given level of FT (α), while I _nb simultaneously increased. This decrease in correlation results naturally from the increase of variance, which appears in the denominator of the formula used to compute the correlation coefficient. However, this decrease in correlation does not preclude an increase of I _nb, demonstrating that the relation between I _nb and correlation is not completely straightforward. This is because of the increased variance in reproductive success, which means that a higher value of I _nb can be reached when variance is increased, even if the correlation is lower.

The other factor that affected the relation between I _nb and FT is population size (N). An increase in population size led to an increase in variance and correlation for a given value of α (Fig. 2). Hence, in small populations, variances and covariances between generations were limited by the total size of the population. As a result, I _nb was higher for large population sizes than for small ones, for moderate FT values (1<α<1·6). However, the opposite pattern was observed for lower levels of FT (α<1), indicating a rather complex interaction between the parameters. From a theoretical perspective, it is interesting to observe that under FT the topology of the tree consequently depends on population size. This contrasts strongly with the classical Kingman's coalescent process, in which population size does not affect the shape of the coalescent tree, but is only a scaling factor for its branch lengths (Kingman, 1982; Hudson, 1990). Thus, under FT, trees cannot be simply normalized by population size as in the classical Kingman's model.

Regarding the possibility to detect FT in natural populations from the inferred coalescent trees, without heterogeneity in family size, the I _nb value hardly deviates from 0·5 for α-values below 0·8 (Fig. 2 c). Thus, this value of 0·8 appears as the minimal value for which FT could be detected. This would correspond to the correlation of 0·394 (Fig. 2 b), which is higher than the highest correlation ever observed in human populations, namely the Hutterite population (Pluzhnikov et al., 2007). Here, our conclusions differ from those of Blum et al. (2006), who stated that even without heterogeneity in family size, FT could be detected in human populations. However, their inferences were based on the simulations of Sibert et al. (2002), which considered populations of 50 individuals. In such small populations, when α<1·0, correlations are expected to be lower and I _nb values higher than in larger populations. Thus, the conclusion that FT can be detected in populations without heterogeneity in family size does not hold in larger populations (N⩾500). However, when there is heterogeneity in family size, I _nb deviates substantially from 0·5 for α-values as low as 0·5 (Fig. 3 c), corresponding to a correlation value of 0·22, which is realistic for human populations. Thus, it is probable that the populations, in which FT was detected through tree imbalance estimations such as HGPs (Blum et al., 2006), were also subjected to other factors such as heterogeneity in family size, which is a common phenomenon in human populations (Vaupel et al., 1979; Ronsmans, 1995; Sastry, 1997; Austerlitz & Heyer, 1998). In this context, it is interesting to note that the high frequency of rare diseases alleles in Saguenay–Lac-Saint-Jean was also explained by an interaction between FT and high heterogeneity in family size (Austerlitz & Heyer, 1998).

(ii) Diploid model

Furthermore, simulating diploid individuals with autosomal, X-linked, Y-linked and mitochondrial genes allowed us to predict the level of variance and correlation in GRS, as well as gene tree imbalance, for the different kinds of genes under biparental, patrilineal or matrilineal FT. It is clear that the haploid model is a good approximation of the impact of FT on mitochondrial genes for matrilineal scenarios (Fig. 5) and Y-linked genes for patrilineal scenarios (Fig. S2). This approximation does not hold, however, for autosomal and X-linked genes, for which the pairing process of individuals has to be taken into account.

Here we have demonstrated that the variance, correlation and tree imbalance associated with the different compartments depended on the characteristics of FT. Firstly, under matrilineal transmission tree imbalance and correlation in GRS were higher for mitochondrial genes than for autosomal and X-linked genes, and were absent for Y-linked genes as expected. However, it is interesting to note that even when FT is strictly matrilineal, as is probably the case for the Maoris (Murray-McIntosh et al., 1998) and the cetaceous species (Whitehead, 1998; Frère et al., 2010), the variance in GRS is the same for all compartments.

Although the Y-chromosome is not directly affected by matrilineal transmission, the application of strict monogamy in our model (pairing each unique male with a unique female) results in the variance in reproductive success being the same for both sexes. The effective population size will, therefore, be decreased for the Y-chromosome due to FT occurring between mothers and daughters. The reason for this was pointed out by Sibert et al. (2002), who noted that individuals are no longer equivalent in the presence of FT because, unlike in the classical Wright–Fisher model, they no longer have the same propensity to reproduce. Some male reproductive strategies, such as serial or simultaneous polygamy should, to some extent, decouple this effect, but the variance in reproductive success of males will still be affected by the variance in the reproductive success of the females they marry.

Conversely, for a patrilineal FT transmission, such as in the Mongol population in Eurasia (Zerjal et al., 2003), we expect higher correlation and imbalance for Y-linked genes than for X-linked and autosomal genes, and neither correlation nor imbalance for mitochondrial genes. However, the effective population size of these mitochondrial genes should still be decreased as a result of the increased variance in GRS. In contrast, biparental FT, as for example described in the French Canadian population (Austerlitz & Heyer, 1998), will have a similar impact on all the compartments. Investigating different genetic compartments, therefore, could allow researchers to assess whether FT is sex-biased or not in their study population, provided that the criteria for the detection of FT are met. Contrasting the autosomes and X-chromosomes should be particularly relevant in this context, as they harbour many independent neutral loci; while the non-recombining parts of the Y- and mitochondrial chromosomes may be subjected to selective processes, which may affect their tree imbalance.

One of the prerequisites to detect FT is the occurrence of heterogeneity in family size, as it increases the level of imbalance for a given level (α) of FT. However, the random mating of individuals in the standard diploid model leads to a decrease of imbalance, rendering it potentially more difficult to detect FT in populations. The introduction of homogamy in family size to our model, however, reduced the strong averaging effects between very dissimilar mates, leading to an increase in the variance and correlation in GRS in proportion to the level of homogamy (Fig. S6). This effect also led to an increase of I _nb for intermediate levels of FT (0·6<α<1·4) (Fig. 6). Interestingly, homogamy in family size has been observed in several human populations such as the Arthez d'Asson village in France (Bocquet-Appel & Jakobi, 1993), the English (Murphy, 2006) and the Uto in Japan (Imaizumi et al., 1970). Combined with heterogeneity in family size, it can substantially increase I _nb and their presence should facilitate the improved detection of FT in human populations.

(iii) Detecting FT in practice

We showed that increasing the number of loci allows one to detect lower levels of FT (Table 1). If only one locus is studied, the threshold value of α above which FT can be detected is of 1·65, which corresponds to a correlation of 0·32 in GRS (Fig. 4 b), which is quite a high value for human populations (Pluzhnikov et al., 2007); whereas for 20 loci this correlation drops to a more realistic value (~0·21). Studying as many loci as possible, therefore, is crucial to an increase in the power of detection for the presence of FT in human populations. The analysis of many autosomal neutral markers could provide a means to distinguish between FT and selection on a single locus, as for instance in the case of HGPs, where FT was inferred from mitochondrial HVR1 sequence data only (Blum et al., 2006). FT should affect all neutral loci in the same way, whereas single-locus selection should only affect the target locus. Inferring tree imbalance for several neutral nuclear DNA sequences could, therefore, facilitate the separation of these two phenomena. Finally, it should be noted that Blum et al. (2006) demonstrated that population structure can lead to an imbalance of the coalescent tree in rather extreme cases. Therefore, it may be helpful to perform an analysis with a clustering program, such as Structure (Pritchard et al., 2000), in order to detect any spurious structure within a population under study.

(iv) Future studies

One practical problem envisaged is that nuclear DNA sequences are prone to intragenic recombination. This can lead to some distortions when reconstructing the genealogical tree using phylogenetic methods (Schierup & Hein, 2000), necessitating an appropriate design for the analysis of nuclear DNA sequences. One solution to this could be to restrict the analyses to ‘haploblocks’, i.e. portions of sequences that have not undergone any recombination events. Detecting these haploblocks can be achieved through different methods, such as the level of linkage disequilibrium (measured for instance by D or D′), or the four gamete test (Hudson & Kaplan, 1985). If the number of mutations is sufficiently large on any given haploblock to build a phylogenetic tree, we may expect to be able to analyse the imbalance of these trees and thus detect FT.

The haploblocks identified by the HapMap project (The International HapMap Consortium, 2003) show, on average, between 19 and 25 single-nucleotide polymorphisms (SNPs) (depending on the population), with some blocks showing much higher numbers. There should be sufficient information in such polymorphic haploblocks to reconstruct the phylogenetic trees. Otherwise, the process of recombination may need to be taken into account, through the development and testing of alternative methods, such as Approximate Bayesian Computation (Beaumont et al., 2002). Additional theoretical studies could also be performed, in particular on the impact of FT on parameters such as the reproductive value, which was shown to be a central parameter in the prediction of the genetic contribution of individuals to their population (Barton & Etheridge, 2011).