Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T02:19:26.989Z Has data issue: false hasContentIssue false
  • English
  • Français

In situ measurement of bulk modulus and yield response of glassy thin films via confined layer compression

Published online by Cambridge University Press:  02 March 2020

Owen Brazil Open the ORCID record for Owen Brazil [Opens in a new window] ,
Johann P. de Silva ,
Mithun Chowdhury ,
Heedong Yoon ,
Gregory B. McKenna ,
Warren C. Oliver ,
Jason Kilpatrick ,
John B. Pethica  and
Graham L.W. Cross
Owen Brazil
Affiliation:
School of Physics, CRANN & AMBER, Trinity College, Dublin 2, Ireland
Johann P. de Silva
Affiliation:
School of Physics, CRANN & AMBER, Trinity College, Dublin 2, Ireland
Mithun Chowdhury
Affiliation:
School of Physics, CRANN & AMBER, Trinity College, Dublin 2, Ireland
Heedong Yoon
Affiliation:
Department of Chemical Engineering, Texas Tech University, Lubbock, Texas 79409-3121, USA
Gregory B. McKenna
Affiliation:
Department of Chemical Engineering, Texas Tech University, Lubbock, Texas 79409-3121, USA
Warren C. Oliver
Affiliation:
Nanomechanics Inc., KLA-Tencor, Oak Ridge, Tennessee 37830, USA
Jason Kilpatrick
Affiliation:
Adama Innovations Ltd., CRANN, Trinity College, Dublin 2, Ireland
John B. Pethica
Affiliation:
School of Physics, CRANN & AMBER, Trinity College, Dublin 2, Ireland
Graham L.W. Cross*
Affiliation:
School of Physics, CRANN & AMBER, Trinity College, Dublin 2, Ireland; and Adama Innovations Ltd., CRANN, Trinity College, Dublin 2, Ireland
*
a)Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

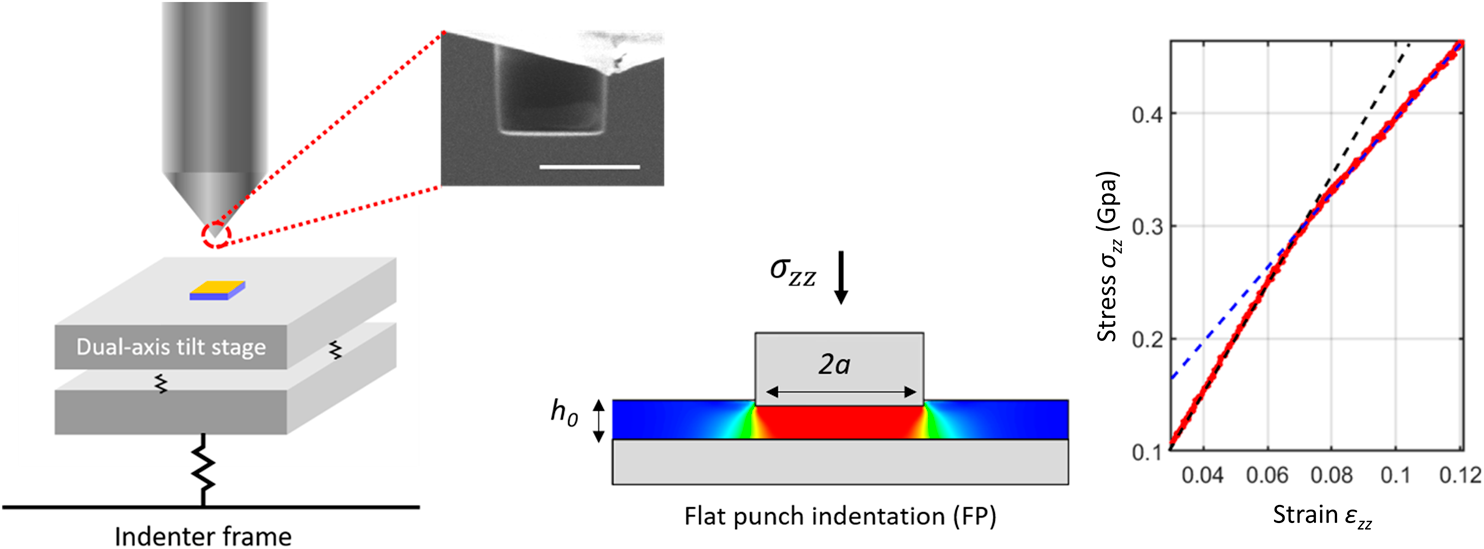
The measurement of thin film mechanical properties free from substrate influence remains one of the outstanding challenges in nanomechanics. Here, a technique based on indentation of a supported film with a flat punch whose diameter is many times the initial film thickness is introduced. This geometry generates a state of confined uniaxial strain for material beneath the punch, allowing direct access to intrinsic stress versus strain response. For simple elastic–plastic materials, this enables material parameters such as elastic modulus, bulk modulus, Poisson's ratio, and yield stress to be simultaneously determined from a single loading curve. The phenomenon of confined plastic yield has not been previously observed in thin films or homogeneous materials, which we demonstrate here for 170 -470 nm thick polystyrene (PS), polymethyl-methacrylate (PMMA) and amorphous Selenium films on silicon. As well as performing full elastic -plastic parameter extraction for these materials at room temperature, we used the technique to study the variation of yield stress in PS to temperatures above the nominal glass transition of 100 °C.

Keywords

elastic propertiesstress/strain relationshipthin film
Type
Article
Information
Journal of Materials Research , Volume 35 , Issue 6 , 30 March 2020 , pp. 644 - 653
Copyright
Copyright © Materials Research Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

b)

Present address: Metallurgical Engineering and Materials Science, Indian Institute of Technology Bombay, Mumbai 400076, India.

*

This article has been corrected since its original publication. An erratum notice detailing these changes was also published (doi: 10.1557/jmr.2020.67)

References

Alcoutlabi, M. and McKenna, G.B.: Effects of confinement on material behaviour at the nanometre size scale. J. Phys.: Condens. Matter 17, R461–R524 (2005).Google Scholar
Rowland, H.D., King, W.P., Pethica, J.B., and Cross, G.L.W.: Molecular confinement accelerates deformation of entangled polymers during squeeze flow. 322, Science. 720–724 (2008).CrossRefGoogle ScholarPubMed
Oliver, W.C. and Pharr, G.M.: An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 7, 1564–1583 (1992).CrossRefGoogle Scholar
Pethica, J.B., Hutchings, R., and Oliver, W.C.: Hardness measurement at penetration depths as small as 20 nm. Philos. Mag. A 48, 593–606 (1983).CrossRefGoogle Scholar
Saha, R. and Nix, W.D.: Effects of the substrate on the determination of thin film mechanical properties by nanoindentation. Acta Mater. 50, 23–38 (2002).CrossRefGoogle Scholar
Pharr, G.M. and Oliver, W.C.: Measurement of thin film mechanical properties using nanoindentation. MRS Bull. 17, 28–33 (1992).CrossRefGoogle Scholar
Uchic, M.D., Dimiduk, D.M., Florando, J.N., and Nix, W.D.: Sample dimensions influence strength and crystal plasticity. Science 305, 986–989 (2004).CrossRefGoogle ScholarPubMed
Stafford, C.M., Harrison, C., Beers, K., Alamgir, K., Amis, E., Vanlandingham, M.R., Kim, H.C., Volksen, W., Miller, R.D., and Simonyi, E.: A buckling-based metrology for measuring the elastic moduli of polymeric thin films. Nat. Mater. 3, 545–550 (2004).CrossRefGoogle ScholarPubMed
Connell, P.A. and McKenna, G.B.: Rheological measurements of the thermoviscoelastic response of ultrathin polymer films. Science. 307, 1760–1763 (2005).CrossRefGoogle Scholar
Mavko, G., Mukerji, T., and Dvorkin, J.: The Rock Physics Handbook (Cambridge University Press, Cambridge, England, 2009); pp. 22–23.CrossRefGoogle Scholar
Davies, R.O. and Selvadurai, A.P.S.: Plasticity and Geomechanics (Cambridge University Press, Cambridge, England, 2005); p. 44.Google Scholar
Ma, Z. and Ravi-Chandar, K.: Confined compression: A stable homogeneous deformation for constitutive characterization. Exp. Mech. 40, 38–45 (2000).CrossRefGoogle Scholar
Ravi-Chandar, K. and Ma, Z.: Inelastic deformation in polymers under multiaxial compression. Mech. Time-Dependent Mater. 4, 333–357 (2000).CrossRefGoogle Scholar
Cross, G.L.W., O'Connell, B.S., Pethica, J.B., Rowland, H., and King, W.P.: Variable temperature thin film indentation with a flat punch. Rev. Sci. Instrum. 79, 013904 (2008).CrossRefGoogle ScholarPubMed
Argon, A.S.: The Physics of Deformation and Fracture of Polymers (Cambridge University Press, Cambridge, England, 2013); p. 112.CrossRefGoogle Scholar
Lindsey, G., Schapery, R.A., Williams, M.L., and Zak, A.R.: The triaxial tension failure of viscoelastic materials, Internal report, US Aerospace Research Laboratories. (Pasedena, California, September 1963).CrossRefGoogle Scholar
Kim, J.W., Medvedev, G.A., and Caruthers, J.M.: Observation of yield in triaxial deformation of glassy polymers. Polymer 54, 2821–2833 (2013).CrossRefGoogle Scholar
Johnson, K.L.: Contact Mechanics (Cambridge University Press, Cambridge, England, 1985); p. 171.CrossRefGoogle Scholar
Johnson, K.L.: The correlation of indentation experiments. J. Mech. Phys. Solids 18, 115–126 (1970).CrossRefGoogle Scholar
Quinson, R., Perez, J., Rink, M., and Pavan, A.: Yield criteria for amorphous glassy polymers. J. Mater. Sci. 32, 1371–1379 (1997).CrossRefGoogle Scholar
Roth, C.B.: Polymer Glasses (CRC Press, Boca Raton, 2016); pp. 31, 161.Google Scholar
Böhmer, R. and Angell, C.A.: Elastic and viscoelastic properties of amorphous selenium and identification of the phase transition between ring and chain structures. Phys. Rev. B 48, 5857–5864 (1993).CrossRefGoogle ScholarPubMed
Brandrup, J., Immergut, E.H., and Grulke, E.A.: Polymer handbook (Wiley-Interscience, New Jersey, 1999).Google Scholar
Mott, P.H., Dorgan, J.R., and Roland, C.M.: The bulk modulus and Poisson's ratio of “incompressible” materials. J. Sound Vib. 312, 572–575 (2008).CrossRefGoogle Scholar
Yoon, H. and McKenna, G.B.: Dynamic and temperature dependent response of physical vapor deposited Se in freely standing nanometric thin films. J. Chem. Phys. 144 (2016).CrossRefGoogle Scholar
Bernatz, K.M., Echeverría, I., Simon, S.L., and Plazek, D.J.. Characterization of the molecular structure of amorphous selenium using recoverable creep compliance measurements. J. Non-Cryst. Solids 307–310, 790–801 (2002).CrossRefGoogle Scholar
Online Source: Stephens, D.R., Heard, H.C., and Schock, R.N.: High-pressure mechanical properties of polymethylmethacrylate (1972). Available at: https://www.osti.gov/servlets/purl/4249322.Google Scholar
Brazil, O.: Deformation and yield of polymer thin films under confinement. Thesis (Trinity College Dublin, Dublin 2, Ireland, 2019).Google Scholar
Quach, A. and Simha, R.: Pressure-volume-temperature properties and transitions of amorphous polymers; polystyrene and poly(orthomethylstyrene). J. Appl. Phys. 42, 4592–4606 (1971).CrossRefGoogle Scholar
Oels, H-J. and Rehage, G.: Pressure-volume-temperature measurements on atactic polystyrene. A thermodynamic view. Macromolecules 10, 1036–1043 (1977).CrossRefGoogle Scholar
Connell, P.A.O. and Mckenna, G.B.: Novel nanobubble inflation method for determining the viscoelastic properties of ultrathin polymer films. Rev. Sci. Instrum. 78, 013901 (2012).CrossRefGoogle Scholar
Rowland, H.D., King, W.P., Cross, G.L.W., and Pethica, J.B.: Measuring glassy and viscoelastic polymer flow in molecular-scale gaps using a flat punch mechanical probe. ACS Nano 2, 419–428 (2008).CrossRefGoogle ScholarPubMed
Wald, M.J., Considine, J.M., and Turner, K.T.: Determining the elastic modulus of compliant thin films supported on substrates from flat punch indentation measurements. Exp. Mech. 53, 931–941 (2013).CrossRefGoogle Scholar
Wald, M.J., Considine, J.M., and Turner, K.T.: Measuring the elastic modulus of soft thin films on substrates. Exp. Appl. Mech. 6, 741–747 (2011).Google Scholar
Cross, G.L.W., O'Connell, B.S., and Pethica, J.B.: Influence of elastic strains on the mask ratio in glassy polymer nanoimprint. Appl. Phys. Lett. 86, 1–3 (2005).CrossRefGoogle Scholar
Supplementary material: File

Brazil et al. supplementary material

Brazil et al. supplementary material

Download Brazil et al. supplementary material(File)
File 27.9 KB