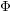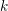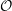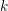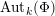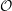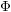1 Introduction
Let
![]() $\unicode[STIX]{x1D6F7}$
be a
$\unicode[STIX]{x1D6F7}$
be a
![]() $d$
-dimensional formal group of height
$d$
-dimensional formal group of height
![]() $h$
over a perfect field
$h$
over a perfect field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p>0$
, and
$p>0$
, and
![]() ${\mathcal{O}}$
denote the ring of Witt vectors over
${\mathcal{O}}$
denote the ring of Witt vectors over
![]() $k$
. The deformation functor
$k$
. The deformation functor
![]() ${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}$
assigns to any Artinian local
${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}$
assigns to any Artinian local
![]() ${\mathcal{O}}$
-algebra
${\mathcal{O}}$
-algebra
![]() $R$
the set of
$R$
the set of
![]() $\star$
-isomorphism classes of deformations of
$\star$
-isomorphism classes of deformations of
![]() $\unicode[STIX]{x1D6F7}$
over
$\unicode[STIX]{x1D6F7}$
over
![]() $R$
, where two deformations of
$R$
, where two deformations of
![]() $\unicode[STIX]{x1D6F7}$
are
$\unicode[STIX]{x1D6F7}$
are
![]() $\star$
-isomorphic if there exists an isomorphism between them with identity reduction. Grothendieck [Reference Illusie11] proved that
$\star$
-isomorphic if there exists an isomorphism between them with identity reduction. Grothendieck [Reference Illusie11] proved that
![]() ${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}$
is representable by the formal spectrum of the ring of formal power series in
${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}$
is representable by the formal spectrum of the ring of formal power series in
![]() $d(h-d)$
variables with coefficients in
$d(h-d)$
variables with coefficients in
![]() ${\mathcal{O}}$
. In other words, there exists a formal group
${\mathcal{O}}$
. In other words, there exists a formal group
![]() $\unicode[STIX]{x1D6E4}$
over
$\unicode[STIX]{x1D6E4}$
over
![]() ${\mathcal{O}}[[t_{1},\ldots ,t_{d(h-d)}]]$
called a universal deformation of
${\mathcal{O}}[[t_{1},\ldots ,t_{d(h-d)}]]$
called a universal deformation of
![]() $\unicode[STIX]{x1D6F7}$
such that for any deformation
$\unicode[STIX]{x1D6F7}$
such that for any deformation
![]() $F$
of
$F$
of
![]() $\unicode[STIX]{x1D6F7}$
over
$\unicode[STIX]{x1D6F7}$
over
![]() $R$
, there is a unique homomorphism
$R$
, there is a unique homomorphism
![]() $\unicode[STIX]{x1D707}:{\mathcal{O}}[[t_{1},\ldots ,t_{d(h-d)}]]\rightarrow R$
such that
$\unicode[STIX]{x1D707}:{\mathcal{O}}[[t_{1},\ldots ,t_{d(h-d)}]]\rightarrow R$
such that
![]() $\unicode[STIX]{x1D707}_{\ast }\unicode[STIX]{x1D6E4}$
is
$\unicode[STIX]{x1D707}_{\ast }\unicode[STIX]{x1D6E4}$
is
![]() $\star$
-isomorphic to
$\star$
-isomorphic to
![]() $F$
. Notice that Grothendieck’s proof does not allow one to construct
$F$
. Notice that Grothendieck’s proof does not allow one to construct
![]() $\unicode[STIX]{x1D6E4}$
explicitly. In the case where
$\unicode[STIX]{x1D6E4}$
explicitly. In the case where
![]() $\unicode[STIX]{x1D6F7}$
is one-dimensional, an explicit universal deformation was constructed by Hazewinkel [Reference Hazewinkel9]. For arbitrary
$\unicode[STIX]{x1D6F7}$
is one-dimensional, an explicit universal deformation was constructed by Hazewinkel [Reference Hazewinkel9]. For arbitrary
![]() $\unicode[STIX]{x1D6F7}$
it was done by the authors in [Reference Demchenko and Gurevich5].
$\unicode[STIX]{x1D6F7}$
it was done by the authors in [Reference Demchenko and Gurevich5].
For the
![]() $\star$
-isomorphism classes of the deformations of
$\star$
-isomorphism classes of the deformations of
![]() $\unicode[STIX]{x1D6F7}$
over
$\unicode[STIX]{x1D6F7}$
over
![]() ${\mathcal{O}}$
, there is another explicit description due to the Dieudonné theory. The Dieudonné module
${\mathcal{O}}$
, there is another explicit description due to the Dieudonné theory. The Dieudonné module
![]() ${\mathcal{D}}(\unicode[STIX]{x1D6F7})$
of
${\mathcal{D}}(\unicode[STIX]{x1D6F7})$
of
![]() $\unicode[STIX]{x1D6F7}$
is a certain profinite module over the Dieudonné ring
$\unicode[STIX]{x1D6F7}$
is a certain profinite module over the Dieudonné ring
![]() $E$
. Fontaine [Reference Fontaine7] assigned a submodule of
$E$
. Fontaine [Reference Fontaine7] assigned a submodule of
![]() ${\mathcal{D}}(\unicode[STIX]{x1D6F7})$
to any deformation of
${\mathcal{D}}(\unicode[STIX]{x1D6F7})$
to any deformation of
![]() $\unicode[STIX]{x1D6F7}$
over
$\unicode[STIX]{x1D6F7}$
over
![]() ${\mathcal{O}}$
so that
${\mathcal{O}}$
so that
![]() $\star$
-isomorphic deformations correspond to the same submodule. Honda [Reference Honda10] described
$\star$
-isomorphic deformations correspond to the same submodule. Honda [Reference Honda10] described
![]() ${\mathcal{D}}(\unicode[STIX]{x1D6F7})$
as a factor module of
${\mathcal{D}}(\unicode[STIX]{x1D6F7})$
as a factor module of
![]() $E^{d}$
. Thus one can show that
$E^{d}$
. Thus one can show that
![]() ${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}({\mathcal{O}})$
is naturally identified with the set of certain double cosets in
${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}({\mathcal{O}})$
is naturally identified with the set of certain double cosets in
![]() $\text{GL}_{d}(E)$
. The first purpose of the present paper is to establish an explicit relation between two parameterizations of
$\text{GL}_{d}(E)$
. The first purpose of the present paper is to establish an explicit relation between two parameterizations of
![]() ${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}({\mathcal{O}})$
: through the explicit universal deformation and through the Dieudonné theory. For a formal group of dimension one such relation was established in the authors’ work [Reference Demchenko and Gurevich4] where a period map was constructed and an explicit formula for it was obtained. In order to treat the general case we exercise a similar approach. In addition to Hazewinkel’s universal
${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}({\mathcal{O}})$
: through the explicit universal deformation and through the Dieudonné theory. For a formal group of dimension one such relation was established in the authors’ work [Reference Demchenko and Gurevich4] where a period map was constructed and an explicit formula for it was obtained. In order to treat the general case we exercise a similar approach. In addition to Hazewinkel’s universal
![]() $p$
-typical formal group [Reference Hazewinkel9] and Honda theory [Reference Honda10] that were involved in [Reference Demchenko and Gurevich4], we make use of covariant Honda theory developed in [Reference Demchenko3].
$p$
-typical formal group [Reference Hazewinkel9] and Honda theory [Reference Honda10] that were involved in [Reference Demchenko and Gurevich4], we make use of covariant Honda theory developed in [Reference Demchenko3].
It is necessary to mention that in his fundamental work [Reference Zink13], Zink introduced the theory of
![]() $3n$
-displays which describes formal groups of finite height over an excellent ring
$3n$
-displays which describes formal groups of finite height over an excellent ring
![]() $R$
. Moreover, he developed a corresponding deformation theory which generalizes the description of
$R$
. Moreover, he developed a corresponding deformation theory which generalizes the description of
![]() ${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}({\mathcal{O}})$
based on the Dieudonné module
${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}({\mathcal{O}})$
based on the Dieudonné module
![]() ${\mathcal{D}}(\unicode[STIX]{x1D6F7})$
. It would be highly interesting to relate Zink’s description of
${\mathcal{D}}(\unicode[STIX]{x1D6F7})$
. It would be highly interesting to relate Zink’s description of
![]() ${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}(R)$
and the parametrization obtained through the explicit universal deformation. Being more involved, this task is left to a future investigation.
${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}(R)$
and the parametrization obtained through the explicit universal deformation. Being more involved, this task is left to a future investigation.
The group of the automorphisms of
![]() $\unicode[STIX]{x1D6F7}$
over
$\unicode[STIX]{x1D6F7}$
over
![]() $k$
acts naturally on the right on the functor
$k$
acts naturally on the right on the functor
![]() ${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}$
. For
${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}$
. For
![]() $\unicode[STIX]{x1D719}\in \text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
and
$\unicode[STIX]{x1D719}\in \text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
and
![]() $F\in {\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}({\mathcal{O}})$
, the action is defined by
$F\in {\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}({\mathcal{O}})$
, the action is defined by
![]() $[F]\unicode[STIX]{x1D719}=[g^{-1}\circ F(g,g)]$
, where
$[F]\unicode[STIX]{x1D719}=[g^{-1}\circ F(g,g)]$
, where
![]() $g$
is a lift of
$g$
is a lift of
![]() $\unicode[STIX]{x1D719}$
over
$\unicode[STIX]{x1D719}$
over
![]() ${\mathcal{O}}$
. In the one-dimensional case, this action was introduced by Lubin and Tate [Reference Lubin and Tate12]. Its deep importance for the representation theory was revealed by Drinfeld [Reference Drinfeld6] and in a more specific way by Carayol [Reference Carayol1]. Later on, it was investigated by several researchers. Gross and Hopkins [Reference Gross and Hopkins8] defined the
${\mathcal{O}}$
. In the one-dimensional case, this action was introduced by Lubin and Tate [Reference Lubin and Tate12]. Its deep importance for the representation theory was revealed by Drinfeld [Reference Drinfeld6] and in a more specific way by Carayol [Reference Carayol1]. Later on, it was investigated by several researchers. Gross and Hopkins [Reference Gross and Hopkins8] defined the
![]() $p$
-adic period map from the generic fiber of the deformation functor to the projective space and proved that it is equivariant with respect to the action of the automorphism group. It provides a linearization of the action for the deformations over
$p$
-adic period map from the generic fiber of the deformation functor to the projective space and proved that it is equivariant with respect to the action of the automorphism group. It provides a linearization of the action for the deformations over
![]() ${\mathcal{O}}$
. Chai [Reference Chai2] studied this action on the closed fiber of the deformation space and described it by certain recurrence relation. Another explicit description for the action which also involved the
${\mathcal{O}}$
. Chai [Reference Chai2] studied this action on the closed fiber of the deformation space and described it by certain recurrence relation. Another explicit description for the action which also involved the
![]() $p$
-adic period map was established by the authors [Reference Demchenko and Gurevich4]. Our second purpose in the present work is to study this action in the higher dimensional case. We proceed similarly to what was done in [Reference Demchenko and Gurevich4]. Namely, applying Honda’s description of
$p$
-adic period map was established by the authors [Reference Demchenko and Gurevich4]. Our second purpose in the present work is to study this action in the higher dimensional case. We proceed similarly to what was done in [Reference Demchenko and Gurevich4]. Namely, applying Honda’s description of
![]() $\text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
and the explicit formula for the period map we obtain an explicit expression for the action in terms of the parametrization introduced in [Reference Demchenko and Gurevich5].
$\text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
and the explicit formula for the period map we obtain an explicit expression for the action in terms of the parametrization introduced in [Reference Demchenko and Gurevich5].
The outline of the paper is as follows. Section 2 recalls the basic definitions related to formal groups and describing the main results of Honda theory [Reference Honda10] and covariant Honda theory [Reference Demchenko3] which are our main tools. In Section 3, Hazewinkel’s universal
![]() $d$
-dimensional
$d$
-dimensional
![]() $p$
-typical formal group
$p$
-typical formal group
![]() $F_{V}$
over the ring
$F_{V}$
over the ring
![]() $\mathbb{Z}[V]$
of polynomials in an infinite set
$\mathbb{Z}[V]$
of polynomials in an infinite set
![]() $V$
of independent variables is introduced. Any
$V$
of independent variables is introduced. Any
![]() $p$
-typical formal group
$p$
-typical formal group
![]() $\unicode[STIX]{x1D6F7}$
over
$\unicode[STIX]{x1D6F7}$
over
![]() $k$
can be obtained from
$k$
can be obtained from
![]() $F_{V}$
by a specialization of the variables of
$F_{V}$
by a specialization of the variables of
![]() $V$
in
$V$
in
![]() $k$
. We recall the main result of [Reference Demchenko and Gurevich5] which states that it is possible to choose a finite set
$k$
. We recall the main result of [Reference Demchenko and Gurevich5] which states that it is possible to choose a finite set
![]() $\{{v_{\unicode[STIX]{x1D713}}\}}_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}$
of variables from
$\{{v_{\unicode[STIX]{x1D713}}\}}_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}$
of variables from
![]() $V$
and to define a homomorphism
$V$
and to define a homomorphism
![]() $\unicode[STIX]{x1D6FE}:\mathbb{Z}[V]\rightarrow {\mathcal{O}}[[t_{\unicode[STIX]{x1D713}}]]_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}$
so that
$\unicode[STIX]{x1D6FE}:\mathbb{Z}[V]\rightarrow {\mathcal{O}}[[t_{\unicode[STIX]{x1D713}}]]_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}$
so that
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6FE}_{\ast }F_{V}$
is a universal deformation of
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6FE}_{\ast }F_{V}$
is a universal deformation of
![]() $\unicode[STIX]{x1D6F7}$
. In particular, it gives a one-to-one correspondence between
$\unicode[STIX]{x1D6F7}$
. In particular, it gives a one-to-one correspondence between
![]() ${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}({\mathcal{O}})$
and
${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}({\mathcal{O}})$
and
![]() $p{\mathcal{O}}^{|\unicode[STIX]{x1D6F9}^{+}|}$
.
$p{\mathcal{O}}^{|\unicode[STIX]{x1D6F9}^{+}|}$
.
In Section 4, a period map from the set of
![]() $\star$
-isomorphism classes of
$\star$
-isomorphism classes of
![]() ${\mathcal{O}}$
-deformations of
${\mathcal{O}}$
-deformations of
![]() $\unicode[STIX]{x1D6F7}$
to
$\unicode[STIX]{x1D6F7}$
to
![]() $\text{GL}_{d}({\mathcal{O}})\backslash \text{GL}_{d}(E)/I+\text{M}_{d}(E)\widehat{u}$
is constructed, where
$\text{GL}_{d}({\mathcal{O}})\backslash \text{GL}_{d}(E)/I+\text{M}_{d}(E)\widehat{u}$
is constructed, where
![]() $E={\mathcal{O}}[[\blacktriangle ]]$
is an
$E={\mathcal{O}}[[\blacktriangle ]]$
is an
![]() ${\mathcal{O}}$
-algebra with multiplication rule
${\mathcal{O}}$
-algebra with multiplication rule
![]() $\blacktriangle a=\unicode[STIX]{x1D6E5}(a)\blacktriangle$
,
$\blacktriangle a=\unicode[STIX]{x1D6E5}(a)\blacktriangle$
,
![]() $a\in {\mathcal{O}}$
,
$a\in {\mathcal{O}}$
,
![]() $\unicode[STIX]{x1D6E5}$
denotes the Frobenius automorphism, and
$\unicode[STIX]{x1D6E5}$
denotes the Frobenius automorphism, and
![]() $\widehat{u}\in \text{M}_{d}(E)$
is Honda type of a deformation of
$\widehat{u}\in \text{M}_{d}(E)$
is Honda type of a deformation of
![]() $\unicode[STIX]{x1D6F7}$
. It gives another parametrization of
$\unicode[STIX]{x1D6F7}$
. It gives another parametrization of
![]() ${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}({\mathcal{O}})$
. Then an explicit relation between these two parameterizations is established. For a natural example, we deduce an explicit formula which expresses the parameters obtained from the cosets in
${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}({\mathcal{O}})$
. Then an explicit relation between these two parameterizations is established. For a natural example, we deduce an explicit formula which expresses the parameters obtained from the cosets in
![]() $\text{GL}_{d}(E)$
via the parameters obtained from the universal deformation with the aid of certain rigid analytic functions. It turns out that in the one-dimensional case, these functions coincide up to a constant factor with the functions used by Gross and Hopkins [Reference Gross and Hopkins8] for the definition of their
$\text{GL}_{d}(E)$
via the parameters obtained from the universal deformation with the aid of certain rigid analytic functions. It turns out that in the one-dimensional case, these functions coincide up to a constant factor with the functions used by Gross and Hopkins [Reference Gross and Hopkins8] for the definition of their
![]() $p$
-adic period map.
$p$
-adic period map.
Section 5 describes the action of the automorphism group of
![]() $\unicode[STIX]{x1D6F7}$
on
$\unicode[STIX]{x1D6F7}$
on
![]() ${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}({\mathcal{O}})$
in the coordinate system introduced in Section 3. Honda theory implies that
${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}({\mathcal{O}})$
in the coordinate system introduced in Section 3. Honda theory implies that
![]() $\text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
acts on
$\text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
acts on
![]() $\text{GL}_{d}({\mathcal{O}})\backslash \text{GL}_{d}(E)/I+\text{M}_{d}(E)\widehat{u}$
by the right multiplication. We show that this action agrees with the natural action on
$\text{GL}_{d}({\mathcal{O}})\backslash \text{GL}_{d}(E)/I+\text{M}_{d}(E)\widehat{u}$
by the right multiplication. We show that this action agrees with the natural action on
![]() ${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}({\mathcal{O}})$
(Theorem 5.1). Thus our period map linearizes the action of the automorphism group on the moduli space which provides its explicit description (Theorem 5.2). In the case of a formal group of dimension 1, this result implies the equivariance of the Gross–Hopkins period map [Reference Gross and Hopkins8, Proposition 23.5].
${\mathcal{D}}ef_{\unicode[STIX]{x1D6F7}}({\mathcal{O}})$
(Theorem 5.1). Thus our period map linearizes the action of the automorphism group on the moduli space which provides its explicit description (Theorem 5.2). In the case of a formal group of dimension 1, this result implies the equivariance of the Gross–Hopkins period map [Reference Gross and Hopkins8, Proposition 23.5].
Throughout the paper, the following notations are used.
![]() $\text{M}_{d^{\prime },d}(A)$
denotes the set of
$\text{M}_{d^{\prime },d}(A)$
denotes the set of
![]() $d^{\prime }\times d$
-matrices with entries in the ring
$d^{\prime }\times d$
-matrices with entries in the ring
![]() $A$
,
$A$
,
![]() $\text{M}_{d}(A)=\text{M}_{d,d}(A)$
,
$\text{M}_{d}(A)=\text{M}_{d,d}(A)$
,
![]() $\text{GL}_{d}(A)$
stands for the subset of
$\text{GL}_{d}(A)$
stands for the subset of
![]() $\text{M}_{d}(A)$
consisting of the invertible matrices. The identity matrix is denoted by
$\text{M}_{d}(A)$
consisting of the invertible matrices. The identity matrix is denoted by
![]() $I$
. An entry of a matrix
$I$
. An entry of a matrix
![]() $M\in \text{M}_{d}(A)$
in the
$M\in \text{M}_{d}(A)$
in the
![]() $i$
th row and the
$i$
th row and the
![]() $j$
th column is denoted by
$j$
th column is denoted by
![]() $M(i,j)$
. The matrix obtained from
$M(i,j)$
. The matrix obtained from
![]() $M$
by raising all its entries to the
$M$
by raising all its entries to the
![]() $q$
th power is denoted by
$q$
th power is denoted by
![]() $M^{(q)}$
, i.e.,
$M^{(q)}$
, i.e.,
![]() $M^{(q)}(i,j)=M(i,j)^{q}$
,
$M^{(q)}(i,j)=M(i,j)^{q}$
,
![]() $1\leqslant i,j\leqslant d$
. If
$1\leqslant i,j\leqslant d$
. If
![]() $\unicode[STIX]{x1D707}:A\rightarrow A^{\prime }$
is a ring homomorphism and
$\unicode[STIX]{x1D707}:A\rightarrow A^{\prime }$
is a ring homomorphism and
![]() $f\in A[[X]]$
, then
$f\in A[[X]]$
, then
![]() $\unicode[STIX]{x1D707}_{\ast }f\in A^{\prime }[[X]]$
denotes a power series obtained by applying
$\unicode[STIX]{x1D707}_{\ast }f\in A^{\prime }[[X]]$
denotes a power series obtained by applying
![]() $\unicode[STIX]{x1D707}$
to the coefficients of
$\unicode[STIX]{x1D707}$
to the coefficients of
![]() $f$
.
$f$
.
2 Formal groups and Honda theory
Let
![]() $A$
be a ring. We denote by
$A$
be a ring. We denote by
![]() $X$
the
$X$
the
![]() $d$
-tuple of independent variables
$d$
-tuple of independent variables
![]() $(x_{1},\ldots ,x_{d})$
and write
$(x_{1},\ldots ,x_{d})$
and write
![]() $X^{q},q\in \mathbb{N}$
, for the
$X^{q},q\in \mathbb{N}$
, for the
![]() $d$
-tuple
$d$
-tuple
![]() $(x_{1}^{q},\ldots ,x_{d}^{q})$
. We also consider the ring
$(x_{1}^{q},\ldots ,x_{d}^{q})$
. We also consider the ring
![]() $A[[X]]_{0}$
of formal power series over
$A[[X]]_{0}$
of formal power series over
![]() $A$
in variables
$A$
in variables
![]() $x_{1},\ldots ,x_{d}$
without constant term.
$x_{1},\ldots ,x_{d}$
without constant term.
A
![]() $d$
-dimensional formal group over
$d$
-dimensional formal group over
![]() $A$
is a
$A$
is a
![]() $d$
-tuple of formal power series
$d$
-tuple of formal power series
![]() $F\in A[[X,Y]]^{d}$
satisfying the following properties
$F\in A[[X,Y]]^{d}$
satisfying the following properties
(i)
 $F(X,0)=X$
;
$F(X,0)=X$
;(ii)
 $F(X,F(Y,Z))=F(F(X,Y),Z)$
;
$F(X,F(Y,Z))=F(F(X,Y),Z)$
;(iii)
 $F(X,Y)=F(Y,X)$
.
$F(X,Y)=F(Y,X)$
.
Let
![]() $F$
and
$F$
and
![]() $F^{\prime }$
be
$F^{\prime }$
be
![]() $d$
- and
$d$
- and
![]() $d^{\prime }$
-dimensional formal groups over
$d^{\prime }$
-dimensional formal groups over
![]() $A$
. A
$A$
. A
![]() $d^{\prime }$
-tuple of formal power series
$d^{\prime }$
-tuple of formal power series
![]() $g\in A[[X]]_{0}^{d^{\prime }}$
is called a homomorphism from
$g\in A[[X]]_{0}^{d^{\prime }}$
is called a homomorphism from
![]() $F$
to
$F$
to
![]() $F^{\prime }$
, if
$F^{\prime }$
, if
![]() $g(F(X,Y))=F^{\prime }(g(X),g(Y))$
. The matrix
$g(F(X,Y))=F^{\prime }(g(X),g(Y))$
. The matrix
![]() $D\in \text{M}_{d^{\prime },d}(A)$
satisfying
$D\in \text{M}_{d^{\prime },d}(A)$
satisfying
![]() $g(X)\equiv DX\hspace{0.6em}{\rm mod}\hspace{0.2em}\deg 2$
is called the linear coefficient of
$g(X)\equiv DX\hspace{0.6em}{\rm mod}\hspace{0.2em}\deg 2$
is called the linear coefficient of
![]() $g$
. It is easy to see that a homomorphism
$g$
. It is easy to see that a homomorphism
![]() $g$
is an isomorphism if and only if its linear coefficient is an invertible matrix. A homomorphism with identity linear coefficient is called a strict isomorphism.
$g$
is an isomorphism if and only if its linear coefficient is an invertible matrix. A homomorphism with identity linear coefficient is called a strict isomorphism.
If
![]() $A$
is a
$A$
is a
![]() $\mathbb{Q}$
-algebra, then for any
$\mathbb{Q}$
-algebra, then for any
![]() $d$
-dimensional formal group
$d$
-dimensional formal group
![]() $F$
over
$F$
over
![]() $A$
, there exists a unique strict isomorphism
$A$
, there exists a unique strict isomorphism
![]() $f$
from
$f$
from
![]() $F$
to
$F$
to
![]() $F_{a}^{d}(X,Y)=X+Y$
(see for instance [Reference Honda10, Theorem 1]). This
$F_{a}^{d}(X,Y)=X+Y$
(see for instance [Reference Honda10, Theorem 1]). This
![]() $f$
is called the logarithm of
$f$
is called the logarithm of
![]() $F$
. It determines the formal group
$F$
. It determines the formal group
![]() $F$
uniquely, since
$F$
uniquely, since
![]() $F(X,Y)=f^{-1}(f(X)+f(Y))$
.
$F(X,Y)=f^{-1}(f(X)+f(Y))$
.
If
![]() $A$
is a ring of characteristic
$A$
is a ring of characteristic
![]() $0$
and
$0$
and
![]() $F$
is a formal group over
$F$
is a formal group over
![]() $A$
, the logarithm of
$A$
, the logarithm of
![]() $F$
is by definition the logarithm of
$F$
is by definition the logarithm of
![]() $F_{A\otimes \mathbb{Q}}$
. If, in addition,
$F_{A\otimes \mathbb{Q}}$
. If, in addition,
![]() $F^{\prime }$
is another formal group over
$F^{\prime }$
is another formal group over
![]() $A$
and
$A$
and
![]() $g$
is a homomorphism from
$g$
is a homomorphism from
![]() $F$
to
$F$
to
![]() $F^{\prime }$
with linear coefficient
$F^{\prime }$
with linear coefficient
![]() $D$
, then
$D$
, then
![]() $g={f^{\prime }}^{-1}\circ (Df)$
, where
$g={f^{\prime }}^{-1}\circ (Df)$
, where
![]() $f$
,
$f$
,
![]() $f^{\prime }$
are the logarithms of
$f^{\prime }$
are the logarithms of
![]() $F$
,
$F$
,
![]() $F^{\prime }$
, respectively (see [Reference Honda10, Proposition 1.6]).
$F^{\prime }$
, respectively (see [Reference Honda10, Proposition 1.6]).
Let
![]() $k$
be a perfect field of characteristic
$k$
be a perfect field of characteristic
![]() $p\neq 0$
,
$p\neq 0$
,
![]() ${\mathcal{O}}$
be the ring of Witt vectors over
${\mathcal{O}}$
be the ring of Witt vectors over
![]() $k$
,
$k$
,
![]() ${\mathcal{K}}$
be the quotient field of
${\mathcal{K}}$
be the quotient field of
![]() ${\mathcal{O}}$
, and
${\mathcal{O}}$
, and
![]() $\unicode[STIX]{x1D6E5}:{\mathcal{K}}\rightarrow {\mathcal{K}}$
be the Frobenius automorphism. Let
$\unicode[STIX]{x1D6E5}:{\mathcal{K}}\rightarrow {\mathcal{K}}$
be the Frobenius automorphism. Let
![]() $E={\mathcal{O}}[[\blacktriangle ]]$
denote the
$E={\mathcal{O}}[[\blacktriangle ]]$
denote the
![]() ${\mathcal{O}}$
-algebra of noncommutative formal power series in the variable
${\mathcal{O}}$
-algebra of noncommutative formal power series in the variable
![]() $\blacktriangle$
over
$\blacktriangle$
over
![]() ${\mathcal{O}}$
with the multiplication rule
${\mathcal{O}}$
with the multiplication rule
![]() $\blacktriangle a=a^{\unicode[STIX]{x1D6E5}}\blacktriangle$
for any
$\blacktriangle a=a^{\unicode[STIX]{x1D6E5}}\blacktriangle$
for any
![]() $a\in {\mathcal{O}}$
. Extend the
$a\in {\mathcal{O}}$
. Extend the
![]() ${\mathcal{O}}$
-module structure on
${\mathcal{O}}$
-module structure on
![]() ${\mathcal{K}}[[X]]_{0}$
to a left
${\mathcal{K}}[[X]]_{0}$
to a left
![]() $E$
-module structure by the formula
$E$
-module structure by the formula
![]() $\blacktriangle f(X)=f^{\unicode[STIX]{x1D6E5}}(X^{p})$
. It determines a bilinear map
$\blacktriangle f(X)=f^{\unicode[STIX]{x1D6E5}}(X^{p})$
. It determines a bilinear map
![]() $\text{M}_{d^{\prime },d}(E)\times {\mathcal{K}}[[X]]_{0}^{d}\rightarrow {\mathcal{K}}[[X]]_{0}^{d^{\prime }}$
. In particular, it gives a left
$\text{M}_{d^{\prime },d}(E)\times {\mathcal{K}}[[X]]_{0}^{d}\rightarrow {\mathcal{K}}[[X]]_{0}^{d^{\prime }}$
. In particular, it gives a left
![]() $\text{M}_{d}(E)$
-module structure on
$\text{M}_{d}(E)$
-module structure on
![]() ${\mathcal{K}}[[X]]_{0}^{d}$
.
${\mathcal{K}}[[X]]_{0}^{d}$
.
Denote
![]() $\mathfrak{P}=p{\mathcal{O}}[[X]]_{0}^{d}$
. Let
$\mathfrak{P}=p{\mathcal{O}}[[X]]_{0}^{d}$
. Let
![]() $u\in \text{M}_{d}(E)$
be such that
$u\in \text{M}_{d}(E)$
be such that
![]() $u\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
. We say that
$u\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
. We say that
![]() $u$
is a type of
$u$
is a type of
![]() $f\in {\mathcal{K}}[[X]]_{0}^{d}$
if
$f\in {\mathcal{K}}[[X]]_{0}^{d}$
if
![]() $f(X)\equiv X\hspace{0.6em}{\rm mod}\hspace{0.2em}\deg 2$
and
$f(X)\equiv X\hspace{0.6em}{\rm mod}\hspace{0.2em}\deg 2$
and
![]() $uf\in \mathfrak{P}$
.
$uf\in \mathfrak{P}$
.
The next technical result will be employed in what follows.
Lemma 2.1. [Reference Honda10, Lemmas 4.2 and 2.3]
(1) Let
 $u\in \text{M}_{d}(E)$
,
$u\in \text{M}_{d}(E)$
,
 $u\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
,
$u\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
,
 $f\in {\mathcal{K}}[[X]]_{0}^{d}$
be of type
$f\in {\mathcal{K}}[[X]]_{0}^{d}$
be of type
 $u$
,
$u$
,
 $\unicode[STIX]{x1D713}_{1}\in {\mathcal{K}}[[X]]_{0}^{d}$
and
$\unicode[STIX]{x1D713}_{1}\in {\mathcal{K}}[[X]]_{0}^{d}$
and
 $\unicode[STIX]{x1D713}_{2}\in {\mathcal{O}}[[X]]_{0}^{d}$
. Then
$\unicode[STIX]{x1D713}_{2}\in {\mathcal{O}}[[X]]_{0}^{d}$
. Then
 $f\circ \unicode[STIX]{x1D713}_{1}\equiv f\circ \unicode[STIX]{x1D713}_{2}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
iff
$f\circ \unicode[STIX]{x1D713}_{1}\equiv f\circ \unicode[STIX]{x1D713}_{2}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
iff
 $\unicode[STIX]{x1D713}_{1}\equiv \unicode[STIX]{x1D713}_{2}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
.
$\unicode[STIX]{x1D713}_{1}\equiv \unicode[STIX]{x1D713}_{2}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
.(2) Let
 $u,v\in \text{M}_{d}(E)$
,
$u,v\in \text{M}_{d}(E)$
,
 $u\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
,
$u\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
,
 $f\in {\mathcal{K}}[[X]]_{0}^{d}$
be of type
$f\in {\mathcal{K}}[[X]]_{0}^{d}$
be of type
 $u$
and
$u$
and
 $g\in {\mathcal{O}}[[X]]_{0}^{d}$
. Then
$g\in {\mathcal{O}}[[X]]_{0}^{d}$
. Then
 $v(f\circ g)\equiv (vf)\circ g\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
.
$v(f\circ g)\equiv (vf)\circ g\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
.
Honda theory [Reference Honda10] describes the logarithms of formal groups over
![]() ${\mathcal{O}}$
as formal power series of certain Honda type.
${\mathcal{O}}$
as formal power series of certain Honda type.
Theorem 2.2. [Reference Honda10, Theorem 2 and Proposition 3.3]
(1) Let
 $u\in \text{M}_{d}(E)$
,
$u\in \text{M}_{d}(E)$
,
 $u\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
,
$u\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
,
 $f\in {\mathcal{K}}[[X]]_{0}^{d}$
be of type
$f\in {\mathcal{K}}[[X]]_{0}^{d}$
be of type
 $u$
. Then
$u$
. Then
 $f$
is the logarithm of a formal group over
$f$
is the logarithm of a formal group over
 ${\mathcal{O}}$
.
${\mathcal{O}}$
.(2) Let
 $F$
be a formal group over
$F$
be a formal group over
 ${\mathcal{O}}$
with the logarithm
${\mathcal{O}}$
with the logarithm
 $f\in {\mathcal{K}}[[X]]_{0}^{d}$
. Then there exists
$f\in {\mathcal{K}}[[X]]_{0}^{d}$
. Then there exists
 $u\in \text{M}_{d}(E)$
,
$u\in \text{M}_{d}(E)$
,
 $u\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
, such that
$u\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
, such that
 $f$
is of type
$f$
is of type
 $u$
.
$u$
.
With the aid of Honda theory, the category of formal groups over
![]() $k$
can be also described and the Dieudonné module can be constructed. Under reduction of a formal power series with coefficients in
$k$
can be also described and the Dieudonné module can be constructed. Under reduction of a formal power series with coefficients in
![]() ${\mathcal{O}}$
, we always mean the reduction modulo
${\mathcal{O}}$
, we always mean the reduction modulo
![]() $p$
.
$p$
.
Proposition 2.3. Let
![]() $F_{1},F_{2}$
be formal groups over
$F_{1},F_{2}$
be formal groups over
![]() ${\mathcal{O}}$
with the logarithms
${\mathcal{O}}$
with the logarithms
![]() $f_{1},f_{2}\in {\mathcal{K}}[[X]]_{0}^{d}$
, respectively. Then the reductions of
$f_{1},f_{2}\in {\mathcal{K}}[[X]]_{0}^{d}$
, respectively. Then the reductions of
![]() $F_{1}$
and
$F_{1}$
and
![]() $F_{2}$
are equal iff there exists
$F_{2}$
are equal iff there exists
![]() $v\in I+\blacktriangle \text{M}_{d}(E)$
such that
$v\in I+\blacktriangle \text{M}_{d}(E)$
such that
![]() $f_{1}\equiv vf_{2}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
.
$f_{1}\equiv vf_{2}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
.
Proof. The “if” part follows immediately from [Reference Demchenko and Gurevich5, Proposition 1]. To prove the “only if” part suppose that the reductions of
![]() $F_{1}$
and
$F_{1}$
and
![]() $F_{2}$
are equal. According to [Reference Demchenko and Gurevich5, Proposition 1], there exists
$F_{2}$
are equal. According to [Reference Demchenko and Gurevich5, Proposition 1], there exists
![]() $q\in \text{GL}_{d}(E)$
such that
$q\in \text{GL}_{d}(E)$
such that
![]() $f_{1}\equiv qf_{2}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
. Let
$f_{1}\equiv qf_{2}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
. Let
![]() $c\in \text{M}_{d}({\mathcal{O}})$
be such that
$c\in \text{M}_{d}({\mathcal{O}})$
be such that
![]() $q\equiv c\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
. Since
$q\equiv c\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
. Since
![]() $X\equiv f_{1}(X)\equiv qf_{2}(X)\equiv cX\;\text{mod}\,(\mathfrak{P},\deg 2)$
, we conclude
$X\equiv f_{1}(X)\equiv qf_{2}(X)\equiv cX\;\text{mod}\,(\mathfrak{P},\deg 2)$
, we conclude
![]() $I\equiv c\hspace{0.6em}{\rm mod}\hspace{0.2em}p$
, i.e., there exists
$I\equiv c\hspace{0.6em}{\rm mod}\hspace{0.2em}p$
, i.e., there exists
![]() $c^{\prime }\in \text{M}_{d}({\mathcal{O}})$
such that
$c^{\prime }\in \text{M}_{d}({\mathcal{O}})$
such that
![]() $c-I=pc^{\prime }$
. Let
$c-I=pc^{\prime }$
. Let
![]() $u_{2}\in \text{M}_{d}(E)$
be such that
$u_{2}\in \text{M}_{d}(E)$
be such that
![]() $u_{2}\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
and
$u_{2}\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
and
![]() $f_{2}$
is of type
$f_{2}$
is of type
![]() $u_{2}$
. Denote
$u_{2}$
. Denote
![]() $v=q-c^{\prime }u_{2}$
. Then
$v=q-c^{\prime }u_{2}$
. Then
![]() $v\equiv I\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
and
$v\equiv I\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
and
![]() $f_{1}\equiv qf_{2}=vf_{2}+c^{\prime }u_{2}f_{2}\equiv vf_{2}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
.◻
$f_{1}\equiv qf_{2}=vf_{2}+c^{\prime }u_{2}f_{2}\equiv vf_{2}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
.◻
Proposition 2.4. [Reference Honda10, Proposition 2.6]
Let
![]() $v\in \text{M}_{d^{\prime },d}(E)$
,
$v\in \text{M}_{d^{\prime },d}(E)$
,
![]() $u\in \text{M}_{d}(E)$
,
$u\in \text{M}_{d}(E)$
,
![]() $u\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
and
$u\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
and
![]() $f\in {\mathcal{K}}[[X]]_{0}^{d}$
be of type
$f\in {\mathcal{K}}[[X]]_{0}^{d}$
be of type
![]() $u$
. If
$u$
. If
![]() $vf\in p{\mathcal{O}}[[X]]_{0}^{d^{\prime }}$
, then there exists
$vf\in p{\mathcal{O}}[[X]]_{0}^{d^{\prime }}$
, then there exists
![]() $s\in \text{M}_{d^{\prime },d}(E)$
such that
$s\in \text{M}_{d^{\prime },d}(E)$
such that
![]() $v=su$
.
$v=su$
.
Let
![]() $F$
be a
$F$
be a
![]() $d$
-dimensional formal group over
$d$
-dimensional formal group over
![]() ${\mathcal{O}}$
with logarithm
${\mathcal{O}}$
with logarithm
![]() $f\in {\mathcal{K}}[[X]]_{0}^{d}$
of type
$f\in {\mathcal{K}}[[X]]_{0}^{d}$
of type
![]() $u\in \text{M}_{d}(E)$
, and
$u\in \text{M}_{d}(E)$
, and
![]() $\bar{F}$
denote the reduction of
$\bar{F}$
denote the reduction of
![]() $F$
. The
$F$
. The
![]() $E$
-module
$E$
-module
![]() ${\mathcal{D}}(\bar{F})=\text{M}_{1,d}(E)f/\text{M}_{1,d}(E)f\cap p{\mathcal{O}}[[X]]_{0}$
is called the Dieudonné module of
${\mathcal{D}}(\bar{F})=\text{M}_{1,d}(E)f/\text{M}_{1,d}(E)f\cap p{\mathcal{O}}[[X]]_{0}$
is called the Dieudonné module of
![]() $\bar{F}$
. Proposition 2.3 implies that
$\bar{F}$
. Proposition 2.3 implies that
![]() ${\mathcal{D}}(\bar{F})$
depends only on
${\mathcal{D}}(\bar{F})$
depends only on
![]() $\bar{F}$
. Since
$\bar{F}$
. Since
![]() $uf\in \mathfrak{P}$
, the
$uf\in \mathfrak{P}$
, the
![]() $E$
-linear map
$E$
-linear map
![]() $\text{M}_{1,d}(E)\rightarrow {\mathcal{D}}(\bar{F})$
defined by
$\text{M}_{1,d}(E)\rightarrow {\mathcal{D}}(\bar{F})$
defined by
![]() $s\mapsto sf+p{\mathcal{O}}[[X]]_{0}$
induces a homomorphism
$s\mapsto sf+p{\mathcal{O}}[[X]]_{0}$
induces a homomorphism
![]() $\text{M}_{1,d}(E)/\text{M}_{1,d}(E)u\rightarrow {\mathcal{D}}(\bar{F})$
which is an isomorphism by Proposition 2.4. A formal group
$\text{M}_{1,d}(E)/\text{M}_{1,d}(E)u\rightarrow {\mathcal{D}}(\bar{F})$
which is an isomorphism by Proposition 2.4. A formal group
![]() $\bar{F}$
is said to be of finite height if
$\bar{F}$
is said to be of finite height if
![]() ${\mathcal{D}}(\bar{F})$
is a free
${\mathcal{D}}(\bar{F})$
is a free
![]() ${\mathcal{O}}$
-module of finite rank (see [Reference Fontaine7, Proposition III.6.1]). In this case the rank of
${\mathcal{O}}$
-module of finite rank (see [Reference Fontaine7, Proposition III.6.1]). In this case the rank of
![]() ${\mathcal{D}}(\bar{F})$
is called the height of
${\mathcal{D}}(\bar{F})$
is called the height of
![]() $\bar{F}$
.
$\bar{F}$
.
The following theorem describes
![]() $\text{Aut}_{k}(\bar{F})$
in terms of Honda types.
$\text{Aut}_{k}(\bar{F})$
in terms of Honda types.
Theorem 2.5. [Reference Honda10, Theorems 5 and 6]
Let
![]() $F$
be a formal group over
$F$
be a formal group over
![]() ${\mathcal{O}}$
with the logarithm
${\mathcal{O}}$
with the logarithm
![]() $f\in {\mathcal{K}}[[X]]_{0}^{d}$
of type
$f\in {\mathcal{K}}[[X]]_{0}^{d}$
of type
![]() $u\in \text{M}_{d}(E)$
, and
$u\in \text{M}_{d}(E)$
, and
![]() $w\in \text{M}_{d}(E)$
. Then
$w\in \text{M}_{d}(E)$
. Then
(1)
 $f^{-1}\circ (wf)\in {\mathcal{O}}[[X]]_{0}^{d}$
iff there exists
$f^{-1}\circ (wf)\in {\mathcal{O}}[[X]]_{0}^{d}$
iff there exists
 $z\in \text{M}_{d}(E)$
such that
$z\in \text{M}_{d}(E)$
such that
 $uw=zu$
.
$uw=zu$
.(2) If
 $f^{-1}\circ (wf)\in {\mathcal{O}}[[X]]_{0}^{d}$
, then its reduction is an automorphism of the reduction of
$f^{-1}\circ (wf)\in {\mathcal{O}}[[X]]_{0}^{d}$
, then its reduction is an automorphism of the reduction of
 $F$
.
$F$
.(3) If
 $\unicode[STIX]{x1D719}$
is an automorphism of the reduction of
$\unicode[STIX]{x1D719}$
is an automorphism of the reduction of
 $F$
, then there exists
$F$
, then there exists
 $w\in \text{M}_{d}(E)$
such that
$w\in \text{M}_{d}(E)$
such that
 $f^{-1}\circ (wf)\in {\mathcal{O}}[[X]]_{0}^{d}$
and
$f^{-1}\circ (wf)\in {\mathcal{O}}[[X]]_{0}^{d}$
and
 $\unicode[STIX]{x1D719}$
is the reduction of
$\unicode[STIX]{x1D719}$
is the reduction of
 $f^{-1}\circ (wf)$
.
$f^{-1}\circ (wf)$
.
Let
![]() ${\mathcal{K}}[[t]]_{p}=\{\sum _{i=0}^{\infty }b_{i}t^{p^{i}}|b_{i}\in {\mathcal{K}}\}$
and
${\mathcal{K}}[[t]]_{p}=\{\sum _{i=0}^{\infty }b_{i}t^{p^{i}}|b_{i}\in {\mathcal{K}}\}$
and
![]() ${\mathcal{K}}[[X]]_{p}=\{\sum _{j=1}^{d}f_{j}(x_{j})|f_{j}\in {\mathcal{K}}[[t]]_{p}\}$
. For any
${\mathcal{K}}[[X]]_{p}=\{\sum _{j=1}^{d}f_{j}(x_{j})|f_{j}\in {\mathcal{K}}[[t]]_{p}\}$
. For any
![]() $\sum _{i=0}^{\infty }a_{i}\blacktriangle ^{i}\in E$
, define
$\sum _{i=0}^{\infty }a_{i}\blacktriangle ^{i}\in E$
, define
![]() $t^{p^{j}}\sum _{i=0}^{\infty }a_{i}\blacktriangle ^{i}=\sum _{i=0}^{\infty }a_{i}^{\unicode[STIX]{x1D6E5}^{j}}t^{p^{i+j}}$
. This provides to
$t^{p^{j}}\sum _{i=0}^{\infty }a_{i}\blacktriangle ^{i}=\sum _{i=0}^{\infty }a_{i}^{\unicode[STIX]{x1D6E5}^{j}}t^{p^{i+j}}$
. This provides to
![]() ${\mathcal{K}}[[t]]_{p}$
a right
${\mathcal{K}}[[t]]_{p}$
a right
![]() $E$
-module structure which in general looks as follows:
$E$
-module structure which in general looks as follows:
 $$\begin{eqnarray}\left(\mathop{\sum }_{j=0}^{\infty }b_{j}t^{p^{j}}\right)\left(\mathop{\sum }_{i=0}^{\infty }a_{i}\blacktriangle ^{i}\right)=\mathop{\sum }_{i=0}^{\infty }\left(\mathop{\sum }_{j=0}^{i}b_{j}a_{i-j}^{\unicode[STIX]{x1D6E5}^{j}}\right)t^{p^{i}}.\end{eqnarray}$$
$$\begin{eqnarray}\left(\mathop{\sum }_{j=0}^{\infty }b_{j}t^{p^{j}}\right)\left(\mathop{\sum }_{i=0}^{\infty }a_{i}\blacktriangle ^{i}\right)=\mathop{\sum }_{i=0}^{\infty }\left(\mathop{\sum }_{j=0}^{i}b_{j}a_{i-j}^{\unicode[STIX]{x1D6E5}^{j}}\right)t^{p^{i}}.\end{eqnarray}$$
It determines a right
![]() $\text{M}_{d}(E)$
-module structure on
$\text{M}_{d}(E)$
-module structure on
![]() ${\mathcal{K}}[[X]]_{p}^{d}$
. In fact, associating
${\mathcal{K}}[[X]]_{p}^{d}$
. In fact, associating
![]() $\sum _{i=0}^{\infty }b_{i}t^{p^{i}}$
with
$\sum _{i=0}^{\infty }b_{i}t^{p^{i}}$
with
![]() $\sum _{i=0}^{\infty }b_{i}\blacktriangle ^{i}$
identifies
$\sum _{i=0}^{\infty }b_{i}\blacktriangle ^{i}$
identifies
![]() ${\mathcal{K}}[[t]]_{p}$
with
${\mathcal{K}}[[t]]_{p}$
with
![]() ${\mathcal{K}}[[\blacktriangle ]]$
provided with screw multiplication
${\mathcal{K}}[[\blacktriangle ]]$
provided with screw multiplication
![]() $\blacktriangle a=a^{\unicode[STIX]{x1D6E5}}\blacktriangle$
. Then the right action of
$\blacktriangle a=a^{\unicode[STIX]{x1D6E5}}\blacktriangle$
. Then the right action of
![]() $E$
on
$E$
on
![]() ${\mathcal{K}}[[t]]_{p}$
corresponds to the right multiplication in
${\mathcal{K}}[[t]]_{p}$
corresponds to the right multiplication in
![]() ${\mathcal{K}}[[\blacktriangle ]]$
. Similarly,
${\mathcal{K}}[[\blacktriangle ]]$
. Similarly,
![]() ${\mathcal{K}}[[X]]_{p}^{d}$
and
${\mathcal{K}}[[X]]_{p}^{d}$
and
![]() $\text{M}_{d}({\mathcal{K}}[[\blacktriangle ]])$
can be identified, and the right action of
$\text{M}_{d}({\mathcal{K}}[[\blacktriangle ]])$
can be identified, and the right action of
![]() $\text{M}_{d}(E)$
on
$\text{M}_{d}(E)$
on
![]() ${\mathcal{K}}[[X]]_{p}^{d}$
corresponds to the right multiplication in
${\mathcal{K}}[[X]]_{p}^{d}$
corresponds to the right multiplication in
![]() $\text{M}_{d}({\mathcal{K}}[[\blacktriangle ]])$
.
$\text{M}_{d}({\mathcal{K}}[[\blacktriangle ]])$
.
Covariant Honda theory [Reference Demchenko3] gives an alternative description of the category of
![]() $p$
-typical formal groups over
$p$
-typical formal groups over
![]() ${\mathcal{O}}$
and can be considered as dual to Honda theory. Only one result from this theory will be used hereafter.
${\mathcal{O}}$
and can be considered as dual to Honda theory. Only one result from this theory will be used hereafter.
Proposition 2.6. [Reference Demchenko3, Proposition 1(i) and (iii)]
(1) The left
 $\text{M}_{d}(E)$
-module structure on
$\text{M}_{d}(E)$
-module structure on
 ${\mathcal{K}}[[X]]_{p}^{d}$
induced from
${\mathcal{K}}[[X]]_{p}^{d}$
induced from
 ${\mathcal{K}}[[X]]_{0}^{d}$
commutes with the right
${\mathcal{K}}[[X]]_{0}^{d}$
commutes with the right
 $\text{M}_{d}(E)$
-module structure.
$\text{M}_{d}(E)$
-module structure.(2) Let
 $f\in {\mathcal{K}}[[X]]_{p}^{d}$
and
$f\in {\mathcal{K}}[[X]]_{p}^{d}$
and
 $u\in \text{M}_{d}(E)$
,
$u\in \text{M}_{d}(E)$
,
 $u\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
. Then
$u\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
. Then
 $uf=pX$
iff
$uf=pX$
iff
 $fu=pX$
.
$fu=pX$
.
3 Universal
 $p$
-typical formal group and universal deformation
$p$
-typical formal group and universal deformation
We consider polynomial rings with integer coefficients in an infinite number of variables which are grouped together in matrices for convenience. Let
![]() $V_{n}$
be
$V_{n}$
be
![]() $d\times d$
-matrices of independent variables
$d\times d$
-matrices of independent variables
![]() $V_{n}(i,j)$
. The set of these independent variables is denoted by
$V_{n}(i,j)$
. The set of these independent variables is denoted by
![]() $V=(V_{1},V_{2},\ldots )$
.
$V=(V_{1},V_{2},\ldots )$
.
According to Hazewinkel’s functional equation lemma [Reference Hazewinkel9, Section 10.2], the
![]() $d$
-tuple of power series
$d$
-tuple of power series
![]() $f_{V}\in \mathbb{Q}[V][[X]]_{0}^{d}$
defined by the recursion formula
$f_{V}\in \mathbb{Q}[V][[X]]_{0}^{d}$
defined by the recursion formula
where
![]() $\unicode[STIX]{x1D70E}(V_{n}(i,j))=V_{n}(i,j)^{p}$
, is the logarithm of a
$\unicode[STIX]{x1D70E}(V_{n}(i,j))=V_{n}(i,j)^{p}$
, is the logarithm of a
![]() $d$
-dimensional formal group
$d$
-dimensional formal group
![]() $F_{V}$
defined over
$F_{V}$
defined over
![]() $\mathbb{Z}[V]$
.
$\mathbb{Z}[V]$
.
Let
![]() $a_{n}(V)\in \mathbb{Q}[V]$
denote the coefficients of
$a_{n}(V)\in \mathbb{Q}[V]$
denote the coefficients of
![]() $f_{V}$
, that means
$f_{V}$
, that means
![]() $f_{V}(X)=\sum _{n=0}^{\infty }a_{n}(V)X^{p^{n}}$
. It is clear that
$f_{V}(X)=\sum _{n=0}^{\infty }a_{n}(V)X^{p^{n}}$
. It is clear that
![]() $a_{0}(V)=I$
. The following recurrence relation will be employed hereafter.
$a_{0}(V)=I$
. The following recurrence relation will be employed hereafter.
Lemma 3.1. [Reference Hazewinkel9, Formula 10.4.5]
![]() $p\,a_{n}(V)=\sum _{k=1}^{n}a_{n-k}(V)V_{k}^{(p^{n-k})}$
.
$p\,a_{n}(V)=\sum _{k=1}^{n}a_{n-k}(V)V_{k}^{(p^{n-k})}$
.
Corollary.
![]() $p^{n}\,a_{n}(V)\in \mathbb{Z}[V]$
.
$p^{n}\,a_{n}(V)\in \mathbb{Z}[V]$
.
Proof. It follows immediately by induction on
![]() $n$
.◻
$n$
.◻
For a ring
![]() $A$
, denote by
$A$
, denote by
![]() $A^{\infty }$
the
$A^{\infty }$
the
![]() $A$
-module consisting of the infinite sequences of elements of
$A$
-module consisting of the infinite sequences of elements of
![]() $A$
. Then
$A$
. Then
![]() $A_{m}^{\infty }$
is the submodule of
$A_{m}^{\infty }$
is the submodule of
![]() $A^{\infty }$
consisting of the sequences starting with
$A^{\infty }$
consisting of the sequences starting with
![]() $m$
zeros.
$m$
zeros.
A formal group
![]() $F$
over a ring
$F$
over a ring
![]() $A$
is called
$A$
is called
![]() $p$
-typical, if there exists
$p$
-typical, if there exists
![]() $\unicode[STIX]{x1D6EF}:\mathbb{Z}[V]\rightarrow A$
such that
$\unicode[STIX]{x1D6EF}:\mathbb{Z}[V]\rightarrow A$
such that
![]() $\unicode[STIX]{x1D6EF}_{\ast }F_{V}=F$
. A morphism
$\unicode[STIX]{x1D6EF}_{\ast }F_{V}=F$
. A morphism
![]() $\unicode[STIX]{x1D6EF}:\mathbb{Z}[V]\rightarrow A$
is uniquely defined by the sequence
$\unicode[STIX]{x1D6EF}:\mathbb{Z}[V]\rightarrow A$
is uniquely defined by the sequence
![]() $(\unicode[STIX]{x1D6EF}(V_{1}),\unicode[STIX]{x1D6EF}(V_{2}),\ldots )\in \text{M}_{d}(A)^{\infty }$
where
$(\unicode[STIX]{x1D6EF}(V_{1}),\unicode[STIX]{x1D6EF}(V_{2}),\ldots )\in \text{M}_{d}(A)^{\infty }$
where
![]() $\unicode[STIX]{x1D6EF}(V_{n})\in \text{M}_{d}(A)$
is defined by
$\unicode[STIX]{x1D6EF}(V_{n})\in \text{M}_{d}(A)$
is defined by
![]() $(\unicode[STIX]{x1D6EF}(V_{n}))(i,j)=\unicode[STIX]{x1D6EF}(V_{n}(i,j))$
. Thus we can write by abuse of the notation
$(\unicode[STIX]{x1D6EF}(V_{n}))(i,j)=\unicode[STIX]{x1D6EF}(V_{n}(i,j))$
. Thus we can write by abuse of the notation
![]() $\unicode[STIX]{x1D6EF}=(\unicode[STIX]{x1D6EF}(V_{1}),\unicode[STIX]{x1D6EF}(V_{2}),\ldots )$
. We will also write
$\unicode[STIX]{x1D6EF}=(\unicode[STIX]{x1D6EF}(V_{1}),\unicode[STIX]{x1D6EF}(V_{2}),\ldots )$
. We will also write
![]() $F_{V(\unicode[STIX]{x1D6EF})}$
instead of
$F_{V(\unicode[STIX]{x1D6EF})}$
instead of
![]() $\unicode[STIX]{x1D6EF}_{\ast }F_{V}$
.
$\unicode[STIX]{x1D6EF}_{\ast }F_{V}$
.
Let
![]() $k$
,
$k$
,
![]() ${\mathcal{O}}$
,
${\mathcal{O}}$
,
![]() $E$
be as in Section 2. Let
$E$
be as in Section 2. Let
![]() $\unicode[STIX]{x1D6F7}$
be a
$\unicode[STIX]{x1D6F7}$
be a
![]() $d$
-dimensional formal group over
$d$
-dimensional formal group over
![]() $k$
of height
$k$
of height
![]() $h$
. According to [Reference Hazewinkel9, Corollary 25.4.29],
$h$
. According to [Reference Hazewinkel9, Corollary 25.4.29],
![]() $\unicode[STIX]{x1D6F7}$
is isomorphic to a
$\unicode[STIX]{x1D6F7}$
is isomorphic to a
![]() $p$
-typical formal group over
$p$
-typical formal group over
![]() $k$
. Thus without loss of generality we can suppose that
$k$
. Thus without loss of generality we can suppose that
![]() $\unicode[STIX]{x1D6F7}$
is
$\unicode[STIX]{x1D6F7}$
is
![]() $p$
-typical, i.e., there exists
$p$
-typical, i.e., there exists
![]() $\unicode[STIX]{x1D6EF}=(\unicode[STIX]{x1D6EF}_{1},\unicode[STIX]{x1D6EF}_{2},\ldots )\in \text{M}_{d}(k)^{\infty }$
such that
$\unicode[STIX]{x1D6EF}=(\unicode[STIX]{x1D6EF}_{1},\unicode[STIX]{x1D6EF}_{2},\ldots )\in \text{M}_{d}(k)^{\infty }$
such that
![]() $\unicode[STIX]{x1D6F7}=F_{V(\unicode[STIX]{x1D6EF})}$
. Let
$\unicode[STIX]{x1D6F7}=F_{V(\unicode[STIX]{x1D6EF})}$
. Let
![]() $\widehat{\unicode[STIX]{x1D6EF}}=(\widehat{\unicode[STIX]{x1D6EF}}_{1},\widehat{\unicode[STIX]{x1D6EF}}_{2},\ldots )\in \text{M}_{d}({\mathcal{O}})^{\infty }$
be the sequence of matrices which are composed of the multiplicative representatives in
$\widehat{\unicode[STIX]{x1D6EF}}=(\widehat{\unicode[STIX]{x1D6EF}}_{1},\widehat{\unicode[STIX]{x1D6EF}}_{2},\ldots )\in \text{M}_{d}({\mathcal{O}})^{\infty }$
be the sequence of matrices which are composed of the multiplicative representatives in
![]() ${\mathcal{O}}$
of the entries of the matrices
${\mathcal{O}}$
of the entries of the matrices
![]() $\unicode[STIX]{x1D6EF}_{1},\unicode[STIX]{x1D6EF}_{2},\ldots$
Then
$\unicode[STIX]{x1D6EF}_{1},\unicode[STIX]{x1D6EF}_{2},\ldots$
Then
![]() $\widehat{F}=F_{V(\widehat{\unicode[STIX]{x1D6EF}})}$
is a formal group over
$\widehat{F}=F_{V(\widehat{\unicode[STIX]{x1D6EF}})}$
is a formal group over
![]() ${\mathcal{O}}$
, and its reduction is equal to
${\mathcal{O}}$
, and its reduction is equal to
![]() $\unicode[STIX]{x1D6F7}$
.
$\unicode[STIX]{x1D6F7}$
.
Given a sequence
![]() $T=(T_{1},T_{2},\ldots )\in \text{M}_{d}(k)^{\infty }$
, we introduce
$T=(T_{1},T_{2},\ldots )\in \text{M}_{d}(k)^{\infty }$
, we introduce
for
![]() $n\geqslant 2$
and
$n\geqslant 2$
and
![]() $Y_{1}(\unicode[STIX]{x1D6EF},T)=0$
. Then
$Y_{1}(\unicode[STIX]{x1D6EF},T)=0$
. Then
![]() $Y_{\unicode[STIX]{x1D6EF}}(T)=(Y_{1}(\unicode[STIX]{x1D6EF},T),Y_{2}(\unicode[STIX]{x1D6EF},T),\ldots )$
defines a
$Y_{\unicode[STIX]{x1D6EF}}(T)=(Y_{1}(\unicode[STIX]{x1D6EF},T),Y_{2}(\unicode[STIX]{x1D6EF},T),\ldots )$
defines a
![]() $k$
-linear operator on
$k$
-linear operator on
![]() $\text{M}_{d}(k)^{\infty }$
.
$\text{M}_{d}(k)^{\infty }$
.
For
![]() $n\geqslant 1$
,
$n\geqslant 1$
,
![]() $1\leqslant i,j\leqslant d$
, denote by
$1\leqslant i,j\leqslant d$
, denote by
![]() $B_{(n,i,j)}\in \text{M}_{d}(k)^{\infty }$
the sequence of matrices with the only nonzero entry which is equal to 1 and appears in the
$B_{(n,i,j)}\in \text{M}_{d}(k)^{\infty }$
the sequence of matrices with the only nonzero entry which is equal to 1 and appears in the
![]() $n$
th matrix at the
$n$
th matrix at the
![]() $(i,j)$
th position. According to [Reference Demchenko and Gurevich5, Proposition 8], there exists a set
$(i,j)$
th position. According to [Reference Demchenko and Gurevich5, Proposition 8], there exists a set
such that
![]() $\{B_{\unicode[STIX]{x1D713}}+\text{Im}Y_{\unicode[STIX]{x1D6EF}}|\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}\}$
is a basis of
$\{B_{\unicode[STIX]{x1D713}}+\text{Im}Y_{\unicode[STIX]{x1D6EF}}|\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}\}$
is a basis of
![]() $\text{Coker}Y_{\unicode[STIX]{x1D6EF}}$
. Moreover,
$\text{Coker}Y_{\unicode[STIX]{x1D6EF}}$
. Moreover,
![]() $|\unicode[STIX]{x1D6F9}|=dh$
.
$|\unicode[STIX]{x1D6F9}|=dh$
.
Since
![]() $Y_{1}(V,T)=0$
, one has
$Y_{1}(V,T)=0$
, one has
![]() $\text{Im}Y_{\unicode[STIX]{x1D6EF}}\subset \text{M}_{d}(k)_{1}^{\infty }$
, and hence
$\text{Im}Y_{\unicode[STIX]{x1D6EF}}\subset \text{M}_{d}(k)_{1}^{\infty }$
, and hence
![]() $\{(1,i,j)|1\leqslant i,j\leqslant d\}\subset \unicode[STIX]{x1D6F9}$
. Define
$\{(1,i,j)|1\leqslant i,j\leqslant d\}\subset \unicode[STIX]{x1D6F9}$
. Define
![]() $\unicode[STIX]{x1D6F9}^{+}=\{(n,i,j)|(n+1,i,j)\in \unicode[STIX]{x1D6F9}\}$
. Clearly,
$\unicode[STIX]{x1D6F9}^{+}=\{(n,i,j)|(n+1,i,j)\in \unicode[STIX]{x1D6F9}\}$
. Clearly,
![]() $|\unicode[STIX]{x1D6F9}^{+}|=d(h-d)$
.
$|\unicode[STIX]{x1D6F9}^{+}|=d(h-d)$
.
Let
![]() $R$
be a complete Noetherian local ring with residue field
$R$
be a complete Noetherian local ring with residue field
![]() $k$
, and
$k$
, and
![]() $\unicode[STIX]{x1D6F7}$
be a formal group over
$\unicode[STIX]{x1D6F7}$
be a formal group over
![]() $k$
. A formal group
$k$
. A formal group
![]() $F$
over
$F$
over
![]() $R$
with reduction
$R$
with reduction
![]() $\unicode[STIX]{x1D6F7}$
is called a deformation of
$\unicode[STIX]{x1D6F7}$
is called a deformation of
![]() $\unicode[STIX]{x1D6F7}$
over
$\unicode[STIX]{x1D6F7}$
over
![]() $R$
. Let
$R$
. Let
![]() $F,F^{\prime }$
be deformations of
$F,F^{\prime }$
be deformations of
![]() $\unicode[STIX]{x1D6F7}$
over
$\unicode[STIX]{x1D6F7}$
over
![]() $R$
. An isomorphism from
$R$
. An isomorphism from
![]() $F$
to
$F$
to
![]() $F^{\prime }$
with identity reduction is called a
$F^{\prime }$
with identity reduction is called a
![]() $\star$
-isomorphism.
$\star$
-isomorphism.
Similarly to
![]() $B_{(n,i,j)}$
, denote by
$B_{(n,i,j)}$
, denote by
![]() $\widehat{B}_{(n,i,j)}\in \text{M}_{d}(R)^{\infty }$
the sequence of matrices with the only nonzero entry being equal to 1 and appearing in the
$\widehat{B}_{(n,i,j)}\in \text{M}_{d}(R)^{\infty }$
the sequence of matrices with the only nonzero entry being equal to 1 and appearing in the
![]() $n$
th matrix at the
$n$
th matrix at the
![]() $(i,j)$
th position.
$(i,j)$
th position.
Now we can formulate the main result of [Reference Demchenko and Gurevich5].
Theorem 3.2. [Reference Demchenko and Gurevich5, Theorem 2]
Let
![]() $\unicode[STIX]{x1D6F7}=F_{V(\unicode[STIX]{x1D6EF})}$
. Then for any complete Noetherian local
$\unicode[STIX]{x1D6F7}=F_{V(\unicode[STIX]{x1D6EF})}$
. Then for any complete Noetherian local
![]() ${\mathcal{O}}$
-algebra
${\mathcal{O}}$
-algebra
![]() $R$
with maximal ideal
$R$
with maximal ideal
![]() $\mathfrak{M}$
containing
$\mathfrak{M}$
containing
![]() $p$
and residue field
$p$
and residue field
![]() $k$
, and for any deformation
$k$
, and for any deformation
![]() $F$
of
$F$
of
![]() $\unicode[STIX]{x1D6F7}$
over
$\unicode[STIX]{x1D6F7}$
over
![]() $R$
:
$R$
:
(1) there exists a unique
 $dh$
-tuple
$dh$
-tuple
 $(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}})_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}}$
,
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}})_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}}$
,
 $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\in \mathfrak{M}$
, such that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\in \mathfrak{M}$
, such that
 $F$
is strictly
$F$
is strictly
 $\star$
-isomorphic to the formal group
$\star$
-isomorphic to the formal group
 $F_{V(Z)}$
, where
$F_{V(Z)}$
, where
 $Z=\widehat{\unicode[STIX]{x1D6EF}}+\sum _{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\widehat{B}_{\unicode[STIX]{x1D713}}\in \text{M}_{d}(R)^{\infty }$
;
$Z=\widehat{\unicode[STIX]{x1D6EF}}+\sum _{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\widehat{B}_{\unicode[STIX]{x1D713}}\in \text{M}_{d}(R)^{\infty }$
;(2) there exists a unique
 $d(h-d)$
-tuple
$d(h-d)$
-tuple
 $(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}})_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}$
,
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}})_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}$
,
 $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\in \mathfrak{M}$
, such that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\in \mathfrak{M}$
, such that
 $F$
is
$F$
is
 $\star$
-isomorphic to the formal group
$\star$
-isomorphic to the formal group
 $F_{V(Z)}$
, where
$F_{V(Z)}$
, where
 $Z=\widehat{\unicode[STIX]{x1D6EF}}+\sum _{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\widehat{B}_{\unicode[STIX]{x1D713}}\in \text{M}_{d}(R)^{\infty }$
.
$Z=\widehat{\unicode[STIX]{x1D6EF}}+\sum _{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\widehat{B}_{\unicode[STIX]{x1D713}}\in \text{M}_{d}(R)^{\infty }$
.
Corollary.
Let
![]() $(t_{\unicode[STIX]{x1D713}})_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}$
be a set of independent variables, and put
$(t_{\unicode[STIX]{x1D713}})_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}$
be a set of independent variables, and put
![]() $\widehat{\unicode[STIX]{x1D6EF}}^{\ast }=\widehat{\unicode[STIX]{x1D6EF}}+\sum _{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}t_{\unicode[STIX]{x1D713}}\widehat{B}_{\unicode[STIX]{x1D713}}$
. Then
$\widehat{\unicode[STIX]{x1D6EF}}^{\ast }=\widehat{\unicode[STIX]{x1D6EF}}+\sum _{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}t_{\unicode[STIX]{x1D713}}\widehat{B}_{\unicode[STIX]{x1D713}}$
. Then
![]() $\unicode[STIX]{x1D6E4}=F_{V(\widehat{\unicode[STIX]{x1D6EF}}^{\ast })}$
is a universal deformation of
$\unicode[STIX]{x1D6E4}=F_{V(\widehat{\unicode[STIX]{x1D6EF}}^{\ast })}$
is a universal deformation of
![]() $\unicode[STIX]{x1D6F7}$
, i.e., for any complete Noetherian local
$\unicode[STIX]{x1D6F7}$
, i.e., for any complete Noetherian local
![]() ${\mathcal{O}}$
-algebra
${\mathcal{O}}$
-algebra
![]() $R$
with residue field
$R$
with residue field
![]() $k$
and for any deformation
$k$
and for any deformation
![]() $F$
of
$F$
of
![]() $\unicode[STIX]{x1D6F7}$
over
$\unicode[STIX]{x1D6F7}$
over
![]() $R$
there exists a unique
$R$
there exists a unique
![]() ${\mathcal{O}}$
-homomorphism
${\mathcal{O}}$
-homomorphism
![]() $\unicode[STIX]{x1D707}:{\mathcal{O}}[[t_{\unicode[STIX]{x1D713}}]]_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}\rightarrow R$
such that
$\unicode[STIX]{x1D707}:{\mathcal{O}}[[t_{\unicode[STIX]{x1D713}}]]_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}\rightarrow R$
such that
![]() $\unicode[STIX]{x1D707}_{\ast }\unicode[STIX]{x1D6E4}$
is
$\unicode[STIX]{x1D707}_{\ast }\unicode[STIX]{x1D6E4}$
is
![]() $\star$
-isomorphic to
$\star$
-isomorphic to
![]() $F$
.
$F$
.
4 Period map for deformations over
 ${\mathcal{O}}$
${\mathcal{O}}$
We keep the notation of the previous section. First, we prove an auxiliary result needed for the definition of the period map.
Proposition 4.1. Let
![]() $F_{1},F_{2}$
be formal groups over
$F_{1},F_{2}$
be formal groups over
![]() ${\mathcal{O}}$
with the logarithms
${\mathcal{O}}$
with the logarithms
![]() $f_{1},f_{2}\in {\mathcal{K}}[[X]]_{0}^{d}$
, respectively, such that their reductions coincide. Then
$f_{1},f_{2}\in {\mathcal{K}}[[X]]_{0}^{d}$
, respectively, such that their reductions coincide. Then
(1)
 $F_{1}$
and
$F_{1}$
and
 $F_{2}$
are strictly
$F_{2}$
are strictly
 $\star$
-isomorphic iff
$\star$
-isomorphic iff
 $f_{1}\equiv f_{2}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
.
$f_{1}\equiv f_{2}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
.(2)
 $F_{1}$
and
$F_{1}$
and
 $F_{2}$
are
$F_{2}$
are
 $\star$
-isomorphic iff there exists
$\star$
-isomorphic iff there exists
 $c\in \text{GL}_{d}({\mathcal{O}})$
such that
$c\in \text{GL}_{d}({\mathcal{O}})$
such that
 $f_{1}\equiv cf_{2}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
.
$f_{1}\equiv cf_{2}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
.
Proof. By definition formal groups
![]() $F_{1},F_{2}$
are strictly
$F_{1},F_{2}$
are strictly
![]() $\star$
-isomorphic (resp.
$\star$
-isomorphic (resp.
![]() $\star$
-isomorphic) iff
$\star$
-isomorphic) iff
![]() $f_{1}^{-1}\circ f_{2}\equiv X\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
(resp.
$f_{1}^{-1}\circ f_{2}\equiv X\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
(resp.
![]() $f_{1}^{-1}\circ (cf_{2})\equiv X\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
for some
$f_{1}^{-1}\circ (cf_{2})\equiv X\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
for some
![]() $c\in \text{GL}_{d}({\mathcal{O}})$
). According to Theorem 2.2(2), there exists
$c\in \text{GL}_{d}({\mathcal{O}})$
). According to Theorem 2.2(2), there exists
![]() $u\in \text{M}_{d}(E)$
with
$u\in \text{M}_{d}(E)$
with
![]() $u\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
such that
$u\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
such that
![]() $f_{1}$
is of type
$f_{1}$
is of type
![]() $u$
. Then Lemma 2.1(1) implies the required statement.◻
$u$
. Then Lemma 2.1(1) implies the required statement.◻
Denote
![]() $\widehat{f}=f_{V(\widehat{\unicode[STIX]{x1D6EF}})}$
. Clearly,
$\widehat{f}=f_{V(\widehat{\unicode[STIX]{x1D6EF}})}$
. Clearly,
![]() $\widehat{f}$
is the logarithm of
$\widehat{f}$
is the logarithm of
![]() $\widehat{F}$
. Further, denote
$\widehat{F}$
. Further, denote
![]() $\widehat{u}=pI-\sum _{n=1}^{\infty }\widehat{\unicode[STIX]{x1D6EF}}_{n}\blacktriangle ^{n}\in \text{M}_{d}(E)$
.
$\widehat{u}=pI-\sum _{n=1}^{\infty }\widehat{\unicode[STIX]{x1D6EF}}_{n}\blacktriangle ^{n}\in \text{M}_{d}(E)$
.
Lemma 4.2. [Reference Demchenko and Gurevich5, Lemma 3]
![]() $\widehat{u}\widehat{f}=pX$
.
$\widehat{u}\widehat{f}=pX$
.
Let
![]() $F$
be a deformation of
$F$
be a deformation of
![]() $\unicode[STIX]{x1D6F7}$
over
$\unicode[STIX]{x1D6F7}$
over
![]() ${\mathcal{O}}$
with logarithm
${\mathcal{O}}$
with logarithm
![]() $f$
. We denote the strict
$f$
. We denote the strict
![]() $\star$
-isomorphism classes of
$\star$
-isomorphism classes of
![]() $F$
by
$F$
by
![]() $[F]$
, and the
$[F]$
, and the
![]() $\star$
-isomorphism classes of
$\star$
-isomorphism classes of
![]() $F$
by
$F$
by
![]() $[F]^{\prime }$
. By Proposition 2.3, there is
$[F]^{\prime }$
. By Proposition 2.3, there is
![]() $v\in I+\blacktriangle \text{M}_{d}(E)$
such that
$v\in I+\blacktriangle \text{M}_{d}(E)$
such that
![]() $f\equiv v\widehat{f}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
. Then one can define the map
$f\equiv v\widehat{f}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
. Then one can define the map
![]() $\unicode[STIX]{x1D712}$
from the set of the strict
$\unicode[STIX]{x1D712}$
from the set of the strict
![]() $\star$
-isomorphism classes of deformations of
$\star$
-isomorphism classes of deformations of
![]() $\unicode[STIX]{x1D6F7}$
over
$\unicode[STIX]{x1D6F7}$
over
![]() ${\mathcal{O}}$
to
${\mathcal{O}}$
to
and the map
![]() $\unicode[STIX]{x1D712}^{\prime }$
from the set of the
$\unicode[STIX]{x1D712}^{\prime }$
from the set of the
![]() $\star$
-isomorphism classes of deformations of
$\star$
-isomorphism classes of deformations of
![]() $\unicode[STIX]{x1D6F7}$
over
$\unicode[STIX]{x1D6F7}$
over
![]() ${\mathcal{O}}$
to
${\mathcal{O}}$
to
as follows:
![]() $\unicode[STIX]{x1D712}([F])=v(I+\,\text{M}_{d}(E)\widehat{u})$
,
$\unicode[STIX]{x1D712}([F])=v(I+\,\text{M}_{d}(E)\widehat{u})$
,
![]() $\unicode[STIX]{x1D712}^{\prime }([F]^{\prime })=(I+\text{M}_{d}(p{\mathcal{O}}))v(I+\,\text{M}_{d}(E)\widehat{u})$
.
$\unicode[STIX]{x1D712}^{\prime }([F]^{\prime })=(I+\text{M}_{d}(p{\mathcal{O}}))v(I+\,\text{M}_{d}(E)\widehat{u})$
.
Proposition 4.3. The maps
![]() $\unicode[STIX]{x1D712}$
and
$\unicode[STIX]{x1D712}$
and
![]() $\unicode[STIX]{x1D712}^{\prime }$
are well defined and bijective.
$\unicode[STIX]{x1D712}^{\prime }$
are well defined and bijective.
Proof. By Proposition 4.1(1), deformations of
![]() $\unicode[STIX]{x1D6F7}$
with logarithms
$\unicode[STIX]{x1D6F7}$
with logarithms
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
are strictly
$f_{2}$
are strictly
![]() $\star$
-isomorphic if and only if
$\star$
-isomorphic if and only if
![]() $f_{1}\equiv f_{2}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
, i.e.,
$f_{1}\equiv f_{2}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
, i.e.,
![]() $(v_{2}-v_{1})\widehat{f}\in \mathfrak{P}$
. According to Lemma 4.2 and Proposition 2.4, it is equivalent to the existence of
$(v_{2}-v_{1})\widehat{f}\in \mathfrak{P}$
. According to Lemma 4.2 and Proposition 2.4, it is equivalent to the existence of
![]() $r\in \text{M}_{d}(E)$
such that
$r\in \text{M}_{d}(E)$
such that
![]() $v_{2}=v_{1}(I+v_{1}^{-1}r\widehat{u})$
, i.e.,
$v_{2}=v_{1}(I+v_{1}^{-1}r\widehat{u})$
, i.e.,
![]() $v_{2}\in v_{1}(I+\text{M}_{d}(E)\widehat{u})$
. Thus
$v_{2}\in v_{1}(I+\text{M}_{d}(E)\widehat{u})$
. Thus
![]() $\unicode[STIX]{x1D712}$
is well defined and injective. For any
$\unicode[STIX]{x1D712}$
is well defined and injective. For any
![]() $v\in I+\text{M}_{d}(p{\mathcal{O}}+\blacktriangle E)$
, one can find
$v\in I+\text{M}_{d}(p{\mathcal{O}}+\blacktriangle E)$
, one can find
![]() $b\in \text{M}_{d}({\mathcal{O}})$
such that
$b\in \text{M}_{d}({\mathcal{O}})$
such that
![]() $\tilde{v}=v(I+b\widehat{u})\in I+\text{M}_{d}(\blacktriangle E)$
. Then
$\tilde{v}=v(I+b\widehat{u})\in I+\text{M}_{d}(\blacktriangle E)$
. Then
![]() $\widehat{u}\tilde{v}^{-1}\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
and
$\widehat{u}\tilde{v}^{-1}\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
and
![]() $\widehat{u}\tilde{v}^{-1}(\tilde{v}\widehat{f})=pX$
. Hence, Theorem 2.2(1) implies that
$\widehat{u}\tilde{v}^{-1}(\tilde{v}\widehat{f})=pX$
. Hence, Theorem 2.2(1) implies that
![]() $\tilde{v}\widehat{f}$
is the logarithm of a formal group over
$\tilde{v}\widehat{f}$
is the logarithm of a formal group over
![]() ${\mathcal{O}}$
. By Proposition 2.3, this formal group must be a deformation of
${\mathcal{O}}$
. By Proposition 2.3, this formal group must be a deformation of
![]() $\unicode[STIX]{x1D6F7}$
, and thus
$\unicode[STIX]{x1D6F7}$
, and thus
![]() $\unicode[STIX]{x1D712}$
is surjective.
$\unicode[STIX]{x1D712}$
is surjective.
Further, according to Proposition 4.1(2), formal groups with logarithms
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
are
$f_{2}$
are
![]() $\star$
-isomorphic iff
$\star$
-isomorphic iff
![]() $f_{1}\equiv cf_{2}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
for some
$f_{1}\equiv cf_{2}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
for some
![]() $c\in \text{GL}_{d}({\mathcal{O}})$
, i.e.,
$c\in \text{GL}_{d}({\mathcal{O}})$
, i.e.,
![]() $(v_{2}-cv_{1})\widehat{f}\in \mathfrak{P}$
. Proposition 2.4 implies that this holds iff there exists
$(v_{2}-cv_{1})\widehat{f}\in \mathfrak{P}$
. Proposition 2.4 implies that this holds iff there exists
![]() $r\in \text{M}_{d}(E)$
such that
$r\in \text{M}_{d}(E)$
such that
![]() $v_{2}=cv_{1}(I+v_{1}^{-1}r\widehat{u})$
, i.e.,
$v_{2}=cv_{1}(I+v_{1}^{-1}r\widehat{u})$
, i.e.,
![]() $v_{2}\in \text{GL}_{d}({\mathcal{O}})v_{1}(I+\text{M}_{d}(E)\widehat{u})$
. Thus
$v_{2}\in \text{GL}_{d}({\mathcal{O}})v_{1}(I+\text{M}_{d}(E)\widehat{u})$
. Thus
![]() $\unicode[STIX]{x1D712}^{\prime }$
is well defined and injective. Since
$\unicode[STIX]{x1D712}^{\prime }$
is well defined and injective. Since
![]() $\unicode[STIX]{x1D712}$
is surjective,
$\unicode[STIX]{x1D712}$
is surjective,
![]() $\unicode[STIX]{x1D712}^{\prime }$
is also surjective.◻
$\unicode[STIX]{x1D712}^{\prime }$
is also surjective.◻
One can see that
![]() $\unicode[STIX]{x1D712}$
and
$\unicode[STIX]{x1D712}$
and
![]() $\unicode[STIX]{x1D712}^{\prime }$
describe deformations of
$\unicode[STIX]{x1D712}^{\prime }$
describe deformations of
![]() $\unicode[STIX]{x1D6F7}$
over
$\unicode[STIX]{x1D6F7}$
over
![]() ${\mathcal{O}}$
up to strict
${\mathcal{O}}$
up to strict
![]() $\star$
-isomorphism and up to
$\star$
-isomorphism and up to
![]() $\star$
-isomorphism, respectively. Theorem 3.2 provides an alternative description of the same deformations. Our aim is to establish an explicit connection between these two descriptions.
$\star$
-isomorphism, respectively. Theorem 3.2 provides an alternative description of the same deformations. Our aim is to establish an explicit connection between these two descriptions.
For
![]() $Z=(Z_{1},Z_{2},\ldots )\in \text{M}_{d}({\mathcal{O}})^{\infty }$
such that
$Z=(Z_{1},Z_{2},\ldots )\in \text{M}_{d}({\mathcal{O}})^{\infty }$
such that
![]() $Z\equiv \widehat{\unicode[STIX]{x1D6EF}}\hspace{0.6em}{\rm mod}\hspace{0.2em}p$
, we define
$Z\equiv \widehat{\unicode[STIX]{x1D6EF}}\hspace{0.6em}{\rm mod}\hspace{0.2em}p$
, we define
Since
![]() $Z\equiv \widehat{\unicode[STIX]{x1D6EF}}\hspace{0.6em}{\rm mod}\hspace{0.2em}p$
, we conclude that
$Z\equiv \widehat{\unicode[STIX]{x1D6EF}}\hspace{0.6em}{\rm mod}\hspace{0.2em}p$
, we conclude that
![]() $Z^{(p^{m})}\equiv \widehat{\unicode[STIX]{x1D6EF}}^{(p^{m})}\;\text{mod}\,p^{m+1}$
for any
$Z^{(p^{m})}\equiv \widehat{\unicode[STIX]{x1D6EF}}^{(p^{m})}\;\text{mod}\,p^{m+1}$
for any
![]() $m\geqslant 0$
. Moreover, Corollary of Lemma 3.1 implies
$m\geqslant 0$
. Moreover, Corollary of Lemma 3.1 implies
![]() $p^{m}a_{m}(Z)\in \text{M}_{d}({\mathcal{O}})^{\infty }$
for any
$p^{m}a_{m}(Z)\in \text{M}_{d}({\mathcal{O}})^{\infty }$
for any
![]() $m\geqslant 0$
. Therefore
$m\geqslant 0$
. Therefore
![]() $a_{n-k}(Z)\left(Z_{k}^{(p^{n-k})}-\widehat{\unicode[STIX]{x1D6EF}}_{k}^{(p^{n-k})}\right)\in \text{M}_{d}(p{\mathcal{O}})$
for any
$a_{n-k}(Z)\left(Z_{k}^{(p^{n-k})}-\widehat{\unicode[STIX]{x1D6EF}}_{k}^{(p^{n-k})}\right)\in \text{M}_{d}(p{\mathcal{O}})$
for any
![]() $n\geqslant k$
, and hence
$n\geqslant k$
, and hence
![]() $v_{Z}\in \text{GL}_{d}(E)$
.
$v_{Z}\in \text{GL}_{d}(E)$
.
Proposition 4.4.
(1) If
 $Z=\widehat{\unicode[STIX]{x1D6EF}}+\sum _{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\widehat{B}_{\unicode[STIX]{x1D713}}$
, for some
$Z=\widehat{\unicode[STIX]{x1D6EF}}+\sum _{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\widehat{B}_{\unicode[STIX]{x1D713}}$
, for some
 $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\in p{\mathcal{O}}$
,
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\in p{\mathcal{O}}$
,
 $\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}$
, then
$\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}$
, then
 $\unicode[STIX]{x1D712}([F_{V(Z)}])=v_{Z}(I+\text{M}_{d}(E)\widehat{u})$
.
$\unicode[STIX]{x1D712}([F_{V(Z)}])=v_{Z}(I+\text{M}_{d}(E)\widehat{u})$
.(2) If
 $Z=\widehat{\unicode[STIX]{x1D6EF}}+\sum _{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\widehat{B}_{\unicode[STIX]{x1D713}}$
, for some
$Z=\widehat{\unicode[STIX]{x1D6EF}}+\sum _{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\widehat{B}_{\unicode[STIX]{x1D713}}$
, for some
 $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\in p{\mathcal{O}}$
,
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\in p{\mathcal{O}}$
,
 $\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}$
, then
$\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}$
, then
 $\unicode[STIX]{x1D712}^{\prime }([F_{V(Z)}]^{\prime })=(I+\text{M}_{d}(p{\mathcal{O}}))v_{Z}(I+\text{M}_{d}(E)\widehat{u})$
.
$\unicode[STIX]{x1D712}^{\prime }([F_{V(Z)}]^{\prime })=(I+\text{M}_{d}(p{\mathcal{O}}))v_{Z}(I+\text{M}_{d}(E)\widehat{u})$
.
Proof. Since
![]() $\widehat{\unicode[STIX]{x1D6EF}}_{n}^{(p)}=\widehat{\unicode[STIX]{x1D6EF}}_{n}^{\unicode[STIX]{x1D6E5}}$
for any
$\widehat{\unicode[STIX]{x1D6EF}}_{n}^{(p)}=\widehat{\unicode[STIX]{x1D6EF}}_{n}^{\unicode[STIX]{x1D6E5}}$
for any
![]() $n\geqslant 1$
, the recurrence formula of Lemma 3.1 can be rewritten as follows
$n\geqslant 1$
, the recurrence formula of Lemma 3.1 can be rewritten as follows
Then according to Proposition 2.6 and Lemma 4.2, one gets
Since
![]() $\widehat{u}\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
and the right multiplication by
$\widehat{u}\equiv pI\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
and the right multiplication by
![]() $\widehat{u}$
in
$\widehat{u}$
in
![]() ${\mathcal{K}}[[X]]_{p}^{d}$
corresponds to the right multiplication by
${\mathcal{K}}[[X]]_{p}^{d}$
corresponds to the right multiplication by
![]() $\widehat{u}$
in
$\widehat{u}$
in
![]() $\text{M}_{d}({\mathcal{K}}[[\blacktriangle ]])$
, we deduce that it is injective, and hence
$\text{M}_{d}({\mathcal{K}}[[\blacktriangle ]])$
, we deduce that it is injective, and hence
![]() $f_{V(Z)}=v_{Z}\widehat{f}$
. This implies (1). Clearly, (2) follows from (1).◻
$f_{V(Z)}=v_{Z}\widehat{f}$
. This implies (1). Clearly, (2) follows from (1).◻
We have a natural bijection from the set
![]() $I+\text{M}_{d}(p{\mathcal{O}}+\blacktriangle E)/I+\text{M}_{d}(E)\widehat{u}$
to the set
$I+\text{M}_{d}(p{\mathcal{O}}+\blacktriangle E)/I+\text{M}_{d}(E)\widehat{u}$
to the set
![]() $\text{M}_{d}(p{\mathcal{O}}+\blacktriangle E)/\text{M}_{d}(E)\widehat{u}$
which maps
$\text{M}_{d}(p{\mathcal{O}}+\blacktriangle E)/\text{M}_{d}(E)\widehat{u}$
which maps
![]() $v(I+\text{M}_{d}(E)\widehat{u})$
to
$v(I+\text{M}_{d}(E)\widehat{u})$
to
![]() $v-I+\text{M}_{d}(E)\widehat{u}$
. The correspondence
$v-I+\text{M}_{d}(E)\widehat{u}$
. The correspondence
![]() $pcI+\blacktriangle q+\text{M}_{d}(E)\widehat{u}\mapsto (pcI-cu)\blacktriangle ^{-1}+q+\text{M}_{d}(E)\widehat{u}$
is an
$pcI+\blacktriangle q+\text{M}_{d}(E)\widehat{u}\mapsto (pcI-cu)\blacktriangle ^{-1}+q+\text{M}_{d}(E)\widehat{u}$
is an
![]() ${\mathcal{O}}$
-module isomorphism from
${\mathcal{O}}$
-module isomorphism from
![]() $\text{M}_{d}(p{\mathcal{O}}+\blacktriangle E)/\text{M}_{d}(E)\widehat{u}$
to
$\text{M}_{d}(p{\mathcal{O}}+\blacktriangle E)/\text{M}_{d}(E)\widehat{u}$
to
![]() $\text{M}_{d}(E)/\text{M}_{d}(E)\widehat{u}$
. The latter module is isomorphic as an
$\text{M}_{d}(E)/\text{M}_{d}(E)\widehat{u}$
. The latter module is isomorphic as an
![]() ${\mathcal{O}}$
-module to the direct sum of
${\mathcal{O}}$
-module to the direct sum of
![]() $d$
copies of
$d$
copies of
![]() ${\mathcal{D}}(\unicode[STIX]{x1D6F7})$
. Therefore
${\mathcal{D}}(\unicode[STIX]{x1D6F7})$
. Therefore
![]() $\text{M}_{d}(p{\mathcal{O}}+\blacktriangle E)/\text{M}_{d}(E)\widehat{u}$
is a free
$\text{M}_{d}(p{\mathcal{O}}+\blacktriangle E)/\text{M}_{d}(E)\widehat{u}$
is a free
![]() ${\mathcal{O}}$
-module of rank
${\mathcal{O}}$
-module of rank
![]() $dh$
. Fix an
$dh$
. Fix an
![]() ${\mathcal{O}}$
-basis of
${\mathcal{O}}$
-basis of
![]() $\text{M}_{d}(p{\mathcal{O}}+\blacktriangle E)/\text{M}_{d}(E)\widehat{u}$
. Taking into account that
$\text{M}_{d}(p{\mathcal{O}}+\blacktriangle E)/\text{M}_{d}(E)\widehat{u}$
. Taking into account that
![]() $\unicode[STIX]{x1D712}$
is bijective (Proposition 4.3), one obtains a parametrization of the set of strict
$\unicode[STIX]{x1D712}$
is bijective (Proposition 4.3), one obtains a parametrization of the set of strict
![]() $\star$
-isomorphism classes of deformations of
$\star$
-isomorphism classes of deformations of
![]() $\unicode[STIX]{x1D6F7}$
over
$\unicode[STIX]{x1D6F7}$
over
![]() ${\mathcal{O}}$
. Another parametrization of the same set is provided by Theorem 3.2(1) applied for
${\mathcal{O}}$
. Another parametrization of the same set is provided by Theorem 3.2(1) applied for
![]() $R={\mathcal{O}}$
. Using Proposition 4.4(1) and the arithmetic properties of the ring
$R={\mathcal{O}}$
. Using Proposition 4.4(1) and the arithmetic properties of the ring
![]() $\text{M}_{d}(E)$
, one can give an explicit formula which expresses the first parametrization through the second one. The same applies to two parameterizations of the set of
$\text{M}_{d}(E)$
, one can give an explicit formula which expresses the first parametrization through the second one. The same applies to two parameterizations of the set of
![]() $\star$
-isomorphism classes of deformations, one constructed with the aid of
$\star$
-isomorphism classes of deformations, one constructed with the aid of
![]() $\unicode[STIX]{x1D712}^{\prime }$
and the other coming from Theorem 3.2(2).
$\unicode[STIX]{x1D712}^{\prime }$
and the other coming from Theorem 3.2(2).
We illustrate the last observation for the set of
![]() $\star$
-isomorphism classes of deformations in a particular example where
$\star$
-isomorphism classes of deformations in a particular example where
![]() $\unicode[STIX]{x1D6EF}_{m}=I$
, for some
$\unicode[STIX]{x1D6EF}_{m}=I$
, for some
![]() $m\geqslant 1$
,
$m\geqslant 1$
,
![]() $\unicode[STIX]{x1D6EF}_{n}=0$
for
$\unicode[STIX]{x1D6EF}_{n}=0$
for
![]() $n\neq m$
. This example is a direct generalization of the setting considered by Gross and Hopkins [Reference Gross and Hopkins8] for one-dimensional formal groups. In this case, one has
$n\neq m$
. This example is a direct generalization of the setting considered by Gross and Hopkins [Reference Gross and Hopkins8] for one-dimensional formal groups. In this case, one has
![]() $\widehat{u}=pI-I\blacktriangle ^{m}$
and the height of
$\widehat{u}=pI-I\blacktriangle ^{m}$
and the height of
![]() $\unicode[STIX]{x1D6F7}$
is equal to
$\unicode[STIX]{x1D6F7}$
is equal to
![]() $dm$
. Moreover,
$dm$
. Moreover,
![]() $\unicode[STIX]{x1D6F9}=\{(n,i,j)|1\leqslant i,j\leqslant d;1\leqslant n\leqslant m\}$
(see [Reference Demchenko and Gurevich5, Example 1]), and hence,
$\unicode[STIX]{x1D6F9}=\{(n,i,j)|1\leqslant i,j\leqslant d;1\leqslant n\leqslant m\}$
(see [Reference Demchenko and Gurevich5, Example 1]), and hence,
![]() $\unicode[STIX]{x1D6F9}^{+}=\{(n,i,j)|1\leqslant i,j\leqslant d;1\leqslant n\leqslant m-1\}$
.
$\unicode[STIX]{x1D6F9}^{+}=\{(n,i,j)|1\leqslant i,j\leqslant d;1\leqslant n\leqslant m-1\}$
.
For any
![]() $(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}})_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}$
,
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}})_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}$
,
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\in p{\mathcal{O}}$
, denote by
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\in p{\mathcal{O}}$
, denote by
![]() $C_{n}$
the matrix in
$C_{n}$
the matrix in
![]() $\text{M}_{d}(p{\mathcal{O}})$
such that
$\text{M}_{d}(p{\mathcal{O}})$
such that
![]() $C_{n}(i,j)=\unicode[STIX]{x1D70F}_{(n,i,j)}$
,
$C_{n}(i,j)=\unicode[STIX]{x1D70F}_{(n,i,j)}$
,
![]() $(n,i,j)\in \unicode[STIX]{x1D6F9}^{+}$
. If
$(n,i,j)\in \unicode[STIX]{x1D6F9}^{+}$
. If
![]() $Z=\widehat{\unicode[STIX]{x1D6EF}}+\sum _{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\widehat{B}_{\unicode[STIX]{x1D713}}$
, then
$Z=\widehat{\unicode[STIX]{x1D6EF}}+\sum _{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\widehat{B}_{\unicode[STIX]{x1D713}}$
, then
![]() $Z_{n}=C_{n}$
for
$Z_{n}=C_{n}$
for
![]() $1\leqslant n\leqslant m-1$
,
$1\leqslant n\leqslant m-1$
,
![]() $Z_{m}=I$
,
$Z_{m}=I$
,
![]() $Z_{n}=0$
for
$Z_{n}=0$
for
![]() $n\geqslant m+1$
, and
$n\geqslant m+1$
, and
We can write
![]() $v_{Z}$
in the form
$v_{Z}$
in the form
![]() $v_{Z}=\sum _{n=0}^{\infty }\unicode[STIX]{x1D708}_{n}\blacktriangle ^{n}$
with
$v_{Z}=\sum _{n=0}^{\infty }\unicode[STIX]{x1D708}_{n}\blacktriangle ^{n}$
with
![]() $\unicode[STIX]{x1D708}_{n}\in \text{M}_{d}({\mathcal{O}})$
,
$\unicode[STIX]{x1D708}_{n}\in \text{M}_{d}({\mathcal{O}})$
,
![]() $\unicode[STIX]{x1D708}_{0}=I$
. Since
$\unicode[STIX]{x1D708}_{0}=I$
. Since
![]() $\widehat{u}=pI-I\blacktriangle ^{m}$
, one gets
$\widehat{u}=pI-I\blacktriangle ^{m}$
, one gets
![]() $I\blacktriangle ^{km}\equiv p^{k}I\;\text{mod}\,\text{M}_{d}(E)\widehat{u}$
and therefore
$I\blacktriangle ^{km}\equiv p^{k}I\;\text{mod}\,\text{M}_{d}(E)\widehat{u}$
and therefore
![]() $v_{Z}\equiv \sum _{i=0}^{m-1}\unicode[STIX]{x1D6FC}_{i}\blacktriangle ^{i}\;\text{mod}\,\text{M}_{d}(E)\widehat{u}$
where
$v_{Z}\equiv \sum _{i=0}^{m-1}\unicode[STIX]{x1D6FC}_{i}\blacktriangle ^{i}\;\text{mod}\,\text{M}_{d}(E)\widehat{u}$
where
![]() $\unicode[STIX]{x1D6FC}_{i}=\sum _{j=0}^{\infty }p^{j}\unicode[STIX]{x1D708}_{jm+i}\in \text{M}_{d}({\mathcal{O}})$
. This means that there exists
$\unicode[STIX]{x1D6FC}_{i}=\sum _{j=0}^{\infty }p^{j}\unicode[STIX]{x1D708}_{jm+i}\in \text{M}_{d}({\mathcal{O}})$
. This means that there exists
![]() $r\in \text{M}_{d}(E)$
such that
$r\in \text{M}_{d}(E)$
such that
![]() $\sum _{i=0}^{m-1}\unicode[STIX]{x1D6FC}_{i}\blacktriangle ^{i}=v_{Z}+r\widehat{u}=v_{Z}(I+v_{Z}^{-1}r\widehat{u})$
. Thus
$\sum _{i=0}^{m-1}\unicode[STIX]{x1D6FC}_{i}\blacktriangle ^{i}=v_{Z}+r\widehat{u}=v_{Z}(I+v_{Z}^{-1}r\widehat{u})$
. Thus
![]() $\sum _{i=0}^{m-1}\unicode[STIX]{x1D6FC}_{i}\blacktriangle ^{i}\in v_{Z}(I+\text{M}_{d}(E)\widehat{u})$
, and it is obviously a unique element of this form in
$\sum _{i=0}^{m-1}\unicode[STIX]{x1D6FC}_{i}\blacktriangle ^{i}\in v_{Z}(I+\text{M}_{d}(E)\widehat{u})$
, and it is obviously a unique element of this form in
![]() $v_{Z}(I+\text{M}_{d}(E)\widehat{u})$
. Moreover,
$v_{Z}(I+\text{M}_{d}(E)\widehat{u})$
. Moreover,
![]() $\unicode[STIX]{x1D6FC}_{0}\equiv I\hspace{0.6em}{\rm mod}\hspace{0.2em}p$
which implies that
$\unicode[STIX]{x1D6FC}_{0}\equiv I\hspace{0.6em}{\rm mod}\hspace{0.2em}p$
which implies that
![]() $\unicode[STIX]{x1D6FC}_{0}$
is invertible in
$\unicode[STIX]{x1D6FC}_{0}$
is invertible in
![]() $\text{M}_{d}({\mathcal{O}})$
and
$\text{M}_{d}({\mathcal{O}})$
and
![]() $\unicode[STIX]{x1D6FC}_{0}^{-1}\equiv I\hspace{0.6em}{\rm mod}\hspace{0.2em}p$
. For
$\unicode[STIX]{x1D6FC}_{0}^{-1}\equiv I\hspace{0.6em}{\rm mod}\hspace{0.2em}p$
. For
![]() $1\leqslant i\leqslant m-1$
, denote
$1\leqslant i\leqslant m-1$
, denote
![]() $\unicode[STIX]{x1D6FD}_{i}=\unicode[STIX]{x1D6FC}_{0}^{-1}\unicode[STIX]{x1D6FC}_{i}$
. Then
$\unicode[STIX]{x1D6FD}_{i}=\unicode[STIX]{x1D6FC}_{0}^{-1}\unicode[STIX]{x1D6FC}_{i}$
. Then
We consider
![]() $\unicode[STIX]{x1D6FD}_{i}$
,
$\unicode[STIX]{x1D6FD}_{i}$
,
![]() $1\leqslant i\leqslant m-1$
, as functions of
$1\leqslant i\leqslant m-1$
, as functions of
![]() $(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}})_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}$
and establish explicit formulas for them.
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}})_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}$
and establish explicit formulas for them.
Proposition 4.5. For any
![]() $(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}})_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}$
,
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}})_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}$
,
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\in p{\mathcal{O}}$
,
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}\in p{\mathcal{O}}$
,
![]() $1\leqslant i\leqslant m-1$
$1\leqslant i\leqslant m-1$
Proof. We write as above
![]() $v_{Z}=\sum _{n=0}^{\infty }\unicode[STIX]{x1D708}_{n}\blacktriangle ^{n}$
,
$v_{Z}=\sum _{n=0}^{\infty }\unicode[STIX]{x1D708}_{n}\blacktriangle ^{n}$
,
![]() $\unicode[STIX]{x1D708}_{n}\in \text{M}_{d}({\mathcal{O}})$
. Then
$\unicode[STIX]{x1D708}_{n}\in \text{M}_{d}({\mathcal{O}})$
. Then
![]() $\unicode[STIX]{x1D708}_{0}=I$
and
$\unicode[STIX]{x1D708}_{0}=I$
and
According to Lemma 3.1,
![]() $\unicode[STIX]{x1D708}_{n}=a_{n}(Z)$
for
$\unicode[STIX]{x1D708}_{n}=a_{n}(Z)$
for
![]() $0\leqslant n\leqslant m-1$
,
$0\leqslant n\leqslant m-1$
,
![]() $\unicode[STIX]{x1D708}_{n}=a_{n}(Z)-p^{-1}a_{n-m}(Z)$
for
$\unicode[STIX]{x1D708}_{n}=a_{n}(Z)-p^{-1}a_{n-m}(Z)$
for
![]() $n\geqslant m$
. These formulas imply
$n\geqslant m$
. These formulas imply
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}_{i} & = & \displaystyle \mathop{\sum }_{j=0}^{\infty }p^{j}\unicode[STIX]{x1D708}_{jm+i}=\lim _{k\rightarrow \infty }\mathop{\sum }_{j=0}^{k}p^{j}\unicode[STIX]{x1D708}_{jm+i}\nonumber\\ \displaystyle & = & \displaystyle \lim _{k\rightarrow \infty }\left(a_{i}(Z)+\mathop{\sum }_{j=1}^{k}p^{j}(a_{jm+i}(Z)-p^{-1}a_{(j-1)m+i}(Z))\right)\nonumber\\ \displaystyle & = & \displaystyle \lim _{k\rightarrow \infty }p^{k}a_{km+i}(Z),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}_{i} & = & \displaystyle \mathop{\sum }_{j=0}^{\infty }p^{j}\unicode[STIX]{x1D708}_{jm+i}=\lim _{k\rightarrow \infty }\mathop{\sum }_{j=0}^{k}p^{j}\unicode[STIX]{x1D708}_{jm+i}\nonumber\\ \displaystyle & = & \displaystyle \lim _{k\rightarrow \infty }\left(a_{i}(Z)+\mathop{\sum }_{j=1}^{k}p^{j}(a_{jm+i}(Z)-p^{-1}a_{(j-1)m+i}(Z))\right)\nonumber\\ \displaystyle & = & \displaystyle \lim _{k\rightarrow \infty }p^{k}a_{km+i}(Z),\nonumber\end{eqnarray}$$
for any
![]() $0\leqslant i\leqslant m-1$
. The required formula for
$0\leqslant i\leqslant m-1$
. The required formula for
![]() $\unicode[STIX]{x1D6FD}_{i}$
follows immediately.◻
$\unicode[STIX]{x1D6FD}_{i}$
follows immediately.◻
Remark that for any
![]() $0\leqslant i\leqslant m-1$
, the infinite sequence
$0\leqslant i\leqslant m-1$
, the infinite sequence
![]() $p^{k}a_{km+i}(\widehat{\unicode[STIX]{x1D6EF}}^{\ast })\in \text{M}_{d}({\mathcal{O}}[[t_{\unicode[STIX]{x1D713}}]]_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}})$
of matrices of polynomials converges in the rigid metric to a matrix of rigid analytic functions. Thus
$p^{k}a_{km+i}(\widehat{\unicode[STIX]{x1D6EF}}^{\ast })\in \text{M}_{d}({\mathcal{O}}[[t_{\unicode[STIX]{x1D713}}]]_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}})$
of matrices of polynomials converges in the rigid metric to a matrix of rigid analytic functions. Thus
![]() $\unicode[STIX]{x1D6FC}_{i}$
can be considered as a matrix of rigid analytic functions of variables
$\unicode[STIX]{x1D6FC}_{i}$
can be considered as a matrix of rigid analytic functions of variables
![]() $(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}})_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}$
.
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}})_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}$
.
When
![]() $d=1$
, the functions
$d=1$
, the functions
![]() $\unicode[STIX]{x1D6FC}_{i}$
,
$\unicode[STIX]{x1D6FC}_{i}$
,
![]() $0\leqslant i\leqslant m-1$
, coincide up to a constant factor with the homogeneous coordinates of the
$0\leqslant i\leqslant m-1$
, coincide up to a constant factor with the homogeneous coordinates of the
![]() $p$
-adic period map introduced by Gross and Hopkins; see [Reference Gross and Hopkins8, 21.6, 21.13 and 23.6].
$p$
-adic period map introduced by Gross and Hopkins; see [Reference Gross and Hopkins8, 21.6, 21.13 and 23.6].
5 Action of the automorphism group
Let
![]() $F$
be a deformation of
$F$
be a deformation of
![]() $\unicode[STIX]{x1D6F7}$
over
$\unicode[STIX]{x1D6F7}$
over
![]() ${\mathcal{O}}$
. For
${\mathcal{O}}$
. For
![]() $\unicode[STIX]{x1D719}\in \text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
, we put
$\unicode[STIX]{x1D719}\in \text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
, we put
![]() $[F]^{\prime }\unicode[STIX]{x1D719}=[g^{-1}(F(g,g))]^{\prime }$
, where
$[F]^{\prime }\unicode[STIX]{x1D719}=[g^{-1}(F(g,g))]^{\prime }$
, where
![]() $g\in {\mathcal{O}}[[X]]_{0}^{d}$
is such that its reduction is equal to
$g\in {\mathcal{O}}[[X]]_{0}^{d}$
is such that its reduction is equal to
![]() $\unicode[STIX]{x1D719}$
. This defines a right action of
$\unicode[STIX]{x1D719}$
. This defines a right action of
![]() $\text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
on the set of
$\text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
on the set of
![]() $\star$
-isomorphism classes of the deformations of
$\star$
-isomorphism classes of the deformations of
![]() $\unicode[STIX]{x1D6F7}$
over
$\unicode[STIX]{x1D6F7}$
over
![]() ${\mathcal{O}}$
. In the case of dimension one, this definition is due to Lubin and Tate [Reference Lubin and Tate12]. We give an explicit description of this action in terms of the parametrization provided by Theorem 3.2(2).
${\mathcal{O}}$
. In the case of dimension one, this definition is due to Lubin and Tate [Reference Lubin and Tate12]. We give an explicit description of this action in terms of the parametrization provided by Theorem 3.2(2).
It is easy to notice that the correspondence
![]() $(I+\text{M}_{d}(p{\mathcal{O}}))v(I+\text{M}_{d}(E)\widehat{u})\mapsto \text{GL}_{d}({\mathcal{O}})v(I+\text{M}_{d}(E)\widehat{u})$
is a bijection from
$(I+\text{M}_{d}(p{\mathcal{O}}))v(I+\text{M}_{d}(E)\widehat{u})\mapsto \text{GL}_{d}({\mathcal{O}})v(I+\text{M}_{d}(E)\widehat{u})$
is a bijection from
![]() $I+\text{M}_{d}(p{\mathcal{O}})\backslash I+\text{M}_{d}(p{\mathcal{O}}+\blacktriangle E)/I+\text{M}_{d}(E)\widehat{u}$
to
$I+\text{M}_{d}(p{\mathcal{O}})\backslash I+\text{M}_{d}(p{\mathcal{O}}+\blacktriangle E)/I+\text{M}_{d}(E)\widehat{u}$
to
![]() $\text{GL}_{d}({\mathcal{O}})\backslash \text{GL}_{d}(E)/I+\text{M}_{d}(E)\widehat{u}$
. Thus we can identify these two sets. Define a right action of
$\text{GL}_{d}({\mathcal{O}})\backslash \text{GL}_{d}(E)/I+\text{M}_{d}(E)\widehat{u}$
. Thus we can identify these two sets. Define a right action of
![]() $\text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
on
$\text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
on
![]() $\text{GL}_{d}({\mathcal{O}})\backslash \text{GL}_{d}(E)/I+\text{M}_{d}(E)\widehat{u}$
in the following way: by Theorem 2.5(3), for any
$\text{GL}_{d}({\mathcal{O}})\backslash \text{GL}_{d}(E)/I+\text{M}_{d}(E)\widehat{u}$
in the following way: by Theorem 2.5(3), for any
![]() $\unicode[STIX]{x1D719}\in \text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
there exists
$\unicode[STIX]{x1D719}\in \text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
there exists
![]() $w\in \text{GL}_{d}(E)$
such that
$w\in \text{GL}_{d}(E)$
such that
![]() $\unicode[STIX]{x1D719}$
is equal to the reduction of
$\unicode[STIX]{x1D719}$
is equal to the reduction of
![]() $\widehat{f}^{-1}(w\widehat{f})$
modulo
$\widehat{f}^{-1}(w\widehat{f})$
modulo
![]() $p$
. For
$p$
. For
![]() $v\in \text{GL}_{d}(E)$
, put
$v\in \text{GL}_{d}(E)$
, put
![]() $\text{GL}_{d}({\mathcal{O}})v(I+\text{M}_{d}(E)\widehat{u})\unicode[STIX]{x1D719}=\text{GL}_{d}({\mathcal{O}})vw(I+\text{M}_{d}(E)\widehat{u})$
. Theorem 2.5(1) implies that this expression does not depend on the choice of
$\text{GL}_{d}({\mathcal{O}})v(I+\text{M}_{d}(E)\widehat{u})\unicode[STIX]{x1D719}=\text{GL}_{d}({\mathcal{O}})vw(I+\text{M}_{d}(E)\widehat{u})$
. Theorem 2.5(1) implies that this expression does not depend on the choice of
![]() $v$
in the corresponding coset. If
$v$
in the corresponding coset. If
![]() $w^{\prime }\in \text{GL}_{d}(E)$
is such that the reduction of
$w^{\prime }\in \text{GL}_{d}(E)$
is such that the reduction of
![]() $\widehat{f}^{-1}(w^{\prime }\widehat{f})$
modulo
$\widehat{f}^{-1}(w^{\prime }\widehat{f})$
modulo
![]() $p$
is equal to
$p$
is equal to
![]() $\unicode[STIX]{x1D719}$
, then by Lemma 2.1(1),
$\unicode[STIX]{x1D719}$
, then by Lemma 2.1(1),
![]() $w\widehat{f}\equiv w^{\prime }\widehat{f}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
and Proposition 2.4 implies that there exists
$w\widehat{f}\equiv w^{\prime }\widehat{f}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
and Proposition 2.4 implies that there exists
![]() $s\in \text{M}_{d}(E)$
such that
$s\in \text{M}_{d}(E)$
such that
![]() $w^{\prime }-w=s\widehat{u}$
, i.e.,
$w^{\prime }-w=s\widehat{u}$
, i.e.,
![]() $w^{\prime }=w(1+w^{-1}s\widehat{u})\in w(I+\text{M}_{d}(E)\widehat{u})$
. Thus the definition does not depend on the choice of
$w^{\prime }=w(1+w^{-1}s\widehat{u})\in w(I+\text{M}_{d}(E)\widehat{u})$
. Thus the definition does not depend on the choice of
![]() $w$
.
$w$
.
Theorem 5.1.
![]() $\unicode[STIX]{x1D712}^{\prime }$
is equivariant with respect to the action of
$\unicode[STIX]{x1D712}^{\prime }$
is equivariant with respect to the action of
![]() $\text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
.
$\text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
.
Proof. Let
![]() $F$
be a deformation of
$F$
be a deformation of
![]() $\unicode[STIX]{x1D6F7}$
over
$\unicode[STIX]{x1D6F7}$
over
![]() ${\mathcal{O}}$
with logarithm
${\mathcal{O}}$
with logarithm
![]() $f$
and
$f$
and
![]() $\unicode[STIX]{x1D719}\in \text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
. By Proposition 2.3, there exists
$\unicode[STIX]{x1D719}\in \text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
. By Proposition 2.3, there exists
![]() $v\in I+\text{M}_{d}(\blacktriangle E)$
such that
$v\in I+\text{M}_{d}(\blacktriangle E)$
such that
![]() $v\widehat{f}\equiv f\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
. By Theorem 2.5(3),
$v\widehat{f}\equiv f\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
. By Theorem 2.5(3),
![]() $\unicode[STIX]{x1D719}$
is equal to the reduction of
$\unicode[STIX]{x1D719}$
is equal to the reduction of
![]() $g=\widehat{f}^{-1}(w\widehat{f})$
for some
$g=\widehat{f}^{-1}(w\widehat{f})$
for some
![]() $w\in \text{GL}_{d}(E)$
. The formal group with logarithm
$w\in \text{GL}_{d}(E)$
. The formal group with logarithm
![]() $w_{0}^{-1}f\circ g$
belongs to the coset
$w_{0}^{-1}f\circ g$
belongs to the coset
![]() $[F]^{\prime }\unicode[STIX]{x1D719}$
, where
$[F]^{\prime }\unicode[STIX]{x1D719}$
, where
![]() $w_{0}\in \text{GL}_{d}({\mathcal{O}})$
is such that
$w_{0}\in \text{GL}_{d}({\mathcal{O}})$
is such that
![]() $w\equiv w_{0}\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
. On the other hand, Lemma 2.1(2) implies
$w\equiv w_{0}\hspace{0.6em}{\rm mod}\hspace{0.2em}\blacktriangle$
. On the other hand, Lemma 2.1(2) implies
![]() $w_{0}^{-1}f\circ g\equiv w_{0}^{-1}(v\widehat{f})\circ \widehat{f}^{-1}(w\widehat{f})\equiv w_{0}^{-1}vw\widehat{f}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
, and hence,
$w_{0}^{-1}f\circ g\equiv w_{0}^{-1}(v\widehat{f})\circ \widehat{f}^{-1}(w\widehat{f})\equiv w_{0}^{-1}vw\widehat{f}\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{P}$
, and hence,
![]() $\unicode[STIX]{x1D712}^{\prime }([F]^{\prime }\unicode[STIX]{x1D719})=\text{GL}_{d}({\mathcal{O}})vw(I+\text{M}_{d}(E)\widehat{u})=\unicode[STIX]{x1D712}^{\prime }([F]^{\prime })\unicode[STIX]{x1D719}$
.◻
$\unicode[STIX]{x1D712}^{\prime }([F]^{\prime }\unicode[STIX]{x1D719})=\text{GL}_{d}({\mathcal{O}})vw(I+\text{M}_{d}(E)\widehat{u})=\unicode[STIX]{x1D712}^{\prime }([F]^{\prime })\unicode[STIX]{x1D719}$
.◻
Theorem 5.2. Let
![]() $w\in \text{GL}_{d}(E)$
and
$w\in \text{GL}_{d}(E)$
and
![]() $Z^{(i)}\in \text{M}_{d}({\mathcal{O}})^{\infty }$
be such that the reduction of
$Z^{(i)}\in \text{M}_{d}({\mathcal{O}})^{\infty }$
be such that the reduction of
![]() $\widehat{f}^{-1}(w\widehat{f})$
is equal to
$\widehat{f}^{-1}(w\widehat{f})$
is equal to
![]() $\unicode[STIX]{x1D719}\in \text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
and
$\unicode[STIX]{x1D719}\in \text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
and
![]() $Z^{(i)}=\widehat{\unicode[STIX]{x1D6EF}}+\sum _{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}^{(i)}\widehat{B}_{\unicode[STIX]{x1D713}}$
for some
$Z^{(i)}=\widehat{\unicode[STIX]{x1D6EF}}+\sum _{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}^{+}}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}^{(i)}\widehat{B}_{\unicode[STIX]{x1D713}}$
for some
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}^{(i)}\in p{\mathcal{O}}$
,
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}^{(i)}\in p{\mathcal{O}}$
,
![]() $i=1,2$
. Then
$i=1,2$
. Then
![]() $[F_{V(Z^{(1)})}]^{\prime }\unicode[STIX]{x1D719}=[F_{V(Z^{(2)})}]^{\prime }$
iff there exist
$[F_{V(Z^{(1)})}]^{\prime }\unicode[STIX]{x1D719}=[F_{V(Z^{(2)})}]^{\prime }$
iff there exist
![]() $c\in \text{GL}_{d}({\mathcal{O}})$
and
$c\in \text{GL}_{d}({\mathcal{O}})$
and
![]() $q\in \text{M}_{d}(E)$
such that
$q\in \text{M}_{d}(E)$
such that
![]() $v_{Z^{(2)}}=cv_{Z^{(1)}}w(I+q\widehat{u})$
.
$v_{Z^{(2)}}=cv_{Z^{(1)}}w(I+q\widehat{u})$
.
Proof. According to Theorem 5.1, Proposition 4.4 and the definition of the action of
![]() $\unicode[STIX]{x1D719}\in \text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
on
$\unicode[STIX]{x1D719}\in \text{Aut}_{k}(\unicode[STIX]{x1D6F7})$
on
![]() $\text{GL}_{d}({\mathcal{O}})\backslash \text{GL}_{d}(E)/I+\text{M}_{d}(E)\widehat{u}$
, we get
$\text{GL}_{d}({\mathcal{O}})\backslash \text{GL}_{d}(E)/I+\text{M}_{d}(E)\widehat{u}$
, we get
On the other hand,
![]() $\unicode[STIX]{x1D712}^{\prime }([F_{V(Z^{(2)})}]^{\prime })=\text{GL}_{d}({\mathcal{O}})v_{Z^{(2)}}(I+\text{M}_{d}(E)\widehat{u})$
. This implies the required statement.◻
$\unicode[STIX]{x1D712}^{\prime }([F_{V(Z^{(2)})}]^{\prime })=\text{GL}_{d}({\mathcal{O}})v_{Z^{(2)}}(I+\text{M}_{d}(E)\widehat{u})$
. This implies the required statement.◻
Corollary.
In the setting of Theorem 5.2, suppose that
![]() $\unicode[STIX]{x1D6EF}_{m}=I$
,
$\unicode[STIX]{x1D6EF}_{m}=I$
,
![]() $\unicode[STIX]{x1D6EF}_{n}=0$
for
$\unicode[STIX]{x1D6EF}_{n}=0$
for
![]() $n\neq m$
, and choose
$n\neq m$
, and choose
![]() $w_{i}\in \text{M}_{d}({\mathcal{O}})$
such that
$w_{i}\in \text{M}_{d}({\mathcal{O}})$
such that
![]() $w\equiv \sum _{i=0}^{m-1}w_{i}\blacktriangle ^{i}\;\text{mod}\,\text{M}_{d}(E)\widehat{u}$
. Then
$w\equiv \sum _{i=0}^{m-1}w_{i}\blacktriangle ^{i}\;\text{mod}\,\text{M}_{d}(E)\widehat{u}$
. Then
![]() $[F_{V(Z^{(1)})}]^{\prime }\unicode[STIX]{x1D719}=[F_{V(Z^{(2)})}]^{\prime }$
iff there exists
$[F_{V(Z^{(1)})}]^{\prime }\unicode[STIX]{x1D719}=[F_{V(Z^{(2)})}]^{\prime }$
iff there exists
![]() $c\in \text{GL}_{d}({\mathcal{O}})$
such that
$c\in \text{GL}_{d}({\mathcal{O}})$
such that
where
 $$\begin{eqnarray}C(w)=\left(\begin{array}{@{}ccccc@{}}w_{0} & w_{1} & w_{2} & & w_{m-1}\\ pw_{m-1}^{\unicode[STIX]{x1D6E5}} & w_{0}^{\unicode[STIX]{x1D6E5}} & w_{1}^{\unicode[STIX]{x1D6E5}} & \cdots \, & w_{m-2}^{\unicode[STIX]{x1D6E5}}\\ pw_{m-2}^{\unicode[STIX]{x1D6E5}^{2}} & pw_{m-1}^{\unicode[STIX]{x1D6E5}^{2}} & w_{0}^{\unicode[STIX]{x1D6E5}^{2}} & & w_{m-3}^{\unicode[STIX]{x1D6E5}^{2}}\\ & \vdots & & \ddots & \vdots \\ pw_{1}^{\unicode[STIX]{x1D6E5}^{m-1}} & pw_{2}^{\unicode[STIX]{x1D6E5}^{m-1}} & pw_{3}^{\unicode[STIX]{x1D6E5}^{m-1}} & \cdots \, & w_{0}^{\unicode[STIX]{x1D6E5}^{m-1}}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}C(w)=\left(\begin{array}{@{}ccccc@{}}w_{0} & w_{1} & w_{2} & & w_{m-1}\\ pw_{m-1}^{\unicode[STIX]{x1D6E5}} & w_{0}^{\unicode[STIX]{x1D6E5}} & w_{1}^{\unicode[STIX]{x1D6E5}} & \cdots \, & w_{m-2}^{\unicode[STIX]{x1D6E5}}\\ pw_{m-2}^{\unicode[STIX]{x1D6E5}^{2}} & pw_{m-1}^{\unicode[STIX]{x1D6E5}^{2}} & w_{0}^{\unicode[STIX]{x1D6E5}^{2}} & & w_{m-3}^{\unicode[STIX]{x1D6E5}^{2}}\\ & \vdots & & \ddots & \vdots \\ pw_{1}^{\unicode[STIX]{x1D6E5}^{m-1}} & pw_{2}^{\unicode[STIX]{x1D6E5}^{m-1}} & pw_{3}^{\unicode[STIX]{x1D6E5}^{m-1}} & \cdots \, & w_{0}^{\unicode[STIX]{x1D6E5}^{m-1}}\end{array}\right).\end{eqnarray}$$
Proof. As we showed above
![]() $\sum _{i=0}^{m-1}\unicode[STIX]{x1D6FC}_{i}^{(2)}\blacktriangle ^{i}\in v_{Z^{(2)}}(I+\text{M}_{d}(E)\widehat{u})$
. Besides, Theorem 5.2 implies
$\sum _{i=0}^{m-1}\unicode[STIX]{x1D6FC}_{i}^{(2)}\blacktriangle ^{i}\in v_{Z^{(2)}}(I+\text{M}_{d}(E)\widehat{u})$
. Besides, Theorem 5.2 implies
 $$\begin{eqnarray}\displaystyle \text{GL}_{d}({\mathcal{O}})v_{Z^{(2)}}(I+\text{M}_{d}(E)\widehat{u}) & = & \displaystyle \text{GL}_{d}({\mathcal{O}})v_{Z^{(1)}}w(I+\text{M}_{d}(E)\widehat{u})\nonumber\\ \displaystyle & = & \displaystyle \text{GL}_{d}({\mathcal{O}})\left(\mathop{\sum }_{i=0}^{m-1}\unicode[STIX]{x1D6FC}_{i}^{(1)}\blacktriangle ^{i}\right)w(I+\text{M}_{d}(E)\widehat{u}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{GL}_{d}({\mathcal{O}})v_{Z^{(2)}}(I+\text{M}_{d}(E)\widehat{u}) & = & \displaystyle \text{GL}_{d}({\mathcal{O}})v_{Z^{(1)}}w(I+\text{M}_{d}(E)\widehat{u})\nonumber\\ \displaystyle & = & \displaystyle \text{GL}_{d}({\mathcal{O}})\left(\mathop{\sum }_{i=0}^{m-1}\unicode[STIX]{x1D6FC}_{i}^{(1)}\blacktriangle ^{i}\right)w(I+\text{M}_{d}(E)\widehat{u}).\nonumber\end{eqnarray}$$
Hence, there exist
![]() $c\in \text{GL}_{d}({\mathcal{O}})$
and
$c\in \text{GL}_{d}({\mathcal{O}})$
and
![]() $q\in \text{M}_{d}(E)$
such that
$q\in \text{M}_{d}(E)$
such that
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{i=0}^{m-1}\unicode[STIX]{x1D6FC}_{i}^{(2)}\blacktriangle ^{i} & = & \displaystyle c\left(\mathop{\sum }_{i=0}^{m-1}\unicode[STIX]{x1D6FC}_{i}^{(1)}\blacktriangle ^{i}\right)w(1+q\widehat{u})\nonumber\\ \displaystyle & \equiv & \displaystyle c\left(\mathop{\sum }_{i=0}^{m-1}\unicode[STIX]{x1D6FC}_{i}^{(1)}\blacktriangle ^{i}\right)w\;\text{mod}\,\text{M}_{d}(E)\widehat{u}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{i=0}^{m-1}\unicode[STIX]{x1D6FC}_{i}^{(2)}\blacktriangle ^{i} & = & \displaystyle c\left(\mathop{\sum }_{i=0}^{m-1}\unicode[STIX]{x1D6FC}_{i}^{(1)}\blacktriangle ^{i}\right)w(1+q\widehat{u})\nonumber\\ \displaystyle & \equiv & \displaystyle c\left(\mathop{\sum }_{i=0}^{m-1}\unicode[STIX]{x1D6FC}_{i}^{(1)}\blacktriangle ^{i}\right)w\;\text{mod}\,\text{M}_{d}(E)\widehat{u}.\nonumber\end{eqnarray}$$
It is easy to check directly that
Therefore
This means that there exists
![]() $r\in \text{M}_{d}(E)$
such that
$r\in \text{M}_{d}(E)$
such that
Since the highest power of
![]() $\blacktriangle$
which appears in the left side of the equality is less or equal to
$\blacktriangle$
which appears in the left side of the equality is less or equal to
![]() $m-1$
, we conclude that
$m-1$
, we conclude that
![]() $r$
must be equal to
$r$
must be equal to
![]() $0$
, which implies the required statement.◻
$0$
, which implies the required statement.◻
In the case
![]() $d=1$
, the last Corollary provides the result by Gross and Hopkins on equivariance of their
$d=1$
, the last Corollary provides the result by Gross and Hopkins on equivariance of their
![]() $p$
-adic period map [Reference Gross and Hopkins8, Proposition 23.5].
$p$
-adic period map [Reference Gross and Hopkins8, Proposition 23.5].
Acknowledgment
The authors thank the referee for a careful reading and several helpful suggestions.